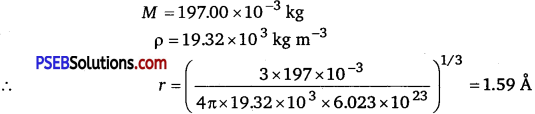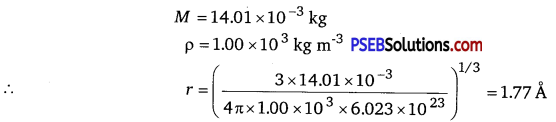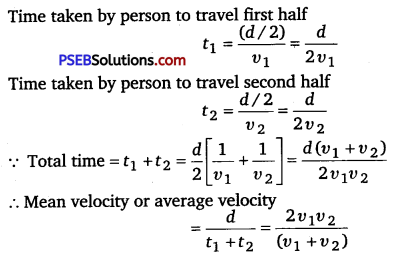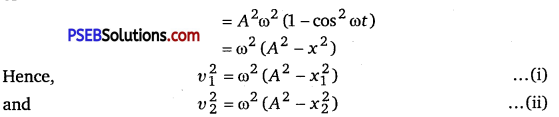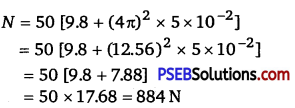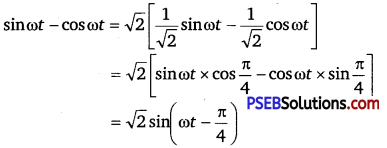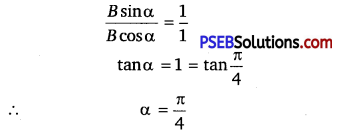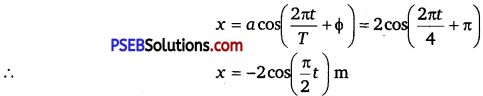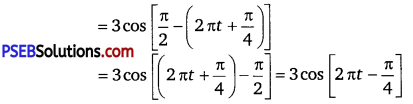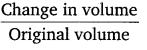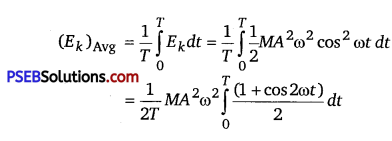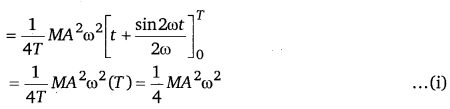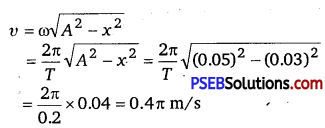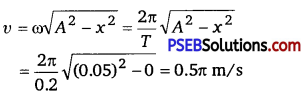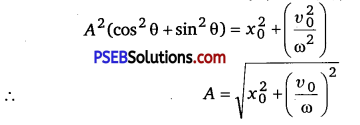Prasanna

Punjab State Board PSEB 11th Class Biology Book Solutions Chapter 18 Body Fluids and Circulation Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Biology Chapter 18 Body Fluids and Circulation

PSEB 11th Class Biology Guide Body Fluids and Circulation Textbook Questions and Answers

Question 1.
Name the components of the formed elements in the blood and mention one major function of each of them.
Answer:
(a) Erythrocytes: They are also known as Red Blood Cells (RBC). They are the most abundant of all the cells in blood. A healthy’adult man has, on an average, 5 millions to 5.5 millions of RBCs mm ^-3 of blood. RBCs are formed in the red bone marrow in the adults.
RBCs are devoid of nucleus in most of the mammals and are biconcave in shape. They have a red coloured, iron containing complex protein called haemoglobin. A healthy individual has 12-16 gms of haemoglobin in every 100 ml of blood.
these molecules play a significant role in transport of respiratory gases. RBCs have an average life span of 120 days after which they are destroyed in the spleen. Hence, spleen is also known as the graveyard of RBCs.

(b) Leucocytes: They are also known as White Blood Cells (WBC) as they are colourless due to the lack of haemoglobin. They are nucleated and are relatively lesser in number which averages 6000-8000 mm^-3 of blood. Leucocytes are generally short-lived.

There are two main categories of WBCs :
1. Granulocytes, e.g., neutrophils, eosinophils and basophils
2. Agranulocytes. e.g., lymphocytes and monocytes.
Neutrophils are the most abundant cells (60-65 per cent) of the total WBCs and basophils are the least (0.5-1 per cent) among them. Neutrophils and monocytes (6-8 per cent) are phagocytic cells which destroy foreign organisms entering the body.

Basophils secrete histamine, serotonin, heparin, etc., and are involved in inflammatory reactions. Eosinophils (2-3 per cent) resist infections and are also associated with allergic reactions. Lymphocytes (20-25 per cent) are of two major types- ‘B’ and T forms. Both B and T lymphocytes are responsible for immune responses of the body.

(c) Platelets: Platelets or thrombocytes, are involved in the coagulation or clotting of blood. A reduction in their number can lead to clotting disorders, which will lead to excessive loss of blood from the body.

Question 2.
What is the importance of plasma proteins?
Answer:
Fibrinogen, globulins and albumins are the major plasma proteins. Fibrinogens are needed for clotting or coagulation of blood. Globulins primarily are involved in defense mechanisms of the body and the albumins help in osmotic balance.

Question 3.
Match column I with column II.

Column I	Column II
A. Eosinophils	1. Coagulation
B. RBC	2. Universal recipient
C. AB group	3. Resist infections
D. Platelets	4. Contraction of heart
E. Systole	5. Gas transport

Answer:

Column I	Column II
A. Eosinophils	3. Resist infections
B. RBC	5. Gas transport
C. AB group	2. Universal recipient
D. Platelets	1. Coagulation
E. Systole	4. Contraction of heart

Question 4.
Why do we consider blood as a connective tissue?
Answer:
Blood is a mobile connective tissue derived from mesoderm which consists of fibre-free fluid matrix, plasma and other cells. It regularly circulates in the body, takes part in the transport of materials.

Question 5.
What is the difference between blood and lymph?
Answer:
Differences between Blood and Lymph

Blood	Lymph
It is red in colour due to the presence of haemoglobin in red cells.	It is colourless as red blood cells are absent.
It consists of plasma, RBC, WBC and platelets.	It consists of plasma and less number of WBC.
Glucose concentration is low.	Glucose concentration is higher than blood.
Clotting of blood is a fast process.	Clotting of lymph is comparatively slow.
It transports materials from one organ to other.	It transports materials from tissue cells into the blood.
Flow of blood is fast.	Lymph flows very slowly.
Its plasma has more proteins, calcium and phosphorus.	Its plasma has less protein, calcium and phosphorus.
It moves away from the heart and towards the heart.	It moves in one direction, i. e., from tissues to sub-clavians.

Question 6.
What is meant by double circulation? What is its significance?
Answer:
Double Circulation: In double circulation, the blood passes twice through the heart during one complete cycle. Double circulation is carried out by two ways :
1. Pulmonary circulation,
2. Systemic circulation

Significance: In birds and mammals, oxygenated and deoxygenated blood received by the left and right atria respectively passes on to the ventricles of the same sides. The ventricles pump it out without mixing up, i.e., two separate circulatory pathways are present in these organisms. This is the importance of double circulation.

Question 7.
Write the differences between:
(a) Blood and lymph
(b) Open and closed system of circulation
(c) Systole and diastole
(d) P-wave and T-wave
Answer:
(a)

Blood	Lymph
It is red in colour due to the presence of haemoglobin in red cells.	It is colourless as red blood cells are absent.
It consists of plasma, RBC, WBC and platelets.	It consists of plasma and less number of WBC.
Glucose concentration is low.	Glucose concentration is higher than blood.
Clotting of blood is a fast process.	Clotting of lymph is comparatively slow.
It transports materials from one organ to other.	It transports materials from tissue cells into the blood.
Flow of blood is fast.	Lymph flows very slowly.
Its plasma has more proteins, calcium and phosphorus.	Its plasma has less protein, calcium and phosphorus.
It moves away from the heart and towards the heart.	It moves in one direction, i. e., from tissues to sub-clavians.

(b) Differences between Open and Closed Circulatory Systems

Open Circulatory System	Closed Circulatory System
1. It is present in arthropods and molluscs.	It is present in annelids and chordates.
2. Blood pumped by heart passes through large vessels into open spaces or body cavities called sinuses.	Blood pumped by the heart is circulated through a loosed network of blood vessels.
3. Flow of blood is not regulated precisely.	It is more advantageous as the blood flow is more precisely regulated.

(c) Differences between Systole and Diastole

Systole	Diastole
1. The contraction of the muscles of auricles and ventricles is called systole.	It is the relaxation of atria and ventricle muscle.
2. It increases the ventricular pressure causing the closure of tricuspid and bicuspid valves due to attempted backflow of blood into atria.	The ventricular pressure falls causing the closure of semilunar valves which prevent backflow of blood into the ventricle.
3. Systolic pressure is higher and occurs during ventricular contraction.	Diastolic pressure is lower and occurs during ventricular expansion.

(d) Differences between P-wave and T-wave

P-wave	T-wave
The P-wave represents the electrical excitation (or depolarisation) of the arrÍa, which leads to the contraction of both the arria.	The T-wave represents the return of the ventricles from excited to normal state (repolarisation). The end of the T-wave marks the end of systole.

Question 8.
Describe the evolutionary change in the pattern of heart among the vertebrates.
Answer:
The heart among the vertebrates shows different patterns of evolution. Different groups of animals have evolved different methods for this transport. All vertebrates possess a muscular chambered heart.
Fishes have a 2-chambered heart with an atrium and a ventricle.
Amphibians and the reptiles (except crocodiles) have a 3-chambered heart with two atria and a single ventricle.
In crocodiles, birds and mammals possess a 4-chambered heart with two atria and two ventricles.

In fishes, the heart pumps out deoxygenated blood which is oxygenated by the gills and supplied to the body parts from where deoxygenated blood is returned to the heart.

In amphibians and reptiles, the left atrium receives oxygenated blood from the gills/lungs/skin and the right atrium gets the deoxygenated blood from other body parts. However, they get mixed up in the single ventricle which pumps out mixed blood.

In birds and mammals, oxygenated and deoxygenated blood received by the left and right atria respectively passes on to the ventricles of the same sides. The ventricles pump it out without any mixing up, i. e., two separate circulatory pathways are present in these organisms, hence, these animals have double circulation.

Question 9.
Why do we call our heart myogenic?
Answer:
Heart is myogenic in origin because the cardiac impulse is initiated in our heart muscles.

Question 10.
The sino-atrial node is called the pacemaker of our heart. Why?
Answer:
The sino-atrial node of heart is responsible for initiating and maintaining the rhythmic activity, therefore it is known as pacemaker of the heart.

Question 11.
What is the significance of atrioventricular node and atrioventricular bundle in the functioning of heart?
Answer:
Atrioventricular Node (AVN): It is the mass of tissue present in the lower-left corner of the right atrium close to the atrioventricular septum. It is stimulated by the impulses that sweep over the atrial myocardium. It is too capable of initiating impulses that cause contraction but at slower rate than SA node.

Atrioventricular Bundle (AV Bundle): It is a bundle of nodal fibres, which continues from AVN and passes through the atria-ventricular septa to emerge on the top of interventricular septum. The AV bundle, bundle branches and Purkinje fibres convey impulses of contraction from the AV node to the apex of the myocardium. Here the wave of ventricular contraction begins, then sweeps upwards and outwards, pumping blood into the pulmonary artery and the aorta.
This nodal musculature has the ability to generate action potentials without any external stimuli.

Question 12.
Define a cardiac cycle and the cardiac output.
Answer:
Cardiac Cycle: The sequential event in the heart which is cyclically repeated is called the cardiac cycle. It consists of systole and diastole of both the atria and ventricles.

Cardiac Output: It is the volume of blood pumped out by each ventricle per minute and averages 5000 mL or 5 L in a healthy individual. The body has the ability to alter the stroke volume as well as the heart rate and thereby the cardiac output. For example, the cardiac output of an athlete will be much higher than that of an ordinary man.

Question 13.
Explain heart sounds.
Answer:
During each cardiac cycle, two prominent sounds are produced which can be easily heard through a stethoscope. The first heart sound (lub) is associated with the closure of the tricuspid and bicuspid valves, whereas the second heart sound (dup) is associated with the closure of the semilunar valves. These sounds are of clinical diagnostic significance.

Question 14.
Draw a standard ECG and explain the different segments in it.
Answer:
Electrocardiograph (ECG): ECG is a graphical representation of the electrical activity of the heart during a cardiac cycle. A patient is connected to the machine with three electrical leads (one to each wrist and to the left ankle) that continuously monitor the heart activity. For a detailed evaluation of the heart’s function, multiple leads are attached to the chest region.

Each peak in, the ECG is identified with a letter from P to T that corresponds to a specific electrical activity of the heart. The P-wave represents the electrical excitation (or depolarization) of the atria, which leads to the contraction of both the atria. The QRS complex represents the depolarization of the ventricles, which initiates the ventricular contraction. The contraction starts shortly after Q and marks the beginning of the systole.

• The T-wave represents the return of the ventricles from excited to normal state (repolarisation).
• The end of the T-wave marks the end of systole.
• Obviously, by counting the number of QRS complexes that occur in a given time period, one can determine the heartbeat rate of an individual.
• Since the ECGs obtained from different individuals have roughly the same shape for a given lead configuration, any deviation from this shape indicates a possible abnormality or disease.
• Hence, it is of a great clinical significance.

Punjab State Board PSEB 11th Class Biology Book Solutions Morphology of Flowering Plants Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Biology Morphology of Flowering Plants

PSEB 11th Class Biology Guide Morphology of Flowering Plants Textbook Questions and Answers

Question 1.
What is meant by modification of root? What type of modification of root is found in the:
(a) Banyan tree
(b) Turnip
(c) Mangrove trees
Answer:
Modification of Root: Roots in some plants change their shape and
structure and become modified to perform functions, other than absorption and conduction of water and minerals. The roots are modified for water, absorption, support, storage of food and respiration.
(a) A banyan tree have hanging roots known as prop roots.
(b) The roots of turnip get modified to become swollen and store food.
(c) The roots of mangrove trees get modified to grow vertically upwards and help to get oxygen for respiration. These are known as pneumatophores.

Question 2.
Justify the following statements on the basis of external features:
(a) Underground parts of a plant are not always roots.
(b) Flower is a modified shoot.
Answer:
(a) Underground parts of a plant are not always roots, they are subterranean stems which do not have root hairs and root cap. Have terminal bud, nodes and internodes. Have leaves on the nodes.
Most of the underground stems such as sucker, rhizome, corm, tubers, bulb, etc., store food, form aerial shoots.
(b) Flower is a modified shoot because:

• It possess nodes and internodes.
• It may develop in the axil of small leaf-like structure called bract.
• Flowers get modified into bulbils or fleshy buds in some plants.
• Anatomically the pedicel and thalamus of a flower resemble that of stem.
• The vascular supply of different organs of flower resemble that of normal leaves.
• In the flower of Degeneria, the stamens are expanded like leaves and the carpels appear like folded leaves.

Question 3.
How is a pinnately compound leaf different from a palmately compound leaf?
Answer:
In pinnately compound leaf, the number of leaflets are present on a common axis, the rachis, which represents the midrib of the leaf as in neem. In case of a palmately compound leaf, the leaflets are attached at a common point, i e., at the tip of petiole as in silk cotton.

Question 4.
Explain with suitable examples the different types of phyllotaxy.
Answer:
Phyllotaxy is the pattern of arrangement of leaves on the stem or branch. This is usually of three types—alternate, opposite and whorled.

• In alternate phyllotaxy, a single leaf arises at each node in alternate manner, as in China rose, mustard and sunflower plants.
• In opposite type of phyllotaxy, a pair of leaves arise at each node and lie opposite to each other as in Calotropis and guava plants.
• If more than two leaves arise at each node and form, a whorl, it is called as whorled, as in Alstonia.

Question 5.
Define the following terms:
(i) Aestivation
(ii) Placentation
(iii) Actinomorphic
(iv) Zygomorphic
(v) Superior ovary
(vi) Perigynous flower
(vii) Epipetalous stamen
Answer:
(i) Aestivation: The mode of arrangement of sepals or petals in relation to one another in a flower bud is called aestivation.
(ii) Placentation: The pattern by which the ovules are attached in an ovary is called placentation.

(iii) Actinomorphic: A flower having radial symmetry. The parts of each whorl are similar in size and shape. The flower can be divided in two equal halves along more than one median longitudinal plane.

(iv) Zygomorphic: A flower having bilateral symmetry. The parts of one or more whorls are dissimilar. The flower can be divided into two equal halves in only one vertical plane.

(v) Superior ovary: The ovary is called superior when it is borne above the point attachment of perianth and stamens on the thalamus.

(vi) Perigynous flower: It is the condition in which gynoecium of a flower is situated in the centre and other parts of the flower are located on the rim of the thalamus almost at the same level.

(vii) Epipetalous stamen: Stamens adhere to the petals by their filaments so, appear to arise from them.

Question 6.
Differentiate between:
(a) Racemose and cymose inflorescence
(b) Fibrous root and adventitious root
(c) Apocarpous and syncarpous ovary
Answer:
(a) Differences between Racemose and Cymose Inflorescence.

Racemose	Cymose
1. This is further divided into (a) Raceme (b) Catkin (c) Spike (d) Spadix (e) Corymb (f) Umbel or capitutum	It is further divided into (a) Monochasial cyme (b) Dichasial Cyme (c) Polychasial Cyme.
2. Branches develop indefinitely and further branches arise laterally in acropetal manner.	The branches arise from terminal buds and stop growing after some time Lateral branches grow much vigorously and spread like a dome.

(b) Differences between Fibrous Root and Adventitious Root

Fibrous Root	Adventitious Root
In monocotyledonous plants, the primary root is short lived and is replaced by a latge number of roots. These roots originate from the base of the fibrous root system say, for example in wheat plants.	In some plants, say for example, in grass and banyan tree there are roots arising from parts of the plant other than the radicle. These are called adventitious roots.

(c) Differences between Apocarpous Ovaiy and Syncarpous Ovary

Apocarpous Ovary	Syncarpous Ovary
When more than one carpel is present, they may be free (as in lotus and rose) and are called apocarpous ovary.	They are termed syncarpous ovary when fused, as in mustard and tomato. After fertilisation, the ovules develop into seeds and like ovary matures into a fruit.

Question 7.
Draw the labelled diagram of the following:
(a) gram seed
(b) V.S. of maize seed
Answer:
(a) Gram Seed

(b) V.S. of maize seed

Question 8.
Describe modifications of stem with suitable examples. [NCERT]
Answer:
Modifications of stem are as follows:

• Tendrils help plants to climb on the support, e. g., Cucumber.
• Thorns are woody, pointed, straight structures to protect plants from browsing animals, e. g., Bougainvillea.
• The plants in arid regions modify their stems into flattened (Opuntia) or fleshy cylindrical (Euphorbia) structures. They contain chlorophyll and carry out photosynthesis.
• Underground stems of some plants such as grass and snawberry, etc., spread to new riches and when older parts die, new plants are formed.
• In Pistia and Eichhornia, a lateral branch with short internodes and each node bearing a rosette of leaves and a tuft of roots is found.
• Stolons or runners help in vegetative propagation in jasmine and grass, respectively.

Question 9.
Take one flower each of the families Fabaceae and Solanaceae and write its semi-technical description. Also draw their floral diagram after studying them.
Answer:
(i) Fabaceae: This family was earlier called Papilionoideae, a subfamily of family Leguminosae.
(a) Habit: Trees, shrubs, herbs, climbers, etc.
(b) Root System: Tap root system with root nodules, that harbour nitrogen fixing bacterium.
(c) Leaves: Leaves are alternate, simple or pinnately compound, pulvinate, and stipulate; venation reticulate.
(d) Inflorescence: Racemose usually, a raceme.
(e) Flowers: Bracteate, bracteolate, bisexual, zygomorphic, hypogynous, and pentamerous.
(f) Calyx: Five sepals, gamosepalous, irregular, odd sepal anterior (characteristic feature of the family) and valvate aestivation.

(g) Corolla: Corolla consists of five petals, polypetalous, characteristically papilionaceous, with an odd posterior large petal called standard or vexillum, a pair of lateral petals, called wing or alae and two anterior keel or carina, which enclose the essential organs; aestivation is vexillary.
(h) Androecium: Ten stamens, diadelphous, [(9) + 1] and anthers dithecous.
(i) Gynoecium: Ovary is superior, monocarpellary, unilocular with many ovules on marginal placenta; style single, curved or bent at right angles to the ovary.
(j) Fruits and Seeds: Characteristically a legume/pod and seeds are non-endospermic.
(k) Floral Formula:
(l) Economic Importance: Plants of this family yield pulses, edible oil, dye, fodder, fibres and wood; some yield products of medicinal value,

(ii) Solanaceae (Potato family)
(a) Habit: Plants are mostly herbs or shrubs or small trees; stem is erect, cylindrical, branched (cymose type); stem is underground in potato CSolarium tuberosum).
(b) Leaves: Simple, alternate, exstipulate with reticulate venation.
(c) Inflorescence: Axillary or extra-axillary cymose, or solitary.
(d) Flowers: Bisexual, actinomorphic, hypogynous and pentamerous.
(e) Calyx: Five sepals, gamosepalous, persistant and valvate aestivation.
(f) Corolla: Five petals, gamopetalous, valvate or imbricate, rotate/wheel-shaped.
(g) Androecium: Five stamens, epipetalous and alternating with the petals.
(h) Gynoecium: Bicarpellary, syncarpous, superior with many ovules on swollen axile placenta; carpels are obliquely placed.
(i) Fruits and Seeds: A berry (tomato and brinjal) or a capsule; seeds are endospermic.
(j) Floral Formula :
(k) Economic Importance: Many plants are used as source of food (vegetables), spice, medicines of fumigatory; some are ornamental plants.

Question 10.
Describe the various types of placentations found in flowering plants.
Answer:
Types of Placentations: The arrangement of ovules within the ovary is known as placentation. The placentations are of different types – marginal, axile, parietal, free central and basal.

Marginal placentation: In this placentation, the placenta forms a ridge along the ventral suture of the ovary and the ovules are borne on this ridge forming two rows as in pea.

Axile placentation: In this placentation, the placenta is axile and the ovules are attached to it in a multilocular ovary as in China rose, tomato, etc.

Parietal placentation: In this placentation, the ovules develop on the inner wall of the ovary or on peripheral part. Ovary is one chambered but it becomes two chambered due to the formation of a false septum known as replam, e.g., mustard.

Free central placentation: In this type of placentation, the ovules are present on the central axis of ovary and septa are absent as in Dianthus and primrose.

Basal placentation: In this placentation the placenta develops at the base of ovary and a single ovule is attached to it, as in sunflower.

Question 11.
What is a flower? Describe the parts of a typical angiospermic flower.
Answer:
Flower: It is a condensed modified reproductive shoot found in angiosperms. It often develops in the axile of a small leaf-like structure called bract. The stalk of the flower is called pedicel. The tip of the pedicel or the base of flower has a broad highly condensed multinodal region called thalamus.
A flower has following four floral structures:

• Calyx: It is made up of sepals. These are green in colour and help in photosynthesis.
• Corolla: It is the brightly coloured part containing petals.
• Androecium: It is the male reproductive part which consists of stamens. A stamen has a long filament and terminal anther. The anther produces the pollen grains.
• Gynoecium: It is the female reproductive part which consists of
  carpels. A carpel has three parts, i.e., style, stigma and ovary. The ovary bears the ovules.

Question 12.
How do the various leaf modifications help plants?
Answer:
Leaf Modifications in Plants
(i) In some plants, the leaf and leaf parts get modified to form green, long, thin unbranched and sensitive thread-like structures called tendrils. The tendrils coil around the plant and provide support to the plant in climbing. Tendrils are present in pea, garden Nasturtium, Clematis, Smilax, etc.

(ii) In some plants, the leaves get modified to form curved stiff claw like hooks to help the plant in clinging to the support. Leaflet hooks are present in Bignonia.

(iii) In case of Acacia and Zizyphus, the leaves get modified to form vasculated, hard, stiff and pointed structures.

(iv) In case of Acacia longifolia, the expanded petiole gets modified and perform the function of photosynthesis in absence of lamina.

(v) In plants such as Nepenthes, the lamina is modified to form large pitcher. It is used for storing water and for digesting insect protein.

(vi) In case of Utricularia, the leaf segments are modified into small bladders, to trap small animals.

Question 13.
Define the term inflorescence. Explain the basis for the different types of inflorescence in flowering plants.
Answer:
The arrangement of flowers on the floral axis is termed as inflorescence. Depending on whether the apex gets converted into a flower or continues to grow, two major types of inflorescences are defined – racemose and cymose. In racemose type of inflorescence the main axis continues to grow, the flowers are borne laterally in an acropetal succession.

In cymose type of inflorescence the main axis terminates in a flower, hence is limited in growth. The flowers are borne in a basipetal order, as depicted in figure.

Question 14.
Write the floral formula of a actinomorphic, bisexual, hypogynous flower with five united sepals, five free petals, five f free stamens and two united carpels with superior ovary and axile placentation.
Answer:
Floral formula

Question 15.
Describe the arrangement of floral members in relation to their ‘ insertion on thalamus.
Answer:
A flower is a condensed specialised reproductive shoot found in angiosperms. The stalk of the flower is known as pedicel. The tip of the pedicel or the base of the flower has a broad highly condensed multinodal region called thalamus. The floral parts of a flower are present on the thalamus. Starting from below they are green sepals or calyx, coloured petals or corolla, stamens or androecium and carpels or gynoecium.

Punjab State Board PSEB 11th Class Physics Book Solutions Chapter 13 Kinetic Theory Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Physics Chapter 13 Kinetic Theory

PSEB 11th Class Physics Guide Kinetic Theory Textbook Questions and Answers

Question 1.
Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at SIP. Take the diameter of an oxygen molecule to be 3Å.
Solution:
Diameter of an oxygen molecule, d = 3Å
Radius, r = \(\frac{d}{2}=\frac{3}{2}\) =1.5 Å = 1.5 x 10^-8 cm
Actual volume occupied by 1 mole of oxygen gas at STP = 22400 cm³
Molecular volume of oxygen gas, V = \(\frac{4}{3}\) πr³N

where, N is Avogadro’s number = 6.023 x 10²³ molecules/mole
∴ V = \(\frac{4}{3}\) x 3.14 x (1.5 x 10^-8)3 x 6.023 x 10²³ = 8.51cm³

Ratio of the molecular volume to the actual volume of oxygen = \(\frac{8.51}{22400}\) = 3.8 x 10^-4 ≈ 4 x 10^-4

Question 2.
Molar volume is the volume occupied by 1 mol of any (ideal) gas at standard temperature and pressure (STP: 1 atmospheric pressure, 0°C). Show that it is 22.4 litres.
Solution:
The ideal gas equation relating pressure (P), volume (V), and absolute temperature (T) is given as PV = nRT
where, R is the universal gas constant = 8.314 J mol^-1 K^-1
n = Number of moles = 1
T = Standard temperature = 273 K
P = Standard pressure = 1 atm = 1.013 x 10⁵ Nm^-2
∴ V = \(\frac{n R T}{P}\)

Hence, the molar volume of a gas at STP is 22.4 litres.

Question 3.
Given figure shows plot of PV IT versus P for 1.00 x 10^-3 kg of oxygen gas at two different temperatures.

(a) What does the dotted plot signify?
(b) Which is true: T₁ > T₂ or T₁ <T₂?
(c) What is the value of PVIT where the curves meet on the y-axis?
(d) If we obtained similar plots for 1.00 x 10³ kg of hydrogen, would we get the same value of PV/T at the point where the curves meet on the y-axis? If not, what mass of hydrogen yields the same value of PV/T (for low-pressure high-temperature region of the plot)? (Molecular mass of H₂=2.02u,of O₂ =32.0 u, R= 8.31Jmol^-1K^-1)
Solution:
(a) The dotted plot in the graph signifies the ideal behaviour of the gas, i. e., the ratio \(\frac{\bar{P} V}{T}\) is equal. μR(μ is the number of moles and R is the universal gas constant) is a constant quantity. It is not dependent on the pressure of the gas.

(b) The dotted plotmn the given graph represents an ideal gas. The curve of the gas at temperatureT₁ is closer to the dotted plot than the curve of the gas at temperature T₂. A real gàs approaches the behaviour of an ideal gas when its temperature increases. Therefore, T₁ > T₂ is true for the given plot.

(c) The value of the ratio PV/T, where the two curves meet, is μ.R. This is because the ideal gas equation is given as:
PV=μRT
\(\frac{P V}{T}\) = μR
where P is the pressure
T is the temperature
V is the volume
μ is the number of moles
R is the unìversal constant
Molecular mass of oxygen = 32.0 g
Mass of oxygen =1 x 10^-3 kg = 1 g
R =8.314J mole^-1K^-1
∴ \(\frac{P V}{T}=\frac{1}{32} \times 8.314\) =0.26JK^-1
Therefore, the value of the ratio PV/T, where the curves meet on the y-axis, is 0.26JK^-1.

(d) If we obtain similar plots for 1.00 x 10^-3 kg of hydrogen, then we will not get the same value of PV/T at the point where the curves meet the y-axis. This is because the molecular mass of hydrogen (2.02 u) is different from that of oxygen (32.0 u).
We have \(\frac{P V}{T}\) = 0.26JK^-1
R = 8.314 J mole^-1 K^-1
Molecular mass (M) of H₂ =2.02 u PV
\(\frac{P V}{T}\) = μR at constant temperature
where, μ = \(\frac{m}{M}\) , m = Mass of H₂
∴ m = \(\frac{P V}{T} \times \frac{M}{R}=\frac{0.26 \times 2.02}{8.314}\)
= 6.3 x 10^-2 g = 6.3 x 10^-5 kg
Hence, 6.3 x 10^-5 kg of H₂ will yield the same value of PV/T.

Question 4.
An oxygen cylinder of volume 30 litres has an initial gauge pressure of 15 atm and a temperature of 27°C. After some oxygen is withdrawn from the cylinder, the gauge pressure drops to 11 atm and its temperature drops to 17°C. Estimate the mass of oxygen taken out of the cylinder (R = 8.31 J mol-1 K -1, molecular mass of O 2 =32 u).
Solution:
Absolute pressure, p₁ = (15 + 1) atm
[∵ Absolute pressure = Gauge pressure +1 atm] = 16 x 1.013 x 10⁵ Pa
V₁ = 30 L = 30 x 10^-3 m³
T₁ = 273.15 + 27 = 300.15K
Using ideal gas equation,
pV = nRT

Hence, moles removed = 19.48-15.12 = 4.36
Mass removed = 4.36 x 32 g = 139.52 g = 0.1396 kg.
Therefore, 0.14 kg of oxygen is taken out of the cylinder.

Question 5.
An air bubble of volume 1.0 cm³ rises from the bottom of a lake 40 cm deep at a temperature of 12°C. To what volume does it grow when it reaches the surface, which is at a temperature of 35°C?
Solution:
Volume of the air bubble, = 1.0 cm³ = 1.0 x 10^-6 m³
Bubble rises to height, d = 40 m
Temperature at a depth of 40 m, T₁ = 12°C = 273 + 12 = 285K
Temperature at the surface of the lake, T₂ = 35°C = 273 + 35 = 308K
The pressure on the surface of the lake,
P₂ =1 atm = 1 x 1.013 x 10⁵Pa
The pressure at the depth of 40 m,
P₁ = 1 atm + dρg
where, ρ is the density of water = 10³ kg/m³
g is the acceleration due to gravity = 9.8 m/s²
∴ P₁ = 1.013 X10⁵+40 X 10³ X 9.8 = 493300 Pa
We have \(\frac{P_{1} V_{1}}{T_{1}}=\frac{P_{2} V_{2}}{T_{2}}\)
where, V₂ is the volume of the air bubble when it reaches the surface
V₂= \(\frac{P_{1} V_{1} T_{2}}{T_{1} P_{2}}=\frac{(493300)\left(1.0 \times 10^{-6}\right) 308}{285 \times 1.013 \times 10^{5}}\)
= 5.263 x 10^-6 m³ or 5.263 cm³
Therefore, when the air bubble reaches the surface, its volume becomes 5.263 cm³.

Question 6.
Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity 25.0 m³ at a temperature of 27°C and 1 atm pressure.
Solution:
Volume of the room, V = 25.0 m³
Temperature of the room, T = 27°C = 273 + 27°C = 300 K
Pressure in the room, P = 1 atm = 1 x 1.013 x 10⁵ Pa
The ideal gas equation relating pressure (?), Volume (V), and absolute temperature (T) can be written as PV = k_BNT
where,
KB is Boltzmann constant = 1.38 x 10 ^-23 m² kg s^-2 K^-1
N is the number of air molecules in the room
∴ N = \(\frac{P V}{k_{B} T}\)
= \(\frac{1.013 \times 10^{5} \times 25}{1.38 \times 10^{-23} \times 300}\) = 6.11 x 10²⁶ molecules
Therefore, the total number of air molecules in the given room is 6.11 x 10²⁶.

Question 7.
Estimate the average thermal energy of a helium atom at (i) room temperature (27°C),
(ii) the temperature on the surface of the Sun (6000K),
(iii) the temperature of 10 million Kelvin (the typical core temperature in the case of a star).
Solution:
(i) At room temperature, T = 27°C = 273 +27 = 300 K
Average thermal energy, E = \(\frac{3}{2}\)kT
where k is Boltzmann constant = 1.38 x 10^-23 m² kg s^-2 K^-1
∴ E = \(\frac{3}{2}\) x 1.38 x 10^-23 x 300 = 6.21 x 10^-21 J
Hence, the average thermal energy of a helium atom at room temperature (27°C) is 6.21 x 10^-23 J

(ii) On the surface of the Sun, T = 6000 K
Average thermal energy = \(\frac{3}{2}\) kT = \(\frac{3}{2}\) x 1.38 x 10^-23 x 6000
= 1.241 x 10^-19J
Hence, the average thermal energy of a helium atom on the surface of the Sun is 1.241 x 10^-19J.

(iii) At temperature, T =10⁷ K
Average thermal energy = \(\frac{3}{2}\)kT = \(\frac{3}{2}\) x 1.38 x 10^-23 x 10⁷
= 2.07 x 10^-16 J
Hence, the average thermal energy of a helium atom at the core of a star is 2.07 x 10^-16 J.

Question 8.
Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (polyatomic). Do the vessels contain equal number of respective molecules? Is the root mean square speed of molecules the same in the three cases? If not, in which case is υ_rms the largest?
Solution:
Yes. All contain the same number of the respective molecules.
No. The root means square speed of neon is the largest.
Since the three vessels have the same capacity, they have the same volume.

Hence, each gas has the same pressure, volume, and temperature. According to Avogadro’s law, the three vessels will contain an equal number of the respective molecules. This number is equal to Avogadro’s number, N = 6.023 x 10²³.
The root mean square speed (υ_rms)oi a gas of mass m, and temperature T, is given by the relation: υ_rms = \(\sqrt{\frac{3 k T}{m}} \)
where k is Boltzmann constant
For the given gases, k and T are constants.

Hence, υ_rms depends only on the mass of the atoms, i.e., υ_rms ∝ \(\sqrt{\frac{1}{m}}\)
Therefore, the root mean square speed of the molecules in the three cases is not the same.

Among neon, chlorine, and uranium hexafluoride, the mass of neon is the smallest.
Hence, neon has the largest root mean square speed among the given gases.

Question 9.
At what temperature is the root mean square speed of an atom in an argon gas cylinder equal to the rms speed of a helium gas atom at -20°C? (atomic mass of Ar = 39.9 u, of He = 4.0u).
Solution:
Temperature of the helium atom, T_He = -20°C = 273 – 20 = 253K
Atomic mass of argon, M_Ar= 39.9 u
Atomic mass of helium, M_He = 4.0 u
Let, (υ_rms)be the rms speed of argon.
Let (υ_rms )He be the rms speed of helium.
The rms speed of argon is given by
(υ_rms)_Ar = \(\sqrt{\frac{3 R T_{\mathrm{Ar}}}{M_{\mathrm{Ar}}}}\) …………………………….. (i)
where, R is the universal gas constant
T_Ar is temperature of argon gas
The rms speed of helium is given by:
(υ_rms)_He = \(\sqrt{\frac{3 R T_{\mathrm{He}}}{M_{\mathrm{He}}}}\) …………………………. (ii)

It is given that: (υ_rms)_Ar = (υ_rms)_He

Therefore, the temperature of the argon atom is 2.52 x 10³ K.

Question 10.
Estimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at 2.0 atm and temperature 17°C. Take the radius of a nitrogen molecule to be roughly 1.0 Å. Compare the collision time with the time the molecule moves freely between two successive collisions (Molecular mass of N₂ = 28.0u).
Solution:
Pressure inside the cylinder containing nitrogen,
P =2.0atm = 2 x 1.013 x 10⁵ Pa = 2.026 x 10⁵ Pa
Temperature inside the cylinder, T = 17°C = 273 +17 = 290 K
Radius of a nitrogen molecule, r = 1.0 Å = 1 x 10,sup>-10 m
Diameter, d = 2 x 1 x 10^-10 = 2 x 10^-10 m
Molecular mass of nitrogen, M = 28.0 g = 28 x 10^-3 kg
The root mean square speed of nitrogen is given by the relation
υ_rms = \(\sqrt{\frac{3 R T}{M}}\)
where, R is the universal gas constant = 8.314 J mole ^-1 K^-1
∴ υ_rms = \(\sqrt{\frac{3 \times 8.314 \times 290}{28 \times 10^{-3}}}\) = 508.26m/s
The mean free path (l) is given by the relation:
l = \(\frac{k T}{\sqrt{2} \times d^{2} \times P}\)
where,
k is the Boltzmann constant = 1.38 x 10^-23 kgm²s^-2 K^-1

Time is taken between successive collisions,

Hence, the time taken between successive collisions is 500 times the time taken for a collision.

Additional Exercises

Question 11.
A metre long narrow bore held horizontally (and closed at one end) contains a 76 cm long mercury thread, which traps a 15 cm column of air. What happens if the tube is held vertically with the open end at the bottom?
Solution:
Length of the narrow bore, L=1 m = 100 cm
Length of the mercury thread, l = 76 cm
Length of the air column between mercury and the closed-end, l_a = 15cm
Since the bore is held vertically in air with the open end at the bottom, the mercury length that occupies the air space is 100-(76+15) = 9 cm

Hence, the total length of the air column = 15 + 9 = 24 cm
Let h cm of mercury flow out as a result of atmospheric pressure.
∴ Length of the air column in the bore = 24 + h cm
and, length of the mercury column = 76 – h cm
Initial pressure, P₁ = 76 cm of mercury
Initial volume,V₁ =15 cm³
Final pressure, P₂ = 76 – (76 – h) = h cm of mercury
Final volume, V₂ = (24 + h) cm³
The temperature remains constant throughout the process.

Height cannot be negative. Hence, 23.8cm of mercury will flow out from the bore and 52.2 cm of mercury will remain in it. The length of the air column will be 24 +23.8 = 47.8 cm.

Question 12.
From a certain apparatus, the diffusion rate of hydrogen has an average value of 28.7cm³s^-1. The diffusion of another gas under the same conditions is measured to have an average rate of 7.2 cm³ s^-1. Identify the gas. [Hint: Use Graham’s law of diffusion: R₁/R₂ =(M₂/M₁)^1/2, where R₁, R₂ are diffusion rates of gases 1 and 2, and M₁ and M₂ their respective molecular masses. The law is a simple consequence of the kinetic theory.]
Solution:
Rate of diffusion of hydrogen, R₁ = 28.7cm³ s^-1
Rate of diffusion of another gas, R₂ = 7.2 cm³ s^-1
According to Graham’s Law of diffusion, we have
\(\frac{R_{1}}{R_{2}}=\sqrt{\frac{M_{2}}{M_{1}}}\)
where, M₁ is the molecular mass of hydrogen 2.020 g
M₂ is the molecular mass of the unknown gas
∴ M₂ = M₁\(\left(\frac{R_{1}}{R_{2}}\right)^{2}\) = 2.01 \(\left(\frac{28.7}{7.2}\right)^{2}\) = 32.09 g
32g is the molecular mass of oxygen. Hence, the unknown gas is oxygen.

Question 13.
A gas in equilibrium has uniform density and pressure throughout its volume. This is strictly true only if there are no external influences. A gas column under gravity, for example, does not have a uniform density (and pressure). As you might expect, its density decreases with height. The precise dependence is given by the so-called law of atmospheres n₂ =n₁ exp[-mg(h₂ -h₁) / k_B T]
where n₂,n₁ refer to number density at heights h₂ and h₁ respectively.
Use this relation to derive the equation for sedimentation equilibrium of a suspension in a liquid column: n₂ = n₁ exp [-mg N_A (ρ -ρ’)(h₂ -h₁) / (ρRT)]
where ρ is the density of the suspended particle, and ρ’ that of surrounding medium. [N_A is Avogadro’s number and R the universal gas constant.] [Hint: Use Archimedes principle to find the apparent weight of the suspended particle.]
Solution:
According to the law of atmospheres, we have
n₂=n₁ exp [-mg(h₂ – h₁])/k_BT] ………………………………. (i)
where, n₁ is the number density at height h₁, and n₂ is the number density at height h₂
mg is the weight of the particle suspended in the gas column
Density of the medium = ρ’
Density of the suspended particle = ρ
Mass of one suspended particle = m’
Mass of the medium displaced = m
Volume of a suspended particle = V
According to Archimedes’ principle for a particle suspended in a liquid column, the effective weight of the suspended particle is given as

Weight of the medium displaced – Weight of the suspended particle
= mg – m’g
= mg – Vρ’g = mg – \(\left(\frac{m}{\rho}\right)\) ρ’g
= mg – \(\left(1-\frac{\rho^{\prime}}{\rho}\right)\) …………………………….. (ii)
Gas constant, R = k_BN
k_B = \(\frac{R}{N}\) …………………………………….. (iii)
Substituting equation (ii) in place of mg in equation (i) and then using equation (iii), we get

Question 14.
Given below are densities of some solids and liquids. Give rough estimates of the size of their atoms:

Substance	Atomic Mass (u)	Density (103 kg m-3)
Carbon (diamond)	12.01	2.22
Gold	197.00	19.32
Nitrogen (liquid)	14.01	1.00
Lithium	6.94	0.53
Fluorine (liquid)	19.00	1.14

[Hint: Assume the atoms to be ‘tightly packed’ in a solid or liquid phase, and use the known value of Avogadro’s number. You should, however, not take the actual numbers you obtain for various atomic sizes too literally. Because of the crudeness of the tight packing approximation, the results only indicate that atomic sizes are in the range of a few Å].
Atomic mass of a substance = M
Density of the substance = ρ

Avogadro’s number = N = 6.023 x 10²³
Volume of each atom = \(\frac{4}{3} \pi r^{3}\)
Volume of N number of molecules = \(\frac{4}{3} \pi r^{3}\) N …………………………….. (i)
Volume of one mole of a substance = \(\frac{M}{\rho}\) ………………………………….. (ii)

For gold

Hence, the radius of a gold atom is 1.59 Å
For liquid nitrogen

Hence, the radius of a liquid nitrogen atom is 1.77 Å

For lithium

Hence, the radius of a lithium atom is 1.73 Å.

For liquid fluorine

Hence, the radius of liquid fluorine atom is 1.88 Å.

Punjab State Board PSEB 11th Class Physics Book Solutions Chapter 3 Motion in a Straight Line Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Physics Chapter 3 Motion in a Straight Lines

PSEB 11th Class Physics Guide Motion in a Straight Line Textbook Questions and Answers

Question 1.
In which of the following examples of motion, can the body be considered approximately a point object:
(a) a railway carriage moving without jerks between two stations.
(b) a monkey sitting on top of a man cycling smoothly on a circular track.
(c) a spinning cricket ball that turns sharply on hitting the ground.
(d) a tumbling beaker that has slipped off the edge of a table.
Answer:
(a), (b)

Explanation
(a) The size of a carriage is very small as compared to the distance between two stations. Therefore, the carriage can be treated as a point sized object.
(b) The size of a monkey is very small as compared to the size of a circular track. Therefore, the monkey can be considered as a point sized object on the track.
(c) The size of a spinning cricket ball is comparable to the distance through which it turns sharply on hitting the ground. Hence, the cricket ball cannot be considered as a point object.
(d) The size of a beaker is comparable to the height of the table from which it slipped. Hence, the beaker cannot be considered as a point object.

Question 2.
The position-time (x – t) graphs for two children A and B returning from their school O to their homes P and Q respectively are shown in below figure. Choose the correct entries in the brackets below;
(a) (A / B) lives closer to the school than (B / A)
(b) (A / B) starts from the school earlier than (B/ A)
(c) (A / B) walks faster than (B / A)
(d) A and B reach home at the (same/different) time
(e) (A / B) overtakes (B / A) on the road (once/twice).

Solution:
(a) Draw normals on graphs from points P and Q. It is clear that OQ > OP. Therefore, child A lives closer to the school than child B.

(b) Child A start from school at time t =0 (become its graph starts from origin) whild child B starts from school at time t = OC. Therefore, child A starts from school earlier than B.

(c) The slope of distance-time graph represents the speed. More the slope of the graph, more will be the speed. As the slope of the x-t graph of B is higher than the slope of the x – t graph of A, therefore child B walks faster than child A.
(d) Corresponding to points P and Q, the value of t from x – t graphs for children A and B is same i. e.,OE. Therefore, children A and B will reach their homes P and Q at the same time.

(e) x – t graphs for children A and B intersect each other at a point D. Child B starts later but reaches home at the same time as that of child A, therefore child B overtake child A on the road once.

Question 3.
A woman starts from her home at 9.00 am, walks with a speed of 5kmh^-1 on a straight road up to her office 2.5 km away, stays at the office up to 5.00 pm, and returns home by an auto with a speed of 25 km h^-1. Choose suitable scales and plot the x – t graph of her motion.
Solution:
Speed of the woman = 5 km/h
Distance between her office and home = 2.5 km
Time taken = \(\frac{\text { Distance }}{\text { Speed }}\)
= \(\frac{2.5}{5}\) = 0.5 h = 30 min
Time of arival at office = 9.00 am + 30 min = 9.30 am i. e., at 9.30 am the distance covered will be 2.5 km. This part of journey is represented in graph by OA.
It is given that she covers the same distance in the evening by an auto. Now, speed of the auto = 25 km/h
= \(\frac{2.5}{25}=\frac{1}{10}\) = 0.1 h = 6 mm

She leaves the office at 5.00 pm and take 6 min to reach home. Therefore, she reaches her home at 5.06 pm at this time the distance is zero. This part of journey is represented in graph by BC.

Question 4.
A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Plot the x – t graph of bis motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.
Solution:
The x – t graph of the drunkard is shown in figure.

Length of each step =1 m, time taken for each step = 1 s
Time taken to move by 5 steps = 5 s
5 steps forward and 3 steps backward means that the net distance covered by him in first 8 steps i. e., in8s = 5m-3m = 2m
Distance covered by him in first 16 steps orl6s = 2 + 2 = 4m
Distance covered the drunkard in first 24 s i. e., 24 steps = 2 + 2 + 2= 6m
and distance covered in 32 steps i. e. 32 s = 8 m
Distance covered in37 steps = 8 + 5 = 13m
Distance of the pit from the start = 13 m
Total time taken by the drunkard to fall in the pit = 37 s
Since, 1 step requires 1 s of time, so we arrive at the same result from the graph shown.

Question 5.
A jet airplane travelling at the speed of 500 km h^-1 ejects its products of combustion at the speed of 1500 km h^-1 relative to the jet plane. What is the speed of the latter with respect to an observer on the ground?
Speed of the jet airplane, υ_jet = 500 km/h
Relative speed of its products of combustion with respect to the plane,
υ_smoke = -1500 km/h
Speed of its products of combustion with respect to the ground V’_smoke Relative speed of its products of combustion with respect to the airplane,
υ_smoke = υ’_smoke υ _jet
-1500 = υ’_smoke – 500
υ’_smoke = -1000 km/h
The negative sign indicates that the direction of its products of combustion is opposite to the direction of motion of the jet airplane.

Question 6.
A car moving along a straight highway with speed of 126 km h^-1 is brought to a stop within a distance of 200 m, What is the retardation of the car (assumed uniform), and how long does it take for the car to stop?
Solution:
Initial velocity of the car, u= 126 km/h = 126 × \(\frac{5}{18}\) m/s
= 35 m/s (∵ 1 km/h \(\frac{5}{10}\) m/s)
Final velocity of the car, υ = 0
Distance covered by the car before coming to rest, s = 200 m
From third equation of motion,
υ² – u² = 2as
(0)² – (35)² = 2 × a × 200
a = \(\frac{35 \times 35}{2 \times 200}\) = -3.06 m/s²
From first equation of motion,
v = u +at
t = \(\frac{v-u}{a}=\frac{0-35}{-3.06}=\frac{-35}{-3.06}\) = 11.44s
∴ Car will stop after 11.4 s.

Question 7.
Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km h^-1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 m/s². If after 50 s, the guard of B just brushes past the driver of A, what was the original distance between them?
Solution:
For train A:
Initial velocity, u = 72 km/h = 72 × \(\frac{5}{18}\) m/s = 20 m/s
Time, t = 50 s
Acceleration, a_I =0 (Since it is moving with a uniform velocity)
From second equation of motion, distance (S_I) covered by train A can be obtained as :
S_I = ut + \(\frac {1}{2}\)a_It²
= 20 × 50 + 0 = 1000 m

For train B:
Initial velocity, u = 7 2 km/h = 72 × \(\frac{5}{18}\) m/ s = 20 m/ s
Acceleration, a_II = 1 m/s²
Time, t = 50 s
From second equation of motion, distance (S_II) covered by train B can be obtained as :
s_II = ut + \(\frac {1}{2}\) a_IIt²
= 20 × 50 + \(\frac {1}{2}\) × 1 × (50)² = 2250 m
Hence, the original distance between the driver of train A and the guard of train B is 2250 – 1000 = 1250 m.

Question 8.
On a two lane road, car A is travelling with a speed of 36 kmh^-1. Two cars B and C approach car A in opposite directions with a speed of 54 km h 1 each. At a certain instant, when the distance AB is equal to AC, both being 1 km, B decides to overtake A before C does. What minimum acceleration of car B is required to avoid an accident?
Solution:
Velocity of car A, υ_A = 36 km/h = 36 × \(\frac {5}{18}\) m/s = 10 m/s
Velocity of car B, υ_B =54 km/h = 54 × \(\frac {5}{18}\) m/s = 15 m/s
Velocity of car C,υ_C = 54 km/h 54 × \(\frac {5}{18}\) m/s = 15 m/s
Relative velocity of car B with respect to car A,
υ_BA = υ_B – υ_A = 15 – 10 = 5 m/s
Relative velocity of car C with respect to car A,
υ_CA – υ_C – (-υ_A) = 15 + 10 = 25m/s
At a certain instance, both cars B and C are at the same distance from car Ai.e.,
s = 1 km = 1000 m
Time taken (t) by car C to cover 1000 m = \(\frac {1000}{25}\) = 40 s
Hence, to avoid an accident, car B must cover the same distance in a maximum of 40 s. From second equation of motion, minimum acceleration (a) produced by car B can be obtained as:
s = ut + \(\frac {1}{2}\)at²
1000 = 5 × 40 + \(\frac {1}{2}\) × a × (40)²
a = \(\frac {1600}{1600}\) = 1ms²

Question 9.
Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20 km h^-1 in the direction AtoB notices that a bus goes past him every 18 min in the direction of his motion, and eveiy 6 min in opposite direction. What is the period T of the bus service and with what speed (assumed constant) do the buses ply on the road?
Solution:
Let V be the speed of the bus running between towns A and B.
Speed of the cyclist, υ = 20 km/h
Relative speed of the bus moving in the direction of the cyclist
= V- υ = (V – 20)km/h
The bus went past the cyclist every 18 min i.e., \(\frac{18}{60}\) h (when he moves in the direction of the bus).
Distance covered by the bus = (V – 20) × \(\frac{18}{60}\) km ……………….. (i)
Since one bus leaves after every T minutes, the distance travelled by the bus will be equal to V × \(\frac{T}{60}\) ……………. (ii)
Both equations (i) and (ii) are equal.
V – 20 \(\frac{18}{60}=\frac{V T}{60}\) ……………… (iii)
Relative speed of the bus moving in the opposite direction of the cyclist
= (V + 20)km/h
Time taken by the bus to go past the cyclist = 6 min = \(\frac{6}{60}\)h
∴ (V + 20) \(\frac{6}{60}\) = \(\frac{VT}{60}\) …………………. (iv)
From equations (iii) and (iv), we get
(V + 20) × \(\frac{6}{60}\) = (V – 20) × \(\frac{18}{60}\)
V + 20 = 3 V – 60
2V = 80
V = 4 km/h
Substituting the value of V in equation (iv), we get
(40 + 20) × \(\frac{6}{60}=\frac{40 T}{60}\)
T = \(\frac{360}{40}\) = 9 min

Question 10.
A player throws a hall upwards with an initial speed of 29.4 ms^-1 .
(a) What is the direction of acceleration during the upward motion of the hall?
(b) What are the velocity and acceleration of the ball at the highest point of its motion?
(c) Choose the x = 0 m and t₀ = 0 s to be the location and time of
the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward, and downward motion.
(d) To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s^-2 and neglect air resistance).
Solution:
(a) The ball is moving under the effect of gravity and therefore the direction of acceleration is vertically downward, in the direction of acceleration due to gravity.
(b) At the highest point of its motion velocity is zero and acceleration is equal to the acceleration due to gravity (9.8 m/s) in vertically downward direction.
(c) If we choose the highest point as x = 0 m and t₀ = 0 s and vertically downward direction to be the positive direction of X- axis then,

During upward motion
Sign of position is negative.
Sign of velocity is negative.
Sign of acceleration is positive.

During downward motion Sign of position is positive.
Sign of velocity is positive.
Sign of acceleration is positive.

(d) Let the ball rises upto maximum height h.
Initial velocity of ball (u) = 29.4 m/s
g = 9.8 m/s
Final velocity at maximum height (υ) = 0
Using equation of motion, υ² = u² – 2gh
0 = (29.4)² – 2 × 9.8 × h
or h = \(\frac{29.4 \times 29.4}{2 \times 9.8}\) = 44.1
Again using equation of motion, υ = u – gt
0 = 29.4 -9.8t
or t = \(\frac{29.4}{9.8}\) = 3s
Time of ascent is always equal to the time of descent.
Total time after which the ball returns to the player’s hand = 2t = 2 × 3 = 6s

Question 11.
Read each statement below carefully and state with reasons and examples, if it is true or false;
A particle in one-dimensional motion
(a) with zero speed at an instant may have non-zero acceleration at that instant’
(b) with zero speed may have non-zero velocity,
(c) with constant speed must have zero acceleration,
(d) with positive value of acceleration must be speeding up.
Answer:
(a) True
Explanation: When an object is thrown vertically up in the air, its speed becomes zero at maximum height. However, it has acceleration equal to the acceleration due to gravity (g) that acts in the downward direction at that point.
Speed is the magnitude of velocity. When speed is zero, the magnitude of velocity along with the velocity is zero.

(b) False
Explanation: A car moving on a straight highway with constant speed will have constant velocity. Since acceleration is defined as the rate of change of velocity, acceleration of the car is also zero.

(c) True
Explanation: This statement is false in the situation when acceleration is positive and velocity is negative at the instant time taken as origin. Then, for all the time before velocity becomes zero, there is slowing down of the particle. Such a case happens when a particle is projected upwards.

(d) False
Explanation: This statement is true when both velocity and acceleration are positive, at the instant time taken as origin. Such a case happens when a particle is moving with positive acceleration or falling vertically downwards from a height.

Question 12.
A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one tenth of its speed. Plot the speed-time graph of its motion between t = 0 to 12 s.
Solution:
Ball is dropped from a height, s = 90 m
Initial velocity of the ball, u = 0
Acceleration, a = g = 9.8 m/s²
Final velocity of the ball = υ
From second equation of motion, time (t) taken by the ball to hit the ground can be obtained as:
s = ut + \(\frac {1}{2}\)at²
90 = 0 + \(\frac {1}{2}\) × 9.8t²
t = \(\sqrt{18.38}\) = 4.29 s
From first equation of motion, final velocity is given as:
υ = u + at
= 0 + 9.8 × 4.29 = 42.04 m/s
Rebound velocity of the ball, u_r = \(\frac {9}{10}\) υ = \(\frac {9}{10}\) × 42.04 = 37.84 m/s

Time (t) taken by the ball to reach maximum height is obtained with the help of first equation of motion as:
υ =u_r + at’
0 = 37.84 + (-9.8) t’
t’ = \(\frac{-37.84}{-9.8}\) = 3.86s
Total time taken by the ball = t + t’ = 4.29 + 3.86 = 8.15 s
As the time of ascent is equal to the time of descent, the ball takes 3.86 s to strike back on the floor for the second time.
The velocity with which the ball rebounds from the floor
= \(\frac {9}{10}\) × 37.84 = 34.05m/s
Total time taken by the ball for second rebound = 8.15 + 3.86 = 12.01 s The speed-time graph of the ball is represented in the given figure as :

Question 13.
Explain clearly, with examples, the distinction between the following:
(a) magnitude of displacement (sometimes called distance) over an interval of time, and the total length of path covered by a particle over the same interval;

(b) magnitude of average velocity over an interval of time, and the average speed over the same interval. [Average speed of a particle over an interval of time is defined as the total path length divided by the time interval].
Show in both (a) and (h) that the second quantity is either greater than or equal to the first.
When is the equality sign true? [For simplicity, consider one-dimensional motion only].
Solution:
(a) The magnitude of displacement over an interval of time is the shortest distance (which is a straight line) between the initial and final positions of the particle.
The total path length of a particle is the actual path length covered by the particle in a given interval of time.
For example, suppose a particle moves from point A to point B and then, comes back to a point, C taking a total time t, as shown below. Then, the magnitude of displacement of the particle = AC.

Whereas, total path length = AB+BC
It is also important to note that the magnitude of displacement can never be greater than the total path length. However, in some cases, both quantities are equal to each other.

(b)
For the given particle,
Average velocity = \(\frac{A C}{t}\)

= \(\frac{A B+B C}{t}\)
Since (AB + BC)> AC, average speed is greater than the magnitude of average velocity. The two quantities will be equal if the particle continues to move along a straight line.

Question 14.
A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km h^-1. Finding the market closed, he instantly turns and walks back home with a speed of 7.5 km h^-1. What is the
(a) magnitude of average velocity, and
(b) average speed of the man over the interval of time? (i) 0 to 30 min, (ii) 0 to 50 min, (iii) 0 to 40 min?
[Note: You will appreciate from this exercise why it is better to define average speed as total path length divided by time, and not as magnitude of average velocity. You would not like to tell the tired man on his return home that his average speed was zero.]
Solution:
(a) A man return his home, therefore total displacement of the man = 0

(b) Speed of man during motion from his home to the market υ₁ = 5 km/h
Speed of man during from market his home υ₂ =7.5 km/h
Distance between his home and market = 2.5 km
(i) Taking time interval 0 to 30 min.
Time taken by the man to reach the market from home,
t₁ = \(\frac{2.5}{5}=\frac{1}{2}\) = h = 30 min
Hence, the man moves from his home to the market in t = 0 to 30 min.

(ii) Taking time interval 0 to 50 min.
Time taken by man in returning to his home from the market

(iii) Taking time interval 0 to 40 min.
Distance travelled in first 30 min = 2.5 km
Distance travelled by the man (from market to home) in the next 10 min
= 7.5 × \(\frac{10}{60}\) =1.25 km
Net displacement 2.5 -1.25 = 1.25 km
Total distance travelled = 2.5 +1.25 = 3.75 km
Average velocity = \(\frac{1.25}{\left(\frac{40}{60}\right)}\) = \(\frac{1.25 \times 3}{2}\) = 1.875 km/h
Average speed = \(\frac{3.75}{\left(\frac{40}{60}\right)}\) = 5.625 km/h

Question 15.
In questions 13 and 14, we have carefully distinguished between average speed and magnitude of average velocity. No such distinction is necessary when we consider instantaneous speed and magnitude of velocity. The instantaneous speed is always equal to the magnitude of instantaneous velocity. Why?
Solution:
Instantaneous velocity is given by the first derivative of distance with respect to time i. e.,
υ_m = \(\frac{d x}{d t}\)
Here, the time interval dt is so small that it is assumed that the particle does not change its direction of motion. As a result, both the total path length and magnitude of displacement become equal is this interval of time.
Therefore, instantaneous speed is always equal to instantaneous velocity.

Question 16.
Look at the graphs (a) to (d) carefully and state, with reasons, which of these cannot possibly represent one-dimensional motion of a particle.

Solution:
(a) The given x – t graph, shown in (a), does not represent one-dimensional motion of the particle. This is because a particle cannot have two positions at the same instant of time.
(b) The given υ – t graph, shown in (b), does not represent one-dimensional motion of the particle. This is because a particle can never have two values of velocity at the same instant of time.
(c) The given υ – t graph, shown in (c), does not represent one-dimensional motion of the particle. This is because speed being a scalar quantity cannot be negative.
(d) The given total path length-time graph, shown in (d), does not represent one dimensional motion of the particle. This is because the total path length travelled by the particle cannot decrease with time.

Question 17.
Figure shows the x – t plot of one-dimensional motion of a particle. Is it correct to say from the graph that the particle’ moves in a straight line for t< 0 and on a parabolic path for t > 0 ? If not, suggest a suitable physical context for this graph.

Solution:
No; The x – t graph of a particle moving in a straight line for t < 0 and on a parabolic path for t > 0 cannot be shown as the given graph. This is because, the given particle does not follow the trajectory of path followed by the particle as t = 0, x = 0. A physical situation that resembles the above graph is of a freely falling body held for sometime at a height.

Question 18.
A police van moving on a highway with a speed of 30 km h^-1 fires a bullet at a theifs car speeding away in the same direction with a speed of 192 km h^-1. If the muzzle speed of the bullet is 150 m s^-1, with what speed does the bullet hit the thief’s car ?
(Note: Obtain that speed which is relevant for damaging the thief’s car).
Solution:
Speed of the police van, υ_p = 30 km/h = 8.33 m/s
Muzzle speed of the bullet, υ_b = 150 m/s
Speed of the thief s car, υ_t =192 km/h = 53.33 m/s
Since the bullet is fired from a moving van, its resultant speed can be obtained as:
= 150 +8.33 = 158.33 m/s
Since, both the vehicles are moving in the same direction, the velocity with which the bullet hits the thief s car can be obtained as:
υ_bt = υ_b – υ_t
= 158.33 – 53.33 = 105 m/s

Question 19.
Suggest a suitable physical situation for each of the following graphs:

Solution:
(a) The given x – t graph shows that initially a body was at rest. Then, its velocity increases with time and attains an instantaneous constant value. The velocity then reduces to zero with an increase in time. Then, its velocity increases with time in the opposite direction and acquires a constant value. A similar physical situation arises when a football (initially kept at rest) is kicked and gets rebound from a rigid wall so that its speed gets reduced. Then, it passes from the player who has kicked it and ultimately gets stopped after sometime.

(b) In the given v-t graph, the sign of velocity changes and its magnitude decreases with a passage of time. A similar situation arises when a ball is dropped on the hard floor from a height. It strikes the floor with some velocity and upon rebound, its velocity decreases by a factor. This continues till the velocity of the ball eventually becomes zero.

(c) The given a – t graph reveals that initially the body is moving with a certain uniform velocity. Its acceleration increases for a short interval of time, which again drops to zero. This indicates that the body again starts moving with the same constant velocity. A similar physical situation arises when a hammer moving with a uniform velocity strikes a nail.

Question 20.
Figure gives the x – t plot of a particle executing one-dimensional simple harmonic motion. (You will learn about this motion in more detail in Chapter 14). Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s,-1.2 s.

Solution:
For simple harmonic motion (SHM) of a particle, acceleration (a) is given by the relation:
a = -ω²x ……. (i)
where, ω → angular frequency
At t = 0.3 s
In this time interval, x is negative. Thus, the slope of the x – t plot will also be negative. Therefore, both position and velocity are negative. However, using equation (i), acceleration of the particle will be positive.
At t = 1.2s
In this time interval, x is positive. Thus, the slope of the x – t plot will also be positive. Therefore, both position and velocity are positive. However, using equation (i), acceleration of the particle comes to be negative.
t = -1.2s
In this time interval, x is negative. Thus, the slope of the x – t plot will also be negative. Since both x and t are negative, the velocity comes to be positive. From equation (i), it can be inferred that the acceleration of the particle will be positive.

Question 21.
Figure gives the x – t plot of a particle in one-dimensional motion. Three different equal intervals of time are shown. In which interval is the average speed greatest, and in which is it the least? Give the sign of average velocity for each interval.

Solution:
The average speed of a particle shown in the x – t graph is obtained from the slope of the graph in a particular interval of time.
It is clear from the graph that the slope is maximum and minimum restively in intervals 3 and 2 respectively. Therefore, the average speed of the particle is the greatest in interval 3 and is the least in interval 2. The
sign of average velocity is positive in both intervals 1 and 2 as the slope is positive in these intervals. However, it is negative in interval 3 because the slope is negative in this interval.

Question 22.
Figure gives a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude? In which interval is the average speed greatest? Choosing the positive direction as the constant direction of motion, give the signs of v and a in the three intervals. What are the accelerations at the points A, B, C and D?

Solution:
Acceleration is given by the slope of the speed-time graph. In the given case, it is given by the slope of the speed-time graph within the,given interval of time.

Since the slope of the given speed-time graph is maximum in interval 2, average acceleration will be the greatest in this interval.
Height of the curve from the time-axis gives the average speed of the particle. It is clear that the height is the greatest in interval 3. Hence, . average speed of the particle is the greatest in interval 3.

In interval 1: The slope of the speed-time graph is positive. Hence, acceleration is positive. Similarly, the speed of the particle is positive in this interval.

In interval 2: The slope of the speed-time graph is negative. Hence, acceleration is negative in this interval. However, speed is positive because it is a scalar quantity.

In interval 3: The slope of the speed-time graph is zero. Hence, acceleration is zero in this interval. However, here the particle acquires some uniform speed. It is positive in this interval.

Points A, B, C and D are all parallel to the time-axis. Hence, the slope is zero at these points. Therefore, at points A, B, C and D, acceleration of the particle is zero.

Question 23.
A three-wheeler starts from rest, accelerates uniformly with 1 m s^-2 on a straight road for 10 s, and then moves with uniform velocity. Plot the distance covered by the vehicle during the n^th second (n = 1, 2, 3,…)versus n. What do you expect this plot to be during accelerated motion: a straight line or a parabola?
Solution:
Distance covered by a body in n^th second is given by the relation
D_n = u + \(\frac{a}{2}\)(2n – 1) ……………(i)
where, u = Initial velocity, a = Acceleration, n = Time = 1, 2, 3, …. , n
In the given case,
u = 0 and a = 1 m/s²
.-. D_n = \(\frac {1}{2}\)(2n – 1) ……………… (ii)
This relation shows that
D_n ∝ n ………………(iii)
Now, substituting different values of n in equation (ii), we get the following table:

Since the three-wheeler acquires uniform velocity after 10 s, the line , will be parallel to the time-axis after n = 10 s.

Question 24.
A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m/s. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m/s and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
Solution:
Initial velocity of the ball, u = 49 m/s
Acceleration, a = -g = – 9.8 m/s2
Case I:
When the lift was stationary, the boy throws the ball.
Taking upward motion of the ball,
Final velocity, υ of the ball becomes zero at the highest point.
From first equation of motion, time of ascent (t) is given as
υ = u + at
t = \(\frac{v-u}{a}\)
\(\frac{-49}{-9.8}\) = 5s
But, the time of ascent is equal to the time of descent.
Hence, the total time taken by the ball to return to the boy’s hand
= 5 + 5 = 10 s
Motion in a Straight Line 53

Case II:
The lift was moving up with a uniform velocity of 5 m/s. In this case, the relative velocity of the ball with respect to the boy remains the same i. e., 49 m/s. Therefore, in this case also, the ball will return back to the boy’s hand after 10 s.

Question 25.
On a long horizontally moving belt (see figure) a child runs to and fro with a speed 9 km h^-1 (with respect to the belt) between his father and mother located 50 m apart on the moving belt. The belt moves with a speed of 4 km h^-1. For an observer on a stationary platform outside, what is the
(a) speed of the child running in the direction of motion of the belt?
(b) speed of the child running opposite to the direction of motion of the belt?
(c) time taken by the child in (a) and (b) ?
Which of the answers alter if motion is viewed by one of the parents?

Solution:
Speed of the belt, υ_B = 4 km/h
Speed of the child, υ_C = 9 km/h

(a) Since the child is running in the same direction of the motion of the belt, his speed (as observed by the stationary observer) can be obtained as
υ_CB = υ_C + υ_B = 9 + 4 = 13 km/h

(b) Since the child is running in the direction opposite to the direction of the motion of the belt, his speed (as observed by the stationary observer) can be obtained as
υ_CB = υ_C + (-υ_B) = 9 – 4 = 5 km/h

(c) Distance between the child’s parents = 50 m
As both parents are standing on the moving belt, the speed of the child in either direction as observed by the parents will remain the same i. e.,
9 km/h = 9 x \(\frac{5}{18}\) m/s = 2.5 m/s.
18
Hence, the time taken by the child in case (a) and (b) is given by
\(\frac{\text { Distance }}{\text { Speed }}=\frac{50}{2.5}\) = 20 s.
If the motion is viewed by any one of the parents, answers obtained in (a) and (b) get altered. This is because the child and his parents are standing on the same belt and hence, are equally affected by the motion of the belt. Therefore, for both parents (irrespective of the direction of motion) the speed of the child remains the same i.e., 9 km/h.

For this reason, it can be concluded that the time taken by the child to reach any one of his parents remains unaltered.

Question 26.
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 m/s and 30 m/s. Verify that the graph shown in figure correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 m/s². Give the equations for the linear and curved parts of the plot.

Solution:
For first stone:
Initial velocity, u₁ =15 m/s
Acceleration, a = -g = -10 m/s²
Using the relation,
x₁ = x₀ + u₁t + \(\frac {1}{2}\)at²
where, x₀ = Height of the cliff = 200 m
x₁ =200 + 15t – 5t² ………………. (i)
When this stone hits the ground, x₁ = 0
-5t² +15t + 200 = 0
t² – 3t – 40 =0
t² – 8t + 5t – 40 = 0
t(t – 8) + 5(t – 8) = 0
(t – 8)(t + 5) = 0
t = 8 s or t = -5s
Since the stone was projected at time t = 0, the negative sign before time is meaningless.
∴ t = 8s

For second stone:
Initial velocity, u₂ = 30 m/s
Acceleration, a = -g = -10 m/s²
Using the relation,
x₂ = x₀ + u₂t + \(\frac {1}{2}\)at²
= 200 + 30t – 5t² ……………. (ii)
At the moment when this stone hits the ground; x₂ = 0
-5t² + 30t + 200 = 0
t² – 6t – 40 = 0
t² -10t + 4t + 40 = 0
t(t – 10) + 4(t – 10) = 0
(t – 10)(t + 4) = 0
t = 10 s or t = -4 s
Here again, the negative sign before time is meaningless.
∴ t = 10 s
Subtracting eq. (i) from eq. (ii), we get
x₂ – x₁ = (200 +30t – 5t²) – (200 + 15t – 5t²)
x₂ – x₁ = 15t …………….. (iii)
Equation (iii) represents the linear path of both stones. Due to this linear relation between
(x₂ – x₁) and t, the path remains a straight line till 8 s.
Maximum separation between the two stones is at t = 8 s.
(x₂ – x₁] )_max = 15 × 8 = 120 m
This is in accordance with the given graph.
After 8 s, only second stone is in motion whose variation with time is given by the quadratic equation :
x₂ – x₁ = 200 + 30t – 5t²
Hence, the equation of linear and curved path is given by
x₂ – x₁ = 15t (Linear path)
x₂ – x₁ = 200 + 30t – 5t² (Curved path)

Question 27.
The speed-time graph of a particle moving along a fixed direction is shown in figure given below. Obtain the distance traversed by the particle between (a) t = 0 s to 10 s, (b) t = 2 s to 6 s.

What is the average speed of the particle over the intervals in (a) and (b)?
Solution:
(a) Distance travelled by the particle = Area under the given graph
= \(\frac{1}{2}\) × (10 – 0) × (12 – 0) = 60 m
Average speed = \(\frac{\text { Distance }}{\text { Time }}\) = \(\frac{60}{10}\) = 6 m/s

(b) Let s₁ and s₂ be the distances covered by the particle between time t = 2 s to 5 s and t = 5 s to 6 s respectively.
Total distance (s) covered by the particle in time t = 2 s to 6 s
S = S₁ + s₂ ……………… (i)

For distance S₁:
Let u’ be the velocity of the particle after 2 s and a’ be the acceleration of the particle in t = 0 to t = 5 s.
Since the particle undergoes uniform acceleration in the interval t = 0 to t = 5 s, from first equation of motion, acceleration can be obtained as:
υ = u + at
Where, υ = Final velocity of the particle
12. = 0 + a’ × 5
a’ = \(\frac{12}{5}\) = 2.4 m/s² .
Again, from first equation of motion, we have
υ = u + at
= 0 + 2.4 × 2 = 4.8 m/s
Distance travelled by the particle between time 2 s and 5 s i. e., in 3 s
S₁ = u’t + \(\frac{1}{2}\) a’t²
= 4.8 × 3 + \(\frac{1}{2}\) × 2.4 × (3)²
= 25.2 m ……………… (ii)

For distance S₂:
Let a” be the acceleration of the particle between time t = 5 s and t = 10s.
From first equation of motion,
υ = u + at (where υ = 0 as the particle finally comes to rest)
0 = 12 + a” × 5
a” = \(\frac{-12}{5}\)
= -2.4 m/s²
Distance travelled by the particle in Is (i. e., between t = 5 s and t = 6 s)
S₂ = u”t + \(\frac{1}{2}\) at²
= 12 × a + \(\frac{1}{2}\)(-2.4) × (1)²
= 12 – 1.2 = 10.8 m ……………… (iii)
From equations (i), (ii), and (iii), we get
S = 25.2 + 10.8 = 36 m
∴ Average speed = \(\frac{36}{4}\) = 9 m/s

Question 28.
The velocity-time graph of a particle in one-dimensional motion is shown in figure.

Which of the following formulae are correct for describing the motion of the particle over the time-interval t₁ to t₂ ?
(a) x(t₂) = x(t₁) + υ(t₁)(t₂ – t₁) + \(\frac {1}{2}\) a(t₂ – t₁)2
(b) υ(t₂) = υ(t₁)+a(t₂ – t₁)
(c) _Average = [x(t₂) – x(t₁)] /(t₂ – t₁)
(d) _Average = [(t₂ ) – υ(t₁)] / (t₂ – t₁)
(e) x(t₂) = x(t₁) + υ_Average (t₂ – t₁) + (\(\frac {1}{2}\)) a_Average (t₂ – t₁)²
(f) x (tsub>2) – x (tsub>1) = area under the υ – t curve bounded by the t-axis and the dotted line shown.
Solution:
The slope of the given graph over the time interval tsub>1 to tsub>2 is not constant and is not uniform. It means acceleration is not constant and is not uniform, therefore, relation (a), (b) and (e) are not correct which is for uniform accelerated motion, but relations (c), (d) and (f) are correct, because these relations are true for both uniform or non-uniform accelerated motion.

Punjab State Board PSEB 11th Class Physics Book Solutions Chapter 14 Oscillations Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Physics Chapter 14 Oscillations

PSEB 11th Class Physics Guide Oscillations Textbook Questions and Answers

Question 1.
Which of the following examples represent periodic motion?
(a) A swimmer completing one (return) trip from one bank of a river to the other and back.
(b) A freely suspended bar magnet displaced from its N-S direction and released.
(c) A hydrogen molecule rotating about its center of mass.
(d) An arrow released from a bow.
Solution:
(b) and (c)
Explanations :
(a) The swimmer’s motion is not periodic. The motion of the swimmer between the banks of a river is back and forth. However, it does not have a definite period. This is because the time taken by the swimmer during his back and forth journey may not be the same.

(b) The motion of a freely-suspended magnet, if displaced from its N-S direction and released, is periodic. This is because the magnet oscillates about its position with a definite period of time.

(c) When a hydrogen molecule rotates about its center of mass, it comes to the same position again and again after an equal interval of time. Such motion is periodic.

(d) An arrow released from a bow moves only in the forward direction. It does not come backward. Hence, this motion is not a periodic.

Question 2.
Which of the following examples represent (nearly) simple harmonic motion and which represent periodic but not simple harmonic motion?
(a) the rotation of earth about its axis.
(b) motion of an oscillating mercury column in a 17-tube.
(c) motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lowermost point.
(d) general vibrations of a polyatomic molecule about its equilibrium position.
Solution:
(b) and (c) are SHMs; (a) and (d) are periodic, but not SHMs
Explanations :
(a) During its rotation about its axis, earth comes to the same position again and again in equal intervals of time. Hence, it is a periodic motion. However, this motion is not simple harmonic. This is because earth does not have a to and fro motion about its axis.

(b) An oscillating mercury column in a [/-tube is simple harmonic. This is because the mercury moves to and fro on the same path, about the fixed position, with a certain period of time.

(c) The ball moves to and fro about the lowermost point of the bowl when released. Also, the ball comes back to its initial position in the same period of time, again and again. Hence, its motion is periodic as well as simple harmonic.

(d) A polyatomic molecule has many natural frequencies of oscillation. Its vibration is the superposition of individual simple harmonic motions of a number of different molecules. Hence, it is not simple harmonic, but periodic.

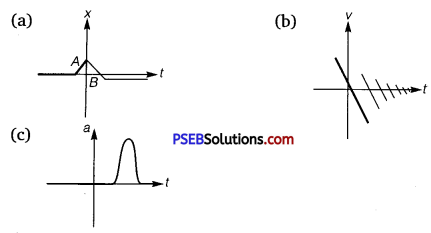
Question 3.
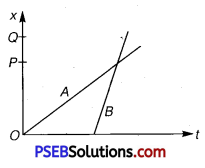
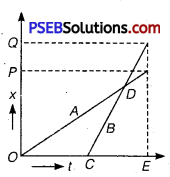
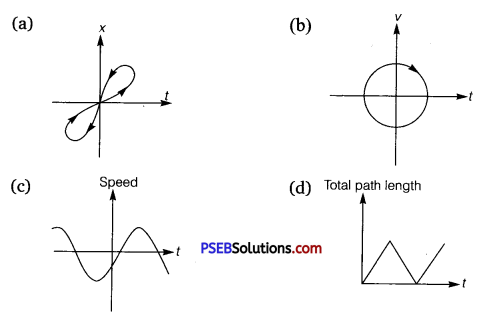
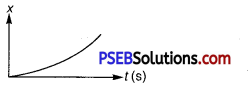
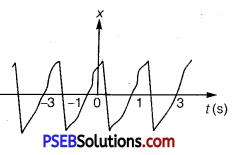
Figure depicts four x-t plots for linear motion of a particle. Which of the plots represents periodic motion? What is the period of motion (in case of periodic motion)?
(a)

(b)

(c)

(d)

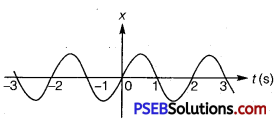
Solution:
(b) and (d) are periodic
Explanation :
(a) It is not a periodic motion. This represents a unidirectional, linear uniform motion. There is no repetition of motion in this case.
(b) In this case, the motion of the particle repeats itself after 2 s. Hence, it is a periodic motion, having a period of 2 s.
(c) It is not a periodic motion. This is because the particle repeats the motion in one position only. For a periodic motion, the entire motion of the particle must be repeated in equal intervals of time. In this case, the motion of the particle repeats itself after 2 s. Hence, it is a periodic motion, having a period of 2 s.

Question 4.
Which of the following functions of time represent (a) simple ‘ harmonic, (b) periodic but not simple harmonic, and (c) non¬periodic motion? Give period for each case of periodic motion (a is any positive constant):
(a) sin ωt – cos ωt
(b) sin ³ωt
(c) 3cos(\(\pi / 4 \) -2ωt)
(d) cos ωt +cos 3 ωt+cos 5ωt
(e) exp(-ω²t²)
(f) 1+ ωt+ω^2t
Solution:
(a) SHM
The given function is:

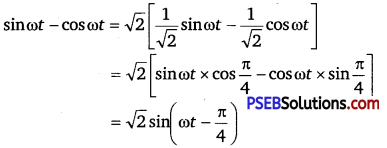
This function represents SHM as it can be written in the form: a sin (ωt +Φ)
Its period is: \(\frac{2 \pi}{\omega}\)

(b) Periodic, but not SHM The given function is:
sin³ ωt = \(\frac{1}{4}\) [3sinωt -sin3ωt] (∵ sin3θ = 3sinθ – 4sin³ θ)
The terms sin cot and sin 3 ωt individually represent simple harmonic motion (SHM). However, the superposition of two SHM is periodic and not simple harmonic.

Period of\(\frac{3}{4}\)sin ωt = \(\frac{2 \pi}{\omega}\) = T
Period of\(\frac{1}{4}\)sin3ωt = \(\frac{2 \pi}{3 \omega}\) = T’ = \(\frac{T}{3}\)
Thus, period of the combination
= Minimum time after which the combined function repeats
= LCM of T and \(\frac{T}{3}\) = T
Its period is 2 \(\pi / \omega\)

(c) SHM
The given function is:
3 cos \(\left[\frac{\pi}{4}-2 \omega t\right]\) = 3 cos \(\left[2 \omega t-\frac{\pi}{4}\right]\)
This function represents simple harmonic motion because it can be written in the form:
acos(ωt +Φ)

Its period is :
\(\frac{2 \pi}{2 \omega}=\frac{\pi}{\omega}\)

(d) Periodic, but not SHM
The given function is cosωt +cos3ωt +cos5ωt. Each individual cosme function represents SHM. However, the superposition of threc simple harmonic motions is periodic, but not simple harmonic.

cosωt represents SHM with period = \(\frac{2 \pi}{\omega}\) T (say)
cos 3ωt represents SHM with period = \(\frac{2 \pi}{3 \omega}=\frac{T}{3}\)
cos 5ωt represents SHM with period = \(\frac{2 \pi}{5 \omega}=\frac{T}{5}\)
The minimum time after which the combined function repeats its value is T. Hence, the given function represents periodic function but not SHM, with period T.

(e) Non-periodic motion: .
The given function exp(- ω²t²) is an exponential function. Exponential functions do not repeat themselves. Therefore, it is a non-periodic motion.

(f) Non-periodic motion
The given function is 1+ ωt + ω²t²
Here no repetition of values. Hence, it represents non-periodic motion.

Question 5.
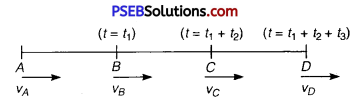
A particle Is in linear simple harmonic motion between two points, A and B, 10 cm apart Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when It Is
(a) at the end A,
(b) at the end B,
(c) at the midpoint of AB going towards A,
(d) at 2 cm away from B going towards A,
(e) at 3 cm away from A going towards B, and
(f) at 4 cm away from B going towards A.
Solution:
The given situation is shown in the following figure. Points A and B are the two endpoints, with AB =10cm. 0 is the midpoint of the path.

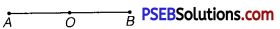
A particle is in linear simple harmonic motion between the endpoints
(a) At the extreme point A, the particle is at rest momentarily. Hence, its velocity is zero at this point.
Its acceleration is positive as it is directed along with AO.
Force is also positive in this case as the particle is directed rightward.

(b) At the extreme point B, the particle is at rest momentarily. Hence, its velocity is zero at this point.
Its acceleration is negative as it is directed along B.
Force is also negative in this case as the particle is directed leftward.

(c)
The particle is extending a simple harmonic motion. O is the mean position of the particle. Its velocity at the mean position O is the maximum. The value for velocity is negative as the partide Is directed leftward. The acceleration and force of a particle executing SHM is zero at the mean position.

(d)
The particle is moving towards point O from the end B. This direction of motion is opposite to the conventional positive direction, which is from A to R. Hence, the particle’s velocity and acceleration, and the force on it are all negative.

(e)

The particle is moving towards point O from the end A. This direction of motion is from A to B, which is the conventional positive direction. Hence, the value for velocity, acceleration, and force are all positive.

(f)

This case is similar to the one given in (d).

Question 6.
Whi ch of the following relationships between the acceleration a and the displacement x of a particle involves simple harmonic motion?
(a) a=0.7x
(b) a=-200x²
(c) a= – 10 x (d) a=100x³
Solution:
A motion represents simple harmonic motion if it is governed by the force law:
F=-kx
ma’= -kx
∴ a = – \(\frac{k}{m}\) x

where F is the force
m is the mass (a constant for a body)
x is the displacement
a is the acceleration.
k is a constant
Among the given equations, only equation a = -10 x is written in the
above form with \( \frac{k}{m}\) =10. Hence, this relation represents SHM.

Question 7.
The motion of a particle executing simple harmonic motion is described by the displacement function,
x(t) = A cos (ωt+Φ)
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ω cm/s, what are its amplitude and initial phase angle? The angular frequency of the particle is πs^-1. If instead of the cosine function, we choose the sine function to describe the SHM:x = B sin(ωt + α), what are the amplitude and initial phase of the particle with the above initial conditions.
Solution:
Initially, at t = 0:
Displacement, x = 1 cm Initial velocity, ν = ω cm/s.
Angular frequency, ω = π rad s^-1
It is given that:
x(t) = Acos (ωt+Φ)
1 = Acos(ω x 0 +Φ) = AcosΦ
AcosΦ =1 ……………………………….. (i)

Velocity, ν = \(\frac{d x}{d t}\)
ω = -Aω sin(ωt +Φ)
1 = -Asin(ω x 0 +Φ) = -AsinΦ
Asin Φ = -1 ………………………… (ii)
Squaring and adding equations (i) and (ii), we get
A²(sin²Φ +cos²Φ) = 1+1
A² = 2
∴ A = \(\sqrt{2}\) cm

Dividing equation (ii) by equation (i), we get
tanΦ = -1

SHM is given as
x = Bsin(ωt + α)
Putting the given values in this equation, we get 1 =B sin (ωt + α)
B sin α =1 …………………………… (iii)

Velocity, ν = \(\frac{d x}{d t}\)
ω =(ωB cos (ωt + a)
1 =B cos (ω x 0+α ) = B cos α …………………………………… (iv)
Squaring and adding equations (iii) and (iv), we get
B² [sin²α +cos² α] =1+1
B² =2
B = \(\sqrt{2}\) cm
Dividing equation (iii) by equation (iv), we get

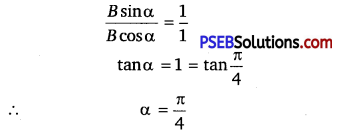
Question 8.
A spring balance has a scale that reads from 0 to 50kg. The length of the scale is 20 cm. A body suspended from this balance, when displaced and released, oscillates with a period of 0.6 s. What is the weight of the body?
Solution:
Maximum mass that the scale can read, M = 50 kg
Maximum displacement of the spring = Length of the scale, l = 20 cm = 0.2 m Time period, T =0.6s
Maximum force exerted on the spring, F = Mg where,
g = acceleration due to gravity = 9.8 m/s²
F = 50 × 9.8 = 490 N
∴ Spring constant , K = \(\frac{F}{l}=\frac{490}{0.2}\) = 2450Nm^-1

Mass m, is suspended from the balance,
Time period, T = \(2 \pi \sqrt{\frac{m}{k}}\)
∴ m = \(\left(\frac{T}{2 \pi}\right)^{2} \times k=\left(\frac{0.6}{2 \times 3.14}\right)^{2} \times 2450 \) = 22.36 kg
∴ Weight of the body = mg = 22.36 x 9.8 = 219.167N
Hence, the weight of the body is about 219 N.

Question 9.
Aspringhavingwith aspiring constant 1200Nm^-1 is mounted on a horizontal table as shown in figure. A mss of 3kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0cm and released.

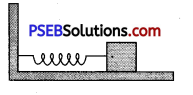
Determine (i) the frequency of oscillations,
(ii) maximum acceleration of the mass, and
(iii) the maximum speed of the mass.
Solution:
Spring constant, k = 1200 Nm^-1
mass,m = 3 Kg
Displacement,A = 2.0 cm = 0.02 m
(i) Frequency of oscillation y, is gyen by the relation
V = \(\frac{1}{T}=\frac{1}{2 \pi} \sqrt{\frac{k}{m}}\)
where, T is the time period
∴ v = \(\frac{1}{2 \times 3.14} \sqrt{\frac{1200}{3}}\) = 3.18 s^-1
Hence, the frequency of oscillations is 3.18 s^-1.

(ii) Maximum acceleration a is given by the relation:
a = ω²A
where,
ω = Angular frequency = \(\sqrt{\frac{k}{m}}\)
A = Maximum displacement
∴ a = \(\frac{k}{m} A=\frac{1200 \times 0.02}{3}\) = 8 ms^-2
Hence, the maximum acceleration of the mass is 8.0 ms²

(iii) Maximum speed, ν_max = Aω
= \(A \sqrt{\frac{k}{m}}=0.02 \times \sqrt{\frac{1200}{3}}\) = 0.4 m/s
Hence, the maximum speed of the mass is 0.4 m/s.

Question 10.
In question 9, let us take the position of mass when the spring is unstretched as x =0, and the direction from left to right as the positive direction of x-axis. Give x as a function of time t for the oscillating massif at the moment we start the stopwatch (t = 0), the mass is
(a) at the mean position,
(b) at the maximum stretched position, and
(c) at the maximum compressed position.
In what way do these functions for SHM differ from each other, in frequency, in amplitude br the initial phase?
Solution:
(a) The functions have the same frequency and amplitude, but different initial phases.
Distance travelled by the mass sideways, A = 2.0 cm
Force constant of the spring, k =1200 N m^-1
Mass, m =3kg
Angular frequency of oscillation,
ω = \(\sqrt{\frac{k}{m}}=\sqrt{\frac{1200}{3}} \) = \(\sqrt{400}\) = 20 rad s^-1
When the mass is at the mean position, initial phase is 0.
Displacement,
x = A sinωt = 2 sin20 t

(b) At the maximum stretched position, the mass is toward the extreme right. Hence, the initial phase is \(\frac{\pi}{2}\)
Displacement, x = Asin \(\left(\omega t+\frac{\pi}{2}\right)\)
=2sin\(\left(20 t+\frac{\pi}{2}\right)\)
= 2 cos 20t

(c) At the maximum compressed position, the mass is toward the extreme left. Hence, the initial phase is \(\frac{3 \pi}{2}\)
Displacement, x = A sin \(\left(\omega t+\frac{3 \pi}{2}\right)\)
= 2sin \(\left(20 t+\frac{3 \pi}{2}\right)\) = -2cos 20t
The functions have the same frequencyl \(\left(\frac{20}{2 \pi} \mathrm{Hz}\right)\) land amplitude (2cm),
but different initial phases \(\left(0, \frac{\pi}{2}, \frac{3 \pi}{2}\right)\)

Question 11.
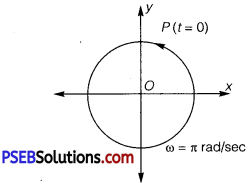
Figures correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i. e., clockwise or anti-clockwise) are indicated on each figure.

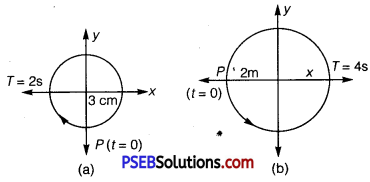
Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.
solution:
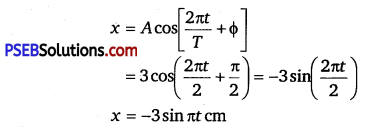
Time period,T =2s
Amplitude, A = 3cm
At time, t = O, the radius vector OP makes an angle \(\frac{\pi}{2}\) with the positive x -axis, i.e., phase angle Φ = + \(\frac{\pi}{2}\)
Therefore, the equation of simple harmonic motion for the x —projection of OP, at time t, is given by the displacement equation

(b) Time period, T = 4s
Amplitude, a =2 m
At time t = 0, OP makes an angle ir with the x-axis, in the anticlockwise direction. Hence, phase angle, Φ = +π
Therefore, the equation of simple harmonic motion for the x -projection of OP, at time t, is given as

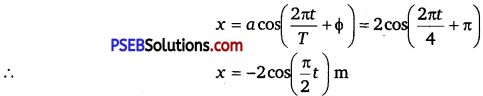
Question 12.
Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t = 0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anticlockwise in every case: (x is in cm and t is in s).
(a) x= – 2sin(3t+\(\pi / \mathbf{3}\) )
(b) x=cos (\(\pi / 6\) – t)
(c) x=3 sin (2πt + \(\pi / 4 \) )
(d) x=2 cos πt
Solution:
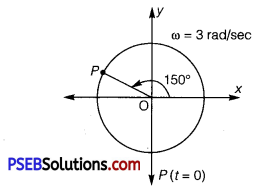
(a) x = -2 sin \(\left(3 t+\frac{\pi}{3}\right)=+2 \cos \left(3 t+\frac{\pi}{3}+\frac{\pi}{2}\right)=2 \cos \left(3 t+\frac{5 \pi}{6}\right) \)

If this equation is compared with the standard SHM equation,
x =A cos \(\left(\frac{2 \pi}{T} t+\phi\right)\) then we get
Amplitude, A = 2cm
Phase angle, Φ = \(\frac{5 \pi}{6}\) =150°
Angular velocity, ω = \(\frac{2 \pi}{T}\) =3 rad/sec
The motion of the particle can be pokted as shown in the following figure.

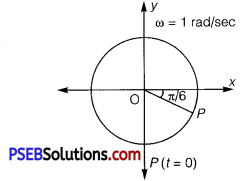
(b) x=cos \(\left(\frac{\pi}{6}-t\right)\) =cos \(\left(t-\frac{\pi}{6}\right)\)
If this equation is compared with the standard SHM equation,
x = A cos \(\left(\frac{2 \pi}{T} t+\phi\right)\) then we get
Amplitude, A = 1 cm
Phase angle, Φ = \(-\frac{\pi}{6} \) = – 30°
Angular velocity, ω = \(\frac{2 \pi}{T}\) =1 rad/s
The motion of the particle can be plotted as shown in the following figure.

(c) x =3sin \(\left(2 \pi t+\frac{\pi}{4}\right)\)

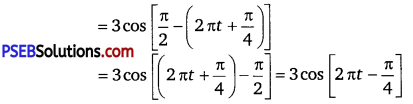
If this equation is compared with the standard SHM equation
x = Acos \(\left(\frac{2 \pi}{T} t+\phi\right)\) then we get
Amplitude, A = 3cm
Phase angle, Φ = \(-\frac{\pi}{4}\)
Angular velocity, ω = \(\frac{2 \pi}{T}\) = 2π rad/s
The motion of the particle can be plotted as shown in the following figure.

(d) x=2cosπt
If this equation is compared with the standard SHM equation,
x = A cos \(\left(\frac{2 \pi}{T} t+\phi\right) \) then we get
Amplitude, A = 2cm
Phase angle, Φ = 0
Angular velocity, ω = π rad/s
The motion of the particle can be plotted as shown in the following figure.

Question 13.
Figure (a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure (b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure (b) is stretched by the same force F.

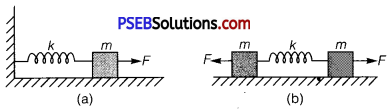
(a) What is the minimum extension of the spring in the two cases?
(b) If the mass in Fig. (a) and the two masses in Fig. (b) are released, what is the period of oscillation in each case?
Solution:
(a) For the one block system:
When a force F, is applied to the free end of the spring, an extension l, is produced. For the maximum extension, it can be written as:
F=kl
where k is the spring constant
Hence, the maximum extension produced in the spring, l = \(\frac{F}{k}\)
For the two blocks system:
The displacement (x) produced in this case is:
x = \(\frac{l}{2}\)
Net force, F = +2kx =2k \(\frac{l}{2}\)
∴ l = \(\frac{F}{k}\)

(b) For the one blocks system:
For mass (m) of the block, force is written as
F = ma = m \(\frac{d^{2} x}{d t^{2}}\)
where, x is the displacement of the block in time t
∴ m \(\frac{d^{2} x}{d t^{2}}\) = -kx
It is negative because the direction of elastic force is opposite to the direction of displacement.

where, ω is angular frequency of the oscillation
∴ Time period of the oscillation,
T= \(\frac{2 \pi}{\omega}=\frac{2 \pi}{\sqrt{\frac{k}{m}}}=2 \pi \sqrt{\frac{m}{k}}\)

For the two blocks system:
F=m \(\frac{d^{2} x}{d t^{2}}\)
m \(\frac{d^{2} x}{d t^{2}}\) =-2kx

It is negative because the direction of elastic force is opposite to the direction of displacement.
\(\frac{d^{2} x}{d t^{2}}\) = \(-\left[\frac{2 k}{m}\right] x \) = – ω²x
where, Angular frequency, ω = \(\sqrt{\frac{2 k}{m}}\)
∴ Time period T = \(\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{m}{2 k}} \)

Question 14.
The piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 1.0 in. If the piston moves with simple harmonic motion with an angular frequency of 200 rad/min, what is its maximum speed?
Solution:
Angular frequency of the piston, ω = 200 rad/min.
Stroke =1.0 m
Amplitude, A = \(\frac{1.0}{2}\) = 0.5m
The maximum speed (ν_max) of the piston is given by the relation
ν_max =Aω = 200 x 0.5=100 m/min

Question 15.
The acceleration due to gravity on the surface of moon is 1.7 ms^-2. What is the time period of a simple pendulum on the surface of moon If Its time period on the surface of earth is 3.5 s? (gon the surface of earth is 9.8 ms^-2)
Solution:
Acceleration due to gravity on the surface of moon, g’ = 1.7m s^-2
Acceleration due to gravity on the surface of earth, g = 9.8 ms^-2
Time period of a simple pendulum on earth, T = 3.5 s
T= \(2 \pi \sqrt{\frac{l}{g}}\)

where l is the length of the pendulum
∴ l = \(\frac{T^{2}}{(2 \pi)^{2}} \times g=\frac{(3.5)^{2}}{4 \times(3.14)^{2}} \times 9.8 \mathrm{~m} \)

The length of the pendulum remains constant.
On Moon’s surface, time period,
T’ = \(2 \pi \sqrt{\frac{l}{g^{\prime}}}=2 \pi \sqrt{\frac{(3.5)^{2}}{\frac{4 \times(3.14)^{2}}{1.7}} \times 9.8} \) = 8.4 s
Hence, the time period of the simple pendulum on the surface of Moon is 8.4 s.

Question 16.
Answer the following questions:
(a) Time period of a particle in SHM depends on the force constant k and mass m of the particle:
T = \(2 \pi \sqrt{\frac{m}{k}}\) A simple pendulum executes SHM approximately. Why then is the time period of a pendulum independent of the mass of the pendulum?

(b) The motion of a simple pendulum is approximately simple harmonic for small-angle oscillations. For larger angles of oscillation a more involved analysis shows that T is greater than \(2 \pi \sqrt{\frac{l}{g}}\) Think of a qualitative argument to appreciate this result.

(c) A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall?

(d) What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity?
Solution :
(a) The time period of a simple pendulum, T = \(2 \pi \sqrt{\frac{m}{k}}\)
For a simple pendulum, k is expressed in terms of mass m, as
k ∝ m
\(\frac{m}{k}\) = Constant
Hence, the time period T, of a simple pendulum is independent of the mass of the bob.

(b) In the case of a simple pendulum, the restoring force acting on the bob of the pendulum is given as
F = -mg sinθ
where, F = Restoring force; m = Mass of the bob; g = Acceleration due to
gravity; θ = Angle of displacement
For small θ, sinθ ≈ θ
For large 0,sin0 is greater than 0.
This decreases the effective value of g.
Hence, the time period increases as
T = \(2 \pi \sqrt{\frac{l}{g}}\)
where, l is the length of the simple pendulum

(c) The time shown by the wristwatch of a man falling from the top of a tower is not affected by the fall. Since a wristwatch does not work on the principle of a simple pendulum, it is not affected by the acceleration due to gravity during free fall. Its working depends on spring action.

(d) When a simple pendulum mounted in a cabin falls freely under gravity, its acceleration is zero. Hence the frequency of oscillation of this simple pendulum is zero.

Question 17.
A simple pendulum of length l and having a bob of mass M is suspended in a car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small f oscillations in a radial direction about its equilibrium position, what will be its time period?
Solution:
The bob of the simple pendulum will experience the acceleration due to gravity and the centripetal acceleration provided by the circular motion of the car.
Acceleration due to gravity = g
Centripetal acceleration = \(\frac{v^{2}}{R}\)
where, v is the uniform speed of the car R is the radius of the track
Effective acceleration (a_eff) is given as
a_eff = \(\sqrt{g^{2}+\left(\frac{v^{2}}{R}\right)^{2}}\)

Time period, T = \( 2 \pi \sqrt{\frac{l}{a_{e f f}}}\)
where, l is the length of the pendulum
∴ Time period, T = \(2 \pi \sqrt{\frac{l}{g^{2}+\frac{v^{4}}{R^{2}}}} \)

Question 18.
A cylindrical piece of cork of density of base area A and height h floats in a liquid of density ρ_l. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T = \(2 \pi \sqrt{\frac{\boldsymbol{h} \rho}{\rho_{\boldsymbol{l}} \boldsymbol{g}}}\)
where ρ is the density of cork. (Ignore damping due to viscosity of the liquid).
Solution:
Base area of the cork = A
Height of the cork = h
Density of the liquid = ρ_l
Density of the cork = ρ

In equilibrium:
Weight of the cork = Weight of the liquid displaced by the floating cork Let the cork be depressed slightly by x. As a result, some extra water of a certain volume is displaced. Hence, an extra up-thrust acts upward and provides the restoring force to the cork.
Up-thrust = Restoring force, F = Weight of the extra water displaced
F = -(Volume x Density x g)
Volume = Area x Distance through which the cork is depressed Volume = Ax
∴ F = -Ax ρ_lg ………………………… (i)
According to the force law,
F = kx
k = \(\frac{F}{x}\)

where k is a constant
k = \(\frac{F}{x}\) = -Aρ_lg ………………………………. (ii)
The time period of the oscillations of the cork,
T = \(2 \pi \sqrt{\frac{m}{k}} \) …………………………………… (iii)

where,
m = Mass of the cork
= Volume of the cork x Density
= Base area of the cork x Height of the cork x Density of the cork = Ahρ
Hence, the expression for the time period becomes
T = \(2 \pi \sqrt{\frac{A h \rho}{A \rho_{l} g}}\) = 2\(\pi \sqrt{\frac{h \rho}{\rho_{l} g}} \)

Question 19.
One end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
Solution:
Area of cross-section of the U-tube = A
Density of the mercury column = ρ
Acceleration due to gravity = g
Restoring force, F = Weight of the mercury column of a certain height
F = -(Volume x Density x g)
F = -(A x 2h x ρ x g) = -2Aρgh = -k x Displacement in one of the arms (h)

where, 2h is the height of the mercury column in the two arms
k is a constant, given by k = \(-\frac{F}{h}\) = 2Aρg
Time period = \(2 \pi \sqrt{\frac{m}{k}}=2 \pi \sqrt{\frac{m}{2 A \rho g}}\)
where, m is the mass of the mercury column
Let l be the length of the total mercury in the U-tube.
Mass of mercury, m = Volume of mercury x Density of mercury = Alρ
∴ T = \(2 \pi \sqrt{\frac{A l \rho}{2 A \rho g}}=2 \pi \sqrt{\frac{l}{2 g}} \)

Hence the mercury column executes simple harmonic motion with time period \(2 \pi \sqrt{\frac{l}{2 g}} \)

Additional Exercises

Question 20.
An air chamber of volume V has a neck area of cross-section a into which a ball of mass m just fits and can move up and down without any friction (see figure). Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal.

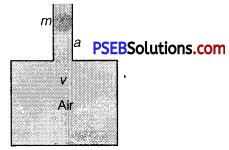
Solution:
Volume of the air chamber = V
Area of cross-section of the neck = a
Mass of the ball = m
The pressure inside the chamber is equal to the atmospheric pressure. Let the ball be depressed by x units. As a result of this depression, there would be a decrease in the volume and an increase in the pressure inside the chamber.
Decrease in the volume of the air chamber, ΔV = ax
Volumetric strain =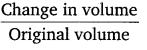
⇒ \(\frac{\Delta V}{V}=\frac{a x}{V}\)

Bulk Modulus of air, B = \(\frac{\text { Stress }}{\text { Strain }}=\frac{-p}{\frac{a x}{V}}\)
In this case, stress is the increase in pressure. The negative sign indicates that pressure increases with a decrease in volume.
p = \(\frac{-B a x}{V}\)
The restoring force acting on the ball,
F = p × a = \(\frac{-B a x}{V} \cdot a=\frac{-B a^{2} x}{V}\) ……………………………. (i)
In simple harmonic motion, the equation for restoring force is
F = -kx …………………………………….. (ii)
where, k is the spring constant Comparing equations (i) and (ii), we get
k = \(\frac{B a^{2}}{V}\)
Time period, T = \(2 \pi \sqrt{\frac{m}{k}}=2 \pi \sqrt{\frac{V m}{B a^{2}}}\)

Question 21.
You are riding in an automobile of mass 3000kg. Assuming that you are examining the oscillation characteristics of its suspension system. The suspension sags 15 cm when the entire automobile is placed on it. Also, the amplitude of oscillation decreases by 50% during one complete oscillation. Estimate the values of (a) the spring constant k and (6) the damping constant b for the spring and shock absorber system of one wheel, assuming that each wheel supports 750 kg.
Solution:
Mass of the automobile, m = 3000 kg
Displacement in the suspension system, x = 15cm = 0.15 m
There are 4 springs in parallel to the support of the mass of the automobile.
The equation for the restoring force for the system:
F = -4 kx = mg

where, k is the spring constant of the suspension system
Time period, T = \(2 \pi \sqrt{\frac{m}{4 k}}\)
and, k = \(\frac{m g}{4 x}=\frac{3000 \times 10}{4 \times 0.15}\) = 50000 = 5 x 10 ⁴N/m
Spring constant, k = 5 x 10⁴ N/m

Each wheel supports a mass, M = \(\frac{3000}{4}\) = 750 kg
For damping factor b, the equation for displacement is written as:
x = x₀e^-bt/2M

The amplitude of oscillation decreases by 50%

where, Time petiod,t =\(2 \pi \sqrt{\frac{m}{4 k}}=2 \pi \sqrt{\frac{3000}{4 \times 5 \times 10^{4}}}\) =0.7691s
∴ b =\(\frac{2 \times 750 \times 0.693}{0.7691}\) =1351.58kg/s
Therefore, the damping constant of the spring is 1351.58 kg/s.

Question 22.
Show that for a particle in linear SHM the average kinetic energy over a period of oscillation equals the average potential energy over the same period.
Solution:
The equation of displacement of a particle executing SHM at an instant t is given as
x = Asinωt
where,
A = Amplitude of oscillation
ω = Angular frequency = \(\sqrt{\frac{k}{M}}\)
The velocity of the particle is
ν = \(\frac{d x}{d t}\) = Aωcosωt

The kinetic energy of the particle is
E_k = \(\frac{1}{2} M v^{2}=\frac{1}{2} M A^{2} \omega^{2} \cos ^{2} \omega t \)
The potential energy of the particle is
E_p = \( \frac{1}{2} k x^{2}=\frac{1}{2} M \omega^{2} A^{2} \sin ^{2} \omega t\)

For time period T, the average kinetic energy over a single cycle is given as


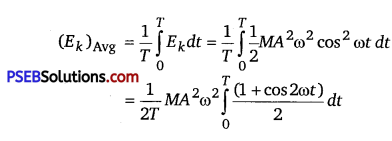
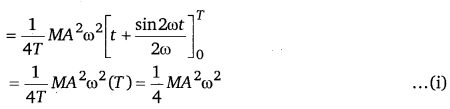
And, average potential energy over one cycle is given as

It can be inferred from equations (i) and (ii) that the average kinetic energy for a given time period is equal to the average potential energy for the same time period.

Question 23.
A circular disc of mass 10 kg is suspended by a wire attached to its center. The wire is twisted by rotating the disc and released. The period of torsional oscillations is found to be 1.5s. The radius of the disc is 15 cm. Determine the torsional spring constant of the wire. (Torsional spring constant a is defined by the relation J = -αθ, where J is the restoring couple and 0 the angle of twist).
Solution:
Mass of the circular disc, m = 10 kg
Radius of the disc, r = 15cm = 0.15 m
The torsional oscillations of the disc has a time period, T = 1.5 s The moment of inertia of the disc is
I = \(\frac{1}{2}\) mr² = \(\frac{1}{2} \times(10) \times(0.15)^{2}\) = 0.1125kg-m²

Time period, T = \(2 \pi \sqrt{\frac{I}{\alpha}}\)
where, α is the torsional constant.
An21 4 x(3.14)2x 0.1125 , M
α = \(\frac{4 \pi^{2} I}{T^{2}}=\frac{4 \times(3.14)^{2} \times 0.1125}{(1.5)^{2}} \) = 1.972 N-m/rad
Hence, the torsional spring constant of the wire is 1.972 N-m rad^-1.

Question 24.
A body describes simple harmonic motion with amplitude of 5 cm and a period of 0.2 s. Find the acceleration and velocity of the body when the displacement is (a) 5 cm, (b) 3 cm, (c) 0 cm.
Solution:
Amplitude, A = 5 cm = 0.05m
Time period, T = 0.2 s
(a) For displacement, x = 5 cm = 0.05m
Acceleration is given by
a = -ω²x = \(-\left(\frac{2 \pi}{T}\right)^{2} x=-\left(\frac{2 \pi}{0.2}\right)^{2} \times 0.05\)
Velocity is given by
ν = ω \(\sqrt{A^{2}-x^{2}}=\frac{2 \pi}{T} \sqrt{(0.05)^{2}-(0.05)^{2}}\) = 0
When the displacement of the body is 5 cm, its acceleration is -5π² m/s² and velocity is 0.

(b) For displacement, x =3 cm = 0.03 m
Acceleration is given by
a = – ω²x = – \(\left(\frac{2 \pi}{T}\right)^{2}\)x = \(\left(\frac{2 \pi}{0.2}\right)^{2}\) 0.03 = -3π² m/s²
Velocity is given by

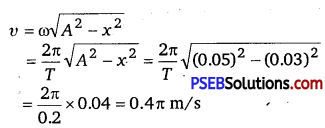
When the displacement of the body is 3 cm, its acceleration is -3π m/s² and velocity is 0.4π m/s.

(c) For displacement, x = 0
Acceleration is given by
a = – ω²x = 0
Velocity is given by

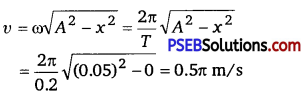
When the displacement of the body is 0, its acceleration is 0, and velocity is0.5π m/s.

Question 25.
A mass attached to a spring is free to oscillate, with angular velocity ω, in a horizontal plane without friction or damping. It is pulled to a distance x₀ and pushed towards the center with a velocity v₀ at time t = 0. Determine the amplitude of the resulting oscillations in terms of the parameters ω, x_0, and v₀. [Hint: Start with the equation x = a cos(ωt + θ) and note that the initial velocity is negative.]
Solution:
The displacement equation for an oscillating mass is given by
x = Acos(ωt + θ) …………………………… (i)
where A is the amplitude
x is the displacement
θ is the phase constant

Squaring and adding equations (iii) and (iv), we get

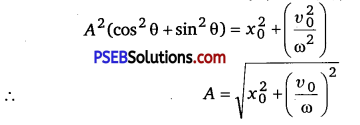
Hence, the amplitude of the resulting oscillation is \(\sqrt{x_{0}^{2}+\left(\frac{v_{0}}{\omega}\right)^{2}}\)