Punjab State Board PSEB 11th Class Physics Book Solutions Chapter 3 Motion in a Straight Line Textbook Exercise Questions and Answers.
PSEB Solutions for Class 11 Physics Chapter 3 Motion in a Straight Lines
PSEB 11th Class Physics Guide Motion in a Straight Line Textbook Questions and Answers
Question 1.
In which of the following examples of motion, can the body be considered approximately a point object:
(a) a railway carriage moving without jerks between two stations.
(b) a monkey sitting on top of a man cycling smoothly on a circular track.
(c) a spinning cricket ball that turns sharply on hitting the ground.
(d) a tumbling beaker that has slipped off the edge of a table.
Answer:
(a), (b)
Explanation
(a) The size of a carriage is very small as compared to the distance between two stations. Therefore, the carriage can be treated as a point sized object.
(b) The size of a monkey is very small as compared to the size of a circular track. Therefore, the monkey can be considered as a point sized object on the track.
(c) The size of a spinning cricket ball is comparable to the distance through which it turns sharply on hitting the ground. Hence, the cricket ball cannot be considered as a point object.
(d) The size of a beaker is comparable to the height of the table from which it slipped. Hence, the beaker cannot be considered as a point object.
![]()
Question 2.
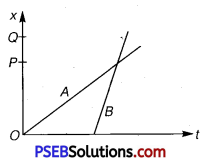
The position-time (x – t) graphs for two children A and B returning from their school O to their homes P and Q respectively are shown in below figure. Choose the correct entries in the brackets below;
(a) (A / B) lives closer to the school than (B / A)
(b) (A / B) starts from the school earlier than (B/ A)
(c) (A / B) walks faster than (B / A)
(d) A and B reach home at the (same/different) time
(e) (A / B) overtakes (B / A) on the road (once/twice).
Solution:
(a) Draw normals on graphs from points P and Q. It is clear that OQ > OP. Therefore, child A lives closer to the school than child B.
(b) Child A start from school at time t =0 (become its graph starts from origin) whild child B starts from school at time t = OC. Therefore, child A starts from school earlier than B.
(c) The slope of distance-time graph represents the speed. More the slope of the graph, more will be the speed. As the slope of the x-t graph of B is higher than the slope of the x – t graph of A, therefore child B walks faster than child A.
(d) Corresponding to points P and Q, the value of t from x – t graphs for children A and B is same i. e.,OE. Therefore, children A and B will reach their homes P and Q at the same time.
(e) x – t graphs for children A and B intersect each other at a point D. Child B starts later but reaches home at the same time as that of child A, therefore child B overtake child A on the road once.
Question 3.
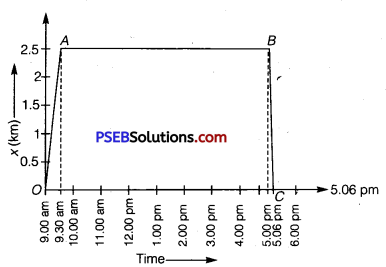
A woman starts from her home at 9.00 am, walks with a speed of 5kmh-1 on a straight road up to her office 2.5 km away, stays at the office up to 5.00 pm, and returns home by an auto with a speed of 25 km h-1. Choose suitable scales and plot the x – t graph of her motion.
Solution:
Speed of the woman = 5 km/h
Distance between her office and home = 2.5 km
Time taken = \(\frac{\text { Distance }}{\text { Speed }}\)
= \(\frac{2.5}{5}\) = 0.5 h = 30 min
Time of arival at office = 9.00 am + 30 min = 9.30 am i. e., at 9.30 am the distance covered will be 2.5 km. This part of journey is represented in graph by OA.
It is given that she covers the same distance in the evening by an auto. Now, speed of the auto = 25 km/h
= \(\frac{2.5}{25}=\frac{1}{10}\) = 0.1 h = 6 mm
She leaves the office at 5.00 pm and take 6 min to reach home. Therefore, she reaches her home at 5.06 pm at this time the distance is zero. This part of journey is represented in graph by BC.
![]()
Question 4.
A drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is 1 m long and requires 1 s. Plot the x – t graph of bis motion. Determine graphically and otherwise how long the drunkard takes to fall in a pit 13 m away from the start.
Solution:
The x – t graph of the drunkard is shown in figure.
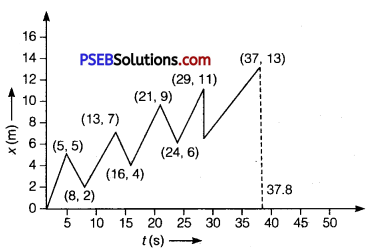
Length of each step =1 m, time taken for each step = 1 s
Time taken to move by 5 steps = 5 s
5 steps forward and 3 steps backward means that the net distance covered by him in first 8 steps i. e., in8s = 5m-3m = 2m
Distance covered by him in first 16 steps orl6s = 2 + 2 = 4m
Distance covered the drunkard in first 24 s i. e., 24 steps = 2 + 2 + 2= 6m
and distance covered in 32 steps i. e. 32 s = 8 m
Distance covered in37 steps = 8 + 5 = 13m
Distance of the pit from the start = 13 m
Total time taken by the drunkard to fall in the pit = 37 s
Since, 1 step requires 1 s of time, so we arrive at the same result from the graph shown.
Question 5.
A jet airplane travelling at the speed of 500 km h-1 ejects its products of combustion at the speed of 1500 km h-1 relative to the jet plane. What is the speed of the latter with respect to an observer on the ground?
Speed of the jet airplane, υjet = 500 km/h
Relative speed of its products of combustion with respect to the plane,
υsmoke = -1500 km/h
Speed of its products of combustion with respect to the ground V’smoke Relative speed of its products of combustion with respect to the airplane,
υsmoke = υ’smoke υ jet
-1500 = υ’smoke – 500
υ’smoke = -1000 km/h
The negative sign indicates that the direction of its products of combustion is opposite to the direction of motion of the jet airplane.
![]()
Question 6.
A car moving along a straight highway with speed of 126 km h-1 is brought to a stop within a distance of 200 m, What is the retardation of the car (assumed uniform), and how long does it take for the car to stop?
Solution:
Initial velocity of the car, u= 126 km/h = 126 × \(\frac{5}{18}\) m/s
= 35 m/s (∵ 1 km/h \(\frac{5}{10}\) m/s)
Final velocity of the car, υ = 0
Distance covered by the car before coming to rest, s = 200 m
From third equation of motion,
υ2 – u2 = 2as
(0)2 – (35)2 = 2 × a × 200
a = \(\frac{35 \times 35}{2 \times 200}\) = -3.06 m/s2
From first equation of motion,
v = u +at
t = \(\frac{v-u}{a}=\frac{0-35}{-3.06}=\frac{-35}{-3.06}\) = 11.44s
∴ Car will stop after 11.4 s.
Question 7.
Two trains A and B of length 400 m each are moving on two parallel tracks with a uniform speed of 72 km h-1 in the same direction, with A ahead of B. The driver of B decides to overtake A and accelerates by 1 m/s2. If after 50 s, the guard of B just brushes past the driver of A, what was the original distance between them?
Solution:
For train A:
Initial velocity, u = 72 km/h = 72 × \(\frac{5}{18}\) m/s = 20 m/s
Time, t = 50 s
Acceleration, aI =0 (Since it is moving with a uniform velocity)
From second equation of motion, distance (SI) covered by train A can be obtained as :
SI = ut + \(\frac {1}{2}\)aIt2
= 20 × 50 + 0 = 1000 m
For train B:
Initial velocity, u = 7 2 km/h = 72 × \(\frac{5}{18}\) m/ s = 20 m/ s
Acceleration, aII = 1 m/s2
Time, t = 50 s
From second equation of motion, distance (SII) covered by train B can be obtained as :
sII = ut + \(\frac {1}{2}\) aIIt2
= 20 × 50 + \(\frac {1}{2}\) × 1 × (50)2 = 2250 m
Hence, the original distance between the driver of train A and the guard of train B is 2250 – 1000 = 1250 m.
![]()
Question 8.
On a two lane road, car A is travelling with a speed of 36 kmh-1. Two cars B and C approach car A in opposite directions with a speed of 54 km h 1 each. At a certain instant, when the distance AB is equal to AC, both being 1 km, B decides to overtake A before C does. What minimum acceleration of car B is required to avoid an accident?
Solution:
Velocity of car A, υA = 36 km/h = 36 × \(\frac {5}{18}\) m/s = 10 m/s
Velocity of car B, υB =54 km/h = 54 × \(\frac {5}{18}\) m/s = 15 m/s
Velocity of car C,υC = 54 km/h 54 × \(\frac {5}{18}\) m/s = 15 m/s
Relative velocity of car B with respect to car A,
υBA = υB – υA = 15 – 10 = 5 m/s
Relative velocity of car C with respect to car A,
υCA – υC – (-υA) = 15 + 10 = 25m/s
At a certain instance, both cars B and C are at the same distance from car Ai.e.,
s = 1 km = 1000 m
Time taken (t) by car C to cover 1000 m = \(\frac {1000}{25}\) = 40 s
Hence, to avoid an accident, car B must cover the same distance in a maximum of 40 s. From second equation of motion, minimum acceleration (a) produced by car B can be obtained as:
s = ut + \(\frac {1}{2}\)at2
1000 = 5 × 40 + \(\frac {1}{2}\) × a × (40)2
a = \(\frac {1600}{1600}\) = 1ms2
Question 9.
Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20 km h-1 in the direction AtoB notices that a bus goes past him every 18 min in the direction of his motion, and eveiy 6 min in opposite direction. What is the period T of the bus service and with what speed (assumed constant) do the buses ply on the road?
Solution:
Let V be the speed of the bus running between towns A and B.
Speed of the cyclist, υ = 20 km/h
Relative speed of the bus moving in the direction of the cyclist
= V- υ = (V – 20)km/h
The bus went past the cyclist every 18 min i.e., \(\frac{18}{60}\) h (when he moves in the direction of the bus).
Distance covered by the bus = (V – 20) × \(\frac{18}{60}\) km ……………….. (i)
Since one bus leaves after every T minutes, the distance travelled by the bus will be equal to V × \(\frac{T}{60}\) ……………. (ii)
Both equations (i) and (ii) are equal.
V – 20 \(\frac{18}{60}=\frac{V T}{60}\) ……………… (iii)
Relative speed of the bus moving in the opposite direction of the cyclist
= (V + 20)km/h
Time taken by the bus to go past the cyclist = 6 min = \(\frac{6}{60}\)h
∴ (V + 20) \(\frac{6}{60}\) = \(\frac{VT}{60}\) …………………. (iv)
From equations (iii) and (iv), we get
(V + 20) × \(\frac{6}{60}\) = (V – 20) × \(\frac{18}{60}\)
V + 20 = 3 V – 60
2V = 80
V = 4 km/h
Substituting the value of V in equation (iv), we get
(40 + 20) × \(\frac{6}{60}=\frac{40 T}{60}\)
T = \(\frac{360}{40}\) = 9 min
![]()
Question 10.
A player throws a hall upwards with an initial speed of 29.4 ms-1 .
(a) What is the direction of acceleration during the upward motion of the hall?
(b) What are the velocity and acceleration of the ball at the highest point of its motion?
(c) Choose the x = 0 m and t0 = 0 s to be the location and time of
the ball at its highest point, vertically downward direction to be the positive direction of x-axis, and give the signs of position, velocity and acceleration of the ball during its upward, and downward motion.
(d) To what height does the ball rise and after how long does the ball return to the player’s hands? (Take g = 9.8 m s-2 and neglect air resistance).
Solution:
(a) The ball is moving under the effect of gravity and therefore the direction of acceleration is vertically downward, in the direction of acceleration due to gravity.
(b) At the highest point of its motion velocity is zero and acceleration is equal to the acceleration due to gravity (9.8 m/s) in vertically downward direction.
(c) If we choose the highest point as x = 0 m and t0 = 0 s and vertically downward direction to be the positive direction of X- axis then,
During upward motion
Sign of position is negative.
Sign of velocity is negative.
Sign of acceleration is positive.
During downward motion Sign of position is positive.
Sign of velocity is positive.
Sign of acceleration is positive.
(d) Let the ball rises upto maximum height h.
Initial velocity of ball (u) = 29.4 m/s
g = 9.8 m/s
Final velocity at maximum height (υ) = 0
Using equation of motion, υ2 = u2 – 2gh
0 = (29.4)2 – 2 × 9.8 × h
or h = \(\frac{29.4 \times 29.4}{2 \times 9.8}\) = 44.1
Again using equation of motion, υ = u – gt
0 = 29.4 -9.8t
or t = \(\frac{29.4}{9.8}\) = 3s
Time of ascent is always equal to the time of descent.
Total time after which the ball returns to the player’s hand = 2t = 2 × 3 = 6s
Question 11.
Read each statement below carefully and state with reasons and examples, if it is true or false;
A particle in one-dimensional motion
(a) with zero speed at an instant may have non-zero acceleration at that instant’
(b) with zero speed may have non-zero velocity,
(c) with constant speed must have zero acceleration,
(d) with positive value of acceleration must be speeding up.
Answer:
(a) True
Explanation: When an object is thrown vertically up in the air, its speed becomes zero at maximum height. However, it has acceleration equal to the acceleration due to gravity (g) that acts in the downward direction at that point.
Speed is the magnitude of velocity. When speed is zero, the magnitude of velocity along with the velocity is zero.
(b) False
Explanation: A car moving on a straight highway with constant speed will have constant velocity. Since acceleration is defined as the rate of change of velocity, acceleration of the car is also zero.
(c) True
Explanation: This statement is false in the situation when acceleration is positive and velocity is negative at the instant time taken as origin. Then, for all the time before velocity becomes zero, there is slowing down of the particle. Such a case happens when a particle is projected upwards.
(d) False
Explanation: This statement is true when both velocity and acceleration are positive, at the instant time taken as origin. Such a case happens when a particle is moving with positive acceleration or falling vertically downwards from a height.
![]()
Question 12.
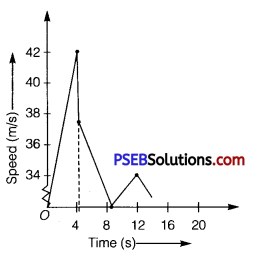
A ball is dropped from a height of 90 m on a floor. At each collision with the floor, the ball loses one tenth of its speed. Plot the speed-time graph of its motion between t = 0 to 12 s.
Solution:
Ball is dropped from a height, s = 90 m
Initial velocity of the ball, u = 0
Acceleration, a = g = 9.8 m/s2
Final velocity of the ball = υ
From second equation of motion, time (t) taken by the ball to hit the ground can be obtained as:
s = ut + \(\frac {1}{2}\)at2
90 = 0 + \(\frac {1}{2}\) × 9.8t2
t = \(\sqrt{18.38}\) = 4.29 s
From first equation of motion, final velocity is given as:
υ = u + at
= 0 + 9.8 × 4.29 = 42.04 m/s
Rebound velocity of the ball, ur = \(\frac {9}{10}\) υ = \(\frac {9}{10}\) × 42.04 = 37.84 m/s
Time (t) taken by the ball to reach maximum height is obtained with the help of first equation of motion as:
υ =ur + at’
0 = 37.84 + (-9.8) t’
t’ = \(\frac{-37.84}{-9.8}\) = 3.86s
Total time taken by the ball = t + t’ = 4.29 + 3.86 = 8.15 s
As the time of ascent is equal to the time of descent, the ball takes 3.86 s to strike back on the floor for the second time.
The velocity with which the ball rebounds from the floor
= \(\frac {9}{10}\) × 37.84 = 34.05m/s
Total time taken by the ball for second rebound = 8.15 + 3.86 = 12.01 s The speed-time graph of the ball is represented in the given figure as :
Question 13.
Explain clearly, with examples, the distinction between the following:
(a) magnitude of displacement (sometimes called distance) over an interval of time, and the total length of path covered by a particle over the same interval;
(b) magnitude of average velocity over an interval of time, and the average speed over the same interval. [Average speed of a particle over an interval of time is defined as the total path length divided by the time interval].
Show in both (a) and (h) that the second quantity is either greater than or equal to the first.
When is the equality sign true? [For simplicity, consider one-dimensional motion only].
Solution:
(a) The magnitude of displacement over an interval of time is the shortest distance (which is a straight line) between the initial and final positions of the particle.
The total path length of a particle is the actual path length covered by the particle in a given interval of time.
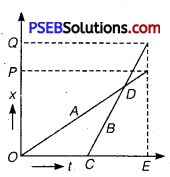
For example, suppose a particle moves from point A to point B and then, comes back to a point, C taking a total time t, as shown below. Then, the magnitude of displacement of the particle = AC.

Whereas, total path length = AB+BC
It is also important to note that the magnitude of displacement can never be greater than the total path length. However, in some cases, both quantities are equal to each other.
(b)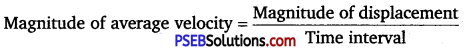
For the given particle,
Average velocity = \(\frac{A C}{t}\)
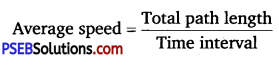
= \(\frac{A B+B C}{t}\)
Since (AB + BC)> AC, average speed is greater than the magnitude of average velocity. The two quantities will be equal if the particle continues to move along a straight line.
![]()
Question 14.
A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km h-1. Finding the market closed, he instantly turns and walks back home with a speed of 7.5 km h-1. What is the
(a) magnitude of average velocity, and
(b) average speed of the man over the interval of time? (i) 0 to 30 min, (ii) 0 to 50 min, (iii) 0 to 40 min?
[Note: You will appreciate from this exercise why it is better to define average speed as total path length divided by time, and not as magnitude of average velocity. You would not like to tell the tired man on his return home that his average speed was zero.]
Solution:
(a) A man return his home, therefore total displacement of the man = 0
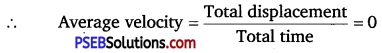
(b) Speed of man during motion from his home to the market υ1 = 5 km/h
Speed of man during from market his home υ2 =7.5 km/h
Distance between his home and market = 2.5 km
(i) Taking time interval 0 to 30 min.
Time taken by the man to reach the market from home,
t1 = \(\frac{2.5}{5}=\frac{1}{2}\) = h = 30 min
Hence, the man moves from his home to the market in t = 0 to 30 min.

(ii) Taking time interval 0 to 50 min.
Time taken by man in returning to his home from the market

(iii) Taking time interval 0 to 40 min.
Distance travelled in first 30 min = 2.5 km
Distance travelled by the man (from market to home) in the next 10 min
= 7.5 × \(\frac{10}{60}\) =1.25 km
Net displacement 2.5 -1.25 = 1.25 km
Total distance travelled = 2.5 +1.25 = 3.75 km
Average velocity = \(\frac{1.25}{\left(\frac{40}{60}\right)}\) = \(\frac{1.25 \times 3}{2}\) = 1.875 km/h
Average speed = \(\frac{3.75}{\left(\frac{40}{60}\right)}\) = 5.625 km/h
Question 15.
In questions 13 and 14, we have carefully distinguished between average speed and magnitude of average velocity. No such distinction is necessary when we consider instantaneous speed and magnitude of velocity. The instantaneous speed is always equal to the magnitude of instantaneous velocity. Why?
Solution:
Instantaneous velocity is given by the first derivative of distance with respect to time i. e.,
υm = \(\frac{d x}{d t}\)
Here, the time interval dt is so small that it is assumed that the particle does not change its direction of motion. As a result, both the total path length and magnitude of displacement become equal is this interval of time.
Therefore, instantaneous speed is always equal to instantaneous velocity.
![]()
Question 16.
Look at the graphs (a) to (d) carefully and state, with reasons, which of these cannot possibly represent one-dimensional motion of a particle.
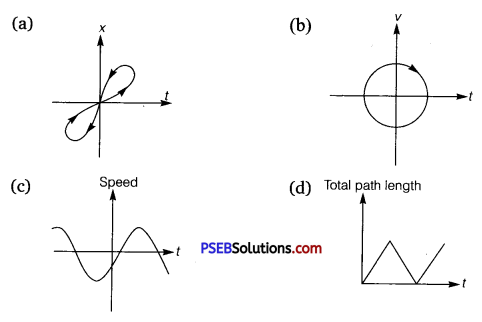
Solution:
(a) The given x – t graph, shown in (a), does not represent one-dimensional motion of the particle. This is because a particle cannot have two positions at the same instant of time.
(b) The given υ – t graph, shown in (b), does not represent one-dimensional motion of the particle. This is because a particle can never have two values of velocity at the same instant of time.
(c) The given υ – t graph, shown in (c), does not represent one-dimensional motion of the particle. This is because speed being a scalar quantity cannot be negative.
(d) The given total path length-time graph, shown in (d), does not represent one dimensional motion of the particle. This is because the total path length travelled by the particle cannot decrease with time.
Question 17.
Figure shows the x – t plot of one-dimensional motion of a particle. Is it correct to say from the graph that the particle’ moves in a straight line for t< 0 and on a parabolic path for t > 0 ? If not, suggest a suitable physical context for this graph.
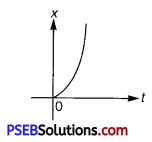
Solution:
No; The x – t graph of a particle moving in a straight line for t < 0 and on a parabolic path for t > 0 cannot be shown as the given graph. This is because, the given particle does not follow the trajectory of path followed by the particle as t = 0, x = 0. A physical situation that resembles the above graph is of a freely falling body held for sometime at a height.
![]()
Question 18.
A police van moving on a highway with a speed of 30 km h-1 fires a bullet at a theifs car speeding away in the same direction with a speed of 192 km h-1. If the muzzle speed of the bullet is 150 m s-1, with what speed does the bullet hit the thief’s car ?
(Note: Obtain that speed which is relevant for damaging the thief’s car).
Solution:
Speed of the police van, υp = 30 km/h = 8.33 m/s
Muzzle speed of the bullet, υb = 150 m/s
Speed of the thief s car, υt =192 km/h = 53.33 m/s
Since the bullet is fired from a moving van, its resultant speed can be obtained as:
= 150 +8.33 = 158.33 m/s
Since, both the vehicles are moving in the same direction, the velocity with which the bullet hits the thief s car can be obtained as:
υbt = υb – υt
= 158.33 – 53.33 = 105 m/s
Question 19.
Suggest a suitable physical situation for each of the following graphs:
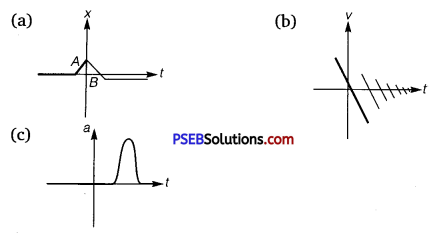
Solution:
(a) The given x – t graph shows that initially a body was at rest. Then, its velocity increases with time and attains an instantaneous constant value. The velocity then reduces to zero with an increase in time. Then, its velocity increases with time in the opposite direction and acquires a constant value. A similar physical situation arises when a football (initially kept at rest) is kicked and gets rebound from a rigid wall so that its speed gets reduced. Then, it passes from the player who has kicked it and ultimately gets stopped after sometime.
(b) In the given v-t graph, the sign of velocity changes and its magnitude decreases with a passage of time. A similar situation arises when a ball is dropped on the hard floor from a height. It strikes the floor with some velocity and upon rebound, its velocity decreases by a factor. This continues till the velocity of the ball eventually becomes zero.
(c) The given a – t graph reveals that initially the body is moving with a certain uniform velocity. Its acceleration increases for a short interval of time, which again drops to zero. This indicates that the body again starts moving with the same constant velocity. A similar physical situation arises when a hammer moving with a uniform velocity strikes a nail.
![]()
Question 20.
Figure gives the x – t plot of a particle executing one-dimensional simple harmonic motion. (You will learn about this motion in more detail in Chapter 14). Give the signs of position, velocity and acceleration variables of the particle at t = 0.3 s, 1.2 s,-1.2 s.
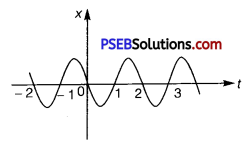
Solution:
For simple harmonic motion (SHM) of a particle, acceleration (a) is given by the relation:
a = -ω2x ……. (i)
where, ω → angular frequency
At t = 0.3 s
In this time interval, x is negative. Thus, the slope of the x – t plot will also be negative. Therefore, both position and velocity are negative. However, using equation (i), acceleration of the particle will be positive.
At t = 1.2s
In this time interval, x is positive. Thus, the slope of the x – t plot will also be positive. Therefore, both position and velocity are positive. However, using equation (i), acceleration of the particle comes to be negative.
t = -1.2s
In this time interval, x is negative. Thus, the slope of the x – t plot will also be negative. Since both x and t are negative, the velocity comes to be positive. From equation (i), it can be inferred that the acceleration of the particle will be positive.
Question 21.
Figure gives the x – t plot of a particle in one-dimensional motion. Three different equal intervals of time are shown. In which interval is the average speed greatest, and in which is it the least? Give the sign of average velocity for each interval.
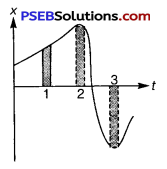
Solution:
The average speed of a particle shown in the x – t graph is obtained from the slope of the graph in a particular interval of time.
It is clear from the graph that the slope is maximum and minimum restively in intervals 3 and 2 respectively. Therefore, the average speed of the particle is the greatest in interval 3 and is the least in interval 2. The
sign of average velocity is positive in both intervals 1 and 2 as the slope is positive in these intervals. However, it is negative in interval 3 because the slope is negative in this interval.
![]()
Question 22.
Figure gives a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude? In which interval is the average speed greatest? Choosing the positive direction as the constant direction of motion, give the signs of v and a in the three intervals. What are the accelerations at the points A, B, C and D?
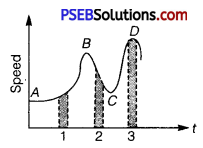
Solution:
Acceleration is given by the slope of the speed-time graph. In the given case, it is given by the slope of the speed-time graph within the,given interval of time.
Since the slope of the given speed-time graph is maximum in interval 2, average acceleration will be the greatest in this interval.
Height of the curve from the time-axis gives the average speed of the particle. It is clear that the height is the greatest in interval 3. Hence, . average speed of the particle is the greatest in interval 3.
In interval 1: The slope of the speed-time graph is positive. Hence, acceleration is positive. Similarly, the speed of the particle is positive in this interval.
In interval 2: The slope of the speed-time graph is negative. Hence, acceleration is negative in this interval. However, speed is positive because it is a scalar quantity.
In interval 3: The slope of the speed-time graph is zero. Hence, acceleration is zero in this interval. However, here the particle acquires some uniform speed. It is positive in this interval.
Points A, B, C and D are all parallel to the time-axis. Hence, the slope is zero at these points. Therefore, at points A, B, C and D, acceleration of the particle is zero.
Question 23.
A three-wheeler starts from rest, accelerates uniformly with 1 m s-2 on a straight road for 10 s, and then moves with uniform velocity. Plot the distance covered by the vehicle during the nth second (n = 1, 2, 3,…)versus n. What do you expect this plot to be during accelerated motion: a straight line or a parabola?
Solution:
Distance covered by a body in nth second is given by the relation
Dn = u + \(\frac{a}{2}\)(2n – 1) ……………(i)
where, u = Initial velocity, a = Acceleration, n = Time = 1, 2, 3, …. , n
In the given case,
u = 0 and a = 1 m/s2
.-. Dn = \(\frac {1}{2}\)(2n – 1) ……………… (ii)
This relation shows that
Dn ∝ n ………………(iii)
Now, substituting different values of n in equation (ii), we get the following table:
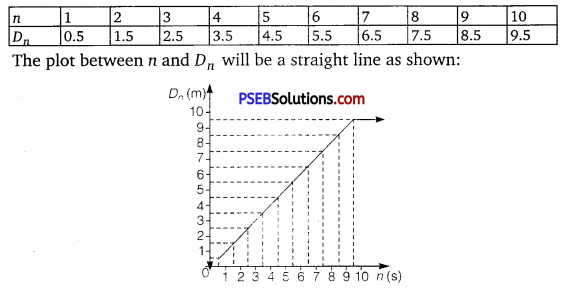
Since the three-wheeler acquires uniform velocity after 10 s, the line , will be parallel to the time-axis after n = 10 s.
![]()
Question 24.
A boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49 m/s. How much time does the ball take to return to his hands? If the lift starts moving up with a uniform speed of 5 m/s and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands?
Solution:
Initial velocity of the ball, u = 49 m/s
Acceleration, a = -g = – 9.8 m/s2
Case I:
When the lift was stationary, the boy throws the ball.
Taking upward motion of the ball,
Final velocity, υ of the ball becomes zero at the highest point.
From first equation of motion, time of ascent (t) is given as
υ = u + at
t = \(\frac{v-u}{a}\)
\(\frac{-49}{-9.8}\) = 5s
But, the time of ascent is equal to the time of descent.
Hence, the total time taken by the ball to return to the boy’s hand
= 5 + 5 = 10 s
Motion in a Straight Line 53
Case II:
The lift was moving up with a uniform velocity of 5 m/s. In this case, the relative velocity of the ball with respect to the boy remains the same i. e., 49 m/s. Therefore, in this case also, the ball will return back to the boy’s hand after 10 s.
Question 25.
On a long horizontally moving belt (see figure) a child runs to and fro with a speed 9 km h-1 (with respect to the belt) between his father and mother located 50 m apart on the moving belt. The belt moves with a speed of 4 km h-1. For an observer on a stationary platform outside, what is the
(a) speed of the child running in the direction of motion of the belt?
(b) speed of the child running opposite to the direction of motion of the belt?
(c) time taken by the child in (a) and (b) ?
Which of the answers alter if motion is viewed by one of the parents?
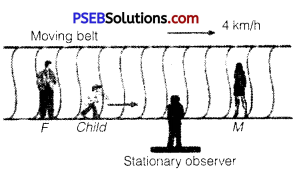
Solution:
Speed of the belt, υB = 4 km/h
Speed of the child, υC = 9 km/h
(a) Since the child is running in the same direction of the motion of the belt, his speed (as observed by the stationary observer) can be obtained as
υCB = υC + υB = 9 + 4 = 13 km/h
(b) Since the child is running in the direction opposite to the direction of the motion of the belt, his speed (as observed by the stationary observer) can be obtained as
υCB = υC + (-υB) = 9 – 4 = 5 km/h
(c) Distance between the child’s parents = 50 m
As both parents are standing on the moving belt, the speed of the child in either direction as observed by the parents will remain the same i. e.,
9 km/h = 9 x \(\frac{5}{18}\) m/s = 2.5 m/s.
18
Hence, the time taken by the child in case (a) and (b) is given by
\(\frac{\text { Distance }}{\text { Speed }}=\frac{50}{2.5}\) = 20 s.
If the motion is viewed by any one of the parents, answers obtained in (a) and (b) get altered. This is because the child and his parents are standing on the same belt and hence, are equally affected by the motion of the belt. Therefore, for both parents (irrespective of the direction of motion) the speed of the child remains the same i.e., 9 km/h.
For this reason, it can be concluded that the time taken by the child to reach any one of his parents remains unaltered.
![]()
Question 26.
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15 m/s and 30 m/s. Verify that the graph shown in figure correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect air resistance and assume that the stones do not rebound after hitting the ground. Take g = 10 m/s2. Give the equations for the linear and curved parts of the plot.
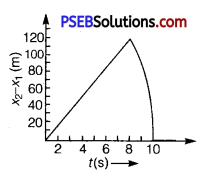
Solution:
For first stone:
Initial velocity, u1 =15 m/s
Acceleration, a = -g = -10 m/s2
Using the relation,
x1 = x0 + u1t + \(\frac {1}{2}\)at2
where, x0 = Height of the cliff = 200 m
x1 =200 + 15t – 5t2 ………………. (i)
When this stone hits the ground, x1 = 0
-5t2 +15t + 200 = 0
t2 – 3t – 40 =0
t2 – 8t + 5t – 40 = 0
t(t – 8) + 5(t – 8) = 0
(t – 8)(t + 5) = 0
t = 8 s or t = -5s
Since the stone was projected at time t = 0, the negative sign before time is meaningless.
∴ t = 8s
For second stone:
Initial velocity, u2 = 30 m/s
Acceleration, a = -g = -10 m/s2
Using the relation,
x2 = x0 + u2t + \(\frac {1}{2}\)at2
= 200 + 30t – 5t2 ……………. (ii)
At the moment when this stone hits the ground; x2 = 0
-5t2 + 30t + 200 = 0
t2 – 6t – 40 = 0
t2 -10t + 4t + 40 = 0
t(t – 10) + 4(t – 10) = 0
(t – 10)(t + 4) = 0
t = 10 s or t = -4 s
Here again, the negative sign before time is meaningless.
∴ t = 10 s
Subtracting eq. (i) from eq. (ii), we get
x2 – x1 = (200 +30t – 5t2) – (200 + 15t – 5t2)
x2 – x1 = 15t …………….. (iii)
Equation (iii) represents the linear path of both stones. Due to this linear relation between
(x2 – x1) and t, the path remains a straight line till 8 s.
Maximum separation between the two stones is at t = 8 s.
(x2 – x1] )max = 15 × 8 = 120 m
This is in accordance with the given graph.
After 8 s, only second stone is in motion whose variation with time is given by the quadratic equation :
x2 – x1 = 200 + 30t – 5t2
Hence, the equation of linear and curved path is given by
x2 – x1 = 15t (Linear path)
x2 – x1 = 200 + 30t – 5t2 (Curved path)
Question 27.
The speed-time graph of a particle moving along a fixed direction is shown in figure given below. Obtain the distance traversed by the particle between (a) t = 0 s to 10 s, (b) t = 2 s to 6 s.
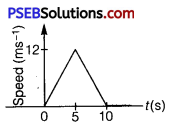
What is the average speed of the particle over the intervals in (a) and (b)?
Solution:
(a) Distance travelled by the particle = Area under the given graph
= \(\frac{1}{2}\) × (10 – 0) × (12 – 0) = 60 m
Average speed = \(\frac{\text { Distance }}{\text { Time }}\) = \(\frac{60}{10}\) = 6 m/s
(b) Let s1 and s2 be the distances covered by the particle between time t = 2 s to 5 s and t = 5 s to 6 s respectively.
Total distance (s) covered by the particle in time t = 2 s to 6 s
S = S1 + s2 ……………… (i)
For distance S1:
Let u’ be the velocity of the particle after 2 s and a’ be the acceleration of the particle in t = 0 to t = 5 s.
Since the particle undergoes uniform acceleration in the interval t = 0 to t = 5 s, from first equation of motion, acceleration can be obtained as:
υ = u + at
Where, υ = Final velocity of the particle
12. = 0 + a’ × 5
a’ = \(\frac{12}{5}\) = 2.4 m/s2 .
Again, from first equation of motion, we have
υ = u + at
= 0 + 2.4 × 2 = 4.8 m/s
Distance travelled by the particle between time 2 s and 5 s i. e., in 3 s
S1 = u’t + \(\frac{1}{2}\) a’t2
= 4.8 × 3 + \(\frac{1}{2}\) × 2.4 × (3)2
= 25.2 m ……………… (ii)
For distance S2:
Let a” be the acceleration of the particle between time t = 5 s and t = 10s.
From first equation of motion,
υ = u + at (where υ = 0 as the particle finally comes to rest)
0 = 12 + a” × 5
a” = \(\frac{-12}{5}\)
= -2.4 m/s2
Distance travelled by the particle in Is (i. e., between t = 5 s and t = 6 s)
S2 = u”t + \(\frac{1}{2}\) at2
= 12 × a + \(\frac{1}{2}\)(-2.4) × (1)2
= 12 – 1.2 = 10.8 m ……………… (iii)
From equations (i), (ii), and (iii), we get
S = 25.2 + 10.8 = 36 m
∴ Average speed = \(\frac{36}{4}\) = 9 m/s
![]()
Question 28.
The velocity-time graph of a particle in one-dimensional motion is shown in figure.
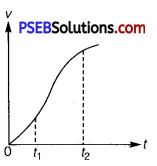
Which of the following formulae are correct for describing the motion of the particle over the time-interval t1 to t2 ?
(a) x(t2) = x(t1) + υ(t1)(t2 – t1) + \(\frac {1}{2}\) a(t2 – t1)2
(b) υ(t2) = υ(t1)+a(t2 – t1)
(c) Average = [x(t2) – x(t1)] /(t2 – t1)
(d) Average = [(t2 ) – υ(t1)] / (t2 – t1)
(e) x(t2) = x(t1) + υAverage (t2 – t1) + (\(\frac {1}{2}\)) aAverage (t2 – t1)2
(f) x (tsub>2) – x (tsub>1) = area under the υ – t curve bounded by the t-axis and the dotted line shown.
Solution:
The slope of the given graph over the time interval tsub>1 to tsub>2 is not constant and is not uniform. It means acceleration is not constant and is not uniform, therefore, relation (a), (b) and (e) are not correct which is for uniform accelerated motion, but relations (c), (d) and (f) are correct, because these relations are true for both uniform or non-uniform accelerated motion.