Punjab State Board PSEB 11th Class Physics Important Questions Chapter 3 Motion in a Straight Line Important Questions and Answers.
PSEB 11th Class Physics Important Questions Chapter 3 Motion in a Straight Line
Very short answer type questions
Question 1.
What is the condition for an object to be considered as a point object?
Answer:
An object can be considered as a point object if the distance travelled by it is very large than its size.
Question 2.
For which condition, the distance and the magnitude of displacement of an object have the same values?
Answer:
The distance and the magnitude of displacement of an object have the same values, when the body is moving along a straight line path in a fixed direction.
![]()
Question 3.
Speed of a particle cannot be negative. Why?
Answer:
Speed is the distance travelled in unit time and distance cannot be negative.
Question 4.
Is it possible that a body could have constant speed but varying velocity?
Answer:
Yes, a body could have constant speed but varying velocity if only the direction of motion changes.
Question 5.
For which condition, the average velocity will be equal to the instantaneous velocity?
Answer:
When a body moves with a uniform velocity, then
υav = υinst
Question 6.
Give an example of uniformly accelerated linear motion.
Answer:
Motion of a body under gravity.
Question 7.
Give example of motion where x > 0, υ < 0, a > 0 at a particular instant. (NCERT Exemplar)
Solution:
Let the motion is represented by
x(t) = A + Be-γt ……………. (i)
Let A>B and γ > 0
Now velocity x(t) = \(\frac{d x}{d t}\) = -Bγe-γt
Acceleration a(t) = \(\frac{d x}{d t}\) = Bγ2e-γt
Suppose we are considering any instant t, then from Eq. (i) we can say that
x(t)>0,υ(t)< 0 and a>0
![]()
Short answer type questions
Question 1.
Explain how an object could have zero average velocity but non-zero average speed?
Solution:
υ = \(=\frac{\text { Net displacement }}{\text { Total time taken }}\)
and average speed,

If an object moves along a straight line starting from origin and then returns back to origin.
Average velocity = 0
and Average speed = \(\frac{2 s}{t}\)
Question 2.
If the displacement of a body is zero, is distance necessarily zero? Answer with one example.
Answer:
No, because the distance covered by an object is the path length of the path covered by the object. The displacement of an object is given by the change in position between the initial position and final position.
Question 3.
Is earth inertial or non-inertial frame of reference?
Answer:
Since, earth revolves around the sun and also spins about its own axis, so it is an accelerated frame of reference. Hence, earth is a non-inertial frame of reference.
However, if we do not take large scale motion such as wind and ocean currents into consideration, we can say that approximation the earth is an inertial frame.
![]()
Question 4.
A person travels along a straight road for the first half with a velocity υ 1 and the second half with velocity υ 2. What is the mean velocity of the person?
Solution:
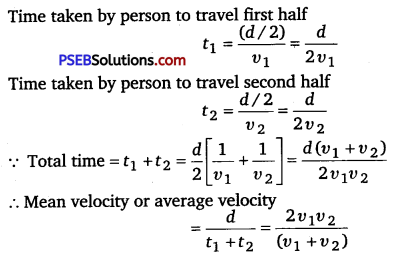
Question 5.
The displacement of a particle is given by at2 What is dependency of acceleration on time?
Solution:
Let x be the displacement. Then, x = at2
∴ Velocity of the object, υ = \(\frac{d x}{d t}\) = 2 at
Acceleration of the object, a = \(\frac{d v}{d t}\) = 2 a
It means that a is constant.
Question 6.
What are uses of a velocity-time graph?
Solution:
From a velocity-time graph, we can find out
(i) The velocity of a body at any instant.
(ii) The acceleration of the body and
(iii) The net displacement of the body in a given time-interval.
![]()
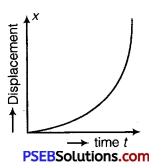
Question 7.
Draw displacement-time graph for a uniformly accelerated motion. What is its shape?
Solution:
Displacement-time graph for a uniformly accelerated motion has been shown in adjoining fig. The graph is parabolic in shape.
Question 8.
The distance travelled by a body is proportional to the square of time. What type of motion this body has?
Solution:
Let x be the distance travelled in time t. Then,
x ∝ t2 [given]
x = kt2 [here, k = constant of proportionality]
We know that velocity is given
υ = \(\frac{d x}{d t}\) = 2kt
and acceleration is given by
a = \(\frac{d v}{d t}\) = 2 k [constant]
Thus, the body has uniform accelerated motion.
Long answer type questions
Question 1.
It is a common observation that rain clouds can be at about a kilometre altitude above the ground.
(i) If a rain drop falls from such a height freely under gravity, what will be its speed? Also, calculate in km/h (g = 10m/s2).
(ii) A typical rain drop is about 4 mm diameter. Momentum is mass × speed in magnitude. Estimate its momentum when it hits ground.
(iii) Estimate time required to flatten the drop.
(iv) Rate of change of momentum is force. Estimate how much force such a drop would exert on you?
(v) Estimate the order of magnitude force on umbrella. Typical lateral separation between two rain drops is 5 cm.
(Assume that umbrella is circular and has a diameter of 1 m and cloth is not pierced through it.) (NCERT Exemplar)
Solution:
Here, height (h) = 1 km = 1000 m, g = 10 m/2
(i) Velocity attained by the rain drop in freely falling through a height h.
υ = \(\sqrt{2 g h}=\sqrt{2 \times 10 \times 1000}\)
= 100√2 m/s
= 100√2 \(\frac{60 \times 60}{1000}\) km/h
= 360√2 km/h ≈ 510 km/h
(ii) Diameter of the drop (d) = 2 r = 4 mm
∴ Radius of the drop (r) = 2 mm = 2 × 10-3 m
Mass of a rain drop (m) = V × ρ
= \(\frac{4}{3}\) πr3ρ = \(\frac{4}{3} \times \frac{22}{7}\) x (2 × 10-3)3 × 103
[ v density of water = 103 kg/m3 ]
≈ 3.4 × 10-5 kg
Momentum of the rain drop (p) = mυ
= 3.4 × 10-5 × 100√2
≈ 4.7 × 10-3 kg-m/s
(iii) Time required to flatten the drop = time taken by the drop to travel the distance equal to the diameter of the drop near the ground
t = \(\frac{d}{v} \times \frac{4 \times 10^{-3}}{100 \sqrt{2}}\) = 0.028 × 10-3 s
= 2.8 × 10-5 s
(iv) Force exerted by a rain drop
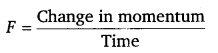
= \(\frac{p-0}{t}=\frac{4.7 \times 10^{-3}}{2.8 \times 10^{-5}}\) ≈ 168 N
(v) Radius of the umbrella (R) = \(\frac{1}{2}\) m
∴ Area of the umbrella (A) = πR2 = \(\frac{22}{7}\) x (\(\frac{1}{2}\))2 = \(\frac{22}{28}=\frac{11}{14}\) ≈ 0.8M2
Number of drops striking the umbrella
simultaneously with average separation of 5 cm or 5 × 10-2 m
= \(\frac{0.8}{\left(5 \times 10^{-2}\right)^{2}}\) = 320
∴ Net force exerted on umbrella = 320 × 168 = 53760 N
![]()
Question 2.
If a body moving with uniform acceleration in straight line describes successive equal distance in time interval t1, t2 and t3, then show that
\(\frac{1}{t_{1}}-\frac{1}{t_{2}}+\frac{1}{t_{3}}=\frac{3}{t_{1}+t_{2}+t_{3}}\)
Solution:
As shown in figure, let three successive equal distances be represented by AB, BC and CD
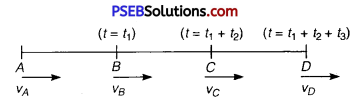
Let each distance berm. Let υA,υB,υC and υD be the velocities at points A, B, C and D respectively.
Average velocity between A and B = \(\frac{v_{A}+v_{B}}{2}\)
