Punjab State Board PSEB 11th Class Physics Book Solutions Chapter 13 Kinetic Theory Textbook Exercise Questions and Answers.
PSEB Solutions for Class 11 Physics Chapter 13 Kinetic Theory
PSEB 11th Class Physics Guide Kinetic Theory Textbook Questions and Answers
Question 1.
Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at SIP. Take the diameter of an oxygen molecule to be 3Å.
Solution:
Diameter of an oxygen molecule, d = 3Å
Radius, r = \(\frac{d}{2}=\frac{3}{2}\) =1.5 Å = 1.5 x 10-8 cm
Actual volume occupied by 1 mole of oxygen gas at STP = 22400 cm3
Molecular volume of oxygen gas, V = \(\frac{4}{3}\) πr3N
where, N is Avogadro’s number = 6.023 x 1023 molecules/mole
∴ V = \(\frac{4}{3}\) x 3.14 x (1.5 x 10-8)3 x 6.023 x 1023 = 8.51cm3
Ratio of the molecular volume to the actual volume of oxygen = \(\frac{8.51}{22400}\) = 3.8 x 10-4 ≈ 4 x 10-4
Question 2.
Molar volume is the volume occupied by 1 mol of any (ideal) gas at standard temperature and pressure (STP: 1 atmospheric pressure, 0°C). Show that it is 22.4 litres.
Solution:
The ideal gas equation relating pressure (P), volume (V), and absolute temperature (T) is given as PV = nRT
where, R is the universal gas constant = 8.314 J mol-1 K-1
n = Number of moles = 1
T = Standard temperature = 273 K
P = Standard pressure = 1 atm = 1.013 x 105 Nm-2
∴ V = \(\frac{n R T}{P}\)

Hence, the molar volume of a gas at STP is 22.4 litres.
![]()
Question 3.
Given figure shows plot of PV IT versus P for 1.00 x 10-3 kg of oxygen gas at two different temperatures.
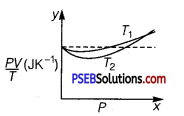
(a) What does the dotted plot signify?
(b) Which is true: T1 > T2 or T1 <T2?
(c) What is the value of PVIT where the curves meet on the y-axis?
(d) If we obtained similar plots for 1.00 x 103 kg of hydrogen, would we get the same value of PV/T at the point where the curves meet on the y-axis? If not, what mass of hydrogen yields the same value of PV/T (for low-pressure high-temperature region of the plot)? (Molecular mass of H2=2.02u,of O2 =32.0 u, R= 8.31Jmol-1K-1)
Solution:
(a) The dotted plot in the graph signifies the ideal behaviour of the gas, i. e., the ratio \(\frac{\bar{P} V}{T}\) is equal. μR(μ is the number of moles and R is the universal gas constant) is a constant quantity. It is not dependent on the pressure of the gas.
(b) The dotted plotmn the given graph represents an ideal gas. The curve of the gas at temperatureT1 is closer to the dotted plot than the curve of the gas at temperature T2. A real gàs approaches the behaviour of an ideal gas when its temperature increases. Therefore, T1 > T2 is true for the given plot.
(c) The value of the ratio PV/T, where the two curves meet, is μ.R. This is because the ideal gas equation is given as:
PV=μRT
\(\frac{P V}{T}\) = μR
where P is the pressure
T is the temperature
V is the volume
μ is the number of moles
R is the unìversal constant
Molecular mass of oxygen = 32.0 g
Mass of oxygen =1 x 10-3 kg = 1 g
R =8.314J mole-1K-1
∴ \(\frac{P V}{T}=\frac{1}{32} \times 8.314\) =0.26JK-1
Therefore, the value of the ratio PV/T, where the curves meet on the y-axis, is 0.26JK-1.
(d) If we obtain similar plots for 1.00 x 10-3 kg of hydrogen, then we will not get the same value of PV/T at the point where the curves meet the y-axis. This is because the molecular mass of hydrogen (2.02 u) is different from that of oxygen (32.0 u).
We have \(\frac{P V}{T}\) = 0.26JK-1
R = 8.314 J mole-1 K-1
Molecular mass (M) of H2 =2.02 u PV
\(\frac{P V}{T}\) = μR at constant temperature
where, μ = \(\frac{m}{M}\) , m = Mass of H2
∴ m = \(\frac{P V}{T} \times \frac{M}{R}=\frac{0.26 \times 2.02}{8.314}\)
= 6.3 x 10-2 g = 6.3 x 10-5 kg
Hence, 6.3 x 10-5 kg of H2 will yield the same value of PV/T.
Question 4.
An oxygen cylinder of volume 30 litres has an initial gauge pressure of 15 atm and a temperature of 27°C. After some oxygen is withdrawn from the cylinder, the gauge pressure drops to 11 atm and its temperature drops to 17°C. Estimate the mass of oxygen taken out of the cylinder (R = 8.31 J mol-1 K -1, molecular mass of O 2 =32 u).
Solution:
Absolute pressure, p1 = (15 + 1) atm
[∵ Absolute pressure = Gauge pressure +1 atm] = 16 x 1.013 x 105 Pa
V1 = 30 L = 30 x 10-3 m3
T1 = 273.15 + 27 = 300.15K
Using ideal gas equation,
pV = nRT

Hence, moles removed = 19.48-15.12 = 4.36
Mass removed = 4.36 x 32 g = 139.52 g = 0.1396 kg.
Therefore, 0.14 kg of oxygen is taken out of the cylinder.
Question 5.
An air bubble of volume 1.0 cm3 rises from the bottom of a lake 40 cm deep at a temperature of 12°C. To what volume does it grow when it reaches the surface, which is at a temperature of 35°C?
Solution:
Volume of the air bubble, = 1.0 cm3 = 1.0 x 10-6 m3
Bubble rises to height, d = 40 m
Temperature at a depth of 40 m, T1 = 12°C = 273 + 12 = 285K
Temperature at the surface of the lake, T2 = 35°C = 273 + 35 = 308K
The pressure on the surface of the lake,
P2 =1 atm = 1 x 1.013 x 105Pa
The pressure at the depth of 40 m,
P1 = 1 atm + dρg
where, ρ is the density of water = 103 kg/m3
g is the acceleration due to gravity = 9.8 m/s2
∴ P1 = 1.013 X105+40 X 103 X 9.8 = 493300 Pa
We have \(\frac{P_{1} V_{1}}{T_{1}}=\frac{P_{2} V_{2}}{T_{2}}\)
where, V2 is the volume of the air bubble when it reaches the surface
V2= \(\frac{P_{1} V_{1} T_{2}}{T_{1} P_{2}}=\frac{(493300)\left(1.0 \times 10^{-6}\right) 308}{285 \times 1.013 \times 10^{5}}\)
= 5.263 x 10-6 m3 or 5.263 cm3
Therefore, when the air bubble reaches the surface, its volume becomes 5.263 cm3.
![]()
Question 6.
Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity 25.0 m3 at a temperature of 27°C and 1 atm pressure.
Solution:
Volume of the room, V = 25.0 m3
Temperature of the room, T = 27°C = 273 + 27°C = 300 K
Pressure in the room, P = 1 atm = 1 x 1.013 x 105 Pa
The ideal gas equation relating pressure (?), Volume (V), and absolute temperature (T) can be written as PV = kBNT
where,
KB is Boltzmann constant = 1.38 x 10 -23 m2 kg s-2 K-1
N is the number of air molecules in the room
∴ N = \(\frac{P V}{k_{B} T}\)
= \(\frac{1.013 \times 10^{5} \times 25}{1.38 \times 10^{-23} \times 300}\) = 6.11 x 1026 molecules
Therefore, the total number of air molecules in the given room is 6.11 x 1026.
Question 7.
Estimate the average thermal energy of a helium atom at (i) room temperature (27°C),
(ii) the temperature on the surface of the Sun (6000K),
(iii) the temperature of 10 million Kelvin (the typical core temperature in the case of a star).
Solution:
(i) At room temperature, T = 27°C = 273 +27 = 300 K
Average thermal energy, E = \(\frac{3}{2}\)kT
where k is Boltzmann constant = 1.38 x 10-23 m2 kg s-2 K-1
∴ E = \(\frac{3}{2}\) x 1.38 x 10-23 x 300 = 6.21 x 10-21 J
Hence, the average thermal energy of a helium atom at room temperature (27°C) is 6.21 x 10-23 J
(ii) On the surface of the Sun, T = 6000 K
Average thermal energy = \(\frac{3}{2}\) kT = \(\frac{3}{2}\) x 1.38 x 10-23 x 6000
= 1.241 x 10-19J
Hence, the average thermal energy of a helium atom on the surface of the Sun is 1.241 x 10-19J.
(iii) At temperature, T =107 K
Average thermal energy = \(\frac{3}{2}\)kT = \(\frac{3}{2}\) x 1.38 x 10-23 x 107
= 2.07 x 10-16 J
Hence, the average thermal energy of a helium atom at the core of a star is 2.07 x 10-16 J.
Question 8.
Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (polyatomic). Do the vessels contain equal number of respective molecules? Is the root mean square speed of molecules the same in the three cases? If not, in which case is υrms the largest?
Solution:
Yes. All contain the same number of the respective molecules.
No. The root means square speed of neon is the largest.
Since the three vessels have the same capacity, they have the same volume.
Hence, each gas has the same pressure, volume, and temperature. According to Avogadro’s law, the three vessels will contain an equal number of the respective molecules. This number is equal to Avogadro’s number, N = 6.023 x 1023.
The root mean square speed (υrms)oi a gas of mass m, and temperature T, is given by the relation: υrms = \(\sqrt{\frac{3 k T}{m}} \)
where k is Boltzmann constant
For the given gases, k and T are constants.
Hence, υrms depends only on the mass of the atoms, i.e., υrms ∝ \(\sqrt{\frac{1}{m}}\)
Therefore, the root mean square speed of the molecules in the three cases is not the same.
Among neon, chlorine, and uranium hexafluoride, the mass of neon is the smallest.
Hence, neon has the largest root mean square speed among the given gases.
![]()
Question 9.
At what temperature is the root mean square speed of an atom in an argon gas cylinder equal to the rms speed of a helium gas atom at -20°C? (atomic mass of Ar = 39.9 u, of He = 4.0u).
Solution:
Temperature of the helium atom, THe = -20°C = 273 – 20 = 253K
Atomic mass of argon, MAr= 39.9 u
Atomic mass of helium, MHe = 4.0 u
Let, (υrms)be the rms speed of argon.
Let (υrms )He be the rms speed of helium.
The rms speed of argon is given by
(υrms)Ar = \(\sqrt{\frac{3 R T_{\mathrm{Ar}}}{M_{\mathrm{Ar}}}}\) …………………………….. (i)
where, R is the universal gas constant
TAr is temperature of argon gas
The rms speed of helium is given by:
(υrms)He = \(\sqrt{\frac{3 R T_{\mathrm{He}}}{M_{\mathrm{He}}}}\) …………………………. (ii)
It is given that: (υrms)Ar = (υrms)He

Therefore, the temperature of the argon atom is 2.52 x 103 K.
Question 10.
Estimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at 2.0 atm and temperature 17°C. Take the radius of a nitrogen molecule to be roughly 1.0 Å. Compare the collision time with the time the molecule moves freely between two successive collisions (Molecular mass of N2 = 28.0u).
Solution:
Pressure inside the cylinder containing nitrogen,
P =2.0atm = 2 x 1.013 x 105 Pa = 2.026 x 105 Pa
Temperature inside the cylinder, T = 17°C = 273 +17 = 290 K
Radius of a nitrogen molecule, r = 1.0 Å = 1 x 10,sup>-10 m
Diameter, d = 2 x 1 x 10-10 = 2 x 10-10 m
Molecular mass of nitrogen, M = 28.0 g = 28 x 10-3 kg
The root mean square speed of nitrogen is given by the relation
υrms = \(\sqrt{\frac{3 R T}{M}}\)
where, R is the universal gas constant = 8.314 J mole -1 K-1
∴ υrms = \(\sqrt{\frac{3 \times 8.314 \times 290}{28 \times 10^{-3}}}\) = 508.26m/s
The mean free path (l) is given by the relation:
l = \(\frac{k T}{\sqrt{2} \times d^{2} \times P}\)
where,
k is the Boltzmann constant = 1.38 x 10-23 kgm2s-2 K-1

Time is taken between successive collisions,

Hence, the time taken between successive collisions is 500 times the time taken for a collision.
Additional Exercises
Question 11.
A metre long narrow bore held horizontally (and closed at one end) contains a 76 cm long mercury thread, which traps a 15 cm column of air. What happens if the tube is held vertically with the open end at the bottom?
Solution:
Length of the narrow bore, L=1 m = 100 cm
Length of the mercury thread, l = 76 cm
Length of the air column between mercury and the closed-end, la = 15cm
Since the bore is held vertically in air with the open end at the bottom, the mercury length that occupies the air space is 100-(76+15) = 9 cm
Hence, the total length of the air column = 15 + 9 = 24 cm
Let h cm of mercury flow out as a result of atmospheric pressure.
∴ Length of the air column in the bore = 24 + h cm
and, length of the mercury column = 76 – h cm
Initial pressure, P1 = 76 cm of mercury
Initial volume,V1 =15 cm3
Final pressure, P2 = 76 – (76 – h) = h cm of mercury
Final volume, V2 = (24 + h) cm3
The temperature remains constant throughout the process.

Height cannot be negative. Hence, 23.8cm of mercury will flow out from the bore and 52.2 cm of mercury will remain in it. The length of the air column will be 24 +23.8 = 47.8 cm.
Question 12.
From a certain apparatus, the diffusion rate of hydrogen has an average value of 28.7cm3s-1. The diffusion of another gas under the same conditions is measured to have an average rate of 7.2 cm3 s-1. Identify the gas. [Hint: Use Graham’s law of diffusion: R1/R2 =(M2/M1)1/2, where R1, R2 are diffusion rates of gases 1 and 2, and M1 and M2 their respective molecular masses. The law is a simple consequence of the kinetic theory.]
Solution:
Rate of diffusion of hydrogen, R1 = 28.7cm3 s-1
Rate of diffusion of another gas, R2 = 7.2 cm3 s-1
According to Graham’s Law of diffusion, we have
\(\frac{R_{1}}{R_{2}}=\sqrt{\frac{M_{2}}{M_{1}}}\)
where, M1 is the molecular mass of hydrogen 2.020 g
M2 is the molecular mass of the unknown gas
∴ M2 = M1\(\left(\frac{R_{1}}{R_{2}}\right)^{2}\) = 2.01 \(\left(\frac{28.7}{7.2}\right)^{2}\) = 32.09 g
32g is the molecular mass of oxygen. Hence, the unknown gas is oxygen.
![]()
Question 13.
A gas in equilibrium has uniform density and pressure throughout its volume. This is strictly true only if there are no external influences. A gas column under gravity, for example, does not have a uniform density (and pressure). As you might expect, its density decreases with height. The precise dependence is given by the so-called law of atmospheres n2 =n1 exp[-mg(h2 -h1) / kB T]
where n2,n1 refer to number density at heights h2 and h1 respectively.
Use this relation to derive the equation for sedimentation equilibrium of a suspension in a liquid column: n2 = n1 exp [-mg NA (ρ -ρ’)(h2 -h1) / (ρRT)]
where ρ is the density of the suspended particle, and ρ’ that of surrounding medium. [NA is Avogadro’s number and R the universal gas constant.] [Hint: Use Archimedes principle to find the apparent weight of the suspended particle.]
Solution:
According to the law of atmospheres, we have
n2=n1 exp [-mg(h2 – h1])/kBT] ………………………………. (i)
where, n1 is the number density at height h1, and n2 is the number density at height h2
mg is the weight of the particle suspended in the gas column
Density of the medium = ρ’
Density of the suspended particle = ρ
Mass of one suspended particle = m’
Mass of the medium displaced = m
Volume of a suspended particle = V
According to Archimedes’ principle for a particle suspended in a liquid column, the effective weight of the suspended particle is given as
Weight of the medium displaced – Weight of the suspended particle
= mg – m’g
= mg – Vρ’g = mg – \(\left(\frac{m}{\rho}\right)\) ρ’g
= mg – \(\left(1-\frac{\rho^{\prime}}{\rho}\right)\) …………………………….. (ii)
Gas constant, R = kBN
kB = \(\frac{R}{N}\) …………………………………….. (iii)
Substituting equation (ii) in place of mg in equation (i) and then using equation (iii), we get

Question 14.
Given below are densities of some solids and liquids. Give rough estimates of the size of their atoms:
| Substance | Atomic Mass (u) | Density (103 kg m-3) |
| Carbon (diamond) | 12.01 | 2.22 |
| Gold | 197.00 | 19.32 |
| Nitrogen (liquid) | 14.01 | 1.00 |
| Lithium | 6.94 | 0.53 |
| Fluorine (liquid) | 19.00 | 1.14 |
[Hint: Assume the atoms to be ‘tightly packed’ in a solid or liquid phase, and use the known value of Avogadro’s number. You should, however, not take the actual numbers you obtain for various atomic sizes too literally. Because of the crudeness of the tight packing approximation, the results only indicate that atomic sizes are in the range of a few Å].
Atomic mass of a substance = M
Density of the substance = ρ
Avogadro’s number = N = 6.023 x 1023
Volume of each atom = \(\frac{4}{3} \pi r^{3}\)
Volume of N number of molecules = \(\frac{4}{3} \pi r^{3}\) N …………………………….. (i)
Volume of one mole of a substance = \(\frac{M}{\rho}\) ………………………………….. (ii)

For gold
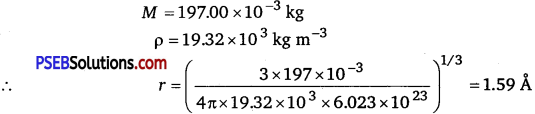
Hence, the radius of a gold atom is 1.59 Å
For liquid nitrogen
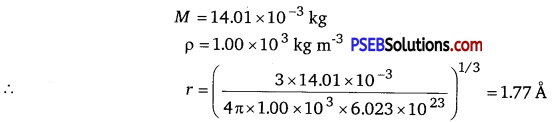
Hence, the radius of a liquid nitrogen atom is 1.77 Å
For lithium

Hence, the radius of a lithium atom is 1.73 Å.
For liquid fluorine

Hence, the radius of liquid fluorine atom is 1.88 Å.