Punjab State Board PSEB 11th Class Physics Important Questions Chapter 13 Kinetic Theory Important Questions and Answers.
PSEB 11th Class Physics Important Questions Chapter 13 Kinetic Theory
Very Short Answer Type Questions
Question 1.
Under what conditions, real gases behave as an ideal gas?
Answer:
At low pressure and high temperature, real gases behave as an ideal gas.
Question 2.
When air is pumped into a cycle tyre, the volume and pressure of the air in the tyre, both are increased. What about Boyle’s law in this case? (NCERT Exemplar]
Answer:
When air is pumped, more molecules are pumped in Boyle’s law is stated for situation where number of molecules remain constant.
Question 3.
What is the minimum possible temperature on the basis of Charles’ law?
Answer:
The minimum possible temperature on the basis of Charles’ law is -273.15°C.
Question 4.
If a vehicle runs on the road for a long time, then the air pressure in the tyres increases. Explain.
Answer:
Due to the presence of friction between the road and tyres, the tyres get heated as a result of which temperature of air inside the tyre increases and hence pressure in tyre also increases.
![]()
Question 5.
What is the number of degree of freedom of a bee flying in a room?
Answer:
Three, because bee is free to move along x-direction or y-direction or z-direction.
Question 6.
How degree of freedom of a gas molecule is related with the temperature?
Answer:
Degree of freedom will increase when temperature is very high because at high temperature, vibrational motion of the gas will contribute to the kinetic energy. Hence, there is an additional kinetic energy associated with the gas, as a result of increased degree of freedom.
Question 7.
Is molar specific heat of a solid a constant quantity?
Answer:
Yes, the molar specific heat of a solid is a constant quantity and its value is 3 cal/mol-K.
Question 8.
Name experimental evidence in support of random motion of gas molecules.
Answer:
Brownian motion and diffusion of gases provide experimental evidence in support of random motion of gas molecules.
Question 9.
What is mean free path of a gas?
Answer:
The average distance travelled by a molecule between two successive collisions is known as mean free path of the molecule.
![]()
Short Answer Type Questions
Question 1.
State ideal gas equation. Draw a graph to check whether a real gas obeys this equation. What is the conclusion drawn?
Answer:
According to the ideal gas equation, we have PV = µRT
Thus, according to this equation \(\frac{P V}{\mu T}\) = R i.e., value of \( \frac{P V}{\mu T}\) must be a constant having a value 8.31 J mol-1 K-1. Experimentally value of \(\frac{P V}{\mu T}\) for real gases was calculated by altering the pressure of gas at different temperatures. The graphs obtained have been shown in the figure.
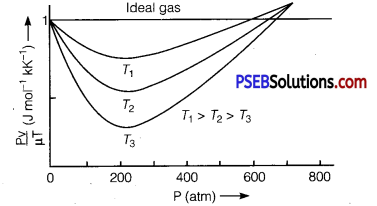
Here, for the purpose of comparison, graph for an ideal gas has also been drawn, which is a straight line parallel to pressure axis. From the graph it is clear that behaviour of real gases differ from an ideal gas. However, at high temperatures and low pressures behaviour is nearly same as that of an ideal gas.
Question 2.
Explain, why
(i) there is no atmosphere on Moon.
(ii) there is fall in temperature with altitude. (NCERT Exemplar)
Answer:
(i) The Moon has small gravitational force and hence the escape velocity is small. As the Moon is in the proximity of the Earth as seen from the Sun, the Moon has the same amount of heat per unit area as that of the Earth. The air molecules have large range of speeds.
Even though the rms speed of the air molecules is smaller than escape velocity on the Moon, a significant number of molecules have speed greater than escape velocity and they escape. Now, rest of the molecules arrange the speed distribution for the equilibrium temperature. Again, a significant number of molecules escape as their speeds exceed escape speed. Hence, over a long time, the Moon has lost most of its atmosphere.
(ii) As the molecules move higher, their potential energy increases and hence kinetic energy decreases and temperature reduces. At greater height, more volume is available and gas expands. Hence, some cooling takes place.
Question 3.
Two perfect gases at absolute temperatures T1 and T2 are mixed. There is no loss of energy. Find the temperature of the mixture if the masses of the molecules are m1 and m2 and the number of the molecules in the gases are n1 and n2 respectively.
Solution:
According to kinetic theory, the average kinetic energy per molecule of a
gas = \(\frac{3}{2} \) KBT
Before mixing the two gases,the average K.E. of all the molecules of two gases
= \(\frac{3}{2} \)KBn1T1 + \(\frac{3}{2} \)KBn1T2
After mixing, the average K.E. of both the gases
= \(\frac{3}{2} \)kB (n1 +n2)T
where, T is the temperature of mixture.
Since there is no loss of energy,
Hence, \(\frac{3}{2} \)kB (n1 +n2)T = \(\frac{3}{2} k_{B} n_{1} T_{1}+\frac{3}{2} k_{B} n_{2} T_{2}\)
or T = \(\frac{n_{1} T_{1}+n_{2} T_{2}}{\left(n_{1}+n_{2}\right)}\).
![]()
Question 4.
At room temperature, diatomic gas molecule has five degrees of freedom. At high temperatures, it has seven degrees of freedom. Explain.
Answer:
At low temperatures, diatomic gas has three translational and two rotational degrees of freedom, so total number of degrees of freedom is 5. But at high temperature, gas molecule starts to vibrate which give two additional degrees of freedom. So the total numbers of degrees of freedom is 7.
Question 5.
What is basic law followed by equipartition of energy?
Answer:
The law of equipartiüon of energy for any dynamical system in thermal equilibrium, the total energy is distributed equally amongst all the degrees of freedom. The energy associated with each molecule per degree of freedom is \(\frac{1}{2}\) kBT, where kB is Boltzmann’s constant and T is temperature of the system.
Question 6.
On what parameters does the λ (mean free path) depends?
Solution:
We know that,
λ = \(\frac{k T}{\sqrt{2} \pi d^{2} P}=\frac{m}{\sqrt{2} \pi d^{2} \rho}=\frac{1}{\sqrt{2} \pi n d^{2}}\)
Therefore, A depends upon:
(i) diameter (d) of the molecule, smaller the ‘d’, larger is the mean free path λ .
(ii) λ ∝ T i. e., higher the temperature larger is the λ.
(iii) λ ∝ \(\frac{1}{P}\) i.e., smaller the pressure larger is the λ.
(iv) λ ∝ \(\frac{1}{\rho}\) i.e., smaller the density (ρ), larger will be the λ.
(v) λ ∝ \(\frac{1}{n}\) i. e., smaller the number of molecules per unit volume of the gas, larger is the λ.
Question 7.
Although velocity of air molecules is very fast but fragrance of a perfume spreads at a much slower rate. Explain?
Answer:
This is because perfume vapour molecules do not travel uninterrupted, they undergo a number of collisions and trace a zig-zag path, due to which their effective displacement per unit time is small, so spreading is at a much slower rate.
Long Answer Type Questions
Question 1.
Consider an ideal gas with following distribution of speeds:
| Speed (m/s) | % of molecules |
| 200 | 10 |
| 400 | 20 |
| 600 | 40 |
| 800 | 20 |
| 1000 | 10 |
(i) Calculate υrms and hence T(m = 3.0 x 10-26 kg)
(ii) If all the molecules with speed 1000 m/s escape from the system, calculate newvma and hence T.(NCERTExemplar)
Solution:
This problem is designed to give an idea about cooling by evaporation.
(i) υ2rms = \(\frac{\sum n_{i} v_{i}^{2}}{\sum n_{i}}\)
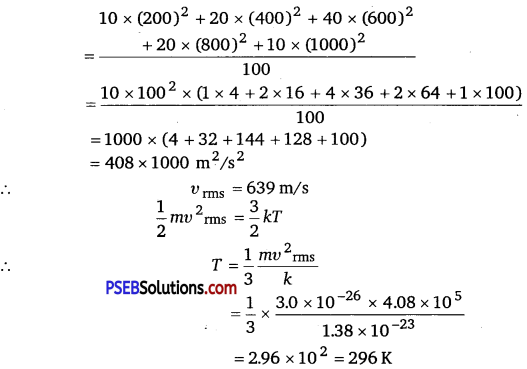
(ii)

![]()
Question 2.
A box of 1.00 m3 is filled with nitrogen at 1.50 atm at 300 K. The box has a hole of an area Is 0.010 mm2. How much time is required for the pressure to reduce by 0.10 atm., if the pressure outside is 1 atm.
Solution:
Given, the volume of the box, V 1.00 m3
Area of hole, a = 0.010 mm3 = 0.01 x 10-6 m2
Temperature outside = Temperature inside
Initial pressure inside the box = 1.50 atm
Final pressure inside the box = 0.10 atm
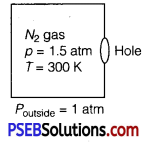
Assuming,
υix= Speed of nitrogen molecule inside the box along x-direction.
n1 = Number of molecules per unit volume in a time interval of Δt, all the particles at a distance (υixΔt) will collide the hole and the wall, the particle colliding along the hole will escape out reducing the pressure in the box.
Let the area of the wall is A, Number of particles colliding in time, Δt = \(\frac{1}{3}\) n1(υixΔt)A \(\frac{1}{2}\) is the factor because all the particles along x-direction are behaving randomly. Hence, half of these are colliding against the walls on either side.
Inside the box, υ2ix + υ2iy + υ2iz = υ2rms
⇒ υ2ix = \(\frac{v_{r m s}^{2}}{3}\) [∵ υix = υiy= υiz]
If particles collide along hole, they move out. Similarly, outer particles colliding along hole will move in.
Ifa = area of hole
Then, net particle flow in time,
Δt = \(\frac{1}{2}\left(n_{1}-n_{2}\right) \frac{k_{B} T}{m} \Delta t a\) [∵υrms = \(\sqrt{\frac{3 k_{B} T}{m}} \)]
[Temperature inside and outside the box are equal]
Let n = number of density of nitrogen
n = \(\frac{\mu N_{A}}{V}=\frac{p N_{A}}{R T}\) [∵ \(\frac{\mu}{V}=\frac{p}{R T}\)]
where, NA = Avogadro’s number
If after time Δt, pressure inside changes from p1 to p2
n’1 = \(\frac{p_{1}^{\prime} N_{A}}{R T}\)
Now, number of molecules gone out = n1V -n’1V
