PSEB 11th Class Physics Important Questions Chapter 15 Waves

Punjab State Board PSEB 11th Class Physics Important Questions Chapter 15 Waves Important Questions and Answers.

PSEB 11th Class Physics Important Questions Chapter 15 Waves

very Short Answer Type Questions

Question 1.
Why should the difference between the frequencies be less than 10 to produce beats?
Answer:
Human ear cannot identify any change in intensity is less than \(\left(\frac{1}{10}\right)^{\mathrm{th}} \)‘ of a second. So, difference should be less than 10.

Question 2.
Does a vibrating source always produce sound?
Answer:
A vibrating source produces sound when it vibrates in a medium and frequency of vibration lies within the audible range (10 Hz to 20 kHz).

Question 3.
What is the nature of water waves produced by a motorboat sailing in water? (NCERT Exemplar)
Answer:
Water waves produced by a motorboat sailing in water are both longitudinal and transverse.

Question 4.
In a hot summer day, pitch of an organ pipe will be higher or lower?
Solution:
The speed of sound in air is more at higher temperatures, as υ ∝ \(\sqrt{T}\) if. As we know frequency υ = \(\frac{v}{\lambda}\) as y is more, hence y will be more and accordingly pitch will be more.

Question 5.
When two waves of almost equal frequencies n₁ and n₂ reach at a point simultaneously. What is the time interval between successive maxima? (NCERT Exemplar)
Solution:
Number of beats/sec = (n₁ – n₂)
Hence, time interval between two successive beats time interval between two successive maxima = \(\frac{1}{n_{1}-n_{2}}\)

Short Answer Type Questions

Question 1.
Transverse waves are generated in two uniform steel wires A and B of diameters 10^-3 m and 0.5 x 10^-3 m respectively, by attaching their free end to a vibrating source of frequency 500 Hz. Find the ratio of the wavelengths if they are stretched with the same tension.
Solution:
The density ρ of a wire of mass M, length L and diameter ‘d’ is given by
ρ = \(\frac{4 M}{\pi d^{2} L}=\frac{4 m}{\pi d^{2}}\)
Now υ_A = \(\sqrt{\frac{T}{m_{A}}}\)
and
υ_B = \(\sqrt{\frac{T}{m_{B}}}\)
∴ \(\frac{v_{A}}{v_{B}}=\sqrt{\frac{m_{B}}{m_{A}}}=\frac{d_{B}}{d_{A}} \)
but υ_A = νλ_A and ν_B = νλ_B, n being the frequency of the source.
Hence, \(\frac{\lambda_{A}}{\lambda_{B}}=\frac{v_{A}}{v_{B}}=\frac{d_{B}}{d_{A}}=\frac{0.5 \times 10^{-3}}{10^{-3}} \) = 0.5

Question 2.
What are the uses of ultrasonic waves?
Answer:
Ultrasonic waves are used for the following purposes

• They are used in SONAR for finding the range and direction of submarines.
• They are used for detecting the presence of cracks and other inhomogeneities in solids.
• They are used to kill the bacteria and hence for sterilising milk.
• They are used for cleaning the surface of solid.

Question 3.
A progressive and a stationary wave have frequency 300 Hz and the same wave velocity 360 in/s. Calculate
(i) the phase difference between two points on the progressive wave which are 0.4 m apart,
(ii) the equation of motion of progressive wave if its amplitude is 0.02 m,
(iii) the equation of the stationary wave if its amplitude is 0.01 m and
(iv) the distance between consecutive nodes in the stationary wave.
Solution:
Wave velocity υ = 360 rn/s
Frequency,f= 300 Hz
∴ Wavelength, λ = \(\frac{v}{f}=\frac{360}{300}\) = 1.2 m

(i) The phase difference between two points at a distance one wavelength apart is 2π. Phase difference between points 0.4 m apart is given by
\(\frac{2 \pi}{\lambda} \times 0.4\) = \(\frac{2 \pi}{1.2} \times 0.4=\frac{2 \pi}{3}\) rad

(ii) The equation of motion of a progressive wave is
y=A sin 2π \(\left(\frac{t}{T}-\frac{x}{\lambda}\right)\)
In the case given
y=0.02sin2π\(\left(300 t-\frac{x}{1.2}\right)\)

(iii) The equation of the stationary wave is
y=2Acos\(\frac{2 \pi x}{\lambda} \sin \frac{2 \pi t}{T}\)
Here, 2A=2×0.01=0.02m
λ =1.2m
\(\frac{1}{T}\) =300Hz

∴ y=0.02 cos \(\frac{2 \pi x}{1.2} \sin 600 \pi t\)

(iv) The distance between the two consecutive nodes in the stationary wave is given by
\(\frac{\lambda}{2}=\frac{1.2}{2}\)m = 0.6m

Question 4.
Write basic conditions for formation õf stationary waves.
Answer:
The basic conditions for formation of stationary waves are listed below:

• The direct and reflected waves must be traveling along the same line.
• For stationary wave formation, the superposing waves should either be longitudinal or transverse. A longitudinal and a transverse wave cannot superposition.
• For formation of stationary waves, there should not be any relative motion between the medium and oppositely traveling waves.
• Amplitude and period of the superposing waves should be same.

Question 5.
The intensity of sound in a normal conversation at home is about 3 x 10^-6 w m^-2 and the frequency of normal human voice Is about 1000 Hz. Find the amplitude of waves, assuming that the air is at standard conditions.
Solution:
At standard conditions (STP)
density (ρ) of air = 129 kg m^-3
velocity of sound,
v=332.5ms^-1
Now, I= 2π²ρn²A²υ
where, n =1000 Hz,
I=3 x 10^-6 Wm^-2
∴ A= \(\frac{1}{\pi n} \sqrt{\frac{I}{2 \rho v}}\)
= \(\frac{1}{3.142 \times 1000} \times \sqrt{\frac{3 \times 10^{-6}}{2 \times 1.29 \times 332.5}}\)
= \(\frac{5.91 \times 10^{-5}}{3.142 \times 10^{3}}\)
=1.88 x 10^-8 m
Note that the amplitude of sound waves in normal conversation is extremely small.

Question 6.
The Intensities due to two sources of sound are I₀ and 4I₀. What is the intensity at a point where the phase difference between two waves is (i) 0⁰ (ii) \(\frac{\pi}{2}\) (iii) π?
Solution:
If a₁ and a₂ are the amplitudes of two waves, then the resultant amplitude is given by
A = \(\sqrt{a_{1}^{2}+a_{2}^{2}+2 a_{1} a_{2} \cos \phi}\)
where Φ is the phase difference between two waves.

Now, A²=a₁² +a₂² +2a₁a₂cos θ
Expressing this equation in terms of intensity.
I= I₁+4I₂+2\(\sqrt{I_{1}} \sqrt{I_{2}} \cos \phi\)
(j) I = I₀ + 4I₀ + 2 \(\sqrt{I_{1}} \sqrt{I_{2}}\) cos 0° = 9I₀
(ii) I = I₀ + 4I₀ + 2\(\sqrt{I_{0}} \sqrt{4 I_{0}} \cos \frac{\pi}{2}\) = 5I₀
(iii) I = I₀ + 4I₀ + 2 \(\sqrt{I_{0}} \sqrt{4 I_{0}} \cos \pi \) = I₀

Question 7.
Compare the velocities of sound In hydrogen (H₂) and carbon dioxide (CO₂) The ratio (γ) of specific beats of H₂ and CO₂ are respectively 1.4 and 1.3.
Solution:

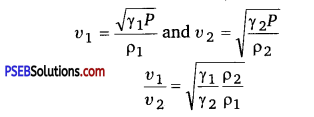
Since density of a gas is proportional to its molecular weight.

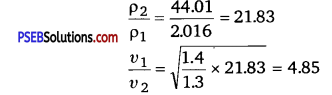
Question 8.
Two loudspeakers have been installed in an open space to listen to a speech. When both the loudspeakers are in operation, a listener sitting at a particular place receives a very feeble sound. Why? What will happen if one loudspeaker is kept off?
Solution:
When the distance between two loudspeakers from the position of listener is an odd multiple of \(\frac{\lambda}{2} \) then due to destructive interference between sound waves from two loudspeakers, a feeble sound is heard by the listener. When one loudspeaker is kept off, no interference will take place and the listener will hear the full sound of the operating loudspeaker.

Question 9.
The second overtone of an open pipe has the same frequency as the first overtone of a closed pipe 2m long. What is the length of the open pipe?
Solution:
Let L₀ be the length of the open pipe. The fundamental frequency of the pipe is given by
ν₀ = \(\frac{v}{\lambda_{f}}=\frac{v}{2 L_{0}}\)
where, ν = velocity of sound in air
The second overtone of the open pipe has a frequency
3ν₀ = \(\frac{3 v}{2 L_{0}} \) Hz

The length of the closed pipe
L_c = 2m
The frequency of the fundamental omitted by the closed pipe
v_c = \(\frac{v}{\lambda}=\frac{v}{4 L_{C}} \)
The first overtone of the closed pipe has a frequency
3v_c=\(\frac{3 v}{4 L_{c}}=\frac{3 v}{4 \times 2}=\frac{3 v}{8}\) Hz
Now, 3v₀ = 3v_c
or 2L₀=8 or L₀=4m

Question 10.
Calculate the number of beata heard per second is there are three sources of sound of frequencies 400, 401, and 402 of equal Intensity sounded together.
Solution:
Let us consider the case of three disturbances each of amplitude a and frequencies (n -1), and (n + 1)respectìvely. The resultant displacement is given by
y=a sin 2π(n-1)t +asin2πnt +asin2π(n +1)x
=2a sin 2πnrcos2πt +asin2π(n+1)t
=a(1 +2cos2πt)sin 2πtnt
So the resultant amplitude is a (1 + 2 cos 2πt)
which is maximum when cos2πt = + 1
∴ 2πt=2k where k=0,1,2,3 ………………..
t =0, 1,2, 3 ……………………

Thus the time interval between two consecutive maxima is one. This shows that the frequency of maxima is one.
Similarly, the amplitude is minimum when
1 +2 cos 2πt = 0
or
cos2πt= – \(\frac{1}{2}\)
or
2πt = 2kπ +\(\frac{2 \pi}{3}\)
(Where k 0,1,2 )
or
t= \(\left(k+\frac{1}{3}\right)=\frac{1}{3}, \frac{4}{3}, \frac{7}{3}, \frac{10}{3}\)
Thus the minima occurs after an interval of one second, i.e., the frequency of minima is also one. Hence, the frequency of beats is also one.
Thus, one beat is heard per second.

Long Answer Type Quèstions

Question 1.
Derive expressions for apparent frequency when
(i) source Is moving towards an observer at rest.
(ii) observer Is moving towards source at rest.
(iii) both source and observer are in motion.
Solution:
Let S and O be the positions of source and observer respectively.
ν = frequency of sound waves emitted by the source.
υ = velocity of sound waves.

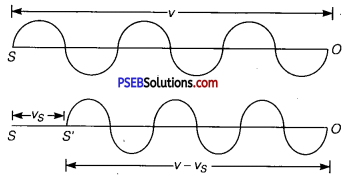
Case (i) Source (S) ¡n motion and observer at rest: When S is at rest, it will emit waves in one second and these will occupy a space of length ν in one second.
If λ = wavelength of these waves, then
λ = \(\frac{v}{v}\)
Let υ_s = velocity of a source moving towards O at rest and let S reaches to S’ in one second. Thus the sound waves wifi be crowded in length (υ – υ_s).
So if λ’ be the new wavelength,
Then ,
λ’ = \(\frac{v-v_{S}}{v}\)
if v’ be the apparent frequency, then
v’ = \(\frac{v}{\lambda^{\prime}}=\frac{v}{v-v_{s}} v\)

∴ v’ > v i. e., when S moves towards O, the apparent frequency of sound waves is greater than the actual frequency.

(ii) If the observer moves towards the source at rest:

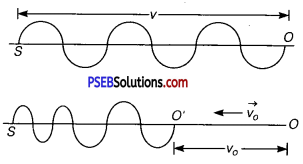
Let v₀ = velocity of observer moving towards S at rest.
As the observer moves towards S at rest, so the velocity of sound waves w.r.t. the observer is v + v₀.
If v’ = apparent frequency, then
v’ = \(\frac{v+v_{o}}{\lambda}=\frac{v+v_{o}}{v} v\)
Clearly v’ > v

(iii) If both S and O are moving
(a) towards each other : We know that when S moves towards stationary observer,

then v’ = \(\frac{v}{v-v_{s}}\)
When O moves towards S, then
v”= \(\left(\frac{v+v_{o}}{v}\right) \mathrm{v}^{\prime}=\left(\frac{v+v_{o}}{v-v_{S}}\right) \mathrm{v} \)

(b) If both S and O move in the direction of sound waves:
Then the apparent frequency is given by

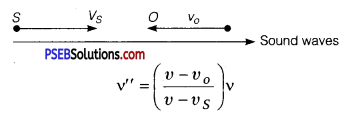
(c) When both S and O are moving away from each other:
When source moves away from O at rest, then apparent frequency is given by

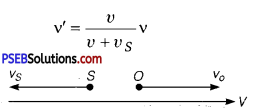
When observer is also moving away from the source, the frequency v’ will change to v” and is given by

Question 2.
Give the analytical treatment of beats.
Solution:
Consider two simple harmonic progressive waves traveling simultaneously in the same direction and in the same medium. Let
(i) A be the amplitude of each wave.
(ii) There is no initial phase difference between them.
(iii) Let v₁ and v₂ be their frequencies.
If y₁ and y₂ be displacements of the two waves, then
y₁ =Asin2πv₁t
and Y₁ =Asin2πv₂t
If y be the result and displacement at any instant, then
y = y₁ + y₂
= A (sin2πv₂t) + Asin (2πv₂t)

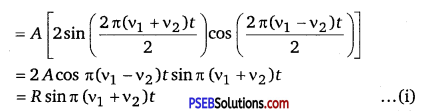
where R = 2Acos π (v₁ – v₂)t ……………………………… (ii)
is the amplitude of the resultant displacement and depends upon t. The following cases arise
(a) If R is maximum, then
cos π (v₁ — v₂ )t = max. = ± 1 = cos nπ
∴ π (v₁ — v₂ )t = n π
or t= \(\frac{n}{v_{1}-v_{2}}\) …………………………. (iii)

where, n =0,1,2, …
∴ Amplitude becomes maximum at times given by
t=0, \(\frac{1}{v_{1}-v_{2}}, \frac{2}{v_{1}-v_{2}}, \frac{3}{v_{1}-v_{2}}, \ldots \)
∴ Time interval between two consecutive maxima is
= \(\frac{1}{v_{1}-v_{2}} \)
∴ Beat period = \(\frac{1}{v_{1}-v_{2}}\)
∴ Beat frequency = v₁ — v₂
∴ no. of beasts formed per sec = v₁ — v₂

(b) If R is minimum, then
cosπ (v₁ – v₂)t = min. = O = cos (2n +1) \(\frac{\pi}{2}\)

where, n 0,1, 2, …
∴ Amplitude becomes minimum at times given by
t = \(\frac{1}{2\left(v_{1}-v_{2}\right)}, \frac{3}{2\left(v_{1}-v_{2}\right)}, \frac{5}{2\left(v_{1}-v_{2}\right)}, \ldots \)

∴ Time interval between two consecutive minima is = \(\frac{1}{v_{1}-v_{2}}\)
∴ Beatperiod = \(\frac{1}{v_{1}-v_{2}}\)
∴ Beat frequency = v₁ – v₂
∴ No. of beats formed per sec = v₁ – v₂
Hence the number of beats formed per second is equal to the difference between the frequencies of two-component waves.