Punjab State Board PSEB 11th Class Physics Important Questions Chapter 2 Units and Measurements Important Questions and Answers.
PSEB 11th Class Physics Important Questions Chapter 2 Units and Measurements
Very short answer type questions
Question 1.
Is it possible to have length and velocity both as fundamental quantities? Why?
Answer:
No, since length is fundamental quantity and velocity is the derived quantity.
Question 2.
Which of these is largest: astronomical unit, light year and par sec?
Answer:
Par sec is larger than light year which in turn is larger than an astronomical unit.
![]()
Question 3.
Define one Bam. How it is related with metre?
Answer:
One bam is a small unit of area used to measure area of nuclear cross-section.
∴ 1 barn = 10-28 m2
Question 4.
What is meant by angular diameter of moon?
Answer:
Angular diameter of moon is the angle subtended at a point on the earth, by two diameterically opposite ends of the moon. Its value is about 0.5°.
Question 5.
Name the device used for measuring the mass of atoms and molecules. (NCERT Exemplar)
Answer:
Spectrograph.
Question 6.
Write the dimensional formula of wavelength and frequency of a wave.
Answer:
Wavelength [λ] = [L]
Frequency [v] = [T-1]
![]()
Question 7.
Obtain the dimensional formula for coefficient of viscosity.
Answer:
Coefficient of viscosity (η) = \(\frac{F d x}{A \cdot d v}\)
= \(\frac{\left[\mathrm{MLT}^{-2}\right][\mathrm{L}]}{\left[\mathrm{L}^{2}\right]\left[\mathrm{LT}^{-1}\right]}\) = [M1L-1T-1]
Question 8.
Write three pairs of physical quantities, which have same dimensional formula.
Answer:
- Work and energy
- Energy and torque
- Pressure and stress
Short answer type questions
Question 1.
Does AU and Å represent the same unit of length?
Answer:
No, AU and Å represent two different units of length.
1 AU = 1 astronomical unit = 1.496 x 1011 m
1Å = 1 angstrom = 10-10 m
Question 2.
What is common between bar and torr?
Solution:
Both bar and torr are the units of pressure.
1 bar =1 atmospheric pressure = 760 mm of Hg column .
= 105 N/m2
1 torr = 1 mm of Hg column
bar 760 torr
Question 3.
Why has second been defined in term of periods of radiations from cesium-133?
Answer:
Second has been defined in terms of periods of radiation, because
- this period is accurately defined.
- this period is not affeced by change of physical conditions like temperature, pressure and volume etc.
- the unit is easily reproducible in any good laboratoty.
![]()
Question 4.
Why parallax method cannot be used for measuring distances of stars more than 100 light ýears away?
Answer:
When a star is more than loo light years away, then the parallax angle is so small that it cannot be measured accurately.
Question 5.
What is the technique used for measuring large time intervals?
Answer:
For measuring large time intervals, we use the technique of radioactive dating. Large time intervals are measured by studying the ratio of number of radioactive atoms decayed to the number of surviving atoms in the
specimen.
Question 6.
Using the relation E = hv, obtain the dimensions of Planck’s constant.
Answer:
We know that dimensional formula of energy E of photon is [M1L2T-2
and dimensional formula of frequency is y is [T-1].
The given relation is E = hv
[h] = \(\frac{[E]}{[v]}=\frac{\left[M^{1} \mathrm{~L}^{2} \mathrm{~T}^{-2}\right]}{\left[\mathrm{T}^{-1}\right]}\) = M1L2T-1
Question 7.
The rotational kinetic energy of a body is given by E = \(\frac {1}{2}\)Iω2, where ω is the angular velocity of the body. Use the equation to obtain dimensional formula for moment of inertia I. Also write
its SI unit.
Solution:
The given relation is E = \(\frac {1}{2}\)Iω2

Its SI unit is Joule.
![]()
Question 8.
Distinguish between dimensional variables and dimensional constants. Give example too.
Answer:
Dimensional variables are those quantities which have dimensions and whose numerical value may change. Speed, velocity, acceleration etc. are dimensional variables.
Dimensional constants are quantities having dimensions but having a constant value, e.g., gravitation constant (G), Planck’s constant (H), Stefan’s constant (σ) etc.
Question 9.
Dow will you convert a physical quantity from one unit system to another by method of dimensions?
Solution:
If a given quantity is measured in two different unit system, then Q = n1u1 = n2u2.
Let the dimensional formula of the quantity be [MaLbTc], then we have n1 [M1aL1bT1c ] = n2 [M2aL2bT2c]
Here M1, L1, T1 are the fundamental units of mass, length and time in
first unit system and M2, L2, T2
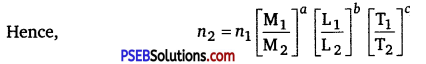
This relation helps us to convert a physical quantity from one unit system to another.
Question 10.
The displacement of a progressive wave is represented by y = A sin (ωt – kx), where x is distance, and t is time. Write the dimensional formula of (i) ω and (ii) k. (NCERT Exemplar)
Solution:
Now, by the principle of homogeneity, i. e., dimensions of LHS and RHS should be equal, hence
[LHS] = [RHS]
⇒ [L] = [A] = L
As ωt – kx should be dimensionless,
[ωt] [kx] = 1
⇒ [ω]T = [k]L= 1
⇒ [ω] = T-1 and [k] = L-1
![]()
Question 11.
Which of the following time measuring devices is most precise?
(a) A wall clock
(b) A stop watch
(c) A digital watch
(d) An atomic clock
Give reason for your answer. (NCERT Exemplar)
Solution:
A wall clock can measure time correctly upto one second. A stop watch can measure time correctly upto a fraction of a second. A digital watch can measure time up to a fraction of second. An atomic clock can measure time most precisely as its precision is 1 s in 1013 s.
Long answer type questions
Question 1.
A large fluid star oscillates in shape under the influence of its own gravitational field. Using dimensional analysis, find the expression for period of oscillation (T) in terms of radius of star (R), Mean density of fluid (ρ) and universal gravitational constant (G).
Solution:
Suppose period of oscillation T depends on radius of star R, mean density of fluid p and universal gravitational constant (G) as
T = kRa ρb Gc,where kis a dimensionless constant
Writing dimentions on both sides of the equation, we have
[M0L0T1]=[L]a[ML-3]b[M-1L3T-2]c
= Mb – cLa – 3b + 3cT-2c
Comparing powers of M, L and T, we have
b – c = 0;
a – 3b + 3c = 0 and -2c = 1
On simplifying these equations, we get
c = -1/2,b = -1/2, a = 0
Thus, we have T = kρ-1/2G-1/2 = \(\frac{k}{\sqrt{\rho G}}\)
![]()
Question 2.
Find an expression for viscous force F acting on a tiny steel ball of radius,r,moving in a viscous liquid of viscosity q with a constant speed υ by the niethod of dimensional analysis.
Solution:
It is given that viscous force F depends on (i) radius r of steel ball, (ii) coefficient of viscosity η of viscous liquid (iii), Speed υ of the ball i.e.,F = kraηbυc,where kis dimensionless constant
Writing dimensions on both sides of equation, we have
[MLT-2] = [L]a[M1L-1T-1]b[LT-1]c
= [MaLa – b + cT-b -c]
Comparing powers of M, L and T on two sides of equation, we get
a = 1
a – b + c = 1
-b -c =-2
On solving, these above equations, we get ,
a = 1, b = 1 and c = 1
Hence, the relation becomes
F = krηυ