Prasanna

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 12 Atoms Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 12 Atoms

PSEB 12th Class Physics Guide Atoms Textbook Questions and Answers

Question 1.
Choose the correct alternative from the clues given at the end of the each statement:
(a) The size of the atom in Thomson’s model is ………………….. the atomic size in Rutherford’s model, (much greater than/no different from/much less than.)
(b) In the ground state of ………………………………… electrons are in stable equilibrium, while in …………………….. electrons always experience a net force. (Thomson’s model/Rutherford’s model.)
(c) A classical atom based on ……………………………. is doomed to collapse. (Thomson’s model/Rutherford’s model.)
(d) An atom has a nearly continuous mass distribution in a ………………………… but has a highly non-uniform mass distribution in …………………….. (Thomson’s model/Rutherford’s model.)
(e) The positively charged part of the atom possesses most of ………………………. the mass in ………………….. (Rutherford’s model/both the models.)
Answer:
(a) The size of the atom in Thomson’s model is no different from the atomic size in Rutherford’s model.
(b) In the ground state of Thomson’s model, electrons are in stable equilibrium while, in Rutherford’s model, electrons always experience a net force.
(c) A classical atom based on Rutherford’s model is doomed to collapse.
(d) An atom has a nearly continuous mass distribution in Thomson’s model but has a highly non-uniform mass distribution in Rutherford’s model.
(e) The positively charged part of the atom possesses most of the mass in both the models.

Question 2.
Suppose you are given a chance to repeat the alpha-particle scattering experiment using a thin sheet of solid hydrogen in place of the gold foil. (Hydrogen is a solid at temperatures below 14 K.) What results do you expect?
Answer:
The basic purpose of scattering experiment is not completed because solid hydrogen will be a much lighter target as compared to the alpha particle acting as a projectile. By using the conditions of elastic collisions, the hydrogen will move much faster as compared to alpha after the collision. We cannot determine the size of hydrogen nucleus.

Question 3.
What is the shortest wavelength present in the Paschen series of spectral lines?
Answer:
Rydberg’s formula is given as
\(\frac{h c}{\lambda}\) = \(21.76 \times 10^{-19}\left[\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right]\)
where, h = Planck’s constant = 6.63 x 10^-34 Js
c=Speed oflight=3 x 10⁸ m/s (n₁ and n₂ are integers)
The shortest wavelength present in the Paschen series of the spectral lines
is given for values n₁ = 3 and n₂ = ∞

= 822.65 nm

Question 4.
A difference of 2.3 eV separates two energy levels in an atom. What is the frequency of radiation emitted when the atom makes a transition from the upper level to the lower level?
Answer:
According to Bohr’s postulate
E₂ – E₁ = hv
∴ Frequency of emitted radiation

Question 5.
The ground state energy of hydrogen atom is -13.6 eV. What are the kinetic and potential energies of the electron in this state?
Answer:
Given, the ground state energy of hydrogen atom
E=-13.6eV
We know that,
Kinetic Energy, E_K = -E = 13.6 eV
Potential Energy E_p = -2KE =-2 x 13.6 = -27.2eV

Question 6.
A hydrogen atom initially In the ground level absorbs a photon, which excites it to the n = 4 level. Determine the wavelength and frequency of photons.
Answer:
The energy levels of H-atom are given by
E_n = \(-\frac{R h c}{n^{2}}\)
For given transition n₁ =1, n₂ = 4
∴ E₁ = \(-\frac{R h c}{1^{2}}\) ,E₂= \(-\frac{R h c}{4^{2}}\)
∴ Energy of absorbed photon
ΔE=E₂ -E₁ =Rhc \(\left(\frac{1}{1^{2}}-\frac{1}{4^{2}}\right)\)
or
ΔE = \(\frac{15}{16}\) Rhc ………………………….. (1)
∴ The wavelength of absorbed photon λ is given by

Question 7.
(a) Using the Bohr’s model, calculate the speed of the electron in a hydrogen atom in the n =1, 2, and 3 levels.
(b) Calculate the orbital period in each of these levels.
Answer:
(a) Let y1 be the orbital speed of the electron in a hydrogen atom in the ground state level, n₁ =1.
For charge (e) of an electron, v₁ is given by the relation,
v₁ = \(\frac{e^{2}}{n_{1} 4 \pi \varepsilon_{0}\left(\frac{h}{2 \pi}\right)}=\frac{e^{2}}{2 \varepsilon_{0} h} \)
where, e=1.6 x 10^-19 C
\(\varepsilon_{0}\) = Permittivity of free space = 8.85 x 10^-12 N^-1 C²m²
h = Planck’s constant = 6.63 x 10^-34 Js
∴ v₁ = \(\frac{\left(1.6 \times 10^{-19}\right)^{2}}{2 \times 8.85 \times 10^{-12} \times 6.63 \times 10^{-34}}\)
= 0.0218 x 10⁸ =2.18 x 10⁶ m/s

For level n₂ =2, we can write the relation for the corresponding orbital speed as
v₂ = \(\frac{e^{2}}{n_{2} 2 \varepsilon_{0} h}\) = \(\frac{\left(1.6 \times 10^{-19}\right)^{2}}{2 \times 2 \times 8.85 \times 10^{-12} \times 6.63 \times 10^{-34}}\) = 1.09 x 10⁶ m/s
And, for n₃ =3, we can write the relation for the corresponding orbital speed as


Hence, the speed of the electron in a hydrogen atom in n = 1, n = 2 and n = 3 is 2.18 x 10⁶ m/s,
1.09 x 10⁶ m/s, 7.27 x 10⁵ m/s respectively.

(b) Orbital period of electron is given by
T = \(\frac{2 \pi r}{v}\)
Radius of nth orbit
r_n = \(\frac{n^{2} h^{2}}{4 \pi^{2} K m e^{2}}\)
∴ r₁ = \(\frac{(1)^{2} \times\left(6.63 \times 10^{-34}\right)^{2}}{4 \times 9.87 \times\left(9 \times 10^{9}\right) \times 9 \times 10^{-31} \times\left(1.6 \times 10^{-19}\right)}\)
= 0.53 x 10^-10 m
For n=1, T₁ = \(\frac{2 \pi r_{1}}{v_{1}}\)
= \(\frac{2 \times 3.14 \times 0.53 \times 10^{-10}}{2.19 \times 10^{6}}\) = 1.52 x 10^-16s

For n = 2, radius r_n = n²r₁
∴ r₂ =’2².r₁ =4 x0.53 x 10^-10
and velocity v_n, = \(\frac{v_{1}}{n}\)
∴ v₂ = \(\frac{v_{1}}{2}=\frac{2.19 \times 10^{6}}{2}\)
Time period T₂ = \(\frac{2 \times 3.14 \times 4 \times 0.53 \times 10^{-10} \times 2}{2.19 \times 10^{6}}\)
=1216 x 10^-15 s
For n=3,radius r³ =3²,r₁ =9r₁ =9 x 0.53 x 10^-10m and velocity v₃ = \(\frac{v_{1}}{3}=\frac{2.19 \times 10^{6}}{3}\) m/s
Time period T₃ = \(\frac{2 \pi r_{3}}{v_{3}}=\frac{2 \times 3.14 \times 9 \times 0.53 \times 10^{-10} \times 3}{2.19 \times 10^{6}}\) = 4.1 x 10^-15 s

Question 8.
The radius of the innermost electron orbit of a hydrogen atom is 5.3 x 10^-11 m. What are the radii of the n = 2 and n = 3 orbits?
Answer:
The radius of the innermost electron orbit of a hydrogen atom, r₁ = 5.3 x 10^-11 m.
Let r₂ be the radius of the orbit at n = 2.
It is related to the radius of the innermost orbit as r₂ = (n)²r₁ = (2)² x 5.3 x 10^-11
= 4 x 5.3 x 10^-11 = 2.12 x 10^-10m
For n = 3, we can write the corresponding electron radius as
r³ =(n)²r₁ = (3)² x 5.3 x 10^-11
n = 9 x 5.3 x 10^-11 = 4.77 x 10^-10m
Hence, the radii of an electron for n = 2 and n = 3 orbits are 2.12 x 10^-10 m and 4.77 x 10^-10 m respectively.

Question 9.
A 12.5 eV electron beam is used to bombard gaseous hydrogen at room temperature. What series of wavelengths will be emitted?
Answer:
It is given that the energy of the electron beam used to bombard gaseous hydrogen at room temperature is 12.5 eV. Also, the energy of the gaseous hydrogen in its ground state at room temperature is -13.6 eV. When gaseous hydrogen is bombarded with an electron beam, the energy of the gaseous hydrogen becomes -13.6 + 12.5 eV i. e., -1.1 eV.

Orbital energy is related to orbit level (n) as
E = \(\frac{-13.6}{(n)^{2}}\)eV
For n=3, E = \(\frac{-13.6}{(3)^{2}}=\frac{-13.6}{9}\) = -1.5 eV
This energy is approximately equal to the energy of gaseous hydrogen. it can be concluded that the electron has jumped from n I to n = 3 level.

During its de-excitation, the electrons can jump from n = 3 to n = 1 directly, which forms a line of the Lyman series of the hydrogen spectrum.
We have the relation for wave number for Lyman series as
\(\frac{1}{\lambda}=R_{y}\left(\frac{1}{1^{2}}-\frac{1}{n^{2}}\right)\)
where, R_y =Rydberg constant = 1.097 x 10⁷ m^-1,
λ = Wavelength of radiation emitted by the transition of the electron for
n =3,
We can obtain λ as
\(\frac{1}{\lambda}\) = 1.097 x 10⁷\(\left(\frac{1}{1^{2}}-\frac{1}{3^{2}}\right)\)
= 1.097 x 10⁷ \(\left(1-\frac{1}{9}\right)\) = 1.097 x 10⁷x \(\frac{8}{9}\)

λ = \(\frac{9}{8 \times 1.097 \times 10^{7}}\) = 102.55nm
If the electron jumps from n = 2 to n = 1, then the wavelength of the radiation is given as
\(\frac{1}{\lambda}\) = 1.097 x 10⁷ \(\left(\frac{1}{1^{2}}-\frac{1}{2^{2}}\right)\)
= 1.097 x 10⁷\(\left(1-\frac{1}{4}\right)\) = 1.097 x 10⁷x \(\frac{3}{4}\)
λ = \(\frac{4}{1.097 \times 10^{7} \times 3}\) = 121.54 nm

If the transition takes place from n = 3 to n = 2, then the wavelength of the radiation is given as

This radiation corresponds to the Balmer series of the hydrogen spectrum. Hence, in Lyman series, two wavelengths i. e., 102.54 nm, and 121.55 nm are emitted. And in the Balmer series, one wavelength i. e., 656.33 nm is emitted.

Question 10.
In accordance with the Bohr’s model, find the quantum number that characterizes the earth’s revolution around the sun in an orbit of radius 1.5 x 10¹¹ m with orbital speed 3 x 10⁴ m/s. (Mass of earth = 6.0 x 10²⁴ kg.)
Answer:
Radius of the orbit of the Earth around the Sun, r = 1.5 x 10¹¹ m
Orbital speed of the Earth, v = 3 x 10⁴ m/s
Mass of the Earth, m = 6.0 x 10²⁴ kg
According to Bohr’s model, angular momentum is quantized and given as
mvr = \(\frac{n h}{2 \pi}\)

where, h = Planck’s constant = 6.63 x 10^-34 Js
n = Quantum number
∴ n = \(\frac{m v r 2 \pi}{h}\)
= \(\frac{2 \pi \times 6 \times 10^{24} \times 3 \times 10^{4} \times 1.5 \times 10^{11}}{6.63 \times 10^{-34}} \) = 25.61 x 10⁷³ = 2.6 x 10⁷⁴
Hence, the quanta number that characterizes the Earth’s revolution is 2.6 x 10⁷⁴.

Additional Exercises

Question 11.
Answer the following questions, which help you to understand the difference between Thomson’s model and Rutherford’s model better.
(a) Is the average angle of deflection of α-particles by a thin gold foil predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model?

(b) Is the probability of backward scattering (i. e., scattering of α-particles at angles greater than 90°) predicted by Thomson’s model much less, about the same, or much greater than that predicted by Rutherford’s model?

(c) Keeping other factors fixed, it is found experimentally that for small thickness t, the number of α-particles scattered at moderate angles is proportional to t. What clue does this linear dependence on t provide?

(d) In which model is it completely wrong to ignore multiple scattering for the calculation of average angle of scattering of α-particles by. a thin foil?
Answer:
(a) The average angle of deflection of α-particles by a thin gold foil predicted by Thomson’s model is about the same size as predicted by Rutherford’s model. This is because the average angle was taken in both models.

(b) The probability of scattering of α-particles at angles greater than 90° predicted by Thomson’s model is much less than that predicted by Rutherford’s model. This is because there is no such massive central core called the nucleus in Rutherford’s model.

(c) Scattering is mainly due to single collisions. The chances of a single collision increase linearly with the number of target atoms. Since the number of target atoms increases with an increase in thickness, the collision probability depends linearly on the thickness of the target.

(d) It is wrong to ignore multiple scattering in Thomson’s model for the calculation of average angle of scattering of α-particles by a thin foil. This is because a single collision causes very little deflection in this model. Hence, the observed average scattering angle can be explained only by considering multiple scattering.

Question 12.
The gravitational attraction between electron and proton in a hydrogen atom is weaker than the Coulomb attraction by a factor of about 10^-40. An alternative way of looking at this fact is to estimate the radius of the first Bohr orbit of a hydrogen atom if the electron and proton were bound by gravitational attraction. You will find the answer interesting.
Answer:
Radius of the first Bohr orbit is given by the relation,
r₁ = \(\frac{4 \pi \varepsilon_{0}\left(\frac{h}{2 \pi}\right)^{2}}{m_{e} e^{2}}\) ……………….. (i)
where, ε₀ = Permittivity of free space
h = Planck’s constant = 6.63 x 10^-34 Js
m_e = Mass of an electron = 9.1 x 10^-31 kg
e = Charge of an electron = 1.9x 10^-19C
m_p = Mass of a proton = 1.67 x 10^-27 kg
r = Distance between the electron and the proton Coulomb attraction between an electron and a proton is given as
F_C = \(\frac{e^{2}}{4 \pi \varepsilon_{0} r^{2}} \) ………………………….. (2)

Gravitational force of attraction between an electron and a proton is
F_G = \(\frac{G m_{p} m_{e}}{r^{2}}\) ……………………………………. (3)
where, G = Gravitational constant = 6.67 x 10^-11 N m²/kg²
If the electrostatic (Coulomb) force and the gravitational force between an electron and a proton are equal, then we can write
∴ F_G = F_C
\(\frac{G m_{p} m_{e}}{r^{2}}\) = \(\frac{e^{2}}{4 \pi \varepsilon_{0} r^{2}}\)
\(\frac{e^{2}}{4 \pi \varepsilon_{0} r^{2}}\) = Gm_pm_e …………………………. (4)
Putting the value of equation (4) in equation (1), we get

Question 13.
Obtain an expression for the frequency of radiation emitted when a hydrogen atom de-excites from level n to level (n -1). For large n, show that this frequency equals the classical frequency of revolution of the electron in the orbit.
Answer:
It is given that a hydrogen atom de-excites from an upper level (n) to a lower level (n —1). We have the relation for energy (E₁) of radiation at level n as
E₁ = hv₁ = \(\frac{h m e^{4}}{(4 \pi)^{3} \varepsilon_{0}^{2}\left(\frac{h}{2 \pi}\right)^{3}} \times\left(\frac{1}{n^{2}}\right)\)
where, v₁ = Frequency of radiation at level n
h = Planck’s constant
m = Mass of hydrogen atom
e = Charge on an electron
ε_o = Permittivity of free space

Now, the relation for energy (E₂) of radiation at level (n -1) is given as
E₂ = hv₂ = \(\frac{h m e^{4}}{(4 \pi)^{3} \varepsilon_{0}^{2}\left(\frac{h}{2 \pi}\right)^{3}} \times \frac{1}{(n-1)^{2}}\) ………………………… (2)
where, v₂ = Frequency of radiation at level (n -1)
Energy (E) released as a result of de-excitation
E = E₂ – E₁ hv= E₂ – E ₁ ………………….. (3)
where, v = Frequency of radiation emitted
Putting values from equations (1) and (2) in equation (3), we get

For large n, we can write (2 n -1) ≈ 2 n and (n-1) ≈ n.
V = \(\frac{m e^{4}}{32 \pi^{3} \varepsilon_{0}^{2}\left(\frac{h}{2 \pi}\right)^{3} n^{3}} \)
∵ v = \(\frac{m e^{4}}{32 \pi^{3} \varepsilon_{0}^{2}\left(\frac{h}{2 \pi}\right)^{3} n^{3}}\) ………………….. (4)
Classical relation of frequency of revolution of an electron is given as
V_c = \(\frac{v}{2 \pi r}\) ……………………………….. (5)
where, velocity of the electron in the n^th orbit is given as
v = \(\frac{e^{2}}{4 \pi \varepsilon_{0}\left(\frac{h}{2 \pi}\right) n}\) ……………………………… (5)
And, radius of the n^th orbit is given as
v = \(\frac{e^{2}}{4 \pi \varepsilon_{0}\left(\frac{h}{2 \pi}\right) n}\) ………………………………(6)
Putting the values of equations (6) and (7) in equation (5), we get
V_c = \( \frac{m e^{4}}{32 \pi^{3} \varepsilon_{0}^{2}\left(\frac{h}{2 \pi}\right)^{3} n^{3}}\)
Hence, the frequency of radiation emitted by the hydrogen atom is equal to its classical orbital frequency.

Question 14.
Classically, an electron can be in any orbit around the nucleus of an atom. Then what determines the typical atomic size? Why is an atom not, say, a thousand times bigger than its typical size? The question had greatly puzzled Bohr before he arrived at his famous model of the atom that you have learnt in the text.

To simulate what he might well have done before his discovery, let us play as follows with the basic constants of nature and see if we can get a quantity with the dimensions of length that is roughly equal to the known size of an atom (~10^-10 m).

(a) Construct a quantity with the dimensions of length from the fundamental constants e, me and c. Determine its numerical value.

(b) You will find that the length obtained in (a) is many orders of magnitude smaller than the atomic dimensions. Further, it involves c. But energies of atoms are mostly in non-relativistic domain where c is not expected to play any role. This is what may have suggested Bohr to discard c and look for ‘something else’ to get the right atomic size. Now, the Planck’s constant h had already made its appearance elsewhere. Bohr’s great insight lay in recognizing that h, me, and e will yield the right atomic size.

Construct a quantity with the dimension of length from h, me, and e and confirm that its numerical value has indeed the correct order of magnitude.
Answer:
(a) Charge on an electron, e = 1.6 x 10^-19 C
Mass of an electron, m_e = 9.1 x 10^-31 kg
Speed of light, c = 3 x 10⁸ m/s
Let us take a quantity involving the given quantities as \(\left(\frac{e^{2}}{4 \pi \varepsilon_{0} m_{e} c^{2}}\right)\)
where, ε₀ = Permittivity of free space and, \(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 x 10⁹ Nm²C^-2 .
The numerical value of the taken quantity will be

Hence, the numerical value of the taken quantity is much smaller than the typical size of an atom.

(b) Charge on an electron, e = 1.6 x 10^-19 C
Mass of an electron, me = 9.1 x 10^-31 kg
Planck’s constant, h = 6.63 x 10^-34 Js
Let us take a quantity involving the given quantities as \(\frac{4 \pi \varepsilon_{0}\left(\frac{h}{2 \pi}\right)^{2}}{m_{e} e^{2}}\)
where, ε₀ = Permittivity of free space
and, \(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 x 10⁹Nm²C^-2

The numerical value of the taken quantity will be
\(\frac{1}{4 \pi \varepsilon_{0}} \times \frac{\left(\frac{h}{2 \pi}\right)^{2}}{m_{e} e^{2}}=9 \times 10^{9} \times \frac{\left(\frac{6.63 \times 10^{-34}}{2 \times 3.14}\right)^{2}}{9.1 \times 10^{-31} \times\left(1.6 \times 10^{-19}\right)^{2}} \)
= 0.53 x 10^-10 m
Hence, the value of the quantity taken is of the order of the atomic size.

Question 15.
The total energy of an electron in the first excited state of the hydrogen atom is about -3.4 eV.
(a) What is the kinetic energy of the electron in this state?
(b) What is the potential energy of the electron in this state?
(c) Which of the answers above would change if the choice of the zero of potential energy is changed?
Answer:
(a) Total energy of the electron, E = -3.4 eV ’
Kinetic energy of the electron is equal to the negative of the total energy.
⇒ K = -E
= -(-3.4) = + 3.4 eV
Hence, the kinetic energy of the electron in the given state is + 3.4 eV.

(b) Potential energy (JJ) of the electron is equal to the negative of twice of its kinetic energy.
⇒ U = -2 K
= -2 x 3.4 = -6.8 eV
Hence, the potential energy of the electron in the given state is -6.8 eV.

(c) The potential energy of a system depends on the reference point taken. Here, the potential energy of the reference point is taken as zero. If the reference point is changed, then the value of the potential energy of the system also changes. Since total energy is the sum of kinetic and potential energies, total energy of the system will also change.

Question 16.
If Bohr’s quantization postulate (angular momentum = nh/2π) is a basic law of nature, it should be equally valid for the case of planetary motion also. Why then do we never speak of quantization of orbits of planets around the sun?
Answer:
We never speak of quantization of orbits of planets around the Sun because the angular momentum associated with planetary motion is largely relative to the value of Planck’s constant (h).
The angular momentum of the Earth in its orbit is of the order of 10⁷⁰h. This leads to a very high value of quantum levels n of the order of 10⁷⁰.
For large values of n, successive energies and angular momenta are relatively very small. Hence, the quantum levels for planetary motion are considered continuous.

Question 17.
Obtain the first Bohr’s radius and the ground state energy of a muonic hydrogen atom an atom in which a negatively
charged muon (μ^– ) of mass about 207 m_e orbits around a proton.
Answer:
Muonic hydrogen is the atom in which a negatively charged muon of mass about 207 m_e revolves around a proton.
In Bohr’s atom model, r ∝ \(\frac{1}{m}\)
∵ \(\frac{r_{\text {muon }}}{r_{\text {electron }}}=\frac{m_{e}}{m_{\mu}}=\frac{m_{e}}{207 m_{e}}=\frac{1}{207}\) [ ∵m_μ = 207 m_e]
Here, r_e is radius of orbit of electron in hydrogen atom is 0.53 Å.

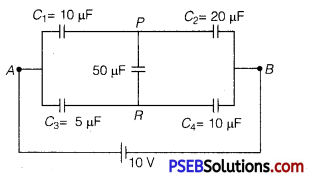
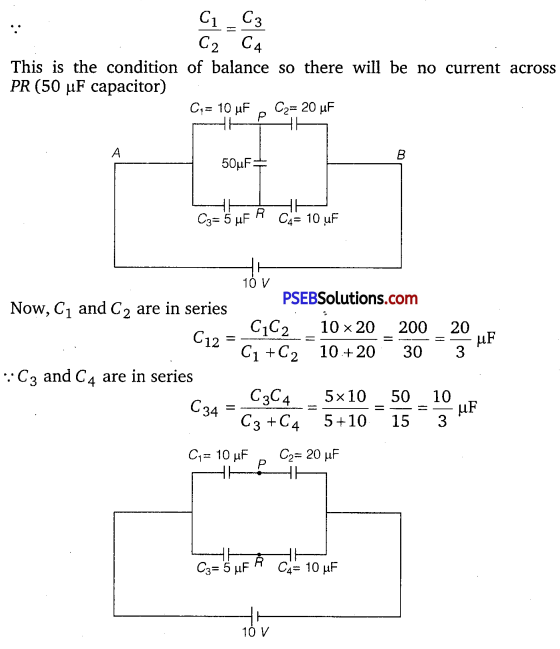
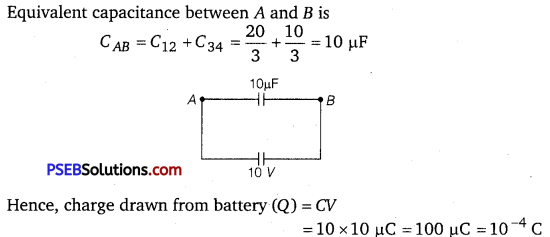
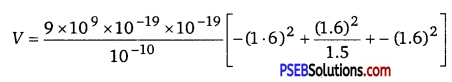Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 3 Current Electricity Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 3 Current Electricity

PSEB 12th Class Physics Guide Current Electricity Textbook Questions and Answers

Question 1.
The storage battery of a car has an emf of 12 V. If the internal resistance of the battery is 0.4 Ω, what is the maximum current that can be drawn from the battery?
Answer:
Emf of the battery, E = 12 V
Internal resistance of the battery, r = 0.4 Ω
Maximum current drawn from the battery = I
According to Ohm’s law,
E = Ir
I = \(\frac{12}{0.4}\) = 30
The maximum current drawn from the given battery is 30 A.

Question 2.
A battery of emf 10 V and internal resistance 3 Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistor? What is the terminal voltage of the battery when the circuit is closed?
Answer:
Emf of the battery, E = 10 V
Internal resistance of the battery, r = 3 Ω
Current in the circuit, I = 0.5 A
Resistance of the resistor = R
The relation for current using Ohm’s law is,
I = \(\frac{E}{R+r}\)
R + r = \(\frac{E}{I}\)
= \(\frac{10}{0.5}\) = 20Ω
∴ R = 20 – 3 = 17Ω
Terminal voltage of the battery = V
According to Ohm’s law,
V = IR
= 0.5 × 17 = 8.5 V
Therefore, the resistance of the resistor is 17 Ω and the terminal voltage of the battery is 8.5 V.

Question 3.
(a) Three resistors 1Ω, 2 Ω and 3 Ω are combined in series. What is the total resistance of the combination?
(b) If the combination is connected to a battery of emf 12 V and negligible internal resistance, obtain the potential drop across each resistor.
Answer:
(a) r₁ = 1Ω, r₂ = 2Ω, r₃ = 3Ω
R_S = ?
R_S = r₁ + r₂ + r₃ = 6Ω

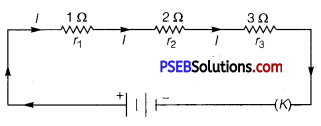
(b) ∵ V = 12 V
R_S = 6Ω
I = ?
∵ V = IR_S
⇒ I = \(\) = 2A
Let V₁,V₂, V₃ be the potential drops across r₁ r₂, r₃. Then,
> V = V₁ + V₂ + V₃
V₁ = =Ir₁ = 2 × 1 = 2V
V₂ =Ir₂ = 2 × 2 = 4 V
V₃ = Ir₃ = 2 × 3 = 6V

Question 4.
(a) Three resistors 2 Ω, 4 Ω and 5 Ω are combined in parallel. What is the total resistance of the combination?
(b) If the combination is connected to a battery of emf 20 V and negligible internal resistance, determine the current through each resistor and the total current drawn from the battery.
Answer:
(a) r₁ = 2Ω,r₂ = 4Ω,r₃ = 5Ω

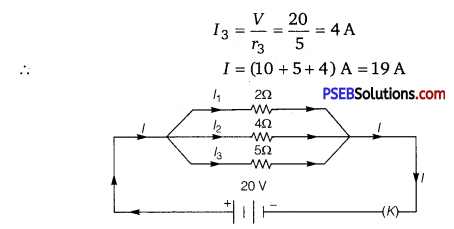
Question 5.
At room temperature (27.0°C) the resistance of a heating element is 100 Ω. What is the temperature of the element if the resistance is found to be 117 Ω, given that the temperature coefficient of the material of the resistor is 1.70 × 10^-4 C^-1.
Answer:
Room temperature, T = 27°C
Resistance of the heating element at T, R = 100 Ω
Let Ti is the increased temperature of the element.
Resistance of the heating element at T₁,R₁ = 117 Ω
Temperature co-efficient of the material of the element,
α = 1.70 × 10^-4°C^-1
α is given by the relation,
α = \(\frac{R_{1}-R}{R\left(T_{1}-T\right)}\)
T₁ – T = \(\frac{R_{1}-R}{R \alpha}\)
T₁ – 27 = \(\frac{117-100}{100\left(1.7 \times 10^{-4}\right)}\)
T₁ – 27 = 1000
T₁ = 1000 + 27
T₁ = 1027°C
Therefore, at 1027°C the resistance of the element is 117 Ω.

Question 6.
A negligibly small current is passed through a wire of length 15 m and uniform cross-section 6.0 × 10^-7 m², and its resistance is measured to be 5.0 Ω. What is the resistivity of the material at the temperature of the experiment?
Answer:
Length of the wire, l = 15 m
Area of cross-section of the wire, A = 6.0 × 10^-7 m²
Resistance of the material of the wire, R = 5.0 Ω
Resistivity of the material of the wire = ρ
Resistance is related with the resistivity as
R = ρ\(\frac{l}{A}\)
ρ = \(\frac{R A}{l}\)
= \(\frac{5 \times 6 \times 10^{-7}}{15}\) = 2 × 10^-7Ωm
Therefore, the resistivity of the material is 2 × 10^-7 Ωm.

Question 7.
A silver wire has a resistance of 2.1 Ω at 27.5°C, and a resistance of 2.7Ω at 100°C. Determine the temperature coefficient of resistivity of silver.
Answer:
Temperature, T₁ = 27.5°C
Resistance of the silver wire at T₁, R₁ = 2.1 Ω
Temperature, T₂ = 100 °C
Resistance of the silver wire at T₂, R₂ = 2.7 Ω
Temperature coefficient of resistivity of silver = a It is related with temperature and resistance as
α = \(\frac{R_{2}-R_{1}}{R_{1}\left(T_{2}-T_{1}\right)}\)
= \(\frac{2.7-2.1}{2.1(100-27.5)}\) = 0.0039°C^-1
Therefore, the temperature coefficient of resistivity of silver is 0.0039 °C^-1.

Question 8.
A heating element using nichrome connected to a 230 V supply draws an initial current of 3.2 A which settles after a few seconds to a steady value of 2.8 A. What is the steady temperature of the heating element if the room temperature is 27.0°C? Temperature coefficient of resistance of nichrome averaged over the temperature range involved is 1.70 x 10^-4°C^-1.
Answer:
Supply voltage, V = 230 V
Initial current drawn, I₁ = 3.2 A
Initial resistance = R₁, which is given by the relation,
R₁ = \(\frac{V}{I_{1}}=\frac{230}{3.2}\) = 71.87 Ω
Steady state value of the current, I₂ = 2.8 A
Resistance at the steady state = R₂, which is given as
R₂ = \(\frac{230}{2.8}\) = 82.14 Ω
Temperature coefficient of resistance of nichrome, α = 1.70 × 10^-4°C^-1
Initial temperature of nichrome, T₁ = 27.0 °C
Steady state temperature reached by nichrome = T₂
T₂ can be obtained by the relation for α,
α = \(\frac{R_{2}-R_{1}}{R_{1}\left(T_{2}-T_{1}\right)}\)
T₂ – 27°C = \(\frac{82.14-71.87}{71.87 \times 1.7 \times 10^{-4}}\) = 840.5
T₂ = 840.5 + 27 = 867.5°C
Therefore, the steady temperature of the heating element is 867.5°C.

Question 9.
Determine the current in each branch of the network shown in ‘ Fig. 3.30.

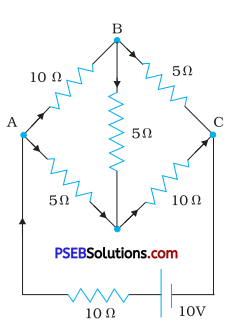
Let I be the total current in the circuit.
I₁ = Current flowing through AB.
∴ I – I₁ = Current flowing through AD.
I₂ = Current flowing through BD.
∴ I₁ – I₂ = Current flowing through BC.
and I₁ – I₁ + I₂ = Current flowing through DC.
Applying loop law to ABDA, we get

10I₁ + 5I₂ – 5(I – I₁) = 10
or 3I₁ + I₂ – I = 0 …………….. (1)
Again applying loop law to BCDB, we get
5(I₁ – I₂) – 10(I – I₁ + I₂) -5I₂ = 0 or 15I₁ – 20I₂ – 10I = 0
or 3I₁ – 4I₂ – 2I = 0 …………….. (2)
Applying loop law to ABCEFA, we get
10I + 10I₁ + 5(I₁ – I₂) = 10
or 3F₁ – I₂ + 2I = 2 ………….. (3)
Eqn. (2) + (3) gives, 6I₁ – 5I₂ = 2 …………… (4)
Multiplying eqn. (1) by 2 and then adding to eqn. (4), we get
9I₁ + I₂ = 2 …………… (5)
Eqn. (4) + 5 x eqn. (5) gives,
6I₁ – 5I₂ + 45I₁ +5I₂ = 2 + 10
or 51I₁ = 12
or I₁ = \(\frac{4}{17}\) A …………….. (6)
∴ Current in branch AB,I₁ = \(\frac{4}{17}\)A
∴ From eqns. (5) and (6), we get
I₂ = 2 – 9 x \(\frac{4}{17}\) = –\(\frac{2}{17}\)A
-ve sign shows that 12 is actually from D to B. Now from eqn. (1), we get

Question 10.
(a) In a metre bridge [Fig. 3.27], the balance point is found to be at 39.5 cm from the end A, when the resistor Y is of 12.5 Ω. Determine the resistance of X. Why are the connections between resistors in a Wheatstone or meter bridge made of thick copper strips?
(b) Determine the balance point of the bridge above if X and Y are interchanged.
(c) What happens if the galvanometer and cell are interchanged at the balance point of the bridge? Would the galvanometer show any current?
Answer:
(a) A metre bridge with resistors X and Y is represented in the given figure.

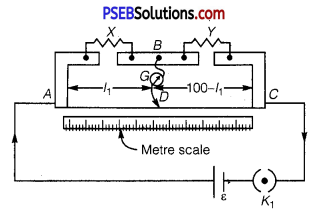
Balance point from end A,l₁ = 39.5 cm
Resistance of the resistor Y = 12.5 Ω
Condition for the balance is given as,

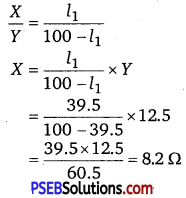
Therefore, the resistance of resistor X is 8.2 Ω.
The connection between resistors in a Wheatstone or metre bridge is made of thick copper strips to minimize the resistance, which is not taken into consideration in the bridge formula.

(b) If X and Y are interchanged, then l₁ and 100 – l₁ get interchanged.
The balance point of the bridge will be 100 – l₁ from A.
100 – l₁ =100 – 39.5 = 60.5 cm
Therefore, the balance point is 60.5 cm from A.

(c) When the galvanometer and cell are interchanged at the balance point of the bridge, the galvanometer will show no deflection. Hence, no current would flow through the galvanometer.

Question 11.
A storage battery of emf 8.0 V and internal resistance 0.5 Ω is being charged by a 120 V dc supply using a series resistor of 15.5 Ω. What is the terminal voltage of the battery during charging? What is the purpose of having a series resistor in the charging circuit?
Answer:
Emf of the storage battery, E = 8.0 V
Internal resistance of the battery, r = 0.5 Ω
DC supply voltage, V = 120 V
Resistance of the resistor, R = 15.5 Ω
Effective voltage in the circuit = V’
R is connected to the storage battery in series. Hence, it can be written as
V’ = V – E
V’= 120 – 8 = 112 V
Current flowing in the circuit = I, which is given by the relation,
I = \(\frac{V^{\prime}}{R^{\prime}+r}\)
= \(\frac{112}{15.5+0.5}=\frac{112}{16}\) = 7A
15.5 + 0.5 16
Voltage across resistor R given by the product, IR = 7 × 15.5 = 108.5 V
∵ DC supply voltage = Terminal voltage of battery+Voltage drop across R
∴ Terminal voltage of battery = 120 -108.5 = 11.5 V
A series resistor in a charging circuit limits the current drawn from the external source. The current will be extremely high in its absence. This is very dangerous.

Question 12.
In a potentiometer arrangement, a cell of emf 1.25 V gives a balance point at 35.0 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63.0 cm, what is the emf of the second cell?
Answer:
Emf of the cell, E₁ = 1.25 V
Balance point of the potentiometer,l₁ = 35 cm
The cell is replaced by another cell of emf E₂.
New balance point of the potentiometer, l₂ = 63 cm
The balance condition is given by the relation,
\(\frac{E_{1}}{E_{2}}=\frac{l_{1}}{l_{2}}\)
E₂ = E₁ × \(\frac{l_{2}}{l_{1}}\) = 1.25 × \(\frac{63}{35}\) = 2.25V
Therefore, emf of the second cell is 2.25 V.

Question 13.
The number density of free electrons in a copper conductor estimated in Example 3.1 is 8.5 × 10²⁸ m^-3. How long does an electron take to drift from one end of a wire 3.0 m long to its other end? The area of cross-section of the wire is 2.0 × 10^-6 m² and it is carrying a current of 3.0 A.
Answer:
Here, n = number density of free electrons = 8.5 × 10²⁸ m^-3
l = length of wire = 3m
A = Area of cross-section of wire = 2.0 × 10^-6 m²
I = current in the wire = 3.0 A
e = 1.6 × 10^-19C
Let t = time taken by electron to drift from one end to another of the wire = ?
Using the relation, I – neA v_d, we get
v_d = I/neA
= \(\frac{3}{8.5 \times 10^{28} \times 1.6 \times 10^{-19} \times 2.0 \times 10^{-6}}\) ms^-1
= 1.103 × 10^-4 ms^-1
∴ t = \(\frac{l}{v_{d}}\) = \(\frac{3}{1.103 \times 10^{-4}}\) = 2.72 × 10⁴ s = 7 h 33 min.

Question 14.
The earth’s surface has a negative surface charge density of 10^-9 Cm^-2. The potential difference of 400 kV between the top of the atmosphere and the surface results (due to the low conductivity of the lower atmosphere) in a current of only 1800 A over the entire globe. If there were no mechanism of sustaining atmospheric electric field, how much time (roughly) would be required to neutralise the earth’s surface? (This never happens in practice because there is a mechanism to replenish electric charges, namely the continual thunderstorms and lightning in different parts of the globe.) (Radius of earth = 6.37 × 10⁶m.)
Answer:
Surface charge density of the earth, σ = 10^-9 Cm ^-2
Current over the entire globe, I = 1800 A .
Radius of the earth, r = 6.37 × 10⁶ m
Surface area of the earth,
A = 4πr²
= 4π × (6.37 × 10⁶)²
= 5.09 × 10¹⁴ m²
Charge on the earth surface,
q = σ × A
= 10^-9 × 5.09 × 10¹⁴
= 5.09 × 10⁵ C
Time taken to neutralise the earth’s surface = t
Current, I = \(\frac{q}{t}\)
t = \(\frac{q}{I}\)
= \(\frac{5.09 \times 10^{5}}{1800}\) = 282.77 s
Therefore, the time taken to neutralize the earth’s surface is 282.77 s.

Question 15.
(a) Six lead-acid type of secondary cells each of emf 2.0 V and internal resistance 0.015 Ω are joined in series to provide a supply to a resistance of 8.5 Ω. What are the current drawn from the supply and its terminal voltage?
(b) A secondary cell after long use has an emf of 1.9 V and a large internal resistance of 380 Ω. What maximum current can be drawn from the cell? Could the cell drive the starting motor of a car?
Answer:
(a) Number of secondary cells, n = 6
Emf of each secondary cell, E = 2.0 V
Internal resistance of each cell, r = 0.015 Ω
Series resistor is connected to the combination of cells.
Resistance of the resistor, R – 8.5 Ω
Current drawn from the supply = I, which is given by the relation,
I = \(\frac{n E}{R+n r}\)
= \(\frac{6 \times 2}{8.5+6 \times 0.015}\)
= \(\frac{12}{8.59}\) = 1.39 A
Terminal voltage, V = IR = 1.39 × 8.5 =11.87 A
Therefore, the current drawn from the supply is 1.39 A and terminal voltage is 11.87 A.

(b) After a long use, emf of the secondary cell, E = 1.9 V
Internal resistance of the cell, r = 380 Ω
Hence, maximum current, I_max = \(\frac{E}{r}=\frac{1.9}{380}\) = 0.005 A

Therefore, the maximum current drawn from the cell is 0.005 A. Since a large current is required to start the motor of a car, the cell cannot be used to start a motor.

Question 16.
Two wires of equal length, one of aluminium and the other of copper have the same resistance. Which of the two wires is lighter? Hence explain why aluminium wires are preferred for overhead power cables. (ρAl = 2.63 × 10^-8 Ω m, ρCu = 1.72 × 10^-8 Ω m, Relative density of A1 = 2.7, of Cu = 8.9.)
Answer:
Resistivity of aluminium, ρAl = 2.63 × 10^-8 Ωm
Relative density of aluminium, d₁ = 2.7
Let l₁be the length of aluminium wire and ₁ be its mass.
Resistance of the aluminium wire = R₁
Area of cross-section of the aluminium wire = A₁
Resistivity of copper, ρCu = 1.72 × 10^-8 Ωm
Relative density of copper, d₂ = 8.9
Let l₂ be the length of copper wire and m₂ be its mass.
Resistance of the copper wire = R₂
Area of cross-section of the copper wire = A₂
R₁ = ρ₁\(\frac{l_{1}}{A_{1}}\) …………… (1)
R₂ = ρ₂\(\frac{l_{2}}{A_{2}}\) …………… (2)
It is given that,

It can be inferred from this ratio that m₁ is less than m₂. Hence, aluminium is lighter than copper.
Since aluminium is lighter, it is preferred for overhead power cables over copper.

Question 17.
What conclusion can you draw from the following observations on a resistor made of alloy manganin?

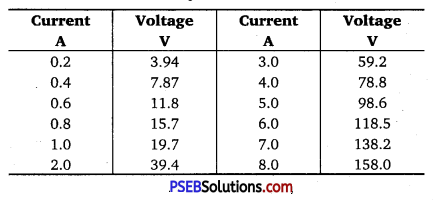
Answer:
It can be inferred from the given table that the ratio of voltage with current is a Constant, which is equal to 19.7. Hence, manganin is an ohmic conductor i. e., the alloy obeys Ohm’s law. According to Ohm’s law, the ratio of voltage with current is the resistance of the conductor. Hence, the resistance of manganin is 19.7 Ω.

Question 18.
Answer the following questions :
(a) A steady current flows in a metallic conductor of non-uniform cross-section. Which of these quantities is constant along the conductor : current, current density, electric field, drift speed?
(b) Is Ohm’s law universally applicable for all conducting elements?
If not, give examples of elements which do not obey Ohm’s law.
(c) A low voltage supply from which one needs high currents must have very low internal resistance. Why?
(d) A high tension (HT) supply of, say 6 kV must have a very large internal resistance. Why?
Answer:
(a) When a steady current flows in a metallic conductor of non-uniform cross-section, the current flowing through the conductor is constant. Current density, electric field, and drift speed are inversely proportional to the area of cross-section. Therefore, they are not constant.

(b) No, Ohm’s law is not universally applicable for all conducting elements. Vacuum diode semi-conductor is a non-ohmic conductor. Ohm’s law is not valid for it.

(c) According to Ohm’s law, the relation for the potential is V = IR
Voltage (V) is directly proportional to current (I).
R is the internal resistance of the source.
I = \(\frac{V}{R}\)
If V is low, then R must be very low, so that high current can be drawn from the source.

(d) In order to prohibit the current from exceeding the safety limit, a high tension supply must have a very large internal resistance. If the internal resistance is not large, then the current drawn can exceed the safety limits in case of a short circuit.

Question 19.
Choose the correct alternative:
(a) Alloys of metals usually have (greater/less) resistivity than that of their constituent metals.
(b) Alloys usually have much (lower/higher) temperature coefficients of resistance than pure metals.
(c) The resistivity of the alloy manganin is nearly independent of/increases rapidly with increase of temperature.
(d) The resistivity of a typical insulator (e. g., amber) is greater than that of a metal by a factor of the order of (10²² /10³).
Answer:
(a) Alloys of metals usually have greater resistivity than that of their constituent metals.
(b) Alloys usually have much lower temperature coefficients of resistance than pure metals.
(c) The resistivity of the alloy, manganin, is nearly independent of increase of temperature.
(d) The resistivity of a typical insulator is greater than that of a metal by a factor of the order of 10²².

Question 20.
(a) Given n resistors each of resistance R, how will you combine them to get the (i) maximum (ii) minimum effective resistance? What is the ratio of the maximum to minimum resistance?
(b) Given the resistances of 1 Ω, 2 Ω, 3 Ω, how will be combine them to get an equivalent resistance of (i) (11/3) Ω (ii) (11/5) Ω, (iii) 6 Ω, (iv) (6/11) Ω?
(c) Determine the equivalent resistance of networks shown in Fig. 3.31.

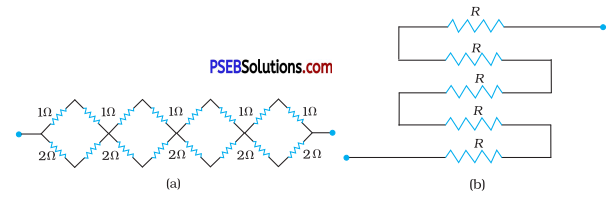
Answer:
(a) For maximum resistance, we shall connect all the resistors in series. Maximum resistance
R_max = nR
For minimum resistance, we shall connect all the resistors in parallel. Minimum resistance,
R_min = \(\frac{R}{n}[latex]
Ratio, [latex]\frac{R_{\max }}{R_{\min }}=\frac{n R}{R / n}\) = n²

(b) The combinations are shown in figure.

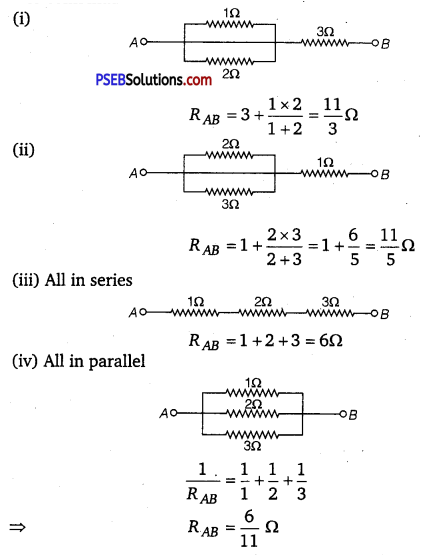
(c) (a) It can be observed from the given circuit that in the first small loop, two resistors of resistance 1 Ω each are connected in series.
Hence, their equivalent resistance = (1 + 1) = 2Ω
It can also be observed that two resistors of resistance 2Ω each,are
connected in series.
Hence, their equivalent resistance = (2 + 2) = 4Ω.
Therefore, the circuit can be redrawn as:

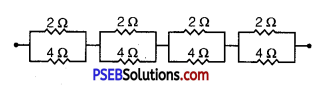
It can be observed that 2 Ω and 4 Ω resistors are connected in parallel in all the four loops. Hence, equivalent resistance (R’) of each loop is given by,
R’ = \(\frac{2 \times 4}{2+4}=\frac{8}{6}=\frac{4}{3}\)Ω
The circuit reduces to,

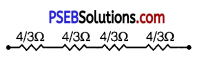
All the four resistors are connected in series.
Hence, equivalent resistance of the given circuit is \(\frac{4}{3}\) × 4 = \(\frac{16}{3}\) Ω

(b) It can be observed from the given circuit that five resistors of resistance R each are connected in series.
Hence, equivalent resistance of the circuit = R + R + R + R + R
= 5 R

Question 21.
Determine the current drawn from a 12 V supply with internal resistance 0.5 Ω by the infinite network shown in Fig. 3.32. Each resistor has 1Ω resistance.

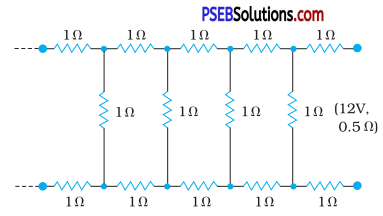
Answer:
Let X be the equivalent resistance of the network. Since network is infinite adding one more set of three resistances each of value R = 1 Ω across the terminals will not affect the total resistance i.e., it should still remain equal to X. Thus this network can be represented as :

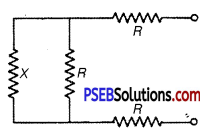
Let R_eq be the equivalent resistance of this network, then
R_eq = R + equivalent resistance of parallel combination of X and R + R
= R + \(\frac{X R}{X+R}\) + R
= 2 R + \(\frac{X R}{X+R}\)
Addition of 3 resistances to resistance X of infinite network should not alter the total resistance of the infinite network. Thus
R_eq =X
or 2R + \(\frac{X R}{X+R}\) = X
or 2 × 1 + \(\frac{X \times 1}{X+1}\) = 1 (∵ R = 1Ω)
or 2(X + 1) + X = X(X + 1)
or X² – 2X – 2 = 0

Question 22.
Figure 3.33 shows a potentiometer with a cell of 2.0 V and internal resistance 0.40 Ω maintaining a potential drop across the resistor wire AB. A standard cell which maintains a constant emf of 1.02 V (for very moderate currents upto a few mA) gives a balance point at 67.3 cm length of the wire. To ensure very low currents drawn from the standard cell, a very high resistance, of 600 kΩ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf e and the balance point found similarly, turns out to be at 82.3 cm length of the wire.

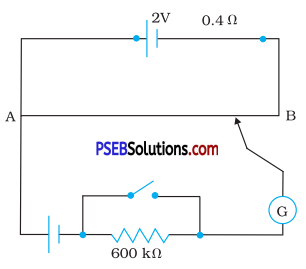
(a) What is the value of e ?
(b) What purpose does the high resistance of 600 kΩ have?
(c) Is the balance point affected by this high resistance?
(d) Is the balance point affected by the internal resistance of the driver cell?
(e) Would the method work in the above situation if the driver cell of the potentiometer had an emf of 1.0 V instead of 2.0 V?
(f) Would the circuit work well for determining an extremely small emf, say of the order of a few mV (such as the typical emf of thermo-couple)? If not, how will you modify the circuit?
Answer:
Constant emf of the given standard cell, E₁ = 1.02 V
Balance point on the wire, l₁ = 67.3 cm
A cell of unknown emf, ε, replaced the standard cell. Therefore, new balance point on the wire, l = 82.3 cm.
(a) The relation between connecting emf and balance point is,
\(\frac{E_{1}}{l_{1}}=\frac{\varepsilon}{l}\)
ε = \(\frac{l}{l_{1}}\) × E₁
= \(\frac{82.3}{67.3}[latex] × 1.02 = 1.247 V
The value of unknown emf is 1.247 V.

(b) The purpose of using the high resistance of 600 kΩ is to reduce the current through the galvanometer when the movable contact is far from the balance point.

(c) The balance point is not affected by the presence of high resistance.

(d) The balance point is not affected by the internal resistance of the driver cell.

(e) The method would not work if the driver cell of the potentiometer had an emf of 1.0 V instead of 2.0 V. This is because if the emf of the driver cell of the potentiometer is less than the’ emf of the other cell, then there would be no balance point on the wire.

(f) The circuit would not work well for determining an extremely small emf. As the circuit would be unstable, the balance point would be close to end A. Hence, there would be a large percentage of error.
The given circuit can be modified if a series resistance is connected with the wire AB. The potential drop across AB is slightly greater than the emf measured. The percentage error would be small.

Question 23.
Figure 3.34 shows a potentiometer circuit for comparison of two resistances. The balance point with a standard resistor R = 10.0 Ω is found to be 58.3 cm, while that with the unknown resistance X is 68.5 cm. Determine the value of X. What might you do if you failed to find a balance point with the given cell of emf ε?

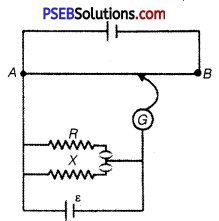
Answer:
Resistance of the standard resistor, R = 10.0 Ω
Balance point for this resistance, l₁ = 58.3 cm
Current in the potentiometer wire = i
Hence, potential drop across R,E₁ = iR
Resistance of the unknown resistor = X
Balance point for this resistor, l₂ = 68.5 cm
Hence, potential drop across X, E₂ = iX
The relation between connecting emf and balance point is,
[latex]\frac{E_{1}}{E_{2}}=\frac{l_{1}}{l_{2}}\)
\(\frac{i R}{i X}=\frac{l_{1}}{l_{2}}\)
X = \(\frac{l_{2}}{l_{1}}\) x R = \(\frac{68.5}{58.3}\) x 10 = 11.749 Ω
Therefore, the value of the unknown resistance, X is 11.75 Ω.
If we fail to find a balance point with the given cell of emf, ε, then the potential drop across R and X must be reduced by putting a resistance in series with it. Only if the potential drop across R or X is smaller than the potential drop across the potentiometer wire AB, a balance point is
obtained.

Question 24.
Figure 3.35 shows a 2.0 V potentiometer used for the determination of internal resistance of a 1.5 V cell. The balance point of the cell in open circuit is 76.3 cm. When a resistor of 9.5 Ω is used in the external circuit of the cell, the balance point shifts to 64.8 cm length of the potentiometer wire. Determine the internal resistance of the cell.

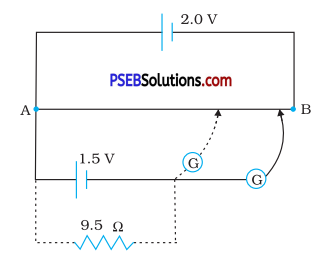
Internal resistance of the cell = r
Balance point of the cell in open circuit, l₁ = 76.3 cm
An external resistance (JR) is connected to the circuit with R = 9.5 Ω.
New balance point of the circuit, l₂ = 64.8 cm
Current flowing through the circuit = I
The relation connecting resistance and emf is,
r = (\(\frac{l_{1}-l_{2}}{l_{2}}\))R
= \(\frac{76.3-64.8}{64.8}\) x 9.5 = 1.68 Ω.
Therefore, the internal resistance of the cell is 1.68 Q.

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 13 Nuclei Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 13 Nuclei

PSEB 12th Class Physics Guide Nuclei Textbook Questions and Answers

Question 1.
(a) Two stable isotopes of lithium ₃⁶Li and ₃⁷Li have respective
abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium.
Boron has two stable isotopes, ₅¹⁰B and ₅¹¹B. Their respective masses are 10.01294 u and 11.00931 u, and the atomic mass of boron is 10.811 u. Find the abundances of ₅¹⁰B and ₅¹¹B.
Answer:
(a) Mass of ₃⁶Li lithium isotope, m₁ = 6.01512 u
Mass of ₃⁷Li lithium isotope, m₂ = 7.01600 u
Abundance of ₃⁶Li, n₁ = 7.5%
Abundance of ₃⁷Li, n₂ = 92.5%
The atomic mass of lithium atom is given as
m = \(\frac{m_{1} n_{1}+m_{2} n_{2}}{n_{1}+n_{2}}\)
= \(\frac{6.01512 \times 7.5+7.01600 \times 92.5}{7.5+92.5}\) = 6.940934 u
Mass of boron isotope ₅¹⁰B, m₁=10.01294 u
Mass of boron isotope ₅¹¹B, m₂ = 11.00931 u
Abundance of ₅¹⁰B,n₁ = x%
Abundance of ₅¹¹B, n₂ = (100 – x)%

Atomic mass of boron, m = 10.811 u.
The atomic mass of boron atom is given as
m = \(\frac{m_{1} n_{1}+m_{2} n_{2}}{n_{1}+n_{2}}\)
10.811 = \(\frac{10.01294 \times x+11.00931 \times(100-x)}{x+100-x}\)
1081.11 = 10.01294 x + 1100.931 – 11.00931 x
∴ x = \(\frac{19.821}{0.99637}\) = 19.89%
And 100 – x = 100 -19.89 = 80.11%
Hence, the abundance of ₅¹⁰B is 19.89% and that of ₅¹¹B is 80.11%.

Question 2.
The three stable isotopes of neon: ₁₀²⁰Ne, ₁₀²¹Ne and ₁₀²²Ne have respective abundances of 90.51%, 0.27%, and 9.22%. The atomic masses of the three isotopes are 19.99 u, 20.99 u, and 21.99 u, respectively. Obtain the average atomic mass of neon.
Answer:
Atomic mass of ₁₀²⁰Ne,m₁ = 19.99%u
Abundance of ₁₀²⁰Ne,n₁ = 90.51%
Atomic mass of ₁₀²¹Ne, m₂ = 20.99u
Abundance of ₁₀²¹Ne,n₂ = 0.27%
Atomic mass of ₁₀²²Ne,m₃ = 21.99u
Abundance of ₁₀²²Ne,n₃ = 9.22%
m = \(\frac{m_{1} n_{1}+m_{2} n_{2}+m_{3} n_{3}}{n_{1}+n_{2}+n_{3}} \)
= \(\frac{19.99 \times 90.51+20.99 \times 0.27+21.99 \times 9.22}{90.51+0.27+9.22}\)
= 20.1771 u

Question 3.
Obtain the binding energy (in MeV) of a nitrogen nucleus (₇¹⁴ N), given m (₇¹⁴ N) = 14.00307 u.
Answer:
Atomic mass of (₇N¹⁴) nitrogen, m = 14.00307 u
A nucleus of ₇N¹⁴ nitrogen contains 7 protons and 7 neutrons.
Hence, the mass defect of this nucleus, Δ m = 7 m_H +7m_n -m
where, Mass of a proton, m_H = 1.007825 u (∵ m_p = m_H)
Mass of a neutron, m_n = 1.008665 u
∴ Δm = 7 x 1.007825 + 7 x 1.008665 -14.00307
= 7.054775 + 7.06055 -14.00307
= 0.112255 u
But 1 u = 931.5 MeV/c²

Δm = 0.112255 x 931.5 MeV/c²
Hence, the binding energy of the nucleus is given as
E_b = Δ mc² .
where, c = speed of light
∴ E_b = 0.112255 x 93.15 \(\left(\frac{\mathrm{MeV}}{\mathrm{c}^{2}}\right)\) x c²
= 104.565532 MeV
Hence, the binding energy of a nitrogen nucleus is 104.565532 MeV.

Question 4.
Obtain the binding energy of the nuclei _56²⁶Fe and _83²⁰⁹Bi in units of MeV from the following data : m (_56²⁶Fe) = 55.934939 u, m (_83²⁰⁹Bi) = 208.980388 u
Answer:
Atomic mass of _56²⁶Fe, m₁ = 55.934939 u
_56²⁶Fe nucleus has 26 protons and (56 -26) = 30 neutrons
Hence, the mass defect of the nucleus, Δ m = 26 x m_H +30 x m_n – m₁
where, mass of a proton, m_H = 1.007825 u
Mass of a neutron, m_n = 1.008665 u
∴Δm = 26 x 1.007825 + 30 x 1.008665 – 55.934939
= 26.20345 + 30.25995 – 55.934939
= 0.528461 u
But 1u = 931.5 MeV/c²
∴ Δm = 0.528461×931.5 MeV/c²

The binding energy of this nucleus is given as
E_b1 = Δmc²
Where, c = speed of light
∴ E_b1 = 0.528461 x 931.5 \(\left(\frac{\mathrm{MeV}}{\mathrm{c}^{2}}\right)\) x c²
= 492.26 MeV
Average binding energy per nucleon = \(\frac{492.26}{56}\) = 8.79 MeV

Atomic mass of _83²⁰⁹Bi, m₂ = 208.980388 u
_83²⁰⁹Bi nucleus has 83 protons and (209 -83) 126 neutrons.
Hence, the mass defect of this nucleus is given as
Δm’ = 83 x m_H +126 x m_n -m₂
where, mass of a proton, m_H = 1.007825 u
Mass of a neutron, m_n = 1.008665 u
∴Δm’ = 83 x 1.007825 +126 x 1.008665 – 208.980388
= 83.649475 + 127.091790 – 208.980388
= 1.760877 u

But 1u = 931.5 MeV/c²
∴Δm’=1.760877×931.5 MeV/c²
Hence, the binding energy of this nucleus is given as
Eb₂ =Δ m’c²
∴ Eb₂ =1.760877 x 931.5 \(\left(\frac{\mathrm{MeV}}{\mathrm{c}^{2}}\right)\) x c²
= 1640.26 MeV
Average binding energy per nucleon = \(\frac{1640.26}{209}\) =7.848 MeV.

Question 5.
A given coin has a mass of 3.0 g. Calculate the nuclear energy that would be required to separate all the neutrons and protons from each other. For simplicity assume that the coin is entirely made of _29⁶³Cu atoms (of mass 62.92960 u).
Answer:
Mass of the copper coin, m’ = 3 g
Atomic mass of 29 Cu⁶³ atom, m = 62.92960 u
The total number of 29Cu⁶³ atoms in the coin, N = \(\frac{N_{A} \times m^{\prime}}{\text { Mass number }}\)
where, NA = Avogadro’s number = 6.023 x 1023 atoms/g
Mass number =63 g
∴N = \(\frac{6.023 \times 10^{23} \times 3}{63}\) = 2.868 x 10²² atoms

29Cu⁶³ nucleus has 29 protons and (63 -29)34 neutrons
∴ Mass defect of this nucleus, Δ m’ = 29 x m_H +34 x m_n -m
where, mass of a proton, m_H = 1.007825 u
Mass of a neutron, m_n = 1.008665 u
∴Δ m’ = 29 x 1.007825 + 34 x 1.008665 – 62.92960
= 29.226925 + 34.29461 – 62.92960 = 0.591935 u

Mass defect of all the atoms present in the coin,
Δm = 0.591935 x 2.868 x 10²²
= 1.69766958 x 10²² u
But 1 u = 931.5MeV/c²
∴ Δm =1.69766958 x 10²² x 931.5MeV/c²

Hence, the binding energy of the nuclei of the coin is given as
E_b = Δmc²
E_b = 1.69766958 x 10²² x 93.15 \(\left(\frac{\mathrm{MeV}}{\mathrm{c}^{2}}\right)\) x c²
= 1.581 x 10²⁵ MeV
But 1 MeV =1.6 x 10^-13 J
E_b= 1.581 x 10²⁵ x 1.6x 10^-13
= 2.53026 x 10¹² J
This much energy is required to separate all the neutrons and protons from the given coin.

Question 6.
Write nuclear reaction equations for
(i) α-decay of _88²²⁶Ra
(ii) α-decay of \(\frac{242}{94}\) Pu
(iii) β^– – decay of _15³²P
(iv) β^– -decay of _83²¹⁰Bi
(y) β⁺ -decay of _6¹¹C
(vi) β⁺ -decay of _43⁹⁷ Tc
(vii) Electron capture of _54¹²⁰ Xe
Answer:

Question 7.
A radioactive isotope has a half-life of T years. How long will it take the activity to reduce to (a) 3.125% (b) 1% of its original value?
Answer:
Half-life of the radioactive isotope = T years
Original amount of the radioactive isotope = N₀
(a) After decay, the amount of the radioactive isotope = N
It is given that only 3.125% of N₀ remains after decay. Hence, we can write
\(\frac{N}{N_{0}}\) = 3.125% = \(\frac{3.125}{100}=\frac{1}{32}\)
But \(\frac{N}{N_{0}}=e^{-\lambda t}\)
where, λ = Decay constant t = Time

Hence, the isotope will take about 5T years to reduce to 3.125% of its original value.

(b) After decay, the amount of the radioactive isotope = N
It is given that only 1% of N₀ remains after decay. Hence, we can write

Hence, the isotope will take about 6.645 T years to reduce to 1% of its original value.

Question 8.
The normal activity of living carbon-containing matter is found to be about 15 decays per minute for every gram of carbon. This activity arises from the small proportion of radioactive _6¹⁴C present with the stable carbon isotope _6¹⁴C. When the organism is dead, its interaction with the atmosphere (which maintains the above equilibrium activity) ceases and its activity begins to drop. From the known half-life (5730 years) of _6¹²C, and the measured activity, the age of the specimen can be approximately estimated. This is the principle of dating _6¹²C used in archaeology. Suppose a specimen from Mohenjodaro gives an activity of 9 decays per minute per gram of carbon. Estimate the approximate age of the Indus-Valley civilization.
Answer:
Decay rate of living carbon-containing matter, R = 15 decays/min
Let N be the number of radioactive atoms present in a normal carbon-containing matter.
Half-life of _6¹²C, T_1/2 = 5730 years
The decay rate of the specimen obtained from the Mohenjodaro site
R’ = 9 decays/min
Let N be the number of radioactive atoms present in the specimen during the Mohenjodaro period.
Therefore, we can relate the decay constant, λ and time, t as

Hence, the approximate age of the Indus-Valley civilization is 4223.5 years.

Question 9.
Obtain the amount of _27⁶⁰Co necessary to provide a radioactive source of 8.0 mCi strength.
The half-life of _27⁶⁰Co is 5.3 years.
Answer:
The strength of the radioactive source is given as
\(\frac{d N}{d t}\) = 8.0 mCi
= 8 x 10^-3 x 3.7 x 10¹⁰
= 29.6 x 10⁷ decay/s
where, N = Required number of atoms
Half-life of _27⁶⁰Co, T_1/2 = 5.3 years
= 5.3 x 365 x 24 x 60 x 60
= 1.67 x 10⁸ s
For decay constant λ, we have the rate of decay as \(\frac{d N}{d t}\) =λN
Where λ = \(\frac{0.693}{T_{1 / 2}}=\frac{0.693}{1.67 \times 10^{8}} \mathrm{~s}^{-1}\)
∴ N = \(\frac{1}{\lambda} \frac{d N}{d t} \)
= \(\frac{\frac{29.6 \times 10^{7}}{0.693}}{1.67 \times 10^{8}}\) = 7.133 x 10¹⁶ atoms
For ₂₇Co⁶⁰
Mass of 6.023 x 10²³ (Avogadro’s number) atoms = 60 g
∴ Mass of 7.133 x 10¹⁶ atoms = \(\frac{60 \times 7.133 \times 10^{16}}{6.023 \times 10^{23}}\) = 7.106 x 10^-6g
Hence, the amount of ₂₇Co⁶⁰ necessary for the purpose is 7.106 x 10^-6g.

Question 10.
The half-life of _38⁹⁰Sr is 28 years. What is the disintegration rate of 15 mg of this isotope?
Answer;
Half-life of _38⁹⁰Sr, t_1/2 = 28 years
= 28 x 365 x 24 x 60 x 60
= 8.83 x 10⁸s
Mass of the isotope, m = 15 mg
90 g of _38⁹⁰Sr atom contains 6.023 x 10²³ (Avogadro’s number) atoms.
Therefore 15 mg of _38⁹⁰ Sr contains \(\frac{6.023 \times 10^{23} \times 15 \times 10^{-3}}{90}\)
i. e.,1.0038 x 10²⁰ number of atoms
Rate of disintegration, = \(\frac{d N}{d t}=\lambda N\)
where, λ = Decay constant = \(\frac{0.693}{8.83 \times 10^{8}} \mathrm{~s}^{-1}\)
∴ \(\frac{d N}{d t}=\frac{0.693 \times 1.0038 \times 10^{20}}{8.83 \times 10^{8}}\)
= 7.878 x 10¹⁰ atoms/s
Hence, the disintegration rate of 15 mg of the given isotope is 7.878 x 10¹⁰ atoms/s.

Question 11.
Obtain approximately the ratio of the nuclear radii of the gold isotope _79¹⁹⁷Au and the silver isotope _47¹⁰⁷Ag.
Answer:
Nuclear radius of the gold isotope _79¹⁹⁷Au = R_Au
Nuclear radius of the silver isotope _47¹⁰⁷Ag =R_Ag
Mass number of gold, A_AU = 197
Mass number of silver, A_Ag =107
The ratio of the radii of the two nuclei is related with their mass numbers as
\(\frac{R_{\mathrm{Au}}}{R_{\mathrm{Ag}}}=\left(\frac{A_{\mathrm{Au}}}{A_{\mathrm{Ag}}}\right)^{1 / 3}\)
= \(=\left(\frac{197}{107}\right)^{1 / 3}\) = 1.2256
Hence, the ratio of the nuclear radii’of the gold and silver isotopes is about 1.23.

Question 12.
Find the Q- value and the kinetic energy of the emitted α-particle in the a-decay of
(a) _88²²⁶ Ra and (b) _86²²⁰ Rn.
Given m (_88²²⁶Ra) = 226.02540u, m (_86²²²Rn) = 222.01750u,
m(_86²²⁶Rn) = 220.01137 u, (_84²¹⁶Po) = 216.00189 u.
Answer:
(a) Alpha particle decay of _88²²⁶Ra emits a helium nucleus. As a result, its
mass number reduces to (226 – 4) 222 and its atomic number reduces to (88 – 2) 86.
This is shown in the following nuclear reaction
_88²²⁶Ra → _86²²²Rn+ _2⁴He

Q-value of emitted α-particle
= (Sum of initial mass – Sum of final mass) c²
where c = speed of light It is given that
m (_88²²⁶Ra) =226.02540 u
m (_86²²²Rn) = 222.01750 u
m (_2⁴He) = 4.002603 u
Q-value =[226.02540 – (222.01750 + 4.002603)] u c²
= 0.005297 u c²
But 1 u = 931.5 MeV/c²
∴ Q = 0.005297 x 931.5 ≈ 4.94 MeV
I Mass number after decay
Kinetic energy of the α -particle = \(\left(\frac{\text { Mass number after decay }}{\text { Mass number before decay }}\right)\) x Q
=\(\frac{222}{226}\) x 4.94=4.85MeV ,

(b) Alpha particle decay of (_86²²²Rn)
_86²²²Rn + _84²¹⁶Po + _2⁴He
It is given that
Mass of (_86²²⁰Rn) = 220.01137 u
Mass of (_84²¹⁶P0) = 216.00189 u
∴ Q-value =[220.01137 – (216.00189 + 4.002603)] x 931.5 ≈ 641 MeV
Kinetic energy of the α -particle = \(\left(\frac{220-4}{220}\right)\) x 6.41 = 6.29 MeV

Question 13.
The radionuclide ¹¹C decays according to _6¹¹C → _5¹¹B + e⁺ + v: T_1/2 = 20.3 min
The maximum energy of the emitted positron is 0.960 MeV. Given the mass values.
m (_6¹¹C) = 11.011434 u and (_5¹¹B) = 11.009305 u,
calculate Q and compare it with the maximum energy of the positron emitted.
Answer:
Mass difference Δm = m_N(_6¹¹C) – {m_N(_5¹¹B) + m_e}
where, m_N denotes that masses of atomic nuclei.
If we take the masses of atoms, then we have to add 6m_e for ¹¹C and 5m_e
for ¹¹B, then Mass difference
= m(_6¹¹C -6m_e) -{m(_5¹¹B – 5m_e + m_e)}
= {m(¹¹C)-m(_6¹¹B)-2m_e}
= 11.011434 -11.009305 – 2 x 0.000548
= 0.001033 u
Q = 0.001033 x 931.5 MeV
= 0.962 MeV
This energy is nearly the same as energy carried by positron (0.960 MeV). The reason is that the daughter nucleus is too heavy as compared to e⁺ and v, so it carries negligible kinetic energy. Total kinetic energy is shared by positron and neutrino; here energy carried by neutrino (E_v) is minimum so that energy carried by positron (E_e) is maximum (practically, E_e ≈ Q).

Question 14.
The nucleus _10²³Ne decays by β^– emission. Write down the β decay equation and determine the maximum kinetic energy of the electrons emitted. Given that: m (_10²³Ne) = 22.994466 u m (_11²³Na) = 22.089770 u
Answer:
In β^– emission, the number of protons increases by 1, and one electron and an antineutrino are emitted from the parent nucleus. β^– emission of the nucleus _10²³Ne
_10²³Ne → _11²³Na +e^–+\(\bar{v}\) +Q
It is given that
Atomic mass m of (_10²³Ne) = 22.994466 u
Atomic mass m of (_11²³ Na) = 22.089770 u
Mass of an electron, m_e = 0.000548 u
Q-value of the given reaction is given as
Q = [m(_10²³Ne)-{m(_11²³Na) + m_e}]c²
There are 10 electrons in _10²³Ne and 11 electrons in _11²³Na.
Hence, the mass of the electron is cancelled in the Q-value equation.
∴ Q = [22.994466 -22.089770] c²
= 0.004696 uc²
But 1 u = 981.5 MeV/c²
∴ Q = 0.004696 uc² x 931.5 = 4.374 MeV
The daughter nucleus is too fifeavy as compared to e^– and \(\bar{v}\).
Hence, it carries negligible energy. The kinetic energy of the antineutrino is nearly zero.
Hence, the maximum kinetic energy of the emitted electrons is almost equal to the Q-value, i. e., 4.374 MeV.

Question 15.
The Q value of a nuclear reaction A + b → C + d is defined by Q = [m_A + m_b -m_c -m_d]c²
where the masses refer to the respective nuclei. Determine from the given data the Q-value of the following reactions and state whether the reactions are exothermic or endothermic.
(i) _1¹H + _1³H → _1²H + _1²H
(ii) _6¹² C + _6¹² C → _10²⁰Ne + ₂He
Atomic masses are given to be
m (₁₂H) = 2.014102 u
m(_1³H) = 3.016049 u
m(_6¹²C) = 12.000000 u
m(_10²⁰Ne) = 19.992439 u
Answer:
(i) The given nuclear reaction is
_1¹H + _1³H → _1²H + _1²H
It is given that
Atomic mass m of (_1¹H) = 1.007825 u
Atomic mass m of (_1³H) = 3.016049 u
Atomic mass m of (_1²H) = 2.014102 u

According to the question, the Q-value of the reaction can be written as
Q = [m (_1¹H) + m (_1³H) -2m (_1²H)] c²
= [1.007825 + 3.016049 – 2 x 2.014102] c²
Q = (-0.00433 c²)u
But 1 u = 931.5MeV/c²
∴ Q = -0.00433 x 931.5 = -4.0334 MeV
The negative Q-value of the reaction shows that the reaction is endothermic.

(ii) The given nuclear reaction is
_12⁶C + _12⁶C → _10²⁰Ne + _2⁴He
It is given that
Atomic mass m of (_12⁶C) = 12.0 u
Atomic mass m of (_10²⁰Ne) = 19.992439 u
Atomic mass m of (_2⁴He) = 4.002603 u
The Q-value of this reaction is given as
Q = [2m (_12⁶C) – m (_10²⁰Ne) – m (_2⁴He)] c²
= [2 x 12.0 -19.992439 – 4.002603] c²
= (0.004958 c²) u
But 1 u = 931.5 MeV/c²
Q = 0.004958 x 931.5 = 4.618377 MeV
The positive Q-value of the reaction shows that the reaction is exothermic.

Question 16.
Suppose, we think of fission of a _26⁵⁶Fe nucleus into two equal fragments, _13²⁸Al. Is the fission energetically possible? Argue by working out Q of the process. Given m (_26⁵⁶Fe) = 55.93494 u and m(_13²⁸Al) = 27.98191 u.
Answer:
The fission of _26⁵⁶Fe can be given as
_26⁵⁶ Fe →2 _13²⁸Al
It is given that
Atomic mass m of (_26⁵⁶Fe) = 55.93494 u
Atomic mass m of (_13²⁸Al) = 27.98191 u
The Q-value of this nuclear reaction is given as
Q = [m (_26⁵⁶Fe) -2m (_13²⁸Al)] c²
= [55.93494 – 2 x 27.98191] c²
= (-0.02888 c²) u
Butl u = 931.5 MeV/c2
∴ Q =-0.02888 x 931.5 =-26.902 MeV
The Q-value of the fission is negative. Therefore, the fission is not possible energetically. For an energetically-possible fission reaction, the Q-value must be positive.

Question 17.
The fission properties of _94²³⁹Pu are very similar to those of _94²³⁹U. The average energy released per fission is 180 MeV. How much energy, in MeV, is released if all the atoms in 1 kg of pure _94²³⁹Pu undergo fission?
Answer:
Average energy released per fission of _94²³⁹Pu, E_av = 180 MeV
Amount of pure 94Pu²³⁹, m = 1 kg = 1000 g
N_A = Avogadro number = 6.023 x 10²³
Mass number of _94²³⁹Pu = 239 g

1 mole of ₉₄Pu²³⁹ contains N_A atoms
∴ 1 kg of 94Pu²³⁹ contains \(\left(\frac{N_{A}}{\text { Mass number }} \times m\right)\) atoms
= \(\frac{6.023 \times 10^{23}}{239} \times 1000\) = 2.52 x 10²⁴ atoms
∴ Total energy released during the fission of 1 kg of _94²³⁹ Pu is calculated as
E = E_av x 2.52 x10²⁴
= 180 x 2.52 x 10²⁴
= 4.536 x 10²⁶ MeV
Hence, 4.536 x10²⁶ MeV is released if all the atoms in 1 kg of pure ₉₄Pu²³⁹ undergo fission.

Question 18.
A 1000 MW fission reactor consumes half of its fuel in 5.00 y. How much _92²³⁵U did it contain initially? Assume that the reactor operates 80% of the time, that all the energy generated arises from the fission of _92²³⁵U, and that this nuclide is consumed only by the fission process.
Answer:
Half-life of the fuel of the fission reactor, t_1/2 =5 years.
= 5 x 365 x 24 x 60 x 60 s
We know that in the fission of 1 g of _92²³⁵ U nucleus, the energy released is equal to 200 MeV.
1 mole, i. e., 235 g of _92²³⁵ U contains 6.023 x 10²³ atoms.
∴ 1 g of _92²³⁵ U= \(\frac{6.023 \times 10^{23}}{235} \) atoms

The total energy generated per gram of _92²³⁵U is calculated as
E= \(\frac{6.023 \times 10^{23}}{235} \times 200 \mathrm{MeV} / \mathrm{g}\)
= \(\frac{200 \times 6.023 \times 10^{23} \times 1.6 \times 10^{-19} \times 10^{6}}{235}\)
= 8.20 x 10¹⁰ J/g
The reactor operates only 80% of the time.

Hence, the amount of _92²³⁵ U consumed in 5 years by the 1000 MW fission
reactor is calculated as
= \(\frac{5 \times 80 \times 60 \times 60 \times 365 \times 24 \times 1000 \times 10^{6}}{100 \times 8.20 \times 10^{10}} \mathrm{~g}\)
≈1538 kg
∴ Initial amount of _92²³⁵U = 2 x 1538 = 3076 kg.

Question 19.
How long can an electric lamp of 100 W be kept glowing by fusion of 2.0 kg of deuterium? Take the fusion reaction as The given fusion reaction is _1²H + _1²H → _2³He+n +3.27 MeV
Answer:
The given fusion reaction is
_1²H + _1²H → _2³He+n +3.27 MeV
Amount of deuterium, m = 2 kg
1 mole, i.e., 2 g of deuterium contains 6.023 x 10²³ atoms.
∴ 2.0 kg of deuterium contains = \(\frac{6.023 \times 10^{23}}{2} \times 2000\)
= 6.023 x 10 ²⁶ atoms

It can be inferred from the given reaction that ‘when two atoms of deuterium fuse, 3.27 MeV energy is released. ” ‘
∴ Total energy per nucleus released in the fusion reaction
E = \(\frac{3.27}{2} \times 6,023 \times 10^{26} \mathrm{MeV}\)
= \(\frac{3.27}{2} \times 6.023 \times 10^{26} \times 1.6 \times 10^{-19} \times 10^{6}\)
= 1.576 x 10¹⁴ J
Power of the electric lamp, P = 100 W = 100 J/s
Hence, the energy consumed by the lamp per second = 100 J
The total time for which the electric lamp will glow is calculated as \(\frac{1.576 \times 10^{14}}{100 \times 60 \times 60 \times 24 \times 365}\)
≈ 4.9 x 10⁴ years

Question 20.
Calculate the height of the potential harrier for a head-on collision of two deuterons. (Hint: The height of the potential barrier is given by the Coulomb repulsion between the two deuterons when they just touch each other. Assume that they can be taken as hard spheres of radius 2.0 fm).
Answer:
When two deuterons collide head-on, the distance between their centres, d is given as Radius of 1st deuteron + Radius of 2 nd deuteron
Radius of a deuteron nucleus = 2 fm =2 x 10^-15 m
∴ d = 2x 10^-15 +2 x 10^-15
=4 x 10^-15 m
Charge on a deuteron nucleus = Charge on an electron = e =1.6 x 10^-19C
Potential energy of the two-deuteron system
V = \(\frac{e^{2}}{4 \pi \varepsilon_{0} d} \)
where, \(\varepsilon_{0}\) = permittivity of free space


= 360 keV
Hence, the height of the potential barrier of the two-deuteron system is 360 keV.

Question 21.
From the relation R = R₀A^1/3, where R₀ is a constant and A is the mass number of a nucleus, show that the nuclear matter density is nearly constant (i. e., independent of A).
Answer:
We have the expression for nuclear radius as
R=R₀A^1/3
where, R0 = Constant.
Nuclear matter density, ρ = \(\frac{\text { Mass of the nucleus }}{\text { Volume of the nucleus }}\)
Let m be the average mass of the nucleus.
Hence, mass of the nucleus = mA

Hence, the nuclear matter density is independent; of A. It is nearly constant.

Question 22.
For the β⁺ (positron) emission from a nucleus, there is another competing process known as electron capture (electron from an inner orbit, say, the K-shell, is captured by the nucleus, and a neutrino is emitted.)
e⁺ + _A^Z X → _z-1^AY+ u
Show that if β⁺ emission is energetically allowed, electron capture is necessarily allowed but not vice-Versa.
Answer:
Let the amount of energy released during the electron capture process be Q₁.
The nuclear reaction can be written as
e⁺ + _A^Z X → _z-1Y+ v+ Q₁ …………..(1)
Let the amount of energy released during the positron capture process be Q₂.
The nuclear reaction can be written as
e⁺ + _A^Z X → _z-1Y+e⁺+ v+ Q₂ ……………………..(2)
m_N (_z^AX) = Nuclear mass of _z^A X
m_N (_z-1^AY) = Nuclear mass of ^z-1AY
m(_ZAX) = Atomic mass of _Z^A X
m (_z-1^A Y) = Atomic mass of _z-1^AY
m_e = Mass of an electron
c = Speed of light
Q-value of the electron capture reaction is given as


It can be inferred that if Q₂ > 0, then Q₁ > 0; Also, if Q₁> 0, it does not necessarily mean that Q₂ > 0.
In other words, this means that if β⁺ emission is energetically allowed, then the electron capture process is necessarily allowed, but not vice-versa. This is because the Q-value must be positive for an energetically-allowed nuclear reaction.

Additional Exercises

Question 23.
In a periodic table the average atomic mass of magnesium is given as 24.312 u. The average value is based on their relative natural abundance on earth. The three isotopes and their masses are _12²⁴ Mg (23.98504 u), _12²⁵Mg (24.98584 u) and _12²⁶Mg (25.98259 u). The natural abundance of _12²⁴Mg is 78.99% by mass. Calculate the abundances of other two isotopes.
Answer:
Average atomic mass of magnesium, m = 24.312 u
Mass of magnesium _12²⁴Mg isotope, m₁ = 23.98504 u
Mass of magnesium _12²⁵Mg isotope, m₂ = 24.98584 u
Mass of magnesium _12²⁶ Mg isotope, m₃ = 25.98259 u
Abundance of _12²⁴Mg, n₁ = 78.99%
Abundance of _12²⁵Mg, n₂ = x%
Hence, abundance of _12²⁶ Mg, n₃ = 100 – x- 78.99% = (21.01 – x)%

We have the relation for the average atomic mass as
m = \(\frac{m_{1} n_{1}+m_{2} n_{2}+m_{3} n_{3}}{n_{1}+n_{2}+n_{3}}\)
243.12 = \(\frac{23.98504 \times 78.99+24.98584 \times x+25.98259 \times(21.01-x)}{100}\)
2431.2 = 1894.5783096 + 24.98584x + 545.8942159- 25.98259 x
0.99675x =9.2725255
∴ x ≈ 9.3%
and 21.01-x =11.71%
Hence, the abundance of _12²⁵Mg is 9.3% and that of _12²⁶ Mg is 11.71%.

Question 24.
The neutron separation energy is defined as the energy required to remove a neutron from the nucleus.
Obtain the neutron separation energies of the nuclei _20⁴¹Ca and _13²⁷Al from
the following data:
m(_20⁴⁰Ca) = 39-962591u
m (_20⁴¹ Ca) = 40.962278 u
m (_26¹³Al) = 25.986895 u
m (_27¹³Al) = 26.981541 u
Answer:
For _20⁴¹Ca : Separation energy = 8.363007 MeV
For _27¹³ A1: Separation energy = 13.059 MeV
(_on¹) is removed from a _20⁴¹Ca.

Thus, the corresponding nuclear reaction can be written as
_20⁴¹Ca → _20⁴⁰Ca + _0¹n
It is given that
m(_20⁴⁰Ca) = 39.962591 u
m(_20⁴¹Ca )= 40.962278 u
m(_on¹) = 1.008665 u
The mass defect of this reaction is given as
Δm = m(_20⁴⁰Ca) + (_0¹n )-m(_20⁴¹Ca)
= 39.962591 +1.008665 – 40.962278
= 0.008978 u

But 1 u = 931.5 MeV/c²
∴ Δm = 0.008978×931.5 MeV/c²
Hence, the energy required for neutron removal is calculated as
E = Δmc²
= 0.008978 x 931.5 = 8.363007 MeV
For _13²⁷ Al, the neutron removal reaction can be written as
_13²⁷Al → _13²⁶ Al + _0¹n
It is given that
m (_13²⁷Al) = 26.981541 u
m (_13²⁶ Al) = 25.986895 u
The mass defect of this reaction is given as
Δm = m (_13²⁶ Al) + m (_0¹n) – m (_13²⁷ Al)
= 25.986895 +1.008665 – 26.981541
= 0.014019 u

But 1 u = 931.5 MeV/c2
∴ Δm = 0.014019 x 931.5 MeV/c²
Hence, the energy required for neutron removal is calculated as
E = Δmc²
= 0.014019 x 931.5 = 13.059 MeV

Question 25.
A source contains two phosphorous radio nudides _15³²P (TM_1/2 =14.3d)
and _15³³P (T_1/2 =253d). Initially, 10% of the
decays come from _15³³P. How long one must wait until 90% do so?
Answer:
Let radionuclide be represented as P₁ (T_1/2 =14.3 days) and
P₂(T_1/2 = 25.3 days).
Initial decay is 90% from P₁ and 10% from P₂. With the passage of rime,
amount of P₁ will decrease faster than that of P₂.

As rate of disintegration ∝ N or mass M. Initial ratio of P₁ to P₂ is 9: 1. Let mass of P₁ be 9x and that of P₂ be x. Let after t days mass of P₁ become y and that of P₂ become 9y.
Using half-life formula, \(\frac{M}{M_{0}}=\left(\frac{1}{2}\right)^{n}\) , where n is number of half lives,
n = \(\frac{t}{T_{1}}\)
\( \frac{y}{9 x}=\left(\frac{1}{2}\right)^{n_{i}}\) ……………………. (1)
Where, n₁ = \(\frac{t}{T_{2}}\)
\(\frac{9 y}{x}=\left(\frac{1}{2}\right)^{n_{2}}\) …………………………… (2)
On dividing eq.(1) by eq(2), we get

log 1- log 81 = t\(\left(\frac{1}{T_{1}}-\frac{1}{T_{2}}\right)\) \((\log 1-\log 2)\)

Question 26.
Under certain circumstances, a nucleus can decay by emitting a particle more massive than an a-particle. Consider the following decay processes:
_88²²³Ra → _82²⁰⁹Pb+ _6¹⁴C
_88²²³Ra → _86²¹⁹Rn + _2⁴He
Calculate the Q-values for these decays and determine that both are energetically allowed.
Answer:
Take a _6¹⁴C emission nuclear reaction
_88²²³Ra → _82²⁰⁹Pb+ _6¹⁴C
We know that
Mass of _88²²³Ra, m₁ = 223.01850 u
Mass of _82²⁰⁹ Pb, m₂ = 208.98107 u
Mass of _6¹⁴C, m₃ = 14.00324 u
Hence, the Q-value of the reaction is given as
Q = (m₁-m₂-m₃‘)c²
= (223.01850 -208.98107-14.00324)c²
= (0.03419 c²)u
But 1u = 931.5 MeV/c²
∴ Q = 0.03419 x 931.5 = 31.848 MeV

Hence, the Q-value of the nuclear reaction is 31.848 MeV. Since the value is positive, the reaction is energetically allowed.
Now take a _2⁴He emission nuclear reaction
_88²²³Ra → _86²¹⁹Rn + _2⁴He
We know that
Mass of _88²²³Ra, m₁ = 223.01850
Mass of _86²¹⁹Rn, m₂ = 219.00948
Mass of _2⁴He, m₃ = 4.00260
Q-value of this nuclear reaction is given as
Q = (m₁-m₂-m₃)c²
= (223.01850 -219.00948-4.00260)c²
= (0.00642 c²)u
= 0.00642 x 931.5 = 5.98 MeV
Hence, the Q value of the second nuclear reaction is 5.98 MeV. Since the value is positive, the reaction is energetically allowed.

Question 27.
Consider the fission of _92²³⁸U by fast neutrons. In one fission event, no neutrons are emitted and the final end products, after the beta decay of the primary fragments, are _58¹⁴⁰Ce and _44⁹⁹Ru.
Calculate Q for this fission process. The relevant atomic and particle masses are .
m = ( _92²³⁸U) = 238.05079 u
m = ( _58¹⁴⁰Ce) = 139.90543 u
m = ( _44⁹⁹Ru) = 98.90594 u
Answer:
In the fission of _92²³⁸U, 10β^– particles decay from the parent nucleus. The nuclear reaction can be written as
_92²³⁸U +_0¹n → _58¹⁴⁰Ce+_44⁹⁹Ru+10_-1⁰e

It is given that
Mass of a nucleus, m₁(_92²³⁸U) = 238.05079 u
Mass of a nucleus, m₂(_58¹⁴⁰Ce) = 139.90543 u
Mass of a nucleus,m₃ (_44⁹⁹Ru) = 98.90543 u
Mass of a neutron,m₄ (_0¹n) = 1.008665 u
Q-value of the above equation,
Q = [m'(_92²³⁸U) + m(_0¹n) – m'(_58¹⁴⁰Ce) – m'(_44⁹⁹Ru) -10 m_e]c²
Where, m’ represents the corresponding atomic masses of the nuclei,
m'(_92²³⁸U) = m1 – 92 m_e
m’ (_58¹⁴⁰Ce) = m₂ – 58m_e
m’ (_44⁹⁹Ru) = m₂ – 44 m_e
m(_0¹n) = m₄

But 1u = 931.5 MeV/c²
∴ Q = 0.247995 x 931.5 = 231.007 MeV
Hence, the Q-value of the fission process is 231.007 MeV.

Question 28.
Consider the D-T reaction (deuterium-tritium fusion)
_1²H +H _1³ →_2⁴He + n
(a) Calculate the energy released in MeV in this reaction from the data
m (_1²H) = 2.014102 u
m(H _1³) = 3.016049 u

(b) Consider the radius of both deuterium and tritium to be approximately 2.0 fm. What is the kinetic energy needed to overcome the coulomb repulsion between the two nuclei? To what temperature must the gas be heated to initiate the reaction? (Hint: Kinetic energy required for one fusion event = average thermal kinetic energy available with the interacting particles =2(3kT/2);k = Boltzman’s constant, T = absolute temperature.)
Answer:
(a) Take the D-T nuclear reaction :
_1²H +H _1³ →_2⁴He + n
It is given that
Mass of _1²H, m₁ = 2.014102 u
Mass of H _1³, m₂ = 3.016049 u
Mass of _2⁴He, m₃ = 4.002603 u
Mass of _0¹n, m₄ = 1.008665 u
Q-value of the given D-T reaction is
Q = [m₁ + m₂ – m₃ – m₄]c²
= [2.014102 + 3.016049 – 4.002603 -1.008665]c²
= [0.018883 c²]u
But 1 u = 931.5 MeV/c²
∴ Q = 0.018883 x 931.5 = 17.59 MeV

(b) Radius of deuterium and tritium, r ≈ 2.0 fm = 2 x 10^-15 m
Distance between the two nuclei at the moment when they touch each other,
d = r + r = 4 x 10^-15 m
Charge on the deuterium nucleus = e
Charge on the tritium nucleus = e
Hence, the repulsive potential energy between the two nuclei is given as
V = \(\frac{e^{2}}{4 \pi \varepsilon_{0}(d)}\)
Where, \(\varepsilon_{0}\) = Permittivity of free space

Hence, 5.76 x 10^-14 J or 360 key of kinetic energy (KE) is needed to overcome the Coulomb repulsion between the two nuclei.
However, it is given that
K.E = 2 x \(\frac{3}{2}\) kt
where, k = Boltzmann constant = 1.38 x 10^-23 m² kg s^-2 K^-1
T = Temperature required for triggering the reaction
T = \(\frac{K E}{3 K}\)
= \(\frac{5.76 \times 10^{-14}}{3 \times 1.38 \times 10^{-23}}\)
= 1.39 x 10⁹ K
Hence, the gas must be heated to a temperature of1.39 x 10⁹ K to initiate the reaction.

Question 29.
Obtain the maximum kinetic energy of β-particles, and the radiation frequencies of y decays in the decay scheme shown in Fig. 13.6. You are given that

It can be observed from the given γ-decay diagram that γ₁ decays from 1.088 MeV
energy level to the O’MeV energy level.
Hence, the energy corresponding to γ₁-decay is given as
E₁ =1.088-0 =1.088 MeV
hv₁ = 1.088 x 1.6 x 10^-19 x 10⁶
where, h = Planck’s constant = 6.63 x 10^-34 Js
v₁ = frequency of radiation radiated by γ₁ -decay.
∴ v₁ = \(\frac{E_{1}}{h}\)
= \(\frac{1.088 \times 1.6 \times 10^{-19} \times 10^{6}}{6.63 \times 10^{-34}}\)
= 2.637 x 10²⁰ Hz
It can be observed from the given γ-decay diagram that γ₂ decays from 0.412 MeV energy level to the 0 MeV energy level.
Hence, the energy corresponding to γ₂-decay is given as :
E₂ =0.412-0 =0.412 MeV
hv₂ = 0.412 x 1.6 x 10^-19 x 10⁶ J
where, v₂ = frequency of radiation radiated by γ₂-decay

It can be observed from the given γ-decay diagram that γ₂ decays from the 1.088 MeV energy level to the 0.412 MeV energy level.
Hence, the energy corresponding to γ₃ -decay is given as
E₃ =1.088- 0.412 = 0.676 MeV
hv₃ = 0.676 x 1.6 x 10 ^-19 J

where, v₃ = frequency of radiation radiated by γ₃-decay
∴ v₃ = \(\frac{E_{3}}{h}=\frac{0.676 \times 1.6 \times 10^{-19} \times 10^{6}}{6.63 \times 10^{-34}}\)
= 1.639 x 10²⁰ Hz
Mass of m (_79¹⁹⁸ Au) = 197.968233 u
Mass of m (_80¹⁹⁸Hg) = 197.966760 u
1 u = 931.5 MeV/c²
Energy of the highest level is given as
E =[ (_79¹⁹⁸ Au) – m (_80¹⁹⁸Hg)]
= 197.968233 -197.966760
= 0.001473 u
= 0.001473 x 931.5 = 1.3720995 MeV
β₁ decays from the 1.3720995 MeV level to the 1.088 MeV level
Maximum kinetic energy of the β₁ particle = 1.3720995 – 1.088
= 0.2840995 MeV
β₂ decays from the 1.3720995.MeV level to the 0.412 MeV level ,
∴ Maximum kinetic energy of the β₂ particle = 1.3720995-0.412
= 0.9600995 MeV

Questions 30.
Calculate and compare the energy released by
(a) fusion of 1.0 kg of hydrogen deep within Sun and
(b) the fission of 1.0 kg of _92²³⁵U in a fission reactor.
Answer:
(a) Amount of hydrogen, m = 1 kg = 1000 g
1 mole, i. e, 1 g of hydrogen (_1¹H) contains 6.023 x 10²³ atoms.
∴ 1000 g of _1¹H contains 6.023 x 10²³ x 1000 atoms.
Within the sun, four _1¹H nuclei combine and form one _2⁴He nucleus. In this process 26 MeV of energy is released.
Hence, the energy released from the fusion of 1 kg _1¹H is
E₁ = \(\frac{6.023 \times 10^{23} \times 26 \times 10^{3}}{4}\)
= 39.1495 x 10²⁶MeV

(b) Amount of _92²³⁵U = 1 kg = 1000 g
1 mole, i. e., 235 g of _92²³⁵U contains 6.023 x 10²³ atoms.
∴1000 g of _92²³⁵U contains \(\frac{6.023 \times 10^{23} \times 1000}{235}\)atoms
It is known that the amount of energy released in the fission of one atom of _92²³⁵U is 200 MeV.
Hence, energy released from the fission of 1 kg of _92²³⁵U is
E₂ = \(\frac{6.023 \times 10^{23} \times 1000 \times 200}{235}\)
= 5.106 x 10²⁶ MeV
∴ \(\frac{E_{1}}{E_{2}}=\frac{39.1495 \times 10^{26}}{5.106 \times 10^{26}}\) = 7.67 ≈ 8
Therefore, the energy released in the fusion of 1 kg of hydrogen is nearly 8 times the energy released in the fission of 1 kg of uranium.

Question 31.
Suppose India had a target of producing by 2020 AD, 200,000 MW of electric power, ten percent of which was to be obtained from nuclear power plants. Suppose we are given that, on an average, the efficiency of utilization (i. e., conversion to electric energy) of thermal energy produced in a reactor was 25%. How much amount of fissionable uranium would our country need per year by 2020? Take the heat energy per fission of ²³⁵U to be about 200 MeV.
Answer:
Amount of electric power to be generated, P = 2 x10⁵ MW
10% of this amount has to be obtained from nuclear power plants.
P₁ = \(\frac{10}{100}\) x 2 x 10⁵
∴ Amount of nuclear power,
= 2 x 10⁴ MW
= 2x 104 x 10⁶ J/s
= 2 x 1010 x 60 x 60 x 24 x 365 J/y
Heat energy released per fission of a ²³⁵ U nucleus, E = 200 MeV
Efficiency of a reactor = 25%
Hence, the amount of energy converted into the electrical energy per fission is calculated as
\(\frac{25}{100} \times 200=50 \mathrm{MeV}=50 \times 1.6 \times 10^{-19} \times 10^{6}=8 \times 10^{-12} \mathrm{~J} \)
Number of atoms required for fission per year
\(\frac{2 \times 10^{10} \times 60 \times 60 \times 24 \times 365}{8 \times 10^{-12}}\) = 78840 x 10²⁴ atoms
1 mole, i. e., 235 g of U²³⁵ contains 6.023 x 10²³ atoms.
∴ Mass of 6.023 x 10²³ atoms of U²³⁵ = 235 g = 235 x 10^-3 kg
∴ Mass of 78840×10²⁴ atoms of U²³⁵ = \(\frac{235 \times 10^{-3}}{6.023 \times 10^{23}} \times 78840 \times 10^{24}\)
= 3.076 x10⁴ kg
Hence, the mass of uranium needed per year is 3.076 x 10⁴ kg.

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 2 Electrostatic Potential and Capacitance Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance

PSEB 12th Class Physics Guide Electrostatic Potential and Capacitance Textbook Questions and Answers

Question 1.
Two charges 5 × 10^-8 C and -3 × 10^-8 C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
Answer:
There are two charges,
q ₁ = 5 × 10^-8 C
q₂ = -3 × 10^-8 C
Distance between the two charges, d =16 cm = 0.16 m
Consider a point P on the line joining the two charges, as shown in the given figure

r = Distance of point P from charge q₁
Let the electric potential (V) at point P be zero. r.
Potential at point P is the sum of potentials caused by charges q₁ and q₂ respectively.

∴ r = 0.1m = 10 cm
Therefore, the potential is zero at a distance of 10 cm from the positive charge between the charges.

Suppose point P is outside the system of two charges at a distance s from the negative charge, where potential is zero, as shown in the following figure:

For this arrangement, potential is given by,

∴ s = 0.4 m = 40 cm
Therefore, the potential is zero at a distance of 40 cm from the positive charge outside the system of charges.

Question 2.
A regular hexagon of side 10 cm has a charge 5 μC at each of its vertices. Calculate the potential at the centre of the hexagon.
Answer:
The given figure shows six equal amount of charges q, at the vertices of a regular hexagon.

where, charge, q = 5μC = 5 × 10^-6C
Side of the hexagon,
l = AB = BC = CD = DE = EF = FA = 10 cm
Distance of each vertex from centre, O, d = 10 cm = 0.1 m
Electric potential at point O,
V = \(\frac{6 \times q}{4 \pi \varepsilon_{0} d}\)
∴ \(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 × 10⁹NC^-2m^-2
∴ V = \(\frac{6 \times 9 \times 10^{9} \times 5 \times 10^{-6}}{0.1}\) = 2.7 × 10⁶ V
Therefore, the potential at the centre of the hexagon is 2.7 × 10⁶ V.

Question 3.
Two charges 2 μC and -2μC are placed at points A and B 6 cm apart.
(a) Identify an equipotential surface of the system.
(b) What is the direction of the electric field at every point on this surface?
Answer:
(a) Here, two charges 2 μC and -2μC are situated at points A and B.
∴ AB = 6 cm = 0.06 m

For the given system of two charges, the equipotential surface is a plane normal to the line joining points A and B. The plane passes through the mid point C of the line AB. The potential at C is

Thus potential at all points lying on this plane is equal and is zero, so it is an equipotential surface.

(b) We know that the electric field always acts from +ve to -ve charge, thus here the electric field acts from point A (having +ve charge) to point B (having -ve charge) and is normal to the equipotential surface.

Question 4.
A spherical conductor of radius 12 cm has a charge of 1.6 x 10^-7 C distributed uniformly on its surface. What is the electric field
(a) inside the sphere
(b) just outside the sphere
(c) at a point 18 cm from the centre of the sphere?
Answer:
Radius of the spherical conductor, r = 12cm = 0.12m
Charge is uniformly distributed over the conductor, q = 1.6 x 10^-7C
(a) Electric field inside a spherical conductor is zero. This is because if there is field inside the conductor, then charges will move to neutralize it.

(b) Electric field E just outside the conductor is given by the relation,
E = \(\frac{q}{4 \pi \varepsilon_{0} r^{2}}\)
\(=\frac{1.6 \times 10^{-7} \times 9 \times 10^{5}}{(0.12)^{2}}[latex] = 10⁵ NC ^-1
(0.12) 2
Therefore, the electric field just outside the sphere is 10⁵ NC^-1

(c) Electric field at a point 18 m from the centre of the sphere = E₁
Distance of the point from the centre, d=18cm = 0.18m
E₁ = [latex]\frac{q}{4 \pi \varepsilon_{0} d^{2}}\)
= \(\frac{9 \times 10^{9} \times 1.6 \times 10^{-7}}{\left(18 \times 10^{-2}\right)^{2}}\)
= 4.4 × 10⁴ N/C
Therefore, the electric field at a point 18 cm from the centre of the sphere is 4.4 × 10⁴N/C.

Question 5.
A parallel plate capacitor with air between the plates has a capacitance of 8 pF (1 pF = 10^-2 F). What will be the capacitance if the distance between the plates is reduced by half, and the space between them is filled with a substance of dielectric constant 6?
Answer:
Capacitance between the parallel plates of the capacitor, C = 8 pF
Initially, distance between the parallel plates was d and it was filled with air. Dielectric constant of air, k = 1
Capacitance, C is given by the formula,
C = \(\frac{k \varepsilon_{0} A}{d}[latex]
= [latex]\frac{\varepsilon_{0} A}{d}\) …………… (1)

If distance between the plates is reduced to half, then new distance,
d’ = \(\frac{d}{2}\)
Dielectric constant of the substance filled in between the plates, k’ Hence, capacitance of the capacitor becomes
C’ = \(\frac{k^{\prime} \varepsilon_{0} A}{d^{\prime}}=\frac{6 \varepsilon_{0}^{*} A}{\frac{d}{2}}\) …………….. (2)
Taking ratios of equations (1) and (2), we obtain
C’ = 2 × 6C
= 12C
= 12 × 8 = 96 pF
Therefore, the capacitance between the plates is 96 pF.

Question 6.
Three capacitors each of capacitance 9 pF are connected in series.
(a) What is the total capacitance of the combination?
(b) What is the potential difference across each capacitor if the combination is connected to a 120 V supply?
Answer:
(a) Given C₁ = C₂ = C₃ = 9 pF
When capacitors are connected in series, the equivalent capacitance Cs is given by
\(\frac{1}{C_{S}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}=\frac{1}{9}+\frac{1}{9}+\frac{1}{9}=\frac{3}{9}=\frac{1}{3}\)
C_S 3PF

(b) In series charge on each capacitor remains the same, so charge on each capacitor.
q = C_SV = (3 × 10^-12 F) × (120 V)
= 3.6 × 10^-10 coulomb
Potential difference across each capacitor, q 3.6 × 10^-10
V = \(\frac{q}{C_{1}}=\frac{3.6 \times 10^{-10}}{9 \times 10^{-12}}\) = 40V

Question 7.
Three capacitors of capacitances 2 pF, 3 pF and 4pF are connected in parallel
(a) What is the total capacitance of the combination?
(b) Determine the charge on each capacitor if the combination is connected to a 100 V supply.
Answer:
C₁ = 2 pF, C₂ = 3 pF, C₃ = 4 pF
(a) Total capacitance when connected in parallel,
C_p = C₁ + C₂ + C₃ = 2 + 3 + 4 = 9 pF,

(b) In parallel, the potential difference across each capacitor remains the same, i.e.,
V = 100 V.
Charge on C₁ = 2 pF,
q₁ = C₁V = 2 × 10^-12 × 100
= 2 × 10 ^-10C

Charge on C₂ = 3pF,
q₂ = C₂V = 3 × 10^-10 × 100
= 3 × 10^-10 C

Charge on C₃ = 4 pF,
q₃ = C₃V = 4 × 10^-12 × 100
= 4 × 10^-10C

Question 8.
In a parallel plate capacitor with air between the plates, each plate has an area of 6 × 10^-3 m² and the distance between the plates is 3 mm. Calculate the capacitance of the capacitor. If this capacitor is connected to a 100 V supply, what is the charge on each plate of the capacitor?
Answer:
Area of each plate of the parallel plate capacitor, A = 6 10^-3m²
Distance between the plates, d = 3 mm = 3 × 10^-3 m
Supply voltage, V = 100 V
Capacitance C of a parallel plate capacitor is given by,
C = \(\frac{\varepsilon_{0} A}{d}\)
where, ε₀ = 8.854 × 10^-12 N^-1m^-2C^-2
C = \(\frac{8.854 \times 10^{-12} \times 6 \times 10^{-3}}{3 \times 10^{-3}}\)
= 17.71 × 10^-12F
= 17.71 pF or 18 pF

Potential V is related with the charge q and capacitance C as
V = \(\frac{q}{C}\)
∴ q = VC = 100 × 17.71 × 10^-12
= 1.771 × 10⁹C
Therefore, capacitance of the capacitor is 17.71 pF and charge on each plate is 1.771 × 10^-9 C.

Question 9.
Explain what would happen if in the capacitor given in Exercise 2.8, a 3 mm thick mica sheet (of dielectric constant = 6) were inserted between the plates,
(a) while the voltage supply remained connected.
(b) after the supply was disconnected.
Answer:
(a) Here C₀ = Capacitance of the capacitor with air as medium = 18 pF
d = distance between the plates = 3 × 10^-3 m
t = thickness of mica sheet = 3 × 10^-3 m = d
K = dielectric constant of the mica sheet = 6

As the mica sheet completely fills the space between the plates, thus the capacitance of the capacitor (C) is given by
C =KC₀ = 6 × 18 × 10^-12 F
= 108 × 10^-12 F = 108 pF
Thus the capacitance of the capacitor increases by K times on inserting the mica sheet.
Potential difference across this capacitor, V = 100 V
∴ Charge q’ on the capacitor with mica sheet as medium is given by
q’ = CV= 108 × 10^-12 × 100
= 108 × 10^-8 C
Now clearly q’ = KC₀V = Kq = 6 × 1.8 × 10^-9
= 1.08 × 10^-8C

Clearly charge becomes K times the charge on the plates with air as medium, i.e., charge on the plates increases when supply remains connected and mica sheet is inserted.

(b) Here, capacitance of capacitor with mica as medium C = KC₀ 108 × 10^-12F
When supply is disconnected, i. e., mV = 0,
The potential difference across on the plates of the reduces by K times.
i.e., V’ = \(\frac{100}{6}\) 16.67V
C-becomes 6 times.
Thus if qi be the charge on its plates after disconnecting the supply,
Then q₁ = CV’ = KC₀ × \(\frac{100}{6}\)
= 6 × 18 × 10^-12 × \(\frac{100}{6}\)
= 18 × 10^-10C
q₀ = 1.8 × 10^-9C =1.8 nC
i.e., the charge on the capacitor with mica as medium remains same as with air medium.

Question 10.
A 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor?
Answer:
Given, C = 12 pF = 12 × 10^-12 F and V = 50 V, U = ?
Using the relation U = \(\frac{1}{2}\) CV², we have
U = \(\frac{1}{2}\)CV² = \(\frac{1}{2}\) × 12 × 10^-12(50)²
= 1.5 × 10⁸ J

Question 11.
A 600 pF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 600 pF capacitor. How much electrostatic energy is lost in the process?
Answer:
Given, C₁ = C₂ = 600 pF = 600 × 10_-12F, V = 200 V, ∆U = ?
Using the relation ∆U = \(\frac{C_{1} C_{2}\left(V_{1}-V_{2}\right)^{2}}{2\left(C_{1}+C_{2}\right)}\) , we get
∆U = \(\frac{600 \times 600 \times 10^{-24}(200-0)^{2}}{2(600+600) \times 10^{-12}}[latex] = 6 × 10^-6 j

Question 12.
A charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of -2 × 10^-9 C from a point P(0, 0, 3 cm) to a point Q (0, 4 cm, 0), viaa point R (0,6 cm, 9 cm). Answer:
Charge located at the origin, q = 8 mC = 8 × 10^-3 C
Magnitude of a small charge, which is taken from a point P to point R to point Q, = -2 × 10^-9 C
All the points are represented in the given figure

Point P is at a distance, d₁ = 3 cm, from the origin along z-axis.
Point Q is at a distance, d₂ = 4 cm, from the origin along y-axis.

Therefore, work done during the process is 1.27 J.

Question 13.
A cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.
Answer:
Length of the side of a cube = b
Charge at each of its vertices = q
A cube of side b is shown in the following figure:

is the distance between the centre of the cube and one of the eight vertices.

The electric potential (V) at the centre of the cube is due to the presence of eight charges at the vertices.
V = [latex]\frac{8 q}{4 \pi \varepsilon_{0} r}\)
= \(\frac{8 q}{4 \pi \varepsilon_{0}\left(b \frac{\sqrt{3}}{2}\right)}\)
= \(\frac{4 q}{\sqrt{3} \pi \varepsilon_{0} b}\)
Therefore, the potential at the centre of the cube is \(\frac{4 q}{\sqrt{3} \pi \varepsilon_{0} b}\)
The electric field at the centre of the cube, due to the eight charges, gets cancelled. This is because the charges are distributed symmetrically with respect to the centre of the cube. Hence, the electric field is zero at the centre.

Question 14.
Two tiny spheres carrying charges 1.5 μC and 2.5 μC are located 30 cm apart. Find the potential and electric field :
(a) at the mid-point of the line joining the two charges, and
(b) at a point 10 cm from this midpoint in a plane normal to the line and passing through the mid-point.
Answer:
Two charges placed at points A and B are represented in the given figure. O is the mid-point of the line joining the two charges.

Magnitude of charge located at A, q₁ = 1.5 μC
Magnitude of charge located at B, q₂ = 2.5 μC
Distance between the two charges, d = 30 cm = 0.3 m

(a) Let V₁ and E₁ are the electric potential and electric field respectively at O.
V₁ = Potential due to charge at A + Potential due to charge at B


Therefore, the potential at mid-point is 2.4 x 10⁵ V and the electric field at mid-point is 4 x 10⁵Vm^-1. The field is directed from the larger charge to the smaller charge.

(b) Consider a point Z such that normal distance OZ =10 cm = 0.1 m, as shown in the following figure:

V₂ and E₂ are the electric potential and electric field respectively at Z. It can be observed from the figure that distance,

θ = cos^-1 (0.5556) = 56.25
∴ 2θ = 112.5°
cos 2θ = -0.38

E = 6.6 × 10⁵ Vm^-1
Therefore, the potential at a point 10 cm (perpendicular to the mid point) is 2.0 × 10⁵ V and electric field is 6.6 × 10⁵ Vm^-1.

Question 15.
A spherical conducting shell of inner radius and r₁outer radius r₂ has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell?
(b) Is the electric field inside a cavity (with no charge) zero, even if the shell is not spherical, but has any irregular shape? Explain.
Answer:
(a) Charge placed at the centre of a shell is+q. Hence, a charge of magnitude -q will be induced to the inner surface of the shell. Therefore, total charge on the inner surface of the shell is -q.
Surface charge density at the inner surface of the shell is given by the relation,
σ₁ = \(\frac{\text { Total charge }}{\text { Inner surface area }}=\frac{-q}{4 \pi r_{1}^{2}}\) ……………… (1)

A charge of + q is induced on the outer surface of the shell. A charge of magnitude Q is placed on the outer surface of the shell. Therefore, total charge on the outer surface of the shell is Q + q. Surface charge density at the outer surface of the shell,
σ₂ = \(=\frac{\text { Total charge }}{\text { Outer surface area }}=\frac{Q+q}{4 \pi r^{2}}\) …………… (2)

(b) Yes.
The electric field intensity inside a cavity is zero, even if the shell is not spherical and has any irregular shape. Take a closed loop such that a part of it is inside the cavity along a field line while the rest is inside the conductor. Net work done by the field in carrying a test charge over a closed loop is zero because the field inside the conductor is zero.
Hence, electric field is zero, whatever is the shape.

Question 16.
(a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by
(E₂ – E₁)n̂ = \(\frac{\sigma}{\varepsilon_{0}}\)
where n is a unit vector normal to the surface at a point ando is the surface charge density at that point. (The direction of n is from side 1 to side 2.) Hence show that just outside a conductor, the electric field is σ = n̂ ε₀.

(b) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another.
[Hint : For (a), use Gauss’s law. For, (b) use the fact that work done by electrostatic field on a closed loop is zero.]
Answer:
(a) Let AB be a charged surface having two sides as marked in the figure.
A cylinder enclosing a small area element ∆ S of the charged surface is the , Gaussian surface.

Let σ = surface charge density
∴ q = charge enclosed by the Gaussian cylinder = σ . ∆ S.
∴ According to Gauss’s Theorem,

where \(\overrightarrow{E_{1}}+\overrightarrow{E_{2}}\) are the electric fields through circular cross-sections of cylinder at II and III respectively.

It is clear from the figure that \(\overrightarrow{E_{1}}\) lies inside the conductor. Also we know that the electric field inside the conductor is zero.
∴ \(\overrightarrow{E_{1}}\) = 0
Thus from eq. (1)
\(\overrightarrow{E_{2}} \cdot \hat{n}=\frac{\sigma}{\varepsilon_{0}}[latex]
or [latex]\left(\overrightarrow{E_{2}} \cdot \hat{n}\right) \cdot \hat{n}=\frac{\sigma}{\varepsilon_{0}} \hat{n}\)
or \(\overrightarrow{E_{2}}=\frac{\sigma}{\varepsilon_{0}} \hat{n}\)
or electric field just outside the conductor = \(\frac{\sigma}{\varepsilon_{0}} \hat{n}\) Hence proved

(b) Let AaBbA be a charged surface in the field of a point charge q lying at origin.
Let \(\overrightarrow{r_{A}}\) and \(\overrightarrow{r_{B}}\) be its position vectors at points A and B respectively.

Let \(\vec{E}\) be the electric field at point P, thus E cosG is the tangential component of electric field \(\vec{E}\).

Question 17.
A long charged cylinder of linear charged density λ is surrounded by a hollow co-axial conducting cylinder. What is tihe electric field in the space between the two cylinders?
Answer:
Charge density of the long charged cylinder of length L and radius r is λ. Another cylinder of same length surrounds the previous cylinder. The radius of this cylinder is R.
Let £ be the electric field produced in the space between the two cylinders.
Electric flux through the Gaussian surface is given by Gauss’s theorem as,
Φ = E (2πd)L
where d = Distance of a point from the common axis of the cylinders Let q be the total charge on the cylinder.
It can be written as
Φ = E (2πdL) = \(\frac{q}{\varepsilon_{0}}\)
where, q = Charge on the inner sphere of the outer cylinder, ε₀ = Permittivity of free space
E (2πdL) = \(\frac{\lambda L}{\varepsilon_{0}}\)
E = \(\frac{\lambda}{2 \pi \varepsilon_{0} d}\)
Therefore, the electric field in the space between the two cylinders is \(\frac{\lambda}{2 \pi \varepsilon_{0} d}\)

Question 18.
In a hydrogen atom, the electron and proton are bound at a distance of about 0.53 Å.
(a) Estimate the potential energy of the system in eV, taking the zero of the potential energy at infinite separation of the electron from proton.
(b) What is the minimum work required to free the electron, given that its kinetic energy in the orbit is half the magnitude of potential energy obtained in (a)?
(c) What are the answers to (a) and (b) above if the zero of potential energy is taken as 1.06 A separation?
Answer:
The distance between electron-proton of a hydrogen atom, d = 0.53 Å
Charge on an electron,q₁ = -1.6 × 10^-19 C
Charge on a proton, q₂ = +1.6 × 10^-19 C
(a) Potential energy at infinity is zero.
Potential energy of the system,
P.E. = P.E. at ∞ – P.E. at d
= 0 – \(\frac{q_{1} q_{2}}{4 \pi \varepsilon_{0} d}\)
∴ P.E 0 = – \(\frac{9 \times 10^{9} \times\left(1.6 \times 10^{-19}\right)^{2}}{0.53 \times 10^{-10}}\)
= -43.47 × 10^-19J
Since 1.6 × 10^-19 J = 1eV
∴ P.E. = -43.47 × 10^-19

= \(\frac{-43.47 \times 10^{-19}}{1.6 \times 10^{-19}}\) = -27.2 eV
Therefore, the potential energy of the system is -27.2 eV.

(b) Kinetic energy is half of the magnitude of potential energy
Kinetic energy = \(\frac{1}{2}\) × (-27.2) = 13.6 eV
[v K.E. of the system is always +ve]
Total energy = 13.6 – 27.2 = 13.6 eV
Therefore, the minimum work required to free the electron is 13.6 eV.

(c) When zero of potential energy is taken, d₁ = 1.06 A
Potential energy of the system = P.E. at – P.E. at d₁ – P.E. at d
= \(\frac{q_{1} q_{2}}{4 \pi \varepsilon_{0} d_{1}}\) -27.2 eV
= \(\frac{9 \times 10^{9} \times\left(1.6 \times 10^{-19}\right)^{2}}{1.06 \times 10^{-10}}\) -27.2 eV
= 21.73 × 10^-19 J -27.2 eV
= 13.58 eV- 27.2 eV .
= -13.6 eV

Question 19.
If one of the two electrons of aH₂ molecule is removed, we get a hydrogen molecular ion H₂⁺. In the ground state of an H₂⁺ the two protons are separated by roughly 1.5 Å, and the electron is roughly 1 Å from each proton. Determine the potential energy of the system. Specify your choice of the zero of potential energy.
Answer:
The system of two protons and one electron is represented in the given figure

Charge on proton 1, q₁ = 1.6 × 10^-19 C
Charge on proton 2, q₂ = 1.6 × 10^-19 C
Charge on electron, q₃ = -1.6 × 10^-19 C
Distance between protons 1 and 2, dj = 1.5 × 10^-10 m
Distance between proton 1 and electron, d₂ = 1 × 10^-10 m
Distance between proton 2 and electron, d₃ = 1 × 10^-10 m The potential energy at infinity is zero.
Potential energy of the system,
V = \(\frac{q_{1} q_{2}}{4 \pi \varepsilon_{0} d_{1}}\) + \(\frac{q_{2} q_{3}}{4 \pi \varepsilon_{0} d_{3}}\) + \(\frac{q_{3} q_{1}}{4 \pi \varepsilon_{0} d_{2}}\)
Substituting \(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 × 10⁹ Nm²C^-2, we obtain

= -30.7 × 10^-19 J
= -19.2 eV
Therefore, the potential energy of the system is -19.2 eV.

Question 20.
Two charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.
Answer:
Let a be the radius of a sphere A, Q_A be the charge on the sphere, and C_A be the capacitance of the sphere. Let b be the radius of a sphere B, Q_B be the charge on the sphere, and CB be the capacitance of the sphere. Since the two spheres are connected with a wire, their potential (V) will become equal.
Let E_A be the electric field of sphere A and E_B be the electric field of sphere B. Therefore, their ratio,

Putting the value of eqn. (2) in eqn. (1), we obtain
\(\frac{E_{A}}{E_{B}}=\frac{a b^{2}}{b a^{2}}=\frac{b}{a}\)
Therefore, the ratio of electric fields at the surface is b/a.
A flat portion may be taken as a spherical surface of large radius and a pointed portion may be taken as a spherical surface of small radius.
As ε ∝ \(\frac{l}{\text { radius }}\),
thus pointed portion has larger fields than the flat one. Also we know that
E = \(\frac{\sigma}{\varepsilon_{0}}\)
i.e., E ∝ σ,
thus clearly the surface charge density on the sharp and pointed ends will be large.

Question 21.
Two charges -q and +q are located at points (0, 0, – a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0)?
(b) Obtain the dependence of potential on the distance r of a point from the origin when r/ a >> 1.
(c) How much work is done in moving a small test charge from the point (5, 0, 0) to (-7, 0, 0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?
Answer:
(a) Here -q and + q are situated at points A (0, 0, -a) and B (0, 0, a) respectively.

∴ Dipole length = 2a
If p be the dipole moment of the dipole, then
p = 2aq
Let P₁ (0, 0, z) be the point at which V is to be calculated. It lies on the axial line of the dipole.

Now point P₂ (x, y, O’) lies in XY plane which is normal to the axis of the dipole, i. e., lies on the line parallel to the equitorial line on which potential due to the dipole is zero as given below:

(b) Let r = distance of the point P from the centre (O) of the dipole at which
V is to be calculated. Let ∠POB = θ, i.e., OP makes an angle θ with \(\).
Also let r₁ and r₂ be the distances of the point P from -q and +q respectively. To find r₁ and r₂, draw AC and BD ⊥ arc to OP.

∴ In Δ ACO, OC = a cos θ
and in Δ BDO, OD = a cos θ
Thus, if V₁ and V₂ be the potentials at P due to – q and + q respectively, then total potential V at P is given by
V = V₁ + V₂

Thus,V = \(=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{p \cos \theta}{r^{2}}\) ………….. (2)
Thus, we see that the dependence of V on r is of \(\frac{1}{r^{2}}\) type, i.e.,V ∝ \(\frac{1}{r^{2}}\).

(c) Let W₁ and W₂ be the work done in moving a test charge q₀ from E(5,0,0) to F(-7, 0,0) in the fields of + q(0, 0, a) and -q(0, 0,-a) respectively.


No, because work done in moving a test charge in an electric field between two points is independent of the path connecting the two point.

Question 22.
Figure 2.34 shows a charge array known as an electric quadrupole. For a point on the axis of the quadrupole, obtain the dependence of potential on r for r/a >> 1, and contrast your results with that due to an electric dipole, and an electric monopole (i. e., a single charge).

Answer:
Four charges of same magnitude are placed at points X, Y, Y and Z respectively, as shown in the following figure:

A point is located at P, which is r distance away from point Y.
The system of charges forms an electric quadrupole.
It can be considered that the system of the electric quadrupole has three charges.
Charge + q placed at point X
Charge -2q placed at point Y
Charge + q placed at point Z
XY = YZ = a
YP = r
PX = r + a
PZ = r – a
Electrostatic potential caused by the system of three charges at point P is given by,

It can be inferred that potential, V ∝ \(\frac{1}{r^{3}}\).
However, it is known that for a dipole, V ∝ \(\frac{1}{r^{2}}\). and, for monopole V ∝ \(\frac{1}{r}\)

Question 23.
An electrical technician requires a capacitance of 2 μF in a circuit across a potential difference of 1 kV. A large number of 1 μF capacitors are available to him each of which can withstand a potential difference of not more than 400 V. Suggest a possible arrangement that requires the minimum number of capacitors.
Answer:
Total required capacitance, C = 2 μF
Potential difference, V = 1 kV = 1000 V
Capacitance of each capacitor, C = 1 μF
Each capacitor can withstand a potential difference, V₁ = 400 V
Suppose a number of capacitors are connected in series and these series circuits are connected in parallel (row) to each other. The potential difference across each row must be 1000 V and potential difference across each capacitor must be 400 V. Hence, number of capacitors in each row is given as
\(\frac{1000}{400}\) = 25 .
Hence, there are three capacitors in each row.
Capacitance of each row = \(\frac{1}{1+1+1}=\frac{1}{3}\) μF
Let there are n rows, each having three capacitors, which are connected in parallel.
Hence, equivalent capacitance of the circuit is given as
\(\frac{1}{3}+\frac{1}{3}+\frac{1}{3}\) + ….. + n terms = \(\frac{n}{3}\)
However, capacitance of the circuit is given as 2 μF.
∴ \(\frac{n}{3}\) = 2
n = 6
Hence, 6 rows of three capacitors are present in the circuit. A minimum of 6 × 3, i.e., 18 capacitors are required for the given arrangement.

Question 24.
What is the area of the plates of a 2 F parallel plate capacitor, given that the separation between the plates is 0.5 cm? [You will realize from your answer why ordinary capacitors are in the range of μF or less. However, electrolytic capacitors do have a much larger capacitance (0.1 F) because of very minute separation between the conductors.]
Answer:
Capacitance of a parallel capacitor, C = 2 F
Distance between the two plates, d = 0.5 cm = 0.5 × 10^-2 m
Capacitance of a parallel plate capacitor is given by the relation,
C = \(\frac{\varepsilon_{0} A}{d}\)
A = \(\frac{C d}{\varepsilon_{0}}\)
Where ε₀ = 8.85 × 10^-12C²N^-1m^-2
∴ A = \(\frac{2 \times 0.5 \times 10^{-2}}{8.85 \times 10^{-12}}\) = 1130 km²
Hence, the area of the plates is too large. To avoid this situation, the capacitance is taken in the range of μF.

Question 25.
Obtain the equivalent capacitance of the network in Fig. 2.35. For a 300 V supply, determine the charge and voltage across each capacitor.

Answer:

Question 26.
he plates of a parallel plate capacitor have an area of 90 cm² each and are separated by 2.5 nun. The capacitor is charged by connecting it to a 400 V supply.
(a) How much electrostatic energy is stored by the capacitor?
(b) View this energy as stored in the electrostatic field between the plates, and obtain the energy per unit volume u. Hence arrive at a relation between u and the magnitude of electric field E between the plates.
Answer:
Area of the plates of a parallel plate capacitor,
A = 90 cm² = 90 × 10^-4 m²
Distance between the plates, d = 2.5mm 2.5 × 10^-3 m
Potential difference across the plates, V = 4OO V
Capacitance of the capacitor is given by the relation,
C = \(\)
(a) Electrostatic energy stored in the capacitor is given by the relation,

Hence, the electrostatic energy stored by the capacitor is 2.55 × 10^-6 J

(b) Volume of the given capacitor,
V’= A × d
= 90 × 10^-4 × 2.5 × 10^-3
= 2.25 × 10^-5 m³
Energy stored in the capacitor per unit volume is given by,

Question 27.
A 4 μF capacitor is charged by a 200 V supply. It is then disconnected from the supply, and is connected to another uncharged 2 μF capacitor. How much electrostatic energy of the first capacitor is lost in the form of heat and electromagnetic radiation?
Answer:

Question 28.
Show that the force on each plate of a parallel plate capacitor has a magnitude equal to (\(\frac{1}{2}\)) QE, where Q is the charge on the capacitor, and E is the magnitude of electric field between the plates. Explain the origin of the factor \(\frac{1}{2}\).
Answer:
Let F be the force applied to separate the plates of a parallel plate capacitor by a distance of Δx. Hence, work done by the force to do so = FΔx
As a result, the potential energy of the capacitor increases by an amount given as uA Δx.
where, u = Energy density
A = Area of each plate
The work done will be equal to the increase in the potential energy, i. e.,
FΔx = uA Δx

The physical origin of the factor, 1/2 in the force formula lies in the fact that just outside the conductor, field is E and inside it is zero. Hence, it is the averge value, E/2 of the field that contributes to the force.

Question 29.
A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports (Fig. 2.36). Show that the capacitance of a spherical capacitor is given by
C = \(\frac{4 \pi \varepsilon_{0} r_{1} r_{2}}{r_{1}-r_{2}}\)
where r ₁and r₂ are the radii of outer and inner spheres, respectively.

Answer:
Radius of the outer shell = r₁
Radius of the inner shell = r₂
The inner surface of the outer shell has charge +Q
The outer surface of the inner shell has induced charge -Q.
Potential difference between the two shells is given by,

Question 30.
A spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5 µC. The space between the concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor.
(b) What is the potential of the inner sphere?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm. Explain why the latter is much smaller.
Answer:
Radius of the inner sphere, r₂ = 12 cm = 0.12m
Radius of the outer sphere, r₁ = 13 cm = 0.13m
Charge on the inner sphere, q = 2.5 µC = 2.5 × 10^-6 C
Dielectric constant of the liquid, ε_r = 32
Capacitance of the capacitor is given by the relation,
C = \(\frac{4 \pi \varepsilon_{0} \varepsilon_{r} r_{1} r_{2}}{r_{1}-r_{2}}\)
C = \(\frac{32 \times 0.12 \times 0.13}{9 \times 10^{9} \times(0.13-0.12)}\)
≈ 5.5 × 10^-9 F
Hence, the capacitance of the capacitor is approximately 5.5 × 10^-9 F.

(b) Potential of the inner sphere is given by,
V = \(\frac{q}{C}=\frac{2.5 \times 10^{-6}}{5.5 \times 10^{-9}}\) = 4.5 × 10²V
Hence, the potential of the inner sphere is 4.5 × 10² V

(c) Radius of an isolated sphere, r = 12cm = 12 × 10^-2m
Capacitance of the sphere is given by the relation,
C’ = 4πε₀r
= 4π × 8.85 × 10^-12 × 12 × 10^-12
= 1.33 × 10^-11F
The capacitance of the isolated sphere is less in comparison to the concentric spheres. This is because the outer sphere of the concentric spheres is earthed. Hence, the potential difference is less and the capacitance is more than the isolated sphere.

Question 31.
Answer carefully:
(a) Two large conducting spheres carrying charges Q₁ and Q₂ are brought close to each other. Is the magnitude of electrostatic force between them exactly given by Q₁Q₂ / πε₀ r², where r is the distance between their centres?
(b) If Coulomb’s law involved 1/r³ dependence (instead of 1/r²), would Gauss’s law be still true?
(c) A small test charge is released at rest at a point in an electrostatic field configuration. Will it travel along the field line passing through that point?
(d) What is the work done by the field of a nucleus in a complete circular orbit of the electron? What if the orbit is elliptical?
(e) We know that electric field is discontinuous across the surface of a charged conductor. Is electric potential also discontinuous there?
(f) What meaning would you give to the capacitance of a single conductor?
(g) Guess a possible reason why water has a much greater dielectric constant (= 80) than say, mica (= 6).
Answer:
(a) The force between two conducting spheres is not exactly given by the expression,Q₁Q₂ / πε₀ r², because there is a non-uniform charge distribution on the spheres.

(b) Gauss’s law will not be true, if Coulomb’s law involved 1/r³ dependence, instead of 1/r², on r.

(c) Yes, If a small test charge is released at rest at a point in an electrostatic field configuration, then it will travel along the field lines passing through the point, only if the field lines are straight. This is because the field lines give the direction of acceleration and not of velocity.

(d) Whenever the electron completes an orbit, either circular or elliptical, the work done by the field of a nucleus is zero.

(e) No, electric field is discontinuous across the surface of a charged conductor. However, electric potential is continuous.

(f) The capacitance of a single conductor is considered as a parallel plate capacitor with one of its two plates at infinity.

(g) Water has an unsymmetrical space as compared to mica. Since it has a permanent dipole moment, it has a greater dielectric constant than mica.

Question 32.
A cylindrical capacitor has two co-axial cylinders of length 15 cm and radii 1.5 cm and 1.4 cm. The outer cylinder is earthed and the inner cylinder is given a charge of 3.5 μC. Determine the capacitance of the system and the potential of the inner cylinder. Neglect end effects (i. e., bending of field lines at the ends).
Answer:
Length of a co-axial cylinder, l = 15 cm = 0.15 m
Radius of outer cylinder, r₁ = 1.5 cm = 0.015 m
Radius of inner cylinder, r₂ = 1.4 cm = 0.014 m
Charge on the inner cylinder, q = 3.5 μC = 3.5 × 10^-6 C

Capacitance of a co-axial cylinder of radii r₁ and r₂ is given by the relation,

Question 33.
A parallel plate capacitor is to be designed with a voltage rating 1 kV, using a material of dielectric constant 3 and dielectric strength about 10⁷ Vm^-1. (Dielectric strength is the maximum electric field a material can tolerate without breakdown, i. e., without starting to conduct electricity through partial ionisation.) For safety, we should like the field never to exceed, say 10% of the dielectric strength. What minimum area of the plates is required to have a capacitance of 50 pF?
Answer:
Potential rating of the parallel plate capacitor, V = 1 kV = 1000 V
Dielectric constant of the material, ε_r = 3
Dielectric strength = 10⁷ V/m
For safety, the field intensity never exceeds 10% of the dielectric strength.
Hence, electric field intensity, E = 10% of 10⁷ =10⁶V/m
Capacitance of the parallel plate capacitor C = 50 pF = 50 × 10^-12F
Distance between the plates is given by,
d = \(\frac{V}{E}=\frac{1000}{10^{6}}\) = 10^-3 m
Capacitance is given by the relation,
C = \(\frac{\varepsilon_{0} \varepsilon_{r} A}{d}\)
∴ A = \(\frac{C d}{\varepsilon_{0} \varepsilon_{r}}\) = \(\frac{50 \times 10^{-12} \times 10^{-3}}{8.85 \times 10^{-12} \times 3}\) ≈ 19cm ²
Hence, the area of each plate is about 19 cm² .

Question 34.
Describe schematically the equipotential surfaces corresponding to
(a) a constant electric field in the z-direction,
(b) a field that uniformly increases in magnitude but remains in a constant (say, z) direction,
(c) a single positive charge at the origin, and
(d) a uniform grid consisting of long equally spaced parallel charged wires in a plane.
Answer:
Equipotential surface is a surface having the same potential at each of its points. In the given cases the equipotential surface are

(a) The planes are parallel to XY plane. For same potential difference, the planes are equidistant.

(b) The planes are parallel to XY plane, but for the same potential difference, the separation between the planes decreases.

(c) Concentric spheres centred at the origin.

(d) A periodically varying shape near the grid which gradually attains the shape of planes parallel to grid at far distances.

Question 35.
In a Van de Graff type generator a spherical metal shell is to be a 15 × 10⁶ V electrode. The dielectric strength of the gas surrounding the electrode is 5 × 10⁷ Vm^-1. What is the minimum radius of the spherical shell required? (You will learn from this exercise why one cannot build an electrostatic generator using a very small shell which requires a small charge to acquire a high potential.)
Answer:

Question 36.
A small sphere of radius r₁and charge q₁ is enclosed by a spherical shell of radius r₂ and charge q₂. Show that if q₁ is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q₂ on the shell is.
Answer:
Here r₁, r₂ are the radii of small sphere and the spherical shell respectively. The shell surrounds the sphere +q₁ is the charge on the sphere +q₂ is the charge on the shell. We know that the electric field
inside a conductor is zero, i.e.,\(\vec{E}\) = 0. Thus according to Gauss’s Theorem

Hence q₂ must reside on the outer surface of the spherical shell.
Now the sphere having +q₁ charge is enclosed inside the spherical shell. So – q₁ charge will be induced on the inside side and +q₁ charge will be induced on the outer surface the spherical shell.

∴ Total charge on the outer surface of the shell = q₂ + q₁.
As the charge always resides on the outer surface, thus charge q₁ from the outer surface of sphere will flow to the other surface of spherical shell when connected with a wire.

Question 37.
Answer the following:
(a) The top of the atmosphere is at about 400 kV with respect to the surface of the earth, corresponding to an electric field that decreases with altitude. Near the surface of the earth, the field is about 100 Vm^-1. Why then do we not get an electric shock as we step out of our house into the open? (Assume the house to be a steel cage so there is no field inside.)

(b) A man fixes outside his house one evening a two metre high insulating slab carrying on its top a large aluminium sheet of area 1 m². Will he get an electric shock if he touches the metal sheet next morning?

(c) The discharging current in the atmosphere due to the small conductivity of air is known to be 1800 A on an average over the globe. Why then does the atmosphere not discharge itself completely in due course and become electrically neutral? In other words, what keeps the atmosphere charged?

(d) What are the forms of energy into which the electrical energy of the atmosphere is dissipated during a lightning? (Hint : The earth has an electric field of about 100 Vm-1 at its surface in the downward direction, corresponding to a surface charge density = -10^-9 Cm^-2. Due to the slight conductivity of the atmosphere up to about 50 km (beyond which it is good conductor), about +1800 C is pumped every second into the earth as a whole. The earth, however, does not get discharged since thunderstorms and lightning occurring continually all over the globe pump an equal amount of negative charge on the earth.)
Answer:
(a) We do not get an electric shock as we step out of our house because the original equipotential surfaces of open air changes, keeping our body and the ground at the same potential.

(b) Yes, the man will get an electric shock if he touches the metal slab next morning. The steady discharging current in the atmosphere charges up the aluminium sheet. As a result, its voltage rises gradually. The raise in the voltage depends on the capacitance of the capacitor formed by the aluminium slab and the ground.

(c) The occurrence of thunderstorms and lightning charges the atmosphere continuously. Hence, even with the presence of discharging current of 1800 A, the atmosphere is not discharged completely. The two opposing currents are in equilibrium and the atmosphere remains electrically neutral.

(d) During lightning and thunderstorm, light energy, heat energy and sound energy are dissipated in the atmosphere.