Punjab State Board PSEB 12th Class Physics Important Questions Chapter 13 Nuclei Important Questions and Answers.
PSEB 12th Class Physics Important Questions Chapter 13 Nuclei
Very short answer type questions
Question 1.
Write the relationship between the size of a nucleus and Its mass number (A).
Answer:
The relationship is R = RoA1/3
where, R = radius of nucleus, A = mass number.
Question 2.
Define the activity of a given radioactive substance. Write its SI unit.
Answer:
The activity of a sample is defined as the rate of disintegration taking place in the sample of radioactive substances.
SI unit of activity is Becquerel (Bq).
1 Bq = 1 disintegration/second
Question 3.
Why is it found experimentally difficult to detect neutrinos in nuclear p-decay?
Answer:
Neutrinos are difficult to detect because they are massless, have no charge, and do not interact with nucleons.
Question 4.
A nucleus undergoes p-decay. How does its :
(i) mass number
(ii) atomic number change?
Answer:
During p-decay,
(i) no change in mass number.
(ii) atomic number increases by 1.
![]()
Question 5.
In pair annihilation, an electron and a positron destroy each other to produce gamma radiations. How is the momentum conserved? (NCERT Exemplar)
Answer:
In pair annihilation, an electron and a positron destroy each other to produce 2γ photons which move in opposite directions to conserve linear momentum.
The annihilation is shown below 0e+1 + 0 e+1 →2γ ray photons.
Question 6.
Which one of the following cannot emit radiation and why? Excited nucleus, excited electron. (NCERT Exemplar)
Answer:
Excited electrons cannot emit radiation because energy of electronic energy levels is in the range of eV and not MeV (mega electron volt). y-radiations have energy of the order of MeV.
Question 7.
He23 and He13 nuclei have the same mass number.
Do they have the same binding energy? (NCERT Exemplar)
Answer:
Nuclei He23 and He13 have the same mass number.
He23 has two protons and one neutron. He13 has one proton arid two neutrons.
The repulsive force between protons is missing in 1He3, so the binding energy of 1He3 is greater than that of 2He3.
Question 8.
Which sample, A or B as shown in figure has shorter mean-life? (NCERT Exemplar)
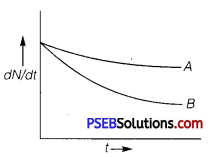
Answer:
B has shorter mean life as λ is greater for B.
Short answer type questions
Question 1.
(i) Define the terms (a) half-life (b) average life. Find out the relationship with the decay constant (λ).
(ii) A radioactive nucleus has a decay constant ) λ = 0.346 (day)-1
How long would it take the nucleus of decay to 75% of Its Initial amount?
Answer:
(i)
(a) Half-life of a radioactive element is defined as the time during which half number of atoms present initially in the sample of the element decay or it is the time during which number of atoms left undecayed in the sample is half the total number of atoms present in the sample.
it is represented by T1/2.
From the equation N = N0e-λt ,
At half-life, t = T1/2,N = \(\frac{N_{0}}{2}\)

On taking log both sides, we get
λT1/2 = log e2
T 1/2 = \(\frac{\log _{e} 2}{\lambda}=\frac{\log _{10} 2 \times 2.303}{\lambda}\)
= \(\frac{0.3010 \times 2.303}{\lambda}\)
After n half-life, the number of atoms left undecayed is given by
N = N0\(\left(\frac{1}{2}\right)^{n}\)
T1/2 = \(\frac{0.6932}{\lambda}\)
(b) Average life of a radioactive element can be obtained by calculating the total life time of all atoms of the element and dividing it by the total number of atoms present initially in the sample of the element.
Average life or mean life of radioactive element is
τ = \(\frac{\text { Total life of all atoms }}{\text { Total number of atoms }}\)
τ = \(=\int_{0}^{N_{0}} \frac{t d N}{N_{0}}=\int_{\infty}^{0-\lambda N_{0} e^{-\lambda t} d t \times t}{N_{0}}\)
[when N =N0,t = 0 and when N = 0, t = ∞] [∵dN =-λ(N0e–λt)dt]
= λ0∫∞ te -λtdt

(ii) Given, λ = 0.3465 (day)
According to the radioactive decay law, we have
R = R0e-λt

⇒ t = 0.830 s
![]()
Question 2.
(i) Write three characteristic properties of nuclear force.
(ii) Draw a plot of potential energy of a pair of nucleons as a function of their separation. Write two important conclusions that can be drawn from the graph.
Answer:
(i) Characteristic Properties of Nuclear Force
(a) Nuclear force act between a pair of neutrons, a pair of protons and also between a neutron-proton pair, with the same strength. This shows that nuclear forces are independent of charge.
(b) The nuclear forces are dependent on spin or angular momentum of nuclei.
(c) Nuclear forces are non-central forces. This shows that the distribution of nucleons in a nucleus is not spherically symmetric. From the plot, it is concluded that
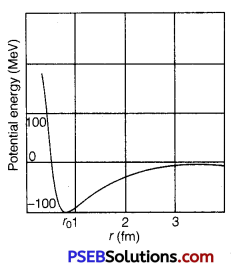
(ii)
(a) The potential energy is minimum at a distance r0(=0.8fm) which means that the force is attractive for distance larger than 0.8 fm and repulsive for the distance less than 0.8 fm between the nucleons.
(b) Nuclear forces are negligible when the distance between the nucleons is more than 10 fm.
Question 3.
Explain giving necessary reaction, how energy is released during:
(i) fission
(ii) fusion
Answer:
(i) Nuclear Fission: The phenomenon of splitting of heavy nuclei (mass number > 120) into smaller nuclei of nearly equal masses is known as nuclear fission. In nuclear fission, the sum of the masses of the product is less than the sum of masses of the reactants. This difference of mass gets converted into energy E = me and hence sample amount of energy is released in a nuclear fission.
e.g., 92235 U + 01n → 56141Ba + 3692Kr + 3 01 + Q
Masses of reactant = 235.0439 amu + 1.0087 amu
= 236.0526 amu
Masses of product = 140.9139 + 91.8973 + 3.0261
= 235.8373 amu
Mass defect = 236.0526 -235.8373
= 0.2153 amu
∵ 1 amu = 931MeV
⇒ Energy released = 0.2153 x 931
⇒ 200 MeV nearly
(ii) Nuclear Fusion: The phenomenon of conversion of two lighter nuclei into a single heavy nucleus is called.nuclear fusion. Since the mass of the heavier product nucleus is less than the sum of masses of reactant nuclei and therefore certain mass defect occurs which converts into energy as per Einstein’s mass-energy relation. Thus, energy is released during nuclear fusion.
e.g., 1H1 + 1H1 → 1H2 + e+ + v + 0.42 MeV
Also, 1H2 + 1H2 → 1H3 + 1H1 + 4.03 MeV
Question 4.
Give reasons for :
(a) Lighter elements are better moderators for a nuclear reactor than heavier elements.
(b) In a natural uranium reactor, heavy water is preferred moderator as compared to ordinary water.
(c) Cadmium rods are provided in a reactor.
(d) Very high temperatures as those obtained in the interior of the sun are required for fusion reaction.
Answer:
(a) A moderator slows down fast neutrons released in a nuclear reactor. The basic principle of mechanics is that the energy transfer in a collision is the maximum when the colliding particles have equal masses. As lighter elements have mass close to that of neutrons, lighter elements are better moderators than heavier elements.
(b) Ordinary water has hydrogen nuclei (11H) which have greater absorption capture for neutrons; so ordinary water will absorb neutrons rather than slowing them; on the other hand, the heavy hydrogen nuclei (21H) have negligible absorption capture for neutrons, so they share energy with neutrons and neutrons are slowed down.
(c) Cadmium has high absorption capture for neutrons; so cadmium rods are used to absorb extra neutrons; so nuclear fission in a nuclear reactor is controlled; therefore cadmium rods are called control rods.
(d) In nuclear fusion, two positively charge nuclei fuse together. When two positively charged nuclei come near each other to fuse together, strong electrostatic repulsive force acts between them.
To overcome this repulsive force, extremely high temperatures of the order of 108 K are required.
This may be calculated as follows: For fusion of H-nuclei,

The temperature in the interior of sun is about 2 x 107 K.
Therefore, very high temperatures of the order 107 K are required for fusion reaction to take place.
![]()
Question 5.
Deuteron is a bound state of a neutron and a proton with a binding energy B 2.2 Mev. A γ-ray of energy E is aimed at a deuteron nucleus to try to break it into a (neutron + proton) such that the n and p move in the direction of the incident y-ray. If E = B, show that this cannot happen. Hence, calculate how much bigger than B must be E be for such a process to happen. (NCERT Exemplar)
Answer:
Given binding energy B = 2.2 MeV
From the energy conservation law,
E-B=Kn+Kp = \(\frac{p_{n}^{2}}{2 m}+\frac{p_{p}^{2}}{2 m}\) ………………….. (1)
From conservation of momentum,
Pn +Pp = \(\frac{E}{c}\)
As E = B,Eq. (1) pn2+ Pp2 =0 ……………………………. (2)
It only happen if pn = pp = 0
So, the Eq. (2) cannot satisfied and the process cannot take place.
Let E = B +X, when X<< B for the process to take place.
Put value of p1 from Eq. (2) in Eq. (1), we get
X = \(\frac{\left(\frac{E}{c}-p_{p}\right)}{2 m}+\frac{p_{p}^{2}}{2 m}\)
or 2pp2 – \(\frac{2 E p_{p}}{c}+\frac{E^{2}}{c^{2}}\) – 2mx = 0
Using the formula of quadratic equation, we get
Pp = \(\frac{\frac{2 E}{c} \pm \sqrt{\frac{4 E^{2}}{c^{2}}-8\left(\frac{E^{2}}{c^{2}}-2 m X\right)}}{4}\)
For the real value pp, the discriminant is positive

Long answer type questions
Question 1.
Define the term: Half-life period and decay constant of a radioactive sample. Derive the relation between these terms.
Answer:
Half-life Period: The half-life period of an element is defined as the time in which the number of radioactive nuclei decay to half of its initial value.
Decay Constant: The decay constant of a radioactive element is defined as the reciprocal of time in which the number of undecayed nuclei of that radioactive element falls to times of its initial value. Relation between Half-life and Decay Constant:
The radioactive decay equation is N = N0e-λt …………………………. (i)
When t = T,N= \(\frac{N_{0}}{2}\)
∴ \(\frac{N_{0}}{2}\) = N0e-λT or e-λT = \(\frac{1}{2}\)
……………………. (2)
Taking log on both sides, we get
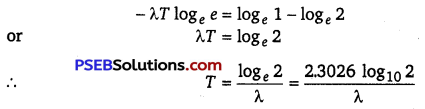
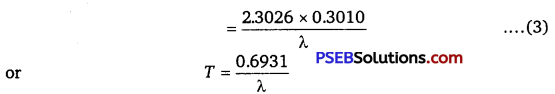
![]()
Question 2.
Draw the graph showing the variation of binding energy per nucleon with the mass number for a large number of nuclei 2 < A < 240. What are the main inferences from the graph? How do you explain the constancy of binding energy in the range 30<A<170 using the property that the nuclear force is short-ranged? Explain with the help of this plot the release of energy in the processes of nuclear fission and fusion.
Answer:
The variation of binding energy per nucleon versus mass number is shown in figure.
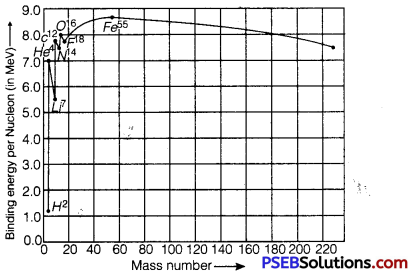
Inferences from Graph
1. The nuclei having mass numbers below 20 and above 180 have relatively small binding energy and hence they are unstable.
2. The nuclei having mass numbers 56 and about 56 have maximum binding energy – 5.8 MeV and so they are most stable.
3. Some nuclei have peaks, e.g., 2He4, 6C12, 8O16; this indicates that these nuclei are relatively more stable than their neighbors.
(i) Explanation of constancy of binding energy: Nuclear force is short-ranged, so every nucleus interacts with its neighbors only, therefore binding energy per nucleon remains constant.
(ii) Explanation of nuclear fission: When a heavy nucleus (A ≥ 235 say) breaks into two lighter nuclei (nuclear fission), the binding energy per nucleon increases i.e., nucleons get more tightly bound. This implies that energy would be released in nuclear fission,
(iii) Explanation of nuclear fusion: When two very light nuclei (A ≤ 10) join to form a heavy nucleus, the binding energy per nucleon of fused heavier nucleus is more than the binding energy per nucleon of lighter nuclei, so again energy would be released in nuclear fusion.