PSEB 12th Class Physics Solutions Chapter 1 Electric Charges and Fields

Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 1 Electric Charges and Fields Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Physics Chapter 1 Electric Charges and Fields

PSEB 12th Class Physics Guide Electric Charges and Fields Textbook Questions and Answers

Question 1.
What is the force between two small charged spheres having charges of 2 × 10^-7 C and 3 × 10^-7 C placed 30 cm apart in air?
Answer:
Charge on the first sphere, q₁ = 2 × 10^-7 C
Charge on the second sphere, q₂ = 3 × 10^-7 C
Distance between the spheres, r = 30 cm = 0.3 m
Electrostatic force between the spheres is given by the relation,
F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r^{2}}\)
where, ε₀ = Permittivity of free space
F = \(\frac{9 \times 10^{9} \times 2 \times 10^{-7} \times 3 \times 10^{-7}}{(0.3)^{2}}\)
= 6 × 10^-3 N
Hence, force between the two small charged spheres is 6 × 10^-3 N. The charges are of same nature. Hence, force between them will be repulsive.

Question 2.
The electrostatic force on a small sphere of charge
0.4 μC due to another small sphere of charge -0.8 μC in air is 0.2 N.
(a) What is the distance between the two spheres?
(b) What is the force on the second sphere due to the first?
Answer:
Electrostatic force on the first sphere, F = 0.2 N
Charge on this sphere, q₁ = 0.4 μC = 0.4 × 10^-6C
Charge on the second sphere, q₂ = -0.8 μC = -0.8 × 10^-6C

(a) Electrostatic force between the spheres is given by the relation,
F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r^{2}}\)
where, ε₀ = Permittivity of free space
r² = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{F}\)
= \(=\frac{0.4 \times 10^{-6} \times 0.8 \times 10^{-6} \times 9 \times 10^{9}}{0.2}\)
= 16 × 9 × 10^-4 = 144 × 10^-4
= \(\sqrt{144 \times 10^{-4}}\) = 0.12 m
The distance between the two spheres is 0.12 m.

(b) Force on q₂ due to q₁= ?
We know that electrostatic forces always, appear in priors and follow Newton’s 3rd law of motion.
∴ \(\left|\vec{F}_{21}\right|\) = Force on q₂ due to q₁
= 0.2 N and it is attractive in nature
We now that,
F₂₁ = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r_{21}^{2}}\)

On substituting the values, we get
F₂₁ = 9 × 10⁹ × \(\frac{\left(0.4 \times 10^{-6}\right) \times\left(0.8 \times 10^{-6}\right)}{(0.12)^{2}}\)
= 0.2 N

Question 3.
Check that the ratio ke² / Gm_em_p is dimensionless. Look up a
table of physical constants and determine the value of this ratio. What does the ratio signify?
Answer:
The given ratio is \(\frac{k e^{2}}{G m_{e} m_{p}}\)
where, G = Gravitational constant
Its unit is Nm²kg^-2.
m_p and m_p = Masses of electron and proton
Their unit is kg.
e = Electric charge Its unit is C.
k = A constant = \(=\frac{1}{4 \pi \varepsilon_{0}}\)
Its unit is N m²C^-2.
Therefore, unit of the given ratio
\(\frac{k e^{2}}{G m_{e} m_{p}}\) = \(\frac{\left[\mathrm{Nm}^{2} \mathrm{C}^{-2}\right]\left[\mathrm{C}^{-2}\right]}{\left[\mathrm{Nm}^{2} \mathrm{~kg}^{-2}\right][\mathrm{kg}][\mathrm{kg}]}\) = M⁰L⁰T⁰
Hence, the given ratio is dimensionless.
e = 1.6 × 10^-19 C
G = 6.67 × 10^-11 N m²kg^-2
m_e = 9.1 × 10^-31 kg
m_p = 1.67 × 10^-27 kg
Hence, the numerical value of the given ratio is
\(\frac{k e^{2}}{G m_{e} m_{p}}\) = \(\frac{9 \times 10^{9} \times\left(1.6 \times 10^{-19}\right)^{2}}{6.67 \times 10^{-11} \times 9.1 \times 10^{-31} \times 1.67 \times 10^{-27}}\)
≈ 2.3 × 10³⁹
This is the ratio of electric force to the gravitational force between a proton and an electron, keeping distance between them constant.

Question 4.
(a) Explain the meaning of the statement ‘electric charge of a body is quantised’.
(b) Why can one ignore quantisation of electric charge when dealing with macroscopic i. e., large scale charges?
Answer:
(a) Electric charge of a body is quantised. This means that only integral (1, 2 …………,n) number of electrons can be transferred from one body to the other. Charges are not transferred in fraction. Hence, a body possesses total charge only in integral multiples of electric charge.

(b) In macroscopic or large scale charges, the charges used are huge as compared to the magnitude of electric charge. Hence, quantisation of electric charge is of no use on macroscopic scale. Therefore, it is ignored and it is considered that electric charge is continuous.

Question 5.
When a glass rod is rubbed with a silk cloth, charges appear on both. A similar phenomenon is observed with many other pairs of bodies. Explain how this observation is consistent with the law of conservation of charge.
Answer:
Rubbing produces charges of equal magnitude but of opposite nature on the two bodies because charges are created in pairs. This phenomenon of charging is called charging by friction. The net charge on the system of two rubbed bodies is zero. This is because equal amount of opposite charges annihilate each other. When a glass rod is rubbed with a silk cloth, opposite natured charges appear on both the bodies. This phenomenon is in consistence with the law of conservation of energy. A similar phenomenon is observed with many other pairs of bodies.

Question 6.
Four point charges q_A = 2 μC, q_B = -5 μC, q_C = 2 μC and q_D) = -5 μC are located at the comers of a square ABCD of side 10 cm. What is the force on a charge of 1 μC placed at the centre of the square?
Answer:
Consider the square ABCD of each side 10 cm and centre O. The charge of 1 μC is placed at O.
Now clearly, OA = OB =OC = OD
AB = BC – 10 cm = 0.1 m
AO = \(\frac{1}{2}\) AC = \(\frac{1}{2} \sqrt{A B^{2}+B C^{2}}\) = \(\frac{1}{2}\) × √2 AB
= \(\frac{1}{\sqrt{2}}\) × 0.1 m = OB = OC = OD

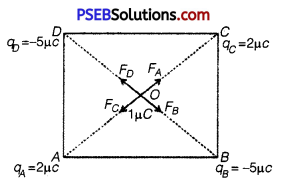
Here,q_A = 2μC, q_B = -5μC,q_C = 2 μC,q_D = -5μC
Clearly q_A = q_C = 2μC = 2 × 10^-6C
and q_B = q_D = -5 μC = -5 × 10^-6C
Since q_A = q_C, the charge of 1 μC will experience equal and opposite forces due to the charges q_A and q_C i. e., along OC and OA respectively. Their magnitudes are
F_A = F_C = \(\frac{1}{4 \pi \varepsilon_{0}} \times \frac{q_{A} \times 1 \mu \mathrm{C}}{A O^{2}}\)
\(\frac{9 \times 10^{9} \times 2 \times 10^{-6} \times 10^{-6}}{\left(\frac{1}{\sqrt{2}} \times 0.1\right)^{2}}\) = 3.6N
∴ \(\vec{F}_{A}=-\vec{F}_{C}\)
Similarly F_B = F_D, the charge of 1 μC will experience equal and opposite forces due to the charge q_B and q_D i. e., along OB and OD respectively, thus
\(\overrightarrow{F_{B}}=-\overrightarrow{F_{D}}\).
Thus the net force on the charge ofl μC due to the given arrangement of charges is zero i.e.,
\(\vec{F}=\vec{F}_{A}+\vec{F}_{B}+\vec{F}_{C}+\vec{F}_{D}\) = 0

Question 7.
(a) An electrostatic field line is a continuous curve. That is, a field line cannot have sudden breaks. Why not?
Explain why two field lines never cross each other at any point?
Answer:
(a) An electrostatic field line is a continuous curve because a charge experiences a continuous force when traced in an electrostatic field. The field line cannot have sudden breaks because the charge moves continuously and does not jump from one point to the other.

(b) If two field lines cross each other at a point, then electric field intensity will show two directions at that point. This is not possible. Hence, two field lines never cross each other.

Question 8.
Two point charges q_A = 3 μC and q_B = -3 μC are located 20 cm apart in vacuum.
(a) What is the electric field at the midpoint O of the line AB joining the two charges?
(b) If a negative test charge of magnitude 1.5 × 10^-9C is placed at this point, what is the force experienced by the test charge?
Answer:
(a) The situation is represented in the given figure. O is the mid-point of line AB.

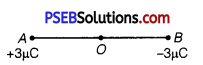
Distance between the two charges, AB = 20 cm
∴ AO = OB =10 cm
Net electric field at point O = E
Magnitude of electric field at point 0 caused by + 3 μC charge,

[Since the values of E₁ and E₂ are same, the value is multiplied with 2]
= 5.4 × 10⁶ N/C along OB
Therefore, the electric field at mid-point O is 5.4 × 10⁶ NCT^-1 along OB.

(b) A test charge of amount 1.5 × 10^-9 C is placed at mid-point O.
According to question, q = -1.5 × 10^-9 C
Force experienced by the test charge = F
F = qE
= -1.5 × 10^-9 × 5.4 × 10⁶
= -8.1 × 10^-3 N
The force is directed along line QA. This is because the negative test charge is repelled by the charge placed at point B but attracted towards point A.

Question 9.
A system has two chargesg q_A = 2.5 × 10^-7C andq_A = -2.5 × 10^-7 located at points A : (0, 0, -15 cm) and B: (0, 0, +15 cm), respectively. What are the total charge and electric dipole moment of the system?
Answer:
Both the charges can be located in a coordinate frame of reference as shown in the given figure At A, amount of charge,
q_A =2.5 × 10^-7C
At B, amount of charge,
q_B = -2.5 × 10^-7C

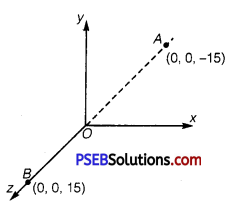
Total charge of the system,
q = q_A + q_B
= 2.5 × 10^-7 C-2.5 × 10^-7C
= 0
Distance between two charges at points A and B,
d. =15 + 15 = 30 cm = 0.3 m
Electric dipole moment of the system is given by,
p = q_A × d = q_B × d.
= 2.5 × 10^-7 × 0.3
= 7.5 × 10^-8 Cm along positive z-axis
Therefore, the electric dipole moment of the system is 7.5 × 10^-8C m along positive z-axis.

Question 10.
An electric dipole with dipole moment 4 × 10^-9 C m is aligned at 30° with the direction of a uniform electric field of magnitude 5 × 10⁴NC^-1. Calculate the magnitude of the torque acting on the dipole.
Answer:
Electric dipole moment, p = 4 × 10^-9 C m
Angle made by p with a uniform electric field, 0 = 30°
Electric field, E = 5 × 10⁴NC^-1
Torque acting on the dipole is given by the relation,
τ = pE sinθ
= 4 × 10^-9 × 5 × 10⁴ × sin30
= 20 × 10^-5 \(\frac{1}{2}\)
= 10^-4 Nm
Therefore, the magnitude of the torque acting on the dipole is 10^-4 N m.

Question 11.
A polythene piece rubbed with wool is found to have a negative charge of 3 × 10^-7C.
(a) Estimate the number of electrons transferred (from which to which?)
(b) Is there a transfer of mass from wool to polythene?
Answer:
(a) When polythene is rubbed with wool, a number of electrons get transferred from wool to polythene. Hence, wool becomes positively charged and polythene becomes negatively charged.
Amount of charge on the polythene piece, q = -3 × 10^-7 C
Amount of charge on an electron, e = -1.6 × 10^-19C
Number of electrons transferred from wool to polythene = n
n can be calculated using the relation,
> q = ne
n = \(\frac{q}{e}\)
= \(\frac{-3 \times 10^{-7}}{-1.6 \times 10^{-19}}\)
= 1.87 × 10¹²
Therefore, the number of electrons transferred from wool to polythene is 1.87 × 10¹².

(b) Yes.
There is a transfer of mass taking place. This is because an electron has mass,
m_e = 9.1 × 10^-31 kg
Total mass transferred to polythene from wool,
m = m_e × n
= 9.1 × 10^-31 × 1.87 × 10¹²
= 1.706 × 10^-18 kg
Hence, a negligible amount of mass is transferred from wool to polythene.

Question 12.
(a) Two insulated charged copper spheres A and B have their centres separated by a distance of 50 cm. What is the mutual force of electrostatic repulsion if the charge on each is 6.5 × 10^-7 C ? The radii of A and B are negligible compared to the distance of separation.
(b) What is the force of repulsion if each sphere is charged double the above amount, and the distance between them is halved?
Answer:
(a) Charge on sphere A, q_A = Charge on sphere B, q_B = 6.5 × 10^-7 C
Distance between the spheres, r = 50 cm = 0.5 m
Force of repulsion between the two spheres,
F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{A} q_{B}}{r^{2}}\)
∴ F = \(=\frac{9 \times 10^{9} \times\left(6.5 \times 10^{-7}\right)^{2}}{(0.5)^{2}}[latex]
= 1.52 × 10^-2 N
Therefore, the force between the two spheres is 1.52 × 10^{-2 N.}

(b) After doubling the charge, charge on sphere A, q_A = charge on sphere
B, q_B = 2 × 6.5 × 10^-7 C = 1.3 × 10<>-6 C
The distance between the spheres is halved
∴ r = [latex]\frac{0.5}{2}\) = 0.25 m
Force of repulsion between the two spheres,
F = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{A} q_{B}}{r^{2}}\)
∴ F = \(\frac{9 \times 10^{9} \times 1.3 \times 10^{-6} \times 1.3 \times 10^{-6}}{(0.25)^{2}}\)
= 16 × 1.52 × 10^-2 = 0.243 N Therefore, the force between the two spheres is 0.243 N.

Question 13.
Suppose the spheres A and B in exercise 1.12 have identical sizes. A third sphere of the same size but uncharged is brought in contact with the first, then brought in contact with the second, and finally removed from both. What is the new force of repulsion between A and B ?
Answer:
Distance between the spheres, A and B,r = 0.5 m
Initially, the charge on each sphere, q = 6.5 × 10 ^-7 C
When sphere A is touched with an uncharged sphere C, \(\frac{q}{2}[latex] amount of
charge from A will transfer to sphere C. Hence, charge on each of the spheres, A and C is [latex]\frac{q}{2}\).
When sphere C with charge \(\frac{q}{2}\) is brought in contact with sphere B with
charge q, total charges on the system will divide into two equal halves given as,
\(\frac{\frac{q}{2}+q}{2}=\frac{3 q}{4}\)
Each sphere will each half. Hence, charge on each of the spheres, C and B, is \(\frac{3 q}{4}\).
Force of repulsion between sphere A having charge \(\frac{q}{2}\) and sphere B having
charge \(\frac{3 q}{4}\)

= 5.703 × 10^-3 N
Therefore, the force of attraction between the two spheres is 5.703 × 10^-3 N.

Question 14.
Figure 1.33 shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?

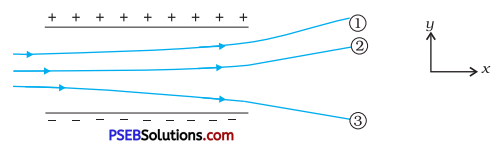
Answer:
Opposite charges attract each other and same charges repel each other. It can be observed that particles 1 and 2 both move towards the positively charged plate and repel away from the negatively charged plate. Hence, these two particles are negatively charged. It can also be observed that particle 3 moves towards the negatively charged plate and repels away from the positively charged plate. Hence, particle 3 is positively charged. The charge to mass ratio (emf) is directly proportional to the displacement or amount of deflection for a given velocity. Since the deflection of particle 3 is the maximum, it has the highest charge to mass ratio.

Question 15.
Consider a uniform electric field E = 3 × 10³ î N/C. (a) What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane? (b) What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?
Answer:
Here, \(\overrightarrow{\vec{E}}\) = 3 × 10³ î NC^-1 i.e., the electric field acts along positive direction of x-axis.
Side of square = 10 cm
∴ Its surface area, ΔS = (10 cm)² = 10^-2 m²
or Δ\(\overrightarrow{\vec{S}}\) = 10^-2 î m²
as normal to the square is along x-axis.

(a) If Φ be the electric flux through the square, then

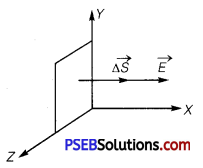
Φ = \(\vec{E} \cdot \Delta \vec{S}\)
= (3 × 10³î) .(10^-2)
= 3 × 10³ × 10^-2 î .î
= 3 × 10 = 30 Nm²C^-1

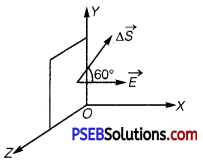
(b) Here, angle between normal to the square i.e., area vector and the electric field is 60°. i.e.,
θ = 60°
∴ Φ = \(\overrightarrow{\vec{E}}\). Δ \(\overrightarrow{\vec{S}}\) = E. Δ S cos60°
= 3 × 10³ × 10^-2 × \(\frac{1}{2}\)
= 15Nm²C^-1

Question 16.
What is the net flux of the uniform electric field of exercise 1.15 through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
Answer:
All the faces of a cube are parallel to the coordinate axes. Therefore, the number of field lines entering the cube is equal to the number of field lines piercing out of the cube. As a result, net flux through the cube is zero.

Question 17.
Careful measurement of the electric field at the surface of a black box indicates that the net outward flux through the surface of the box is 8.0 × 10³ N m² / C. (a) What is the net charge inside the box? (b) If the net outward flux through the surface of the box were zero, could you conclude that there were no charges inside the box? Why or Why not?
Answer:
(a) Net outward flux through the surface of the box Φ = 8.0 × 10³ N m² / C
For a body containing net charge q, flux is given by the relation,
Φ = \(\)
q = ε₀Φ)
= 8.854 × 10^-12 × 8.0 × 10³
(∵ ε₀ = 8.854 × 10^-12N^-1C²m^-2) = 7.08 × 10^-8
= 0.07 µC
Therefore, the net charge inside the box is 0.07 pC.

(b) No.
Net flux piercing out through a body depends on the net charge contained in the body. If net flux is zero, then it can be inferred that net charge inside the body is zero. The body may have equal amount of positive and negative charges.

Question 18.
A point charge +10 µC is a distance 5 cm directly above the centre of a square of side 10 cm, as shown in Fig. 1.34. What is the magnitude of the electric flux through the square? (Hint : Think of the square as one face of a cube with edge 10 cm.)

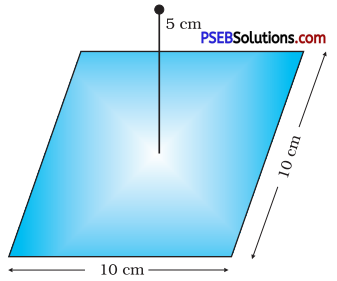
Answer:
The square can be considered as one face of a cube of edge 10 cm with a centre where charge q is placed. According to Gauss’s theorem for a cube, total electric flux is through all its six faces.
Φ total = \(\frac{q}{\varepsilon_{0}}\)

Hence, electric flux through one face of the cube i. e., through the square,
Φ = \(\frac{\phi_{\text {Total }}}{6}=\frac{1}{6} \frac{q}{\varepsilon_{0}}\)
ε₀ = 8.854 × 10^-12 N^-1C²m^-2
q = 10 µC =10 × 10^-6C
Φ = \(\frac{1}{6} \times \frac{10 \times 10^{-6}}{8.854 \times 10^{-12}}\)
= 1.88 × 10⁵ N m² C^-1
Therefore, electric flux through the square is 1.88 × 10⁵ N m² C^-1.

Question 19.
A point charge of 2.0 µC is at the centre of a cubic Gaussian surface 9.0 cm on edge. What is the net electric flux through the surface?
Answer:
Net electric flux (Φ _Net) through the cubic surface is given by,
Φ _Net = \(\frac{q}{\varepsilon_{0}}\)
ε₀ = 8.854 × 10^-12 N^-1C²m^-22 q q = Net charge contained inside the cube
= 20 µC = 2 × 10^-6C
∴ Φ _Net = \(\frac{2 \times 10^{-6}}{8.854 \times 10^{-12}}\)
∴ Φ _Net = \(\frac{2 \times 10^{-6}}{8.854 \times 10^{-12}}\)
= 2.26 × 10⁵ Nm²C^-1
The net electric flux through the surface is = 2.26 × 10⁵ Nm²C^-1

Question 20.
A point charge causes an electric flux of -1.0 × 10³ Nm² /C to pass through a spherical Gaussian surface of 10.0 cm radius centred on the charge, (a) If the radius of the Gaussian surface were doubled, how much flux would pass through the surface? (b) What is the value of the point charge?
Answer:
Electric flux, Φ = -1.0 × 10³ Nm²/C
Radius of the Gaussian surface,
r = 10.0 cm

(a) Electric flux piercing out through a surface depends on the net charge enclosed inside a body. It does not depend on the size of the body. If the radius of the Gaussian surface is doubled, then the flux passing through the surface remains the same i. e., -1.0 × 10³ 

(b) Electric flux is given by the relation,
Φ = \(\frac{q}{\varepsilon_{0}}\)
q = Φε₀
= -1.0 × 10³ × 8.854 × 10^-12
= -8.854 × 10^-9 C
= -8.854 nC
Therefore, the value of the point charge is -8.854 nC.

Question 21.
A conducting sphere of radius 10 cm has an unknown charge. If the electric field 20 cm from the centre of the sphere is 1.5 × 10³ N/C and points radially inward, what is the net charge on the sphere?
Answer:
Here R = radius of the conducting sphere = 10 cm = 0.10 m
r = distance of the point from centre of sphere = 20 cm = 0.20 m Clearly
r > R
E = electric field at a point at a distance of 20 cm from the sphere = 1.5 × 10³ NC ^-1acting inward.
q = net charge on the sphere = ?
Using the formula, E = \(\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{r^{2}}\) We get
q = 4πε₀Er² = \(\frac{1}{9 \times 10^{9}}\) × 1.5 × 10<>3 × (0.20)²
= 6.67 × 10^-9C =6.67 nC
Also as E acts in the inward direction, so charge on the sphere is negative.
q = -6.67 × 10^-9C -6.67nC

Question 22.
A uniformly charged conducting sphere of 2.4 m diameter has a surface charge density of 80.0 μC / m². (a) Find the charge on the sphere, (b) What is the total electric flux leaving the surface of the sphere?
Answer:
Diameter of the sphere, d = 2.4 m
Radius of the sphere, r = 1.2 m
Surface charge density, σ = 80.0 μC / m² = 80 × 10 ^-6C / m²

(a) Total charge on the surface of the sphere,
q = Charge density × Surface area = σ × 4πr²
= 80 × 10^-6 × 4 × 3.14 × (1.2)² = 1.447 × 10^-3 C
Therefore, the charge on the sphere is 1.447 × 10^-3 C.

(b) Total electric flux (Φ _Total) leaving out the surface of a sphere containing net charge q is given by the relation,
Φ _Total = \(\frac{q}{\varepsilon_{0}}\)
ε₀ = 8.854 × 10^-12 N^-1C²m^-2
q = 1.447 × 10^-3 C
Φ _Total = \(\frac{1.44 \times 10^{-3}}{8.854 \times 10^{-12}}\)
= 1.63 × 10⁸ NC^-1 m²
Therefore, the total electric flux leaving the surface of the sphere is 1.63 × 10⁸ NC^-1 m².

Question 23.
An infinite line charge produces a field of 9 × 10⁴ N/C^-1 at a distance of 2 cm. Calculate the linear charge density.
Answer:
Here E = electric field produced by infinite line charge = 9 × 10⁴ NC^-1.
r = distance of the point where E is produce = 2 cm = 0.02 m.
λ = linear charge density = ?

Question 24.
Two large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 17.0 × 10^-22 C/m². What is E : (a) in the outer region of the first plate, (b) in the outer region of the second plate, and (c) between the plates?
Answer:
The situation is represented in the following figure:

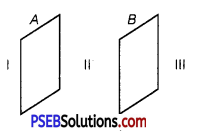
A and B are two parallel plates close to each other. Outer region of plate A is labelled as I, outer region of plate B is labelled as III, and the region between the plates, A and B is labelled as II.

(a) Charge density of plate A,
σ = 17.0 × 10^-22 C/m²
Charge density of plate B,
σ = -17.0 × 10^-22 C/ m²
In the regions, I and III, electric field E is zero. This is because charge is not enclosed by the respective plates.

(b) Electric field E in region II is given by the relation,
E = \(\frac{\sigma}{\varepsilon_{0}}\)
where, ε₀ = Permittivity of free space
= 8.854 × 10^-12N^-1C²m^-2
E = \(\frac{17.0 \times 10^{-22}}{8.854 \times 10^{-12}}\)
= 1.92 × 10^-10 N/C
Therefore, electric field between the plates is 1.92 × 10^-10 N/C.

Question 25.
An oil drop of 12 excess electrons is held stationary under a constant electric field of 2.55 × 10⁴ NC^-1 in Millikan’s oil drop experiment. The density of the oil is 1.26 g cm^-3. Estimate the radius of the drop. (g = 9.81 ms^-2, e = 1.60 × 10^-9 C).
Answer:
Here, E = constant electric field = 2.55 × 10⁴ NC^-1, e = charge of an electron = 1.6 × 10^-19 C, n = no. of electrons = 12
If q = charge on the drop, then
q = ne = 12 × 1.6 × 10^-19 C = 19.2 × 10^-19 C
If F_e be the electrostatic force on the oil drop due to electric field, then
F_e = qE = 19.2 × 10^-19 × 2.55 × 10⁴ …………..(1)
Also let F_g = Force on the drop due to gravity, then
F_g = mg = \(\frac{4}{3}\) πr³ρg …………… (2)
Here ρ = density of oil = 1.26 g cm^-3
= 1.26 × 10^-3 kg(10^-2 m)^-3
= 1.26 × 10³ kg m^-3 g
g = 9.81 ms^-2
r = radius of the drop = ?
Putting these values in equation (2), we get

Question 26.
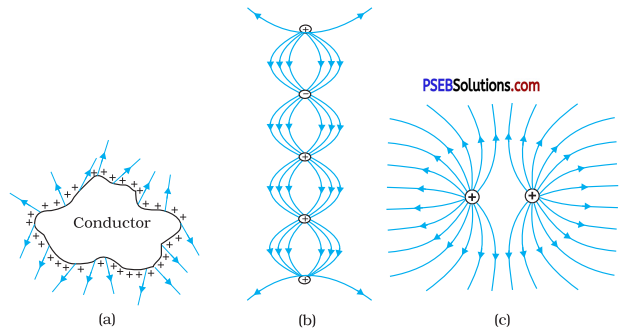
Which among the curves shown in Fig. 1.35 cannot possibly represent electrostatic field lines?


Answer:
(a) The field lines showed in (a) do not represent electrostatic field lines because field lines must be normal to the surface of the conductor.
(b) The field lines showed in (b) do not represent electrostatic field lines because the field lines cannot emerge from a negative charge and cannot terminate at a positive charge.
(c) The field lines showed in (c) represent electrostatic field lines. This is because the field lines emerge from the positive charges and repel each other.
(d) The field lines showed in (d) do not represent electrostatic field lines because the field Hnes should not intersect each other.
(e) The field lines showed in (e) do not represent electrostatic field lines because closed loops are not formed in the area between the field lines.

Question 27.
In a certain region of space, electric Held is along the z-direction throughout. The magnitude of electric field is, however, not constant but increases uniformly along the positive z-direction, at the rate of 10⁵ NC^-1 per metre. What are the force and torque experienced by a system having a total dipole moment equal to 10^-7 Cm in the negative z-direction?
Answer:
Dipole moment of the system, p = q × dl = -10^-7Cm
Rate of increase of electric field per unit length,
\(\frac{d E}{d l}\) = 10⁺⁵ NC^-1
Force (F) experienced by the system is given by the relation,
F = qE
F = q\(\frac{d E}{d l}\) × dl
= p × \(\frac{d E}{d l}\)
= -10^-7 × 10⁵ .
= -10^-2 N
The force is -10^-2 N in the negative z-direction i.e., opposite to the direction of electric field. Hence, the angle between electric field and dipole moment is 180°.
Torque (τ) is given by the relation,
τ = pEsin180°
= 0
Therefore, the torque experienced by the system is zero.

Question 28.
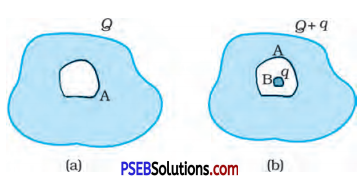
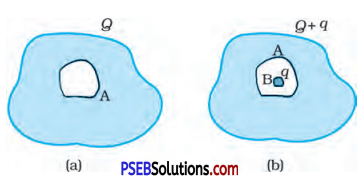
(a) A conductor A with a cavity as shown in Fig. 1.36 (a) is given a charge Q. Show that the entire charge must appear on the outer surface of the conductor.

(b) Another conductor B with charge q is inserted into the cavity keeping B insulated from A. Show that the total charge on the outside surface of A is Q q [Fig. 1.36 (b)].

(c) A sensitive instrument is to be shielded from the strong electrostatic fields in its environment. Suggest a possible way.

Answer:
(a) Let us consider a Gaussian surface that is lying wholly within a conductor and enclosing the cavity. The electric field intensity E inside the charged conductor is zero.
Let q is the charge inside the conductor and e 0 is the permittivity of free space.
According to Gauss’s law,
Flux, Φ = \(\vec{E} \cdot \overrightarrow{d s}\) = \(\frac{q}{\varepsilon_{0}}\)
Here, E = 0
\(\frac{q}{\varepsilon_{0}}\) = 0
∵ ε₀ ≠ 0
∴ q = 0
Therefore, charge inside the conductor is zero.
The entire charge Q appears on the outer surface of the conductor.

The outer surface of conductor A has a charge of amount Q. Another conductor B having charge +q is kept inside conductor A and it is insulated from A. Hence, a charge of amount -q will be induced in the inner surface of conductor A and + q is induced on the outer surface of conductor A. Therefore, total charge on the outer surface of conductor A is Q + q.

A sensitive instrument can be shielded from the strong electrostatic field in its environment by enclosing it fully inside a metallic surface. A closed metallic body acts as an electrostatic shield.

Question 29.
A hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hole is (\(\)) n̂, where n̂ is the unit vector in the outward normal direction and a is the surface charge density near the hole.
Answer:
Let us consider a conductor with a cavity or a hole. Electric field inside the cavity is zero.

Let E is the electric field just outside the conductor, q is the electric charge, σ is the charge density, and ε₀ is the permittivity of free space.
Charge \(|q|=\vec{\sigma} \times \overrightarrow{d s}\)
According to Gauss’s law,
Flux Φ = \(\vec{E} \cdot \overrightarrow{d s}\) = \(\frac{|q|}{\varepsilon_{0}}\)
Eds = \(\frac{\vec{\sigma} \times \overrightarrow{d s}}{\varepsilon_{0}}\)
∴ E = \(\frac{\sigma}{\varepsilon_{0}} \hat{n}\)

Therefore, the electric field just outside the conductor is \(\frac{\sigma}{\varepsilon_{0}} \hat{n}\) . This field is

a superposition of field due to the cavity (\(\vec{E}\)) and the field due to the rest of the charged conductor (E). These fields are equal and opposite inside the conductor, and equal in magnitude and direction outside the conductor.
∴ E’ + E’ = E
E’ = \(=\frac{E}{2}=\frac{\sigma}{2 \varepsilon_{0}} \hat{n}\)
Therefore, the field due to the rest of the conductor is \(\frac{\sigma}{\varepsilon_{0}} \hat{n}\) .
Hence, proved.

Question 30.
Obtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss’s law. [Hint: Use Coulomb’s law directly and evaluate the necessary integral.]
Answer:
Take a long thin wire XY (as shown in the figure) of uniform linear charge density λ.

Consider a point A at a perpendicular distance l from the mid-point O of the wire, as shown in the following figure:

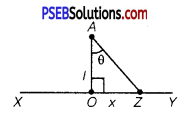
Let E be the electric field at point A due to the wire, XY.
Consider a small length element dx on the wire section with OZ = x
Let q be the charge on this piece.
∴ q = λ dx
Electric field due to the piece,
dE = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{\lambda d x}{(A Z)^{2}}\)
However, AZ = \(\sqrt{\left(l^{2}+x^{2}\right)}\)
∴ dE = \(\frac{\lambda d x}{4 \pi \varepsilon_{0}\left(l^{2}+x^{2}\right)}\)

The electric field is resolved into two rectangular components. dE cos θ is the perpendicular component and dE sin0 is the parallel component. When the whole wire is considered, the component dE sin0 is cancelled. Only the perpendicular component dE cosO affects point A.

Hence, effective electric field at point A due to the element dx is dE₁.
∴ dE₁ = \(\frac{\lambda d x \cos \theta}{4 \pi \varepsilon_{0}\left(x^{2}+l^{2}\right)}\) ……………. (1)
In Δ AZO, tanθ = \(\frac{x}{l}\)
x = ltanθ ……………. (2)

On differentiating equation (2), we obtain
\(\frac{d x}{d \theta}\) = l sin²θ
dx = lsin²θ dθ ……………… (3)

Question 31.
It is now believed that protons and neutrons (which constitute nuclei of ordinary matter) are themselves built out of more elementary units called quarks. A proton and a neutron consist of three quarks each. Two types of quarks, the so called ‘up* quark (denoted by u) of charge (+2/3)e, and the ‘down’ quark (denoted by d) of charge (-1/3) e, together with electrons build up ordinary matter. (Quarks of other types have also been found which give rise to different unusual varieties of matter.) Suggest a possible quark composition of a proton and neutron.
Answer:
A proton has three quarks. Let there be n up quarks in a proton, each having a charge of + \(\frac{2}{3}\) e.
Charge due to n up quarks = (\(\frac{2}{3}\)e)n
Number of down quarks in a proton = 3 – n
Each down quark has a charge of – \(\frac{1}{3}\) e.
Charge due to (3 – n) down quarks = (-\(\frac{1}{3}\)e) (3 – n)
Total charge on a proton = + e
e = (\(\frac{2}{3}\)e)n + (-\(\frac{1}{3}\)e) (3 – n)
e = (\(\frac{2 \text { ne }}{3}\)) – e + \(\frac{n e}{3}\)
2e = ne
n = 2
Number of up quarks in a proton, n = 2
Number of down quarks in a proton = 3 – n = 3 – 2 = 1
Therefore, a proton can be represented as ‘uud’.
A neutron also has three quarks. Let there be n up quarks in a neutron,
each having a charge of + \(\frac{2}{3}\) e.
Charge on a neutron due to n up quarks (+\(\frac{2}{3}\)e) n

Number of down quarks is 3 -n, each having a charge of (-\(\frac{1}{3}\))e
Charge on a neutron due to (3 – n) down quarks = (-\(\frac{1}{3}\)e) (3 – n)
Total charge on a neutron = 0
0 = (\(\frac{2}{3}\)e)n + (-\(\frac{1}{3}\)e) (3 – n)
0 = \(\frac{2}{3}\) en – e + \(\frac{n e}{3}\)
e = ne
n = 1
Number of up quarks in a neutron, n = 1
Number of down quarks in a neutron = 3 – n = 3 – 1 = 2
Therefore, a neutron can be represented as ‘udd’.

Question 32.
(a) Consider an arbitrary electrostatic field configuration. A small test charge isplaced at a null point (i. e., where E = 0) of the configuration. Shew that the equilibrium of the test charge is necessarily unstable.
(b) Verify this result for the simple configuration of two charges of the same magnitude and sign placed a certain distance apart.
Answer:
(a) An arbitrary electrostatic configuration consists of two charges of unequal charges of unequal magnitude and of same sign. e. g., consider a system of two fixed charges + ve and + e separated by a distance r placed at point A and B respectively. Let a test charge q0 be placed at a point C at a distance x from + 4 e. C is the point is resultant field or force on 90 is zero.

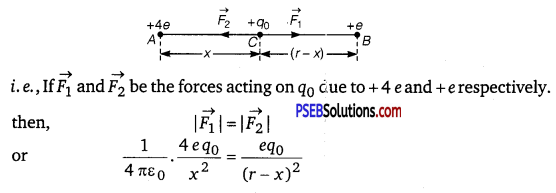
or 4(r – x)² = x² or 2(r – x) = ±x
∴ x = \(\frac{2 r}{3}\) or 2r
For equilibrium, the charge q0 can be either + ve or – ve.

Case I: If q0 is – ve, then it experiences equal attractive force due to both the charges. When it is displaced on either side along the line joining the two charges from its equilibrium position, the attractive force due to one charge gets increased while due to the other, it is decreased. As a result of this, charge -q0 no longer returns to its equilibrium position i.e., equilibrium of – ve charge is necessarily unstable.

Case II: If q0 is the + ve but displaced perpendicular to line joining the two charges, then resultant force tends to displace it further more i.e., it will not come back to its equilibrium position i. e., equilibrium will be unstable.

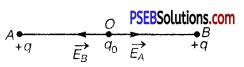
(b) Let the simple configuration consists of two equal charges +q at point A and B. As now the two charges are of same nature and have same magnitude hence their resultant \(\vec{E}\) will be zero at the mid-point O of the line joining them being equal and opposite and system will be unstable if the charge is slightly displaced, it executes S.H.M.

Question 33.
A particle of mass m and charge (~q) enters the region between the two charged plates initially moving along x-axis with speed vx (like particle 1 in Fig. 1.33). The length of plate is L and an uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is q EL² (2m v²x).
Compare this motion with motion of a projectile in gravitational field discussed in section 4.10 of Class XI Textbook of Physics.
Answer:
Charge on a particle of mass m = -q
Velocity of the particle = v_x
Length of the plates = L
Magnitude of the uniform electric field between the plates = E
Mechanical force,F = Mass (m) x Acceleration (a)
a = \(\frac{F}{m}\)
However, electric force, F = qE
Therefore, acceleration, a = \(\frac{q E}{m}\) …………. (1)
Time taken by the particle to cross the field of length L is given by,
= \(\frac{\text { Length of the plate }}{\text { Velocity of the particle }}=\frac{L}{v_{x}}\) …………… (2)

Velocity of the particle vx In the vertical direction, initial velocity, u = 0
According to the third equation of motion, vertical deflection s of the particle can be obtained as,
s = ut + \(\frac{1}{2}\)at²
s = 0 + \(\frac{1}{2}\) (\(\frac{q E}{m}\))(\(\frac{L}{v_{x}}\))²
s = \(\frac{q E L^{2}}{2 m v_{x}^{2}}\) ……………. (3)

Hence, vertical deflection of the particle at the far edge of the plate is qEL² / (2m v_x²). This is similar to the motion of horizontal projectiles under gravity.

Question 34.
Suppose that the particle in Exercise in 1.33 is an electron projected with velocity v_x = 2.0 x 10⁶ ms^-1. If E between the plates separated by 0.5 cm is 9.1 x 10² N/C, where will the electron strike the upper plate? (|e| = 1.6 x 10^-19 C, me = 9.1 x 10^-31 kg.)
Answer:
Velocity of the particle, v_x = 2.0 x 10⁶ m/ s
Separation of the two plates, d = 0.5 cm = 0.005 m
Electric field between the two plates, E = 9.1 x 10² N / C
Charge on an electron, q = 1.6 x 10^-19 C
Mass of an electron, m_e = 9.1 x 10^-31 kg
Let the electron strike the upper plate at the end of plate L, when deflection is s. Therefore,

Therefore, the electron will strike the upper plate after travelling 1.6 cm.