Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 2 Electrostatic Potential and Capacitance Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance
PSEB 12th Class Physics Guide Electrostatic Potential and Capacitance Textbook Questions and Answers
Question 1.
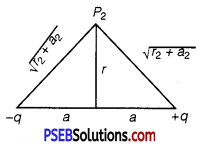
Two charges 5 × 10-8 C and -3 × 10-8 C are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.
Answer:
There are two charges,
q 1 = 5 × 10-8 C
q2 = -3 × 10-8 C
Distance between the two charges, d =16 cm = 0.16 m
Consider a point P on the line joining the two charges, as shown in the given figure

r = Distance of point P from charge q1
Let the electric potential (V) at point P be zero. r.
Potential at point P is the sum of potentials caused by charges q1 and q2 respectively.

∴ r = 0.1m = 10 cm
Therefore, the potential is zero at a distance of 10 cm from the positive charge between the charges.
Suppose point P is outside the system of two charges at a distance s from the negative charge, where potential is zero, as shown in the following figure:

For this arrangement, potential is given by,

∴ s = 0.4 m = 40 cm
Therefore, the potential is zero at a distance of 40 cm from the positive charge outside the system of charges.
![]()
Question 2.
A regular hexagon of side 10 cm has a charge 5 μC at each of its vertices. Calculate the potential at the centre of the hexagon.
Answer:
The given figure shows six equal amount of charges q, at the vertices of a regular hexagon.
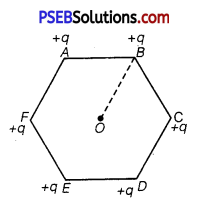
where, charge, q = 5μC = 5 × 10-6C
Side of the hexagon,
l = AB = BC = CD = DE = EF = FA = 10 cm
Distance of each vertex from centre, O, d = 10 cm = 0.1 m
Electric potential at point O,
V = \(\frac{6 \times q}{4 \pi \varepsilon_{0} d}\)
∴ \(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 × 109NC-2m-2
∴ V = \(\frac{6 \times 9 \times 10^{9} \times 5 \times 10^{-6}}{0.1}\) = 2.7 × 106 V
Therefore, the potential at the centre of the hexagon is 2.7 × 106 V.
Question 3.
Two charges 2 μC and -2μC are placed at points A and B 6 cm apart.
(a) Identify an equipotential surface of the system.
(b) What is the direction of the electric field at every point on this surface?
Answer:
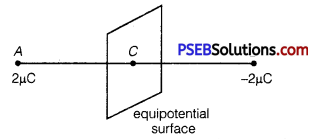
(a) Here, two charges 2 μC and -2μC are situated at points A and B.
∴ AB = 6 cm = 0.06 m
For the given system of two charges, the equipotential surface is a plane normal to the line joining points A and B. The plane passes through the mid point C of the line AB. The potential at C is
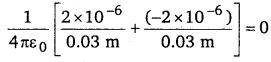
Thus potential at all points lying on this plane is equal and is zero, so it is an equipotential surface.
(b) We know that the electric field always acts from +ve to -ve charge, thus here the electric field acts from point A (having +ve charge) to point B (having -ve charge) and is normal to the equipotential surface.
Question 4.
A spherical conductor of radius 12 cm has a charge of 1.6 x 10-7 C distributed uniformly on its surface. What is the electric field
(a) inside the sphere
(b) just outside the sphere
(c) at a point 18 cm from the centre of the sphere?
Answer:
Radius of the spherical conductor, r = 12cm = 0.12m
Charge is uniformly distributed over the conductor, q = 1.6 x 10-7C
(a) Electric field inside a spherical conductor is zero. This is because if there is field inside the conductor, then charges will move to neutralize it.
(b) Electric field E just outside the conductor is given by the relation,
E = \(\frac{q}{4 \pi \varepsilon_{0} r^{2}}\)
\(=\frac{1.6 \times 10^{-7} \times 9 \times 10^{5}}{(0.12)^{2}}[latex] = 105 NC -1
(0.12) 2
Therefore, the electric field just outside the sphere is 105 NC-1
(c) Electric field at a point 18 m from the centre of the sphere = E1
Distance of the point from the centre, d=18cm = 0.18m
E1 = [latex]\frac{q}{4 \pi \varepsilon_{0} d^{2}}\)
= \(\frac{9 \times 10^{9} \times 1.6 \times 10^{-7}}{\left(18 \times 10^{-2}\right)^{2}}\)
= 4.4 × 104 N/C
Therefore, the electric field at a point 18 cm from the centre of the sphere is 4.4 × 104N/C.
![]()
Question 5.
A parallel plate capacitor with air between the plates has a capacitance of 8 pF (1 pF = 10-2 F). What will be the capacitance if the distance between the plates is reduced by half, and the space between them is filled with a substance of dielectric constant 6?
Answer:
Capacitance between the parallel plates of the capacitor, C = 8 pF
Initially, distance between the parallel plates was d and it was filled with air. Dielectric constant of air, k = 1
Capacitance, C is given by the formula,
C = \(\frac{k \varepsilon_{0} A}{d}[latex]
= [latex]\frac{\varepsilon_{0} A}{d}\) …………… (1)
If distance between the plates is reduced to half, then new distance,
d’ = \(\frac{d}{2}\)
Dielectric constant of the substance filled in between the plates, k’ Hence, capacitance of the capacitor becomes
C’ = \(\frac{k^{\prime} \varepsilon_{0} A}{d^{\prime}}=\frac{6 \varepsilon_{0}^{*} A}{\frac{d}{2}}\) …………….. (2)
Taking ratios of equations (1) and (2), we obtain
C’ = 2 × 6C
= 12C
= 12 × 8 = 96 pF
Therefore, the capacitance between the plates is 96 pF.
Question 6.
Three capacitors each of capacitance 9 pF are connected in series.
(a) What is the total capacitance of the combination?
(b) What is the potential difference across each capacitor if the combination is connected to a 120 V supply?
Answer:
(a) Given C1 = C2 = C3 = 9 pF
When capacitors are connected in series, the equivalent capacitance Cs is given by
\(\frac{1}{C_{S}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}=\frac{1}{9}+\frac{1}{9}+\frac{1}{9}=\frac{3}{9}=\frac{1}{3}\)
CS 3PF
(b) In series charge on each capacitor remains the same, so charge on each capacitor.
q = CSV = (3 × 10-12 F) × (120 V)
= 3.6 × 10-10 coulomb
Potential difference across each capacitor, q 3.6 × 10-10
V = \(\frac{q}{C_{1}}=\frac{3.6 \times 10^{-10}}{9 \times 10^{-12}}\) = 40V
Question 7.
Three capacitors of capacitances 2 pF, 3 pF and 4pF are connected in parallel
(a) What is the total capacitance of the combination?
(b) Determine the charge on each capacitor if the combination is connected to a 100 V supply.
Answer:
C1 = 2 pF, C2 = 3 pF, C3 = 4 pF
(a) Total capacitance when connected in parallel,
Cp = C1 + C2 + C3 = 2 + 3 + 4 = 9 pF,
(b) In parallel, the potential difference across each capacitor remains the same, i.e.,
V = 100 V.
Charge on C1 = 2 pF,
q1 = C1V = 2 × 10-12 × 100
= 2 × 10 -10C
Charge on C2 = 3pF,
q2 = C2V = 3 × 10-10 × 100
= 3 × 10-10 C
Charge on C3 = 4 pF,
q3 = C3V = 4 × 10-12 × 100
= 4 × 10-10C
![]()
Question 8.
In a parallel plate capacitor with air between the plates, each plate has an area of 6 × 10-3 m2 and the distance between the plates is 3 mm. Calculate the capacitance of the capacitor. If this capacitor is connected to a 100 V supply, what is the charge on each plate of the capacitor?
Answer:
Area of each plate of the parallel plate capacitor, A = 6 10-3m2
Distance between the plates, d = 3 mm = 3 × 10-3 m
Supply voltage, V = 100 V
Capacitance C of a parallel plate capacitor is given by,
C = \(\frac{\varepsilon_{0} A}{d}\)
where, ε0 = 8.854 × 10-12 N-1m-2C-2
C = \(\frac{8.854 \times 10^{-12} \times 6 \times 10^{-3}}{3 \times 10^{-3}}\)
= 17.71 × 10-12F
= 17.71 pF or 18 pF
Potential V is related with the charge q and capacitance C as
V = \(\frac{q}{C}\)
∴ q = VC = 100 × 17.71 × 10-12
= 1.771 × 109C
Therefore, capacitance of the capacitor is 17.71 pF and charge on each plate is 1.771 × 10-9 C.
Question 9.
Explain what would happen if in the capacitor given in Exercise 2.8, a 3 mm thick mica sheet (of dielectric constant = 6) were inserted between the plates,
(a) while the voltage supply remained connected.
(b) after the supply was disconnected.
Answer:
(a) Here C0 = Capacitance of the capacitor with air as medium = 18 pF
d = distance between the plates = 3 × 10-3 m
t = thickness of mica sheet = 3 × 10-3 m = d
K = dielectric constant of the mica sheet = 6
As the mica sheet completely fills the space between the plates, thus the capacitance of the capacitor (C) is given by
C =KC0 = 6 × 18 × 10-12 F
= 108 × 10-12 F = 108 pF
Thus the capacitance of the capacitor increases by K times on inserting the mica sheet.
Potential difference across this capacitor, V = 100 V
∴ Charge q’ on the capacitor with mica sheet as medium is given by
q’ = CV= 108 × 10-12 × 100
= 108 × 10-8 C
Now clearly q’ = KC0V = Kq = 6 × 1.8 × 10-9
= 1.08 × 10-8C
Clearly charge becomes K times the charge on the plates with air as medium, i.e., charge on the plates increases when supply remains connected and mica sheet is inserted.
(b) Here, capacitance of capacitor with mica as medium C = KC0 108 × 10-12F
When supply is disconnected, i. e., mV = 0,
The potential difference across on the plates of the reduces by K times.
i.e., V’ = \(\frac{100}{6}\) 16.67V
C-becomes 6 times.
Thus if qi be the charge on its plates after disconnecting the supply,
Then q1 = CV’ = KC0 × \(\frac{100}{6}\)
= 6 × 18 × 10-12 × \(\frac{100}{6}\)
= 18 × 10-10C
q0 = 1.8 × 10-9C =1.8 nC
i.e., the charge on the capacitor with mica as medium remains same as with air medium.
Question 10.
A 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor?
Answer:
Given, C = 12 pF = 12 × 10-12 F and V = 50 V, U = ?
Using the relation U = \(\frac{1}{2}\) CV2, we have
U = \(\frac{1}{2}\)CV2 = \(\frac{1}{2}\) × 12 × 10-12(50)2
= 1.5 × 108 J
![]()
Question 11.
A 600 pF capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 600 pF capacitor. How much electrostatic energy is lost in the process?
Answer:
Given, C1 = C2 = 600 pF = 600 × 10-12F, V = 200 V, ∆U = ?
Using the relation ∆U = \(\frac{C_{1} C_{2}\left(V_{1}-V_{2}\right)^{2}}{2\left(C_{1}+C_{2}\right)}\) , we get
∆U = \(\frac{600 \times 600 \times 10^{-24}(200-0)^{2}}{2(600+600) \times 10^{-12}}[latex] = 6 × 10-6 j
Question 12.
A charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of -2 × 10-9 C from a point P(0, 0, 3 cm) to a point Q (0, 4 cm, 0), viaa point R (0,6 cm, 9 cm). Answer:
Charge located at the origin, q = 8 mC = 8 × 10-3 C
Magnitude of a small charge, which is taken from a point P to point R to point Q, = -2 × 10-9 C
All the points are represented in the given figure
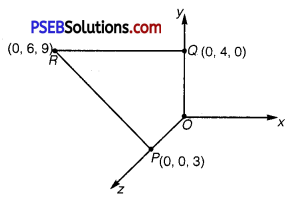
Point P is at a distance, d1 = 3 cm, from the origin along z-axis.
Point Q is at a distance, d2 = 4 cm, from the origin along y-axis.

Therefore, work done during the process is 1.27 J.
Question 13.
A cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.
Answer:
Length of the side of a cube = b
Charge at each of its vertices = q
A cube of side b is shown in the following figure:

is the distance between the centre of the cube and one of the eight vertices.
The electric potential (V) at the centre of the cube is due to the presence of eight charges at the vertices.
V = [latex]\frac{8 q}{4 \pi \varepsilon_{0} r}\)
= \(\frac{8 q}{4 \pi \varepsilon_{0}\left(b \frac{\sqrt{3}}{2}\right)}\)
= \(\frac{4 q}{\sqrt{3} \pi \varepsilon_{0} b}\)
Therefore, the potential at the centre of the cube is \(\frac{4 q}{\sqrt{3} \pi \varepsilon_{0} b}\)
The electric field at the centre of the cube, due to the eight charges, gets cancelled. This is because the charges are distributed symmetrically with respect to the centre of the cube. Hence, the electric field is zero at the centre.
![]()
Question 14.
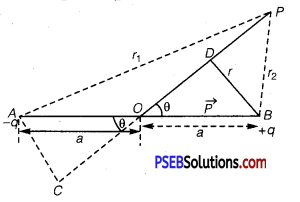
Two tiny spheres carrying charges 1.5 μC and 2.5 μC are located 30 cm apart. Find the potential and electric field :
(a) at the mid-point of the line joining the two charges, and
(b) at a point 10 cm from this midpoint in a plane normal to the line and passing through the mid-point.
Answer:
Two charges placed at points A and B are represented in the given figure. O is the mid-point of the line joining the two charges.
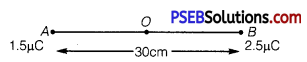
Magnitude of charge located at A, q1 = 1.5 μC
Magnitude of charge located at B, q2 = 2.5 μC
Distance between the two charges, d = 30 cm = 0.3 m
(a) Let V1 and E1 are the electric potential and electric field respectively at O.
V1 = Potential due to charge at A + Potential due to charge at B

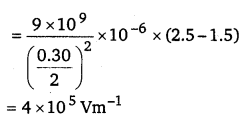
Therefore, the potential at mid-point is 2.4 x 105 V and the electric field at mid-point is 4 x 105Vm-1. The field is directed from the larger charge to the smaller charge.
(b) Consider a point Z such that normal distance OZ =10 cm = 0.1 m, as shown in the following figure:
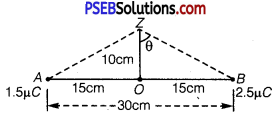
V2 and E2 are the electric potential and electric field respectively at Z. It can be observed from the figure that distance,

θ = cos-1 (0.5556) = 56.25
∴ 2θ = 112.5°
cos 2θ = -0.38
![]()
E = 6.6 × 105 Vm-1
Therefore, the potential at a point 10 cm (perpendicular to the mid point) is 2.0 × 105 V and electric field is 6.6 × 105 Vm-1.
![]()
Question 15.
A spherical conducting shell of inner radius and r1outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell?
(b) Is the electric field inside a cavity (with no charge) zero, even if the shell is not spherical, but has any irregular shape? Explain.
Answer:
(a) Charge placed at the centre of a shell is+q. Hence, a charge of magnitude -q will be induced to the inner surface of the shell. Therefore, total charge on the inner surface of the shell is -q.
Surface charge density at the inner surface of the shell is given by the relation,
σ1 = \(\frac{\text { Total charge }}{\text { Inner surface area }}=\frac{-q}{4 \pi r_{1}^{2}}\) ……………… (1)
A charge of + q is induced on the outer surface of the shell. A charge of magnitude Q is placed on the outer surface of the shell. Therefore, total charge on the outer surface of the shell is Q + q. Surface charge density at the outer surface of the shell,
σ2 = \(=\frac{\text { Total charge }}{\text { Outer surface area }}=\frac{Q+q}{4 \pi r^{2}}\) …………… (2)
(b) Yes.
The electric field intensity inside a cavity is zero, even if the shell is not spherical and has any irregular shape. Take a closed loop such that a part of it is inside the cavity along a field line while the rest is inside the conductor. Net work done by the field in carrying a test charge over a closed loop is zero because the field inside the conductor is zero.
Hence, electric field is zero, whatever is the shape.
Question 16.
(a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by
(E2 – E1)n̂ = \(\frac{\sigma}{\varepsilon_{0}}\)
where n is a unit vector normal to the surface at a point ando is the surface charge density at that point. (The direction of n is from side 1 to side 2.) Hence show that just outside a conductor, the electric field is σ = n̂ ε0.
(b) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another.
[Hint : For (a), use Gauss’s law. For, (b) use the fact that work done by electrostatic field on a closed loop is zero.]
Answer:
(a) Let AB be a charged surface having two sides as marked in the figure.
A cylinder enclosing a small area element ∆ S of the charged surface is the , Gaussian surface.
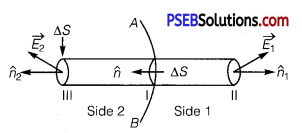
Let σ = surface charge density
∴ q = charge enclosed by the Gaussian cylinder = σ . ∆ S.
∴ According to Gauss’s Theorem,

where \(\overrightarrow{E_{1}}+\overrightarrow{E_{2}}\) are the electric fields through circular cross-sections of cylinder at II and III respectively.

It is clear from the figure that \(\overrightarrow{E_{1}}\) lies inside the conductor. Also we know that the electric field inside the conductor is zero.
∴ \(\overrightarrow{E_{1}}\) = 0
Thus from eq. (1)
\(\overrightarrow{E_{2}} \cdot \hat{n}=\frac{\sigma}{\varepsilon_{0}}[latex]
or [latex]\left(\overrightarrow{E_{2}} \cdot \hat{n}\right) \cdot \hat{n}=\frac{\sigma}{\varepsilon_{0}} \hat{n}\)
or \(\overrightarrow{E_{2}}=\frac{\sigma}{\varepsilon_{0}} \hat{n}\)
or electric field just outside the conductor = \(\frac{\sigma}{\varepsilon_{0}} \hat{n}\) Hence proved
(b) Let AaBbA be a charged surface in the field of a point charge q lying at origin.
Let \(\overrightarrow{r_{A}}\) and \(\overrightarrow{r_{B}}\) be its position vectors at points A and B respectively.
Let \(\vec{E}\) be the electric field at point P, thus E cosG is the tangential component of electric field \(\vec{E}\).

![]()
Question 17.
A long charged cylinder of linear charged density λ is surrounded by a hollow co-axial conducting cylinder. What is tihe electric field in the space between the two cylinders?
Answer:
Charge density of the long charged cylinder of length L and radius r is λ. Another cylinder of same length surrounds the previous cylinder. The radius of this cylinder is R.
Let £ be the electric field produced in the space between the two cylinders.
Electric flux through the Gaussian surface is given by Gauss’s theorem as,
Φ = E (2πd)L
where d = Distance of a point from the common axis of the cylinders Let q be the total charge on the cylinder.
It can be written as
Φ = E (2πdL) = \(\frac{q}{\varepsilon_{0}}\)
where, q = Charge on the inner sphere of the outer cylinder, ε0 = Permittivity of free space
E (2πdL) = \(\frac{\lambda L}{\varepsilon_{0}}\)
E = \(\frac{\lambda}{2 \pi \varepsilon_{0} d}\)
Therefore, the electric field in the space between the two cylinders is \(\frac{\lambda}{2 \pi \varepsilon_{0} d}\)
Question 18.
In a hydrogen atom, the electron and proton are bound at a distance of about 0.53 Å.
(a) Estimate the potential energy of the system in eV, taking the zero of the potential energy at infinite separation of the electron from proton.
(b) What is the minimum work required to free the electron, given that its kinetic energy in the orbit is half the magnitude of potential energy obtained in (a)?
(c) What are the answers to (a) and (b) above if the zero of potential energy is taken as 1.06 A separation?
Answer:
The distance between electron-proton of a hydrogen atom, d = 0.53 Å
Charge on an electron,q1 = -1.6 × 10-19 C
Charge on a proton, q2 = +1.6 × 10-19 C
(a) Potential energy at infinity is zero.
Potential energy of the system,
P.E. = P.E. at ∞ – P.E. at d
= 0 – \(\frac{q_{1} q_{2}}{4 \pi \varepsilon_{0} d}\)
∴ P.E 0 = – \(\frac{9 \times 10^{9} \times\left(1.6 \times 10^{-19}\right)^{2}}{0.53 \times 10^{-10}}\)
= -43.47 × 10-19J
Since 1.6 × 10-19 J = 1eV
∴ P.E. = -43.47 × 10-19
= \(\frac{-43.47 \times 10^{-19}}{1.6 \times 10^{-19}}\) = -27.2 eV
Therefore, the potential energy of the system is -27.2 eV.
(b) Kinetic energy is half of the magnitude of potential energy
Kinetic energy = \(\frac{1}{2}\) × (-27.2) = 13.6 eV
[v K.E. of the system is always +ve]
Total energy = 13.6 – 27.2 = 13.6 eV
Therefore, the minimum work required to free the electron is 13.6 eV.
(c) When zero of potential energy is taken, d1 = 1.06 A
Potential energy of the system = P.E. at – P.E. at d1 – P.E. at d
= \(\frac{q_{1} q_{2}}{4 \pi \varepsilon_{0} d_{1}}\) -27.2 eV
= \(\frac{9 \times 10^{9} \times\left(1.6 \times 10^{-19}\right)^{2}}{1.06 \times 10^{-10}}\) -27.2 eV
= 21.73 × 10-19 J -27.2 eV
= 13.58 eV- 27.2 eV .
= -13.6 eV
![]()
Question 19.
If one of the two electrons of aH2 molecule is removed, we get a hydrogen molecular ion H2+. In the ground state of an H2+ the two protons are separated by roughly 1.5 Å, and the electron is roughly 1 Å from each proton. Determine the potential energy of the system. Specify your choice of the zero of potential energy.
Answer:
The system of two protons and one electron is represented in the given figure
Charge on proton 1, q1 = 1.6 × 10-19 C
Charge on proton 2, q2 = 1.6 × 10-19 C
Charge on electron, q3 = -1.6 × 10-19 C
Distance between protons 1 and 2, dj = 1.5 × 10-10 m
Distance between proton 1 and electron, d2 = 1 × 10-10 m
Distance between proton 2 and electron, d3 = 1 × 10-10 m The potential energy at infinity is zero.
Potential energy of the system,
V = \(\frac{q_{1} q_{2}}{4 \pi \varepsilon_{0} d_{1}}\) + \(\frac{q_{2} q_{3}}{4 \pi \varepsilon_{0} d_{3}}\) + \(\frac{q_{3} q_{1}}{4 \pi \varepsilon_{0} d_{2}}\)
Substituting \(\frac{1}{4 \pi \varepsilon_{0}}\) = 9 × 109 Nm2C-2, we obtain
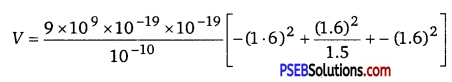
= -30.7 × 10-19 J
= -19.2 eV
Therefore, the potential energy of the system is -19.2 eV.
Question 20.
Two charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.
Answer:
Let a be the radius of a sphere A, QA be the charge on the sphere, and CA be the capacitance of the sphere. Let b be the radius of a sphere B, QB be the charge on the sphere, and CB be the capacitance of the sphere. Since the two spheres are connected with a wire, their potential (V) will become equal.
Let EA be the electric field of sphere A and EB be the electric field of sphere B. Therefore, their ratio,

Putting the value of eqn. (2) in eqn. (1), we obtain
\(\frac{E_{A}}{E_{B}}=\frac{a b^{2}}{b a^{2}}=\frac{b}{a}\)
Therefore, the ratio of electric fields at the surface is b/a.
A flat portion may be taken as a spherical surface of large radius and a pointed portion may be taken as a spherical surface of small radius.
As ε ∝ \(\frac{l}{\text { radius }}\),
thus pointed portion has larger fields than the flat one. Also we know that
E = \(\frac{\sigma}{\varepsilon_{0}}\)
i.e., E ∝ σ,
thus clearly the surface charge density on the sharp and pointed ends will be large.
![]()
Question 21.
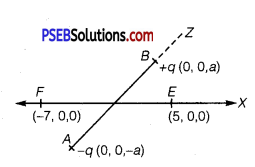
Two charges -q and +q are located at points (0, 0, – a) and (0, 0, a), respectively.
(a) What is the electrostatic potential at the points (0, 0, z) and (x, y, 0)?
(b) Obtain the dependence of potential on the distance r of a point from the origin when r/ a >> 1.
(c) How much work is done in moving a small test charge from the point (5, 0, 0) to (-7, 0, 0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?
Answer:
(a) Here -q and + q are situated at points A (0, 0, -a) and B (0, 0, a) respectively.
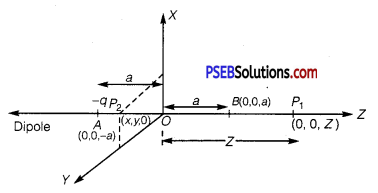
∴ Dipole length = 2a
If p be the dipole moment of the dipole, then
p = 2aq
Let P1 (0, 0, z) be the point at which V is to be calculated. It lies on the axial line of the dipole.

Now point P2 (x, y, O’) lies in XY plane which is normal to the axis of the dipole, i. e., lies on the line parallel to the equitorial line on which potential due to the dipole is zero as given below:

(b) Let r = distance of the point P from the centre (O) of the dipole at which
V is to be calculated. Let ∠POB = θ, i.e., OP makes an angle θ with \(\).
Also let r1 and r2 be the distances of the point P from -q and +q respectively. To find r1 and r2, draw AC and BD ⊥ arc to OP.
∴ In Δ ACO, OC = a cos θ
and in Δ BDO, OD = a cos θ
Thus, if V1 and V2 be the potentials at P due to – q and + q respectively, then total potential V at P is given by
V = V1 + V2

Thus,V = \(=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{p \cos \theta}{r^{2}}\) ………….. (2)
Thus, we see that the dependence of V on r is of \(\frac{1}{r^{2}}\) type, i.e.,V ∝ \(\frac{1}{r^{2}}\).
(c) Let W1 and W2 be the work done in moving a test charge q0 from E(5,0,0) to F(-7, 0,0) in the fields of + q(0, 0, a) and -q(0, 0,-a) respectively.

No, because work done in moving a test charge in an electric field between two points is independent of the path connecting the two point.
![]()
Question 22.
Figure 2.34 shows a charge array known as an electric quadrupole. For a point on the axis of the quadrupole, obtain the dependence of potential on r for r/a >> 1, and contrast your results with that due to an electric dipole, and an electric monopole (i. e., a single charge).

Answer:
Four charges of same magnitude are placed at points X, Y, Y and Z respectively, as shown in the following figure:
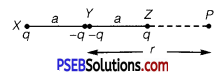
A point is located at P, which is r distance away from point Y.
The system of charges forms an electric quadrupole.
It can be considered that the system of the electric quadrupole has three charges.
Charge + q placed at point X
Charge -2q placed at point Y
Charge + q placed at point Z
XY = YZ = a
YP = r
PX = r + a
PZ = r – a
Electrostatic potential caused by the system of three charges at point P is given by,

It can be inferred that potential, V ∝ \(\frac{1}{r^{3}}\).
However, it is known that for a dipole, V ∝ \(\frac{1}{r^{2}}\). and, for monopole V ∝ \(\frac{1}{r}\)
Question 23.
An electrical technician requires a capacitance of 2 μF in a circuit across a potential difference of 1 kV. A large number of 1 μF capacitors are available to him each of which can withstand a potential difference of not more than 400 V. Suggest a possible arrangement that requires the minimum number of capacitors.
Answer:
Total required capacitance, C = 2 μF
Potential difference, V = 1 kV = 1000 V
Capacitance of each capacitor, C = 1 μF
Each capacitor can withstand a potential difference, V1 = 400 V
Suppose a number of capacitors are connected in series and these series circuits are connected in parallel (row) to each other. The potential difference across each row must be 1000 V and potential difference across each capacitor must be 400 V. Hence, number of capacitors in each row is given as
\(\frac{1000}{400}\) = 25 .
Hence, there are three capacitors in each row.
Capacitance of each row = \(\frac{1}{1+1+1}=\frac{1}{3}\) μF
Let there are n rows, each having three capacitors, which are connected in parallel.
Hence, equivalent capacitance of the circuit is given as
\(\frac{1}{3}+\frac{1}{3}+\frac{1}{3}\) + ….. + n terms = \(\frac{n}{3}\)
However, capacitance of the circuit is given as 2 μF.
∴ \(\frac{n}{3}\) = 2
n = 6
Hence, 6 rows of three capacitors are present in the circuit. A minimum of 6 × 3, i.e., 18 capacitors are required for the given arrangement.
Question 24.
What is the area of the plates of a 2 F parallel plate capacitor, given that the separation between the plates is 0.5 cm? [You will realize from your answer why ordinary capacitors are in the range of μF or less. However, electrolytic capacitors do have a much larger capacitance (0.1 F) because of very minute separation between the conductors.]
Answer:
Capacitance of a parallel capacitor, C = 2 F
Distance between the two plates, d = 0.5 cm = 0.5 × 10-2 m
Capacitance of a parallel plate capacitor is given by the relation,
C = \(\frac{\varepsilon_{0} A}{d}\)
A = \(\frac{C d}{\varepsilon_{0}}\)
Where ε0 = 8.85 × 10-12C2N-1m-2
∴ A = \(\frac{2 \times 0.5 \times 10^{-2}}{8.85 \times 10^{-12}}\) = 1130 km2
Hence, the area of the plates is too large. To avoid this situation, the capacitance is taken in the range of μF.
![]()
Question 25.
Obtain the equivalent capacitance of the network in Fig. 2.35. For a 300 V supply, determine the charge and voltage across each capacitor.
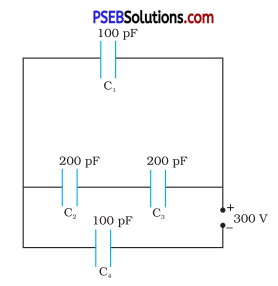
Answer:


Question 26.
he plates of a parallel plate capacitor have an area of 90 cm2 each and are separated by 2.5 nun. The capacitor is charged by connecting it to a 400 V supply.
(a) How much electrostatic energy is stored by the capacitor?
(b) View this energy as stored in the electrostatic field between the plates, and obtain the energy per unit volume u. Hence arrive at a relation between u and the magnitude of electric field E between the plates.
Answer:
Area of the plates of a parallel plate capacitor,
A = 90 cm2 = 90 × 10-4 m2
Distance between the plates, d = 2.5mm 2.5 × 10-3 m
Potential difference across the plates, V = 4OO V
Capacitance of the capacitor is given by the relation,
C = \(\)
(a) Electrostatic energy stored in the capacitor is given by the relation,
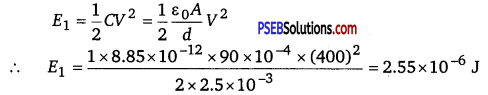
Hence, the electrostatic energy stored by the capacitor is 2.55 × 10-6 J
(b) Volume of the given capacitor,
V’= A × d
= 90 × 10-4 × 2.5 × 10-3
= 2.25 × 10-5 m3
Energy stored in the capacitor per unit volume is given by,

Question 27.
A 4 μF capacitor is charged by a 200 V supply. It is then disconnected from the supply, and is connected to another uncharged 2 μF capacitor. How much electrostatic energy of the first capacitor is lost in the form of heat and electromagnetic radiation?
Answer:

![]()
Question 28.
Show that the force on each plate of a parallel plate capacitor has a magnitude equal to (\(\frac{1}{2}\)) QE, where Q is the charge on the capacitor, and E is the magnitude of electric field between the plates. Explain the origin of the factor \(\frac{1}{2}\).
Answer:
Let F be the force applied to separate the plates of a parallel plate capacitor by a distance of Δx. Hence, work done by the force to do so = FΔx
As a result, the potential energy of the capacitor increases by an amount given as uA Δx.
where, u = Energy density
A = Area of each plate
The work done will be equal to the increase in the potential energy, i. e.,
FΔx = uA Δx

The physical origin of the factor, 1/2 in the force formula lies in the fact that just outside the conductor, field is E and inside it is zero. Hence, it is the averge value, E/2 of the field that contributes to the force.
Question 29.
A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports (Fig. 2.36). Show that the capacitance of a spherical capacitor is given by
C = \(\frac{4 \pi \varepsilon_{0} r_{1} r_{2}}{r_{1}-r_{2}}\)
where r 1and r2 are the radii of outer and inner spheres, respectively.
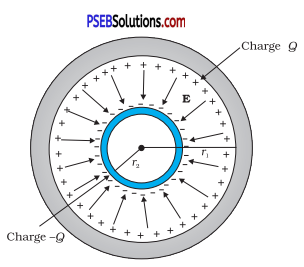
Answer:
Radius of the outer shell = r1
Radius of the inner shell = r2
The inner surface of the outer shell has charge +Q
The outer surface of the inner shell has induced charge -Q.
Potential difference between the two shells is given by,

Question 30.
A spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5 µC. The space between the concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor.
(b) What is the potential of the inner sphere?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm. Explain why the latter is much smaller.
Answer:
Radius of the inner sphere, r2 = 12 cm = 0.12m
Radius of the outer sphere, r1 = 13 cm = 0.13m
Charge on the inner sphere, q = 2.5 µC = 2.5 × 10-6 C
Dielectric constant of the liquid, εr = 32
Capacitance of the capacitor is given by the relation,
C = \(\frac{4 \pi \varepsilon_{0} \varepsilon_{r} r_{1} r_{2}}{r_{1}-r_{2}}\)
C = \(\frac{32 \times 0.12 \times 0.13}{9 \times 10^{9} \times(0.13-0.12)}\)
≈ 5.5 × 10-9 F
Hence, the capacitance of the capacitor is approximately 5.5 × 10-9 F.
(b) Potential of the inner sphere is given by,
V = \(\frac{q}{C}=\frac{2.5 \times 10^{-6}}{5.5 \times 10^{-9}}\) = 4.5 × 102V
Hence, the potential of the inner sphere is 4.5 × 102 V
(c) Radius of an isolated sphere, r = 12cm = 12 × 10-2m
Capacitance of the sphere is given by the relation,
C’ = 4πε0r
= 4π × 8.85 × 10-12 × 12 × 10-12
= 1.33 × 10-11F
The capacitance of the isolated sphere is less in comparison to the concentric spheres. This is because the outer sphere of the concentric spheres is earthed. Hence, the potential difference is less and the capacitance is more than the isolated sphere.
![]()
Question 31.
Answer carefully:
(a) Two large conducting spheres carrying charges Q1 and Q2 are brought close to each other. Is the magnitude of electrostatic force between them exactly given by Q1Q2 / πε0 r2, where r is the distance between their centres?
(b) If Coulomb’s law involved 1/r3 dependence (instead of 1/r2), would Gauss’s law be still true?
(c) A small test charge is released at rest at a point in an electrostatic field configuration. Will it travel along the field line passing through that point?
(d) What is the work done by the field of a nucleus in a complete circular orbit of the electron? What if the orbit is elliptical?
(e) We know that electric field is discontinuous across the surface of a charged conductor. Is electric potential also discontinuous there?
(f) What meaning would you give to the capacitance of a single conductor?
(g) Guess a possible reason why water has a much greater dielectric constant (= 80) than say, mica (= 6).
Answer:
(a) The force between two conducting spheres is not exactly given by the expression,Q1Q2 / πε0 r2, because there is a non-uniform charge distribution on the spheres.
(b) Gauss’s law will not be true, if Coulomb’s law involved 1/r3 dependence, instead of 1/r2, on r.
(c) Yes, If a small test charge is released at rest at a point in an electrostatic field configuration, then it will travel along the field lines passing through the point, only if the field lines are straight. This is because the field lines give the direction of acceleration and not of velocity.
(d) Whenever the electron completes an orbit, either circular or elliptical, the work done by the field of a nucleus is zero.
(e) No, electric field is discontinuous across the surface of a charged conductor. However, electric potential is continuous.
(f) The capacitance of a single conductor is considered as a parallel plate capacitor with one of its two plates at infinity.
(g) Water has an unsymmetrical space as compared to mica. Since it has a permanent dipole moment, it has a greater dielectric constant than mica.
Question 32.
A cylindrical capacitor has two co-axial cylinders of length 15 cm and radii 1.5 cm and 1.4 cm. The outer cylinder is earthed and the inner cylinder is given a charge of 3.5 μC. Determine the capacitance of the system and the potential of the inner cylinder. Neglect end effects (i. e., bending of field lines at the ends).
Answer:
Length of a co-axial cylinder, l = 15 cm = 0.15 m
Radius of outer cylinder, r1 = 1.5 cm = 0.015 m
Radius of inner cylinder, r2 = 1.4 cm = 0.014 m
Charge on the inner cylinder, q = 3.5 μC = 3.5 × 10-6 C
Capacitance of a co-axial cylinder of radii r1 and r2 is given by the relation,

Question 33.
A parallel plate capacitor is to be designed with a voltage rating 1 kV, using a material of dielectric constant 3 and dielectric strength about 107 Vm-1. (Dielectric strength is the maximum electric field a material can tolerate without breakdown, i. e., without starting to conduct electricity through partial ionisation.) For safety, we should like the field never to exceed, say 10% of the dielectric strength. What minimum area of the plates is required to have a capacitance of 50 pF?
Answer:
Potential rating of the parallel plate capacitor, V = 1 kV = 1000 V
Dielectric constant of the material, εr = 3
Dielectric strength = 107 V/m
For safety, the field intensity never exceeds 10% of the dielectric strength.
Hence, electric field intensity, E = 10% of 107 =106V/m
Capacitance of the parallel plate capacitor C = 50 pF = 50 × 10-12F
Distance between the plates is given by,
d = \(\frac{V}{E}=\frac{1000}{10^{6}}\) = 10-3 m
Capacitance is given by the relation,
C = \(\frac{\varepsilon_{0} \varepsilon_{r} A}{d}\)
∴ A = \(\frac{C d}{\varepsilon_{0} \varepsilon_{r}}\) = \(\frac{50 \times 10^{-12} \times 10^{-3}}{8.85 \times 10^{-12} \times 3}\) ≈ 19cm 2
Hence, the area of each plate is about 19 cm2 .
![]()
Question 34.
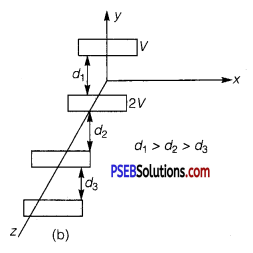
Describe schematically the equipotential surfaces corresponding to
(a) a constant electric field in the z-direction,
(b) a field that uniformly increases in magnitude but remains in a constant (say, z) direction,
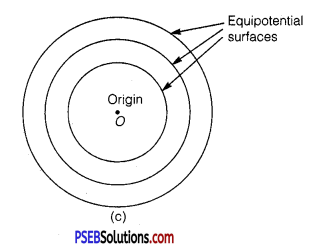
(c) a single positive charge at the origin, and
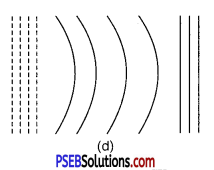
(d) a uniform grid consisting of long equally spaced parallel charged wires in a plane.
Answer:
Equipotential surface is a surface having the same potential at each of its points. In the given cases the equipotential surface are
(a) The planes are parallel to XY plane. For same potential difference, the planes are equidistant.
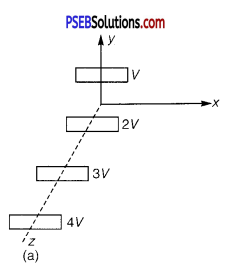
(b) The planes are parallel to XY plane, but for the same potential difference, the separation between the planes decreases.
(c) Concentric spheres centred at the origin.
(d) A periodically varying shape near the grid which gradually attains the shape of planes parallel to grid at far distances.
Question 35.
In a Van de Graff type generator a spherical metal shell is to be a 15 × 106 V electrode. The dielectric strength of the gas surrounding the electrode is 5 × 107 Vm-1. What is the minimum radius of the spherical shell required? (You will learn from this exercise why one cannot build an electrostatic generator using a very small shell which requires a small charge to acquire a high potential.)
Answer:

Question 36.
A small sphere of radius r1and charge q1 is enclosed by a spherical shell of radius r2 and charge q2. Show that if q1 is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q2 on the shell is.
Answer:
Here r1, r2 are the radii of small sphere and the spherical shell respectively. The shell surrounds the sphere +q1 is the charge on the sphere +q2 is the charge on the shell. We know that the electric field
inside a conductor is zero, i.e.,\(\vec{E}\) = 0. Thus according to Gauss’s Theorem
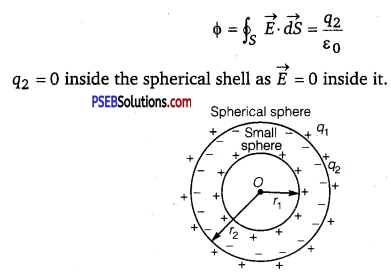
Hence q2 must reside on the outer surface of the spherical shell.
Now the sphere having +q1 charge is enclosed inside the spherical shell. So – q1 charge will be induced on the inside side and +q1 charge will be induced on the outer surface the spherical shell.
∴ Total charge on the outer surface of the shell = q2 + q1.
As the charge always resides on the outer surface, thus charge q1 from the outer surface of sphere will flow to the other surface of spherical shell when connected with a wire.
![]()
Question 37.
Answer the following:
(a) The top of the atmosphere is at about 400 kV with respect to the surface of the earth, corresponding to an electric field that decreases with altitude. Near the surface of the earth, the field is about 100 Vm-1. Why then do we not get an electric shock as we step out of our house into the open? (Assume the house to be a steel cage so there is no field inside.)
(b) A man fixes outside his house one evening a two metre high insulating slab carrying on its top a large aluminium sheet of area 1 m2. Will he get an electric shock if he touches the metal sheet next morning?
(c) The discharging current in the atmosphere due to the small conductivity of air is known to be 1800 A on an average over the globe. Why then does the atmosphere not discharge itself completely in due course and become electrically neutral? In other words, what keeps the atmosphere charged?
(d) What are the forms of energy into which the electrical energy of the atmosphere is dissipated during a lightning? (Hint : The earth has an electric field of about 100 Vm-1 at its surface in the downward direction, corresponding to a surface charge density = -10-9 Cm-2. Due to the slight conductivity of the atmosphere up to about 50 km (beyond which it is good conductor), about +1800 C is pumped every second into the earth as a whole. The earth, however, does not get discharged since thunderstorms and lightning occurring continually all over the globe pump an equal amount of negative charge on the earth.)
Answer:
(a) We do not get an electric shock as we step out of our house because the original equipotential surfaces of open air changes, keeping our body and the ground at the same potential.
(b) Yes, the man will get an electric shock if he touches the metal slab next morning. The steady discharging current in the atmosphere charges up the aluminium sheet. As a result, its voltage rises gradually. The raise in the voltage depends on the capacitance of the capacitor formed by the aluminium slab and the ground.
(c) The occurrence of thunderstorms and lightning charges the atmosphere continuously. Hence, even with the presence of discharging current of 1800 A, the atmosphere is not discharged completely. The two opposing currents are in equilibrium and the atmosphere remains electrically neutral.
(d) During lightning and thunderstorm, light energy, heat energy and sound energy are dissipated in the atmosphere.