Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 1 Relations and Functions Ex 1.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 Maths Chapter 1 Relations and Functions Ex 1.1
Question 1.
Determine whether each of the following relations are reflexive, symmetric and transitive:
(i) Relation R in the set A – {1, 2, 3,.. .13,14} defined as, R = {(x, y) : 3x – y = 0}
Solution:
(i) A = {1, 2, 3 ……. 13, 14};
R = {(x, y): 3x – y = 0}
∴ R = {(1, 3), (2, 6), (3, 9), (4, 12)}
R is not reflexive since (1, 1), (2, 2) … (14, 14) ∉ R.
Also, R is not symmetric as (1, 3) ∈ R, but (3, 1) ∉ R. [3(3) – 1 ≠ 0]
Also, R is not transitive as (1, 3), (3, 9) ∈ R, but (1, 9) ∉ R. [3(1) – 9 ≠ 0]
Hence, R is neither reflexive, nor symmetric, nor transitive.

(ii) Relation R in the set N of natural numbers defined as, R = {(x, y): y = x + 5 and x < 4}
Solution:
R = {(x, y) : y = x + 5 and x < 4} = {(1,6), (2, 7), (3, 8)} It is seen that (1, 1) ∉ R. ∴ R is not reflexive. (1, 6) ∈ R But, (6, 1) ∉ R.
∴ R is not symmetric. Now, since there is no pair in R such that (x, y) and (y, z) ∈ R. So, we need not look for the ordered pair (x, z) in R.
R is transitive Hence, R is neither reflexive, nor symmetric but it is transitive.
(iii) Relation R in the set A = {1, 2, 3, 4, 5, 6} as R = {(x, y): y is divisible by x}
Solution:
A = {1, 2, 3, 4, 5, 6} R = {(x, y) y is divisible by x} We know that any number (x) is divisible by itself. ⇒ (x, x) ∈ R
∴ R is reflexive. Now, (2, 4) ∈ R [as 4 is divisible by 2] But, (4, 2) ∉ R. [as 2 is not divisible by 4]
∴ R is not symmetric. Let (x, y), (y, z) ∈ R. Then, y is divisible by x and z is divisible by y.
∴ z is divisible by x. ⇒ (x, z) ∈ R ∴ R is transitive.
Hence, R is reflexive and transitive but not symmetric.\

(iv) Relation R in the set Z of all integers defined as, R = {(x, y): x – y is an integer}
Solution:
R = {(x, y): x – y is an integer} Now, for every x ∈ Z, (x, x) ∈ R as x – x = 0 is an integer.
∴ R is reflexive. Now, for every x, y ∈ Z if (x, y) E R as x – y is an integer. ⇒ – (x – y) is also an integer. ⇒ (y – x) is an integer. (y, x) ∈ r ∴ R is symmetric. Now, let (x, y) and (y, z) ∈ R, where x, y, z ∈ Z. ⇒ (x – y) and (y – z) are integers. ⇒ x – z = (x – y) + (y – z) is an integer. ∴ (x, z) ∈ R ∴ R is transitive. Hence, R is reflexive, symmetric and transitive.
(v) Relation R in the set A of human beings in a town at a particular time given by, (a) R = {(x, y): x and y work at the same place} Solution: (a) R = {(x, y): x and y work at the same place} ⇒ (x, x) ∈ R R is reflexive. ⇒ y and x work at the same place. ⇒ (y, X) ∈ R. ∴ R is symmetric. Now, let (x, y), (y, z) ∈ R ⇒ x and y work at the same place and y and z work at the same place. => x and z work at the same place.
⇒ (x, z) ∈ R
∴ R is transitive.
Hence, R is reflexive, symmetric, and transitive.

(b) R = {(x, y) : x and y live in the same locality}
Solution:
R = { (x, y) : x and y live in the same locality}
Clearly (x, x) ∈ R as x and x is the same human being.
∴ R is reflexive.
If (x, y) ∈ R, then x and y live in the same locality.
⇒ y and x live in the same locality.
⇒ (y, x) ∈ R
∴ R is symmetric.
Now, let (x, y) ∈ R and (y, z) ∈ R.
⇒ x and y live in the same locality and y and z live in the same locality. =} x and z live in the same locality.
⇒ (x, z) ∈ R
∴ R is transitive.
Hence, R is reflexive, symmetric, and transitive.
(c) R = {(x, y): x is exactly 7 cm taller than y}
Solution:
R = {(x, y): x is exactly 7 cm taller than y}
Now, (x, x) ∉ R
Since, human being x cannot be taller than himself.
∴ R is not reflexive.
Now, let (x, y) ∈ R.
=> x is exactly 7 cm taller than y.
Then, y is not taller than x.
∴ (y, x) ∉ R
Indeed if x is exactly 7 cm taller than y, then y is exactly 7 cm shorter than x.
∴ R is not symmetric.
Now, let (x, y), (y, z) ∈ R.
⇒ x is exactly 7 cm taller than y and y is exactly 7 cm taller than z.
⇒ x is exactly 14 cm taller than z.
∴ (x, z) ∈ R
∴ R is not transitive.
Hence, R is neither reflexive, nor symmetric, nor transitive.

(d) R = {(x, y) : x is wife of y}
Solution:
R = {(x, y): x is the wife of y}
Now, (x, x) ∉ R
Since, x cannot be the wife of herself.
∴ R is not reflexive.
Now, let (x, y) ∈ R ⇒ x is the wife of y.
Clearly, y is not the wife of x.
∴ (y, x) ∉ R
Indeed if x is the wife of y, then y is the husband of x.
∴ R is not symmetric.
Let (x, y),(y, z) ∈ R
⇒ x is the wife of y and y is the wife of z.
This case is not possible. Also, this does not imply that x is the wife of z.
∴ (x, z) ∉ R
∴ R is not transitive.
Hence, R is neither reflexive, nor symmetric, nor transitive.
(e) R = {(x, y): x is father of y}
Solution:
R = {(x, y): x is the father of y}
(x, x) ∉ R
As x cannot be the father of himself.
∴ R is not reflexive.
Now, let (x, y) G R ⇒ x is the father of y.
⇒ y cannot be the father of x. Indeed y is the son or the daughter of x.
∴ (y, x) ∉ R
R is not symmetric.
Now, let (x, y) ∈ R and (y, z) ∈ R.
⇒ x is the father of y and y is the father of z.
⇒ x is not the father of z.
Indeed x is the grandfather of z.
∴ (x, z) ∉ R
∴ R is not transitive.
Hence, R is neither reflexive, nor symmetric, nor transitive.

Question 2.
Show that the relation R in the set R of real numbers, defined as R = {(a, b) : a ≤ b2} is neither reflexive nor symmetric nor transitive.
Solution:
R = {(a, b) : a ≤ b2}
It can be observed that (\(\frac{1}{2}\), \(\frac{1}{2}\)) ∉ R, since \(\frac{1}{2}\) > (\(\frac{1}{2}\))2 = \(\frac{1}{4}\)
∴ R is not reflexive.
Now, (1, 4) ∈ R as 1 < 42 But, 4 is not less than 12.
∴ (4, 1) ∉ a
∴ R is not symmetric.
Now, (3 2), (2, 1.5) ∈ R [as 3 < 22 = 4 and 2 < (1.5)2 = 2.25]
But, 3 > (1.5)2 = 2.25
∴ (3, 1.5) ∉ R
∴ R is not transitive.
Hence, R is neither reflexive, nor symmetric, nor transitive.
Question 3.
Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b): 6 = a +1} is reflexive, symmetric or transitive.
Solution:
Let A = {1, 2, 3, 4,5,6}
A relation R is defined on set A as: R = {(a, b):b = a +1}
∴ R = {(1,2), (2, 3), (3, 4), (4, 5), (5, 6)}
∴ R is not reflexive.
It can be observed that (1, 2) ∈ R, but (2,1) £ R.
∴ R is not symmetric.
Now, (1, 2), (2, 3) ∈ R But, (1, 3) ∉ R
∴ R is not transitive
Hence, R is neither reflexive, nor symmetric, nor transitive.

Question 4.
Show that the relation B in R defined as R = {(a, b):a < b}, is reflexive and transitive hut not symmetric.
Solution:
R = {(a, b) : a < b}
(i) R is reflexive : Replacing b by a, a < a ⇒ a = a is true.
(ii) R is not symmetric : a < b, and b < a which is not true. 2 < 3, but 3 is not less than 2.
(iii) R is transitive : If a < b and b < c then a < c. e.g 2 < 3, 3 < 4 ⇒ 2 < 4.
Question 5.
Check whether the relation R in R defined as R = {(a, b) : a ≤ b3} is reflexive, symmetric or transitive.
Solution:
R = {(a, b) : a ≤ b3}
Now, (\(\frac{1}{2}\), \(\frac{1}{2}\)) ∉ R as \(\frac{1}{2}\) > \(\frac{1}{2}\)3 = \(\frac{1}{8}\))
∴ R is not Reflexive.
Now, (1, 2) ∈ R (as 1 < 23 = 8)
But, (2, 1) ∉ R (as (\(\frac{4}{4}\)) > 1)
∴ R is not symmetric.
(3, \(\frac{3}{2}\)), (\(\frac{3}{2}\), \(\frac{6}{5}\)) ∈ R as 3 < (\(\frac{3}{2}\))3 and \(\frac{3}{2}\) < (\(\frac{6}{5}\))3
But (3, \(\frac{6}{5}\)) ∉ R as 3 > (\(\frac{6}{5}\))3
∴ R is not transitive.
Hence, R is neither reflexive, nor symmetric, nor transitive.

Question 6.
Show that the relation R in the set {1, 2, 3} given by R = {(1, 2), (2, 1)} is symmetric but neither reflexive nor transitive.
Solution.
Let A = {1, 2, 3}.
A relation R on A is defined as R = {(1, 2), (2,1)}
It is seen that (1, 1), (2, 2), (3, 3) ∉ R.
R is not reflexive.
Now, as (1, 2) ∈ R and (2, 1) ∈ R, then R is symmetric.
Now, as (1, 2) and (2,1) ∈ R – However, (1, 1) ∈ R
∴ R is not transitive.
Hence, R is symmetric but neither reflexive nor transitive.
Question 7.
Show that the relation R in the set A of all the books in a library of a college, given by
R = {(x, y) : x and y have same number of pages} is an equivalence relation.
Solution:
Set A is the set of all books in the library of a college.
R = {(x, y) : x and y have the same number of pages}
Now, R is reflexive since (x, x) ∈ R as x and x have the same number of pages.
Let (x, y) ∈ R
⇒ x and y have the same number of pages.
⇒ y and x have the same number of pages.
⇒ (y, x) ∈ R
∴ R is symmetric.
Now, let (x, y) ∈ R and (y, z) ∈ R.
⇒ x and y have the same number of pages and y and z have the same number of pages.
⇒ x and z have the same number of pages.
⇒ (x, z) ∈ R
∴ R is transitive.
Hence, R is a equivalence relation.

Question 8.
Show that the relation R in the set A = {1, 2, 3, 4, ,5} given by R = {(a, b): | a – b| is even}, is an equivalence relation. Show that all the elements of {1, 3, 5} are related to each other and all the elements of {2,4} are related to each other. But no element of {1, 3, 5} is related to any element of {2, 4}.
Solution.
A = {1, 2, 3, 4, 5}
R = { (a, b) : |a – b| is even}
It is clear that for any element a e∈ A, we have |a – a| = 0 (which is even).
∴ R is reflexive.
Let (a, b) ∈ R.
⇒ |a – b| is even.
⇒ |-(a – b)| = |b – a| is also even.
⇒ (b, a) ∈ R
∴ R is symmetric.
Now, let (a, b) ∈ R and (b, c) ∈ R.
⇒ | a – b | is even and | b – c | is even.
⇒ (a – b) is even and (b – c) is even.
⇒ (a – c) = (a – b) + (b – c) is even [Sum of two even integers is even] => | a – c | is even.
⇒ (a, c) ∈ R
∴ R is transitive.
Hence, R is an equivalence relation.
Now, all elements of the set {1, 2, 3} are related to each other as all the elements of this subset are odd. Thus, the modulus of the difference between any two elements will be even.
Similarly, all elements of the set {2, 4} are related to each other as all the elements of this subset are even.
Also, no element of the subset {1, 3, 5} can be related to any element of {2, 4} as all elements of {1, 3, 5} are odd and elements of (2, 4} are even. Thus, the modulus of the difference between the two elements (from each of these two subsets) will not be even.

Question 9.
Show that each of the relation R in the set A = {x ∈ Z: 0 < x ≤ 12}, given by
(i) R = {(a, b) : |a – b| is a multiple of 4}
(ii) R = {(a, b) : a – b} is an equivalence relation. Find the set of all elements related to 1 in each case.
Solution.
A = {x ∈ Z : 0 < x ≤ 12} = {0,1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,12} (i) R = {(a, b): |a – b | is a multiple of 4. For any element a ∈ A, we have (a, a) ∈ R as | a – a | = 0 is a multiple of 4. ∴ R is reflexive. Now, let (a, b) e R => | a – b | is a multiple of 4.
⇒ |- (a – b) | =| b – a| is multiple of 4.
⇒ (b, a) ∈ R
R is symmetric.
Now, let (a, b), (b, c) ∈ R.
⇒ | a – b | is a multiple of 4 and | b – c| is a multiple of 4.
⇒ (a – b) is a multiple of 4 and (b – c) is a multiple of 4.
⇒ (a – c) = (a – b) + (b – c) is a multiple of 4.
⇒ | a – c | is a multiple of 4.
⇒ (a, c) ∈ R
∴ R is transitive.
Hence, R is an equivalence relation.
The set of elements related to 1 is {1, 5, 9} since
|1 – 1| = 0 is a multiple of 4
| 5 – 1| = 4 is a multiple of 4, and
|9 – 1| = 8 is a multiple of 4.
(ii) R = {(a, b) : a = b}
For any element a ∈ A, we have (a, a) ∈ R, since a = a.
∴ R is reflexive.
Now, let (a, b) ∈ R.
⇒ a = b ⇒ b = a ⇒ (b, a) ∈ R
∴ R is symmetric.
Now, let (a, b) ∈ R and (b, c) ∈ R.
⇒ a = b and b = c ⇒ a = c ⇒ (a, c) ∈ R
∴ R is transitive.
Hence, R is an equivalence relation.
The elements in R that are related to 1, will be those elements form set A which are equal to 1.
Hence, the set of elements related to 1 is {1}.

Question. 10.
Given an example of a relation. Which is
(i) Symmetric but neither reflexive nor transitive.
(ii) Transitive but neither reflexive nor symmetric.
(iii) Reflexive and symmetric but not transitive.
(iv) Reflexive and transitive but not symmetric.
(v) Symmetric and transitive but not reflexive.
Solution.
Let A – set of straight lines in a plane.
(i) R = {(a, b): a is perpendicular to b}
Let a, b be two perpendicular lines
(a) If line a is perpendicular to b then b is perpendicular to a ⇒ R is symmetric.
(b) But ‘a’ is not a perpendicular to itself.
∴ R is not reflexive.
(c) If ‘a’ is a perpendicular to to ‘b’ and ‘b’ is perpendicular to ‘o’, but ‘a’ is not perpendicular to ‘c’.
∴ R is not transitive.
Thus, R is symmetric but neither reflexive nor transitive.
(ii) Let A = set of real numbers R = {(a, b) : a>b}
(a) An element is not greater than itself .-. R is not reflexive.
(b) If a > b than b is not greater than a.
⇒ R is not symmetric.
(c) If a > b also b> c, then a > c Thus, R is transitive.
Hence, R is transitive but neither reflexive nor symmetric.

(iii) The relation R in the set {1, 2, 3}, is given by
R = {(a, b) : a + b ≤ 4}
R = {(1, 1), (a, 2), (2, 1), (1, 3), (3, 1), (2, 2)}
Here (1, 1), (2, 2) ∈ R ⇒ R is reflexive.
(1, 2), (2, 1), (1, 3), (3, 1) ⇒ R is symmetric
But it is not transitive, since (2, 1) ∈ R, (1, 3) ∈ R but (2, 3) ∉ R.
(iv) The relation R in the set {1, 2, 3} given by
R = {(a, b) : a ≤ b) = {(1, 2), (2, 2), (3, 3), (2, 3), (1, 3)}
(a) (1, 1), (2, 2), (3, 3) ∈ R ⇒ R is reflexive.
(b) (1, 2) ∈ R, but (2, 1) ∈ R ⇒ R is not symmetric.
(c) (1, 2) ∈ R, (2, 3) ∈ R, Also (1, 3) e R ⇒ R is transitive.
(v) The relation R in the set {1, 2, 3} given by
R = {(a, b): 0 < |a – b | ≤ 2} = {(1, 2), (2,1), (1, 3), (3,1), (2, 3), (3, 2)}
(a) R is not reflexive, (1, 1), (2, 2), (3, 3) do not belong to R.
(b) R is symmetric. (1, 2), (2,1), a, 3), (3,1), (2, 3), (3, 2) ∈ R
(c) R is transitive (1, 2) ∈ R, (2, 3) ∈ R, Also (1, 3) ∈ R.

Question. 11.
Show that the relation R in the set A of points in a plane given by R = {(P, Q): distance of the point P form the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further, show that the set of all points related to a point P ≠ (0, 0) is the circle passing through P with origin as centre.
Solution.
R – {(P, Q) : distance of point P from the origin is the same as the distance of point Q from the origin}
Clearly, (P, P) ∈ R, since the distance of point P from the origin is always the same as the distance of the same point P from the origin.
∴ R is reflexive.
Now, let (P, Q) ∈ R.
⇒ The distance of point P from the origin is the same as the distance of point Q from the origin. y’
⇒ The distance of point Q from the origin! is the same as the distance of point P from the origin.
⇒ (Q, P) ∈ P
⇒ R is symmetric.
Now, let (P, Q), (Q, S) ∈ R.
⇒ The distance of points P and Q from the origin is the same and also, the distance of points Q and S from the origin is the same.
⇒ The distance of points P and S from the origin is the same.
⇒ (P, S) ∈ P
∴ R is transitive.
Therefore, R is an equivalence relation.
The set of all points related to P ≠ (0 ,0) will be those points whose distances from the origin are the same as the distance of point P from the origin.
In other words, if O (0, 0) is the origin and OP = k, then the set of all points related to P is at a distance of k from the origin.
Hence, this set of points forms a circle with the centre as the origin and this circle passes through point P.

Question. 12.
Show that the relation R defined in the set A of all triangles as R = {(T1, T2) : T1 is similar to T2}, is equivalence relation. Consider three right angled triangles T1 with sides (3, 4, 5), T2 with sides (5, 12, 13) and T3 with sides (6, 8, 10). Which triangles among T1, T2 and T3 are related?
Solution.
R = { (T1, T2): T1 is similar to T2}
R is reflexive since every triangle is similar to itself.
Further, if (T1, T2) ∈ R, then T1 is similar to T2.
⇒ T2 is similar to T1.
⇒ (T2, T1)E R R is symmetric.
Now, let (T1, T2), (T2, T3) ∈ R.
⇒ T1 is similar to T2 and T2 is similar to T3.
⇒ T1 is similar to T3.
⇒ (T1, T3) ∈ R
∴ R is transitive.
Thus, R is an equivalence relation.
Now, we can observe that : \(\frac{3}{6}=\frac{4}{8}\) = \(\frac{5}{10}=\frac{1}{2}\)
∴ The corresponding sides of triangles T1 and T3 are in the same ratio.
Then, triangle T1 is similar to triangle T3.
Hence, T1 is related to T3.

Question 13.
Show that the relation R defined in the set A of all polygons as R = {(P1, P2) : P1 and P2 have same number of sides}, is an equivalence relation. What is the set of all elements in A related to the right angled triangle T with sides 3, 4 and 5?
Solution.
R = {(P1, P2) : Px and P2 have same number of sides.}
R is reflexive since (P1, P1) e R as the same polygon has the same number of sides with itself.
Let (P1, P2) ∈ R.
⇒ P1 and P2 have the same number of sides.
⇒ P2 and P1 have the same number of sides.
⇒ (P2, P1) ∈ R
∴ R is symmetric.
Now, let (P1, P2), (P2, P3) e R.
⇒ P1 and P2 have the same number of sides.
Also, P2 and P3 have the same number of sides.
⇒ P1 and P3 have the same number of sides.
⇒ (P1, P3) ∈ R
∴ R is transitive. Hence, R is an equivalence relation.
The elements in A related to the right-angled triangle (T) with sides 3, 4 and 5 are those polygons which have 3 sides (since T is a polygon with 3 sides).
Hence, the set of all elements in A related to triangle T is the set of all triangles.

Question. 14.
Let L be the set of all lines in XY-plane and R be the relation in L defined as R = {(L1, L2): L1 is parallel to L2}. Show that R is an equivalence relation. Find the set of all lines related to the line y = 2x + 4.
Solution.
R = {(L1, L2) : L1 is parallel to L2}
R is reflexive as any line L1 is parallel to itself i.e., (L1, L1) ∈ R.
Now, let (L1, L2) ∈ R
⇒ L1 is parallel to L2.
⇒ L2 is parallel to L1.
⇒ (L2, L1) ∈ R R is symmetric.
Now, let (L1, L2), (L2, L3) ∈ R.
⇒ L1 is parallel to L2. Also, L2 parallel to L3.
⇒ L1 is parallel to L3.
∴ R is transitive.
Hence, R is an equivalence relation.
The set of all lines related to the line y = 2x + 4 is the set of all lines that are parallel to the line y – 2x + 4.
Slope of line y = 2x + 4 is m = 2. It is known that parallel lines have the same slopes.
The line parallel to the given line is of the form y = 2x + c, where c ∈ R. Hence, the set of all lines related to the given line is given by y = 2x + c, where c ∈ R.

Question 15.
Let R be the relation in the set {1, 2, 3, 4} given by R = {(1, 2), (2, 2), (1, 1), (4, 4), (1, 3), (3, 3), (3, 2)}. Choose the correct answer.
(A) R is reflexive and symmetric but not transitive.
(B) R is reflexive and transitive but not symmetric.
(C) R is symmetric and transitive but not reflexive.
(D) R is an equivalence relation.
Solution.
R = {(1, 2), (2, 2), (1,1), (4, 4), (1, 3), (3, 3), (3, 2)}
It is seen that (a, a) ∈ R, for every a ∴ {1, 2, 3, 4}
∴ R is reflexive.
It is seen that (1, 2) ∈ R, but (2, 1) $ R.
∴. R is not symmetric.
Also, it is observed that (a, b), (b, c) ∈ R
⇒ (a, c) ∈ R for all a, b, c ∈ {1, 2, 3, 4}
∴ R is transitive.
Hence, R is reflexive and transitive but not symmetric.
Thus, the correct answer is (B).
Question 16.
Let R be the relation in the set N given by
R = {a, b): a = b – 2, b > 6}. Choose the correct answer.
(A) (2, 4) ∈ R
(B) (3, 8) ∈ R
(C) (6, 8) ∈ R
(D) (8, 7) ∈ R
Solution.
R = {(a, b): a = b – 2, b > 6}
Now, since b > 6, (2, 4) ∉ R
Also, as 3 ≠ 8 – 2, (3, 8) ∉ R
And, as 8 ≠ 7 – 2
∴ (8, 7) ∉ R
Now, consider (6, 8). We have 8 > 6 and also, 6 = 8 – 2.
∴ (6, 8) ∈ R
Thus, the correct answer is (C).
![]()
![]()
![]()
![]()
![]()
![]()
![]()


 ]
]
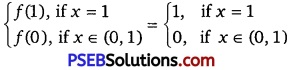 gof(x) = g(f(x))= g(1) [∵ x > 0]
gof(x) = g(f(x))= g(1) [∵ x > 0]