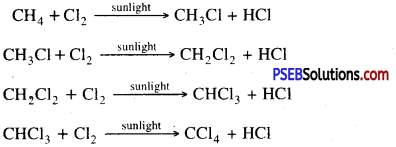
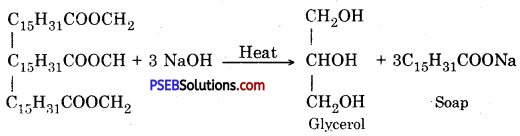
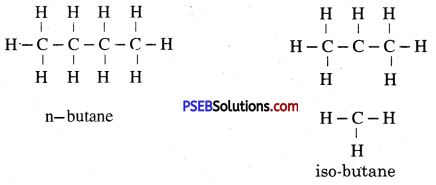
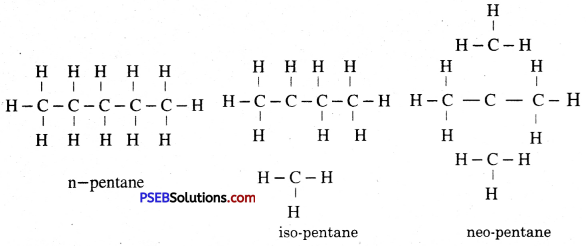
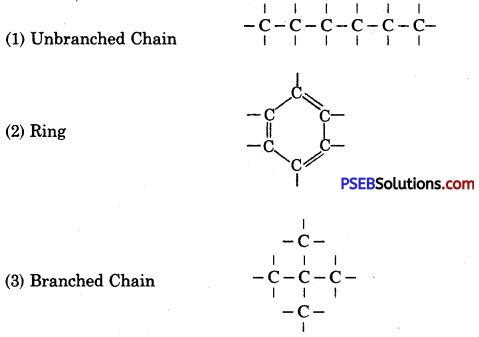
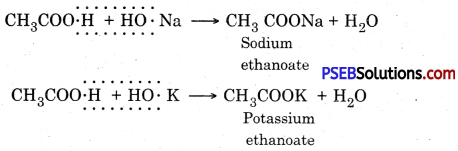
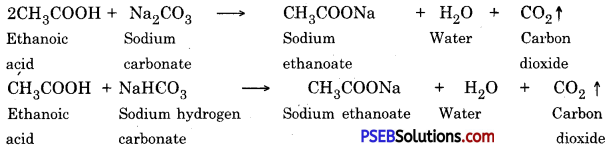
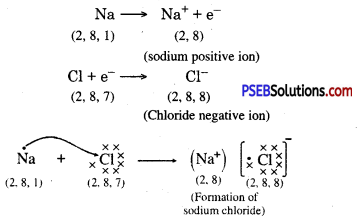
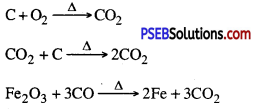
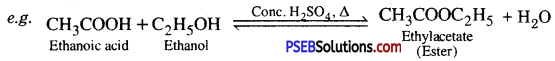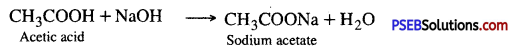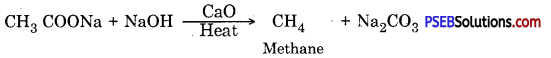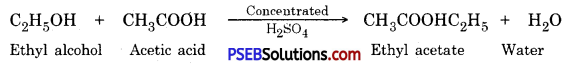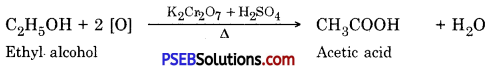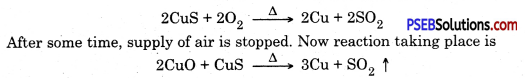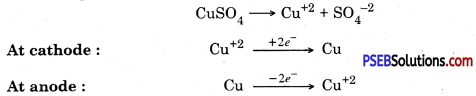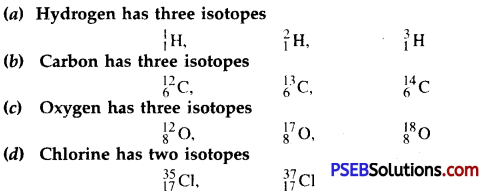Punjab State Board PSEB 10th Class Science Important Questions Chapter 5 Periodic Classification of Elements Important Questions and Answers.
PSEB 10th Class Science Important Questions Chapter 5 Periodic Classification of Elements
Long Answer Type Questions
Question 1.
What do you understand by Dobereiner’s triads? Give some examples to support it.
Answer:
In 1817, a German Chemist, Dobereiner, gave a classification in which the similar elements were arranged in groups of three called Triads. The arrangement was such that the atomic mass of the middle element was almost the average of the atomic masses of the first and third elements. For example, if A, B and C are the elements present in the triad, then
Atomic mass of B =\(\frac{\text { Atomic mass of } \mathrm{A}+\text { Atomic mass of } \mathrm{C}}{2}\)
Examples of triads.
A few examples of triads are listed as given ahead :
1. Lithium, Sodium. Potassium
Atomic mass of Lithium (Li) = 7
Atomic mass of Potassium (K) = 39
Atomic mass of Sodium (Na) = \(\frac{39+7}{2}\) = 23
Actual atomic mass of sodium = 23
This group of triads is called Alkali Metal Group. All the elements present are metals, have valency equal to one (1) and dissolve in water to form soluble hydroxides called alkalis.
2. Calcium, Strontium, Barium
Atomic mass of Calcium (Ca) = 40
Atomic mass of Barium (Ba) = 137
Atomic mass of Strontium (Sr) = \(\frac{137+40}{2}=\frac{177}{2}\) = 88.5
Actual atomic mass of strontium = 88
This group of triads is called Alkaline Earth Metals Group. All the elements present are metals, have valency equal to two (2) and their oxides dissolve in water to form hydroxides which are alkaline in nature.
Question 2.
(a) What was Dobereiner’s basis of classifying elements?
Answer:
Dobereiner gave a classification in which the elements were arranged in a group of three elements called triads. The arrangement was such that the atomic masses of the middle elements were almost the average of the atomic masses of the first and third elements.
(b) What is the basis of classification of elements according to Mendeleev?
Answer:
The major contribution in the classification of the elements is by Mendeleev, a Russian chemist. He studied in detail the properties of the elements and made a very important observation. He stated that when elements are arranged in order of increasing atomic masses, the elements with similar properties recur after a definite gap. He based his classification of law called Mendeleev’s Periodic Law. The law may be stated as:
Physical and chemical properties of the elements are periodic function of their atomic weights or atomic masses.
![]()
Question 3.
Give a brief discussion of the Mendeleev’s classification of the elements.
Answer:
Mendeleev’s classification of the elements is based upon the Mendeleev’s periodic law. The law helped him to develop a table called Mendeleev’s Periodic Table. The table has been divided into vertical columns which are called Groups and horizontal rows which are known as Periods.
These are briefly discussed as follows :
1. Groups: These are the vertical rows. There are in all eight groups. The elements present in first seven groups are called Normal Elements. The elements present in group VIII are called the Transition Elements. Each group (I to VII) has been further divided into sub-groups which are called A and B. The inert gas or noble gas elements (He, Ne, Ar, Kr, Xe) were not known at that time. Therefore, they were not shown in the table. All the elements placed in a group have the same valency. Ail the elements present in a sub-group have the similar properties. For example, group I-B includes element Cu (Copper), Ag (Silver) and Au (Gold). They have similar properties.
2. Periods: In the periodic table horizontal rows are called periods. There were in all six periods in the original periodic table. The seventh period was added later on and this is not shown in the periodic table. The properties of the elements present in a period change systematically. For example, in every period, the first element is a typical metal. As we move from left to right, the metallic character gradually decreases and non- metallic character increases. For example, in period 2, the first element Li (Lithium) is a metal while the last element F (Fluorine) is a non-metal. The Mendeleev’s Periodic Table is shown below :
Mendeleev’S Periodic Table
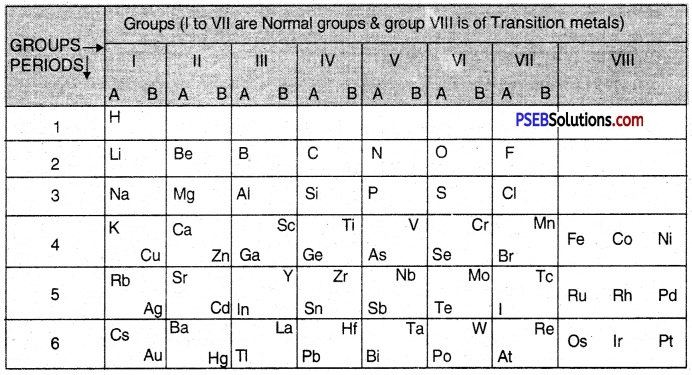
Question 4.
(a) Why do we classify elements?
Answer:
To simplify and systematize the study of known elements.
(b) What were the two criteria used by Mendeleev in creating his Periodic Table?
Answer:
- Mendeleev arranged the elements in order of increasing atomic masses.
- Mendeleev considered the compounds formed by the elements oxygen and hydrogen.
(c) Why did Mendeleev leave some gaps in his Periodic Table?
Answer:
For the discovery of new elements.
(d) In Mendeleev’s Periodic Table, why was there no mention of Noble gases like7 Helium, Neon and Argon?
Answer:
Because noble gases were not known at that time.
(e) Would you place the two isotopes of chlorine, Cl-35 and Cl-37 in different slots because of their different atomic masses or in the same slot because their chemical properties are the same? Justify your answer.
Answer:
In the same slot because Cl-35 and Cl-37 have same chemical properties.
Question 5.
How did Mendeleev’s Periodic Table help in the discovery of new elements?
Answer:
When Mendeleev gave the periodic table, only 63 elements were known. The classification was based on two major properties :
- Elements are arranged in order of increasing atomic masses.
- Elements present in a group have similar properties.
Many elements were not known at the time the periodic table was given. Therefore, Mendeleev left gaps for these elements in the periodic table. But the properties of these elements could be predicted. For example, let us suppose that Rb (Rubidium) a member of group IA was not known when Mendeleev framed the periodic table. But its properties could be predicted. It was expected to be a metal with valency equal to 1. It was expected to be soluble in water to form a soluble hydroxide RbOH which is an alkali. This helped in the discovery of the element. In this manner, a number of elements could be discovered.
![]()
Question 6.
Discuss some major merits of the Mendeleev’s Periodic Table.
Answer:
Merits of Mendeleev’s Periodic Table
Mendeleev’s periodic table was the first proper systematic classification of the elements. The important merits of the table are listed as follows :
1. Systematic study of elements. With the classification of elements into groups and periods, their study became quite systematic. For example, if the properties of one particular element in a group are known, those of the other elements could be predicted. Actually, elements placed in a group are expected to show similar characteristics.
2. Correction of wrong atomic masses. The periodic table helped in correcting the atomic masses of some of the elements because the elements were arranged in order of their increasing atomic masses.
3. Prediction of new elements. At the time Mendeleev gave the periodic table, only 63 elements were known. While arranging these elements in groups and periods, certain gaps were left. These gaps represented some undiscovered elements. But the properties of these unknown elements could be predicted from their positions in the respective groups. This helped, later on, to discover these elements.
Question 7.
On the basis of Mendeleev’s Periodic Table given following, answer the questions that follow the table :
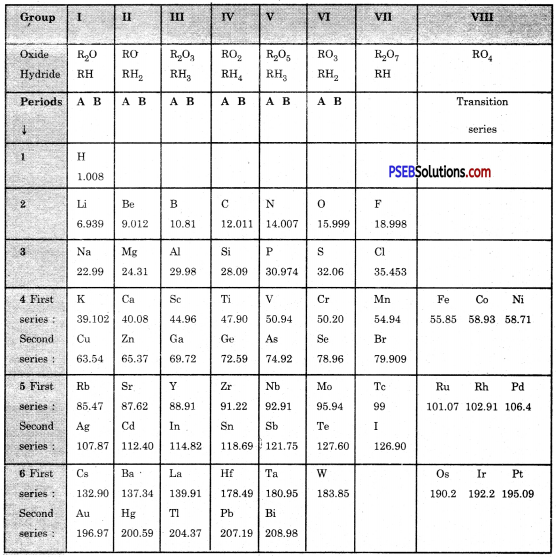
(a) Name the element which is in
(i) 1st group and 3rd period
Answer:
Sodium
(ii) VII group and 2nd period.
Answer:
Fluorine
(b) Suggest the formula for the following :
(i) oxide of nitrogen
Answer:
N2O5
(ii) hydride of oxygen.
Answer:
H2O.
(c) In group VIII of the Periodic Table, why does cobalt with atomic mass 58.93 appear before nickel having atomic mass 58.71?
Answer:
Because the elements with similar properties could be grouped together.
(d) Besides gallium, which two other elements have since been discovered for which Mendeleev had left gaps in his Periodic Table?
Answer:
Scandium and Germanium.
(e) Using atomic masses of Li, Na and K, find the average atomic mass of Li and K and compare it with the atomic mass of Na. State the conclusion drawn from this activity.
Answer:
Average atomic mass of Li and K = \(\frac{6.939+39.102}{2}=\frac{46.04}{2}\) = 23.02
Atomic mass of Na = 22.99
Hence Atomic mass of Na = Average of atomic masses of Li and K = \(\frac{46.04}{2}\) = 23.02
Question 8.
Point out the major defects in Mendeleev’s Periodic Table.
Answer:
Defects in Mendeleev’s Periodic Table:
Mendeleev’s periodic table was quite helpful in the classification of the elements.
But it had certain defects also. These are discussed as follows :
1. Position of hydrogen. Hydrogen was placed at the top of group LA. It is a non-metal where all other elements included in the group are metals.
2. Position of isotopes. The periodic table is based on the basis of the atomic masses of the elements and the elements with different atomic masses must be given separate places in the table. If this is correct, all the isotopes of an element must be allotted separate positions. For example, there are three isotopes for hydrogen and they must be given three separate places in the table. But only one position for hydrogen has been given.
3. Wrong order of atomic masses of some elements. In the table, the elements are arranged in order of increasing atomic masses. This means that the element with higher atomic mass must be placed after the element with the lower atomic mass. But in the table, there are some anomalies. For example, Co (Cobalt) with atomic mass 58-9 should be placed after Ni (Nickel) with atomic mass 58-7. But it has been placed before nickel.
4. Elements with similar properties placed in different groups. In the periodic table, it has been found that the elements with similar properties are placed in different groups. For example, copper and mercury have many common properties. But copper has been placed in group I B and mercury in group II B.
5. No similarity in the elements placed in sub-groups. The elements present in different sub-groups of the same group are expected to have common properties. But these are quite different. For example, elements in group I A are very soft and reactive metals but elements in group IB are hard and less reactive in nature.
6. No explanation for the cause of periodicity. Mendeleev was not in a position to explain why the elements included in a group show similar properties.
Question 9.
Give a brief description of Long Form of Periodic Table.
Answer:
The Long form of periodic table has been formed by arranging the elements in order of increasing atomic numbers. It is based upon Modern periodic law which states that the properties of the elements are the periodic function of their atomic numbers. Just as in case of the Mendeleev’s table, this periodic table has also been divided into Periods and Groups.
(A) Groups
These are the vertical columns. In all, there are eighteen groups in the table. The details of the groups are as follows :
Long Form of Periodic Table of Modern Periodic Table
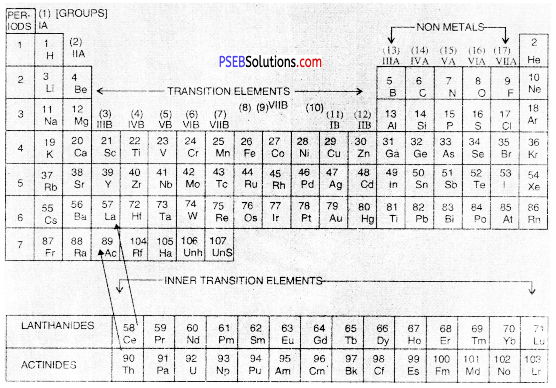
- Group 1: The elements present in group I or 1 are called Alkali Metals.
- Group 2: The elements which are present in group IIA or 2 are called Alkaline Earth Metals.
- Groups 13 to Group 18: There are in all six groups. The Groups 13 to 16 are named after the first element present in the family. For example, Group IIIA or 13 is called Boron Family because first member is boron.
- Group 17 consists of a family called Halogen Family.
- The group 18 is also called zero group because the elements have zero valency. These elements are ail gases. They have very little tendency to take part in chemical combination. These are also called Noble Gases.
In the latest Long Form of Periodic Table, groups of Alkali metals and Alkaline erttH metals are given numbers 1 and 2. The transition of elements are numbered from its,2 The non-metals are included in groups 13 to 18.
| Group No. | Name of Family |
| Group 13 | Boron Family |
| Group 14 | Carbon Family |
| Group 15 | Nitrogen Family |
| Group 16 | Oxygen Family |
| Group 17 | Halogens |
| Group 18 or zero group | Noble Gases |
- Group 3 to Group 12: There are in all ten groups. These are all metals and are called Transition elements. When we go down each group, the metallic character further increases.
- Group 3: Group 3 also includes fourteen elements belonging to Lanthanide family. These are called Lanthanides because they start after Lanthanum (La) with Z = 57. These are present in the 6th period as shown in the table.
- It also includes another fourteen elements called Actinides. These are present in 7th period. These are so called as they come after Actinium (Ac) with Z = 89. These are placed at the bottom of the table for convenience.
(B) Periods
Periods are the horizontal rows which are present in the Long Form of Periodic Table. Different periods have different number of elements and their atomic numbers are continuous. There are in all seven periods. The seventh period is still incomplete. The number of elements which are included in each period are given below :
| Period | No. of elements | Name of the Period |
| 1 | 2 | Shortest Period |
| 2 | 8 | Short Period |
| 3 | 8 | Short Period |
| 4 | 18 | Long Period |
| 5 | 18 | Long Period |
| 6 | 32 | Longest Period |
| 7 | 20 | Incomplete Period |
![]()
Question 10.
What is periodicity? What is the cause of periodicity?
Answer:
Periodicity may be defined as the repetition of the similar properties of the elements placed in a group and separated by definite gaps of atomic numbers (8, 8, 18, 18, 32).
Cause of Periodicity. The properties of the elements, particularly the chemical properties, are linked with number of electrons present in the outermost shell of their atoms which is also called Valence shell. Elements with similar valence shell electronic configurations are expected to have similar properties.
It may be noted that all the elements which are present in a group have the same number of electrons in the valence shells of their atoms. In other words, the same valence shell electronic arrangement gets repeated after definite gaps of atomic numbers (8, 8, 18, 18, 32). Therefore, the elements placed in a group show similar properties.
Example, Let us write the electronic distribution of the first four members of the alkali metals present in group I.
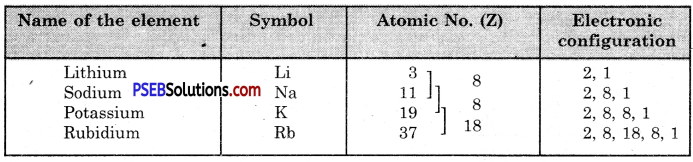
All the four elements have one electron each in the valence shell of their atoms. They have, therefore, similar properties.
Question 11.
(a) What were the two major shortcomings of Mendeleev’s periodic table? How have these been removed in the modern periodic table?
Answer:
The shortcomings of Mendeleev’s periodic table are :
- Isotopes of an element find different positions in periodic table.
- Some chemically similar elements have been separated and some dissimilar elements are placed together.
In these Modern Periodic Table
Modern Table
- Isotopes of an element occupy the same position because they have same atomic number.
- The similar elements are grouped together and dissimilar elements are separated.
(b) Two elements X and Y have atomic numbers 12 and 16 respectively. Write the electronic configuration for these elements. To which period of the modern periodic table do these two elements belong? What type of bond will be formed between them and why?
Answer:
| Element | Electronic Configuration | Period |
| X12 | 2, 8, 2 | 3rd |
| Y16 | 2, 8, 6 | 3rd |
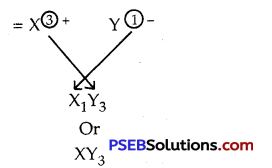
They will form ionic bonds because two electrons are transferred from X to Y so that they get their octets complete :
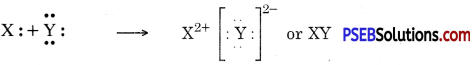
Question 12.
Why is Long Form of Periodic Table regarded better than Mendeleev’s Periodic Table?
Or
How could Modern Periodic Table remove various anomalies of Mendeleev’s Periodic Table?
Answer:
Long Form of Periodic Table is regarded better than the Mendeleev’s periodic table due to the following reasons:
- It is based upon atomic number which is considered better than the atomic mass because the properties of the elements are related to the atomic number.
- It explains why the elements placed in a group show similar properties but Mendeleev’s Periodic Table gives no explanation for the same.
- All groups in the Periodic Table are independent groups and there are no sub¬groups as in Mendeleev’s Periodic Table.
- Many defects in the Mendeleev’s Periodic Table have been removed.
- There is no confusion regarding the position of isotopes because all the isotopes of an element have the same atomic number.
- The periodic table is more systematic than the Mendeleev’s table and is easy to remember.
Question 13.
The following tables shows the position of six elements A, B, C, D, E and F in the periodic table.
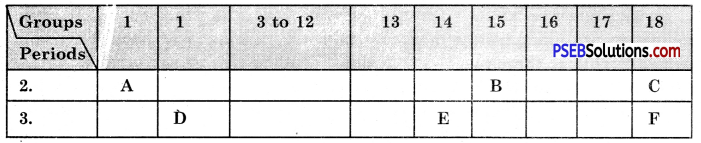
Using the above table answer the following questions :
(a) Which element will form only covalent compounds?
Answer:
E
(b) Which element is a metal with valency 2?
Answer:
D
(c) Which element is non-metal with valency of 3?
Answer:
B
(d) Out of D and E, which one has a bigger atomic radius and why?
Answer:
D
(e) Write a common name for the family of elements C and F,
Answer:
The noble gases.
Question 14.
The question refers to the elements of the periodic table with atomic number from 3 to 18.
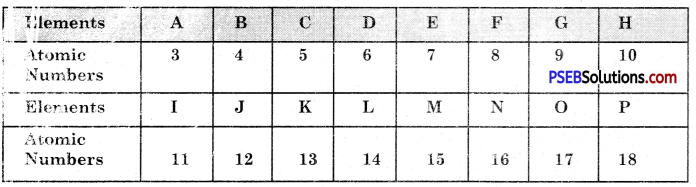
(a) Which of these :
(i) is/are noble gas?
Answer:
H, P
(ii) is it a halogen?
Answer:
G, O
(iii) is an alkali metal?
Answer:
A, I
(iv) is it a metal with valency 2?
Answer:
A, I
(b) Write the electronic arrangement of G.
Answer:
G has the electronic configuration = 2, 7
(c) If A combines with F, what would be the formula of resulting compound?
Answer:
Short Answer Type Questions
Question 1.
Atomic number is considered to be a more appropriate parameter than atomic mass classification of elements in a periodic table. Why?
How does atomic size of elements vary on moving from
(i) Left to right in a period.
(ii) from top to bottom in a group.
Give reasons for your answers.
Answer:
- This is because atomic number is a more fundamental property of an atom.
- As we move from left to right along a period atomic radius decreases due to increase in effective nuclear charge.
- As we move from top to bottom in a group, atomic radius increases. This is due to addition of new electronic shells.
![]()
Question 2.
Define periodic law. Why was it necessary to change the basis of classification from atomic masses to atomic numbers?
Answer:
Periodic Law: The properties of elements are a periodic function of their atomic numbers. It was necessary to change the basis of classification from atomic masses to atomic numbers because atomic number and not atomic mass is the fundamental property of an element.
Question 3.
What do you understand by the term periodicity? Do the properties of two elements placed in a group the same? Illustrate.
Answer:
The repetition of the similar properties of the elements placed in a group and separated by definite gaps of atomic numbers (8, 8, 18, 18, 32) is called periodicity. The elements placed in a group show similar properties, e.g. consider group 1 elements.
| Element | Symbol | Electronic configuration |
| Lithium | (3) | Li – 2, 1 |
| Sodium | (11) | Na – 2, 8, 1 |
| Potassium | (19) | K – 2, 8, 8, 1 |
| Rubidium | (37) | Rb – 2, 8, 18, 8, 1 |
| Cesium | (55) | Cs – 2, 8, 18, 18, 1 |
| Francium | (87) | Fr – 2, 8, 18, 32, 18, 8, 1 |
These elements show similar properties because they have similar outer electronic configurations.
Question 4.
What was wrong with Dobereiner’s classification of elements?
Answer:
Dobereiner classified the elements in group of three in such a way that the atomic mass of the middle element was the mean of the first and the third elements. But he could not find many triads of elements. Therefore, the classification was rejected.
Question 5.
What properties do ail elements in the same column of the periodic table as boron have in common?
Answer:
The elements of Boron family in the periodic table show
- Tricovalency
- Form trihalides
- Form trioxides
- React with halogens to form halides.
Question 6.
Indicate the atomic number of elements of period 3 of Modern periodic table :
(a) non-metals
Answer:
14, 15, 16, 17
(b) elements forming negative ions.
Answer:
15, 16, 17
(c) elements with high melting points.
Answer:
11, 12, 13, 14
(d) elements forming positive ions.
Mention the atomic number only.
Answer:
11, 12, 13
Question 7.
Define atomic radius. Give its units.
Answer:
Atomic radius. It may be defined as the distance between the centre of nucleus and the outermost shell of an isolated atom.
Also the atomic radius of a non-metallic element is defined as half the distance between the nuclei of two atoms bound by a single covalent bond.
Units = Å or pm (picometre)
e.g. atomic radius of hydrogen atom = 37 pm.
Question 8.
How does atomic radius vary down a group and along a period?
Answer:
Variation in a group. The atomic radius generally increases from top to bottom in a group due to the addition of a new shell.
Variation along a period. The atomic radius decreases on moving from left to right due to the increase in nuclear charge.
Question 9.
Write down the electronic configuration of elements with atomic numbers 2, 14, 17, 19. Indicate the group of the periodic table to which they belong.
Answer:
The information is being given in a tabular form.
| Atomic number | Electronic configuration K L M N | Group |
| 2 | 2 | 18 |
| 14 | 2, 8, 4 | 14 |
| 17 | 2, 8, 7 | 17 |
| 19 | 2, 8, 8, 1 | 1 |
Question 10.
Locate the following group in the periodic table :
(a) Alkali metals
Answer:
Alkali metals: Group 1 or IA
(b) Halogens
Answer:
Halogens: Group 17 or VIIA
(c) Alkaline earth metals
Answer:
Alkaline earth metals: Group 2 or IIA
(d) Noble gases.
Answer:
Noble gases: Group 18 or zero
![]()
Question 11.
What properties do the elements in the same vertical column of the periodic table as fluorine have in common?
Answer:
These are :
- They form diatomic molecules F2, Cl2, Br2 I2
- They are non-metals.
- They show a valency of one.
Question 12.
Write the chemical electronic configuration of nitrogen (N = 7) and phosphorous (P = 15).
Answer:

Question 13.
(i) Name the members of the alkaline earth family.
Answer:
The members of the alkaline earth family are :
Be, Mg, Ca, Sr, Ba, Ra.
(ii) To which group do they belong?
Answer:
They belong to group 2.
(iii) Which member is radioactive in nature?
Answer:
The radioactive member in them is Radium (Ra).
(iv) Which member is the least reactive?
Answer:
The least reactive member of the family is Beryllium (Be).
Question 14.
Why are the members of group 1 called alkali metals?
Answer:
The members of group 1 are called alkali metals because all of them are water soluble. They react with water to form soluble hydroxides. The soluble hydroxides of the metals are called alkalies.
![]()
Question 15.
An atom has the electronic configuration 2, 8, 7.
(a) What is the atomic number of this element?
Answer:
The atomic number of the element = Total number of electrons
= 2 + 8 + 7 = 17
(b) To which of the following elements would it be chemically similar? (atomic numbers are given) N (7), F (9), P (15), Ar (18).
Answer:
The electronic configurations of given atom and N, F, P and Ar are.
| Atom | Electronic configuration | ||
| K | L | M | |
| 2 | 8 | 7 | |
| N | 2 | 5 | |
| F | 2 | 7 | |
| P | 2 | 8 | 5 |
| Ar | 2 | 8 | 8 |
Since F has same number of electrons in the outermost shell as the given atom. Hence, the given atom is chemically similar to F.
Question 16.
What physical and chemical properties of elements were used by Mendeleev in creating his periodic table? List two observations which posed a challenge to Mendeleev’s Periodic Law.
Answer:
He selected the compounds of the elements with oxygen and hydrogen. He gave a table based upon atomic weights of the elements.
Limitations of Mendeleev’s Classification
- The position of hydrogen was uncertain.
- The isotopes of elements were not given proper positions in the periodic table.
Question 17.
(a) What are amphoteric oxides? Choose the amphoteric oxides from amongst the following oxides :
Na2O, ZnO, Al2O3, CO2, HaO
Answer:
The oxides which can react both with acids as well as bases to produce salts and water.
(b) Why is it that non-metals do not displace hydrogen from dilute acids?
Answer:
This is because non-metals cannot lose electrons and cannot reduce H+ ions from acid to H2.
![]()
Question 18.
What are noble gas elements? Why are they so called?
Answer:
Noble gas elements are the. elemehts present in group 18 of the periodic table which is also called zero group, It means that the valency of the elements is zero. Actually, whereas the first member helium has two electrons in its only shell, the atoms of the remaining elements (Neon, Argon, Krypton, Xenon and Radon) have eight electrons in their outermost shells. They do not have any tendency to combine with atoms of other elements. Hence, they show zero valency. These are also called noble gases because they do not take part in chemical combination.
Question 19.
How is metallic character of an element defined? How does the metallic character of the elements change in a group?
Answer:
The metallic character of an element may be expressed in terms of its tendency to lose electrons and to form positive ion.
M (Element) → M+ + e–
In a group the metallic character increases’ downwards. For example, among the elements of group 2, Beryllium (Be) is the least metallic. At the same time, radium (Ra) which is the last element is maximum metallic in nature.
Question 20.
Why do the elements present in a group show similar chemical properties?
Answer:
The properties of the elements, particularly the chemical properties are related to valence shell electronic distribution. The elements with the same valence shell electronic distribution have the similar chemical properties. For example, the members, of alkaline earth metal family (Group 2) have two electrons in the valence shell of their atoms. They therefore, show similar chemical properties.
Question 21.
How does the reactivity of the metals vary in a group?
Answer:
In a group, containing metals, the reactivity increases down the group. For example, in the metals of group 1 (Alkali metals), Lithium reacts with water very slowly. Sodium is more reactive and potassium is. still more reactive than sodium.
Question 22.
Name the elements present in the second period. Give their electronic configuration.
Answer:
The second period of the Long Form of Periodic Table has eight elements. The first element is Lithium and the last element is Neon. The electronic configuration of the elements are given below:

Question 23.
Why do not the elements present in a period show same valency?
Answer:
The valency of the element is related to the number of electrons in the outermost energy shell of its atom. Since the elements present in a period have different number of valence electrons or outermost electrons, they show different valencies.
Question 24.
The metallic character of the elements in a period decreases from left to the right. Justify.
Answer:
In every period, as we move from left to right, the metallic character of the elements decreases gradually. This is shown with the elements present in the third period.

Question 25.
Give symbols for :
(a) a metal belonging to second group of the periodic table.
Answer:
The metal belonging to second group is calcium (Ca).
(b) a metal belonging to the third group of the periodic table.
Answer:
The metal belonging to third group is aluminium (Al).
(c) two non-metals belonging to the halogen family.
Answer:
The two non-metals of halogen family are fluorine (F) and chlorine (Cl).
Question 26.
Write electronic structures of:
(i) Potassium
(ii) Lithium
(iii) Fluorine.
Answer:
The electronic configurations of the atoms are given below :

Question 27.
Name two other elements which are in the same family as
(i) carbon
Answer:
Carbon belongs to the group 16. Two other elements are silicon (Si) and germanium (Ge).
(ii) fluorine
Answer:
Fluorine belongs to group 17. Two other elements are chlorine (Cl) and bromine (Br).
(iii) sodium.
Answer:
Sodium belongs to group 1. Two other elements are lithium (Li) and potassium (K).
![]()
Question 28.
Carbon (atomic number 6) and silicon (atomic number 14) are elements in the same group of the periodic table. Give the electronic arrangements of the carbon and silicon atoms and state the groups in which these elements occur.
Answer:
The required information may be given in a tabular form as follows :
| Element | Atomic no. | Electronic arrangement | Group |
| Carbon (C) | 6 | 2, 4 | 14 |
| Silicon (Si) | 14 | 2, 8, 4 | 14 |
Question 29.
Sodium and aluminium have atomic numbers of 11 and 13 respectively. They are separated by one element in the periodic table and have valencies of 1 and 3 respectively. Chlorine and potassium are also separated by one element in the periodic table (their atomic numbers are 17 and 19 respectively) and yet both have valency of one. Explain your answer.
Answer:
Sodium and aluminium: The electronic configurations of the elements are given below :
Sodium (Na) = 2, 8, 1
Aluminium (Al) = 2, 8, 3
The valency in this case is given by the number of valence electrons. Therefore, the valency of sodium is 1 and that of aluminium is 3.
Chlorine and potassium: The electronic configurations of the elements are given below :
Chlorine (Cl) = 2, 8, 7
Potassium (K) = 2, 8, 1
Question 30.
Give the atomic number and electronic distribution of:
(i) The third alkali metal
Answer:
Potassium (19) 2, 8, 8, 1
(ii) The second alkaline earth metal
Answer:
Magnesium (12) 2, 8, 2
(iii) The first halogen
Answer:
Fluorine (9) 2, 7
(iv) The second noble gas.
Answer:
Neon (10) 2, 8.
Question 31.
Observe the following elements in the Modern Periodic Table.
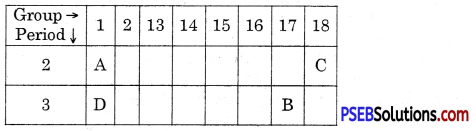
Name the elements A, B, C and D. Also indicate noble gas
Answer:
(A) Lithium
(B) Chlorine
(C) Neon
(D) Potassium C is a noble gas
Question 32.
Match the following :
| (a) Fluorine | (i) Metalloid |
| (b) Neon | (ii) Halogen |
| (c) Sodium | (iii) Noble gas |
| (d) Arsenic | (iv) Alkali metal |
Answer:
| (a) Fluorine | (ii) Halogen |
| (b) Neon | (iii) Noble gas |
| (c) Sodium | (iv) Alkali metal |
| (d) Arsenic | (i) Metalloid |
![]()
Question 33.
How many electrons can be present in the valence shells of metal atoms and non-metal atoms?
Answer:
Metal atoms have 1, 2 or 3 electrons in their valence shells whereas non-metal atoms have 4 to 7 electrons in their valence shells.
Question 34.
How are the various groups of the Modern Periodic Table designated according to the IUPAC system and old system?
Answer:
The designations of various groups of the Modern periodic table are :

Question 35.
What are the uses of Modern Periodic Table?
Answer:
- Systematic study of the elements. In the periodic table, the elements with similar properties are placed together in the same group. If we know the properties of one element of the group, the properties of other elements belonging to the same group can be predicted. Thus, there is no need to study the properties of all the elements.
- Properties of an element can be predicted from the position of the element in the periodic table. For example, if the element belongs to group IA or IIA it is likely to be a reactive metal, and if it belongs to group VII A it is likely to be a reactive non-metal.
- It has led to the discovery of many new elements.
Very Short Answer Type Questions
Question 1.
How many elements have been discovered so far?
Answer:
114.
Question 2.
How are elements classified?
Answer:
The elements have been classified on the basis of their properties.
Question 3.
Why are group IA elements called alkali metals?
Answer:
This is because all these elements are metals and their oxides and hydroxides give alkaline solutions in water.
Question 4.
What is the basis of Modern Periodic table?
Answer:
It is based upon Modern Periodic law.
![]()
Question 5.
Name the family to which halogens belongs?
Answer:
Halogen family.
Question 6.
Name the second elements of group 14.
Answer:
Silicon.
Question 7.
How many valence electrons and present in halogen elements?
Answer:
Seven.
Question 8.
How many elements are present in 4th period?
Answer:
18.
Question 9.
How many electrons are present in Mg2+ ion?
Answer:
Ten.
Question 10.
Out of Na and Mg which was larger size?
Answer:
Na
Question 11.
What is the valency of nitrogen?
Answer:
Three.
Question 12.
Out of Na and K which is more reactive?
Answer:
Sodium (Na).
Question 13.
Name the group number of halogen family.
Answer:
Group 17 (or VII-A).
Question 14.
Name the last element of third period?
Answer:
Argon.
![]()
Question 15.
What is Dobereiner’s Triad?
Answer:
A group of three elements having similar properties is called Dobereiner’s Triad.
Question 16.
A, B and constitute the Dobereiner s Traid. Atomic mass of A and C are 7 and 23 respectively. Calculate atomic mass of B.
Answer:
\(\frac{7+23}{2}=\frac{30}{2}\) = 15
Question 17.
Name the elements discovered after Mendeleev’s Periodic Table?
Answer:
Scandium (Se), Gallium (Ga), Germanium (Ge) etc.
Question 18.
Name the groups and periods in Mendeleev’s Periodic Table?
Answer:
8 groups and 7 periods.
Question 19.
How does atomic radii as we move from left along a period in the Periodic Table?
Answer:
It decreases.
Question 20.
An element has the electronic configuration 2, 8, 3. What is its group number in Modern Periodic Table?
Answer:
Group 13.
Question 21.
Give the basis of Dobereiner’s classification.
Answer:
Doberenier Triads.
Question 22.
Give the characteristics of Dobereiner’s Triads.
Answer:
The atomic mass of the central element is the average of masses of the other two elements.
Question 23.
What is the drawback of Doberenier’s Triads?
Answer:
All the known elements could be grouped into Triads.
Question 24.
There are three alements A, B and C. The atomic masses of A and C are 7 and 39. What is the atomic mass of B on the bais of Dobereiner’s Traids?
Answer:
Atomic mass of B = \(\frac{7+39}{2}\) = 23.
Question 25.
There are three elements X, Y, Z. Atomic masses of X and Z are 35.5 and 127. What will be atomic mass of Y on the basis of Dobereiner’s Traids?
Answer:
Atomic mass of Y
\(\frac{35.5+127}{2}=\frac{162.5}{2}\) = 81.25
Question 26.
Write Newland’s Law of Octaves for classification of elements.
Answer:
When the elements are arranged in order of increasing atomic masses, eighth elements has properties similar to the first element.
Question 27.
How many element were classified by Newland.
Answer:
Upto mass number 40.
Question 28.
Indicate the group number and period number of P in the modern Periodic Table.
Answer:
Group-15, Period-3.
Question 29.
An element has the electronic configuration 2, 8, 8, 2. Indicate its group and Period in the Modern Periodic Table.
Answer:
Group-12, Period-4.
Question 30.
An element M is in the group 13 of Modern Periodic Table write the formula of its oxide.
Answer:
M2O3.
Question 31.
Give the groups and periods in the Modern Periodic Table.
Answer:
Group-18, Periods-7.
Question 32.
Give the electronic configuration of 17Cl35. Also indicate its position in the Periodic Table.
Answer:
Electronic configuation of 17Cl35 = 2, 8, 7
Period number = 3
Group number =17. (VII A)
Question 33.
Give the name and electronic configuation of element with atomic number 9.
Answer:
Fluorine and it has the electronic configuation = 2, 7.
Question 34.
What is Modern Periodic Law?
Answer:
It states that the properties of the elements are the periodic functions of their atomic numbers.
Question 35.
Who gave Newland’s Law of Octaves.
Answer:
Newland.
Question 36.
Define Mendeleev’s periodic law.
Answer:
It states that the properties of the elements are the periodic functions of their atomic masses.
Question 37.
What is the basis of Mendeleev’s Modern Table?
Answer:
It is based upon Mendeleev periodic law and in this table the elements are arranged in order of increasing atomic masses.
Question 38.
How many groups are present in Mendeleev’s Period Table.
Answer:
Eight.
Question 39.
Name the next elements after P in Modern Periodic Table.
Answer:
Sulphur (S).
Question 40.
Give the group number of nitrogen and phosphorus.
Answer:
They belong to group number 15.
Question 41.
Out of Mg and Al which is more metallic?
Answer:
Mg.
Question 42.
Out of Be, Mg, Ca, Al which does not belong to same group?
Answer:
Al.
Question 43.
In which group noble gases are present?
Answer:
Group 18 or group zero.
![]()
Question 44.
Na and S are present in the third period of Modern Periodic Table. Which is more metallic and why?
Answer:
Na is more metallic due to larger size than S.
Question 45.
What is metallic character?
Answer:
It is the tendency of an atom of the element to form positive ions by losing electrons.
Question 46.
What is the trend in metallic character on moving from left to right along a period?
Answer:
It decreases.
Multiple Choice Questions:
Question 1.
Who gave Law of octaves?
(A) Newland
(B) Dobereiner
(C) Mendeleef
(D) Lother Mayer.
Answer:
(A) Newland
Question 2.
In Mendeleef’s periodic table which element was discovered in the gap between Boron and Aluminium ?
(A) Na
(B) Ca
(C) Ga
(D) Ba.
Answer:
(C) Ga
Question 3.
According to Mendeleef’s periodic law, the elements are arranged in order of A increasing:
(A) Atomic numbers
(B) Decreasing atomic number
(C) Increasing atomic masses
(D) Decreasing atomic masses.
Answer:
(C) Increasing atomic masses
Question 4.
Which element occupied gap left in Mendeleers periodic table?
(A) Germanium
(B) chlorine
(C) Oxygen
(D) Silicon.
Answer:
(A) Germanium
Question 5.
An element has the electronic configuration 2, 8, 2. It is present in group:
(A) 2
(B) is
(C) 8
(D) 10.
Answer:
(A) 2
Question 6.
Which element shows metallic character?
(A) 2, 8, 2
(B) 2, 8, 4
(C) 2, 8, 8
(D) 2, 7.
Answer:
(A) 2, 8, 2
Question 7.
Which shell is largest shell?
(A) K
(B)L
(C) M
(D) N.
Answer:
(D) N
Fill in the blanks :
Question 1.
Out of Na and Mg, ______ has bigger size.
Answer:
Na.
Question 2.
Number of elements known in Mendeleefs periodic table were ______
Answer:
63.
Question 3.
Oxygen and sulphur belong to same ______
Answer:
group.
Question 4.
The elements of group 17 are called ______
Answer:
halogens.
![]()
Question 5.
The valency of the members of noble gas family is ______
Answer:
zero.
Question 6.
The halogens belong to group ______
Answer:
17.