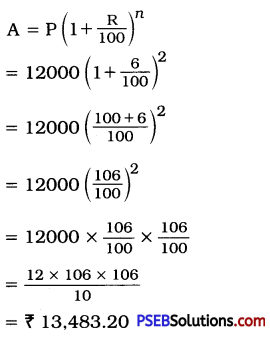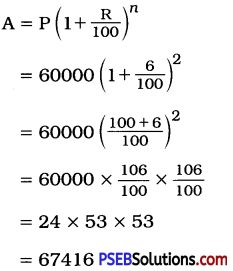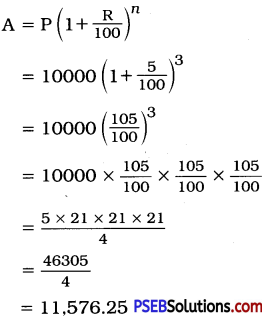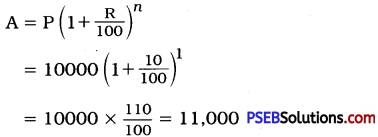Class 8

Punjab State Board PSEB 8th Class Punjabi Book Solutions Chapter 1 ਰਾਸ਼ਟਰੀ ਝੰਡਾ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Punjabi Chapter 1 ਰਾਸ਼ਟਰੀ ਝੰਡਾ

(i) ਛੋਟੇ ਉੱਤਰ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਨੂੰ ਤਿਰੰਗਾ ਕਿਉਂ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ :
ਇਸ ਵਿਚ ਤਿੰਨ ਰੰਗ ਹੋਣ ਕਰਕੇ ।

ਪ੍ਰਸ਼ਨ 2.
ਹਰਾ ਰੰਗ ਕਿਸ ਗੱਲ ਦਾ ਪ੍ਰਤੀਕ ਹੈ ?
ਉੱਤਰ :
ਖ਼ੁਸ਼ਹਾਲੀ ਦਾ ।

ਪ੍ਰਸ਼ਨ 3.
ਅਮਨ ਦੀ ਨਿਸ਼ਾਨੀ ਕਿਹੜਾ ਰੰਗ ਦਰਸਾਉਂਦਾ ਹੈ ?
ਉੱਤਰ :
ਚਿੱਟਾ ਰੰਗ ।

ਪ੍ਰਸ਼ਨ 4.
ਕੇਸਰੀ ਰੰਗ ਕਿਸ ਗੱਲ ਦਾ ਪ੍ਰਤੀਕ ਹੈ ?
ਉੱਤਰ :
ਕੁਰਬਾਨੀ ਦਾ ।

(ii) ਸੰਖੇਪ ਉੱਤਰ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਹਰੇ, ਚਿੱਟੇ ਤੇ ਕੇਸਰੀ ਰੰਗ ਦੀ ਕੀ ਮਹੱਤਤਾ ਹੈ ?
ਉੱਤਰ :
ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਵਿਚਲਾ ਹਰਾ ਰੰਗ ਦੇਸ਼ ਦੀ ਖ਼ੁਸ਼ਹਾਲੀ, ਚਿੱਟਾ ਰੰਗ ਅਮਨ-ਸ਼ਾਂਤੀ ਤੇ ਕੇਸਰੀ ਰੰਗ ਦੇਸ਼ ਲਈ ਕੁਰਬਾਨੀ ਕਰਨ ਦੀ ਮਹੱਤਤਾ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਕਵੀ ਨੇ ਕਿਨ੍ਹਾਂ ਸਤਰਾਂ ਵਿਚ ਭਾਰਤ ਲਈ ਪਿਆਰ ਪ੍ਰਗਟ ਕੀਤਾ ਹੈ ?
ਉੱਤਰ :
ਕਵੀ ਨੇ ਇਨ੍ਹਾਂ ਸਤਰਾਂ ਵਿਚ ਭਾਰਤ ਲਈ ਪਿਆਰ ਪ੍ਰਗਟ ਕੀਤਾ ਹੈ-
ਗੀਤ ਤਿਰੰਗੇ ਦੇ ਰਲ ਕੇ ਗਾਈਏ ।
ਭਾਰਤ ਮਾਂ ਦੀ ਸ਼ਾਨ ਵਧਾਈਏ ।

ਪ੍ਰਸ਼ਨ 3.
ਖੇਤਾਂ ਵਿਚ ਖ਼ੁਸ਼ਹਾਲੀ ਕਿਵੇਂ ਟਹਿਕ ਰਹੀ ਹੈ ?
ਉੱਤਰ :
ਖੇਤਾਂ ਵਿਚ ਹਰੀਆਂ-ਭਰੀਆਂ ਬਹੁਮੁੱਲੀਆਂ ਫ਼ਸਲਾਂ ਪੈਦਾ ਹੋਣ ਨਾਲ ਖੁਸ਼ਹਾਲੀ ਟਹਿਕ ਰਹੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਤੁਸੀਂ ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਬਾਰੇ ਹੋਰ ਕੀ ਜਾਣਕਾਰੀ ਰੱਖਦੇ ਹੋ ?
ਉੱਤਰ :
ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਵਿਚ ਤਿੰਨ ਰੰਗਾਂ ਤੋਂ ਇਲਾਵਾ ਵਿਚਕਾਰਲੀ ਚਿੱਟੀ ਪੱਟੀ ਵਿਚ ਨੇਵੀ ਬਲਿਊ ਰੰਗ ਦੇ ਅਸ਼ੋਕ ਚੱਕਰ ਦਾ ਚਿੰਨ੍ਹ ਵੀ ਹੈ, ਜਿਸਨੂੰ ਸਾਰਨਾਥ ਵਿਚ ਬਣੇ ਅਸ਼ੋਕ ਥੰਮ ਤੋਂ ਲਿਆ ਗਿਆ ਹੈ, ਜੋ ਵਿਕਾਸ ਤੇ ਤਰੱਕੀ ਦਾ ਚਿੰਨ੍ਹ ਹੈ । 26 ਜਨਵਰੀ ਨੂੰ ਰਾਸ਼ਟਰਪਤੀ ਜੀ ਇਸ ਝੰਡੇ ਨੂੰ ਰਾਜ-ਪੱਥ ਉੱਤੇ ਝੁਲਾਉਂਦੇ ਹਨ ਤੇ 15 ਅਗਸਤ ਨੂੰ ਪ੍ਰਧਾਨ ਮੰਤਰੀ ਜੀ ਇਸਨੂੰ ਲਾਲ ਕਿਲ੍ਹੇ ਉੱਤੇ ਝੁਲਾਉਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
‘ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਕਵਿਤਾ ਵਿਚ ਮੁੱਖ ਤੌਰ’ ਤੇ ਕੀ ਵਰਣਨ ਕੀਤਾ ਗਿਆ ਹੈ ?
ਉੱਤਰ :
ਇਸ ਕਵਿਤਾ ਵਿਚ ਮੁੱਖ ਤੌਰ ਤੇ ਆਪਣੇ ਭਾਰਤ ਦੇਸ਼ ਦੇ ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਦੀ ਮਹਿਮਾ ਗਾਈ ਗਈ ਹੈ ਤੇ ਇਸ ਦੇ ਤਿੰਨਾਂ ਰੰਗਾਂ ਦੇ ਮਹੱਤਵ ਨੂੰ ਉਜਾਗਰ ਕੀਤਾ ਗਿਆ ਹੈ । ਇਸ ਦੇ ਨਾਲ ਹੀ ਸਾਨੂੰ ਤਿਰੰਗੇ ਝੰਡੇ ਦਾ ਗੀਤ ਗਾਉਣ ਤੇ ਭਾਰਤ ਮਾਂ ਦੀ ਸ਼ਾਨ ਵਧਾਉਣ ਦੀ ਪ੍ਰੇਰਨਾ ਦਿੱਤੀ ਗਈ ਹੈ ।

(iii) ਕੁੱਝ ਹੋਰ ਪ੍ਰਸ਼ਨ

ਪ੍ਰਸ਼ਨ 1.
ਖ਼ਾਲੀ ਸਥਾਨ ਭਰੋ :
(ੳ) ਰਾਸ਼ਟਰੀ ਝੰਡਾ …………… ਪਿਆਰਾ ।
(ਅ) ਹਰੇ ਰੰਗ ਦੀ ਏ ………. !
(ਈ) ………. ਰੰਗ ਹੈ ਚਿੱਟਾ !
(ਸ) ਭਾਰਤ ਮਾਂ ਦੀ ………….. ।
(ਹ) ……….. ਦੇਸ਼ ਦਾ ਸਿਤਾਰਾ ॥
ਉੱਤਰ :
(ਉ) ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਪਿਆਰਾ ॥
(ਅ) ਹਰੇ ਰੰਗ ਦੀ ਏ ਸ਼ਾਨ ਨਿਰਾਲੀ ।
(ਈ ਅਮਨ ਦੀ ਨਿਸ਼ਾਨੀ ਰੰਗ ਹੈ ਚਿੱਟਾ ।
(ਸ) ਭਾਰਤ ਮਾਂ ਦੀ ਸ਼ਾਨ ਵਧਾਈਏ ।
(ਹ) ਸੂਰਜ ਬਣ ਕੇ ਚਮਕੇ ਦੇਸ਼ ਦਾ ਸਿਤਾਰਾ ।

ਪ੍ਰਸ਼ਨ 2.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਵਿਚੋਂ ਵਿਸ਼ੇਸ਼ਣ ਚੁਣੋ :ਤਿਰੰਗਾ, ਖ਼ੁਸ਼ਹਾਲ, ਨਿਸ਼ਾਨੀ, ਗੀਤ, ਸ਼ਾਨ, ਸੂਰਜ ।
ਉੱਤਰ :
ਤਿਰੰਗਾ
ਖ਼ੁਸ਼ਹਾਲ ।

ਪ੍ਰਸ਼ਨ 3.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਨਾਲ ਰਲਦੇ ਸ਼ਬਦ ਲਿਖੋ :
ਪਿਆਰਾ – ……………
ਨਿਰਾਲੀ – ……………
ਚਿੱਟਾ – ……………
ਸਿਤਾਰਾ – ……………
ਗਾਈਏ – ……………
ਉੱਤਰ :
ਪਿਆਰਾ – ਨਿਆਰਾ
ਨਿਰਾਲੀ – ਖ਼ੁਸ਼ਹਾਲੀ
ਚਿੱਟਾ – ਮਿੱਠਾ
ਸਿਤਾਰਾ – ਧਾਰਾ
ਗਾਈਏ – ਵਧਾਈਏ ।

ਪ੍ਰਸ਼ਨ 4.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਦੀ ਵਾਕਾਂ ਵਿਚ ਵਰਤੋਂ ਕਰੋ :
(ਨਿਰਾਲੀ, ਨਿਸ਼ਾਨੀ, ਖ਼ੁਸ਼ਹਾਲੀ, ਮੇਵਾ, ਧਾਰਾ, ਕੁਰਬਾਨੀ, ਸ਼ਾਨ)
ਉੱਤਰ :
1. ਨਿਰਾਲੀ (ਵੱਖਰੀ, ਦੂਜਿਆਂ ਤੋਂ ਭਿੰਨ, ਅਨੋਖੀ) – ਭਾਰਤ ਮਾਂ ਦੀ ਸ਼ਾਨ ਨਿਰਾਲੀ ਹੈ ।
2. ਨਿਸ਼ਾਨੀ (ਚਿੰਨ੍ਹ) – ਤਿਰੰਗੇ ਝੰਡੇ ਵਿਚਲਾ ਹਰਾ ਰੰਗ ਖ਼ੁਸ਼ਹਾਲੀ ਦੀ ਨਿਸ਼ਾਨੀ ਹੈ ।
3. ਖ਼ੁਸ਼ਹਾਲੀ (ਖ਼ੁਸ਼ੀ ਦਾ ਪਸਾਰ ਹੋਣਾ) – ਜਦੋਂ ਦੇਸ਼ ਸਚਮੁੱਚ ਤਰੱਕੀ ਕਰੇ, ਤਾਂ ਹਰ ਪਾਸੇ ਖ਼ੁਸ਼ਹਾਲੀ ਫੈਲ ਜਾਂਦੀ ਹੈ ।
4. ਮੇਵਾ (ਸੁੱਕੇ ਮਿੱਠੇ ਫਲ) – ਮੇਵੇ ਵਿਚ ਛੁਹਾਰੇ ਤੇ ਸੌਗੀ ਸ਼ਾਮਿਲ ਹੁੰਦੇ ਹਨ ।
5. ਧਾਰਾ (ਵਹਿਣ, ਰੌ) – ਸਾਡੇ ਖੇਤਾਂ ਕੋਲ ਛੋਟੀ ਜਿਹੀ ਨਦੀ ਦੀ ਧਾਰਾ ਵਹਿੰਦੀ ਹੈ ।
6. ਕੁਰਬਾਨੀ (ਜਾਨ ਦੇ ਦੇਣੀ) – ਸ਼ਹੀਦ ਭਗਤ ਸਿੰਘ ਦੀ ਦੇਸ਼ ਲਈ ਕੀਤੀ ਕੁਰਬਾਨੀ ਨੂੰ ਕੌਣ ਭੁਲਾ ਸਕਦਾ ਹੈ ?
7. ਸ਼ਾਨ (ਵਡਿਆਈ) – ਸਾਨੂੰ ਹਮੇਸ਼ਾ ਆਪਣੇ ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਦੀ ਸ਼ਾਨ ਉੱਚੀ ਰੱਖਣੀ ਚਾਹੀਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਹੇਠ ਲਿਖੀਆਂ ਸਤਰਾਂ ਨੂੰ ਸੁੰਦਰ ਲਿਖਾਈ ਕਰ ਕੇ ਲਿਖੋ-
ਗੀਤ ਤਿਰੰਗੇ ਦੇ ਰਲ ਗਾਈਏ ।
ਭਾਰਤ ਮਾਂ ਦੀ ਸ਼ਾਨ ਵਧਾਈਏ ।
ਉੱਤਰ :
………………………………………………..
………………………………………………..

ਪ੍ਰਸ਼ਨ 6.
‘ਰਾਸ਼ਟਰੀ ਝੰਡਾ’ ਕਵਿਤਾ ਨੂੰ ਰਲ ਕੇ ਗਾਓ ।
ਉੱਤਰ :
(ਨੋਟ-ਇਸ ਕਵਿਤਾ ਨੂੰ ਵਿਦਿਆਰਥੀ ਜ਼ਬਾਨੀ ਯਾਦ ਕਰਨ ਤੇ ਰਲ ਕੇ ਗਾਉਣ )

ਪ੍ਰਸ਼ਨ 7.
‘ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਕਵਿਤਾ ਦੀਆਂ ਪੰਜ-ਛੇ ਸਤਰਾਂ ਜ਼ਬਾਨੀ ਲਿਖੋ-
ਉੱਤਰ :
ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਪਿਆਰਾ ।
ਝੱਲੇ ਹਵਾ ਵਿਚ ਲਗਦਾ ਪਿਆਰਾ !
ਹਰੇ ਰੰਗ ਦੀ ਏ ਸ਼ਾਨ ਨਿਰਾਲੀ ।
ਖੇਤਾਂ ਬੰਨੇ ਖੇਡੇ ਖ਼ੁਸ਼ਹਾਲੀ ।
ਸੋਨਾ ਉਪਜੇ ਹਰ ਖੇਤ ਦਾ ਕਿਆਰ ।
ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਪਿਆਰਾ ॥

ਬਹੁਵਿਕਲਪੀ ਅਤੇ ਬਹੁਤ ਸੰਖੇਪ ਉੱਤਰ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

(ਉ) ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਪਿਆਰਾ ।
ਭੁੱਲੇ ਹਵਾ ਵਿਚ ਲਗਦਾ ਨਿਆਰਾ ॥
ਹਰੇ ਰੰਗ ਦੀ ਏ ਸ਼ਾਨ ਨਿਰਾਲੀ ॥
ਖੇਤਾਂ ਬੰਨੇ ਖੇਡੇ ਖੁਸ਼ਹਾਲੀ |
ਸੋਨਾ ਉਪਜੇ ਹਰ ਖੇਤ ਦਾ ਕਿਆਰਾ ।
ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਪਿਆਰਾ ।

ਪ੍ਰਸ਼ਨ 1.
(i) ਉਪਰੋਕਤ ਕਾਵਿ-ਟੋਟੇ ਦੇ ਭਾਵ-ਅਰਥ ਲਿਖੋ ।
(ii) ਇਹ ਸਤਰਾਂ ਕਿਸ ਕਵਿਤਾ ਵਿਚੋਂ ਹਨ ?
(iii) ਇਹ ਕਵਿਤਾ ਕਿਸੇ ਦੀ ਲਿਖੀ ਹੋਈ ਹੈ ?
(iv) ਸਾਡੇ ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਦਾ ਕੀ ਨਾਂ ਹੈ ?
(v) ਸਾਡੇ ਝੰਡੇ ਵਿਚ ਹਰਾ ਰੰਗ ਕਿਸ ਗੱਲ ਦਾ ਪ੍ਰਤੀਕ ਹੈ ?
(vi) ਸਾਡੇ ਖੇਤ ਕੀ ਪੈਦਾ ਕਰਦੇ ਹਨ ?
ਉੱਤਰ :
(i) ਸਾਡਾ ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਸਾਨੂੰ ਪਿਆਰਾ ਤੇ ਨਿਆਰਾ ਲਗਦਾ ਹੈ । ਇਸ ਵਿਚਲਾ ਹਰਾ ਰੰਗ ਬਹੁਮੁੱਲੀਆਂ ਫ਼ਸਲਾਂ ਪੈਦਾ ਕਰ ਕੇ ਵਰਤੀ ਖ਼ੁਸ਼ਹਾਲੀ ਦਾ ਚਿੰਨ੍ਹ ਹੈ ।
(ii) ਰਾਸ਼ਟਰੀ ਝੰਡਾ
(iii) ਡਾ: ਹਰਨੇਕ ਸਿੰਘ ਕਲੇਰ ।
(iv) ਤਿਰੰਗਾ !
(v) ਖ਼ੁਸ਼ਹਾਲੀ ਦਾ ।
(vi) ਬਹੁਮੁੱਲੀਆਂ ਫ਼ਸਲਾਂ ਰੂਪੀ ਸੋਨਾ ।

(ਅ) ਅਮਨ ਦੀ ਨਿਸ਼ਾਨੀ, ਰੰਗ ਹੈ ਚਿੱਟਾ ।
ਜੀਣ ਤੇ ਜੀਣ ਦਿਓ, ਮੇਵਾ ਹੈ ਮਿੱਠਾ ।
ਵਗਦੀ ਰਹੇ ਸਦਾ ਸ਼ਾਂਤੀ ਦੀ ਧਾਰਾ ।
ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਪਿਆਰਾ ।

ਪ੍ਰਸ਼ਨ 2.
(i) ਉਪਰੋਕਤ ਕਾਵਿ-ਟੋਟੇ ਦੇ ਭਾਵ-ਅਰਥ ਲਿਖੋ ।
(ii) ਤਿਰੰਗੇ ਵਿਚਲਾ ਚਿੱਟਾ ਰੰਗ ਕਿਸ ਚੀਜ਼ ਦੀ ਨਿਸ਼ਾਨੀ ਹੈ ?
(iii) ਅਮਨ ਦੀ ਨਿਸ਼ਾਨੀ ਕਿਹੜਾ ਰੰਗ ਹੈ ?
(iv) ਕਿਸ ਮੇਵੇ ਨੂੰ ਮਿੱਠਾ ਕਿਹਾ ਗਿਆ ਹੈ ?
(v) ਕਿਹੜੀ ਧਾਰਾ ਵਗਦੀ ਰਹਿਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ :
(i) ਸਾਡੇ ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਤਿਰੰਗੇ ਵਿਚ ਚਿੱਟਾ ਰੰਗ ਅਮਨ ਦਾ ਚਿੰਨ੍ਹ ਹੈ, ਜਿਹੜਾ ਜੀਓ ਤੇ ਜਿਉਣ ਦਿਓ ਦਾ ਸੁਨੇਹਾ ਦਿੰਦਾ ਹੈ, ਤਾਂ ਜੋ ਦੁਨੀਆ ਵਿਚ ਹਮੇਸ਼ਾ ਸ਼ਾਂਤੀ ਦਾ ਵਾਤਾਵਰਨ ਬਣਿਆ ਰਹੇ ।
(ii) ਅਮਨ ਦੀ ।
(iii) ਚਿੱਟਾ ।
(iv) “ਜੀਓ ਅਤੇ ਜੀਣ ਦਿਓ’ ਦੇ ਸਿਧਾਂਤ ਰੂਪ ਮੇਵੇ ਨੂੰ ।
(v) ਸ਼ਾਂਤੀ ਦੀ ।

(ਬ) ਕੇਸਰੀ ਰੰਗ ਹੈ ਕੁਰਬਾਨੀ ਵਾਲਾ ।
ਜੀਵੇ ਸਰਹੱਦਾਂ ਦਾ ਰਖਵਾਲਾ ॥
ਸੂਰਜ ਬਣ ਕੇ ਚਮਕੇ, ਦੇਸ਼ ਦਾ ਸਿਤਾਰਾ ।
ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਪਿਆਰਾ ॥

ਪ੍ਰਸ਼ਨ 3.
(i) ਉਪਰੋਕਤ ਕਾਵਿ-ਟੋਟੇ ਦੇ ਭਾਵ-ਅਰਥ ਲਿਖੋ ।
(ii) ਤਿਰੰਗੇ ਵਿਚਲਾ ਕੇਸਰੀ ਰੰਗ ਕਿਸ ਚੀਜ਼ ਦਾ ਚਿੰਨ੍ਹ ਹੈ ?
(iii) ਸਰਹੱਦਾਂ ਦਾ ਰਖਵਾਲਾ ਕੌਣ ਹੈ ?
(iv) ਦੇਸ਼ ਦਾ ਸਿਤਾਰਾ ਕਿਸ ਤਰ੍ਹਾਂ ਚਮਕਣ ਦੀ ਇੱਛਾ ਕੀਤੀ ਗਈ ਹੈ ?
ਉੱਤਰ :
(i) ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਤਿਰੰਗੇ ਵਿਚਲਾ ਕੇਸਰੀ ਰੰਗ ਕੁਰਬਾਨੀ ਦਾ ਪ੍ਰਤੀਕ ਹੈ । ਅਸੀਂ ਚਾਹੁੰਦੇ ਹਾਂ ਕਿ ਦੇਸ਼ ਦਾ ਰਾਖਾ ਫ਼ੌਜੀ ਸਿਪਾਹੀ ਸਦਾ ਜਿਉਂਦਾ ਰਹੇ, ਤਾਂ ਜੋ ਦੇਸ਼ ਦਾ ਸਿਤਾਰਾ ਸੂਰਜ ਵਾਂਗ ਚਮਕਦਾ ਰਹੇ ।
(ii) ਕੁਰਬਾਨੀ ਦਾ ।
(iii) ਫ਼ੌਜੀ ਸਿਪਾਹੀ ।
(iv) ਸੂਰਜ ਵਾਂਗ ।

(ਸ) ਗੀਤ ਤਿਰੰਗੇ ਦੇ ਰਲ ਕੇ ਗਾਈਏ ।
ਭਾਰਤ ਮਾਂ ਦੀ ਸ਼ਾਨ ਵਧਾਈਏ ।
ਸਿਫ਼ਤਾਂ ਕਰਦਾ ਏ ਜੱਗ ਸਾਰਾ ।
ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਪਿਆਰਾ ਹੈ।

ਪ੍ਰਸ਼ਨ 4.
(i) ਉਪਰੋਕਤ ਕਾਵਿ-ਟੋਟੇ ਦੇ ਭਾਵ-ਅਰਥ ਲਿਖੋ ।
(ii) ਸਾਨੂੰ ਰਲ ਕੇ ਕਿਸਦੇ ਗੀਤ ਗਾਉਣੇ ਚਾਹੀਦੇ ਹਨ ?
(iii) ਸਾਨੂੰ ਕਿਸ ਦੀ ਸ਼ਾਨ ਵਧਾਉਣ ਲਈ ਕੰਮ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ?
(iv) ਸਾਰਾ ਜਗਤ ਕਿਸ ਦੀਆਂ ਸਿਫ਼ਤਾਂ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ :
(i) ਸਾਨੂੰ ਸਭ ਨੂੰ ਰਲ ਕੇ ਆਪਣੇ ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਤਿਰੰਗੇ ਦੇ ਗੀਤ ਗਾ ਕੇ ਭਾਰਤ ਮਾਂ ਦੀ ਸ਼ਾਨ ਵਧਾਉਣੀ ਚਾਹੀਦੀ ਹੈ । ਸਾਰਾ ਸੰਸਾਰ ਸਾਡੇ ਦੇਸ਼ ਦੀਆਂ ਸਿਫ਼ਤਾਂ ਕਰਦਾ ਹੈ । ਸਾਨੂੰ ਇਹ ਤਿਰੰਗਾ ਝੰਡਾ ਬਹੁਤ ਪਿਆਰਾ ਹੈ ।
(ii) ਤਿਰੰਗੇ ਦੇ !
(iii) ਭਾਰਤ ਮਾਂ ਦੀ ।
(iv) ਭਾਰਤ ਮਾਂ ਦੀਆਂ ।

ਕਾਵਿ-ਟੋਟਿਆਂ ਦੇ ਸਰਲ ਅਰਥ

(ਉ) ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਪਿਆਰਾ ॥
ਝੱਲੇ ਹਵਾ ਵਿਚ ਲਗਦਾ ਨਿਆਰਾ ।
ਹਰੇ ਰੰਗ ਦੀ ਏ ਸ਼ਾਨ ਨਿਰਾਲੀ ।
ਖੇਤਾਂ ਬੰਨੇ ਖੇਡੇ ਖ਼ੁਸ਼ਹਾਲੀ ॥
ਸੋਨਾ ਉਪਜੇ ਹਰ ਖੇਤ ਦਾ ਕਿਆਰਾ ।
ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਪਿਆਰਾ ॥

ਔਖੇ ਸ਼ਬਦਾਂ ਦੇ ਅਰਥ : ਨਿਆਰਾ-ਵੱਖਰਾ, ਦੂਜਿਆਂ ਤੋਂ ਵੱਖਰਾ । ਨਿਰਾਲੀ-ਵੱਖਰੀ, ਦੁਜਿਆਂ ਨਾਲੋਂ ਭਿੰਨ ( ਬੰਨੇ-ਵਲ, ਬੰਨੇ ਉੱਤੇ । ਉਪਜੇ-ਪੈਦਾ ਕਰੇ । ਕਿਆਰਾ-ਖੇਤ ਦਾ ਛੋਟਾ ਹਿੱਸਾ, ਜੋ ਵੱਟ ਪਾ ਕੇ ਵੱਖਰਾ ਕੀਤਾ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 1.
(i) ਉੱਪਰ ਲਿਖੇ ਕਾਵਿ-ਟੋਟੇ ਦੇ ਸਰਲ ਅਰਥ ਲਿਖੋ ।
(ii) ਸਾਡੇ ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਦਾ ਕੀ ਨਾਂ ਹੈ ?
(iii) ਕਿਹੜੀ ਚੀਜ਼ ਪਿਆਰੀ ਲੱਗਦੀ ਹੈ ?
(iv) ਝੰਡੇ ਦਾ ਹਰਾ ਰੰਗ ਕਿਸ ਚੀਜ਼ ਦਾ ਚਿੰਨ੍ਹ ਹੈ ?
(v) ਹਰ ਖੇਤ ਵਿਚ ਕੀ ਪੈਦਾ ਹੁੰਦਾ ਹੈ ।
ਉੱਤਰ :
(i) ਕਵੀ ਕਹਿੰਦਾ ਹੈ ਕਿ ਸਾਨੂੰ ਆਪਣੇ ਭਾਰਤ ਦੇਸ਼ ਦਾ ਤਿਰੰਗਾ ਝੰਡਾ ਬਹੁਤ ਪਿਆਰਾ ਹੈ । ਇਹ ਜਦੋਂ ਹਵਾ ਵਿਚ ਭੁੱਲ ਰਿਹਾ ਹੁੰਦਾ ਹੈ, ਤਾਂ ਸਾਨੂੰ ਹੋਰ ਵੀ ਵਧੇਰੇ ਪਿਆਰਾ ਲਗਦਾ ਹੈ । ਇਸ ਦੇ ਹਰੇ ਰੰਗ ਦੀ ਸ਼ਾਨ ਹੀ ਵੱਖਰੀ ਹੈ । ਇਹ ਖੇਤਾਂ ਵਿਚ ਖੇਡ ਰਹੀਆਂ ਹਰੀਆਂ ਫ਼ਸਲਾਂ ਤੋਂ ਪੈਦਾ ਹੋਣ ਵਾਲੀ ਖ਼ੁਸ਼ਹਾਲੀ ਦਾ ਚਿੰਨ੍ਹ ਹੈ । ਇਹ ਇਸ ਗੱਲ ਦਾ ਪ੍ਰਤੀਕ ਹੈ ਕਿ ਇਸ ਦੇਸ਼ ਦੇ ਖੇਤਾਂ ਦਾ ਹਰ ਕਿਆਰਾ ਸੋਨੇ ਵਰਗੀਆਂ ਬਹੁਮੁੱਲੀਆਂ ਫ਼ਸਲਾਂ ਪੈਦਾ ਕਰਦਾ ਹੈ । ਸਾਨੂੰ ਦੇਸ਼ ਦੇ ਖੇਤਾਂ ਵਿਚਲੀ ਹਰਿਆਵਲ ਨੂੰ ਦਰਸਾਉਣ ਵਾਲਾ ਆਪਣਾ ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਬਹੁਤ ਪਿਆਰਾ ਹੈ ।
(ii) ਤਿਰੰਗਾ ।
(iii) ਹਵਾ ਵਿਚ ਭੁੱਲਦਾ ਤਿਰੰਗਾ ਝੰਡਾ ।
(iv) ਖ਼ੁਸ਼ਹਾਲੀ ਦਾ ।
(v) ਸੋਨੇ ਵਰਗੀਆਂ ਬਹੁਮੁੱਲੀਆਂ ਫ਼ਸਲਾਂ ।

(ਅ) ਅਮਨ ਦੀ ਨਿਸ਼ਾਨੀ, ਰੰਗ ਹੈ ਚਿੱਟਾ ।
ਜੀਣ ਤੇ ਜੀਣ ਦਿਓ, ਮੇਵਾ ਹੈ ਮਿੱਠਾ ।
ਵਗਦੀ ਰਹੇ ਸਦਾ ਸ਼ਾਂਤੀ ਦੀ ਧਾਰਾ ॥
ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਪਿਆਰਾ ।

ਔਖੇ ਸ਼ਬਦਾਂ ਦੇ ਅਰਥ : ਮੇਵਾ-ਫਲ, ਸੁੱਕਾ ਮਿੱਠਾ ਫਲ ਧਾਰਾ-ਰੌ, ਵਹਿਣ, ਨਦੀ ।

ਪ੍ਰਸ਼ਨ 2.
(i) ਉੱਪਰ ਲਿਖੇ ਕਾਵਿ-ਟੋਟੇ ਦੇ ਸਰਲ ਅਰਥ ਲਿਖੋ ।
(ii) ਸਾਡੇ ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਦਾ ਕੀ ਨਾਂ ਹੈ ?
(iii) ਝੰਡੇ ਵਿਚਲਾ ਚਿੱਟਾ ਰੰਗ ਕਿਸ ਗੱਲ ਦੀ ਨਿਸ਼ਾਨੀ ਹੈ ?
(iv) “ਮਿੱਠਾ ਮੇਵਾ ਕਿਸਨੂੰ ਕਿਹਾ ਗਿਆ ਹੈ ?
(v) ਕਿਹੜੀ ਧਾਰਾ ਸਦਾ ਵਗਦੀ ਰਹਿਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ :
(i) ਕਵੀ ਕਹਿੰਦਾ ਹੈ ਕਿ ਸਾਡੇ ਦੇਸ਼ ਦੇ ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਤਿਰੰਗੇ ਵਿਚਲਾ ਚਿੱਟਾ ਰੰਗ ਅਮਨ ਦਾ ਚਿੰਨ੍ਹ ਹੈ । ਇਹ ਸਾਨੂੰ ਸੰਦੇਸ਼ ਦਿੰਦਾ ਹੈ ਕਿ ਸਾਨੂੰ ਆਪ ਵੀ ਅਮਨ-ਸ਼ਾਂਤੀ ਵਿਚ ਜਿਉਣਾ ਚਾਹੀਦਾ ਹੈ ਤੇ ਦੂਜਿਆਂ ਨੂੰ ਵੀ ਜਿਉਣ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ | ਅਮਨ ਤੇ ਪ੍ਰੇਮ-ਪਿਆਰ ਨਾਲ ਰਹਿਣ ਦਾ ਸੁਆਦ ਮਿੱਠੇ ਮੇਵੇ ਵਰਗਾ ਹੁੰਦਾ ਹੈ | ਸਾਡੇ ਤਿਰੰਗੇ ਝੰਡੇ ਵਿਚਲਾ ਚਿੱਟਾ ਰੰਗ ਸਾਨੂੰ ਸਦਾ ਅਮਨ ਤੇ ਸ਼ਾਂਤੀ ਦੀ ਧਾਰਾ ਵਗਦੀ ਰੱਖਣ ਦੀ ਇੱਛਾ ਕਰਨ ਦਾ ਸੰਦੇਸ਼ ਦਿੰਦਾ ਹੈ । ਇਸੇ ਕਰਕੇ ਸਾਨੂੰ ਆਪਣਾ ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਬਹੁਤ ਪਿਆਰਾ ਹੈ ।
(ii) ਤਿਰੰਗਾ ।
(iii) ਅਮਨ ਦੀ ।
(iv) ‘ਆਪ ਜੀਉ ਤੇ ਦੂਜਿਆਂ ਨੂੰ ਜਿਊਣ ਦਿਓ’ ਦੇ ਵਿਚਾਰ ਨੂੰ ।
(v) ਸ਼ਾਂਤੀ ਦੀ ।

(ਇ) ਕੇਸਰੀ ਰੰਗ ਹੈ ਕੁਰਬਾਨੀ ਵਾਲਾ ॥
ਜੀਵੇ ਸਰਹੱਦਾਂ ਦਾ ਰਖਵਾਲਾ ॥
ਸੂਰਜ ਬਣ ਕੇ ਚਮਕੇ, ਦੇਸ਼ ਦਾ ਸਿਤਾਰਾ ।
ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਪਿਆਰਾ ।

ਔਖੇ ਸ਼ਬਦਾਂ ਦੇ ਅਰਥ : ਸਰਹੱਦਾਂ ਦਾ ਰਖਵਾਲਾ-ਫ਼ੌਜ ਦਾ ਸਿਪਾਹੀ ।

ਪ੍ਰਸ਼ਨ 3.
(i) ਉੱਪਰ ਲਿਖੇ ਕਾਵਿ-ਟੋਟੇ ਦੇ ਸਰਲ ਅਰਥ ਲਿਖੋ ।
(ii) ਕੇਸਰੀ ਰੰਗ ਕਿਸ ਚੀਜ਼ ਦਾ ਪ੍ਰਤੀਕ ਚਿੰਨ ਹੈ ?
(iii) ਸਰਹੱਦਾਂ ਦਾ ਰਖਵਾਲਾ ਕੌਣ ਹੈ ?
(iv) ਦੇਸ਼ ਦਾ ਸਿਤਾਰਾ ਕਿਸ ਤਰ੍ਹਾਂ ਚਮਕਣਾ ਚਾਹੀਦਾ ਹੈ ?
(v) ਤਿਰੰਗੇ ਦੇ ਕਿੰਨੇ ਰੰਗ ਹਨ ?
ਉੱਤਰ :
(i) ਕਵੀ ਕਹਿੰਦਾ ਹੈ ਕਿ ਸਾਡੇ ਦੇਸ਼ ਦੇ ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਤਿਰੰਗੇ ਵਿਚਲਾ ਕੇਸਰੀ ਰੰਗ ਕੁਰਬਾਨੀ ਦਾ ਚਿੰਨ੍ਹ ਹੈ । ਇਹ ਸਾਨੂੰ ਦੇਸ਼ ਦੀ ਅਜ਼ਾਦੀ ਲਈ ਜਾਨਾਂ ਵਾਰਨ ਵਾਲੇ ਦੇਸ਼ਭਗਤਾਂ ਤੇ ਦੇਸ਼ ਦੀਆਂ ਸਰਹੱਦਾਂ ਉੱਤੇ ਇਸ ਦੇ ਦੁਸ਼ਮਣਾਂ ਤੋਂ ਇਸ ਦੀ ਰਾਖੀ ਕਰਨ ਲਈ ਹਿੱਕਾਂ ਡਾਹ ਕੇ ਕੁਰਬਾਨੀਆਂ ਕਰਨ ਵਾਲੇ ਫ਼ੌਜ ਦੇ ਸਿਪਾਹੀਆਂ ਦੀ ਯਾਦ ਦੁਆਉਂਦਾ ਹੈ । ਇਹ ਸਾਨੂੰ ਦੇਸ਼ ਦੇ ਸਿਤਾਰੇ ਨੂੰ ਦੁਨੀਆ ਵਿਚ ਚਮਕਦਾ ਰੱਖਣ ਲਈ ਕੁਰਬਾਨੀਆਂ ਕਰਨ ਦੀ ਪ੍ਰੇਰਨਾ ਦਿੰਦਾ ਹੈ । ਅਜਿਹਾ ਮਹਾਨ ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਸਾਨੂੰ ਬਹੁਤ ਪਿਆਰਾ ਹੈ !
(ii) ਕੁਰਬਾਨੀ ਦਾ ।
(iii) ਫ਼ੌਜੀ ਜਵਾਨ ।
(iv) ਸੂਰਜ ਵਾਂਗ ।
(v) ਤਿੰਨ-ਹਰਾ, ਚਿੱਟਾ ਤੇ ਕੇਸਰੀ ।

(ਸ) ਗੀਤ ਤਿਰੰਗੇ ਦੇ ਰਲ ਕੇ ਗਾਈਏ ।
ਭਾਰਤ ਮਾਂ ਦੀ ਸ਼ਾਨ ਵਧਾਈਏ ।
ਸਿਫ਼ਤਾਂ ਕਰਦਾ ਏ ਜੱਗ ਸਾਰਾ ॥
ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਪਿਆਰਾ ।

ਔਖੇ ਸ਼ਬਦਾਂ ਦੇ ਅਰਥ : ਜੱਗ-ਦੁਨੀਆ, ਜਗਤ ।

ਪ੍ਰਸ਼ਨ 4.
(i) ਉਪਰੋਕਤ ਕਾਵਿ-ਟੋਟੇ ਦੇ ਸਰਲ ਅਰਥ ਲਿਖੋ ।
(ii) ਸਾਨੂੰ ਰਲ ਕੇ ਕਿਸ ਦੇ ਗੀਤ ਗਾਉਣ ਲਈ ਕਿਹਾ ਗਿਆ ਹੈ ?
(iii) ਭਾਰਤ ਮਾਂ ਦੀ ਸ਼ਾਨ ਕਿਸ ਤਰ੍ਹਾਂ ਵਧਦੀ ਹੈ ?
(iv) ਕਿਸ ਦੀਆਂ ਸਾਰਾ ਸੰਸਾਰ ਸਿਫ਼ਤਾਂ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ :
(i) ਕਵੀ ਕਹਿੰਦਾ ਹੈ ਕਿ ਸਾਨੂੰ ਸਭ ਨੂੰ ਰਲ਼ ਕੇ ਆਪਣੇ ਦੇਸ਼ ਦੇ ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਤਿਰੰਗੇ ਦੀ ਮਹਿਮਾ ਦੇ ਗੀਤ ਗਾਉਂਦੇ ਰਹਿਣਾ ਚਾਹੀਦਾ ਹੈ ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਭਾਰਤ ਮਾਂ ਦੀ ਸ਼ਾਨ ਨੂੰ ਵਧਾਉਣਾ ਚਾਹੀਦਾ ਹੈ । ਸਾਰਾ ਸੰਸਾਰ ਸਾਡੇ ਦੇਸ਼ ਦੀ ਸੁੰਦਰਤਾ ਤੇ ਬਰਕਤਾਂ ਦੀਆਂ ਸਿਫ਼ਤਾਂ ਕਰਦਾ ਹੈ । ਇਸੇ ਕਰਕੇ ਸਾਨੂੰ ਸਾਡਾ ਰਾਸ਼ਟਰੀ ਝੰਡਾ ਤਿਰੰਗਾ ਬਹੁਤ ਪਿਆਰਾ ਲਗਦਾ ਹੈ ।
(ii) ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਤਿਰੰਗੇ ਦੇ ।
(iii) ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਤਿਰੰਗੇ ਦੇ ਗੀਤ ਗਾਉਣ ਨਾਲ ।
(iv) ਸਾਡੇ ਰਾਸ਼ਟਰੀ ਝੰਡੇ ਤਿਰੰਗੇ ਦੀਆਂ ।

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 8 Comparing Quantities InText Questions and Answers.

PSEB 8th Class Maths Solutions Chapter 8 Comparing Quantities InText Questions

Try These (Textbook Page No. 119)

In a primary school, the parents were asked about the number of hours they spend per day in helping their children to do homework. There were 90 parents who helped for \(\frac {1}{2}\) hour to 1\(\frac {1}{2}\) hours. The distribution of parents according to the time for which, they said they helped is given in the figure;
20 % helped for more than 1\(\frac {1}{2}\) hours per day;
30 % helped for \(\frac {1}{2}\) hour to 1\(\frac {1}{2}\) hours;
50 % did not help at all.

Using this, answer the following:

Question (i).
How many parents were surveyed ?
Solution:
90 parents helped their children for \(\frac {1}{2}\) h to 1\(\frac {1}{2}\) h.
Given, percentage in pie chart = 30 %
Let x parents be surveyed.
30 % of x helped for \(\frac {1}{2}\) h to 1\(\frac {1}{2}\) h = 90
∴ 30 % of x = 90
∴ \(\frac {30}{100}\) × x = 90
∴ x = \(\frac{90 \times 100}{30}\)
∴ x = 300
Thus, 300 parents were surveyed.

Question (ii).
How many said that they did not help ?
Solution:
50% parents did not help.
So the number of parents who did not help :
= 50 % of 300
= \(\frac {1}{2}\) × 300
= 50 × 3
= 150
Thus, 150 parents did not help.

Question (iii).
How many said that they helped for more than 1\(\frac {1}{2}\) hours ?
Solution:
20% parents helped for more than 1\(\frac {1}{2}\)h.
So the number of parents who helped for more than 1 \(\frac {1}{2}\) h
= 20% of 300
= \(\frac {20}{100}\) × 300
= 20 × 3
= 60
Thus, 60 parents helped for more than 1\(\frac {1}{2}\) h.

Try These (Textbook Page No. 121)

1. A shop gives 20% discount. What would the sale price of each of these be?

Question (a).
A dress marked at ₹ 120
Solution:
Marked price of the dress = ₹ 120
Discount offered = 20 % )
∴ Discount = 20% of MP
= \(\frac {20}{100}\) × 120 = ₹ 24
∴ Sale price of the dress = MP – Discount
= ₹ (120 – 24)
= ₹ 96
Thus, sale price of the dress is ₹ 96.

Question (b).
A pair of shoes marked at ₹ 750
Solution:
Marked price of the pair of shoes = ₹ 750
Discount offered = 20 %
∴ Discount = 20 % of MP
= \(\frac {20}{100}\) × 750 = ₹ 150
∴ Sale price of the pair of shoes
= MP – Discount s
= ₹ (750 – 150) = ₹ 600
Thus, sale price of the pair of shoes is ₹ 600.

Question (c).
A bag marked at ₹ 250
Solution:
Marked price of the bag = ₹ 250
Discount offered = 20 %
∴ Discount = 20 % of MP
= \(\frac {20}{100}\) × 250 = ₹ 50
∴ Sale price of the bag = MP – Discount
= ₹ (250 – 50)
= ₹ 200
Thus, sale price of the bag is ₹ 200.

2. A table marked at ₹ 15,000 is available for ₹ 14,400. Find the discount given and the discount per cent.
Solution:
Marked price of the table = ₹ 15,000
Sale price of the table = ₹ 14,400
Discount = MP – SP
= ₹ (15000 – 14400)
= ₹ 600
Discount per cent = \(\frac{\text { Discount }}{\text { MP }}\) × 100
= \(\frac{600}{15000}\) × 100
= \(\frac {60}{15}\)
= 4 %
Thus, the discount = ₹ 600 and discount per cent = 4%.

3. An almirah is sold at ₹ 5225 after allowing a discount of 5%. Find its marked price.
Solution:
Sale price of the almirah = ₹ 5225
Discount per cent = 5 %
Let marked price of the almirah be ₹ x.
∴ Discount = 5 % of x
= \(\frac {5}{100}\) × x
= \(\frac{5 x}{100}\)
Sale price = MP – Discount
= x – \(\frac{5 x}{100}\)
=\(\frac{100 x-5 x}{100}\)
= \(\frac{95 x}{100}\)
Sale price of the almirah = ₹ 5225 (Given)
∴ \(\frac{95 x}{100}\) = 5225
∴ x = \(\frac{5225 \times 100}{95}\)
= 5500
Thus, the marked price of the almirah is ₹ 5500.

Try These (Textbook Page No. 123)

1. Find selling price (SP) if a profit of 5 % is made on:

Question (a).
A cycle of ₹ 700 with ₹ 50 as overhead charges.
Solution:
Cost price of the cycle = ₹ 700
Overhead charges = ₹ 50
Total cost price = Cost price + Overhead charges
= ₹ (700 + 50)
= ₹ 750
Profit per cent = 5 %
Profit amount = 5% of total cost of the cycle
= ₹ \(\left(\frac{5}{100} \times 750\right)\)
= ₹ \(\frac{3750}{100}\)
= ₹ 37.50
∴ Selling price of the cycle = Total cost of the cycle + Profit
= ₹ (750 + 37.50)
= ₹ 787.50
Thus, the selling price of the cycle is ₹ 787.50.

Question (b).
A lawn mower bought at ₹ 1150 with ₹ 50 as transportation charges.
Solution:
Cost price of the lawn mower = ₹ 1150
Transportation (overhead) charges = ₹ 50
Total cost price = Cost price + Overhead charges
= ₹ (1150 + 50)
= ₹ 1200
Profit per cent = 5 %
Profit amount = 5 % of total cost price of the lawn mower
= \(\frac {5}{100}\) × 1200
= ₹ \(\left(\frac{5}{100} \times 1200\right)\)
= ₹ 60
∴ Selling price of the lawn mower = Total cost price of the lawn mower + Profit
= ₹ (1200 + 60)
= ₹ 1260
Thus, the selling price of the lawn mower is ₹ 1260.

Question (c).
A fan bought for ₹ 560 and expenses of ₹ 40 made on its repairs.
Solution:
Cost price of the fan = ₹ 560
Repair (overhead) charges = ₹ 40
Total cost price = Cost price + Overhead charges
= ₹ (560 + 40)
= ₹ 600
Profit per cent = 5 %
Profit amount = 5% of total cost of the fan
= ₹ \(\left(\frac{5}{100} \times 600\right)\)
= ₹ 30
∴ Selling price of the fan = Total cost price of the fan + Profit
= ₹ (600 + 30)
= ₹ 630
Thus, the selling price of the fan is ₹ 630.

Try These (Textbook Page No. 123)

1. A shopkeeper bought two TV sets at ₹ 10,000 each. He sold one at a profit of 10% and the other at a loss of 10%. Find whether he made an overall profit or loss.
Solution:
Cost price of each TV set = ₹ 10,000
Cost price of two TV sets = 2 × ₹ 10000
= ₹ 20,000
For TV set sold at a profit:
Profit per cent =10% |
∴ Profit amount =10% of a cost price
= \(\left(\frac{10}{100} \times 10000\right)\)
= ₹ 1000
Selling price = Cost price + Profit
= ₹ (10000 + 1000)
= ₹ 11,000

For TV set sold at a loss:
Loss per cent = 10%
∴ Loss amount = 10% of a cost price
= \(\left(\frac{10}{100} \times 10000\right)\)
= ₹ 1000
Selling price = Cost price – Loss
= ₹ (10000 – 1000)
= ₹ 9000
Total selling price of 2 TV sets
= ₹ (11000 + 9000)
= ₹ 20,000
∴ Cost price of 2 TV sets = Selling price of 2 TV sets
Thus, there is neither profit nor loss.

Think, Discuss and Write (Textbook Page No. 125)

1. Two times a number is a 100% increase in the number. If we take half the number what would be the decrease in per cent?
Solution:
Let the number be x
∴ Half the number = \(\frac{x}{2}\)
Now, decrease in number = x – \(\frac{x}{2}\)
= \(\frac{2 x-x}{2}\)
= \(\frac{x}{2}\)
Decrease per cent = \(\left(\frac{\text { Decrease }}{\text { Original value }} \times 100\right) \%\)
= \(\left(\frac{\frac{x}{2}}{x} \times 100\right) \%\)
= \(\left(\frac{x}{2} \div \frac{x}{1} \times 100\right) \%\)
= \(\left(\frac{x}{2} \times \frac{1}{x} \times 100\right) \%\)
= 50%
Thus, 50% would be the decrease in number, if we take half the number.

2. By what per cent is ₹ 2000 less than ₹ 2400? Is it the same as the per cent by which ₹ 2400 is more than ₹ 2000?
Solution:
(a) ₹ (2400 – 2000) = ₹ 400
i.e., ₹ 2000 is less than ₹ 2400 by ₹ 400.
∴ Percentage decrease = \(\left(\frac{\text { Decrease in value }}{\text { Original value }} \times 100\right) \%\)
= \(\left(\frac{400}{2400} \times 100\right) \%\)
= \(\left(\frac{400}{24}\right) \%\)
= 6\(\frac {1}{2}\)%
Thus, percentage decrease is 16\(\frac {2}{3}\)%%

(b) ₹ (2400 – 2000) = ₹ 400
i.e., ₹ 2400 is more than ₹ 2000 by ₹ 400.
∴ Percentage increase = \(\left(\frac{\text { Increase in value }}{\text { Original value }} \times 100\right) \%\)
= \(\left(\frac{400}{2000} \times 100\right) \%\)
= (4 × 5) %
= 20%
∴ Percentage increase is 20 %.
Thus, percentage increase and percentage decrease are not the same.

Try These (Textbook Page No. 126)

Find interest and amount to be paid on f 15,000 at 5% per annum after 2 years.
Solution:
Here, P = ₹ 15,000; R = 5%, T = 2 years
SI = \(\frac{P \times R \times T}{100}\)
= \(\frac{15000 \times 5 \times 2}{100}\)
= ₹ 1500
Amount = Principal + Interest
= ₹ (15000 + 1500)
= ₹ 16,500
OR
∴ interest on ₹ 15,000 for 1 year
= ₹ \(\frac {15000}{100}\) × 5
= ₹ 750
∴ interest on ₹ 15,000 for 2 years
= ₹ 750 × 2
= 1500
Amount = Principal + Interest
= ₹ (15000 + 1500)
= ₹ 16500
Thus, interest ₹ 1500 and amount ₹ 16,500.

Try These (Textbook Page No. 129)

1. Find CI on a sum of ₹ 8000 for 2 years at 5% per annum compounded annually.
Solution:
Here, P = ₹ 8000, R = 5 %, n = 2 years
A = P\(\left(1+\frac{\mathrm{R}}{100}\right)^{n}\)
= 8000\(\left(1+\frac{5}{100}\right)^{2}\)
= 8000\(\left(\frac{100+5}{100}\right)^{2}\)
= 8000\(\left(\frac{105}{100}\right)^{2}\)
= 8000 × \(\frac {21}{20}\) × \(\frac {21}{20}\) = 8820
Thus, amount = ₹ 8820
Compound interest = Amount – Interest
= ₹ (8820 – 8000)
= ₹ 820
Thus, compound interest = ₹ 820

Try These (Textbook Page No. 130)

Find the time period and rate for each:

1. A sum taken for 1\(\frac {1}{2}\) years at 8% per annum is compounded half yearly.
Solution:
[Note : If interest is compounded half yearly, then the rate of interest (R) will be half i.e., \(\frac{\mathrm{R}}{2}\)% and time (n) will be double i.e., 2n years.]
n (time period) = 1\(\frac {1}{2}\) years
= \(\frac {3}{2}\) years
For half yearly, time period = \(\frac {3}{2}\) × 2 = 3
R (rate of interest) = 8%
For half yearly, rate of interest = \(\frac {8}{2}\)% = 4%
Thus, here n = 3 and R = 4%

2. A sum taken for 2 years at 4% per annum compounded half yearly.
Solution:
n (time period) = 2 years
For half yearly period = 2 × 2 = 4
R (rate of interest) = 4%
For half yearly, rate of interest = \(\frac {2}{2}\) % = 2 %

Think, Discuss and Write (Textbook Page No. 130)

A sum is taken for one year at 16% p.a. If interest is compounded after every three months, how many times will interest be charged in one year?
Solution:
Here, the interest is compounded after every three months (quarterly).
For quarterly,
R = 16% p.a.
= \(\frac {16}{4}\)% = 4%.
n = 1 year
= 1 × 4
= 4
Thus, interest will be charged 4 times in one year.

Try These (Textbook Page No. 131)

Find the amount to be paid:

1. At the end of 2 years on ₹ 2400 at 5 % per annum compounded annually.
Solution:
Here, P = ₹ 2400, n = 2 years, R = 5%

Thus, amount to be paid = ₹ 2646

2. At the end of 1 year on ₹ 1800 at 8% per annum compounded quarterly.
Solution:
Here, the interest is compounded quarterly.
P = ₹ 1800, R = \(\frac {8}{4}\) = 2 %, T = 1 year
n = 4 × 1 = 4

Thus, amount to be paid = ₹ 1948.38

Try These (Textbook Page No. 133)

1. A machinery worth ₹ 10,500 depreciated by 5%. Find its value after one year.
Solution:
Here, P = ₹ 10,500; R = – 5 %; T = 1 year
∴ n = 1
A = \(\mathrm{P}\left(1-\frac{\mathrm{R}}{100}\right)^{n}\)
(∵ R = -5 – means depreceation)
∴ A = 10500\(\left(1-\frac{5}{100}\right)^{1}\)
∴ A = 10500\(\left(\frac{100-5}{100}\right)\)
= 10500 × \(\frac {95}{100}\)
= 9975
Thus, the valu of a machinery after one year will be ₹ 9975.

2. Find the population of a city after 2 years, which is at present 12 lakh, if the rate of increase is 4%.
Solution:
Here, P = 12,00,000; Rate of increase R = 4 %; T = 2 years; n = 2
Population after 2 years = \(\mathrm{P}\left(1+\frac{\mathrm{R}}{100}\right)^{n}\)
= 120000\(\left(1+\frac{4}{100}\right)^{2}\)
= 120000\(\left(\frac{100+4}{100}\right)^{2}\)
= 120000\(\left(\frac{104}{100}\right)^{2}\)
= 1200000 x \(\frac {104}{100}\) × \(\frac {104}{100}\)
= 120 × 104 × 104
= 12,97,920
Thus, the population of a city after 2 years will be 12,97,920.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 8 Comparing Quantities Ex 8.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.3

1. Calculate the amount and compound interest on:

Question (a)
₹ 10,800 for 3 years at 12\(\frac {1}{2}\) per annum compounded annually.
Solution:
Here, P = ₹ 10,800;
R = 12\(\frac {1}{2}\) % = \(\frac {25}{2}\) %;
T = 3 years; ∴ n = 3

Amount = ₹ 15,377.34
Compound’interest = Amount – Principal
= ₹ (15377.34 – 10800)
= ₹ 4577.34

Question (b)
₹ 18,000 for 2\(\frac {1}{2}\) years at 10% per annum compounded annually.
Solution:
Here, P = ₹ 18,000; R = 10 %;
T = 2\(\frac {1}{2}\) years; ∴ n = 2 + \(\frac {1}{2}\)

Amount = ₹ 22,869
Compoimd interest = Amount – Principal
= ₹ (22869 – 18000)
= ₹ 4869

Question (c)
₹ 62,500 for 1\(\frac {1}{2}\) years at 8% per annum compounded half yearly.
Solution:
Here, the interest is compounded half-yearly.
Here, P = ₹ 62,500; R = \(\frac {8}{2}\) = 4 %
T = 1\(\frac {1}{2}\) years ∴ n = \(\frac {3}{2}\) × 2 = 3

Amount = ₹ 70,304
Compound interest = Amount – Principal
= ₹ (70304 – 62500)
= ₹ 7804

Question (d)
₹ 8000 for 1 year at 9 % per annum compounded half-yearly.
(You could use the year-by-year calculation using SI formula to verify.)
Solution:
Here, the interest is compounded half-yearly.
Here, P = ₹ 8000; R = \(\frac {9}{2}\) %;
T = 1 year ∴ n = 2

Amount = ₹ 8736.20
Compound interest = Amount – Principal
= ₹ (8736.20 – 8000)
= ₹ 736.20
[Note : By finding simple interest also we can calculate.)
SI = \(\frac {PRT}{100}\)
= \(\frac{8000 \times 9 \times 1}{2 \times 100}\)
= ₹ 376.20
Thus, total interest of 1 year
= ₹ (360 + 376.20)
= ₹ 736.20

Question (e)
₹ 10,000 for 1 year 8% per annum compounded half yearly.
Solution:
Here, the interest is compounded half-yearly.
Here, P = ₹ 10,000; R = \(\frac {8}{2}\) = 4 %;
T = 1 year ∴ n = 1 × 2 = 2

Amount = ₹ 10,816
Compound interest = Amount – Principal
= ₹ (10816 – 10000)
= ₹ 816

2. Kamala borrowed ₹ 26,400 from a Bank to buy a scooter at a rate of 15% p.a. compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan?
(Hint: Find A for 2 years with interest is compounded yearly and then find SI on the 2nd year amount for \(\frac {4}{12}\) years)
Solution:
[Note: Here, find amount after 2 years by compound interest. This amount is principal for \(\frac {4}{12}\) year. For this \(\frac {4}{12}\) year, find simple interest.)
Here, P = ₹ 26,400; R = 15%;
T = 2 years ∴ n = 2

Now, ₹ 34,914 will be principal to find interest of 4 months.
SI = \(\frac {PRT}{100}\)
= \(\frac{34914 \times 15 \times 4}{100 \times 12}\)
= \(\frac{174570}{100}\)
= ₹ 174570
= ₹ 1745.70
Amount = ₹ (34914 + 1745.70)
= ₹ 36,659.70
Thus, Kamala Mil have to pay ₹ 36,659.70 to clear the loan.

3. Fabina borrows ₹ 12,500 at 12% per annum for 3 years at simple interest and Radha borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest and by how much?
Solution:
For Fabina:
Here, P = ₹ 12,500; R = 12%; T = 3 years
SI = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{12500 \times 12 \times 3}{100}\)
= 125 × 12 × 3
= ₹ 4500
Simple interest = ₹ 4500

For Radha:
Here, P = ₹ 12,500; R = 10%;
T = 3 years ∴ n = 3


Amount = ₹ 16,637.50
Compound interest = Amount – Principal
= ₹ (16637.50 – 12500)
= ₹ 4137.50
Fabina has to pay ₹ 4500 as interest and Radha has to pay ₹ 4137.50 as interest.
∴ Fabina has to pay more interest.
Difference in interest = ₹ (4500 – 4137.50)
= ₹ 362.50
Thus, Fabina has to pay ₹ 362.50 more than Radha as interest.

4. I borrowed ₹ 12,000 from Jamshed at 6 % per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest, what extra amount would I have to pay?
Solution:
For Simple Interest:
Here, P = ₹ 12,000; R = 6 %; T = 2 years
SI = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{12000 \times 6 \times 2}{100}\)
= 120 × 6 × 2
= ₹ 1440
SI = ₹ 1440

For Compound Interest:
Here, P = ₹ 12,000, R = 6 %
T = 2 years ∴ n = 2

= ₹ 13,483.20
Amount = ₹ 13,483.20
CI = A – P
= ₹ (13483.20 – 12000)
= ₹ 1483.20
∴ Extra amount to be paid
= ₹ (1483.20 – 1440)
= ₹ 43.20
Thus, I have to pay ₹ 43.20 as extra amount.

5. Vasudevan invested ₹ 60,000 at an interest rate of 12% per annum compounded half-yearly. What amount would he get.

Question (i)
after 6 months?
Solution:
Interest after 6 months:
Here, P = ₹ 60,000; R = \(\frac {12}{2}\) = 6%;
T = 6 months ∴ n = 1

∴ Amount = ₹ 63,600

Question (ii)
after 1 year?
Solution:
After 1 year:
∴ Amount = ₹ 67,416
Here, P = ₹ 60,000; R = \(\frac {12}{2}\) = 6 %;
T = 1 year ∴ n = 2

∴ Amount = ₹ 67, 146
Thus, Vasudevan will get ₹ 63,600 after 6 months and ₹ 67,416 after 1 year.

6. Arif took a loan of ₹ 80,000 from a bank. If the rate of interest is 10% per annum, find the difference in amounts he would be paying after 1\(\frac {1}{2}\) years if the interest is

Question (i)
compounded annually.
Solution:
Calculation of CI annually:
Here, P = ₹ 80,000; R = 10 %;
T = 1\(\frac {1}{2}\) year

For 1st year:
R = 10% and n = 1

∴ Amount of CI after 1 year = ₹ 88,000
Now, calculate simple interest of ₹ 88,000 for 6 months.
P = ₹ 88,000; R = 10 %;
T = 6 months = \(\frac {1}{2}\) year
∴ Interest = \(\frac{P \times R \times T}{100}\)
= \(\frac{88000 \times 10 \times 1}{100 \times 2}\)
= 4400
∴ Interest of 6 months = ₹ 4400
Thus, A = P + I
= ₹ (88000 + 4400)
= ₹ 92,400
Thus, according to CI, Arif has to pay ₹ 92,400

Question (ii)
compounded half yearly.
Solution:
If interest is compounded half yearly
Here, P = ₹ 88000, R = \(\frac {10}{2}\) = 5%
T = 1\(\frac {1}{2}\) years ∴ n = 3

∴ Amount = ₹ 92,610
Thus, according to half-yearly CI, Arif has to pay ₹ 92,610
∴ Difference = ₹ (92,610 – 92,400)
= ₹ 210

7. Maria invested ₹ 8,000 in a business. She would be paid interest at 5% per annum compounded annually. Find

Question (i)
The amount credited against her name at the end of the second year,
Solution:
(i) Here, P = ₹ 8000, R = 5 %,
T = 2 years ∴ n = 2


Thus, amount credited against Marlas name at the end of second year is ₹ 8820.

Question (ii)
The interest for the 3rd year.
Solution:
To find the interest for the 3rd year:
P = ₹ 8820, R = 5%, T = 1 years
SI = \(\frac{\mathrm{PRT}}{100}=\frac{8820 \times 5 \times 1}{100}\) = 441
The interest for 3rd year is ₹ 441
OR
The interest for the 3rd year:
Here, P = ₹ 8000, R = 5 %, T = 3 years ∴ n = 3

∴ At the end of 3rd year ₹ 9261 will be credited against Maria’s name.
∴ Interest of the 3rd year = Amount of 3 years – Amount of 2 years
= ₹ (9261 – 8820)
= ₹ 441

8. Find the amount and the compound interest on ₹ 10,000 for 1\(\frac {1}{2}\) years at 10% per annum, compounded half-yearly. Would this interest be more than the interest he would get if it was compounded annually?
Solution:
(i) Here, interest is compounded half-yearly.
Here, P = ₹ 10,000; R = \(\frac {10}{2}\) = 5 %;
T = 1\(\frac {1}{2}\) years ∴ n = 3

Amount = ₹ 11,576.25
CI = A – P
= ₹ (11576.25 – 10000)
= ₹ 1576.25

(ii) Here, interest is compounded yearly. CI for 1 year:
Here, P = ₹ 10,000; R = 10%;
T = 1 year ∴ n = 1

Amount at the end of 1 year = ₹ 11,000
∴ CI = A – P
= ₹ (11000 – 10000)
= ₹ 1000
Now, calculate SI for 6 months.
Here, P = ₹ 11,000; R = 10%; T = \(\frac {1}{2}\) year
SI = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}=\frac{11000 \times 10 \times 1}{100 \times 2}\)
= 550
∴ Total interest of 1\(\frac {1}{2}\) years = ₹ (1000 + 550)
= ₹ 1550
After comparing (i) and (ii), we can conclude ₹ 1576.25 > ₹ 1550
∴ Yes, the interest is more if compounded half-yearly.

9. Find the amount which Ram will get on ₹ 4096, if he gave it for 18 months at 12\(\frac {1}{2}\) % per annum, interest being compounded half-yearly.
Solution:
Here, interest is compounded half-yearly.
Here, P = ₹ 4096, R = 12\(\frac{1}{2} \times \frac{1}{2}=\frac{25}{4}\)
T = 18 months = 1\(\frac {1}{2}\) years ∴ n = 3

Amount = ₹ 4913
Thus, Ram will get ₹ 4913 at the end of period.

10. The population of a place increased to 54,000 in 2003 at a rate of 5% per annum

Question (i)
find the population in 2001.
Solution:
[Note: In 1st case, we have to find P as population of 2003 is given. From that we have to find population of 2001.]
Population in 2003 = 54,000
Here, A = 54,000; R = 5%; T = 2 years ∴ n = 2

∴ P = 48979.59 (approx)
P = 48980 (approx)
Thus, the population in 2001 is 48,980.

Question (ii)
What would be its population in 2005?
Solution:
Here, P = 54,000; R = 5 %;
T = 2 years ∴ n = 2

Thus, the population in 2005 is 59,535.

11. In a Laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5,06,000.
Solution:
Initial count of bacteria = 5,06,000
Rate of increasing = 2.5% per hour
Bacteria count after 2 hours
Here, P = 5,06,000, R = 2.5 % = \(\frac {5}{2}\)%;
T = 2 hours ∴ n = 2

A = 531616 (approx)
Thus, the number of bacteria count after 2 hours will be 5,31,616 (approx).

12. A scooter was bought at ₹ 42,000. Its value depreciated at the rate of 8 % per annum. Find its value after one year.
Solution:
CP of a scooter = ₹ 42,000
Here, P = ₹ 42,000; R = 8 %; T = 1 ∴ n = 1
R = – 8 % (as depreciation)

Thus, the value of a scooter after 1 year will be ₹ 38,640.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 8 Comparing Quantities Ex 8.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.2

1. A man got a 10% increase in his salary. If his new salary is ₹ 1,54,000, find his original salary.
Solution:
Let the original salary be ₹ 100.
After 10% increase, the new salary = ₹ (100 + 10)
= ₹ 110
If his new salary is ₹ 110,
then the original salary = ₹ 100
If new salary is ₹ 1,54,000,
then original salary = (\(\frac {100}{110}\) × 1,54,000)
= 100 × 1400
= ₹ 140000
Thus, his original salary was ₹ 1,40,000.

2. On Sunday 845 people went to the Zoo. On Monday only 169 people went. What is the per cent decrease in the people visiting the Zoo on Monday?
Solution:
Number of people went to the zoo on Sunday = 845
Number of people went to the zoo on Monday = 169
∴ Decrease in the number of people visiting the zoo on Monday = (845 – 169) = 676
Percentage decrease = \(\left(\frac{\text { Decrease }}{\text { Original number }} \times 100\right) \%\)
= (\(\frac {676}{845}\) × 100) %
= 80 %
Thus, 80% decrease in the number of people visiting the zoo on Monday.

3. A shopkeeper buys 80 articles for ₹ 2400 and sells them for a profit of 16%. Find the selling price of one article.
Solution:
Cost price of 80 articles = ₹ 2400
∴ Cost price of 1 article = ₹ \(\frac {2400}{80}\) = ₹ 30
Profit = 16%
∴ Profit on 1 article = ₹ \(\left(\frac{16}{100} \times 30\right)\)
= ₹ 4.80
∴ Selling price of 1 article
= Cost price + Profit
= ₹ 30 + ₹ 4.80
= ₹ 34.80
Thus, selling price of one article is ₹ 34.80.

4. The cost of an article was ₹ 15,500. ₹ 450 were spent on its repairs. If it is sold for a profit of 15%, find the selling price of the article.
Solution:
Cost price of an article = ₹ 15,500
Repair charge (overhead charge) = ₹ 450
∴ Total cost price = Cost price of an article + Overhead expenses
= ₹ (15500 + 450) = ₹ 15,950
Profit per cent = 15%
Amount of profit = 15% of ₹ 15,950
= ₹ \(\left(\frac{15}{100} \times 15950\right)\)
= ₹ \(\left(\frac{23925}{10}\right)\)
= ₹ 2392.50
∴ Selling price = Total cost + Profit
= ₹ (15950 + 2392.50)
= ₹ 18342.50
Thus, the selling price of an article is ₹ 18,342.50.

5. A VCR and TV were bought for ₹ 8000 each. The shopkeeper made a loss of 4% on the VCR and a profit of 8% on the TV. Find the gain or loss per cent on the whole transaction.
Solution:
(i) Cost price of a VCR = ₹ 8000,
Loss per cent = 4 %
∴ Loss amount = 4% of cost
= ₹ \(\left(\frac{4}{100} \times 8000\right)\)
= ₹ (4 × 80)
= ₹ 320
∴ Selling price = Cost price – Loss
= ₹ (8000 – 320)
= ₹ 7680

(ii) Cost price of a TV = ₹ 8000
Profit per cent = 8%
∴ Profit amount = 8 % of cost
= ₹ \(\left(\frac{8}{100} \times 8000\right)\)
= ₹ (8 × 80)
= ₹ 640
∴ Selling price = Cost price + Profit
= ₹ (8000 + 640)
= ₹ 8640
Total cost price of a VCR and TV = ₹ (8000 + 8000)
= ₹ 16,000
Total selling price of a VCR and TV = ₹ (7680 + 8640)
= ₹ 16,320
SP > CR
∴ profit = SP – CP
= ₹ (16,320 – 16,000)
= ₹ 320
∴ Profit per cent = \(\left(\frac{\text { Profit }}{\text { Cost price }} \times 100\right) \%\)
= \(\left(\frac{320}{16000} \times 100\right) \%\)
= 2%
Thus, there is 2% profit on the whole transaction.

6. During a sale, a shop offered a discount of 10% on the marked prices of all the items. What would a customer have to pay for a pair of jeans marked at ₹ 1450 and two shirts marked at ₹ 850 each ?
Solution:
MP of a pair of jeans = ₹ 1450
MP of one shirt = ₹ 850
∴ MP of two shirts = ₹ (2 × 850)
= ₹ 1700
∴ Total MP of three items = ₹ (1450 + 1700)
= ₹ 3150
Discount per cent = 10%
∴ Amount of discount = 10% of total cost
= ₹ \(\left(\frac{10}{100} \times 3150\right)\)
= ₹ 315
Bill amount = MP – Discount
= ₹ (3150 – 315)
= ₹ 2835
Thus, customer would have to pay ₹ 2835 for a pair of jeans and two shirts.

7. A milkman sold two of his buffaloes for ₹ 20,000 each. On one he made a gain of 5 % and on the other a loss of 10%. Find his overall gain or loss. (Hint: Find CP of each)
Solution:
Let CP of 1st buffalo be ₹ x
Gain (Profit) per cent = 5%
Amount of profit = 5 % of CP
= ₹ \(\left(\frac{5}{100} \times x\right)\)
= ₹ \(\frac{5 x}{100}\)
∴ SP = CP + Profit
= ₹ \(\left(x+\frac{5 x}{100}\right)\)
= ₹ \(\left(\frac{100 x+5 x}{100}\right)\)
= ₹ \(\frac{105 x}{100}\)
But, SP of a buffalo = ₹ 20,000 (Given)
∴ \(\frac{105 x}{100}\) = ₹ 20,000
∴ x = ₹ \(\left(\frac{20000 \times 100}{105}\right)\)
= ₹ 19047.62

Let the cost price of 2nd buffalo = ₹ y
Loss per cent = 10%
Amount of loss = 10% of CP
= ₹ \(\left(\frac{10}{100} \times y\right)\)
= ₹ \(\frac{10 y}{100}\)
SP = CP – Loss
= ₹ \(\left(y-\frac{10 y}{100}\right)\)
= ₹ \(\left(\frac{100 y-10 y}{100}\right)\)
= ₹ \(\frac{90 y}{100}\)
But SP of a buffalo = ₹ 20,000 (Given)
∴ \(\frac{90 y}{100}\) = ₹ 20,000
∴ y = ₹ \(\left(\frac{20000 \times 100}{90}\right)\)
= ₹ 22222.22

Total CP of both buffaloes = ₹ (x + y)
= ₹ (19047.62 + 22222.22)
= ₹ 41,269.84

Total SP of both buffaloes = ₹ (20000 + 20000)
= ₹ 40,000
∴ SP < CP
Amount of loss = CP – SP
= ₹ (41269.84 – 40000)
= ₹ 1269.84
Thus, there is overall loss of ₹ 1269.84.

8. The price of a TV is ₹ 13,000. The GST charged on it is at the rate of 12%. Find the amount that Vinod will have to pay if he buys it.
Solution:
Price of a TV = ₹ 13,000
GST per cent = 12%
∴ Amount of GST = 12% of price
= ₹ \(\left(\frac{12}{100} \times 13,000\right)\)
= ₹ 1560
∴ Total amount = Price of a TV + GST
= ₹ (13,000 + 1560)
= ₹ 14,560
Thus, Vinod will have to pay ₹ 14,560.

9. Aran bought a pair of skates at a sale where the discount given was 20%. If the amount he pays is ₹ 1600, find the marked price.
Solution:
Let the MP of a pair of skates be ₹ x.
Discount per cent = 20%
∴ Amount of discount = 20% of MP
= ₹ \(\left(\frac{20}{100} \times x\right)\)
= ₹ \(\frac{20 x}{100}\)
∴ Selling price = MP – Discount
= ₹ \(\left(x-\frac{20 x}{100}\right)\)
= ₹ \(\left(\frac{100 x-20 x}{100}\right)\)
= ₹ \(\frac{80 x}{100}\)
= ₹ \(\frac{4}{5} x\)
But, SP of a pair of skates = ₹ 1600 (Given).
∴ \(\frac{4}{5} x\) = 1600
∴ x = ₹ \(\left(\frac{1600 \times 5}{4}\right)\)
∴ x = ₹ 2000
Thus, the marked price of a pair of skates is ₹ 2000.

10. I purchased a hair dryer for ₹ 5400 including 18% GST. Find the price before GST was added.
Solution:
Cost price of hair dryer with GST = ₹ 5400
GST per cent = 18%
Let the price of a hair dryer before GST ) was added be ₹ x.
∴ Amount of GST = 18% of x
= ₹ \(\left(\frac{18}{100} \times x\right)\)
= ₹ \(\frac{18 x}{100}\)
∴ Price after adding GST = ₹ \(\left(x+\frac{18}{100} x\right)\)
= ₹ \(\left(\frac{100 x+18 x}{100}\right)\)
= ₹ \(\frac{118 x}{100}\)
But, price after adding GST = ₹ 5400 (Given)
∴ \(\frac{118 x}{100}\) = 5400
∴ x = ₹ \(\left(\frac{5400 \times 100}{118}\right)\)
= ₹ 4576.27
Thus, the price of a hair dryer before adding GST is ₹ 4576.27.

11. An article was purchased for ₹ 1239 including GST of 18%. Find the price of the article before GST was added.
Solution:
Such type of sums can be done by two methods.
One method:
Let the price of an article before adding GST be ₹ 100.
GST = 18%
∴ price including GST = ₹ (100 + 18)
= ₹ 118
If price including GST is ₹ 118,
then price before adding GST = ₹ 100
∴ if price including GST is ₹ 1239,
then price before adding GST = ₹ \(\left(\frac{1239}{118} \times 100\right)\)
= ₹ 1050
Thus, the price of an article before adding GST was ₹ 1050.

Another method:
Let the price of an article before adding GST be ₹ x.
GST = 18%
Amount of GST = 18% of ₹ x
= ₹ \(\left(\frac{18}{100} \times x\right)\)
= ₹ \(\frac{18 x}{100}\)
Price after adding GST = ₹ \(\left(x+\frac{18 x}{100}\right)\)
= ₹ \(\left(\frac{118 x}{100}\right)\)
But, the price of an article = ₹ 1239 (Given)
∴ \(\frac{118 x}{100}\) = 1239
∴ x = ₹ \(\left(\frac{1239 \times 100}{118}\right)\)
= ₹ 1050
Thus, the price of an article before adding GST was ₹ 1050.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 9 Algebraic Expressions and Identities InText Questions and Answers.

PSEB 8th Class Maths Solutions Chapter 9 Algebraic Expressions and Identities InText Questions

Try These: [Textbook Page No. 139]

1. Write two terms which are like:

Question (i)
7xy
Solution:
14xy, 21xy

Question (ii)
4mn²
Solution:
8mn² , – 11mn²

Question (iii)
21
Solution:
– 5l, 9l

Try These : [Textbook Page No. 142]

1. Can you think of two more such situations, where we may need to multiply algebraic expressions?
Solution:
1. Aarush purchased x notebooks and y pens. If cost of a notebook and a pen is same ₹ z, what amount has he to pay? → ₹ z (x + y)
2. Shailja wants to spread a carpet in her room having length (l + 5) m and breadth (b – 2) m. Find the area of the carpet. → (l + 5) (b – 2) m²

Try These: [Textbook Page No. 143]

1. Find 4x × 5y × 7z.
Solution:
4x × 5y × 7z = 4 × 5 × 7 × x × y × z
= 140 xyz

2. Find 4x × 5y × 7z. First find (4x × 5y) and multiply it by 7z; or first find (5y × 7z) and multiply it by 4x. Is the result the same? What do you observe? Does the order in which you carry out the multiplication matter?
Solution:
(4x × 5 y) = 4 × 5 × x × y
= 20xy
Now, 20xy × 7z = 20 × 7 × xy × z
= 140xyz … (i)
Also, (5y × 7z) = 5 × 7 × y × z = 35 yz
Now, 35yz × 4x = 35 × 4 × yz × x
= 140xyz … (ii)
Yes, the result is same.
We can conclude that product remains same if we change order of the terms.

3. Complete the table for area of a rectangle with given length and breadth.
Solution:

length	breadth	area
3x	5y	3x × 5y = 15xy
9y	4y2	9y × 4y2 = 36y3
4ab	5bc	4ab × 5be = 20ab2c
2l2m	3lm2	2l2m × 3lm2 = 6l3m3

Try These : [Textbook Page No. 144]

1. Find the product:

Question (i)
2x (3x + 5xy)
Solution:
= (2x × 3x) + (2x × 5xy)
= 6x² + 10x²y

Question (ii)
a² (2ab – 5c)
Solution:
= (a² × 2ab) – (a² × 5c)
= 2a³b – 5a²c

Try These: [Textbook Page No. 145]

1. Find the product: (4p² + 5p + 7) × 3p
Solution:
(4p² + 5p + 7) × 3p
= (4p² × 3p) + (5p × 3p) + (7 × 3p)
= 12p³ + 15p² + 21p

Try These : [Textbook Page No. 149]

1. Put -b in place of b in Identity (I). Do you get Identity (II)?
Solution:
Identity (I): (a + b)² = a² + 2ab + b²
Let us put (- b) instead of b [a + (- b)]²
= a² + 2a (- b) + (- b)²
∴ (a – b)²
= a² – 2ab + b²
Identity (II): (a – b)² = a² – 2ab + b²
Yes, we get Identity (II).

Try These : [Textbook Page No. 149]

1. Verify Identity (IV), for a = 2, b = 3, x = 5.
Solution:
Identity (IV):
(x + a) (x + b) = x² + (a + b) x + ab
Substitute a = 2, b = 3 and x = 5
LHS
= (x + a) (x + b)
= (5 + 2) (5 + 3)
= (7)(8)
= 56

RHS
= x² + (a + b) x + ab
= (5)² + (2 + 3) × 5 + (2 × 3)
= 25 + (5) × 5 + (6)
= 25 + 25 + 6 = 56
∴ LHS = RHS
∴ The given identity is true for the given values.

2. Consider, the special case of Identity (IV) with a = b, what do you get ? Is it related to Identity (I)?
Solution:
When a = b (∴ Take y for both)
(x + a) (x + b) = x² + (a + b) x + ab
Substitute a = y and b = y
(x + y)(x + y) = x² + (y + y)x + (y × y)
= x² + (2y) x + (y × y) = x² + 2xy + y²
∴ Yes, it is the same as Identity ( I).

3. Consider, the special case of Identity (IV) with a = -c and b = -c. What do you get ? Is it related to Identity (II) ?
Solution:
Identity (IV):
(x + a)(x + b) = x² + (a + b) x + ab
Substitute (- c) instead of a and (- c) instead of b,
(x – c) (x – c)
= x² + [(-c) + (-c)]x + [(-c) × (-c)]
= x² + [- 2c] x + (c²)
= x² – 2cx + c²
∴ Yes, it is the same as Identity (II).

4. Consider the special case of Identity (IV) with b = – a. What do you get ? Is it related to Identity (III)?
Solution :
Identity (IV):
(x + a) (x + b) = x² + (a + b) x + ab
Substitute (-a) instead of b,
(x + a) (x – a)
= x² + [a + (- a)] x + [a × (- a)]
= x² + (a – a) x + [- a²]
= x² + (0) x – a²
= x² – a²
∴ Yes, it is the same as Identity (III).

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5

1. Use a suitable identity to get each of the following products:

Question (i)
(x + 3) (x + 3)
Solution:
= (x + 3)²
= (x)² + 2(x)(3) + (3)²
[∵ (a + b)² = a² + 2ab + b²]
= x² + 6x + 9

Question (ii)
(2y + 5) (2y + 5)
Solution:
= (2y + 5)²
= (2y)² + 2 (2y)(5) + (5)²
[∵ (a – b)² = a² – 2ab + b²]
= 4y² + 20y + 25

Question (iii)
(2a – 7) (2a – 7)
Solution:
= (2a – 7)²
= (2a)² – 2(2a)(7) + (7)²
[∵ (a – b)² = a² – 2ab + b²]
= 4a² – 28a + 49

Question (iv)
(3a – \(\frac {1}{2}\))(3a – \(\frac {1}{2}\))
Solution:
= (3a – \(\frac {1}{2}\))²
= (3a)² – 2(3a)(\(\frac {1}{2}\)) + (\(\frac {1}{2}\))²
[∵ (a – b)² = a² – 2ab + b²]
= 9a² – 3a + \(\frac {1}{4}\)

Question (v)
(1.1m – 0.4) (1.1m + 0.4)
Solution:
= (1.1m)² – (0.4)²
[∵ (a + b) (a – b) = a² – b²]
= 1.21m² – 0.16

Question (vi)
(a² + b²) (-a² + b²)
Solution:
= (b² + a²) (b² – a²)
= (b²)² – (a²)²
[∵ (a + b) (a – b) = a² – b²]
= b⁴ – a⁴

Question (vii)
(6x – 7) (6x + 7)
Solution:
= (6x)² – (7)²
[∵ (a + b) (a – b) = a² – b²]
= 36x² – 49

Question (viii)
(-a + c) (-a + c)
Solution:
= (-a + c)²
= (-a)² + 2 (-a) (c) + (c)²
[∵ (a + b)² = a² + 2ab + b²]
= a² – 2ac + c²

Question (ix)
(\(\frac{x}{2}+\frac{3 y}{4}\))
Solution:
= (\(\frac{x}{2}+\frac{3 y}{4}\))²
= (\(\frac {x}{2}\))² + 2(\(\frac {x}{2}\))(\(\frac {3y}{4}\)) + (\(\frac {3y}{4}\))²
[∵ (a + b)² = a² + 2ab + b²]
= \(\frac{x^{2}}{4}+\frac{3 x y}{4}+\frac{9 y^{2}}{16}\)

Question (x)
(7a – 9b) (7a – 9b)
Solution:
= (7a – 9b)²
= (7a)² – 2(7a)(9b) + (9b)²
[∵ (a – b)² = a² – 2ab + bsup>2]
= 49a² – 126ab + 81b²

2. Use the identity (x + a) (x + b) = x² + (a + b) x + ab to find the following products:

Question (i)
(x + 3) (x + 7)
Solution:
Identity : (x + a) (x + b) = x² + (a + b) x + ab
= (x)² + (3 + 7)x + (3) (7)
= x² + (10) x + 21
= x² + 10x + 21

Question (ii)
(4x + 5) (4x + 1)
Solution:
= (4x)² + (5 + 1) 4x + (5)(1)
= 16x² + (6) 4x + 5
= 16x² + 24x + 5

Question (iii)
(4x – 5) (4x – 1)
Solution:
= (4x)² + (- 5 – 1) 4x + (- 5) (- 1)
= 16x² + (- 6) 4x + 5
= 16x² – 24x + 5

Question (iv)
(4x + 5) (4x- 1)
Solution:
= (4x)² + (5 – 1) 4x + (5) (- 1)
= 16x² + (4) 4x – 5
= 16x² + 16x – 5

Question (v)
(2x + 5y) (2x + 3y)
Solution:
= (2x)² + (5y + 3y) 2x + (5y) (3y)
= 4x² + (8y) 2x + 15y²
= 4x² + 16xy + 15y²

Question (vi)
(2a² + 9) (2a² + 5)
Solution:
= (2a²)² + (9 + 5) 2a² + (9)(5)
= 4a⁴ + (14)2a² + 45
= 4a⁴ + 28a² + 45

Question (vii)
(xyz – 4) (xyz – 2)
Solution:
= (xyz)² + (- 4 – 2) xyz + (- 4)(- 2)
= x²y²z² + (- 6) xyz + 8
= x²y²z² – 6xyz + 8

3. Find the following squares by using the identities:

Question (i)
(b – 7)²
Solution:
= (b)² – 2 (b)(7) + (7)²
[∵ (a – b)² = a² – 2ab + b²]
= b² – 14 b + 49

Question (ii)
(xy + 3z)²
Solution:
= (xy)² + 2 (xy)(3z) + (3z)²
[∵ (a + b)² = a² + 2ab + b²]
= x²y² + 6xyz + 9z²

Question (iii)
(6x² – 5y)²
Solution:
= (6x²)² – 2 (6x²) (5y) + (5y)²
[∵ (a – b)² = a² – 2ab + b²]
= 36x⁴ – 60x²y + 25y²

Question (iv)
(\(\frac {2}{3}\)m + \(\frac {3}{2}\)n)²
Solution:
= (\(\frac {2}{3}\)m)² + 2(\(\frac {2}{3}\)m)(\(\frac {3}{2}\)n) + (\(\frac {3}{2}\)n)²
[∵ (a + b)² = a² + 2ab + b²]
= \(\frac {4}{9}\)m² + 2mn + \(\frac {9}{4}\)n²

Question (v)
(0.4p – 0.5q)²
Solution:
= (0.4p)² – 2 (0.4p)(0.5q) + (0.5q)²
[∵ (a – b)² = a² – 2ab + b²]
= 0.16p² – 0.4pq + 0.25q²

Question (vi)
(2xy + 5y)²
Solution:
= (2xy)² + 2 (2xy)(5y) + (5y)²
[∵ (a + b)² = a² + 2ab + b²]
= 4x²y² + 20xy² + 25 y²

4. Simplify:

Question (i)
(a² – b²)²
Solution:
= (a²)² – 2(a²)(b²) + (b²)²
= a⁴ – 2a²b² + b⁴

Question (ii)
(2x + 5)² – (2x – 5)²
Solution:
= [(2x)² + 2(2x)(5) + (5)²] – [(2x)² – 2 (2x)(5) + (5)²]
= [4x² + 20x + 25] – [4x² – 20x + 25]
= 4x² + 20x + 25 – 4x² + 20x – 25
= 4x² – 4x² + 20x + 20x + 25 – 25
= 40x

Question (iii)
(7m – 8n)² + (7m + 8n)²
Solution:
= [(7m)² – 2(7m)(8n) + (8n)²] + [(7m)² + 2 (7m)(8n) + (8n)²]
= [49m² – 112mn + 64n²] + [49m² + 112mn + 64n²]
= 49m² – 112mn + 64n² + 49m² + 112mn + 64n²
= 49m² + 49m² – 112mn + 112mn + 64n² + 64n²
= 98m² + 128n²

Question (iv)
(4m + 5n)² + (5m + 4n)²
Solution:
= [(4m)² + 2 (4m)(5n) + (5n)²] + [(5m)² + 2 (5m)(4n) + (4n)²]
= 16m² + 40mn + 25n² + 25m² + 40mn + 16n²
= 16m² + 25m² + 40mn + 40 mn + 25n² + 16n²
= 41m² + 80mn + 41n²

Question (v)
(2.5p – 1.5q)² – (1.5p – 2.5q)²
Solution:
= [(2.5p)² – 2 (2.5p)(1.5q) + (1.5q)²] – [(1.5p)² – 2 (1.5p)(2.5q) + (2.5q)²]
= [6.25p² – 7.5pq + 2.25q²] – [2.25p² – 7.5pq + 6.25q²]
= 6.25p² – 7.5pq + 2.25q² – 2.25p² + 7.5pq – 6.25q²
= 6.25p² – 2.25p² – 7.5pq + 7.5pq + 2.25q² – 6.25q²
= 4p² – 4q²

Question (vi)
(ab + bc)² – 2ab²c
Solution:
= [(ab)² + 2 (ab)(bc) + (bc)²] – 2ab²c
= a²b² + 2ab²c + b²c² – 2ab²c
= a²b² + 2ab²c – 2ab²c + b²c²
= a²b² + b²c²

Question (vii)
(m² – n²m)² + 2m³n²
Solution:
= [(m²)² – 2 (m²)(n²m)² + (n²m)²] + 2m³n²
= m⁴ – 2 m³n² + n⁴m² + 2 m³ n²
= m⁴ – 2 m³n² + 2 m³n² + n⁴m²
= m⁴ + m²n⁴

5. Show that:

Question (i)
(3x + 7)² – 84x = (3x – 7)²
Solution:
LHS = (3x + 7)² – 84x
= (3x)² + 2(3x)(7) + (7)² – 84x
= 9x² + 42x + 49 – 84x
= 9x² + 42x – 84x + 49
= 9x² – 42x + 49

RHS = (3x – 7)²
= (3x)² – 2(3x)(7) + (7)²
= 9x² – 42x + 49
Thus, LHS = RHS
∴ (3x + 7)² – 84x = (3x – 7)²

Question (ii)
(9p – 5q)² + 180pq = (9p + 5q)²
Solution:
LHS = (9p – 5q)² + 180pq
= (9p)² – 2(9p)(5q) + (5q)² + 180pq
= 81p² – 90pq + 25q² + 180pq
= 81p² – 90pq + 180pq + 25q²
= 81p² + 90pq + 25q²

RHS = (9p + 5q)²
= (9p)² + 2(9p)(5q) + (5q)²
= 81p² + 90pq + 25q²
Thus, LHS = RHS
∴ (9p – 5q)² + 180pq = (9p + 5q)²

Question (iii)
(\(\frac {4}{3}\)m – \(\frac {3}{4}\)n)² + 2mn = \(\frac {16}{9}\)m² + \(\frac {9}{16}\)n²
Solution:
LHS = [\(\frac {4}{3}\)m – \(\frac {3}{4}\)n]² + 2mn
= [(\(\frac {4}{3}\)m)² – 2(\(\frac {4}{3}\)m)(\(\frac {3}{4}\)n) + (\(\frac {3}{4}\)n)²] + 2mn
= \(\frac {16}{9}\)m² – 2mn + \(\frac {9}{16}\)n² + 2mn
= \(\frac {16}{9}\)m² – 2mn + 2mn + \(\frac {9}{16}\)n²
= \(\frac {16}{9}\)m² + \(\frac {9}{16}\)n² = RHS
Thus, LHS = RHS
∴ (\(\frac {4}{3}\)m – \(\frac {3}{4}\)n)² + 2mn = \(\frac {16}{9}\)m² + \(\frac {9}{16}\)n²

Question (iv)
(4pq + 3q)² – (4pq – 3q)² = 48pq²
Solution:
LHS = (4pq + 3q)² – (4pq – 3q)²
= [(4pq)² + 2 (4pq)(3q) + (3q)²] – [(4pq)² – 2 (4pq)(3q) + (3q)²]
= [16p²q² + 24pq² + 9q²] – [16p²q² – 24pq² + 9q²]
= 16p²q² + 24pq² + 9q² – 16p²q² + 24pq² – 9q²
= 16p²q² – 16p²q² + 24pq² + 24pq² + 9q² – 9q²
= 48pq² = RHS
Thus, LHS = RHS
∴ (4pq + 3q)² – (4pq – 3q)² = 48pq²

Question (v)
(a – b) (a + b) + (b – c) (b + c) + (c – a) (c + a) = 0
Solution:
LHS = (a – b)(a + b) + (b – c)(b + c) + (c – a) (c + a)
= (a² – b²) + (b² – c²) + (c² – a²)
= a² – b² + b² – c² + c² – a²
= a² – a² + b² – b² + c² – c²
= 0 = RHS
Thus, LHS = RHS
∴ (a -b)(a + b) + (b- c) (b + c) + (c – a) (c + a) = 0

6. Using identities, evaluate:

Question (i)
71²
Solution:
= (70 + 1)²
= (70)² + 2 (70)(1) + (1)²
[∵ (a + b)² = a² + 2ab + b²]
= 4900 + 140 + 1
= 5041

Question (ii)
99²
Solution:
= (100 – 1)2
= (100)² – 2(100)(1) + (1)²
[∵ (a – b)² – a² – 2ab + b²]
= 10000 – 200 + 1
= 9801

Question (iii)
102²
Solution:
= (100 + 2)²
= (100)² + 2 (100)(2) + (2)²
[∵ (a + b)² = a² + 2ab + b²]
= 10000 + 400 + 4
= 10404

Question (iv)
998²
Solution:
= (1000 – 2)²
= (1000)² – 2 (1000)(2) + (2)²
[∵ (a – b)² = a² – 2ab + b²]
= 1000000 – 4000 + 4
= 996004

Question (v)
5.2²
Solution:
= (5 + 0.2)²
= (5)² + 2 (5)(0.2) + (0.2)²
[∵ (a + b)² = a² + 2ab + b²]
= 25 + 2 + 0.04
= 27 + 0.04
= 27.04

Question (vi)
297 × 303
Solution:
= (300 – 3) × (300 + 3)
= (300)² – (3)²
[∵ (a – b)(a + b) = a² – b²]
= 90000 – 9
= 89991

Question (vii)
78 × 82
Solution:
= (80 – 2) × (80 + 2)
= (80)² – (2)²
[∵ (a – b)(a + b) = a² – b²]
= 6400 – 4
= 6396

Question (viii)
8.9²
Solution:
= (9 – 0.1)²
= (9)² – 2(9)(0.1) + (0.1)²
[∵ (a – b)² = a² – 2ab + b²]
= 81 – 1.8 + 0.01
= 81.01 – 1.8
= 79.21

Question (ix)
10.5 × 9.5
Solution:
= (10 + 0.5) × (10 – 0.5)
= (10)² – (0.5)²
[∵ (a + b)(a – b) = a² – b²]
= 100 – 0.25
= 99.75

7. Using a² – b² = (a + b) (a – b), find:

Question (i)
51² – 49²
Solution:
= (51 + 49) (51 – 49)
= (100) × (2)
= 200

Question (ii)
(1.02)² – (0.98)²
Solution:
= (1.02 + 0.98) (1.02 – 0.98)
= (2.0) × (0.04)
= 0.08

Question (iii)
153² – 147²
Solution:
= (153 + 147) (153 – 147)
= (300) × (6)
= 1800

Question (iv)
12.1² – 7.9²
Solution:
= (12.1 + 7.9) (12.1 – 7.9)
= 20 × 4.2
= 84

8. Using (x + a)(x + b) = x² + (a + b) x + ab, find:

Question (i)
103 × 104
Solution:
= (100 + 3) × (100 + 4)
= (100)² + (3 + 4) × 100 + (3)(4)
= 10000 + 700 + 12
=10712

Question (ii)
5.1 × 5.2
Solution:
= (5 + 0.1) (5 + 0.2)
= (5)² + (0.1 + 0.2) × 5 + (0.1)(0.2)
= 25 + (0.3) × 5 + 0.02
= 25 + 1.5 + 0.02
= 26.52

Question (iii)
103 × 98
Solution:
= (100 + 3) (100-2)
= (100)² + (3 – 2) 100 + (3)(-2)
= 10000 + 100 – 6
= 10094

Question (iv)
9.7 × 9.8
Solution:
= (10 – 0.3) (10 – 0.2)
= (10)² + [(-0.3) + (-0.2)] 10 + (-0.3) (-0.2)
= 100 + [-0.5] × 10 + 0.06
= 100 – 5 + 0.06
= 95.06

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 8 Comparing Quantities Ex 8.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.1

1. Find the ratio of the following.

Question (a).
Speed of a cycle 15 km per hour to the speed of scooter 30 km per hour.
Solution:
Speed of a cycle = 15 km/h
Speed of a scooter = 30 km / h
∴ Ratio of the speed of a cycle to the speed of a scooter
= \(\frac{15 \mathrm{~km} / \mathrm{h}}{30 \mathrm{~km} / \mathrm{h}}\)
= \(\frac {1}{2}\)
= 1 : 2

Question (b).
5 m to 10 km
Solution:
[Note : Unit of both quantities should be same.]
1 km = 1000 m
∴ 10 km = 10 × 1000 m
= 10,000 m
∴ Ratio of 5 m to 10 km = \(\frac{5 \mathrm{~m}}{10 \mathrm{~km}}\)
= \(\frac{5 \mathrm{~m}}{10000 \mathrm{~m}}\)
= \(\frac{1}{2000}\)
= 1 : 2000

Question (c).
50 paise to ₹ 5
Solution:
[Note : Unit of both quantities should be same.]
₹ 1 = 100 paise
∴ ₹ 5 = 500 paise
∴ Ratio of 50 paise to ₹ 5 = \(\frac{50 \text { paise }}{₹ 5}\)
= \(\frac{50 \text { paise }}{500 \text { paise }}\)
= \(\frac{1}{10}\)
= 1 : 10

2. Convert the following ratios to percentages.

Question (a).
3 : 4
Solution:
Given ratio = 3 : 4
∴ Percentage = (\(\frac{3}{4}\) × 100) %
= (3 × 25) %
= 75 %

Question (b).
2 : 3
Solution:
Given ratio = 2 : 3
∴ Percentage = (\(\frac{2}{3}\) × 100) %
= (\(\frac{200}{3}\)) %
= 66 \(\frac{2}{3}\)%

3. 72% of 25 students are interested in Mathematics. How many are not interested in Mathematics?
Solution:
Total number of students = 25
Students interested in Mathematics = 72%
∴ Students who are not interested in Mathematics = (100 – 72) %
= 28 %
Number of students who are not interested in Mathematics = 28% of 25
= \(\frac{28}{100}\) × 25
= \(\frac{28}{4}\)
= 7
Thus, 7 students are not interested in Mathematics.

4. A football team won 10 matches out of the total number of matches they played. If their win percentage was 40, then how many matches did they play in all ?
Solution:
Number of matches won by the football team = 10
Let x matches be played by the team.
∴ 40% of x = 10
∴ \(\frac{40}{100}\) × x = 10
∴ x = \(\frac{10 \times 100}{40}\)
= 25
Thus, the football team played 25 matches in all.

5. If Chameli had ₹ 600 left after spending 75% of her money, how much did she have in the beginning?
Solution:
Let Chameli had in the beginning ₹ x
Percentage of money spent by Chameli = 75 %
Percentage of money left with Chameli = (100 – 75)%
= 25%
But money left = ₹ 600 (Given)
∴ 25% of x = 600
∴ \(\frac{25}{100}\) × x = 600
∴ x = \(\frac{600 \times 100}{25}\)
∴ x = 2400
Thus, Chameli had ₹ 2400 in the beginning.

6. If 60% people in a city like cricket, 30% like football and the remaining like other games, then what per cent of the people like other games? If the total number of people is 50 lakh, find the exact number who like each type of game.
Solution:
Percentage of people who like cricket = 60 %
Percentage of people who like football = 30 %
∴ Percentage of people who like other games = [ 100 – (60 + 30)]%
= (100 – 90)%
= 10 %
Total number of people = 50,00,000 (Given)
Now,
People who like cricket
= 60% of 50,00,000
= \(\frac {1}{2}\) × 50,00,000
= 60 × 50000
= 3000000
= 30 lakh

People who like football
= 30% of 5000000
= \(\frac {30}{100}\) × 5000000
= 30 × 50000
= 1500000
= 15 lakh

People who like other games
= 10% of 5000000
= \(\frac {10}{100}\) × 5000000
= 500000
= 5 lakh
Thus, number of people who like
cricket = 30 lakh,
football = 15 lakh
and other games = 5 lakh

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 7 Cubes and Cube Roots InText Questions and Answers.

PSEB 8th Class Maths Solutions Chapter 7 Cubes and Cube Roots InText Questions

Try These (Textbook Page No. 111)

Find the one’s digit of the cube of each of the following numbers:
(i) 3331
(ii) 8888
(iii) 149
(iv) 1005
(v) 1024
(vi) 77
(vii) 5022
(viii) 53
Solution:

Sl. No.	Number	Number ending in	Units place digit of the cube
(i)	3331	1	1
(ii)	8888	8	2
(iii)	149	9	9
(iv)	1005	5	5
(v)	1024	4	4
(vi)	77	7	3
(vii)	5022	2	8
(viii)	53	3	7

Some interesting patterns: (Textbook Page No. 111)

Observe the following pattern of sums of odd numbers.

Try These (Textbook Page No. 111)

1. Express the following numbers as the sum of odd numbers using the above pattern ?
(a) 6³
(b) 8³
(c) 7³
Solution:
From above pattern, we can conclude n³ = [n(n – 1) + 1] + [n(n – 1) + 3] + [n(n – 1) + 5]… + n terms
(a) 6³
Here, n = 6, n- 1=5
6 (6 – 1) + 1 → 6 × 5 + 1 → 31

OR
= [6(6 – 1) + 1] + [6(6 – 1) + 3] + [6(6 – 1) + 5] + [6(6 – 1) + 7] + [6(6 – 1) + 9] + [6(6 – 1) + 11]
= (6 × 5 + 1) + (6 × 5 + 3) + (6 × 5 + 5) + (6 × 5 + 7) + (6 × 5 + 9) + (6 × 5 + 11)
= (30 + 1) + (30 + 3) + (30 + 5) + (30 + 7) + (30 + 9) + (30 + 11)
= 31 +33 + 35 + 37 + 39 + 41
= 216

(b) 8³
Here, n = 8, n – 1 = 7
8 (8 – 1) + 1 → 8 × 7 + 1 → 57

OR
= [8(8 – 1) + 1] + (8(8 – 1) + 3] + [8(8 – 1) + 5] + [8(8 – 1) + 7] + [8(8 – 1) + 9] + [8(8 – 1) + 11] + [8(8 – 1) + 13] + [8(8 – 1) + 15]
= (8 × 7 + 1) + (8 × 7 + 3) + (8 × 7 + 5) + (8 × 7 + 7) + (8 × 7 + 9) + (8 × 7 + 11) + (8 × 7 + 13) + (8 × 7 + 15)
= (56 + 1) + (56 + 3) + (56 + 5) + (56 + 7) + (56 + 9) + (56 + 11) + (56 + 13) + (56 + 15)
= 57 + 59 + 61 + 63 + 65 + 67 + 69 + 71
= 512

(c) 7³
Here, n = 7, n – 1 = 6
7 × 6 + 1 → 42 + 1 → 43

OR
= [7(7 – 1) + 1] + [7(7 – 1) + 3] + [7(7 – 1) + 5] + [7(7 – 1) + 7] + [7(7 – 1) + 9] + [7(7 – 1) + 11] + [7(7 – 1) + 13]
= (7 × 6 + 1) + (7 × 6 + 3) + (7 × 6 + 5) + (7 × 6 + 7) + (7 × 6 + 9) + (7 × 6 + 11) + (7 × 6 + 13)
= (42 + 1) + (42 + 3) + (42 + 5) + (42 + 7) + (42 + 9) + (42 + 11) + (42 + 13)
= 43 + 45 + 47 + 49 + 51 + 53 + 55
= 343

Consider the following pattern:
2³ – 1³ = 1 + 2 × 1 × 3
3³ – 2³ = 1 + 3 × 2 × 3
4³ – 3³ = 1 + 4 × 3 × 3
Using the above pattern, find the value of the following:
(i) 7³ – 6³
(ii) 12³– 11³
(iii) 20³ – 19³
(iv) 51³ – 50³
Solution:
From above pattern, we can conclude
n³ – (n – 1)³ = 1 + n × (n – 1) × 3
(i) 7³ – 6³ = 1 + 7 × 6 × 3
= 1 + 126
= 127

(ii) 12³ – 11³ = 1 + 12 × 11 × 3
= 1 + 396
= 397

(iii) 20³ – 19³ = 1 + 20 × 19 × 3
= 1 + 1140
= 1141

(iv) 51³ – 50³ = 1 + 51 × 50 × 3
= 1 + 7650
= 7651

Try These (Textbook Page No. 112)

1. Which of the following are perfect cubes?

Question (1).
400
Solution:
\(\begin{array}{l|l}
2 & 400 \\
\hline 2 & 200 \\
\hline 2 & 100 \\
\hline 2 & 50 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
400 = 2 × 2 × 2 × 2 × 5 × 5
Here, the prime factors 2 and 5 do not appear in triples.
∴ 2 × 5 × 5 is left over.
∴ 400 is not a perfect cube.

Question (2).
3375
Solution:
\(\begin{array}{l|l}
3 & 3375 \\
\hline 3 & 1125 \\
\hline 3 & 375 \\
\hline 5 & 125 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
3375 = 3 × 3 × 3 × 5 × 5 × 5
Here, the prime factors 3 and 5 appear in triples.
No factor is left over.
∴ 3375 is a perfect cube.
3375 = 3³ × 5³

Question (3).
8000
Solution:
\(\begin{array}{l|l}
2 & 8000 \\
\hline 2 & 4000 \\
\hline 2 & 2000 \\
\hline 2 & 1000 \\
\hline 2 & 500 \\
\hline 2 & 250 \\
\hline 5 & 125 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
8000 = 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5
Here, the prime factors 2 and 5 appear in triples.
No factor is left over.
∴ 8000 is a perfect cube.
8000 = 2³ × 2³ × 5³

Question (4).
15625
Solution:
\(\begin{array}{l|l}
5 & 15625 \\
\hline 5 & 3125 \\
\hline 5 & 625 \\
\hline 5 & 125 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
15625 = 5 × 5 × 5 × 5 × 5 × 5
Here, the prime factor 5 appear in triples.
No factor is left over.
∴ 15625 is a perfect cube.
15625 = 5³ × 5³

Question (5).
9000
Solution:
\(\begin{array}{l|l}
2 & 9000 \\
\hline 2 & 4500 \\
\hline 2 & 2250 \\
\hline 3 & 1125 \\
\hline 3 & 375 \\
\hline 5 & 125 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
9000 = 2 × 2 × 2 × 3 × 3 × 5 × 5 × 5
Here, among the prime factors 2 and 5 appear in triples but 3 does not appear in triple.
3 × 3 is left over.
∴ 9000 is not a perfect cube.

Question (6).
6859
Solution:
\(\begin{array}{l|l}
19 & 6859 \\
\hline 19 & 361 \\
\hline 19 & 19 \\
\hline & 1
\end{array}\)
6859 = 19 × 19 × 19
Here, the prime factor 19 appears in triple.
No factor is left over.
∴ 6859 is a perfect cube.
6859 = 193

Question (7).
2025
Solution:
\(\begin{array}{l|l}
3 & 2025 \\
\hline 3 & 675 \\
\hline 3 & 225 \\
\hline 3 & 75 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
2025 = 3 × 3 × 3 × 3 × 5 × 5
Here, the prime factor 3 appears in triple, but 3 × 5 × 5 is left over.
∴ 2025 is not a perfect cube.

Question (8).
10648
Solution:
\(\begin{array}{r|l}
2 & 10648 \\
\hline 2 & 5324 \\
\hline 2 & 2662 \\
\hline 11 & 1331 \\
\hline 11 & 121 \\
\hline 11 & 11 \\
\hline & 1
\end{array}\)
10648 = 2 × 2 × 2 × 11 × 11 × 11
Here, the prime factors 2 and 11 appear in triples.
No factor is left over.
∴ 10648 is a perfect cube.
10648 = 2³ × 11³

Think, Discuss and Write (Textbook Page No. 113)

1. Check which of the following are perfect cubes:
(i) 2700
(ii) 16000
(iii) 64000
(iv) 900
(v) 125000
(vi) 36000
(vii) 21600
(viii) 10000
(ix) 27000000
(x) 1000
What pattern do you observe in these perfect cubes ?
Solution:
(i) 2700
The number is ending with two zeros. If a number ends with three zeros or a multiple of 3 zeros, it may be a perfect cube.
∴ 2700 is not a perfect cube.

(ii) 16000
The number is ending with three zeros.
So it may be a perfect cube.
But, 16 is not a perfect cube.
∴ 16000 is not a perfect cube.

(iii) 64000
The number is ending with three zeros.
So it may be a perfect cube.
64 is a perfect cube. (∵ 4³ = 64)
∴ 64000 is a perfect cube.

(iv) 900
The number is ending with two zeros.
So it is not a perfect cube.
∴ 900 is not a perfect cube.

(v) 125000
The number is ending with three zeros.
So it may be a perfect cube.
125 is a perfect cube. (∵ 5³ = 125)
∴ 125000 is a perfect cube.

(vi) 36000
The number is ending with three zeros.
So it may be a perfect cube.
But, 36 is not a perfect cube.
∴ 36000 is not a perfect cube.

(vii) 21600
The number is ending with two zeros.
So it is not a perfect cube.
∴ 21600 is not a perfect cube.

(viii) 10000
The number is ending with four zeros.
So it is not a perfect cube.
∴ 10000 is not a perfect cube.

(ix) 27000000
The number is ending with six zeros.
So it may be a perfect cube.
27 is a perfect cube. (∵ 3³ = 27)
∴ 27000000 is a perfect cube.

(x) 1000
The number is ending with three zeros.
So it may be a perfect cube.
1 is a perfect cube, (∵ 1³ = 1)
∴ 1000 is a perfect cube.

Think, Discuss and Write (Textbook Page No. 115)

1. State true or false for any integer m, m² < m³. Why ?
Solution:
It seems true, but not always true.
m × m = m² and m × m × m = m³
∴ m² < m³
e.g. if m = 1
∴ m² = 1² = 1 and m³ = 1³ = 1
∴ m² ≮  m³, but m² = m³
If m = (- 1)
∴ m² = (- 1)² = 1 and m³ = (- 1)³ = (- 1)
∴ m² ≮  m³, but m2 > m³
So the above statement is not always true.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 9 Algebraic Expressions and Identities Ex 9.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.4

1. Multiply the binomials:

Question (i)
(2x + 5) and (4x – 3)
Solution:
= (2x + 5)(4x – 3)
= 2x(4x – 3) + 5 (4x – 3)
= 8x² – 6x + 20x – 15
= 8x² + 14x – 15

Question (ii)
(y – 8) and (3y – 4)
Solution:
= (y -8) (3y – 4)
= y (3y – 4) – 8 (3y – 4)
= 3y² – 4y – 24y + 32
= 3y² – 28y + 32

Question (iii)
(2.51 – 0.5m) and (2.51 + 0.5m)
Solution:
= (2.5l – 0.5m) (2.5l + 0.5m)
= 2.5l(2.5l + 0.5m) – 0.5m (2.5l + 0.5m)
= 6.25l² + 1.25lm – 1.25lm – 0.25m²
= 6.25l² – 0.25m²

Question (iv)
(a + 3b) and (x + 5)
Solution:
= (a + 3b) (x + 5)
= a (x + 5) + 3b (x + 5)
= ax + 5a + 3bx + 15b

Question (v)
(2pq + 3q²) and (3pq – 2q²)
Solution:
= (2pq + 3q²) (3pq – 2q²)
= 2pq (3pq – 2q²) + 3q² (3pq – 2q²)
= 6p²q² – 4pq³ + 9pq³ – 6q⁴
= 6p²q² + 5pq³ – 6q⁴

Question (vi)
(\(\frac {3}{4}\)a² + 3b²) and 4 (a² – \(\frac {2}{3}\)b²)
Solution:
= (\(\frac {3}{4}\)a² + 3b²) (4a² – \(\frac {8}{3}\)b²)
= \(\frac {3}{4}\)a⁴ (4a² – \(\frac {8}{3}\)b²) + 3b² (4a² – \(\frac {8}{3}\)b²)
= 3a₄ – 2a²b² + 12a²b² – 8b₄
= 3a⁴ + 10a²b² – 8b⁴

2. Find the product:

Question (i)
(5 – 2x) (3 + x)
Solution:
= 5 (3 + x) – 2x (3 + x)
= 15 + 5x – 6x – 2x²
= 15 – x – 2x²

Question (ii)
(x + 7y) (7x – y)
Solution:
= x(7x – y) + 7y (7x – y)
= 7x² – xy + 49xy – 7y²
= 7x² + 48xy – 7y²

Question (iii)
(a² + b) (a + b²)
Solution:
= a² (a + b²) + b (a + b²)
= a³ + a²b² + ab + b³

Question (iv)
(p² – q²) (2p + q)
Solution:
= p²(2p + q) – q²(2p + q)
= 2p³ + p²q – 2pq² – q³

3. Simplify:

Question (i)
(x² – 5) (x + 5) + 25
Solution:
= x² (x + 5) – 5 (x + 5) + 25
= x³ + 5x² – 5x – 25 + 25
= x³ + 5x² – 5x

Question (ii)
(a² + 5) (b³ + 3) + 5
Solution:
= a²(b³ + 3) + 5 (b³ + 3) + 5
= a²b³ + 3a² + 5b³ + 15 + 5
= a²b³ + 3a² + 5b³ + 20

Question (iii)
(t + s²)(t² – s)
Solution:
= t (t² – s) + s² (t² – s)
= t³ – st + s²t² – s³

Question (iv)
(a + b) (c – d) + (a – b) (c + d) + 2 (ac + bd)
Solution:
= a(c – d) + b(c – d) + a(c + d) – b(c + d) + 2 (ac + bd)
= ac – ad + bc – bd + ac + ad – bc – bd + 2ac + 2bd
= ac + ac + 2ac – ad + ad + bc – bc – bd – bd + 2 bd
= 4 ac

Question (v)
(x + y) (2x + y) + (x + 2y) (x – y)
Solution:
= x (2x + y) + y (2x + y) +x(x – y) + 2y (x – y)
= 2x² + xy + 2xy + y² + x² – xy + 2xy – 2y²
= 2x² + x² + xy + 2xy – xy + 2xy + y² – 2y²
= 3x² + 4xy – y²

Question (vi)
(x + y) (x² – xy + y²)
Solution:
= x (x² – xy + y²) + y (x² – xy + y²)
= x³ – x²y + xy² + x²y – xy² + y³
= x³ – x²y + x²y + xy² – xy² + y³
= x³ + y³

Question (vii)
(1.5x – 4y) (1.5x + 4y + 3) – 4.5x + 12y
Solution:
= 1.5x (1.5x + 4y + 3) – 4y (1.5x + 4y + 3) – 4.5x + 12y
= 2.25x² + 6xy + 4.5x – 6xy – 16y² – 12y – 4.5x + 12y
= 2.25x² + 6xy – 6xy + 4.5x – 4.5x – 16y² – 12y + 12y
= 2.25x² – 16y²

Question (viii)
(a + b + c) (a + b – c)
Solution:
= a (a + b – c) + b (a + b – c) + c (a + b – c)
= a² + ab – ac + ab + b² – bc + ac + bc – c²
= a² + ab + ab – ac + ac + b² – bc + bc – c²
= a² + 2ab + b² – c²
= a² + b² – c² + 2 ab

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 7 Cubes and Cube Roots Ex 7.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.2

1. Find the cube root of each of the following numbers by prime factorisation method.

Question (i).
64
Solution:
\(\begin{array}{l|l}
2 & 64 \\
\hline 2 & 32 \\
\hline 2 & 16 \\
\hline 2 & 8 \\
\hline 2 & 4 \\
\hline 2 & 2 \\
\hline & 1
\end{array}\)
By prime factorisation,
64 = 2 × 2 × 2 × 2 × 2 × 2
∴ \(\sqrt[3]{64}\) = 2 × 2
= 4
Thus, cube root of 64 is 4.

Question (ii).
512
Solution:
\(\begin{array}{l|l}
2 & 512 \\
\hline 2 & 256 \\
\hline 2 & 128 \\
\hline 2 & 64 \\
\hline 2 & 32 \\
\hline 2 & 16 \\
\hline 2 & 8 \\
\hline 2 & 4 \\
\hline 2 & 2 \\
\hline & 1
\end{array}\)
By prime factorisation,
512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
∴ \(\sqrt[3]{512}\) = 2 × 2 × 2
= 8
Thus, cube root of 512 is 8.

Question (iii).
10648
Solution:
\(\begin{array}{r|l}
2 & 10648 \\
\hline 2 & 5324 \\
\hline 2 & 2662 \\
\hline 11 & 1331 \\
\hline 11 & 121 \\
\hline 11 & 11 \\
\hline & 1
\end{array}\)
By prime factorisation,
10648 = 2 × 2 × 2 × 11 × 11 × 11
∴ \(\sqrt[3]{10648}\) = 2 × 11
= 22
Thus, cube root of 10648 is 22.

Question (iv).
27000
Solution:
\(\begin{array}{l|l}
2 & 27000 \\
\hline 2 & 13500 \\
\hline 2 & 6750 \\
\hline 3 & 3375 \\
\hline 3 & 1125 \\
\hline 3 & 375 \\
\hline 5 & 125 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
By prime factorisation
27000 = 2 × 2 × 2 × 3 × 3 × 3 × 5 × 5 × 5
∴ \(\sqrt[3]{27000}\) = 2 × 3 × 5
= 30
Thus, cube root of 27000 is 30.

Question (v).
15625
Solution:
\(\begin{array}{l|l}
5 & 15625 \\
\hline 5 & 3125 \\
\hline 5 & 625 \\
\hline 5 & 125 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
By prime factorisation,
15625 = 5 × 5 × 5 × 5 × 5 × 5
∴ \(\sqrt[3]{15625}\) = 5 × 5
= 25
Thus, cube root of 15625 is 25.

Question (vi).
13824
Solution:
\(\begin{array}{l|l}
2 & 13824 \\
\hline 2 & 6912 \\
\hline 2 & 3456 \\
\hline 2 & 1728 \\
\hline 2 & 864 \\
\hline 2 & 432 \\
\hline 2 & 216 \\
\hline 2 & 108 \\
\hline 2 & 54 \\
\hline 3 & 27 \\
\hline 3 & 9 \\
\hline 3 & 3 \\
\hline & 1
\end{array}\)
By prime factorisation,
13824 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
∴ \(\sqrt[3]{13824}\) = 2 × 2 × 2 × 3
= 24

Question (vii).
110592
Solution:
\(\begin{array}{l|l}
2 & 110592 \\
\hline 2 & 55296 \\
\hline 2 & 27648 \\
\hline 2 & 13824 \\
\hline 2 & 6912 \\
\hline 2 & 3456 \\
\hline 2 & 1728 \\
\hline 2 & 864 \\
\hline 2 & 432 \\
\hline 2 & 216 \\
\hline 2 & 108 \\
\hline 2 & 54 \\
\hline 3 & 27 \\
\hline 3 & 9 \\
\hline 3 & 3 \\
\hline & 1
\end{array}\)
By prime factorisation,
110592 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
∴ \(\sqrt[3]{110592}\) = 2 × 2 × 2 × 2 × 3
= 48
Thus, cube root of 110592 is 48.

Question (viii).
46656
Solution:
\(\begin{array}{l|l}
2 & 46656 \\
\hline 2 & 23328 \\
\hline 2 & 11664 \\
\hline 2 & 5832 \\
\hline 2 & 2916 \\
\hline 2 & 1458 \\
\hline 3 & 729 \\
\hline 3 & 243 \\
\hline 3 & 81 \\
\hline 3 & 27 \\
\hline 3 & 9 \\
\hline 3 & 3 \\
\hline & 1
\end{array}\)
By prime factorisation,
46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
∴ \(\sqrt[3]{46656}\) = 2 × 2 × 3 × 3
= 36
Thus, cube root of 46656 is 36.

Question (ix).
175616
Solution:
\(\begin{array}{l|l}
2 & 175616 \\
\hline 2 & 87808 \\
\hline 2 & 43904 \\
\hline 2 & 21952 \\
\hline 2 & 10976 \\
\hline 2 & 5488 \\
\hline 2 & 2744 \\
\hline 2 & 1372 \\
\hline 2 & 686 \\
\hline 7 & 343 \\
\hline 7 & 49 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)
By prime factorisation,
175616 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 7 × 7 × 7
∴ \(\sqrt[3]{175616}\) = 2 × 2 × 2 × 7
= 56
Thus, cube root of 175616 is 56.

Question (x).
91125
Solution:
\(\begin{array}{l|l}
3 & 91125 \\
\hline 3 & 30375 \\
\hline 3 & 10125 \\
\hline 3 & 3375 \\
\hline 3 & 1125 \\
\hline 3 & 375 \\
\hline 5 & 125 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
By prime factorisation,
91125 = 3 × 3 × 3 × 3 × 3 × 3 × 5 × 5 × 5
∴ \(\sqrt[3]{91125}\) =3 × 3 × 5
= 45
Thus, cube root of 91125 is 45.

2. State true or false.

Question (i).
Cube of any odd number is even.
Solution:
False, cube of any odd number is odd.

Question (ii).
A perfect cube does not end with two zeros.
Solution:
True, a perfect cube ending with zero will always have a triplet of zeros.

Question (iii).
If square of a number ends with 5, then its cube ends with 25.
Solution:
False, let us understand with an example.
15² = 15 × 15 = 225
15³ = 15 × 15 × 15 = 3375

Question (iv).
There is no perfect cube which ends with 8.
Solution:
False, let us understand with an example.
8 = 2³, 1728 = 12³

Question (v).
The cube of a two-digit number may be a three-digit number.
Solution:
False, let us take an example.
The smallest two-digit number is 10.
10³ = 1000
which is a four-digit number and not a three-digit number.

Question (vi).
The cube of a two-digit number may have seven or more digits.
Solution:
False, let us take an example.
The greatest two-digit number is 99.
99³ = 970299
which is a six-digit number.

Question (vii).
The cube of a single digit number may be a single digit number.
Solution:
True, let us take examples.
1³ = 1 and 2³ = 8

3. You are told that 1,331 is a perfect cube. Can you guess without factorisation what is its cube root? Similarly, guess the cube roots of 4913, 12167, 32768.
Solution:
Yes, we can guess without prime factorisation.
1331 : Separate given number into two groups.
1331 → 1 and 331
331 → Units place digit of 331 is 1.
∴ Unit place digit of cube root of 1331 = 1 (∵ 1³ = 1)
1 → 1³ = 1 and 2³ = 8
∴ Tens digit of cube root of 1331 = 1
Thus, the cube root of 1331 is 11.

(i) 4913 : Separate given number into two groups.
4913 → 4 and 913
913 → Units place digit of 913 is 3.
∴ Unit digit of cube root of 4913 = 7 (∵ 7³ = 343)
4 → 1³ = 1 and 2³ = 8
1 < 4 < 8 (∴ 1³ < 4 < 2³)
∴ The tens digit of cube root of 4913 = 1
Thus, the cube root of 4913 is 17.

(ii) 12167 : Separate given number into two groups.
12167 → 12 and 167
167 → Units place digit of 167 is 7.
∴ Unit digit of cube root of 12167 = 3
(∵ 3³ = 27)
12 → 2³ = 8 and 3³ = 27
8 < 12 < 27 (∵ 2³ < 12 < 3³)
∴ Tens place digit of cube root of 12167 = 2
Thus, the cube root of 12167 is 23.

(iii) 32768 : Separate given number into two groups.
32768 → 32 and 768
768 → Units place digit of 768 is 8.
∴ Unit digit of cube root of 32768 = 2 (∵ 2³ = 8)
32 → 3³ = 27 and 4³ = 64
27 < 32 < 64 (∵ 3³ < 32 < 4³)
∴ The tens digit of cube root of 32768 = 3
Thus, the cube root of 32768 is 32.