Bhagya

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 14 Statistics MCQ Questions with Answers.

PSEB 9th Class Maths Chapter 14 Statistics MCQ Questions

Multiple Choice Questions and Answer

Answer each question by selecting the proper alternative from those given below each question to make the statement true:

Question 1.
The marks scored by Kavya in 10 tests of Mathematics are 35, 18, 41, 24, 45, 10, 28, 32, 40, 15. Then, the range of the data is …………….. .
A. 45
B. 10
C. 35
D. 28.8
Answer:
C. 35

Question 2.
The average of the observations 3, 4, 5, 8, 12, 10, 13, 16, 18, 11 is …………………. .
A. 100
B. 10
C. 18
D. 3
Answer:
B. 10

Question 3.
The mean of first five odd natural numbers is ……………….. .
A. 3
B. 5
C. 4
D. 25
Answer:
B. 5

Question 4.
The mean of first four even natural numbers is ……………….. .
A. 5
B. 10
C. 20
D. 4
Answer:
A. 5

Question 5.
The mean of first five prime numbers is
A. 28
B. 2.8
C. 5.6
D. 1.4
Answer:
C. 5.6

Question 6.
If the mean of 2x, 5, 3x, 12, 5x, 17 and 6 is 20, then x = ………………….. .
A. 10
B. 20
C. 15
D. 40
Answer:
A. 10

Question 7.
The mean of the following distribution is ………………. .

A. 3.9
B. 7.8
C. 78
D. 39
Answer:
A. 3.9

Question 8.
If the mean of 12, 13, x, 17, 18 and 20 is 16, then x = ………………. .
A. 8
B. 4
C. 16
D. 32
Answer:
C. 16

Question 9.
For a given frequency distribution, n = 20 and Σf_ix_i = 140, then X̄ = ………………… .
A. 20
B. 14
C. 7
D. 28
Answer:
C. 7

Question 10.
The mean of \(\frac{2}{5},\), \(\frac{5}{7},\), \(\frac{3}{5},\) and \(\frac{2}{7},\) is ……………… .
A. \(\frac{1}{2},\)
B. \(\frac{3}{5},\)
C. \(\frac{5}{7},\)
D. 2
Answer:
A. \(\frac{1}{2},\)

Question 11.
The median of 14, 6, 2, 13, 9, 15 and 12 is …………………. .
A. 12
B. 10
C. 2
D. 15
Answer:
A. 12

Question 12.
The median of 21, 17, 13, 33, 19, 23 is ………………… .
A. 21
B. 20
C. 33
D. 19
Answer:
B. 20

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 14 Statistics Ex 14.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 14 Statistics Ex 14.4

Question 1.
The following number of goals were scored by a team in a series of 10 matches:
2, 3. 4, 5, 0. 1, 3, 3, 4, 3
Find the mean, median and mode of these scores.
Answer:
Here, n = 10.
Mean X̄ = \(\frac{\Sigma x_{i}}{n}\)
= \(\frac{2+3+4+5+0+1+3+3+4+3}{10}\)
= \(\frac{28}{10}\)
= 2.8
Thus, the mean of the given scores is 2.8 goals.

Arranging the observations in the ascending order, we get:
0, 1, 2, 3, 3, 3, 3, 4, 4, 5
Since n = 10 is an even number, \(\frac{n}{2}\) = 5 and \(\frac{n}{2}\) + 1 = 6.

Median M
= \(\frac{\left(\frac{n}{2}\right) \text { th observation }+\left(\frac{n}{2}+1\right) \text { th observation }}{2}\)
= \(\frac{5 \text { th } \text { observation }+6 \text { th } \text { observation }}{2}\)
= \(\frac{3+3}{2}\) = 3
Thus, the median of the given scores is 3 goals.
In the given data, observation 3 occurs most frequently (4 times). Hence, the mode of the data is 3 goals.

Question 2.
In a mathematics test given to 15 students, the following marks (out of 100) are recorded :
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60
Find the mean, median and mode of this data.
Answer:
Here, n = 15.
Mean X̄ = \(\frac{\Sigma x_{i}}{n}\)
= \(\begin{gathered}
41+39+48+52+46+62+54+40 \\
+96+52+98+40+42+52+60 \\
\hline 15
\end{gathered}\)
= \(\frac{822}{15}\) = 54.8
Thus, the mean of the data is 54.8 marks.
Arranging the observations in the ascending order, we get:
39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98
Here, n = 15 is an odd number.
Median M = \(\left(\frac{n+1}{2}\right)\)th observation
= \(\left(\frac{15+1}{2}\right)\)th observation
= 8 th observation
= 52
Thus, the median of the data is 52 marks.
In the given data, observation 52 occurs most frequently (3 times). Hence, the mode of the data is 52 marks.

Question 3.
The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x.
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
Answer:
Here, the median = 63 and n = 10.
∴ \(\frac{n}{2}\) = 5 and \(\frac{n}{2}\) + 1 = 6

Median M
= \(\frac{\left(\frac{n}{2}\right) \text { th observation }+\left(\frac{n}{2}+1\right) \text { th observation }}{2}\)
∴ 63 = \(\frac{5 \text { th } \text { observation }+6 \text { th } \text { observation }}{2}\)
∴ 63 = \(\frac{(x)+(x+2)}{2}\)
∴63 × 2 = x + x + 12
∴126 = 2x + 2
∴ 2x = 124
∴ x = 62

Question 4.
Find the mode of 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18.
Answer:
Here, just by simple observation, it is clearly seen that observation 14 occurs most frequently, i.e., 4 times.
Hence, the mode of the data is 14.

Question 5.
Find the mean salary of 60 workers of a factory from the following table:

Answer:

Mean X̄ = \(\frac{\Sigma f_{i} x_{i}}{n}\)
= \(\) = \(\frac{3,05,000}{60}\) = 5083.33
Thus, the mean salary is ₹ 5083.33.

Question 6.
Give one example of a situation in which
(i) the mean is an appropriate measure of central tendency.
Answer:
For the students studying in the same class, usually their level of knowledge and understanding would be more or less equal. There would be a few student having this level low and there would be a few students having this level high. Their level of knowledge and understanding would be reflected in the marks scored by them at an examination. Hence, the mean of marks scored by them at an examination is an appropriate measure of central tendency.

(ii) the mean is not an appropriate measure of central tendency but the median is an appropriate measure of central tendency.
Answer:
If we consider the monthly income of the people of certain region, the mean is not an appropriate measure of central tendency but the median is an appropriate measure of central tendency.

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 14 Statistics Ex 14.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 14 Statistics Ex 14.3

Question 1.
A survey conducted by an organisation for the cause of illness and death among the women between the ages 15-44 (in years) worldwide, found the following figures (in %):

Causes	Female fatality rate (%)
1. Reproductive health conditions	31.8
2. Neuropsychiatric conditions	25.4
3. Injuries	12.4
4. Cardiovascular conditions	4.3
5. Respiratory conditions	4.1
6. Other causes	22.0

(i) Represent the information given above graphically.
Answer:

(ii) Which condition is the major cause of women’s ill health and death worldwide?
Answer:
‘Reproductive health conditions’ is the major cause of womens ill health and death worldwide.

(iii) Try to find out, with the help of your teacher, any two factors which play a major role in the cause in (ii) above being the major cause.
Answer:
‘Malnutrition’ and ‘Lack of necessary medical facilities’ can be considered as two other factors which play a major role in female fatality.

Question 2.
The following data on the number of girls (to the nearest ten) per thousand boys in different sections of Indian society is given below:

Section	Number of girls per thousand bays
Scheduled Caste (SC)	940
Scheduled Tribe (ST)	970
Non-SC/ST	920
Backward districts	950
Non-backward districts	920
Rural	930
Urban	910

(i) Represent the information above by a bar graph.
(ii) In the classroom discuss what conclusions can be arrived at from the graph.
Answer:

Question 3.
Given below are the seats won by different political parties in the polling outcome of a state assembly elections:

(i) Draw a bar graph to represent the polling results.
Answer:
Seats won by different political parties

(ii) Which political party won the maximum number of seats?
Answer:
Political party: A won the maximum number of seats.

Question 4.
The length of 40 leaves of a plant are measured correct to one millimetre, and the obtained data is represented in the following table:

Length (in mm)	Number of leaves
118-126	3
127-135	5
136-144	9
145-153	12
154-162	.5
163-171	4
172-180	2

(i) Draw a histogram to represent the given data. [Hint: First make the class intervals continuous.]
(ii) Is there any other suitable graphical representation for the same data?
(iii) Is it correct to conclude that the maximum number of leaves are 153 mm long? Why?
Answer:
Making the class intervals continuous, we get the following table:

Length (in mm)	Number of leaves
117.5-126.5	3
126.5- 135.5	5
135.5-144.5	9
144.5-153.5	12
153.5- 162.5	5
162.5-171.5	4
171.5-180.5	2

(i) Length of leaves in millimetre

(ii) Yes. The given data can also be represented by ‘Frequency polygon’.

(iii) It is not correct to conclude that the maximum number of leaves are 153 mm long, because even if the frequency of class 145-153 is 12, we do not have the information about the length of each of those 12 leaves individually.

Question 5.
The following table gives the life times of 400 neon lamps:

Life time (in hours)	Number of lamps
300 – 400	14
400 – 500	56
500 – 600	60
600 – 700	86
700 – 800	74
800 – 900	62
900 – 1000	48

(i) Represent the given information with the help of a histogram.
Answer:

(ii) How many lamps have a life time of 700 hours or more than 700 hours ?
Answer:
The-frequencies of classes 700-800, 800-900 and 900-1000 are 74, 62 and 48 respectively.
Hence, the life time of 184 (74 + 62 + 48) lamps is 700 hours or more than 700 hours.

Question 6.
The following table gives the distribution of students of two sections according to the marks obtained by them:

Represent the marks of the students of both the sections on the same graph by two frequency polygons. From the two polygons compare the performance of the two sections.
Answer:
To draw the frequency polygons of both the sections, we find the class marks of each class and prepare the following tables:

Section A

Marks	Class mark	Frequency
0-10	5	3
10-20	15	9
20-30	25	17
30-40	35	12
40-50	45	9

Section B

Marks	Class mark	Frequency
0-10	5	5
10-20	15	19
20-30	25	15
30-40	35	10
40-50	45	1

Comparing the performance of both the sections from the frequency polygons, we observe that the performance of students of section A is better than the performance of students of section B.

Question 7.
The runs scored by two teams A and B on the first 60 balls in a cricket match are given below:

Number of balls	Team A	Team B
1-6	2	5
7-12	1	6
13-18	8	2
19-24	9	10
25-30	4	5
31-36	5	6
37-42	6	3
43-48	10	4
49-54	6	8
55-60	2	10

Represent the data of both the teams on the same graph by frequency polygons.
[Hint: First make the class intervals continuous.]
Answer:

Number of runs made by Team A and Team B in first 60 balls.

Question 8.
A random survey of the number of children of various age groups playing in a park was found as follows:

Age (in years)	Number of children
1-2	5
2-3	3
3-5	6
5-7	12
7-10	9
10-15	10
15-17	4

Draw a histogram to represent the data above.
Answer:

Children of various age groups playing in a park

Question 9.
100 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letters in the English alphabet in the surnames was found as follows:

Number of letters	Number of surnames
1-4	6
4-6	30
6-8	44
8-12	16
12-20	4

(i) Draw a histogram to depict the given information.
(ii) Write the class interval in which the maximum number of surnames lie.
Answer:

(i) Information regarding the number of surnames having given number of letters
Answer:

(ii) Write the class interval in which the maximum number of surnames lie.
Answer:
The maximum number of surnames lie in the class interval 6-8.

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 13 Surface Areas and Volumes Ex 13.9 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.9

Question 1.
A wooden bookshelf has external dimensions as follows : Height =110 cm, Depth = 25 cm, Breadth = 85 cm (see the given figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.

Answer:
Outer faces to be polished:

• One face on back side of the bookshelf, measuring 110 cm × 85 cm.
• Two faces on the sides, each of those measuring 110 cm × 25 cm.
• The top and the base, each of those measuring 85 cm × 25 cm.
• Two vertical strips on the front side, each of those measuring 110 cm × 5 cm.
• Four horizontal strips on the front side, each of those measuring 75 cm × 5 cm.

Thus, total area of region to be polished
= [(110 × 85) + 2(110 × 25) + 2 (85 × 25) + 2(110 × 5) + 4(75 × 5)] cm²
= (9350 + 5500 + 4250 + 1100+ 1500) cm²
= 21700 cm²
20 paise per cm² = ₹ 0.20 per cm²
Cost of polishing 1 cm2 region = ₹ 0.20
∴ Cost of polishing 21700 cm² region
= ₹ (21700 × 0.20)
= ₹ 4340

Inner faces to be painted:

• Two faces on the sides each of those measuring 90 cm × 20 cm.
• Two faces each of two shelves, the top face and the bottom face, in all six face, each of those measuring 75 cm × 20 cm.
• Face on the back side, measuring 90 cm × 75 cm.

Thus, total area of the region to be painted
= [2 (90 × 20) + 6 (75 × 20) + (90 × 75)] cm²
= (3600 + 9000 + 6750) cm²
= 19350 cm²
10 paise per cm² = ₹0.10 per cm²
Cost of painting 1 cm² region = ₹ 0.10
∴ Cost of painting 19350 cm² region = ₹ (19350 × 0.10) = ₹ 1935
Then, the total expense of polishing and painting = ₹ 4340 + ₹ 1935 = ₹ 6275

Question 2.
The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in the given figure. Eight such spheres are used for this purpose, and are to be ‘ painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm² and black paint costs 5 paise per cm².

Answer:
For each wooden sphere,
radius r = \(\frac{\text { diameter }}{2}\) = \(\frac{21}{2}\) cm
Curved surface area of 1 sphere
= 4πr²
= 4 × \(\frac{22}{7}\) × \(\frac{21}{2}\) × \(\frac{21}{2}\) cm²
= 1386 cm²
For each cylindrical support, radius r = 1.5 cm and height h = 7 cm.
Area of top of cylindrical support
= πr²
= \(\frac{22}{7}\) × 1.5 × 1.5 cm²
= 7.07 cm² (approx.)
Hence, the area of each sphere to be painted silver = 1386 cm² – 7.07 cm² = 1378.93 cm²
∴ Total area of eight spheres to be painted silver = 1378.93 cm² × 8 = 11031.44 cm²
25 paise per cm² = ₹ 0.25 per cm²
Cost of painting silver in 1 cm² region = ₹ 0.25
∴ Cost of painting silver in 11031.44 cm² region
= ₹ (11031.44 x 0.25)
= ₹ 2757.86 (approx.)
Curved surface area of 1 cylindrical support
= 2πrh
= 2 × \(\frac{22}{7}\) × 1.5 × 7 cm
= 66 cm²
∴ Total area of eight cylindrical supports to be painted black = 66 cm² × 8 = 528 cm²
5 paise per cm² = ₹ 0.05 per cm²
Cost of painting black in 1 cm² region = ₹ 0.05
∴ Cost of painting black in 528 cm² region = ₹ (528 × 0.05)
= ₹ 26.40
Thus, the total cost of painting = ₹ 2757.86 + ₹ 26.40
= ₹ 2784.26 (approx.)

Question 3.
The diameter of a sphere is decreased by 25 %. By what per cent does its curved surface area decrease?
Answer:
Suppose, the initial diameter of the sphere is d units and radius is r units.
∴ d = 2r
Original curved surface area of the sphere
= 4πr²
= π (4r²)
= π (2r)²
= πd² unit²
Now, the diameter of the sphere is reduced by 25 %. Hence, the new diameter of the sphere is 0.75d units.
New curved surface area of the sphere
= π (diameter)
= π (0.75d)² unit²
= 0.5625 πd² unit²
∴ The decrease in the curved surface area of the sphere = πd² – 0.5625 πd²
= 0.4375 πd² unit²
∴Percentage decrease in the curved surface area of the sphere = \(\frac{0.4375 \pi d^{2}}{\pi d^{2}}\) × 100 = 43.75 %
Thus, when the diameter of a sphere is decreased by 25 %, its curved surface area decreases by 43.75 %.

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 Introduction to Trigonometry Ex 8.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.2

Question 1.
Evaluate the following:
(i) sin 60° cos 30° + sin 30° cos 60°

(ii) 2 tan² 45° + cos² 30° – sin² 60°

(iii)

(iv)

(v) \(\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}\)
Solution:
(i) sin 60° cos 30° + sin 30° cos 60°
= \(\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{3}}{2}\right)+\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)\)

= \(\left(\frac{\sqrt{3}}{2}\right)^{2}+\left(\frac{1}{2}\right)^{2}\)
= \(\frac{3}{4}+\frac{1}{4}\) = 1.

(ii) 2 tan² 45° + cos² 30° – sin² 60° = 2 (tan 45°)² + (cos 30°)² – (sin 60°)²
= 2 (1)² + (\(\frac{\sqrt{3}}{2}\))² – (\(\frac{\sqrt{3}}{2}\))² = 2.

(iii)
= \(\frac{\frac{1}{\sqrt{2}}}{\left(\frac{2}{\sqrt{3}}\right)+(2)}=\frac{\frac{1}{\sqrt{2}}}{\frac{2+2 \sqrt{3}}{\sqrt{3}}}\)

= \(\frac{1}{\sqrt{2}}: \frac{\sqrt{3}}{2+2 \sqrt{3}}=\frac{\sqrt{3}}{2 \sqrt{2}(\sqrt{3}+1)}\)

= \(\frac{\sqrt{3}(\sqrt{3}-1)}{2 \sqrt{2}(\sqrt{3}+1)(\sqrt{3}-1)}\)

= \(\frac{\sqrt{2} \times \sqrt{3} \times(\sqrt{3}-1)}{4(3-1)}=\frac{3 \sqrt{2}-\sqrt{6}}{8}\).

(iv)

= \(\frac{\frac{1}{2}+1-\frac{2}{\sqrt{3}}}{\frac{2}{\sqrt{3}}+\frac{1}{2}+1}=\frac{\frac{3}{2}-\frac{2}{\sqrt{3}}}{\frac{2}{\sqrt{3}}+\frac{3}{2}}\)

= \(\frac{3 \sqrt{3}-4}{4+3 \sqrt{3}}\)

= \(\frac{(3 \sqrt{3}-4)(3 \sqrt{3}-4)}{(3 \sqrt{3}+4)(3 \sqrt{3}-4)}\)

= \(\frac{27+16-24 \sqrt{3}}{27-16}\)

= \(\frac{43-24 \sqrt{3}}{11}\)

(v) \(\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}\)

= \(\begin{array}{r}
5\left(\cos 60^{\circ}\right)^{2}+4\left(\sec 30^{\circ}\right)^{2} \\
\frac{-\left(\tan 45^{\circ}\right)^{2}}{\left(\sin 30^{\circ}\right)^{2}+\left(\cos 30^{\circ}\right)^{2}}
\end{array}\)

= \(\frac{5\left(\frac{1}{2}\right)^{2}+4\left(\frac{2}{\sqrt{3}}\right)^{2}-(1)^{2}}{\left(\frac{1}{2}\right)^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}}\)

= \(\frac{\frac{5}{4}+4 \times \frac{4}{3}-1}{\frac{1}{4}+\frac{3}{4}}=\frac{\frac{5}{4}+\frac{1}{3}-1}{\frac{1}{4}+\frac{3}{4}}\)

= \(\frac{5}{4}+\frac{16}{3}-1=\frac{15+64-12}{12}=\frac{67}{12}\).

Question 2.
Choose the correct option and justify your choice.

(i) \(\frac{2 \tan 30^{\circ}}{1+\tan 30^{\circ}}\)
(A) sin 60°
(B) cos 60°
(C) tan 60°
(D) sin 30°

(ii) \(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan 45^{\circ}}\)
(A) tan 90°
(B) 1
(C) sin 45°
(D) 0.

(iii) sin 2A = 2 sin A is true when
(A) 0°
(B) 30°
(C) 45°
(D) 60°

(iv) \(\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}\)
(A) cos 60°
(B) sin 60°
(C) tan 60°
(D) sin 30°.

Solution:
(i) \(\frac{2 \tan 30^{\circ}}{1+\tan 30^{\circ}}=\frac{2\left(\frac{1}{\sqrt{3}}\right)}{1+\left(\frac{1}{\sqrt{3}}\right)^{2}}\)

\(\frac{\frac{2}{\sqrt{3}}}{1+\frac{1}{3}}=\frac{2}{\sqrt{3}} \times \frac{3}{4}=\frac{\sqrt{3}}{2}\) = sin 60°.
So, correct anwer is (A).

(ii) \(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}=\frac{1-(1)^{2}}{1+(1)^{2}}\) = 0
So, correct anwer is (D).

(iii) Here when A = 0°
L.H.S. = sin 2A = sin 0° = 0
and R.H.S. = 2 sin A = 2 sin 0°
= 2 × 0 = 0
∴ Option (A) is correct.

(iv) \(\frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}=\frac{2\left(\frac{1}{\sqrt{3}}\right)}{1-\left(\frac{1}{\sqrt{3}}\right)^{2}}\)

= \(\frac{\frac{2}{\sqrt{3}}}{1-\frac{1}{3}}=\frac{2}{\sqrt{3}} \times \frac{3}{2}=\sqrt{3}\)

= tan 60°
∴ Option (C) is correct.

Question 3.
If tan (A + B) = \(\sqrt{3}\) and tan (A – B) = \(\frac{1}{\sqrt{3}}\); 0° ∠A + B ≤ 90°; A > B. find A and B.
Solution:
tan (A + B) = \(\sqrt{3}\). Given
tan (A + B) = tan 60°
⇒ A + B = 60° ……………..(1)
tan (A – B) = \(\frac{1}{\sqrt{3}}\) (Given)
or tan (A – B) = tan 30°
⇒ A – B = 30° …………….(2)
On adding (1) and (2),

A = 45°

Pu value of A = 45° in (1)
45° + B = 60°
B = 60° – 45°
B = 15°
Hence A = 45° and B = 15°.

Question 4.
State whether the following are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin q increases as q increases.
(iii) The value of cos q Increases as q increases
(iv) sin q = cos q for all value of q.
(v) cot A is not defined for A = 0°.
Solution:
(i) False.
When A = 60°, B = 30°
L.H.S. = sin (A + B) = sin (60° + 30°) = sin 90° = 1
R.H.S. = sin A + sin B
= sin 60° + sin 30°
= \(\frac{\sqrt{3}}{2}+\frac{1}{2}\) ≠ 1
i.e., L.H.S. ≠ R.H.S.

(ii) True, sin 30° = \(\frac{1}{2}\) = 0.5,
Note that sin 0° = 0,
sin 45° = \(\frac{1}{\sqrt{2}}\) = 0.7 (approx.)
sin 60° = \(\frac{\sqrt{3}}{2}\) = 0.87 (approx.)
and sin 90° = 1
i.e., value of sin θ increases as θ increases from 0° to 90°.

(iii) False.
Note that cos 0° = 1,
cos 30° = \(\frac{\sqrt{3}}{2}\) = 0.87(approx.)
cos 45° = \(\frac{1}{\sqrt{2}}\) = 0.7.(approx.)
cos 60° = \(\frac{1}{2}\) = 0.5
and cos 90° = 0.
Hence, value of θ decreases as θ increases from 0° to 90°.

(iv) False
Since sin 30° = \(\frac{1}{2}\)
and cos 30° = \(\frac{\sqrt{3}}{2}\)
or sin 30° ≠ cos 30°
Only we have: sin 45° = cos 45°.
\(\frac{1}{\sqrt{2}}\) = \(\frac{1}{\sqrt{2}}\)

(v) True.
cot 0° = \(\frac{1}{\tan 0^{\circ}}=\frac{1}{0}\), or not defined.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 1 Rational Numbers Ex 1.1Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1

1. Represent these numbers on the number line:

Question (i).
\(\frac {7}{4}\)
Solution:
To represent \(\frac {7}{4}\), make 7 markings each of a distance equal to \(\frac {1}{4}\) on the right side of 0. The 7th point represents the rational number \(\frac {7}{4}\).

The point A is \(\frac {7}{4}\).

Question (ii).
\(\frac {-5}{6}\)
Solution:
To represent (\(\frac {-5}{6}\)) on the number line, make 5 markings each of a distance equal to on the left side of 0. The 5th point represents the rational number (\(\frac {-5}{6}\)).

The point B is (\(\frac {-5}{6}\))

2. Represent \(\frac{-2}{11}, \frac{-5}{11}, \frac{-9}{11}\) on the number line.
Solution:
To represent the given rational numbers on a number line, make 11 markings each being equal to distance \(\frac {1}{11}\) on the left of 0.

Here, the point A is (\(\frac {-2}{11}\)).
the point B is (\(\frac {-5}{11}\)).
the point C is (\(\frac {-9}{11}\)).

3. Write five rational numbers which are smaller than 2.
Solution:
There are infinite rational numbers below 2, positive as well as negative.
Five of them are 1, \(\frac {1}{3}\), \(\frac {1}{4}\), 0, – 1.

4. Find ten rational numbers between \(\frac {-2}{5}\) and \(\frac {1}{2}\).
Solution:
First, convert \(\frac {-2}{5}\) and \(\frac {1}{2}\) having the same denominator, such that the difference between the numerators is more than 10.
\(\frac{-2}{5}=\frac{-2}{5} \times \frac{4}{4}=\frac{-8}{20}\);
\(\frac{1}{2}=\frac{1}{2} \times \frac{10}{10}=\frac{10}{20}\)
∴ The ten rational numbers between \(\frac {-8}{20}\) and \(\frac {10}{20}\) are
\(\frac{-7}{20}, \frac{-6}{20}, \frac{-5}{20}, \frac{-4}{20}, \frac{-3}{20}, \ldots, 0, \frac{1}{20}, \ldots, \frac{9}{20} .\)
(There can be many more such rational numbers.)

5. Find five rational numbers between

Question (i).
\(\frac {2}{3}\) and \(\frac {4}{5}\)
Solution:
First, convert \(\frac {2}{3}\) and \(\frac {4}{5}\) having the same denominator, such that the difference between the numerators is more than 5.
\(\frac{2}{3}=\frac{2}{3} \times \frac{20}{20}=\frac{40}{60}\);
\(\frac{4}{5}=\frac{4}{5} \times \frac{12}{12}=\frac{48}{60}\)
∴ The five rational numbers between \(\frac {2}{3}\) and \(\frac {4}{5}\) are \(\frac{42}{60}, \frac{43}{60}, \frac{44}{60}, \frac{45}{60}, \frac{46}{60}\).

Question (ii).
\(\frac {-3}{2}\) and \(\frac {5}{3}\)
Solution:
First, convert \(\frac {-3}{2}\) and \(\frac {5}{3}\) having the same denominator, such that the difference between the numerators is more than 5.
\(\frac{-3}{2}=\frac{-3}{2} \times \frac{3}{3}=\frac{-9}{6}\);
\(\frac{5}{3}=\frac{5}{3} \times \frac{2}{2}=\frac{10}{6}\)
∴ The five rational numbers between \(\frac {-3}{2}\) and \(\frac {5}{3}\) are \(\frac{-8}{6}, \frac{-7}{6}, 0, \frac{7}{6}, \frac{8}{6}\).

Question (iii).
\(\frac {1}{4}\) and \(\frac {1}{2}\)
Solution:
First, convert \(\frac {1}{4}\) and \(\frac {1}{2}\) having the same denominator, such that the difference between the numerators is more than 5.
\(\frac{1}{4}=\frac{1}{4} \times \frac{8}{8}=\frac{8}{32}\);
\(\frac{1}{2}=\frac{1}{2} \times \frac{16}{16}=\frac{16}{32}\)
∴ The five rational numbers between \(\frac {1}{4}\) and \(\frac {1}{2}\) are \(\frac{10}{32}, \frac{11}{32}, \frac{12}{32}, \frac{13}{32}, \frac{14}{32}\).
(There can be many more such rational numbers.)
[Note : You can write rational numbers of your choice.]

6. Write five rational numbers greater than -2.
Solution:
There can be many rational numbers greater than – 2. Five of them are \(\frac{-3}{2}, \frac{-1}{4}, 0, \frac{1}{2}, \frac{1}{5}\).

7. Find ten rational numbers between \(\frac {3}{5}\) and \(\frac {3}{4}\).
Solution:
First, convert \(\frac {3}{5}\) and \(\frac {3}{4}\) having the same denominator, such that the difference between the numerators is more than 10.
\(\frac{3}{5}=\frac{3}{5} \times \frac{20}{20}=\frac{60}{100}\);
\(\frac{3}{4}=\frac{3}{4} \times \frac{25}{25}=\frac{75}{100}\)
∴ The ten rational numbers between \(\frac {3}{5}\) and \(\frac {3}{4}\) are \(\frac{61}{100}, \frac{62}{100}, \frac{63}{100}, \frac{64}{100}, \frac{65}{100}, \frac{66}{100}, \frac{67}{100}, \frac{68}{100},\)\(\frac{69}{100}, \frac{70}{100}\)

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 Introduction to Trigonometry Ex 8.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1

Question 1.
In ∆ABC, right angled at B, AB = 24 cm; BC = 7 cm. Determine
(i) sin A, cos A
(ii) sin C, cos C.
Solution:
(i) We are to find sin A .cos A AB = 24 cm; BC = 7 cm
By using Pythagoras Theorem,

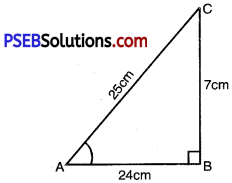
AC² = AB² + BC²
AC² = (24)² + (7)²
AC² = 576 + 49
AC² = 625
AC = \(\sqrt{625}\)
AC = 25 cm.
sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)

sin A = \(\frac{7 \mathrm{~cm}}{25 \mathrm{~cm}}=\frac{7}{25}\)

cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{24 \mathrm{~cm}}{25 \mathrm{~cm}}\)

cos A = \(\frac{24}{25}\)

Hence sin A = \([latex]\frac{7}{25}\)[/latex] and cos A = \([latex]\frac{24}{25}\)[/latex].

(ii) sin C = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{24 \mathrm{~cm}}{25 \mathrm{~cm}}\)

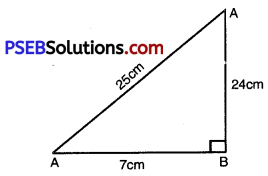
sin C = \(\frac{24}{25}\)

cos C = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7 \mathrm{~cm}}{25 \mathrm{~cm}}\)

cos C = \(\frac{7}{25}\)

Hence sin C = \(\frac{24}{25}\) and cos C = \(\frac{7}{25}\).

Question 2
In fig., find tan P – cot R.

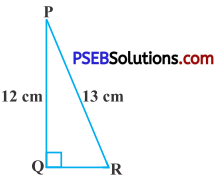
Solution:
Hyp. PR = 13 cm

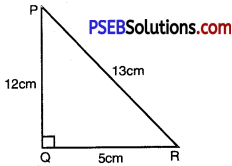
By using Pythagoras Theorem,
PR² = PQ² + QR²
or (13)² = (12)² + QR²
or 169 = 144 + (QR)²
or 169 – 144 = (QR)²
or 25 = (QR)²
or QR = ± \(\sqrt{25}\)
or QR = 5, – 5.
But QR = 5 cm.
[QR ≠ – 5, because side cannot be negative]
tan P = \(\frac{R Q}{Q P}=\frac{5}{12}\)

cot R = \(\frac{R Q}{P Q}=\frac{5}{12}\)

∴ tan P – cot R = \(\frac{5}{12}-\frac{5}{12}\) = 0
Hence tan P – cot R = 0.

Question 3.
If sin A = \(\frac{3}{4}\) calculate cos A and tan A.
Solution:
Let ABC be any triangle with right angle at B.

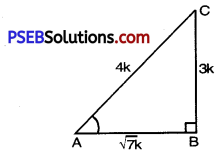
sin A = \(\frac{3}{4}\)
But sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}\) [From figure]
∴ \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3}{4}\)
But \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3}{4}\) = K
where K, is constant of proportionality.
⇒ BC = 3K, AC = 4K
By using Pythagoras Theorem,
AC² = AB² + BC²
or (4K)² = (AB)² + (3K)²
or 16K² = AB² + 9K²
or 16K² – 9K² = AB²
or 7K² = AB²
or AB = ± \(\sqrt{7 K^{2}}\)
or AB = ± \(\sqrt{7} \mathrm{~K}\)
[AB ≠ \(\sqrt{7 K}\) because side of a triangle cannot be negative]

⇒ AB = \(\sqrt{7} \mathrm{~K}\)
cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
cos A = \(\frac{\sqrt{7} K}{4 K}=\frac{\sqrt{7}}{4}\)
tan A = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{3 \mathrm{~K}}{\sqrt{7} \mathrm{~K}}=\frac{3}{\sqrt{7}}\)

Hence cos A = \(\frac{\sqrt{7}}{4}\) and tan A = \(\frac{3}{\sqrt{7}}\).

Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution:
Let ABC be any right angled triangle where A is an acute angle with right angle at B.

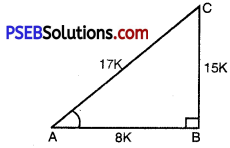
15 cot A = 8
cot A = \(\frac{8}{15}\)
But cot A = \(\frac{A B}{B C}\) (fromfig.)
⇒ \(\frac{A B}{B C}=\frac{8}{15}\) = K
where K is constant of proportionality.
AB = 8 K, BC = 15 K
By using Pythagoras Theorem.
AC² = (AB)² + (BC)²
(AC)² = (8 K)² + (15 K)²
(AC)² = 64K² + 225 K²
(AC)² = 289 K²
AC = ± \(\sqrt{289 K^{2}}\)
AC = ± 17 K
⇒ AC = 17K
[AC = – 17 K, Because side cannot be negative]
sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{15 \mathrm{~K}}{17 \mathrm{~K}}=\frac{15}{17}\)

sin A = \(\frac{15}{17}\)

sec A = \(\frac{\mathrm{AC}}{\mathrm{AB}}\)

sec A = \(\frac{17 \mathrm{~K}}{8 \mathrm{~K}}=\frac{17}{8}\)

sec A = \(\frac{17}{8}\)

Hence, sin A = \(\frac{15}{17}\) and sec A = \(\frac{17}{8}\).

Question 5.
Given sec θ = \(\frac{13}{2}\), calculate all other trigonometric ratios.
Solution:
Let ABC be any right angled triangle with right angle at B.
Let ∠BAC = θ

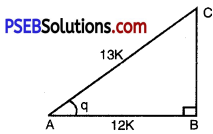
sec θ = \(\frac{13}{12}\)

But sec θ = \(\frac{\mathrm{AC}}{\mathrm{AB}}\) ……….[from fig.]

\(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{13}{12}\)

But \(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{13}{12}\) = k where k is constant of proportionality.
AC = 13 k and AB = 12 k
By using Pythagoras Theorem,
AC² = (AB)² + (BC)²
or (13k)² = (12k)² + (BC)²
or 169k² = 144k² + (BC)²
or 169k² – 144k² = (BC)
or (BC)² = 25k²
or BC = ± \(\sqrt{25 k^{2}}\)
or BC = ± 5k
or BC = 5k.
[BC ≠ – 5k because side cannot be negative]

sin θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{5 k}{13 k}=\frac{5}{13}\)
cos θ = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{12 k}{13 k}=\frac{12}{13}\)
tan θ = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{5 k}{12 k}=\frac{5}{12}\)
cosec θ = \(\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{13 k}{5 k}=\frac{13}{5}\)
cot θ = \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{12 k}{5 k}=\frac{12}{5}\).

Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B, show that LA = LB.
Solution:
Let ABC be any triangle, where ∠A and ∠B are acute angles. To find cos A and cos B.

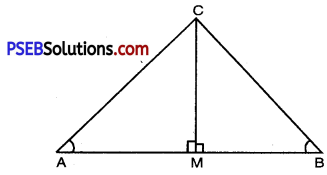
Draw CM ⊥ AB
∠AMC = ∠BMC = 90°
In right angled ∆AMC,
\(\frac{\mathrm{AM}}{\mathrm{AC}}\) = cos A ……………(1)
In right angled ∆BMC,
\(\frac{\mathrm{BM}}{\mathrm{BC}}\) = cos B ……………(2)
But cos A = cos B [given] ………..(3)
From (1), (2) and (3),
\(\frac{\mathrm{AM}}{\mathrm{AC}}=\frac{\mathrm{BM}}{\mathrm{BC}}\)
\(\frac{\mathrm{AM}}{\mathrm{BM}}=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{CM}}{\mathrm{CM}}\)
∴ ∆AMC = ∆BMC [By SSS similarity]
⇒ ∠A = ∠B [∵ Corresponding angles of two similar triangles are equal].

Question 7.
If cot θ = \(\frac{7}{8}\) evaluate
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) cot² θ.
Solution:
(i) ∠ABC = θ.
In right angled triangle ABC with right angle at C.

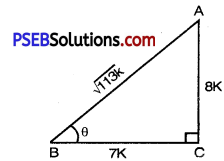
Given that, cot θ = \(\frac{7}{8}\)
But cot θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}\) [From fig.]
⇒ \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7}{8}\)
Let \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7}{8}\) = k
where k is constant of proportionality.
⇒ BC = 7k, AC = 8k
By using Pythagoras Theorem,
AB² = (BC)² + (AC)²
or (AB)² = (7k)² + (8k)²
or (AB)² = 49k² + 64k²
or (AB)² = 113 k²
or AB = ± \(\)
AB = \(\sqrt{113 k^{2}}\) k
AB = \(\sqrt{113}\) k
[AB ≠ \(\sqrt{113}\) k because side cannot be negative]

sin θ = \(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{8 k}{\sqrt{113} k}\)
sin θ = \(\frac{8}{\sqrt{113}}\)
cos θ = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{7 k}{\sqrt{113} k}=\frac{7}{\sqrt{113}}\)
cos θ = \(\frac{7}{\sqrt{113}}\)

(1 + sin θ) (1 – sin θ) = (1 + \(\frac{8}{\sqrt{113}}\)) (1 – \(\frac{8}{\sqrt{113}}\))
= (1)² – (\(\frac{8}{\sqrt{113}}\))²
[By using formula (a + b) (a – b) = a² – b²]
= 1 – \(\frac{64}{113}\)
(1 + sin θ) (1 – sin θ) = \(\frac{113-64}{113}=\frac{49}{113}\)
(1 + sin θ)(1 – sin θ) = \(\frac{49}{113}\) ……………..(1)

(1 + cos θ) (1 – cos θ) = (1 + \(\frac{8}{\sqrt{113}}\)) (1 – \(\frac{8}{\sqrt{113}}\))
(1)² – (\(\frac{7}{\sqrt{113}}\))²
[By using formula(a + b) (a – b) = a² – b²]
= 1 – \(\frac{49}{113}\) = \(\frac{113-49}{113}\)
(1 + cos θ) (1 – cos θ) = \(\frac{64}{113}\) ……….(2)

Consider, \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}=\frac{\frac{49}{113}}{\frac{64}{113}}\) [From (1) and (2)]

Hence \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}=\frac{49}{64}\)

(ii) cot θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7}{8}\)
cot² θ = (cot θ)²
cot² θ= (\(\frac{7}{8}\))²
⇒ cot² θ = \(\frac{49}{64}\).

Question 8.
If 3 cot A = 4 check whether \(\frac{1-\tan ^{2} A}{1+\tan ^{2} A}\) = cos² A – sin² A or not.
Solution:
Let ABC be a right angled triangle with right angled at B.

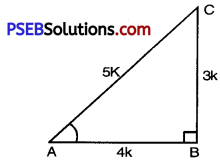
It is given that 3 cot A = 4
cot A = \(\frac{4}{3}\)
But cot A = \(\frac{\mathrm{AB}}{\mathrm{BC}}\) [From fig.]
⇒ \(\frac{A B}{B C}=\frac{4}{3}\)
But \(\frac{A B}{B C}=\frac{4}{3}\) = k
⇒ AB = 4k, BC = 3k
By using Pythagoras Theorem,
(AC)² = (AB)² + (BC)²
(AC)² = (4k)² + (3k)²
(AC)² = 16 k² + 9 k²
(AC)² = 25 k²
AC=± \(\sqrt{25 k^{2}}\)
AC = ± 5k

But AC = 5k.
[AC ≠ – 5k. because side cannot be negative]
sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3 k}{5 k}=\frac{3}{5}\)

tan A = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{3 k}{4 k}=\frac{3}{4}\)

cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{4 k}{5 k}=\frac{4}{5}\)

L.H.S. = \(\frac{1-\tan ^{2} \mathrm{~A}}{1+\tan ^{2} \mathrm{~A}}\)

∴ cos² A – sin² A = \(\frac{7}{25}\) ………..(2)

From (1) and (2),
L.H.S = R.H.S
Hence, \(\frac{1-\tan ^{2} \mathrm{~A}}{1+\tan ^{2} \mathrm{~A}}\) = cos² A – sin² A.

Question 9.
In triangle ABC, right angled at B, if tan A = \(\frac{1}{\sqrt{3}}\). Find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C.
Solution:
(i) Given: ABC with right angled at B

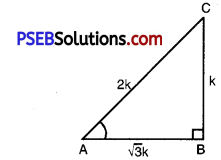
tan A = \(\frac{1}{\sqrt{3}}\) ……………..(1)
But tan A = \(\frac{B C}{A B}\) ……………(2)
From (1) and (2),
\(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{1}{\sqrt{3}}\)
Let \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{1}{\sqrt{3}}\) = k
BC = k, AB = k
where k is constant of proportionality.
In right angled triangle ABC,
By using Pythagoras Theorem,
(AC)² = (AB)² + (BC)²
or (AC)² = (Jk)² + (k)²
or AC² = 3k² + k²
or AC² = 4k²
or AC = ± \(\sqrt{4 k^{2}}\)
AC = ± 2k.
where AC = 2k
[AC ≠ – 2k side cannot be negative]

[sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{k}{2 k}=\frac{1}{2}\)

cos C = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{k}{2 k}=\frac{1}{2}\)

cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\sqrt{3} k}{2 k}=\frac{\sqrt{3}}{2}\)

sin C = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\sqrt{3} k}{2 k}=\frac{\sqrt{3}}{2}\)] …………….(3)

sin A cos C = \(\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)=\frac{1}{4}\)
cos A sin C = \(\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{3}}{2}\right)=\frac{3}{4}\)
sin A cos C + cos A sin C = \(\frac{1}{4}+\frac{3}{4}\)
= \(\frac{1+3}{4}\)
= \(\frac{4}{4}\) = 1
∴ sin A cos C + cos A sin C = 1.

(ii) cos A cos C = \(\left(\frac{\sqrt{3}}{2}\right)\left(\frac{1}{2}\right)=\frac{\sqrt{3}}{4}\) [From (3)]
sin A sin C = \(\left(\frac{1}{2}\right)\left(\frac{\sqrt{3}}{2}\right)=\frac{\sqrt{3}}{4}\) [From (3)]

cos A cos C – sin A sin C = \(\left(\frac{\sqrt{3}}{4}\right)-\left(\frac{\sqrt{3}}{4}\right)\) = 0.

Question 10.
In ∆PQR, right angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:
Given: ∆PQR, right angled at Q

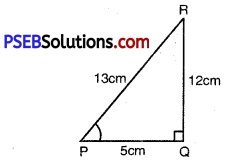
PR + QR = 25 cm
PQ = 5 cm
In right angled triangle PQR
By using Pythagoras Theorem,
(PR)² = (PQ)² + (RQ)²
or (PR)² = (5)² + (RQ)²
[∴ PR + QR = 25, QR = 25 – PR]
or (PR)² = 25 + [25 – PR]²
or (PR)² = 25 + (25)² + (PR)² – 2 × 25 × PR
or (PR)² = 25 + 625 + (PR)² – 50
or (PR)² – (PR)² + 50 PR = 650
or 50 PR = 650
or PR = \(\frac{650}{50}\)
or PR = 13 cm
QR = 25 – PR
QR = (25 – 13) cm
or QR = 12 cm.

sin P = \(\frac{Q R}{P R}=\frac{12}{13}\)

cos P = \(\frac{P Q}{P R}=\frac{5}{13}\)

tan P = \(\frac{Q R}{P Q}=\frac{12}{5}\)

Question 11.
State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1
(ii) sec A = \(\frac{12}{5}\) for some value of angle A.
(iii) cos A is abbreviation used for cosecant of angle A.
(iv) cot A is product of cot and A.
(v) sin θ = \(\frac{4}{3}\) for some angle θ.
Solution:
(i) False
∵ tan 60° = √3 = 1.732 > 1.

(ii) True; sec A = \(\frac{12}{5}\) = 240 > 1
∵ Sec A is always greater than 1.

(iii) False.
Because cos A is used for cosine A.

(iv) False.
Because cot A is cotangent of the angle A not the product of cot and A.

(v) False; sin θ = \(\frac{4}{3}\) = 1.666 > 1
Because sin θ is always less than 1.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 1 Rational Numbers Ex 1.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1

1. Using appropriate properties find.

Question (i).
\(-\frac{2}{3} \times \frac{3}{5}+\frac{5}{2}-\frac{3}{5} \times \frac{1}{6}\)
Solution:
\(-\frac{2}{3} \times \frac{3}{5}+\frac{5}{2}-\frac{3}{5} \times \frac{1}{6}\)
= \(-\frac{2}{3} \times \frac{3}{5}-\frac{3}{5} \times \frac{1}{6}+\frac{5}{2}\) (Commutative)
= \(\frac{3}{5} \times\left[-\frac{2}{3}-\frac{1}{6}\right]+\frac{5}{2}\) (Distributive)
= \(\frac{3}{5}\left[\frac{-4-1}{6}\right]+\frac{5}{2}\)
= \(\frac{3}{5}\left[\frac{-5}{6}\right]+\frac{5}{2}\)
= \(\frac{3}{5} \times \frac{-5}{6}+\frac{5}{2}\)
= \(-\frac{1}{2}+\frac{5}{2}\)
= \(\frac{-1+5}{2}\)
= \(\frac {4}{2}\)
= 2

Question (ii).
\(\frac{2}{5} \times\left(-\frac{3}{7}\right)-\frac{1}{6} \times \frac{3}{2}+\frac{1}{14} \times \frac{2}{5}\)
Solution:
\(\frac{2}{5} \times\left(-\frac{3}{7}\right)-\frac{1}{6} \times \frac{3}{2}+\frac{1}{14} \times \frac{2}{5}\)
= \(\frac{2}{5} \times\left(\frac{-3}{7}\right)+\frac{1}{14} \times \frac{2}{5}-\frac{1}{6} \times \frac{3}{2}\) (Commutative)
= \(\frac{2}{5} \times\left(\frac{-3}{7}+\frac{1}{14}\right)-\frac{1}{6} \times \frac{3}{2}\) (Distributive)
= \(\frac{2}{5} \times\left[\frac{-6+1}{14}\right]-\frac{1}{4}\)
= \(\frac{2}{5} \times \frac{-5}{14}-\frac{1}{4}\)
= \(-\frac{1}{7}-\frac{1}{4}=\frac{-4-7}{28}\)
= \(\frac{-11}{28}\)

2. Write the additive inverse of each of the following:

Question (i).
\(\frac{2}{8}\)
Solution:
Additive inverse of \(\frac{2}{8}\) = \(\frac{-2}{8}\)

Question (ii).
\(\frac{-5}{9}\)
Solution:
Additive inverse of \(\frac{-5}{9}\) = \(\frac{5}{9}\)

Question (iii).
\(\frac{-6}{-5}\)
Solution:
Additive inverse of \(\frac{-6}{-5}\) means \(\frac{6}{5}\) = \(\frac{-6}{5}\)

Question (iv).
\(\frac{2}{-9}\)
Solution:
Additive inverse of \(\frac{2}{-9}\) = \(\frac{2}{9}\)

Question (v).
\(\frac{19}{-6}\)
Solution:
Additive inverse of \(\frac{19}{-6}\) = \(\frac{19}{6}\)

3. Verify that – (- x) = x for

(i) x = \(\frac {11}{15}\)
Solution:
x = \(\frac {11}{15}\)
∴ (-x) = \(\left(\frac{-11}{15}\right)\)
-(-x) = –\(\left(\frac{-11}{15}\right)\)
= \(\frac {11}{15}\) = x
∴ -(-x) = x

(ii) x = \(\frac {-13}{17}\)
Solution:
x = \(\frac {-13}{17}\)
∴ (-x) = \(\left(\frac{-13}{17}\right)\)
= \(\frac {13}{17}\)
-(-x) = –\(\left(\frac{-13}{17}\right)\)
= \(\frac {-13}{17}\) = x
∴ -(-x) = x

4. Find the multiplicative inverse of the following:

Question (i).
-13
Solution:
Multiplicative inverse of -13 = \(\frac {-1}{13}\)

Question (ii).
\(\frac {-13}{19}\)
Solution:
Multiplicative inverse of \(\frac {-13}{19}\) \(\frac {-19}{13}\)

Question (iii).
\(\frac {1}{5}\)
Solution:
Multiplicative inverse of \(\frac {1}{5}\) = 5

Question (iv).
\(\frac{-5}{8} \times \frac{-3}{7}\)
Solution:
\(\left(\frac{-5}{8}\right) \times\left(\frac{-3}{7}\right)\)
= \(\frac{(-5 \times-3)}{8 \times 7}\)
= \(\frac {15}{56}\)
Multiplicative inverse of \(\frac {15}{56}\) = \(\frac {56}{15}\)

Question (v) .
1 × \(\frac {-2}{5}\)
Solution:
-1 × \(\frac {-2}{5}\) = \(\frac{(-1 \times-2)}{5}\)
= \(\frac {2}{5}\)
Multiplicative inverse of \(\frac {2}{5}\) = \(\frac {5}{2}\)

Question (vi).
-1
Solution:
Multiplicative inverse of -1 = (-1)
(∵ \(\frac{1}{(-1)}\) = (-1))

5. Name the property under multiplication used in each of the following:

Question (i).
\(\frac{-4}{5} \times 1=1 \times \frac{-4}{5}=-\frac{4}{5}\)
Solution:
1 is the multiplicative identity.

Question (ii).
\(-\frac{13}{17} \times \frac{-2}{7}=\frac{-2}{7} \times \frac{-13}{17}\)
Solution:
Commutative property of multiplication.

Question (iii).
\(\frac{-19}{29} \times \frac{29}{-19}=1\)
Solution:
Existence of multiplicative inverse.

6. Multiply \(\frac {6}{13}\) by the reciprocal of \(\frac {-7}{16}\).
Solution:
Reciprocal of \(\frac{-7}{16}=\frac{-16}{7}\)
∴ \(\frac{6}{13} \times \frac{-16}{7}\)
= \(\frac{6 \times(-16)}{13 \times 7}\)
= \(\frac {-96}{91}\)

7. Tell what property allows you to compute.
\(\frac{1}{3} \times\left(6 \times \frac{4}{3}\right)\) as \(\left(\frac{1}{3} \times 6\right) \times \frac{4}{3}\)
Solution:
In computing
\(\frac{1}{3} \times\left(6 \times \frac{4}{3}\right)\) as \(\left(\frac{1}{3} \times 6\right) \times \frac{4}{3}\)
we use the associativity.

8. Is \(\frac {8}{9}\) the multiplicative inverse of – 1 \(\frac {1}{8}\) ? Why or why not ?
Solution:
\(-1 \frac{1}{8}=\frac{-9}{8}\)
\(\frac{8}{9} \times \frac{-9}{8}\) = (-1)
∴ \(\frac {8}{9}\) is is not the multiplicative inverse of -1 \(\frac {1}{8}\) as product of two multiplicative inverse is always 1.

9. Is 0.3 the multiplicative inverse of 3 \(\frac {1}{3}\) ? Why or why not?
Solution:
0.3 = \(\frac {3}{10}\) and 3 \(\frac {1}{3}\) = \(\frac {10}{3}\)
\(\frac{3}{10} \times \frac{10}{3}\) = 1
∴ the multiplicative inverse of 3 \(\frac {1}{3}\) is 0.3.

10. Write:

Question (i).
The rational number that does not have a reciprocal.
Solution:
The rational number that does not have a reciprocal is 0.

Question (ii).
The rational numbers that are equal to their reciprocals.
Solution:
The rational numbers that are equal to their reciprocals are 1 and (-1).

Question (iii).
The rational number that is equal to its negative.
Solution:
The rational number that is equal to its negative is zero (0).

11. Fill in the blanks:

Question (i).
Zero has ……………. reciprocal.
Solution:
Zero has no reciprocal.

Question (ii).
The numbers ……………. and ……………. are their own reciprocals.
Solution:
The numbers 1 and -1 are their own reciprocals.

Question (iii).
The reciprocal of – 5 is …………….
Solution:
The reciprocal of – 5 is \(\frac {-1}{5}\)

Question (iv).
Reciprocal of \(\frac{1}{x}\), where x ≠ 0 is …………….
Solution:
Reciprocal of \(\frac{1}{x}\), where x ≠ 0 is x

Question (v) .
The product of two rational numbers is always a …………….
Solution:
The product of two rational numbers is always a rational number.

Question (vi).
The reciprocal of a positive rational number is …………….
Solution:
The reciprocal of a positive rational number is positive.

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 10 Practical Geometry Ex 10.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 10 Practical Geometry Ex 10.4

1. Draw a circle of the following radius:

Question (i)
3.5 cm
Solution:
Steps of construction.

1. Mark a point O on the page of your note book, where a circle is to be drawn.
2. Take compasses fixed with sharp pencil and measure OA = 3.5 cm using a scale.
3. Without changing the opening of the compasses, keep the needle at point O and draw a complete arc by holding the compasses from its knob, we get the required circle.

Question (ii)
4 cm
Solution:
Steps of construction.

1. Mark a point O on the page of your note book, where a circle is to be drawn.
2. Take compasses fixed with sharp pencil and measure OA = 4 cm using a scale.
3. Without changing the opening of the compasses, keep the needle at point O and draw a complete arc by holding the compasses from its knob.

Question (iii)
2.8 cm
Solution:
Steps of construction

1. Mark a point O on the page of your note book, where a circle is to be drawn.
2. Take compasses fixed with sharp pencil and measures OA = 2.8 cm using a scale.
3. Without changing the opening of the compasses, keep the needle at point O and draw a complete arc by holding the compasses from its knob, we get the required circle.

Question (iv)
4.7 cm
Solution:
Steps of construction

1. Mark a point O on the page of your note book.
2. Take compasses fixed with sharp pencil and measures OA = 4.7 cm using a scale.
3. Without changing the opening of the compasses, keep the needle at point O and draw a complete arc by holding the compasses from its knob, we get the required circle.

Question (v)
5.2 cm.
Solution:
Steps of construction

1. Mark a point O on the page of your note book.
2. Take compasses fixed with sharp pencil and measures OA = 5.2 cm using a scale.
3. Without changing the opening of the compasses, keep the needle at point O and draw a complete arc by holding the compasses from its knob, we get the required circle.

2. Draw a circle of diameter 6 cm.
Solution:
Steps of construction

1. Draw a line segment PQ = 6 cm.
2. Draw the perpendicular bisector of PQ intersecting PQ at O.
3. With O as centre and radius = OQ = 3 cm (= OP), draw a circle.
The circle thus drawn is the required circle.

3. With the same centre O, draw two concentric circles of radii 3.2 cm and 4.5 cm.
Solution:
Steps of Construction

1. Mark a point O on the page of your note book, where a circle is drawn.
2. Take compasses fixed with sharp pencil measuring OA = 4.5 cm using scale.
3. Without changing the opening of the compasses, keep the needle at point O and draw complete arc by holding the compasses from its knob.
After completing one round, we get circle I.
4. Again with the same centre O and new radius = 3.2 cm draw another circle II following the same step 3.

4. Draw a circle of radius 4.2 cm with centre at O. Mark three points A, B and C such that point A is on the circle, B is in the interior and C is in the exterior of the circle.
Solution:
Steps of Construction

1. Mark a point O on the page of your note book, where a circle is to be drawn
2. Take compasses fixed with sharp pencil and measure OA = 4.2 cm using scale (∴ A is on the circle).
3. Without changing the opening of the compasses, keep the needle at point O and draw complete arc by rotating the compasses from the knob. After completing one round, we get required circle.
4. Mark point B in the interior of the circle and point C in the exterior of the circle.

5. Draw a circle of radius 3 cm and draw any chord. Draw the perpendicular bisector of the chord. Does the perpendicular bisector passes through the centre?
Solution:
Steps of Construction.

1. Draw a circle with C as centre and radius 3 cm.
2. Draw AB the chord of the circle.
3. Draw PQ the perpendicular bisector of chord AB.
4. We see that the perpendicular bisector of chord AB passes through the centre C of the circle.

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 10 Practical Geometry Ex 10.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 10 Practical Geometry Ex 10.3

1. Draw a line r and mark a point P on it. Construct a line perpendicular to r at point P.

Question (i)
Using a ruler and compasses.
Solution:
Using ruler and compasses

Steps of Construction.

1. Draw a line r and mark a point P on it.

2. Draw an arc from P to the line r of any suitable radius which intersects line r at A and B.

3. Draw arcs of any radius which is more than half of arc made in step (2) from A and B which intersect at Q.

4. Join PQ.

Thus PQ is perpendicular to AB or line l or PQ ⊥ A.
Here P is called foot of perpendicular.

Question (ii)
Using a ruler and a set square.
Solution:
Using a ruler and a set square

Steps of Construction

1. Draw a line r and a point P on it.
2. Place one of the edges of a ruler along the line l and hold if firmly.

3. Place the set square in such a way that one of its edges contaning the right angle coincides with the ruler.
4. Holding the ruler, slide the set square along the line l till the vertical side reaches the point P.

5. Firmly hold the set square in this position. Draw PQ along its vertical edge. Now PQ is the required perpendicular to l ie. PQ ⊥ r.

2. Draw a line p and mark a point z above it. Construct a line perpendicular to p, from the point z.

Question (i)
Using a ruler and compasses.
Solution:
1. Draw a line p and mark a point z not lying on it.
2. From point z draw an arc which intersects line p at two points P and Q.


3. Using any radius and taking P and Q as centre, draw two arcs that intersect at point say B. On the other side (a shown in figure).
4. Join AB to obtain altitude to the line p.

Thus xz is altitude to line p.
i.e. xz ⊥ p.

Question (ii)
Using a ruler and set square
Solution:
Steps of constructions:
1. Draw a line p and mark a point z which is not lying on it.
2. Place one of the edge of a ruler along the line p and hold it firmly.

3. Place the set square in such a way that one of its edges containing the right angle coincides with the ruler.
4. Holding the ruler firmly, slide the set square along the line p till its vertical side reaches the point z.

5. Firmly hold the set square in this position, Draw xz along its vertical edge. Now xz is the required altitude to p i.e. xz ⊥ p.

3. Draw a line AB and mark two points P and Q on either side of line AB, Construct two lines perpendicular to AB, from P and Q using a ruler and compasses.
Solution:
1. Draw a line AB and Mark two points P and Q on either side of AB.

2. From point P draw an arc which intersect line AB at two points C and D.
3. Using any radius and taking C and D as centre draw two arcs that intersects at point say E on the other side as shown in figures.

4. Join PE to obtain perpendicular to AB.
5. From point Q draw an arc which intersects AB at two points X and Y.

6. Using any radius and taking X and Y as centre draw two arcs that intersects at point say R on the other side of line AB as shown in figures.
7. Join QR to obtain perpendicular to AB.
Thus, PE ⊥ AB and QR ⊥ AB

4. Draw a line segment of 7 cm and draw perpendicular bisector of this line segment.
Solution:
Steps of Construction:
1. Draw a line segment AB = 7 cm.
2. With A as centre and radius more than half of AB, draw an arc on both sides of AB.

3. With B as centre and the same radius as in step 2, draw an arc intersecting the first arc at C and D.
4. Join CD intersecting AB at O. Then CD is the perpendicular bisector of AB.

5. Draw a line segment PQ = 6.8 cm and draw its perpendicular bisector XY which bisect PQ at M. Find the length of PM and QM. Is PM = QM ?
Solution:
Steps of Construction:

1. Draw a line segment PQ = 6.8 cm
2. With P as centre and radius more than half of PQ draw arcs on both sides of PQ.

3. Now with Q as centre and the same radius as in step 2 draw arcs intersecting the previous drawn arcs at A and B respectively.
4. Join AB intersecting PQ at M. Then M bisects the line segment.
5. Measure the length of PM and QM
PM = 3.4 cm and QM = 3.4 cm
∴ PM = QM.

6. Draw perpendicular bisector of line segment AB = 5.4 cm. Mark point X anywhere on perpendicular bisector Join X with A and B. Is AX = BX ?
Solution:
Steps of construction.
1. Draw a line segment AB = 5.4 cm.
2. With A as centre and radius more than half of AB, draw an arc in both sides of AB.

3. With B as centre and the same radius as in step 2, draw an arc intersecting the first arc at C and D.
4. Join CD intersecting AB at O.
Then CD is the perpendicular bisector of AB.
Mark any point X on the perpendicular bisector CD. Drawn. Then join AX and BX.
On examination, we find that AX = BX.

7. Draw perpendicular bisectors of line segment of the following lengths.

Question (i)
8.2 cm
Solution:
Steps of Construction.
1. Draw a line regment AB = 8.2 cm

2. With A as centre and radius more than half of AB, draw arcs on both sides of AB.
3. With B as centre and the same radius as in step 2, draw an arcs intersecting the previous arc at C and D.
4. Join CD intersecting AB at O. Then CD is the perpendicular bisector of AB.

Question (ii)
7.8 cm
Solution:
Steps of Construction.

1. Draw a line segment AB = 7.8 cm

2. With A as centre and radius more than half of AB draw arcs on both sides of AB.
3. With B as centre and the same radius as in step 2, draw arcs intersecting the previous arcs at C and D.
4. Join CD intersecting AB at O. Then CD is the perpendicular bisector of AB.

Question (iii)
6.5 cm.
Solution:
Steps of Construction.
1. Draw a line segment AB = 6.5 cm

2. With A as centre and radius more than half of AB draw arcs on both sides of AB.
3. With B as centre and the same radius as in step 2 draw arcs intersecting the previous arcs at C and D.
4. Join CD intersecting AB at O. Then CD is the perpendicular bisector of AB.

8. Draw a line segment of length 8 cm and divide it into four equal parts Using compasses. Measure each part.
Solution:
Steps of construction.

1. Draw a line segment AB of length 8 cm
2. With A as centre and radius more than half of AB, draw arcs on both sides of AB.
3. With B as centre and the same radius as in step 2, draw arcs intersecting the previous arcs at P and Q.
4. Join PQ intersecting AB at C then PQ is the perpendicular bisector of AB intersecting AB at C.
5. Similarly draw the perpendicular bisector of AC intersecting AC at D.
6. Draw the perpendicular bisector of CB intersecting CB at E.
By actual measurement, it can be verified that
AD = DC = CE = EB