Class 9

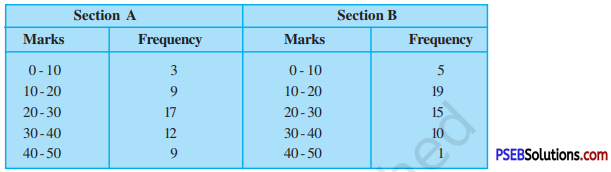
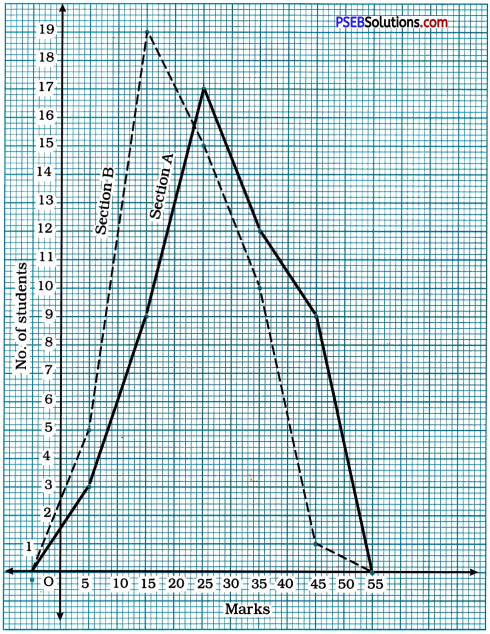
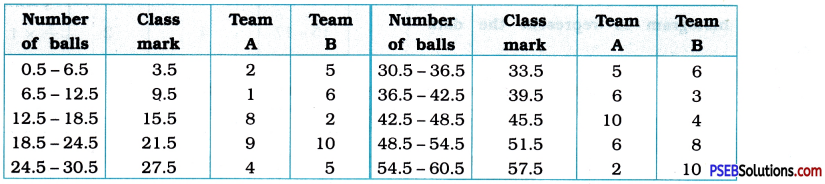
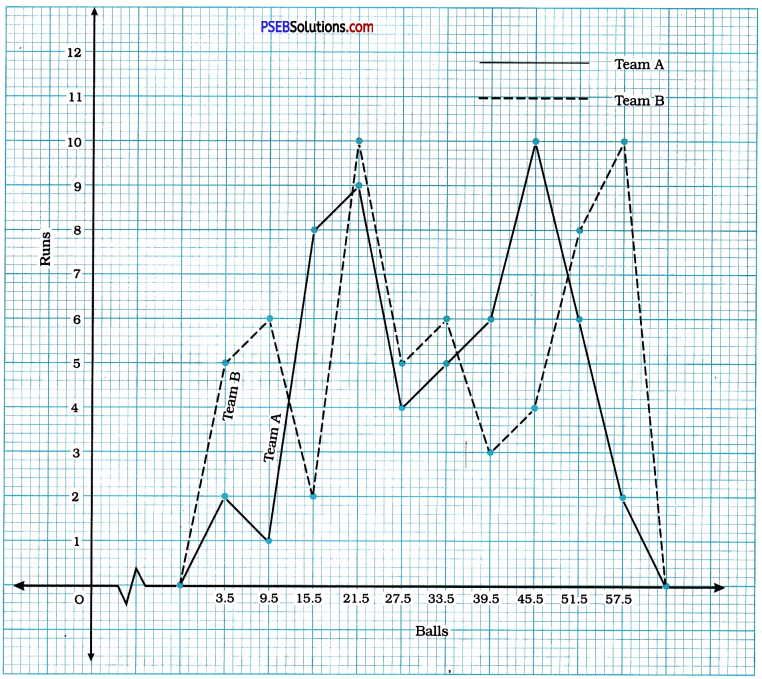
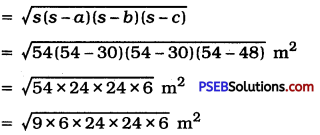Punjab State Board PSEB 9th Class Social Science Book Solutions Geography Chapter 3b पंजाब : जलतन्त्र Exercise Questions and Answers.

PSEB Solutions for Class 9 Social Science Geography Chapter 3b पंजाब : जलतन्त्र

SST Guide for Class 9 PSEB पंजाब : जलतन्त्र Textbook Questions and Answers

(क) नक्शा कार्य (Map Work):

प्रश्न 1.
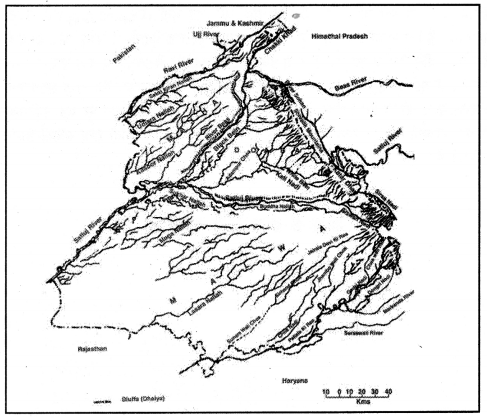
पंजाब के रेखाचित्र में दिखाएं :
(i) रावी, ब्यास, सतलुज तथा घग्गर
(ii) कोई चार नहरें
(iii) कोई चार चो।
उत्तर-
यह प्रश्न विद्यार्थी MBD Map Master की सहायता से स्वयं करें।

प्रश्न 2.
नदियों का प्रदूषण कैसे रोका जाए, इस विषय पर कक्षा में अध्यापक से चर्चा करें।
उत्तर-
यह प्रश्न विद्यार्थी स्वयं करें।

प्रश्न 3.
अपने समीप नदी या नहर में हो रहे प्रदूषण के लिए अध्यापक व अधिकारियों को सूचना दें।
उत्तर-
यह प्रश्न विद्यार्थी स्वयं करें।

PSEB 9th Class SST Solutions Geography Chapter 3a भारत : जलप्रवाह

(ख) निम्न वस्तुनिष्ठ प्रश्नों के उत्तर दें:

प्रश्न 1.
कौन-सी नदी का उद्गम स्थान मान सरोवर के पास रक्षताल झील है ?
(i) घग्गर
(ii) ब्यास
(iii) सतलुज
(iv) ब्रह्मपुत्र।
उत्तर-
(iii) सतलुज।

प्रश्न 2.
पंजाब में कितनी नदियां हैं-
(i) तीन
(ii) चार
(iii) पाँच
(iv) आठ।
उत्तर-(i) तीन।

प्रश्न 3.
रणजीत सागर अथवा थीन डैम का निर्माण कौन-सी नदी पर हुआ है ?
(i) ब्यास
(ii) रावी
(iii) सतलुज
(iv) इनमें से कोई नहीं।
उत्तर-
(ii) रावी।

प्रश्न 4.
भंगी और बाशा चोअ कौन-से जिले में पड़ते हैं ?
(i) फिरोज़पुर
(ii) गुरदासपुर
(iii) होशियारपुर
(iv) कोई भी नहीं।
उत्तर-
(iii) होशियारपुर।

प्रश्न 5.
कौन-सा कथन गलत है और कौन-सा सही है
(i) रावी, ब्यास व सतलुज बारामारसी नदियां हैं।
(ii) काली बेई व पावर्ती, ब्यास की सहायक नदियां हैं।
(iii) प्राकृतिक जल का शुद्धतम रूप वर्षा का जल है। .
(iv) पंजाब में 10 हैडवर्क्स तथा 20,786 किलोमीटर नहरें हैं।
उत्तर-

1. सही,
2. सही,
3. सही,
4. गलत।

प्रश्न 6.
बिस्त दोआब में बिस्त से क्या अभिप्राय है ?
उत्तर-
ब्यास तथा सतलुज दरियाओं के पहले शब्दों ‘बि’ तथा ‘सत’ को मिला. कर बिस्त शब्द बना है।

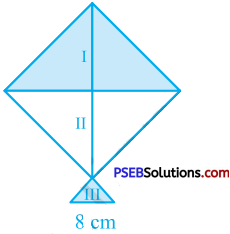
प्रश्न 7.
हरीके झील से राजस्थान को पानी ले जाने वाली दो नहरें कौन-कौन सी हैं ?
उत्तर-
राजस्थान फीडर नहर जिसे इंदिरा गांधी कमांड नहर भी कहा जाता है।

प्रश्न 8.
पंजाब की कौन-सी नहर हरियाणा को जल प्रदान करती है ?
उत्तर-
घग्गर नदी।

प्रश्न 9.
अपर बारी दोआब नहर का स्त्रोत क्या है ?
उत्तर-
माधोपुर हैडवर्कस।

प्रश्न 10.
पौंग डैम का निर्माण कौन-सी नदी पर किया गया है ?
उत्तर-
ब्यास दरिया।

(ग) प्रश्नों के संक्षेप उत्तर दें:

प्रश्न 1.
ब्यास व रावी की सहायक नदियों की सारणी बनाएं।
उत्तर-
व्यास-ब्यास की सहायक नदियां हैं-सुकन्तरी, पार्वती, सोहां, उहल तथा काली बेईं।
रावी-ऊज, सक्की किरन नाला रावी की प्रमुख नदियां हैं।

प्रश्न 2.
चोअ क्या होते हैं ? किन्हीं चार के नाम लिखें।
उत्तर-
चोअ छोटी मौसमी नदियां होती हैं जो वर्षा की ऋतु में पानी से पूर्णतया भर जाती हैं। बहुत सी चौएं कटारधार तथा सोलहासिंगी पहाड़ियों से शुरू होती हैं। पंजाब के कण्डी क्षेत्र में बहुत सी मौसमी चौएं हैं। बाणा चोअ, टोसां चोअ, बलाचौर चोअ, गढ़शंकर चोअ, नरियाला चोअ, मैली चोअ इत्यादि कुछ प्रमुख चौ हैं।

प्रश्न 3.
पंजाब के नदी, नहरों के प्रदूषण से अवगत करवायें।
उत्तर-
जब पानी में अनावश्यक वस्तुएं मिला दी जाती हैं जिस से पानी प्रयोग करने लायक नहीं रहता, इसे जल प्रदूषण कहते हैं। इसमें कोई शंका नहीं है कि पंजाब की सभी नदियों तथा नहरों में काफ़ी अधिक जल प्रदूषण है। भारत सरकार के कई विभागों तथा मन्त्रालयों का भी मानना है कि पंजाब की नहरों में काफ़ी अधिक जल प्रदूषण है तथा इनमें खतरनाक ज़हर भर रहा है। यह ज़हर पानी की सहायता से हमारी भोजन प्रणाली में पहुँच रहा है तथा लोग इससे खतरनाक बिमारियों का शिकार हो रहे हैं। उदाहरण के लिए बुड्ढा नाला पूर्णतया तेजाबी हो चुका है। हमें सभी नदियों को बचाने की आवश्यकता है ताकि हम पानी के साथ-साथ अपने जीवन को बचा कर रख सकें।

(घ) निम्न प्रश्नों के विस्तृत उत्तर दें

प्रश्न 1.
सतलुज नदी, उस पर बनाये डैमों तथा उसकी सहायक नदियों की जानकारी दें।
उत्तर-
सतलुज नदी तिब्बत में 4630 मीटर की ऊँचाई पर स्थित मानसरोवर झील से रक्षताल नामक स्थान से शुरू होता है। जब यह हिमालय पर्वत को पार कर रहा होता है तो गहरी खाइयां बनाता है। सतलुज मैदानों में भाखड़ा में दाखिल होता है तथा यहां ही भाखड़ा डैम बनाया गया है। नंगल से सतलुज दरिया दक्षिण दिशा की तरफ बढ़ता है तथा जब यह रोपड़ पहुँचता है तो इसमें सुआं, सरसा नदियां, मौसमी चोअ मिल जाते हैं। फिरोजपुर जिले में यह हरीके पत्तण से 60 किलोमीटर की दूरी पर स्थित सुलेमानकी नामक स्थान से पाकिस्तान में चला जाता है। सतलुज दरिया पर भाखड़ा बाँध के साथ-साथ कोटला बाँध, नाथपा झाखड़ी तथा नंगल बाँध भी बनाए गए हैं। सुआं, ब्यास तथा चिट्टी बेईं सतलुज की सहायक नदियां हैं। मक्खु में गिद्दड़ पिण्डी तथा चिट्टी बेईं सतलुज में मिल जाती है। सतलुज दरिया पर कई बाँधों के साथ-साथ रोपड़ तथा हरीके हैडवर्क्स भी बनाए गए हैं।

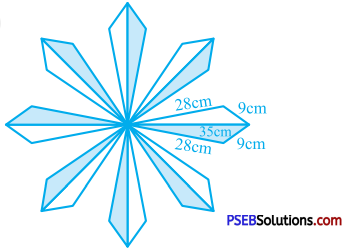
प्रश्न 2.
पंजाब के नहर प्रबन्ध के विषय में लिखें। इससे कृषि को क्या लाभ हैं ?
उत्तर-
पंजाब की अधिकतर जनता कृषि या इससे संबंधित कार्यों में लगी हुई है तथा पंजाब में ही 1960 के दशक में हरित क्रान्ति की शुरूआत हुई। हरित क्रान्ति में सिंचाई की बहुत बड़ी भूमिका थी क्योंकि किसान फसलों की सिंचाई के लिए केवल वर्षा पर निर्भर नहीं रह सकता। इस कारण पंजाब ने समय-समय पर अपनी नहरी व्यवस्था को काफी विकसित किया। पंजाब में 14500 किलोमीटर लंबी नहरें तथा 5 हैडवर्क्स हैं। यहां 10 नहरें भी हैं जिनके नाम हैंसरहिन्द नहर, अपर बारी दोआब नहर, बिस्त दोआब नहर, भाखड़ा मेन लाइन नहर, फिरोज़पुर/सरहिन्द फीडर प्रबन्ध, कश्मीर नहर, मक्खु, नहर, शाह नहर, राजस्थान फीडर तथा बीकानेर नहर। इन 10 नहरों में से 8 नहरों का वर्णन इस प्रकार है-

नहर	उत्पात का स्थान	लंबाई
1. भाखड़ा मेन लाइन	नंगल बैराज	161.36 कि०मी०
2. राजस्थान फीडर	हरीके हैडवर्क्स	149.53 कि०मी०
3. सरहिन्द फीडर II	हरीके हैडवर्क्स	136.53 कि०मी०
4. सरहिन्द	रोपड़ हैडवर्क्स	59.44 कि०मी०
5. बिस्त दोआब	रोपड़ हैडवर्क्स	43.00 कि०मी०
6. अपर बारी दोआब	माधोपुर हैडवर्क्स	42.35 कि०मी०
7. पूर्वी नहर	हुसैनीवाला हैडवर्क्स	8.02 कि०मी०
8. शाह नहर	मुकेरियां हाईडल चैनल	2.23 कि०मी०

कृषि को लाभ-इस नहरी व्यवस्था से पंजाब की कृषि को काफी लाभ हुआ जिसका वर्णन इस प्रकार है-

1. इन नहरों से पंजाब की कृषि को सारा साल पानी मिलता रहता है।
2. सिंचाई के साधन बढ़ने से किसान साल में दो या अधिक फसलें उगाने में सफल हो गए हैं।
3. अधिक फसलें उगाने से किसानों को काफ़ी फायदा हुआ है तथा उनकी आय भी बढ़ गई है।
4. दरियाओं तथा नहरों पर डैम बना कर पानी को रोका गया ताकि वर्षा न होने की स्थिति में किसानों तक पानी पहुँचाया जा सके।
5. डैमों से बिजली तैयार की गई जिससे उद्योगों तथा घरों को 24 घण्टे बिजली प्राप्त हुई।

प्रश्न 3.
पंजाब के चोअ और रौअ कौन-कौन से हैं ? विस्तत नोट लिखें।
उत्तर-
चौएं छोटी छोटी वर्षा पर आधारित तथा मौसमी नदियां होती हैं जो वर्षा के मौसम में पानी से भर जाती हैं। पंजाब में एक कण्डी क्षेत्र है जहां बहुत-सी चौएं मौजूद हैं। इनमें से कई चौओं का जन्म कटारधार तथा सेलासिंगी की पहाड़ियों में होता है। जब वर्षा आती है तो इन चौओं में पानी भर जाता है। पंजाब सरकार ने इनमें से कई चौओं को बंद करने में सफलता प्राप्त कर ली है तथा इनमें आने वाले वर्षा के पानी को कृषि अथवा अन्य कार्यों के लिए प्रयोग किया जा रहा है।

होशियारपुर जिले के दक्षिण पश्चिम में 93 चौएं मौजूद हैं जिनमें से बहुत से काली बेईं तथा चिट्टी बेईं में जाकर मिल जाते हैं। होशियारपुर में बहुत से चौएं हैं जिनमें कुछ काफी प्रमुख हैं जैसे कि टोसां चौ, बणा चौ, गढ़शंकर चौ, बलाचौर चौ, मैली चौ, नरियाला चौ, नंगल शहीदां चौ, गोंदपुर चौ, दसूहा चौ इत्यादि। इन पर नियन्त्रण रखने के लिए पंजाब सरकार ने कण्डी क्षेत्र विकास (Kandi Area Development) को भी शुरू किया है। पंजाब में कुछ बरसाती नाले भी हैं जैसे कि पटियाला की राव, जैंतिया देवी की रौ, बुड्ढ़ा नाला इत्यादि।

PSEB 9th Class Social Science Guide पंजाब : जलतन्त्र Important Questions and Answers

बहुविकल्पीय प्रश्न (Multiple Choice Questions)

प्रश्न 1.
पंजाब कौन-से दो शब्दों से मिलकर बना है ?
(क) पंज + आब
(ख) पंजा + आहब
(ग) पंज + अहाब
(घ) पं + जाहब।
उत्तर-
(क) पंज + आब

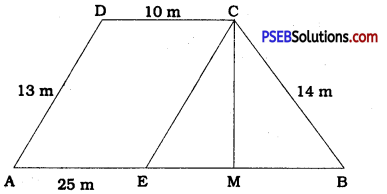
प्रश्न 2.
अब पंजाब में कितने दरिया हैं ?
(क) दो
(ख) तीन
(ग) चार
(घ) पाँच।
उत्तर-
(ख) तीन

प्रश्न 3.
इनमें से कौन-सा मौसमी दरिया है ?
(क) घग्गर
(ख) सकी किरन
(ग) काली बेई
(घ) उपर्युक्त सभी।
उत्तर-
(घ) उपर्युक्त सभी।

प्रश्न 4.
इनमें से कौन-सा बारहमासी दरिया है ?
(क) रावी
(ख) ब्यास
(ग) सतलुज
(घ) उपर्युक्त सभी।
उत्तर-
(घ) उपर्युक्त सभी।

प्रश्न 5.
रणजीत सागर डैम किस दरिया पर बना है ?
(क) रावी
(ख) सतलुज
(ग) ब्यास
(घ) चिनाब।
उत्तर-
(क) रावी

प्रश्न 6.
पौंग डैम किस दरिया पर बना है ?
(क) रावी
(ख) सतलुज
(ग) ब्यास
(घ) जेहलम।
उत्तर-
(ग) ब्यास

प्रश्न 7.
होशियारपुर में कितने चौएं हैं ?
(क) 70
(ख) 93
(ग) 84
(घ) 54.
उत्तर-
(ख) 93

रिक्त स्थान की पूर्ति करें (Fill in the Blanks)

1. सन् …………. में भारत तथा पाकिस्तान के विभाजन का सबसे बड़ा नुकसान …….. को हुआ।
2. रावी, ब्यास तथा सतलुज ……….. दरिया हैं।
3. रणजीत सागर डैम का कार्य ………… में पूर्ण हुआ था।
4. सुकन्तरी ………. की प्रमुख सहायक नदी है।
5. ………… किसी समय सरस्वती नदी का हिस्सा थी।

उत्तर-

1. 1947, पंजाब,
2. बारहमासी,
3. 2001,
4. ब्यास,
5. घग्गर

सही/ग़लत (True/False)

1. जेहलम, चिनाब तथा सिन्धु पाकिस्तान वाले पंजाब में रह गए।
2. रावी ककझ मंझ नाम के स्थान पर पाकिस्तान में प्रवेश करता है।
3. रणजीत सागर डैम से 1600 वाट बिजली उत्पन्न होती है।
4. ब्यास दरिया पर पौंग डैम बनाया गया है।
5. रावी दरिया से राजस्थान फीडर नहर निकाली गई है।

उत्तर-

1. ✓
2. ✓
3. ✗
4. ✓
5. ✗

अति लघु उत्तरों वाले प्रश्न।।

प्रश्न 1.
पंजाब शब्द का क्या अर्थ है ?
उत्तर-
पंजाब शब्द दो शब्दों ‘पंज-आब’ से मिलकर बना है जिसका अर्थ है पाँच दरियाओं की धरती।

प्रश्न 2.
1947 के पश्चात् कौन-से दरिया पंजाब में रह गए।
उत्तर-
सतलुज, रावी तथा ब्यास।

प्रश्न 3.
1947 के पश्चात् कौन-से दरिया पाकिस्तान वाले पंजाब में चले गए ?
उत्तर-
जेहलम, चिनाब तथा सिन्धु।

प्रश्न 4.
बारहमासी दरिया कौन-से होते हैं ?
उत्तर-
वह दरिया जिनमें सम्पूर्ण वर्ष पानी रहता है उन्हें बारहमासी दरिया कहते हैं।

प्रश्न 5.
बारहमासी दरियाओं में सम्पूर्ण वर्ष पानी कहां से आता है ?
उत्तर-
बारहमासी दरियाओं में पहाड़ों से पिघली बर्फ का पानी सम्पूर्ण वर्ष आता रहता है।

प्रश्न 6.
पंजाब के कुछ मौसमी दरियाओं के नाम लिखो।
उत्तर-
घग्गर, काली बेईं, चिट्टी बेईं, ऊज, चक्की खड्ड, स्वात इत्यादि।

प्रश्न 7.
किन्हीं दो अवशेषी दरियाओं के नाम लिखें।
उत्तर-
बुड्डा नाला तथा सक्की किरन नाला।

प्रश्न 8.
रावी दरिया का जन्म कहां पर होता है ?
उत्तर-
रावी दरिया कुल्लू की पहाड़ियों में स्थित रोहतांग दर्रे के उत्तर में 4116 मीटर की ऊंचाई से शुरू होता है।

प्रश्न 9.
रावी दरिया पर कौन-सा डैम बनाया गया है तथा इसमें से कौन-सी नहर निकाली गई है ?
उत्तर-
रावी दरिया पर रणजीत सागर डैम बनाया गया है तथा इससे अपर बारी दोआब नहर निकाली गई है।

प्रश्न 10.
रावी दरिया पर कौन-से हैडवर्क्स बनाए गए हैं ?
उत्तर-
शाहपुर कण्डी के नज़दीक धाना या बसन्तपुर, कटारधार, माधोपुर हैडवर्क्स तथा माधोपुर ब्यास लिंक पर कठुआ फीडर।

प्रश्न 11.
रणजीत सागर डैम के बारे में बताएं।
उत्तर-
यह रावी दरिया पर बनाया गया डैम है जिससे 600 मेगावाट बिजली पैदा होती है। यह 1981 में शुरू हुआ था तथा मार्च 2011 में इसका कार्य पूर्ण हुआ था।

प्रश्न 12.
ब्यास दरिया कहां से निकलता है ?
उत्तर-
ब्यास दरिया ब्यास कुण्ड से निकलता है जो हिमाचल प्रदेश में रोहतांग दर्रे के पास 4060 मीटर की ऊंचाई पर स्थित है।

प्रश्न 13.
व्यास दरिया पर कौन-से डैम बनाए गए हैं ?
उत्तर-
हिमाचल प्रदेश में पंडोह तथा पंजाब में पौंग डैम।

प्रश्न 14.
ब्यास से कौन सी नहर निकाली गई है ?
उत्तर-
ब्यास से राजस्थान फीडर नहर निकाली गई है जिसे इंदिरा गांधी कमांड नहर का नाम भी दिया गया है।

प्रश्न 15.
ब्यास की सहायक नदियों के नाम लिखें।
उत्तर–
पार्वती, सुकन्तरी, सौहां, उम्मन तथा काली बेईं।

प्रश्न 16.
सतलुज दरिया कहां पर शुरू होता है ?
उत्तर-
सतलुज दरिया तिब्बत में मानसरोवर झील के नज़दीक स्थित रक्षताल से शुरू होता है।

प्रश्न 17.
सतलुज दरिया कहां पर पाकिस्तान में प्रवेश करता है ?
उत्तर-
सतलुज दरिया फिरोज़पुर में सुलेमान की नामक स्थान से पाकिस्तान में प्रवेश करता है।

प्रश्न 18.
सतलुज दरिया पर कौन-से डैम बनाए गए हैं ?
उत्तर-
नाथपा झाखड़ी, नंगल डैम, कौटला डैम।

प्रश्न 19.
घग्गर किस प्रकार की नदी है ?
उत्तर-
घग्गर दक्षिणी पंजाब में बहने वाली एक मौसमी नदी है ।

प्रश्न 20.
घग्गर कहां से निकलती है ?
उत्तर-
घग्गर नदी सिरमौर की पहाड़ियों से निकलती है।

प्रश्न 21.
पंजाब के किस क्षेत्र में बहुत से चोअ मिलते हैं ?
उत्तर-
कण्डी क्षेत्र में।

प्रश्न 22.
चोअ क्या होता है ?
उत्तर-
चोअ एक छोटी सी नदी होती है जो वर्षा के मौसम में पानी से भर जाती है।

प्रश्न 23.
पंजाब के किस जिले में बहुत से चोअ हैं ?
उत्तर-
होशियारपुर जिले में।

प्रश्न 24.
पंजाब की नहरों की लंबाई बताएं।
उत्तर-
पंजाब की नहरों की लंबाई 14500 किलोमीटर है।

प्रश्न 25.
पंजाब की सबसे लंबी नहर कौन-सी है ?
उत्तर-
भाखड़ा मेन लाइन जिसकी लंबाई 161.36 किलोमीटर है।

प्रश्न 26.
कौन-सा दरिया किसी समय सरस्वती नदी का सहायक होता था ?
उत्तर-
घग्गर दरिया किसी समय सरस्वती नदी का सहायक होता था।

लघु उत्तरों वाले प्रश्न

प्रश्न 1.
पंजाब के जलतन्त्र के बारे में बताएं।
उत्तर-
पंजाब दो शब्द ‘पंज’ तथा ‘आब’ से मिलकर बना है जिसका अर्थ है पाँच दरियाओं की धरती। पंजाब में 1947 से पहले कई दरिया होते थे परन्तु देशों के विभाजन के कारण जेहलम, चिनाब, सिन्धु तथा बहुत सी नदियां पाकिस्तान में चली गईं। अब पंजाब में केवल तीन दरिया रावी, ब्यास तथा सतलुज ही हैं। यह तीनों दरिया बारहमासी हैं जिनमें पहाड़ों की बर्फ पिघलने के कारण सारा साल पानी रहता है। यहां बहुत से मौसमी दरिया भी हैं जैसे कि घग्गर, ऊज, काली बेईं, चिट्टी बेईं, स्वान, नूरपुर बेदी चोअ इत्यादि। यहां अवशेषी दरिया, जैसे कि बुड्ढा नाला तथा सक्की किरन नाला भी मिलते हैं।

प्रश्न 2.
रावी की सहायक नदियों के बारे में बताएं।
उत्तर-
जब रावी दरिया माधोपुर पहुँचता है तो इसमें कई सहायक नदियां आकर मिल जाती हैं। इनमें सबसे महत्त्वपूर्ण ऊज नदी है। इसके साथ ही सक्की किरन नाला रावी के साथ-साथ चलता है तथा भारत और पाकिस्तान की सरहद पर इसमें मिल जाता है। रावी दरिया पर चार हैडवर्क्स भी बनाए गए हैं जिनके नाम हैं माधोपुर ब्यास लिंक पर कठुआ फीडर, शाहपुर कण्डी के नज़दीक धाना या बसन्तपुर, माधोपुर हैडवर्क्स तथा कटारधार।

प्रश्न 3.
ब्यास दरिया की सहायक नदियों के बारे में बताएं।
उत्तर-
सुकन्तरी-उग्मन, पारबती, काली बेईं तथा सौहां ब्यास की कुछ सहायक नदियां हैं। तलवाड़ा पहुँच कर सौहां ब्यास में मिल जाती हैं। हरीके के नज़दीक काली बेईं होशियारपुर तथा कपूरथला से होते हुए ब्यास में मिल जाती है। ब्यास दरिया पर पौंग डैम तथा पंडोह डैम को भी बनाया गया है।

प्रश्न 4.
घग्गर पर एक नोट लिखें।
उत्तर-
पंजाब में काफी पहले सरस्वती नदी बहती थी तथा घग्गर भी उसका ही हिस्सा थी। परन्तु अब घग्गर एक मौसमी नदी है जो दक्षिण पंजाब में बहती है। यह सिरमौर की पहाड़ियों से निकलती है। मुबारकपुर नाम के स्थान पर यह मैदानी इलाकों में आ जाती है। इसके पश्चात् यह पटियाला, घनौर तथा हरियाणा के इलाकों को पार करती हैं। इसके पश्चात् यह राजस्थान के रेगिस्तान में जाकर खत्म हो जाती है।

दीर्घ उत्तर वाला प्रश्न

प्रश्न-रावी दरिया पर एक नोट लिखें।
उत्तर-रावी पंजाब का एक बारहमासी दरिया है जिसमें सारा साल पानी रहता है क्योंकि पहाड़ों की बर्फ पिघलने के कारण इसमें लगातार पानी आता रहता है। रावी दरिया कुल्लू की पहाड़ियों में रोहतांग दर्रे के उत्तर से शुरू होता है जिसकी ऊंचाई 4116 मीटर है। रावी दरिया अपने आरंभिक स्थान (Place of Origin) से लगातार बहते हुए धौलाधार तथा पीर पंजाल की पहाड़ियों को पार करता है तथा वहां बनी हुई गतॊ (Depressions) से बहते हुए चम्बा तथा डलहौजी को पार करता है। पठानकोट में माधोपुर नाम के स्थान पर यह मैदानों में प्रवेश कर जाता है। रावी के ऊपर रणजीत सागर डैम तथा थीन डैम बनाए गए हैं तथा इनके लिए माधोपुर हैडवर्क्स बनाया गया है। यहां से अपर बारी दोआब नहर भी निकाली गई है। इसके पश्चात् रावी दरिया पठानकोट, गुरदासपुर तथा अमृतसर जिलों में से निकलता है। यह भारत व पाकिस्तान की सरहद निश्चित करता है। कलझ मंझ नाम के स्थान पर यह पाकिस्तान में चला जाता है। पाकिस्तान में यह सिधानी नाम के स्थान पर चिनाब में मिल जाता है। ऊज नदी तथा सक्की किरन वाला रावी की प्रमुख सहायक नदियां हैं।

पंजाब : जलतन्त्र PSEB 9th Class Geography Notes

• पंजाब-पंजाब को पाँच दरियाओं की धरती कहा जाता है। समय के साथ-साथ पंजाब का कई बार विभाजन हुआ तथा अब इसमें केवल तीन दरिया रावी, ब्यास तथा सतलुज ही रह गए हैं। यह तीनों दरिया सम्पूर्ण वर्ष पानी से भरे रहते हैं।
• पंजाब का जलतन्त्र-पंजाब में तीन प्रकार के दरिया हैं-बारहमासी दरिया, मौसमी दरिया तथा अवशेषी दरिया।
• रावी दरिया-रावी दरिया रोहतांग दर्रे के उत्तर की तरफ 4116 मीटर की ऊंचाई पर शुरू होता है। इसके ऊपर रणजीत सागर डैम तथा थीन डैम के लिए माधोपुर हैड वर्कस को बनाया गया है। इसकी कई सहायक नदियां भी हैं जिनमें ऊज नदी सबसे महत्त्वपूर्ण है।
• ब्यास नदी-ब्यास दरिया हिमाचल प्रदेश के नज़दीक 4060 मीटर की ऊंचाई पर ब्यास कुण्ड से शुरू होता है। यह पंजाब में 160 किलोमीटर का फासला तय करके सतलुज में मिल जाता है। इससे ही राजस्थान फीडर नहर निकाली गई है जो राजस्थान के एक बड़े हिस्से की पानी की आवश्यकताएं पूर्ण करती है।
• सतलुज-सतलुज मानसरोवर झील के नज़दीक रक्षताल से निकलता है। इस पर भाखड़ा डैम बनाया गया है। यह फिरोजपुर जिले में से पाकिस्तान में चला जाता है।
• घग्गर-घग्गर एक मौसमी नदी है जो सिरमौर की पहाड़ियों में से निकल कर पटियाला, घनौर तथा हरियाणा में से होते हुए राजस्थान के रेगिस्तान में खत्म हो जाती है।
• पंजाब की नहरी व्यवस्था-पंजाब में काफी विकसित नहरी व्यवस्था है जिसमें 5 हैडवर्क्स तथा 14500 किलोमीटर लंबी नहरें हैं।3

Punjab State Board PSEB 9th Class Physical Education Book Solutions Chapter 1 शारीरिक शिक्षा-इसके गुण एवं उद्देश्य Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Physical Education Chapter 1 शारीरिक शिक्षा-इसके गुण एवं उद्देश्य

PSEB 9th Class Physical Education Guide शारीरिक शिक्षा-इसके गुण एवं उद्देश्य Textbook Questions and Answers

बहुत छोटे उत्तरों वाले प्रश्न

प्रश्न 1.
शारीरिक शिक्षा का लक्ष्य क्या है ?
उत्तर-
शारीरिक शिक्षा का उद्देश्य व्यक्ति के लिए ऐसा वातावरण प्रदान करना है जो उसके शरीर, दिमाग तथा समाज के लिए लाभदायक हो।

प्रश्न 2.
शारीरिक शिक्षा क्या है ?
उत्तर-
शारीरिक शिक्षा बच्चे के सम्पूर्ण व्यक्तित्व के विकास के लिए शारीरिक कार्यक्रम द्वारा, शरीर, मन तथा आत्मा को पूर्णता की ओर ले जाती है।

प्रश्न 3.
शारीरिक शिक्षा के कोई दो उद्देश्यों के नाम लिखो।
उत्तर-
(1) शारीरिक विकास (2) मानसिक विकास।

प्रश्न 4.
व्यक्ति और समाज के विकास में शारीरिक शिक्षा के कोई दो योगदानों के नाम लिखें।
उत्तर-
(1) खाली समय का उचित प्रयोग, (2) जीवन के लक्ष्य की प्राप्ति में सहायक, 3. सामाजिक भावना।

प्रश्न 5.
खेल के मैदान में आप कौन-कौन से शारीरिक शिक्षा के उद्देश्य ग्रहण करते हो ? किसी दो के नाम लिखें।
उत्तर-
(1) सहनशीलता, (2) अनुशासन, (3) चरित्र विकास ।

प्रश्न 6.
खेलें व्यक्ति में कैसे गुण विकसित करती हैं ?
उत्तर-
नेतृत्व के गुण।

बड़े उत्तरों वाले प्रश्न

प्रश्न 1.
शारीरिक शिक्षा का क्या लक्ष्य है ?
(What is the aim of Physical Education ?)
उत्तर-
शारीरिक शिक्षा का लक्ष्य (Aim of Physical Education)-शारीरिक शिक्षा साधारण शिक्षा की भान्ति उच्च मंजिल पर पहुंचने के लिए शिक्षा प्रदान करती है।
सुप्रसिद्ध शारीरिक शिक्षा शास्त्री जे० एफ० विलिअम्ज (J.F. Williams) का कहना है .. कि यदि हमें शारीरिक शिक्षा की मंजिल प्राप्त करनी है तो यह हमारा उद्देश्य होना चाहिए। शारीरिक शिक्षा का उद्देश्य एक कुशल तथा योग्य नेतृत्व देना तथा ऐसी सुविधाएं प्रदान करना है जो किसी एक व्यक्ति या समुदाय को कार्य करने का अवसर दें तथा ये सभी क्रियाएं शारीरिक रूप से सम्पूर्ण, मानसिक रूप से उत्तेजक तथा सन्तोषजनक तथा सामाजिक रूप से निपुण हों। इसके अनुसार व्यक्ति के लिए केवल उन्हीं क्रियाओं का चयन करना चाहिए जो शारीरिक रूप से लाभदायक हों।

प्रत्येक व्यक्ति केवल वे क्रियाएँ करे जो शरीर को तेज़ करने वाली हों तथा उसकी चिन्तन शक्ति बढ़ाने वाली हों। खेलों में कुछ उलझनें तथा प्रतिबन्ध इस प्रकार लगाये जाते हैं कि व्यक्ति का दिमाग ताज़ा रहे और उसे मानसिक सन्तोष मिले। इन क्रियाओं को समाज का समर्थन भी प्राप्त होना चाहिए। इसके अतिरिक्त समाज के अन्य सदस्य भी इन्हें आदर की दृष्टि से देखें। . संक्षेप में, समूचे तौर पर शारीरिक शिक्षा का लक्ष्य व्यक्ति के लिए ऐसा वातावरण प्रदान करना है जो उसके शारीरिक, मानसिक तथा सामाजिक पक्ष के लिए उपयोगी हो। इस प्रकार व्यक्ति का सर्वपक्षीय विकास (All-round Development) ही शारीरिक शिक्षा का एकमात्र लक्ष्य है।

प्रश्न 2.
खाली समय का उचित प्रयोग किस प्रकार किया जा सकता है ? संक्षेप में लिखो।
(How can Leisure time be usefully spent ? Describe in brief.)
उत्तर-
किसी ने ठीक ही कहा है कि “खाली मन शैतान का घर होता है।” (“An idle brain is a devil’s workshop.”) यह प्रायः देखा भी जाता है कि बेकार आदमी को शरारतें ही सूझती हैं। कई बार तो वह ऐसे गलत काम करने लगता है जो सामाजिक तथा नैतिक दृष्टि से उचित नहीं ठहराये जा सकते। इसका कारण यह है कि उसके पास फालतू समय तो है परन्तु उसके पास इसे व्यतीत करने का ढंग नहीं है। फालतू समय का उचित प्रयोग न होने के कारण उसका दिमाग कुरीतियों में फंस जाता है और कई बार अनेक उलझनों में उलझ कर रह जाता है जिनसे बाहर निकलना उसके वश से बाहर होता है।

यदि व्यक्ति इस फालतू समय का सदुपयोग जानता हो तो वह जीवन में उच्च शिखरों को छू सकता है। संसार के अनेक आविष्कार उन व्यक्तियों ने किये जो फालतू समय को कुशल ढंग से व्यतीत करने की कला से परिचित थे। इस प्रकार संसार के अनेक आविष्कार फालतू समय की ही देन हैं।।

यदि बच्चों के फालतू समय व्यतीत करने के लिए कोई उचित प्रबन्ध न हो तो वे बुरी आदतों का शिकार हो जाएंगे। इस प्रकार वे समाज पर बोझ बनने के साथ-साथ इसके लिए कलंक भी बन जाएंगे। इसलिए उनके फालतू समय के उचित प्रयोग की अच्छी व्यवस्था करनी चाहिए। स्कूलों, कॉलेजों, पंचायतों या नगरपालिकाओं या सरकार को अच्छे खेल के मैदानों तथा खेलों के सामान का पूरा प्रबन्ध करना चाहिए ताकि बच्चे खेलों में भाग लेकर अपने खाली समय का उचित प्रयोग कर सकें। इस प्रकार हम देखते हैं कि फालतू समय के प्रभावशाली उपयोग का सर्वोत्तम साधन खेलें हैं।

प्रश्न 3.
‘खेलें अच्छे नेता बनाती हैं।’ कैसे ?
(Games make good Leader. How ?)
अथवा
खेलें एक अच्छे नेता के गुण कैसे पैदा करती हैं?
(How sports produce the qualities of a good Leader ?)
उत्तर-
खेलें व्यक्ति में अच्छे नेतृत्व के गुण विकसित करती हैं। शारीरिक शिक्षा का क्षेत्र अत्यधिक विशाल है। खेलों में एक खिलाड़ी को अनेक ऐसे अवसर मिलते हैं जब उसे टीम के कप्तान, सैक्रेटरी, रैफरी या अम्पायर की भूमिका निभानी पड़ती है। इन परिस्थितियों में वह अपनी योग्यता के अनुसार आचरण करता है। एक कप्तान के रूप में वह अपनी टीम के खिलाड़ियों को समय-समय पर निर्देश देकर उन्हें उचित ढंग से तथा पूर्ण विश्वास के साथ खेलने की प्रेरणा देता है। एक रैफरी या अम्पायर के रूप में वह निष्पक्ष रूप से उचित निर्णय देता है। सैक्रेटरी के रूप में वह टीम का ठीक ढंग से गठन एवं संचालन करता है। इस प्रकार उसमें एक सफल और अच्छे नेता के गुण विकसित हो जाते हैं।

एक नेता में अच्छे चारित्रिक गुणों का होना आवश्यक है। उसमें आज्ञा-पालन, समय की पाबन्दी, सभी के साथ समान व्यवहार, प्रेम, सहानुभूति, सहनशीलता आदि गुण प्रचुर मात्रा में होने चाहिएं। ये सभी गुण वह खेल के मैदान से ग्रहण कर सकता है। एक नेता को अपने आस-पास के लोगों के साथ सद्भावना से रहना चाहिए। खेलें उसमें यह गुण विकसित करती हैं। जब एक खिलाड़ी अन्य स्थानों के खिलाड़ियों के साथ मिल-जुल कर खेलता है, वह उनके स्वभाव तथा सभ्यता के साथ भली-भान्ति परिचित हो जाता है। उसमें उनके प्रति सद्भावना उत्पन्न हो जाती है। यह सद्भावना ही एक नेता का महत्त्वपूर्ण गुण है।

नेता को चुस्त और फुर्तीला होना चाहिए। खेलों में भाग लेने से व्यक्ति में चुस्ती और स्फूर्ति आती है। इस प्रकार खेलें अच्छे नेताओं के निर्माण में विशेष योगदान देती हैं।

बड़े स्तरों वाले प्रश्न

प्रश्न 1.
शारीरिक शिक्षा के मुख्य उद्देश्य कौन-कौन से हैं ?
(Describe the main objectives of Physical Education.)
उत्तर-
शारीरिक शिक्षा के उद्देश्य (Objectives of Physical Education)किसी भी कार्य को आरम्भ करने से पहले उसके उद्देश्य निर्धारित कर लेना आवश्यक है। बिना उद्देश्य के किया गया काम छाछ को मथने के समान है। उद्देश्य निश्चित कर लेने से
हमारे यत्नों को प्रोत्साहन मिलता है और उस काम को करने में लगाई गई शक्ति व्यर्थ नहीं जाती है। आज तो शारीरिक शिक्षा के उद्देश्य की जानकारी प्राप्त करना और भी ज़रूरी हो गया है क्योंकि अब तो स्कूलों में एक विषय (Subject) के रूप में इसका अध्ययन किया जाता है।

साधारणतया शारीरिक शिक्षा के निम्नलिखित उद्देश्य हैं-

• शारीरिक वृद्धि एवं विकास (Physical Growth and Development)
• मानसिक विकास (Mental Development) (3) सामाजिक विकास (Social Development)
• चरित्र निर्माण या नैतिक विकास (Formation of Character or Moral Development)
• नाड़ियों और मांसपेशियों में समन्वय (Neuro-muscular Co-ordination )
• बीमारियों से बचाव (Prevention of Diseases)

1. शारीरिक वृद्धि एवं विकास (Physical Growth and Development)अच्छा, सफल तथा सुखद जीवन व्यतीत करने के लिए सुदृढ़, सुडौल तथा स्वस्थ शरीर का होना परमावश्यक है। हमारे शरीर का निर्माण मज़बूत हड्डियों से हुआ है। इसमें काम करने वाले सभी अंग उचित रूप से अपने कर्तव्य का पालन कर रहे हैं। शरीर के अंगों के सुचारु रूप से कार्य करते रहने से शरीर का निरन्तर विकास होता है। इसके विपरीत इनके भलीभान्ति काम न करने से शारीरिक विकास भी रुक जाता है। इस प्रकार शारीरिक प्रफुल्लता के उद्देश्य की प्राप्ति के लिए शारीरिक शिक्षा सुखद वातावरण जुटाती है।

2. मानसिक विकास (Mental Development)- शारीरिक विकास के साथसाथ मानसिक विकास की भी आवश्यकता है। शारीरिक शिक्षा ऐसी क्रियाएं प्रदान करती हैं जो व्यक्ति के मस्तिष्क को उत्तेजित करती हैं। उदाहरणस्वरूप, बास्केटबाल के खेल में एक टीम के खिलाड़ियों को विरोधी टीम के खिलाड़ियों से गेंद (बॉल) को बचा कर रखना होता है तथा इसके साथ-साथ अपना लक्ष्य भी देखना पड़ता है । अपनी शक्ति का अनुमान लगा कर बॉल को ऊपर लगी बास्केट में भी डालना होता है। कोई भी खिलाड़ी जो शारीरिक रूप से हृष्ट-पुष्ट है, परन्तु मानसिक रूप में विकसित नहीं है, कभी भी अच्छा खिलाड़ी नहीं बन सकता है। शारीरिक शिक्षा मानसिक विकास के लिए उचित वातावरण प्रदान करती है। इसलिए खेलों में भाग लेने वाले व्यक्ति का शारीरिक विकास के साथ-साथ मानसिक विकास भी हो जाता है।

प्रायः शारीरिक रूप से अस्वस्थ तथा मानसिक रूप से सुस्त व्यक्ति बहुत ही भावुक हो जाते हैं। वे जीवन की साधारण समस्याओं को हंसी-हंसी में सुलझा लेने के स्थान पर उनमें उलझ कर रह जाते हैं। वे अपनी खुशी, गम, पसन्द तथा नफ़रत को आवश्यकता से कहीं अधिक महत्त्व देने लगते हैं और वे अपना कीमती समय तथा शक्ति व्यर्थ ही गंवा देते हैं। इस प्रकार कोई महान् सफलता प्राप्त करने से वंचित रह जाते हैं। शारीरिक शिक्षा इन भावनाओं पर नियन्त्रण पाने की कला सिखाती है।

3. सामाजिक विकास (Social Development) शारीरिक शिक्षा व्यक्ति को अपने इर्द-गिर्द के लोगों के साथ सद्भावना से रहने की शिक्षा प्रदान करती है। जब एक व्यक्ति विभिन्न स्थानों के खिलाड़ियों के साथ मिल कर खेलता है तो सामाजिक विकास का अच्छा वातावरण पनपता रहता है। प्रत्येक खिलाड़ी अन्य खिलाड़ियों के स्वभाव, रीति-रिवाज, पहनावा, सभ्यता तथा संस्कृति से भली-भान्ति परिचित हो जाता है। कई बार दूसरों की अच्छी बातें तथा गुण ग्रहण कर लिए जाते हैं। देखने में आता है कि यूनिवर्सिटी, राज्यीय, राष्ट्रीय तथा अन्तर्राष्ट्रीय स्तरों पर खेल मुकाबलों का आयोजन किया जाता है। इनका मुख्य उद्देश्य लोगों में प्रेम तथा आदर की भावनाएं विकसित करना होता है।

4. चरित्र-निर्माण अथवा नैतिक विकास (Character Formation or Moral Development)-खेल का मैदान चरित्र-निर्माण की पाठशाला है। इसका कारण यह है कि खेल के मैदान में ही व्यक्ति खेल के नियमों को निभाते हैं। यहीं से वे अच्छा जीवन व्यतीत करने की कला सीखते हैं तथा सुलझे हुए इन्सान बन जाते हैं। खेल खेलते समय यदि रैफरी कोई ऐसा निर्णय दे देता है जो उन्हें पसन्द नहीं तो भी वे खेल जारी रखते हैं और कोई अभद्र व्यवहार नहीं करते। खेल के मैदान में ही आज्ञा-पालन, अनुशासन, प्रेम तथा दूसरों से सहयोग आदि के गुण सीखे जाते हैं। इस प्रकार प्रत्येक व्यक्ति का चरित्र-निर्माण और नैतिक विकास होता है।

5. नाड़ियों और मांसपेशियों में समन्वय (Neuro-muscular Coordination)-हमारी प्रतिदिन की क्रियाओं को समुचित ढंग से पूर्ण करना अनिवार्य है ताकि नाड़ियों और मांसपेशियों में समन्वय पैदा हो। शारीरिक शिक्षा इनमें समन्वय पैदा करने में सहायता देती है।

6. बीमारियों से बचाव (Prevention from Diseases) शारीरिक शिक्षा का उद्देश्य विद्यार्थियों को बीमारी से बचाना भी है। बहुत-सी बीमारियां अज्ञानता के कारण लग जाती हैं। शारीरिक शिक्षा का उद्देश्य बच्चों की बीमारियों के कारणों का ज्ञान देना है। वे इन कारणों से बच कर स्वयं भी बीमारियों से बच सकते हैं।

अन्त में, हम कह सकते हैं कि शारीरिक शिक्षा मनुष्य के सर्वपक्षीय विकास के लिए, नागरिकता के लिए, मानवीय भावनाओं के निर्माण तथा राष्ट्रीय एकता के लिए बहुत ही उपयोगी है।

प्रश्न 2.
हॉकी के खेल के मैदान में आप कौन-कौन से शारीरिक शिक्षा के उद्देश्य ग्रहण करते हो ?
(What are the objectives of Physical Education that one acquires in the game of Hockey ?)
उत्तर-
हॉकी का मैदान भी एक तरह की पाठशाला है जहां से विद्यार्थी शारीरिक शिक्षा के अनेक गुण ग्रहण करता है जिनसे वह जीवन में उन्नति के उच्च शिखर को छूता है और जीवन का हर पक्ष से भरपूर आनन्द उठाता है। हॉकी के क्रीड़ा-क्षेत्र में हम शारीरिक शिक्षा के निम्नलिखित गुणों को ग्रहण करते हैं –

1. सहनशीलता (Toleration) खेल के मैदान में हम सहनशीलता का पाठ पढ़ते हैं। वैसे तो सभी खिलाड़ी चाहते हैं कि जीत उनकी टीम की ही हो। परन्तु कई बार लाख चाहने पर भी विरोधी टीम विजयी हो जाती है। ऐसी स्थिति में पराजित टीम के खिलाड़ी दिल छोड़ कर नहीं बैठ जाते बल्कि अपना मनोबल ऊंचा रखते हैं। वे हार-जीत को एक ही समान समझते हैं। इस प्रकार खेल के मैदान से विद्यार्थियों को सहनशीलता की व्यावहारिक ट्रेनिंग मिलती है।

2. अनुशासन (Discipline)-खेल के मैदान में खिलाड़ी अनुशासन में रहने की कला सीखते हैं। उन्हें पता चलता है कि अनुशासन ही सफलता की कुंजी है। वे खेल में भाग लेते समय अनुशासन का पालन करते हैं। वे अपने कप्तान की आज्ञा मानते हैं तथा रैफरी के निर्णयों को सहर्ष स्वीकार करते हैं। खेल में पराजय को सामने स्पष्ट शारीरिक शिक्षा-इसके गुण एवं उद्देश्य देखते हुए भी वे कोई ऐसा अभद्र व्यवहार नहीं करते जिससे कोई उन्हें अनुशासनहीन – कह सके।

3. चरित्र विकास (Character Development) हॉकी के खेल में भाग लेने से विद्यार्थियों में सहयोग, प्रेम, सहनशीलता, अनुशासन आदि गुणों का विकास होता है जिनसे उनके चरित्र का विकास होता है। इस खेल में भाग लेने से उनमें सहयोग की भावना विकसित होती है। वे निजी हितों को समूचे हितों पर न्योछावर कर देते हैं।

4. व्यक्तित्व का विकास (Development of Personality) हॉकी के खेल में भाग लेने से विद्यार्थियों में कुछ ऐसे गुण विकसित हो जाते हैं, जिनसे उनके व्यक्तित्व का विकास हो जाता है। उनमें सहयोग तथा सहनशीलता आदि गुण विकसित होते हैं तथा उनका शरीर सुन्दर एवं आकर्षक बन जाता है। ये सभी अच्छे व्यक्तित्व के चिन्ह हैं।

5. अच्छे नागरिक बनाना (Creation of Good Citizens)-हॉकी के मैदान में खिलाड़ी में कर्त्तव्य-पालन, आज्ञा पालन, सहयोग, सहनशीलता आदि गुण विकसित हो जाते हैं जो उन्हें एक अच्छा नागरिक बनने में पर्याप्त सहायता पहुंचाते हैं। वे नागरिकता के सभी कर्तव्यों का भली-भान्ति पालन करते हैं। इस प्रकार हॉकी का मैदान अच्छे नागरिकों के निर्माण में महत्त्वपूर्ण भूमिका निभाता है।

6. सहयोग (Co-operation) हॉकी के खेल में भाग लेने वाला खिलाड़ी प्रत्येक खिलाड़ी का कहना मानता है। वह अपना विचार दूसरों पर बलात् लागू नहीं करवाता है, अपितु अपने विचार विनिमय के द्वारा खेल के मैदान में संयुक्त विचारधारा बनाता है। इस प्रकार सहयोग की भावना उत्पन्न होती है।

7. राष्ट्रीय भावना (National Spirit)-हॉकी का मैदान एक ऐसा स्थान है जहां हम बिना धर्म और वर्ग के आधार पर भाग ले सकते हैं। कोई भी खिलाड़ी खेल के मैदान में से किसी खिलाड़ी को धर्म के आधार पर टीम से बाहर नहीं निकाल सकता। इस प्रकार . खेल के मैदान में समानता और राष्ट्रीय एकता की भावना पैदा होती है।

8. आत्म-विश्वास की भावना (Self-Confidence) हॉकी के खेल के मैदान में खिलाड़ियों में आत्म-विश्वास की भावना पैदा होती है। जैसे, वह विजय-पराजय को एक समान समझता है। वही खिलाड़ी खेल के मैदान में सफल होता है जो धैर्य
और विश्वास के साथ खेले। इससे सिद्ध होता है कि हॉकी के खेल के द्वारा खिलाड़ियों में आत्म-विश्वास की भावना पैदा होती है।

9. विजय-पराजय को समान समझने की भावना (Spirit of giving equal importance to Victory of Defeat) हॉकी के खेल के द्वारा खिलाड़ियों में विजय-पराजय को एक समान समझने की भावना पैदा होती है।

हमें कभी भी विरोधी टीम का मज़ाक नहीं उड़ाना चाहिए या विजय की प्रसन्नता में पागल नहीं होना चाहिए। पराजित टीम को सदैव प्रोत्साहन देना चाहिए। यदि उसकी पराजय होती है तो उसे निराश और उत्साहहीन नहीं होने देना चाहिए अपितु उसका हौसला बढ़ाना चाहिए।

10. त्याग की भावना (Spirit of Sacrifice)-हॉकी के खेल के मैदान में त्याग की भावना अत्यावश्यक है। जब हम खेल में भाग लेते हैं तो हम अपने स्कूल, प्रान्त, क्षेत्र और सारे राष्ट्र के लिए अपने हित का त्याग करके उसकी विजय का श्रेय राष्ट्र को देते हैं। अत: यह सिद्ध होता है कि खेलें सदैव त्याग चाहती हैं। – ड्यूक ऑफ़ विलिंग्टन ने नेपोलियन को वाटरलू (Waterloo) के युद्ध में पराजित करने के पश्चात् कहा था, “वाटरलू का युद्ध एटन और हैरो के खेल के मैदानों में जीता गया।” (“The Battle of Waterloo was won at the playing-fields of Eton and Harrow.”)
इससे यह सिद्ध होता है कि खेलें अच्छे नेता पैदा करने में सहायक होती हैं।

शारीरिक शिक्षा-इसके गुण एवं उद्देश्य PSEB 9th Class Physical Education Notes

• .शारीरिक शिक्षा-शारीरिक क्रियाओं से हमें जो अनुभव प्राप्त होता है, उसे शारीरिक शिक्षा कहते हैं।
• शारीरिक शिक्षा का लक्ष्य-मनुष्य का सर्वोन्मुखी विकास ही शारीरिक शिक्षा का लक्ष्य है।
• शारीरिक शिक्षा के उद्देश्य-शारीरिक, मानसिक और नैतिक विकास ही शारीरिक शिक्षा के उद्देश्य हैं।
• खेल के मैदान में शारीरिक शिक्षा का उद्देश्य-खेल के मैदान से सहनशीलता, अनुशासन और चरित्र का विकास होता है।
• खाली समय का उचित प्रयोग-खेलों में भाग लेने से बच्चे खाली समय का उचित प्रयोग करते हैं जिससे उनमें बुरी आदतें नहीं पनपती हैं।
• खेलों के नेतृत्व का गुण-एक नेता में अच्छे चारित्रिक गुणों का होना आवश्यक है और ये खेलें मनुष्य में नेतृत्व के गुण पैदा करती हैं।

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 15 Probability MCQ Questions with Answers.

PSEB 9th Class Maths Chapter 15 Probability MCQ Questions

Multiple Choice Questions and Answer

Answer each question by selecting the proper alternative from those given below each question to make the statement true:

Question 1.
When a balanced die is thrown, the probability of getting 3 is …………….. .
A. \(\frac{1}{3}\)
B. \(\frac{1}{2}\)
C. \(\frac{1}{4}\)
D. \(\frac{1}{6}\)
Answer:
D. \(\frac{1}{6}\)

Question 2.
A card is drawn at random from a well shuffled pack of cards. The probability of that card being a king is …………………. .
A. \(\frac{1}{52}\)
B. \(\frac{1}{26}\)
C. \(\frac{1}{13}\)
D. 1
Answer:
C. \(\frac{1}{13}\)

Question 3.
A card is drawn at random from a well shuffled pack of cards. The probability of that card being a card other than picture cards is ……………….. .
A. \(\frac{4}{13}\)
B. \(\frac{10}{13}\)
C. \(\frac{3}{13}\)
D. \(\frac{1}{13}\)
Answer:
B. \(\frac{10}{13}\)

Question 4.
When an unbiased coin is tossed thrice, the probability of receiving three heads is ………………… .
A. \(\frac{1}{8}\)
B. \(\frac{1}{4}\)
C. \(\frac{1}{2}\)
D. \(\frac{3}{8}\)
Answer:
A. \(\frac{1}{8}\)

Question 5.
When three unbiased coins are tossed simultaneously, the probability of receiving exactly one tail is ………………… .
A. \(\frac{1}{8}\)
B. \(\frac{1}{2}\)
C. \(\frac{1}{4}\)
D. \(\frac{3}{8}\)
Answer:
D. \(\frac{3}{8}\)

Question 6.
When a balanced die is thrown, the probability of receiving an even number is ………………… .
A. \(\frac{1}{6}\)
B. \(\frac{5}{6}\)
C. \(\frac{1}{2}\)
D. \(\frac{1}{4}\)
Answer:
C. \(\frac{1}{2}\)

Question 7.
When a balanced die is thrown, the probability of receiving a prime number is ……………….. .
A. \(\frac{2}{3}\)
B. \(\frac{3}{4}\)
C. \(\frac{1}{3}\)
D. \(\frac{1}{2}\)
Answer:
D. \(\frac{1}{2}\)

Question 8.
When two balanced dice are thrown simultaneously, the probability of getting the total of numbers on dice as 9 is ………………. .
A. \(\frac{1}{9}\)
B. \(\frac{1}{6}\)
C. \(\frac{1}{3}\)
D. \(\frac{1}{12}\)
Answer:
A. \(\frac{1}{9}\)

Question 9.
Out of 100 days, the forecast predicted by the wheather department proved to be true on 20 days. Chosen any one day from these 100 days, the probability that the forecast proved to be false is ………………… .
A. \(\frac{1}{3}\)
B. \(\frac{1}{4}\)
C. \(\frac{3}{4}\)
D. \(\frac{4}{5}\)
Answer:
D. \(\frac{4}{5}\)

Question 10.
The probability of a month of January having 5 Sundays is ………………….. .
A. \(\frac{2}{7}\)
B. \(\frac{3}{7}\)
C. \(\frac{5}{7}\)
D. \(\frac{1}{7}\)
Answer:
B. \(\frac{3}{7}\)

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 15 Probability Ex 15.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 15 Probability Ex 15.1

Question 1.
In a cricket match, a batswoman hits a boundary 6 times out of 30 balls she plays. Find the probability that she did not hit a boundary.
Answer:
The batswoman played 30 balls. Hence, the total number of trials = 30. If the event that she did not hit a boundary is denoted by A, then. the number of trials when event A occured is 30 – 6 = 24.
∴ p(A) = \(\frac{\text { No. of trials in which event A occured }}{\text { The total number of trials }}\)
= \(\frac{24}{30}\)
= \(\frac{4}{5}\)
Thus, the probability that she did not hit a boundary is \(\frac{4}{5}\).

Question 2.
1500 families with 2 children were selected randomly, and the following data were s recorded:

Compute the probability of a family, chosen at random, having
(i) 2 girls
(ii) 1 girl
(iii) No girl. Also check whether the sum of these probabilities is 1.
Answer:
Here, the total number of families is 1500.
Hence, the total number of trials = 1500

(i) Let event A denote the event that the family chosen at random is having 2 girls.
Then, the number of trials when event A occured is 475.
∴ P(A) = \(\frac{\text { No. of trials in which event A occured }}{\text { The total number of trials }}\)
= \(\frac{475}{1500}\)
= \(\frac{19}{60}\)

(ii) Let event B denote the event that the family chosen at random is having 1 girl.
Then, the number of trials when event B occured is 814.
∴ P(B) = \(\frac{\text { No. of trials in which event B occured }}{\text { The total number of trials }}\)
= \(\frac{814}{1500}\)
= \(\frac{407}{750}\)

(iii) Let event C denote the event that the family chosen at random Is having no girl.
Then, the number of trials when event C occured is 211.
∴ p(C) = \(\frac{\text { No. of trials in which event } \mathrm{C} \text { occured }}{\text { The total number of trials }}\)
= \(\frac{211}{1500}\)
Now,
P(A) + P(B) + P(C) = \(\frac{19}{60}+\frac{407}{750}+\frac{211}{1500}\)
= \(\frac{475+814+211}{1500}\)
= \(\frac{1500}{1500}\)
= 1

Question 3.
Refer to sum no. 5 of “Sums to Enrich ‘Remember’” in chapter 14. Find the probability that a student of the class was born in August.
Answer:
From the Bar graph in the sum which is referred here, we get the following information:

Total number of students = 40 and the number of students born in August = 6.
Hence, if event A denotes the event that a student of the class is born in August, then the number of trials when event A occured is 6 and the total number of trials is 40.
∴ P(A) = \(\frac{\text { No. of trials in which event A occured }}{\text { The total number of trials }}\)
= \(\frac{6}{40}\)
= \(\frac{3}{20}\)

Question 4.
Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes:

If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up.
Answer:
Here, the total number of trials = 200. If event A denotes the event that 2 heads come up, then the number of trials when event A occured is 72.
∴ P(A) = \(\frac{\text { No. of trials in which event A occured }}{\text { The total number of trials }}\)
= \(\frac{72}{200}\)
= \(\frac{9}{25}\)

Question 5.
An organisation selected 2400 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a family. The information gathered is listed in the table below :

Suppose a family is chosen. Find the probability that the family chosen is ( i ) earning ? 10000- ? 13000 per month and owning exactly 2 vehicles.
(ii) earning ₹ 16000 or more per month and owning exactly 1 vehicle.
(iii) earning less than ₹ 7000 per month and does not .own any vehicle.
(iv) earning ₹ 13000 – ₹ 16000 per month and owning more than 2 vehicles.
(v) owning not more than 1 vehicle.
Answer:
Here, the total number of families is 2400. Hence, the total number of trials = 2400

(i) Let event A denote the event that the family is earning ₹ 10000 – ₹ 13000 per month and owning exactly 2 vehicles.
Then, the number of trials when event A occured = 29.
∴ P(A) = \(\frac{\text { No. of trials in which event A occured }}{\text { The total number of trials }}\)
= \(\frac{29}{2400}\)

(ii) Let event B denote the event that the family is earning ₹ 16000 or more per month and owning exactly 1 vehicle.
Then, the number of trials when even B occured = 579.
∴ P(B) = \(\frac{\text { No. of trials in which event B occured }}{\text { The total number of trials }}\)
= \(\frac{579}{2400}\)
= = \(\frac{193}{800}\)

(iii) Let event C denote the event that the family is earning less than ₹ 7000 per month and does not own any vehicle.
Then, the number of trials when event C occured = 10.
∴ P(C) = \(\frac{\text { No. of trials in which event C occured }}{\text { The total number of trials }}\)
= \(\frac{10}{2400}\)
= = \(\frac{1}{240}\)

(iv) Let event D denote the event that the family is earning ? 13000 -? 16000 per month and is owning more than 2 vehicles. Then, the number of trials when event D occured = 25.
∴ P(D) = \(\frac{\text { No. of trials in which event D occured }}{\text { The total number of trials }}\)
= \(\frac{25}{2400}\)
= \(\frac{1}{96}\)

(v) Let event E denote the event that the family is owning not more than 1 vehicle, i.e., 1 vehicle or no vehicle.
Then, the number of trials when event E occured.
= 10 + 160 + 0 + 305 + 1 + 535 + 2 + 469 + 1 + 579 = 2062
∴ P(E) = \(\frac{\text { No. of trials in which event E occured }}{\text { The total number of trials }}\)
= \(\frac{2062}{2400}\)
= \(\frac{1031}{1200}\)

Question 6.
Refer to table 7 of sum no. 7 in “Sums to Enrich ‘Remember’” in chapter 14.
(i) Find the probability that a student obtained less than 20 marks in the mathematics test.
(ii) Find the probability that a student obtained marks 60 or above.
Answer:
According to the table referred here, the total number of students = 90.
Hence, the total number of trials = 90.
(i) According to the same table, the number of students who obtained less than 20 marks in the mathematics test is 7. So, if the event that a student obtained less than 20 marks in mathematics test is called event A, then the number of trials when event A occured is 7.
∴ P(A) = \(\frac{\text { No. of trials in which event A occured }}{\text { The total number of trials }}\)
= \(\frac{7}{90}\)

(ii) Let event B denote the event that a student obtained 60 or more marks. Then, , according to the same table, the number of trials when event B occured = 15 + 8 = 23.
∴ P(B) = \(\frac{\text { No. of trials in which event B occured }}{\text { The total number of trials }}\)
= \(\frac{23}{90}\)

Question 7.
To know the opinion of the students about the subject statistics, a survey of 200 students was conducted. The data is recorded in the following table:

Opinion	Number of students
Like	135
Dislike	65

Find the probability that a student chosen at random
(i) Likes statistics,
(ii) Does not like it.
Answer:
Here, the total number of students = 200.
Hence, the total number of trials = 200.

(i) Let event A denote the event that a student likes statistics.
Then, the number of trials when event A occured = 135
∴ P(A) = \(\frac{\text { No. of trials in which event A occured }}{\text { The total number of trials }}\)
= \(\frac{135}{200}\)
= \(\frac{27}{40}\)

(ii) Let event B denote the event that a student does not like statistics. Then, the number of trials when event B occured = 65.
∴ P(B) = \(\frac{\text { No. of trials in which event B occured }}{\text { The total number of trials }}\)
= \(\frac{65}{200}\)
= \(\frac{13}{40}\)

Question 8.
Refer to sum no. 2, Exercise 14.2. What is the empirical probability that an engineer lives:
(i) less than 7 km from her place of work ?
(ii) more than or equal to 7km from her place of work ?
(iii) within \(\frac{1}{2}\)km from her place to work?
Answer:
The total number of observations in the question referred here is 40.
Hence, the total number of trials = 40.

(i) Let event A denote the event that the distance between her residence and the place of work is less than 7 km. Then there are 9 such observations, viz., 5, 3, 2, 3, 6, 5, 6, 2, 3.
Hence, the number of trials when event A occured = 9.
∴ P(A) = \(\frac{\text { No. of trials in which event A occured }}{\text { The total number of trials }}\)
= \(\frac{9}{40}\)

(ii) Let event B denote the event that the said distance is 7 km or more than 7 km. Then, all the remaining 31(40-9) observations refer to event B.
Hence, the number of trials when event B occured = 31
∴ P(A) = \(\frac{\text { No. of trials in which event A occured }}{\text { The total number of trials }}\)
= \(\frac{31}{40}\)

(iii) Let event C denote the event that the engineer lives within \(\frac{1}{2}\) km from her place of work. There is no observation which is \(\frac{1}{2}\) or less than \(\frac{1}{2}\).
Hence, the number of trials when event C occured = 0.
∴ P(C) = \(\frac{\text { No. of trials in which event C occured }}{\text { The total number of trials }}\)
= \(\frac{0}{40}\)
= 0

Question 9.
Activity: Note the frequency of two-wheelers, three-wheelers and four-wheelers going past during a time interval, in front of your school gate. Find the probability that any one vehicle out of the total vehicles you have observed is a two-wheeler.
Answer:
Note: Students should do this Activity themselves.

Question 10.
Activity: Ask all the students in your class to write a 3-digit number. Choose any student from the room at random. What is the probability that the number written by her / him is divisible by 3 ? Remember that a number is divisible by 3, if the sum of its digits is divisible by 3.
Answer:
Note: Students should do this Activity themselves.

Question 11.
Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour (in kg) :
4.97 5.05 5.08 5.03 5.00 5.06 5.08 4.98 5.04 5.07 5.00
Find the probability that any of these bags chosen at random contains more than 5 kg of flour.
Answer:
The total number of bags = 11.
Hence, the total number of trials = 11.
Let event A denote the event that a bag contains more than 5 kg of flour.
There are 7 bags weighing more than 5 kg.
Their weights (in kg) are 5.05, 5.08, 5.03, 5.06, 5.08, 5.04 and 5.07. Hence, the number of trials when event A occured = 7.
∴ P(A) = \(\frac{\text { No. of trials in which event A occured }}{\text { The total number of trials }}\)
= \(\frac{7}{11}\)

Question 12.
In sum no. 5, Exercise 14.2, you were asked to prepare a frequency distribution table, regarding the concentration of sulphur dioxide in the air in parts per million of a certain city for 30 days. Using this table, find the probability of the concentration of sulphur dioxide in the interval 0.12 – 0.16 on any of these days.
Answer:
In sum no. 5, Exercise 14.2, total number of days is 30.
Hence, the total number of trials = 30.
In the table prepared there, we see that the frequency of class 0.12 – 0.16 is 2.
Hence, during 2 days the concentration of sulphur dioxide (in ppm) was in the interval 0.12 – 0.16.
Let event A denote the event that the concentration of sulphur dioxide (in ppm) is in the interval 0.12 – 0.16.
Hence, the number of trials when event A occured = 2.
∴ P(A) = \(\frac{\text { No. of trials in which event A occured }}{\text { The total number of trials }}\)
= \(\frac{2}{30}\)
= \(\frac{1}{15}\)

Question 13.
In sum no. 1, Exercise 14.2, you were asked) to prepare a frequency distribution table regarding the blood groups of 30 students of a class. Use this table to determine the probability that a student of this class, selected at random, has blood group AB.
Answer:
In sum no. 1, Exercise 14.2, the total number of students is 30.
Hence, the total number of trials = 30.
Let event A denote the event that a student has blood group AB. The number of students having blood group AB is 3.
Hence, the number of trials when event A occured = 3.
∴ P(A) = \(\frac{\text { No. of trials in which event A occured }}{\text { The total number of trials }}\)
= \(\frac{3}{30}\)
= \(\frac{1}{10}\)

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 14 Statistics MCQ Questions with Answers.

PSEB 9th Class Maths Chapter 14 Statistics MCQ Questions

Multiple Choice Questions and Answer

Answer each question by selecting the proper alternative from those given below each question to make the statement true:

Question 1.
The marks scored by Kavya in 10 tests of Mathematics are 35, 18, 41, 24, 45, 10, 28, 32, 40, 15. Then, the range of the data is …………….. .
A. 45
B. 10
C. 35
D. 28.8
Answer:
C. 35

Question 2.
The average of the observations 3, 4, 5, 8, 12, 10, 13, 16, 18, 11 is …………………. .
A. 100
B. 10
C. 18
D. 3
Answer:
B. 10

Question 3.
The mean of first five odd natural numbers is ……………….. .
A. 3
B. 5
C. 4
D. 25
Answer:
B. 5

Question 4.
The mean of first four even natural numbers is ……………….. .
A. 5
B. 10
C. 20
D. 4
Answer:
A. 5

Question 5.
The mean of first five prime numbers is
A. 28
B. 2.8
C. 5.6
D. 1.4
Answer:
C. 5.6

Question 6.
If the mean of 2x, 5, 3x, 12, 5x, 17 and 6 is 20, then x = ………………….. .
A. 10
B. 20
C. 15
D. 40
Answer:
A. 10

Question 7.
The mean of the following distribution is ………………. .

A. 3.9
B. 7.8
C. 78
D. 39
Answer:
A. 3.9

Question 8.
If the mean of 12, 13, x, 17, 18 and 20 is 16, then x = ………………. .
A. 8
B. 4
C. 16
D. 32
Answer:
C. 16

Question 9.
For a given frequency distribution, n = 20 and Σf_ix_i = 140, then X̄ = ………………… .
A. 20
B. 14
C. 7
D. 28
Answer:
C. 7

Question 10.
The mean of \(\frac{2}{5},\), \(\frac{5}{7},\), \(\frac{3}{5},\) and \(\frac{2}{7},\) is ……………… .
A. \(\frac{1}{2},\)
B. \(\frac{3}{5},\)
C. \(\frac{5}{7},\)
D. 2
Answer:
A. \(\frac{1}{2},\)

Question 11.
The median of 14, 6, 2, 13, 9, 15 and 12 is …………………. .
A. 12
B. 10
C. 2
D. 15
Answer:
A. 12

Question 12.
The median of 21, 17, 13, 33, 19, 23 is ………………… .
A. 21
B. 20
C. 33
D. 19
Answer:
B. 20

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 14 Statistics Ex 14.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 14 Statistics Ex 14.4

Question 1.
The following number of goals were scored by a team in a series of 10 matches:
2, 3. 4, 5, 0. 1, 3, 3, 4, 3
Find the mean, median and mode of these scores.
Answer:
Here, n = 10.
Mean X̄ = \(\frac{\Sigma x_{i}}{n}\)
= \(\frac{2+3+4+5+0+1+3+3+4+3}{10}\)
= \(\frac{28}{10}\)
= 2.8
Thus, the mean of the given scores is 2.8 goals.

Arranging the observations in the ascending order, we get:
0, 1, 2, 3, 3, 3, 3, 4, 4, 5
Since n = 10 is an even number, \(\frac{n}{2}\) = 5 and \(\frac{n}{2}\) + 1 = 6.

Median M
= \(\frac{\left(\frac{n}{2}\right) \text { th observation }+\left(\frac{n}{2}+1\right) \text { th observation }}{2}\)
= \(\frac{5 \text { th } \text { observation }+6 \text { th } \text { observation }}{2}\)
= \(\frac{3+3}{2}\) = 3
Thus, the median of the given scores is 3 goals.
In the given data, observation 3 occurs most frequently (4 times). Hence, the mode of the data is 3 goals.

Question 2.
In a mathematics test given to 15 students, the following marks (out of 100) are recorded :
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60
Find the mean, median and mode of this data.
Answer:
Here, n = 15.
Mean X̄ = \(\frac{\Sigma x_{i}}{n}\)
= \(\begin{gathered}
41+39+48+52+46+62+54+40 \\
+96+52+98+40+42+52+60 \\
\hline 15
\end{gathered}\)
= \(\frac{822}{15}\) = 54.8
Thus, the mean of the data is 54.8 marks.
Arranging the observations in the ascending order, we get:
39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98
Here, n = 15 is an odd number.
Median M = \(\left(\frac{n+1}{2}\right)\)th observation
= \(\left(\frac{15+1}{2}\right)\)th observation
= 8 th observation
= 52
Thus, the median of the data is 52 marks.
In the given data, observation 52 occurs most frequently (3 times). Hence, the mode of the data is 52 marks.

Question 3.
The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x.
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
Answer:
Here, the median = 63 and n = 10.
∴ \(\frac{n}{2}\) = 5 and \(\frac{n}{2}\) + 1 = 6

Median M
= \(\frac{\left(\frac{n}{2}\right) \text { th observation }+\left(\frac{n}{2}+1\right) \text { th observation }}{2}\)
∴ 63 = \(\frac{5 \text { th } \text { observation }+6 \text { th } \text { observation }}{2}\)
∴ 63 = \(\frac{(x)+(x+2)}{2}\)
∴63 × 2 = x + x + 12
∴126 = 2x + 2
∴ 2x = 124
∴ x = 62

Question 4.
Find the mode of 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18.
Answer:
Here, just by simple observation, it is clearly seen that observation 14 occurs most frequently, i.e., 4 times.
Hence, the mode of the data is 14.

Question 5.
Find the mean salary of 60 workers of a factory from the following table:

Answer:

Mean X̄ = \(\frac{\Sigma f_{i} x_{i}}{n}\)
= \(\) = \(\frac{3,05,000}{60}\) = 5083.33
Thus, the mean salary is ₹ 5083.33.

Question 6.
Give one example of a situation in which
(i) the mean is an appropriate measure of central tendency.
Answer:
For the students studying in the same class, usually their level of knowledge and understanding would be more or less equal. There would be a few student having this level low and there would be a few students having this level high. Their level of knowledge and understanding would be reflected in the marks scored by them at an examination. Hence, the mean of marks scored by them at an examination is an appropriate measure of central tendency.

(ii) the mean is not an appropriate measure of central tendency but the median is an appropriate measure of central tendency.
Answer:
If we consider the monthly income of the people of certain region, the mean is not an appropriate measure of central tendency but the median is an appropriate measure of central tendency.

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 14 Statistics Ex 14.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 14 Statistics Ex 14.3

Question 1.
A survey conducted by an organisation for the cause of illness and death among the women between the ages 15-44 (in years) worldwide, found the following figures (in %):

Causes	Female fatality rate (%)
1. Reproductive health conditions	31.8
2. Neuropsychiatric conditions	25.4
3. Injuries	12.4
4. Cardiovascular conditions	4.3
5. Respiratory conditions	4.1
6. Other causes	22.0

(i) Represent the information given above graphically.
Answer:

(ii) Which condition is the major cause of women’s ill health and death worldwide?
Answer:
‘Reproductive health conditions’ is the major cause of womens ill health and death worldwide.

(iii) Try to find out, with the help of your teacher, any two factors which play a major role in the cause in (ii) above being the major cause.
Answer:
‘Malnutrition’ and ‘Lack of necessary medical facilities’ can be considered as two other factors which play a major role in female fatality.

Question 2.
The following data on the number of girls (to the nearest ten) per thousand boys in different sections of Indian society is given below:

Section	Number of girls per thousand bays
Scheduled Caste (SC)	940
Scheduled Tribe (ST)	970
Non-SC/ST	920
Backward districts	950
Non-backward districts	920
Rural	930
Urban	910

(i) Represent the information above by a bar graph.
(ii) In the classroom discuss what conclusions can be arrived at from the graph.
Answer:

Question 3.
Given below are the seats won by different political parties in the polling outcome of a state assembly elections:

(i) Draw a bar graph to represent the polling results.
Answer:
Seats won by different political parties

(ii) Which political party won the maximum number of seats?
Answer:
Political party: A won the maximum number of seats.

Question 4.
The length of 40 leaves of a plant are measured correct to one millimetre, and the obtained data is represented in the following table:

Length (in mm)	Number of leaves
118-126	3
127-135	5
136-144	9
145-153	12
154-162	.5
163-171	4
172-180	2

(i) Draw a histogram to represent the given data. [Hint: First make the class intervals continuous.]
(ii) Is there any other suitable graphical representation for the same data?
(iii) Is it correct to conclude that the maximum number of leaves are 153 mm long? Why?
Answer:
Making the class intervals continuous, we get the following table:

Length (in mm)	Number of leaves
117.5-126.5	3
126.5- 135.5	5
135.5-144.5	9
144.5-153.5	12
153.5- 162.5	5
162.5-171.5	4
171.5-180.5	2

(i) Length of leaves in millimetre

(ii) Yes. The given data can also be represented by ‘Frequency polygon’.

(iii) It is not correct to conclude that the maximum number of leaves are 153 mm long, because even if the frequency of class 145-153 is 12, we do not have the information about the length of each of those 12 leaves individually.

Question 5.
The following table gives the life times of 400 neon lamps:

Life time (in hours)	Number of lamps
300 – 400	14
400 – 500	56
500 – 600	60
600 – 700	86
700 – 800	74
800 – 900	62
900 – 1000	48

(i) Represent the given information with the help of a histogram.
Answer:

(ii) How many lamps have a life time of 700 hours or more than 700 hours ?
Answer:
The-frequencies of classes 700-800, 800-900 and 900-1000 are 74, 62 and 48 respectively.
Hence, the life time of 184 (74 + 62 + 48) lamps is 700 hours or more than 700 hours.

Question 6.
The following table gives the distribution of students of two sections according to the marks obtained by them:

Represent the marks of the students of both the sections on the same graph by two frequency polygons. From the two polygons compare the performance of the two sections.
Answer:
To draw the frequency polygons of both the sections, we find the class marks of each class and prepare the following tables:

Section A

Marks	Class mark	Frequency
0-10	5	3
10-20	15	9
20-30	25	17
30-40	35	12
40-50	45	9

Section B

Marks	Class mark	Frequency
0-10	5	5
10-20	15	19
20-30	25	15
30-40	35	10
40-50	45	1

Comparing the performance of both the sections from the frequency polygons, we observe that the performance of students of section A is better than the performance of students of section B.

Question 7.
The runs scored by two teams A and B on the first 60 balls in a cricket match are given below:

Number of balls	Team A	Team B
1-6	2	5
7-12	1	6
13-18	8	2
19-24	9	10
25-30	4	5
31-36	5	6
37-42	6	3
43-48	10	4
49-54	6	8
55-60	2	10

Represent the data of both the teams on the same graph by frequency polygons.
[Hint: First make the class intervals continuous.]
Answer:

Number of runs made by Team A and Team B in first 60 balls.

Question 8.
A random survey of the number of children of various age groups playing in a park was found as follows:

Age (in years)	Number of children
1-2	5
2-3	3
3-5	6
5-7	12
7-10	9
10-15	10
15-17	4

Draw a histogram to represent the data above.
Answer:

Children of various age groups playing in a park

Question 9.
100 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letters in the English alphabet in the surnames was found as follows:

Number of letters	Number of surnames
1-4	6
4-6	30
6-8	44
8-12	16
12-20	4

(i) Draw a histogram to depict the given information.
(ii) Write the class interval in which the maximum number of surnames lie.
Answer:

(i) Information regarding the number of surnames having given number of letters
Answer:

(ii) Write the class interval in which the maximum number of surnames lie.
Answer:
The maximum number of surnames lie in the class interval 6-8.

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 13 Surface Areas and Volumes Ex 13.9 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes Ex 13.9

Question 1.
A wooden bookshelf has external dimensions as follows : Height =110 cm, Depth = 25 cm, Breadth = 85 cm (see the given figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.

Answer:
Outer faces to be polished:

• One face on back side of the bookshelf, measuring 110 cm × 85 cm.
• Two faces on the sides, each of those measuring 110 cm × 25 cm.
• The top and the base, each of those measuring 85 cm × 25 cm.
• Two vertical strips on the front side, each of those measuring 110 cm × 5 cm.
• Four horizontal strips on the front side, each of those measuring 75 cm × 5 cm.

Thus, total area of region to be polished
= [(110 × 85) + 2(110 × 25) + 2 (85 × 25) + 2(110 × 5) + 4(75 × 5)] cm²
= (9350 + 5500 + 4250 + 1100+ 1500) cm²
= 21700 cm²
20 paise per cm² = ₹ 0.20 per cm²
Cost of polishing 1 cm2 region = ₹ 0.20
∴ Cost of polishing 21700 cm² region
= ₹ (21700 × 0.20)
= ₹ 4340

Inner faces to be painted:

• Two faces on the sides each of those measuring 90 cm × 20 cm.
• Two faces each of two shelves, the top face and the bottom face, in all six face, each of those measuring 75 cm × 20 cm.
• Face on the back side, measuring 90 cm × 75 cm.

Thus, total area of the region to be painted
= [2 (90 × 20) + 6 (75 × 20) + (90 × 75)] cm²
= (3600 + 9000 + 6750) cm²
= 19350 cm²
10 paise per cm² = ₹0.10 per cm²
Cost of painting 1 cm² region = ₹ 0.10
∴ Cost of painting 19350 cm² region = ₹ (19350 × 0.10) = ₹ 1935
Then, the total expense of polishing and painting = ₹ 4340 + ₹ 1935 = ₹ 6275

Question 2.
The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in the given figure. Eight such spheres are used for this purpose, and are to be ‘ painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm² and black paint costs 5 paise per cm².

Answer:
For each wooden sphere,
radius r = \(\frac{\text { diameter }}{2}\) = \(\frac{21}{2}\) cm
Curved surface area of 1 sphere
= 4πr²
= 4 × \(\frac{22}{7}\) × \(\frac{21}{2}\) × \(\frac{21}{2}\) cm²
= 1386 cm²
For each cylindrical support, radius r = 1.5 cm and height h = 7 cm.
Area of top of cylindrical support
= πr²
= \(\frac{22}{7}\) × 1.5 × 1.5 cm²
= 7.07 cm² (approx.)
Hence, the area of each sphere to be painted silver = 1386 cm² – 7.07 cm² = 1378.93 cm²
∴ Total area of eight spheres to be painted silver = 1378.93 cm² × 8 = 11031.44 cm²
25 paise per cm² = ₹ 0.25 per cm²
Cost of painting silver in 1 cm² region = ₹ 0.25
∴ Cost of painting silver in 11031.44 cm² region
= ₹ (11031.44 x 0.25)
= ₹ 2757.86 (approx.)
Curved surface area of 1 cylindrical support
= 2πrh
= 2 × \(\frac{22}{7}\) × 1.5 × 7 cm
= 66 cm²
∴ Total area of eight cylindrical supports to be painted black = 66 cm² × 8 = 528 cm²
5 paise per cm² = ₹ 0.05 per cm²
Cost of painting black in 1 cm² region = ₹ 0.05
∴ Cost of painting black in 528 cm² region = ₹ (528 × 0.05)
= ₹ 26.40
Thus, the total cost of painting = ₹ 2757.86 + ₹ 26.40
= ₹ 2784.26 (approx.)

Question 3.
The diameter of a sphere is decreased by 25 %. By what per cent does its curved surface area decrease?
Answer:
Suppose, the initial diameter of the sphere is d units and radius is r units.
∴ d = 2r
Original curved surface area of the sphere
= 4πr²
= π (4r²)
= π (2r)²
= πd² unit²
Now, the diameter of the sphere is reduced by 25 %. Hence, the new diameter of the sphere is 0.75d units.
New curved surface area of the sphere
= π (diameter)
= π (0.75d)² unit²
= 0.5625 πd² unit²
∴ The decrease in the curved surface area of the sphere = πd² – 0.5625 πd²
= 0.4375 πd² unit²
∴Percentage decrease in the curved surface area of the sphere = \(\frac{0.4375 \pi d^{2}}{\pi d^{2}}\) × 100 = 43.75 %
Thus, when the diameter of a sphere is decreased by 25 %, its curved surface area decreases by 43.75 %.

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 12 Heron’s Formula Ex 12.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 12 Heron’s Formula Ex 12.2

Question 1.
A park, in the shape of a quadrilateral ABCD has ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m and AD = 8 m. How much area does it occupy?
Answer:

In ∆ BCD, ∠C = 90°
∴ BD² = BC² + CD²
= (12)² + (5)²
= 144 + 25
= 169
= (13)²
∴ BD = 13 m

In ∆ BCD, a = 5 m, b = 12 m and c = 13 m
∴ Semiperimeter s = \(\frac{a+b+c}{2}\)
= \(\frac{5+12+13}{2}\) = \(\frac{30}{2}\) = 15 m
Then, s – a = 15 – 5 = 10m,
s – b = 15 – 12 = 3m and
s – c = 15 – 13 = 2 m.

Area of ∆ BCD = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{15 \times 10 \times 3 \times 2}\) m²
= \(\sqrt{900}\) m²
= 30 m²

Note: ∆ BCD is a right triangle.
∴ Area of ∆ BCD = \(\frac{1}{2}\) × BC × CD
= \(\frac{1}{2}\) × 12 × 5 = 30 m²

Now, in ∆ ABD, a = 9 m, b = 13 m arid c = 8 m
∴ Semiperimeter s = \(\frac{a+b+c}{2}\)
= \(\frac{9+13+8}{2}\) = \(\frac{30}{2}\) = 15 m
Then,
s – a = 15 – 9 = 6m,
s – b = 15 – 13 = 2m and
s – c = 15 – 8 = 7 m.

Area of ∆ ABD = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{15 \times 6 \times 2 \times 7}\) m²
= \(\sqrt{5 \times 3 \times 3 \times 2 \times 2 \times 7}\) m²
= 6 √35 m²
= 35.5 m² (approx.)
Then, the area of park in the shape of quadrilateral ABCD
= Area of ∆ BCD + Area of ∆ ABD
= (30 + 35.5) m² (approx.)
= 65.5 m² (approx.)
Thus, the area of the park is 65.5 m² (approx.)

Question 2.
Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm.
Answer:

In ∆ ABC, a = 3 cm; b = 4 cm and c = 5 cm
∴ Semiperimeter s = \(\frac{a+b+c}{2}\)
= \(\frac{3+4+5}{2}\)
= \(\frac{12}{2}\) = 6 cm
Then,
s – a = 6 – 3 = 3 cm,
s – b = 6 – 4 = 2 cm and,
s – c = 6 – 5 = 1 cm.
Area of ∆ ABC = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{6 \times 3 \times 2 \times 1}\) cm²
= 6 cm²
Note: Proving that ∆ ABC is a right triangle, Area of ∆ ABC = \(\frac{1}{2}\) × 3 × 4 = 6 cm² can be obtained easily.
In ∆ ACD, a = 4 cm; b = 5 cm and c = 5 cm

Area of quadrilateral ABCD
= Area of ∆ ABC + Area of ∆ ACD
= (6 + 9.2) cm² (approx.)
= 15.2 cm² (approx.)

Question 3.
Radha made a picture of an aeroplane with coloured paper as shown in the given figure, s Find the total area of the paper used. ;

Answer:
The sides of the triangle in part 1 measure 5 cm, 5 cm and 1 cm.
∴ a = 5 cm, b = 5 cm and c = 1 cm
∴ Semiperimeter s = \(\frac{a+b+c}{2}\)
= \(\frac{5+5+1}{2}\) = \(\frac{11}{2}\) cm
Area of part 1
= Area of triangle

The length and breadth of rectangle in part II are 6.5 cm and 1 cm respectively.
Area of part II = Area of rectangle
= length × breadth
= (6.5 × 1) cm²
= 6.5 cm²
For the trapezium in part III, the parallel sides measure 1 cm and 2 cm, while both the non-parallel sides measure 1 cm each.

Drawing DM ⊥ AB and CN ⊥ AB. we get
AM = BM = \(\frac{2-1}{2}\) = \(\frac{1}{2}\) cm.
In ∆ DMA, ∠M = 90°
Area of trapezium ABCD
= \(\frac{1}{2}\) × Sum of parallel sides X Distance between parallel sides
= \(\frac{1}{2}\) × (AB + CD) × DM
= \(\frac{1}{2}\) × (2 + 1) × \(\frac{\sqrt{3}}{2}\)cm²
= \(\frac{1}{2}\) × 3 × \(\frac{\sqrt{3}}{2}\) cm²
= 1.3 cm² (approx.)
For the right triangle in part IV the sides forming the right angle measure 6 cm and 1.5 cm.
Area of right triangle in part IV.
= \(\frac{1}{2}\) × Product of sides forming the right angle
= \(\frac{1}{2}\) × 6 × 1.5 cm²
= 4.5 cm²
The right triangle in part V is congruent to the right triangle in part IV.
∴ Area of right triangle in part V = 4.5 cm²
Now, total area of the paper used
= Areas of figures in part I to part V
= (2.5 + 6.5 + 1.3 + 4.5 + 4.5) cm²
= 19.3 cm²

Question 4.
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Answer:
In the given triangle, a = 26 cm, b = 28 cm and c = 30 cm
∴ Semiperimeter s = \(\frac{a+b+c}{2}\)
= \(\frac{26+28+30}{2}\) = \(\frac{84}{2}\) = 42 cm
Area of triangle

= 7 × 6 × 4 × 2 cm²
= 336 cm²
The area of the triangle and the area of the parallelogram are equal.
∴ Area of the parallelogram = 336 cm²
∴ Base × Corresponding altitude = 336 cm²
∴ 28 cm × Corresponding altitude = 336 cm²
∴ Corresponding altitude = \(\frac{336}{28}\) cm
∴ Corresponding altitude = 12 cm
Thus, the height of the parallelogram is 12 cm.

Question 5.
A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
Answer:

Rhombus ABCD in the given figure represents the field.
A diagonal of a rhombus divides it into two congruent triangles.
∴ Area of rhombus ABCD = 2 × Area of ∆ ABC
In ∆ ABC, a = 30 m; b = 30 m; and c = 48 m.
∴ Semiperimeter s = \(\frac{a+b+c}{2}\)
= \(\frac{30+30+48}{2}\) = \(\frac{108}{2}\) = 54 cm
Area of ∆ ABC

= 3 × 6 × 24 m²
= 432 m²
Now, area of the field
= area of rhombus ABCD
= 2 × area of ∆ ABC
= 2 × 432 m²
= 864 m²
Now, area of grass field available for 18 cows to graze = 864 m²
∴ Area of grass field available for 1 cow to graze = \(\frac{864}{18}\) m² = 48 m²
Thus, each cow gets 48 m² of grass field to graze.

Question 6.
An umbrella is made by stitching 10 triangular pieces of cloth of two different colours (see the given figure), each piece measuring 20 cm, 50 cm and 50 cm. How much cloth of each colour is required for the umbrella?

Answer:
Out of 10 triangular pieces, 5 are dark coloured and 5 are light coloured.
For each triangle, a = 20 cm, b = 50 cm and c = 50 cm

Hence, the total area of 5 dark coloured cloth pieces = 5 × 200 √6 cm² = 1000 √6 cm²
Similarly, the total area of 5 light coloured cloth pieces = 5 × 200 √6 cm² = 1000 √6 cm²

Question 7.
A kite in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and sides 6 cm each is to be made of three different shades as shown in the given figure. How much paper of each shade has been used in it?

Answer:
Let us name the square part as ABCD and the triangular part as CMN.
Suppose the length of square ABCD is xcm.
∴ In ∆ ABD, AB = AD = x cm and ∠A = 90°
The length of hypotenuse BD is given to be 32 cm.
AB² + AD² = BD² (Pythagoras’ theorem)
∴ (x)² + (x)² = (32)²
∴ 2x² = 1024
∴ x² = 512
∴ x = √512
∴ x = \(\sqrt{256 \times 2}\)
∴ x = 16√2
Thus, the length of each side of square ABCD is 16 √2 cm.
Area of part I = Area of ∆ ABD
= \(\frac{1}{2}\) × AB × AD (∠A is a right angle.)
= \(\frac{1}{2}\) × 16 √2 × 16 √2 cm²
= 256 cm²
Area of part II = Area of A BCD
= \(\frac{1}{2}\) × BD × CD (∠A is a right angle.)
= \(\frac{1}{2}\) × 16 √2 × 16 √2 cm²
= 256 cm²
Note: Here, area of square ABCD can easily be found as below:
Area of square ABCD = \(\frac{(\text { Hypotenuse })^{2}}{2}\)
= \(\frac{(32)^{2}}{2}\)
= \(\frac{1024}{2}\)
= 512 cm²
To find the area of part III, we find the area of ∆ CMN.
In ∆ CMN, a = 6 cm, b = 8 cm and c = 6 cm.
∴ Semiperimeter s = \(\frac{a+b+c}{2}\)
= \(\frac{6+8+6}{2}\) = \(\frac{20}{2}\) = 10 cm

Area of part III
= Area of ∆ CMN

= 8 × 2.24 cm² (approx.)
= 17.92 cm² (approx.)

Question 8.
A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9 cm, 28 cm and 35 cm (see the given figure). Find the cost of polishing the tiles at the rate of 50 p per cm².

Answer:
For each of 16 triangular tiles,
a = 9 cm; b = 28 cm and c = 35 cm

= 88.2 cm² (approx.)
∴ Area of 16 tiles = 16 × 88.2 cm²
= 1411.2 cm²
50 paise = ₹ 0.50
Cost of polishing 1 cm² region = ₹ 0.50
∴ Cost of polishing 1411.2 cm² region
= ₹ (1411.2 × 0.50)
= ₹ 705.60

Question 9.
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Answer:

In the given figure, trapezium ABCD represents the field in which AB || CD,
AB = 25 m, BC = 14 m, CD = 10 m and DA = 13 m.
Through C, draw a line parallel to DA to intersect AB at E.
In quadrilateral AECD, AE || CD and DA || CE
∴ AECD is a parallelogram.
∴ CE = DA = 13 m and AE = CD = 10 m
Now, BE = AB – AE = 25 – 10 = 15 m
In ∆ CEB, a = 13 m; b = 15 m and c = 14 m

In ∆ CEB, draw CM ⊥ BE.
Area of ∆ CEB = \(\frac{1}{2}\) × BE × CM
∴ 84 m² = \(\frac{1}{2}\) × 15 m × CM
∴ CM = \(\frac{84 \times 2}{15}\) m
∴ CM = 11.2 m
Area of parallelogram AECD
= Base × Corresponding altitude
= AE × CM
= 10 × 11.2 m²
= 112 m²
Hence, area of the field
= Area of trapezium ABCD
= Area of ∆ CEB + Area of parallelogram AECD
= 84 m² + 112 m²
= 196 m²
Note: After finding CM = 11.2m, the area of . the field can also be found as below:
Area of the field
= Area of trapezium ABCD
= \(\frac{1}{2}\) × sum of parallel sides × distance between parallel sides
= \(\frac{1}{2}\) × (AB + CD) × CM
= \(\frac{1}{2}\) × (25 + 10) × 11.2 m²
= \(\frac{1}{2}\) × 35 × 11.2 m²
= 196 m²

Punjab State Board PSEB 9th Class English Book Solutions English Paragraph Writing Exercise Questions and Answers, Notes.

PSEB 9th Class English Paragraph Writing

1. My Father

My father is an able person. He is a farmer. He is not well-educated. But he knows his work well. He is very hard-working. He is truthful and honest. So people respect him. They greet him respectfully. My father has an open mind. He tries to settle the quarrels among the people of the village. He is the wisest man of the village. He leads a simple and clean life. He does not lose temper with anybody. He is respected by one and all. I am proud of my father.

2. My Mother

Shrimati Asha is my mother. She is 40 years old. She is a kind and noble lady. She is active and smart. She is an M.A. She is a very simple lady. She has good habits. She gets up early in the morning. Then she cleans the house. She takes a bath and prays to God. She goes to temple daily. She prepares food for us. She looks after us all. She helps me in my studies. At night, she tells us stories. She loves me very much. I am proud of my mother. May she live long !

3. My Younger Brother

Surinder is my younger brother. He is twelve years old. He is strong and healthy. He is tall for his age. He is very intelligent. He is honest. He never tells a lie. He is hard-working and obedient. He reads in the 6th class. He is the monitor of his class. He stands first in his class. He does his homework daily. He does not mix with bad boys. All the teachers love him. He is very fond of cricket. He is a member of the school cricket team. He is a good singer also. He is fond of reading storybooks. We are proud of him.

4. The Person I Dislike Most

Mr. Chaudhry, our next-door neighbour, is the person I dislike most. He has made our life miserable. Whenever he sees that we are studying, he switches on his TV at full volume. He has a big dog. He keeps it unchained. Many a time the dog bites people going through the street. Mr. Chaudhry’s wife is a very quarrelsome lady. She quarrels over trifles. She has six children. They make mischiefs all the day. Their mother never scolds them. These children are very rude. They know no manners. They write dirty words on the walls. But nobody dares complain against them to their parents. It is really a curse to have such a neighbour.

5. My School

I read in Arya High School, Ludhiana. It is a very big school. It has one huge gate. It has two storeys. There are fifty rooms. The rooms are airy. Each room has two electric fans. The hall of our school is very big. The school has two big playgrounds. It has a beautiful garden also. There are ten classes in our school.

Each class has four sections. Each section has about sixty students. Our Headmaster is very able. He is very kind to the students. He is very hardworking. The teachers of our school are also able and hard-working. They love the students and the students respect them. Our school shows very good results every year. I love my school. I am proud of it. May it propser day and night!

6. Our Headmaster

Sh. Sohan Lal is the headmaster of our school. He is forty years old. He is tall and strong. He is active and smart. He is an M.A., B.Ed. Our headmaster is true to his duty. He is very punctual. He comes to school in time. He sits in his office. He works very hard. He plans his work well. He is very intelligent. He watches the working of the school. All the teachers and students respect him. He is a good teacher. He is a good speaker. He is a good writer also. He has written many books. He is a good player. He plays games in the evening. He is all in all in our school. We are proud of him. May he live long !

7. The Prize Distribution Function

The prize distribution function of our school was held on the seventh of March this year. The Education Minister presided over the function. The Minister took his seat and the function began. The Headmaster spoke a few words to welcome the guests and the Minister. Then the Headmaster requested the Minister to give away the prizes. The Minister shook hands with the prize-winners. All the prize-winners were loudly cheered. After giving away the prizes, the Minister made a short speech. He congratulated the prize-winners. He congratulated the Headmaster and the staff on their excellent work. In the end, the Headmaster thanked the Minister and the function was over. Tea was served to the guests and the prize-winners.

8. Our School Peon

Ramu is our school peon. He is twenty-five years old. He is tall and strong. He wears a khaki uniform. He is obedient and honest. He is true to his duty. He respects the teachers. He always speaks the truth. He knows his job well. Ramu lives in the school. He gets up early in the morning. He sweeps the school. He dusts the office. He rings the bell at the right time. He is busy the whole day. He is loyal to the school. He looks after the school property. His duty is hard, but his pay is small. I pity his lot.

9. A Postman

The postman is a very useful public servant. His duty is very hard. He has to do his duty in sun and rain. He goes to the Head Post Office in the morning. There he gets the dak. He arranges the letters. He puts them in a bag. Then he goes on his beat. He goes from door to door. He is eagerly waited for. He brings good as well as bad news. He helps to bring the world closer. A postman has to work hard. But his pay is small. He can hardly make both ends meet. I pity his lot.

10. A Rickshaw-Puller 

The life of a rickshaw-puller is very hard. He lives by the sweat of his brow. He pulls heavy loads. He pulls men, women and children. It is very painful to look at him. A rickshaw-puller hardly gets as much as he deserves. People try to give him as little as possible. He has to work in sun and rain from morning till evening. Even then, he gets very little to eat. He is in rags. It is unlucky that even in this age of science men have to work like beasts of burden to earn their bread.

11. The Diwali Festival

Diwali is an important Indian festival. It falls in the month of October or November. It comes twenty days after Dussehra. Shri Ram came back to Ayodhya on this day. Shri Guru Hargobind was set free by the Mughal Emperor on this day. This festival is celebrated in every village and town. Houses and shops are painted in new colours. People light their homes with candles and electric lights. They buy sweets and toys. They distribute gifts among friends and relatives. Children enjoy fireworks at night. On this day, people worship goddess Lakshmi Some people gamble on this day. It is evil. It should be ended.

12. The Dussehra Festival

Dussehra is an important Hindu festival. It comes off in October. Rama defeated Ravar on this day. It marks the victory of good over evil. The festival lasts for ten days. Ram Lila staged at night. Many people come to see this Lila. On the last day, a fair is held. Many people come to see the fair. Everyone looks happy. Effigies of Ravana, Meghnada and Kumbhakarn are set up. Rama shoots arrows at the effigies. At about sunset, Hanumana sets them on fire After this people come back to their homes. They feel happy.

13. The Independence Day

India became a free country on August 15, 1947. So, August 15 is called the Independence Day of India. The British rule came to an end on this day. It is a red-letter day in the history of the country. It is celebrated all over the country with great enthusiasm. On this day, all schools, colleges and offices remain closed. It is a national holiday. Public meetings are held in all towns and cities. A big function is held in Delhi. The Prime Minister unfurls the national flag at the Red Fort. Our freedom is a hard-won freedom. We should protect it.

14. The Republic Day

India became a Republic on January 26, 1950. The Constitution of the country came into force on this day. India became a secular democratic country. The power of government passed into the hands of the common people. All castes, creeds and religions are to be equal in the eyes of the law. It is a red-letter day in the history of the country. It is celebrated all over the country with great enthusiasm. The national flag is unfurled at all the public buildings. A big function is held in Delhi. The President of the country presides over this function. It is worth seeing. This day is a national holiday.

15. Mahatma Gandhi

Mahatma Gandhi was born on October 2, 1869. He was unlike other boys. He was very gentle. He loved truth. He respected his teachers. After doing law he started practice in India. He did not take up false cases. He went to Africa to fight a case. There he saw the poor Indians. The English treated them badly. Gandhiji fought for their rights for ten years. Then he came back to India. He fought for the freedom of India. He gave us a new way of fighting. It was ‘ahimsa’. It was more powerful than violence. He was able to free India in 1947. He was a real Mahatma. He led a very simple life. He is called the Father of our Nation. A mad person shot him dead on January 30, 1948. Gandhiji’s name will always be remembered.

16. An Ideal Student

An ideal student is a knowledge-seeker in the real sense. He obeys his teachers. He has full confidence in them. He is regular and punctual. He works hard at studies. But he takes part in games also. He does not read cheap and dirty literature. He reads only good and useful books. An ideal student believes in simple living and high thinking. He knows the value of discipline. He does not waste the hard-earned money of his parents. An ideal student is a true patriot. In short, he has all the qualities of head and heart.

17. The Recess Period

The recess is the period of enjoyment. In this period, the students feel happy. They enjoy freedom for some time. As soon as the recess period begins, students rush out of their classrooms. Some of them run to the vendors. They buy things to eat. Others go to the taps to drink water. There is great rush in the playground. Some love to play there while others like to sit under the shady trees. They talk about their friends and teachers. Soon the bell goes. Students run back to their classes. The students feel fresh and start their studies once again.

18. A One-Day Cricket Match

Last Sunday, a one-day cricket match was played between our school and Arya High School. Each team played 40 overs. The match started at 10 a.m. We won the toss. We decided to bat first. Mohan and Gopal were our openers. Mohan made 30 runs and was out. Now Raja came in to bat. He did not play well. He was out for a duck. The next four players made 60 runs. Our team was out at 120 runs. Now it was the turn of Arya High School. They had good openers. They made 60 runs. Their third batsman was a hitter. He made 30 runs. But the other players were soon out. Their team could make only one hundred runs. We won the match by 20 runs. It was really a very interesting match.

19. A Football Match

Last Monday, a football match was played between our school and Khalsa School. It was played on our school grounds. Sh. Jaswant Singh was the referee. He blew the whistle. There was a toss. We won the toss. We chose our side. The match began. At first, the game was slow, but soon it became brisk. All the players played well. Our defence was very strong. There was no goal. The referee blew the whistle for interval. In the second half, Vinod passed the ball on to me. I ran with it into the Then I kicked it hard. It went through the poles. It was a goal. There were loud cheers. The referee blew the whistle. The game was over. We won the march by one goal.

20. A Kabaddi Match

I saw a kabaddi match last Sunday. It was played between our school and New High School. Sh. Mohan Lal was the referee. Many people came to see the match. There was a toss. We won the toss. We chose our side. Then the match began. First of all, our captain went running to the other side. He shouted, “Kabaddi, Kabaddi.” He came back. There was no point. Now it was the turn of New High School.

One of their players came to our side. He was caught. He could not go back. We scored a point. There were loud cheers. We scored more points. New High School team got only 8 points. We had gained 20 points. The referee blew a long whistle. The match came to an end. We won the match by 12 points. It was an interesting match.

21. Morning Walk

Morning walk is the best form of exercise. It costs nothing. It is very useful for our health. It refreshes our mind. It strengthens our body. It saves us from many diseases. Morning walk keeps us fresh for the whole day. It develops in us the habit of rising early. It brings pure thoughts in our mind. The dew drops, the fresh flowers, the chirping birds and the rustling leaves charm our mind. We start loving these objects of natural beauty. Thus, morning walk is useful not only for our body but for our mind also.

22. A Journey by Bus

Last Sunday, I went to Delhi by bus. I went to the bus stand and bought a ticket. A bus bound for Delhi was standing there. I got in and took the front seat. The conductor gave a whistle and the bus started. ‘We were soon out of the city. The driver drove very fast. But he was very good at his job. We felt quite safe. He left many buses behind. I saw farmers working in their fields. Here and there, I saw carts going on the road. The conductor was a jolly fellow. He made the journey pleasant by his witty talk. The bus reached Delhi at 6 p.m. It was a very pleasant journey.

23. A Journey by Train

Last year, I went to Delhi by train. I packed my luggage. I hired a rickshaw. I reached the station. I bought a ticket. I went to the platform. Soon the train arrived. I got into it. There was a great rush. But I was lucky. I got a seat near the window. The train started. I saw many things on the way. Farmers were ploughing the fields. Children were playing. A ticket-checker came. He checked our tickets. A young man was without ticket. He was fined. The train stopped at many stations. I bought a newspaper, I read it. It was 10 a.m. The train reached Delhi. It was a happy journey.

24. A Visit to a Zoo

There is a zoo in our city. I visited it last Sunday. I went with my parents. We bought tickets and went in. First of all, we saw birds. There were many beautiful and rare kinds of birds. We saw parrots, canaries, swallows, peacocks, ducks, cranes, herons, gulls and geese. Then we saw some wild beasts. A lioness and her cub were basking in the sun. They roared now and then. We also saw wolves, tigers, elephants and rhinos. When we were coming back, we saw a muddy pond. There were many big snakes in it. It was fearful to look at them. We stayed in the zoo for about three hours. Then we came back home.

25. A Visit to a Fair 

I went to see a fair last Tuesday. This fair is held every year in our town. It is held in the memory of a pious faqir. Many people go to see this fair. They include men of all religions and faiths. This year I went to see the fair with my parents. We offered flowers at the faqir’s tomb.

Then we went round the fair. There was a temporary bazaar. Stalls were arranged on either side. There was a great hustle and bustle. Sweets were in great demand. Children were enjoying rides in merry-go-rounds. A big shamiana was set up on one side of the fair. Qawalis were being sung there. We sat there for some time. Then we came back home.

26. A Visit to a Circus

A circus came to our town last month. I went to see it with my parents. We bought tickets and went in. We took our seats in the front row. First of all, a young girl came in. She had an umbrella in her hand. She walked on a rope. Then some more girls joined her. They showed various feats in gymnastics. They looked like rubber dolls. One of the girls jumped through a fire ring. Then there were animal shows. An elephant drank water from a bottle. A lion and a goat played with each other. A monkey drove a mini-cycle. The show came to an end at 7 p.m. I liked it very much.

27. A Visit to a Historical Place

During the last spring holidays, I went to Agra. There I visited the Taj. It is built outside the city on the bank of the Yamuna. A large gateway of red stone provides the entrance. The Taj is a large and beautiful building. It stands on a raised platform. In the middle of the platform, there is a splendid white dome. At its four corners, there are four stately towers. Underneath the white dome are the marble tombs of Mumtaz Mahal and Shah Jahan. The whole building is surrounded by a garden on three sides. On the fourth side, the river Yamuna grazes it. No words can describe the beauty of the Taj.

28. A Scene at the Railway Station

Last Sunday, my father went to Delhi. I went to the station to see him off. I bought a ticket and a platform ticket. We went to the platform. There was great hustle and bustle. Some men were buying books at the bookstall. The hawkers were going up and down the platform. The coolies were busy. People were waiting for the train. Soon the train arrived. There was a great rush in it. Some passengers got down. Others got in and took their seats. I got a seat for my father. The engine gave a whistle. The guard waved a green flag. The train again whistled and steamed off. Now there was all quiet on the platform. I came back home.

29. A Scene at the Bus Stand

Last Monday, I went to the bus stand to see off my uncle. The bus stand was humming with life. There were separate parking stands for different routes. A bus was parked at each stand. Men behind the counter were issuing tickets. The conductors were shouting to attract passengers for their respective buses. As soon as a bus was full, the conductor blew his whistle and the bus moved out of the stand. Another one immediately took its place. This activity was going on endlessly. I bought a ticket for my uncle, got him a good seat and then came back home.

30. A House on Fire

It was Sunday. I was sitting in my room with my friend, Atul. Suddenly, we saw clouds of smoke rising in the sky. There was a big fire in the next street. People were running to the site of fire. Children were shouting for help. People brought buckets of water. We also joined them. We threw sand and water on the flames. The fire was put out after half an hour. It was the house of a carpenter. The poor man suffered a big loss. All his wood, grain and money were gone. The house was reduced to ashes. He was very sad at his loss. People felt sorry for him. They gave him food, clothes and some money. The poor carpenter thanked them with folded hands.

31. A Bus Accident

Last Monday, I was travelling from Panipat to Delhi by bus. We had hardly gone twenty kilometres when a dreadful accident took place. All of a sudden a scooterist, coming from a side-road, came in front of the bus. The driver at once applied the brakes, and also turned the bus to one side. All the passengers were thrown off their seats. In no time, the bus went off the road and fell into a ditch. There were loud cries. Many passengers were badly wounded. I, too, got a deep cut on my forehead. Many people gathered there. They helped us to get out of the bus. Luckily there was no death. The scooterist had sped away. I reached home with a bandaged head.

32. A Street Quarrel

Last evening, I was sitting near the window of my room. I saw two children playing in the street. Suddenly, they fell out. Other boys of the street gathered there. None tried to separate them. They kept looking on. Soon, the mothers of both the children reached there. They started abusing each other. They used very dirty words for each other. From hot words, they came to blows. They pulled each other’s hair. Luckily, an elderly woman came there. She separated the fighting ladies. She spoke to them very wisely. The two women realised their mistake. They went back to their homes. Both the children started playing together once again.

33. A Rainy Day

It was the month of July last year. One day, it was very hot. Men and animals were panting. All were perspiring. We longed for a shower of rain. In the afternoon, some clouds appeared in the east. Soon the whole sky was overcast with dark clouds. It started raining heavily. Streets and bazaars were flooded with water. Little children came out and played in the rain. They splashed water over one another. The rain stopped after two hours. It became very cool and pleasant. Streets and bazaars were washed clean. The city gave a fresh look.

34. Life in a Village

The three words that can amply describe the life in a village are — Simple, Pure and Fresh. The villagers are very simple-hearted people. They know no cunning. They are pure in their thoughts and actions. They are very hospitable. They live simply and happily. They have no anxiety. Life in a village is very calm and peaceful. It is free from the noise and din of cities. The air is fresh and health-giving. Says Leo Tolstoy in one of his stories, “A villager’s life is not a fat one, but it is a long one.” He may never grow rich, but he has always enough to eat. In short, we can say that life in a village is worth living.

35. How I Celebrated My Birthday

I gave a party on my birthday. I invited all my friends. The party was held at my house. The party began at 6 p.m. A big cake was placed on a table. All my friends stood round the table. I cut the cake with a knife. My friends and parents chanted three times : ‘Happy Birthday To You.’ Then everybody set to eating. The cake was served to all. It was very tasty. There were many things to eat. Everybody ate to their heart’s content. There was singing and dancing also. Everyone enjoyed the party. It was over by 8 p.m. My friends congratulated me once again and went back to their homes.

36. A Drowning Tragedy

One day, I was picnicking with some of my friends on the riverbank. A boy named Kamal fell into the river. He didn’t know how to swim. I saw him struggling with water. It was a painful sight. I at once jumped into the river. I swam to him and brought him out with great difficulty. He had swallowed a lot of water. He was unconscious. We, at once called a doctor. Someone ran to inform Kamal’s parents. The doctor pressed out the water from Kamal’s belly. Kamal opened his eyes. We felt great relief. After some time Kamal’s parents reached the place. They thanked me and the doctor again and again.

37. The Golden Temple

Amritsar is also called Guru-ki-nagri. It is famous for the Golden Temple. The Temple is situated in the city. It is surrounded by many narrow lanes. The golden shrine built in the middle of the sarover shines at sunrise and sunset. It was built by Guru Arjun Dev Ji. It is a unique experience when Granth Sahib is brought out from the Akal Takhat Sahib amidst chanting of hymns and blowing of bugles.

The Akal Takhat Sahib, facing the Harmandir Sahib, was built by Guru Hargobind Ji. It was used for holding courts. The complex has a museum of rare paintings, books, shashtras, etc. The lives of the Gurus are described through them. There is a big bazaar near Darshani Deori. Gutakas, karas and other articles related to the Sikh religion are sold there. Home-made papad-varian, chura-bangles, dry fruit are also sold in many shops. There are number of hotels and guest houses near the Temple for tourists to stay. There is a sarai also for pilgrims in the Temple. The Golden Temple is indeed a worth-visiting place.

38. Canada

Canada is one of the largest country of the world. Its area is 9,976,139 sq. km. and population is about 32 million. The capital city of Canada is Ottawa. The currency of the country is Canadian dollar. English and French are the official languages of Canada. In winter, the climate of Canada is bitterly cold. In some regions, the mercury may dip to -65°C. The average temperature in Ottawa is from -15°C to -6°C in January.

In July, the average temperature is 15°C to 26°C. The main products of Canada are fruit, vegetables, livestock, tobacco, copper, zinc, iron, salt, oil and natural gas. And major industries of the country are agriculture, forestry, food processing, transport, chemicals, oil and gas refining and cement. Vehicles, machinery, food stuffs, natural gas, meat, coal and timber are exported to other countries. Canada is one of the most developed nations of the world.

39. Aruna Asif Ali

Aruna Asif Ali is known as the Grand Old Lady of India. She took active part in the Independence movement. She was born in an orthodox Hindu Bengali family in 1909 at Kalka. She married a Muslim, Mr. Asif Ali, thus breaking all conventions regarding marriage. Her husband, Mr. Asif Ali, was also involved in the freedom struggle. Aruna Asif Ali took part in Salt Satyagrah under the leadership of Gandhiji.

She addressed many public meetings and led processions for the cause of India’s independence from the British rule. As a result, she was sentenced to one-year imprisonment. But she didn’t give up the cause for which she was fighting against the British rule. She was again sentenced to jail.

She became the editor of the newspaper ‘Inquilab’. After Independence, she became a social worker. She fought for the rights of women. In 1992 she received Nehru Award for International Understanding. She passed away in July 1996. She was honoured with Bharat Ratna posthumously.

40. The Tribals of Odisha 

There are many tribal groups in Odisha. They live in remote places. One such group lives in the forests of Kalahandi. These people are one of most backward tribes in the world. They have dark skin and black hair. The women wear bright-coloured saris while the men wear nothing but loincloth.

They still believe that India is ruled by kings. These people are illiterate as they do not have any facility of schooling, means of transportation and proper motorable roads. As a result, they are cut off from the rest of the world. They do not have any idea of currency notes. They still use barter system.

They usually live in groups and each group has common property. They cure diseases with herbs and set bones by rubbing oils. The government should launch schemes to educate them and bring them to the mainstream of the nation.

41. An Incident of Burglary

Mr. Ramanathan is an affluent businessman of our town. One day, he with his family went out of the town to attend a wedding. There was nobody at home and the house was locked from outside. A thief broke into the house at night. He decamped with the jewellery, valuables and money.

But the neighbours had seen the lights on and they informed the police about it. The police came along with a dog. They found the thief’s glove. The dog sniffed the scent of the thief. It took the policemen to the thief’s place. Thus the thief was arrested and the case was solved. The policemen were rewarded by the department for their efficiency.

42. Floods in Mumbai

On July 26, 2005, I was busy shopping in a famous crowded market, although it was raining. Gradually, it started raining heavily. Now, it was impossible to go from there. Therefore, I took shelter in a shop. Soon, the place got flooded and water started entering the shops. The articles in the shops started floating in the water and the shopkeeper tried to retrieve valuable articles. The entire area was submerged in the flood water.

Many vehicles couldn’t move in the flood water. The people had to stay in them. Some other people took shelter in shops and houses. Suddenly, it started raining like hell. Now water in the shops and houses rose up to 6-7 feet. The people had to move to first floor. In no time the army swung into action. The volunteers of many NGO’s started helping the affected people with food and water. All this went on for more than 24 hours. It was really a horrifying experience which I can never forget.

43. The Lohri Festival

Lohri is a festival of fun and frolic. It is generally celebrated on 13th of January every year. This festival is related to the folklore of Dulla Bhatti. At sunset, people light up bonfires in the open in front of their houses. Lohri is celebrated with more enthusiasm in the families where there is a newborn son or a newly married person.

Giddha or Bhangra is performed to the beats of the drums. On the day of Lohri, children go singing from house to house asking for money and sweets. Lohri is a busy festival. People meet their friends and relatives and exchange greetings and gifts.

44. How to Make Papier-mache -Toys

In order to make toys with papier-mache, old newspaper sheets are taken. They are torn into small pieces. These pieces are soaked in water overnight. Next day, the mixture is boiled for half an hour. After that, the mixture is whipped till it becomes soft and pulpy.

The water is squeezed out from the mixture and two tablespoons of white gum are added into it. The mixture is stirred well and then the toys are made from it. These toys are left to dry overnight or more. Then they are painted with water-based colour. To make these toys waterproof, two or three coats of lacquer are given on them. Masks can also be made in the same manner.

45. How to Make Gajrela

It is very easy to make gajrela at home. Take three kilograms of large carrots and wash them properly. Then grate the carrots. Mix 242 litres milk with the carrots. After that put the mixture in a pan and boil it till the mixture becomes very thick. Add 3/4 cup of sugar and 250 gm of khoya in the mixture.

Stir the mixture till it becomes thick. Stir it continuously as the mixture should not stick to the pan. Now remove the pan from the fire. Add nuts to it. Your gajrela is ready. Let it cool before serving. It can also be served hot.