Punjab State Board PSEB 9th Class Social Science Book Solutions Geography Chapter 4 जलवायु Exercise Questions and Answers.
PSEB Solutions for Class 9 Social Science Geography Chapter 4 जलवायु
SST Guide for Class 9 PSEB जलवायु Textbook Questions and Answers
(क) नक्शा कार्य (Map Work):
प्रश्न 1.
भारत के रेखाचित्र में दिखायें :
(i) ग्रीष्म ऋतु की मानसून पवनों की दिशा
(ii) शीत ऋतु की मानसून पवनों की दिशा
(iii) 200 सै०मी० या इससे अधिक वर्षा वाले दो क्षेत्र
(iv) 100 सै०मी० से 200 सै०मी० वर्षा वाले दो क्षेत्र
(v) 50 सै०मी० से 100 सै०मी० वर्षा वाले दो क्षेत्र।
उत्तर-
विद्यार्थी इस प्रश्न को MBD Map Master की सहायता से स्वयं करें।
प्रश्न 2.
कक्षा क्रिया (Class Activity) :
(i) मार्च माह के समाचार पत्रों में से जानकारी लीजिए कि पंजाब के किन क्षेत्रों में साधारण से अधिक वर्षा हुई। अध्यापक की मदद से ज़मीनदोज़ जल पर वर्षा के प्रभाव पर चर्चा कक्षा में कीजिए।
(ii) समाचार पत्रों के आधार पर अगस्त माह में सूर्योदय व अस्त का समय नोट करें तथा फिर ‘सूर्य की स्थिति और पृथ्वी’ विषय पर अध्यापक से चर्चा करें।
उत्तर-
इस प्रश्न को विद्यार्थी अपने अध्यापक की सहायता से स्वयं करें।
(ख) निम्न प्रश्नों के उत्तर एक शब्द से एक वाक्य में दें:
प्रश्न 1.
शीत ऋतु में तमिलनाडु के तट पर वर्षा का क्या कारण है :
(i) दक्षिण-पश्चिम मानसून
(ii) उत्तर-पूर्वीय मानसून
(iii) स्थानीय कारण
(iv) इनमें से कोई नहीं।
उत्तर-
(ii) उत्तर-पूर्वीय मानसून।
प्रश्न 2.
भारत में अधिकतम वर्षा वाला शहर इनमें से कौन-सा है:
(i) मुम्बई
(ii) धर्मशाला
(iii) मासिनराम
(iv) कोलकाता।
उत्तर-
(iii) मासिनराम।
प्रश्न 3.
पंजाब में शीत ऋतु की वर्षा का क्या कारण है ?
(i) व्यापारिक पवनें
(ii) पश्चिमी चक्रवात
(iii) ध्रुवीय पवनें
(iv) पर्वतों की दिशा।
उत्तर-
(ii) पश्चिमी चक्रवात।
प्रश्न 4.
सूनामी कौन सी भाषा का शब्द है ?
(i) फ्रांसीसी
(ii) जापानी
(iii) पंजाबी
(iv) अंग्रेजी।
उत्तर-
(ii) जापानी।
प्रश्न 5.
नक्शे पर समान वर्षा, क्षेत्र को जोड़ने वाली रेखाओं को क्या कहते हैं ?
(i) आइसोथर्म
(ii) आईसोहाईट
(iii) आईसोबार
(iv) कोई नहीं।
उत्तर-
(ii) आईसोहाईट।
प्रश्न 6.
लू क्या होती है ?
उत्तर-
गर्म ऋतु में कम दबाव का क्षेत्र उत्पन्न होने के कारण चलने वाली धूल भरी हवाओं को लू कहा जाता है।
प्रश्न 7.
जलवायु विज्ञान को अंग्रेजी में क्या कहते हैं ?
उत्तर-
Climatology.
प्रश्न 8.
मानसून का क्या अर्थ है ?
उत्तर-
मानसून शब्द की उत्पत्ति अरबी भाषा के शब्द मौसम (Mausam) से हुई है, जिसका अर्थ है मौसम में परिवर्तन आना तथा स्थानीय हवा के तत्त्वों अर्थात् तापमान, नमी, दबाव तथा दिशा में परिवर्तन आना।
प्रश्न 9.
तापमान व वायुदबाव का संबंध कैसा होता है ?
उत्तर-
इनमें काफी गहरा संबंध है। तापमान के बढ़ने से वायुदबाव कम है तथा तापमान के कम होने से ही अधिक दबाव का क्षेत्र बन जाता है।
प्रश्न 10.
भारत में सबसे अधिक और सबसे कम वर्षा वाले स्थानों के नाम लिखें।
उत्तर-
अधिक वर्षा वाले क्षेत्र-मासिनराम, चिरापुंजी।।
कम वर्षा वाले क्षेत्र-पश्चिमी राजस्थान, गुजरात का कच्छक्षेत्र, जम्मू-कश्मीर का लद्दाख क्षेत्र।
(ग) निम्नलिखित प्रश्नों के सक्षेप उत्तर लिखें:
प्रश्न 1.
जलवायु तथा मौसम में अंतर स्पष्ट कीजिए।
उत्तर-
- जलवायु-किसी भी भौगोलिक क्षेत्र में कम-से-कम 30 वर्षों के लिए मौसम की औसत का जो परिणाम निकाला जाता है, उसे जलवायु कहते हैं। इसका अर्थ है कि जलवायु लंबे समय के लिए किसी भी क्षेत्र के तापमान वर्षा, वायु दबाव, हवाओं इत्यादि की औसत होती है।
मौसम-किसी निश्चित स्थान पर किसी विशेष दिन में वातावरण के तत्त्वों जैसे कि तापमान, दबाव तथा हवा, वर्षा इत्यादि को इकट्ठा मिलाकर मौसम की स्थिति में बदला जाता है। मौसम एक दैनिक चक्र है तथा यह प्रत्येक दिन तथा प्रत्येक घण्टे में भी बदल सकता है।
प्रश्न 2.
कैरियोलिस शक्ति या फैरल का नियम क्या है ?
उत्तर-
पृथ्वी सूर्य के इर्द-गिर्द एक समान गति से घूमती है। पृथ्वी की दैनिक गति के कारण उत्तरार्द्ध गोले के बीच हवाओं तथा अन्य स्वतन्त्र हवाएं अपने Right तरफ तथा दक्षिणी अर्द्ध गोले में अपनी Left तरफ मुड़ जाते हैं। इस शक्ति को ही कैरियोलिस शक्ति अथवा फैरल का नियम कहते हैं।
प्रश्न 3.
भारतीय वर्षा अनियमित तथा अनिश्चित है, कैसे।
उत्तर-
मानसून की अनियमितता तथा अनिश्चितता से अभिप्राय यह है कि भारत में न तो मानसूनी वर्षा की मात्रा निश्चित है और न ही इसके आगमन का समय। उदाहरण के लिए
- यहां बिना वर्षा वाले तथा वर्षा वाले दिनों की संख्या घटती-बढ़ती रहती है।
- किसी वर्ष भारी वर्षा होती है तो कभी हल्की। परिणामस्वरूप कभी बाढ़ आती है तो किसी वर्ष सूखा पड़ जाता है।
- नसून का आगमन और वापसी भी अनियमित तथा अनिश्चित है।
- इस प्रकार कुछ क्षेत्र भारी वर्षा प्राप्त करते हैं, तो कुछ क्षेत्र बिल्कुल शुष्क रह जाते हैं।
प्रश्न 4.
वायु वेग मापक तथा वायु वेग सूचक में अंतर बतायें।
उत्तर-
- वायु वेग मापक-वायु वेग मापक को Anemometer कहा जाता है जिसे हवा की गति मापने के लिए प्रयोग किया जाता है। इसमें चार सीखों के साथ खाली कौलियां लगी होती हैं। चारों सीखें एक स्टैंड पर एक-दूसरे के साथ जोड़ी जाती हैं तथा यह सीखें पृथ्वी में समांतर होती हैं। जब हवा चलती है तो खाली कौलियां घूमने लग जाती हैं। इनके घूमने से स्टैंड पर लगी सुई भी घूमती है तथा हवा की गति उस पर लगे हुए आंकड़े से पता चल जाती है।
- वायु वेग सूचक-वायु वेग सूचक को Wind Wane कहते हैं तथा इसे हवा की दिशा पता करने के लिए प्रयोग किया जाता है। इस यन्त्र पर मुर्गे की शक्ल अथवा तीर का निशान बना होता है। यह मुर्गा या तीर एक सीधी लंबी धुरी पर घूमता है। इस मुर्गे के नीचे चार दिशाओं के नाम नीचे लगी सीखों के द्वारा दर्शाए जाते हैं। जब हवा चलती है तो मुर्गे अथवा तीर का निशान घूम कर उस तरफ हो जाता है जिस तरफ हवा आती है। इस प्रकार सीख पर लगे निशान से हवा की दिशा का पता चल जाता है।
प्रश्न 5.
भारत में शीत ऋतु की वर्षा पर संक्षेप नोट लिखें।
उत्तर-
सर्दियों में देश में दो स्थानों पर वर्षा होती है। देश के उत्तर-पश्चिमी भागों के पंजाब, हरियाणा, उत्तरी राजस्थान, जम्मू कश्मीर तथा उत्तर प्रदेश के उत्तर पश्चिमी क्षेत्रों में औसतन 20 से 50.सैंटीमीटर तक चक्रवाती वर्षा होती है। कश्मीर, हिमाचल प्रदेश तथा कुमाऊँ के पहाड़ी क्षेत्रों में बर्फ पड़ती है। दूसरी तरफ तमिलनाडु तथा केरल के तटीय क्षेत्रों पर उत्तर-पूर्वी मानसून हवाओं के कारण दिसंबर में वर्षा होती है।
प्रश्न 6.
पर्वतीय वर्षा केवल पर्वतों पर होती है, स्पष्ट करें।
उत्तर-
जब मानसून के बादल समुद्र से धरातल की तरफ आते हैं तो समुद्र के ऊपर से आने के कारण उनमें काफी नमी हो जाती है। कई बार इनके रास्ते में पर्वत रुकावट बन जाते हैं तथा यह बादल ऊपर उठ जाते हैं। ऊपर जाकर यह ठण्डे हो जाते हैं तथा इनमें संघनन शुरू हो जाता है। इस कारण वहाँ पर वर्षा शुरू हो जाती है। क्योंकि इस प्रकार की वर्षा का कारण पर्वत होते हैं इसलिए यह केवल पर्वतीय क्षेत्रों में होती है।
प्रश्न 7.
निम्न पर नोट लिखें :
1. जेट स्ट्रीम
2. समताप रेखाएं
3. सूखी व गीली गोली थर्मामीटर।
उत्तर-
- जेट स्ट्रीम-धरातल से तीन किलोमीटर की ऊँचाई पर बहने वाली हवाओं अथवा संचार चक्र को जैट स्ट्रीम कहते हैं। जेट स्ट्रीम का जलवायु पर काफी प्रभाव पड़ता है। सर्दियों में पश्चिमी चक्रवात भारत में जेट स्ट्रीम के कारण ही आते हैं। इनकी ऊँचाई लगभग 12 किलोमीटर तक होती है। यह गर्मियों में लगभग 110 किलोमीटर प्रति घण्टा की गति से चलते हैं तथा सर्दियों में 184 किलोमीटर प्रति घण्टा की गति से चलते हैं।
- समताप रेखाएं-मानचित्र के ऊपर कुछ रेखाएं खिंची होती हैं जो लगभग समान तापमान वाले स्थानों को एकदूसरे से मिलाती हैं। समताप रेखाएं किसी स्थान पर किसी विशेष समय पर तापमान के विभाजन को दिखाने के लिए प्रयोग की जाती हैं।
- सूखी व गीली गोली थर्मामीटर-हवा में नमी को मापने के लिए इस प्रकार के थर्मामीटर का प्रयोग किया जाता है। इसमें दो अलग-अलग थर्मामीटर होते हैं। एक थर्मामीटर के निचले भाग पर मलमल के कपड़े की पट्टी बन्धी होती है तथा पट्टी का निम्न भाग पानी में रखा जाता है। यह थर्मामीटर कम तापमान बताता है। सूखी तथा गीली गोली थर्मामीटर के तापमान के अंतर का पता करके उसके साथ दिए गए पैमानों की सहायता से हवा की नमी का पता किया जाता है। हवा की नमी हमेशा प्रतिशत में बताई जाती है।
प्रश्न 8.
‘कुदरती आफतों में जानी-माली नुकसान होता है’ में जानी-माली क्या है ?
उत्तर-
इसमें कोई शंका नहीं है कि जब भी प्राकृतिक आपदाएं आती हैं तो जानी-माली का बहुत नुकसान होता है। यहां जानी का अर्थ है कि इससे बहुत से लोगों की मृत्यु हो जाती है। माली का अर्थ है कि बहुत से पशु पक्षी मर जाते हैं तथा बहुत से पैसे का भी नुकसान होता है।
(घ) निम्नलिखित के विस्तृत उत्तर दें:
प्रश्न 1.
किसी स्थान की जलवायु किन तत्त्वों पर निर्भर है ? व्याख्या करें।
उत्तर-
भारत की जलवायु विविधताओं से परिपूर्ण है। इन विविधताओं को अनेक तत्त्व प्रभावित करते हैं, जिनका वर्णन इस प्रकार है
- भूमध्य रेखा से दूरी-भारत उत्तरी गोलार्द्ध में भूमध्य रेखा के समीप स्थित है। परिणामस्वरूप पर्वतीय क्षेत्रों को छोड़कर देश के अधिकांश क्षेत्रों में लगभग पूरे वर्ष तापमान ऊंचा रहता है। इसीलिए भारत को गर्म जलवायु वाला देश भी कहा जाता है।
- धरातल-एक ओर हिमालय पर्वत श्रेणियां देश को एशिया के मध्यवर्ती भागों से आने वाली बर्फीली व शीत पवनों से बचाती हैं तो दूसरी ओर ऊंची होने के कारण ये बंगाल की खाड़ी से आने वाली मानसून पवनों के रास्ते में बाधा बनती हैं और उत्तरी मैदान में वर्षा का कारण बनती हैं।
- वायु-दबाव प्रणाली-गर्मियों की ऋतु में सूर्य की किरणें कर्क रेखा की ओर सीधी पड़ने लगती हैं। परिणामस्वरूप देश के उत्तरी भागों में तापमान बढ़ने लगता है और उत्तरी विशाल मैदानों में कम हवा के दबाव (994 मिलीबार) वाले केन्द्र बनने प्रारम्भ हो जाते हैं। सर्दियों में हिन्द महासागर पर कम दबाव पैदा हो जाता है।
- मौसमी पवनें-
- देश के भीतर गर्मी तथा सर्दी के मौसम में हवा के दबाव में परिवर्तन होने के कारण गर्मियों के छ: महीने समुद्र से स्थल की ओर तथा सर्दियों के छ: महीने स्थल से समुद्र की ओर पवनें चलने लगती हैं।
- धरातल पर चलने वाली इन मौसमी पवनों तथा मानसूनी पवनों को दिशा संचार चक्र अथवा जेट स्ट्रीम भी प्रभावित करता है। इस प्रभाव के कारण ही गर्मियों के चक्रवात और भूमध्य सागरीय क्षेत्रों का पश्चिमी मौसमी हलचल
का प्रभाव देश के उत्तरी भागों तक आ पहुंचता है तथा भरपूर वर्षा प्रदान करता है।
- हिन्द महासागर से समीपता-
- सम्पूर्ण देश की जलवायु पर हिन्द महासागर का प्रभाव है। हिन्द महासागर की सतह समतल है। परिणामस्वरूप भूमध्य रेखा के दक्षिणी भागों से दक्षिणी-पश्चिमी मानसूनी पवनें पूरे वेग से देश की ओर बढ़ती हैं। ये पवनें समुद्री भागों से लाई नमी को सारे देश में वितरित करती हैं।
- प्रायद्वीपीय भाग के तीन ओर से समुद्र से घिरे होने के कारण तटवर्ती क्षेत्रों में सम जलवायु मिलती है। उससे गर्मियों में कम गर्मी तथा सर्दियों में कम सर्दी पडती है। सच तो यह है कि भारत में गर्म-उष्ण मानसूनी खण्ड (Tropical Monsoon Region) वाली जलवायु मिलती है। इसलिए मानसूनी पवनें अलग-अलग समय में देश के प्रत्येक भाग में गहरा प्रभाव डालती हैं।
प्रश्न 2.
वर्षा कितने प्रकार की होती है ? विस्तार से लिखें।
उत्तर-
मुख्यत: वर्षा तीन प्रकार की होती है। वह है-
- संवहनी वर्षा (Convectional Rainfall)
- पर्वतीय वर्षा (Orographic Rainfall)
- Elshanit af (Cyclonic Rainfall)
1. संवहनी वर्षा (Convectional Rainfall)—भूमध्य रेखा पर सम्पूर्ण वर्ष सूर्य की सीधी किरणें पड़ती हैं तथा इस कारण वहां पर काफी गर्मी होती है। गर्मी के कारण वायु दबाव (Air Pressure) काफी कम हो जाता है। इस क्षेत्र में पानी गर्म होकर वाष्प बनकर ऊपर उठ जाता है तथा बादल बन जाते हैं। इस क्षेत्र में बादल ठण्डे होकर वर्षा करते हैं तथा इसे संवणीय वर्षा कहते हैं। यह वर्षा अधिक समय के लिए नहीं होती क्योंकि कम वायु दबाव होने कारण ऊपर उठती हवा अपने साथ अधिक नमी लेकर नहीं जा सकती। इस प्रकार की वर्षा में बादलों की आवाज़ तथा बिजली काफी चमकती है।
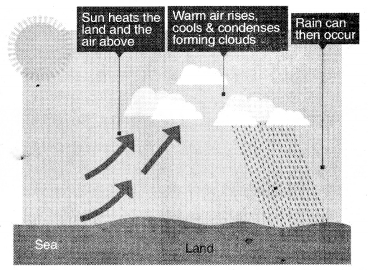
संवहनी वर्षा चित्र
2. पर्वतीय वर्षा (Orographic Rainfall)-जब मानसून के बादल समुद्र से पृथ्वी की तरफ आते हैं तो समुद्र के ऊपर से लांघने के कारण उनमें काफी नमी आ जाती है। कई बार इनके रास्ते में पर्वत रुकावट बन जाते हैं तथा यह पवन या बादल ऊपर उठ जाते हैं। ऊपर जाकर यह ठण्डे हो जाते हैं तथा घने हो जाते हैं। इस कारण वर्षा हो जाती है। इस वर्षा को ही पर्वतीय वर्षा कहते हैं। गर्मियों में हिमालय पर्वत के नज़दीक होने वाली वर्षा इस प्रकार की वर्षा ही होती है।
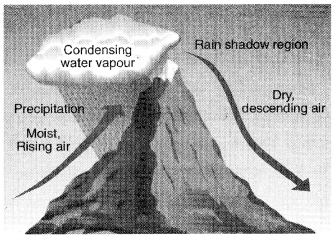
पर्वतीय वर्षा चित्र
3. चक्रवाती वर्षा (Cyclonic Rainfall)—जब वातावरण में बाहर की तरफ अधिक वायु दबाव तथा अंदर कम वायु दबाव की स्थिति उत्पन्न हो जाए तो चक्रवात उत्पन्न होते हैं। पवनें अधिक दबाव से कम वायु अधिक दबाव की तरफ घूमती हैं तथा कम वायु दबाव वाली हवाएं ऊपर उठ जाती हैं। जब यह ठण्डी हो जाती हैं तो वर्षा करती हैं।
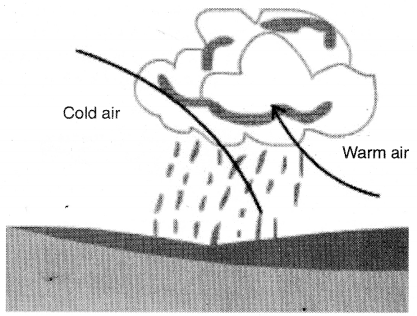
चक्रवाती वर्षा चित्र
सर्दियों में भारत के उत्तर तथा उत्तर पश्चिमी क्षेत्रों में फारस की खाड़ी तथा मैडिटेरिनियन समुद्र की तरफ से चक्रवात आते हैं तथा वर्षा करते हैं। सर्दियों में पंजाब में आने वाली वर्षा फसलों के लिए काफी लाभदायक होती है।
प्रश्न 3. मानसून पवनों की अरब सागर शाखा व बंगाल की खाड़ी की शाखा के विषय में बताएं।
उत्तर- भारतीय मानसून पवनों को दो भागों में विभाजित किया जाता है तथा वह हैं-
- अरब सागर की शाखा तथा
- बंगाल की खाड़ी शाखा। इनका वर्णन इस प्रकार है
1. अरब सागर की शाखा (Arabian Sea Branch)—भारत के पश्चिम की तरफ अरब सागर मौजूद है तथा यहां से ही गर्मियों में मानसून पवनें शुरू होती हैं। जून के पहले हफ्ते तक मानसून पवनों की यह शाखा केरल तक पहुँच जाती है। जून के दूसरे हफ़्ते अर्थात् 10 जून तक यह पश्चिमी घाट पर पहुँच कर वर्षा करती हैं। पश्चिमी घाट में रुकावटें हैं जिस कारण यह पवनें पश्चिमी घाट के मुख्य मैदानों में भारी वर्षा करती हैं। फिर यह पवनें दक्षिण के पठार तथा मध्य प्रदेश के क्षेत्रों में भी वर्षा करती हैं। इसके पश्चात् पवनों की यह शाखा उत्तर भारत की तरफ बढ़ जाती है तथा उत्तर में जाकर यह बंगाल की खाड़ी शाखा के साथ मिलकर गंगा के मैदानों में चली जाती है। इकट्ठी होकर पश्चिमी भारत की तरफ चली जाती है। जुलाई के प्रथम सप्ताह में यह पंजाब, हरियाणा तथा राजस्थान में वर्षा करती हैं। इन पवनों से हुई वर्षा की मात्रा पूर्वी भारत की तरफ अधिक होती है तथा पश्चिम की तरफ जाते हुए वर्षा की मात्रा कम होती जाती है।
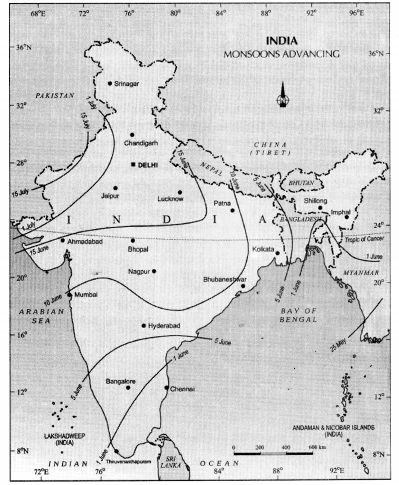
चित्र
2. बंगाल की खाड़ी शाखा-मानसून की यह शाखा बंगाल की खाड़ी से शुरू होती है तथा उत्तर भारत की तरफ बढ़ती है। यह आगे जाकर दो भागों में विभाजित हो जाती है। इसका एक भाग भारत के उत्तर तथा उत्तर पूर्व की तरफ चला जाता है तथा दूसरा भाग पश्चिम की तरफ चला जाता है। गंगा के मैदानों में जाकर यह शाखा अरब सागर शाखा के साथ मिल जाती है। इस शाखा का एक भाग उत्तर-पूर्वी भारत की तरफ जाकर, ब्रह्मपुत्र की घाटी तक पहुँचता है तथा गारो, खासी, जैंतिया पहाड़ियों पर काफी वर्षा करता है। मासिनराम में 1221 सैंटीमीटर औसत वर्षा देखी गई है। चेरापुंजी भी खासी पहाड़ियों में स्थित है जहां 1102 सेंटीमीटर औसत वर्षा होती है।
प्रश्न 4.
जलवायु की जानकारी देने के लिए कौन-कौन से यन्त्र प्रयोग किए जाते हैं ? संक्षेप में लिखें।
उत्तर-
किसी भी क्षेत्र की जलवायु की जानकारी के लिए बहुत से यन्त्रों का प्रयोग किया जाता है जिनका वर्णन इस प्रकार है:
- उच्चतम व न्यूनतम थर्मामीटर (Maximum and Minimum Thermometer)-तापमान का पता करने के लिए इस प्रकार के थर्मामीटर का प्रयोग किया जाता है। अगर किसी स्थान की जलवायु की जानकारी प्राप्त करनी है तो हमें वहां के तापमान की जानकारी का होना आवश्यक है। इस प्रकार का थर्मामीटर दो जुड़ी हुई नालियों के साथ बना होता है। एक नाली से रात्रि का न्यूनतम तापमान पता किया जाता है तथा दूसरी नाली से दिन का उच्चतम तापमान पता किया जाता है। तापमान को सैंटीमीटर ग्रेड अथवा फारेनहाइट की डिग्री में मापा जाता है।
- एनीराइड बैरोमीटर (Aniroid Barometer)-एनीराइड बैरोमीटर से वायु दबाव का पता किया जाता है। यह बैरोमीटर धातु की एक डिब्बी में से हवा निकाल कर उसे एक पतली सी चादर से बाँध दिया जाता है। डिब्बी में एक स्परिंग होता है। हवा के दबाव के कारण अंदर स्परिंग से लगी हुई सुई घूमती है। दबाव के अनुसार सुई अन्दर लिखे हुए आंकड़ों पर टिकेगी तथा इससे हमें वायु दबाव अथवा हवा के दबाव का पता चल जाएगा। हवा के दबाव को हमेशा मिली बार में बताया जाता है।
- सूखी व गीली गोली का थर्मामीटर (Dry and Wet Bulb Thermometer)-वायु में नमी को मापने के लिए इस प्रकार के थर्मामीटर को प्रयोग किया जाता है। इसमें दो अलग-अलग थर्मामीटर होते हैं। एक थर्मामीटर ने निचले सिरे पर मलमल के कपड़े की पट्टी बाँधी जाती है तथा पट्टी का निचला भाग पानी में रखा जाता है। यह कम तापमान बताता है। सूखी व गीली गोली थर्मामीटरों के तापमान के अन्तर का पता करके, उसके साथ दिए गए पैमाने की सहायता से हवा में नमी का पता किया जाता है। हवा में नमी हमेशा प्रतिशत में बताई जाती है।
- वर्षा मापक यन्त्र (Rain Gauge)-वर्षा को मापने के लिए वर्षा मापक यन्त्र का प्रयोग किया जाता है। वर्षा मापक यन्त्र के बीच लोहे या पीतल का एक गोल बर्तन होता है। इस बर्तन के मुँह पर एक कीप लगी होती है जिससे बारिश का पानी साथ लगी हुई बोतल में इकट्ठा हो जाता है। इस कारण यह वाष्प बनकर नहीं उड़ सकता। इस यन्त्र को एक खुले स्थान पर रखा जाता है ताकि बारिश का पानी इसमें आसानी से इकट्ठा हो सके। बारिश खत्म होने के पश्चात् पानी को एक शीशे के बर्तन में डाल दिया जाता है। जिस पर निशान लगे होते हैं। इन निशानों की सहायता से बताया जाता है कि कितनी वर्षा हुई है। वर्षा को इंच या सेंटीमीटर में बताया जाता है। .
- वायु वेग मापक (Anemometer) वायु वेग मापक को Anemometer कहा जाता है जिसे हवा की गति मापने के लिए प्रयोग किया जाता है। इसमें चार सींखों के साथ खाली कौलियां लगी होती हैं। चारों सीखें एक स्टैंड पर एक-दूसरे के साथ जोड़ी जाती हैं तथा यह सींखें पृथ्वी के समांतर होती हैं। जब हवा चलती है तो खाली कौलियां घूमने लग जाती हैं। इनके घूमने से स्टैंड पर लगी सुई भी घूमती है तथा हवा की गति उस पर लगे हुए आंकड़ों से पता चल जाती है।
- वायु वेग सूचक (Wind Wane)-वायु वेग सूचक को Wind Wane कहते हैं तथा इसे हवा की दिशा पता करने के लिए प्रयोग किया जाता है। इस यन्त्र पर मुर्गे की शक्ल तथा तीर का निशान बना होता है। यह मुर्गा या तीर एक सीधी लंबी धुरी पर घूमता है। इस मुर्गे के नीचे चार दिशाओं के नाम नीचे लगी सींखों के द्वारा दर्शाए जाते हैं। जब हवा चलती है तो मुर्गे अथवा तीर का निशान घूमकर उस तरफ हो जाता है जिस तरफ हवा आती है। इस प्रकार सीख पर लगे निशान से हवा की दिशा का पता चल जाता है।
प्रश्न 5.
कुदरती आफतों का जनजीवन पर क्या बुरा प्रभाव पड़ता है ?
उत्तर-
कुदरती आफतों अथवा प्राकृतिक आपदाओं के बुरे प्रभाव निम्नलिखित हैं:
- भौतिक नुकसान-प्राकृतिक आपदाओं से भवनों तथा सेवाओं को नुकसान होता है। इससे आग लग सकती है, बाँध टूटने के कारण बाढ़ आ सकती है तथा भू-क्षरण हो सकता है।
- मृत्यु-भूकम्प के कारण उन क्षेत्रों में अधिक लोग मरते हैं, जो भूकम्प का केन्द्र (Epicentre) होते हैं, जिन स्थानों पर जनसंख्या अधिक होती है तथा मकान भूकम्प रोधी नहीं होते वहां पर मरने वालों की संख्या अधिक होती
- जनस्वास्थ्य-प्राकृतिक आपदाओं विशेषतया भूकम्प का जनता के स्वास्थ्य पर प्रतिकूल प्रभाव पड़ता है। हड्डियां टूटना, जख्मी होना एक न्यायिक समस्या होती है। सफाई व्यवस्था के भंग होने से महामारी पैदा हो जाती है।
- यातायात बाधित होना-सड़कें, पुल, रेल की लाइनें इत्यादि टूट जाती हैं तथा यातायात बाधित हो जाता है। 5. बिजली व संचार-सभी सम्पर्क प्रभावित हो जाते हैं। बिजली की समस्या भी आ जाती है।
PSEB 9th Class Social Science Guide जलवायु Important Questions and Answers
बहुविकल्पीय प्रश्न (Multiple Choice Questions)
प्रश्न 1.
भारत के दक्षिणी भागों में कौन-सी ऋतु नहीं होती ?
(क) गर्मी
(ख) वर्षा
(ग) सर्दी
(घ) बसन्त।
उत्तर-
(ग) सर्दी
प्रश्न 2.
तूफानी चक्रवातों को पश्चिमी बंगाल में कहा जाता है
(क) काल बैसाखी
(ख) मानसून
(ग) लू
(घ) सुनामी।
उत्तर-
(क) काल बैसाखी
प्रश्न 3.
देश के उत्तरी मैदानों में गर्मियों में चलने वाली धूल भरी स्थानीय पवन को कहा जाता है-
(क) सुनामी
(ख) मानसून
(ग) काल वैसाखी
(घ) लू।
उत्तर-
(घ) लू।
प्रश्न 4.
दक्षिण-पश्चिमी मानसून की बंगाल की खाड़ी वाली शाखा के द्वारा सर्वाधिक प्रभावित स्थान है-
(क) चेन्नई
(ख) अमृतसर
(ग) मासिनराम
(घ) शिमला।
उत्तर-
(ग) मासिनराम
प्रश्न 5.
लौटती हुई तथा पूर्वी मानसून से प्रभावित स्थान है-
(क) चेन्नई
(ख) अमृतसर
(ग) दिल्ली
(घ) शिमला।
उत्तर-
(क) चेन्नई
प्रश्न 6.
सम्पूर्ण भारत में सर्वाधिक वर्षा वाले दो महीने हैं-
(क) जून तथा जुलाई
(ख) जुलाई तथा अगस्त
(ग) अगस्त तथा सितम्बर
(घ) जून और अगस्त।
उत्तर-
(ख) जुलाई तथा अगस्त
प्रश्न 7.
सुनामी कब आई थी ?
(क) 26 दिसम्बर 2004
(ख) 26 दिसम्बर 2006
(ग) 25 नवम्बर 2003
(घ) 25 नवम्बर 2002.
उत्तर-
(क) 26 दिसम्बर 2004
प्रश्न 8.
वायु दबाव का पता करने के लिए ……………….. प्रयोग किया जाता है।
(क) वर्षा मापक यन्त्र
(ख) एनीराइड बैरोमीटर
(ग) वायु वेग मापक
(घ) वायु दिशा सूचक।
उत्तर-
(ख) एनीराइड बैरोमीटर
रिक्त स्थान की पूर्ति करें (Fill in the Blanks)
- भारत में अधिकतर (75 से 90 प्रतिशत तक) वर्षा जून से ………… तक होती है।
- भारत में पश्चिमी चक्रवातों से होने वाली वर्षा ……………. की फसल के लिए लाभप्रद होती है।
- आम्रवृष्टि ……………. की फसल के लिए लाभदायक होती है।
- भारत के …………. तट पर सर्दियों में वर्षा होती है।
- भारत के तटवर्ती क्षेत्रों में ……………. जलवायु मिलती है।
- वायु की कमी मापने के लिए ……………. प्रयोग किया जाता है।
- सुनामी से भारत में कई राज्यों में …………….. लोग मर गए थे।
उत्तर-
- सितम्बर,
- रबी,
- फूलों,
- कोरोमण्डल,
- सम,
- सूखी व गीली गोली का थर्मामीटर,
- 10.500.
सही/ग़लत (True/False)
- भारत गर्म जलवायु वाला देश है। ( )
- भारत की जलवायु पर मानसून पवनों का गहरा प्रभाव है। ( )
- भारत के सभी भागों में वर्षा का वितरण एक समान है। ( )
- मानसूनी वर्षा की यह विशेषता है कि इसमें कोई शुष्ककाल नहीं आता। ( )
- भारत में गर्मी का मौसम सबसे लम्बा होता है। ( )
- एनीराइड बैरोमीटर से तापमान मापा जाता है। ( )
- वायु की गति वायु वेग मापक से मापी जाती है। ( )
उत्तर-
- (✓)
- (✓)
- (✗)
- (✗)
- (✓)
- (✗)
- ( ✓)
अति लघु उत्तरों वाले प्रश्न
प्रश्न 1.
भारत के लिए कौन-सा भू-भाग प्रभावकारी जलवायु विभाजक का कार्य करता है ?
उत्तर-
भारत के लिए विशाल हिमालय प्रभावकारी जलवायु विभाजक का कार्य करता है।
प्रश्न 2.
भारत कौन-सी पवनों के प्रभाव में आता है ?
उत्तर-
भारत उपोष्ण उच्च वायुदाब से चलने वाली स्थलीय पवनों के प्रभाव में आता है।
प्रश्न 3.
वायुधाराओं तथा पवनों में क्या अन्तर है ?
उत्तर-
वायुधाराएं भू-पृष्ठ से बहुत ऊंचाई पर चलती हैं जबकि पवनें भू-पृष्ठ पर ही चलती हैं।
प्रश्न 4.
उत्तरी भारत में मानसून के अचानक ‘फटने’ के लिए कौन-सा तत्त्व उत्तरदायी है ?
उत्तर-
इसके लिए 15° उत्तरी अक्षांश के ऊपर विकसित पूर्वी जेट वायुधारा उत्तरदायी है।
प्रश्न 5.
भारत में अधिकतर वर्षा कब से कब तक होती है ?
उत्तर-
भारत में अधिकतर (75 से 90 प्रतिशत तक) वर्षा जून से सितम्बर तक होती है।
प्रश्न 6.
(i) भारत के किस भाग में पश्चिमी चक्रवातों के कारण वर्षा होती है ?
(ii) यह वर्षा किस फसल के लिए लाभप्रद होती है ?
उत्तर-
- पश्चिमी चक्रवातों के कारण भारत के उत्तरी भाग में वर्षा होती है।
- यह वर्षा रबी की फसल विशेष रूप से गेहूं के लिए लाभप्रद होती है।
प्रश्न 7.
पीछे हटते हुए मानसून की ऋतु की कोई एक विशेषता बताइए।
उत्तर-
इस ऋतु में मानसून का निम्न वायुदाब का गर्त कमजोर पड़ जाता है तथा उसका स्थान उच्च वायुदाब ले लेता है।
अथवा
इस ऋतु में पृष्ठीय पवनों की दिशा उलटनी शुरू हो जाती है। अक्तूबर तक मानसून उत्तरी मैदानों से पीछे हट जाता है।
प्रश्न 8.
भारत में दक्षिण-पश्चिमी मानसून की कौन-कौन सी शाखाएं हैं ?
उत्तर-
भारत में दक्षिण-पश्चिमी मानसून की दो मुख्य शाखाएं हैं-अरब सागर की शाखा तथा बंगाल की खाड़ी की शाखा।
प्रश्न 9.
ग्रीष्म ऋतु के प्रारम्भ (मार्च मास) में किस भाग पर तापमान सबसे अधिक होता है ?
उत्तर-
ग्रीष्म ऋतु के प्रारम्भ में दक्कन के पठार पर तापमान सबसे अधिक होता है।
प्रश्न 10.
संसार की सबसे अधिक वर्षा कहां होती है ?
उत्तर-
संसार की सबसे अधिक वर्षा माउसिनराम (Mawsynram) नामक स्थान पर होती है।
प्रश्न 11.
भारत के किस तट पर सर्दियों में वर्षा होती है ?
उत्तर-
कोरोमण्डल।
प्रश्न 12.
भारत के तटवर्ती क्षेत्रों में किस प्रकार की जलवायु मिलती है ?
उत्तर-
सम।
प्रश्न 13.
‘मानसून’ शब्द की उत्पत्ति किस शब्द से हुई है ?
उत्तर-
‘मानसून’ शब्द की उत्पत्ति अरबी भाषा के मौसम शब्द से हुई है।
प्रश्न 14.
भारत की वार्षिक औसत वर्षा कितनी है ?
उत्तर-
118 सें० मी०।
प्रश्न 15.
किस भाग में तापमान लगभग सारा साल ऊंचे रहते हैं ?
उत्तर-
दक्षिणी भाग में।
प्रश्न 16.
तूफानी चक्रवातों को पश्चिमी बंगाल में क्या कहा जाता है ?
उत्तर-
काल बैसाखी।
प्रश्न 17.
देश के उत्तरी मैदानों में गर्मियों में चलने वाली धूल भरी स्थानीय पवन का क्या नाम है ?
उत्तर-
लू।
प्रश्न 18.
देश की सबसे अधिक वर्षा कौन-सी पहाड़ियों में होती है ?
उत्तर-
मेघालय की पहाड़ियों में।
प्रश्न 19.
मासिनराम की वार्षिक वर्षा की मात्रा कितनी है ?
उत्तर-
1141 से० मी०।
प्रश्न 20.
तिरुवन्नतपुरम् की जलवायु सम क्यों है ?
उत्तर-
इसका कारण यह है कि तिरुवन्नतपुरम् सागरीय जलवायु के प्रभाव में रहता है।
प्रश्न 21.
भारत की जलवायु को प्रभावित करने वाले तत्त्वों को बताइए।(कोई दो)
उत्तर-
भारत की जलवायु को प्रभावित करने वाले मुख्य तत्त्व हैं-
- भूमध्य रेखा से दूरी,
- धरातल का स्वरूप,
- वायुदाब प्रणाली,
- मौसमी पवनें और
- हिन्द महासागर से समीपता।
प्रश्न 22.
देश में सर्दियों के मौसम में
(i) सबसे अधिक और
(ii) सबसे कम तापक्रम वाले दो-दो स्थानों के नाम बताइए।
उत्तर-
क्रमशः-
- मुम्बई तथा चेन्नई
- अमृतसर तथा लेह।
प्रश्न 23.
देश में गर्मियों में
(i) सबसे ठण्डे व
(ii) गर्म स्थानों के नाम बताओ।
उत्तर-
- सबसे ठण्डे स्थान लेह तथा शिलांग
- सबसे गर्म स्थान-उत्तर-पश्चिमी मैदान।
प्रश्न 24.
‘काल बैसाखी’ किसे कहते हैं ?
उत्तर-
बैसाख मास में पश्चिमी बंगाल में चलने वाले तूफ़ानी चक्रवातों को ‘काल बैसाखी’ कहते हैं।
प्रश्न 25.
‘आम्रवृष्टि’ से क्या अभिप्राय है ?
उत्तर-
ग्रीष्म ऋतु के अन्त में केरल तथा कर्नाटक के तटीय भागों में होने वाली पूर्व मानसूनी वर्षा जो आमों अथवा फूलों की फसल के लिए लाभदायक होती है।
प्रश्न 26.
अरब सागर व बंगाल की खाड़ी वाली मानसून पवनें किन स्थानों पर एक-दूसरे से मिल जाती हैं ?
उत्तर-
अरब सागर व बंगाल की खाड़ी वाली मानसून पवनें पंजाब तथा हिमाचल प्रदेश में आपस में मिलती हैं।
प्रश्न 27.
वर्षा कितने प्रकार की होती है ?
उत्तर-
वर्षा तीन प्रकार की होती है-संवहणीय वर्षा, पर्वतीय वर्षा तथा चक्रवाती वर्षा।
प्रश्न 28.
पर्वतीय वर्षा क्यों लगातार तथा लंबे समय तक बरसती रहती है ?
उत्तर-
पवनें समुद्र से धरातल की तरफ लगातार चलती रहती हैं जिस कारण पर्वतीय वर्षा लगातार लंबा समय चलती रहती है।
प्रश्न 29.
पंजाब की फसलों के लिए कौन-सी वर्षा सर्दियों में लाभदायक होती है ?
उत्तर-
सर्दियों की चक्रवाती वर्षा पंजाब की फसलों के लिए लाभदायक होती है।
प्रश्न 30.
‘मानसून का फटना’ किसे कहते हैं ?
उत्तर-
मानसून पवनें लगभग 1 जून को पश्चिमी तट पर पहुंचती हैं और बहुत तेजी से वर्षा करती हैं जिसे मानसूनी धमाका या ‘मानसून का फटना’ (Monsoon Burst) कहते हैं।
प्रश्न 31.
लू (Loo) से आप क्या समझते हैं ?
उत्तर-
ग्रीष्म ऋतु में कम दबाव का क्षेत्र पैदा होने के कारण चलने वाली धूल भरी आंधियां लू कहलाती हैं।
प्रश्न 32.
जलवायु का अनुमान किन यन्त्रों से लगाया जाता है ?
उत्तर-
जलवायु का अनुमान कई यन्त्रों से लगाया जाता है जैसे कि उच्चतम व न्यूनतम थर्मामीटर, एनीराइड बैरोमीटर, सूखी व गीली गोली का थर्मामीटर, वर्षा मापक यन्त्र, वायु वेग मापक, वायु दिशा सूचक इत्यादि।
प्रश्न 33.
प्राकृतिक आपदाओं के मुख्य रूप बताओ।
उत्तर-
प्राकृतिक आपदाएं कई रूपों में आती हैं, जैसे कि-भूकम्प, सुनामी, ज्वालामुखी, चक्रवात, बाढ़, सूखा इत्यादि।
प्रश्न 34.
भारत में सुनामी कब तथा कौन से राज्यों में आई थी ?
उत्तर-
भारत में सुनामी दिसम्बर 2004 में अंडेमान-निकोबार, तमिलनाडु के तट, आन्ध्र प्रदेश, केरल इत्यादि प्रदेशों में आई थी।
प्रश्न 35.
सुनामी का एक गलत प्रभाव बताएं।
उत्तर-
सुनामी से काफ़ी जान-माल का नुकसान हुआ था।
लघु उत्तरों वाले प्रश्न
प्रश्न 1.
परम्परागत भारतीय ऋतु प्रणाली के बारे में बताइए।
उत्तर-
| ऋतु | परम्परागत ऋतु प्रणाली |
| 1.सर्दी | हेमन्त तथा शिशिर का मिश्रण |
| 2. गर्मी | गर्मी |
| 3. वर्षा | वर्षा |
| 4. वापसी मानसून की ऋतु | शरद |
प्रश्न 2.
नागपुर मुम्बई की अपेक्षा ठण्डा है।
उत्तर-
मुम्बई सागर तट पर बसा है। समुद्र के प्रभाव के कारण मुम्बई की जलवायु सम रहती है और यहां सर्दी कम पड़ती है।
इसके विपरीत नागपुर समुद्र से दूर स्थित है। समुद्र के प्रभाव से मुक्त होने के कारण वहां विषम जलवायु पाई जाती है। अत: नागपुर मुम्बई की अपेक्षा ठण्डा है।
प्रश्न 3.
भारत की अधिकांश वर्षा चार महीनों में होती है।
उत्तर-
भारत में अधिकांश वर्षा मध्य जून से मध्य सितम्बर तक होती है। इन चार महीनों में समुद्र से आने वाली मानसूनी पवनें चलती हैं। नमी से युक्त होने के कारण ये पवनें भारत के अधिकांश भाग में खूब वर्षा करती हैं।
प्रश्न 4.
चेरापूंजी में विश्व की लगभग सबसे अधिक वर्षा होती है।
उत्तर-
चेरापूंजी गारो तथा खासी की पहाड़ियों के दक्षिणी भाग में स्थित है। इसकी स्थिति कीप की आकृति वाली घाटी के शीर्ष पर है। यहां बंगाल की खाड़ी की मानसून पवनों की एक शाखा वर्षा करती है। इन पवनों की दिशा तथा अनोखी स्थिति के कारण चेरापूंजी संसार में सबसे अधिक वर्षा वाला स्थान बन गया है।
प्रश्न 5.
दक्षिणी-पश्चिमी मानसून द्वारा कोलकाता में 145 सेंटीमीटर वर्षा जबकि जैसलमेर में केवल 12 सेंटीमीटर वर्षा होती है।
उत्तर-
कलकत्ता (कोलकाता) बंगाल की खाड़ी से उठने वाली मानसून पवनों के पूर्व की ओर बढ़ते समय पहले पड़ता है। जलकणों से लदी ये पवनें यहां 145 सेंटीमीटर वर्षा करती हैं।
जैसलमेर अरावली पर्वत के प्रभाव में आता है। अरावली पर्वत अरब सागर से आने वाली पवनों के समानान्तर स्थित है और यह पवनों को रोकने में असमर्थ है। अतः पवनें बिना वर्षा किए आगे निकल जाती हैं। यही कारण है कि जैसलमेर में केवल 12 सेंटीमीटर वर्षा होती है।
प्रश्न 6.
चेन्नई में अधिकांश वर्षा सर्दियों में होती है।
उत्तर-
चेन्नई भारत के पूर्वी तट पर स्थित है। यह उत्तर-पूर्वी मानसून पवनों के प्रभाव में आता है। ये पवनें शीत ऋतु में स्थल से समुद्र की ओर चलती हैं। परन्तु बंगाल की खाड़ी से लांघते हुए ये जलवाष्प ग्रहण कर लेती हैं। तत्पश्चात् पूर्वी घाट से टकरा कर ये चेन्नई में वर्षा करती हैं।
प्रश्न 7.
पश्चिमी जेट धारा का चक्रवातीय वर्षा लाने में योगदान को बताइए।
उत्तर-
पश्चिमी जेट वायुधारा शीत ऋतु में हिमालय के दक्षिणी भाग के ऊपर समताप मण्डल में स्थिर रहती है। जून मास में यह उत्तर की ओर खिसक जाती है और 25° उत्तरी अक्षांश तक पहुंच जाती है। तब इसकी स्थिति मध्य एशिया में स्थित तियेनशान पर्वत श्रेणी के उत्तर में हो जाती है। इस प्रभाव के कारण ही गर्मियों के चक्रवात और भूमध्य सागरीय क्षेत्रों का पश्चिमी मौसमी हलचल का प्रभाव देश के उत्तरी भागों तक आ पहुंचता है तथा भरपूर वर्षा प्रदान करता है।
प्रश्न 8.
राजस्थान अरब सागर के नज़दीक होते हुए भी शुष्क क्यों रहता है ?
उत्तर-
इसमें कोई सन्देह नहीं कि राजस्थान अरब सागर के निकट स्थित है। परन्तु फिर भी यह शुष्क रह जाता है। इसके निम्नलिखित कारण हैं
- राजस्थान में पहुंचते समय मानसून पवनों में नमी की मात्रा काफ़ी कम हो जाती है, जिसके कारण राजस्थान का थार मरुस्थल का भाग शुष्क ही रह जाता है।
- इस मरुस्थलीय क्षेत्र की तापमान विरोध की स्थिति के कारण ये पवनें तेजी से दाखिल नहीं हो पातीं।
- अरावली पर्वत इन पवनों के समानान्तर तथा कम ऊंचाई में होने के कारण ये पवनें बिना ऊपर उठे ही सीधी निकल जाती हैं।
प्रश्न 9.
हिमालय पर्वत भारत के लिए किस प्रकार ‘जलवायु विभाजक’ का कार्य करता है ?
उत्तर-
हिमालय पर्वत की उच्च श्रृंखला उत्तरी पवनों के सामने एक दीवार की भान्ति खड़ी है। उत्तरी ध्रुव वृत्त के निकट उत्पन्न होने वाली ये ठण्डी और बर्फीली पवनें हिमालय को पार करके भारत में प्रवेश नहीं कर सकतीं। परिणामस्वरूप सम्पूर्ण उत्तर-भारत में उष्ण कटिबन्धीय जलवायु पाई जाती है। अतः स्पष्ट है कि हिमालय पर्वत की श्रृंखला भारत के लिए जलवायु विभाजक का कार्य करती है।
प्रश्न 10.
भारत की स्थिति को स्पष्ट करते हुए देश की जलवायु पर इसके प्रभाव को समझाइए।(कोई तीन बिन्दु)।
उत्तर-
- भारत 8° उत्तर से 37° अक्षांशों के बीच स्थित है। इसके मध्य से कर्क वृत्त गुज़रता है। इसके कारण देश का दक्षिणी आधा भाग उष्ण कटिबन्ध में आता है, जबकि उत्तरी आधा भाग उपोष्ण कटिबन्ध में आता है।
- भारत के उत्तर में हिमालय की ऊंची-ऊंची अटूट पर्वत मालाएं हैं। देश के दक्षिण में हिन्द महासागर फैला है। इस सुगठित भौतिक विन्यास ने देश की जलवायु को मोटे तौर पर समान बना दिया है।
- देश के पूर्व में बंगाल की खाड़ी तथा पश्चिम में अरब सागर की स्थिति का भारतीय उप-महाद्वीप की जलवायु पर समताकारी प्रभाव पड़ता है। ये देश में वर्षा के लिए अनिवार्य आर्द्रता भी जुटाते हैं।
प्रश्न 11.
‘आम्रवृष्टि’ और ‘काल बैसाखी’ में अन्तर स्पष्ट कीजिए।
उत्तर-
आम्रवृष्टि-ग्रीष्म ऋतु के अन्त में केरल तथा कर्नाटक के तटीय भागों में मानसून से पूर्व की वर्षा का यह स्थानीय नाम इसलिए पड़ा है क्योंकि यह आम के फलों को शीघ्र पकाने में सहायता करती है।
काल बैसाखी-ग्रीष्म ऋतु में बंगाल तथा असम में भी उत्तरी-पश्चिमी तथा उत्तरी पवनों द्वारा वर्षा की तेज़ बौछारें पड़ती हैं। यह वर्षा प्रायः सायंकाल में होती है। इसी वर्षा को ‘काल बैसाखी’ कहते हैं। इसका अर्थ है-बैसाख मास का काल।
प्रश्न 12.
भारत में पीछे हटते हुए मानसून ऋतु की तीन विशेषताएं बताओ।
उत्तर-
भारत में पीछे हटते मानसून की ऋतु अक्तूबर तथा नवम्बर के महीने में रहती है। इस ऋतु की तीन विशेषताएं अग्रलिखित हैं
- इस ऋतु में मानसून का निम्न वायुदाब का गर्त कमज़ोर पड़ जाता है और उसका स्थान उच्च वायुदाब ले लेता है।
- भारतीय भू-भागों पर मानसून का प्रभाव क्षेत्र सिकुड़ने लगता है।
- पृष्ठीय पवनों की दिशा उलटनी शुरू हो जाती है। आकाश स्वच्छ हो जाता है और तापमान फिर से बढ़ने लगता है।
प्रश्न 13.
मानसून पूर्व की वर्षा (Pre-Monsoonal Rainfal) किन कारणों से होती है ?
उत्तर-
गर्मियों में भूमध्य रेखा की कम दबाव की पेटी कर्क रेखा की ओर खिसक (सरक) जाती है। इस दबाव को भरने के लिए दक्षिणी हिन्द महासागर से दक्षिणी-पूर्वी व्यापारिक पवनें भू-मध्य रेखा को पार करते ही धरती की दैनिक गति के कारण घड़ी की सुई की दिशा में दक्षिण-पश्चिम से उत्तर-पूर्व की ओर मुड़ जाती हैं। ये पवनें 1 जून को देश के पश्चिमी तट पर पहुंचकर बहुत तेज़ी से वर्षा करती हैं। परन्तु 1 जून से पहले भी केरल तट के आस-पास जब समुद्री पवनें पश्चिमी तट को पार करती हैं, तब भी मध्यम स्तर की वर्षा होती है। इसी वर्षा को पूर्व मानसून (PreMonsoon) की वर्षा भी कहा जाता है। इस वर्षा का मुख्य कारण, पश्चिमी घाट की पवनमुखी ढालें हैं।
प्रश्न 14.
देश की जलवायु को प्रभावित करने वाले दो तत्त्वों का वर्णन करें।
उत्तर-
- भूमध्य रेखा से दूरी-भारत उत्तरी गोलार्द्ध में भूमध्य रेखा के समीप स्थित है। परिणामस्वरूप पर्वतीय क्षेत्रों को छोड़कर देश के अधिकांश क्षेत्रों में लगभग पूरे वर्ष तापमान ऊंचा रहता है। इसीलिए भारत को गर्म जलवायु वाला देश भी कहा जाता है।
- धरातल-एक ओर हिमालय पर्वत श्रेणियां देश को एशिया के मध्यवर्ती भागों से आने वाली बीली व शीत पवनों से बचाती हैं तो दूसरी ओर ऊंची होने के कारण ये बंगाल की खाड़ी से आने वाली मानसून पवनों के रास्ते में बाधा बनती हैं और उत्तरी मैदान में वर्षा का कारण बनती हैं।
प्रश्न 15.
मानसून पवनों में मुख्य लक्षण बताएं।
उत्तर-
- मानसून पवनें लगभग कर्क रेखा व मकर रेखा के बीच के क्षेत्रों में चलती है।
- उष्णपूर्ति जेट स्ट्रीम तथा पश्चिमी जेट स्ट्रीम भी देश के मानसून को प्रभावित करती है।
- गर्मियों में सूर्य के उत्तर की तरफ सरकने के साथ वायु दबाव पेटी भी उत्तर की तरफ चली जाती है तथा स्थिति मानसून पवनों के चलने के लिए बढ़िया हो जाती है।
प्रश्न 16.
सर्दी की ऋतु के बारे में बताएं।
उत्तर-
इस मौसम में सूर्य दक्षिणी गोलार्द्ध में मकर रेखा पर सीधा चमकता है। इसीलिए भारत में दक्षिणी भागों से उत्तर की ओर तापमान लगातार घटता जाता है। सम्पूर्ण उत्तरी भारत में तापमान में गिरावट के कारण उच्च वायुदाब का क्षेत्र पाया जाता है। कभी-कभी देश के पश्चिमी और उत्तर-पश्चिमी भागों में निम्नदाब के केन्द्र बन जाते हैं। उन्हें पश्चिमी गड़बड़ी विक्षोभ अथवा चक्रवात कहा जाता है। इस समय मध्य तथा पश्चिमी एशिया के क्षेत्रों में उच्चदाब का केन्द्र होता है। वहां की शुष्क तथा शीत पवनें उत्तर-पश्चिमी भागों में से देश के अन्दर प्रवेश करती हैं। इससे पूरे विशाल मैदानों का तापमान काफ़ी नीचे गिर जाता है। 3 से 5 किलोमीटर प्रति घण्टे की गति से बहने वाली इन पवनों के द्वारा शीत लहर का जन्म होता है। सर्दियों में देश के दो भागों में वर्षा होती है। देश के उत्तरी-पश्चिमी भागों में पंजाब, हरियाणा, उत्तरी राजस्थान, उत्तराखण्ड, जम्मू-कश्मीर व पश्चिमी उत्तर प्रदेश में औसत 20 से 25 सेंटीमीटर तक चक्रवातीय वर्षा होती है। दूसरी ओर तमिलनाडु तथा केरल के तटीय भागों में उत्तर-पूर्व मानसून से पर्याप्त वर्षा होती है। सर्दियों में मौसम सुहावना होता है। दिन मुख्य रूप से गर्म (सम) तथा रातें ठण्डी होती हैं। कभी-कभी रात के तापमान में गिरावट आने के कारण सघन कोहरा भी पड़ता है।
प्रश्न 17.
गर्मी की ऋतु के बारे में बताएं।
उत्तर-
भारत में गर्मी की ऋतु सबसे लम्बी होती है। 21 मार्च के बाद से ही देश के आन्तरिक भागों का तापमान बढ़ने लगता है। दिन का अधिकतम तापमान मार्च में नागपुर में 380 सें०, अप्रैल में मध्यप्रदेश में 40° सें० तथा मईजून में उत्तर-पश्चिम भागों में 45° सें० से भी अधिक रहता है। रात के समय न्यूनतम तापमान 21° से 27° सें० तक बना रहता है। दक्षिणी भागों का औसत तापमान समुद्र की समीपता के कारण अपेक्षाकृत कम (25° सें०) रहता है। तापमान में वृद्धि के कारण हवा के कम दबाव का क्षेत्र देश के उत्तरी भागों की ओर खिसक जाता है। मई-जून में देश के उत्तरी-पश्चिमी भागों में कम दबाव का चक्र सबल हो जाता है तथा दक्षिणी ‘जेट’ धारा हिमालय के उत्तर की ओर सरक जाती है। धरातल के ऊपर हवा में भी कम दबाव का चक्र उत्पन्न हो जाता है। कम दबाव के ये दोनों चक्र मानसून पवनों को तेजी से अपनी ओर खींचते हैं।
प्रश्न 18.
उच्चतम व न्यूनतम थर्मामीटर को किस लिए तथा किस प्रकार प्रयोग किया जाता है ?
उत्तर-
तापमान का पता करने के लिए इस प्रकार के थर्मामीटर का प्रयोग किया जाता है। अगर किसी स्थान की जलवायु की जानकारी प्राप्त करनी हो तो हमें वहां के तापमान की जानकारी का होना आवश्यक है। इस प्रकार का थर्मामीटर दो जुड़ी हुई नालियों के साथ बना होता है। इस नाली से रात्रि का न्यूनतम तापमान पता किया जाता है तथा दूसरी नाली से दिन का उच्चतम तापमान पता किया जाता है। तापमान को सैंटीग्रेड अथवा फारेनहाइड की डिग्री में मापा जाता है।
प्रश्न 19.
एनीराइड बैरोमीटर का वर्णन करें।
उत्तर-
एनीराइड बैरोमीटर से वायु दबाव का पता किया जाता है। यह बैरोमीटर धातु की एक डिब्बी में से हवा निकाल कर उसे एक पतली सी चादर से बांध दिया जाता है। डिब्बी में एक स्परिंग होता है। हवा के दबाव के कारण अंदर स्परिंग से लगी हुई सूई घूमती है। दबाव से अनुसार सूई अन्दर लिखे हुए आंकड़ों पर टिकेगी तथा इससे हमें वायु दबाव अथवा हवा के दबाव का पता चल जाएगा। हवा के दबाव को हमेशा मिली बार में बताया जाता है।
परिणामस्वरूप सम्पूर्ण उत्तर-भारत में उष्ण कटिबन्धीय जलवायु पाई जाती है। अतः स्पष्ट है कि हिमालय पर्वत की श्रृंखला भारत के लिए जलवायु विभाजक का कार्य करती है।
प्रश्न 20.
वर्षा मापक यन्त्र क्यों तथा कैसे प्रयोग किया जाता है ?
उत्तर-
वर्षा को मापने के लिए वर्षा मापक यन्त्र का प्रयोग किया जाता है। वर्षा मापक यन्त्र के बीच लोहे या पीतल का एक गोल बर्तन होता है। इस बर्तन के मुंह पर एक कीप लगी होती है जिससे बारिश का पानी साथ लगी हुई बोतल में इक्ट्ठा हो जाता है। इस कारण यह वाष्प बन कर नहीं उड़ सकता। इस यन्त्र को एक खुले स्थान पर रखा जाता है। ताकि बारिश का पानी इसमें आसानी से इक्ट्ठा हो सके। बारिश खत्म होने के पश्चात् पानी को एक शीशे के बर्तन में डाल दिया जाता है। जिस पर निशान लगे होते हैं। इन निशानों की सहायता से बताया जाता है कि कितनी वर्षा हुई है। वर्षा को इंच या सैंटमीटर में बताया जाता है।
प्रश्न 21.
सुनामी का संक्षेप में वर्णन करें।
उत्तर-
सुनामी जापानी भाषा का शब्द है। जिसका अर्थ है-बंदगाह की लहर। अगर किसी स्थान पर सुनामी आती है तो समुद्र में काफी ऊंची-ऊंची लहरें उठने लग जाती हैं। समुद्र के किनारों पर तो इनकी ऊंचाई 10 मीटर से 30 मीटर तक हो जाती है। इनकी गति काफी तेज़ होती है तथा खुले समुद्र में यह 40 कि०मी० से 1000 कि०मी० प्रति घण्टा की गति से चलती है। वास्तव में अगर समुद्र तल से नीचे भूकम्प आए तो सुनामी आती है। 26 दिसम्बर, 2004 को दक्षिण पूर्वी एशिया में सुनामी आई थी जिससे काफी नुक्सान हुआ था। अकेले भारत में ही 10,500 लोगों की मृत्यु हो गई थी तथा दस हज़ार करोड़ रुपये का नुकसान हो गया था।
दीर्घ उत्तरों वाले प्रश्न
प्रश्न 1.
भारतीय जलवायु की प्रादेशिक विभिन्नताएं कौन-कौन सी हैं ?
उत्तर-
भारतीय जलवायु की प्रादेशिक विभिन्नताएं निम्नलिखित हैं
- सर्दियों में हिमालय पर्वत के कारगिल क्षेत्रों में तापमान-45° सेन्टीग्रेड तक पहुंच जाता है परन्तु उसी समय तमिलनाडु के चेन्नई (मद्रास) महानगर में यह 20° सेन्टीग्रेड से भी अधिक होता है। इसी प्रकार गर्मियों की ऋतु में अरावली पर्वत की पश्चिमी दिशा में स्थित जैसलमेर का तापमान 50° सेन्टीग्रेड को भी पार कर जाता है, जबकि श्रीनगर में 20° सेन्टीग्रेड से कम तापमान होता है। –
- खासी पर्वत श्रेणियों में स्थित माउसिनराम (Mawsynaram) में 1141 सेंटीमीटर औसतन वार्षिक वर्षा दर्ज की जाती है। परन्तु दूसरी ओर पश्चिमी थार मरुस्थल में वार्षिक वर्षा का औसत 10 सेंटीमीटर से भी कम है।
- बाड़मेर और जैसलमेर में लोग बादलों के लिए तरस जाते हैं परन्तु मेघालय में,सारा साल आकाश बादलों से ढका रहता है।
- मुम्बई तथा अन्य तटवर्ती नगरों में समुद्र का प्रभाव होने के कारण तापमान वर्ष भर लगभग एक जैसा ही रहता है। इसके विपरीत राष्ट्रीय राजधानी क्षेत्र दिल्ली और आसपास के क्षेत्रों में सर्दी एवं गर्मी के तापमान में भारी अन्तर पाया जाता है।
प्रश्न 2.
देश में जलवायु विभिन्नताओं के कारण बताओ।
उत्तर-
भारत के सभी भागों की जलवायु एक समान नहीं है। इसी प्रकार सारा साल भी जलवायु एक जैसी नहीं रहती। इसके मुख्य कारण निम्नलिखित हैं
- देश के उत्तरी पर्वतीय क्षेत्र ऊंचाई के कारण वर्ष भर ठण्डे रहते हैं। परन्तु समुद्र तटीय प्रदेशों का तापमान वर्ष भर लगभग एक समान रहता है। दूसरी ओर, देश के भीतरी भागों में कर्क रेखा की समीपता के कारण तापमान ऊंचा रहता है।
- पवनमुखी ढालों पर स्थित स्थानों पर भारी वर्षा होती है, जबकि वृष्टि छाया क्षेत्र में स्थित प्रदेश सूखे रह जाते हैं।
- गर्मियों में मानसून पवनें समुद्र से स्थल की ओर चलती हैं। जलवाष्प से भरपूर होने के कारण ये खूब वर्षा करती हैं। परन्तु आगे बढ़ते हुए इनके जलवाष्प कम होते जाते हैं। परिणामस्वरूप वर्षा की मात्रा कम होती जाती है।
- सर्दियों में मानसून पवनें विपरीत दिशा अपना लेती हैं। इनके जलवाष्प रहित होने के कारण देश में अधिकांश भाग शुष्क रह जाते हैं। इस ऋतु में अधिकांश वर्षा केवल देश के दक्षिण-पूर्वी तट पर ही होती है।
प्रश्न 3.
भारत की वर्षा ऋतु का वर्णन करो।
उत्तर-
वर्षा ऋतु को दक्षिण-पश्चिम मानसून की ऋतु भी कहते हैं। यह ऋतु जून से लेकर मध्य सितम्बर तक रहती है। इस ऋतु की मुख्य विशेषताओं का वर्णन निम्नलिखित है
- भारत के उत्तर-पश्चिमी क्षेत्र में निम्न दाब का क्षेत्र अधिक तीव्र हो जाता है।
- समुद्र से पवनें भारत में प्रवेश करती हैं और गरज के साथ घनघोर वर्षा करती हैं।
- आर्द्रता से भरी ये पवनें 30 किलोमीटर प्रति घण्टा की दर से चलती हैं और एक मास के अन्दर-अन्दर पूरे देश में फैल जाती हैं।
- भारतीय प्रायद्वीप मानसून को दो शाखाओं में विभाजित कर देता है-अरब सागर की मानसून पवनें तथा खाड़ी बंगाल की मानसून पवनें।
- खाड़ी बंगाल की मानसून पवनें भारत के पश्चिमी घाट और उत्तर-पूर्वी क्षेत्र में अत्यधिक वर्षा करती हैं। पश्चिमी घाट की पवनाभिमुख ढालों पर 250 सें०मी० से भी अधिक वर्षा होती है। इसके विपरीत इस घाट की पवनाविमुख ढालों पर केवल 50 सें०मी० वर्षा होती है। मुख्य कारण वहां की उच्च पहाड़ी श्रृंखलाएं तथा पूर्वी हिमालय हैं। दूसरी ओर उत्तरी मैदानों में पूर्व से पश्चिम की ओर जाते हुए वर्षा की मात्रा घटती जाती है।
प्रश्न 4.
भारत की मानसूनी वर्षा की मुख्य विशेषताओं का वर्णन करो।
उत्तर-
भारत में वार्षिक वर्षा की मात्रा 118 सेंटीमीटर के लगभग है। यह सारी वर्षा मानसून पवनों द्वारा ही प्राप्त होती है। इस मानसूनी वर्षा की निम्नलिखित मुख्य विशेषताएं हैं_-
- वर्षा का समय व मात्रा-देश की अधिकांश वर्षा (87%) मानसून पवनों द्वारा गर्मी के मौसम में प्राप्त होती है। 3% वर्षा सर्दियों में और 10% मानसून आने से पहले मार्च से मई तक हो जाती है। वर्षा ऋतु जून से मध्य सितम्बर के बीच होती है।
- अस्थिरता-भारत में मानसून पवनों से प्राप्त वर्षा भरोसे योग्य नहीं है। यह आवश्यक नहीं है कि वर्षा एकसमान होती रहे। वर्षा की यह अस्थिरता देश के आन्तरिक भागों तथा राजस्थान में अपेक्षाकृत अधिक है।
- असमान वितरण-देश में वर्षा का वितरण समान नहीं है। पश्चिमी घाट की पश्चिमी ढलानों और मेघालय तथा असम की पहाड़ियों में 250 सेंटीमीटर से भी अधिक वर्षा होती है। दूसरी ओर पश्चिमी राजस्थान, पश्चिमी गुजरात, उत्तरी जम्मू-कश्मीर आदि में 25 सेंटीमीटर से भी कम वर्षा होती है।
- अनिश्चितता-भारत में होने वाली मानसूनी वर्षा की मात्रा पूरी तरह निश्चित नहीं है। कभी तो मानसून पवनें समय से पहले पहुंच कर भारी वर्षा करती हैं। कई स्थानों पर तो बाढ़ तक आ जाती है। कभी यह वर्षा इतनी कम होती है या निश्चित समय से पहले ही खत्म हो जाती है कि सूखे की स्थिति पैदा हो जाती है।
- शुष्क अन्तराल-कई बार गर्मियों में मानसूनी वर्षा लगातार न होकर कुछ दिन या सप्ताह के अन्तराल से होती है। इसके फलस्वरूप वर्षा-चक्र टूट जाता है और वर्षा ऋतु में एक लम्बा व शुष्क काल (Long & Dry Spell) आ जाता है।
- पर्वतीय वर्षा-मानसूनी वर्षा पर्वतों के दक्षिणी ढलान और पवनोन्मुखी ढलान (Windward sides) पर अधिक होती है। पर्वतों की उत्तरी और पवन विमुखी ढलाने (Leaward sides) वर्षा-छाया क्षेत्र (Rain-Shadow Zone) में स्थित होने के कारण शुष्क रह जाती हैं।
- मूसलाधार वर्षा-मानसूनी वर्षा अत्यधिक मात्रा में और कई-कई दिनों तक लगातार होती है। इसीलिए ही यह कहावत प्रसिद्ध है कि भारत में वर्षा पड़ती नहीं है बल्कि गिरती है।’ सच तो यह है कि मानसूनी वर्षा अनिश्चित तथा असमान स्वभाव लिए हुए है।
प्रश्न 5.
भारतीय जीवन पर मानसनी पवनों के प्रभाव का उदाहरण सहित वर्णन करो।
उत्तर-
किसी भी देश या क्षेत्र के आर्थिक, धार्मिक तथा सामाजिक विकास में वहां की जलवायु का गहरा प्रभाव होता है। इस सम्बन्ध में भारत कोई अपवाद नहीं है। मानसून पवनें भारत की जलवायु का सर्वप्रमुख प्रभावी कारक हैं। इसलिए इनका महत्त्व और भी बढ़ जाता है। भारतीय जीवन पर इन पवनों के प्रभाव का वर्णन इस प्रकार है
- आर्थिक प्रभाव-भारतीय अर्थव्यवस्था लगभंग पूर्णतया से कृषि पर आधारित है। इसके विकास के लिए मानसूनी वर्षा ने एक सुदृढ़ आधार प्रदान किया है। जब मानसूनी वर्षा समय पर तथा उचित मात्रा में होती है, तो कृषि उत्पादन बढ़ जाता है तथा चारों ओर हरियाली एवं खुशहाली छा जाती है। परन्तु इसकी असफलता से फसलें सूख जाती हैं, देश में सूखा पड़ जाता है तथा अनाज के भण्डारों में कमी आ जाती है। इसी प्रकार यदि मानसून देरी से आए तो फसलों की बुआई समय पर नहीं हो पाती जिससे उत्पादन कम हो जाता है। इस प्रकार कृषि के विकास और मानसूनी जलवायु वर्षा के बीच गहरा सम्बन्ध बना हुआ है। इसी बात को देखते हुए ही भारत के बजट को मानसूनी पवनों का जुआ (Gamble of Monsoon) भी कहा जाता है।
- सामाजिक प्रभाव-भारत के लोगों की वेशभूषा, खानपान तथा सामाजिक रीति-रिवाजों पर मानसून पवनों का गहरा प्रभाव दिखाई देता है। मानसूनी वर्षा आरम्भ होते ही तापमान कुछ कम होने लगता है और इसके साथ ही लोगों का पहरावा बदलने लगता है। इसी प्रकार मानसून द्वारा देश में एक ऋतु-चक्र चलता रहता है, जो खान-पान तथा पहरावे में बदलाव लाता रहता है। कभी लोगों को गर्म वस्त्र पहनने पड़ते हैं तो कभी हल्के सूती वस्त्र।
- धार्मिक प्रभाव-भारतीयों के अनेक त्योहार मानसून से जुड़े हुए हैं। कुछ का सम्बन्ध फसलों की बुआई से है तो कुछ का सम्बन्ध फसलों के पकने तथा उसकी कटाई से। पंजाब का त्योहार बैसाखी इसका उदाहरण है। इस त्योहार पर पंजाब के किसान फसल पकने की खुशी में झूम उठते हैं। सच तो यह है कि समस्त भारतीय जन-जीवन मानसून के गिर्द ही घूमता है।
प्रश्न 6.
भारत में विशाल मानसूनी एकता होते हुए भी क्षेत्रीय विभिन्नताएं क्यों मिलती हैं ? उदाहरण सहित लिखो।
उत्तर-
इसमें कोई सन्देह नहीं कि हिमालय के कारण देश में मानसूनी एकता देखने को मिलती है परन्तु इस एकता के बावजूद भारत के सभी क्षेत्रों में समान मात्रा में वर्षा नहीं होती है और कुछ क्षेत्रों में बहुत कम वर्षा होती है। इस विभिन्नता के कारण निम्नलिखित हैं
- स्थिति-भारत के जो क्षेत्र पर्वतोन्मुख भागों में स्थित हैं, वहां समुद्र से आने वाली मानसून पवनें पहले पहंचती हैं और खूब वर्षा करती हैं। इसके विपरीत पवन विमुख ढालों वाले क्षेत्रों में वर्षा कम होती है। उत्तर-पूर्वी मैदानी भागों, हिमाचल तथा पश्चिमी तटीय मैदान में अत्यधिक वर्षा होती है। इसके विपरीत प्रायद्वीपीय पठार के बहुत-से भागों तथा कश्मीर में कम वर्षा होती है।
- पर्वतों की दिशा-जो पर्वत पवनों के सम्मुख स्थित होते हैं, वे पवनों को रोकते हैं और वर्षा का कारण बनते हैं। इसके विपरीत पवनों के समानान्तर स्थित पर्वत पवनों को रोक नहीं पाते और उनके समीप स्थित क्षेत्र शुष्क रह जाते हैं। राजस्थान का एक बहुत बड़ा भाग अरावली पर्वत के कारण शुष्क मरुस्थल बन कर रह गया है।
- पवनों की दिशा-मानसूनी पवनों के मार्ग में जो क्षेत्र पहले आते हैं, उनमें वर्षा अधिक होती है और जो क्षेत्र बाद में आते हैं, उनमें वर्षा क्रमशः कम होती जाती है। कोलकाता में बनारस से अधिक वर्षा होती है।
- समुद्र से दूरी-समुद्र के निकट स्थित स्थानों में अधिक वर्षा होती है। परन्तु जो स्थान समुद्र से दूर स्थित होते हैं, वहां वर्षा की मात्रा कम होती है। सच तो यह है कि विभिन्न क्षेत्रों की स्थिति तथा पवनों एवं पर्वतों की दिशा के कारण वर्षा के वितरण में क्षेत्रीय विभिन्नता पाई जाती है।
प्रश्न 7.
भारत में वर्षा का वार्षिक वितरण कैसा है ?
उत्तर-
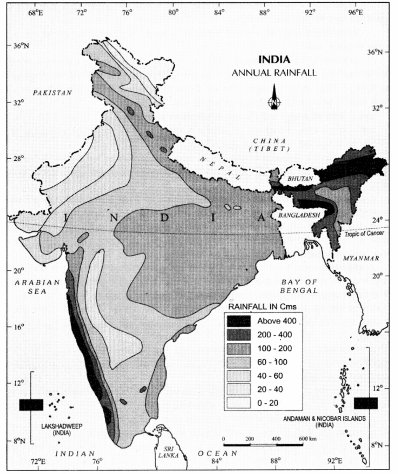
भारत में 118 सें०मी० औसत वार्षिक वर्षा होती है। परन्तु देश में वर्षा का वितरण बहुत ही असमान है। मेघालय की पहाड़ियों में 1000 सेंटीमीटर से भी अधिक वर्षा होती है जबकि थार मरुस्थल में एक वर्ष में केवल 20 सें०मी० से भी कम वर्षा होती है। वार्षिक वर्षा की मात्रा के आधार पर देश को निम्नलिखित पांच क्षेत्रों में बांटा जा सकता है
- भारी वर्षा वाले क्षेत्र-
- दादरा तथा नगर हवेली से लेकर दक्षिण में तिरुवन्तपुरम् तक फैली लम्बी और तंग पट्टी में पश्चिमी घाट की पश्चिमी ढलान तथा पश्चिमी तटीय क्षेत्र सम्मिलित हैं। यहां के कोंकण तथा मालाबार के तटों पर लगातार पांच महीने वर्षा होती रहती है।
- भारी वर्षा का दूसरा क्षेत्र देश के उत्तर-पूर्वी भाग में है। इसमें दार्जिलिंग, बंगाल द्वार, असम की मध्यवर्ती तथा निम्नवर्ती घाटियां, दक्षिणी अरुणाचल प्रदेश और मेघालय के पर्वतीय भाग सम्मिलित हैं। शिलांग के पठार तथा बंगलादेश की ओर वाली ढलानों पर अत्यधिक वर्षा होती है। यहां चेरापूंजी में 1087 सेंटीमीटर और इसी के पास स्थित माउसिनराम में 1141 सेंटीमीटर वर्षा होती है जो विश्व की सबसे अधिक वर्षा है।
- अण्डमान तथा निकोबार द्वीप समूह तथा लक्षद्वीप आदि क्षेत्र भी भारी वर्षा वाले क्षेत्रों में आते हैं।
- अधिक वर्षा वाले क्षेत्र-इन क्षेत्रों में निम्नलिखित क्षेत्र सम्मिलित हैं-
- पश्चिमी घाट के साथ-साथ उत्तर-दक्षिण दिशा में ताप्ती नदी के मुहाने से केरल के मैदानों तक फैली हुई पट्टी।
- दूसरी पट्टी हिमालय की दक्षिणी ढलानों के साथ-साथ हिमाचल प्रदेश से होकर कुमाऊं हिमालय से गुज़रती हुई असम की निचली घाटी तक पहुंचती है।
- तीसरी पट्टी उत्तर-दक्षिण दिशा में फैली हुई है। इसमें त्रिपुरा, मणिपुर, मीकिर की पहाड़ियां आती हैं।
- मध्यम वर्षा वाले क्षेत्र-इन क्षेत्रों में 100 से 150 सेंटीमीटर तक की वार्षिक वर्षा होती है। देश में मध्यम वर्षा वाले तीन क्षेत्र मिलते हैं।
- इसका सबसे बड़ा क्षेत्र उड़ीसा, उत्तरी आन्ध्र प्रदेश, मध्य प्रदेश, झारखण्ड, पूर्वी उत्तर प्रदेश तथा शिवालिक की पहाड़ियों के साथ-साथ तंग पट्टी के रूप में जम्मू की पहाड़ियों तक फैला हुआ है।
- दूसरी पट्टी पूर्वी तट से 80 किलोमीटर की चौड़ाई में फैली हुई है। इसे कोरोमण्डल तट भी कहते हैं।
- तीसरी पट्टी का विस्तार पश्चिमी घाट की पूर्वी ढलानों में नर्मदा नदी के मुहाने से लेकर कन्याकुमारी तक है।
- कम वर्षा वाले क्षेत्र-इस श्रेणी में देश के वे अर्ध-शुष्क क्षेत्र सम्मिलित हैं, जहां पर पूरे वर्ष में औसतन 50 से 100 सेंटीमीटर तक वर्षा होती है। इस क्षेत्र का विस्तार उत्तर में जम्मू के साथ लगी हुई देश की सीमा से लेकर सुदूर दक्षिण में कन्याकुमारी तक है।
- बहुत कम वर्षा वाले क्षेत्र-इन शुष्क क्षेत्रों में 50 सेंटीमीटर से भी कम वर्षा होती है। ऐसे क्षेत्रों में से जस्कर पर्वत श्रेणी के पीछे स्थित लद्दाख से कराकोरम तक का क्षेत्र, कच्छ तथा पश्चिमी राजस्थान का क्षेत्र और पंजाब तथा हरियाणा राज्यों के दक्षिणी-पश्चिमी क्षेत्र शामिल हैं। इन क्षेत्रों में पश्चिमी घाट की पूर्वी ढलानें भी सम्मिलित हैं।
जलवायु PSEB 9th Class Geography Notes
- जलवायु – किसी भी स्थान के लंबे समय के मौसम की औसत | निकाल कर जो परिणाम निकाला जाता है उस परिणाम को | उस स्थान की जलवायु कहते हैं। भारत में जलवायु की अलग-अलग परिस्थितियां पाई जाती हैं।
- जलवायु को प्रभावित करने वाले तत्त्व – किसी भी स्थान की जलवायु को कई कारक प्रभावित करते हैं; जैसे कि भूमध्य रेखा से दूरी, समुद्र से दूरी, समुद्री तल से ऊंचाई, धरातल का स्वरूप, जेट स्ट्रीम | इत्यादि। हमारे देश की भौगोलिक संरचना ने देश की जलवायु को एक जैसा ही बना दिया है।
- वर्षा – नमी भरी हवा ऊपर उठती है तथा ऊँचाई पर जाकर ठंडी हो जाती है। ठंडी होने के कारण यह नमी को संभालकर नहीं रख सकती तथा पानी के कण बादलों का रूप ले लेते हैं। जब बादलों में से यह पानी के कण पृथ्वी पर गिरते हैं तो इसे वर्षा करते हैं। वर्षा तीन प्रकार की होती है-संवहनी वर्षा, पर्वतीय वर्षा तथा चक्रवाती वर्षा।
- मानसून का अर्थ – ‘मानसून’ शब्द की व्युत्पत्ति अरबी भाषा के ‘मौसिम’ शब्द से हुई है। इसका शाब्दिक अर्थ है-ऋतु। इस प्रकार मानसून से अभिप्राय एक ऐसी ऋतु से है जिसमें पवनों की दिशा पूरी तरह उलट जाती है।
- मानसून प्रणाली – मानसून की रचना उत्तरी गोलार्द्ध में प्रशान्त महासागर तथा हिन्द महासागर के दक्षिणी भाग पर वायुदाब की विपरीत स्थिति के कारण होती है। वायुदाब की यह स्थिति परिवर्तित होती रहती है। इस कारण विभिन्न ऋतुओं में विषुवत् वृत्त के आर-पार पवनों की स्थिति बदल जाती है। इस प्रक्रिया को दक्षिणी दोलन कहते हैं। इसके अतिरिक्त जेट वायुधाराएं भी मानसून के रचनातन्त्र में महत्त्वपूर्ण भूमिका निभाती हैं।
- भारत की ऋतुएं – भारत के वार्षिक ऋतु चक्र में चार प्रमुख ऋतुएं होती हैंशीत ऋतु, ग्रीष्म ऋतु, आगे बढ़ते मानसून की ऋतु तथा पीछे हटते मानसून की ऋतु।
- शीत ऋतु – लगभग सारे देश में दिसम्बर से फरवरी तक शीत ऋतु होती है। इस ऋतु में देश के ऊपर उत्तर-पूर्वी व्यापारिक पवनें चलती हैं। इस ऋतु में दक्षिण से उत्तर की ओर जाने पर तापमान घटता | जाता है। कुछ ऊँचे स्थानों पर पाला भी पड़ता है। शीत ऋतु से चलने वाली उत्तरी पूर्वी पवनों द्वारा केवल तमिलनाडु राज्य को लाभ पहुंचता है। ये पवनें खाड़ी बंगाल से गुजरने के बाद वहां पर्याप्त वर्षा करती हैं।
- ग्रीष्म ऋतु – यह ऋतु मार्च से मई तक रहती है। मार्च मास में सबसे | अधिक तापमान (लगभग 38° सें०) दक्कन के पठार पर होता है। धीरे-धीरे ऊष्मा की यह पेटी उत्तर की ओर खिसकने लगती है और उत्तरी भाग में तापमान बढ़ता जाता है। मई के अन्त तक एक लम्बा संकरा निम्न वायु दाब क्षेत्र विकसित हो जाता है, जिसे ‘मानसून का निम्न वायुदाब गर्त’ कहते हैं। देश के उत्तर-पश्चिमी भाग में चलने वाली | गर्म-शुष्क पवनें (लू), केरल तथा कर्नाटक के तटीय भागों में होने वाली ‘आम्रवृष्टि’ और बंगाल तथा असम की ‘काल बैसाखी’ ग्रीष्म ऋतु की अन्य मुख्य विशेषताएं हैं।
- आगे बढ़ते मानसून की ऋतु – यह ऋतु जून से सितम्बर तक रहती है। देश में दक्षिणपश्चिमी मानसून चलती है जो दो शाखाओं में भारत में प्रवेश करती है-अरब सागर की शाखा तथा बंगाल की
खाड़ी की शाखा। ये पवनें देश में पर्याप्त वर्षा करती हैं। | उत्तर-पूर्वी भारत में भारी वर्षा होती है, जबकि देश के उत्तरी-पश्चिमी कुछ भाग शुष्क रह जाते हैं। जुलाई तथा अगस्त के महीनों में देश की 75 से 90 प्रतिशत तक वार्षिक वर्षा हो जाती है। गारो तथा खासी की पहाड़ियों की दक्षिणी श्रेणी के शीर्ष पर स्थित माउसिनराम में संसार भर में सबसे अधिक वर्षा होती है। दूसरा स्थान यहां से कुछ ही दूरी पर स्थित चेरापूंजी को प्राप्त है। दक्षिणी भारत में पश्चिमी घाट की पवनाभिमुख ढालों पर अरब सागर की मानसून शाखा द्वारा भारी वर्षा होती है। - पीछे हटते मानसून की ऋतु – अक्तूबर तथा नवम्बर के महीनों में मानसून पीछे हटने लगता है। क्षीण हो जाने के कारण इसका प्रभाव कम हो जाता है। पृष्ठीय पवनों की दिशा भी उलटने लगती है। आकाश साफ़ हो जाता है और तापमान फिर से बढ़ने लगता है। उच्च तापमान तथा भूमि की आर्द्रता के कारण मौसम कष्टदायक हो जाता है। इसे ‘क्वार की उमस’ कहते हैं। इस ऋतु में दक्षिणी प्रायद्वीप के तटों पर उष्ण कटिबन्धीय चक्रवात भारी वर्षा करते हैं। इस प्रकार ये बहुत ही विनाशकारी सिद्ध होते हैं।
- वर्षा का वितरण – भारत में सबसे अधिक वर्षा पश्चिमी तटों तथा उत्तरी पूर्वी | भागों में होती (300 सें० मी० से भी अधिक) है। परन्तु पश्चिमी राजस्थान तथा इसके निकटवर्ती पंजाब, हरियाणा तथा गुजरात के क्षेत्रों में 50 सें० मी० से भी कम वार्षिक वर्षा होती है। देश के उच्च भागों (हिमालय क्षेत्र) में हिमपात होता है। वर्षण की यह मात्रा प्रति वर्ष घटती बढ़ती रहती है। मानसून की स्वेच्छाचारिता के कारण कहीं तो भयंकर बाढ़ें आ जाती हैं और कहीं सूखा पड़ जाता है।
- जलवायु के यन्त्र – जलवायु का अनुमान लगाने के लिए कई प्रकार में यन्त्रों | का प्रयोग किया जाता है। जैसे कि थर्मामीटर एनीराइड बैरोमीटर, सूखी तथा गीली गोली का थर्मामीटर, वर्षा मापक यन्त्र, वायुवेग मापक, वायु दिशा सूचक इत्यादि।
- प्राकृतिक आपदाएं – प्रकृति के ऊपर किसी का ज़ोर नहीं चलता। इस प्रकार जब प्राकृतिक आपदाएं आती हैं तो काफी जान-माल का नुकसान होता है। सुनामी भी इन प्राकृतिक आपदाओं में से एक थी जो दिसंबर 2004 में दक्षिण एशिया के देशों में आई तथा हज़ारों लोगों की मृत्यु हो गई थी।