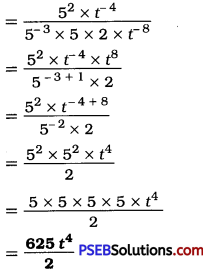Class 8

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 5 Data Handling Ex 5.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1

Question 1.
For which of these would you use a histogram to show the data?
(a) The number of letters for different areas in a postman’s bag.
(b) The height of competitors in an athletics meet.
(c) The number of cassettes produced by 5 companies.
(d) The number of passengers boarding trains from 7:00 a.m. to 7:00 p.m. at a station.
Give reasons for each.
Solution:
We represent those data by a histogram which can be grouped into class intervals. Obviously, for (b) and (d), the data can be represented by histograms.

Question 2.
The shoppers who come to a departmental store are marked as: man (M), woman (W), boy (B) or girl (G). The following list gives the shoppers who came during the first hour in the morning:
W W W G B W W M G G M M W W W W G B M W B G G M W W M M W W W M W B W G M W W W W G W M M W W M W G W M G W M M B G G W
Make a frequency distribution table using tally marks. Draw a bar graph to illustrate it.
Solution:
The frequency distribution table for the above data can be done as follows :

We can represent the above data by a bar graph as given below:

Question 3.
The weekly wages (in ₹) of 30 workers in a factory are:
830, 835, 890, 810, 835, 836, 869, 845, 898, 890, 820, 860, 832, 833, 855, 845, 804, 808, 812, 840, 885, 835, 835, 836, 878, 840, 868, 890, 806, 840
Using tally marks make a frequency table with intervals as 800-810, 810-820 and so on.
Solution:
The lowest observation = 804
The highest observation = 898
The classes are 800-810, 810-820, etc.
∴ The frequency distribution table is

Question 4.
Draw a histogram for the frequency table made for the data in Question 3, and answer the following questions:
(i) Which group has the maximum number of workers?
(ii) How many workers earn ₹ 850 and more ?
(iii) How many workers earn less than ₹ 850 ?
Solution:
The histogram from the above frequency table is given below.
Here we have represented the class intervals along X-axis and frequencies of the class intervals along the Y-axis.

(i) The group 830 – 840 has the maximum number of workers.
(ii) Number of workers earning ₹ 850 or more = 1 + 3 + 1 + 1 – 1 – 4 = 10
(iii) Number of workers earning less than ₹ 850 = 3 + 2 + 1 + 9 + 5 = 20

Question 5.
The number of hours for which students of a particular class watched television during holidays is shown through the given graph.
Answer the following:
(i ) For how many hours did the maximum number of students watch TV ?
(ii) How many students watched TV for less than 4 hours ?
(iii) How many students spent more than 5 hours in watching TV ?

Solution:
(i) The maximum number of students watched TV for 4 to 5 hours.
(ii) 34 students watched TV for less than 4 hours (4 + 8 + 22 = 34).
(iii) 14 students spent more than 5 hours in watching TV (8 + 6 = 14).

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 11 Mensuration Ex 11.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.1

1. A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?

Question (a)

Solution:
Side of a square field = 60 m
∴ Perimeter of a square field = 4 × side
= 4 × 60 = 240 m
Area of a square field = (side)²
= (60)²
= 60 × 60
= 3600m²

Question (b)

Solution:
Perimeter of a rectangular field = Perimeter of square field
∴ Perimeter of a rectangular held = 240
∴ 2 (length + breadth) = 240
∴ 2 (80 + breadth) = 240
∴ 80 + breadth = \(\frac {240}{2}\)
∴ 80 + breadth =120
∴ breadth = 120 – 80
∴ breadth = 40
Breadth of rectangular field = 40 m
∴ Area of rectangular field = length × breadth
= (80 × 40)
= 3200 m²
Area of square field > Area of rectangular field
Thus, area of square field (a) is larger.

2. Mrs. Kaushik has a square plot with the measurement as shown g in the figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of ₹ 55 per m².

Solution:
Side of the square plot = 25 m
∴ Area of the square plot = (side)²
= (25 × 25) m²
= 625 m²
In square plot, a rectangular-shaped house is to be constructed.
∴ Area of the constructed house
= length × breadth
= (20 × 15) m²
= 300 m²
∴ Area of the garden = Area of square plot – Area of constructed house
= 625 – 300 = 325 m²
Cost of developing garden of 1 m² is ₹ 55
∴ Cost of developing garden of 325 m²
= ₹ (55 × 325)
= ₹ 17,875
Thus, total cost of developing garden is ₹ 17,875.

3. The shape of a garden is rectangular in the middle and semicircular at the ends as shown in the diagram. Find the area and the perimeter of this garden [Length of rectangle is 20 – (3.5+ 3.5) metres].

Solution:
[Note: Here 2 semicircles at the ends of a rectangular garden makes a whole circle. So first find area of a circle and then area of a rectangle. Sum of these two areas is total area. Follow same pattern to find perimeter too. For perimeter of a garden, take only length as rectangle is between two semicircles. Diameter of a circle = Breadth of a rectangle = 7 m]
For semicircle:
∴ Radius = \(\frac{\text { diameter }}{\text { 2 }}\) = \(\frac {7}{2}\)m
Area of circle = πr²
Area of a semicircle = \(\frac {1}{2}\)πr²
∴ Area of 2 semicircles = 2(\(\frac {1}{2}\)πr²)
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\)m²
= 38.5 m²
Circumference of two semicircles = 2πr
= 2 × \(\frac {22}{7}\) × \(\frac {7}{2}\)
= 22 m

For rectangle:
length = 20 – (3.5 + 3.5) = 20 – 7 = 13 m
breadth = 7 m
Area of the rectangle = length × breadth
= 13 × 7 = 91 m²
Perimeter of the rectangle
= 2 (length × breadth)
= 2 (13 + 0)
= 2 × 13 = 26 m
∴ Total area of the garden = (38.5 + 91) m²
= 129.5 m²
∴ Perimeter of the garden = (22 + 26) m
= 48 m
Thus, area of the garden is 129.5 m² and the perimeter is 48 m.

4. A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m²? (If required you can split the tiles in whatever way you want to fill up the corners.)
Solution:
[Note : To find number of tiles, divide the area of the floor by area of a tile. Let us do it in a simple way. Unit of floor area and tile area should be same.] Here, tile is parallelogram shaped.
So it’s area = base × corresponding height
Area of a floor = 1080 m²
Base of a tile = 24 cm = \(\frac {24}{100}\) m
Corresponding height of a tile = 10 cm = \(\frac {10}{100}\) m
Number of tiles = \(\frac{\text { Area of a floor }}{\text { Area of a title }}\)
= \(\frac{1080}{\frac{24}{100} \times \frac{10}{100}}\)
= \(\frac{1080 \times 100 \times 100}{24 \times 10}\)
= 45,000
Thus, 45,000 tiles are required to cover the given floor.

5. An ant is moving around a few food pieces of different shapes scattered on the floor. For which food piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression c = 2 πr, where r is the radius of the circle.

Question (a)

Solution:
Here, the shape is semi-circular.
Diameter = 2.8 cm
Radius = \(\frac{\text { Diameter }}{2}=\frac{2.8}{2}\) = 1.4 cm
Circumference of a semicircle = πr
Perimeter of the given figure
= πr + diameter
= (\(\frac {22}{7}\) × 1.4) + 2.8
= 4.4 + 2.8
= 7.2 cm

Question (b)

Solution:
Here, given shape is semicircular at one side, (radius = \(\frac {2.8}{2}\) = 1.4 cm)
So perimeter of semicircular region (circumference) = πr
= \(\frac {22}{7}\) × 1.4
= \(\frac {22}{7}\) × \(\frac {14}{10}\)
= 4.4 cm … (i)
Perimeter of the other portion
= breadth + length + breadth
= (1.5 + 2.8 + 1.5) cm
= 5.8 cm … (ii)
∴ Perimeter of the given figure
= (4.4 + 5.8) cm [from (i) and (ii)]
= 10.2 cm

Question (c)

Solution:
Perimeter of a given part
(semi circular circumference) = πr
= \(\frac {22}{7}\) × 1.4
= 4.4 cm
∴ Perimeter of the given figure
= (4.4 + 2 + 2) cm
= 8.4 cm
Thus, 7.2 cm < 8.4 cm < 10.2 cm.
Thus, the ant would has to take a longer round for food piece (b), as it has a larger perimeter.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 12 Exponents and Powers InText Questions and Answers.

PSEB 8th Class Maths Solutions Chapter 12 Exponents and Powers InText Questions

Try These : [Textbook Page No. 194]

1. Find the multiplicative inverse of the following:

Question (i)
2^-4
Solution:
Multiplicative inverse of 2^-4 = 2⁴

Question (ii)
10^-5
Solution:
Multiplicative inverse of 10^-5 = 10⁵

Question (iii)
7^-2
Solution:
Multiplicative inverse of 7^-2 = 7²

Question (iv)
5^-3
Solution:
Multiplicative inverse of 5^-3 = 5³

Question (v)
10^-100
Solution:
Multiplicative inverse of 10^-100 =10¹⁰⁰

Try These : [Textbook Page No. 194]

1. Expand the following numbers using exponents:
(i) 1025.63
(ii) 1256.249
Solution:

Number	Expanded form
(i) 1025.63	(1 × 1000) + (0 × 100) + (2 × 10) + (5 × 1) + (6 × \(\frac {1}{10}\)) + (3 × \(\frac {1}{100}\)) OR (1 × 103) + (2 × 101) + (5 × 100) + (6 × 10-1) + (3 × 10-2)
(ii) 1256.249	(1 × 1000) + (2 × 100) + (5 × 10) + (6 × 1) + (2 × \(\frac {1}{10}\))+ (4 x \(\frac {1}{100}\)) + (9 × \(\frac {1}{1000}\)) OR (1 × 103) + (2 × 102) + (5 × 101) + (6 × 100) + (2 × 10-1) + (4 × 10-2) + (9 × 10-3)

Try These : [Textbook Page No. 195]

1. Simplify and write in exponential form:

Question (i)
(- 2)^-3 × (- 2)^-4
Solution:
= (-2)^-3+(-4)
= (-2)^-3-4
= (-2)^-7 or \(\frac{1}{(-2)^{7}}\)

Question (ii)
p³ × p^-10
Solution:
= p^3+(-10)
= p^3-10
= (p)^-7 or \(\frac{1}{(p)^{7}}\)

Question (iii)
3² × 3^-5 × 3⁶
Solution:
= 3^2+(-5)+6
= 3^2-5+6
= 3^2+6-5
= 3³

Try These : [Textbook Page No. 199]

1. Write the following numbers in standard form:

Question (i)
0.000000564
Solution:
= \(\frac{564}{1000000000}\)
(The decimal point is shifted to nine places to the right.)
= \(\frac{5.64}{10^{9}}\)
= \(\frac{5.64}{10^{7}}\)
= 5.64 × 10^-7
∴ 0.000000564 = 5.64 × 10^-7

Question (ii)
0.0000021
Solution:
\(\frac{21}{10000000}\)
= \(\frac{2.1 \times 10}{10000000}\)
= \(\frac{2.1}{10^{6}}\)
= 2.1 × 10^-6
∴ 0.0000021 = 2.1 × 10^-6

Question (iii)
21600000
Solution:
= 216 × 100000
= 216 × 10⁵
= 2.16 × 10² × 10⁵
= 2.16 × 10⁷
∴ 21600000 = 2.16 × 10⁷

Question (iv)
15240000
Solution:
= 1524 × 10000
= 1.524 × 1000 × 10000
= 1.524 × 10³ × 10⁴
= 1.524 × 10⁷
∴ 15240000 = 1.524 × 10⁷

2. Write all the facts given in the standard form. Observe the following facts: [Textbook Page No. 198 ]

Question 1.
The distance from the Earth to the Sun is 150,600,000,000 m.
Solution:
150,600,000,000 m
= 1.506 × 10¹¹ m

Question 2.
The speed of light is 300,000,000 m/sec.
Solution:
300,000,000 m / sec
= 3 × 10⁸m/sec

Question 3.
Thickness of Class VII Mathematics book is 20 mm.
Solution:
20 = 2 × 10¹ mm

Question 4.
The average diameter of a Red Blood Cell is 0.000007 m.
Solution:
0.000007 = 7 × 10^-6 m

Question 5.
The thickness of human hair is in the range of 0.005 cm to 0.01 cm.
Solution:
0.005 = 5 × 10^-3cm and
0.01 = 1 × 10^-2 cm

Question 6.
The distance of moon from the Earth is 384,467,000 m (approx).
Solution:
384,467,000 = 3.84467 × 10⁸ m

Question 7.
The size of a plant cell is 0.00001275 m.
Solution:
0.00001275 = 1.275 × 10^-5m

Question 8.
Average radius of the Sun is 695000 km.
Solution:
695000 = 6.95 × 10⁵ km

Question 9.
Mass of propellant in a space shuttle solid rocket booster is 503600 kg.
Solution:
503600 = 5.036 × 10⁵ kg

Question 10.
Thickness of a piece of paper is 0.0016 cm.
Solution:
0.0016 = 1.6 × 10^-3 cm

Question 11.
Diameter of a wire on a computer chip is 0.000003 m.
Solution:
0.000003 = 3 × 10^-6 cm

Question 12.
The height of Mount Everest is 8848 m.
Solution:
8848 = 8.848 × 10³ m

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 4 Practical Geometry InText Questions and Answers.

PSEB 8th Class Maths Solutions Chapter 4 Practical Geometry InText Questions

Think, Discuss and Write (Textbook Page No. 58)

Question 1.
Arshad has five measurements of a quadrilateral ABCD. These are AB = 5 cm, ∠A = 50°, AC = 4 cm, BD = 5 cm and AD = 6 cm. Can he construct a unique quadrilateral ? Give reasons for your answer.
Solution:
No, the quadrilateral ABCD cannot be constructed with the given combination of measurements. If the length of side BC or DC is given, then only □ ABCD can be constructed.

Think, Discuss and Write (Textbook Page No. 60)

Question (i).
We saw that 5 measurements of a quadrilateral can determine a quadrilateral uniquely. Do you think any five measurements of the quadrilateral can do this ?
Solution:
No, any 5 measurements can’t determine a s quadrilateral. To construct a quadrilateral, specific combination of measurements should be needed such as :

• Four sides and one diagonal
• Four sides and one angle
• Three sides and two diagonals
• Two adjacent sides and three angles
• Three sides and two included angles
• Some special properties should be given,

Question (ii).
Can you draw a parallelogram BATS where BA = 5 cm, AT = 6 cm and AS = 6.5 cm? Why?
Solution:

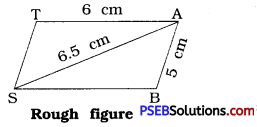
Here, to draw a parallelogram BATS, BA = 5 cm, AT = 6 cm and AS = 6.5 cm are given. In parallelogram length of opposite sides are equal. So ST = AB = 5 cm and SB = AT = 6 cm. First we can draw A ASB where SB = 6 cm, AB = 5 cm and AS = 6.5 cm. Then draw ΔATS where AT = 6 cm, ST = 5 cm.
Thus, we can draw a parallelogram from given measurements.

Question (iii).
Can you draw a rhombus ZEAL where ZE = 3.5 cm, diagonal EL = 5 cm ? Why?
Solution:

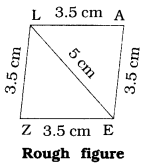
Here, to draw a rhombus ZEAL, ZE = 3.5 cm and EL = 5 cm are given. All of rhombus are equal to each other. So ZE = EA = AL = LZ = 3.5 cm. Moreover, diagonal EL = 5 cm Is given.
So We know all necessary measurements to draw rhombus. Yes, we can draw a rhombus ZEAL.

Question (iv).
A student attempted to draw a quadrilateral PLAY where PL = 3 cm, LA = 4 cm, AY = 4.5 cm, PY = 2 cm and LY = 6 cm, but could not draw it. What is the reason?
[Hint: Discuss it using a rough sketch. ]
Solution :
Here, to draw a quadrilateral PLAY,
PL = 3 cm, LA = 4 cm, AY = 4.5 cm, PY = 2 cm and LY = 6 cm are given.

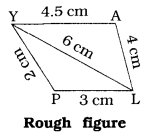
Now, let us look at measurements of
ΔPLY. PL + PY = 3 cm + 2 cm = 5 cm while YL = 6 cm.
We know that the sum of the lengths of any two sides of triangle is always greater than the length of the third side.
So point P cannot be determined even after constructing ΔLAY. Thus, a student failed s due to this reason.

Think, Discuss and Write (Textbook Page No. 62)

Question 1.
In the above example, can we draw the quadrilateral by drawing ΔABD first and then find the fourth point C ?
Solution:
Since, the measurement of AB is not given, we cannot draw ΔABD, so question does not arise to find the foruth point C.

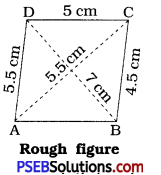
Thus, we cannot draw the quadrilateral

Question 2.
Can you construct a quadrilateral PQRS with PQ = 3 cm, RS = 3 cm, PS = 7.5 cm, PR = 8 cm and SQ = 4 cm ? Justify your answer.
Solution:
No, the quadrilateral PQRS cannot be constructed as in ΔQSP, SQ + PQ ≯ SP

Think, Discuss and Write (Textbook Page No. 64)

Question 1.
Can you construct the above quadrilateral MIST if we have 100° at M instead of 75° ?
Solution:
Yes. The quadrilateral MIST can be constructed with ∠M = 100° instead of 75°.
[Note : Only size of quadrilateral is changed.]

Question 2.
Can you construct the quadrilateral PLAN if PL = 6 cm, LA = 9.5 cm, ∠P = 75°, ∠L = 150° and ∠A = 140° ?
[Hint: Recall angle sum property.]
Solution:
Here, ∠P + ∠L + ∠A + ∠N
= 75° + 150° + 140° + ∠N
= 365° + ∠N
∴ Construction of quadrilateral PLAN is not possible as according to angle sum property. The sum of all the angles of a quadrilateral is 360°. Here, 365° + N > 360°.

Question 3.
In a parallelogram, the lengths of adjacent sides are known. Do we still need measures of the angles to construct as in the example above?
Solution :
In a parallelogram, the opposite sides are parallel and of equal length. Here, we know the lengths of adjacent sides, so measures of the angles are not needed.
If we know the length of a diagonal the quadrilateral can be drawn.

Think, Discuss and Write (Textbook Page No. 66)

Question 1.
In the above example, we first drew BC. Instead, what could have been be the other starting points?
Solution :
Instead of drawing BC, we can start with \(\overline{\mathrm{AB}}\) or \(\overline{\mathrm{CD}}\).

Question 2.
We used some five measurements to draw quadrilaterals so far. Can there be different sets of five measurements (other than seen so far) to draw a quadrilateral ? The following problems may help you in answering the question.
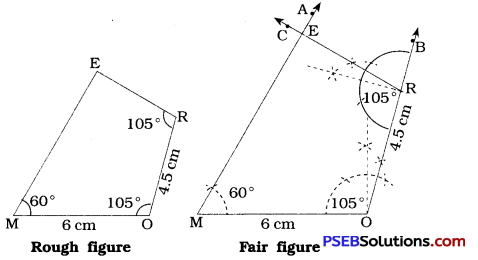
(i) Quadrilateral ABCD with AB = 5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm and ∠B = 80°.
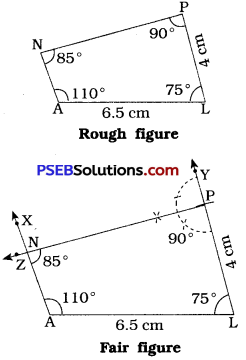
(ii) Quadrilateral PQRS with PQ = 4.5 cm, ∠P = 70°, ∠Q = 100°, ∠R = 80° and ∠S = 110°.
Construct a few more examples of your own to find sufficiency/insufficiency of the data for construction of a quadrilateral.
Solution:
(i) Here, four sides and one angle are given. So given data is sufficient to construct quadrilateral ABCD.
(ii) We cannot locate the points R and S with the help of given data. So given data is insufficient to construct quadrilateral PQRS.

Few examples of sufficient data to construct quadrilaterals :

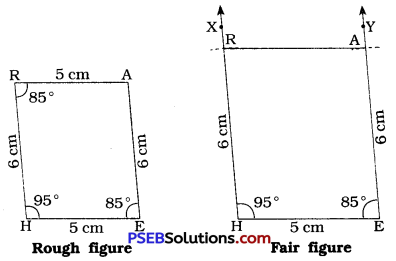
• Quadrilateral PQRS in which RS = 6 cm, QR = 5 cm, PQ = 5 cm, ∠Q = 135°, ∠R = 90°. (three sides and two angles)
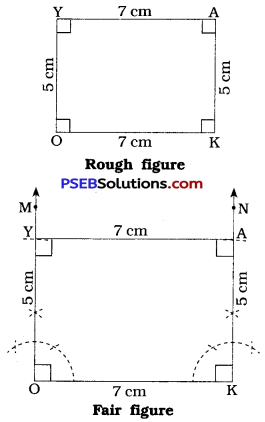
• Quadrilateral ABCD in which AB = 5 cm, BC = 4 cm, ∠B = 60°, ∠A = 90° and ∠C = 135°. (two sides and three angles)

Try these (Textbook Page No. 67)

Question 1.
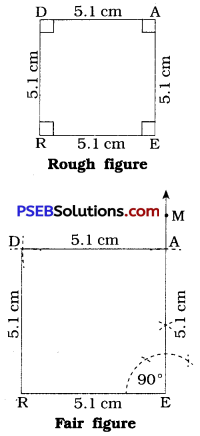
How will you construct a rectangle PQRS if you know only the lengths PQ and QR?
Solution:

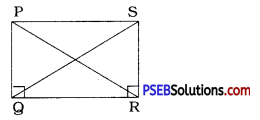
Each angle of a rectangle is a right angle. Rectangle has opposite sides of equal lengths. Here, PQ is given, So PQ = RS.
ΔPQR can be drawn using PQ, QR and ∠Q = 90°.
ΔQRS can be drawn using QR, RS and ∠R = 90°.
Thus, the required rectangle PQRS can be constructed.

Question 2.
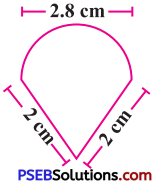
Construct the kite EASY if AY = 8 cm, EY = 4 cm and SY = 6 cm. Which properties of the kite did you use in the process ?
Solution:

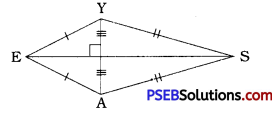
Diagonals intersect each other at right angle. ? In kite pairs of consecutive sides are of equal lengths.
While constructing, E cannot be located.
∴ Kite EASY cannot be constructed
(∵ For Δ EYA, the sum of lengths of two sides EY + EA (4 + 4) is not greater than length of third side AY (8).

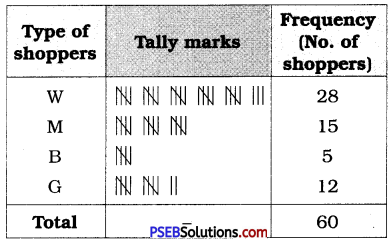
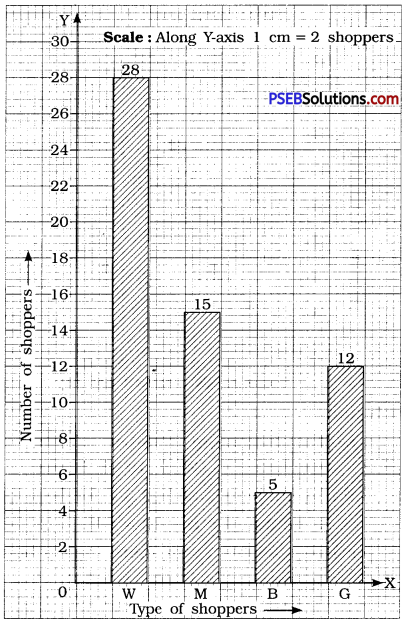
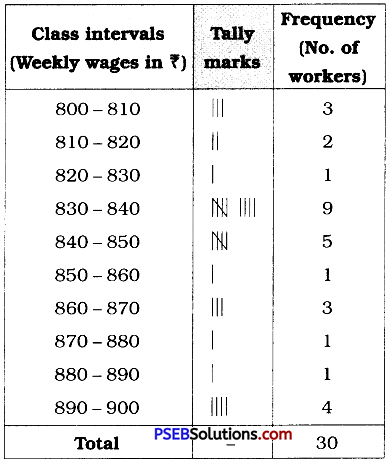
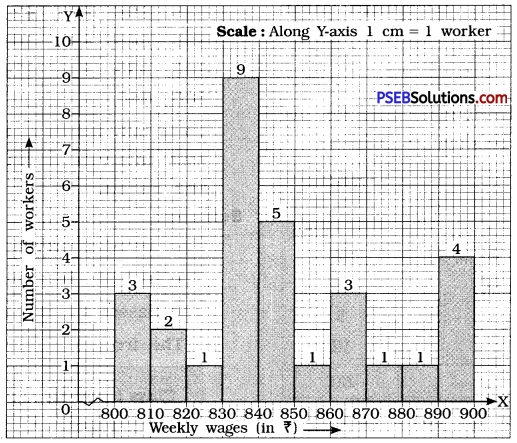
Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 12 Exponents and Powers Ex 12.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.2

1. Express the following numbers in standard form:

Question (i)
0.0000000000085
Solution:
= \(\frac{85}{10000000000000}\)
= \(\frac{85}{10^{13}}\)
= \(\frac{8.5 \times 10}{10^{13}}\)
= 8.5 × 10 × 10^-13
= 8.5 × 10^-12

Question (ii)
0.00000000000942
Solution:
= \(\frac{942}{100000000000000}\)
= \(\frac{942}{10^{14}}\)
= \(\frac{9.42 \times 10^{2}}{10^{14}}\)
= 9.42 × 10² × 10^-14
= 9.42 × 10^-12

Question (iii)
6020000000000000
Solution:
= 602 × 10000000000000
= 602 × 10¹³
= 6.02 × 10² × 10¹³
= 6.02 × 10¹⁵

Question (iv)
0.00000000837
Solution:
= \(\frac{837}{100000000000}\)
= \(\frac{837}{10^{11}}\)
= \(\frac{8.37 \times 10^{2}}{10^{11}}\)
= 8.37 × 10² × 10^-11
= 8.37 × 10^2+(-11)
= 8.37 × 10^-9

Question (v)
31860000000
Solution:
= 3186 × 10000000
= 3186 × 10⁷
= 3.186 × 10³ × 10⁷
= 3.186 × 10^{3 + 7}
= 3.186 × 10¹⁰

2. Express the following numbers in usual form:

Question (i)
3.02 × 10^-6
Solution:
= 302 × 10^-2 × 10^-6
= 302 × 10^-8
= \(\frac{302}{100000000}\)
= 0.00000302

Question (ii)
4.5 × 10⁴
Solution:
= \(\frac {45}{10}\) × 10000
= 45 × 1000
= 45000

Question (iii)
3 × 10^-8
Solution:
= \(\frac{3}{100000000}\)
= 0.00000003

Question (iv)
1.0001 × 10⁹
Solution:
= \(\frac{10001}{10000}\) × 1000000000
= 10001 × 100000
= 1000100000

Question (v)
5.8 × 10¹²
Solution:
= \(\frac {58}{10}\) × 100000000000
= 58 × 10000000000
= 5800000000000

Question (vi)
3.61492 × 10⁶
Solution:
= \(\frac{361492}{100000}\) × 1000000
= 361492 x 10
= 3614920

3. Express the number appearing in the following statements in standard form:

Question (i)
1 micron is equal to \(\frac{1}{1000000}\) m.
Solution:
1 micron = \(\frac{1}{1000000}\)m
= \(\frac{1}{10^{6}}\)m
∴ 1 micron = 1 × 10^-6 m

Question (ii)
Charge of an electron is 0.000,000,000,000,000,000,16 coulomb.
Solution:
Charge of an electron
= 0.000,000,000,000,000,000,16 coulomb
= \(\frac{16}{100000000000000000000}\) coulomb
= \(\frac{1.6 \times 10}{10^{20}}\) coulomb
= \(\frac{1.6}{10^{19}}\) coulomb
= 1.6 × 10^-19 coulomb
∴ Charge of an electron = 1.6 × 10^-19 coulomb

Question (iii)
Size of a bacteria is 0.0000005 m.
Solution:
Size of a bacteria = 0.0000005 m
= \(\frac{5}{10000000}\)m
= \(\frac{5}{10^{7}}\)m
= 5 × 10^-7 m
∴ Size of a bacteria = 5 × 10^-7 m

Question (iv)
Size of a plant cell is 0.00001275 m.
Solution:
Size of a plant cell = 0.00001275 m
= \(\frac{1275}{100000000}\)m
= \(\frac{1275}{10^{8}}\)m
= \(\frac{1.275 \times 10^{3}}{10^{8}}\) m
= 1.275 × 10^3-8
= 1.275 × 10^-5
∴ Size of a plant cell
= 1.275 × 10^-5 m

Question (v)
Thickness of a thick paper is 0.07 mm.
Solution:
Thickness of a thick paper = 0.07 mm
= \(\frac {7}{100}\) mm
= \(\frac{7}{10^{2}}\) mm
= 7 × 10^-2 mm
∴ Thickness of a thick paper
= 7 × 10^-2 mm

4. In a stack there are 5 books each of thickness 20 mm and 5 paper sheets each of thickness 0.016 mm. What is the total thickness of the stack.
Solution:
Thickness of a book = 20 mm
∴ Thickness of 5 books = (5 × 20) mm
= 100 mm
Thickness of a paper sheet = 0.016 mm
∴ Thickness of 5 paper sheets
= (5 × 0.016) mm
= 0.08 mm
∴ Total thickness of a stack = Thickness of books + Thickness of paper sheets
= (100 + 0.08) mm
= 100.08 mm
In standard form 100.08 is written as 1.0008 × 10².
Thus, the total thickness of the stack is 1.0008 × 10² mm.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 12 Exponents and Powers Ex 12.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.1

1. Evaluate:

Question (i)
3^-2
Solution:
= \(\frac{1}{3^{2}}\)
= \(\frac{1}{3 \times 3}\)
= \(\frac {1}{9}\)

Question (ii)
(-4)^-2
Solution:
= \(\frac{1}{(-4)^{2}}\)
= \(\frac{1}{(-4) \times(-4)}\)
= \(\frac {1}{9}\)

Question (iii)
(\(\frac {1}{2}\))^-5
Solution:
= \(\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}\)
= \(\frac{1}{\frac{1}{32}}\)
= 32

2. Simplify and express the result in power notation with positive exponent:

Question (i)
(-4)⁵ ÷ (-4)⁸
Solution:
= (-4)^{5 – 8} (∵ a^m ÷ aⁿ = a^m-n)
= (-4)^{– 3}
= \(\frac{1}{(-4)^{3}}\)

Question (ii)
\(\left(\frac{1}{2^{3}}\right)\)²
Solution:
= \(\frac{(1)^{2}}{\left(2^{3}\right)^{2}}\) [∵ \(\left(\frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}}\)]
= \(\frac{1}{2^{3 \times 2}}\) [∵ (a^m)ⁿ = a^mn
= \(\frac{1}{2^{6}}\)

Question (iii)
(-3)⁴ × (\(\frac {5}{3}\))⁴
Solution:
= [(-3) × \(\frac {5}{3}\)]⁴ [∵ a^m × b^m = (ab)^m]
= [(-1) × 5]⁴
= (-1)⁴ × 5⁴
= 1 × 5⁴
= 5⁴

Question (iv)
(3^-7 ÷ 3^-10) × 3^-5
Solution:
= (3^(-7)-(-10)) × 3^-5 (∵ a^m ÷ aⁿ = a^m-n)
= (3^-7+10 × 3^-5
= 3³ × 3^-5
= 3³ + (-5) (∵ a^m × aⁿ = a^m+n)
= 3^-2
= \(\frac{1}{3^{2}}\)

Question (v)
2^-3 × (-7)^-3
Solution:
= [2 × (-7)]^-3 [∵ a^m × b^m = (ab)^m
= (-14)^-3
= \(\frac{1}{(-14)^{3}}\)

3. Find the value of:

Question (i)
(3⁰ + 4^-1) × 2²
Solution:
= (1 + \(\frac {1}{4}\)) × 2²
= (\(1 \frac{1}{4}\)) × 2²
= (\(\frac {5}{4}\)) × 4
= 5

Question (ii)
(2^{– 1} × 4^-1) ÷ 2²
Solution:
= (\(\frac {1}{2}\) × \(\frac {1}{4}\)) ÷ \(\frac{1}{2^{2}}\)
= (\(\frac {1}{8}\)) ÷ \(\frac {1}{4}\)
= \(\frac {1}{8}\) × \(\frac {4}{1}\)
= \(\frac {1}{2}\)

Question (iii)
(\(\frac {1}{2}\))^{– 2} + (\(\frac {1}{3}\))^{– 2} + (\(\frac {1}{4}\))^{– 2}
Solution:
=\(\frac{1}{\left(\frac{1}{2}\right)^{2}}+\frac{1}{\left(\frac{1}{3}\right)^{2}}+\frac{1}{\left(\frac{1}{4}\right)^{2}}\)
= \(\frac{1}{\frac{1}{4}}+\frac{1}{\frac{1}{9}}+\frac{1}{\frac{1}{16}}\)
= 4 + 9 + 16
= 29

Question (iv)
(3^{– 1} + 4^{– 1} + 5^{– 1})⁰
Solution:
(3^-1 + 4^-1 + 5^-1)⁰
∴ [3^-1 + 4^-1 + 5^-1]⁰ = 1
[∵ a⁰ = 1]

Question (v)
\(\left\{\left(\frac{-2}{3}\right)^{-2}\right\}\)²
Solution:
= \(\left(\frac{-2}{3}\right)^{(-2) \times 2}\) [∵ (a^m)^m = a^mn]
= (\(\frac {-2}{3}\))^-4
= \(\frac{(-2)^{-4}}{(3)^{-4}}\) [∵ \(\left(\frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}}\)]
= \(\frac{3^{4}}{(-2)^{4}}\)
= \(\frac{3 \times 3 \times 3 \times 3}{(-2) \times(-2) \times(-2) \times(-2)}\)
= \(\frac {81}{16}\)

4. Evaluate:

Question (i)
\(\frac{8^{-1} \times 5^{3}}{2^{-4}}\)
Solution:
= \(\frac{2^{4} \times 5^{3}}{8}\)
= \(\frac{2^{4} \times 5^{3}}{2^{3}}\)
= 2^4-3 × 5³
= 2 × 125
= 250

Question (ii)
(5^-1 × 2^-1) × 6^-1
Solution:
= (\(\frac {1}{5}\) × \(\frac {1}{2}\)) × \(\frac {1}{6}\)
= (\(\frac {1}{10}\)) × \(\frac {1}{6}\)
= \(\frac {1}{60}\)

Another method:
= 5^-1 × 2^-1 × 6^-1
= (5 × 2 × 6)^-1
= (60)^-1
= \(\frac {1}{60}\)

5. Find the value of m for which 5^m ÷ 5^-3 = 5⁵.
Solution:
∴ 5^m-(-3) = 5⁵.
∴ 5^{m + 3} = 5⁵
∴ m + 3 = 5 (∵ a^m = aⁿ then m = n)
∴ m = 5 – 3
∴ m = 2
Thus, value of m is 2.

6. Evaluate:

Question (i)
\(\left\{\left(\frac{1}{3}\right)^{-1}-\left(\frac{1}{4}\right)^{-1}\right\}^{-1}\)
Solution:
= {\(\frac{3}{1}-\frac{4}{1}\)}^-1 (∵ a^-m = \(\frac {1}{a^m}\))
= {3 – 4}^-1
= {-1}^-1
= \(\frac {1}{-1}\)
= -1

Question (ii)
(\(\frac {5}{8}\))^-7 × (\(\frac {8}{5}\))^-4
Solution:
(\(\frac {5}{8}\))^-7 × (\(\frac {5}{8}\))⁴
(∵ a^-m = \(\frac{1}{a^{m}}\))
= (\(\frac {5}{8}\))^-7+4 (∵ a^m × aⁿ = a^m+n)
= (\(\frac {5}{8}\))^-3
= (\(\frac {8}{5}\))³
= \(\frac{8 \times 8 \times 8}{5 \times 5 \times 5}\)
= \(\frac {512}{125}\)

7. Simplify:

Question (i)
\(\frac{25 \times t^{-4}}{5^{-3} \times 10 \times t^{-8}}\) (t ≠ 0)
Solution:

Question (ii)
\(\frac{3^{-5} \times 10^{-5} \times 125}{5^{-7} \times 6^{-5}}\)
Solution:

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 4 Practical Geometry Ex 4.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.5

Draw the following.

Question 1.
The square READ with RE = 5.1 cm.
Solution:

Steps of construction :

• Draw a line segment RE = 5.1 cm.
• At E, draw \(\overrightarrow{\mathrm{EM}}\), such that ∠REM = 90°.
• With E as centre and radius =5.1 cm, draw an arc intersecting \(\overrightarrow{\mathrm{EM}}\) at A.
• With R as centre and radius = 5.1 cm, draw an arc.
• With A as centre and radius = 5.1 cm, draw an arc which intersect the previous arc at D.
• Draw \(\overline{\mathrm{RD}}\) and \(\overline{\mathrm{AD}}\).

Thus, READ is the required square.

Question 2.
A rhombus whose diagonals are 5.2 cm and 6.4 cm long.
Solution:

[Note : The diagonals of a rhombus bisect each other at right angle.]
Here, in rhombus XYZW, YW 6.4 cm.
∴ OW = OY = 3.2 cm

Steps of construction:

• Draw a line segment XZ = 5.2 cm.
• Draw \(\overleftrightarrow{\mathrm{AB}}\), the perpendicular bisector of \(\overline{\mathrm{XZ}}\), which intersect \(\overline{\mathrm{XZ}}\) at O.
• With O as centre and radius = 3.2 cm, draw an arc intersecting \(\overleftrightarrow{\mathrm{AB}}\) above \(\overline{\mathrm{XZ}}\) at W.
• With O as centre and radius = 3.2 cm, draw another arc which intersects \(\overleftrightarrow{\mathrm{AB}}\) below \(\overline{\mathrm{XZ}}\) at Y.
• Draw \(\overline{\mathrm{XY}}\), \(\overline{\mathrm{YZ}}\), \(\overline{\mathrm{ZW}}\) and \(\overline{\mathrm{XW}}\).

Thus, XYZW is the required rhombus.

Question 3.
A rectangle with adjacent sides of lengths 5 cm and 4 cm.
Solution:

[Note: Each angle of a rectangle is a right angle.]
Steps of construction :

• Draw a line segment AB = 5 cm.
• At A, draw \(\overrightarrow{\mathrm{AX}}\), such that ∠XAB = 90°.
• With A as centre and radius = 4 cm, draw an arc intersecting \(\overrightarrow{\mathrm{AX}}\) at D.
• With B as centre and radius = 4 cm, draw an arc.
• With D as centre and radius = 5 cm, draw an arc which intersects the previous arc at C.
• Draw \(\overline{\mathrm{BC}}\) and \(\overline{\mathrm{CD}}\).

Thus, ABCD is the required rectangle.

Question 4.
A parallelogram OKAY where OK = 5.5 cm and KA = 4.2 cm. Is it unique ?
Solution:

A parallelogram cannot be constructed as sufficient measurements are not given. It is not unique as angles may vary in parallelogram drawn by given measurements.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 4 Practical Geometry Ex 4.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.4

1. Construct the following quadrilaterals:

Question (i).
Quadrilateral DEAR
DE = 4 cm
EA = 5 cm
AR = 4.5 cm
∠E = 60°
∠A = 90°
Solution:

Steps of construction:

• Draw a line segment DE = 4 cm.
• At E, draw \(\overrightarrow{\mathrm{EM}}\) such that ∠DEM = 60°.
• With E as centre and radius = 5 cm, draw an arc intersecting \(\overrightarrow{\mathrm{EM}}\) at A.
• At A, draw \(\overrightarrow{\mathrm{AN}}\) such that ∠EAN = 90°.
• With A as centre and radius = 4.5 cm, draw an arc intersecting \(\overrightarrow{\mathrm{AN}}\) at R.
• Draw \(\overline{\mathrm{DR}}\).

Thus, DEAR is the required quadrilateral.

Question (ii).
Quadrilateral TRUE
TR = 3.5 cm
RU = 3 cm
UE = 4 cm
∠R = 75°
∠U = 120°
Solution:

Steps of construction :

• Draw a line segment TR = 3.5 cm.
• At R, draw a \(\overrightarrow{\mathrm{RM}}\) such that ∠TRM = 75°.
• With R as centre and radius = 3 cm, draw an arc intersecting \(\overrightarrow{\mathrm{RM}}\) at U.
• At U, draw \(\overrightarrow{\mathrm{UN}}\) such that ∠RUN = 120°.
• With U as centre and radius = 4 cm, draw an arc intersecting \(\overrightarrow{\mathrm{UN}}\) at E.
• Draw \(\overline{\mathrm{ET}}\).

Thus, TRUE is the required quadrilateral.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 4 Practical Geometry Ex 4.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.3

1. Construct the following quadrilaterals:

Question (i).
Quadrilateral MORE
MO = 6 cm
OR = 4.5 cm
∠M = 60°
∠O = 105°
∠R = 105°
Solution:

• Draw a line segment MO = 6 cm.
• At M, draw \(\overrightarrow{\mathrm{MA}}\), such that ∠OMA = 60°
• At O, draw \(\overrightarrow{\mathrm{OB}}\) such that ∠MOB = 105°.
• With O as centre and radius = 4.5 cm, draw an arc intersecting \(\overrightarrow{\mathrm{OB}}\) at R.
• At R, draw \(\overrightarrow{\mathrm{RC}}\) such that ∠ORC = 105°.
• Locate E at intersection of \(\overrightarrow{\mathrm{RC}}\) and \(\overrightarrow{\mathrm{MA}}\).

Thus, MORE is the required quadrilateral.

Question (ii).
Quadrilateral PLAN
PL = 4 cm
LA = 6.5 cm
∠P = 90°
∠A = 110°
∠N = 85°
Solution:

[Note : In □ PLAN, m∠P = 90°, m∠A = 110° and m∠N = 85°)
∴ m∠L = 360°- (m∠P + m∠A + m∠N)
= 360° – (90° + 110° + 85°)
= 360° – 285°
= 75°

Steps of construction:

• Draw a line segment AL = 6.5 cm.
• At A, draw \(\overrightarrow{\mathrm{AX}}\) such that ∠XAL = 110°. (Use protractor)
• At L, draw \(\overrightarrow{\mathrm{LY}}\) such that ∠YLA = 75°. (Use protractor)
• With L as centre and radius = 4 cm, draw an arc intersecting \(\overrightarrow{\mathrm{LY}}\) at P.
• At P, draw \(\overrightarrow{\mathrm{PZ}}\) such that ∠ZPL = 90°. (∵ ∠ ZPY = 90°)
• Locate N at intersection of \(\overrightarrow{\mathrm{AX}}\) and \(\overrightarrow{\mathrm{PZ}}\).

Thus, PLAN is the required quadrilateral.

Question (iii).
Parallelogram HEAR
HE = 5 cm
EA = 6 cm
∠R = 85°
Solution:

[Note : □ HEAR is a parallelogram.
Opposite sides of parallelogram are of equal lengths.]
HE = 5 cm, ∴ AR = 5 cm, EA = 6 cm, ∴ HR = 6 cm
Adjacent angles of a parallelogram arc supplementary.
m∠R = 85° (given)
∴ m∠H = 180° – 85° = 95°
Opposite angles of a parallelogram are of equal measures,
m ∠ R = 85°
∴ m ∠ E = 85°

Steps of construction:

• Draw a line segment HE = 5 cm.
• At H, draw \(\overrightarrow{\mathrm{HX}}\), such that ∠ XHE = 95°. (Use protractor)
• With H as centre and radius = 6 cm, draw an arc intersecting \(\overrightarrow{\mathrm{HX}}\) at R.
• At E, draw \(\overrightarrow{\mathrm{EY}}\) such that ∠ HEY = 85°. (Use protractor)
• With E as centre and radius = 6 cm, draw an arc intersecting \(\overrightarrow{\mathrm{EY}}\) at A.
• Draw \(\overline{\mathrm{AR}}\).

Thus, HEAR is the required parallelogram.

Question (iv).
Rectangle OKAY
OK = 7 cm
KA = 5 cm
Solution:

[Note: Here, OKAY is a rectangle. Opposite sides of a rectangle are of equal lengths.]
OK = 7 cm, ∴ AY = 7 cm and KA = 5 cm, ∴ OY = 5 cm
Moreover, all angles of a rectangle are right angles.

Steps of construction:

• Draw a line segment OK = 7 cm.
• At O, draw \(\overrightarrow{\mathrm{OM}}\) such that ∠ MOK = 90°.
• With O as centre and radius = 5 cm, draw an arc intersecting \(\overrightarrow{\mathrm{OM}}\) at Y.
• At K, draw \(\overrightarrow{\mathrm{KN}}\) such that ∠ NKO = 90°.
• With K as centre and radius = 5 cm, draw an arc intersecting \(\overrightarrow{\mathrm{KN}}\) at A.
• Draw \(\overline{\mathrm{AY}}\).

Thus, OKAY is the required rectangle.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 13 Direct and Inverse Proportions InText Questions and Answers.

PSEB 8th Class Maths Solutions Chapter 13 Direct and Inverse Proportions InText Questions

Try These : [Textbook Page No. 204]

1. Observe the following tables and find if x and y are directly proportional.

Question (i)

X	20	17	14	11	8	5	2
y	40	34	28	22	16	10	4

Solution:
\(\begin{aligned}
&\frac{20}{40}=\frac{1}{2}, \frac{17}{34}=\frac{1}{2}, \frac{14}{28}=\frac{1}{2}, \frac{11}{22}=\frac{1}{2}, \frac{8}{16}=\frac{1}{2} \\
&\frac{5}{10}=\frac{1}{2}, \frac{2}{4}=\frac{1}{2}
\end{aligned}\)
The value of \(\frac{\text {x}}{\text {y}}\) is same for different values of x and y. So these values x and y are directly proportional.

Question (ii)

X	6	10	14	18	22	26	30
y	4	8	12	16	20	24	28

Solution:
\(\begin{aligned}
&\frac{6}{4}=\frac{3}{2}, \frac{10}{8}=\frac{5}{4}, \frac{14}{12}=\frac{7}{6}, \frac{18}{16}=\frac{9}{8}, \frac{22}{20}=\frac{11}{10}, \\
&\frac{26}{24}=\frac{13}{12}, \frac{30}{28}=\frac{15}{14}
\end{aligned}\)
The values of \(\frac{\text {x}}{\text {y}}\) are different for different values of x and y respectively. So these values of x and y are not directly proportional.

Question (iii)

X	5	8	12	15	18	20
y	15	24	36	60	72	100

Solution:
The values of \(\frac{\text {x}}{\text {y}}\) are different for different values of x and y respectively.
So these values of x and y are not directly proportional.

2. Principal = ₹ 1000, Rate = 8 % per annum. Fill in the following table and find which type of interest (simple or compound) changes in direct proportion with time period.

Time Period	1 year	2 years	3 years
Simple Interest (in ₹)
Compound Interest (in ₹)

Solution:
Simple interest : SI = \(\frac{P \times R \times T}{100}\)
For calculation:
P = ₹ 1000, R = 8 %, T = …………….

Time (T) →	1 year: T = 1	2 years : T = 2	3 years : T = 3
Simple interest SI = \(\frac{P \times R \times T}{100}\)	₹ \(\frac{1000 \times 8 \times 1}{100}\) = ₹ 80	₹ \(\frac{1000 \times 8 \times 2}{100}\) = ₹ 160	₹ \(\frac{1000 \times 8 \times 3}{100}\) = ₹ 240
\(\frac{\text { SI }}{\text { T }}\)	\(\frac {80}{1}\) = 80	\(\frac {160}{2}\) = 80	\(\frac {240}{3}\) = 80

Here, the ratio of simple interest with time period is same for every year.
Hence, simple interest changes in direct proportion with time period.
Compound interest:
For calculation:
P = ₹ 1000, R = 8 %, T = ……………

Time →	1 year : n = 1
A = P(1 + \(\frac {R}{100}\))n CI = A – P	A = 1000(1 + \(\frac {8}{100}\))1 = 1000 × \(\frac {108}{100}\) = 1080 ∴ CI = 1080 – 1000 = ₹ 80
\(\frac{\text { CI }}{\text { T }}\)	\(\frac {80}{1}\)

Time →	2 years : n = 2
A = P(1 + \(\frac {R}{100}\))n CI = A – P	A = 1000(1 + \(\frac {8}{100}\))2 = 1000 × \(\frac {108}{100}\) × \(\frac {108}{100}\) = ₹ 1166.40 ∴ CI = ₹ 1166.40 – 1000 = ₹ 166.40
\(\frac{\text { CI }}{\text { T }}\)	\(\frac {166.40}{2}\)

Time →	3 years : n = 3
A = P(1 + \(\frac {R}{100}\))n CI = A – P	A = 1000(1 + \(\frac {8}{100}\))3 = 1000 × \(\frac {108}{100}\) × \(\frac {108}{100}\) × \(\frac {108}{100}\) = ₹ 1259.712 ∴ CI = ₹ 1259.712 – ₹ 1000 = ₹ 259.712
\(\frac{\text { CI }}{\text { T }}\)	\(\frac {259.712}{3}\)

Here, the ratio of CI and T is not same.
Thus, compound interest is not proportional with time period.

Think, Discuss and Write: [Textbook Page No. 204]

1. If we fix time period and the rate of interest, simple interest changes proportionally with principal. Would there be a similar relationship for compound interest? Why?
Solution:
Time period (T) and rate of interest (R) are fixed, then
Simple interest = \(\frac {PRT}{100}\) = P × Constant
So simple interest depends on principal. Simple interest changes proportionally with principal.
Now, compound interest = P(1 + \(\frac {R}{100}\))^T – P
i.e., A – P
= P [(1 + \(\frac {R}{100}\)^T – 1]
= P × Constant
So compound interest depends on principal.
If principal increases or decreases, then compound interest will also increases or decreases.
Thus, compound interest changes with principal.

Think, Discuss and Write : [Textbook Page No. 209]

1. Take a few problems discussed so far under ‘direct variation’. Do you think that they can be solved by ‘unitary method’?
Solution:
Yes, each problem can be solved by unitary method.
e.g. Question 4 of Exercise: 13.1
Number of bottles filled in 6 hours = 840
∴ The number of bottles filled in 1 hour = \(\frac {840}{6}\) = 140
The number of bottles filled in 5 hours = 140 × 5 = 700
Thus, 700 bottles will it fill in five hours.

Try These : [Textbook Page No. 211]

1. Observe the following tables and find which pair of variables (here x and y) are in inverse proportion.

Question (i)

X	50	40	30	20
y	5	6	7	8

Solution:
x₁ = 50 and y₁ = 5
∴ x₁y₁ = 50 × 5
∴ x₁y₁ = 250

x₂ = 40 and y₂ = 6
∴ x₂y₂ = 40 × 6
∴ x₂y₂ = 240

x₃ = 30 and y₃ = 7
∴ x₃y₃ = 30 × 7
∴ x₃y₃ = 210

x₄ = 20 and y₄ = 8
∴ x₄y₄ = 20 × 8
∴ x₄y₄ = 160
Now 250 ≠ 240 ≠ 210 ≠ 160
∴ x₁y₁ ≠ x₂y₂ ≠ x₃y₃ ≠ x₄y₄
∴ x and y are not in inverse proportion.

Question (ii)

X	100	200	300	400
y	60	30	20	15

Solution:
x₁ = 100 and y₁ = 60
∴ x₁y₁ = 100 × 60
∴ x₁y₁ = 6000

x₂ = 200 and y₂ = 30
∴ x₂y₂ = 200 × 30
∴ x₂y₂ = 6000

x₃ = 300 and y₃ = 20
∴ x₃y₃ = 300 × 20
∴ x₃y₃ = 6000

x₄ = 400 and y₄ = 15
∴ x₄y₄ = 400 × 15
∴ x₄y₄ = 6000
Now x₁y₁ = x₂y₂ = x₃y₃ = x₄y₄
∴ x and y are in inverse proportion.

Question (iii)

X	90	60	45	30	20	5
y	10	15	20	25	30	35

Solution:
x₁ = 90 and y₁ = 10
∴ x₁y₁ = 90 × 10
∴ x₁y₁ = 900

x₂ = 60 and y₂ = 15
∴ x₂y₂ = 60 × 15
∴ x₂y₂ = 900

x₃ = 45 and y₃ = 20
∴ x₃y₃ = 45 × 20
∴ x₃y₃ = 900

x₄ = 30 and y₄ = 25
∴ x₄y₄ = 30 × 25
∴ x₄y₄ = 750

x₅ = 20 and y₅ = 30
∴ x₅y₅ = 20 × 30
∴ x₅y₅ = 600

x₆ = 30 and y₆ = 35
∴ x₆y₆ = 5 × 35
∴ x₆y₆ = 175

Now x₁y₁ = x₂y₂ = x₃y₃ ≠ x₄y₄ ≠ x₅y₅ ≠ x₆y₆
∴ x and y are in inverse proportion.