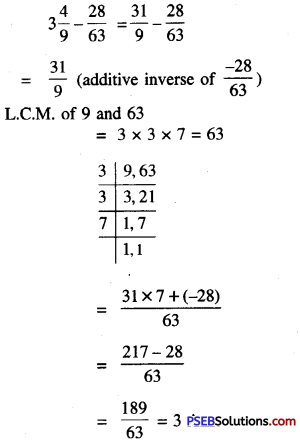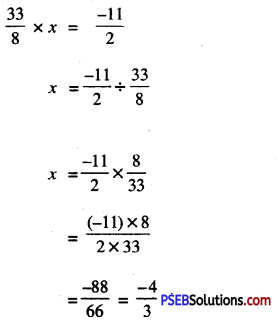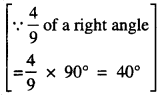Class 7

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 6 Triangles Ex 6.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 6 Triangles Ex 6.1

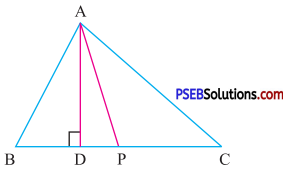
1. In ΔABC, P is midpoint of BC, then
(i) BP = ……………..
(ii) AP is a …………….. of ΔABC
(iii) ∠ADC = ……………..
(iv) BD = BC (True/False)
(v) AD is an …………….. of ΔABC

Solution:
(i) PC
(ii) Median
(iii) 90°
(iv) False
(v) Altitude

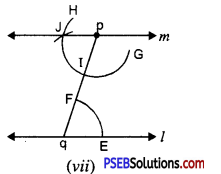
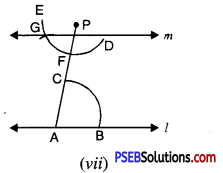
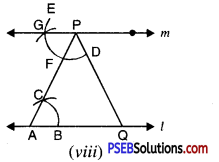
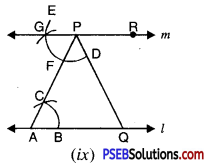
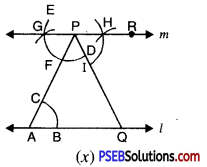
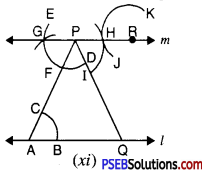
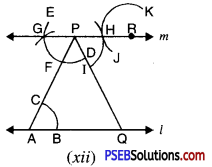
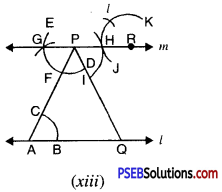
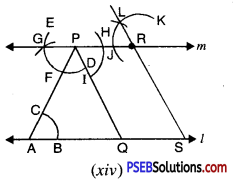
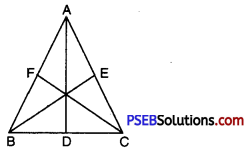
2. (a) Draw AD, BE, CF three medians in a ΔABC.
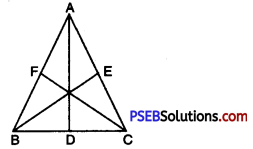
(b) Draw an equilateral triangle and its medians. Also compare the lengths of the medians.
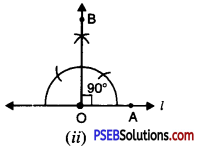
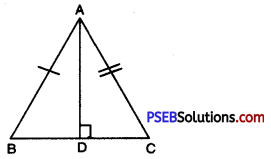
(c) Draw an isosceles triangle ABC in which AB = BC. Also draw its altitudes.
Solutions:
(a) We are given ΔABC D, E and F are mid points of the sides BC, CA and AB respectively. Join AD, BE and CF.
The AD, BE and CF are the required medians.

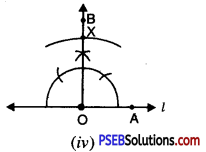
(b) Draw an equilateral triangle ABC, D,E and F are the mid points of sides BC, CA and AB respectively. On joining AD, BE and CF, we get the required medians AD, BE and CF. Measure the lengths of AD, BE and CF we observe that the three medians AD, BE and CF are equal in length.
∴ AD = BE = CF.

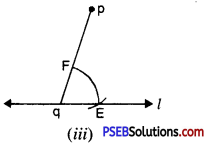
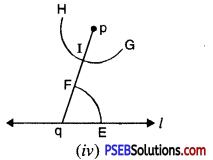
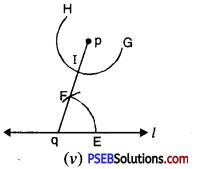
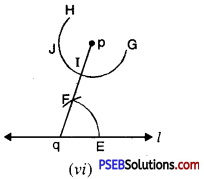
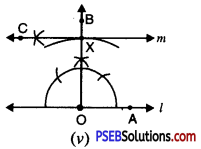
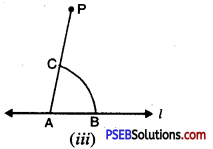
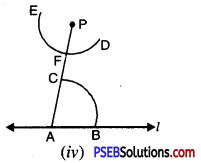
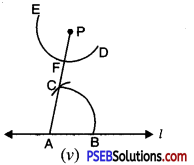
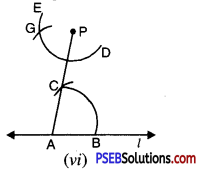
(c) Draw an isosceles ΔABC in which AB = BC Altitude can be drawn as below :
AD is the altitude from A to D.


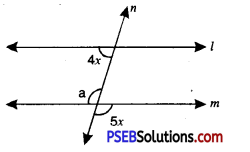
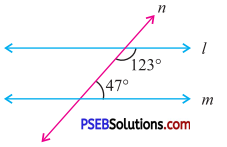
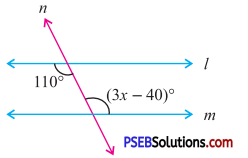
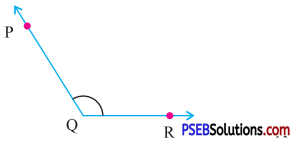
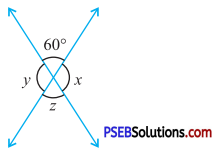
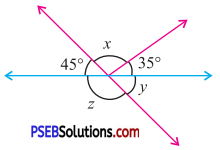
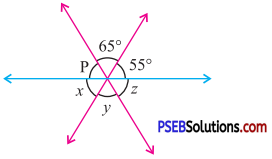
3. Find the value of the unknown exterior angles.

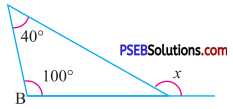
Question (i).

Answer:
In the given triangle,
By exterior angle property of a triangle
Exterior angle = sum of interior opposed angles
x = 100° + 40°
∴ x = 140°

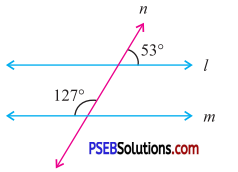
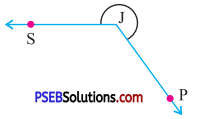
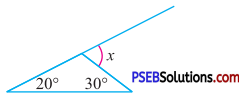
Question (ii).

Answer:
By exterior angle property of a triangle
Exterior angle = Sum of interior opp. angles
x = 20° + 30°
∴ x = 50°

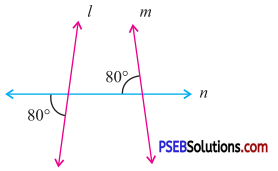
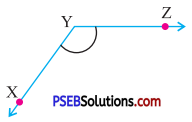
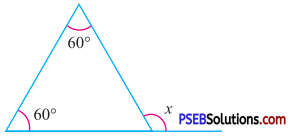
Question (iii).

Answer:
By exterior angle property of a triangle
Exterior angle = Sum of interior opp. angles
x = 60° + 60°
∴ x = 120°

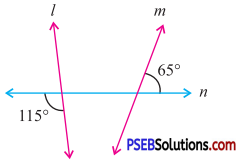
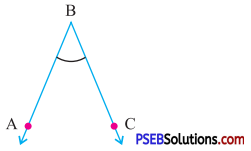
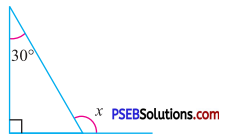
Question (iv).

Answer:
By exterior angle property of a triangle
Exterior angle = Sum of interior opp. angles
x = 90° + 30°
∴ x = 120°

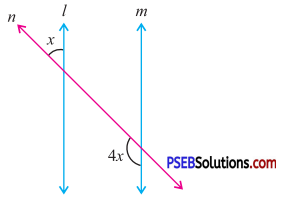
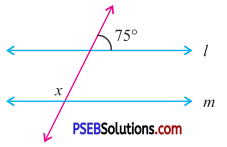
4. Find the value of x in the following figures.

Question (i).

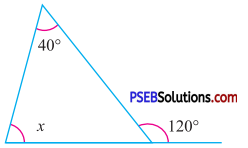
Answer:
By exterior angle property of a triangle
Sum of interior opp. angles = Exterior angle
40° + x = 120°
x = 120° – 40°
x = 80°.

Question (ii).

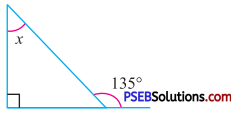
Answer:
By exterior angle property of a triangle
Sum of interior opp. angles = Exterior angle
x + 90° = 135°
x = 135° – 90°
x = 45°

Question (iii).

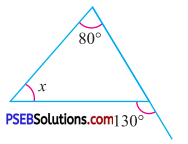
Answer:
By exterior angle property of a triangle
Sum of interior opp. angles = Exterior angle
x + 80° = 130°
x = 130° – 80°
x = 50°

Question (iv).

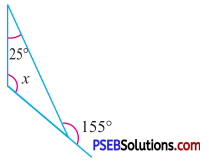
Answer:
By exterior angle property of a triangle
Sum of interior opp. angles = Exterior angle
x + 25° = 155°
x = 155° – 25°
x = 130°

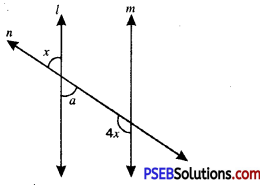
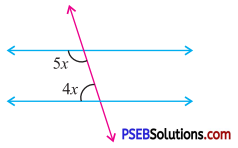
5. Find the value of y in following figures.

Question (i).

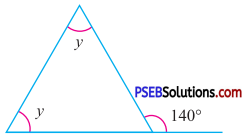
Answer:
By exterior angle property of a triangle
Sum of interior opp. angles = Exterior angle
y + y = 140°
2y = 140°
y = \(\frac{140^{\circ}}{2}\)
y = 70°

Question (ii).

Answer:
By exterior angle property of a triangle
Sum of interior opp. angles = Exterior angle
y + 90° = 160°
y = 160° – 90°
y = 70°

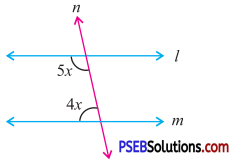
Question (iii).

Answer:
By exterior angle property of a triangle
exterior angle = Sum of interior opp. angles
5y = y + 80°
5y – y = 80°
4y = 80°
y = \(\frac{80^{\circ}}{4}\)
y = 20°.

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 9 Rational Numbers MCQ Questions with Answers.

PSEB 7th Class Maths Chapter 9 Rational Numbers MCQ Questions

Multiple Choice Questions :

Question 1.
Look at the above number line and tell which of the following values is the greatest.
(a) a + b
(b) b – a
(c) a × b
(d) a ÷ b
Answer:
(a) a + b

Question 2.
The product of a rational number and its reciprocal is always :
(a) -1
(b) 0
(c) 1
(d) equal to itself.
Answer:
(c) 1

Question 3.
Which of the following is not an natural number ?
(a) 0
(b) 2
(c) 10
(d) 105.
Answer:
(a) 0

Question 4.
The ascending order of \(\frac{-3}{5}, \frac{-2}{5}, \frac{-1}{5}\) is :
(a) \(\frac{-1}{5}<\frac{3}{5}<\frac{2}{5}\)
(b) \(\frac{-3}{5}<\frac{-2}{5}<\frac{-1}{5}\)
(c) \(\frac{-3}{5}<\frac{-1}{5}<\frac{-2}{5}\)
(d) \(\frac{-2}{5}<\frac{-3}{5}<\frac{-1}{5}\)
Answer:
(b) \(\frac{-3}{5}<\frac{-2}{5}<\frac{-1}{5}\)

Question 5.
Write \(\frac {1}{4}\) as a rational number with 4 denominator 20.
(a) \(\frac{2}{20}\)
(b) \(\frac{3}{20}\)
(c) \(\frac{5}{20}\)
(d) \(\frac{4}{20}\)
Answer:
(c) \(\frac{5}{20}\)

Question 6.
The value of \(\frac{-13}{7}+\frac{6}{7}\) :
(a) \(\frac{19}{7}\)
(b) \(\frac{-7}{7}\)
(c) \(\frac{7}{7}\)
(d) None of these
Answer:
(b) \(\frac{-7}{7}\)

Question 7.
The additive inverse of \(\frac{-9}{11}\) is :
(a) \(\frac{9}{11}\)
(b) \(\frac{-9}{11}\)
(c) \(\frac{11}{9}\)
(d) \(\frac{-11}{9}\)
Answer:
(a) \(\frac{9}{11}\)

Question 8.
The additive inverse of \(\frac{5}{7}\) is :
(a) \(\frac{7}{5}\)
(b) \(\frac{-5}{7}\)
(c) \(\frac{-7}{5}\)
(d) \(\frac{5}{7}\)
Answer:
(b) \(\frac{-5}{7}\)

Fill in the blanks :

Question 1.
The smallest natural number is ………………..
Answer:
1

Question 2.
The numbers which are used for counting are called ………………..
Answer:
natural number

Question 3.
All natural number along with zero (0) are called ………………..
Answer:
whole number

Question 4.
Reciprocal of \(\frac {5}{3}\) is ………………..
Answer:
\(\frac {3}{5}\)

Question 5.
Additive inverse of –\(\frac {3}{4}\) is ………………..
Answer:
\(\frac {3}{4}\)

Write True or False :

Question 1.
The smallest natural number is zero (0). (True/False)
Answer:
False

Question 2.
0 is an integer which is neither negative nor positive. (True/False)
Answer:
True

Question 3.
The smallest whole number is 1. (True/False)
Answer:
False

Question 4.
–\(\frac {2}{5}\) is a fraction. (True/False)
Answer:
False

Question 5.
\(\frac {1}{0}\) not a rational number. (True/False)
Answer:
True

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 9 Rational Numbers Ex 9.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 9 Rational Numbers Ex 9.2

1. Find the sum

Question (i).
\(\frac{6}{9}+\frac{2}{9}\)
Solution:
\(\frac{6}{9}+\frac{2}{9}\) = \(\frac{6+2}{9}\)
= \(\frac {8}{9}\)

Question (ii).
\(\frac{-15}{7}+\frac{9}{7}\)
Solution:
\(\frac{-15}{7}+\frac{9}{7}\) = \(\frac{-15+9}{7}\)
= \(\frac{-6}{7}\)

Question (iii).
\(\frac{17}{11}+\left(\frac{-9}{11}\right)\)
Solution:
\(\frac{17}{11}+\left(\frac{-9}{11}\right)\) = \(\frac{17-9}{11}\)
= \(\frac{8}{11}\)

Question (iv).
\(\frac{-5}{6}+\frac{3}{18}\)
Solution:
\(\frac{-5}{6}+\frac{3}{18}\)
Now, \(\frac{-5}{6}=\frac{-5}{6} \times \frac{3}{3}=\frac{-15}{18}\)

L.C.M. of 6 and 18
= 2 × 3 × 3 = 18
Thus, \(\frac{-5}{6}+\frac{3}{18}=\frac{-15}{18}+\frac{3}{18}\)
= \(\frac{-15+3}{18}\)
= \(\frac {-12}{18}\)
= \(\frac {-2}{3}\)

Question (v).
\(\frac{-7}{19}+\frac{-3}{38}\)
Solution:
\(\frac{-7}{19}+\frac{-3}{38}\)
Now, \(\frac{-7}{19}=\frac{-7}{19} \times \frac{2}{2}\)
= \(\frac {-14}{38}\)
\(\begin{array}{l|l}
2 & 19,38 \\
\hline 19 & 19,19 \\
\hline & 1,1 \\
\hline
\end{array}\)
L.C.M. = 2 × 19
= 38
Thus, \(\frac{-7}{19}+\frac{-3}{38}=\frac{-14}{38}+\frac{-3}{38}\)
= \(\frac{-14-3}{38}\)
= \(\frac{-17}{38}\)

Question (vi).
\(-3 \frac{4}{7}+2 \frac{3}{7}\)
Solution:
\(-3 \frac{4}{7}+2 \frac{3}{7}\)
= \(-\frac{25}{7}+\frac{17}{7}\)
= \(\frac{-25+17}{7}\)
= \(\frac{-8}{7}\)

Question (vii).
\(\frac{-5}{14}+\frac{8}{21}\)
Solution:
\(\frac{-5}{14}+\frac{8}{21}\)
Now, \(\frac{-5}{14}=\frac{-5}{14} \times \frac{3}{3}\)
= \(\frac{-15}{42}\)
\(\begin{array}{l|l}
2 & 14,21 \\
\hline 3 & 7,21 \\
\hline 7 & 7,7 \\
\hline & 1,1
\end{array}\)
L.C.M of 14, 21 = 2 × 3 × 7
= 42
\(\frac{8}{21}=\frac{8}{21} \times \frac{2}{2}\)
= \(\frac{16}{42}\)
Thus, \(\frac{-5}{14}+\frac{8}{21}\)
= \(\frac{-15}{42}+\frac{16}{42}\)
= \(\frac{-15+16}{42}\)
= \(\frac{1}{42}\)

Question (viii).
\(-4 \frac{1}{15}+3 \frac{2}{20}\)
Solution:

2. Find

Question (i).
\(\frac{7}{12}-\frac{11}{36}\)
Solution:
\(\frac{7}{12}-\frac{11}{36}\) = \(\frac{7}{12}\) + (Additive inverse of \(\frac{11}{36}\))
= \(\frac{7}{12}+\left(\frac{-11}{36}\right)\)
= \(\frac{21+(-11)}{36}\)
\(\begin{array}{l|l}
2 & 12,36 \\
\hline 2 & 6,18 \\
\hline 3 & 3,9 \\
\hline 3 & 1,3 \\
\hline & 1,1
\end{array}\)
L.C.M of 12 and 36
= 2 × 2 × 3 × 3
= 36
= \(\frac{10}{36}=\frac{5}{18}\)

Question (ii).
\(\frac{-5}{9}-\frac{3}{5}\)
Solution:
\(\frac{-5}{9}-\frac{3}{5}\) = \(\frac {-5}{9}\) + (additive inverse of \(\frac {3}{5}\))
= \(\frac{-5}{9}+\left(\frac{-3}{5}\right)\)
= \(\frac{-25+(-27)}{45}\)
L.C.M of 9 and 5 is 45 = \(\frac {-52}{45}\)

Question (iii).
\(\frac{-7}{13}-\left(\frac{-5}{91}\right)\)
Solution:
\(\frac{-7}{13}-\left(\frac{-5}{91}\right)\) = \(\frac {-7}{13}\) + (additive inverse of \(\frac {-5}{91}\))
= \(\frac{-7}{13}+\left(\frac{5}{91}\right)\)
= \(\frac{-49+(5)}{91}\)
L.C.M of 13 and 91 = 7 × 13 = 91
\(\begin{array}{l|l}
7 & 13,91 \\
\hline 13 & 13,13 \\
\hline & 1,1
\end{array}\)
= \(\frac {-44}{91}\)

Question (iv).
\(\frac{6}{11}-\frac{-3}{4}\)
Solution:
\(\frac{6}{11}-\frac{-3}{4}\) = \(\frac {6}{11}\) + (additive inverse of \(\frac {-3}{4}\))
= \(\frac{6}{11}+\left(\frac{3}{4}\right)\)
= \(\frac{24+33}{44}\)
L.C.M of 11 and 4 is 44 = \(\frac {57}{44}\)

Question (v).
\(3 \frac{4}{9}-\frac{28}{63}\)
Solution:

3. Find the product of :

Question (i).
\(\frac{5}{9} \times \frac{-3}{8}\)
Solution:
\(\frac{5}{9} \times \frac{-3}{8}\)
= \(\frac{5 \times-3}{9 \times 8}\)
= \(\frac {-5}{24}\)

Question (ii).
\(\frac{-3}{7} \times \frac{7}{-3}\)
Solution:
\(\frac{-3}{7} \times \frac{7}{-3}\)
= \(\frac{-3 \times 7}{7 \times-3}\)
= 1

Question (iii).
\(\frac{3}{13} \times \frac{5}{8}\)
Solution:
\(\frac{3}{13} \times \frac{5}{8}\)
= \(\frac{3 \times 5}{13 \times 8}\)
= \(\frac {15}{104}\)

Question (iv).
\(\frac {3}{10}\) × (-18)
Solution:
\(\frac {3}{10}\) × (-18)
= \(\frac{3 \times-18}{10}\)
= \(\frac{-27}{5}\)

4. Find the value of:

Question (i).
-9 ÷ \(\frac {3}{5}\)
Solution:
-9 ÷ \(\frac {3}{5}\)
= -9 × (Reciprocal of \(\frac {3}{5}\))
= -9 × \(\frac {5}{3}\)
= -15

Question (ii).
\(\frac {-4}{7}\) ÷ 4
Solution:
\(\frac {-4}{7}\) ÷ 4
= \(\frac {-4}{7}\) × (Reciprocal of 4)
= \(\frac{-4}{7} \times \frac{1}{4}\)
= \(\frac {-1}{7}\)

Question (iii).
\(\frac{7}{18} \div \frac{5}{6}\)
Solution:
\(\frac{7}{18} \div \frac{5}{6}\)
= \(\frac {7}{18}\) × (Reciprocal of \(\frac {5}{6}\))
= \(\frac{7}{18} \times \frac{6}{5}\)
= \(\frac {7}{15}\)

Question (iv).
\(\frac{-8}{35} \div\left(\frac{-2}{7}\right)\)
Solution:
\(\frac{-8}{35} \div\left(\frac{-2}{7}\right)\)
= \(\frac {-8}{35}\) × (Reciprocal of \(\frac {-2}{7}\))
= \(\frac{-8}{35} \times \frac{7}{-2}\)
= \(\frac {4}{5}\)

Question (v).
\(\frac {-9}{15}\) ÷ -18
Solution:
\(\frac {-9}{15}\) ÷ -18
= \(\frac {-9}{15}\) × (Reciprocal of -18)
= \(\frac{-9}{15} \times \frac{1}{-18}\)
= \(\frac {1}{30}\)

5. What ratonal number should be added to \(\frac {-5}{12}\) to get \(\frac {-7}{8}\)?
Solution:
Let the required number to be added be x.
then, \(\frac {-5}{12}\) + x = \(\frac {-7}{8}\)

L.C.M of 8, 12 = 2 × 2 × 2 × 3
= 24
= \(\frac{-7 \times 3+5 \times 2}{24}\)
= \(\frac{-21+10}{24}\)
= \(\frac {-11}{24}\)

6. What number should be subtracted from \(\frac {-2}{3}\) to get \(\frac {-5}{6}\) ?
Solution:
Let the required number to be subtracted be x, then
\(\frac{-2}{3}-x=\frac{-5}{6}\)
⇒ \(\frac{-2}{3}-\left(\frac{-5}{6}\right)\) = x
x = \(\frac{-2}{3}+\frac{5}{6}\)
= \(\frac{-4+5}{6}\)
= \(\frac {1}{6}\)

7. The product of two rational numbers is \(\frac {-11}{2}\). If one of them is \(\frac {33}{8}\), find the other number.
Solution:
Let the required number be x, then

8. Multiple Choice Questions

Question (i).
The sum of \(\frac{5}{4}+\left(\frac{25}{-4}\right)\) =
(a) -5
(b) 5
(c) 4
(d) -4
Answer:
(a) -5

Question (ii).
\(\frac{17}{11}-\frac{6}{11}\) =
(a) 1
(b) -1
(c) 6
(d) 3
Answer:
(a) 1

Question (iii).
\(\frac{2}{-5} \times \frac{-5}{2}\) =
(a) 1
(b) -1
(c) 2
(d) -5
Answer:
(a) 1

Question (iv).
\(\frac{7}{12} \div\left(\frac{-7}{12}\right)\) =
(a) 1
(b) -1
(c) 7
(d) -7
Answer:
(b) -1

Question (v).
Which of the following is value of (-4) × [(-5) + (-3)]
(a) -32
(b) 120
(c) 32
(d) -23
Answer:
(c) 32

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 10 Practical Geometry Ex 10.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.1

1. Draw a line, l, take a point p outside it. Through p, draw a line parallel to l using ruler and compass only.
Solution:
Steps of Construction :
Step 1. Draw a line l of any suitable length Mid a point ‘p’ outside l [see Fig. (i)].

Step 2. Take a point ‘q’ on l and join q to p [see Fig. (ii)].

Step 3. With q as centre and a convenient radius, draw an arc cutting l at E and pq at F [see Fig. (iii)].

Step 4. Now with p as a centre and the same radius as in step 3, draw an arc GH cutting pq at I [see Fig. (iv)].

Step 5. Place the pointed tip of the compasses at E and adjust the opening so that the pencil tip is at F [see Fig. (v)].

Step 6. With the same opening as in step 5 and with I as centre, draw an arc cutting the arc GH at J. [see Fig. (vi)].

Step 7. Now, join pand J to draw a line ‘m’ [see Fig. (vii)],

Note that : ∠Jpq and ∠pqE are alternate interior angles and ∠pqE = ∠qpJ
∴ m || l

2. Draw a line parallel to a line l at a distance of 3.5 cm from it.
Solution :
Steps of construction :
Step 1. Take a line ‘l’ and any point say O on it [see Fig. (i)].

Step 2. At O draw ∠AOB = 90°. [see Fig. (ii)].

Step 3. Place the pointed tip of the compasses at ‘0’ (zero) mark on ruler and adjust the opening so that the pencil tip is at 3.5 cm [see Fig. (iii)]

Step 4. With the same opening as in step 3 and with O as centre draw an arc cutting ray OB at X. [see Fig. (iv)].

Step 5. At X draw a line ‘m’ perpendicular to OB. In other words, draw ∠CXO = 90° [see Fig. (v)].

In this way, line m is parallel to l.
Note that. ∠AOX and ∠CXO are alternate angles and ∠AOX = ∠CXO (each = 90°).
∴ m || l.
Note. We may use any of three properties regarding the transversal OX and parallel lines l and m.

3. Let l be a line and P be a point not on l. Through P, draw a line ‘m’ parallel to l. Now, join P to any point Q on l. Choose any other point R on m. Through R, draw a line parallel to PQ. Let this meets l at S. What shape do the two sets of parallel lines enclose ?
Solution:
Steps of Construction :
Step 1. Take a line ‘l’ and a point ‘P’ outside l. [see Fig . (i)]

Step 2. Take any point A on l and join P to A [see Fig. (ii)]

Step 3. With A as centre and convenient radius draw an arc cutting l at B and AP at C. [see Fig. (iii)]

Step 4. Now with P as centre and the same radius as in step 3, draw an arc DE cutting PA at F [see Fig. (iv)].

Step 5. Place the pointed tip of the compasses at B and adjust the opening so that the pencil tip is at C [see Fig. (v)].

Step 6. With the same opening as in step 5 and with F as centre, draw an arc cutting the arc DE at G [see Fig. (vi)].

Step 7. Now join PG to draw line ‘m’ [see Fig. (vii)].

Note that. ∠PAB and ∠APG are alternate interior angles and ∠PAB = ∠APG
∴ m || l
Step 8. Take any point Q on l. Join PQ [see Fig. (viii)].

Step 9. Take any other point R on m [see Fig. (ix)].

Step 10. With P as centre and convenient radius, draw an arc cutting line m at H and PQ at I [see Fig. (x)].

Step 11. Now with R as centre and the same radius as in step 10, draw an arc JK [see Fig. (xi)].

Step 12. Place the pointed tip of compasses at H and adjust the opening so that the pencil tip is at I.

Step 13. With the same opening as in step 12 and with R as centre, draw an arc cutting the arc JK at L [see Fig. (xii)].

Step 14. Now join RL to draw a line parallel to PQ. Let this meet l at S. [see Fig. (xiv)]

Note that. ∠RPQ and ∠LRP are alternate interior angles
and ∠RPQ = ∠LRP
∴ RS || PQ.
Now we have
PR || QS
[∵ m || l and PR is part of m and QS is part of line l]
and PQ || RS
∴ PQSR is a parallelogram.

4.

Question (i).
How many parallel lines can be drawn, passing through a point not lying on the given line ?
(a) 0
(b) 2
(c) 1
(d) 3
Answer:
(c) 1

Question (ii).
Which of the following is used to draw a line parallel to a given line ?
(a) A protractor
(b) A ruler
(c) A compasses
(d) A ruler and compasses.
Answer:
(d) A ruler and compasses.

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 5 Lines and Angles MCQ Questions with Answers.

PSEB 7th Class Maths Chapter 5 Lines and Angles MCQ Questions

Multiple Choice Questions :

Question 1.
If a line intersects three lines, tell the number of intersecting point:
(a) 1
(b) 2
(c) 3
(d) A
Answer:
(c) 3

Question 2.
A line has :
(a) Two ends
(b) One end
(c) No end
(d) None of these
Answer:
(c) No end

Question 3.
The complementary angle of 45° is :
(a) 45°
(b) 135°
(c) 90°
(d) 180°
Answer:
(a) 45°

Question 4.
Supplementary angle of 100° is :
(a) 80°
(b) 100°
(c) 90°
(d) 180°
Answer:
(d) 180°

Fill in the blanks :

Question 1.
It two angles are complementary, then the sum of their measures is
Answer:
90°

Question 2.
If two angles are supplementary, then the sum of their measures is
Answer:
180°

Question 3.
The angle which is equal to its complement is
Answer:
45°

Question 4.
The angle which is equal to its supplement is
Answer:
90°

Question 5.
If two adjacent angles are supplementary they form a
Answer:
linear pair

Write True/False for the following :

Question 1.
Two acute angles can be complementary. (True/False)
Answer:
True

Question 2.
Two obtuse angles can be supplementary. (True/False)
Answer:
False

Question 3.
The complement of a right angle is also a right angle. (True/False)
Answer:
False

Question 4.
Adjacent angle can be complementary. (True/False)
Answer:
False

Question 5.
Complementry angles are always adjacent. (True/False)
Answer:
False

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 5 Lines and Angles Ex 5.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 5 Lines and Angles Ex 5.2

1. In the figure question identify the pair of angles as corresponding angles alternate interior angles, exterior alternate angles, adjacent angles, vertically opposite angles and co-interior angles, linear pair.
(i) ∠3 and ∠6
(ii) ∠3 and ∠7
(iii) ∠2 and ∠4
(iv) ∠2 and ∠7
(v) ∠1 and ∠8
(vi) ∠4 and ∠6
(vii) ∠1 and ∠5
(viii) ∠1 and ∠4
(ix) ∠5 and ∠7

Answer:
(i) Alternate interior angles.
(ii) Corresponding angles.
(iii) Adjacent angles.
(iv) Alternate exterior angles.
(v) Alternate exterior angles.
(vi) Co-interior angles.
(vii) Corresponding angles.
(viii) Vertically opposite angles.
(ix) Linear pair.

2. In the figure identify :

(i) The pairs of corresponding angle.
(ii) The pairs of alternate interior angles.
(iii) The pairs of interior angles on the same side of the transversal.
(iv) The pairs of vertically opposite angles.
Answer:
(i) ∠1 and ∠5, ∠2 and ∠6, ∠3 and ∠7, ∠4 and ∠8.
(ii) ∠1 and ∠7, ∠2 and ∠8.
(iii) ∠1 and ∠8, ∠2 and ∠7.
(iv) ∠1 and ∠3, ∠2 and ∠4, ∠5 and ∠7, ∠6 and ∠8.

3. In the given figures, the intersected lines are parallel to each other. Find the unknown angles.

Question (i).

Answer:
l || m and a is a transversal ∠b = 80°
[Alternate interior angles]
∠a = ∠b
[Vertically opposite angles]
∴ ∠a = 80° [∵ ∠b = 80°]
Also ∠c = 80°
[Vertically opposite ∠5]
Hence a = 80°, b = 80°, c = 80°

Question (ii).

Answer:
∠x° + 70°= 180° (Linear pair)
∠x° = 180° – 70°
∠x° = 110°
∠y° = 70°.
(Vertically opposite angles)
AB || CD and EF is a transversal
∴ ∠z° = 70°
[Alternate interior angles]
Hence x = 110°, y = 70° and z = 70°

Question (iii).

Answer:
110° + a = 180° (Linear pair)
∴ a = 180°- 110° = 70°
b = a
(Corresponding angles)
∴ b = 70°
d = b
(Vertically opposite angles)
∴ d = 70°
b + c = 180° (Linear pair)
70° + c = 180°
∴ c = 180° – 70° = 110°
Hence a = 70°, b = 70°, c = 110°, d = 70°

Question (iv).

Answer:
P + 75° = 180° (Linear pair)
∴ P = 180° – 75° = 105°
R = P
= 105°
(Vertically opposite angles)
Q =75°
(Vertically opposite angles)
AB || CD and EF is a transversal
S = R
(Alternate interior angles)
∴ S = 105°
T = Q
(Alternate interior angles) = 75°
Now U = T
= 75°
(Vertically opposite angles) V = S
(Vertically opposite angles) = 105°
Hence P = 105°, Q = 75°, R = 105°,
S = 105°, T = 75°, U = 75°, V = 105°

4. Find the value of x in the following figures if l || m

Question (i).

Answer:
l || m and n is a transversal
∴ 2x + 3x = 180°
[The pair of co-interior angles are supplementary]
or 5x = 180°
x = \(\frac{180^{\circ}}{5}\) = 36°

Question (ii).

Answer:
a = 5x
(Vertically opposite angles)
Since l || m and n is a transversal
∴ 4x + 5x= 180°
[The pair of co-interior angles are supplementary]

or 9x = 180°
∴ x = \(\frac{180^{\circ}}{9}\) = 20°

Question (iii).

Answer:
a = x
(Vertically opposite angles)
Now l || m and n is a transversal
a + 4x = 180°
[The pair of co-interior angles are supplementary]

∴ a + 4x = 180°
or x + 4x = 180°
or 5x = 180°
Or x = \(\frac{180^{\circ}}{5}\) = 36°

Question (iv).

Answer:
Since l || m and n is a transversal
[The pair of co-interior angles are supplementary]
∴ 5x + 4x = 180°
Or 9x = 180°
x = \(\frac{180^{\circ}}{9}\) = 20°

5. In the given figures arms of two angles are parallel find the following.

Question (a).
(i) ∠DGC
(ii) ∠DEF

Answer:
(i) AB || DE and BC is a transversal
∴ ∠DGC = ∠ABC
(Corresponding angles)
= 65° (∵ ∠ABC = 65°)

(ii) Since BC || EF and DE is the transversal.
∴ ∠DEF = ∠DGC
(Corresponding angles)
= 65° (∵ ∠DGC = 65°)

Question (b).
(i) ∠MNP
(ii) ∠RST

Answer:
(i) Since MN || RS and NP is a transversal
∴ ∠MNP = ∠RQP
(Corresponding angles)
= 70° (∵ ∠RQP = 70°)

(ii) Since NP || ST and RS is a transversal
∴ ∠RST = ∠RQP
(Corresponding angles)
= 70° (∵ ∠RQP = 70°)

6. In the following figure AB || CD and EF || GH, find the measure of ∠x and ∠y.

Solution:
Since AB || CD and EF is a transversal
∴ ∠y = 65°
(Corresponding angles)
Since EF || GH and AB is a transversal.
∴ ∠x = 65°
[alternate interior angles]
Therefore ∠x = 65° and ∠y = 65°

7. PQ ⊥ RS find the value of x in the following figure.

Solution:
Let O be the point of intersection of PQ and RS.
Now PQ and MN intersect each other at O
∴ ∠POM = ∠NOQ
(Vertically opposite angles)
= 3x° (∵ ∠WOQ = 3x°)
Now ∠POS = 90°
∴ ∠POM + ∠MOS = 90°
6x° + 3x° = 90°
9x° = 90°
x = \(\frac{90^{\circ}}{9}\) = 10°

8. In the given figure below, decide whether l is parallel to m.

Question (i).

Answer:
Here 123° + 47° = 170°
But the sum of the pair of co-interior angles is 180°
∴ l is not parallel to m.

Question (ii).

Answer:
Here 127° + 53° = 180°
∴ sum of the pair of co-interior angles is 180°.
Thus l parallel to m.

Question (iii).

Answer:
Since 80° + 80° = 160°
But the sum of the pairs of co-interior angles is 180°
Therefore l is not parallel to m.

Question (iv).

Answer:
115° and 65° are corresponding angles which are not equal.
Therefore l is not parallel to m.

9. Multiple Choice Questions :

Question (i).
A pair of complementary angles is
(a) 130°, 50°
(b) 35°, 55°
(c) 25°, 75°
(d) 27°, 53°
Answer:
(d) 27°, 53°

Question (ii).
A pair of supplementary angles is
(a) 55°, 115°
(b) 65°, 125°
(c) 47°, 133°
(d) 40°, 50°
Answer:
(b) 65°, 125°

Question (iii).
If one angle of a linear pair is acute, then the other angle is
(a) acute
(b) obtuse
(c) right
(d) straight.
Answer:
(b) obtuse

Question (iv).
In the adjoining figure, if l || m, then the value of x is

(a) 50°
(b) 60°
(c) 70°
(d) 45°
Answer:
(a) 50°

Question (v).
In the adjoining figure, if l || m, then

(a) 75°
(b) 95°
(c) 105°
(d) 115°
Answer:
(c) 105°

Question (vi).
In the adjoining figure, the value of x that will make the lines l and m parallel is

(a) 20
(b) 30
(c) 60
(d) 80
Answer:
(a) 20

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 5 Lines and Angles Ex 5.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 5 Lines and Angles Ex 5.1

1. Name each of the following as acute, obtuse, right straight or a reflex angle.

Question (i).

Answer:
Right angle

Question (ii).

Answer:
Obtuse angle

Question (iii).

Answer:
Straight angle

Question (iv).

Answer:
Reflex angle

Question (v).

Answer:
Obtuse angle

Question (vi).

Answer:
Acute angle.

2. Write the complement of each of the following angles :

Question (i).
53°
Answer:
Complement of 53°
= (90° – 53°) = 37°.

Question (ii).
90°
Answer:
Complement of 90°
= (90° – 90°) = 0°.

Question (iii).
85°
Answer:
Complement of 85°
= (90° – 85°) = 5°.

Question (iv).
\(\frac {4}{9}\) of a right angle
Answer:
Complement of \(\frac {4}{9}\) of a right angle
i. e. 40° = (90° – 40°) = 50°

Question (v).
0°
Answer:
Complement of 0° = (90° – 0°)
= 90°.

3. Write the supplement of each of the following angle :

Question (i).
55°
Answer:
Supplement of 55°
= (180° – 55°) = 125°.

Question (ii).
105°
Answer:
Supplement of 105°
= (180° – 105°) = 75°.

Question (iii).
100°
Answer:
Supplement of 100°
= (180° – 100°) = 80°.

Question (iv).
\(\frac {2}{3}\) of a right angle
Answer:
\(\frac {2}{3}\) of a right angle
= \(\frac {2}{3}\) × 90° = 60°.
∴ Supplement of 60°
= (180° – 60°) = 120°.

Question (v).
\(\frac {1}{3}\) of 270°.
Answer:
Supplement of \(\frac {1}{3}\) of 270° i.e. 90°
= (180°- 90°) = 90°.

4. Identify the following pairs of angles as complementary or supplementary.

Question (i).
65° and 115°
Answer:
Since 65° + 115° = 180°.
∴ It is a pair of supplementary angles.

Question (ii).
112° and 68°
Answer:
Since 112° + 68° = 180°
∴ It is a pair of supplementary angles.

Question (iii).
63° and 27°
Answer:
Since 63° + 27° = 90°
∴ It is a pair of complementary angles.

Question (iv).
45° and 45°
Answer:
Since 45° + 45° = 90°
∴ It is a pair of complementary angles.

Question (v).
130° and 50°
Answer:
Since 130° + 50° = 180°.
∴ It is a pair of supplementary angles.

5. Two complementary angles are in the ratio of 4 : 5, find the angles.
Solution:
Ratio of angles = 4 : 5
Let two complementary angles are 4x and 5x
Their sum = 90°
∴ 4x + 5x = 90°
9x = 90°
x = \(\frac{90^{\circ}}{9}\) = 10°
∴ 1st angle = 4x = 4 × 10° = 40°
2nd angle = 5x = 4 × 10° = 50°

6. Two supplementary angles are in the ratio of 5 : 13, find the angles.
Solution:
Ratio of two supplementary angles = 5 : 13
Let 5x and 13x are two supplementary angles
Since their sum = 180°
∴ 5x + 13x = 180°
18x = 180°
x = \(\frac{180^{\circ}}{18}\) = 10°
∴ 1st angle = 5x = 5 × 10° = 50°.
2nd angle = 13x = 13 × 10° = 130°

7. Find the angle which is equal to its complement.
Solution:
Let the angle be = x
Therefore its complement = 90° – x
Since the angle is equal to its complement
∴ x = 90° – x
or x + x = 90°
or 2x = 90°
or x = \(\frac{90^{\circ}}{2}\)
or x = 45°
Therefore the required angle is 45°.

8. Find the angle which is equal to its supplement.
Solution:
Let the angle be x
Therefore its supplement = 180° – x
Since the angle is equal to its supplement
∴ x = 180° – x
or x + x = 180°
or 2x = 180°
or x = \(\frac{180^{\circ}}{2}\) = 90°
Therefore, the required angle is 90°.

9. In the given figure, AOB is straight line. Find the measure of ∠AOC.

Solution:
In the given figure AOB is straight line (see Fig.)
∴ ∠AOB = 180°
∴ ∠AOC + ∠BOC = 180°
or ∠AOC + 50° = 180°
[∵ ∠BOC = 50° (given)]
∴∠AOC = 180° – 50°
= 130°

10. In the given figure, MON is straight line find.
(i) ∠MOP
(ii) ∠NOP

Solution:
Since MON is straight line (see Fig.)
∴ ∠MON = 180°
∴ ∠MOP + ∠NOP = 180°
[∵ ∠MOP = x + 20°
∠NOP = x + 40°]
or 2x + 60° = 180°
or 2x = 180° – 60°
or 2x = 120°
or x = \(\frac{120^{\circ}}{2}\) = 60°.
(i) ∠MOP = x + 20°
= 60° + 20°
= 80°
(ii) ∠NOP = x + 40°
= 60° + 40°
= 100°

11. Find the value of x, y and z in each of following.

Question (i).

Solution:
In fig (i)
x = 100°
(Vertically opposite angles)
y = 80°
(Vertically opposite angles)

Question (ii).

Solution:
In fig (ii)
z = 60°
(Vertically opposite angles)
∠y + 60° = 180° (Linear pair)
or ∠y = 180° – 60°
or ∠y = 120°
x = y
(Vertically opposite angles)
= 120°

12. Find the value of x, y, z and p in each of following.

Question (i).

Solution:
In fig (i)
45° + x + 35°= 180° (Linear pair)
or x + 80° = 180°
or x = 180° – 80°
or x = 100°
y = 45° (Vertically opposite angles)
Also 45° + z = 180° (Linear pair)
z = 180° – 45°
= 135°.
Hence x = 100°,
y = 45°,
z = 135°

Question (ii).

Solution:
In fig (ii)
p + 65° + 55° = 180° (Linear pair)
p + 120°= 180°
∴ p = 180° -120°
i. e. p = 60°
x = 55°
(Vertically opposite angles)
y = 65°
(Vertically opposite angles)
z = p
= 60°
(Vertically opposite angles)
Hence x = 55°,
y = 65°,
z = 60°,
p = 60°

13. Multiple Choice Questions :

Question (i).
If two angles are complementary then the sum of their measure is …………..
(a) 180°
(b) 90°
(c) 360°
(d) None of these.
Answer:
(b) 90°

Question (ii).
Two angles are called ………….. if the sum of their measures is 180°.
(a) supplementary
(b) complementary
(c) right
(d) none of these.
Answer:
(a) supplementary

Question (iii).
If two adjacent angles are supplementary then, they form a …………..
(a) right angle
(b) vertically opposite angles
(c) linear pair
(d) corresponding angles.
Answer:
(c) linear pair

Question (iv).
If two lines intersect at a point, the vertically opposite angles are always …………..
(a) equal
(b) zero
(c) 90°
(d) none of these.
Answer:
(a) equal

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 4 Simple Equations MCQ Questions with Answers.

PSEB 7th Class Maths Chapter 4 Simple Equations MCQ Questions

Multiple Choice Questions :

Question 1.
Choose simple equation out of the following:
(a) 3x + 11
(b) 2x + 5 < 11
(c) x – 5 = 7x + 6
(d) \(\frac{5 x+6}{6}\)
Answer:
(c) x – 5 = 7x + 6

Question 2.
A quantity which takes a fixed numerical value is called :
(a) Constant
(b) Variable
(c) Equation
(d) Expression
Answer:
(a) Constant

Question 3.
In equation 5x = 25 the value of x is :
(a) 0
(b) 5
(c) -5
(d) 1
Answer:
(b) 5

Question 4.
In equation \(\frac{m}{3}\) = 2 the value of m is :
(a) 1
(b) 0
(c) 6
(d) -6
Answer:
(c) 6

Question 5.
In equation 7x + 5 = 19 the value of n is :
(a) 0
(b) -2
(c) 1
(d) 2
Answer:
(d) 2

Question 6.
In equation 4p – 3 = 13, the value of p is :
(a) 1
(b) 4
(c) 0
(d) -4
Answer:
(b) 4

Question 7.
The equation of the statement, the sum of number x and 4 is 9 is :
(a) x + 4 = 9
(b) x – 4 = 9
(c) x = 4 + 9
(d) x – 9 = 4.
Answer:
(a) x + 4 = 9

Question 8.
The equation of the statement, ‘seven times m plus 7 = gives 77’ is.
(a) 1m × 7 = 77
(b) 7m + 7 = 77
(c) 7m = 77 + 7
(d) m + 7 × 7 = 77
Answer:
(a) 1m × 7 = 77

Fill in the blanks :

Question 1.
A quantity which takes a fixed numerical value is called …………….
Answer:
Constant

Question 2.
The equation for the statement seven time a number is 42 is …………….
Answer:
7x = 42

Question 3.
If x + 4 = 15, then the value of x is …………….
Answer:
x = 11

Question 4.
If 2y – 6 = 4, then y is equal to …………….
Answer:
y = 5

Question 5.
If 8x – 4 = 28, then x is equal to …………….
Answer:
x = 4

Write True or False :

Question 1.
An equation of one variable is called linear equation. (True/False)
Answer:
True

Question 2.
If x – 3 = 1, then value of x is 2. (True/False)
Answer:
False

Question 3.
If 7m + 7 = 77, then value of m is 10. (True/False)
Answer:
True

Question 4.
If 3 subtracted from twice a number is 5, then the number is 4. (True/False)
Answer:
True

Question 5.
If one fourth of a number is 10 then the number is 40. (True/False)
Answer:
False

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 4 Simple Equations Ex 4.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.1

1. Complete the following :

Solution:
(i) No
Reason : For x = 5
L.H.S. = x + 5 = 5 + 5 = 10
RHS = 0
Since L.H.S. ≠ R.H.S.
Therefore, given equation is not satisfied for x = 5

(ii) Yes
Reason : For x = -5
L.H.S. = x + 5
= -5 + 5 = 0
R.H.S. = 0
Since L.H.S. = R.H.S.
Therefore, given equation is satisfied for
x = – 5

(iii) NO
Reason : For x = 3
L.H.S. = x – 3
= 3 – 3 = 0
R.H.S. = 1
Since L.H.S. ≠ R.H.S.
Therefore, given equation is not satisfied for x = 3

(iv) No
Reason : x = – 3
L.H.S. = x – 3
= – 3 – 3 = -6
R.H.S. = 1
Since L.H.S. ≠ R.H.S.
Therefore, given equation is not satisfied for x = – 3

(v) Yes
Reason : For x = 5
L.H.S. = 2x
= 2 × 5 = 10
R.H.S. = 10
Since L.H.S. = R.H.S.
Therefore given equation is satisfied for
x = 5

(vi) No
Reason : For x = – 6
L.H.S. = \(\frac{x}{3}\)
= \(\frac {-6}{3}\)
= -2
R.H.S. = 2
Since L.H.S. ≠ R.H.S.
Therefore given equation is not satisfied for x = – 6

(vii) No,
Reason : For x = 0
L.H.S. = \(\frac{x}{2}\)
= \(\frac {0}{2}\) = 0
R.H.S. = 2
Since L.H.S. ≠ R.H.S.
Therefore given equation is not satisfied for x = 0

2. Check whether the value given in the brackets is a solution to the given equation or not.

Question (i).
x + 4 = 11 (x = 7)
Answer:
Yes
Check : For x = 1
L.H.S. = x + 4
= 7 + 4 = 11
R.H.S. = 11
Since L.H.S. = R.H.S.
Therefore x = 7 is the solution to the given equation.

Question (ii).
8x + 4 = 28 (x = 4)
Answer:
No
Check: Forx-4
L.H.S. = 8x + 4
= 8 × 4 + 4
= 32 + 4
= 36
R.H.S. = 28
Since L.H.S. ≠ R.H.S.
Therefore x = 4 is not solution to the given equation.

Question (iii).
3m – 3 = 0 (m = 1)
Answer:
Yes
Check : For m = 1
L.H.S. = 3m – 3
= 3 × 1 – 3 = 3 – 3 = 0
R.H.S.= 0
Since L.H.S. = R.H.S.
Therefore, m = 1 is the solution to the given equation.

Question (iv).
\(\frac{x}{5}\) – 4 = -1 (x = 15)
Answer:
Yes
Check : For x = 15
L.H.S. = \(\frac{x}{5}\) – 4
= \(\frac {15}{5}\) – 4 = 3 – 4 = – 1
R.H.S. = – 1
Since L.H.S. = R.H.S.
Therefore, x = 15 is the solution to the given equation.

Question (v).
4x – 3 = 13 (x = 0)
Answer:
No
Check : For x = 0
L.H.S. = 4x – 3
= 4 × 0 – 3
= 0 – 3
= -3
R.H.S. = 13
Since L.H.S. ≠ R.H.S.
Therefore x = 0 is not the solution to the given equation.

3. Solve the following equations by trial and error method

Question (i).
5x + 2 = 17
Answer:

Value of x	L.H.S	R.H.S
1	5 × 1 + 2 = 5 + 2 = 7	17
2	5 × 2 + 2 = 10 + 2 = 12	17
3	5 × 3 + 2 = 15 + 2 = 17	17

We observe that for x = 3, L.H.S. = R.H.S.
Hence x = 3 is the solution of the given equation.

Question (ii).
3p – 14 = 4
Answer:

Value of p	L.H.S.	R.H.S.
1	3 × 1 – 14 = 3 – 14 = -11	4
2	3 × 2 – 14 = 6 – 14 = -8	4
3	3 × 3- 14 = 9 – 14 = -5	4
4	3 × 4 – 14 = 12 – 14 = -2	4
5	3 × 5 – 14 = 15 – 14 = 1	4
6	3 × 6 – 14 = 18 – 14 = 4	4

We observe that for p = 6, L.H.S. = R.H.S.
Hence p = 6 is the solution of the given equation

4. Write equations for the following statements.

Question (i).
The sum of numbers x and 4 is 9
Answer:
x + 4 = 9

Question (ii).
3 subtracted from y gives 9
Answer:
y – 3 = 9

Question (iii).
Ten times x is 50
Answer:
10x = 50

Question (iv).
Nine times x plus 6 is 87
Answer:
9x + 6 = 87

Question (v).
One fifth of a number y minus 6 gives 3.
Answer:
\(\frac {1}{5}\)x – 6 = 3

5. Write the following equations in statement form :

Question (i).
x – 2 = 6
Answer:
2 substracted from x is 6

Question (ii).
3y – 2 = 10
Answer:
2 subtracted from 3 times a number y is 10.

Question (iii).
\(\frac{x}{6}\) = 6
Answer:
One sixth of a number x is 6

Question (iv).
7x – 15 = 34
Answer:
15 subtracted 7 times a number x is 34.

Question (v).
\(\frac{x}{2}\) + 2 = 8
Answer:
add 2 to half of a number x to get 8.

6. Write an equation for the following statements :

Question (i).
Raju’s father’s age is 4 years more than five times Raju’s age. Raju’s father is 54 years old.
Answer:
Let x years be Raju’s age
Five times Raju’s age is 5x years
His father’s age will be 4 years more than five times
Raju’s age = 5x + 4
But 4 years more han five times Raju’s age = Raju’s father’s age
Therefore 5x + 4 = 54

Question (ii).
A teacher tells that the highest marks obtained by a student in his class is twice the lowest marks plus 6. The highest score is 86. (Take the lowest score to be x).
Answer:
Let the lowest score to be x
Twice the lowest score plus 6 = 2x + 6
The highest score obtained by a student is twice the lowest score plus 6 = 2x + 6
But highest score = 86
Hence 2x + 6 = 86

Question (iii).
In an isosceles triangle, the vertex angle is twice either base angle (Let the base angle be x in degrees. Remember that the sum of angles of a triangle is 180 degrees).
Answer:
Let the base angle be x (in degrees)
Therefore vertex angle is twice the base angle = 2x (in degrees)
Sum of three angles of a triangle = 180°
∴ x + x + 2x = 180° = 4x = 180°

Question (iv).
A shopkeeper sells mangoes in two types of boxes. One small and one large. The large box contains as many as 8 small boxes plus 4 loose mangoes. The number of mangoes in a large box is given to be 100.
Answer:
Let the mangoes in small box be x.
Large box contains mangoes
= 8 small box + 4
= 8x + 4
But mangoes in large box = 100
∴ 8x + 4 = 100

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 3 Data Handling MCQ Questions with Answers.

PSEB 7th Class Maths Chapter 3 Data Handling MCQ Questions

Multiple Choice Questions :

Question 1.
Mean of first five natural numbers is :
(a) 2
(b) 3
(c) 4
(d) 5
Answer:
(b) 3

Question 2.
The mode of the data :
3, 5, 1, 2, 2, 3, 2, 0 is :
(a) 1
(b) 2
(c) 3
(d) 5
Answer:
(b) 2

Question 3.
The probability of possible event is :
(a) 0
(b) 1
(c) 2
(d) -1
Answer:
(b) 1

Question 4.
The probability of impossible event is :
(a) 1
(b) -1
(c) 0
(d) None of these
Answer:
(c) 0

Question 5.
The probability of selecting letter S from the word ‘STUDENT’ is :
(a) \(\frac {1}{2}\)
(b) \(\frac {1}{3}\)
(c) \(\frac {1}{4}\)
(d) \(\frac {1}{7}\)
Answer:
(d) \(\frac {1}{7}\)

Fill in the blanks :

Question 1.
The mean of first five prime numbers is ……………..
Answer:
5.6

Question 2.
The median of the data: 3, 1, 5, 6, 3, 4, 5 is ……………..
Answer:
5

Question 3.
Mode of the data : 1, 0, 1, 2, 3, 1, 2, is ……………..
Answer:
1

Question 4.
The probability of getting a head or tail is ……………..
Answer:
\(\frac {1}{2}\)

Question 5.
When a die is thrown the probability of getting a number 5 is ……………..
Answer:
\(\frac {1}{6}\)

Write True or False :

Question 1.
Mean of the first five whole numbers is 2. (True/False)
Answer:
True

Question 2.
Mode of data : 1, 1, 2,4, 3, 2, 1 is 2. (True/False)
Answer:
False

Question 3.
Median of data : 1, 2, 3, 4, 5 is 3. (True/False)
Answer:
True

Question 4.
An outcome is the result of an experiment. (True/False)
Answer:
True

Question 5.
Events that have many probabilities can have probability between 0 and 1. (True/False)
Answer:
True