Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 5 Lines and Angles Ex 5.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 5 Lines and Angles Ex 5.1
1. Name each of the following as acute, obtuse, right straight or a reflex angle.
Question (i).
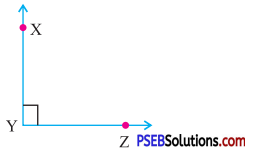
Answer:
Right angle
Question (ii).
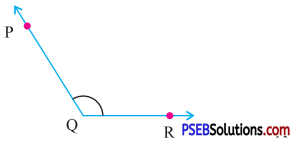
Answer:
Obtuse angle
Question (iii).

Answer:
Straight angle
Question (iv).
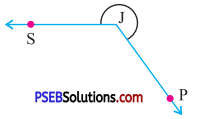
Answer:
Reflex angle
![]()
Question (v).
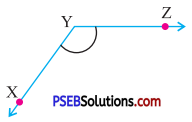
Answer:
Obtuse angle
Question (vi).
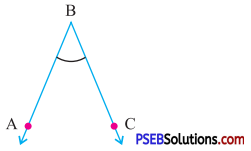
Answer:
Acute angle.
2. Write the complement of each of the following angles :
Question (i).
53°
Answer:
Complement of 53°
= (90° – 53°) = 37°.
Question (ii).
90°
Answer:
Complement of 90°
= (90° – 90°) = 0°.
Question (iii).
85°
Answer:
Complement of 85°
= (90° – 85°) = 5°.
![]()
Question (iv).
\(\frac {4}{9}\) of a right angle
Answer:
Complement of \(\frac {4}{9}\) of a right angle
i. e. 40° = (90° – 40°) = 50°
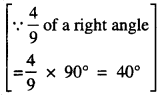
Question (v).
0°
Answer:
Complement of 0° = (90° – 0°)
= 90°.
3. Write the supplement of each of the following angle :
Question (i).
55°
Answer:
Supplement of 55°
= (180° – 55°) = 125°.
Question (ii).
105°
Answer:
Supplement of 105°
= (180° – 105°) = 75°.
Question (iii).
100°
Answer:
Supplement of 100°
= (180° – 100°) = 80°.
![]()
Question (iv).
\(\frac {2}{3}\) of a right angle
Answer:
\(\frac {2}{3}\) of a right angle
= \(\frac {2}{3}\) × 90° = 60°.
∴ Supplement of 60°
= (180° – 60°) = 120°.
Question (v).
\(\frac {1}{3}\) of 270°.
Answer:
Supplement of \(\frac {1}{3}\) of 270° i.e. 90°
= (180°- 90°) = 90°.
4. Identify the following pairs of angles as complementary or supplementary.
Question (i).
65° and 115°
Answer:
Since 65° + 115° = 180°.
∴ It is a pair of supplementary angles.
Question (ii).
112° and 68°
Answer:
Since 112° + 68° = 180°
∴ It is a pair of supplementary angles.
Question (iii).
63° and 27°
Answer:
Since 63° + 27° = 90°
∴ It is a pair of complementary angles.
![]()
Question (iv).
45° and 45°
Answer:
Since 45° + 45° = 90°
∴ It is a pair of complementary angles.
Question (v).
130° and 50°
Answer:
Since 130° + 50° = 180°.
∴ It is a pair of supplementary angles.
5. Two complementary angles are in the ratio of 4 : 5, find the angles.
Solution:
Ratio of angles = 4 : 5
Let two complementary angles are 4x and 5x
Their sum = 90°
∴ 4x + 5x = 90°
9x = 90°
x = \(\frac{90^{\circ}}{9}\) = 10°
∴ 1st angle = 4x = 4 × 10° = 40°
2nd angle = 5x = 4 × 10° = 50°
6. Two supplementary angles are in the ratio of 5 : 13, find the angles.
Solution:
Ratio of two supplementary angles = 5 : 13
Let 5x and 13x are two supplementary angles
Since their sum = 180°
∴ 5x + 13x = 180°
18x = 180°
x = \(\frac{180^{\circ}}{18}\) = 10°
∴ 1st angle = 5x = 5 × 10° = 50°.
2nd angle = 13x = 13 × 10° = 130°
![]()
7. Find the angle which is equal to its complement.
Solution:
Let the angle be = x
Therefore its complement = 90° – x
Since the angle is equal to its complement
∴ x = 90° – x
or x + x = 90°
or 2x = 90°
or x = \(\frac{90^{\circ}}{2}\)
or x = 45°
Therefore the required angle is 45°.
8. Find the angle which is equal to its supplement.
Solution:
Let the angle be x
Therefore its supplement = 180° – x
Since the angle is equal to its supplement
∴ x = 180° – x
or x + x = 180°
or 2x = 180°
or x = \(\frac{180^{\circ}}{2}\) = 90°
Therefore, the required angle is 90°.
9. In the given figure, AOB is straight line. Find the measure of ∠AOC.
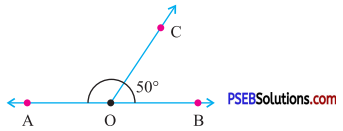
Solution:
In the given figure AOB is straight line (see Fig.)
∴ ∠AOB = 180°
∴ ∠AOC + ∠BOC = 180°
or ∠AOC + 50° = 180°
[∵ ∠BOC = 50° (given)]
∴∠AOC = 180° – 50°
= 130°
![]()
10. In the given figure, MON is straight line find.
(i) ∠MOP
(ii) ∠NOP
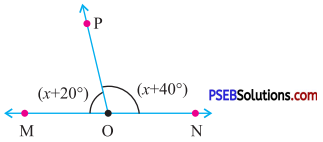
Solution:
Since MON is straight line (see Fig.)
∴ ∠MON = 180°
∴ ∠MOP + ∠NOP = 180°
[∵ ∠MOP = x + 20°
∠NOP = x + 40°]
or 2x + 60° = 180°
or 2x = 180° – 60°
or 2x = 120°
or x = \(\frac{120^{\circ}}{2}\) = 60°.
(i) ∠MOP = x + 20°
= 60° + 20°
= 80°
(ii) ∠NOP = x + 40°
= 60° + 40°
= 100°
11. Find the value of x, y and z in each of following.
Question (i).
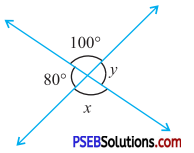
Solution:
In fig (i)
x = 100°
(Vertically opposite angles)
y = 80°
(Vertically opposite angles)
Question (ii).
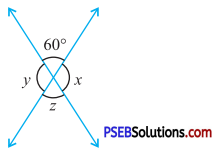
Solution:
In fig (ii)
z = 60°
(Vertically opposite angles)
∠y + 60° = 180° (Linear pair)
or ∠y = 180° – 60°
or ∠y = 120°
x = y
(Vertically opposite angles)
= 120°
![]()
12. Find the value of x, y, z and p in each of following.
Question (i).
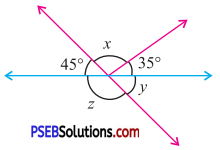
Solution:
In fig (i)
45° + x + 35°= 180° (Linear pair)
or x + 80° = 180°
or x = 180° – 80°
or x = 100°
y = 45° (Vertically opposite angles)
Also 45° + z = 180° (Linear pair)
z = 180° – 45°
= 135°.
Hence x = 100°,
y = 45°,
z = 135°
Question (ii).
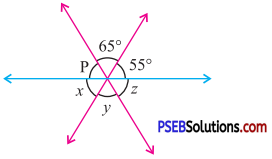
Solution:
In fig (ii)
p + 65° + 55° = 180° (Linear pair)
p + 120°= 180°
∴ p = 180° -120°
i. e. p = 60°
x = 55°
(Vertically opposite angles)
y = 65°
(Vertically opposite angles)
z = p
= 60°
(Vertically opposite angles)
Hence x = 55°,
y = 65°,
z = 60°,
p = 60°
![]()
13. Multiple Choice Questions :
Question (i).
If two angles are complementary then the sum of their measure is …………..
(a) 180°
(b) 90°
(c) 360°
(d) None of these.
Answer:
(b) 90°
Question (ii).
Two angles are called ………….. if the sum of their measures is 180°.
(a) supplementary
(b) complementary
(c) right
(d) none of these.
Answer:
(a) supplementary
Question (iii).
If two adjacent angles are supplementary then, they form a …………..
(a) right angle
(b) vertically opposite angles
(c) linear pair
(d) corresponding angles.
Answer:
(c) linear pair
Question (iv).
If two lines intersect at a point, the vertically opposite angles are always …………..
(a) equal
(b) zero
(c) 90°
(d) none of these.
Answer:
(a) equal