Punjab State Board PSEB 9th Class Science Book Solutions Chapter 11 Work, Energy and Power Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Science Chapter 11 Work, Energy and Power
PSEB 9th Class Science Guide Work, Energy and Power Textbook Questions and Answers
Question 1.
Look at the activities listed below. Reason out whether or not work is done in the light of your understanding of the term ‘work’.
- Suma is swimming in a pond.
- A donkey is carrying a load on its back.
- A wind-mill is lifting water from a well.
- A green plant is carrying out photosynthesis.
- An engine is pulling a train.
- Food grains are getting dried in the sun.
- A sail boat is moving due to wind energy.
Answer:
- Suma while swimming is applying her muscular force in a particular direction and gets displaced. Therefore, work is being done by Suma.
- The load being carried by donkey is acting in the downward direction perpendicular to the horizontal direction of displacement. And when the force acts perpendicular to the direction of displacement then no work is done. Therefore, donkey is not doing any work.
- Work is being done because in lifting water, the displacement, as well as force, are in vertically upward direction.
- A green plant carrying photosynthesis does no work since neither there is force applied nor any displacement in direction of force applied.
- An engine pulling a train is doing work since displacement is in direction of force applied.
- No work is done on food grain. However part of heat suplied coverts moisture of grains into steam which rises up increasing P.E.
- Work is being done since force and displacement is there in the same direction.
![]()
Question 2.
An object thrown at a certain angle to the ground moves in a curved path and falls back to the ground. The initial and final points of the path of object lie on the same horizontal line. What is the work done by the force of gravity on the object?
Answer:
The work done by the force of gravity will be zero. This is because the displacement is in a horizontal direction while the force is acting vertically downward perpendicular to this direction of displacement.
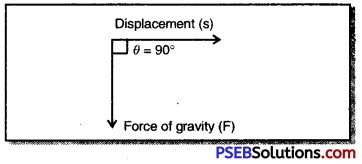
In this situation θ = 90°
∴ cos θ = cos 90° = 0
Now work done (W) = F cos θ × S
= F × 0 × S
W = 0
Question 3.
A battery lights a bulb. Describe the energy changes involved in the process.
Answer:
Chemical energy of the chemicals in the battery is first being converted to electric energy. Then the electric energy of the battery is converted into heat energy and light energy by the bulb.
![]()
Question 4.
Certain force acting on a 20 kg mass changes its velocity from 5 m s-1 to 2 ms-1. Calculate the work done by the force.
Solution:
Here mass (m) = 20 kg
Initial velocity (u) = 5ms-1
Final velocity (v) = 2ms-1
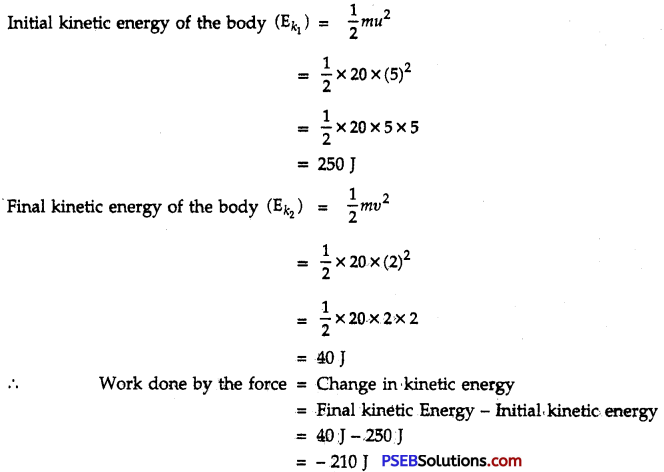
∴ Negative sign shows that there is decrease in velocity due to opposing force which is doing work.
Question 5.
A mass of 10 kg is at a point Aon atable. It is moved to a point B. If line joining A and B is horizontal, what is die work done on fee object by gravitational force ? Explain your answer.
Solution:
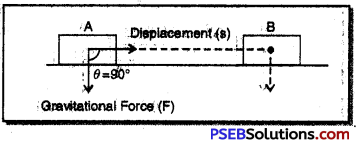
An object of mass 10 kg is displaced in the horizontal direction from point A to point B but the gravitational force is acting vertically downward which makes an angle of 90° with the direction of displacement.
∴ Work done by the gravitational force (W) = F cos θ × S
= F cos 90° × S
= F × 0 × S
= 0
Question 6.
The potential energy of a freely falling object decreases progressively. Does this Violate the law of conservation of energy? Why?
Answer:
- It does not violate the law of conservation of energy. When the height of freely falling body decreases, its potential energy decreases but kinetic energy increases.
- Kinetic energy increases by the same amount as potential energy has decreased.
- At any time the sum of kinetic energy and potential energy remains conserved.
Question 7.
What are the various energy transformations that occur when you are riding a bicycle ?
Answer:
When we are riding a bicycle and pedalling it, the energy of our muscles gets transformed into heat energy and kinetic energy. This kinetic energy is used in doing work against the frictional energy offered by the road.
![]()
Question 8.
Does the transfer of energy takes place when you push a huge rock with all your might and fail to move it ? Where is the energy you spent going?
Answer:
Although you have not been able to move the heavy rock, you are very much tired and this has reduced your energy. Since we have failed to move the heavy rock, work appears to be zero.
While pushing the stone, you had to stretch your muscles, heart had to pump more blood and in making these changes, your energy is definitely lost. The work done by you on your body is not zero. You may have to eat some food to compensate for the work done by your muscles and heart.
Question 9.
A certain household has consumed 250 units of electric energy during a month. How much energy is this in joules ?
Solution:
We know, 1 unit of energy = 1 kilowatt hour (1 kWh)
= 1 kW × 1 h
= (1 × 1000 watt) × (1 × 60 × 60 s)
= 36 × 105 J
= 3.6 × 106 J
∴ 250 units of energy = 250 × 3.6 × 106 J
= 900 × 106 J
= 9 × 108 J
Question 10.
An object of mass 40 kg is raised to a height of 5 m above the ground. What is its potential energy ? If the object is allowed to fall, find its kinetic energy when it is half-way down. Take g – 10 ms “2.
Solution:
Here mass of the object (m) = 40 kg
Height above the ground (h) = 5m
Acceleration due to gravity (g) = 10 ms-2
Potential energy of the object at a height of 5 m (Ep) = m × g × h
= 40 × 10 × 5 J
= 2000 J
Let υ be the velocity of the object when it has come halfway down
Distance moved by the object (S) = \(\frac {5}{2}\) = 2.5 m
using υ2 – u2 = 2gS
υ2 – (0)2 = 2 × 10 × 2.5
υ2 = 2 × 25
or υ2 = 50
Kinetic energy of the object on reaching half way down (Ek) = \(\frac {1}{2}\)mυ2
= \(\frac {1}{2}\) × 40 × 50
= 1000 J
Question 11.
What is the work done by the force of gravity on a satellite moving round the earth ? Justify your answer.
Answer:
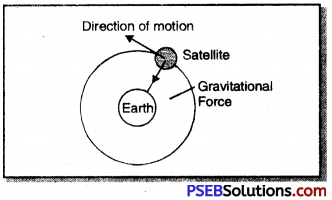
When a satellite moves around the earth the force of gravity is directed inward along the radius of the circular path while the direction of motion is along the tangent which is perpendicular to the radius. In this way force of gravity and displacement are mutually at right angle to each other as a result of which the work done on the satellite is zero.
We know, work done (W) = F cos θ × S
= F cos 90° × S
= F × 0 × S
= 0
![]()
Question 12.
Can there be a displacement of any object in the absence of any external force ?
Answer:
In the absence of any external force the displacement of the object is possible if the object is moving with a uniform velocity. And if the object is in the state of rest then the displacement is not possible in the absence of external force.
Question 13.
A person holds a bundle of hay over his head for 30 minutes and gets tired. Has he done some work or not ? Justify your answer.
Answer:
A person holds a bundle of hay over his head for 30 minutes and gets tired but the force of gravity acting on the bundle does not displace the bundle of hay in the direction of force of gravity. Since there is no displacement in the direction of force, therefore, no work is said to be done by him.
Question 14.
An electric heater is rated 1500 W. How much energy does it use in 10 hours ?
Solution:
Given, Power of the heater (P) = 1500 W
Time for which heater is used (t) = 10 hr
Energy used by the heater in 10 hours (E) = ?
We know, energy used = Power × Time
= 1500 Watt × 10 hrs
= 1500 Wh
= \(\frac {1500}{1000}\)k Wh
= 15kWh
= 15 units
Question 15.
Illustrate the law of conservation of energy by discussing the energy changes which occur when we draw a pendulum bob to one side and allow it to oscillate. Why does the bob eventually come to rest ? What happens to its energy eventually? Is it a violation of the law of conservation of energy?
Answer:
Energy transformation in oscilated pendulum:
Initially bob is at rest at its mean position, thus in kinetic energy is zero. We can consider its potential energy equal to zero in this position.
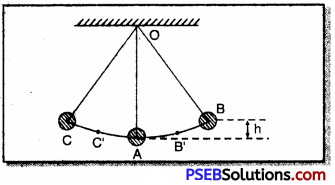
When we take the bob of the pendulum to one side its height goes on increasing and we have to do some work against the force of gravity. This work is stored in the bob as its potential energy. Thus, when a bob is released from one of its extreme position, i.e. state of maximum displacement B at this position its kinetic energy is zero and potential energy is maximum.
Now, the bob is in motion and is moving towards its mean position A its height goes on decreasing that means its potential energy also goes on decreasing whereas its velocity goes on increasing and hence, its kinetic energy increases. Because bob is moving through the air, thus, some energy is consumed, against the force of friction due to air. This causes increase in speed of molecules of air and thus, kinetic energy of the molecules increase.
At the mean position, kinetic energy of the bob becomes maximum and potential energy becomes minimum. Due to inertia of motion bob does not stop here but it moves to the other side of its mean position. Its height again starts increasing so that potential energy also increases, but kinetic energy continues to decrease. When bob reaches at the extreme position ‘O’ its potential energy becomes maximum and kinetic energy becomes zero.
Bob does not stop here it comes back towards its mean position ‘A’. At every point of its motion, sum of kinetic energy and potential energy of the bob along with energy of air molecules remains constant. Thus, during oscillation of the bob of a simple pendulum total energy remains conserved.
Amplitude of the simple pendulum depends on the total energy of the bob. The energy transfered to the molecules of the air by the oscillating bob can never be recovered. Thus total energy of the bob goes on decreasing. When, the bob transfers whole of its energy to the molecules of the air then its total energy becomes zero and it comes to rest at its mean position. Thus there is no violation of the law of conservation of energy.
![]()
Question 16.
An object of mass ‘m’ is moving with velocity V. How much work should be done on the object in order to bring the object at rest?
Solution:
Let an object of mass m be initially moving with velocity υ and finally be brought to rest by the application of an opposing force F after covering a distance S.
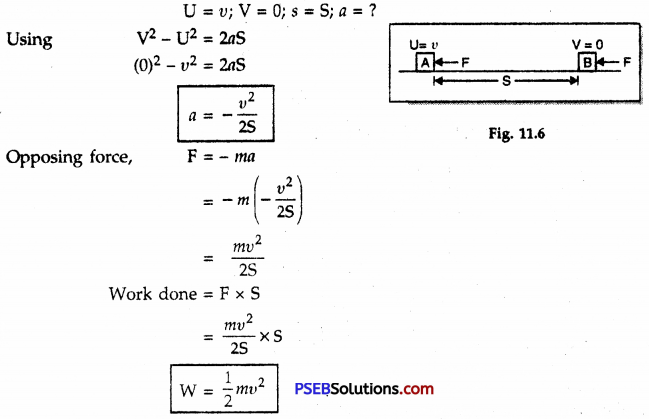
Question 17.
Calculate the work required to be done to stop a car of 1500 kg moving at a velocity of 60 km h-1.
Solution:

Question 18.
In each of the following force F is acting on an object of mass m. The direction of displacement is from west to east shown by the longer arrow. Observe the diagram carefully and state whether the work done by the force in negative, positive or zero
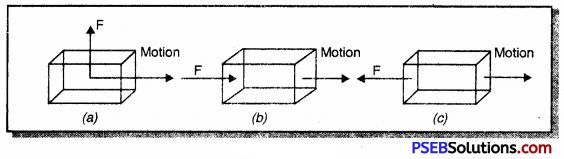
Answer:
- In Fig. (a) displacement is in a direction perpendicular to direction of force applied, therefore work done is zero. There is no displacement in direction of force.
- In Fig. (b), the work done is positive since force and displacement are in the same direction.
- In Fig. (c), the work done is negative since displacement is in a direction opposite to direction of force.
Question 19.
Soni says that acceleration in an object could be zero even when several forces are acting on it. Do you agree with her? Why?
Answer:
Yes, acceleration can be zero when a large number of forces are acting on a body and their resultant is zero.
We kno w, a = \(\frac{\text { F }}{\text { m }}\)
= \(\frac{\text { 0 }}{\text { m }}\)
∴ a = 0
Illustration:
- If two equal and opposite forces are acting on an object, acceleration of the object is zero.
- If three forces are simultaneously acting on an object and can be represented in magnitude and direction by three sides of the triangle in the same order, the body is in equilibrium and will have zero acceleration even when three forces are acting on it.
- Even with more than 3 forces acting on a body, it could have zero acceleration if the resultant of all force is zero.
![]()
Question 20.
Find the energy in kWh consumed in 10 hours by four devices of power 500 W each.
Solution:
Power of 1 device = 500 W
Total power of 4 devices = 4 × 500 W = 2000 W
Time for which 4 devices used (t) = 10 hrs
Energy consumed in 10 hours = Power × Time
= P × t
= 2000W × 10 h
= 20000 Wh
= \(\frac {20000}{1000}\)kWh
= 20 kWh
Question 21.
A freely falling object eventually stops on reaching the ground. What happens to its kinetic energy?
Answer:
A freely falling body on reaching the ground finally stops. Its kinetic energy gets transformed into other forms of energy such as heat, sound and light etc. and then into its potential energy.
Science Guide for Class 9 PSEB Work, Energy and Power InText Questions and Answers
Question 1.
A force of 7 N acts on an object. The displacement is, say 8 m in the direction of the force. Let us take it that the force acts on the object through displacement. What is the work done in this case?
Answer:
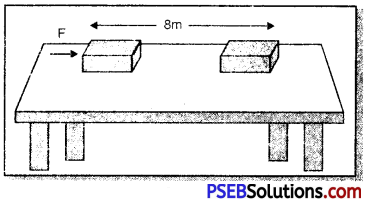
Here force (F) = 7 N
Displacement (S) = 8m
∴ Work done (W) = ?
We know, W = F × S
= 7N × 8m
= 56N – m
= 56 J
![]()
Question 2.
Write an expression for the work done when a force is acting on an object in the direction of its displacment.
Answer:
When the displacement of the object is in the direction of force then,
Work done (W) = Force (F) × Displacement (S)
Question 3.
Define 1 J of work.
Answer:
Joule. Work done on the body is said to be 1 J if IN of the force acting on it displaces the body in its own direction through a distance of 1 m.
We know, W = F × S
or 1 J = 1 N × 1 m
= 1N – m
Question 4.
A pair of bullocks exerts a force of 140 N on a plough. The field being ploughed is 15 m long. How much work is done in ploughing the length of the field ?
Solution:
Force exerted by bullocks (F) = 140 N
Length of the field ploughed (S) = 15 m
Work done in ploughing the field (W) = ?
We know, W = F × S
W = 140 N × 15 m
= 2100 N – m
= 2100 J
Question 5.
What is kinetic energy of an object?
Answer:
Kinetic Energy: Kinetic energy of an object is the quantity of motion possessed by it.
Kinetic energy of an object of mass ‘m moving with velocity υ is = \(\frac {1}{2}\) mυ2
S.I. unit of kinetic energy is Joule
Examples:
- Stone in motion
- Blowing wind
- Rotating wheel
![]()
Question 6.
Write an expression for the kinetic energy of an object.
Answer:
Kinetic energy of an object of mass ‘m’ moving with velocity ‘υ’ is
Ek = \(\frac {1}{2}\) × mass × (velocity)2
= \(\frac {1}{2}\) × m × (υ )2
= \(\frac {1}{2}\)mυ2
∴ Expression for kinetic energy (Ek) = \(\frac {1}{2}\)mυ2
Question 7.
The kinetic energy of an object of mass’m’ moving with a velocity of 5 ms-1 is 25 J. What will be its kinetic energy when its velocity is doubled ? What will be its kinetic energy when its velocity is increased to three times.
Solution:
Given, Mass of an object = m
Velocity of the object (v) = 5 ms-1
Kinetic energy of the object (Efc) = 25 J
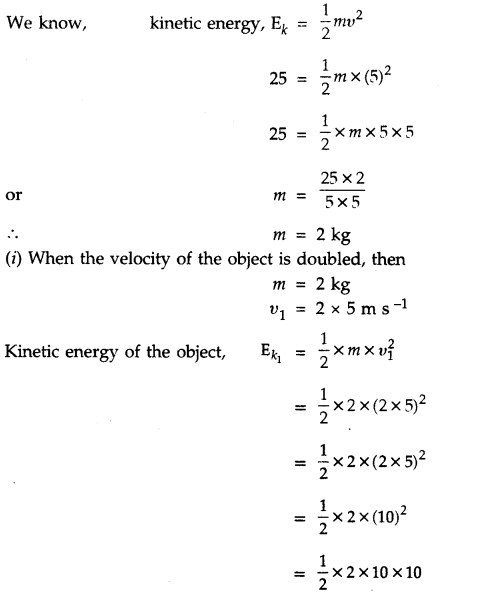
= 100 J
= 4 × 25 J
∴ \(\mathbf{E}_{k_{1}}\) = 4 × Ek
∴ When velocity is doubled, the kinetic energy of the object (\(\mathbf{E}_{k_{1}}\)) becomes four times the first kinetic energy
(ii) When the velocity of the object is made three times the original velocity, then
υ2 = 3 × υ
= 3 × 5m s-1
= 15m s-1
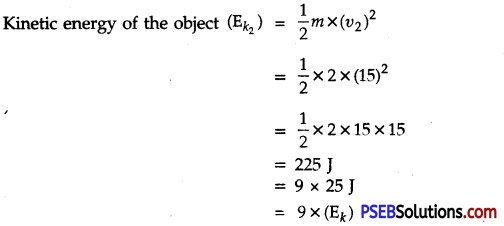
i.e. on increasing the velocity to three times the original velocity, its kinetic energy ( \(\mathbf{E}_{k_{2}}\)) becomes nine times the first kinetic energy (Ek).
![]()
Question 8.
What is Power ?
Answer:
Power: The rate of doing work or the rate of transformation of energy is called power. Its S.I. unit is watt (W) or Joule/sec (J s-1)
If an agent does work /W’ in time ‘t’ then
Power = \(\frac{\text { Work done }}{\text { Time taken to do work }}\)
or P = \(\frac{\text { W }}{\text { t }}\)
Question 9.
Define 1 watt of Power.
Answer:
Watt. It is the power of that agent or machine which can work at the rate of 1 Joule in 1 second.
Question 10.
A lamp consumes 1,000 J of electric energy in 10 s. What is its power ?
Solution:
Here, W = 1000 J
Time (t) = 10 s
Power (P) = ?
We know Power (P) = \(\frac{\text { E }}{\text { t }}\)
= \(\frac{1000 \mathrm{~J}}{10 \mathrm{~s}}\)
= 100 J s-1
∴ p = 100 W
Question 11.
Define Average Power.
Answer:
Average Power: It is defined as the ratio of total energy consumed to the total time taken.
∴ Average Power (Pav) = \(\frac{\text { Total energy consumed }}{\text { Total time taken }}\)