Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 9 Rational Numbers Ex 9.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 9 Rational Numbers Ex 9.2
1. Find the sum
Question (i).
\(\frac{6}{9}+\frac{2}{9}\)
Solution:
\(\frac{6}{9}+\frac{2}{9}\) = \(\frac{6+2}{9}\)
= \(\frac {8}{9}\)
Question (ii).
\(\frac{-15}{7}+\frac{9}{7}\)
Solution:
\(\frac{-15}{7}+\frac{9}{7}\) = \(\frac{-15+9}{7}\)
= \(\frac{-6}{7}\)
Question (iii).
\(\frac{17}{11}+\left(\frac{-9}{11}\right)\)
Solution:
\(\frac{17}{11}+\left(\frac{-9}{11}\right)\) = \(\frac{17-9}{11}\)
= \(\frac{8}{11}\)
Question (iv).
\(\frac{-5}{6}+\frac{3}{18}\)
Solution:
\(\frac{-5}{6}+\frac{3}{18}\)
Now, \(\frac{-5}{6}=\frac{-5}{6} \times \frac{3}{3}=\frac{-15}{18}\)

L.C.M. of 6 and 18
= 2 × 3 × 3 = 18
Thus, \(\frac{-5}{6}+\frac{3}{18}=\frac{-15}{18}+\frac{3}{18}\)
= \(\frac{-15+3}{18}\)
= \(\frac {-12}{18}\)
= \(\frac {-2}{3}\)
![]()
Question (v).
\(\frac{-7}{19}+\frac{-3}{38}\)
Solution:
\(\frac{-7}{19}+\frac{-3}{38}\)
Now, \(\frac{-7}{19}=\frac{-7}{19} \times \frac{2}{2}\)
= \(\frac {-14}{38}\)
\(\begin{array}{l|l}
2 & 19,38 \\
\hline 19 & 19,19 \\
\hline & 1,1 \\
\hline
\end{array}\)
L.C.M. = 2 × 19
= 38
Thus, \(\frac{-7}{19}+\frac{-3}{38}=\frac{-14}{38}+\frac{-3}{38}\)
= \(\frac{-14-3}{38}\)
= \(\frac{-17}{38}\)
Question (vi).
\(-3 \frac{4}{7}+2 \frac{3}{7}\)
Solution:
\(-3 \frac{4}{7}+2 \frac{3}{7}\)
= \(-\frac{25}{7}+\frac{17}{7}\)
= \(\frac{-25+17}{7}\)
= \(\frac{-8}{7}\)
Question (vii).
\(\frac{-5}{14}+\frac{8}{21}\)
Solution:
\(\frac{-5}{14}+\frac{8}{21}\)
Now, \(\frac{-5}{14}=\frac{-5}{14} \times \frac{3}{3}\)
= \(\frac{-15}{42}\)
\(\begin{array}{l|l}
2 & 14,21 \\
\hline 3 & 7,21 \\
\hline 7 & 7,7 \\
\hline & 1,1
\end{array}\)
L.C.M of 14, 21 = 2 × 3 × 7
= 42
\(\frac{8}{21}=\frac{8}{21} \times \frac{2}{2}\)
= \(\frac{16}{42}\)
Thus, \(\frac{-5}{14}+\frac{8}{21}\)
= \(\frac{-15}{42}+\frac{16}{42}\)
= \(\frac{-15+16}{42}\)
= \(\frac{1}{42}\)
Question (viii).
\(-4 \frac{1}{15}+3 \frac{2}{20}\)
Solution:

![]()
2. Find
Question (i).
\(\frac{7}{12}-\frac{11}{36}\)
Solution:
\(\frac{7}{12}-\frac{11}{36}\) = \(\frac{7}{12}\) + (Additive inverse of \(\frac{11}{36}\))
= \(\frac{7}{12}+\left(\frac{-11}{36}\right)\)
= \(\frac{21+(-11)}{36}\)
\(\begin{array}{l|l}
2 & 12,36 \\
\hline 2 & 6,18 \\
\hline 3 & 3,9 \\
\hline 3 & 1,3 \\
\hline & 1,1
\end{array}\)
L.C.M of 12 and 36
= 2 × 2 × 3 × 3
= 36
= \(\frac{10}{36}=\frac{5}{18}\)
Question (ii).
\(\frac{-5}{9}-\frac{3}{5}\)
Solution:
\(\frac{-5}{9}-\frac{3}{5}\) = \(\frac {-5}{9}\) + (additive inverse of \(\frac {3}{5}\))
= \(\frac{-5}{9}+\left(\frac{-3}{5}\right)\)
= \(\frac{-25+(-27)}{45}\)
L.C.M of 9 and 5 is 45 = \(\frac {-52}{45}\)
Question (iii).
\(\frac{-7}{13}-\left(\frac{-5}{91}\right)\)
Solution:
\(\frac{-7}{13}-\left(\frac{-5}{91}\right)\) = \(\frac {-7}{13}\) + (additive inverse of \(\frac {-5}{91}\))
= \(\frac{-7}{13}+\left(\frac{5}{91}\right)\)
= \(\frac{-49+(5)}{91}\)
L.C.M of 13 and 91 = 7 × 13 = 91
\(\begin{array}{l|l}
7 & 13,91 \\
\hline 13 & 13,13 \\
\hline & 1,1
\end{array}\)
= \(\frac {-44}{91}\)
![]()
Question (iv).
\(\frac{6}{11}-\frac{-3}{4}\)
Solution:
\(\frac{6}{11}-\frac{-3}{4}\) = \(\frac {6}{11}\) + (additive inverse of \(\frac {-3}{4}\))
= \(\frac{6}{11}+\left(\frac{3}{4}\right)\)
= \(\frac{24+33}{44}\)
L.C.M of 11 and 4 is 44 = \(\frac {57}{44}\)
Question (v).
\(3 \frac{4}{9}-\frac{28}{63}\)
Solution:
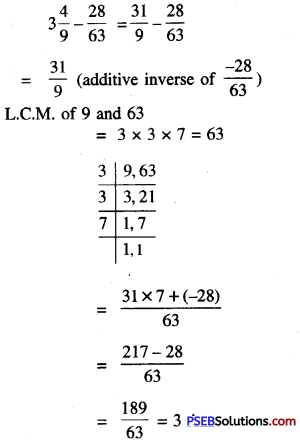
3. Find the product of :
Question (i).
\(\frac{5}{9} \times \frac{-3}{8}\)
Solution:
\(\frac{5}{9} \times \frac{-3}{8}\)
= \(\frac{5 \times-3}{9 \times 8}\)
= \(\frac {-5}{24}\)
Question (ii).
\(\frac{-3}{7} \times \frac{7}{-3}\)
Solution:
\(\frac{-3}{7} \times \frac{7}{-3}\)
= \(\frac{-3 \times 7}{7 \times-3}\)
= 1
![]()
Question (iii).
\(\frac{3}{13} \times \frac{5}{8}\)
Solution:
\(\frac{3}{13} \times \frac{5}{8}\)
= \(\frac{3 \times 5}{13 \times 8}\)
= \(\frac {15}{104}\)
Question (iv).
\(\frac {3}{10}\) × (-18)
Solution:
\(\frac {3}{10}\) × (-18)
= \(\frac{3 \times-18}{10}\)
= \(\frac{-27}{5}\)
4. Find the value of:
Question (i).
-9 ÷ \(\frac {3}{5}\)
Solution:
-9 ÷ \(\frac {3}{5}\)
= -9 × (Reciprocal of \(\frac {3}{5}\))
= -9 × \(\frac {5}{3}\)
= -15
Question (ii).
\(\frac {-4}{7}\) ÷ 4
Solution:
\(\frac {-4}{7}\) ÷ 4
= \(\frac {-4}{7}\) × (Reciprocal of 4)
= \(\frac{-4}{7} \times \frac{1}{4}\)
= \(\frac {-1}{7}\)
![]()
Question (iii).
\(\frac{7}{18} \div \frac{5}{6}\)
Solution:
\(\frac{7}{18} \div \frac{5}{6}\)
= \(\frac {7}{18}\) × (Reciprocal of \(\frac {5}{6}\))
= \(\frac{7}{18} \times \frac{6}{5}\)
= \(\frac {7}{15}\)
Question (iv).
\(\frac{-8}{35} \div\left(\frac{-2}{7}\right)\)
Solution:
\(\frac{-8}{35} \div\left(\frac{-2}{7}\right)\)
= \(\frac {-8}{35}\) × (Reciprocal of \(\frac {-2}{7}\))
= \(\frac{-8}{35} \times \frac{7}{-2}\)
= \(\frac {4}{5}\)
Question (v).
\(\frac {-9}{15}\) ÷ -18
Solution:
\(\frac {-9}{15}\) ÷ -18
= \(\frac {-9}{15}\) × (Reciprocal of -18)
= \(\frac{-9}{15} \times \frac{1}{-18}\)
= \(\frac {1}{30}\)
5. What ratonal number should be added to \(\frac {-5}{12}\) to get \(\frac {-7}{8}\)?
Solution:
Let the required number to be added be x.
then, \(\frac {-5}{12}\) + x = \(\frac {-7}{8}\)

L.C.M of 8, 12 = 2 × 2 × 2 × 3
= 24
= \(\frac{-7 \times 3+5 \times 2}{24}\)
= \(\frac{-21+10}{24}\)
= \(\frac {-11}{24}\)
![]()
6. What number should be subtracted from \(\frac {-2}{3}\) to get \(\frac {-5}{6}\) ?
Solution:
Let the required number to be subtracted be x, then
\(\frac{-2}{3}-x=\frac{-5}{6}\)
⇒ \(\frac{-2}{3}-\left(\frac{-5}{6}\right)\) = x
x = \(\frac{-2}{3}+\frac{5}{6}\)
= \(\frac{-4+5}{6}\)
= \(\frac {1}{6}\)
7. The product of two rational numbers is \(\frac {-11}{2}\). If one of them is \(\frac {33}{8}\), find the other number.
Solution:
Let the required number be x, then
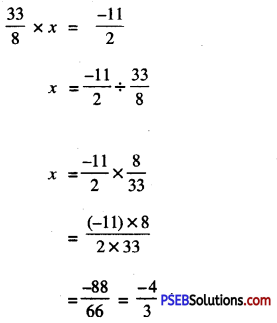
8. Multiple Choice Questions
Question (i).
The sum of \(\frac{5}{4}+\left(\frac{25}{-4}\right)\) =
(a) -5
(b) 5
(c) 4
(d) -4
Answer:
(a) -5
Question (ii).
\(\frac{17}{11}-\frac{6}{11}\) =
(a) 1
(b) -1
(c) 6
(d) 3
Answer:
(a) 1
![]()
Question (iii).
\(\frac{2}{-5} \times \frac{-5}{2}\) =
(a) 1
(b) -1
(c) 2
(d) -5
Answer:
(a) 1
Question (iv).
\(\frac{7}{12} \div\left(\frac{-7}{12}\right)\) =
(a) 1
(b) -1
(c) 7
(d) -7
Answer:
(b) -1
Question (v).
Which of the following is value of (-4) × [(-5) + (-3)]
(a) -32
(b) 120
(c) 32
(d) -23
Answer:
(c) 32