Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 3 Playing with Numbers Ex 3.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 6 Maths Chapter 3 Playing with Numbers Ex 3.4
1. Find H.C.F. of the following numbers by prime factorisation:
Question (i)
30, 42
Solution:
First we write the prime factorization of the given numbers
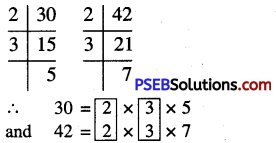
We find that 2 occurs two times and 3 occurs two times as common factors.
∴ HCF of 30 and 42 = 2 × 3 = 6
Question (ii)
135,225
Solution:
First we write the prime factorization of the given number
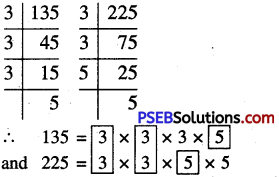
We find that 3 occurs two times and 5 occurs once as common factors
∴ HCF of 135 and 225 = 3 x 3 x 5 = 45
![]()
Question (iii)
180,192
Solution:
First we write the prime factorisation of the given numbers
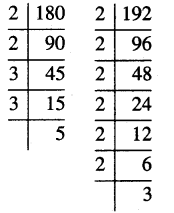
We find that 2 occurs twice and 3 occurs once as common factors
HCF of 180 and 192
= 2 × 2 × 3 = 12
Question (iv)
49,91,175
Solution:
First we write the prime factorization of the given numbers
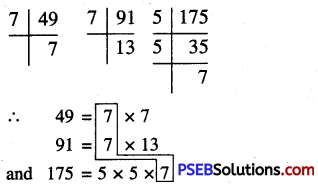
We find that 7 occurs once as a common factor.
∴ HCF of 49, 91 and 175 = 7
Question (v)
144, 252, 630.
Solution:
First we write the prime factorisation of the given numbers

We find that 2 occurs once and 3 occurs twice as common factors.
∴ HCF of 144, 252 and 630
= 2 × 3 × 3 = 18
![]()
2. Find H.C.F. of the following numbers using division method:
Question (i)
170, 238
Solution:
Given numbers are 170 and 238

Hence, H.C.F. of 170 and 238 = 34
Question (ii)
54, 144
Solution:
Given numbers are 54 and 144

Hence, H.C.F. of 54 and 144 = 18
Question (iii)
72, 88
Solution:
Given numbers are 72 and 88.

Hence, H.C.F. of 72 and 88 = 8
![]()
Question (iv)
96, 240, 336
Solution:
Given numbers are 96, 240 and 336 Consider any two numbers say 96 and 240

∴ H.C.F. of 96 and 240 = 48
Now, we find H.C.F. of 48 and 336
∴ H.C.F. of 48 and 336 = 48
Hence, H.C.F. of 96, 240 and 336 = 48
Question (v)
120, 156, 192.
Solution:
Given numbers are 120, 156 and 192 Consider any two numbers say 120 and 156

∴ H.C.F. of 12 and 192 = 12
Hence, H.C.F. of 120, 156 and 192 = 12
3. What is the H.C.F. of two prime numbers?
Solution:
H.C.F. of two prime numbers = 1.
4. What is the H.C.F. of two consecutive even numbers?
Solution:
The H.C.F. of two consecutive even numbers = 2.
![]()
5. What is the H.C.F. of two consecutive natural numbers?
Solution:
H.C.F. of two consecutive natural numbers = 1.
6. What is the H.C.F. of two consecutive odd numbers?
Solution:
H.C.F. of two conseutive odd numbers = 1.
7. Find the greatest number which divides 245 and 1029, leaving a remainder 5 in each case.
Solution:
Given that, required number when divides 245 and 1029, the remainder is 5 in each case.
⇒ 245 – 5 = 240 and 1029 – 5 = 1024 are completely divisible by the required number.
⇒ Required number is the highest common factor of 240 and 1024. Since it is given that required number is the greatest number.
∴ Required number is the H.C.F. 240 and 1024.

Hence, required number (H.C.F.) of 240 and 1024 = 16
8. Find the greatest number that can divide 782 and 460 leaving remainder 2 and 5 respectively.
Solution:
Required greatest number = H.C.F. of (782 – 2) and (460 – 5)
= H.C.F. of 780 and 455 = 65

Hence required greatest number = 65
![]()
9. Find the greatest number that will divide 398,437 and 540 leaving remainders 7,12 and 13 respectively.
Solution:
Required greatest number = H.C.F. of (398 – 7), (437 – 12) and (540 – 13)
= H.C.F. of 391, 425 and 527
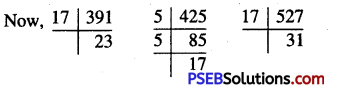
∴ 391 = 17 × 23
425 = 5 × 5 × 17
and 527 = 17 × 31
∴ H.C.F. = 17
Hence, required greatest number = 17
10. Two different containers contain 529 litres and 667 litres of milk respectively. Find the maximum capacity of container which can measure the milk of both containers in exact number of times.
Solution:
We have to find, maximum capacity of a container which measure both conainers in exact number of times.
⇒ We required the maximum number which divides 529 and 667
⇒ Required number = H.C.F. of 529 and 667 = 23

Hence required capacity of container = 23 litres
11. There are 136 apples, 170 mangoes and 255 oranges. These are to be packed in boxes containing the same number of fruits. Find the greatest number of fruits possible in each box.
Solution:
We have to find the greatest number of fruits in each box ,
So, we required greatest numbers which divides 136, 170 and 255
∴ Required greatest number of fruits possible in each box
= H.C.F. of 136, 170 and 255
Now take any two numbers, say 136 and 170
H.C.F. of 136 and 170 = 34
Now find H.C.F. of 34 and 255
∴ H.C.F. of 34 and 255 = 17
H.C.F. of 136, 170 and 255 = 17
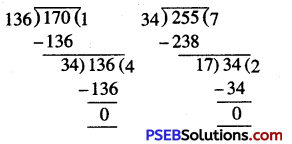
∴ Hence the greatest number of fruits possible in each box = 17
![]()
12. Three pieces of timber 54 m, 36 m and 24 m long, have to be divided into planks of the same length. What is the greatest possible length of each plank?
Solution:
We have to find the greatest possible length of each plank.
So, we required the maximum number which divides 54 m, 36 m and 24 m.
∴ Required length of each plank = H.C.F. of 54 m, 36 m and 24 m
Now, take any two numbers, say 54 and 36
H.C.F. of 54 and 36 = 18
Now find the H.C.F. of 18 and 24
H.C.F. 18 and 24 = 6
H.C.F. 54, 36 and 24 = 6

Hence, the greatest length of each plank = 6m
13. A room Measures 4.8 m and 5.04 m. Find the size of the largest square tile that can be used to tile the floor without cutting any tile.
Solution:
We have to find the size of largest square tile that can be used to the floor without cutting any tile.
∴ Required size of tile = H.C.F. of 4.8 and 5.04 m
= H.C.F. of 480 cm and 504 cm [1 m – 100 cm]
∴ H.C.F. of 480 cm and 504 cm = 24 cm

Hence size of each square tile = 24 cm
![]()
14. Reduce each of the following fractions to lowest forms:
Question (i)
\(\frac {85}{102}\)
Solution:
In order to reduce given fraction to the lowest terms,
We divide numerator and denominator by their H.C.F.
Now we find H.C.F. of 85 and 102 Clearly H.C.F. of 85 and 102 = 17

Question (ii)
\(\frac {52}{130}\)
Solution:
We find H.C.F. of 52 and 130
Clearly H.C.F. of 52 and 130 = 26

![]()
Question (iii)
\(\frac {289}{391}\)
Solution:
We find H.C.F. of 289 and 391
Clearly, H.C.F. of 289 and 391 = 17
