Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 5 Lines and Angles Ex 5.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 5 Lines and Angles Ex 5.2
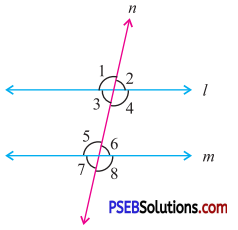
1. In the figure question identify the pair of angles as corresponding angles alternate interior angles, exterior alternate angles, adjacent angles, vertically opposite angles and co-interior angles, linear pair.
(i) ∠3 and ∠6
(ii) ∠3 and ∠7
(iii) ∠2 and ∠4
(iv) ∠2 and ∠7
(v) ∠1 and ∠8
(vi) ∠4 and ∠6
(vii) ∠1 and ∠5
(viii) ∠1 and ∠4
(ix) ∠5 and ∠7
Answer:
(i) Alternate interior angles.
(ii) Corresponding angles.
(iii) Adjacent angles.
(iv) Alternate exterior angles.
(v) Alternate exterior angles.
(vi) Co-interior angles.
(vii) Corresponding angles.
(viii) Vertically opposite angles.
(ix) Linear pair.
2. In the figure identify :
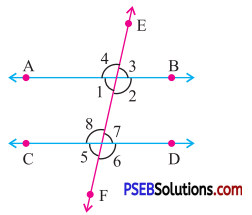
(i) The pairs of corresponding angle.
(ii) The pairs of alternate interior angles.
(iii) The pairs of interior angles on the same side of the transversal.
(iv) The pairs of vertically opposite angles.
Answer:
(i) ∠1 and ∠5, ∠2 and ∠6, ∠3 and ∠7, ∠4 and ∠8.
(ii) ∠1 and ∠7, ∠2 and ∠8.
(iii) ∠1 and ∠8, ∠2 and ∠7.
(iv) ∠1 and ∠3, ∠2 and ∠4, ∠5 and ∠7, ∠6 and ∠8.
![]()
3. In the given figures, the intersected lines are parallel to each other. Find the unknown angles.
Question (i).
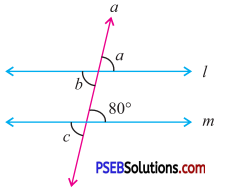
Answer:
l || m and a is a transversal ∠b = 80°
[Alternate interior angles]
∠a = ∠b
[Vertically opposite angles]
∴ ∠a = 80° [∵ ∠b = 80°]
Also ∠c = 80°
[Vertically opposite ∠5]
Hence a = 80°, b = 80°, c = 80°
Question (ii).
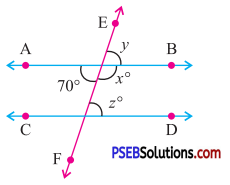
Answer:
∠x° + 70°= 180° (Linear pair)
∠x° = 180° – 70°
∠x° = 110°
∠y° = 70°.
(Vertically opposite angles)
AB || CD and EF is a transversal
∴ ∠z° = 70°
[Alternate interior angles]
Hence x = 110°, y = 70° and z = 70°
Question (iii).
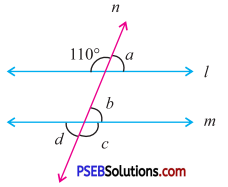
Answer:
110° + a = 180° (Linear pair)
∴ a = 180°- 110° = 70°
b = a
(Corresponding angles)
∴ b = 70°
d = b
(Vertically opposite angles)
∴ d = 70°
b + c = 180° (Linear pair)
70° + c = 180°
∴ c = 180° – 70° = 110°
Hence a = 70°, b = 70°, c = 110°, d = 70°
![]()
Question (iv).
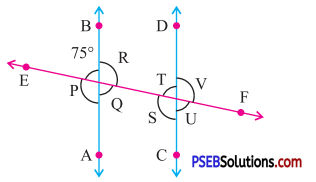
Answer:
P + 75° = 180° (Linear pair)
∴ P = 180° – 75° = 105°
R = P
= 105°
(Vertically opposite angles)
Q =75°
(Vertically opposite angles)
AB || CD and EF is a transversal
S = R
(Alternate interior angles)
∴ S = 105°
T = Q
(Alternate interior angles) = 75°
Now U = T
= 75°
(Vertically opposite angles) V = S
(Vertically opposite angles) = 105°
Hence P = 105°, Q = 75°, R = 105°,
S = 105°, T = 75°, U = 75°, V = 105°
4. Find the value of x in the following figures if l || m
Question (i).
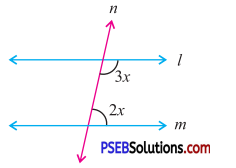
Answer:
l || m and n is a transversal
∴ 2x + 3x = 180°
[The pair of co-interior angles are supplementary]
or 5x = 180°
x = \(\frac{180^{\circ}}{5}\) = 36°
Question (ii).
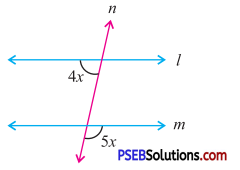
Answer:
a = 5x
(Vertically opposite angles)
Since l || m and n is a transversal
∴ 4x + 5x= 180°
[The pair of co-interior angles are supplementary]
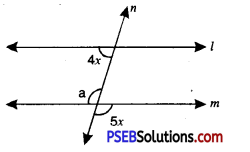
or 9x = 180°
∴ x = \(\frac{180^{\circ}}{9}\) = 20°
![]()
Question (iii).
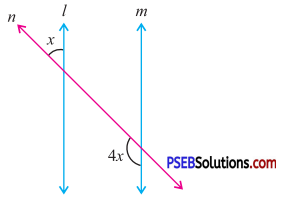
Answer:
a = x
(Vertically opposite angles)
Now l || m and n is a transversal
a + 4x = 180°
[The pair of co-interior angles are supplementary]
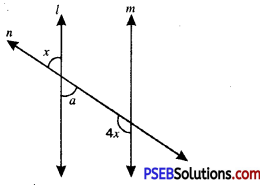
∴ a + 4x = 180°
or x + 4x = 180°
or 5x = 180°
Or x = \(\frac{180^{\circ}}{5}\) = 36°
Question (iv).
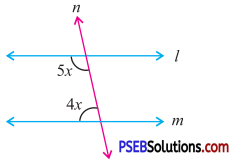
Answer:
Since l || m and n is a transversal
[The pair of co-interior angles are supplementary]
∴ 5x + 4x = 180°
Or 9x = 180°
x = \(\frac{180^{\circ}}{9}\) = 20°
5. In the given figures arms of two angles are parallel find the following.
Question (a).
(i) ∠DGC
(ii) ∠DEF
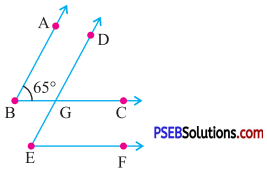
Answer:
(i) AB || DE and BC is a transversal
∴ ∠DGC = ∠ABC
(Corresponding angles)
= 65° (∵ ∠ABC = 65°)
(ii) Since BC || EF and DE is the transversal.
∴ ∠DEF = ∠DGC
(Corresponding angles)
= 65° (∵ ∠DGC = 65°)
![]()
Question (b).
(i) ∠MNP
(ii) ∠RST
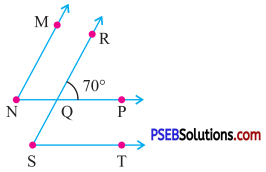
Answer:
(i) Since MN || RS and NP is a transversal
∴ ∠MNP = ∠RQP
(Corresponding angles)
= 70° (∵ ∠RQP = 70°)
(ii) Since NP || ST and RS is a transversal
∴ ∠RST = ∠RQP
(Corresponding angles)
= 70° (∵ ∠RQP = 70°)
6. In the following figure AB || CD and EF || GH, find the measure of ∠x and ∠y.
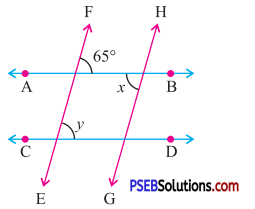
Solution:
Since AB || CD and EF is a transversal
∴ ∠y = 65°
(Corresponding angles)
Since EF || GH and AB is a transversal.
∴ ∠x = 65°
[alternate interior angles]
Therefore ∠x = 65° and ∠y = 65°
7. PQ ⊥ RS find the value of x in the following figure.
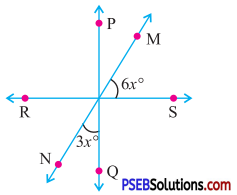
Solution:
Let O be the point of intersection of PQ and RS.
Now PQ and MN intersect each other at O
∴ ∠POM = ∠NOQ
(Vertically opposite angles)
= 3x° (∵ ∠WOQ = 3x°)
Now ∠POS = 90°
∴ ∠POM + ∠MOS = 90°
6x° + 3x° = 90°
9x° = 90°
x = \(\frac{90^{\circ}}{9}\) = 10°
![]()
8. In the given figure below, decide whether l is parallel to m.
Question (i).
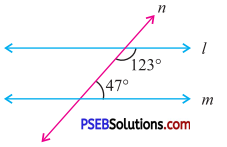
Answer:
Here 123° + 47° = 170°
But the sum of the pair of co-interior angles is 180°
∴ l is not parallel to m.
Question (ii).
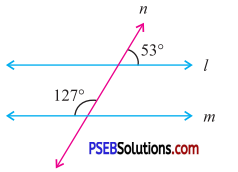
Answer:
Here 127° + 53° = 180°
∴ sum of the pair of co-interior angles is 180°.
Thus l parallel to m.
Question (iii).
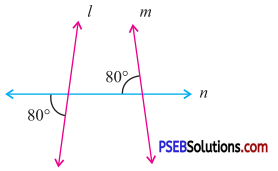
Answer:
Since 80° + 80° = 160°
But the sum of the pairs of co-interior angles is 180°
Therefore l is not parallel to m.
Question (iv).
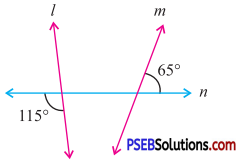
Answer:
115° and 65° are corresponding angles which are not equal.
Therefore l is not parallel to m.
9. Multiple Choice Questions :
Question (i).
A pair of complementary angles is
(a) 130°, 50°
(b) 35°, 55°
(c) 25°, 75°
(d) 27°, 53°
Answer:
(d) 27°, 53°
Question (ii).
A pair of supplementary angles is
(a) 55°, 115°
(b) 65°, 125°
(c) 47°, 133°
(d) 40°, 50°
Answer:
(b) 65°, 125°
![]()
Question (iii).
If one angle of a linear pair is acute, then the other angle is
(a) acute
(b) obtuse
(c) right
(d) straight.
Answer:
(b) obtuse
Question (iv).
In the adjoining figure, if l || m, then the value of x is
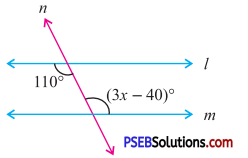
(a) 50°
(b) 60°
(c) 70°
(d) 45°
Answer:
(a) 50°
Question (v).
In the adjoining figure, if l || m, then
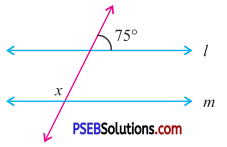
(a) 75°
(b) 95°
(c) 105°
(d) 115°
Answer:
(c) 105°
Question (vi).
In the adjoining figure, the value of x that will make the lines l and m parallel is
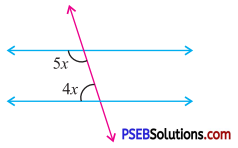
(a) 20
(b) 30
(c) 60
(d) 80
Answer:
(a) 20