Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 10 Practical Geometry Ex 10.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.1
1. Draw a line, l, take a point p outside it. Through p, draw a line parallel to l using ruler and compass only.
Solution:
Steps of Construction :
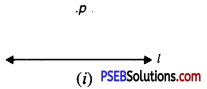
Step 1. Draw a line l of any suitable length Mid a point ‘p’ outside l [see Fig. (i)].
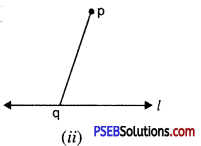
Step 2. Take a point ‘q’ on l and join q to p [see Fig. (ii)].
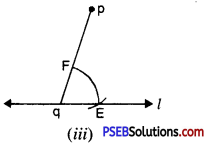
Step 3. With q as centre and a convenient radius, draw an arc cutting l at E and pq at F [see Fig. (iii)].
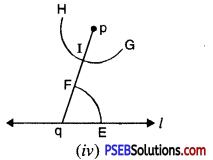
Step 4. Now with p as a centre and the same radius as in step 3, draw an arc GH cutting pq at I [see Fig. (iv)].
Step 5. Place the pointed tip of the compasses at E and adjust the opening so that the pencil tip is at F [see Fig. (v)].
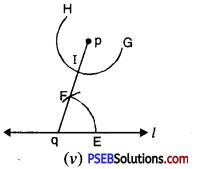
![]()
Step 6. With the same opening as in step 5 and with I as centre, draw an arc cutting the arc GH at J. [see Fig. (vi)].
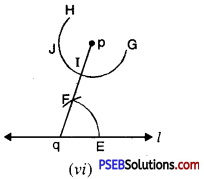
Step 7. Now, join pand J to draw a line ‘m’ [see Fig. (vii)],
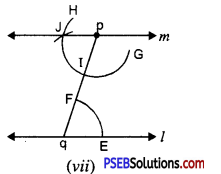
Note that : ∠Jpq and ∠pqE are alternate interior angles and ∠pqE = ∠qpJ
∴ m || l
2. Draw a line parallel to a line l at a distance of 3.5 cm from it.
Solution :
Steps of construction :
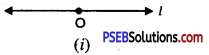
Step 1. Take a line ‘l’ and any point say O on it [see Fig. (i)].
Step 2. At O draw ∠AOB = 90°. [see Fig. (ii)].
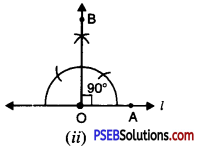
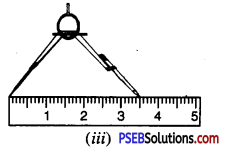
Step 3. Place the pointed tip of the compasses at ‘0’ (zero) mark on ruler and adjust the opening so that the pencil tip is at 3.5 cm [see Fig. (iii)]
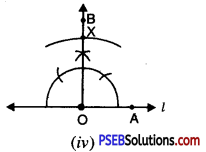
Step 4. With the same opening as in step 3 and with O as centre draw an arc cutting ray OB at X. [see Fig. (iv)].
![]()
Step 5. At X draw a line ‘m’ perpendicular to OB. In other words, draw ∠CXO = 90° [see Fig. (v)].
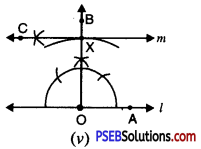
In this way, line m is parallel to l.
Note that. ∠AOX and ∠CXO are alternate angles and ∠AOX = ∠CXO (each = 90°).
∴ m || l.
Note. We may use any of three properties regarding the transversal OX and parallel lines l and m.
3. Let l be a line and P be a point not on l. Through P, draw a line ‘m’ parallel to l. Now, join P to any point Q on l. Choose any other point R on m. Through R, draw a line parallel to PQ. Let this meets l at S. What shape do the two sets of parallel lines enclose ?
Solution:
Steps of Construction :
Step 1. Take a line ‘l’ and a point ‘P’ outside l. [see Fig . (i)]
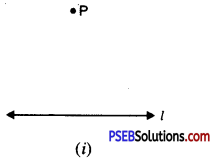
Step 2. Take any point A on l and join P to A [see Fig. (ii)]
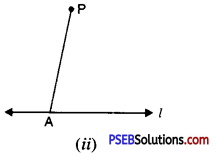
Step 3. With A as centre and convenient radius draw an arc cutting l at B and AP at C. [see Fig. (iii)]
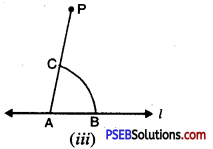
Step 4. Now with P as centre and the same radius as in step 3, draw an arc DE cutting PA at F [see Fig. (iv)].
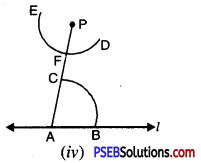
Step 5. Place the pointed tip of the compasses at B and adjust the opening so that the pencil tip is at C [see Fig. (v)].
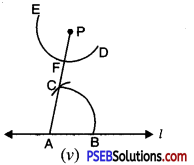
![]()
Step 6. With the same opening as in step 5 and with F as centre, draw an arc cutting the arc DE at G [see Fig. (vi)].
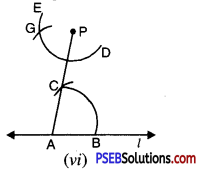
Step 7. Now join PG to draw line ‘m’ [see Fig. (vii)].
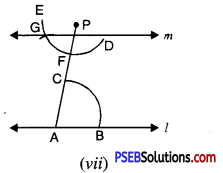
Note that. ∠PAB and ∠APG are alternate interior angles and ∠PAB = ∠APG
∴ m || l
Step 8. Take any point Q on l. Join PQ [see Fig. (viii)].
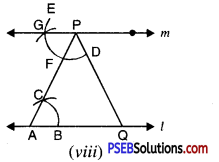
Step 9. Take any other point R on m [see Fig. (ix)].
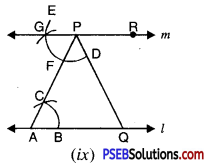
Step 10. With P as centre and convenient radius, draw an arc cutting line m at H and PQ at I [see Fig. (x)].
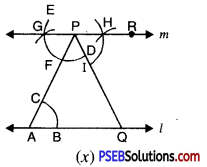
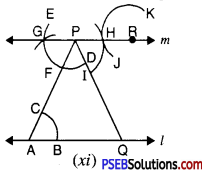
Step 11. Now with R as centre and the same radius as in step 10, draw an arc JK [see Fig. (xi)].
![]()
Step 12. Place the pointed tip of compasses at H and adjust the opening so that the pencil tip is at I.
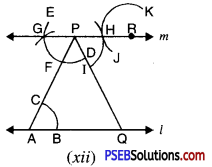
Step 13. With the same opening as in step 12 and with R as centre, draw an arc cutting the arc JK at L [see Fig. (xii)].
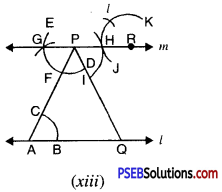
Step 14. Now join RL to draw a line parallel to PQ. Let this meet l at S. [see Fig. (xiv)]
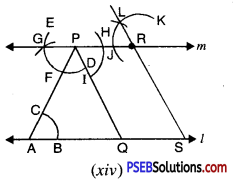
Note that. ∠RPQ and ∠LRP are alternate interior angles
and ∠RPQ = ∠LRP
∴ RS || PQ.
Now we have
PR || QS
[∵ m || l and PR is part of m and QS is part of line l]
and PQ || RS
∴ PQSR is a parallelogram.
![]()
4.
Question (i).
How many parallel lines can be drawn, passing through a point not lying on the given line ?
(a) 0
(b) 2
(c) 1
(d) 3
Answer:
(c) 1
Question (ii).
Which of the following is used to draw a line parallel to a given line ?
(a) A protractor
(b) A ruler
(c) A compasses
(d) A ruler and compasses.
Answer:
(d) A ruler and compasses.