Class 11

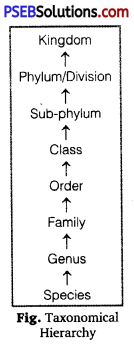
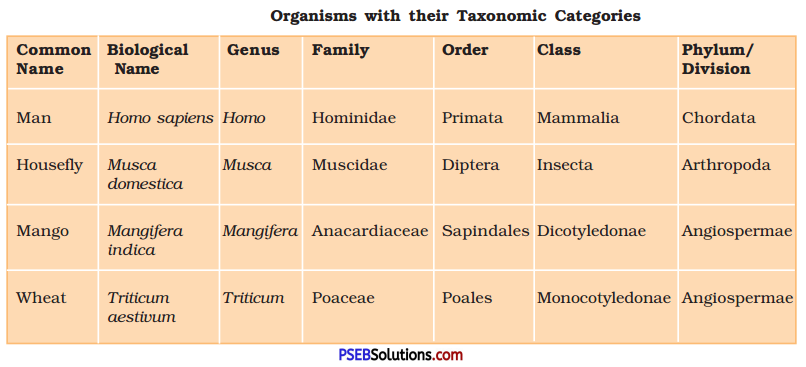
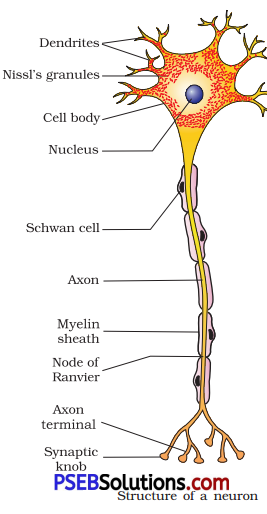
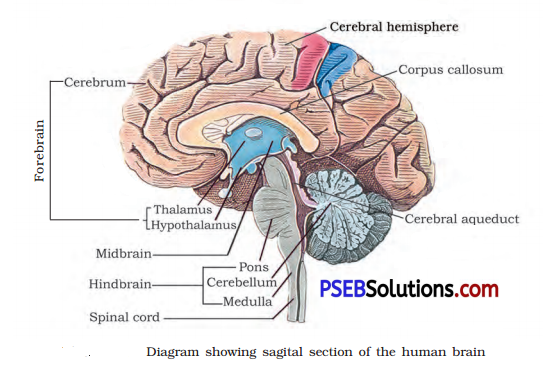
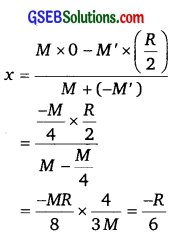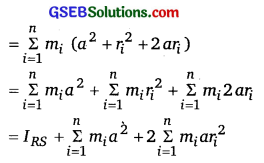Punjab State Board PSEB 11th Class Physics Book Solutions Chapter 8 Gravitation Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Physics Chapter 8 Gravitation

PSEB 11th Class Physics Guide Gravitation Textbook Questions and Answers

Question 1.
Answer the following:
(a) You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means?
(b) An astronaut inside a small spaceship orbiting around the earth cannot detect gravity. If the space station orbiting around the earth has a large size, can he hope to detect gravity?
(c) If you compare the gravitational force on the earth due to the sun to that due to the moon, you would find that the Sun’s pull is greater than the moon’s pull. (You can check this yourself using the data available in the succeeding exercises). However, the tidal effect of the moon’s pull is greater than the tidal effect of sun. Why?
Answer:
(a) No, Gravitational influence of matter on nearby objects cannot be screened by any means. This is because gravitational force unlike electrical forces is independent of the nature of the material medium. Also, it is independent of the status of other objects.

(b) Yes, If the size of the space station is large enough, then the astronaut will detect the change in Earth’s gravity (g).

(c) Tindal effect depends inversely upon the cube of the distance while gravitational force depends inversely on the square of the distance. Since the distance between the Moon and the Earth is smaller than the distance between the Sun and the Earth, the tidal effect of the Moon’s pull is greater than the tidal effect of the Sun’s pull.

Question 2.
Choose the correct alternative:
(a) Acceleration due to gravity increases/decreases with increasing altitude.
(b) Acceleration due to gravity increases/decreases with increasing depth (assume the earth to be a sphere of uniform density).
(c) Acceleration due to gravity is independent of mass of the earth/mass of the body.
(d) The formula -G Mm(1 /r₂ -1/r₁) is more/less accurate than the formula mg (r₂ – r₁) for the difference of potential energy between two points r₂ and r₁ distance away from the centre of the earth.
Solution:
(a) Decreases,
Explanation : Acceleration due to gravity at altitude h is given by the relation:
g_h = \(\left(1-\frac{2 h}{R_{e}}\right) g\)
where, R_e = Radius of the Earth
g = Acceleration due to gravity on the surface of the Earth
It is clear from the given relation that acceleration due to gravity decreases with an increase in height.

(b) Decreases,
Explanation : Acceleration due to gravity at depth d is given by the relation:
g_d = \(\left(1-\frac{d}{R_{e}}\right) g\)
It is clear from the given relation that acceleration due to gravity decreases with an increase in depth.

(c) Mass of the body,
Explanation : Acceleration due to gravity of body of mass m is given by the relation:
g = \(\frac{G M_{e}}{R^{2}}\)
where, G = Universal gravitational constant
M_e = Mass of the Earth
R_e = Radius of the Earth
Hence, it can be inferred that acceleration due to gravity is independent of the mass of the body.

(d) More,
Explanation : Gravitational potential energy of two points r₂ and r₁ distance away from the centre of the Earth is respectively given by:
V(r₁) = -GmM
V(r₂) = – \(\frac{G m M}{r_{2}}\)
V = V (r₂) – V(r₁) = -GmM\(\left(\frac{1}{r_{2}}-\frac{1}{r_{1}}\right)\).
Hence, this formula is more accurate than the formula mg (r₂ – r₁).

Question 3.
Suppose there existed a planet that went around the Sun twice as fast as the Earth. What would be its orbital size as compared to that of the Earth?
Solution:
Time taken by the Earth to complete one revolution around the Sun,
T_e = 1 year
Orbital radius of the Earth in its orbit, R_e = 1 AU
Time taken by the planet to complete one revolution around the Sun,
T_p = \(\frac{1}{2} T_{e}=\frac{1}{2}\) year
Orbital radius of the planet = R_p
From Kepler’s third law of planetary motion, we can write

Hence, the orbital radius of the planet will be 0.63 times smaller than that of the Earth.

Question 4.
I₀, one of the satellites of Jupiter, has an orbital period of 1.769 days and the radius of the orbit is 4.22 x 10⁸ m. Show that the mass of Jupiter is about one-thousandth that of the sun.
Solution:
Orbital period of I₀, TI₀ = 1.769 days = 1.769 x 24 x 60 x 60 s
Orbital radius of I_I0, R_I0 = 4.22 x 108 m
Satellite I₀ is revolving around the Jupiter Mass of the latter is given by the relation:
M_j = \(\frac{4 \pi^{2} R_{I_{O}}^{3}}{G T_{I_{O}}^{2}}\) ……………………….. (i)

where M_j = Mass of Jupiter
G = Universal gravitational constant Orbital period of the Earth,
T_e = 365.25 days = 365.25 x 24 x 60 x 60 s Orbital radius of the Earth,
Re =1 AU = 1.496 x 10¹¹ m
Mass of Sun is given as:
M_s = \(\frac{4 \pi^{2} R_{e}^{3}}{G T_{e}^{2}}\) ………………………. (ii)

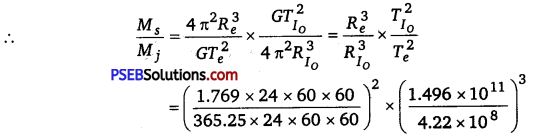
= 1045.04
∴ \(\frac{M_{s}}{M_{j}} \sim 1000\)
\(M_{s} \sim 1000 \times M_{j}\)
Hence, it can be inferred that the mass of Jupiter is about one thousandth that of the Sun.

Question 5.
Let us assume that our only consists of 2.5 x 10¹¹ stars each of one solar mass. How long will a star at a distance of 50,000 ly from the galactic center take to complete one revolution? Take the diameter of the Milky Way to be 10⁵ ly.
Solution:
Number of stars in our galaxy, = 2.5 x 10¹¹
Mass of each star = one solar mass =2 x 10³⁰ kg
Mass of our galaxy,M =2.5 x 10¹¹ x 2 x 10³⁰ = 5 x 10⁴¹ kg
Diameter of Milky Way, d = 10⁵ ly
Radius of Milky Way,r= 5 x 10⁴ ly
∵ 1 ly=946 x 10¹⁵m
∴ r=5 x 10⁴ x 9.46 x 10¹⁵
=4.73 x 10²⁰m

Since a star revolves around the galactic centre of the Milky Way, its time period is given by the relation:
T = \(\left(\frac{4 \pi^{2} r^{3}}{G M}\right)^{1 / 2}\)

1 year = 365 x 324 x 60 x 60 s
∵ 1 s = \(\frac{1}{365 \times 24 \times 60 \times 60} \) years
∴ 1.12 x 10¹⁶ s = \(\frac{1.12 \times 10^{16}}{365 \times 24 \times 60 \times 60}\) = 3.55 x 10 ⁸ years

Question 6.
Choose the correct alternative:
(a) If the zero of potential energy Is at infinity, the total energy of an orbiting satellite is negative of its kinetic/potential energy.
(b) The energy required to launch an orbiting satellite out of Earth’s gravitational influence Is more/less than the energy required to project a stationary object at the same height (as the satellite) out of Earth’s influence.
Solution:
(a) Kinetic energy
Explanation: Total mechanical energy of a satellite is the sum of its kinetic energy (always positive) and potential energy (maybe negative). At infinity, the gravitational potential energy of the satellite is zero. As the Earth-satellite system is a bound system, the total energy of the satellite is negative.

Thus, the total energy of an orbiting satellite at infinity is equal to the negative of its kinetic energy.

(b) Less
Explanation: An orbiting satellite acquires certain amount of energy that enables it to revolve around the Earth. This energy is provided by its orbit. It requires relatively lesser energy to move out of the influence of the Earth’s gravitational field than a stationary object on the Earth’s surface that initially contains no energy.

Question 7.
Does the escape speed of a body from the Earth depend on
(a) the mass of the body,
(b) the location from where it is projected,
(c) the direction of projection,
(d) the height of the location from where the body is launched?
Answer:
(a) No, we know that the escape velocity of the body is given by
V_e = \(\sqrt{\frac{2 G M}{R}} \) , where M and R are mass and radius of Earth. Thus clearly, it does not depend on the grass of the body as V_e is independent of it.

(b) Yes, we know that V_e depends upon the gravitational potential at the point from where the body is launched. Since the gravitational potential depends on the latitude and height of the point, therefore the escape velocity depends on the location of the point from where it is projected. It can also be experienced as:
V_e = \(\sqrt{2 g r}\) . As g has different values at different heights. Therefore, V_e depends upon the height of location.

(c) No, it does not depend on the direction of projection as V_e is independent of the direction of projection.

(d) Yes, it depends on the height of location from where the body is launched as explained in (b).

Question 8.
A comet orbits the Sun in a highly elliptical orbit. Does the comet have a constant
(a) linear speed,
(b) angular speed,
(c) angular momentum,
(d) kinetic energy,
(e) potential energy,
(f) total energy throughout its orbit? Neglect any mass loss of the comet when it comes very close to the Sun.
Solution:
(a) No, according to law of conservation of linear momentum L = mvr constant, therefore the comet moves faster when it is close to the sun and moves slower when it is farther away from the sun. Therefore, the speed of the comet does not remain constant.

(b) No, as the linear speed varies, the angular speed also varies. Therefore, angular speed of the comet does not remain constant.

(c) Yes, as no external torque is acting on the comet, therefore, according to law of conservation of angular momentum, the angular momentum of the comet remain constant.

(d) No, kinetic energy of the comet = \(\frac{1}{2}\) mν² As the linear speed of the comet changes as its kinetic energy also changes. Therefore, its KE does not remains constant.

(e) No, potential energy of the comet changes as its kinetic energy changes.

(f) Yes, total energy of a comet remain constant throughout its orbit.

Question 9.
Which of the following symptoms is likely to afflict an astronaut in space
(a) swollen feet,
(b) swollen face,
(c) headache,
(d) orientational problem?
Answer:
(b), (c), and (d)
Explanations:
(a) Legs hold the entire mass of a body in standing position due to gravitational pull. In space, an astronaut feels weightlessness because of the absence of gravity. Therefore, swollen feet of an astronaut do not affect him/her in space.

(b) A swollen face is caused generally because of apparent weightlessness in space sense organs such as eyes, ears, nose, and mouth constitute a person’s face. This symptom can affect an astronaut in space.

(c) Headaches are caused because of mental strain. It can affect the working of an astronaut in space.

(d) Space has different orientations. Therefore, orientational problems can affect an astronaut in space.

Question 10.
In the following two exercises, choose the correct answer from among the given ones:
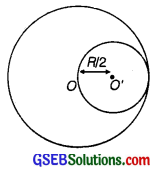
The gravitational intensity at the center of a hemispherical shell of uniform mass density has the direction indicated by the arrow (see figure) (i) a, (ii) b, (iii) c, (iv) 0.

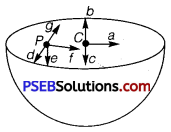
Solution:
(iii) Gravitational potential (V) is constant at all points in a spherical shell.
Hence, the gravitational potential gradient \(\left(\frac{d V}{d r}\right)\) is zero everywhere inside the spherical shell. The gravitational potential gradient is equal to the negative of gravitational intensity. Hence, intensity is also zero at all points inside the spherical shell. This indicates that gravitational forces acting at a point in a spherical shell are symmetric.

If the upper half of a spherical shell is cut out (as shown in the given figure), then the net gravitational force acting on a particle located at center O will be in the downward direction.

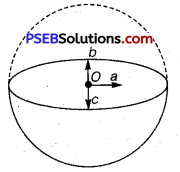
Since gravitational intensity at a point is defined as the gravitational force per unit mass at that point, it will also act in the downward direction. Thus, the gravitational intensity at center O of the given hemispherical shell has the direction as indicated by arrow c.

Question 11.
For the above problem, the direction of the gravitational intensity at an arbitrary point P is indicated by the arrow
(i) d,
(ii) e,
(iii) f,
(iv) g.
Solution:
(ii) Gravitational potential (V) is constant at all points in a spherical shell.
Hence, the gravitational potential gradient \(\left(\frac{d V}{d r}\right)\) inside the spherical shell. The gravitational potential gradient is equal to the negative of gravitational intensity. Hence, intensity is also zero at all points inside the spherical shell. Ibis indicates that gravitational forces acting at a point in a spherical shell are symmetric. If the upper half of a spherical shell is cut out (as shown in the given figure), then the net gravitational force acting on a particle at an arbitrary point P will be in the downward direction.

Since gravitational intensity at a point is defined as the gravitational force per unit mass at that point, it will also act in the downward direction. Thus, the gravitational intensity at an arbitrary point P of the hemispherical shell has the direction as indicated by arrow e.

Question 12.
A rocket Is fired from the Earth towards the Sun. At what distance from the Earth’s centre is the gravitational force on the rocket zero? Mass of the Sun = 2 x 10³⁰kg, mass of the Earth = 6 x 10²⁴ kg. Neglect the effect of other planets etc. (orbital radius = 1.5 x 10¹¹ m)
Solution:
Mass of the Sun, M_s = 2 x 10³⁰ kg
Mass of the Earth, M_e = 6 x 10 ²⁴ kg
Orbital radius, r = 1.5 x 10¹¹ m
Mass of the rocket = m

Let x be the distance from the center of the Earth where the gravitational force acting on satellite P becomes zero.
From Newton’s law of gravitation, we can equate gravitational forces acting on satellite P under the influence of the Sun and the Earth as:

= 2.59 x 10⁸ m

Question 13.
How will you ‘weigh the Sun’, that is estimate its mass? The mean orbital radius of the Earth around the Sun is 1.5 x 10⁸ km.
Solution:
Orbital radius of the Earth around the Sun, r = 1.5 x 10⁸ km = 1.5 x 10¹¹ m
Time taken by the Earth to complete one revolution around the Sun,
T = 1 year = 365.25 days = 365.25 x 24 x 60 x 60 s
Universal gravitational constant, G = 6.67 x 10^-11N-m² kg^-2
Thus, mass of the Sun can be calculated using the relation,
M = \(\frac{4 \pi^{2} r^{3}}{G T^{2}}\)
= \(\frac{4 \times(3.14)^{2} \times\left(1.5 \times 10^{11}\right)^{3}}{6.67 \times 10^{-11} \times(365.25 \times 24 \times 60 \times 60)^{2}}\)
= \(\frac{133.24 \times 10^{33}}{6.64 \times 10^{4}}\) = 2.0 x 10³⁰kg
Hence, the mass of the Sun is 2.0 x 10³⁰ kg.

Question 14.
A Saáurn year is 29.5 times the Earth year. How far is the Saturn from the Sun if the Earth is 1.5 x 10⁸ km away from the Sun?
Solution:
Distance of the Earth from the Sun, r_e = 1.5x 10⁸ km= 1.5 x 10¹¹ m
Time period of the Earth = T_e
Time period of Saturn, T_s = 29.5 T_e
Distance of Saturn from the Sun = r_s
From Kepler’s third law of planetary motion, we have
T=\(\left(\frac{4 \pi^{2} r^{3}}{G M}\right)^{\frac{1}{2}}\)
For Saturn and Sun, we can write

= 1.43 x 10¹² m

Question 15.
A body weigths 63 N on the surface of the Earth. What is the gravitational force on it due to the Earth at a height equal to half the radius of the Earth?
Solution:
Weight of the body, W =63 N
Acceleration due to gravity at height h from the Earth’s surface is given by the relation:
g’ = \(\frac{g}{\left(1+\frac{h}{R_{e}}\right)^{2}}\)
where, g = Acceleration due to gravity on the Earth’s surface
R_e =Radius of the Earth
For h= \(\frac{R_{e}}{2}\)
g’ = \(\frac{g}{\left(1+\frac{R_{e}}{2 \times R_{e}}\right)^{2}}=\frac{g}{\left(1+\frac{1}{2}\right)^{2}}=\frac{4}{9} g\)

Weight of a body of mass m at height h is given as
W’ = mg’
= m x \(\frac{4}{9}\) g = \(\frac{4}{9}\) x mg
= \(\frac{4}{9}\) W
= \(\frac{4}{9}\) x 63 =28 N

Question 16.
Assuming the Earth to be a sphere of uniform mass density, how much would a body weigh halfway down to the centre of the Earth if it weighed 250 N on the surface?
Solution:
Weight of a body of mass m at the Earth’s surface, W = mg = 250 N
Body of mass m is located at depth, d = \(\frac{1}{2}\) R_e
where, R_e = Radius of the Earth
Acceleration due to gravity at depth d is given by the relation
g’ = \(\left(1-\frac{d}{R_{e}}\right) g=\left(1-\frac{R_{e}}{2 \times R_{e}}\right) g=\frac{1}{2} g\)
Weight of the body at depth d,
W’ = mg’
= m x \(\frac{1}{2} g=\frac{1}{2}\) mg = \(\frac{1}{2}\) W
= \(\frac{1}{2}\) x 250 = 125 N

Question 17.
A rocket is fired vertically with a speed of 5 km s^-1 from the Earth’s surface. How far from the Earth does the rocket ‘ go before returning to the earth? Mass of the Earth = 6.0 x 10²⁴ kg; mean radius of the Earth = 6.4 x 10⁶ m;
G = 6.67 x 10 ^-11 N-m² kg^-2.
Solution:
Velocity of the rocket, ν = 5 km/s = 5 x 10³ m/s
Mass of the Earth, M_e = 6.0 x 10²⁴ kg
Radius of the Earth, R_e = 6.4 x 10⁶ m
Height reached by rocket mass, m = h

At the surface of the Earth,
Total energy of the rocket = Kinetic energy + Potential energy
= \(\frac{1}{2} m v^{2}+\left(\frac{-G M_{e} m}{R_{e}}\right)\)
At highest point h,
ν = 0
and, Potential energy = – \(\frac{G M_{e} m}{R_{e}+h}\)
Total energy of the rocket = 0+ \(\left(-\frac{G M_{e} m}{R_{e}+h}\right)=-\frac{G M_{e} m}{R_{e}+h}\)
From the law of conservation of energy, we have
Total energy of the rocket at the Earth’s surface=Total energy at height h


Height achieved by the rocket with respect to the centre of the Earth = R_e +h
= 6.4 x 10⁶ +1.6 x 10⁶ = 8.0 x 10⁶ m

Question 18.
The escape speed of a projectile on the Earth’s surface is 11.2 km s^-1. A body is projected out with thrice this speed. What is the speed of the body far away from the Earth? Ignore the presence of the Sun and other planets.
Solution:
Escape velocity of a projectile from the Earth, υ_esc = 11.2 km/s
Projection velocity of the projectile, v_p = 3 v_esc
Mass of the projectile = m
Velocity of the projectile far away from the Earth = v_f
Total energy of the projectile on the Earth = \(\frac{1}{2} m v_{p}^{2}-\frac{1}{2} m v_{\mathrm{esc}}^{2}\)
The gravitational potential energy of the projectile far away from the Earth is zero.
Total energy of the projectile far away from the Earth = \(\frac{1}{2}\) mv²_f
From the law of conservation of energy, we have

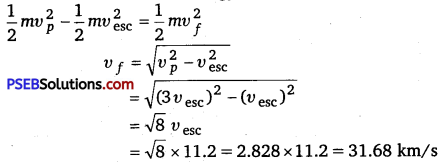
Question 19.
A satellite orbits the Earth at a height of 400 km above the surface. How much energy must be expended to rocket the satellite out Of the Earth’s gravitational influence? Mass of the satellite = 200 kg mass of the Earth = 6.0 x 10²⁴ kg; radius of the Earth=6.4x 10⁶ m;G=6.67 x 10^-11 N-m² kg^-2.
Solution:
Mass of the Earth, M_e =6.0 x 10²⁴ kg
Mass of the satellite, m = 200 kg
Radius of the Earth, Re = 6.4 x 10⁶ m
Universal gravitational constant, G = 6.67 x 10^-11 N-m²kg²
Heightofthesatellite,h =400 km=4 x 10⁵ m=0.4 x 10⁶ m

Total energy of the satellite at height h = \(\frac{1}{2} m v^{2}+\left(\frac{-G M_{e} m}{R_{e}+h}\right)\)
Orbital velocity of the satellite, ν = \(\sqrt{\frac{G M_{e}}{R_{e}+h}}\)
Total energy of height, h = \(\frac{1}{2} m\left(\frac{G M_{e}}{R_{e}+h}\right)-\frac{G M_{e} m}{R_{e}+h}=-\frac{1}{2}\left(\frac{G M_{e} m}{R_{e}+h}\right) \)

The negative sign indicates that the satellite is bound to the Earth. This is called bound energy of the satellite.
Energy required to send the satellite out of its orbit = – (Bound energy)

Question 20.
Two stars each of one solar mass (= 2x 10³⁰ kg) are approaching each other for a head-on collision. When they are a distance 10⁹ km, their speeds are negligible. What is the speed with which they collide? The radius of each star is 10⁴ km. Assume the stars to remain undistorted until they collide. (Use the known value of G).
Solution:
Mass of each star, M = 2 x 10³⁰ kg
Radius of each star, R = 10⁴ km = 10⁷ m
Distance between the stars, r = 10⁹ km = 10¹² m
For negligible speeds, ν = 0 total energy of two stars separated at distance r
= \(\frac{-G M M}{r}+\frac{1}{2} m v^{2}\)
= \(\frac{-G M M}{r}+0\) = 0 ………………………… (i)

Now, consider the case when the stars are about to collide:
The velocity of the stars = ν
Distance between the centers of the stars = 2R
Total kinetic energy of both stars = \(\frac{1}{2} M v^{2}+\frac{1}{2} M v^{2}\) = Mv²
Total potential energy of both stars = \(\frac{-G M M}{2 R}\)
Total energy of the two stars = Mv² – \(\frac{-G M M}{2 R}\) ………………………. (ii)
Using the law of conservation of energy, we can write

Question 21.
Two heavy spheres each of mass 100 kg and radius 0.10 m are placed 1.0 m apart on a horizontal table. What is the gravitational force and potential at the midpoint of the line joining the centers of the spheres? Is an object placed at that point in equilibrium? If so, is the equilibrium stable or unstable?
Solution:
The situation is represented in the following figure :

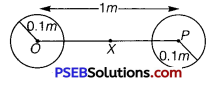
Mass of each sphere, M = 100 kg
Separation between the spheres, r = 1 m
X is the mid-point between the spheres. Gravitational force at point X will be zero. This is because gravitational force exerted by each sphere will act in opposite directions. Gravitational potential at point X

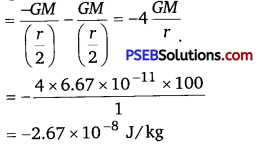
Any object placed at point X will be in equilibrium state, but the equilibrium is unstable. This is because any change in the position of the object will change the effective force in that direction.

Additional Exercises

Question 22.
As you have learnt in the text, a geostationary satellite orbits the Earth at a height of nearly 36,000 km from the surface of the Earth. What is the potential due to Earth’s gravity at the site of this satellite? (Take the potential energy at infinity to be zero). Mass of the Earth = 6.0 x 10²⁴ kg, radius = 6400 km.
Solution:
Mass of the Earth, M = 6.0 x 10²⁴ kg
Radius of the Earth, R = 6400 km = 6.4 x 10⁶ m
Height of a geostationary satellite from the surface of the Earth,
h = 36000 km = 3.6 x 10⁷m
Gravitational potential energy due to Earth’s gravity at height h,

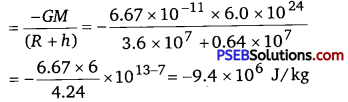
Question 23.
A star 2.5 times the mass of the Sun and collapsed to a size of 12 km rotates with a speed of 1.2 revs. per second. (Extremely compact stars of this kind are known as neutron stars. Certain stellar objects called pulsars belong to this category). Will an object placed on its equator remain stuck to its surface due to gravity? (Mass of the Sun = 2 x 10³⁰ kg).
Solution:
Yes, A body gets stuck to the surface of a star if the inward gravitational force is greater than the outward centrifugal force caused by the rotation of the star.
Gravitational force, fg = \(\frac{G M m}{R^{2}}\)
where,M =Mass of the star=2.5 x 2 x 10³⁰ = 5 x 10³⁰ kg
m = Mass of the body

R=Radiusofthestar=12 km=1.2 x 10⁴ m
∴ f_g = \(\frac{6.67 \times 10^{-11} \times 5 \times 10^{30} \times m}{\left(1.2 \times 10^{4}\right)^{2}}\)
= 2.31 x 10¹² mN
Centrifugal force, f_c = mrω²

where, ω = Angular speed = 2 πv
ν = Angular frequency = 1.2 rev s^-1
f _c=mR(2πv)²
= m x (1.2 x 10⁴) x 4 x(3.14)² x (1.2)² = 1.7 x 10⁵ mN
Since f_g > f_c, the body will remain stuck to the surface of the star.

Question 24.
A spaceship is stationed on Mars. How much energy must be expended on the spaceship to launch it out of the solar system? Mass of the spaceship = 1000 kg; mass of the Sun = 2 x 10³⁰ kg; mass of mars = 6.4 x 10²³ kg; radius of mars = 3395 km; radius of the orbit of mars = 2.28 x 10⁸ km;
G = 6.67 x 10^-11 N-m²kg^-2.
Solution:
Given, mass of the Sun, M = 2 x 10³⁰ kg

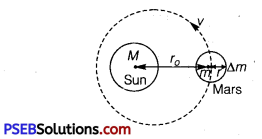
Mass of the mars, m = 6.4 x 10²³ kg
Mass of spaceship, Δm = 1000 kg
Radius of orbit of the mars, r₀ = 2.28 x 10¹¹
Radius of the mars, r = 3.395 x 10⁶ m
If v is the orbital velocity of mars, then

Since the velocity of the spaceship is the same as that of the mars, Kinetic energy of the spaceship,


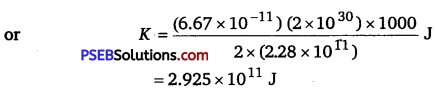
Total potential energy of the spaceship,
U = Potential energy of the spaceship due to its being in the gravitational
field of the mars + potential energy of the spaceship due to its being in the gravitational field of the Sun.

Total energy of the spaceship E=K +U = 2.925 x 10¹¹ J – 5.977 x 10¹¹J
= – 3.025 x 10¹¹ J = -3.1 x 10¹¹ J
Negative energy denotes that the spaceship is bound to the solar system. Thus, the energy needed by the spaceship to escape from the solar system = 3.1 x 10¹¹ J.

Question 25.
A rocket is fired ‘vertically’ from file surface of mars with a speed of 2 kms^-1. If 20% of its initial energy is lost due to martian atmospheric resistance, how far will the rocket go from the surface of Mars before returning to it?
Mass of mars = 6.4x 10²³ kg; radius of mars = 3395 km;
G = 6.67 x 10^-11 N-m² kg².
Solution:
Initial velocity of the rocket, ν = 2 km/s = 2 x 10³ m/s
Mass of Mars, M = 6.4 x 10²³ kg .
Radius of Mars, R = 3395 km = 3.395 x 10⁶ m
Universal gravitational constant, G = 6.67 x 10^-11 N-m² kg^-2
Mass of the rocket = m
Initial kinetic energy of the rocket = \(\frac{1}{2} m v^{2}\)
Initial potential energy of the rocket = \(\frac{-G M m}{R}\)
Total initial energy = \(\frac{1}{2} m v^{2}-\frac{G M m}{R}\)

If 20 % of initial kinetic energy is lost due to martian atmospheric resistance, then only 80 % of its kinetic energy helps in reaching a height.
Total initial energy available = \(\frac{80}{100} \times \frac{1}{2} m v^{2}-\frac{G M m}{R}=0.4 m v^{2}-\frac{G M m}{R} \)
Maximum height reached by the rocket = h
At this height, the velocity and hence, the kinetic energy of the rocket will become zero.
Total energy of the rocket at height h = \(-\frac{G M m}{(R+h)}\)
Applying the law of conservation of energy for the rocket, we can write

= 495 x 10³ m = 495 km

Punjab State Board PSEB 11th Class Biology Book Solutions Chapter 1 The Living World Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Biology Chapter 1 The Living World

PSEB 11th Class Biology Guide The Living World Textbook Questions and Answers

Question 1.
Why are living organisms classified?
Answer:
Living organisms are classified because:

• there are millions of organisms on the earth, which need a proper system of classification for identification.
• a number of new organisms are discovered each year. They require a particular system to be identified and to find out their correct position in a group.

Question 2.
Why are the classification systems changing every now and then?
Answer:
Evolution is the major factor responsible for the change in classification systems. Since, evolution still continues, so many different species of plants and animals are added in the already existed biodiversity. These newly discovered plant and animal specimens are then identified, classified and named according to the already existing classification systems. Due to evolution, animal and plant species keep on changing, so necessary changes in the already existed classification systems are necessary to place every newly discovered plant and animal in their respective ranks.

Question 3.
What different criteria would you choose to classify people that you meet often?
Answer:
The different scientific criteria to classify people that we meet often would be :
(i) Nomenclature: It is the science of providing distinct and proper names to the organisms. It is the determination of correct name as per established universal practices and rules.

(ii) Classification: It is the arrangement of organisms into categories based on systematic planning. In classification various categories used are class, order, family, genus and species.

(iii) Identification: It is the determination of correct name and place of an organism. Identification is used to tell that a particular species is similar to other organism of known identity. This includes assigning an organism to a particular taxonomic group.
The same criteria can be applied to the people we meet daily. We can identify them will their names classify them according to their living areas, profession, etc.

Question 4.
What do we learn from identification of individuals and populations?
Answer:
Identification of individuals and population categorized it into a species. Each species has unique characteristic features. On the basis of these features, it can be distinguished from other closely related species, e. g.,

Question 5.
Given below is the scientific name of Mango. Identify the correctly written name.
(i) Mangifera Indica
(ii) Mangifera indica.
Answer:
(ii) Mangifera indica (the name of species can never begins with a capital letter).

Question 6.
Define a taxon. Give some examples of taxa at different hierarchical levels.
Answer:
Taxon is a grouping of organisms of any level in hierarchical classification, which is based on some common characteristics, e.g., insects represent a class of phylum – Arthropoda. All the insects possess common characters of three pairs of jointed legs. The term ‘taxon’ was introduced by ICBN in 1956. Examples of taxa are kingdom, phylum or division, class, order, family, genus and species. These taxa form taxonomic hierarchy, e.g., taxa for human :
Phylum – Chordata
Class – Mammalia
Order – Primata
Family – Hominidae
Genus – Homo
Species – sapiens

Question 7.
Can you identify the correct sequence of taxonomical categories?
(a) Species → Order → Phylum → Kingdom
(b) Genus → Species → Order → Kingdom
(c) Species → Genus → Order → Phylum
Answer:
The correct sequence of taxonomical categories is as follows :
Species → Genus → Order → Phylum

Question 8.
Try to collect all the currently accepted meanings for the word ‘species’. Discuss with your teacher the meanings of species in case of higher plants and animals on one hand, and bacteria on the other hand.
Answer:
A group of individual organisms with fundamental similarities is called species. It can be distinguished from other closely related species on the basis of distinct morphological differences.
In case of higher plants and animals, one genus may have one or more than one species, e.g.,Panthera leo (lion) and Panthera tigris (tiger).
In this example, Panthera is genus, which includes leo (lion) and tigris (tiger) as species.
In case of bacteria, different categories are present on the basis of shape. These are spherical, coccus, rod-shaped, comma and spiral-shaped. Thus, meaning of species in case of higher organisms and bacteria are different.

Question 9.
Define and understand the following terms:
(i) Phylum,
(ii) Class,
(iii) Family,
(iv) Order,
(v) Genus.
Answer:
(i) Phylum: Phylum comes next to Kingdom in the taxonomical hierarchy. All broad characteristics of an animal or plant are defined in a phylum. For example all chordates have a notochord and gill at some stage of life cycle. Similarly all arthropods have jointed legs made of chitin.

(ii) Class: The category class includes related orders. It is higher than order and lower than phylum. For example, class – Mammalia has order – Carnivora, Primata, etc.

(iii) Family: It is the category higher than genus and lower than order, which has one or more related genera having some common features. For example, Felidae, Canidae, etc.

(iv) Order: Order further zeroes down on characteristics and includes related genus. For example humans and monkeys belong to the order primates. Both humans and monkeys can use their hands to manipulate objects and can walk on their hind legs.

(v) Genus: It comprises a group of related species which has more characters in common in comparison to species of other genera. We can say that genera are aggregates of closely related species. For example, j potato, tomato and brinjal are three different species but all belong to the genus Solatium. Lion (Panthera leo), leopard (P. pardus) and tiger (P. tigris) with several common features, are all species of the genus Panthera. This genus differs from another genus Felis which includes cats.

Question 10.
How is a key helpful in the identification and classification of an
organism?
Answer:
Key is a device (scheme) of diagnostic alternate (contrasting) characters, which provide an easy means for the identification of unknown organism. The keys are taxonomic literature based on the contrasting characters generally a pair called couplet. Each statement in the key is called a lead. Separate taxonomic keys are required for each taxonomic category such as family, genus and species for identification purposes. Being analytical ‘ in nature, two types of keys are commonly used-indented key and bracketed key.

(i) Indented key provides sequence of choice between two or more statements of characters of species. The user has to make correct choise for identification.

(ii) Bracketed key (1) are used for contrasting characters like indented key but they are not repeated by intervening sub-dividing character and each character is given a number in brackets.

Question 11.
Illustrate the taxonomical hierarchy with suitable examples of a plant and an animal.
Answer:

Taxonomical hierarchy is the system of arrangement of taxonomic categories in a descending order depending upon their relative dimensions. It was introduced by Linnaeus (1751) and is therefore, also called Linnaeus hierarchy. Each category, referred to as a unit of classification commonly called as taxon (pi. taxa), e.g., taxonomic categories and hierarchy can be illustrated by a group of organisms, i.e., insects. The common features of insects is ‘three pair of jointed legs’. It means insects are recognisable objects which can be classified, so given a rank or category.
Category further denotes a rank. Each rank or taxon, represents a unit of classification taxonomic studies of all plants and animals led to the development of common categories such as kingdom, phylum or division (for plants), class, order, family, genus and species. All organisms, including those in the plant and animal, kingdoms have ‘species’ as the lowest category.

To place an organism in various categories is to have the knowledge of characters of an individual or group of organism. This helps to identify similarities and dissimilarities among the individual of the same kind of organisms as well as of other kinds of organism. Some organisms with their taxonomical categories are given in following table:

Punjab State Board PSEB 11th Class Biology Book Solutions Chapter 21 Neural Control and Coordination Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination

PSEB 11th Class Biology Guide Neural Control and Coordination Textbook Questions and Answers

Question 1.
Briefly describe the structure of the following:
(a) Brain
(b) Eye
(c) Ear
Answer:
(a) Brain
The human brain has the following parts :
(i) Cerebrum
A deep cleft called longitudinal fissure divides the brain/cerebrum into two halves-cerebral hemispheres.
The two cerebral hemispheres are joined together by bundles of densely packed nerve fibers, called corpus callosum.
The outer surface of cerebrum, the cerebral cortex, is called grey matter, due to its greyish appearance; the cell bodies of the neurons are concentrated in this region; it contains motor areas, sensory areas and association areas.
Inner to the cortex is the white matter, that consists of myelinated nerve fibers in the form of nerve fibre tracts.

(ii) Thalamus
Thalamus is the major coordinating centre for sensory and motor signals.

(iii) Hypothalamus
It has centers to control body temperature, hunger, thirst, etc.
It contains several groups of neurosecretory cells, which secrete hormones.

(iv) Limbic System
The inner parts of the cerebral hemispheres and a group of deep structures called amygdala, hippocampus, etc. form a complex structure, called limbic system. Along with the hypothalamus, it is involved in the regulation of sexual behavior, expression of emotions, motivation, etc.

(v) Midbrain
Midbrain is located between the hypothalamus of the forebrain and the pons of the hindbrain. The dorsal portion of the midbrain consists of four small lobes, called corpora quadrigemina. A canal, called cerebral aqueduct passes through the midbrain.

(vi) Hindbrain
It consists of pons, cerebellum and medulla oblongata. The medulla contains centres which control vital functions like respiration, cardiovascular reflexes and gastric secretions. The medulla continues down as the spinal cord.

(b) Eye

• Each eye ball consists of three concentric layers, the outermost sclera, middle choroid and innermost retina.
• The sclera in the front (l/6th) forms the transparent cornea.
• The middle choroid is highly vascular and pigmented, that prevents internally reflected light within the eye; just behind the junction between cornea and sclera, the choroid becomes thicker forming the ciliary body.
• The iris extends from the ciliary body in front of the lens; it controls the dilation or constriction of pupil.
• The lens is suspended from the ciliary body, by suspensory ligaments.
• The anterior chamber of eye is filled with an aqueous clear fluid, aqueous humor and the posterior chamber has a gelatinous material, vitreous humor.
• The retina is composed of three layers of cells; the photoreceptor layer contains rods and cones, the intermediate layer has bipolar neurons, which synapse with retinal ganglion cells and their axons bundle to form optic nerve.
• The photoreceptor cells (rods and cones) contain the light sensitive proteins, called photopigments.
• The point in the retina where the optic nerve leaves the eye and the retinal blood vessels enter the eye is called a blind spot; there are no photoreceptor cells in this region.
• Lateral to blindspot, there is a yellowish pigmented spot, called macula lutea with a central pit called fovea.
• The fovea is the region where only cones are densely packed and it is the point where acuity (resolution) vision is the greatest.

(c) Ear
The ear performs two sensory functions, namely
(a) hearing and

(b) maintenance of body balance.

• Ear consists of three parts: external ear, middle ear and internal ear.
• The external ear consists of the pinna, and external auditory meatus.
• The tympanic membrane separates the middle ear from the external ear.
• The middle ear (tympanic cavity) is an air- filled chamber, which is connected to pharynx by Eustachian tube.
• The middle ear lodges three small bones, the ear ossicles namely, the malleus, incus and stapes.
• The middle ear communicates with the internal ear through the oval window and round window.
• The inner ear is a fluid-filled chamber and called labyrinth; it has two parts, an outer bony labyrinth, inside
• which a membranous labyrinth is floating in the perilymph; the membranous labyrinth is filled with a fluid, called endolymph.
• The labyrinth is divided into two parts, the cochlea and vestibular apparatus.
• Cochlea is the coiled portion of the labyrinth and its membranes, Reissner’s membrane and basilar membrane divide the perilymph-filled bony labyrinth into an upper scala vestibule, middle scala media and a lower scala tympani; scala media is filled with endolymph.
• At the base of the cochlea, scala vestibuli ends at the oval window, while the scala tympani terminates at the round window, that opens to the middle ear.
• Organ of Corti is the structural unit of hearing; it consists of hair cells which are the auditory receptors and is located on the basilar membrane.
• A thin elastic tectorial membrane lies over the row of hair cells.
• The vestibular apparatus is composed of three semicircular canals and an otolith organ or vestibule.
• The otolith organ has two parts namely the utricle and saccule.
• The utricle and saccule also contain a projecting ridge, called macula.
• The crista ampullar and macula are the specific receptors of the vestibular apparatus, for maintaining body balance.

Question 2.
Compare the following:
(a) Central Neural System (CNS) and Peripheral Neural System (PNS)
(b) Resting potential and action potential
(c) Choroid and retina
Answer:
(a) Comparison between Central Neural System (CNS) and Peripheral Neural System (PNS): The CNS includes the brain and the spinal cord and is the site of information processing and control. The PNS comprises of all the nerves of the body associated with the CNS (brain and spinal cord). The nerve fibers of the PNS are of two types :
(i) Afferent fibers, (ii) Efferent fibers

(b) Comparison between Resting Potential and Action Potential:
The electrical potential difference across the resting plasma membrane A is called the resting potential. The electrical potential difference across the plasma membrane at the site A is called the action potential, which is in fact termed as a nerve impulse.

(c) Comparison between Choroid and Retina: The middle layer of eyeball which contains many blood vessels and looks bluish in colour is known as choroid. The choroid layer is thin over the posterior two-thirds of the eyeball, but it becomes thick in the anterior part to form the ciliary body. The ciliary body itself continues forward to form a pigmented and opaque structure called the iris.

Retina is the inner layer of eye ball and it contains three layers of cells from inside to outside, i. e., ganglion cells, bipolar cells and photoreceptor cells. There are two types of photoreceptor cells, namely, rods and cones. These cells contain the light-sensitive proteins called the photopigments.

Question 3.
Explain the following processes:
(a) Polarisation of the membrane of a nerve fibre
(b) Depolarisation of the membrane of a nerve fibre
(c) Conduction of a nerve impulse along a nerve fibre
(d) Transmission \of a nerve impulse across a chemical synapse
Answer:
(a) Polarisation of the Membrane of a Nerve Fibre: During resting condition, the concentration of K+ ions is more inside the axoplasm while the concentration of Na+ ions is more outside the axoplasm. As a result, the potassium ions move faster from inside to outside as compared to sodium ions. Therefore, the membrane becomes positively charged outside and negatively charged inside. This is known as polarisation of membrane or polarised nerve.

(b) Depolarisation of the Membrane of a Nerve Fibre: When an electrical stimulus is given to a nerve fibre, an action potential is generated. The membrane becomes permeable to sodium ions than to potassium ions. This results into positive charge inside and negative charge outside the nerve fibre. Hence, the membrane is said to be depolarised.

(c) Conduction of a Nerve Impulse Along a Nerve Fibre: There are two types of nerve fibers-myelinated and non-myelinated. In myelinated nerve fibre, the action potential is conducted from node to node in jumping manner. This is because the myelinated nerve fibre is coated with myelin sheath.

The myelin sheath is impermeable to ions. As a result, the ionic exchange and depolarization of nerve fiber is not possible along the whole length of nerve fiber. It takes place only at some point, known as nodes of Ranvier, whereas in non-myelinated nerve fiber, the ionic exchange and depolarization of nerve fiber takes place along the whole length of the nerve fiber. Because of this ionic exchange, the depolarised area becomes repolarised and the next polarised area becomes depolarised.

(d) Transmission of a Nerve Impulse Across a Chemical Synapse:
Synapse is a small gap that occurs between the last portion of the axon of one neuron and the dendrite of next neuron. When an impulse reaches at the endplate of axon, vesicles consisting of chemical substances or neurotransmitters, such as acetylcholine, fuse with the plasma membrane.

This chemical moves across the cleft and attaches to chemo-receptors present on the membrane of the dendrite of next neuron. This binding of chemical with chemo-receptors leads to the depolarization of membrane and generates a nerve impulse across nerve fibre. The chemical, acetylcholine, is inactivated by enzyme acetylcholinesterase. The enzyme is present in the postsynaptic membrane of the dendrite. It hydrolyses acetylcholine and this allows the membrane to repolarise.

Question 4.
Draw labeled diagrams of the following:
(a) Neuron
(b) Brain
(c) Eye
(d) Ear
Answer:
(a) Neuron

(b) Brain

(c) Eye

(d) Ear

Question 5.
Write short notes on the following:
(a) Neural coordination
(b) Forebrain
(c) Midbrain
(d) Hindbrain
(e) Retina
(f) Ear ossicles
(g) Cochlea
(h) Organ of Corti
(i) Synapse
Answer:
(a) Neural Coordination: The organized network of point-to-point connections for quick coordination provided by neural system is called neural coordination. The mechanism of neural coordination involves transmission of nerve impulses, impulse conduction across a synapse, and the physiology of reflex action.

(b) Forebrain: The forebrain consists of :
1. Olfactory lobes: The anterior part of the brain is formed by a pair of short club-shaped structures, the olfactory lobes. These are concerned with the sense of smell.

2. Cerebrum: It is the largest and most complex of all the parts of the human brain. A deep cleft divides the cerebrum longitudinally into two halves, which are termed as the left and right cerebral hemispheres connected by a large bundle of myelinated fibres the corpus callosum. The outer cover of cerebral hemisphere is called cerebral cortex. The cerebral cortex is referred to as the grey matter due to its greyish appearance (as neuron cell bodies are concentrated here).

The cerebral cortex is greatly folded. The upward folds, gyri, alternate with the downward grooves or sulci. Beneath the grey matter, there are millions of medullated nerve fibers, which constitute the inner part of the cerebral hemisphere. The large concentration of medullated nerve fibers gives this tissue an opaque white appearance. Hence, it is called the white matter.

3. Lobes: A very deep and a longitudinal fissure, separates the two cerebral hemispheres. Each cerebral hemisphere of the cerebrum is divided into four lobes, i.e., frontal, parietal, temporal, and occipital lobes.

In each cerebral hemisphere, there are three types of functional areas:
(i) Sensory areas receive impulses from the receptors and motor areas transmit impulses to the effectors.
(ii) Association areas are large regions that are neither clearly sensory nor motor injunction. They interpret the input, store the input and initiate a response in light of similar past experiences. Thus, these areas are responsible for complex functions like memory, learning, reasoning, and other intersensory associations.

(iii) Diencephalon is the posteroventral part of forebrain. Its main parts are as follows :
Epithalamus is a thin membrane of non-neural tissue. It is the posterior segment of the diencephalon. The cerebrum wraps around a structure called thalamus, which is a major coordinating center for sensory and motor signaling. The hypothalamus, that lies at the base of thalamus contains a number of centers, which control body temperature, urge for eating and drinking. It also contains several groups of neurosecretory cells, which secrete hormones called hypothalamic hormones.

(c) Midbrain: The midbrain is located between the thalamus and hypothalamus of the forebrain and pons of the hindbrain. A canal called the cerebral aqueduct passes through, the midbrain.
The dorsal portion of the midbrain mainly consists of two pairs (i.e., four) of rounded swellings (lobes) called corpora qua trigeminal.

(d) Hindbrain: The hindbrain consists of :

(i) Pons: It consists of fiber tracts that interconnect different regions of the brain.

(ii) Cerebellum: It is the second-largest part of the human brain (means little cerebrum). It has very convoluted surface in order to provide the additional space for many more neurons.

(iii) Medulla: It (oblongata) is connected to the spinal cord and contains centers, which control respiration, cardiovascular reflexes, and gastric secretions.

(e) Retina: The inner layer of eyeball is the retina and it contains three layers of cells from inside to outside—ganglion cells, bipolar cells and photoreceptor cells. There are two types of photoreceptor cells namely, rods and cones. These cells contain the light-sensitive proteins called the photopigments.

(f) Ear Ossicles: The middle ear contains three ossicles called malleus, incus and stapes which are attached to one another in a chain-like fashion. The malleus is attached to the tympanic membrane and the stapes is attached to the oval window or the cochlea. The ear ossicles increase the efficiency of transmission of sound waves to the inner ear.

(g) Cochlear: The membranous labyrinth of inner ear is filled with a fluid called endolymph. The coiled portion of the labyrinth is called cochlea. The membranes constituting cochlea, the Meissner’s and basilar, divide the surrounding perilymph-filled bony labyrinth into an upper scale vestibule and a lower scala tympani. The space within cochlea called scala media is filled with endolymph. At the base of the cochlea, the scala vestibule ends at the oval window, while the scala tympani terminates at the round window which opens to the middle ear.

(h) Organ of Corti: The organ of Corti is a structure located on the basilar membrane of inner ear, which contains hair cells that act as auditory receptors. The hair cells are present in rows on the internal side of the organ of Corti. The basal end of the hair cell is in close contact with the afferent nerve fibers. A large number of processes called stereocilia are projected from the apical part of each hair cell. Above the rows of the hair cells is a thin elastic membrane called tectorial membrane.

(i) Synapse: It is a junction between two neurons, where one neuron expands and comes in near contact with another neuron. A synapse is formed by the membranes of a pre-synaptic neuron, and a post-synaptic neuron, which may or may not be separated by a gap called synaptic cleft.

There are two types of synapses-an electrical synapse and a chemical synapse. In electrical synapse, membranes of pre and post-synaptic neurons are is very close proximity field. In chemical synapse, these membranes are separated by a fluid-filled space called synaptic cleft.

Question 6.
Give a brief account of:
(a) Mechanism of synaptic transmission
(b) Mechanism of vision
(c) Mechanism of hearing
Answer:
(a) Mechanism of Synaptic Transmission: Synapse is a junction between two neurons. It is present between the axon terminal of one neuron and the dendrite of next neuron separated by a cleft.

There are two ways of synaptic transmission :
1. Chemical transmission: When a nerve impulse reaches the end plate of axon, it releases a neurotransmitter (acetylcholine) across the synaptic cleft. This chemical is synthesized in cell body of the neuron and is transported to the axon terminal. The acetylcholine diffuses across the cleft and binds to the receptors present on the membrane of next neuron. This causes depolarization of membrane and initiates an action potential.

2. Electrical transmission: In this type of transmission, an electric current is formed in the neuron. This electric current generates an action potential and leads to transmission of nerve impulses across the nerve fiber. This represents a faster method of nerve conduction than the chemical method of transmission.

(b) Mechanism of Vision: Retina is the innermost layer of eye. It contains three layers of cells-inner ganglion cells, middle bipolar cells and outermost photoreceptor cells. A photoreceptor cell is composed of a protein called opsin and an aldehyde of vitamin A called retinal. When light rays are focused on the retina through cornea, it leads to the dissociation of retinal from opsin protein.

This changes the structure of opsin. As the structure of opsin changes, the permeability of membrane changes, generating a potential difference in the cells. This generates an action potential in the ganglionic cells and is transmitted to the visual cortex of the brain via optic nerves. In the cortex region of brain, the impulses are analyzed and image is formed on the retina.

(c) Mechanism of Hearing: The pinna of the external region collects the sound waves and directs it towards ear drum or external auditory canal. These waves strike the tympanic membrane and vibrations are created. Then, these vibrations are transmitted to the oval window, fenestra ovalis, through three ear ossicles, named as malleus, incus, and stapes. These ear ossicles act as lever and transmit the sound waves to internal ear.

These vibrations from fenestra ovalis are transmitted into cochlear fluid. This generates sound waves in the lymph. The formation of waves generates a ripple in the basilar membrane. This movement bends the sensory hair cells present on the organ of corti against tectorial membrane. As a result of this, sound waves are converted into nerve impulses. These impulses are then carried to auditory cortex of brain via auditory nerves. In cerebral cortex of brain, the impulses are analysed and sound is recognised.

Question 7.
Answer briefly:
(a) How do you perceive the colour of an object?
(b) Which part of our body helps us in maintaining the body balance?
(c) How does the eye regulate the amount of light that falls on the retina?
Answer:
(a) The daylight (photopic) vision and colour vision are functions of cones. In the human eye, there are three types of cones which possess their own characteristic photopigments that respond to red, green and blue lights. The sensations of different colours are produced by various combinations of these cones and their photopigments. When these cones are stimulated equally a sensation of white light is produced.

(b) The crista and macula are the specific receptors of the vestibular apparatus of inner ear which are responsible for the maintenance of balance of the body and posture.

(c) The diameter of the pupil is regulated by the muscle fiber of iris. Photoreceptors, rods, and cones regulate the amount of light that falls on the retina.

Question 8.
Explain the following:
(a) Role of Na⁺ in the generation of action potential.
(b) Mechanism of generation of light-induced impulse in the retina.
(c) Mechanism through which a sound produces a nerve impulse in the inner ear.
Answer:
(a) Role of Na⁺ in the Generation of Action Potential: When a stimulus is applied to a nerve, the membrane of the nerve becomes freely permeable to Na ^{+ .} This leads to a rapid influx of Na⁺ followed by the reversal of the polarity at that site, i. e., the outer surface of the membrane becomes negatively charged and the inner side becomes positively charged. The electrical potential difference across plasma membrane at the membrane is called the action potential, which is in fact termed as a nerve impulse. Thus, this shows that Na⁺ ions play an important role in the conduction of nerve impulses.

(b) Mechanism of Generation of Light-induced Impulse in the Retina: Light induces dissociation of the retina from opsin resulting in changes in the structure of the opsin. This causes membrane permeability changes. As a result, potential differences are generated in the photoreceptor cells. This produces a signal that generates action potentials in the ganglion cells through the bipolar cells.

These action potentials (impulses) are transmitted by the optic nerves to the visual corted area of the brain, where the nerve impulses are analysed and the image formed on the retina is recognised.

(c) Mechanism through which a Sound Produces a Nerve Impulse in the Inner Ear: In the inner ear, the vibrations are passed through the oval window on to the fluid of the cochlea, where they generate waves in the lymph.
The waves in the lymphs induce a ripple in the basilar membrane.

These movements of the basilar membrane bend \ the hair cells, pressing them against the tectorial membrane. As a result, nerve impulses are generated in the associated afferent neurons. These impulses are transmitted by the afferent fibres via auditory nerves to the auditory cortex of the brain, where the impulses are analyzed and the sound is recognized.

Question 9.
Differentiate between:
(a) Myelinated and non-myelinated axons
(b) Dendrites and axons
(c) Rods and cones
(d) Thalamus and hypothalamus
(e) Cerebrum and cerebellum
Answer:
(a) Differences between Myelinated and Non-myelinated Axons

Myelinated Axon	Non-myelinated Axon
1. The myelinated nerve fibers are enveloped with Schwann cells, which form a myelin sheath around the axon.	1. Unmyelinatcd nerve fibers are enclosed by a Schwann cell that does not form a myelin sheath around the axon.
2. Myelinated nerve fibres are found in spinal and cranial nerves.	2. They are commonly found in autonomous and the somatic neural systems.

(b) Differences between Dendrite and Axon

Dendrite	Axon
1. These are short fibres which branch repeatedly and project out of the cell body also contain Nissl’s granules	The axon is a long branched fibre, which terminates as a bulb-like structure called. synaptic knob. It possess synaptic vesicles containing chemicals called neurotransmitters.
2. These fibres transmit impulses towards the cell body.	The axons transmit nerve impulses away from the cell body to a synapse.

(c) Differences between Rods and Cones

Rod	Cone
1. The twilight vision is the function of rods.	The daylight vision and colour vision are functions of cones.
2. The rods contain a purplish-red protein called the rhodopsin or visual purple, which contains a derivative of Vitamin-A	In the human eye, there are three types of cones which possess their own characteristic photopigments that respond to red, green and blue lights.

(d) Differences between Thalamus and Hypothalamus

Thalamus	Hypothalamus
1. The cerebrum wraps around a structure called thalamus.	It lies at the base of the thalamus.
2. All types of sensory input passes synapses in the thalamus	It contains neurosecretory cells that secrete hypothalamus hormones.
3. It controls emotional and memory functions.	It regulates, sexual behavior, expression of emotional reactions and motivation.

.(e) Differences between Cerebrum and Cerebellum

Cerebrum	Cerebellum
1. It is the most developed part in brain.	It is the second developed part of brain also called as little cerebrum
2. A deep cleft divides cerebrum into two cerebral hemispheres.	Externally the whole surface contains gyri and sulci.
3. Its functions are intelligence, learning, memory, speech, etc.	It contains centres for coordination and error checking during motor and cognition.

Question 10.
Answer the following:
(a) Which part of the ear determines the pitch of a sound?
(b) Which part of the human brain is the most developed?
(c) Which part of our central neural, system acts as a master clock?
Answer:
(a) Inner ear
(b) Cerebrum
(c) Brain

Question 11.
The region of the vertebrate eye, where the optic nerve passes out of the retina, is called the
(a) fovea
(b) iris
(c) blind spot
(d) optic chiasma
Answer:
(d) Optic Charisma

Question 12.
Distinguish between:
(a) Afferent neurons and efferent neurons.
(b) Impulse conduction in a myelinated nerve fibre and unmyelinated nerve fibre.
(c) Aqueous humour and vitreous humour.
(d) Blind spot and yellow spot.
(e) Cranial nerves and spinal nerves.
Answer:
(a) Differences between Afferent neurons and Efferent neurons

Afferent Neurons	Efferent Neurons
The afferent nerve fibres transmit impulses from tissues/organs to the CNS.	The efferent fibres transmit regulatory impulses from the CNS to the concerned peripheral tissues/organs.

(b) Differences between Myelinated and Non-myelinated Axons

Myelinated Axon	Non-myelinated Axon
1. The myelinated nerve fibers are enveloped with Schwann cells, which form a myelin sheath around the axon.	1. Unmyelinatcd nerve fibers are enclosed by a Schwann cell that does not form a myelin sheath around the axon.
2. Myelinated nerve fibres are found in spinal and cranial nerves.	2. They are commonly found in autonomous and the somatic neural systems.

(c) Differences between Aqueous humour and Vitreous humour

Aqueous Humour	Vitreous Humour
1. It is the space between the cornea and the lens.	The space between the lens and the retina is called the vitreous chamber.
2. It contains a thin watery fluid.	It is filled with a transparent gel.

(d) Differences between Blindspot and Yellow spot

Blind Spot	Yellow Spot
1. Photoreceptor cells are not present in this region.	Yellow spot or macula lutea is located at the posterior pole of the eye lateral to the blind spot. It has a central pit called fovea.
2. The light focuses on that part of the retina is not detected.	The fovea of yellow spot is a thinned-out portion of retina where only the cones are densely packed is the point where visual cavity is greatest.

(e) Differences between Cranial nerves and spinal nerves

Cranial Nerves	Spinal Nerves
1. The cranial nerves originate in the brain and terminate mostly in organs head and upper body.	The spinal nerves originate in the spinal cord and extend to parts of the body below the head.
2. There are 12 pairs of cranial nerves.	There are 31 pairs of spinal nerves.
3. Most of the cranial nerves contain axons and both sensory and motor neurons.	All of the spinal nerves contain axons of both sensory and motor neurons.

Punjab State Board PSEB 11th Class Biology Book Solutions Chapter 22 Chemical Coordination and Integration Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Biology Chapter 22 Chemical Coordination and Integration

PSEB 11th Class Biology Guide Chemical Coordination and Integration Textbook Questions and Answers

Question 1.
Define the following:
(a) Exocrine gland
(b) Endocrine gland
(c) Hormone
Answer:
(a) Exocrine Gland: It is a gland that pours its secretion on the surface or into a particular region by means of ducts for performic a metabolic activity, e.g., sebaceous glands, sweat glands, salivary glands, etc.

(b) Endocrine Gland: It is a gland that pours its secretion into blood or lymph for reaching the target organ because the gland is not connected with the target organ by any duct. It is also known as ductless gland.

(c) Hormone: Hormones are non-nutrient chemicals which act as intercellular messengers and are produced in trace amounts.

Question 2.
Diagrammatically indicate the location of the various endocrine glands in our body.

Fig- Location of Endocrine Glands

Question 3.
List the hormones secreted by the following:
(a) Hypothalamus
(b) Pituitary
(c) Thyroid
(d) Parathyroid
(e) Adrenal
(f) Pancreas
(g) Testis
(h) Ovary
(i) Thymus
(j) Atrium
(k) Kidney
(l) G-I Tract
Answer:
(a) Hypothalamus secrets Thyrotropin-releasing hormone, Adrenocorticotropin releasing hormone, Gonadotropin-releasing hormone, Somatotropin releasing hormone, Prolactin releasing hormone, Melanocyte stimulating hormone, releasing hormone.

(b)
(i) Pars Distalis Part of Pituitary (anterior pituitary) secrets Growth Hormone (GH), Prolactin (PRL), Thyroid Stimulating Hormone (TSH), Adrenocorticotrophic Hormone (ACTH), Luteinising Hormone (LH), Follicle Stimulating Hormone (FSH).
(ii) Pars Intermedia secrets Melanocyte Stimulating Hormone (MSH), Oxytocin, Vasopressin.

(c) Thyroid secrets Thyroxine (T4) and triiodothyronine (T3)
(d) Parathyroid secrets Parathyroid hormone (PTH).

(e) Adrenal
(i) secrets Adrenaline, Noradrenaline from adrenal medulla. ‘
(ii) also secretes corticoids (glucocorticoid and mineralocorticoid) and sexocorticoids from adrenal cortex.

(f) Pancreas: The a-cells secrete glucagon, while the β-cells secrete insulin.
(g) Testis: Androgens mainly testosterone.
(h) Ovary: Estrogen and progesterone.
(i) Thymus: Thymosins.
(j) Atrium: Atrial Natriuretic Factor (ANF).
(k) Kidney: Erythropoietin
(l) G-I Tract: Gastrin, secretin, cholecystokinin (CCK), and Gastric Inhibitory Peptide (GIP).

Question 4.
Fill in the blanks:

Hormones	Target gland
Hypothalamic hormones	……………………………
Thyrotrophin (TSH)	……………………………..
Corticotrophin (ACTH)	………………………………….
Gonadotrophins (LH, FSH)	………………………………..
Melanotrophin (MSH)	………………………………

Answer:

Hormones	Target gland
Hypothalamic hormones	Pituitary gland
Thyrotrophin (TSH)	Thyroid gland
Corticotrophin (ACTH)	Adrenal glands
Gonadotrophins (LH, FSH)	Testis and ovary
Melanotrophin (MSH)	Hypothalamus

Question 5.
Write short notes on the functions of the following hormones:
(a) Parathyroid hormone (PTH)
(b) Thyroid hormones
(c) Thymosins
(d) Androgens
(e) Estrogens
(f) Insulin and Glucagon
Answer:
(a) Parathyroid Hormone (PTH): The parathyroid glands secrete a peptide hormone called parathyroid hormone (PTH). PTH acts on bones and stimulates the process of bone resorption (dissolution/demineralization). PTH also stimulates reabsorption of Ca²⁺ by the renal tubules and increases Ca²⁺ absorption from the digested food. It plays a significant role in calcium balance in the body.

(b) Thyroid Hormones: Thyroid hormones play an important role in the regulation of the basal metabolic rate. These hormones also support the rocess of red blood cell formation. Thyroid hormones control the metabolism of carbohydrates, proteins and fats. The maintenance of water and electrolyte balance is also influenced by thyroid hormones. Thyroid gland also secretes a protein hormone called thyrocalcitonin (TCT), which regulates the blood calcium levels.

(c) Thymosins: The thymus gland secretes the peptide hormones called thymosins. Thymosins play a major role in the differentiation of T-lymphocytes, which provide cell-mediated immunity. In addition, thymosins also promote production of antibodies to provide humoral immunity.

(d) Androgens: Androgens regulate the development, maturation, and functions of the male accessory sex organs like epididymis, vas deferens, seminal vesicles, prostate gland, urethra, etc. These hormones stimulate muscular growth, growth of facial and axillary hair, aggressiveness, low pitch of voice, etc. Androgens play a major stimulatory role in the process of spermatogenesis (formation of spermatozoa), influence the male sexual behavior (libido).

(e) Estrogens: Estrogens produce wide-ranging actions such as stimulation of growth and activities of female secondary sex organs, development of growing ovarian follicles, appearance of female secondary sex characters (e.g., high pitch of voice, etc.), mammary gland development. Estrogens also regulate female sexual behavior.

(f) Insulin and Glucagon: Glucagon acts mainly on the liver cells and stimulates glycogenolysis resulting in increased blood sugar (hyperglycemia). In addition, this hormone stimulates the process of gluconeogenesis, which also contributes to hyperglycemia. Glucagon reduces the cellular glucose uptake and utilization.

Insulin is a peptide hormone, which plays a major role in the regulation of glucose homeostasis. Insulin acts mainly on hepatocytes and adipocytes and enhances cellular glucose uptake and utilization. Insulin also stimulates conversion of glucose to glycogen (glycogenesis) in the target cells. The glucose homeostasis in blood is thus maintained jointly by the two insulin and glucagons.

Question 6.
Give example(s) of:
(a) Hyperglycemic hormone and hypoglycemic hormone
(b) Hypercalcemic hormone
(c) Gonadotrophic hormones
(d) Progestational hormone ‘
(e) Blood pressure lowering hormone
(f) Androgens and estrogens
Answer:
(a) Glucagon and insulin respectively
(b) Parathyroid hormone
(c) Follicle-stimulating hormone and luteinizing hormones
(d) Progesterone
(e) Atrial Natriuretic IFactor (ANF)
(f) Androgens are mainly testosterone and estrogens include estrogen

Question 7.
Which hormonal deficiency is responsible for the following:
(a) Diabetes mellitus
(b) Goitre
(c) Cretinism
Answer:
(a) Diabetes mellitus is due to deficiency of insulin.
(b) Goitre is due to deficiency of thyroxine (T₄) and triiodothyronine (T₃).
(e) Cretinism is due to deficiency of thyroxine hormone.

Question 8.
Briefly mention the mechanism of action of FSH.
Answer:
Follicle Stimulating Hormone (FSH): In males, FSH and androgens regulate spermatogenesis. FSH stimulates growth and development of the ovarian follicles in females. It stimulates the secretion of estrogens in ovaries.

Question 9.
Match the following columns:

Column I	Column II
A. T4	1. Hypothalamus
B. PTH	2. Thyroid
C. GnRH	3. PituItary
D. LH	4. Parathyroid

Answer:

Column I	Column II
A.T4	2. Thyroid
B. PTH	4. Parathyroid
C. GnRH	1. Hypothalamus
D. LH	3. Pituitary

 

Punjab State Board PSEB 11th Class Physics Book Solutions Chapter 7 System of Particles and Rotational Motion Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Physics Chapter 7 System of Particles and Rotational Motion

PSEB 11th Class Physics Guide System of Particles and Rotational Motion Textbook Questions and Answers

Question 1.
Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
Answer:
The centre of mass (C.M.) is a point where the mass of a body is supposed to be concentrated. For the given geometric shapes having a uniform mass density, the C.M. lies at their respective geometric centres.
No, The centre of mass of a body need not necessarily lie within it. For example, the C.M. of bodies such as a ring, a hollow sphere, etc. lies outside the body.

Question 2.
In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1Å = 10^-10 m). Find the approximate location of the C.M. of the molecule, given that a chlorine atom is about 35.5 times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus.
Solution:
The given situation can be shown as:

Distance between H and Cl atoms = 1.27 Å
Mass of H atom = m
Mass of Cl atom = 35.5 m
Let the centre of mass of the system lie at a distance x Å from the Cl atom.
Distance of the centre of mass from the H atom = (1.27 – x) Å.
Let us assume that the centre of mass of the given molecule lies at the origin. Therefore, we can have:
\(\frac{m(1.27-x)+35.5 m x}{m+35.5 m}\) = 0
m (1.27 – x) + 35.5mx = 0
1.27 – x = -35.5x
x = \(\frac{-1.27}{(35.5-1)}\) = -0.037 Å
[the negative sign indicates that the centre of mass lies at the left of the molecule, -ve sign negligible.]
Hence, the centre of mass of the HC1 molecule lies 0.037Å from the Cl atom.
Hence, the centre of mass of the HC1 molecule lies
(1.27 – x) = 1.27 – 0.037 = 1.24 Å from the H atom.

Question 3.
A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system?
Solution:
The child is running arbitrarily on a trolley moving with velocity υ. However, the running of the child will produce no effect on the velocity of the centre of mass of the trolley. This is because the force due to the boy’s motion is purely internal. Internal forces produce no effect on the motion of the bodies on which they act. Since no external force is involved in the boy-trolley system, the boy’s motion will produce no change in the velocity of the centre of mass’of the trolley.

Question 4.
Show that the area of the triangle contained between the vectors [Latex]\vec{a}[/Latex] and [Latex]\vec{b}[/Latex] is one half of the magnitude of \(\vec{a} \times \vec{b}\).
Consider two vecters \(\overrightarrow{O K}=|\vec{a}|\) = and \(\overrightarrow{O M}=|\vec{b}|\) inclined at an angle θ as, shown in the following figure.

In Δ OMN , we can write the relation:
sinθ = \(\frac{M N}{O M}=\frac{M N}{|\vec{b}|}\)
MN = \(|\vec{b}|\) sinθ
\(|\vec{a} \times \vec{a}|=|\vec{a}||\vec{b}|\) sinθ
= OK.MN x \(\frac{2}{2}\)
= 2 x Area of Δ OMK
∴ Area of Δ𝜏 OMK = \(\frac{1}{2}\) \(|\vec{a} \times \vec{b}|\)

Question 5.
Show that \(\vec{a} \cdot(\vec{b} \times \vec{c})\) is equal in magnitude to the volume of the parallelepiped formed on the three vectors, \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\).
Solution:
A parallelepiped with origin O and sides \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) is shown in the following figure.

Volume of the given parallelepiped = abc
\(\overrightarrow{O C}=\vec{a}\)
\(\overrightarrow{O B}=\vec{b}\)
\(\overrightarrow{O C}=\vec{c}\)
Let n̂ be a unit vector perpendicular to both \(\) and \(\). Hence, n̂ and \(\)
have the same direction.
∴ \(\vec{b} \times \vec{c}\) = bc sin n̂
= bc sinθ n̂ bcsin90° n̂ = bc n̂
\(\vec{a} \cdot(\vec{b} \times \vec{c})\) = a.(bc n̂)
= abc cosθ n̂
= abc cos0°= abc
= Volume of the parallelepiped

Question 6.
Find the components along the x, y, z axes of the angular momentum \(\) of a particle, whose position vector is \(\) with components x, y, z and momentum is \(\) with components p_x, p_y and p_z. Show
that if the particle moves only in the x-y plane the angular momentum has only a z-component.
Solution:


The particle moves in the x – y plane. Hence, the z – component of the position vector and linear momentum vector becomes zero, i. e.,
z = P_z = 0
Thus, equation (i) reduces to

Therefore, when the particle is confined to move in the x – y plane, the direction of angular momentum is along the z – direction.

Question 7.
Two particles, each of mass m and speed υ, travel in opposite directions along parallel lines separated by a distance d. Show that the vector angular momentum of the two particle system is the same whatever be the point about which the angular momentum is taken.
Solution:
Let at a certain instant two particles be at points P and Q, as shown in the following figure.

Angular momentum of the system about point P:
\(\vec{L}\)_P = mυ × 0 + mυ × d
= mυd …………. (i)
Angular momentum of the system about point Q:
\(\vec{L}\)_Q = mυ × d + mυ × 0 = mυd …………… (ii)
Consider a point R, which is at a distance y from point Q, i. e.,
QR = y
∴ PR = d – y
Angular momentum of the system about point R:
\(\vec{L}\)_R = mυ × (d – y) + mυ × y = mυd – mυy + mυy
= mυd ……………. (iii)
Comparing equations (i), (ii), and (iii), we get
\(\vec{L}\)_P = \(\vec{L}\)_Q = \(\vec{L}\)_R ……….. (iv)
We infer from equation (iv) that the angular momentum of a system does not depend on the point about which it is taken.

Question 8.
A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in figure given below. The angles made by the strings with the vertical are 36.9° and 53.1° respectively. The bar is 2 m long. Calculate the distance d of the centre of gravity of the bar from its left end.

Solution:
The free body diagram of the bar is shown in the following figure.

Length of the bar, l = 2 m
T₁ and T₂ are the tensions produced in the left and right strings respectively.
At translational equilibrium, we have:
T₁ sin 36.9° = T₂ sin 53.1°
\(\frac{T_{1}}{T_{2}}=\frac{\sin 53.1^{\circ}}{\sin 36.9^{\circ}}=\frac{0.800}{0.600}=\frac{4}{3}\)
⇒ T₁ = \(\frac{4}{3}\) T₂ ……………… (i)
For rotational equilibrium, on taking the torque about the centre of gravity, we have:
T₁ cos 36.9° × d = T₂ cos 53.1° (2 – d)
T₂ × 0.800 d = T₂ 0.600 (2 – d)
\(\frac{4}{3}\) × T₂ × 0.800 d = T₂ [0.600 × 2 – 0.600 d] [from eq. (i)]
1.067 d+ 0.6 d = 1.2
∴ d = \(\frac{1.2}{1.67}\) = 0.72 m
Hence, the C.G. (centre of gravity) of the given bar lies 0.72 m from its left end.

Question 9.
A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its centre of gravity is 1.05 m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.
Solutio:
Mass of the car, m = 1800 kg
Distance between the front and back axles, d = 1.8 m
Distance between the C.G. (centre of gravity) and the back axle
= 1.05 m
The various forces acting on the car are shown in the following figure.

R_f and R_b are the forces exerted by the level ground on the front and back wheels respectively.
At translational equilibrium:
R_f + R_b = mg
= 1800 × 9.8 = 17640 N ………….. (i)
For rotational equilibrium, on taking the torque about the C.G.,
we have
R_f (1.05) = R_b (1.8 – 1.05)
R_f × 1.05 = R_b × 0.75
\(\frac{R_{f}}{R_{b}}=\frac{0.75}{1.05}=\frac{5}{7}\)
\(\frac{R_{b}}{R_{f}}=\frac{7}{5}\)
R_b = 1.4 R_f …………… (ii)
Solving equations (i) and (ii), we get
1.4 R_f + R_f =17640
⇒ 2.4 R_f = 17640
⇒ R_f = \(\frac{17640}{2.4}\)= 7350N
∴ Rb = 17640 – 7350 = 10290 N
Therefore, the force exerted on each front wheel = \(\frac{7350}{2}\) = 3675 N and
The force exerted on each back wheel = \(\frac{10290}{2}\)= 5145 N

Question 10.
(a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2 MR²/15, where M is the mass of the sphere and R is the radius of the sphere.
(b) Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR² /4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge.
Solution:
(a) The moment of inertia (M.I.) of a sphere about its diameter = \(\frac{2}{5}\)MR²

M.I.= \(\frac{2}{5}\)MR²
According to the theorem of parallel axes, the moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.
The M.I. about a tangent of the sphere = \(\frac{2}{5}\) MR² + MR² = \(\frac{7}{5}\) MR²

(b) The moment of inertia of a disc about its diameter = \(\frac{1}{4}\) MR²
According to the theorem of perpendicular axis, the moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes – concurrent with perpendicular axis and lying in the plane of the body.
The M.I. of the disc about its centre = \(\frac{1}{4}\) MR² + \(\frac{1}{4}\) MR² = \(\frac{1}{4}\) MR²
The situation is shown in the given figure.

Applying the theorem of parallel axes,
The moment of inertia about an axis normal to the disc and passing through a point on its edge = \(\frac{1}{2}\)MR² + \(\frac{1}{2}\)MR² = \(\frac{3}{2}\) MR²

Question 11.
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
Solution:
Let m and r be the respective masses of the hollow cylinder and the solid sphere.
The moment of inertia of the hollow cylinder about its standard axis,
I₁ = mr²
The moment of inertia of the solid sphere about an axis passing through its centre, I₂ = \(\frac{2}{5}\) mr²
We have the relation:
τ = Iα
where,
α = Angular acceleration
τ = Torque
I = Moment of inertia
For the hollow cylinder, τ₁ = I₁α₁
For the solid sphere, τ₂ = I₂τ₂
As an equal torque is applied to both the bodies, τ₁ = τ₂
∴ \(\frac{\alpha_{2}}{\alpha_{1}}=\frac{I_{1}}{I_{2}}=\frac{m r^{2}}{\frac{2}{5} m r^{2}}=\frac{5}{2}\)
⇒ α₂ = \(\frac{5}{2}\)α₁
⇒ α₂ > α₁ …………… (i)
Now, using the relation:
ω = ω₀ + αt
where,
ω₀ = Initial angular velocity
t = Time of rotation
ω = Final angular velocity
For equal ω and t, we have:
ω ∝ α ……………. (ii)
From equations (i) and (ii), we can write:
ω₂ > ω₁
Hence, the angular velocity of the solid sphere will be greater than that of the hollow cylinder.

Question 12.
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s^-1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis?
Solution:
Mass of the cylinder, m = 20 kg
Angular speed, ω = 100 rad s^-1
Radius of the cylinder, r = 0.25 m
The moment of inertia of the solid cylinder:
I = \(\frac{m r^{2}}{2}\) = \(\frac{1}{2}\) × 20 × (0.25)²
= 0.625 kg-m²
∴ Kinetic energy = \(\frac{1}{2}\) Iω² = \(\frac{1}{2}\) × 0.625 × (100)² = 3125 J
∴ Angular momentum, L = Iω = 0.625 × 100 = 62.5 J-s

Question 13.
(a) A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of 40 rev/min. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/5 times the initial value? Assume that the turntable rotates without friction.
(b) Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?
Solution:
(a) Initial angular velocity,ω₁ = 40 rev/min
Let, Final angular velocity = ω₂
The moment of inertia of the child with.stretched hands = I₁
The moment of inertia of the child with folded hands = I₂
The two moments of inertia are related as:
I₂ = \(\frac{2}{5}\)I₁
Since no external force acts on the boy, the angular momentum L is a constant.
Hence, for the two situations, we can write:
I₂ω₂ = I₁ω₁
ω₂ = \(\frac{I_{1}}{I_{2}}\) ω₁
= \(\frac{I_{1}}{\frac{2}{5} I_{1}}\) × 40 = \(\frac{5}{2}\) × 40
= 100 rev/min

∴ E_F = 2.5 E_I
The increase in the rotational kinetic energy is attributed to the internal energy of the child.

Question 14.
A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assume that there is no slipping.
Solution:
Mass of the hollow cylinder, m = 3 kg
Radius of the hollow cylinder, r = 40 cm = 0.4 m
Applied force, F = 30 N
The moment of inertia of the hollow cylinder about its geometric axis,
I = mr² = 3 × (0.4)² = 0.48 kg-m²
Torque, τ = F × r = 30 × 0.4 =12 N-m
For angular acceleration α, torque is also given by the relation
τ = Iα
α = \(\frac{\tau}{I}=\frac{12}{0.48}\)= 25 rad s^-2
Linear acceleration = rα = 0.4 × 25 = 10 ms^-2

Question 15.
To maintain a rotor at a uniform angular speed of 200 rad s^-1, an engine needs to transmit a torque of 180 N-m. What is the power required by the engine?
(Note: uniform angular velocity in the absence of friction implies zero torque. In practice, applied torque is needed to counter frictional torque). Assume that the engine is 100 % efficient.
Solution:
Angular speed of the rotor, ω = 200 rad / s
Torque required, τ = 180 N-m
The power of the rotor (P) is related to torque and angular speed by the relation:
P = τω
= 180 × 200 = 36 × 10³ W = 36 kW
Hence, the power required by the engine is 36 kW.

Question 16.
From a uniform disk of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of gravity of the resulting flat body.
Solution:
Let, Mass per unit area of the original disc = σ
Radius of the original disc = R
∴ Mass of the original disc, M = πR² σ
The disc with the cut portion is shown in the following figure:

Radius of the smaller disc = \(\frac{R}{2}\)
Mass of the smaller disc, M’= π(\frac{R}{2})² σ = \(\frac{1}{4}\)πR² σ = \(\frac{M}{4}\)

Let O and O'[]be the respective centres of the original disc and the disc cut off from the original. As per the definition of the centre of mass, the centre of mass of the original disc is supposed to be concentrated at O, while that of the smaller disc is supposed to be concentrated at O’.
It is given that:
00′ = \(\frac{R}{2}\)
After the smaller disc has been cut from the original, the remaining portion is considered to be a system of two masses. The two masses are:
M (concentrated at O), and
– M = (= \(\frac{M}{4}\)) concentrated at O’
(The negative sign indicates that this portion has been removed from the original disc.)
Let x be the distance through which the centre of mass of the remaining portion shifts from point O.
The relation between the centres of masses of two masses is given as:
x = \(\frac{m_{1} r_{1}+m_{2} r_{2}}{m_{1}+m_{2}}\)
For the given system, we can write:

(The negative sign indicates that the centre of mass gets shifted toward the left of point O.)
Hence, the centre of gravity is located at the distance of R/6 from the original centre of the body and opposite to the centre of the cut portion.

Question 17.
A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5 g are put one on top of the other at the 12.0 cm mark, the stick is found to he balanced at 45.0 cm. What is the mass of the metre stick?
Solution:
Let W and W’ be the respective weights of the metre stick and the coin.

The mass of the metre stick is concentrated at its mid-point, i. e., at the 50 cm mark.
Let, mass of the metre stick = m’
Given, mass of each coin, m = 5 g
When the coins are placed 12 cm away from the end P, the centre of mass gets shifted by 5 cm from point R toward the end P. The centre of mass is located at a distance of 45 cm from point P.
The net torque will be conserved for rotational equilibrium about point R.
10 × g (45 -12) – m’ g (50 – 45) = 0
⇒ 10 × 33 = m’ × 5
∴ m’ = \(\frac{10 \times 33}{5}\) = 66 g
Hence, the mass of the metre stick is 66 g.

Question 18.
A solid sphere rolls down two different inclined planes of the same heights hut different angles of inclination, (a) Will it reach the bottom with the same speed in each case? (b) Will it take longer to roll down one plane than the other? (c) If so, which one and why?
Solution:
(a) Yes (b) Yes (c) on the smaller inclination
(a) Mass of the sphere = m
Height of the plane = h
Velocity of the sphere at the bottom of the plane = υ
At the top of the plane, the total energy of the sphere
= Potential energy = mgh
At the bottom of the plane, the sphere has both translational and rotational kinetic energies.
Hence, total energy = –\(\frac{1}{2}\)mυ² + \(\frac{1}{2}\)Iω²
Using the law of conservation of energy, we can write:
\(\frac{1}{2}\)mυ² + \(\frac{1}{2}\)Iω² = mgh ……………. (i)
For a solid sphere, the moment of inertia about its centre, I = \(\frac{2}{5}\) mr²
Hence equation (i) becomes,
\(\frac{1}{2}\)mυ² + \(\frac{1}{2}\) (\(\frac{2}{5}\)mr²)ω² = mgh
\(\frac{1}{2}\)υ² + \(\frac{1}{5}\)r²ω² = gh
But we have the relation, υ = rω
\(\frac{1}{2}\)υ² + \(\frac{1}{5}\)υ² = gh
∴ υ²(\(\frac{7}{10}\)) = gh
υ = \(\sqrt{\frac{10}{7} g h}\)
Hence, the velocity of the sphere at the bottom depends only on height (h) and acceleration due to gravity (g). Both these values are constants. Therefore, the velocity at the bottom remains the same from whichever inclined plane the sphere is rolled.

(b), (c) Consider two inclined planes with inclinations θ₁ and θ₂, related as
θ₁ < θ₂
The acceleration produced in the sphere when it rolls down the plane inclined at θ₁,
θ₁ = g sinθ₁
The various forces acting on the sphere are shown in the following figure.

R₁ is the normal reaction to the sphere.
Similarly, the acceleration produced in the sphere when it rolls down the plane inclined at θ₂,
a₂ = gsinθ₂
The various forces acting on the sphere are shown in the following figure.

R₂ is the normal reaction to the sphere.
θ₂ > 0₁; sinθ₂ > sinθ₁ ……….(i)
∴ a₂ > a₁ ……………. (ii)
Initial velocity, u = 0
Final velocity, υ = Constant
Using the first equation of motion, we can obtain the time of roll as,
υ = u + at
t ∝ \(\frac{1}{a}\)

From equations (ii) and (iii), we get:
t₂ < t₁
Hence, the sphere will take a longer time to reach the bottom of the inclined plane having the smaller inclination.

Question 19.
A hoop of radius 2 m weighs 100 kg. It rolls along a horizontal floor so that its centre of mass has a speed of 20 cm/s. How much work has to he done to stop it?
Solution:
Radius of the hoop, r = 2 m
Mass of the hoop, m = 100 kg
Velocity of the hoop, υ = 20 cm/s = 0.2 m/s
Total kinetic energy of the hoop = Translational KE + Rotational KE
E_T = \(\frac{1}{2}\)mυ² + \(\frac{1}{2}\) Iω²
Moment of inertia of the hoop about its centre, I = mr²
E_T = \(\frac{1}{2}\) mυ² + \(\frac{1}{2}\)(mr² )ω²
But we have the relation, υ = rω
E_T = \(\frac{1}{2}\) mυ² + \(\frac{1}{2}\)mr² ω²
= \(\frac{1}{2}\) mυ² + \(\frac{1}{2}\)mυ² = mυ²
The work required to be done for stopping the hoop is equal to the total energy of the hoop.
□Required work to be done,
W = mυ² =100 × (0.2)² = 4 J

Question 20.
The oxygen molecule has a mass of 5.30 × 10^-26 kg and a moment of inertia of 1.94 × 10^-46 kg-m² about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 m/s and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
Solution:
Mass of an oxygen molecule, m = 5.30 × 10^-26 kg
Moment of inertia, I =1.94 × 10^-46 kg-m²
Velocity of the oxygen molecule, υ = 500 m/s
The separation between the two atoms of the oxygen molecule = 2 r
Mass of each oxygen atom = \(\frac{m}{2}\)
Hence, moment of inertia I, is calculated as

Question 21.
A solid cylinder rolls up an inclined plane of angle of inclination 30°. At the bottom of the inclined plane the centre of mass of the , cylinder has a speed of 5 m/s.
(a) How far will the cylinder go up the plane?
(b) How long will it take to return to the bottom?
Solution:
(a) A solid cylinder rolling up an inclination is shown in the following figure.

Initial velocity of the solid cylinder, υ = 5 m/s
Angle of inclination, θ = 30°
Height reached by the cylinder = h
Energy of the cylinder at point A
KE_rot = KE_trans
\(\frac{1}{2}\) Iω² = \(\frac{1}{2}\)mυ²
Energy of the cylinder at point B = mgh
Using the law of conservation of energy, we can write
\(\frac{1}{2}\) Iω² + \(\frac{1}{2}\)mυ² =mgh

Hence, the cylinder will travel 3.82 m up the inclined plane.

(b) For radius of gyration K, the velocity of the cylinder at the instance
when it rolls back to the bottom is given by the relation:


Therefore, the total time taken by the cylinder to return to the bottom is 2 × 0.764 = 1.53 s.

Question 22.
As shown in figure given below, the two sides of a step ladder BA and CA are 1.6 m long and hinged at A. A rope DE, 0.5 m is tied half way up. A weight 40 kg is suspended from a point F, 1.2 m from B along the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take g = 9.8 m/s²)
(Hint: Consider the equilibrium of each side of the ladder separately.)

Solution:
The given situation can be shown as:

where, N_B = Force exerted on the ladder by the floor point B
N_C = Force exerted on the ladder by the floor point C
T = Tension in the rope
BA = CA =1.6 m
DE = 0.5 m
BF =1.2 m
Mass of the weight, m = 40 kg
Draw a perpendicular from A on the floor BC. This intersects DE at mid-point H.
Δ ABI and Δ AIC are similar
∴ BI = IC
Hence, I is the mid-point of BC.
In Δ ABC, DE || BC
∴ BC = 2 × DE = 1m
and AF = BA – BF= 1.6 – 1.2 = 0.4 m …………… (i)
D is the mid-point of AB.
Hence, we can write:
AD = \(\frac{1}{2}\) × BA = 0.8 m ………….. (ii)
Using equations (i) and (ii), we get
DF = AD – AF = 0.8 – 0.4 = 0.4 m
Hence, F is the mid-point of AD.
FG || DH and F is the mid-point of AD. Hence, G will also be the mid-point ofAH.
Δ AFG and Δ ADH are similar
∴ \(\frac{F G}{D H}=\frac{A F}{A D}\)
\(\frac{F G}{D H}=\frac{0.4}{0.8}=\frac{1}{2}\)
FG = \(\frac{1}{2}\)DH
= \(\frac{1}{2}\) × 0.25 = 0.125 m , [∵ DH = \(\frac{1}{2}\)DE]
In Δ ADH,
AH = \(\sqrt{A D^{2}-D H^{2}}\)
= \(\sqrt{(0.8)^{2}-(0.25)^{2}}\) = 0.76 m
For translational equilibrium of the ladder, the upward force should be equal to the downward force.
N_B + N_C = mg = 40 × 9.8 = 392 …………….. (iii)
For rotational equilibrium of the ladder, the net moment about A is
-N_B × BI + mg × FG + N_C × CI + T × AG – T × AG = 0
-N_B × 0.5 + 40 × 9.8 × 0.125 + N_C × (0.5) = 0
(N_B – N_C) × 0.5 = 49
N_B – N_C = 98 …………. (iv)
Adding equations (iii) and (iv), we get:
N_B = 245 N
N_C = 147N
For rotational equilibrium of the side AB, consider the moment about A
-N_B × BI + mg × FG + T × AG = 0
-245 × 0.5 + 40 × 9.8 × 0.125 + T × 0.76 = 0
0.76 T = 122.5 – 49 = 73.5
T = \(\frac{73.5}{0.76}\)= 96.7N

Question 23.
A man stands on a rotating platform, with his arms stretched horizontally holding a 5 kg weight in each hand. The angular speed of the platform is 30 revolutions per minute. The man ‘ then brings his arms close to his body with the distance of each weight from the axis changing from 90 cm to 20cm. The moment *of inertia of the man together with the platform may be taken to be constant and equal to 7.6 kg-m² .
(a) What is his new angular speed? (Neglect friction.)
(b) Is kinetic energy conserved in the process? If not, from where does the change come about?
Solution:
(a) Moment of inertia of the man-platform system
= 7.6 kg-m²
Moment of inertia when the man stretches his hands to a distance of 90 cm
= 2 × mr² = 2 × 5 × (0.9)²
= 8.1 kg-m²
Initial moment of inertia of the system, I_i = 7.6 + 8.1 = 15.7 kg-m²
Initial angular speed, ω_i = 30 rev/min
Initial angular momentum, L_i = I_iω_i = 15.7 × 30 …………….. (i)
Moment of inertia when the man folds his hands to a distance of 20 cm
= 2 × mr² = 2 × 5(0.2)² = 0.4 kg-m²
Final moment of inertia, I_f = 7.6 + 0.4 = 8 kg-m²
Let, final angular speed = ω_f
Final angular momentum, L_f = I_fω_f = 8ω_f ………….. (ii)
From the conservation of angular momentum, we have
I_iω_i = I_fω_f
∴ ω_f = \(\frac{15.7 \times 30}{8}\)= 58.88 rev/min
Hence, new angular speed is 58.88 revolutions per minute.

(b) No, kinetic energy is not conserved in the given process. In fact, with the decrease in the moment of inertia, kinetic energy increases. The additional kinetic energy comes from the work done by the man to fold his hands toward himself.

Question 24.
A bullet of mass 10 g and speed 500 m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0 m wide and weighs 12 kg. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it. (Hint: The moment of inertia of the door about the vertical axis at one end is ML² /3.)
Solution:
Mass of the bullet, m = 10 g = 10 x 10^-3 kg
Velocity of the bullet, υ = 500 m/s
Thickness of the door, L = 1 m
Radius of the door, r = \(\frac{1}{2}\) m
Mass of the door, M = 12 kg
Angular momentum imparted by the bullet on the door,
α = mυr
= (10 × 10^-3) × (500) × \(\frac{1}{2}\) = 2.5kg-m²s^-1 ………………. (i)
Moment of inertia of the door,
I = \(\frac{1}{2}\)ML² = \(\frac{1}{3}\) × 12 × (1)² = 4 kg-m²
But α = Iω
∴ ω = \(\) = 0.625 rad s^-1

Question 25.
Two discs of moments of inertia I\ and /2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds ω₁ and ω₂ are brought into contact face to face with their axes of rotation coincident, (a) What is the angular speed of the two-disc system? (b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies ‘of the two discs. How do you account for this loss in energy? Take ω₁ ≠ ω₂.
Solution:
(a) Moment of inertia of disc I = I₁
Angular speed of disc I = ω₁
Moment of inertia of disc II = I₂
Angular speed of disc II = ω₂
Angular momentum of disc I, L₁ = I₁ω₁
Angular momentum of disc II, L₂ = I₂ω₂
Total initial angular momentum, L _i = I₁ω₁ + I₂ω₂
When the two discs are joined together, their moments of inertia get added up.
Moment of inertia of the systme of two discs, I = I₁ + I₂
Let ω be the angular speed of the system.
Total final angular momentum, L_f = (I₁ + I₂)ω
Using the law of conservation of angular momentum, we have
L_i = L_f
I₁₁ + I₂₂ (I₁ + I₂)ω
< ω = \(\frac{I_{1} \omega_{1}+\bar{I}_{2} \omega_{2}}{I_{1}+I_{2}}\)

(b) Kinetic energy of disc I, E₁ = \(\frac{1}{2}\)I₁ω₁²
Kinetic energy of disc II, E₂ = \(\frac{1}{2}\)I₂ω₂²
Total initial kinetic energy, E_i = E₁ + E₂ = \(\frac{1}{2}\) (I₁ω₁² + I₂ω₂²)
When the discs are joined, their moments of inertia get added up.
Moment of inertia of the system, I = I₁ + I₂
Angular speed of the system = ω
Final kinetic energy E_f.

All the quantities on RHS are positive
∴ E_i – E_f > 0
E_i > E_f
The loss of KE can be attributed to the frictional force that comes into play when the two discs come in contact with each other.

Question 26.
(a) Prove the theorem of perpendicular axes.
(Hint: Square of the distance of a point (x, y) in the x – y plane from an axis through the origin perpendicular to the plane is x² + y² )
(b) Prove the theorem of parallel axes.
(Hint: If the centre of mass is chosen to be the origin Z m_ir_i = 0).
Solution:
(a) The theorem of perpendicular axes states that the moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with perpendicular axis and lying in the plane of the body.
A physical body with centre O and a point mass m, in the x – y plane at , (x, y) is shown in the following figure.

Moment of inertia about x – axis, I_x = mx²
Moment of inertia about y – axis, I_y = my²
Moment of inertia about z – axis, I_z = \(\left(\sqrt{x^{2}+y^{2}}\right)^{2}\)
I_x + I_y = mx² + my²
= m(x² + y²)
= m\(\left(\sqrt{x^{2}+y^{2}}\right)^{2}\)
I_x + I_y = I_z
Hence, the theorem is proved.

(b) The theorem of parallel axes states that the moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel . axes.

Suppose a rigid body is made up of n particles, having masses m₁, m₂, m₃, …… , m_n, at perpendicular distances r₁, r₂, r₃, ………….. , m_n respectively from the centre of mass O of the rigid body.
The moment of inertia about axis RS passing through the point O,

I_IRS = \(\sum_{i=1}^{n}\) m_ir_i

The perpendicular distance of mass mi, from the axis QP = a + r_i
Hence, the moment of inertia about axis QP,
I_QP = \(\sum_{i=1}^{n}\)_i(a + r_i)²

Now, at the centre of mass, the moment of inertia of all the particles about the axis passing through the centre of mass is zero, that is,
2 \(\sum_{i=1}^{n}\) m_iar_i = 0
∴ m_ir_i = 0
a ≠ 0
Σm_ir_i = 0
Also, \(\sum_{i=1}^{n}\) m_i = M; M = Total mass of the rigid body
∴ I_QP = I_RS + Ma²
Hence, the theorem is proved.

Question 27.
Prove the result that the velocity v of translation of a rolling hody (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height h is given by
υ² = \(\frac{2 g h}{\left(1+k^{2} / R^{2}\right)}\)
using dynamical consideration (i. e., by consideration of forces and torques). Note k is the radius of gyration of the body about its symmetry axis, and R is the radius of the body. The body starts from rest at the top of the plane.
Solution:
A body rolling on an inclined plane of height h, is shown in the following figure :

m = Mass of the body
R = Radius of the body
k = Radius of gyration of the body
υ = Translational velocity of the body
h = Height of the inclined plane
g = Acceleration due to gravity
Total energy at the top of the plane, E_T = mgh
Total energy at the bottom of the plane,
E_b = KE_rot + KE_trains
= \(\frac{1}{2}\)Iω² + \(\frac{1}{2}\)mυ²

Hence, the given result is proved.

Question 28.
A disc rotating about its axis with angular speed (ω₀ is placed lightly (without any translational push) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points A, B and C on the disc shown in figure? Will the disc roll in the direction indicated?

Solution:
Angular speed of the disc = ω₀
Radius of the disc = R
Using the relation for linear velocity, υ = ω₀R
For point A:υ_A = Rω₀; in the direction tangential to the right
For point B:υ_B = Rω₀; in the direction tangential to the left
For point C:υ_C = (\(\frac{R}{2}\))ω₀; in the direction same as that of vA.
The directions of motion of points A, B and C on the disc are shown in the following figure

Since the disc is placed on a frictionless table, it will not roll. This is because the presence of friction is essential for the rolling of a body.

Question 29.
Explain why friction is necessary to make the disc in figure given in question 28 roll in the direction indicated.
(a) Give the direction of frictional force at B, and the sense of frictional torque, before perfect rolling begins.
(b) What is the force of friction after perfect rolling begins?
Solution:
A torque is required to roll the given disc. As per the definition of torque,
the rotating force should be tangential to the disc. Since the frictional force at point B is along the tangential force at point A, a frictional force is required for making the disc roll.

(a) Force of friction acts opposite to the direction of velocity at point B. The direction of linear velocity at point B is tangentially leftward. Hence, frictional force will act tangentially rightward. The sense of frictional torque before the start of perfect rolling is perpendicular to the plane of the disc in the outward direction.

(b) Since frictional force acts opposite to the direction of velocity at point B, perfect rolling will begin when the velocity at that point becomes equal to zero. This will make the frictional force acting on the disc zero.

Question 30.
A solid disc and a ring, both of radius 10 cm are placed on a horizontal table simultaneously, with initial angular speed equal to 10 πrad s^-1. Which of the two will start to roll earlier? The coefficient of kinetic friction is μ_k = 0.2
Solution:
Radii of the ring and the disc, r- = 10 cm = 0.1 m
Initial angular speed, ω₀ = 10 πrad s-^-1
Coefficient of kinetic friction, μ_k = 0.2
Initial velocity of both the objects, u = 0
Motion of the two objects is caused by frictional force. As per Newton’s second law of motion, we have frictional force, f = ma.
μ_kmg = ma
where,
a = Acceleration produced in the objects
m = Mass
∴ a = μ_kg …………… (i)
As per the first equation of motion, the final velocity of the objects can be obtained as
υ = u + at
= 0 + μ_kgt
= μ_kgt ……………. (ii)
The torque applied by the frictional force will act in perpendicularly outward direction and cause reduction in the initial angular speed.
Torque, τ = -Iα
where, α = Angular acceleration
μ_kmgr = -Iα
∴ α = \(\frac{-\mu_{k} m g r}{I}\) ……………… (iii)
Using the first equation of rotational motion to obtain the final angular speed,

Question 31.
A cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination 30°. The coefficient of static friction μ_g, = 0.25.
(a) How much is the force of friction acting on the cylinder?
(b) What is the work done against friction during rolling?
(c) If the inclination θ of the plane is increased, at what value of θ does the cylinder begin to skid, and not roll perfectly?
Solution:
Given, mass of the cylinder, m =10 kg
Radius of the cylinder, r = 15cm = 0.15m
Coefficient of static friction, μ_s = 0.25
Angle of inclination, θ = 30°
Moment of inertia of a solid cylinder about its geometric axis, I = \(\frac{1}{2}\)mr²
The various forces acting on the cylinder are shown in the following figure:

= \(\frac{2}{3}\) × 9.8 × 0.5 = 3.27 m/s²

(a) Using Newton’s second law of motion, we can write net force as
f_netnet = ma
mg sin30° – f = ma
f = mgsin30° – ma
= 10 × 9.8 × 0.5 – 10 × 3.27
= 49 – 32.7 = 16.3 N

(b) During rolling, the instantaneous point of contact with the plane comes to rest. Hence, the work done against frictional force is zero.

(c) For rolling without skid, we have the relation:
μ = \(\frac{1}{3}\)tanθ
tanθ = 3μ = 3 × 0.25
∴ θ = tan^-1 (0.75) = 36.87°

Question 32.
Read each statement below carefully, and state, with reasons, if it is true or false;
(a) During rolling, the force of friction acts in the same direction as the direction of motion of the CM of the body.
(b) The instantaneous speed of the point of contact during rolling is zero.
(c) The instantaneous acceleration of the point of contact during rolling is zero.
(d) For perfect rolling motion, work done against friction is zero.
(e) A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling) motion.
Solution:
(a) False
Reason: Frictional force acts opposite to the direction of motion of the centre of mass of a body. In the case of rolling, the direction of motion of the centre of mass is backward. Hence, frictional force acts in the forward direction.

(b) True
Reason: Rolling can be considered as the rotation of a body about an axis passing through the point of contact of the body with the ground. Hence, its instantaneous speed is zero.

(c) False
Reason: When a body is rolling, its instantaneous acceleration is not equal to zero. It has some value.

(d) True
Reason: When perfect rolling begins, the frictional force acting at the lowermost point becomes zero. Hence, the work done against friction is also zero.

(e) True
Reason: The rolling of a body occurs when a frictional force acts between the body and the surface. This frictional force provides the torque necessary for rolling. In the absence of a frictional force, the body slips from the inclined plane under the effect of its own weight.

Question 33.
Separation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass:
(a) Show \(\overrightarrow{p_{i}}=\overrightarrow{p_{i}^{\prime}}=m_{i} \vec{V}\)
where, \(\overrightarrow{p_{i}}\) is the momentum of the i^th particle (of mass m_i) and \(\overrightarrow{p_{i}^{\prime}}=\vec{m}_{i} \vec{v}_{i}^{\prime}\). Note \(\overrightarrow{\boldsymbol{v}_{\boldsymbol{i}}^{\prime}}\) is the velocity of the i^th particle relative to the centre of mass.
Also, prove using the definition of the centre of mass \(\sum_{i} \overrightarrow{p_{i}^{\prime}}\) = 0

(b) Show K = K’ + \(\frac{1}{2}\) MV²
where, K is the total kinetic energy of the system of particles, K’ is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and MV² /2 is the kinetic energy of the translation of the system as a whole (i. e., of the centre of mass motion of the system). The result has been used in Sec. 7.14.

(c) Show \(\overrightarrow{\boldsymbol{L}}^{\prime}=\overrightarrow{\boldsymbol{L}}^{\prime}+\overrightarrow{\boldsymbol{R}} \times \boldsymbol{M} \overrightarrow{\boldsymbol{V}}\)
where, \(\overrightarrow{\boldsymbol{L}}^{\prime}=\Sigma \overrightarrow{\boldsymbol{r}_{\boldsymbol{i}}^{\prime}} \times \overrightarrow{\boldsymbol{p}_{\boldsymbol{i}}^{\prime}}\) is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember \(\overrightarrow{\boldsymbol{r}_{i}^{\prime}}=\overrightarrow{\boldsymbol{r}_{i}}-\overrightarrow{\boldsymbol{R}}\) rest of the notation is the standard notation used in the chapter. Note \(\overrightarrow{\boldsymbol{L}}\) and \(\boldsymbol{M} \overrightarrow{\boldsymbol{R}} \times \overrightarrow{\boldsymbol{V}}\) can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.

(d) Show = \(\frac{d \vec{L}^{\prime}}{d t}=\sum_{i} \overrightarrow{r_{i}^{\prime}} \times \frac{d}{d t}\left(\overrightarrow{p_{i}^{\prime}}\right)\)
Further, show that
\(\frac{d \vec{L}^{\prime}}{d t}\) = τ’_ext
where, τ’_ext is the sum of all external torques acting on the system about the centre of mass.
(Hint: Use the definition of centre of mass and Newton’s Third Law. Assume the internal forces between any two particles act along the line joining the particles.)
Solution:
(a) Take a system of i moving particles.
Mass of the i^th particle = m_i
Velocity of the t^th particle = υ_i
Hence, momentum of the i^th particle, \(\overrightarrow{p_{i}}\) = m_iυ_i
Velocity of the centre of mass = V
The velocity of the i^th particle with respect to the centre of mass of the system is given as:
\(\overrightarrow{v_{i}^{\prime}}=\overrightarrow{v_{i}}-\vec{V}\) ……………. (i)
Multiplying m; throughout equation (i), we get
\(m_{i} \overrightarrow{v_{i}^{\prime}}=m_{i} \overrightarrow{v_{i}}-m_{i} \vec{V}\)
\(\overrightarrow{p_{i}^{\prime}}=\overrightarrow{p_{i}}-m_{i} \vec{V}\)
where, \(\overrightarrow{p_{i}^{\prime}}=m_{i} \overrightarrow{v_{i}^{\prime}}\) = Momentum of the i^th particle with respect to the centre of mass of the system
∴ \(\overrightarrow{p_{i}}=\overrightarrow{p_{i}^{\prime}}+m_{i} \vec{V}\)
We have the relation: \(\overrightarrow{p_{i}^{\prime}}=m_{i} \overrightarrow{v_{i}^{\prime}}\)
Taking the summation of momentum of all the particles with respect to the centre of mass of the system, we get
\(\Sigma \overrightarrow{p_{i}^{\prime}}=\Sigma_{i} m_{i} \overrightarrow{v_{i}^{\prime}}=\Sigma_{i} m_{i} \frac{d \overrightarrow{r_{i}^{\prime}}}{d t}\)
where, \(\overrightarrow{r_{i}^{\prime}}\) = Position vector of i^th particle with respect to the centre of mass
\(\overrightarrow{v_{i}^{\prime}}=\frac{d \overrightarrow{r_{i}^{\prime}}}{d t}\)
As per the definition of the centre of mass, we have
\(\sum_{i} m_{i} \overrightarrow{r_{i}^{\prime}}\) = 0
\(\sum_{i} m_{i} \frac{d \overrightarrow{r_{i}^{\prime}}}{d t}\) = 0
\(\sum_{i} \overrightarrow{p_{i}^{\prime}}\) = 0

(b) KE. of a system consists of two parts translational K.E. (K_t) and rotational K.E. (K’) i.e., K.E. of motion of C.M. (\(\frac{1}{2}\)mυ²) and K.E. of rotational motion about the C.M. of the system of particles (K’), thus total K.E. of the system is given by
K = \(\frac{1}{2}\)mυ² + \(\frac{1}{2}\) Iω²
= \(\frac{1}{2}\)mυ² + K’
= K’ + \(\frac{1}{2}\)mυ²

(c) Position vector of the i th particle with respect to origin = \(\overrightarrow{r_{i}}\)
position vector of the i th particle with respect to the centre of mass = \(\overrightarrow{r_{i}^{\prime}}\)
Position vector of the centre of mass with respect to the origin = \(\vec{R}\)
It is given that:
\(\overrightarrow{r_{i}^{\prime}}=\overrightarrow{r_{i}}-\vec{R}\)
\(\overrightarrow{r_{i}}=\overrightarrow{r_{i}^{\prime}}+\vec{R}\)
We have from part (a),
\(\overrightarrow{p_{i}}=\overrightarrow{p_{i}^{\prime}}+m_{i} \vec{V}\)
Taking the cross product of this relation by r_i, we get:

Punjab State Board PSEB 11th Class Biology Book Solutions Chapter 19 Excretory Products and their Elimination Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Biology Chapter 19 Excretory Products and their Elimination

PSEB 11th Class Biology Guide Excretory Products and their Elimination Textbook Questions and Answers

Question 1.
Define Glomerular Filtration Rate (GFR).
Answer:
Glomerular Filtration Rate (GFR) is the amount of the filtrate formed by the kidneys per minute. GFR in a healthy individual is approximately 125 mt/mm, i.e., 180 L day.

Question 2.
Explain the autoregulatory mechanism of GFR.
Answer:
Regulation of GFR: The kidneys have built-in mechanisms for the regulation o glomerular filtration rate. One such efficient mechanism is carried out by the juxtaglomerular apparatus (JGA). JGA is a special sensitive region formed by cellular modifications in the distal convoluted tubule and the afferent arteriole at the location of their contact. A fall in GFR can activate the JG cells to release renin which can stimulate the glomerular blood flow and thereby the GFR back to normal.

Question 3.
Indicate whether the following statements are true or false:
(a) Micturition is carried out by a reflex.
(b) Al)H helps In water elimination, making the urine hypotonia.
(c) Protein-free fluid is filtered from blood plasma into the Bowman’s capsule.
(d) Henle’s loop plays an important role in concentrating the urine.
(e) Glucose is actively reabsorbed in the proximal convoluted tubule.
Answer:
(a) True,
(b) False,
(C) True,
(d) True,
(e) True.

Question 4.
Give a brief account of the counter-current mechanism.
Answer:
Counter-current Mechanism

• The counter-current mechanism takes place in Henle’s loop and vasa recta.
• The flow of filtrate in the two limbs of Henle’s loop is in opposite directions and thus, forms a counter-current.
• The flow of blood through the two limbs of vasa recta is also in a counter-current pattern.
• NaCl is transported by the ascending limb of Henle’s loop which is exchanged with the descending limb of vasa recta.
• NaCl is returned to the interstitium by the ascending portion of vasa recta.
• Similarly small amount of urea enters the thin segment of the ascending limb of Henle’ loop, which is transported back to the interstitium by the collecting tubule.
• This transport of substances facilitated by the special arrangement of Henle’s loop and vasa recta is called the counter-current mechanism,
• It helps to maintain a concentration gradient in the medullary interstitium, which facilitates an easy passage of water from the collecting tubule thereby concentrating the filtrate (urine).

Question 5.
Describe the foie of liver, lungs and skin in excretion.
Answer:
Liver, lungs and skin also play an important role in the process of excretion. Role of the Liver: Liver is the largest gland in vertebrates. It helps in the excretion of cholesterol, steroid hormones, vitamins, drugs, and other waste materials through bile. Urea is formed in the liver by the ornithine cycle. Ammonia-a toxic substance is quickly changed into urea in the liver and thence eliminated from the body. Liver also changes the decomposed haemoglobin pigment into bile pigments called bilirubin and biliverdin.

Role of the Lungs: Lungs help in the removing waste materials such as carbon dioxide from the body.
Role of the Skin: Skin has many glands which help in excreting waste products through pores. It has two types of glands-sweat and sebaceous glands.

Sweat glands are highly vascular and tubular glands that separate the waste products from the blood and excrete them in the form of sweat. Sweat excretes excess salt and water from the body.
Sebaceous glands are branched glands that secrete an oily secretion called sebum.

Question 6.
Explain micturition.
Answer:
Micturition: The process of release of urine is called micturition and the neural mechanisms causing it is called the micturition reflex. An adult human excretes on an average 1 to 1.5 L of urine per day. The urine formed is a light yellow coloured watery fluid which is slightly acidic (pH 6.0) and has a characteristic odour.

Question 7.
Match the items of Column-I with those of Column-II:

Column-I	Column-II
(a) Ammonotelism	(i) Birds
(b) Bowman’s capsule	(ii) Water reabsorption
(c) Micturition	(iii) Bony fish
(d) Uricotelism	(iv) Urinary bladder
(e) ADH	(v) Renal tubule

Answer:

Column-I	Column-II
(a) Ammonotelism	(iii) Bony fish
(b) Bowman’s capsule	(v) Renal tubule
(c) Micturition	(iv) Urinary bladder
(d) Uricotelism	(i) Birds
(e) ADH	(ii) Water reabsorption

Question 8.
What is meant by the term osmoregulation?
Answer:
It is the phenomenon of regulation of change in the concentration of body fluids according to the concentration of external environment. Le., most marine invertebrates, some freshwater invertebrates, hagfish (a vertebrate).

Question 9.
Terrestrial animals are generally either republic or uricotelic, not ammonotelic, why?
Answer:
Terrestrial adaptation requires the production of less toxic nitrogenous wastes like urea and uric acid for the conservation of water. Aquatic animals excret atnmonia which requires large amounts of water to dissolve. This huge quantity of water is easily available to such animals from surroundings.

However, for terrestrial animals, such a huge quantity of water is not available, hence, they modify their original water product NH3 to comparatively less toxic products like urea and uric acid which requires less amount of water for their excretion.

Question 10.
What is the significance of juxtaglomerular apparatus (JGA) in Sidney function?
Answer:
The juxtaglomerular apparatus (JGA) plays an important role in monitoring and regulation of kidney functioning by hormonal feedback, mechanism, involving the hypothalamus and to a certain extent, the heart.

Question 11.
Name the following:
(a) A chordate animal having flame cells as excretory structures.
(b) Cortical portions projecting between the medullary pyramids in the human kidney.
(c) A loop of capillary running parallel to the Henle’s loop.
Answer:
(a) Flarworms,
(b) Columns of Bertini,
(c) Vasa recta

Question 12.
Fill in the gaps:
(a) Ascending limb of Henle’s loop is ………………………… to water whereas the descending limb is …………………….. to it.
(b) Reabsorption of water from distal parts of the tubules is facilitated by hormone ……………………………. .
(c) Dialysis fluid contains all the constituents as in plasma except …………………………… .
(d) A healthy adult human excretes (on an average) ………………………… gm of urea/day.
Answer:
(a) impermeable, permeable;
(b) vasopressin or ADH.;
(c) the nitrogenous wastes;
(d) 25-30.

Punjab State Board PSEB 11th Class Biology Book Solutions Chapter 4 Animal Kingdom Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Biology Chapter 4 Animal Kingdom

PSEB 11th Class Biology Guide Animal Kingdom Textbook Questions and Answers

Question 1.
What are the difficulties that you would face in classification of animals, if common fundamental features are not taken into account?
Answer:
The major difficulties in the classification of animals are on the following lines :

• Some show cellular level of organisation, some have tissue level and even some have organ system level of organisation.
• Regarding symmetry, some are radially symmetrical, while some have bilateral symmetry.
• Some have open circulatory system, while others have closed type.
• Regarding digestion, some animals have extracellular digestion, while others have intracellular digestion.
• In case of body cavity, some have true coelom while others are pseudocoelomates.
• Regarding reproduction, some have only asexual reproduction, while others reproduce both by sexual and asexual means.
  So, these are difficulties that zoologists face in the classification of animals.

Question 2.
If you are given a specimen, what are the steps that you would follow to classify it?
Answer:
If I am given an animal specimen, then I will classify it on the basis of fundamental features which are common to all animal types inspite of the presence of some major differences in the structure and form of animals. The features taken into consideration during classification of animal are as follows:

• The type of arrangement of cells.
• Body symmetry.
• Nature of coelom.
• Pattern of digestive system.
• Type of circulatory system.
• Type of methods of reproduction.

Question 3.
How useful is the study of the nature of body cavity and coelom in the classification of animals?
Answer:
Presence or absence of a cavity between the body wall and the gut wall is very important in classification. The body cavity which is lined by, mesoderm, is called coelom.

• Animals possessing coelom are called coelomates, e.g., annelids, molluscs, arthropods, echinoderms, hemichordates and chordates.
• In some animals, the body cavity is not mesoderm, instead the mesoderm is present as scattered pouches in between the ectoderm and endoderm. Such a body cavity is called pseudocoelom and the animals possessing them are called pseudocoelomates, e.g., Aschelminthes.
• The animals in which the body cavity is absent are known as acoelomates, e.g. , Platyhelminthes.

Question 4.
Distinguish between intracellular and extracellular digestion?
Answer:
Differences between intracellular and extracellular digestion are as follows:
(i) Intracellular Digestion: It occurs inside the living cells with the help of lysosomal enzymes. Food particle is taken in through endocytosis. It forms a phagosome which fuses with a lysosome. The digested material pass into the cytoplasm. The undigested matter is throw out by exocytosis. It occurs in Amoeba, Paramecium, etc.,

(ii) Extracellular Digestion: In case of coelentrates digestion occurs in gastrovascular cavity. This cavity has gland cells which secret digestive enzymes over the food. The partially digested fragmented food particles are ingested by nutritive cells. It occurs in Hydra, Aurelia, etc.

Question 5.
What is the difference between direct and indirect development?
Answer:
In direct development the embryo directly develops into an adult, while in indirect development there is an intermediate larval stage. Certain members of arthropods show larval stage of development.

Question 6.
What are the peculiar features that you find in parasitic platyhelminthes?
Answer:
Hooks and suckers are present in the parasitic forms. They are parasitic flatworms commonly called flukes. The body is unsegmented leaf like, which is covered by a thick living tegument. There is no epidermis. The mouth is anterior and is armed with suckers for attachment in the host. Life history includes larval stage and involves more than one hosts.
Examples : Fasciola (the liver fluke), Schistosoma (the blood fluke.)

Question 7.
What are the reasons that you can think of for the arthropods to constitute the largest group of the animal kingdom?
Answer:
Arthropods constitute the largest group of the animal kingdom. It is estimated that the Arthropoda population of the world is approximately a billion (10¹⁸) individuals, in terms of species diversity, number of individuals and geographical distribution. It is the most successful phylum on the Earth that have ever existed. Arthropods are equipped with jointed appendages, which are variously adapted for walking, swimming, feeding, sensory reception and defence. The appendages of abdomen are associated with locomotion, reproduction and in some cases with defence as well.

The appendages of head are related to defence, whereas those of thorax are mainly associated with locomotion. These features are responsible for its large diversity.

Question 8.
Water vascular system is the characteristic of which group of the following?
(a) Porifera
(b) Ctenophora
(c) Echinodermata
(d) Chordata
Answer:
Echinodermata have the water vascular system.

Question 9.
‘All vertebrates are chordates but all chordates are not vertebrates’.’Justify the statement.
Answer:
Notochord is a characteristic feature of all chordates. The members of sub-phylum – Vertebrata possess notochord during the embryonic stage. But in adults the notochord is replaced by a cartilaginous or bony vertebral column. Whereas in member of other Sub-phyla of Chordata the notochord remain as such. The urochordate and cephalochordates retain the notochord during their entire life cycle. Thus, the absence of notochord in adult vertebrates suggest that all vertebrates are chordates but all chordates are not vertebrates.

Question 10.
How important is the presence of air bladder in Pisces?
Answer:
In fishes, air bladder regulates buoyancy and helps in floating in water. If it is absent, animals need to swim constantly to avoid sinking.

Question 11.
What are the modifications that are observed in birds that help them fly?
Answer:
Flight adaptations in birds are as follows :

• Boat-shaped body helps to propel through the air easily.
• Feathery covering of body to reduce the friction of air.
• Holding the twigs automatically by hindlimbs.
• Extremely powerful muscles that enables the wings to work during flight.
• Bones are light, hollow and provide more space for muscle attachment. Presence of pneumatic bones which reduce the weight of body and help in flight.
• The first four thoracic vertebrae are fused to form a furculum for walking of the wings.
• Lungs are solid and elastic and have associated air sacs.
• The power of accomodation of eyes is well developed due to the presence of comb-like structure pecten.
• A single left ovary and oviduct to reduce the body weight.

Question 12.
Could the number of eggs or young ones produced by an oviparous and viviparous mother be equal? Why?
Answer:
The number of eggs or young ones produced by an oviparous or viviparous mother cannot be equal. An oviparous mother gives rise to more number of eggs as some of them die during hatching and as they have to pass through a large number of developmental stages before becoming an adult. On the other hand, a viviparous mother gives rise to fewer number of young ones because there are less chances of their death. Moreover, they did not have to pass through any larval stage.

Question 13.
Segmentation in the body is first observed in which of the following:
(a) Platyhelminthes
(b) Annelida
(c) Aschelminthes
(d) Arthropoda
Answer:
Segmentation in the body is first observed in Annelida. This phenomenon is known as metamerism.

Question 14.
Match the following:

A. Operculum	1. Ctenophora
B. Parapodia	2. Mollusca
C. Scales	3. Porifera
D. Comb plates	4. Reptilia
E. Radula	5. Annelida
F. Hairs	6. Cyclostomata and Chondrichthyes
G. Choanocytes	7. Mammalia
H. Gill slits	8. Osteichthyes

Answer:

A. Operculum	8. Osteichthyes
B. Parapodia	5. Annelida
C. Scales	4. Reptilia
D. Comb plates	1. Ctenophora
E. Radula	2. Mollusca
F. Hairs	7. Mammalia
G. Choanocytes	3. Porifera
H. Gill slits	6. Cyclostomata and Chondrichthyes

Question 15.
Prepare a list of some animals that are found parasitic on human heings.
Answer:
A list of parasitic animals on human beings:

Parasite	In Part of Human Body
Leishmania donovani	Blood
Trichomonas vaginalis	Vagina of human female
Plasmodium vivax	Blood
Taenia solium	Intestine
Ascaris lumbricoides	Small intestine
Wuchereria bancrofti	Lymphatic and muscular system
Loa loa	Eyes
Fasciola hepatica	Liver and bile ducts
Entamoeba histolytica	Intestine
Trypanosoma gambiense	Blood

Punjab State Board PSEB 11th Class Biology Book Solutions Chapter 3 Plant Kingdom Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Biology Chapter 3 Plant Kingdom

PSEB 11th Class Biology Guide Plant Kingdom Textbook Questions and Answers

Question 1.
What is the basis of classification of algae?
Answer:
Basis of classification of algae are as follows:

• Kinds of pigments.
• Nature of reserve food.
• Kinds, number and points of insertion of flagella of motile cells.
• Presence or absence of organised nucleus in the cell.

Question 2.
When and where does reduction division take place in the life cycle of a liverwort, a moss, a fern, a gymnosperm and an angiosperm?
Answer:
Reduction division in the life cycle of a liverwort, a moss, a fern and a gymnosperm take place during the production of spores from spore mother cells. In case of an angiosperm, the reduction division occurs during pollen grain formation from anthers and during production of embryo sac from ovule.

Question 3.
Name three groups of plants that bear archegonia. Briefly describe the life cycle of any one of them.
Answer:
Three groups of plants that bear archegonia are bryophytes, pteridophytes and gymnosperms.
Life Cycle of a Pteridophyte: The life cycle of a pteridophyte consists of two morphologically distinct phases:
1. The gametophytic phase
2. The sporophytic phase.
These two phases come one after another in the life cycle of a pteridophyte. This phenomenon is called alternation of generation. The gametophyte is haploid with single set of chromosomes. It produces male sex organs antheridia and female sex organs archegonia.

• The antheridia may be embedded or projecting type. Each antheridium has single layered sterile jacket enclosing a mass of androcytes.
• The androcytes are flask-shaped, sessile or shortly stalked and differentiated into globular venter and tubular neck.
• The archegonium contains large egg, which is non-mo tile.
• The antherozoids after liberation from antheridium, reaches up to the archegonium fuses with the egg and forms a diploid structure known as zygotes.
• The diploid zygote is the first cell of sporophytic generation. It is retained inside the archegonium and forms the embryo.
• The embryo grows and develop to form sporophyte which is differentiated into roots, stem and leaves.
• At maturity the plant bears sporangia, which encloses spore mother cells.
• Each spore mother cell gives rise to four haploid spores which are usually arranged in tetrads.
• The sporophytic generation ends with the production of spores.
• Each spore is the first cell of gametophytic generation. It germinates to produce gametophyte and completes its life cycle.

Question 4.
Mention the ploidy of the following:
Protonemal cell of a moss, primary endosperm nucleus in dicot, leaf cell of a moss, prothallus cell of a fern, gemma cell in Marchantia, meristem cell of monocot, ovum of a liverwort and zygote of a fern.
Answer:
Protonemal cell of a moss – haploid
Primary endosperm nucleus in dicot – triploid
Leaf cell of a moss – haploid
Prothallus cell of a fern – haploid
Gemma cell in Marchantia – haploid
Meristem cell of monocot – diploid
Ovum of a liverwort – haploid
Zygote of a fern – diploid

Question 5.
Write a note on economic importance of algae and gymnosperms.
Answer:
Economic Importance of Algae

• Red algae provides food, fodder and commercial products. Porphyra tenera is rich in protein, carbohydrates and vitamin-A, B, E and C.
• Corallina has vermifuge properties.
• Agar-agar a gelatin substance used as solidifying agent in culture media is obtained from Gelidium and Gracilaria algae. Funori is a glue used as adhesive and in sizing textiles, papers, etc. Chondrus is most widely used in sea weed in Europe.
• Mucilage extracted from Chondrus is used in sampoos, shoe polish and creams.
• Carrageenin is a sulphated polysaccharide obtained from cell wall of Chondrus crispus and Gigartina and is used in confectionary, bakery, jelly, creams, etc.

Economic Importance of Gymnosperms

• Gymnosperms hold soil particles and thus check soil erosion.
• Many gymnosperms are grown in gardens as ornamental plants, i.e., Cycas, Thiya, Araucaria, Taxus, Agathis, Maiden hair tree, etc.
• Sago is a kind of starch obtained from cortex and pith of stem and seeds of Cycas. Roasted seeds of Pinus geradiana (chilgoza) are used as dry fruit.
• Paper pulp is obtained from wood of Picea (spruce), Gnetum, Pinus (pine) and Larix (larck).
• The wood of Juniperus virginiana (red cedar) is used to make pencils, holders and cigar boxes. Wood of Taxus is heaviest amongst soft woods and is used for making bows for archery.
• Dry leaves of Cycas are used to make baskets and brooms. Needles of Pinus in making fibre board. Electric and telephone poles are made of stem of conifers.
• Essential oils are obtained from Juniperus, Tsugo, Picea, Abies, Cedrus, etc. Resins are obtained from many species of Pinus.

Question 6.
Both gymnosperms and angiosperms bear seeds, then why are they classified separately?
Answer:
Both gymnosperms and angiosperms bear seeds, but they are yet classified separately. Because, in case of gymnosperms the seeds are naked, i.e., the seeds are not produced inside the fruit but in case of angiosperms the seeds are enclosed inside the fruit.

Question 7.
What is heterospory? Briefly comment on its significance. Give two examples.
Answer:
Heterospory is the phenomenon in which a plant produces two types of spores, namely microspores and megaspores.
Heterospory is significant in the following ways:

• Microspores give rise to male gametophyte and megaspores give rise to female gametophyte.
• Female gametophyte is retained on the parent plant. The development of zygote takes place within the female gametophyte.
• This leads to formation of seeds.
  Examples: All gymnosperms and all angiosperms, Pinus, Gnetum, neem, peepal, etc.

Question 8.
Explain briefly the following terms with suitable examples:
(i) Protonema
(ii) Antheridium
(iii) Archegonium
(iv) Diplontic
(v) Sporophyll
(vi) Isogamy.
Answer:
(i) Protonema: It is the juvenile stage of a moss. It results from the germinating meiospore. When fully grown, it consists of a slender green, branching system of filaments called the protonema.

(ii) Antheridium: The male sex organ of bryophyte and pteridophyte is known as antheridium. It has a single-layered sterile jacket enclosing in a large number of androcytes. The androcytes’ metamorphose into flagellated motile antherozoids.

(iii) Archegonium: The female sex organ of bryophytes, which is multicellular and differentiated into neck and venter. The neck consists of neck canal cells and venter contains the venter canal cells and egg.

(iv) Diplontic: A kind of life cycle in which the sporophyte is the dominant, photosynthetic, independent phase of the plant and alternate with haploid gametophytic phase is known as diplontic life cycle.

(v) Sporophyll: The sporangium bearing structure in case of Selaginella is known as sporophyll.

(vi) Isogamy: It is the process of fusion between two similar gametes, i.e., Chlamydomonas.

Question 9.
Differentiate between the following:
(i) red algae and brown algae,
(ii) liverworts and moss,
(iii) homosporous and heterosporous pteridophytes.
(iv) syngamy and triple fusion.
Answer:
(i) Differences between Red Algae and Brown Algae

Red Algae	Brown Algae
1. It belongs to the It belongs to the class-Rhodophyceae	It belongs to the It belongs to the class Phaeophyceae.
2. It is red in colour due to the presence of pigments chlorophyll-a, c and phycoerythrin. Example: Stylolema, Rhodela.	It is brown in colour due to the presence Example: Sargassum, Microcystis.

(ii) Differences between Liverworts and Moss

Liverwort	Moss
1. These are the member of class-Hepaticopsida of bryophyta.	These belongs to class-Bryop’sida of bryophyta.
2. Thallus is dorsoventrally flattened and lobed liver like	Thallus is leafy and radially symmetrical.
3. Rhizoids are unicellular.	Rhizoids are multicellular
4. Elaters are present in capsule to assist dispersal of spores.	Elaters are absent, but peristome teeth are present in the capsule to assist dispersal of spores.

(iii) Differences between Homosporous and Heterosporous Pteridophytes

Homosporous Pteridophyte	Heterosporous Pteridophyte
Pteridophytes, which produce only one kind of spores. Example: Lycopodium	These produce two kinds of spores, i.e., large megaspore and smaller microspore. Example: Selaginella

(iv) Differences between Syngamy and Triple Fusion

Syngamy	Triple Fusion
It is the act of fusion of one male gamete with the egg cell to form zygote.	The act of fusion of second male gamete with secondary nucleus to form triploid enddsperm is called triple endosperm is called triple fusion.

Question 10.
How would you distinguish monocots from dicots?
Answer:

Dicotyledons (Dicots)	Monocotyledons (Monocots)
•» Tap root system	Fibrous root system
•» Two cotyledons	One cotyledon
•» Reticulate Venation	Parallel venation
•» Tetramerous or Pentamerous flowers	Trimerous flowers

Question 11.
Match the followings (column I with column II)

Column I	Column II
(a) Chlamydomonas	(i) Moss
(b) Cycas	(ii) Pteridophyte
(c) Selaginella	(iii) Algae
(d) Sphagnum	(iv) Gymnosperm

Answer:

Column I	Column II
(a) Chlamydomonas	(iii) Algae
(b) Cycas	(iv) Gymnosperm
(c) Selaginella	(ii) Pteridophyte
(d) Sphagnum	(i) Moss

Question 12.
Describe the important characteristics of gymnosperms.
Answer:
Characteristics of gymnosperms are as follows :

• Naked-seeded plants, i.e., their ovules are exposed and not enclosed in ovaries. Hence, the seeds are naked without fruits.
• Tap root system is present. They show symbiotic as speciation with fungi
  to form mycorrhizae or with N₂-fixing cyanobacteria to form colloidal roots as in Cycas.
• Leaves are large and needle-shaped.
• Vascular tissues are well developed.
• Gymnosperms are heterosporous.
• Pollination by wind and deposited in ovules.
• Fertilisation occurs in archegonia.
• Retention of female gametophyte inside the ovule and the ovules on the sporophytic plant for complete development is responsible for the development of seed habit.

Punjab State Board PSEB 11th Class Biology Book Solutions Chapter 20 Locomotion and Movement Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Biology Chapter 20 Locomotion and Movement

PSEB 11th Class Biology Guide Locomotion and Movement Textbook Questions and Answers

Question 1.
Draw the diagram of a sarcomere of skeletal muscle showing different regions.
Answer:

Question 2.
Define sliding-filament theory of muscle contraction.
Answer:
The sliding-filament, theory states that the contraction of a muscle fibre takes place by the sliding of the thin filaments over the thick filaments.

Question 3.
Describe the important steps in muscle contraction.
Answer:
Mechanism of Muscle Contraction:

• The mechanism of muscle contraction is explained by the sliding filament theory.
• This theory states that contraction of a muscle fibre is due to the sliding of the thin (actin) filaments over the thick (myosin) filaments.
• Muscle contraction is initiated by a neural signal from the central nervous system through a motor neuron.
• When the neural signal reaches the neuromuscular junction, it releases a neurotransmitter, i.e., acetylcholine, which generates an action potential in the sarcolemma.
• This spreads through the muscle fibre and causes the release of Ca⁺⁺ ions from the sarcoplasmic reticulum into the sarcoplasm.
• The Ca⁺⁺ ions bind to the subunit of troponin and brings about conformational changes; this removes the masking of the active site for myosin.
• The myosin head binds to the active site on actin to form a cross-bridge; this utilises energy from the hydrolysis of ATP.
• This pulls the actin filaments towards the centre of A-band.
• As a result, the Z-lines limiting the sarcomere are pulled closer together, causing a shortening of the sarcomere or contraction of muscle.
• Thus, during muscle contraction, the length of A band remains unchanged, while that of I-band decreases.
• The myosin goes back to its relaxed state.
• A new ATP binds and the cross-bridge is broken and the actin filaments slide out of A-band.
• The cycle of cross bridge-formation and cross bridge breakage continues till the Ca⁺⁺ ions are pumped back to the sarcoplasmic reticulum which leads to the masking of the active site on F-actin.

Question 4.
Write true or false. If false change the statement so that it is true.
(a) Actin is present in thin filament.
(b) H-zone of striated muscle fibre represents both thick and thin filaments.
(c) Human skeleton has 206 bones.
(d) There are 11 pairs of ribs in man.
(e) Sternum is present on the ventral side of the body.
Answer:
(a) True
(b) False, H-zone represents thick filaments
(c) True
(d) False, there are 12 pairs of ribs in man.
(e) True

Question 5.
Write the difference between:
(a) Actin and Myosin
(b) Red and White Muscles
(c) Pectoral and Pelvic Girdle
Answer:
(a) Differences between Actin and Myosin Filament

Actin Filaments	Myosin Filaments
1. These are found in I-band.	These are found in A-band.
2. These are thin.	These are thick.
3. Cross bridges (heads) are absent.	Cross bridges (heads) are present.
4. It is a globular protein with low molecular weight.	It is a heavy molecular weight polymerised protein.

(b) Differences between Red and White Muscles

Red Muscles	White Muscles
1. In some muscles, myoglobin content is high, which gives a reddish colour to them, such muscles are called red muscles.	Some muscles possess very less quantity of myoglobin, so they appear whitish called as white muscles.
2. These contain plenty of mitochondria.	These have less number of mitochondria but amount of sarcoplasmic reticulum is high.
3. These are called aerobic muscles.	They depend on anaerobic process of energy.

(c) Differences between Pectoral and Pelvic Girdle

Pectoral Girdle	Pelvic Girdle
1. It helps in the articulation of upper limbs.	It helps in the articulation of lower limbs.
2. It is situated in the pectoral region of the body.	It is situated in the pelvic region of the body.
3. Each half of pectoral girdle is formed of a clavicle and a scapula.	Pelvic girdle consists of two coxal bones.
4. Scapula is a large triangular flat bone and clavicle is a long slender bone.	Each coxal bone is formed of three bones, ilium, ischium and pubis.
5. An expanded process, acromion from scapula forms a depression called glenoid cavity, which articulates with the head of humerus to form shoulder joint.	Ilium, ischium and pubis fuse at a point to form a cavity called acetabulum to which the thigh bone articulates.

Question 6.
Match Column-I with Column-II

Column-I	Column-II
(a) Smooth muscle	(i) Myoglobin
(b) Tropomyosin	(ii) Thin filament
(c) Red muscle	(iii) Sutures
(d) Skull	(iv) Involuntary

Answer:

Column-I	Column-II
(a) Smooth muscle	(iv) Involuntary
(b) Tropomyosin	(ii) Thin filament
(c) Red muscle	(i) Myoglobin
(d) Skull	(iii) Sutures

Question 7.
What are the different types of movements exhibited by the cells of human body?
Answer:
Cells of the human body exhibit three main types of movements-amoeboid, ciliary and muscular.
(i) Amoeboid Movement: Some specialised cells in our body like macrophages and leucocytes in blood exhibit amoeboid movement. It is effected by pseudopodia formed by the streaming of protoplasm (as in Amoeba). Cytoskeletal elements like microfilaments are also involved in amoeboid movement.

(ii) Ciliary Movement: Ciliary movement occurs in most of our internal tubular organs which are lined by ciliated epithelium. The coordinated movements of cilia in the trachea help us in removing dust particles and some of the foreign substances inhaled along with the atmospheric air. Passage of ova through the female reproductive tract is also facilitated by the ciliary movement.

(iii) Muscular Movement: Movement of our limbs, jaws, tongue, etc., require muscular movement. Locomotion requires a perfect coordinated activity of muscular, skeletal and neural systems.

Question 8.
How do you distinguish between a skeletal muscle and a cardiac muscle?
Answer:

Skeletal Muscle	Cardiac Muscle
1. The, cells of skeletal muscles are unbranched.	1. The cells of cardiac muscles are branched.
2. Intercalated disks are absent.	2. The cells are joined with one another by intercalated disks that help in coordination or synchronization of the heartbeat.
3. Alternate light and dark bands are present.	3. Faint bands are present.
4. They are voluntary muscles.	4. They are involuntary muscles.
5. They contract rapidly and get fatigued in a short span of time.	5. They contract rapidly but do not get fatigued easily.
6. They are present in body parts such as the legs, tongue, hands, etc.	6. These muscles are present in the heart and control the contraction and relaxation of the heart.

Question 9.
Name the type of joint between the following:
(i) Atlas/Axis
(ii) Carpal/Metacarpal of thumb
(iii) Between phalanges
(iv) Femur/Acetabulum
(v) Between cranial bones
(vi) Between pubic bones in the pelvic girdle.
Answer:
(i) Pivot joint
(ii) Saddle joint
(iii) Hinge joint
(iv) Ball and socket joint
(v) Fibrous joint
(vi) Cartilagenous joint

Question 10.
Fill in the blank spaces.
(a) All mammals (except a few) have ………………………………. cervical vertebra.
(b) The number of phalanges in each limb of human is ……………………………………
(c) Thin filament of myofibril contains 2 ‘F’ actins and two other proteins namely ………………………. and ………………..
(d) In a muscle fibre Ca²⁺ is stored in ………………………..
(e) ………………….. and ……………………………….. pairs of ribs are called floating ribs.
(f) The human cranium is made of …………………………. bones.
Answer:
(a) seven
(b) fourteen.
(c) troponin and tropomyosin
(d) sarcoplasm
(e) 11 th; 12th
(f) eight

Punjab State Board PSEB 11th Class Biology Book Solutions Chapter 2 Biological Classification Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Biology Chapter 2 Biological Classification

PSEB 11th Class Biology Guide Biological Classification Textbook Questions and Answers

Question 1.
Discuss how classification systems have undergone several changes over a period of time?
Answer:
(i) Linnaeus proposed a two kingdom system of classification with Plantae and Animalia kingdoms was developed that included all plants and animals respectively. But as this system did not distinguish between the eukaryotes and prokaryotes, unicellular and multicellular organisms and photosynthetic (green algae) and non-photosynthetic (fungi) organisms, so scientists found it an inadequate system of classification. Classification systems for the living organisms have hence, undergone several changes over time.

(ii) The two kingdom system of classification was replaced by three kingdom system, then by four and finally by five kingdom system of classification of RH Whittaker (1969).

(iii) The five kingdoms included Monera, Protista, Fungi, Plantae and Animalia. This is the most accepted system of classification of living organisms.

(iv) But, Whittaker has not described viruses and lichens. Then Stanley described viruses, viroids, etc.
Thus, over a period of time, classification systems have undergone several changes.

Question 2.
State two economically important uses of:
(a) Heterotrophic bacteria
(b) Archaebacteria
Answer:
(a) Heterotrophic Bacteria

• Maintain soil fertility by nitrogen fixation, ammonification and nitrification, e.g., Rhizobium bacteria (in the root nodules of legumes).
• The milk products such as butter, cheese, curd, etc., are obtained by the action of bacteria. The milk contains bacterial forms like Streptococcus lacti, Escherichia coli, Lactobacillus lactis and Clostridium sp., etc.

(b) Archaebacteria

• Methanogens are responsible for the production of methane (biogas) from the dung of animals.
• Archaebacteria help in the degradation of waste materials.

Question 3.
What is the nature of cell walls in diatoms?
Answer:
In case of diatoms, the cell wall forms two thin overlapping cells, which fit together as in a soap box. The cell wall is made up of silica. Due to siliceous nature of cell wall, it is known as diatomite or diatomaceous Earth. Diatomaceous Earth is a whitish, highly porous, chemically inert, highly absorbant and fire proof substance.

Question 4.
Find out what do the terms ‘algal bloom’ and ‘red tides’ signify?
Answer:
Sometimes, greqn algae such as Chlorella, Scenedesmus and Spirogyra, etc,, grow in excess in water bodies and impart green colour to the water. These are called algal blooms. Red dianoflagellates (Gonyaulax) grow in abundance in sea and impart red colour to the ocean. This looks like red tides. Both due to algal blooms and ‘red tide’ the animal life declines due to toxins and deficiency of oxygen inside water.

Question 5.
How are viroids different from viruses?
Answer:
Viroids different from viruses as follows:

Virus	Viroids
1. These are smaller than bacteria.	Smaller than viruses.
2. Both RNA and DNA present.	Only RNA is present.
3. Protein coat present.	Protein coat absent.
4. Causes diseases like mumps and AIDS.	Causes plant diseases like spindle tuber diseases – potato.

Question 6.
Describe briefly the four major groups of Protozoa.
Answer:
Protozoans are divided into four phyla on the basis of locomotory organelles – Zooflagellata, Sarcodina, Sporozoa and Ciliates.
(i) Zooflagellates: These protozoans possess one to several flagella for locomotion. Zooflagellates are generally uninucleate, occasionally multinucleate.
The body is covered by a firm pellicle. There is also present cyst formation.
Examples: Giardia, Trypanosoma, Leishmania and Trichonympha, etc.

(ii) Sarcodines: These protozoans possess pseudopodia for locomotion. Pseudopodia are of four types, i.e., lobopodia, filopodia, axopodia and reticulopodia. Pseudopodia are also used for engulfing food particles. Sarcodines are mostly free living, found in freshwater, sea water and on damp soil only a few are parasitic. Nutrition is commonly holozoic. Sarcodines are generally uninucleates. Sarcodines are of four types – Amoeboids (i.e.,Amoeba, etc.), radiolarians (i.e., Acanthometra, etc.), foraminiferans (i.e., Elphidium, etc.) and heliozoans (i.e., Actinophrys, etc.).

(iii) Sporozoans: All of them are endoparasites. Locomotoryorganelles (cilia, flagella, pseudopodia, etc.) are absent. Nutrition is parasitic (absorptive), Phogotrophy is rare. The body is covered with an elastic pellicle or cuticle. Nucleus is single. Contractile vacuoles are absent. Life cyle consists of two distinct asexual and sexual phases. They may be passed in one (monogenetic) or two different hosts (digenetic),e.g., Plasmodium, Monocystis, etc.

(iv) Ciliates: These are aquatic, actively moving organisms because of the presence of thousands of cilia. They have a cavity (gullet) that opens to the outside of the cell surface. The coordinated movements of rows of cilia causes the water laden with food to enter into the gullet, e.g., Paramecium.

Question 7.
Plants are autotrophic. Can you think of some plants that are partially heterotrophic?
Answer:
Plants are autotrophs, i.e., they prepare their own food through the process of photosynthesis. But, in nature there are also some other plants which are partjally heterotrophic, i.e., they partially depend upon another organisms for food requirements, e.g.,
(i) Loranthus and Viscum are partial stem parasites which have leathery leaves. They attack several fruit and forest trees and with the help of their haustoria draw sap from the xylem tissue of the host.

(ii) Insectivorous plants have special leaves to trap insects. The trapped insects are killed and digested by proteolytic enzymes secreted by the epidermis of the leaves, e.g., pitcher plant.

(iii) Parasitic plant, e.g., Cuscutta develops haustoria, which penetrate, the vascular bundles of the host plant to absorb water and solutes.

Question 8.
What do the terms phycobiont and mycobiont signify?
Answer:
In case of lichens (t. e., an association of algae and fungi), the algal partner which is capable of carrying out photosynthesis is known as phycobiont, whereas the fungal partner which is heterotrophic in nature is known as mycobiont.

Question 9.
Give a comparative account of the classes of Kingdom Fungi under the following:
(i) Mode of nutrition
(ii) Mode of reproduction

Fungal Class	Mode of Nutrition	Mode of Reproduction
Myxomycetes	Heterotrophic and mostly saprophytic	Asexual and sexual reproduction
Phycomycetes	Mostly parasites	Asexual and sexual methods
Zygomycetes	Mostly saprophytic	Asexual and sexual reproduction
Ascomycetes	Saprophytes or parasites	Asexual and sexual reproduction
Basidiomycetes	Saprophytes or parasites	Asexual and sexual method
Deuteromycetes	Saprophytes or parasites	Only asexual reproduction

Question 10.
What are the characteristic features of Euglenoids?
Answer:
The characteristic features of euglenoids are as follows :

• They occur in freshwater habitats and damp soils.
• A single long flagella present at the anterior end.
• Creeping movements occur by expansion and expansion of their body known as euglenoid movements.
• Mode of nutrition is holophytic, saprobic or holozoic.
• Reserve food material is paramylum.
• Euglenoids are known as plant and animal.
  Plant characters of them are as follows:
  (a) Presence of chloroplasts with chlorophyll.
  (b) Holophytic nutrition
  Animal characters of them are as follows:
  (a) Presence of pellicle, which is made up of proteins and not a cellulose.
  (b) Presence of stigma.
  (c) Presence of contractile vacuole.
  (d) Presence of longitudinal binary fission.
• Under favourable conditions euglenoids multiply by longitudinal binary fission, e.g., Euglena, Phacus, Paranema, etc.

Question 11.
Give a brief account of viruses with respect to their structure ’ and nature of genetic material. Also name four common viral diseases.
Answer:
Viruses are non-cellular, ultramicroscopic, infectious particles. They are made up of envelope, capsid, nucleoid and occasionally one or two enzymes. Viruses possess an outer thin loose covering called envelope. The central portion of nucleoid is surrounded by capsid that is made up of ( smaller sub-units known as capsomeres.

The nucleic acid present in the viruses is known as nucleoid. It is the r infective part of the virus which utilises the host cell machinery. The
genetic material of viruses is of four types –

(i) Double stranded DNA (dsDNA) as found in pox virus, hepatitis-B virus and herpes virus, etc.
(ii) Single stranded DNA (ssDNA) occur in coliphage Φ, coliphage Φ x 174.
(iii) Double stranded RNA (dsRNA) occur in Reo virus,
(iv) Single stranded RNA (ssRNA) occur in TMV virus, polio virus, etc.
Four common viral diseases are – (i) Polio, (ii) AIDS, (iii) Hepatitis-B (iv) Rabies.

Question 12.
Organise a discussion in your class on the topic—Are viruses living or non-living?
Answer:
Viruses are intermediate between living and non-living objects. They resemble non-living objects in:

• Lacking protoplast. ‘
• Ability to get crystallised.
• High specific gravity which is found only in non-living objects.
• Absence of respiration and energy storing system.
• Absence of growth and division.
• Cannot live independent of a living cell.

They resemble living objects in:

• Presence of genetic material (DNA or RNA).
• Property of mutation.
• Irritability.
• Can grow and multiply inside the host cell.