Bhagya

Punjab State Board PSEB 7th Class English Book Solutions English Grammar Adjectives with Degrees Exercise Questions and Answers, Notes.

PSEB 7th Class English Grammar Adjectives with Degrees

An Adjective is a word which qualifies or adds something to the meanings of a Noun or a Pronoun.
जो शब्द किसी Noun अथवा Pronoun की विशेषता प्रकट करता है उसे Adjective (विशेषण) कहते हैं।

Adjective प्रायः Noun के साथ प्रयोग होता है और यह किसी व्यक्ति, पशु अथवा स्थान की विशेषता बताता है या किसी संख्या अथवा मात्रा का बोध कराता है। जैसे:

1. Many years ago there was a miser. (संख्या)
2. He never ate good food. (विशेषता)
3. He spent little money. (मात्रा)
   Adjectives मुख्यत: 9 प्रकार के होते हैं।

1. Adjectives of Quality. जो विशेषण किसी व्यक्ति अथवा वस्तु के गुण- दोष का बोध कराते हैं उन्हें Adjective of Quality (गुणवाचक विशेषण) कहते हैं। जैसे-
good, fresh, bad आदि।।

2. Proper Adjectives. Proper Nouns से बनने वाले विशेषण Proper Adjectives (व्यक्तिवाचक विशेषण) कहलाते हैं। जैसे:-
Indian, Chinese.

3. Adjectives of Quantity. जो विशेषण किसी वस्तु की मात्रा का बोध कराते हैं उन्हें Adjectives of Quantity (परिमाणवाचक विशेषण) कहते हैं। इस प्रकार के Adjective प्रायः कितने (How much) शब्द का उत्तर देते हैं। जैसे:-
some, no, great.

4. Adjectives of Number. जो विशेषण संख्या अथवा क्रम का- बोध कराते हैं उन्हें Adjectives of Number (संख्यावाचक विशेषण) कहते हैं। जैसे:-
two, all आदि।

5. Distributive Adjectives. जो विशेषण किसी विशेष वर्ग के व्यक्ति अथवा वस्तु को अलग-अलग प्रकट करें, उन्हें Distributive Adjectives (विभाजन विशेषण) कहते हैं। जैसे : each, either, every आदि।

6. Demonstrative Adjectives. जो विशेषण सम्बन्धित व्यक्ति अथवा वस्तु की ओर संकेत करते हैं उन्हें Demonstrative Adjectives (संकेतवाचक विशेषण) कहते हैं। जैसे:-
This pen; That girl.

7. Interrogative Adjectives. जो विशेषण प्रश्न पूछने के लिए प्रयोग किए जाते हैं उन्हें Interrogative Adjectives (प्रश्नवाचक विशेषण) कहते हैं। जैसे:-
which, what, whose आदि।

8. Possessive Adjectives. किसी वस्तु या व्यक्ति पर अधिकार व्यक्त करने वाले विशेषण को Possessive Adjectives (सम्बन्धवाचक विशेषण) कहा जाता है। जैसे:-
My book, Your brother, आदि।

9. Emphasizing Adjectives. जो शब्द Possessive Adjectives पर बल देने के लिए प्रयोग किए जाते हैं वे Emphasizing Adjectives कहलाते हैं।
प्रायः Own शब्द इसके लिए प्रयोग किया जाता है। जैसे:-
I became my own servant.

Degree of Adjectives

(1)

इसी प्रकार के कुछ अन्य विशेषण जिनके साथ er तथा est का प्रयोग होता है, निम्नलिखित हैं:
Loud (ऊंची आवाज़), small (छोटा), warm (गर्म), young (आयु में छोटा), cheap (सस्ता), bright (चमकीला) इत्यादि।

(2)

इसी प्रकार के अन्य विशेषण हैं, Busy.(व्यस्त), dirty (गन्दा), dry (शुष्क), early (पहले या जल्दी) इत्यादि।

(5)

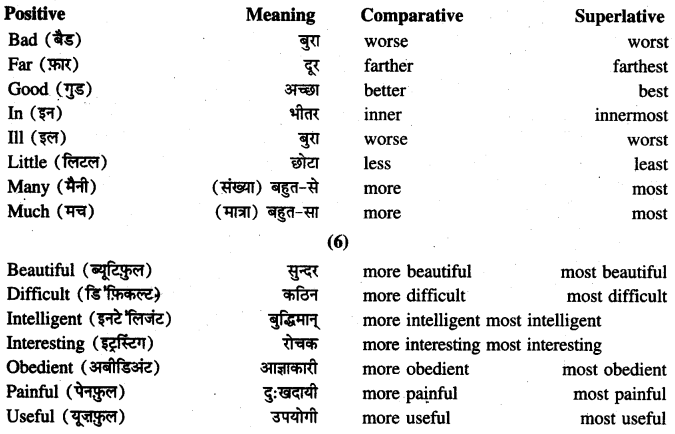
इसी प्रकार के अन्य विशेषण हैं: Stupid (मूर्ख), active (फुर्तीला), expensive (महंगा), powerful (शक्तिशाली) आदि।

Exercise 1

I. Underline the adjectives of quality in the sentences given below. The first one has been done for you:

1. Reema is a good singer.
2. Naina wore a red sari for the party.
3. Johnny Walker was a funny man.
4. Look ! there’s a shiny coin.
5. Abha has chubby cheeks and a dimple chin.
6. Kolkata is a congested city.
7. Pandit Nehru was the first Prime Minister of India.
8. Get the black car from the garage.
9. Many families died in the earthquake.
10. Milk is a healthy drink.
Hints:
2. red
3. funny
4. shiny
5. chubby, dimple
6. congested
7. first
8. black
9. Many
10. healthy.

II. Add an adjective of quality to the following nouns. The first one has been done for you:

1. a tasty meal.
2. a ……….. bread.
3. a ………. dress
4. a ………. night
5. a ………. story
6. a ……… woman.
7. a ………. baby.
8. a ……… class.
9. an ………. play
10. a ……… building.
Hints:
2. fresh
3. new
4. dark
5. funny.
6. fat
7. lovely
8. middle
9. interesting
10. tall.

III. Replace the word in italics with a word from the box to give the opposite meaning and rewrite the sentence. The first one has been done for you:

tidy, short, broad, easy, sour, honest. active, modern, bright, strong, clever, useless.
1. It is a dull day. It is a bright day.
2. The room is untidy
3. The road ahead is narrow. …………..
4. Difficult sums take up time.
5. The sweet litchis are from Dehradun. ……
6. The weak boy won the match. ……………
7. The dishonest servant ran away. ……………
8. Jassi is very lazy. …………….
9. The fort is an example of ancient architecture…..
10. Babita is a foolish girl. ………….
11. The spanner is a useful tool. ………….
12. The tall boy is my brother. …………….
Hints:
2. tidy
3. broad
4. Easy
5. sour
6. strong
7. honest
8. active
9. modern
10. wise
11. useless
12. short.

IV. Choose from these adjectives of quantity and number to fill in the blanks given below. One has been done for you.

a few, ten, some, a little, second, enough, any, two, much, several, few.
(a) Some elephants were seen near a village.
(b) Renu has ……….milk every night.
(c) Sam has ……….money to buy a scooter.
(d) Rafiq found ……….gold coins in the trunk.
(e) The ……….day of the week is Monday.
(f). The ………. brothers live in Delhi.
(g) Very ……….tickets are there for the show.
(h) Put ……….sugar in the tea.
(i) Panna does not spend ……….time on exercise.
(j) I read ……….pages before going to bed.
(k) We have ……….fingers on our hands.
(l) ……… people watch the television everyday.
Hints:
(b) some
(c) enough
(d) several
(e) second
(f) two
(g) few
(h) a little
(i) any
(j) a few
(k) ten
(l) Several.

V. Fill in the blanks with an adjective of your choice:

(a) You will need ………… paper and ……….. ink for your test.
(b) ……… monkeys sat in the compartment.
(c) I have to write ………… letters today.
(d) Father sent ………….. money for my expenses.
(e) There are ………….. boys in the class.
(f) The book has …………. illustrations.
(g) I would like …………. tea.
(h) The ship sank into the ………. sea.
Hints:
(a) white, blue
(b) Some
(c) many
(d) enough
(e) thirty
(f) beautiful
(g) some
(h) deep.

Exercise 2

I. Fill in the blanks with the correct form of the adjective given in the brackets. The first one has been done for you:

1. Samarjit is the best showman in the town. (good)
2. Meena is the ……… girl in her class. (intelligent)
3. Anuj is ………. than Aman. (short)
4. Anita is ………. than Jamuna. (pretty)
5. Iron is the ………. of all metals. (heavy)
6. John is the ……… student in Mathematics. (bad)
7. Raman is ……. than Lalit. (tall)
8. A train journey is ……… than a road journey. (comfortable)
Hints:
2. most intelligent
3. shorter
4. prettier
5. heaviest
6. worst
7. taller
8. more comfortable.

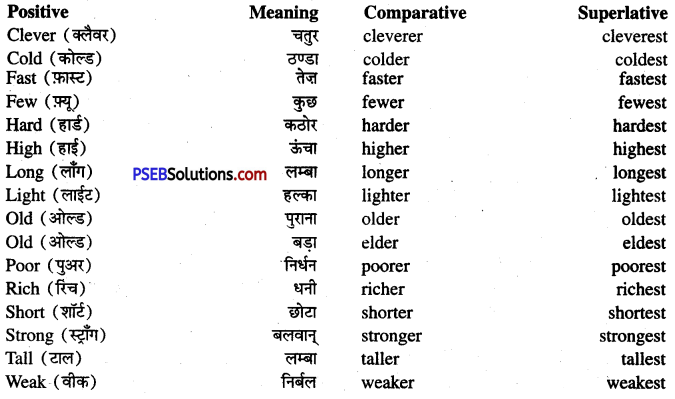
II. Give the comparative and superlative degrees of the following adjectives:

Positive	Comparative	Superlative
bright	brighter	brightest
noble	nobler	noblest
many	more	most
little	less	least
intelligent	more intelligent	most intelligent
strange	stranger	strangest
red	redder	reddest
bad	worse	worst
ugly	uglier	ugliest
Good	better	Best
rich	richer	richest
heavy	heavier	heaviest
wonderful	more wonderful	most wonderful
able	abler	ablest
much	more	most
clever	cleverer	cleverest
courageous	more courageous	most courageous
dirty	dirtier	dirtiest
neat	neater	neatest
wide	wider	widest.

III. Use words from the box to complete the sentences. One has been done for you.

snow, ice, feather, lion, bee, snail, fox, silk, clown, bat.
1. Raj is as brave as a ………… .
2. Her friend proved to be as cunning as a ………… .
3. The room was as cold as …………… .
4. The pages were as white as ………… .
5. My sister is as busy as a …………. .
6. The old man is as blind as a ………….
7. Ramu is as funny as a …………. .
8. The train is as slow as a ……….. .
9. The box weighs as light as a …………. .
10. Her skin is as soft as ………… .
Answer:
1. Raj is as brave as a lion.
2. Her friend proved to be as cunning as a fox.
3. The room was as cold as ice.
4. The pages were as white as snow.
5. My sister is as busy as a bee.
6. The old man is as blind as a bat.
7. Ramu is as funny as a clown.
8. The train is as slow as a snail.
9. The box weighs as light as a feather.
10. Her skin is as soft as silk.

IV. Fill in the blanks with some, little, a little, few, much, any and many. The first one has been done for you:

1. I requested Salil to give me a ……….. money.
2. The trunk holds ……….. clothes.
3. There is ……….. space in the hall.
4. There were very …………. people at the party.
5. There are too ………. poor people in India.
6. I carried ……….. clothes for the trip.
7. Please pour ………. oil in the bottle.
8. Shiela has ………… work to do.
9. Raju has ………… friends in the U.S.A.
10. I take a ………….. food at night.
11. There aren’t ………… students in school today.
12. Rajat gave me ……… tips for the exams.
Answer:
1. I requested Salil to give me a little money.
2. The trunk holds some clothes.
3. There is little space in the hall.
4. There were very few people at the party.
5. There are too many poor people in India.
6. I carried some clothes for the trip.
7. Please pour some oil in the bottle.
8. Shiela has much work to do.
9. Raju has few friends in the U.S.A.
10. I take a little food at night.
11. There aren’t any students in school today.
12. Rajat gave me many tips for the exams.

V. Make sentence of your own with comparative and superlative of the adjectives of much, little, few and many. The first one has been done for you.

Answer:
1. More : I have more clothes than my sister.
Most : She is the most beautiful girl of our class.

2. Less : I spend less than I earn.
Least : I am least worried about his result.

3. Fewer : There are fewer boys than girls in the class.
Fewest : Attendance is the fewest today.

4. More : I have more clothes than my sister.
Most : Most of the students are absent today.

VI. Form adjectives by joining letters from circle ‘B’ with circle ‘A’ and make sentences of your own. One has been done for you.

1. yearly – They are holding yearly meeting.
2. lovely – She is a lovely girl.
3. handy – I have a handy bag.
4. useful – Milk is useful for health.
5. girlish – I don’t like your girlish behaviour.
6. childish – I don’t like your childish talks.
7. costly – The watch is very costly.
8. dutiful – Hira is a dutiful son.
9. thoughtful – He is in a thoughtful mood.
10. noisy – I cannot work in a noisy atmosphere.
11. motherly – She showers motherly love upon me.

VII. Pick out the adjectives in the following sentences and say whether they are adjectives of quality, quantity or number. The first one has been done for you:

1. Sonu is a dishonest man. (quality)
2. Dolly is six years old. (number)
3. There is little hope for her survival. (quantity)
4. There is very little milk to drink (quantity)
5. Those poor children are hungry. (quality)
6. How many marks have you got ? (number)
7. An empty mind is a devil’s workshop. (quality)
8. I have enough cash to buy a mobile. (quantity)

VIII. Underline the adjectives in the given sentences. The first one has been done for you:

1. A small leak can sink a big ship.
2. All work and no play makes Jack a dull boy.
3. He gave me many sweets.
4. These apples are raw.
5. The dog is a faithful animal.
6. Which book do you want to buy ?
7. There is a little milk in the jug.
8. A wise enemy is better than a foolish friend.
9. This is cold water.
10. He has enough milk for tea.

IX. Correct the degrees of adjectives in the sentences. The first one has been done for you:

1. He is the strong man in our village.
He is the strongest man in our village.

2. Ram gets less salary.
Ram gets a little salary.

3. Mohan is my older brother.
Mohan is my elder brother.

4. This mountain is high than that mountain.
This mountain is higher than that mountain.

5. My handwriting is better in the class.
My handwriting is the best in the class.

6. Gita’s left hand is weak than the right hand.
Gita’s left hand is weaker than the right hand.

7. Suman is good than Gurmeet in music.
Suman is better than Gurmeet in music.

Exercise 3

I. Underline demonstrative adjectives in the sentences. The first one has been done for you:

1. This sari is hand-painted.
2. Give me that book.
3. That book belongs to Milan.
4. These mangoes are for distribution.
5. These boys did not appear for the test.
6. Take that pot to the kitchen.
7. Ahmed joined this school recently.
8. Where did you get those flowers from?
9. Mohan presented me this silver plate.
10. We did not go to those places for security reasons.
Hints:
2. that
3. That
4. These
5. These
6. that
7. this
8. those
9. this
10. those.

II. Underline possessive adjectives and underline interrogative adjectives in these sentences:

1. What colour is your hair ?
2. Which is my towel ?
3. Whose car has her sister taken ?
4. What gift have you bought for your friend ?
5. Which desk is yours?
6. What is your name?
7. Whose watch has her brother worn ?
8. Which tools does the gardener need for his work ?
9. Which chocolates do you want for your shop ?
Hints:
1. What, your
2. Which, my
3. Whose, her
4. What, your
5. Which, yours
6. What, your
7. Whose, her
8. Which, his
9. Which, your.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 15 Introduction to Graphs InText Questions and Answers.

PSEB 8th Class Maths Solutions Chapter 15 Introduction to Graphs InText Questions

Try These : [Textbook Page No. 244]

1. In the above example, use the graph to find how much petrol can be purchased for ₹ 800.

Solution:
We can find the quantity of petrol to be got for ₹ 800. For this take a point on the Y-axis (0, 800). Now, draw a line parallel to X-axis to meet the graph at the point B. Now, from the point B, draw a line parallel to Y-axis, which intersect X-axis in the point C. Coordinate of the point C : (16, 0).
Hence, 16 litres of petrol can be purchased for ₹ 800.

Think, Discuss and Write : [Textbook Page No. 243]

1. The number of litres of petrol you buy to fill a car’s petrol tank will decide the amount you have to pay. Which is the independent variable here? Think about it.
Solution:
Here, we clearly understand that graph of quantity of petrol (litre) and amount to pay (₹) should be a line.
Both quantities are in direct proportion. If we fill more litres of petrol, we have to pay more amount and vice versa.
∴ Petrol is the independent variable.

Try These : [Textbook Page No. 245]

1. Is Example 7, a case of direct variation?
Solution:
Yes, Example 7 given on page 245 (Textbook), is a case of direct variation. As the principal increases, the simple interest on it also increases proportionately.

Punjab State Board PSEB 7th Class English Book Solutions English Grammar Adverbs Exercise Questions and Answers, Notes.

PSEB 7th Class English Grammar Adverbs

An Adverb is a word which modifies or adds something to the meanings of a Verb, an Adjective or another Adverb.
जो शब्द किसी Verb, Adjective अथवा किसी अन्य Adverb की विशेषता प्रकट करे उसे Adverb (क्रिया):

1. He speaks loudly.
2. Snowfall was very beautiful.
3. Mr. Sharma walks too slowly.

पहले वाक्य में loudly शब्द speaks (Verb) की विशेषता प्रकट करता है।
दूसरे वाक्य में very शब्द beautiful (Adjective) की विशेषता प्रकट करता है।
तीसरे वाक्य में too शब्द Slowly (Adverb) की विशेषता प्रकट करता है।

Exercise 1

Underline the adverbs in the following sentences:

1. The child slept soundly.
2. Meena works hard for her living.
3. Sam will return tomorrow.
4. Simi lives there.
5. Flies go everywhere.
6. Navjot talks softly.
7. The car stopped outside.
8. We must always speak respectfully to our elders.
9. Pammi looked sadly at Rani.
10. Aunt cooked quickly for us.
Hints:
1. soundly
2. hard
3. tomorrow
4. there
5. everywhere
6. softly
7. outside
8. always, respectfully
9. sadly
10. quickly.

Exercise 2

Fill in the blanks with appropriate adverbs of manner from the box. The first one has been done for you:

rudely
thoughtfully
heavily
politely
sincerely
happily
quickly
quietly
1. The children ate quickly.
2. Samir went ………. to the hostel.
3. The boy looked ………. at me.
4. The father sat …………
5. Teachers work ……….
6. The father spoke ………. to his son.
7. The salesman answered ……….
8. It rained ………. yesterday.
Hints:
2. happily
3. rudely
4. thoughtfully
5. sincerely
6. quietly
7. politely
8. heavily.

Exercise 3

A table has been given below with adverbs of time. Make sentences using words from the different columns. The first one has been done for you.

Answer:
(1) Father has already read the paper.
(2) Grandfather is still in bed.
(3) The bus is already at the gate.
(4) Mother hasn’t yet, had breakfast.
(5) Grandmother is still in the garden.
(6) My sister hasn’t yet left for office.
(7) The dog is still at the gate.
(8) The doctor will soon leave for the hospital.

Exercise 4

I. Underline the adverbs of place in the following sentences. The first one has been done for you:

1. Maya stood therė.
2. Children ran up and down.
3. The hunter looked inside the box.
4. We walked in by the first gate.
5. Tilak ran forward.
6. Raj went everywhere for his test.

II. Match the following verbs and adverbs given below:

Verbs	Adverbs
wait	seriously
drive	patiently
work	soundly
study	fast
sleep	bravely
fight	early
walk	honestly
wake	slowly

Answer:

Verbs	Adverbs
wait	patiently
drive	slowly
work	honestly
study	seriously
sleep	soundly
fight	bravely
walk	fast
wake	early

Exercise 5

I. Using the words given in the box, complete the following sentences. The first one has been done for you:

seldom, twice, often, once, always, frequently
1. The students went ………… to see Gadar.
2. The man dived ………….. into the river.
3. I …………. keep medicines with me.
4. We ………….. go out to eat.
5. My grandmother …………. visits Sri Harmandar Sahib.
6. We …………….. go to watch movies.
7. I …………. dream of going abroad.
8. Sanjay goes …………. for walks.
Answer:
1. The students went twice to see Gadar.
2. The man dived once into the river.
3. I often keep medicines with me.
4. We seldom go out to eat.
5. My grandmother frequently visits Sri Harmandar Sahib.
6. We seldom go to watch movies.
7. I always dream of going abroad.
8. Sanjay goes frequently for walks.

II. Rewrite the sentences using the words given in the brackets. The first one has been done for you:

1. Ajay ……………… borrows books from me. (often)
Ajay often borrows books from me.

2. Children are difficult to get along with. (sometimes)
Children are sometimes difficult to get along with.

3. I will work in a factory (never).
I will never work in a factory.

4. Ludhiana is cold in January (usually)
Ludhiana is usually cold in January.

5. Harpreet is cheerful. (always)
Harpreet is always cheerful.

6. Raman concentrates on his studies. (seldom)
Raman seldom concentrates on his studies.

7. Krishma is a crowd puller (always).
Krishma is always a crowd puller.

8. Anjan drives fast (never).
Anjan never drives fast.

Exercise 6

Use these adverbs of degree : fully, almost, most, very, quite, extremely, nearly in sentences of your own. One has been done for you:

1. The students ……….. agreed with the teacher.
2. It is ………… time to go.
3. Mr. A is ……….. wanted criminal.
4. He is ………… rich.
5. I am ………. well.
6. It is …………. cold.
7. This pot is ………. empty.
Answer:
1. The students fully agreed with the teacher.
2. It is almost time to go.
3. Mr. A is most wanted criminal.
4. He is very rich.
5. I am quite well.
6. It is extremely cold.
7. This pot is nearly empty.

Exercise 7

Write questions to the answers given below. The first one has been done for you:

1. Where did you go?
Answer:
I went to get some water.

2. How many friends has Suraj?
Answer:
Suraj has five friends.

3. When did your mother come?
Answer:
My mother came yesterday.

4. Where were the children?
Answer:
The children were in the house.

5. How is the patient keeping?
Answer:
The patient is keeping well.

6. Where is Tirupati ?
Answer:
Tirupati is in Tamil Nadu.

7. When do you plan to return?
Answer:
I plan to return tomorrow.

8. Why are you sad ?
Answer:
I am sad for I have lost a pen.

Exercise 8

Fill in the blanks with the positive, comparative or the superlative degree of adverbs given in brackets:

1. Raj likes painting best (well) of all.
2. He worked as …………………… (slowly) as he wished.
3. Amarjit walks ……………………. (quickly) than I do.
4. Carl Lewis ran ……………………… (fast) of all.
5. You came …………………… (early) than I expected.
6. Suman acted …………………. (generously) among all.
7. Actions speak ……………………… (loud) than words.
8. It is not correct to go any ……………………. (far) in this storm.
9. The ………………….. (early) you leave, the ……………… (soon) you can return.
10. Fatima doesn’t shout as ………………. (loudly) as you do.

Hints:
2. slowly
3. more quickly
4. fastest
5. earlier
6. most generously
7. louder
8. farther
9. earlier, sooner
10. loudly.

Punjab State Board PSEB 7th Class English Book Solutions English Vocabulary Prefix and Suffix Exercise Questions and Answers, Notes.

PSEB 7th Class English Vocabulary Prefix and Suffix

A- Prefix

Prefix : mid-
mid+way = midway
mid+term = midterm
mid+west = midwest
mid+stream = midstream
mid+day = midday
mid+night = midnight

Prefix : re-
re+read = reread
re+write = rewrite
re+think = rethink
re+start = restart
re+act = react

Prefix : over-
over+do = overdo
over+dose = overdose
over+load = overload
over+throw = overthrow
over+leaf = overleaf
ab+normal = abnormal
ab+sent = absent

Prefix : mis-
mis+manage = mismanage
mis+take = mistake
mis+use = misuse

Prefix : pre-
pre+view = preview
pre+test = pretest
pre+plan = preplan
pre+position = preposition
pre+tend = pretend
pre+caution = precaution
pre+judge = prejudge

Prefix : in-
in+vade = invade
in+ability = inability
in+action = inaction
in+effective = ineffective
in+visible = invisible

Prefix : dis-
dis- dis+agree = disagree
dis+able = disable
dis+grace = disgrace
dis+loyal = disloyal

Prefix : un-
un+well = unwell
un+able = unable
un+trained = untrained
un+do = undo

B-Suffix

Suffix : -able
favour+able = favourable
objection+able = objectionable
reason+able = reasonable
remark+able = remarkable
value+able = valuable

Suffix : -ance
accept+ance = acceptance
allow+ance = allowance
defy+ance = defiance
guide+ance = guidance

Suffix : -ment
agree+ment = agreement
attach+ment = attachment
fulfil+ment = fulfilment
pay+ment = payment
refresh+ment = refreshment
settle+ment = settlement

Suffix : -ful
beauty+ful = beautiful
care+ful = careful
grace+ful = graceful
hope+ful = hopeful

Suffix : -er
begin+er = beginner
build+er = builder
invade+er =invader
make+er = maker
command+er = commander

Suffix : -less
art+less = artless
hope+less = hopeless
noise+less = noiseless
taste+less = tasteless
weight+less = weightless
help+less = helpless

Suffix : -y
cloud+y = cloudy
fault+y = faulty
sand+y = sandy
sleep+y = sleepy
rain+y = rainy

Suffix : -en
gold+en = golden
silk+en = silken
light+en = lighten
soft+en = soften
bright+en = brighten

Suffix : -ous
grace+ous = gracious
nerve+ous = nervous
courage+ous = courageous
mystery+ous = mysterious
danger+ous = dangerous

Punjab State Board PSEB 7th Class English Book Solutions English Grammar Conjunctions Exercise Questions and Answers, Notes.

PSEB 7th Class English Grammar Conjunctions

A conjunction is a word which joins words or sentences together.
वह शब्द जो शब्दों अथवा वाक्यों को आपस में जोड़े, Conjunction (संयोजक) कहलाता है। जैसे:

1. Moti and Narain were friends.
2. I know that he is honest.
3. He failed because he did not work hard.

इन वाक्यों में and, that तथा because शब्दों एवं वाक्यों को आपस में जोड़ते हैं। अतः ये शब्द conjunctions

Exercise 1

I. Rewrite each pair of sentences by using ‘because’, ‘and’, ‘but’, ‘or’, ‘else’, “otherwise and ‘unless’. One has been done for you:

1. You must walk’ fast. You will not reach the station.
You must walk fast or you will not reach the station.

2. Rina is a girl. Tony is a boy.
Rina is a girl but Tony is a boy.

3. Radha is studying. Hardeep is watching cartoons.
Radha is studying but Hardeep is watching cartoons.

4. Find the key. You will be standing out.
Find the key else you will be standing out..

5. Lock the door. Robbers will break into the house.
Lock the door otherwise robbers will break into the house.

6. Study seriously. You will not get promotion.
Unless you study seriously you will not get promotion.

7. Take exercise regularly. You will not keep fit.
Take exercise regularly otherwise you will not keep fit.

8. Put the alarm. You will not wake on time.
Put the alarm or you will not wake on time.

9. Rama sells fruits. She sells vegetables.
Rama sells fruits but she sells vegetables.

10. I like my parents. They encourage me.
I Like my parents because they encourage me.

11. They started well. They failed in the end.
They started well but they failed in the end.

12. Control your ways. You will be punished.
Control your ways or you will be punished.

II. Using the conjunctions “so’, ‘therefore’, ‘because’, “as’, ‘since’, ‘though”, “still and “although’ make sentences of your own. The first one has been done for you:

1. I am not well so I did not go to school today.
2. It was very cold, therefore I did not go for a walk.
3. My father punished me because I stole his pen.
4. I forgave him as he spoke the truth.
5. Since he is my brother, I must help him.
6. Though they played well, they could not win the match.
7. Raj hit the gentleman still he forgave him.
8. Although he ran fast, he could not win the race.

III. Underline the conjunctions in the following sentences. The first one has been done for you:

1. I won’t forgive you unless you return my money.
2. Sanjay is rich yet he is a miser.
3. I am weak but I can run fast.
4. Although I am weak, I can run fast.
5. She is old, so her limbs are weak.
6. I was angry with him because he disobeyed me.
7. You are not an honest man, still I will help you.
8. The lady fed the child since she cared for her.
9. It is very hot, therefore I am drinking a cold drink.
10. As there is no milk, I am not having tea.
11. Take the medicine else you will remain sick.
12. Though he is poor, he is happy and content.
13. It was raining still the children went out to play.
14. We did not start the dinner till the guests arrived.

Exercise 2

I. Combine the following pair of sentences by using neither ……… nor ; either………….. or:

1. Soma is not intelligent. Gopal is not intelligent.
2. Hari doesn’t know the answer. Manjit doesn’t know the answer.
3. I shall write you a letter. I shall telephone you.
4. You can go by bus. You can go by train.
5. Our country isn’t poor. Our country isn’t small.
6. You can play in the playground. You can read in the library.
7. He has not come from England. He has not come from America.
Answer:
1. Neither Soma nor Gopal is intelligent.
2. Neither Hari nor Manjit knows the answer.
3. I shall either write you a letter or telephone you.
4. You can either go by bus or by train.
5. Our country is neither poor nor small.
6. You can either play in the playground or read in the library.
7. He has neither come from England nor from America.

II. Fill in the blanks with appropriate conjunctions and, unless, if, or, but, till, though, neither……. nor, either… or:

1. The beggar sang for a long time……………. nobody gave him anything.
2. He felt sad………….. stopped singing.
3. He is …………….. an actor …………… a teacher. He is a student.
4. The musician said, “Give me your violin ………….. I will play for you.”
5. They …………. eat bread ………………….. chapattis for breakfast.
6. ………….. I ran fast I missed the train.
7. I shall wait …………….. you return.
8. Catch me …………… you can.
9. You will be late …………… you hurry.
10. Raman will sing ……………. you so desire.
11. He saw me …………….. did not talk to me.
12. I have a rupee. You can ………….. take it ………….. leave it.
13. Gopal is not to be seen. He is ……………. at home …………….in his office.
14. He did not come …………… I invited him.
Hints:
1. but
2. and
3. neither, nor
4. and
5. either, or
6. Though
7. till
8. if
9. unless
10. if
11. but
12. either, or
13. neither, nor
14. though.

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 12 Areas Related to Circles Ex 12.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 12 Areas Related to Circles Ex 12.1

Question 1.
The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
Solution:

Radius of first circle (r₁) = 19 cm
Radius of second circle (r₂) = 9 cm
Let radius of third circle be R cm
According to condition
circumference of first circle + circumference of second circle = circumference of third circle
2πr₁ + 2πr₂ = 2πR
2π (r₁ + r₂] = 2πR
19 + 9 = R
∴ R = 28
∴ Radius of third circle (R) = 28 cm.

Question 2.
The Radii of two circles are 8 cm and 6 cm respectively. Find radius of circle which is having area equal to sum of the area of two circles.
Solution:
Radius of first circle (r₁) = 8 cm
Radius of second circle (r₂) = 6 cm
Let radius of third circle be R cm
According to question
Area of third circle = Area of first circle + Area of second circle
πR² = πr₁² + πr₂²
πR² = π[r₁² + r₂²]
R² = (8)² + (6)²
R = \(\sqrt{64+36}=\sqrt{100}\)
R = 10 cm
∴ Radius of required circle (R) = 10 cm.

Question 3.
Fig. depicts an archery target marLed with its five scoring areas from the centre ‘utwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score ¡s 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.

Solution:
Diameter of Gold region = 21 cm
Radius of Gold region (R₁) = 10.5 cm
∴ Area of gold region = πR₁²
= \(\frac{22}{7} \times \frac{21}{2} \times \frac{21}{2}=\frac{690}{2}\) cm²
= 346.5 cm²
Width of each band = 10.5 cm
∴ Radius of Red and Gold region (R₂) = (10.5 + 10.5) = 21 cm
Combined radius of Blue, Red and Gold region (R₃) = R₂ + 10.5 cm
= 21 cm + 10.5 cm = 31.5 cm
Combined radius of Black, Blue, Red and Gold (R₄) = R₃ + 10.5
= 31.5 + 10.5 = 42cm
Area of circle having black radius = (Combined area of Gold, Red, Blue and Black radius) – (Combined Area of Gold, Red and Blue radius)
= πr₄² – πr₃²
= π [(42)² – (31.5)²]
= \(\frac{22}{7}\) [1764 – 992.25]
= \(\frac{22}{7}\) [771.75] = 2425.5 cm²

Combined Radius of white, black, blue, red, gold region (R₅) = R₄ + 10.5
R₅ = 42 + 10.5 = 52.5 cm
Combined radius of black, blue, red and gold = (R₄) = 42 cm.
Area of circle white scoring region = (Combined area of white, bLack, red, blue, gold region) – (Combined Area of Black, blue and gold region)
= πR₅² – πR₄²
= π[R₅² – πR₄²]
= \(\frac{22}{7}\) × [(52.5)² – (42)²]
= \(\frac{22}{7}\) [2756.25 – 1764]
= \(\frac{22 \times 992.25}{7}=\frac{21829.5}{7}\)
= 3118.5 cm²
∴ Area of white scoring region = 3118.5 cm²

∴ Area of red region = Area of red and gold region – Area of gold region
= πR₂² – πR₁²
= π [(21)² – (\(\frac{21}{2}\))²]
= \(\frac{22}{7}\) × 441 [1 – \(\frac{1}{4}\)]
= 22 × 63 \(\frac{3}{4}\)
= \(\frac{11 \times 189}{4}=\frac{2079}{4} \mathrm{~cm}^{2}\)
= 1039.5 cm²

∴ Area of Red region = 1039.5 cm²
Combined Radius of Gold, Red and Blue region R₃ (10.5 + 10.5 + 10.5) = 31.5 cm

Area of blue scoring region = (Combined area of red, blue and gold region) – (Combined area of Gold and red region)
= πR₃² – πR₂²
= π[R₃² – πR₂²]
= \(\frac{22}{7}\) × [(31.5)² – (21)²]
= \(\frac{22}{7}\) [992.25 – 441]
= \(\frac{22}{7}\) × 551.25 = \(\frac{121275}{7}\)
= 1732.5 cm²

Hence, area of gold ring; red ring; blue ring : black ring; white ring are 3465 cm² ; 1039.5 cm²; 1732.5 cm²; 24255 cm² ; 3118.5 cm² respectively.

Question 4.
The wheels of a ca are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a spel of 66 km per hour?
Solution:
Diameter of wheel = 80 cm
Radius of wheel (R) = 40 cm
Circumference of whed = 2πr
= 2 × \(\frac{22}{7}\) × 0.04
= \(\frac{22}{7}\) × 0.08 m
Let us suppose wheel of cr complete n revolutions of the wheel in 10 minutes = n[0.08 × \(\frac{22}{7}\)]
Speed of car = 66 km/hr. = 66 × 1000 m
Distance covered in 60 minutes = \(\frac{66 \times 1000}{60} \times 10\) = 11000 m
According to question.
∴ n[\(\frac{22}{7}\) × 0.08] = 11000
n = \(\frac{11000}{0.08} \times \frac{7}{22}\)
n = 4375
Hence, number of complete revolutions made by wheel in 10 minutes = 4375.

Question 5.
Tick the correct answer in the following and justify your choice : If the perimeter and area of a clrde are numerically equal, then the radius of the circle Is
(A) 2 units
(B) π units
(C) 4 units
(D) n units
Solution:
Perimeter of circle = Area of circle
2πR = πR²
2R = R²
⇒ R = 2
∴ Correct option A is (R) = 2 unit.

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 11 Constructions Ex 11.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2

In each of the following, give also the justification of the construction.

Question 1.
Draw a circle of radius 6 cm from a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution:

Steps of construction:
1. Draw a circle (1) of radius 6 cm.
2. Take a point ‘P’ at a distance of 10 m. from the centre of the circle. Join OP.
3. Draw perpendicular bisector of OP. Let ‘M’ be the mid point OP.
4. With ‘M’ as centre and radius MO, draw a circle (II) which intersects the circle (I) at T and T’.
5. Then FT and PT’ are two required tangents.

Justification of construction:
We know that tangent at a point is always perpendicular to the radius at the point. Now
we have to prove that ∠PTO = ∠PT’O = 90°.
OT is joined.
Now, PMO is the diameter of circle (II) and ∠PTO is in the semicircle.
∴ ∠PTO = 90° [Angle in semicircle is a right angle].
Similarly, ∠PT’O = 90°
∴ PT and PT’ has to be the tangents to the circle at T and T’.
(On measuring, the lengths of tangents
i.e., PT = 8.1 cm
PT’ = 8.1 cm.
Co-centric circles. Two or more circles having same centre but different radii are called CO-CENTRIC circles.

Question 2.
Construct a tangent to a circle of radivs 4 cm from a point on the co-centric circle of radIus 6 cm and measure its length.
Also, erify the measurement by actual calculation.
Solution: Steps of construction:
STEPS OF CONSTRUCTION:
1. Draw a circle with cente O’ and radius 4 cm. Mark it as 1
2. Draw another circle with same centre ‘O’ and radius 6 cm and mark it as II.
3. Take any point ‘P’ on circle II. Join OP.
4. Draw pependicu1ar bisector of OP. Let it intersects ‘OP’ at M.
5. With M is centre and radius MO’ or ‘MP’, draw a circie III which intersects the circle ‘1’ at T and T’.
6. Join PT.
PT is the required tangent.

Justification of the construction :
Join OT.
Now OP is the diameter of the circle III.
∠OTP is in the semicircle.
∴ ∠OTP = 90° …………….(1)
[∴ Angle in a semicircle isa right angle]
Now OT ⊥ PT [using (I)]
∵ A line which makes an angle of 900 with radius at any point on the circle, the line is tangent to the circle.
∴ PT is tangent to the circle ‘I’
i.e. PT is tangent to the circle of radius 4.5 cm.

To calculate the length of tangent:
Consider ∆OTP,
∠OTP = 90° [using (i)]
∴ ∆OTP is a right angled triangle.
OT = 4 cm [Radius of I circle (given)]
OP = 6 cm [Radius of the II circle (given)]
PT = ? [to be calculated]
In rt. triangle ∆OTP,
By Pythagoras theorem
OP² = OT² + PT²
[(Hyp)² = (Base)² + (Perp.)²]
or PT² = OP² – OT²
= 6² – 4²
= 36 – 16 = 20
PT = \(\sqrt{20}\) cm
= 2√5 = 2 × 2.24 = 4.48 cm.
So, length of tangent by actual calculation = 4.48 cm = 4.5 cm.
Length of tangent by measurement = 4.5 cm
Hence, the length of tangent ‘PT’ is verified.

Question 3.
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points ‘P’ and ‘Q’.
Solution:
Steps of construction:
1. Draw a circle of radius 3 cm and centre ‘O’.

2. Draw its diameter ‘AB’ and extend it in both directions as OX and OX’.
3. Take a point P’ on OX” direction and ‘Q’ on OX’ direction such that OP = OQ = 7 cm.
4. Draw perpendicular bisectors of OP and OQ which intersects OP and OQ at ‘M’ and ‘M” respectively.
5. With ‘M’ as centre and radius = ‘MO’ or MP, draw a circle ‘II’ which intersects the circle ‘I’ at T and T’.
6. Similarly with ‘M’’ as centre and radius = M’O or MQ, draw a circle (III) which intersects the circle ‘I’ at S’ and ‘S’’.
7. Join PT, PT’ and QS and QS’.

Justification of construction :
Join OT’ and ‘OT” and ‘OS’ and OS’.
To prove ‘PT & PT’ tangents to the circle
we will prove that ∠PTO = ∠PT’O = 90°.
Now ‘OP’ acts as the diameter of circle ‘II’ and ∠OTP is in the semicircle.
∴ ∠OTP = 90° …………….(1) [∵ Angle in semicircle is 90°]
But ‘OT’ is the radius of circle ‘I’ and line ‘PT’ touches the circle at T’.
∵ The line which touches the circle at a point and makes an angle of 90° with radius at that point, is tangent to the circle.
∴ PT is tangent to the circle I at point T through point ‘P.
Similarly PT’, QS and QS’ are tangents to the circle I.

Question 4.
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°
Solution:
Steps of construction:
1. Draw the rough sketch of required figure.

∵ the tangents make an angle of 60° with each other.
∠OTP = ∠OQT = 90°
[Tangent is perpendicular to the radius of circle]
1. To find inclination of radii with each other
∠TOQ + ∠OTP + ∠OQT + ∠TPQ = 360° [Angle sum property of quad.]
or ∠TOQ + 90° + 90° + 60 = 360°
or ∠TOQ = 360 – 90° – 90° – 60° = 120°
2. Draw a circle of radius 5 cm.
3. Draw two radii of circle which make an angle of 120° with each other.
4. The radii intersect the circle at ‘A’ and
5. Make an angle of 90° at each point A and B, which intersect each other at ‘P’.

6. PA and PB are the required tangents.

Question 5.
Draw a line segment AB of length 8 cm. Taking ‘A’ as centre, draw a circle of radius 4 cm and taking ‘B’ as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution:

Steps of construction :
1. Draw a line segment AB = 8 cm.
2. With ‘A’ as centre and radius 4 cm, draw a circle (I)
3. With ‘B’ as centre and radius 3 cm, draw a circle ‘I’.
4. Draw the perpendicular bisector of line segment AB which inersects ‘AB’ at ‘M’.
5. With ‘M as centre and radius MA or MB. draw a circle (III) which intersects the circle (I) at ‘S’ and ‘T’ and circle (II) at ‘P’ and ‘Q’.
6. Join ‘AP’ and AQ’. These are required tangents to the circle with radius 3 cm. from point ‘A’.
7. Join ‘BS’ and ‘BT’. These are required tangents to the circle with radius 4 cm from point ‘B’.

Justification of Construction:
In circle (III), AB acts as diameter then ∠ASB and ∠BPA are in semicircle.
∴ ∠ASB = 90° ………………(1) [Angle in semicircle]
and ∠BPA = 90° .
But ∠ASB is angle between radius of circle (I) and line segment BS’ and ∠BPA is angle between radius of circle (II) and line segment ‘AP’.
∵ Line segment which is perpendicular to the radius of circle, is tangent to the circle through that point.
∴ BS is tangent to circle (I) at point ‘S’ and AP is tangent to circle (II) at point ‘P’.
Similarly AQ and BT are tangents to the circle (II) and (I) respectively.

Question 6.
Let ABC be a right triangle in which AB = 6 cm, BC = 5 cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from ‘A’ to this circle.
Solution:

Steps of construction:
1. Construct rt. angled triangle. ABC according to given conditions and measurements.
2. Draw BD ⊥ AC.
3. Take mid point of side BC take it as
4. Take ‘M’ as centre and BC as diameter,
draw a circle through B. C, D using property, angle in semicircle is 90° (∠BDC 90°). Take this circle as I.
5. Now join ‘A’ and ‘M.
6. Draw perpendicular bisector of AM intersecting AM in point N. Now with ‘N’ as centre and ‘NA or ‘NM’ as radius, draw a circle (II) which intersects the circle (I) at ‘B’ and ‘P’.
7. Join AP.
8 AP and AB are the required tangents.

Justification of construction:
Line segment AM’ is diameter of circle (II)
∠APM is in semicircle
∴ ∠APM = 90° [Angle in semicircle]
i.e., MP ⊥ AP
But ‘MP’ is the radius of circle (I)
∴ AP is tangent to the circle (II)
[∵ Any line ⊥ to radius of circle at any point on the circle is tangent to the circle.]
Similarly AB is tangent to circle (I).

Question 7.
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this poiñt
to the circle.
Solution:
To draw circle with bangle means the centre of circle is unknown. First find the centre of circle.

Steps of construction:
1. Draw a circle. using a bangle (I).
2. Take any two chords AB and CD (non parallel) on circle.
3. Draw the perpendicular bisectors of chords AB and CD. The perpendicular bisectors intersect each other
[∵ any point lying on perpendicular bisector of line segment is equidistant from its end points
[∵ ‘O’ lies on ⊥ bisector of AH and CD]
∴ OA = OB and OC = OD
∴ OA = OB = OC = OD (Radii of circle)
∴ ‘O’ is the centre of circle.
4. Take any point ‘P’ out side the circle.
5. Join OP.
6. Draw the perpcndicular bisector of OP let ‘M’ the mid point of OP.
7. With ‘M’ as centre and radius ‘MP’ or ‘MO’, draw a circle II which intersects the circle (I) at T and T’.
8. Join PT and PT’, which is required pair of tangents.

Justification of construction:
Tangent at a point is always perpendicular to the radius at the point. Now, we have to prove
that ∠PTO = PT’O = 90°
Join OT.
Now ∠PTO is in the semicircle I.
∵ ∠PTO = 90° [Angle in semicircle is a right angle]
Similarly ∠PT’O = 90°
∴ PT and PT’ has to be the tangents to the circle at T and T’.

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 11 Constructions Ex 11.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.1

In each of the questions, give the justification of the construction also.

Question 1.
Draw a line segment of length 7.6 cm and divide ¡tin the ratio 5 : 8. Measure the two parts.
Solution:
Given: A line segment of length of 7.6 cm.
Steps of construction:
1. Take a line segment AB = 7.6 cm.
2. Draw any ray AX, making an acute angle ∠BAX.
3. Locate 5 + 8 = 13 (given ratio 5: 8) points A₁, A₂, A₃, A₄, A₅, ………….., A₁₀, A₁₁, A₁₂, A₁₃ on ray AX such that A₁A₂ = A₂A₃ = A₃A₄ = …………. = A₁₁A₁₂ = A₁₂ A₁₃.
4. Join BA₁₃.
5. Through point A5, draw a line A₅C || A₁₃B (by making an angle equal to ∠A₁₃B) at A₅ intersecting AB at ‘C’. Then AC : CB = 5 : 8;

Justification:
Let us see how this method gives us the required division.
In ∆AA₁₃B,
Since A₅C || A₁₃B
∴ By Basic Proportionality Theorem
\(\frac{\mathrm{AA}_{5}}{\mathrm{~A}_{5} \mathrm{~A}_{13}}=\frac{\mathrm{AC}}{\mathrm{CB}}\)

By construction, \(\frac{\mathrm{AA}_{5}}{\mathrm{~A}_{5} \mathrm{~A}_{13}}=\frac{5}{8}\)

∴ \(\frac{\mathrm{AC}}{\mathrm{CB}}=\frac{5}{8}\)
This shows that ‘C’ divides AB in the ratio 5 : 8.
On measuring the two parts, AC = 2.9 cm and CB = 4.7 cm.

Alternative Method:
Steps of construction:
1. Take a line segment AB = 7.6 cm
2. Draw any acute angle ∠BAX
3. Draw angle ∠ABY such that ∠ABY = ∠BAX.
4. Locate the points A₁, A₂, A₃, A₄, A₅ on ray AX such that A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅.
5. Locate the points B₁, B₂, B₃, B₄, B₅, B₆, B₇, B₈ on ray BY such that B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇ = B₇B₈
6. Join A₅B₈ let it intersects AB at point Then AC : CB = 5 : 8.

justification:
In ∆ACA₅ and ∆BCB₈,
∠ACA₅ = ∠BCB₈ [vertically opp. ∠s]
∠BAA₅ = ∠ABB₈ [construction]
∴ AACA₅ ~ ABCB₈ [AA-similarity cond.]
∴ Their corresponding sides must be in the same ratio. ,
\(\frac{A C}{B C}=\frac{C A_{5}}{C B_{8}}=\frac{A_{5} A}{B_{8} B}\)
(I)(II) (III)
From I and III, \(\frac{A C}{B C}=\frac{A_{5} A}{B_{8} B}\)

But, \(\frac{A_{5} A}{B_{8} B}=\frac{5}{8}\) [construction]

\(\frac{A C}{C B}=\frac{5}{8}\).

Question 2.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are \(\frac{2}{3}\) of corresponding sides of the first triangle.
Solution:
Steps of construction:
1. Construct a triangle ABC with given measurements. AB = 5 cm, AC = 4 cm and BC = 6 cm.
2. Make any acute angle ∠CBX below the side BC.

3. Locate three points (greater of 2 and 3 in \(\frac{2}{3}\))B₁, B₂, B₃ on BX such that BB₁ = B₁B₂ = B₂B₃.
4. Join B₃C.
5. Through B₂ (smaller of 2 and 3 in \(\frac{2}{3}\) draw a line parallel to B₃C, which intersect BC in C’.
6. Through C’, draw a line parallel to CA meeting BA is A’.
Thus ∆A’BC’ is the required triangle whose sides are of corresponding sides of ∆ABC.

Justification of construction :
First we will show that first triangle and constructed triangle are similar.
i.e. ∆A’BC’ ~ ∆ABC.
Consider ∆A’BC’ and ∆ABC.
∠B = ∠B [Common]
∠A’C’B= ∠ACB [By construction]
∆A’C’B ~ ∆ACB [AA – similarity]
∴ Their corresponding sides must be in the same ratio.
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) …………….(1)
Now, consider ∆B₂BC’ and ∆B₃BC,
∠B = ∠B [common]
∠B₂C’B = ∠B₂CB [construction]
∴ ∆B₂BC’ ~ ∆B₃BC [AA -similarity]
∴ Their corresponding sides must be in the same ratio.

\(\frac{\mathrm{B}_{2} \mathrm{~B}}{\mathrm{~B}_{3} \mathrm{~B}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{B}_{2}}{\mathrm{CB}_{3}}\)

I II III

Taking (I) and (II).
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{B}_{2} \mathrm{~B}}{\mathrm{~B}_{3} \mathrm{~B}}\)

But, \(\frac{\mathrm{B}_{2} \mathrm{~B}}{\mathrm{~B}_{3} \mathrm{~B}}=\frac{2}{3}\) [construction]

\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{2}{3}\) ……………(2)

From (1) & (2),
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}=\frac{2}{3}\)

⇒ A’B = \(\frac{2}{3}\) AB and BC’ = \(\frac{2}{3}\) BC; C’A’ = \(\frac{2}{3}\) CA.
Hence, the construction is Justified.

Question 3.
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are of the corresponding sides of the first triangle.
Solution:

Steps of construction :
1. Construct a triangle ABC in which AB = 7 cm, BC 6 cm and AC =5 cm.
2. Make any acute angle ∠BAX below the base AB.
3. Locate seven points A₁, A₂, A₃, A₄, A₅, A₆, A₇ on the ray AX such that
AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₇.
4. Join BA₅.
5. Through A₇, draw a line parallel A₅B. Let it meets AB at B’ on being produced such that AB’= \(\frac{7}{5}\) AB.
6. Through B’, draw a line parallel to BC which meets AC at C’ on being produced.
∆AB’C’ is the required triangle.

Justification of the construction.
In ∆ABC and ∆AB’C’,
∠A = ∠A [common]
∠ABC = ∠AB’C’ [corresponding ∠s]
∴ ∠ABC – ∠AB’C’ [AA-similarity]
∴ Their corresponding sides must be in the same ratio.
\(\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}=\frac{\mathrm{BC}}{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}=\frac{\mathrm{CA}}{\mathrm{C}^{\prime} \mathrm{A}}\) ……………..(1)

Again, in ∆AA₅B and AA₇B’
∠A = ∠A [common]
∠AA5B = ∠AA7 B’ [corresponding ∠s]
∴ ∆AA5B ~ ∆AA7B’ [AA – similarity]
∴ Their corresponding sides must be in the same ratio.
\(\frac{\mathrm{AA}_{5}}{\mathrm{AA}_{7}}=\frac{\mathrm{A}_{5} \mathrm{~B}}{\mathrm{~A}_{7} \mathrm{~B}^{\prime}}=\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}\)

⇒ \(\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}=\frac{\mathrm{AA}_{5}}{\mathrm{AA}_{7}}\) [construction]

But, \(\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}=\frac{5}{7}\) …………….(2)

From (1) and (2),

\(\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}=\frac{\mathrm{BC}}{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}=\frac{\mathrm{CA}}{\mathrm{C}^{\prime} \mathrm{A}}=\frac{5}{7}\)

or \(\frac{A B^{\prime}}{A B}=\frac{B^{\prime} C^{\prime}}{B C}=\frac{C^{\prime} A}{C A}=\frac{7}{5}\)

⇒ AB’ = \(\frac{7}{5}\) AB; B’C’ = \(\frac{7}{5}\) BC and C’A’ = \(\frac{7}{5}\) CA

Hence, the sides of ∆AB’C’ are \(\frac{4}{4}\) of ∆ABC.

Question 4.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 12 times
the corresponding sides of the isosceles triangle.
Solution:
Given: Base of isosceles triangle is 8 cm and Altitude = 4 cm
To construct: A triangle whose sides are times the sides of isosceles triangle.
Steps of construction:
1. Take base AB = 8 cm.
2. Draw perpendicular bisector of AB. Let it intersect AB at ‘M’.
3. With M as centre and radius = 4 cm, draw an arc which intersects the perpendicular bisector at ‘C’
4. Join CA and CB.
5. ∆ABC is an isosceles with CA = CB.
6. Make any acute angle ∠BAX below the side BC.
7. Locate three (greater of ‘2’ & ‘3’ in 1\(\frac{1}{2}\) or \(\frac{3}{2}\))
A₁, A₂, A₃ on ‘AX’ such that A A₁ = A₁ A₂ = A₂ A₃.

8. Join A₂ (2nd point smaller of ‘2 and ‘3’ in ) and B.
9. Through A₃, draw a line parallel to A₂B meet AB is B’ cm being produced.
10. Through B’, draw a line parallel to BC which meets AC in C’ on being produced. ∆AB’C’ is the required triangle whose sides are 1\(\frac{1}{2}\) times the corresponding sides of ∆ABC.

Justification of construction :
First we will prove ∆AB’C’ are ∆ABC and similar.
Consider ∆ AB’C’ and ∆ ABC
∠A = ∠A [Common]
∠AB’C’ = ∠ABC [By construction]
∠AB’C’ ~ ∠ABC [By AA – similarityj
∴ Their corresponding sides must be in the same ratio
\(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}}{\mathrm{CA}}\) ……………(1)

Now consider ∆ A₃AB’ and ∆ A,AB
∠A = ∠A [common]
∠B’A₃A = ∠BA₂A [By construction]
∴∆ A₃A B’ – ∆A₂AB [AA – similarity]
∴ Their corresponding sides must be in the same ratio
\(\frac{A_{3} A}{A_{2} A}=\frac{A B^{\prime}}{A B}=\frac{B^{\prime} A_{3}}{B A_{2}}\)
I II III
Taking (I) & (II),
\(\frac{A B^{\prime}}{A B}=\frac{A_{3} A}{A_{2} A}\)

But, \(\frac{A_{3} A}{A_{2} A}=\frac{3}{2}\) [construction]
⇒ \(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}=\frac{3}{2}\) ……………..(2)
From (1) & (2)m
\(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}}{\mathrm{CA}}=\frac{3}{2}\left(1 \frac{1}{2}\right)\)

⇒ AB’ = 1\(\frac{1}{2}\) (AB); B’C’ = 1\(\frac{1}{2}\) BC and C’A’ = 1\(\frac{1}{2}\) (CA)
Hence, given result is justified.

Question 5.
Draw a triangle ABC with side BC = 6 cm, AB =5 cm and ¿ABC = 60°. Then construct a triangle whose sides are of the corresponding sides of the triangle ABC.
Solution:
Steps of construction :
1. Take a line segment BC = 6 cm
2. Construct an angle of measure 60° at point B. i.e., ∠CBX = 60°.
3. With B as centre and radius 5 cm draw an arc intersecting BX at ‘A’

4. Join A and C.
5. At B, make any acute angle ∠CBY below the side BC.
6. Locate four points (greater of 3 and 4 in \(\frac{3}{4}\)) B₁, B₂, B₃, B₄ on BY such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄. .
7. Join B₄ and C.
8. Draw a line through B₃ (smaller of 3 and 4 in ) parallel to B₄C making corresponding angles. Let the line through B₃ intersects BC in C’.
9. Through C’, draw a line parallel to CA which intersects BA at A’.
The ∆A’BC’ is the required triangle whose sides are \(\frac{3}{4}\) of sides of ∆ABC.

Justification of the construction:
Consider ∆A’BC’ and ∆ABC
∠B = ∠B [commoni
∠A’C’B = ∠ACB [corresponding ∠s]
∴ ∆A’BC’ ~ ∆ABC [AA – similarity]
∴ Their corresponding sides must be in the same ratio.

∴ \(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) ……………..(1)

Now consider ∆B₃B C’ and ∆B₄BC.
∠B = ∠B [common]
∠ C’ B₃B = ∠CB₄B [corresponding ∠s]
∆B₃BC’ ~ ∆B₄BC [AA – similarity con.]
Their corresponding sides must be in the same ratio.
\(\frac{B_{3} B}{B_{4} B}=\frac{B C^{\prime}}{B C}=\frac{C^{\prime} B_{3}}{C B_{4}}\)
(I) (II) (III)

From (I) and (II),
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{B}_{3} \mathrm{~B}}{\mathrm{~B}_{4} \mathrm{~B}}\)

But, = \(\frac{\mathrm{B}_{3} \mathrm{~B}}{\mathrm{~B}_{4} \mathrm{~B}}=\frac{3}{4}\) [construction]

\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{3}{4}\) ………..(3)

From (1) and (3)
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}=\frac{3}{4}\)

and C’A’= \(\frac{3}{4}\) CA.
∆A’BC’ is the required triangle whose sides are \(\frac{3}{4}\) sides of ∆ABC.

Question 6.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°. ∠A = 105°. Then construct a triangle whose sides are j- times
the corresponding sides of ∆ABC.
Solution:
Steps of construction:
1. Construct the triangle ABC with the given measurements.
BC = 7 cm; ∠B = 45, ∠A = 105°
By angle sum property of triangle
∠A + ∠B + ∠C= 180°
105° + 45° + ∠C = 180°
∠C = 180 – 150° = 30°
2. Make any acute angle ∠CBX at point B, below the sides BC.

3. Locate four points (greater of 3 and 4 in \(\frac{4}{3}\)) B₁, B₂, B₃, B₄ on ‘BX’ such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄.
4. Join B₃C (smaller of 3 and 4 in \(\frac{4}{3}\)).
5. Through B₄, draw a line parallel to B₃C meeting BC in C’ on being produced.
6. Through C’, draw another line parallel to CA meeting BA in A’ on being produced.
7. ∆A’BC’ is the required triangle whose sides are times the triangle ABC.

Justification of construction:
Consider the ∆ A’BC’ and ∆ ABC,
∠B = ∠B [common]
∠A’C’B = ∠ACB [construction]
∴ ∆A’BC’ ~ ∆ABC [AA – similarity]
∴ Their corresponding sides must be in the same ratio

\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) ………….(1)

Again, consider ∆B₄B C’ and ∆B₃BC,
∠B = ∠B [common]
∠C’B4B = ∠CB3B [By consiruction]
∴ BB C’ AB3BC [AA-si niilarity]
∴ Their corresponding sides must be in the same ratio
\(\frac{\mathrm{B}_{4} \mathrm{~B}}{\mathrm{~B}_{3} \mathrm{~B}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{B}_{4}}{\mathrm{CB}_{3}}\)
I II III

Taking I and II members.

\(\frac{B C^{\prime}}{B C}=\frac{B_{4} B}{B_{3} B}\)

But, \(\frac{B_{4} B}{B_{3} B}=\frac{4}{3}\) (construction)

or \(\frac{B C^{\prime}}{B C}=\frac{4}{3}\) ………….(2)

From (1) and (2),

\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}=\frac{4}{3}\)

⇒ A’B = \(\frac{4}{3}\) AB; BC’ = \(\frac{4}{3}\) BC and C’A’ = \(\frac{4}{3}\) CA
Hence the construction is justified.

Question 7.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are \(\frac{5}{3}\) times the corresponding sides of the given triangle.
Solution:
Steps of construction:
1. Draw a right triangle using given conditions. Consider the triangle as ABC in which BC = 4 cm; AB = 3 cm and
∠B = 90°.
2. Make any acute angle ∠CBX below the line BC.
3. Locate five points (greater of 5 and 3 in \(\frac{5}{3}\)) B₁, B₂, B₃, B₄. B₅ on BX such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅.
4. Join B₃ (smaller of ‘5’ and ‘3’ in \(\frac{5}{3}\)) and ‘C’.

5. Through B₅. draw a line parallel to BC meeting BC is C’ on being produced.
6. Again draw a line through C’ parallel to CA meeting BA in A’ on being produced.
∆A’BC’ is the required triangle whose sides are \(\frac{5}{3}\) times the sides of ∆ABC.

Justification of construction :
Consider ∆A’BC’ and ∆ABC
∠B = ∠B [common]
∠A’C’B = ∠ACB [By construction]
∴ ∆A’BC’ ~ ∆ABC [AA-similarity condition]
∴ Their corresponding sides must be in the same ratio
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) ……………..(1)

Again, in ∆B₅C’B and ∆XB₃CB,
∠B = ∠B [common]
∠C’B₅B = ∠CB₃B [By construction]
∴ ∆B₅C’B ~ ∆B₃CB [AA-similarityj
∴ Their corresponding sidcs must be in the same ratio.

\(\frac{\mathrm{B}_{5} \mathrm{C}^{\prime}}{\mathrm{B}_{3} \mathrm{C}}=\frac{\mathrm{C}^{\prime} \mathrm{B}}{\mathrm{CB}}=\frac{\mathrm{BB}_{5}}{\mathrm{BB}_{3}}\)

I II III

Taking II and III members.
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{B}_{5} \mathrm{~B}}{\mathrm{~B}_{3} \mathrm{~B}}\)

But, \(\frac{B_{5} B}{B_{3} B}=\frac{5}{3}\) [construction]

\(\frac{B C^{\prime}}{B C}=\frac{5}{3}\) ……………(2)
From (1) and (2),

\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}=\frac{5}{3}\)

⇒ A’B = \(\frac{5}{3}\) AB; BC’ = \(\frac{5}{3}\) BC and C’A’ = \(\frac{5}{3}\) CA
Hence the construction is justified.

Punjab State Board PSEB 7th Class English Book Solutions English Grammar Noun Exercise Questions and Answers, Notes.

PSEB 7th Class English Grammar Noun

A Noun is the name of a person an animal place or a thing.
किसी व्यक्ति, पशु स्थान अथवा वस्तु के नाम को Noun (संज्ञा) कहते हैं; जैसे,

1. Mr. Amitabh Mukerjee is a Bengali.
2. Geeta went to Patiala.
3. A balloon was flying in the sky.

1. पहले वाक्य में व्यक्ति अर्थात् Mr. Amitabh Mukerjee, दूसरे में स्थान अर्थात् Patiala और तीसरे में वस्तु अर्थात् balloon का नाम दिया गया है। ये तीनों शब्द Nouns हैं।

Kinds:
Nouns चार प्रकार के होते हैं।

• Proper Noun. Proper Noun (व्यक्तिवाचक संज्ञा) किसी विशेष व्यक्ति या स्थान का नाम होता है, जैसे:
• Dinesh is a good boy.
• Chandigarh is the capital of Punjab.

2. Common Noun. जिस शब्द से किसी जाति के प्रत्येक व्यक्ति, स्थान, अथवा वस्तु का बोध हो, उसे Common Noun (जातिवाचक संज्ञा) कहते हैं; जैसे:

• She went to a lawyer.
• Amritsar is a big city.

3. Collective Noun. जिस संज्ञा से समूह का बोध होता है उसे Collective Noun (समुदायवाचक संज्ञा) कहते हैं; जैसे:

• A hockey team has eleven players.
• There are fifty boys in our class.
• She has lost her bunch of keys.

4. Abstract Noun. जिस संज्ञा से किसी वस्तु के गुण, कार्य अथवा अवस्था का बोध होता है, उसे Abstract Noun (भाववाचक संज्ञा) कहते हैं; जैसे:
गुण-Goodness, kindness, honesty, beauty.
कार्य-Laughter, hatred.
अवस्था-Boyhood, sleep, childhood, length, breadth.

Exercise 1

I. Underline the common nouns in the following sentences. Some sentences have more than one common noun. One has been done for you.
1. The baby was afraid of the dark.
2. Many people were being treated in the hospital.
3. The sky was full of dark clouds.
4. My house is very large.
5. I like to play with my favourite toys.
6. Books give us a lot of information.
7. Amarjit has injured his arm.
8. The old lady was very lonely.
9. The train to Jalandhar was late again.
10. The teacher spoke to her students.
11. Simran loves watching the television.
Hints:
2. people, hospital
3. clouds
4. house
5. toys
6. Books
7. arm
8. lady
9. train
10. teacher, students
11. television.

II. Fill in the blanks with suitable common nouns to form meaningful sentences:

1. Ravi could not find his ………….. in his bag.
2. Rahim fell into the
3. The ………… was late today.
4. Our ………….. is very beautiful.
5. We bought some …………. yesterday.
6. I saw a long
Hints:
1. pen
2. river
3. bus
4. garden
5. flowers
6. snake.

Exercise 2

I. Underline the proper nouns in the following sentences. Some sentences have more than one proper noun. The first one has been done for you:
1. Nutan was a great actress of India.
2. Ravana is a character from the Ramayana
3. The Ganges flows down from the Himalayas.
4. Children enjoyed at Appu Ghar.
5. The Esteem is an expensive car.
6. Prince Rana died in a tragic road accident.
7. Mr. Mohan uses a Videocon washing machine.
8. The Charminar is in Hyderabad.
9. The film Sholay was seen by a large number of people.
10. February is the shortest month of the year.
11. Verka ice-cream is available in many flavours.
Hints:
2. Ravana, Ramayana
3. Ganges, Himalayas
4. Appu Ghar
5. Esteem
6. Prince Rana
7. Mr. Mohan, Videocon washing machine
8. Charminar, Hyderabad
9. Sholay
10. February
11. Verka ice-cream.

II. Fill in the blanks with suitable proper nouns to form meaningful sentences.

1. My pet dog …………. is very lovable.
2. …………. is a popular hill station.
3. My favourite television programme is ………
4. The film ………… is running in four theatres.
5. The month of ………….. is very cold.
Hints:
1. Don
2. Shimla
3. Hungama
4. Sholay
5. January.

Exercise 3

I. Underline the collective nouns in the following sentences. The first one has been done for you.

1. The army marched forward to occupy the land.
2. Father bought a packet of sweets.
3. Our class is very noisy.
4. The mob destroyed the furniture.
5. We booked a suite of rooms in the hotel.
6. A herd of cattle was grazing in the field.
Hints:
2. packet
3. class
4. mob, furniture
5. suite
6. herd.

II. Fill in the blanks in the following phrases with collective nouns. Choose from the box given below:

soldiers
grapes
bananas
bees
stick
musicians
sailors
stones
puppies.
wolves
1. a band of musicians
2. a bundle of sticks
3. a heap of stones
4. a bunch of grapes
5. a regiment of soldiers
6. a pack of wolves
7. a swarm of bees
8. a bunch of bananas
9. a crew of sailors
10. a litter of puppies.

III. Choose from the following list of collective nouns to form meaningful sentences:

school
library
pride
audience
committee
1. The …………. held a two hour meeting.
2. The …………. enjoyed the film.
3. We saw a …………. of whales in the sea.
4. The ………….. of lions was an impressive sight.
5. The students collected books from the ………
Hints:
1. committee
2. audience
3. school
4. pride
5. library.

Exercise 4

I. Underline the abstract nouns in the following sentences. The first one has been done for you.

1. Soldiers are known for their bravery.
2. Books provide us with knowledge.
3. My grandfather enjoys good health.
4. We lost hope of finding our stolen jewellery.
5. Raj suffered a loss when he sold his house.
6. Navin was in a lot of pain after he fell.
7. The teacher told the parents about their son’s progress.
8. The little boy cried in fear on seeing the tiger.
9. It is our duty to respect our parents.
10. Most of us are afraid of failure.
Hints.
2. knowledge
3. health
4. hope
5. loss
6. pain
7. progress
8. fear
9. duty
10. failure.

II. Match abstract nouns from the given box that are opposite in meaning to those listed below. One has been done for you:

life
success
war
hatred
wealth
disagreement
cowardice
pain
cruelty
sorrow
noise
dishonesty.
Answer:
1. Silence – noise
2. kindness – cruelty
3. love – hatred
4. happiness – sorrow
5. agreement – disagreement
6. bravery – cowardice
7. peace – war
8. pleasure – pain
9. death – life
10. poverty – wealth
11. honesty – dishonesty
12. failure – success.
Note : A phrase doing the work of a noun is called a noun phrase.

Exercise 5

Underline the noun phrases in the following sentences:

1. I enjoy swimming in the river.
2. Serving our country is our duty.
3. Helping the poor gives me joy.
4. His dislike for me is unjustified.
5. My love for my friends is deep.
Answer:
1. I enjoy swimming in the river.
2. Serving our country is our duty.
3. Helping the poor gives me joy.
4. His dislike for me is unjustified.
5. My love for my friends is deep.
Note : A clause doing the work of a noun is called a noun clause.

Exercise 6

Underline the noun clause in the sentences.

1. I believe that he is honest.
2. Let me know where you are going.
3. No one doubts what he says.
4. I hope that he will pass his examination.
5. I do not know what he wants to do after graduation.
Answer:
1. I believe that he is honest.
2. Let me know where you are going.
3. No one doubts what he says.
4. I hope that he will pass his examination.
5. I do not know what he wants to do after graduation.