Bhagya

Punjab State Board PSEB 4th Class Punjabi Book Solutions Chapter 14 ਮੇਰਾ ਪੰਜਾਬ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 4 Punjabi Chapter 14 ਮੇਰਾ ਪੰਜਾਬ

ਪਾਠ-ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 1.
ਪੰਜਾਬ ਦਾ ਇਹ ਨਾਂ ਕਿਵੇਂ ਪਿਆ ?
ਉੱਤਰ:
“ਪੰਜਾਬ’ ਦੋ ਸ਼ਬਦਾਂ ਦੇ ਸੁਮੇਲ ਤੋਂ ਬਣਿਆ ਹੈ, ਜਿਸ ਤੋਂ ਭਾਵ ਹੈ-ਪੰਜ ਪਾਣੀਆਂ ਦੀ ਧਰਤੀ । ਪੰਜਾਬ ਵਿਚ ਵਗਦੇ ਪੰਜ ਦਰਿਆਵਾ ਤੋਂ ਇਸਦਾ ਇਹ ਨਾਂ ਪਿਆ ਹੈ !

ਪ੍ਰਸ਼ਨ 2.
“ਪੰਜਾਬ” ਸ਼ਬਦ ਦਾ ਕੀ ਅਰਥ ਹੈ ?
ਉੱਤਰ:
“ਪੰਜਾਬ” ਸ਼ਬਦ ਦਾ ਅਰਥ ਹੈ-ਪੰਜ ਪਾਣੀਆਂ ਦੀ ਧਰਤੀ ।

ਪ੍ਰਸ਼ਨ 3.
ਅੱਜ-ਕਲ੍ਹ ਪੰਜਾਬ ਵਿਚ ਵਗਦੇ ਤਿੰਨ ਦਰਿਆਵਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ;
ਸਤਲੁਜ, ਬਿਆਸ ਅਤੇ ਰਾਵੀ ।

ਪ੍ਰਸ਼ਨ 4.
ਪੰਜਾਬ ਦੇ ਕਿਹੜੇ-ਕਿਹੜੇ ਦੋ ਪ੍ਰਮੁੱਖ ਨਾਚ ਹਨ ?
ਉੱਤਰ:
ਗਿੱਧਾ ਤੇ ਭੰਗੜਾ ।

ਪ੍ਰਸ਼ਨ 5.
ਪੰਜਾਬ ਦੀਆਂ ਵਿਰਾਸਤੀ ਖੇਡਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ;
ਲੂਣ-ਮਿਆਣੀ, ਬਾਂਦਰ-ਕਿੱਲਾ, ਭੰਡਾਭੰਡਾਰੀਆ, ਕੋਟਲਾ-ਛਪਾਕੀ, ਈਂਗਣ-ਮੀਂਗਣ, ਪਿੱਠੂ, ਗੁੱਲੀ-ਡੰਡਾ ਆਦਿ ਪੰਜਾਬ ਦੀਆਂ ਵਿਰਾਸਤੀ ਖੇਡਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਪੰਜਾਬ ਦੀ ਧਰਤੀ ਬੰਜਰ ਕਿਉਂ ਹੋ ਰਹੀ ਹੈ ?
ਉੱਤਰ:
ਪੰਜਾਬ ਦੀ ਧਰਤੀ ਦੇ ਬੰਜਰ ਹੋਣ ਦਾ ਇਕ ਕਾਰਨ ਤਾਂ ਝੋਨੇ ਦੀ ਬਿਜਾਈ ਕਾਰਨ ਧਰਤੀ ਹੇਠਲੇ ਪਾਣੀ ਦੇ ਪੱਧਰ ਦਾ ਡੂੰਘਾ ਹੁੰਦਾ ਜਾਣਾ ਹੈ ਤੇ ਦੂਸਰਾ ਕੀਟ-ਨਾਸ਼ਕਾਂ ਅਤੇ ਰਸਾਇਣਾਂ ਦੀ ਜ਼ਿਆਦਾ ਵਰਤੋਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਪੰਜਾਬ ਵਿਚ ਕਿੰਨੇ ਜ਼ਿਲ੍ਹੇ ਹਨ ?
ਉੱਤਰ:
22.

ਪ੍ਰਸ਼ਨ 8.
ਪੰਜਾਬ ਦੀ ਰਾਜਧਾਨੀ ਦਾ ਕੀ ਨਾਂ ਹੈ ?
ਉੱਤਰ:
ਚੰਡੀਗੜ੍ਹ ।

ਪ੍ਰਸ਼ਨ 9.
ਅਸੀਂ ਪੰਜਾਬੀ ਭਾਸ਼ਾ ਨੂੰ ਕਿਹੜੀ ਲਿਪੀ ਵਿਚ ਲਿਖਦੇ ਹਾਂ ?
ਉੱਤਰ:
ਗੁਰਮੁਖੀ ।

ਪ੍ਰਸ਼ਨ 10.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਦੇ ਅਰਥ ਲਿਖੋ
ਪ੍ਰਸਿੱਧ, ਨਾਮਕਰਨ, ਫ਼ੀਸਦੀ, ਰਕਬਾ, ਖੜਗ, ਐਬ, ਸੁਬਾ, ਬਟਵਾਰਾ ।
ਉੱਤਰ:
(ੳ) ਸਿੱਧ – ਮਸ਼ਹੂਰ ।
(ਅ) ਨਾਮਕਰਨ – ਨਾਂ ਰੱਖਣ ਦੀ ਰਸਮ ।
(ਇ) ਫ਼ੀਸਦੀ – ਪ੍ਰਤਿਸ਼ਤ ।
(ਸ) ਰਕਬਾ – ਜ਼ਮੀਨ ਦਾ ਖੇਤਰ, ਖੇਤਰਫਲ ।
(ਹ) ਖੜਗ – ਤਲਵਾਰ ।
(ਕ) ਐਬ – ਬੁਰਾਈ ।
(ਖ) ਸੁਬਾ – ਪਾਂਤ ਜਾਂ ਰਾਜ ।
(ਗ) ਬਟਵਾਰਾ – ਵੰਡ ।

ਪ੍ਰਸ਼ਨ 11.
ਪੰਜਾਬ ਨੂੰ ਭੂਗੋਲਿਕ ਆਧਾਰ ‘ਤੇ ਮੁੱਖ ਰੂਪ ਵਿੱਚ ਤਿੰਨ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ : ਮਾਝਾ, ਦੁਆਬਾ ਅਤੇ ਮਾਲਵਾ । ਬਿਆਸ ਦਰਿਆ ਤੋਂ ਪਾਕਿਸਤਾਨ ਦੀ ਹੱਦ ਤੱਕ ਫੈਲੇ ਖੇਤਰ ਨੂੰ “ਮਾਝਾ’ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਬਿਆਸ ਅਤੇ ਸਤਲੁਜ ਦਰਿਆਵਾਂ ਦੇ ਵਿਚਕਾਰਲੇ ਖੇਤਰ ਨੂੰ ‘ਦੁਆਬਾ’ ਕਹਿੰਦੇ ਹਨ । ਸਤਲੁਜ ਦਰਿਆ ਤੋਂ ਹਰਿਆਣਾ ਅਤੇ ਰਾਜਸਥਾਨ ਦੀ ਹੱਦ ਤੱਕ ਫੈਲਿਆ ਖੇਤਰ ‘ਮਾਲਵਾ ਅਖਵਾਉਂਦਾ ਹੈ । ਪੰਜਾਬ ਦੇ ਕੁੱਲ 22 ਜ਼ਿਲ੍ਹੇ ਹਨ ।

ਚੰਡੀਗੜ੍ਹ ਪੰਜਾਬ ਦੀ ਰਾਜਧਾਨੀ ਹੈ । ਅੰਮ੍ਰਿਤਸਰ, ਪਟਿਆਲਾ, ਲੁਧਿਆਣਾ, ਜਲੰਧਰ, ਬਠਿੰਡਾ ਆਦਿ ਪੰਜਾਬ ਦੇ ਪ੍ਰਮੁੱਖ ਸ਼ਹਿਰ ਹਨ, ਜਿਨ੍ਹਾਂ ਦੇ ਨਾਂ ਵੱਖ-ਵੱਖ ਕਾਰਨਾਂ ਕਰਕੇ ਦੇਸ਼ ਅਤੇ ਸੰਸਾਰ ਵਿਚ ਪ੍ਰਸਿੱਧ ਹਨ । ਅੰਮ੍ਰਿਤਸਰ ਸਿੱਖ ਧਰਮ ਦਾ ਪਵਿੱਤਰ ਸਥਾਨ ਹੈ ਸ੍ਰੀ ਹਰਿਮੰਦਰ ਸਾਹਿਬ ਅੰਮ੍ਰਿਤਸਰ ਵਿੱਚ ਹੀ ਸਥਿਤ ਹੈ ਪਟਿਆਲਾ ਪੰਜਾਬ ਦਾ ਇੱਕ ਪ੍ਰਸਿੱਧ ਇਤਿਹਾਸਿਕ ਸ਼ਹਿਰ ਹੈ । ਇੱਥੇ ਬਹੁਤ ਸਾਰੀਆਂ ਇਤਿਹਾਸਿਕ ਇਮਾਰਤਾਂ ਹਨ । ਇਸ ਰਾਜ ਦਾ ਮੁੱਖ ਉਦਯੋਗਿਕ ਸ਼ਹਿਰ ਲੁਧਿਆਣਾ ਹੈ । ਜਲੰਧਰ ਖੇਡਾਂ ਅਤੇ ਲੁਧਿਆਣਾ ਹੌਜ਼ਰੀ ਦਾ ਸਮਾਨ ਤਿਆਰ ਕਰਨ ਲਈ ਦੁਨੀਆ ਭਰ ਵਿਚ ਪ੍ਰਸਿੱਧ ਹੈ । ਬਠਿੰਡਾ ਵਿੱਚ ਇੱਕ ਇਤਿਹਾਸਿਕ ਕਿਲ੍ਹਾ ਹੈ । ਇੱਥੇ ਏਸ਼ੀਆ ਮਹਾਂਦੀਪ ਦੀ ਸਭ ਤੋਂ ਵੱਡੀ ਛਾਉਣੀ ਅਤੇ ਇੱਕ ਵੱਡਾ ਰੇਲਵੇ ਜੰਕਸ਼ਨ ਹੈ ।

ਪ੍ਰਸ਼ਨ

1. ਇਸ ਪੈਰੇ ਵਿੱਚ ਕਿਹੜੇ-ਕਿਹੜੇ ਸ਼ਹਿਰਾਂ ਦੇ ਨਾਂ ਆਏ ਹਨ ?
2. ਪੰਜਾਬ ਦੀ ਰਾਜਧਾਨੀ ਦਾ ਨਾਂ ਲਿਖੋ ।
3. ਜਲੰਧਰ ਕਿਸ ਕਾਰਨ ਸੰਸਾਰ ਪ੍ਰਸਿੱਧ ਸ਼ਹਿਰ ਹੈ ?

ਉੱਤਰ:

1. ਚੰਡੀਗੜ੍ਹ, ਅੰਮ੍ਰਿਤਸਰ, ਪਟਿਆਲਾ, ਲੁਧਿਆਣਾ, ਜਲੰਧਰ ਤੇ ਬਠਿੰਡਾ ।
2. ਚੰਡੀਗੜ੍ਹ ।
3. ਖੇਡਾਂ ਦੇ ਸਮਾਨ ਕਰਕੇ ।

ਪ੍ਰਸ਼ਨ 12.
ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ
(ਉ) ਬਠਿੰਡੇ ਵਿੱਚ ……….. ਦੀ ਸਭ ਤੋਂ ਵੱਡੀ ਛਾਉਣੀ ਹੈ ।
(ਅ) ਪੰਜਾਬ ਦੇ ਤਿੰਨ ਭਾਗ ……….. ਅਤੇ ਸਭ ਮਾਲਵਾ ਹਨ ।
ਉੱਤਰ;
(ਉ) ਬਠਿੰਡੇ ਵਿਚ ਏਸ਼ੀਆ ਮਹਾਂਦੀਪ ਦੀ ਤੋਂ ਵੱਡੀ ਛਾਉਣੀ ਹੈ ।
(ਅ) ਪੰਜਾਬ ਦੇ ਤਿੰਨ ਭਾਗ ਮਾਝਾ, ਦੁਆਬਾ ਤੇ ਮਾਲਵਾ ਹਨ ।

ਪ੍ਰਸ਼ਨ 13.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਦੇ ਅਰਥ ਦੱਸ ਕੇ ਵਾਕਾਂ ਵਿਚ ਵਰਤੋਂ-
(ਕੁਦਰਤ, ਸੰਸਾਰ, ਸਤਿਕਾਰ, ਪੰਜਾਬੀ, ਧਰਤੀ)
ਉੱਤਰ:

1. ਕੁਦਰਤ ਪ੍ਰਕਿਰਤੀ, ਸਾਡਾ ਆਲਾਦੁਆਲਾ)-ਕੁਦਰਤ ਦੇ ਪਸਾਰੇ ਦਾ ਕੋਈ ਅੰਤ ਨਹੀਂ ।
2. ਸੰਸਾਰ (ਦੁਨੀਆ)-ਇਸ ਸਮੇਂ ਸੰਸਾਰ ਦੀ ਅਬਾਦੀ ਸਵਾ ਸੱਤ ਅਰਬ ਹੈ ।
3. ਸਤਿਕਾਰ (ਇੱਜ਼ਤ)-ਸਾਨੂੰ ਆਪਣੇ ਵੱਡਿਆਂ ਦਾ ਸਤਿਕਾਰ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।
4.  ਪੰਜਾਬੀ ਪੰਜਾਬ ਦੇ ਰਹਿਣ ਵਾਲਾ)-ਪੰਜਾਬੀ ਲੋਕ ਅਣਖੀਲੇ ਤੇ ਬਹਾਦਰ ਹੁੰਦੇ ਹਨ ।
5. ਧਰਤੀ (ਜ਼ਮੀਨ)-ਧਰਤੀ ਗੋਲ ਹੈ ।

ਪ੍ਰਸ਼ਨ 14.
ਮਿਲਾਨ ਕਰੋ-

ਉੱਤਰ:

ਪ੍ਰਸ਼ਨ 15.
ਨਕਸ਼ੇ ਵਿਚ ਪੰਜਾਬ ਦੇ ਤਿੰਨ ਖੇਤਰਾਂ ਬਾਰੇ ਜਾਣਕਾਰੀ ਦਿਓ-
ਉੱਤਰ:

ਪ੍ਰਸ਼ਨ 16.
ਪੰਜਾਬ ਦੇ ਨਕਸ਼ੇ ਵਿਚ ਜ਼ਿਲ੍ਹਿਆਂ ਅਤੇ ਗੁਆਂਢੀ ਦੇਸ਼/ਸੂਬਿਆਂ ਬਾਰੇ ਜਾਣਕਾਰੀ ਦਿਓ ।
ਉੱਤਰ:

Punjab State Board PSEB 4th Class Punjabi Book Solutions Chapter 13 ਮੱਘੂ ਮਗਰਮੱਛ ਤੇ ਪੰਛੀ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 4 Punjabi Chapter 13 ਮੱਘੂ ਮਗਰਮੱਛ ਤੇ ਪੰਛੀ

ਪਾਠ-ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 1.
ਚਿੜੀ ਨੇ ਮੱਧੂ ਨੂੰ ਕੀ ਕਿਹਾ ?
ਉੱਤਰ;
ਚਿੜੀ ਨੇ ਮੱਧੂ ਨੂੰ ਕਿਹਾ ਕਿ ਉਸ ਨੂੰ ਸਾਫ਼-ਸੁਥਰਾ ਰਹਿਣਾ ਚਾਹੀਦਾ ਹੈ ਤੇ ਉਸਨੂੰ ਵੀ ਭੋਜਨ ਖਾਣ ਮਗਰੋਂ ਆਪਣੇ ਦੰਦ ਸਾਫ਼ ਕਰਨੇ ਚਾਹੀਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਚਿੜੀ ਨੇ ਮੱਧੂ ਮਗਰਮੱਛ ਨੂੰ ਮੂੰਹ ਸਾਫ਼ ਕਰਨ ਦੇ ਕੀ-ਕੀ ਲਾਭ ਦੱਸੇ ?
ਉੱਤਰ:
ਚਿੜੀ ਨੇ ਮੱਘੂ ਨੂੰ ਦੱਸਿਆ ਕਿ ਮੂੰਹ ਸਾਫ਼, ਕਰਨ ਨਾਲ ਇਕ ਤਾਂ ਉਹ ਸਾਫ਼-ਸੁਥਰਾ ਹੋ ਜਾਵੇਗਾ, ਦੂਸਰਾ ਉਹ ਸੋਹਣਾ ਦਿਸੇਗਾ, ਤੀਸਰਾ ਉਸ ਕੋਲੋਂ ਬਦਬੂ ਨਹੀਂ ਆਵੇਗੀ ਤੇ ਚੌਥਾ ਉਹ ਅਰੋਗ ਰਹੇਗਾ ।

ਪ੍ਰਸ਼ਨ 3.
ਗੁਟਾਰ ਨੇ ਮੱਧੂ ਮਗਰਮੱਛ ਨੂੰ ਕੀ ਕਿਹਾ ?
ਉੱਤਰ:
ਗੁਟਾਰ ਨੇ ਮੱਧੂ ਮਗਰਮੱਛ ਨੂੰ ਕਿਹਾ ਕਿ ਉਨ੍ਹਾਂ ਨੂੰ ਉਸ ਦੇ ਦੰਦ ਸਾਫ਼ ਕਰਨ ਦਾ ਕੰਮ ਨਹੀਂ ਪੁੱਗਣਾ, ਕਿਉਂਕਿ ਉਹੋ ਵੇਲਾ ਹੀ ਉਨ੍ਹਾਂ ਦੇ ਚੁਗਣ ਦਾ ਹੁੰਦਾ ਹੈ ਤੇ ਉਹੋ ਹੀ ਉਸਦੋਂ ਦੰਦ ਸਾਫ਼ ਕਰਨ ਦਾ ।

ਪ੍ਰਸ਼ਨ 4.
ਮੱਧੂ ਮਗਰਮੱਛ ਨੇ ਪੰਛੀਆਂ ਨੂੰ ਕੀ ਸਮਝਾਇਆ ?
ਉੱਤਰ:
ਮੱਘੂ ਨੇ ਪੰਛੀਆਂ ਨੂੰ ਸਮਝਾਇਆ ਕਿ ਜੇਕਰ ਉਹ ਉਸ ਦੇ ਦੰਦ ਸਾਫ਼ ਕਰਨਗੇ, ਤਾਂ ਉਨ੍ਹਾਂ ਨੂੰ ਉਸ ਦੇ ਦੰਦਾਂ ਵਿਚ ਫਸਿਆ ਭੋਜਨ ਵੀ ਲੱਭੇਗਾ । ਉਸ ਦੇ ਦੰਦ ਸਾਫ਼ ਕਰਨਾ ਤਾਂ ਉਨ੍ਹਾਂ ਲਈ ਫ਼ਾਇਦੇ ਦੀ ਗੱਲ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਮੱਘੂ ਮਗਰਮੱਛ ਨੇ ਪੰਛੀਆਂ ਨਾਲ ਕੀ ਵਾਅਦਾ ਕੀਤਾ ?
ਉੱਤਰ:
ਮੱ ਮਗਰਮੱਛ ਨੇ ਪੰਛੀਆਂ ਨਾਲ ਵਾਅਦਾ ਕੀਤਾ ਕਿ ਜਦੋਂ ਉਹ ਉਸ ਦੇ ਦੰਦ ਸਾਫ਼ ਕਰਿਆ ਕਰਨਗੇ, ਤਾਂ ਉਹ ਆਪਣਾ ਮੂੰਹ ਖੁੱਲਾ ਹੀ ਰੱਖੇਗਾ । ਇਸ ਤਰ੍ਹਾਂ ਉਨ੍ਹਾਂ ਨੂੰ ਉਸ ਤੋਂ ਕੋਈ ਖ਼ਤਰਾ ਨਹੀਂ ।

ਪ੍ਰਸ਼ਨ 6.
ਬੈਕਟਾਂ ਵਿੱਚੋਂ ਠੀਕ ਸ਼ਬਦ ਚੁਣ ਕੇ ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ
(ਪਿੱਠ, ਚੁੰਝਾਂ, ਦੰਦ, ਭੋਜਨ, ਚਿੱਕੜ)
(ਉ) ਨਦੀ ਦੇ ਪਾਣੀ ਨੇ ਉਹਦੇ ਮੂੰਹ ਦਾ ……… ਧੋ ਦਿੱਤਾ ।
(ਅ) ਪੰਛੀਆਂ ਨੂੰ ……….. ਦੀ ਭਾਲ ਵਿਚ ਦੂਰ-ਦੂਰ ਤਕ ਉਡਾਰੀਆਂ ਭਰਨੀਆਂ ਪੈਂਦੀਆਂ ਸਨ ।
(ਇ) ਨਿੱਕੀ ਚਿੜੀ ਮੱਘਾ ਮਗਰਮੱਛ ਦੀ। …………. ਉੱਤੇ ਬੈਠ ਕੇ ਕਈ ਵਾਰ ਨਦੀ ਵਿਚ ਦੂਰ-ਦੂਰ ਤਕ ਸੈਰ ਕਰ ਆਉਂਦੀ ਸੀ ।
(ਸ) ਚਿੜੀ ਉਹਦੇ ਮੂੰਹ ਵਿਚ ਵੜ ਕੇ …….. ਮਾਰਨ ਲੱਗ ਪਈ ।
(ਹ) ਪੰਛੀਆਂ ਨੇ ਭਰ-ਪੇਟ ਭੋਜਨ ਵੀ ਖਾਧਾ ਅਤੇ ਮੱਘੁ ਮਗਰਮੱਛ ਦੇ ……. ਵੀ ਸਾਫ਼ ਹੋ ਗਏ ।
ਉੱਤਰ:
(ਉ) ਨਦੀ ਦੇ ਪਾਣੀ ਨੇ ਉਹਦੇ ਮੂੰਹ ਦਾ ਚਿੱਕੜ ਧੋ ਦਿੱਤਾ |
(ਅ) ਪੰਛੀਆਂ ਨੂੰ ਭੋਜਨ ਦੀ ਭਾਲ ਵਿਚ ਦੂਰ-ਦੂਰ ਤਕ ਉਡਾਰੀਆਂ ਭਰਨੀਆਂ ਪੈਂਦੀਆਂ ਸਨ ।
(ਇ) ਨਿੱਕੀ ਚਿੜੀ ਮੱਘੂ ਮਗਰਮੱਛ ਦੀ ਪਿੱਠ ਉੱਤੇ ਬੈਠ ਕੇ ਕਈ ਵਾਰ ਨਦੀ ਵਿਚ ਦੂਰ-ਦੂਰ ਤਕ ਸੈਰ ਕਰ ਆਉਂਦੀ ਸੀ ।
(ਸ) ਚਿੜੀ ਉਹਦੇ ਮੂੰਹ ਵਿਚ ਵੜ ਕੇ ਚੁੰਝਾਂ ਮਾਰਨ ਲੱਗ ਪਈ ।
(ਹ) ਪੰਛੀਆਂ ਨੇ ਭਰ ਪੇਟ ਭੋਜਨ ਵੀ ਖਾਧਾ ਅਤੇ ਮੱਘੁ ਮਗਰਮੱਛ ਦੇ ਦੰਦ ਵੀ ਸਾਫ਼ ਹੋ ਗਏ ।

ਪ੍ਰਸ਼ਨ 7.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦ ਕਿਸ ਨੇ, ਕਿਸ ਨੂੰ ਕਹੇ ?
(ਉ) ਸਾਨੂੰ ਹਮੇਸ਼ਾਂ ਸਾਫ਼-ਸੁਥਰੇ ਬਣ ਕੇ ਰਹਿਣਾ ਚਾਹੀਦੈ । ਤੂੰ ਵੀ ਭੋਜਨ ਖਾਣ ਤੋਂ ਪਿੱਛੋਂ ਮੂੰਹ ਸਾਫ਼ ਕਰਿਆ ਕਰ ।
(ਅ) ‘‘ਤੇਰਾ ਤਾਂ ਮੂੰਹ ਵੱਡਾ ਸਾਰਾ ਏ ਤੇ ਦੰਦ ਕਿੰਨੇ ਸਾਰੇ । ਏਨਾ ਕੰਮ ਮੈਂ ਇਕੱਲੀ ਕਿਸ ਤਰ੍ਹਾਂ ਕਰੂੰ ?”
(ਇ) “ਇਹ ਕੰਮ ਨਹੀਂ ਸਾਨੂੰ ਪੁੱਗਣਾ ।ਉਹੋ ਵੇਲਾ ਚੋਗਾ ਚੁਗਣ ਦਾ ਤੇ ਉਹ ਵੇਲਾ ਤੇਰੇ ਦੰਦ ਸਾਫ਼ ਕਰਨ ਦਾ ।”
(ਸ) ‘‘ਮੇਰਾ ਪੱਕਾ ਵਾਅਦਾ ਰਿਹਾ, ਦੰਦਾਂ ਦੀ ਸਫ਼ਾਈ ਵੇਲੇ ਮੂੰਹ ਖੁੱਲ੍ਹਾ ਹੀ ਰੱਖਿਆ ਕਰੂੰ. ।”
ਉੱਤਰ:
(ੳ) ਇਹ ਸ਼ਬਦ ਚਿੜੀ ਨੇ ਮੱਧੂ ਮਗਰਮੱਛ ਨੂੰ ਕਹੇ ।
(ਆ) ਇਹ ਸ਼ਬਦ ਚਿੜੀ ਨੇ ਮੱਘੁ ਮਗਰਮੱਛ ਨੂੰ ਕਹੇ ।
(ਈ) ਇਹ ਸ਼ਬਦ ਗੁਟਾਰ ਨੇ ਮੱਘੂ ਮਗਰਮੱਛ ਨੂੰ ਕਹੇ ।
(ਸ) ਇਹ ਸ਼ਬਦ ਮੱਘੂ ਮਗਰਮੱਛ ਨੇ ਪੰਛੀਆਂ ਨੂੰ ਕਹੇ ।

ਪ੍ਰਸ਼ਨ 8.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਨੂੰ ਵਾਕਾਂ ਵਿਚ ਵਰਤੋ
ਕੋਸ਼ਿਸ਼, ਸਹਾਇਤਾ, ਸਾਫ਼-ਸੁਥਰੇ, ਜ਼ਿੰਮੇਵਾਰੀ, ਭਰੋਸਾ, ਬੂਥੀ, ਬਦਬੂ ।
ਉੱਤਰ:

1. ਕੋਸ਼ਿਸ਼ (ਯਤਨ) – ਸਫਲਤਾ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਕੋਸ਼ਿਸ਼ ਕਰਨੀ ਜ਼ਰੂਰੀ ਹੈ ।
2. ਸਹਾਇਤਾ (ਮੱਦਦ) – ਉਸ ਨੇ ਮੇਰੀ ਔਖੇ ਵੇਲੇ ਸਹਾਇਤਾ ਕੀਤੀ ।
3. ਸਾਫ਼-ਸੁਥਰੇ (ਸਾਫ਼) – ਦਾਤਣ ਕਰਨ ਨਾਲ ਦੰਦ ਸਾਫ਼-ਸੁਥਰੇ ਰਹਿੰਦੇ ਹਨ ।
4. ਜ਼ਿੰਮੇਵਾਰੀ (ਸਿਰ ਲੈਣਾ) – ਇਹ ਕੰਮ ਕਰਨਾ ਹੁਣ ਤੇਰੀ ਜ਼ਿੰਮੇਵਾਰੀ ਹੈ ।
5. ਭਰੋਸਾ (ਯਕੀਨ) – ਮੈਨੂੰ ਤੇਰੀ ਗੱਲ ਉੱਤੇ ਪੂਰਾ ਭਰੋਸਾ ਹੈ ।
6. ਬੂਥੀ (ਮੂੰਹ)-ਕੁੱਤਾ ਬੂਥੀ ਚੁੱਕ ਕੇ ਮੇਰੀ ਵਲ ਦੇਖ ਰਿਹਾ ਸੀ !
7. ਬਦਬੂ (ਭੈੜੀ ਬੂ-ਗੰਦਗੀ ਦੇ ਢੇਰ ਆਲੇਦੁਆਲੇ ਵਿਚ ਬਦਬੂ ਫੈਲਾਉਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 9.
ਕਿਸੇ ਮਨ-ਪਸੰਦ ਪੰਛੀ ਦੀ ਤਸਵੀਰ ਬਣਾਓ
ਉੱਤਰ:
ਨੋਟ-ਵਿਦਿਆਰਥੀ ਆਪੇ ਬਣਾਉਣ ਦਾ ਯਤਨ ਕਰਨ ॥

ਪ੍ਰਸ਼ਨ 10.
ਦੰਦਾਂ ਦੀ ਸੰਭਾਲ ਕਿਵੇਂ ਕਰੀਏ ?

ਉੱਤਰ:

ਪ੍ਰਸ਼ਨ 11.
‘ਦੀਵਾਲੀ ਵਿਸ਼ੇ ਉੱਤੇ ਇਕ ਲੇਖ ਲਿਖੋ ।
ਉੱਤਰ:
(ਨੋਟ-ਇਹ ਲੇਖ ਲਿਖਣ ਲਈ ਦੇਖੋ ਅਗਲੇ ਸਫ਼ਿਆਂ ਵਿਚ “ਲੇਖ-ਰਚਨਾ ਵਾਲਾ ਭਾਗ ।)

Punjab State Board PSEB 4th Class Punjabi Book Solutions Chapter 6 ਗੁਟਰ-ਗੂੰ ……. ਗੁਟਰ-ਗੂੰ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 4 Punjabi Chapter 6 ਗੁਟਰ-ਗੂੰ ……. ਗੁਟਰ-ਗੂੰ

ਕਾਵਿ-ਟੋਟਿਆਂ ਦੇ ਸਰਲ ਅਰਥ

(ਉ) ਗੁਟਰ-ਗੂੰ ……………… ਗੁਟਰ ਗੂੰ’।
ਸਰਲ ਅਰਥ-ਕਬੂਤਰ ਕਹਿੰਦਾ ਹੈ, “ਮੈਂ ਗੁਟਰਗੂੰ, ਗੁਟਰ-ਗੂੰ’ ਕਰਦਾ ਹੋਇਆ ਬੋਲਦਾ ਹਾਂ । ਲੋਕ ਮੈਨੂੰ ਚੀਨਾ ਜਾਂ ਗੋਲਾ ਕਹਿੰਦੇ ਹਨ । ਮੇਰਾ ਸਰੀਰ ਰੰਗ-ਬਰੰਗਾ ਹੈ । ਤੂੰ ਆਪ ਬੁੱਝ ਲੈ, ਮੈਂ ਕੌਣ ਹਾਂ ?”
‘‘ਮੇਰੇ ਖੰਭ ਕਈ ਰੰਗਾਂ ਦੇ ਬਣੇ ਹੋਏ ਹਨ । ਮੇਰੇ ਖੰਭ ਚਿੱਟੇ ਵੀ ਹਨ ਤੇ ਕਾਲੇ ਵੀ, ਜੋ ਕਿ ਲੋਕਾਂ ਨੂੰ ਚੰਗੇ ਲੱਗਦੇ ਹਨ । ਮੇਰੇ ਇਨ੍ਹਾਂ ਰੰਗਾਂ ਕਰਕੇ ਹੀ ਕੋਈ ਮੈਨੂੰ ਲਾਲਬਿੰਦਾ ਕਹਿੰਦਾ ਹੈ, ਕੋਈ ਲੋਟਣ ਤੇ ਕੋਈ ਗੋਲਾ । ਇਸ ਤਰ੍ਹਾਂ ਮੇਰੇ ਕਿੰਨੇ ਹੀ ਨਾਂ ਹਨ । ਮੈਂ ‘ਗੁਟਰ-ਗੂੰ, ਗੁਟਰ-ਗੂੰ ਕਰਦਾ ਹੋਇਆ ਬੋਲਦਾ ਹਾਂ।”

(ਅ) ਮੌਜਾਂ ਨਾਲ……….. ਗੁਟਰ-ਗੂੰ ।
ਸਰਲ ਅਰਥ-ਕਬੂਤਰ ਕਹਿੰਦਾ ਹੈ ਕਿ ਮੈਨੂੰ ਜਦੋਂ ਵੀ ਬੱਚੇ ਚੋਗਾ ਪਾਉਂਦੇ ਹਨ, ਤਾਂ ਮੈਂ ਬੜੀ ਮੌਜ ਨਾਲ ‘ ਚੁਗਣ ਲੱਗ ਪੈਂਦਾ ਹਾਂ । ਮੈਂ ਚੋਗਾ ਪਾਉਣ ਵਾਲੇ ਤੇ ਤੋਤਲੀ ਬੋਲੀ ਬੋਲਣ ਵਾਲੇ ਬੱਚਿਆਂ ਨਾਲ ਗੱਲਾਂ ਕਰਦਾ ਹਾਂ ਤੇ ਉਨ੍ਹਾਂ ਦੇ ਖਿਲਾਰੇ ਚੋਗੇ ਵਲ ਵੀ ਮੂੰਹ ਰੱਖਦਾ ਹਾਂ ਤੇ ‘ਗੁਟਰ-ਗੂੰ, ਗੁਟਰ-ਗੂੰ ਕਰ ਕੇ ਵੀ ਬੋਲਦਾ ਹਾਂ |

(ਈ) ਅੰਬਰੀਂ ਜਦੋਂ ……… ਗੁਟਰ-ਗੂੰ ।
ਸਰਲ ਅਰਥ-ਕਬੂਤਰ ਕਹਿੰਦਾ ਹੈ ਕਿ ਜਦੋਂ ਮੈਂ ਅਸਮਾਨਾਂ ਵਿਚ ਉਡਾਰੀ ਮਾਰਦਾ ਹਾਂ, ਤਾਂ ਬੱਦਲਾਂ ਤੋਂ
ਵੀ ਉੱਚਾ ਉੱਡ ਜਾਂਦਾ ਹਾਂ, ਪਰ ਮੈਂ ਘਰ ਦਾ ਰਾਹ ਕਦੇ ਵੀ ਨਹੀਂ ਭੁੱਲਦਾ । ਇਸੇ ਕਰਕੇ ਮੈਂ ਤਿਰਕਾਲਾਂ ਵੇਲੇ ਆਪਣੇ ਘਰ ਵਾਪਸ ਪਰਤ ਆਉਂਦਾ ਹਾਂ । ਮੈਂ “ਗੁਟਰ-ਗੂੰ, ਗੁਟਰ-ਗੂੰ’ ਕਰ ਕੇ ਬੋਲਦਾ ਰਹਿੰਦਾ ਹਾਂ ।

(ਸ) ਕਦੇ ਕਿਸੇ ਢੋਲ………….. ਗੁਟਰਗੂੰ ।
ਸਰਲ ਅਰਥ-ਕਬੂਤਰ ਕਹਿੰਦਾ ਹੈ ਕਿ ਮੈਂ ਕਦੇ ਕਿਸੇ ਪ੍ਰੇਮੀ ਜਾਂ ਪਤੀ ਦੀ ਚਿੱਠੀ ਇਕ ਥਾਂ ਤੋਂ ਦੂਜੀ ਥਾਂ ਉੱਤੇ ਪਹੁੰਚਾਉਂਦਾ ਹਾਂ । ਕਦੇ ਚਿੱਠੀ ਕਿਸੇ ਮੌਤ ਦੇ ਸੁਨੇਹੇ ਜਾਂ ਵਿਆਹ ਦੇ ਸੱਦੇ ਦੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਮੈਂ ਇਕ ਥਾਂ ਤੋਂ ਦੂਜੀ ਥਾਂ ਖ਼ੁਸ਼ੀ ਜਾਂ ਗ਼ਮੀ ਭਰੀਆਂ ਖ਼ਬਰਾਂ ਪਹੁੰਚਾਉਂਦਾ ਰਹਿੰਦਾ ਹਾਂ ਤੇ ਇਹ ਕੰਮ ਕਰਨ ਲਈ ਮੈਂ ਕਦੇ ਵੀ ਕੋਈ ਹਿਚਕਚਾਹਟ ਨਹੀਂ ਕਰਦਾ । ਨਾਲ-ਨਾਲ ਮੈਂ ‘ਗੁਟਰ-ਗੂੰ, ਗੁਟਰ-ਗੂੰ ਕਰ ਕੇ ਬੋਲਦਾ ਰਹਿੰਦਾ ਹਾਂ ।

(ਹ) ਮੈਂ ਕਬੂਤਰ ………….. ਗੁਟਰ-ਗੂੰ ।
ਸਰਲ ਅਰਥ-ਕਬੂਤਰ ਕਹਿੰਦਾ ਹੈ ਕਿ ਉਹ ਅਮਨ ਦਾ ਗੀਤ ਗਾਉਂਦਾ ਹੈ । ਉਹ ਸਭ ਦਾ ਭਲਾ ਮੰਗਦਾ ਹੈ । ਉਹ ਕਹਿੰਦਾ ਹੈ ਕਿ ਮਨੁੱਖੋ, ਤੁਸੀਂ ਮੇਰੇ ਕੋਲੋਂ ਰਲ ਕੇ ਰਹਿਣਾ ਸਿੱਖੋ ਤੇ ਆਪਣੇ ਮਨਾਂ ਵਿਚੋਂ ਨਫ਼ਰਤ ਨੂੰ ਕੱਢ ਦੇਵੋ । ਮੈਂ “ਗੁਟਰ-ਗੂੰ, ਗੁਟਰ ਗੂੰ’ ਕਰਦਾ ਤੁਹਾਨੂੰ ਇਹੋ ਗੱਲ ਕਹਿੰਦਾ ਹਾਂ ।

ਬਹੁਤ ਸੰਖੇਪ ਉੱਤਰ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

1. ਗੁਟਰ-ਗੂੰ……
ਗੁਟਰ-ਗੂੰ…………
ਲੋਕ ਕਹਿਣ ਮੈਨੂੰ ਚੀਨਾ, ਗੋਲਾ
ਰੰਗ-ਬਰੰਗਾ, ਬੁੱਝ ਲੈ ਤੂੰ …….।

ਪ੍ਰਸ਼ਨ

1. ‘ਗੁਟਰ-ਗੂ ਕਿਸ ਪੰਛੀ ਦੀ ਅਵਾਜ਼ ਵਲ ਸੰਕੇਤ ਹੈ ?
2. ਲੋਕ ਕਿਸ ਨੂੰ ਕੀ ਕਹਿੰਦੇ ਹਨ ?
3. ਤੁਸੀਂ ਇਨ੍ਹਾਂ ਸਤਰਾਂ ਤੋਂ ਕੀ ਬੁੱਝਦੇ ਹੋ ਕਿ ਇਹ ਕਿਸ ਬਾਰੇ ਹਨ ?

ਉੱਤਰ:

1. ਇਹ ਸੰਕੇਤ ਕਬੂਤਰ ਦੀ ਅਵਾਜ਼ ਵਲ ਹੈ ।
2. ਲੋਕ ਕਬੂਤਰ ਨੂੰ ਚੀਨਾ, ਗੋਲਾ ਆਦਿ ਕਹਿੰਦੇ ਹਨ ।
3. ਇਹ ਸਤਰਾਂ ਕਬੂਤਰ ਬਾਰੇ ਹਨ ।

2. ਖੰਭ ਨੇ ਮੇਰੇ ਰੰਗ-ਬਰੰਗੇ
ਚਿੱਟੇ, ਕਾਲੇ, ਲੱਗਦੇ ਚੰਗੇ
ਲਾਲ ਬਿੰਦਾ ਤੇ ਲੋਟਣ, ਗੋਲਾ
ਕਿੰਨੇ ਹੀ ਮੇਰੇ ਨਾਂ ਨੂੰ ਉੱ…
ਗੁਟਰ-ਗੂੰ ……. ਗੁਟਰ-ਗੂੰ ।

ਪ੍ਰਸ਼ਨ

1. ਕਿਸ ਦੇ ਖੰਭ ਰੰਗ-ਬਰੰਗੇ ਹਨ ?
2. ਮੇਰੇ ਨਾਂ ਕਿੰਨੇ ਹਨ ?
3. “ਗੁਟਰ-ਗੂੰ…… ਗੁਟਰ-ਗੂੰ’ ਕਵਿਤਾ ਦੀਆਂ ਚਾਰ ਸਤਰਾਂ ਜ਼ਬਾਨੀ ਲਿਖੋ ।

ਉੱਤਰ:

1. ਕਬੂਤਰ ਏਂ, ਖੰਭ ਰੰਗ-ਬਰੰਗੇ ਹਨ |
2. ਮੇਰੇ ਨਾਂ ਲਾਲਬਿੰਦਾ, ਲੋਟਣ ਤੇ ਗੋਲਾ ਹਨ ।
3. (ਨੋਟ-ਉੱਪਰ ਦਿੱਤੀਆਂ ਸਤਰਾਂ ਨੂੰ ਯਾਦ ਕਰੋ ।)

3. ਮੌਜਾਂ ਨਾਲ ਮੈਂ ਚੁਗਦਾ ਦਾਣੇ ,
ਚੋਗਾ ਜਦ ਵੀ ਪਾਉਣ ਨਿਆਣੇ
ਤੋਤਲਿਆਂ ਨਾਲ ਗੱਲਾਂ ਕਰਦਾ
ਚੋਗੇ ਵਲ ਵੀ ਰੱਖਦਾ ਮੂੰਹ ….
ਗੁਟਰ-ਗੂੰ…… ਗੁਟਰ-ਗੂੰ ।

ਪ੍ਰਸ਼ਨ

1. ਮੌਜਾਂ ਨਾਲ ਦਾਣੇ ਕੌਣ ਚੁਗਦਾ ਹੈ ?
2. ਚੋਗਾ ਕੌਣ ਪਾਉਂਦਾ ਹੈ ?
3. ਤੋਤਲੇ ਕੌਣ ਹਨ ?
4. ਚੋਗੇ ਵਲ ਮੂੰਹ ਕੌਣ ਰੱਖਦਾ ਹੈ ?

ਉੱਤਰ:

1. ਮੌਜਾਂ ਨਾਲ ਦਾਣੇ ਕਬੂਤਰ ਚੁਗਦਾ ਹੈ ।
2. ਚੋਗਾ ਨਿਆਣੇ ਪਾਉਂਦੇ ਹਨ ।
3. ਨਿਆਣੇ ।
4. ਕਬੂਤਰ ।

4. ਅੰਬਰੀਂ ਜਦੋਂ ਉਡਾਰੀ ਲਾਵਾਂ
ਬੱਦਲਾਂ ਤੋਂ ਉੱਚਾ ਉੱਡ ਜਾਵਾਂ
ਘਰ ਦਾ ਮੈਂ ਰਾਹ ਨਹੀਂ ਭੁੱਲਦਾ
ਮੁੜ ਆਵਾਂ ਆਥਣ ਨੂੰ…….
ਗੁਟਰ-ਗੂੰ ……… ਗੁਟਰ-ਗੂੰ ।

ਪ੍ਰਸ਼ਨ

1. ਅੰਬਰਾਂ ਵਿਚ ਉਡਾਰੀ ਕੌਣ ਮਾਰਦਾ ਹੈ ?
   ਜਾਂ
   ਬੱਦਲਾਂ ਤੋਂ ਉੱਚਾ ਕੌਣ ਉੱਡਦਾ ਹੈ ।
2. ਮੈਂ ਕਦੋਂ ਘਰ ਮੁੜਦਾ ਹਾਂ ?

ਉੱਤਰ:

1. ਕਬੂਤਰ ।
2. ਮੈਂ ਆਥਣ ਵੇਲੇ ਘਰ ਮੁੜਦਾ ਹਾਂ ।

5. ਕਦੇ ਕਿਸੇ ਢੋਲ, ਦੀ ਚਿੱਠੀ
ਮਰਗ, ਵਿਆਹ ਦੀ ਕੌੜੀ-ਮਿੱਠੀ
ਖ਼ਬਰਾਂ ਮੈਂ ਹੀ ਪਹੁੰਚਾਂਦਾ ਸੀ
ਕਦੇ ਨਾ ਕਰਦਾ ਚੂ, ਚਾਂ, ਊਂ…
ਗੁਟਰ-ਗੂੰ…. ਗੁਟਰ-ਗੂੰ ।

ਪ੍ਰਸ਼ਨ

1. ਕਿਸ-ਕਿਸ ਦੀ ਚਿੱਠੀ ਦੀ ਗੱਲ ਕੀਤੀ ਗਈ ਹੈ ?
2. ਚੂੰ-ਚਾਂ ਕੌਣ ਨਹੀਂ ਕਰਦਾ ?
   ਜਾਂ
   ਖ਼ਬਰਾਂ ਕੌਣ ਪੁਚਾਉਂਦਾ ਹੈ ?

ਉੱਤਰ:

1. ਢੋਲ ਪ੍ਰੇਮੀ, ਮਰਗ ਤੇ ਵਿਆਹ ਦੀ ਚਿੱਠੀ ਦੀ ਗੱਲ ਕੀਤੀ ਗਈ ਹੈ ।
2. ਕਬੂਤਰ ।

6. ਮੈਂ ਗਾਵਾਂ ਗੀਤ ਅਮਨ ਦਾ
ਭਲਾ ਲੋੜਦਾ ਸਭਨਾਂ ਦਾ
ਰਲ਼ ਕੇ ਰਹਿਣਾ ਮੈਥੋਂ ਸਿੱਖੋ
ਮਨ ਚੋਂ ਕੱਢੋ ਨਫ਼ਰਤ ਨੂੰ…
ਗੁਟਰ-ਗੂੰ……. ਗੁਟਰ-ਗੂੰ ।

ਪ੍ਰਸ਼ਨ

1. ਕਬੂਤਰ ਕਿਸ ਦਾ ਗੀਤ ਗਾਉਂਦਾ ਹੈ ?
2. ਕਬੂਤਰ ਕਿਸ ਦਾ ਭਲਾ ਚਾਹੁੰਦਾ ਹੈ ?
3. ਸਾਨੂੰ ਕਿਸ ਤਰ੍ਹਾਂ ਰਹਿਣਾ ਸਿੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ?

ਉੱਤਰ:

1. ਕਬੂਤਰ ਅਮਨ ਦਾ ਗੀਤ ਗਾਉਂਦਾ ਹੈ ।
2. ਕਬੂਤਰ ਸਭ ਦਾ ਭਲਾ ਚਾਹੁੰਦਾ ਹੈ ।
3. ਸਾਨੂੰ ਰਲ ਕੇ ਰਹਿਣਾ ਸਿੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ਤੇ ਮਨ ਵਿਚੋਂ ਨਫ਼ਰਤ ਕੱਢ ਦੇਣੀ ਚਾਹੀਦੀ ਹੈ ।

ਪਾਠ-ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 1.
‘ਗੁਟਰ-ਗੂੰ….ਗੁਟਰ-ਗੂੰ ਕਿਹੜਾ ਪੰਛੀ ਬੋਲਦਾ ਹੈ ?
ਉੱਤਰ:
“ਗੁਟਰ-ਗੂੰ … ਗੁਟਰ-ਗੂੰ’ ਕਬੂਤਰ ਬੋਲਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਕਬੂਤਰ ਦੇ ਖੰਭ ਕਿਹੜੇ-ਕਿਹੜੇ ਰੰਗਾਂ ਦੇ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ:
ਕਬੂਤਰ ਦੇ ਖੰਭ ਰੰਗ-ਬਰੰਗੇ ਹੁੰਦੇ ਹਨ । ਉਹ ਚਿੱਟੇ ਵੀ ਹੁੰਦੇ ਹਨ ਤੇ ਕਾਲੇ ਵੀ ।

ਪ੍ਰਸ਼ਨ 3.
ਕਬੂਤਰ ਦੇ ਹੋਰ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ:
ਚੀਨਾ, ਲਾਲਬਿੰਦਾ, ਗੋਲਾ, ਲੋਟਣ ।

ਪ੍ਰਸ਼ਨ 4.
ਕਬੂਤਰ ਤੋਂ ਕੀ ਕੰਮ ਲਿਆ ਜਾਂਦਾ ਸੀ ?
ਉੱਤਰ:
ਕਬੂਤਰ ਤੋਂ ਇਕ ਥਾਂ ਤੋਂ ਦੂਜੀ ਥਾਂ ਚਿੱਠੀਆਂ ਭੇਜਣ ਦਾ ਕੰਮ ਲਿਆ ਜਾਂਦਾ ਸੀ ।

ਪ੍ਰਸ਼ਨ 5.
ਕਬੂਤਰ ਕਿਹੜਾ ਗੀਤ ਗਾਉਂਦਾ ਹੈ ?
ਉੱਤਰ:
ਕਬੂਤਰ ਅਮਨ ਦਾ ਗੀਤ ਗਾਉਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਸਤਰਾਂ ਪੂਰੀਆਂ ਕਰੋ-
……… ਬਰੰਗੇ ।
……. ਚੰਗੇ ।
ਉੱਤਰ:
ਖੰਭ ਨੇ ਮੇਰੇ ਰੰਗ-ਬਰੰਗੇ ।
ਚਿੱਟੇ ਕਾਲੇ ਲਗਦੇ ਚੰਗੇ ।

ਪ੍ਰਸ਼ਨ 7.
ਸੋਹਣਾ ਕਰਕੇ ਲਿਖੋ
ਮੈਂ ਗਾਵਾਂ ਗੀਤ ਅਮਨ ਦਾ.
ਭਲਾ ਲੋੜਦਾ ਸਭਨਾਂ ਦਾ
ਰਲ ਕੇ ਰਹਿਣਾ, ਮੈਥੋਂ ਸਿੱਖੋ
ਮਨ ਚੋਂ ਕੱਢੋ ਨਫ਼ਰਤ ਨੂੰ
ਗੁਟਰ-ਗੂੰ…… ਗੁਟਰ-ਗੂੰ ।
ਉੱਤਰ:
(ਨੋਟ-ਵਿਦਿਆਰਥੀ ਆਪ ਹੀ ਸੋਹਣੀ ਲਿਖਾਈ ਕਰ ਕੇ ਲਿਖਣ ।)

ਪ੍ਰਸ਼ਨ 8.
ਪੜੋ, ਸਮਝੋ ਤੇ ਲਿਖੋ
ਨਿਆਣੇ : ਸਿਆਣੇ
ਉੱਚਾ : ………
ਆਥਣ : …….
ਕੌੜੀ : …….
ਕਾਲੇ : …….
ਭਲਾ : ………
ਚੰਗੇ : ……..
ਉੱਤਰ:
ਨਿਆਣੇ : ਸਿਆਣੇ
ਉੱਚਾ : ਨੀਵਾਂ
ਆਥਣ : ਉੱਗਣ (ਉਗਮਣੀ)
ਕੌੜੀ : ਮਿੱਠੀ
ਕਾਲੇ : ਚਿੱਟੇ
ਭਲਾ : ਚੰਗੇ
ਮੰਦੇ : ਮੰਦੇ ।

ਪ੍ਰਸ਼ਨ 9.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਦੇ ਅਰਥ ਲਿਖੋ-ਮਰਗ, ਆਥਣ |
ਉੱਤਰ:
ਮਰਗ ਦਾ ਅਰਥ ਹੈ ‘ਮਿਤ` । ਇਸ ਲਈ ‘ਤ’ ਤੇ ‘ਕਾਲ’ ਸ਼ਬਦ ਵੀ ਵਰਤੇ ਜਾਂਦੇ ਹਨ ।
ਆਥਣ ਦਾ ਅਰਥ ਹੈ “ਸੰਝ’ |ਇਸ ਲਈ ‘ਤਿਕਾਲਾਂ ਵੇਲਾ’ ਤੇ ‘ਸ਼ਾਮ’ ਸ਼ਬਦ ਵੀ ਵਰਤੇ ਜਾਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 10.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਦੀ ਵਾਕਾਂ ਵਿਚ ਵਰਤੋਂ ਕਰੋ-
ਲੋਕ, ਰੰਗ-ਬਰੰਗਾ, ਬੁੱਝ, ਦਾਣੇ, ਅੰਬਰ, ਬੱਦਲ, ਵਿਆਹ, ਕੌੜੀ-ਮਿੱਠੀ, ਪ੍ਰਤੀਕ, ਨਫ਼ਰਤ, ਮਰਗ !
ਉੱਤਰ:

1. ਲੋਕ ਬੰਦੇ)-ਮੇਲਾ ਅਣਗਿਣਤ ਲੋਕਾਂ । ਨਾਲ ਭਰਿਆ ਹੋਇਆ ਹੈ ।
2. ਰੰਗ-ਬਰੰਗਾ (ਬਹੁਤ ਸਾਰੇ ਰੰਗਾਂ ਵਾਲਾ)ਤੇਰਾ ਕੁੜਤਾ ਬੜਾ ਰੰਗ-ਬਰੰਗਾ ਹੈ ।
3. ਬੁੱਝ (ਜਾਣ)-ਉਸ ਤੋਂ ਮੇਰੀ ਬਾਤ ਨਾ ਬੁੱਝ ਹੋਈ ।
4. ਦਾਣੇ (ਬਨਸਪਤੀ ਦੇ ਬੀਜ)-ਇਹ ਦਾਣੇ ਪੀਹਣ ਦੀ ਚੱਕੀ ਹੈ ।
5. ਅੰਬਰ (ਅਸਮਾਨ)-ਨੀਲੇ ਅੰਬਰ ਵਿਚ ਸੂਰਜ ਚਮਕ ਰਿਹਾ ਹੈ ।
6. ਬੱਦਲ (ਮੇਘ-ਅਸਮਾਨ ਵਿਚ ਬੱਦਲ ਛਾ ਗਏ ਤੇ ਮੀਂਹ ਪੈਣ ਲੱਗਾ ।
7. ਵਿਆਹ ਸ਼ਾਦੀ)-ਕੱਲ੍ਹ ਨੂੰ ਮੇਰੀ ਭੈਣ ਦਾ ਵਿਆਹ ਹੈ ।
8. ਕੌੜੀ-ਮਿੱਠੀ ਮਾੜੀ-ਚੰਗੀ)-ਗੁਆਂਢੀਆਂ ਨਾਲ ਕਿਤੇ-ਕਿਤੇ ਕੌੜੀ-ਮਿੱਠੀ ਗੱਲ ਹੋ ਹੀ ਜਾਂਦੀ ਹੈ ।
9. ਤੀਕ ਚਿੰਨ੍ਹ)-ਕਬੂਤਰ ਅਮਨ ਦਾ ਪ੍ਰਤੀਕ ਹੈ ।
10. ਨਫ਼ਰਤ (ਘਿਣਾ)-ਕਦੇ ਵੀ ਕਿਸੇ ਨਾਲ ਨਫ਼ਰਤ ਨਾ ਕਰੋ ।
11. ਮਰਗ (ਮੌਤ-ਇਕ ਦੁਕਾਨਦਾਰ ਦੀ ਮਰਗ ਹੋਣ ਕਰਕੇ ਸਾਰਾ ਬਜ਼ਾਰ ਬੰਦ ਹੋ ਗਿਆ ।

ਪ੍ਰਸ਼ਨ 11.
ਹੇਠ ਲਿਖੇ ਚੱਕਰਾਂ ਵਿਚ ਕਬੂਤਰ ਨਾਲ ਸੰਬੰਧਿਤ ਗੱਲਾਂ ਲਿਖੋ ।

ਉੱਤਰ:

ਪ੍ਰਸ਼ਨ 12.
ਦਸ ਪੰਛੀਆਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ:
ਕਾਂ, ਚਿੜੀ, ਘੁੱਗੀ, ਛਾਰਕ, ਇੱਲ, ਬਾਜ਼, ਚੱਕੀਰਾਹਾ, ਕਬੂਤਰ, ਤਿੱਤਰ, ਬਟੇਰਾ ।

 

Punjab State Board PSEB 4th Class Punjabi Book Solutions Chapter 12 ਸਾਡੇ ਰੁੱਖ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 4 Punjabi Chapter 12 ਸਾਡੇ ਰੁੱਖ

ਪਾਠ-ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 1.
ਪੰਜਾਬ ਦਾ ਰਾਜ-ਰੁੱਖ ਕਿਹੜਾ ਹੈ ?
ਉੱਤਰ:
ਟਾਹਲੀ ।

ਪ੍ਰਸ਼ਨ 2.
ਟਾਹਲੀ ਦੀ ਲੱਕੜ ਕਿਹੋ ਜਿਹੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ:
ਟਾਹਲੀ ਦੀ ਲੱਕੜ ਮਜ਼ਬੂਤੇ ਤੇ ਰੇਸ਼ੇਦਾਰ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਨਿੰਮ ਦੇ ਰੁੱਖ ਉੱਤੇ ਲਗਣ ਵਾਲੇ ਫ਼ਲ ਦਾ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ:
ਨਿਮੋਲੀਆਂ ।

ਪ੍ਰਸ਼ਨ 4.
ਪਿੱਪਲ ਦੇ ਰੁੱਖ ਨੂੰ ਕੱਟਿਆ ਕਿਉਂ ਨਹੀਂ ਜਾਂਦਾ ?
ਉੱਤਰ:
ਪਿੱਪਲ ਦੇ ਰੁੱਖ ਨੂੰ ਧਾਰਮਿਕ ਸੰਸਕਾਰਾਂ ਕਰਕੇ ਕੱਟਿਆ ਨਹੀਂ ਜਾਂਦਾ

ਪ੍ਰਸ਼ਨ 5.
ਬੋਹੜ ਦੀ ਉਮਰ ਕਿੰਨੀ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ:
ਸੈਂਕੜੇ ਸਾਲ |

ਪ੍ਰਸ਼ਨ 6.
ਬੋਹੜ ਦਾ ਰੁੱਖ ਸਾਡੇ ਕੀ ਕੰਮ ਆਉਂਦਾ ਹੈ ?
ਉੱਤਰ:
ਬੋਹੜ ਦਾ ਰੁੱਖ ਸਾਨੂੰ ਛਾਂ ਤੇ ਬਾਲਣ ਲਈ ਲੱਕੜ ਦਿੰਦਾ ਹੈ । ਇਸਦੀ ਛਿੱਲ, ਪੱਤੇ ਤੇ ਦੁੱਧ ਨੂੰ ਕਈ ਬਿਮਾਰੀਆਂ ਦੇ ਇਲਾਜ ਲਈ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ । ਬੱਚੇ ਇਸਦੀ ਦਾੜ੍ਹੀ ਨੂੰ ਫੜ ਕੇ ਝੂਟੇ ਲੈਂਦੇ , ਹਨ ।

ਪ੍ਰਸ਼ਨ 7.
ਪਿੱਪਲ ਦੀ ਲਾਖ ਤੋਂ ਕੀ ਕੁੱਝ ਬਣਦਾ ਹੈ ?
ਉੱਤਰ:
ਪਿੱਪਲ ਦੀ ਲਾਖ ਤੋਂ ਬਟਨ, ਬਿਜਲੀ ਦੀਆਂ ਤਾਰਾਂ ਤੇ ਪਲਾਸਟਿਕ ਬਣਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਦੇ ਅਰਥ ਲਿਖੋ-
ਲੋਪ, ਸਦੀ, ਸੱਖਣੇ, ਸੈਂਕੜੇ, ਜੁੱਸਿਆਂ, ਤਨ, ਲੱਖਣ, ਲਾਖ
ਉੱਤਰ:
ਲੋਪ – ਦਿਖਾਈ ਨਾ ਦੇਣਾ, ਖ਼ਤਮ !
ਸਦੀ – ਇਕ ਸੌ ਸਾਲ ਦਾ ਸਮਾਂ ।
ਸੱਖਣੇ – ਖ਼ਾਲੀ ।
ਸੈਂਕੜੇ – ਸੌ ।
ਜੁੱਸਿਆਂ – ਸਰੀਰਾਂ
ਤਨ – ਸਰੀਰਾਂ |
ਲੱਖਣ – ਅੰਦਾਜ਼ਾ ।
ਲਾਖ – ਬੇਰੀ ਜਾਂ ਪਿੱਪਲ ਦੇ ਰਸ ਵਿਚੋਂ ਟਹਿਣੀਆਂ ਉੱਤੇ ਪੈਦਾ ਹੋਣ ਵਾਲਾ ਪਦਾਰਥ ।

ਪ੍ਰਸ਼ਨ 9.
ਠੀਕ ਸ਼ਬਦ ਚੁਣ ਕੇ ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ-
(ਦਾਤਣ, ਪੇਟ, ਆਲ੍ਹਣੇ, ਰੁੱਖ, ‘ਘੋਟਣੇ ।)
(ੳ) ਕੋਈ ਸਮਾਂ ਸੀ, ਜਦੋਂ ਹਰੇਕ ਘਰ ਵਿੱਚ ਕੋਈ ਨਾ ਕੋਈ ……… ਜ਼ਰੂਰ ਹੁੰਦਾ ਸੀ ।
(ਅ) ਨਿੰਮ ਦੀ ………… ਦੰਦਾਂ ਨੂੰ ਰੋਗ-ਰਹਿਤ ਰੱਖਦੀ ਹੈ ।
(ਈ) ਘਰਾਂ ਵਿਚ ਮਸਾਲੇ ਰਗੜਨ ਲਈ ਵਰਤੇ ਜਾਂਦੇ ……… ਜ਼ਿਆਦਾਤਰ ਨਿੰਮ ਦੇ ਰੁੱਖ ਦੇ ਬਣੇ · ਹੁੰਦੇ ਸਨ ।
(ਸ) ਪਿੱਪਲ ਦੀ ਜੜ੍ਹ ਅਤੇ ਛਿੱਲ ਨੂੰ …… ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਦੇ ਇਲਾਜ ਲਈ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ।
(ਹ) ਬੋਹੜ ਦੇ ਵੱਡੇ ਆਕਾਰ ਉੱਤੇ ਸੰਘਣੇ ਪੱਤਿਆਂ ਕਰਕੇ ਬਹੁਤ ਸਾਰੇ ਪੰਛੀ ਇਸ ਉੱਤੇ ਆਪਣੇ ……… ਪਾਉਂਦੇ ਹਨ ।
ਉੱਤਰ:
(ੳ) ਕੋਈ ਸਮਾਂ ਸੀ, ਜਦੋਂ ਹਰੇਕ ਘਰ ਵਿੱਚ ਕੋਈ ਨਾ ਕੋਈ ਰੁੱਖ ਜ਼ਰੂਰ ਹੁੰਦਾ ਸੀ ।
(ਅ) ਨਿੰਮ ਦੀ ਦਾਤਣ ਦੰਦਾਂ ਨੂੰ ਰੋਗ-ਰਹਿਤ ਰੱਖਦੀ ਹੈ ।
(ਈ) ਘਰਾਂ ਵਿਚ ਮਸਾਲੇ ਰਗੜਨ ਲਈ ਵਰਤੇ ਜਾਂਦੇ ਘੋਟਣੇ ਜ਼ਿਆਦਾਤਰ ਨਿੰਮ ਦੇ ਰੁੱਖ ਦੇ ਬਣੇ ਹੁੰਦੇ ਸਨ |
(ਸ) ਪਿੱਪਲ ਦੀ ਜੜ੍ਹ ਅਤੇ ਛਿੱਲ ਨੂੰ ਪੇਟ ਦੀਆਂ । ਬਿਮਾਰੀਆਂ ਦੇ ਇਲਾਜ ਲਈ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ।
(ਹ) ਬੋਹੜ ਦੇ ਵੱਡੇ ਆਕਾਰ ਉੱਤੇ ਸੰਘਣੇ ਪੱਤਿਆਂ ਕਰਕੇ ਬਹੁਤ ਸਾਰੇ ਪੰਛੀ ਇਸ ਉੱਤੇ ਆਪਣੇ ਆਲ੍ਹਣੇ ਪਾਉਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 10.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਦੀ ਵਾਕਾਂ ਵਿਚ ਵਰਤੋਂ ਕਰੋ-
ਰੁੱਖ, ਲੱਕੜ, ਉਮਰ, ਝੂਟੇ, ਛਾਂ ।
ਉੱਤਰ:

1. ਰੁੱਖ (ਦਰੱਖ਼ਤ, ਬਿਰਛ)-ਵਾਤਾਵਰਨ ਦੇ ਬਚਾਓ ਲਈ ਸਾਨੂੰ ਭੁੱਖ ਨਹੀਂ ਵੱਢਣੇ ਚਾਹੀਦੇ ।
2. ਲੱਕੜ ਰੁੱਖ ਦਾ ਅੰਦਰਲਾ ਸਖ਼ਤ ਭਾਗਟਾਹਲੀ ਦੀ ਲੱਕੜ ਬੜੀ ਮਜ਼ਬੂਤ ਤੇ ਰੇਸ਼ੇਦਾਰ ਹੁੰਦੀ ਹੈ ।
3. ਉਮਰ ਆਯੂ, ਜੀਵਨ ਦਾ ਸਮਾਂ-ਬੋਹੜ ਦੇ ਰੁੱਖ ਦੀ ਉਮਰ ਬਹੁਤ ਲੰਮੀ ਹੁੰਦੀ ਹੈ ।
4. ਝੂਟੇ ਹਿਲੋਰੇ)-ਕੁੜੀਆਂ ਪਿੱਪਲ ਤੇ ਪੀਂਘ ਪਾ ਕੇ ਝੂਟੇ ਲੈ ਰਹੀਆਂ ਹਨ ।
5. ਛਾਂ ਧੁੱਪ ਦੇ ਉਲਟ ਸ਼ਬਦ-ਗਰਮੀਆਂ ਵਿਚ ਦਰੱਖ਼ਤਾਂ ਦੀ ਛਾਂ ਬੜੀ ਪਿਆਰੀ ਲਗਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਢੁੱਕਵੇਂ ਮਿਲਾਨ ਕਰੋ-

ਉੱਤਰ:

ਪ੍ਰਸ਼ਨ 12.
ਵੱਖ-ਵੱਖ ਰੁੱਖਾਂ ਬਾਰੇ ਗੀਤਾਂ ਦੀਆਂ ਕੁੱਝ ਸਤਰਾਂ ਸੁੰਦਰ ਕਰ ਕੇ ਲਿਖੋ ।
ਉੱਤਰ:

1. ਟਾਹਲੀ-ਉੱਚੀਆਂ ਲੰਮੀਆਂ ਟਾਹਲੀਆਂ, ਵਿਚ ਗੁਜਰੀ ਦੀ ਪੀਂਘ ਵੇ ਮਾਹੀਆ ।
2. ਕਿੱਕਰ-ਮੁੰਡਾ ਰੋਹੀ ਦੇ ਕਿੱਕਰ ਤੋਂ ਕਾਲਾ, ਬਾਪੂ ਦੇ ਪਸੰਦ ਆ ਗਿਆ ।
3. ਪਿੱਪਲ-ਸਾਉਣ ਮਹੀਨੇ ਤੀਆਂ ਦੀ ਰੁੱਤ, ਪਿੱਪਲੀਂ ਪੀਘਾਂ ਪਈਆਂ |
4. ਨਿੰਮ-ਕੌੜੀ ਨਿੰਮ ਨੂੰ ਪਤਾਸੇ ਲਗਦੇ, ਜਿੱਥੋਂ ਮੇਰਾ ਵੀਰ ਲੰਘ ਜੇ ।
5. ਚੰਦਨ-ਬੇਟੀ ਚੰਨਣ ਦੇ ਓਹਲੇ ਓਹਲੇ ਕਿਉਂ ‘ ਖੜੀ ? ਮੈਂ ਤਾਂ ਖੜੀ ਸਾਂ ਬਾਬਲ ਜੀ ਦੇ ਪਾਸ ਬਾਬਲ ਵਰ ਲੋੜੀਏ ।
6. ਕਰੀਰ-ਸਾਉਣ ਮਹੀਨੇ ਮੀਂਹ ਪੈ ਜਾਂਦਾ,ਲਗਦਾ ਕਰੀਰੀਂ ਬਾਟਾ ।

ਪ੍ਰਸ਼ਨ 13.
ਆਪਣੇ ਚਾਚਾ ਜੀ ਦੇ ਵਿਆਹ ਵਿਚ ਸ਼ਾਮਿਲ ਹੋਣ ਲਈ ਸਕੂਲ ਵਿਚੋਂ ਛੁੱਟੀ ਲੈਣ ਲਈ ਇਕ ਅਰਜ਼ੀ ਲਿਖੋ ।
ਉੱਤਰ;
(ਨੋਟ-ਇਹ ਅਰਜ਼ੀ ਲਿਖਣ ਲਈ ਦੇਖੋ ਅਗਲੇ ਸਫ਼ਿਆਂ ਵਿਚ ਵੱਡੇ ਭਰਾ ਦੇ ਵਿਆਹ ਉੱਤੇ ਸਕੂਲੋਂ ਛੁੱਟੀ ਲੈਣ ਦੀ ਅਰਜ਼ੀ )

Punjab State Board PSEB 4th Class Punjabi Book Solutions Chapter 11 ਮੇਰੇ ਨਿਸ਼ਾਨੇ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 4 Punjabi Chapter 11 ਮੇਰੇ ਨਿਸ਼ਾਨੇ

‘ਕਾਵਿ-ਟੋਟਿਆਂ ਦੇ ਸਰਲ ਅਰਥ

(ੳ) ਮੈਂ ਭਾਰਤ ਦੀ …….. ਸ਼ਾਨ ਬਣਾਂਗਾ ।
ਸਰਲ ਅਰਥ-ਬੱਚਾ ਕਹਿੰਦਾ ਹੈ ਕਿ ਮੈਂ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਬਣਾਂਗਾ ਅਜੇ ਭਾਵੇਂ ਮੈਂ ਛੋਟਾ ਬੱਚਾ ਹਾਂ, ਪਰ ਕਿਸੇ ਵੇਲੇ ਮੈਂ ਮਹਾਨ ਮਨੁੱਖ ਬਣਾਂਗਾ। ਮੈਂ ਮਨ ਲਾ ਕੇ ਪੜ੍ਹਾਈ ਕਰਾਂਗਾ ਤੇ ਉੱਚੀ ਤੋਂ ਉੱਚੀ ਵਿੱਦਿਆ ਪ੍ਰਾਪਤ ਕਰਾਂਗਾ । ਮੈਂ ਸਖ਼ਤ ਮਿਹਨਤ ਕਰ ਕੇ, ਆਪਣੀ ਸੂਝ ਤੇ ਗਿਆਨ ਨੂੰ ਵਧਾ ਕੇ ਇਕ ਚੰਗਾ ਵਿਦਵਾਨ ਬਣਾਂਗਾ ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਮੈਂ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਬਣਾਂਗਾ ।

(ਅ) ਮੇਰੀਆਂ ਅੱਖਾਂ ……… ਸ਼ਾਨ ਬਣਾਂਗਾ ।
ਸਰਲ ਅਰਥ-ਬੱਚਾ ਕਹਿੰਦਾ ਹੈ ਕਿ ਮੇਰੀਆਂ ਨਜ਼ਰਾਂ ਭਾਰਤ ਦੇ ਹੱਦਾਂ-ਬੰਨਿਆਂ ਉੱਤੇ ਟਿਕੀਆਂ ਰਹਿਣਗੀਆਂ । ਕੋਈ ਦੁਸ਼ਮਣ ਮੇਰੇ ਹੁੰਦਿਆਂ ਭਾਰਤ ਵਲ ਤਕ ਵੀ ਨਹੀਂ ਸਕੇਗਾ । ਮੈਂ ਫ਼ੌਜੀ ਕਪਤਾਨ ਬਣ ਕੇ ਭਾਰਤ ਦੀ ਰਾਖੀ ਕਰਾਂਗਾ ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਮੈਂ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਬਣਾਂਗਾ ।

(ਈ) ਹਿੰਦੂ, ਮੁਸਲਿਮ ……. ਦਾ ਜਾਇਆ ।
ਸਰਲ ਅਰਥ-ਬੱਚਾ ਕਹਿੰਦਾ ਹੈ ਕਿ ਮੇਰੇ ਲਈ ਸਾਰੇ ਭਾਰਤ-ਵਾਸੀ ਇਕ ਸਮਾਨ ਹੋਣਗੇ । ਮੇਰੇ ਲਈ ਹਿੰਦੂ, ਮੁਸਲਿਮ, ਸਿੱਖ, ਈਸਾਈ ਵਿੱਚੋਂ ਕੋਈ ਵੀ ਪਰਾਇਆ ਨਹੀਂ ਹੋਵੇਗਾ । ਮੈਨੂੰ ਤਾਂ ਭਾਰਤ ਮਾਂ ਦਾ ਹਰ ਇਕ ਪੁੱਤਰ ਆਪਣਿਆਂ ਵਰਗਾ ਜਾਪਦਾ ਹੈ । ਮੈਂ ਭਾਰਤ ਦੀ ਜਿੰਦ-ਜਾਨ ਬਣਾਂਗਾ ਤੇ ਇਸ ਦੀ ਸ਼ਾਨ ਵਧਾਵਾਂਗਾ ।

(ਸ) ਸੌਂਪ ਦਏਗੀ ………………. ਸ਼ਾਨ ਬਣਾਂਗਾ । ਸਰਲ ਅਰਥ-ਬੱਚਾ ਕਹਿੰਦਾ ਹੈ ਕਿ ਭਾਰਤ ਮਾਤਾ ਮੈਨੂੰ ਯੋਗ ਬਣਾ ਕੇ ਜਿਹੜਾ ਵੀ ਕੰਮ ਸੌਂਪੇਗੀ, ਉਸ ਨੂੰ ਨਿਭਾਉਣਾ ਮੇਰਾ ਧਰਮ ਹੋਵੇਗਾ । ਮੈਂ ਉਸ ਕੰਮ ਨੂੰ ਤਨ-ਮਨ ਲਾ ਕੇ ਸਿਰੇ ਚੜ੍ਹਾਵਾਂਗਾ । ਇਸ ਤਰ੍ਹਾਂ ਮੈਂ ਭਾਰਤ ਦੀ ਚੰਗੀ ਸੰਤਾਨ ਬਣਾਂਗਾ ਤੇ ਇਸ ਦੀ ਸ਼ਾਨ ਵਧਾਵਾਂਗਾ ।

(ਹ) ਇੱਕੋ ਨੂਰ ਹੈ ………. ਸ਼ਾਨ ਬਣਾਂਗਾ ।
ਸਰਲ ਅਰਥ-ਬੱਚਾ ਕਹਿੰਦਾ ਹੈ ਕਿ ਸਾਰੇ ਮਨੁੱਖਾਂ ਵਿਚ ਇੱਕੋ ਰੱਬ ਦਾ ਨੂਰ ਹੈ । ਜਾਤਾਂ-ਪਾਤਾਂ ਦੇ ਸਾਰੇ ਫ਼ਰਕ ਝੂਠੇ ਹਨ । ਮੈਂ ਅਜਿਹਾ ਤੂਫ਼ਾਨ ਬਣਾਂਗਾ ਕਿ ਮੈਨੂੰ ਦੇਖ ਕੇ ਇੱਥੋਂ ਊਚ-ਨੀਚ ਤੇ ਛੂਤ-ਛਾਤ ਦੇ ਵਿਤਕਰੇ ਉੱਡ ਜਾਣਗੇ । ਇਸ ਤਰ੍ਹਾਂ ਮੈਂ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਬਣਾਂਗਾ ।

ਬਹੁਤ ਸੰਖੇਪ ਉੱਤਰ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

1. ਮੈਂ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਬਣਾਂਗਾ,
ਭਾਵੇਂ ਅੱਜ ਹਾਂ ਛੋਟਾ ਬੱਚਾ
ਪਰ ਮੈਂ ਕਦੇ ਮਹਾਨ ਬਣਾਂਗਾ ।
ਮੈਂ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਬਣਾਂਗਾ ।

ਪ੍ਰਸ਼ਨ

1. ਕੌਣ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਬਣਨਾ ਚਾਹੁੰਦਾ ਹੈ ?
2. ਬੱਚਾ ਕਿਸ ਦੀ ਸ਼ਾਨ ਬਣਨਾ ਚਾਹੁੰਦਾ ਹੈ ?
3. “ਮੇਰੇ ਨਿਸ਼ਾਨੇ ਕਵਿਤਾ ਦੀਆਂ ਚਾਰ ਸਤਰਾਂ ਜ਼ਬਾਨੀ ਲਿਖੋ ।

ਉੱਤਰ:

1. ਛੋਟਾ ਬੱਚਾ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਬਣਨਾ ਚਾਹੁੰਦਾ ਹੈ ।
2. ਬੱਚਾ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਬਣਨਾ ਚਾਹੁੰਦਾ ਹੈ ।
3. ਨੋਟ-ਉਪਰੋਕਤ ਸਤਰਾਂ ਨੂੰ ਜ਼ਬਾਨੀ ਯਾਦ ਕਰੋ ਤੇ ਲਿਖੋ ।

2. ਕਰਕੇ ਮਨ ਦੇ ਨਾਲ ਪੜ੍ਹਾਈ,
ਉੱਚੀ-ਉੱਚੀ ਵਿੱਦਿਆ ਪਾ ਕੇ ।
ਪੂਰੀ ਭਰਵੀਂ ਮਿਹਨਤ ਕਰ ਕੇ
ਸੂਝ ਵਧਾ ਕੇ, ਗਿਆਨ ਵਧਾ ਕੇ ।
ਮੈਂ ਚੰਗਾ ਵਿਦਵਾਨ ਬਣਾਂਗਾ,
ਮੈਂ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਬਣਾਂਗਾ ।

ਪ੍ਰਸ਼ਨ

1. ਛੋਟਾ ਬੱਚਾ ਕਿਸ ਤਰ੍ਹਾਂ ਪੜ੍ਹਾਈ ਕਰਨੀ ਚਾਹੁੰਦਾ ਹੈ ?
2. ਬੱਚਾ ਕੀ ਬਣਨਾ ਚਾਹੁੰਦਾ ਹੈ ?

ਉੱਤਰ:

1. ਛੋਟਾ ਬੱਚਾ ਸਖ਼ਤ ਮਿਹਨਤ ਕਰ ਕੇ ਪੜ੍ਹਾਈ ਕਰਨੀ ਚਾਹੁੰਦਾ ਹੈ ।
2. ਬੱਚਾ ਵਿਦਵਾਨ ਬਣਨਾ ਚਾਹੁੰਦਾ ਹੈ ।

3. ਮੇਰੀਆਂ ਅੱਖਾਂ ਦੇ ਵਿਚ ਰਹਿਣ,
ਦੇਸ਼ ਮੇਰੇ ਦੇ ਹੱਦਾਂ-ਬੰਨੇ ।
ਤੱਕੇਗਾ ਨਾ ਮੇਰੇ ਹੁੰਦਿਆਂ,
ਕੋਈ ਮੇਰੇ ਭਾਰਤ ਵੰਨੇ ।
ਮੈਂ ਫ਼ੌਜੀ ਕਪਤਾਨ ਬਣਾਂਗਾ,
ਮੈਂ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਬਣਾਂਗਾ ।

ਪ੍ਰਸ਼ਨ

1. ਬੱਚਾ ਆਪਣੀਆਂ ਅੱਖਾਂ ਅੱਗੇ ਕੀ ਰੱਖਣਾ ਚਾਹੁੰਦਾ ਹੈ ?
2. ਬੱਚਾ ਫ਼ੌਜ ਵਿਚ ਕਿਹੜਾ ਅਹੁਦਾ ਪ੍ਰਾਪਤ ਕਰਨਾ ਚਾਹੁੰਦਾ ਹੈ ?

ਉੱਤਰ:

1. ਬੱਚਾ ਭਾਰਤ ਦੇ ਹੱਦਾਂ-ਬੰਨਿਆਂ ਨੂੰ ਅੱਖਾਂ ਸਾਹਮਣੇ ਰੱਖਣਾ ਚਾਹੁੰਦਾ ਹੈ ।
2. ਬੱਚਾ ਫ਼ੌਜ ਵਿਚ ਕਪਤਾਨ ਦਾ ਅਹੁਦਾ ਪ੍ਰਾਪਤ ਕਰਨਾ ਚਾਹੁੰਦਾ ਹੈ ।

4. ਹਿੰਦੂ, ਮੁਸਲਿਮ, ਸਿੱਖ, ਈਸਾਈ,
ਮੈਨੂੰ ਕੋਈ ਨਹੀਂ ਪਰਾਇਆ ।
ਲੱਗਦਾ ਮੈਨੂੰ ਆਪਣਿਆਂ ਵਾਂਗਰ,
ਹਰ ਇਕ ਭਾਰਤ ਮਾਂ ਦਾ ਜਾਇਆ ।
ਮੈਂ ਭਾਰਤ ਦੀ ਜਿੰਦ-ਜਾਨ ਬਣਾਂਗਾ,
ਮੈਂ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਬਣਾਂਗਾ ।

ਪ੍ਰਸ਼ਨ

1. ਕਿਨ੍ਹਾਂ ਦੇ ਇਕ ਹੋਣ ਦੀ ਗੱਲ ਕੀਤੀ ਗਈ ਹੈ ?
2. ਕਿਹੜਾ ਆਪਣਿਆਂ ਵਰਗਾ ਜਾਪਦਾ ਹੈ ?

ਉੱਤਰ:

1. ਦੇਸ਼ ਦੇ ਹਰ ਇਕ ਵਾਸੀ ਹਿੰਦੂ, ਮੁਸਲਿਮ, ਸਿੱਖ, ਈਸਾਈ ਦੇ ਇਕ ਹੋਣ ਦੀ ਗੱਲ ਕੀਤੀ ਗਈ ਹੈ ।
2. ਭਾਰਤ ਮਾਂ ਦਾ ਹਰ ਇਕ ਜਾਇਆ ਆਪਣਿਆਂ ਵਰਗਾ ਜਾਪਦਾ ਹੈ ।

5. ਸੌਂਪ ਦਏਗੀ ਜੋ ਕੰਮ ਮੈਨੂੰ,
ਭਾਰਤ ਮਾਤਾ ਯੋਗ ਬਣਾ ਕੇ ।
ਉਹੀ ਮੇਰਾ ਧਰਮ ਬਣੇਗਾ,
ਤੋੜ ਚੜ੍ਹਾਸਾ ਤਨ-ਮਨ ਲਾ ਕੇ ।
ਮੈਂ ਚੰਗੀ ਸੰਤਾਨ ਬਣਾਂਗਾ,
ਮੈਂ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਬਣਾਂਗਾ ।

ਪ੍ਰਸ਼ਨ

1. ਬੱਚੇ ਦਾ ਧਰਮ ਕੀ ਹੋਵੇਗਾ ?
2. ਕੌਣ ਚੰਗੀ ਸੰਤਾਨ ਬਣੇਗਾ ?

ਉੱਤਰ:

1. ਜਿਹੜਾ ਕੰਮ ਵੀ ਭਾਰਤ ਮਾਤਾ ਉਸਨੂੰ ਸੌਂਪ ਦੇਵੇਗੀ, ਉਹ ਹੀ ਉਸ ਦਾ ਧਰਮ ਹੋਵੇਗਾ ।
2. ਛੋਟਾ ਬੱਚਾ ।

6. ਇੱਕੋ – ਨੂਰ ਹੈ ਸਭਨਾਂ ਅੰਦਰ,
ਝੂਠੀਆਂ ਨੇ ਸਭ ਜਾਤਾਂ-ਪਾਤਾਂ ।
ਉੱਡ ਜਾਣੇ ਨੇ ਮੈਨੂੰ ਤੱਕ ਕੇ,
ਊਚ-ਨੀਚਤਾ, ਛੂਤਾਂ-ਛਾਤਾਂ ।
ਮੈਂ ਐਸਾ ਤੂਫ਼ਾਨ ਬਣਾਂਗਾ,
ਮੈਂ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਬਣਾਂਗਾ ।

ਪ੍ਰਸ਼ਨ

1. ਸਭਨਾਂ ਅੰਦਰ ਕੀ ਹੈ ?
2. ਕੀ ਉੱਡ ਜਾਵੇਗਾ ?

ਉੱਤਰ:

1. ਇੱਕੋ ਨੂਰ ।
2. ਊਚ-ਨੀਚ ਤੇ ਛੂਤ-ਛਾਤ ।

ਪਾਠ-ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 1.
ਹੇਠ ਲਿਖੀਆਂ ਸਤਰਾਂ ਪੂਰੀਆਂ ਕਰੋ-

(ੳ) ਭਾਵੇਂ ਅੱਜ ਹਾਂ ਛੋਟਾ ਬੱਚਾ,
…………………………
(ਅ) ਤੱਕੇਗਾ ਨਾ ਮੇਰੇ ਹੁੰਦਿਆਂ,
…………………………
(ਈ) ਲੱਗਦਾ ਮੈਨੂੰ ਆਪਣਿਆਂ ਵਾਂਗਰ,
…………………………
(ਸ) ਇੱਕੋ ਨੂਰ ਹੈ ਸਭਨਾਂ ਅੰਦਰ,
…………………………
ਉੱਤਰ:
(ੳ) ਭਾਵੇਂ ਅੱਜ ਹਾਂ ਛੋਟਾ ਬੱਚਾ,
ਪਰ ਮੈਂ ਕਦੇ ਮਹਾਨ ਬਣਾਂਗਾ ।
(ਅ) ਤੱਕੇਗਾ ਨਾ ਮੇਰੇ ਹੁੰਦਿਆਂ,
ਕੋਈ ਮੇਰੇ ਭਾਰਤ ਵੰਨੇ ।
(ਇ) ਲੱਗਦਾ ਮੈਨੂੰ ਆਪਣਿਆਂ ਵਾਂਗਰ,
ਹਰ ਇਕ ਭਾਰਤ ਮਾਂ ਦਾ ਜਾਇਆ ।
(ਸ) ਇੱਕੋ ਨੂਰ ਹੈ ਸਭਨਾਂ ਅੰਦਰ,
ਝੂਠੀਆਂ ਨੇ ਸਭ ਜਾਤਾਂ-ਪਾਤਾਂ ।

ਪ੍ਰਸ਼ਨ 2.
ਇਸ ਕਵਿਤਾ ਵਿਚਲਾ ਵਿਦਿਆਰਥੀ ਕਿਹੜੇ-ਕਿਹੜੇ ਢੰਗਾਂ ਨਾਲ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਵਧਾਉਣੀ ਚਾਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ:
ਵਿਦਿਆਰਥੀ ਸਖ਼ਤ ਮਿਹਨਤ ਨਾਲ ਵਿਦਵਾਨ ਬਣ ਕੇ, ਫ਼ੌਜੀ ਕਪਤਾਨ ਬਣ ਕੇ, ਧਰਮਾਂ ਤੇ ਜਾਤਾਂ-ਪਾਤਾਂ ਦੇ ਵਿਤਕਰੇ ਮਿਟਾ ਕੇ ਅਤੇ ਭਾਰਤ ਮਾਤਾ ਦੁਆਰਾ ਸੌਂਪੇ ਕੰਮ ਨੂੰ ਤਨ, ਮਨ, ਧਨ ਨਾਲ ਨਿਭਾ ਕੇ ਭਾਰਤ ਦੀ ਸ਼ਾਨ ਵਧਾਉਣੀ ਚਾਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਨੂੰ ਵਾਕਾਂ ਵਿਚ ਵਰਤੋ
ਸ਼ਾਨ, ਮਹਾਨ, ਗਿਆਨ, ਮਿਹਨਤ, ਪਰਾਇਆ, ਸੰਤਾਨ, ਜਾਤ-ਪਾਤ ।
ਉੱਤਰ:

1. ਸ਼ਾਨ (ਵਡਿਆਈ)-ਮੈਂ ਤੇਰੀ ਸ਼ਾਨ ਦੇ ਖ਼ਿਲਾਫ਼ ਇਕ ਵੀ ਲਫ਼ਜ਼ ਨਹੀਂ ਬੋਲਿਆ ।
2. ਮਹਾਨ (ਵਿੱਡਾ)-ਭਾਰਤ ਇਕ ਮਹਾਨ ਦੇਸ਼ ਹੈ ।
3. ਗਿਆਨ (ਜਾਣਕਾਰੀ)-ਬੰਦੇ ਨੂੰ ਹਰ ਰੋਜ਼ ਆਪਣਾ ਗਿਆਨ ਵਧਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ।
4. ਮਿਹਨਤ (ਸਖ਼ਤ ਕੰਮ ਕਰਨਾ)-ਉਸਨੇ ਮਿਹਨਤ ਕੀਤੀ ਤੇ ਉਹ ਪਾਸ ਹੋ ਗਿਆ ।
5. ਪਰਾਇਆ (ਬੇਗਾਨਾ)-ਤੁਹਾਨੂੰ ਕਿਸੇ ਪਰਾਏ ਨਾਲ ਸਾਂਝ ਨਹੀਂ ਪਾਉਣੀ ਚਾਹੀਦੀ ।
6. ਸੰਤਾਨ (ਔਲਾਦ-ਉਸਦੇ ਵੱਡੇ ਭਰਾ ਦੀ ਕੋਈ ਸੰਤਾਨ ਨਹੀਂ ।
7. ਜਾਤ-ਪਾਤ (ਸਮਾਜ ਦੇ ਉੱਚੀਆਂ-ਨੀਵੀਆਂ ਜਾਤਾਂ ਵਿਚ ਵੰਡੇ ਹੋਣ ਦੇ ਵਿਚਾਰ ਨੂੰ ਮੰਨਣਾ)-ਗੁਰੂ ਸਾਹਿਬ ਜਾਤ-ਪਾਤ ਵਿਚ ਵਿਸ਼ਵਾਸ ਨਹੀਂ ਸਨ ਕਰਦੇ, ਸਗੋਂ ਸਾਰੀ ਮਨੁੱਖਤਾ ਨੂੰ ਬਰਾਬਰ ਸਮਝਦੇ ਸਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਦੱਸੇ ਅਨੁਸਾਰ ਸ਼ਬਦਾਂ ਨੂੰ ਮਿਲਾਓ-

ਉੱਤਰ:

ਪ੍ਰਸ਼ਨ 5.
ਵਿਸਰਾਮ ਚਿੰਨ੍ਹ ਲਾਓ-
ਹਿੰਦੂ ਮੁਸਲਿਮ ਸਿੱਖ ਈਸਾਈ
ਮੈਨੂੰ ਕੋਈ ਨਹੀਂ ਪਰਾਇਆ
ਲਗਦਾ ਮੈਨੂੰ ਆਪਣਿਆਂ ਵਾਂਗਰ
ਹਰ ਇਕ ਭਾਰਤ ਮਾਂ ਦਾ ਜਾਇਆ
ਉੱਤਰ:
ਹਿੰਦੂ, ਮੁਸਲਿਮ, ਸਿੱਖ, ਈਸਾਈ,
ਮੈਨੂੰ ਕੋਈ ਨਹੀਂ ਪਰਾਇਆ ।
ਲਗਦਾ ਮੈਨੂੰ ਆਪਣਿਆਂ ਵਾਂਗਰ,
ਹਰ ਇਕ ਭਾਰਤ ਮਾਂ ਦਾ ਜਾਇਆ ।

ਪ੍ਰਸ਼ਨ 6.
ਵਿਸਰਾਮ ਚਿੰਨ੍ਹ ਕੀ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ;
‘ਵਿਸਰਾਮ’ ਦਾ ਅਰਥ ਹੈ “ਅਰਾਮ ਜਾਂ “ਠਹਿਰਾਓ’ ਜਦੋਂ ਅਸੀਂ ਇਕ ਵਾਕ ਬੋਲਦੇ ਜਾਂ ਲਿਖਦੇ ਹਾਂ, ਤਾਂ ਉਸ ਤੋਂ ਪਿੱਛੋਂ ਜ਼ਰਾ ਰੁਕ ਕੇ ਅਗਲਾ ਵਾਕ ਬੋਲਦੇ ਜਾਂ ਲਿਖਦੇ ਹਾਂ । ਲਿਖਤ ਵਿਚ ਵਾਕ ਦੇ ਅੰਤ ਵਿਚ ਜਾਂ ਵਿਚਕਾਰ ਆਈ ਰੁਕਾਵਟ ਨੂੰ ਵਿਸਰਾਮ ਚਿੰਨ੍ਹਾਂ ਦੁਆਰਾ ਪ੍ਰਗਟ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਹਰ ਸਧਾਰਨ ਵਾਕ ਦੇ ਅੰਤ ਵਿਚ ਡੰਡੀ (।) ਵਿਸਰਾਮ ਚਿੰਨ੍ਹ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ਕਈ ਵਾਰੀ ਵਾਕ ਵਿਚ ਸਧਾਰਨ ਗੱਲ ਨਹੀਂ ਕਹੀ ਹੁੰਦੀ, ਸਗੋਂ ਕੋਈ ਪ੍ਰਸ਼ਨ ਪੁੱਛਿਆ ਜਾਂਦਾ ਹੈ, ਜਾਂ ਹੈਰਾਨੀ, ਖ਼ੁਸ਼ੀ, ਗ਼ਮੀ ਆਦਿ 1 ਦੇ ਪ੍ਰਗਟ ਕੀਤੇ ਜਾਂਦੇ ਹਨ । ਜਿਸ ਵਾਕ ਵਿਚ ਪ੍ਰਸ਼ਨ ਪੁੱਛਿਆ ਜਾਵੇ, ਉਸਦੇ ਅੰਤ ਵਿਚ ਪ੍ਰਸ਼ਨਿਕ ਚਿੰਨ੍ਹ (?) ਪਾਇਆ ਜਾਂਦਾ ਹੈ । ਹੈਰਾਂਨੀ, ਖੁਸ਼ੀ ਜਾਂ ਗ਼ਮੀ ਆਦਿ ਪ੍ਰਗਟ ਕਰਨ ਵਾਲੇ ਵਾਕ ਦੇ ਅੰਤ ਵਿਚ ਵਿਸਮਿਕ ਚਿੰਨ੍ਹ (!) ਪਾਇਆ ਜਾਂਦਾ ਹੈ; ਜਿਵੇਂ:

(ਉ) ਮੇਰੇ ਪਿਤਾ ਜੀ ਦਾ ਨਾਂ ਸ: ਹਰਨੇਕ ਸਿੰਘ ਹੈ ।
(ਅ) ਤੇਰੇ ਪਿਤਾ ਜੀ ਦਾ ਨਾਂ ਕੀ ਹੈ ?
(ਇ) ਵਾਹਵਾ ! ਸੋਹਣੀ ਖੇਡ ਹੈ ।
ਇਸੇ ਤਰ੍ਹਾਂ ਘੱਟ ਠਹਿਰਾਓ ਨੂੰ ਪ੍ਰਗਟ ਕਰਨ ਲਈ ਕਾਮੇ (,) ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ , ਜਿਵੇਂ :
ਮੈਂ ਬਜ਼ਾਰੋਂ ਆਲੂ, ਗੰਢੇ, ਗਾਜਰਾਂ, ਮਟਰ ਤੇ ਟਮਾਟਰ ਲਿਆਂਦੇ ।

ਕਿਸੇ ਦੀ ਕਹੀ ਹੋਈ ਗੱਲ ਨੂੰ ਇੰਨ-ਬਿੰਨ ਲਿਖਣ ਲਈ ਦੋਹਰੇ ਪੁੱਠੇ. ਕਾਮਿਆਂ (” ”) ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ , ਜਿਵੇਂ :-
ਅਧਿਆਪਕ ਨੇ ਕਿਹਾ, “ਧਰਤੀ ਸੂਰਜ ਦੁਆਲੇ ਘੁੰਮਦੀ ਹੈ ।
ਇਨ੍ਹਾਂ ਤੋਂ ਇਲਾਵਾ ਕੁੱਝ ਹੋਰ ਵਿਸਰਾਮ ਚਿੰਨ੍ਹ ਵੀ ਹਨ, ਜਿਨ੍ਹਾਂ ਦੀ ਲਿਖਤ ਵਿਚ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਤੁਸੀਂ ਜ਼ਿੰਦਗੀ ਵਿਚ ਕੀ ਬਣਨਾ ਚਾਹੁੰਦੇ ਹੋ ?
ਉੱਤਰ:
ਮੈਂ ਜ਼ਿੰਦਗੀ ਵਿਚ ਇਕ ਇੰਜੀਨੀਅਰ ਬਣਨਾ ਚਾਹੁੰਦਾ ਹਾਂ ।

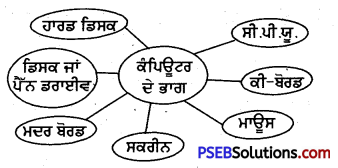
Punjab State Board PSEB 4th Class Punjabi Book Solutions Chapter 10 ਈਦ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 4 Punjabi Chapter 10 ਈਦ

ਪਾਠ-ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 1.
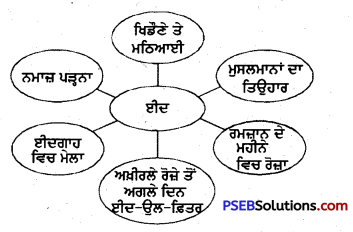
ਈਦ ਕਦੋਂ ਮਨਾਈ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ:
ਈਦ ਰਮਜ਼ਾਨ ਦੇ ਮਹੀਨੇ ਵਿਚ ਰੋਜ਼ੇ ਰੱਖਣ ਤੋਂ ਮਗਰੋਂ ਅਖ਼ੀਰਲੇ ਰੋਜ਼ੇ ਤੋਂ ਅਗਲੇ ਦਿਨ ਮਨਾਈ ਜਾਂਦੀ ਹੈ । ਇਸ ਨੂੰ ਈਦ-ਉਲ-ਫ਼ਿਤਰ ਆਖਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਈਦਗਾਹ ਪਹੁੰਚ ਕੇ ਸਭ ਨੇ ਕੀ ਕੀਤਾ ?
ਉੱਤਰ:
ਈਦਗਾਹ ਪਹੁੰਚ ਕੇ ਸਭ ਨੇ ਕਤਾਰਾਂ ਵਿਚ ਖੜੇ ਹੋ ਕੇ ਨਮਾਜ਼ ਪੜੀ । ਨਮਾਜ਼ ਪੜ੍ਹ ਕੇ ਹੱਥ ਉਠਾ ਕੇ ਖ਼ੁਦਾ ਤੋਂ ਦੁਆ ਮੰਗੀ । ਇਸ ਤੋਂ ਮਗਰੋਂ ਸਾਰੇ ਇਕ ਦੂਜੇ ਦੇ ਗਲ ਨਾਲ ਲੱਗ ਕੇ ਮਿਲੇ । ਸਭ ਨੇ ਇਕ ਦੂਜੇ ਨੂੰ ਈਦ ਦੀ ਮੁਬਾਰਕਬਾਦ ਦਿੱਤੀ ।

ਪ੍ਰਸ਼ਨ 3.
ਮੇਲੇ ਵਿਚ ਕੀ ਕੁੱਝ ਸੀ ?
ਉੱਤਰ:
ਮੇਲੇ ਵਿਚ ਮਠਿਆਈਆਂ ਤੇ ਖਿਡੌਣਿਆਂ ਦੀਆਂ ਦੁਕਾਨਾਂ ਸਜੀਆਂ ਹੋਈਆਂ ਸਨ । ਮੇਲੇ ਵਿਚ . ਝੂਲੇ ਵੀ ਲੱਗੇ ਹੋਏ ਸਨ । ਬੱਚੇ ਝੂਟੇ ਲੈ ਰਹੇ ਸਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਸੁਹੇਲ ਨੇ ਮੇਲੇ ਵਿੱਚੋਂ ਕੀ ਖ਼ਰੀਦਿਆ ?
ਉੱਤਰ:
ਸੁਹੇਲ ਨੇ ਮੇਲੇ ਵਿੱਚੋਂ ਖਿਡੌਣਾ ਜਹਾਜ਼ ਖ਼ਰੀਦਿਆ । ਉਸ ਨੇ ਆਪਣੀ ਭੈਣ ਲਈ ਨੱਚਣ ਵਾਲਾ ਇਕ ਰਿੱਛ ਖ਼ਰੀਦਿਆ ।

ਪ੍ਰਸ਼ਨ 5.
ਅੰਮੀ ਨੇ ਸੁਹੇਲ ਦੇ ਦੋਸਤਾਂ ਨੂੰ ਕੀ ਖੁਆਇਆ ?
ਉੱਤਰ:
ਅੰਮੀ ਨੇ ਸੁਹੇਲ ਦੇ ਦੋਸਤਾਂ ਨੂੰ ਸੇਵੀਆਂ ਤੇ ਮਠਿਆਈ ਖਵਾਈ ।

ਪ੍ਰਸ਼ਨ 6.
ਬੈਕਟਾਂ ਵਿੱਚੋਂ ਠੀਕ ਸ਼ਬਦ ਚੁਣ ਕੇ ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ-
(ਈਦਗਾਹ, ਈਦ, ਰਮਜ਼ਾਨ, ਸੇਵੀਆਂ, ਖੁਦਾ ।)
(ਉ) ……. ਵਿਚ ਤੀਹ ਰੋਜ਼ੇ ਰੱਖੇ ਜਾਂਦੇ ਹਨ।
(ਅ) ਘਰ-ਘਰ …….. ਪਕਾਈਆਂ ਜਾ ਰਹੀਆਂ ਹਨ ।
(ਇ) ਸਭ ਲੋਕ …….. ਪਹੁੰਚ ਗਏ ।
(ਸ) ਨਮਾਜ਼ ਪੜ੍ਹ ਕੇ, ਹੱਥ ਉਠਾ ਕੇ …… ਤੋਂ ਦੁਆ ਮੰਗੀ ।
(ਹ) ਸਭ ਨੇ ਇਕ-ਦੂਜੇ ਨੂੰ …… ਦੀ ਮੁਬਾਰਕਬਾਦ ਦਿੱਤੀ ।
ਉੱਤਰ:
(ੳ) ਰਮਜ਼ਾਨ ਵਿਚ ਤੀਹ ਰੋਜ਼ੇ ਰੱਖੇ ਜਾਂਦੇ ਹਨ ।
(ਅ) ਘਰ-ਘਰ ਸੇਵੀਆਂ ਪਕਾਈਆਂ ਜਾ ਰਹੀਆਂ ਹਨ ।
(ਇ) ਸਭ ਲੋਕ ਈਦਗਾਹ ਪਹੁੰਚ ਗਏ ।
(ਸ) ਨਮਾਜ਼ ਪੜ੍ਹ ਕੇ, ਹੱਥ ਉਠਾ ਕੇ ਖ਼ੁਦਾ ਤੋਂ ਦੁਆ ਮੰਗੀ ।
(ਹ) ਸਭ ਨੇ ਇਕ-ਦੂਜੇ ਨੂੰ ਈਦ ਦੀ ਮੁਬਾਰਕਬਾਦ ਦਿੱਤੀ ।

ਪ੍ਰਸ਼ਨ 7.
ਹੇਠ ਲਿਖਿਆਂ ਬਾਰੇ ਜਾਣਕਾਰੀ ਦਿਓ :
ਈਦ, ਰਮਜ਼ਾਨ, ਰੋਜ਼ਾ …
ਉੱਤਰ:
(ੳ) ਈਦ-ਮੁਸਲਮਾਨਾਂ ਦਾ ਇਕ ਤਿਉਹਾਰ, ਜੋ ਰਮਜ਼ਾਨ ਦੇ ਮਹੀਨੇ ਦੇ ਰੋਜ਼ਿਆਂ ਪਿੱਛੋਂ ਅਗਲੇ ਦਿਨ ਮਨਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਨੂੰ ਈਦੁਲ ਫ਼ਿਤਰ ਕਹਿੰਦੇ ਹਨ ਦੂਜੀ ਈਦ, ਜਿਸਦਾ ਨਾਂ ਈਦੁਲ ਅਜ਼ਹਾ ਹੈ, ਜਿਸਦਾ ਸੰਬੰਧ ਮੱਕੇ ਦਾ ਹੱਜ ਕਰਨ ਤੇ ਪਸ਼ੂ ਦੀ ਬਲੀ ਦੇਣ ਨਾਲ ਹੈ ।
(ਅ) ਰਮਜ਼ਾਨ-ਹਿਜਰੀ ਸਾਲ ਦੇ ਨੌਵੇਂ ਮਹੀਨੇ ਦਾ ਨਾਂ ਰਮਜ਼ਾਨ ਹੈ । ਇਸ ਵਿਚ ਮੁਸਲਮਾਨ ਰੋਜ਼ੇ ਰੱਖਦੇ ਹਨ ।
(ਈ) ਰੋਜ਼ਾ-ਵਰਤ, ਜੋ ਮੁਸਲਮਾਨ ਧਾਰਮਿਕ ਫ਼ਰਜ਼ ਸਮਝ ਕੇ ਰੱਖਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 8.
ਪੜੋ, ਸਮਝੋ ਅਤੇ ਲਿਖੋ
(ੳ) ਬੱਚਾ – ਬੱਚੇ
(ਅ) ਝੂਲਾ – ………
(ਇ) ਰੋਜ਼ਾ – ………..
(ਸ) ਕੱਪੜਾ – …….
(ਹ) ਖਿਡੌਣਾ – …….
(ਕ) ਕੁੜਤਾ – ………..
(ਖ) ਮਹੀਨਾ – ……..
(ਗ) ਮੇਲਾ – ……….
(ਘ) ਝੂਟਾ – …….
(ਝ) ਪਜਾਮਾ – ……
(ਚ) ਟੱਪਦਾ – ……..
(ਛ) ਨੱਚਦਾ – …….
ਉੱਤਰ:

ਪ੍ਰਸ਼ਨ 9.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਨੂੰ ਵਾਕਾਂ ਵਿਚ ਵਰਤੋ-
ਤਿਉਹਾਰ, ਖੁਦਾ, ਦੁਆ, ਮੁਬਾਰਕਬਾਦ, ਮਠਿਆਈ, ਮਹੀਨਾ, ਬਜ਼ਾਰ, ਚੂੜੀਆਂ, ਨਮਾਜ਼, ਦੁਕਾਨ ।
ਉੱਤਰ:

1. ਤਿਉਹਾਰ (ਖ਼ੁਸ਼ੀ ਦਾ ਦਿਨ)-ਅੱਜ ਈਦ ਦਾ ਤਿਉਹਾਰ ਹੈ ।
2. ਖ਼ੁਦਾ (ਬ)-ਖੁਦਾ ਸਭ ਦਾ ਸਾਂਝਾ ਹੈ ।
3. ਦੁਆ-ਸਾਰੇ ਲੋਕਾਂ ਨੇ ਨਮਾਜ਼ ਪੜ੍ਹ ਕੇ ਰੱਬ ਕੋਲੋਂ ਦੁਆ ਮੰਗੀ । ..
4.  ਮੁਬਾਰਕਬਾਦ-ਸਭ ਨੇ ਇਕ-ਦੂਜੇ ਨੂੰ ਈਦ ਦੀ ਮੁਬਾਰਕਬਾਦ ਦਿੱਤੀ ।
5. ਮਠਿਆਈ-ਸੁਹੇਲ ਨੇ ਆਪਣੀ ਭੈਣ ਨੂੰ ਮਠਿਆਈ ਦਿੱਤੀ ।
6.  ਮਹੀਨਾ ਸਾਲ ਦੇ ਸਮੇਂ ਦੇ ਬਾਰਵੇਂ ਹਿੱਸੇ ਦਾ ਨਾਂ, ਜੋ ਆਮ ਕਰਕੇ ਤੀਹ ਜਾਂ ਇਕੱਤੀ ਦਿਨਾਂ ਦਾ ਹੁੰਦਾ ਹੈ)-ਦਸੰਬਰ ਦੇ ਮਹੀਨੇ ਵਿਚ ਠੰਢ ਬਹੁਤ ਹੁੰਦੀ ਹੈ ।
7. ਬਜ਼ਾਰ ਖ਼ਰੀਦਣ-ਵੇਚਣ ਲਈ ਨਾਲ-ਨਾਲ ਤੇ ਆਹਮੋ-ਸਾਹਮਣੇ ਬਣੀਆਂ ਦੁਕਾਨਾਂ)-ਬਜ਼ਾਰ ਵਿਚ ਇਕ ਦੁਕਾਨ ਉੱਤੇ ਘੜੀਆਂ ਵਿਕ ਰਹੀਆਂ ਹਨ.
8. ਚੂੜੀਆਂ ਵੰਗਾਂ)-ਚੂੜੀਆਂ ਦੀ ਦੁਕਾਨ ਉੱਤੇ ਕੁੜੀਆਂ ਦੀ ਭੀੜ ਲੱਗੀ ਹੋਈ ਸੀ ।
9. ਨਮਾਜ਼ (ਮੁਸਲਮਾਨਾਂ ਦੁਆਰਾ ਰੱਬ ਦਾ ਨਾਂ ਲੈਣ ਤੇ ਉਸ ਵਲ ਧਿਆਨ ਲਾਉਣ ਦੀ ਵਿਧੀ)-ਮੁਸਲਮਾਨ ਪੰਜ ਵੇਲੇ ਨਮਾਜ਼ ਪੜ੍ਹਦੇ ਹਨ ।
10. ਦੁਕਾਨ (ਹੱਟੀ)-ਬਜ਼ਾਰ ਵਿਚ ਦੁਕਾਨਾਂ ਤਰ੍ਹਾਂਤਰ੍ਹਾਂ ਦੇ ਸਮਾਨ ਨਾਲ ਭੌਰੀਆਂ ਹੋਈਆਂ ਸਨ |

ਪ੍ਰਸ਼ਨ 10.
ਇਸ ਪਾਠ ਵਿਚ ਆਏ ਜੋੜੇ-ਜੋੜੇ ਸ਼ਬਦ ਲਿਖੋ-
ਜਿਵੇਂ ਉਦਾਹਰਨ ਵਿਚ ਦੱਸਿਆ ਗਿਆ ਹੈ :
ਉਦਾਹਰਨ-ਕੁੜਤਾ-ਪਜਾਮਾ ।
ਉੱਤਰ:
ਕੁੜਤਾ-ਪਜਾਮਾ
ਧੂਮ-ਧਾਮ,
ਖਾਂਦੇ-ਪੀਂਦੇ,
ਨਹਾ-ਧੋ,
ਸਲਵਾਰ-ਕਮੀਜ਼,
ਨੱਚਦੇ-ਟੱਪਦੇ,
ਇਕ-ਦੂਜੇ,
ਖ਼ੁਸ਼ੀ-ਖੁਸ਼ੀ ।

ਪ੍ਰਸ਼ਨ 11.
ਈਦਗਾਹ ਦੇ ਬਾਹਰ ਮੇਲਾ ਲੱਗਿਆ ਹੋਇਆ ਹੈ । ਮਠਿਆਈਆਂ ਤੇ ਖਿਡੌਣਿਆਂ ਦੀਆਂ ਦੁਕਾਨਾਂ ਸਜੀਆਂ ਹੋਈਆਂ ਹਨ ਮੇਲੇ ਵਿਚ ਝੂਲੇ ਵੀ ਲੱਗੇ ਹੋਏ ਹਨ । ਬੱਚੇ ਝੂਟੇ ਲੈ ਰਹੇ ਹਨ । ਸੁਹੇਲ ਦੇ ਅੱਬਾ ਨੇ ਮਠਿਆਈ ਖ਼ਰੀਦੀ । ਖਿਡੌਣਿਆਂ ਦੀ ਦੁਕਾਨ ਤੋਂ ਸੁਹੇਲ ਨੇ ਆਪਣੇ ਲਈ ਇਕ ਖਿਡੌਣਾ ਜਹਾਜ਼ ਖ਼ਰੀਦਿਆਂ ਉਸ ਨੇ ਆਪਣੀ ਭੈਣ ਲਈ ਨੱਚਣ ਵਾਲਾ ਇਕ ਰਿੱਛ ਖ਼ਰੀਦਿਆ ।
ਉਪਰੋਕਤ ਪੈਰੇ ਨੂੰ ਪੜ੍ਹ ਕੇ ਹੇਠ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਦਿਓ :-

1. ਕਿੱਥੇ ਮੇਲਾ ਲੱਗਾ ਹੋਇਆ ਹੈ ?
2. ਕਿਨ੍ਹਾਂ ਚੀਜ਼ਾਂ ਦੀਆਂ ਦੁਕਾਨਾਂ ਸਜੀਆਂ ਹੋਈਆਂ ਹਨ ?
3. ਬੱਚੇ ਕਿੱਥੇ ਝੂਟੇ ਲੈ ਰਹੇ ਹਨ ?
4. ਮਠਿਆਈ ਕਿਸ ਨੇ ਖ਼ਰੀਦੀ ?
5. ਸੁਹੇਲ ਨੇ ਆਪਣੇ ਲਈ ਕੀ ਖ਼ਰੀਦਿਆ ?
6. ਸੁਹੇਲ ਨੇ ਭੈਣ ਲਈ ਕੀ ਖ਼ਰੀਦਿਆ ?

ਉੱਤਰ:

1. ਈਦਗਾਹ ਦੇ ਬਾਹਰ ।
2. ਮਠਿਆਈਆਂ ਤੇ ਖਿਡੌਣਿਆਂ ਦੀਆਂ ।
3. ਝੂਲਿਆਂ ਉੱਤੇ ।
4. ਸੁਹੇਲ ਦੇ ਅੱਬਾ ਨੇ ।
5. ਇਕ ਖਿਡੌਣਾ ਜਹਾਜ਼ ।
6. ਨੱਚਣ ਵਾਲਾ ਇਕ ਰਿੱਛ ।

ਪ੍ਰਸ਼ਨ 12.
ਹੇਠ ਲਿਖੇ ਵਾਕਾਂ ਨੂੰ ਸੁੰਦਰ ਲਿਖਾਈ ਕਰ ਕੇ ਲਿਖੋ :
(ਉ) ਰਮਜ਼ਾਨ ਵਿਚ ਤੀਹ ਰੋਜ਼ੇ ਰੱਖੇ ਜਾਂਦੇ ਹਨ ।
(ਅ) ਸੁਹੇਲ ਦੇ ਅੱਬਾ ਨੇ ਮਠਿਆਈ ਖ਼ਰੀਦੀ ।
(ਇ) ਬਜ਼ਾਰਾਂ ਵਿਚ ਬੜੀ ਰੌਣਕ ਹੈ ।
(ਸ) ਘਰ-ਘਰ ਸੇਵੀਆਂ ਪਕਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ।
(ਹ) ਉਹ ਗੋਟੇ ਵਾਲੀ ਚੁੰਨੀ ਲੈ ਕੇ ਬਹੁਤ ਖੁਸ਼ ਸੀ ।
ਉੱਤਰ:
(ਨੋਟ-ਵਿਦਿਆਰਥੀ ਆਪ ਹੀ ਲਿਖਣ ) ।

ਪ੍ਰਸ਼ਨ 13.
ਆਪਣੇ ਮਾਤਾ-ਪਿਤਾ ਦੀ ਮੱਦਦ ਨਾਲ ਆਪਣੇ ਘਰ ਵਿਚ ਮਨਾਏ ਜਾਂਦੇ ਤਿਉਹਾਰਾਂ ਦੀ ਸੂਚੀ ਬਣਾਉ ।
ਉੱਤਰ:

1. ਲੋਹੜੀ
2. ਬਸੰਤ
3. ਹੋਲੀ
4. ਰੱਖੜੀ
5. ਸਰਾਧ
6. ਨਰਾਤੇ (ਦੁਰਗਾ ਅਸ਼ਟਮੀ)
7. ਸਾਂਝੀ ਮਾਈ
8. ਅਹੋਈ ।
9. ਕਰਵਾ ਚੌਥ
10. ਦੀਵਾਲੀ
11. ਗਣੇਸ਼ ਚਤੁਰਥੀ ।

ਪ੍ਰਸ਼ਨ 14.
ਈਦ ਨਾਲ ਸੰਬੰਧਿਤ ਗੱਲਾਂ ਲਿਖੋ ।

ਉੱਤਰ:

Punjab State Board PSEB 4th Class Punjabi Book Solutions Chapter 9 ਕਬੱਡੀ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 4 Punjabi Chapter 9 ਕਬੱਡੀ

ਪਾਠ-ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 1.
ਕਬੱਡੀ ਦੇ ਕਿੰਨੇ ਤੇ ਕਿਹੜੇ-ਕਿਹੜੇ ਰੂਪ ਹਨ ?
ਉੱਤਰ:
ਕਬੱਡੀ ਦੇ ਦੋ ਰੂਪ ਹਨ-ਨੈਸ਼ਨਲ ਸਟਾਈਲ ਕਬੱਡੀ ਅਤੇ ਸਰਕਲ ਸਟਾਈਲ ਕਬੱਡੀ ।

ਪ੍ਰਸ਼ਨ 2.
ਕਬੱਡੀ ਭਾਰਤ ਦੇ ਕਿਹੜੇ-ਕਿਹੜੇ ਦੇਸ਼ਾਂ ਦੀ ਰਾਜ-ਖੇਡ ਹੈ ?
ਉੱਤਰ:
ਕਬੱਡੀ ਪੰਜਾਬ, ਆਂਧਰਾ ਪ੍ਰਦੇਸ਼, ਹਰਿਆਣਾ, ਬਿਹਾਰ, ਕੰਰਨਾਟਕ, ਮਹਾਂਰਾਸ਼ਟਰ ਤੇ ਤਾਮਿਲਨਾਡੂ ਦੀ ਰਾਜ-ਖੇਡਾਂ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਏਸ਼ੀਅਨ ਖੇਡਾਂ ਵਿਚ ਭਾਰਤ ਨੇ ਲਗਾਤਾਰ ਕਿੰਨੇ ਸੋਨ ਤਗਮੇ ਜਿੱਤੇ ਹਨ ?
ਉੱਤਰ:
ਸੱਤ ।

ਪ੍ਰਸ਼ਨ 4.
ਪੜ੍ਹੋ ਤੇ ਸਮਝੋ-
(ਉ) ਪ੍ਰਫੁਲਤ – ਵਧਣਾ-ਫੁੱਲਣਾ, ਵਧਾਉਣਾ, ਫੈਲਾਉਣਾ ।
(ਅ) ਅਤਿਅੰਤ – ……………………………………………….
(ਈ) ਆਚਾਰ – ……………………………………………….
(ਸ) ਪੋਲਾ – ……………………………………………….
(ਹ) ਸੁਮੇਲ – ……………………………………………….
(ਕ) ਚੋਖੀ – ……………………………………………….
(ਖਿ) ਧਾਵਾ – ……………………………………………….
ਉੱਤਰ
(ਉ) ਪ੍ਰਫੁਲਿਤ – ਵਧਣਾ-ਫੁੱਲਣਾ, ਵਧਾਉਣਾ, ਫੈਲਾਉਣਾ ।
(ਅ) ਅਤਿਅੰਤ – ਬਹੁਤ ਜ਼ਿਆਦਾ ।
(ਈ) ਆਚਾਰ – ਚੱਜ, ਵਰਤੋਂ-ਵਿਹਾਰ ।
(ਸ) ਪੋਲਾ – ਨਰਮ !
(ਹ) ਸੁਮੇਲ – ਵੱਖ-ਵੱਖ ਚੀਜ਼ਾਂ ਜਾਂ ਗੁਣਾਂ ਦਾ ਵਧੀਆ ਮੇਲ ।
(ਕ) ਚੋਖੀ – ਕਾਫ਼ੀ ।
(ਖਿ) ਧਾਵਾ -ਹਮਲਾ ।

ਪ੍ਰਸ਼ਨ 5.
ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਵਿਚ ਢੁੱਕਵੇਂ ਸ਼ਬਦ ਭਰੋ-
(ਪ੍ਰਫੁਲਿਤ, ਮੱਧ, ਟੀਮ, ਜੇਤੂ, ਸੱਤ ।)
(ੳ) ਕਬੱਡੀ ਦੇ ਮੈਦਾਨ ਦੇ ਬਿਲਕੁਲ ਵਿਚਕਾਰ ……….. ਰੇਖਾ ਹੁੰਦੀ ਹੈ ।
(ਅ) ਟੋਲੀਆਂ ਲਈ ਅੱਜ-ਕੱਲ ……… ਸ਼ਬਦ ਪ੍ਰਚਲਿਤ ਹੈ ।
(ਈ) ਅੰਤ `ਤੇ ਵੱਧ ਅੰਕ ਪ੍ਰਾਪਤ ਕਰਨ ਵਾਲੀ ਟੀਮ ਨੂੰ ………. ਕਰਾਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
(ਸ) ਏਸ਼ੀਆ ਖੇਡਾਂ ਵਿਚ ਭਾਰਤ ਨੇ ਕਬੱਡੀ ਵਿਚ ਲਗਾਤਾਰ ………… ਸੋਨ ਤਗਮੇ ਜਿੱਤੇ ਹਨ ।
(ਹ) ਪੰਜਾਬੀ ਕਬੱਡੀ ਨੂੰ ……….. ਕਰਨ ਵਿਚ ਆਪਣਾ ਯੋਗਦਾਨ ਪਾ ਰਹੇ ਹਨ ।
ਉੱਤਰ:
(ੳ) ਕਬੱਡੀ ਦੇ ਮੈਦਾਨ ਦੇ ਬਿਲਕੁਲ ਵਿਚਕਾਰ ਮੱਧ ਰੇਖਾ ਹੁੰਦੀ ਹੈ ।
(ਅ) ਟੋਲੀਆਂ ਲਈ ਅੱਜ-ਕੱਲ੍ਹ ਟੀਮ ਸ਼ਬਦ ਪ੍ਰਚਲਿਤ ਹੈ । ਅੰਤ `ਤੇ ਵੱਧ ਅੰਕ ਪ੍ਰਾਪਤ ਕਰਨ ਵਾਲੀ ਟੀਮ ਨੂੰ ਜੇਤੂ ਕਰਾਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
(ਸ) ਏਸ਼ੀਅਨ ਖੇਡਾਂ ਵਿਚ ਭਾਰਤ ਨੇ ਕਬੱਡੀ ਵਿਚ ਲਗਾਤਾਰ ਸੱਤ ਸੋਨ ਤਗਮੇ ਜਿੱਤੇ ਹਨ ।
(ਹ) ਪੰਜਾਬੀ ਕਬੱਡੀ ਨੂੰ ਪ੍ਰਫੁਲਿਤ ਕਰਨ ਵਿਚ ਆਪਣਾ ਯੋਗਦਾਨ ਪਾ ਰਹੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਕਬੱਡੀ ਦੇ ਕਿਹੜੇ-ਕਿਹੜੇ ਦੋ ਰੂਪ ਹਨ ?
ਉੱਤਰ:
ਨੈਸ਼ਨਲ ਸਟਾਈਲ ਕਬੱਡੀ ਅਤੇ ਸਰਕਲ ਸਟਾਈਲ ਕਬੱਡੀ ।

ਪ੍ਰਸ਼ਨ 7.
ਨੈਸ਼ਨਲ ਸਟਾਈਲ ਕਬੱਡੀ ਦੇ ਮੈਦਾਨ ਦਾ ਆਕਾਰ ਕਿਹੋ-ਜਿਹਾ ਭਾਗ ਲੈਂਦੇ ਹੈ ?
ਉੱਤਰ:
ਨੈਸ਼ਨਲ ਸਟਾਈਲ ਕਬੱਡੀ ਦਾ ਮੈਦਾਨ ਆਇਤਾਕਾਰ ਤੇ ਪੋਲਾ ਹੁੰਦਾ ਹੈ । ਇਸ ਦੇ ਵਿਚਕਾਰ ਇਕ ਮੱਧ-ਰੇਖਾ ਹੁੰਦੀ ਹੈ, ਜੋ ਖੇਡ ਦੇ ਮੈਦਾਨ ਨੂੰ ਦੋ ਬਰਾਬਰ ਹਿੱਸਿਆਂ ਵਿੱਚ ਵੰਡਦੀ ਹੈ । ਯੂਨੀਅਰ ਖਿਡਾਰੀਆਂ ਤੇ ਇਸਤਰੀਆਂ ਲਈ ਮੈਦਾਨ ਛੋਟਾ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਨੈਸ਼ਨਲ ਸਟਾਈਲ ਕਬੱਡੀ ਦੀ ਟੀਮ ਵਿਚ ਕਿੰਨੇ ਖਿਡਾਰੀ ਭਾਗ ਲੈਂਦੇ ਹਨ ?
ਉੱਤਰ;
ਨੈਸ਼ਨਲ ਸਟਾਈਲ ਕਬੱਡੀ ਦੀਆਂ ਦੋਹਾਂ ਟੀਮਾਂ ਵਿਚ ਬਾਰਾਂ-ਬਾਰਾਂ ਖਿਡਾਰੀ ਹੁੰਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਵਿਚੋਂ ਸੱਤ-ਸੱਤ ਖਿਡਾਰੀ ਖੇਡ ਵਿਚ ਭਾਗ ਲੈਂਦੇ ਹਨ, ਪਰੰਤੂ ਉਨ੍ਹਾਂ ਦੇ ਪੰਜ-ਪੰਜ ਖਿਡਾਰੀ ਵਾਧੂ ਹੁੰਦੇ ਹਨ, ਜਿਨ੍ਹਾਂ ਨੂੰ ਲੋੜ ਪੈਣ ‘ਤੇ ਖਿਡਾਰੀਆਂ ਨਾਲ ਬਦਲਿਆ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਕਬੱਡੀ ਖੇਡਣ ਲਈ ਖਿਡਾਰੀ ਵਿਚ ਕਿਹੜੇ-ਕਿਹੜੇ ਗੁਣ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ?
ਉੱਤਰ:
ਕਬੱਡੀ ਖੇਡਣ ਲਈ ਖਿਡਾਰੀ ਵਿਚ ਚੋਖੀ ਸਰੀਰਕ ਸ਼ਕਤੀ, ਤੇਜ਼ ਰਫ਼ਤਾਰੀ, ਲੰਮਾ ਸਾਹ, ਚੁਸਤੀ ਤੇ ਫੁਰਤੀ ਆਦਿ ਗੁਣ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 10.
ਕਬੱਡੀ ਅਤੇ ਕੁਸ਼ਤੀ ਵਿਚ ਕੀ ਸਾਂਝ ਹੈ ?
ਉੱਤਰ:
ਕਬੱਡੀ ਖੇਡਣ ਤੇ ਕੁਸ਼ਤੀ ਦੋਹਾਂ ਲਈ ਖਿਡਾਰੀਆਂ ਵਿਚ ਚੋਖੀ ਸਰੀਰਕ ਸ਼ਕਤੀ ਤੇ ਚੁਸਤੀਫੁਰਤੀ ਆਦਿ ਦਾ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਕਬੱਡੀ ਵਿੱਚ ਖਿਡਾਰੀਆਂ ਨੂੰ ਫੜ ਕੇ ਹਿੱਲਣ ਨਾ ਦੇਣਾ ਇਕ ਤਰ੍ਹਾਂ ਦੀ ਮਿੰਨੀ ਕੁਸ਼ਤੀ ਹੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਕਬੱਡੀ ਤੇ ਕੁਸ਼ਤੀ ਦੋਹਾਂ ਵਿਚ ਕਾਫ਼ੀ ਸਾਂਝ ਹੈ ।

ਪ੍ਰਸ਼ਨ 11.
ਪੜੋ, ਸਮਝੋ ਤੇ ਲਿਖੋ-
(ਉ) ਜਿੱਤ – ਹਾਰ
(ਅ) ਨਫ਼ਰਤ – …..
(ਬ) ਹੌਲੀ – ……..
(ਸ) ਸੁਸਤੀ – ……
(ਹ) ਔਗੁਣ – ……..
(ਕ) ਸਖ਼ਤ – ………..
(ਖ) ਆਖਰੀ – ……..
ਉੱਤਰ:
(ੳ) ਜਿੱਤ – ਹਾਰ
(ਅ) ਨਫ਼ਰਤ – ਮੋਹ, ਪਿਆਰ
(ੲ) ਹੌਲੀ -ਤੇਜ਼
(ਸ) ਸੁਸਤੀ – ਚੁਸਤੀ
(ਹ) ਔਗੁਣ – ਗੁਣ
(ਕ) ਸਖ਼ਤ – ਨਰਮ
(ਖ) ਆਖਰੀ – ਪਹਿਲਾ ।

ਪ੍ਰਸ਼ਨ 12.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਦੇ ਅਰਥ ਦੱਸ ਕੇ ਵਾਕਾਂ ਵਿਚ ਵਰਤੋ
ਮਨਪਸੰਦ, ਖਿਡਾਰੀ, ਅਰਾਮ, ਮੈਦਾਨ, ਚੁਸਤ, ਪਹਿਲਵਾਨ, ਕਬੱਡੀ, ਜਾਫੀ ।
ਉੱਤਰ:
(ੳ) ਮਨਪਸੰਦ ਮਨ ਨੂੰ ਚੰਗਾ ਲੱਗਣ ਵਾਲਾ)-ਕਬੱਡੀ ਮੇਰੀ ਮਨਪਸੰਦ ਖੇਡ ਹੈ ।
(ਅ) ਖਿਡਾਰੀ ਖੇਡਣ ਵਾਲਾ)-ਕਬੱਡੀ ਖੇਡਦਿਆਂ ਖਿਡਾਰੀ ਨੇ ਧਾਵੀ ਦਾ ਗੁੱਟ ਫੜ ਕੇ ਮੁੜ ਨਾ ਛੱਡਿਆ ।
(ਇ) ਅਰਾਮ (ਚੈਨ, ਠੀਕ ਹੋਣਾ, ਬਿਮਾਰੀ ਤੋਂ ਛੁਟਕਾਰਾ)-ਦਵਾਈ ਖਾ ਕੇ ਮੇਰੀ ਸਿਰਦਰਦ ਨੂੰ ਅਰਾਮ ਆ ਗਿਆ ।
(ਸ) ਮੈਦਾਨ ਪੱਧਰੀ ਥਾਂ, ਖੇਡਣ ਜਾਂ ਜੰਗ ਕਰਨ ਲਈ ਖੁੱਲ੍ਹੀ ਥਾਂ)-ਖਿਡਾਰੀ ਖੇਡਣ ਲਈ ਮੈਦਾਨ ਵਿਚ ਆ ਗਏ ।
(ਹ) ਚੁਸਤ ਸਰੀਰਕ ਤੇ ਮਾਨਸਿਕ ਤੌਰ ‘ਤੇ ਤੇਜ਼ਕਬੱਡੀ ਖੇਡਣ ਲਈ ਖਿਡਾਰੀ ਦਾ ਚੁਸਤ-ਫੁਰਤ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ ।
(ਕ) ਪਹਿਲਵਾਨ ਮੱਲ, ਭਲਵਾਨ)-ਪਹਿਲਵਾਨ ਕੁਸ਼ਤੀਆਂ ਵਿਚ ਹਿੱਸਾ ਲੈ ਰਹੇ ਹਨ ।
(ਖ) ਜਾਫੀ (ਕਬੱਡੀ ਵਿਚ ਧਾਵੀ ਨੂੰ ਫੜਨ ਵਾਲਾਜੇਕਰ ਜਾਫੀ ਨੇ ਧਾਵੀ ਨੂੰ ਜੱਫਾ ਮਾਰ ਕੇ ਮੁੜ ਆਪਣੇ ਪਾਸੇ ਵਲ ਜਾਣ ਨਾ ਦਿੱਤਾ, ਤਾਂ ਉਹ ਮਰਿਆ, ਸਮਝਿਆ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 13.
ਢੁੱਕਵੇਂ ਮਿਲਾਨੇ ਕਰੋ-


ਉੱਤਰ:

ਪ੍ਰਸ਼ਨ 14.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਵਿਚੋਂ ਰਾਜਾਂ ਤੇ ਦੇਸ਼ਾਂ ਦੇ ਨਾਂਵਾਂ ਨੂੰ ਵੱਖ-ਵੱਖ ਕਰ ਕੇ ਲਿਖੋ- ‘
ਬੰਗਾਲ, ਪਾਕਿਸਤਾਨ, ਬਰਮਾ, ਤਾਮਿਲਨਾਡੂ, ਪੰਜਾਬ, ਨੇਪਾਲ, ਮਹਾਂਰਾਸ਼ਟਰ, ਤੇਲੰਗਾਨਾ, ਕਰਨਾਟਕ, ਹਰਿਆਣਾ, ਭਾਰਤ, ਲੰਕਾ, ਬਿਹਾਰ, ਆਂਧਰਾ ਪ੍ਰਦੇਸ਼
ਉੱਤਰ:

Punjab State Board PSEB 4th Class Punjabi Book Solutions Chapter 8 ਬੁੱਝ ਤੂੰ ਮੇਰੀ ਬਾਤ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 4 Punjabi Chapter 8 ਬੁੱਝ ਤੂੰ ਮੇਰੀ ਬਾਤ

ਕਾਵਿ-ਟੋਟਿਆਂ ਦੇ ਸਰਲ ਅਰਥ

(ਉ) ਦੀਪੀ ਕਹਿੰਦਾ ……….. ਲਈ ਦਾਤ
ਸਰਲ ਅਰਥ-ਦੀਪੀ ਜੀਤੀ ਨੂੰ ਕਹਿੰਦਾ ਹੈ, ਤੂੰ ਮੇਰੀ ਇਕ ਬੁਝਾਰਤ ਬੁੱਝ । ਤੂੰ ਦੱਸ ਕਿ ਅਜਿਹੀ ਕਿਹੜੀ ਮਸ਼ੀਨ ਹੈ, ਜਿਸ ਨੂੰ ਬੰਦੇ ਲਈ ਇਕ ਬਖ਼ਸ਼ਿਸ਼ ਸਮਝਣਾ ਚਾਹੀਦਾ ਹੈ ।

(ਅ) ਉਹ ਕੇਵਲ ………… ਵਿਚ ਕਰਦੀ । ਸਰਲ ਅਰਥ-ਦੀਪੀ ਜੀਤੀ ਨੂੰ ਕਹਿੰਦਾ ਹੈ, ਤੂੰ ਮੈਨੂੰ ਦੱਸ ਕਿ ਅਜਿਹੀ ਕਿਹੜੀ ਮਸ਼ੀਨ ਹੈ, ਜਿਹੜੀ ਨਾ ਕੇਵਲ ਗਿਣਨਾ ਹੀ ਜਾਣਦੀ ਹੈ, ਸਗੋਂ ਅੱਖਰਾਂ ਨੂੰ ਜੋੜ ਕੇ · ਲਿਖ ਵੀ ਸਕਦੀ ਹੈ । ਉਹ ਹਿਸਾਬ ਲਈ ਜੋੜ, ਘਟਾਓ, ਗੁਣਾ ਤੇ ਵੰਡ ਦੇ ਕੰਮ ਤਾਂ ਮਿੰਟਾਂ-ਸਕਿੰਟਾਂ ਵਿਚ ਕਰ ਦਿੰਦੀ ਹੈ ।

(ਇ) ਇਸ ਨੇ ਹੋਰ ………… ਮੇਰੀ ਬਾਤ ।
ਸਰਲ ਅਰਥ-ਦੀਪੀ ਜੀਤੀ ਨੂੰ ਕਹਿੰਦਾ ਹੈ, ਤੂੰ ਮੇਰੀ ਇਕ ਬੁਝਾਰਤ ਬੁੱਝ ਤੇ ਮੈਨੂੰ ਦੱਸ ਕਿ ਉਹ ਕਿਹੜੀ ਮਸ਼ੀਨ ਹੈ, ਜਿਸਨੇ ਹੋਰ ਮਸ਼ੀਨਾਂ ਨੂੰ ਪਿੱਛੇ ਪਾ ਦਿੱਤਾ ਹੈ ।

(ਸ) ਬਟਨ ਦਬਾ ਕੇ ………… ਭਰ ਲਓ ।
ਸਰਲ ਅਰਥ-ਦੀਪੀ ਜੀਤੀ ਨੂੰ ਕਹਿੰਦਾ ਹੈ, ਤੂੰ ਮੈਨੂੰ ਦੱਸ ਕਿ ਉਹ ਕਿਹੜੀ ਮਸ਼ੀਨ ਹੈ, ਜਿਸਦੇ ਬਟਨ ਦਬਾ ਕੇ ਟਾਈਪ ਵੀ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਤੇ ਉਸ ਵਿਚ ਰਿਕਾਰਡ ਵੀ ਦਰਜ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਜੇਕਰ ਤੁਸੀਂ ਚਾਹੋ, ਤਾਂ ਉਸ ਨਾਲ ਤਸਵੀਰਾਂ ਵੀ ਬਣਾ ਸਕਦੇ ਹੋ ਤੇ ਉਨ੍ਹਾਂ ਵਿਚ ਮਨ-ਮਰਜ਼ੀ ਦੇ ਰੰਗ ਵੀ ਭਰ ਸਕਦੇ ਹੋ ।

(ਹ) ਵਾਇਰਸ ਹੋ ……….. ਮੇਰੀ ਬਾਤ ।
ਸਰਲ ਅਰਥ-ਦੀਪੀ ਜੀਤੀ ਨੂੰ ਕਹਿੰਦਾ ਹੈ, ਤੂੰ ਮੇਰੀ ਬੁਝਾਰਤ ਬੁੱਝ ਤੇ ਦੱਸ ਕਿ ਉਹ ਕਿਹੜੀ ਮਸ਼ੀਨ ਹੈ ਕਿ ਜੇਕਰ ਉਸ ਵਿਚ ਵਾਇਰਸ ਆ ਜਾਵੇ, ਤਾਂ ਉਹ ਕੰਮ ਨਹੀਂ ਕਰਦੀ ਤੇ ਨਾ ਹੀ ਮਿੱਟੀ-ਘੱਟਾ ਤੇ ਬਰਸਾਤ ਨੂੰ ਬਰਦਾਸ਼ਤ ਕਰ ਸਕਦੀ ਹੈ ।

(ਕ) “ਕੀਅ ਬੋਰਡ ……. ਕੀ ਦਫ਼ਤਰ ।
ਸਰਲ ਅਰਥ-ਦੀਪੀ ਜੀਤੀ ਨੂੰ ਕਹਿੰਦਾ ਹੈ ਕਿ ਤੂੰ ਮੈਨੂੰ ਦੱਸ ਕਿ ਉਹ ਕਿਹੜੀ ਮਸ਼ੀਨ ਹੈ, ਜਿਸਦਾ ਮੌਨੀਟਰ ਉਸਦੇ ਕੀ ਬੋਰਡ ਵਾਂਗ ਹੀ ਉਸਦਾ ਮੁੱਖ ਅੰਗ ਹੈ । ਇਹ ਮਸ਼ੀਨ ਘਰ ਤੇ ਦਫ਼ਤਰ ਵਿਚ ਬੰਦੇ ਦੇ ਬਹੁਤ ਸਾਰੇ ਕੰਮ ਕਰਦੀ ਹੈ ।

(ਖ) ਕੰਮ ਕਰਦਿਆਂ …….. ਮੇਰੀ ਬਾਤ ।
ਸਰਲ ਅਰਥ-ਦੀਪੀ ਜੀਤੀ ਨੂੰ ਕਹਿੰਦਾ ਹੈ ਕਿ ਤੂੰ ਮੇਰੀ ਇਕ ਬੁਝਾਰਤ ਸੁਣ ਕੇ ਬੁੱਝ ਤੇ ਦੱਸ ਕਿ ਉਹ ਕਿਹੜੀ ਮਸ਼ੀਨ ਹੈ, ਜਿਹੜੀ ਰਾਤ-ਦਿਨ ਕੰਮ ਕਰਦਿਆਂ ਰਤਾ ਵੀ ਥੱਕਦੀ ਨਹੀਂ ।

(ਗ) ਅੱਜ-ਕੱਲ੍ਹ ਤਾਂ …….. ਰਹੇ ਅਧੂਰੀ ।
ਸਰਲ ਅਰਥ-ਦੀਪੀ ਜੀਤੀ ਨੂੰ ਕਹਿੰਦਾ ਹੈ ਕਿ ਤੂੰ ਮੈਨੂੰ ਦੱਸ ਕਿ ਉਹ ਕਿਹੜੀ ਮਸ਼ੀਨ ਹੈ, ਜਿਸ ਨੂੰ ਚਲਾਉਣਾ ਸਿੱਖਣਾ ਅੱਜ ਦੇ ਸਮੇਂ ਵਿਚ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ । ਜੇਕਰ ਇਸਨੂੰ ਸਿੱਖਿਆ ਨਾ ਜਾਵੇ, ਤਾਂ ਬੰਦੇ ਦੀ ਪੜ੍ਹਾਈ-ਲਿਖਾਈ ਅਧੂਰੀ ਰਹਿ ਜਾਂਦੀ ਹੈ ।

(ਘ) ਦਿਓ ਕਮਾਂਡ ……….. ਮੇਰੀ ਬਾਤ ।
ਸਰਲ ਅਰਥ-ਦੀਪੀ ਜੀਤੀ ਨੂੰ ਕਹਿੰਦਾ ਹੈ, ਤੂੰ ਮੇਰੀ ਇਕ ਬੁਝਾਰਤ ਸੁਣ ਕੇ ਬੁੱਝ ਤੇ ਦੱਸ ਕਿ ਉਹ ਕਿਹੜੀ ਮਸ਼ੀਨ ਹੈ, ਜਿਸ ਨੂੰ ਕਮਾਂਡ ਦੇ ਕੇ ਤੁਸੀਂ ਸੰਗੀਤ ਸੁਣ ਸਕਦੇ ਹੋ, ਜੋ ਕਿ ਇਕ ਅਦਭੁੱਤ ਕਰਾਮਾਤ ਜਾਪਦੀ ਹੈ ।

ਬਹੁਤ ਸੰਖੇਪ ਉੱਤਰ ਵਾਲੇ ਪ੍ਰਸ਼ਨ

1. ਦੀਪੀ ਕਹਿੰਦਾ ਸੁਣ ਓਏ ਜੀਤੀ,
ਬੁੱਝ ਤੂੰ ਮੇਰੀ ਬਾਤ
ਐਸੀ ਇਕ ਮਸ਼ੀਨ ਉਹ ਕਿਹੜੀ,
ਜੋ ਬੰਦੇ ਲਈ ਦਾਤ ।

ਪ੍ਰਸ਼ਨ

1. ਦੀਪੀ ਜੀਤੀ ਨੂੰ ਕੀ ਬੁੱਝਣ ਲਈ ਕਹਿੰਦਾ ਹੈ ?
2. ਮਸ਼ੀਨ ਕਿਹੋ ਜਿਹੀ ਹੈ ?
3. ‘ਬੁੱਝ ਤੂੰ ਮੇਰੀ ਬਾਤ ਕਵਿਤਾ ਦੀਆਂ ਚਾਰ ਸਤਰਾਂ ਜ਼ਬਾਨੀ ਲਿਖੋ ।

ਉੱਤਰ:

1. ਦੀਪੀ ਜੀਤੀ ਨੂੰ ਇਕ ਬੁਝਾਰਤ ਬੁੱਝਣ ਲਈ ਕਹਿੰਦਾ ਹੈ ।
2. ਮਸ਼ੀਨ ਬੰਦੇ ਲਈ ਦਾਤ ਹੈ ।
3. (ਨੋਟ-ਉਪਰੋਕਤ ਸਤਰਾਂ ਹੀ ਲਿਖੋ ।)

2. ਉਹ ਕੇਵਲ ਨਾ ਗਿਣਨਾ ਜਾਣੇ,
ਅੱਖਰ ਜੋੜ ਵੀ ਸਕਦੀ ।
ਜੋੜ, ਘਟਾਓ, ਗੁਣਾ, ਵੰਡ ਤਾਂ,
ਪਲਾਂ, ਛਿਣਾਂ ਵਿਚ ਕਰਦੀ ।

ਪ੍ਰਸ਼ਨ

1. ਮਸ਼ੀਨ ਕੀ-ਕੀ ਕੰਮ ਕਰਦੀ ਹੈ ?
2. ਮਸ਼ੀਨ ਸਾਰੇ ਕੰਮ ਕਿੰਨੇ ਸਮੇਂ ਵਿਚ ਕਰਦੀ ਹੈ ?

ਉੱਤਰ:

1. ਮਸ਼ੀਨ ਗਿਣਤੀ ਤੋਂ ਇਲਾਵਾ ਅੱਖਰ ਜੋੜਨ ਅਰਥਾਤ ਲਿਖਣ ਦਾ ਕੰਮ ਕਰਦੀ ਹੈ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਇਹ ਜੋੜ, ਘਟਾਓ, ਗੁਣਾ ਤੇ ਵੰਡ ਦਾ ਕੰਮ ਵੀ ਕਰਦੀ ਹੈ ।
2. ਪਲਾਂ-ਛਿਣਾਂ ਵਿਚ ।

3. ਇਸ ਨੇ ਹੋਰ ਮਸ਼ੀਨਾਂ ਤਾਈਂ,
ਪਾ ਦਿੱਤੀ ਏ ਮਾਤ ।
ਦੀਪੀ ਕਹਿੰਦਾ ਸੁਣ ਓਏ ਜੀਤੀ,
ਬੁੱਝ ਤੂੰ ਮੇਰੀ ਬਾਤ ।

ਪ੍ਰਸ਼ਨ

1. ਇਸ ਮਸ਼ੀਨ ਨੇ ਕੀ ਕੀਤਾ ਹੈ ?
2. ਦੀਪੀ ਕਿਸ ਅੱਗੇ ਬਾਤ ਪਾਉਂਦਾ ਹੈ ?
3. ਇਸ ਮਸ਼ੀਨ ਦਾ ਨਾਂ ਕੀ ਹੈ ?

ਉੱਤਰ:

1. ਇਸ ਮਸ਼ੀਨ ਨੇ ਹੋਰ ਸਾਰੀਆਂ ਮਸ਼ੀਨਾਂ ਨੂੰ ਮਾਤ ਪਾ ਦਿੱਤਾ ।
2. ਦੀਪੀ ਜੀਤੀ ਅੱਗੇ ਬਾਤ ਪਾਉਂਦਾ ਹੈ ।
3. ਕੰਪਿਊਟਰ ।

4. ਬਟਨ ਦਬਾ ਕੇ ਟਾਈਪ ਕਰੋ,
ਤੇ ਫੀਡ, ਰਿਕਾਰਡ ਵੀ ਕਰ ਲਓ ।
ਚਿਤਰ ਬਣਾ ਲਓ, ਭਾਵੇਂ ਰੰਗ ਵੀ,
ਮਨਮਰਜ਼ੀ ਦੇ ਭਰ ਲਓ ।

ਪ੍ਰਸ਼ਨ

1. ਮਸ਼ੀਨ ਟਾਈਪ ਕਿਸ ਤਰ੍ਹਾਂ ਕਰਦੀ ਹੈ ?
2. ਰੰਗ ਕਿਸ ਵਿਚ ਭਰੇ ਜਾ ਸਕਦੇ ਹਨ ?

ਉੱਤਰ:

1. ਮਸ਼ੀਨ ਬਟਨ ਦਬਾਉਣ ਨਾਲ ਟਾਈਪ ਕਰਦੀ ਹੈ ।
2. ਰੰਗ ਚਿਤਰਾਂ ਵਿਚ ਭਰੇ ਜਾ ਸਕਦੇ ਹਨ ।

5. ਵਾਇਰਸ ਹੋ ਜਾਏ, ਸਹਿ ਨਹੀਂ ਸਕਦੀ,
ਘੱਟਾ ਤੇ ਬਰਸਾਤ ।
ਦੀਪੀ ਕਹਿੰਦਾ ਸੁਣ ਓਏ ਜੀਤੀ,
ਬੁੱਝ ਤੂੰ ਮੇਰੀ ਬਾਤ ।

ਪ੍ਰਸ਼ਨ

1. ਮਸ਼ੀਨ ਕਦੋਂ ਕੰਮ ਨਹੀਂ ਕਰਦੀ ?
2. ਦੀਪੀ ਜੀਤੀ ਨੂੰ ਕੀ ਕਹਿੰਦਾ ਹੈ ?

ਉੱਤਰ:

1. ਵਾਇਰਸ ਆ ਜਾਣ ਜਾਂ ਘੱਟੇ ਤੇ ਬਰਸਾਤ ਦਾ ਅਸਰ ਹੋਣ ਨਾਲ ਮਸ਼ੀਨ ਕੰਮ ਨਹੀਂ ਕਰਦੀ ।
2. ਦੀਪੀ ਜੀਤੀ ਨੂੰ ਕਹਿੰਦਾ ਹੈ ਕਿ ਉਹ ਉਸ ਦੀ ਇਕ ਬਾਤ ਬੁੱਝੇ ।

6. ਕੀਅ-ਬੋਰਡ’ ਦੇ ਵਾਂਗੂੰ ਇਸ ਦਾ,
ਹੈ ਮੁੱਖ ਅੰਗ ਮੌਨੀਟਰ ।
ਬੰਦੇ ਦੇ ਕੰਮ ਕਰੇ ਅਨੇਕਾਂ,
ਕੀ ਘਰ ਤੇ ਕੀ ਦਫ਼ਤਰ ।

ਪ੍ਰਸ਼ਨ

1. ਇਸ ਮਸ਼ੀਨ ਦੇ ਮੁੱਖ ਅੰਗ ਕਿਹੜੇਕਿਹੜੇ ਹਨ ?
2. ਇਹ ਮਸ਼ੀਨ ਬੰਦੇ ਦੇ ਕਿੱਥੇ-ਕਿੱਥੇ ਕੰਮ ਆਉਂਦੀ ਹੈ ?

ਉੱਤਰ:

1. ਕੀ ਬੋਰਡ ਤੇ ਮੌਨੀਟਰ ਇਸ ਮਸ਼ੀਨ ਦੇ ਮੁੱਖ ਅੰਗ ਹਨ ।
2. ਇਹ ਮਸ਼ੀਨ ਬੰਦੇ ਦੇ ਘਰਾਂ ਤੇ ਦਫ਼ਤਰ ਵਿਚ ਕੰਮ ਆਉਂਦੀ ਹੈ ।

7. ਕੰਮ ਕਰਦਿਆਂ ਜ਼ਰਾ ਨਾ ਥੱਕੇ,
ਵੇਖੇ ਨਾ ਦਿਨ-ਰਾਤ ।
ਦੀਪੀ ਕਹਿੰਦਾ ਸੁਣ ਓਏ ਜੀਤੀ,
ਬੁੱਝ ਤੂੰ ਮੇਰੀ ਬਾਤ ।

ਪ੍ਰਸ਼ਨ

1. ਇਹ ਮਸ਼ੀਨ ਕਿੰਨਾ ਚਿਰ ਕੰਮ ਕਰ ਸਕਦੀ ਹੈ ?
2. ਬਾਤ ਕਿਸ ਨੂੰ ਬੁੱਝਣ ਲਈ ਕਿਹਾ ਗਿਆ ਹੈ ?

ਉੱਤਰ:

1. ਇਹ ਮਸ਼ੀਨ ਬਿਨਾਂ ਥਕੇਵੇਂ ਤੋਂ ਰਾਤ- : ਦਿਨ ਕੰਮ ਸਕਦੀ ਹੈ ।
2. ਜੀਤੀ ਨੂੰ ਬਾਤ, ਬੁੱਝਣ ਲਈ ਕਿਹਾ ਗਿਆ

8. ਅੱਜ-ਕਲ੍ਹ ਤਾਂ ਏ ਸਿੱਖਣਾ ਇਸ ਨੂੰ,
ਹੋਇਆ ਬੜਾ ਜ਼ਰੂਰੀ ।
ਨਹੀਂ ਤਾਂ ਅੱਜ-ਕਲ੍ਹ ਸਿੱਖਿਆ ਇਸ ਦੇ,
ਬਾਥੋਂ ਰਹੇ ਅਧੂਰੀ ।

ਪ੍ਰਸ਼ਨ

1. ਕਿਸ ਮਸ਼ੀਨ ਦੀ ਗੱਲ ਹੋ ਰਹੀ ਹੈ ?
2. ਵਿੱਦਿਆ ਕਿਸ ਤੋਂ ਬਿਨਾਂ ਅਧੂਰੀ ਹੈ ?

ਉੱਤਰ:

1. ਕੰਪਿਊਟਰ ਦੀ ।
2. ਕੰਪਿਊਟਰ ਦੀ ਸਿੱਖਿਆ ਤੋਂ ਬਿਨਾਂ ਵਿੱਦਿਆ ਅਧੂਰੀ ਹੈ ।

9. ਦਿਓ ਕਮਾਂਡ ਤੇ ਸੁਣੋ ਮਿਊਜ਼ਕ,
‘ਅਜਬ ਹੈ ਇਹ ਕਰਾਮਾਤ ।
ਦੀਪੀ ਕਹਿੰਦਾ ਸੁਣ ਓਏ ਜੀਤੀ
ਬੁੱਝ ਤੂੰ ਮੇਰੀ ਬਾਤ ।

ਪ੍ਰਸ਼ਨ

1. ਮਿਊਜ਼ਕ ਕਿਸ ਤਰ੍ਹਾਂ ਸੁਣਿਆ ਜਾ ਸਕਦਾ ਹੈ ?
2. ਕੌਣ ਬਾਤ ਪਾਉਂਦਾ ਹੈ ?

ਉੱਤਰ:

1. ਕਮਾਂਡ ਦੇ ਕੇ ।
2. ਦੀਪੀ ।

ਪਾਠ-ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ :

ਪ੍ਰਸ਼ਨ 1.
ਦੀਪੀ ਨੇ ਕਿਹੜੀ ਮਸ਼ੀਨ ਦੀ ਬਾਤ ਪਾਈ ?
ਉੱਤਰ:
ਕੰਪਿਊਟਰ ਦੀ ।

ਪ੍ਰਸ਼ਨ 2.
ਇਹ ਮਸ਼ੀਨ ਪਲਾਂ-ਛਿਣਾਂ ਵਿਚ ਕੀ ਕਰਦੀ ਹੈ ?
ਉੱਤਰ:
ਇਹ ਮਸ਼ੀਨ ਹਿਸਾਬ ਦੇ ਸਾਰੇ ਕੰਮ ਅਰਥਾਤ ਜੋੜ, ਘਟਾਓ, ਗੁਣਾਂ ਤੇ ਵੰਡ ਪਲਾਂ-ਛਿਣਾਂ ਵਿਚ ਕਰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਘੱਟਾ ਤੇ ਬਰਸਾਤ ਹੋਣ ਕਾਰਨ ਮਸ਼ੀਨ ਨੂੰ ਕੀ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ:
ਘੱਟਾ ਤੇ ਬਰਸਾਤ ਹੋਣ ਨਾਲ ਮਸ਼ੀਨ ਖ਼ਰਾਬ ਹੋ ਜਾਂਦੀ ਹੈ ਤੇ ਉਹ ਕੰਮ ਨਹੀਂ ਕਰਦੀ ।

ਪ੍ਰਸ਼ਨ 4.
ਇਸ ਮਸ਼ੀਨ ਦੀ ਵਰਤੋਂ ਕਿੱਥੇ-ਕਿੱਥੇ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ:
ਇਸ ਮਸ਼ੀਨ ਦੀ ਵਰਤੋਂ ਦਫ਼ਤਰਾਂ ਤੇ ਘਰਾਂ ਵਿਚ ਸਭ ਥਾਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਅੱਜ-ਕਲ੍ਹ ਇਸ ਮਸ਼ੀਨ ਨੂੰ ਸਿੱਖਣਾ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹੋ ਗਿਆ ਹੈ ?
ਉੱਤਰ:
ਅੱਜ-ਕਲ੍ਹ ਇਸ ਮਸ਼ੀਨ ਨੂੰ ਸਿੱਖਣਾ ਇਸ ਕਰਕੇ ਜ਼ਰੂਰੀ ਹੈ, ਕਿਉਂਕਿ ਸਾਡੇ ਘਰਾਂ ਤੇ ਦਫ਼ਤਰਾਂ ਦੇ ਬਹੁਤ ਸਾਰੇ ਕੰਮ ਇਸ ਤੋਂ ਬਿਨਾਂ ਨਹੀਂ ਚਲਦੇ ।

ਪ੍ਰਸ਼ਨ 6.
ਪੜੋ, ਸਮਝੋ ਤੇ ਲਿਖੋ ।
ਮਸ਼ੀਨ : ਪੁਰਜ਼ਿਆਂ ਤੇ ਪੇਚਾਂ ਦਾ ਬਣਿਆ ਉਹ ਜੰਤਰ, ਜਿਸ ਨਾਲ ਕੋਈ ਕੰਮ ਜਲਦੀ ਤੇ ਅਸਾਨੀ ਨਾਲ ਹੋ ਜਾਂਦਾ ਹੈ ।
ਦਾਤ :
ਮਾਤ :
ਅਧੂਰੀ :
ਅਜਬ :
ਕਰਾਮਾਤ :
ਉੱਤਰ-ਮਸ਼ੀਨ : ਪੁਰਜ਼ਿਆਂ ਤੇ ਪੇਚਾਂ ਦਾ ਬਣਿਆ ਉਹ ਜੰਤਰ, ਜਿਸ ਨਾਲ ਕੋਈ ਕੰਮ ਜਲਦੀ ਤੇ ਅਸਾਨੀ ਨਾਲ ਹੋ ਜਾਂਦਾ ਹੈ ।
ਦਾਤ : ਦਾਨ ਕੀਤੀ ਹੋਈ ਵਸਤੂ, ਬਖ਼ਸ਼ਿਸ਼ ।
ਮਾਤ : ਸਭ ਨੂੰ ਪਿੱਛੇ ਛੱਡ ਦੇਣਾ ।
ਅਧੂਰੀ : ਜੋ ਪੂਰੀ ਨਹੀਂ, ਅਪੂਰਨ
ਅਜਬ : ਹੈਰਾਨ ਕਰਨ ਵਾਲਾ, ਅਨੋਖਾ
ਕਰਾਮਾਤ : ਅਜੀਬ ਸ਼ਕਤੀ, ਅਣਹੋਣੀ ਬਾਤ ।

ਪ੍ਰਸ਼ਨ 7.
ਇਸ ਕਵਿਤਾ ਵਿਚ ਕੰਪਿਊਟਰ ਨਾਲ ਜੁੜੇ ਅੰਗਰੇਜ਼ੀ ਦੇ ਕੁੱਝ ਸ਼ਬਦ ਆਏ ਹਨ । ਇਨ੍ਹਾਂ ਨੂੰ ਸੋਹਣਾ ਕਰ ਕੇ ਲਿਖੋ :
ਬਟਨ : BUTTON
ਟਾਈਪ : TYPE
ਫੀਡ : FEED
ਵਾਇਰਸ : VIROUS
ਕੀਅ-ਬੋਰਡ : KEY-BOARD
ਮੋਨੀਟਰ : MONITOR
ਉੱਤਰ:
(ਨੋਟ-ਵਿਦਿਆਰਥੀ ਆਪ ਹੀ ਲਿਖਣ ।)

ਪ੍ਰਸ਼ਨ 8.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਦੀ ਵਾਕਾਂ ਵਿਚ ਵਰਤੋਂ ਕਰੋ-
ਦਾਤ, ਰਿਕਾਰਡ, ਅਨੇਕਾਂ, ਬਾਥੂ, ਅਜਬ, ਕਰਾਮਾਤ, ਮਸ਼ੀਨ, ਚਿਤਰ, ਬਰਸਾਤ, ਦਫ਼ਤਰ, ਸਿੱਖਿਆ ।
ਉੱਤਰ:

1. ਦਾਤ (ਦੇਣ, ਬਖ਼ਸ਼ਿਸ਼)-ਕੁਦਰਤ ਨੇ ਬੰਦੇ ਨੂੰ ਬੇਅੰਤ ਦਾਤਾਂ ਦਿੱਤੀਆਂ ਹਨ ।
2. ਰਿਕਾਰਡ (ਹਿਸਾਬ-ਕਿਤਾਬ, ਵੇਰਵਾ)ਕੰਪਿਊਟਰ ਵਿਚ ਇਸ ਦਫ਼ਤਰ ਦਾ ਸਾਰਾ ਰਿਕਾਰਡ ਮੌਜੂਦ ਹੈ ।
3. ਅਨੇਕਾਂ ਬਹੁਤ ਸਾਰੇ)-ਅਜ਼ਾਦੀ ਦੀ ਲਹਿਰ ਵਿਚ ਅਨੇਕਾਂ ਸੂਰਬੀਰਾਂ ਨੇ ਜਾਨ ਦੀ ਬਾਜ਼ੀ ਲਾਈ ।
4. ਬਾਥੋਂ (ਬਿਨਾਂ)-ਭਰਾਵਾ, ਤੇਰੇ ਬਾਝੋ ਅਸੀਂ ਕਿਸੇ ਜੋਗੇ ਨਹੀਂ ।
5. ਅਜਬ ਹੈਰਾਨ ਕਰਨ ਵਾਲੀ)-ਕੰਪਿਊਟਰ ਅਜਬ ਕੰਮ ਕਰ ਦਿਖਾਉਂਦਾ ਹੈ ।
6. ਕਰਾਮਾਤ (ਅਣਹੋਣੀ ਗੱਲ, ਕ੍ਰਿਸ਼ਮਾ-ਗੁਰੂਆਂਪੀਰਾਂ ਦੀਆਂ ਜੀਵਨੀਆਂ ਵਿਚ ਉਨ੍ਹਾਂ ਦੀਆਂ ਬਹੁਤ ਸਾਰੀਆਂ ਕਰਾਮਾਤਾਂ ਦਾ ਜ਼ਿਕਰ ਹੁੰਦਾ ਹੈ ।
7. ਮਸ਼ੀਨ (ਯੰਤਰ)-ਇਸੁ ਮਸ਼ੀਨ ਨਾਲ ਖ਼ਰਾਦ . ਦਾ ਕੰਮ ਹੁੰਦਾ ਹੈ ।
8. ਚਿਤਰ (ਤਸਵੀਰ)-ਇਹ ਇਕ ਸੁੰਦਰ ਕੁਦਰਤੀ ਦ੍ਰਿਸ਼ ਦਾ ਚਿਤਰ ਹੈ ।
9. ਬਰਸਾਤ (ਮੀਂਹ ਦਾ ਲਗਾਤਾਰ ਪੈਣਾ-ਜੁਲਾਈਅਗਸਤ ਬਰਸਾਤ ਦੇ ਮਹੀਨੇ ਹਨ ।
10. ਦਫ਼ਤਰ (ਬੈਠ ਕੇ ਕੰਮ ਕਰਨ ਦੀ ਕੇਂਦਰੀ ਥਾਂ)-ਇਹ ਪੰਜਾਬ ਕਾਂਗਰਸ ਪਾਰਟੀ ਦਾ ਦਫ਼ਤਰ ਹੈ ।
11. ਸਿੱਖਿਆ ਪੜ੍ਹਾਈ)-ਪੰਜਾਬ ਸਕੂਲ ਸਿੱਖਿਆ ਬੋਰਡ ਦਾ ਦਫ਼ਤਰ ਮੁਹਾਲੀ ਵਿਚ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਕੰਪਿਊਟਰ ਦੇ ਹਿੱਸਿਆਂ (ਭਾਗਾਂ) ਦੀ ਮਾਈਂਡ ਮੈਪਿੰਗ ਤਿਆਰ ਕਰੋ ।
ਜਾਂ
ਕੰਪਿਊਟਰ ਦੇ ਭਾਗ ਖ਼ਾਲੀ ਗੋਲਿਆਂ ਵਿਚ ਲਿਖੋ ।

ਉੱਤਰ:

ਪ੍ਰਸ਼ਨ 10.
ਕੰਪਿਊਟਰ ਮਸ਼ੀਨ ਕੋਲ ਜਾ ਕੇ ਅਧਿਆਪਕ ਤੋਂ ਇਸ ਦੇ ਭਾਗਾਂ ਤੇ ਇਸ ਦੇ ਕੰਮ ਬਾਰੇ ਜਾਣਕਾਰੀ ਪ੍ਰਾਪਤ ਕਰੋ ।
ਉੱਤਰ:
(ਨੋ-ਵਿਦਿਆਰਥੀ ਆਪੇ ਹੀ ਕਰਨ ।)

ਪ੍ਰਸ਼ਨ 11.
‘ਮੇਰੀ ਕਿਤਾਬ (ਪੁਸਤਕ) ਵਿਸ਼ੇ ਉੱਤੇ ਲੇਖ ਰਚਨਾ ਕਰੋ ।
ਉੱਤਰ:
(ਨੋਟ-ਇ ਲੇਖ ਲਿਖਣ ਲਈ ਦੇਖੋ ਅਗਲੇ ਸਫ਼ਿਆਂ ਵਿਚ ਲੇਖ-ਰਚਨਾ ਵਾਲਾ ਭਾਗ ।)

Punjab State Board PSEB 4th Class Punjabi Book Solutions Chapter 7 ਨਾਨੀ ਦੀ ਸਿੱਖਿਆTextbook Exercise Questions and Answers.

PSEB Solutions for Class 4 Punjabi Chapter 7 ਨਾਨੀ ਦੀ ਸਿੱਖਿਆ

ਪਾਠ-ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 1.
ਬੁੱਧ ਰਾਮ ਦਾ ਇਹ ਨਾਂ ਕਿਸ ਨੇ ਤੇ ਕਿਉਂ ਰੱਖਿਆ ?
ਉੱਤਰ:
ਬੁੱਧ ਰਾਮ ਦਾ ਇਹ ਨਾਂ ਉਸਦੀ ਨਾਨੀ ਨੇ ਇਸ ਕਰਕੇ ਰੱਖਿਆ ਸੀ, ਕਿਉਂਕਿ ਉਹ ਬੁੱਧਵਾਰ ਵਾਲੇ ਦਿਨ ਜੰਮਿਆ ਸੀ ।

ਪ੍ਰਸ਼ਨ 2.
ਨਾਨਕੇ ਜਾਣ ਸਮੇਂ ਰਸਤੇ ਵਿਚ ਬੁੱਧੂ ਨੂੰ ਕੌਣ-ਕੌਣ ਮਿਲਿਆ ?
ਉੱਤਰ:
ਨਾਨਕੇ ਜਾਣ ਸਮੇਂ ਰਸਤੇ ਵਿਚ ਬੁੱਧੂ ਨੂੰ ਸ਼ਿਕਾਰੀ, ਚੋਰ, ਅਰਥੀ ਚੁੱਕੀ ਜਾਂਦੇ ਪਿੰਡ ਦੇ ਲੋਕ, ਕੁੜੀ ਦਾ ਵਿਆਹ ਕਰ ਰਹੇ ਲੋਕ, ਕਣਕ ਨੂੰ ਲੱਗੀ ਅੱਗ ਬੁਝਾ ਰਹੇ ਲੋਕ ਤੇ ਕਿਰਸਾਨ ਮਿਲੇ ।

ਪ੍ਰਸ਼ਨ 3.
ਨਾਨਕੇ ਪਹੁੰਚ ਕੇ ਬੁੱਧੂ ਨੇ ਕੀ ਕੀਤਾ ?
ਉੱਤਰ:
ਨਾਨਕੇ ਪਹੁੰਚ ਕੇ ਬੁੱਧੂ ਨੇ ਆਪਣੀ ਨਾਨੀ ਨੂੰ ਰਸਤੇ ਵਿਚ ਵਾਪਰੀ ਸਾਰੀ ਹੱਡ-ਬੀਤੀ ਸੁਣਾਈ ।

ਪ੍ਰਸ਼ਨ 4.
ਨਾਨੀ ਨੇ ਬੁੱਧੂ ਨੂੰ ਕੀ ਸਮਝਾਇਆ ?
ਉੱਤਰ:
ਨਾਨੀ ਨੇ ਬੁੱਧੂ ਨੂੰ ਸਮਝਾਇਆ ਕਿ ਉਹ ਅਨਪੜ੍ਹ ਰਹਿਣ ਕਰਕੇ ਬੁੱਧੂ ਰਹਿ ਗਿਆ ਹੈ । ਉਹ ਪੜ੍ਹ ਕੇ ਹੁਸ਼ਿਆਰ ਬਣ ਸਕਦਾ ਸੀ । ਇਸ ਦੇ ਨਾਲ ਹੀ ਉਸਨੂੰ ਬਿਨਾਂ ਮਤਲਬ ਨਹੀਂ ਸੀ ਬੋਲਣਾ ਚਾਹੀਦਾ । ਪੜ੍ਹੇ-ਲਿਖੇ ਮੁੰਡੇ-ਕੁੜੀਆਂ ਬਹੁਤਾ ਨਹੀਂ ਬੋਲਦੇ । ਜੇ ਬੋਲਣ ਦੀ ਲੋੜ ਪਵੇ, ਤਾਂ ਉਹ ਸੋਚ-ਸਮਝ ਕੇ ਬੋਲਦੇ

ਪ੍ਰਸ਼ਨ 5.
ਆਪਣੇ ਘਰ ਪਰਤ ਕੇ ਬੁੱਧੂ ਨੇ ਮਾਂ ਨੂੰ ਕੀ ਕਿਹਾ ?
ਉੱਤਰ:
ਆਪਣੇ ਘਰ ਪਰਤ ਕੇ ਬੁੱਧੂ ਨੇ ਆਪਣੀ ਮਾਂ ਨੂੰ ਕਿਹਾ ਕਿ ਉਹ ਕਲ੍ਹ ਤੋਂ ਪੜ੍ਹਨ ਸਕੂਲ ਜਾਇਆ ਕਰੇਗਾ ।

ਪ੍ਰਸ਼ਨ 6.
ਬੈਕਟਾਂ ਵਿੱਚੋਂ ਠੀਕ ਸ਼ਬਦ ਚੁਣ ਕੇ ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ
(ਚੋਰ, ਫ਼ਸਲ, ਲੜਕੀ, ਨੌਜਵਾਨ, ਜਾਲ )

(ਉ) ਸ਼ਿਕਾਰੀ ਨੇ ਸ਼ਿਕਾਰ ਨੂੰ ਫੜਨ ਲਈ ………… ਵਿਛਾਇਆ ਹੋਇਆ ਸੀ ।
(ਅ) ਕੁੱਝ ………… ਚੋਰੀ ਕਰਨ ਦੀ ਸੋਚ ਰਹੇ ਸਨ ।
(ਇ) ਪਿੰਡ ਦੇ ਲੋਕ ਇਕ ………… ਦੀ ਅਰਥੀ ਚੁੱਕੀ ਮੜੀਆਂ ਵਲ ਜਾ ਰਹੇ ਸਨ ।
(ਸ) ਅਗਲੇ ਪਿੰਡ ਵਿਚ ਇਕ ………… ਦਾ ਵਿਆਹ ਸੀ ।
(ਹ) ਕਿਰਸਾਣ ਦੀ ਪੱਕੀ ………… ਨੂੰ ਅੱਗ ਲੱਗੀ ਹੋਈ ਸੀ ।
ਉੱਤਰ:
(ੳ) ਸ਼ਿਕਾਰੀ ਨੇ ਸ਼ਿਕਾਰ ਨੂੰ ਫੜਨ ਲਈ ਜਾਲ ਵਿਛਾਇਆ ਹੋਇਆ ਸੀ ।
(ਅ) ਕੁੱਝ ਚੋਰ ਚੋਰੀ ਕਰਨ ਦੀ ਸੋਚ ਰਹੇ ਸਨ ।
(ਇ) ਪਿੰਡ ਦੇ ਲੋਕ ਇਕ ਨੌਜਵਾਨ ਦੀ ਅਰਥੀ ਚੁੱਕੀ ਮੜ੍ਹੀਆਂ ਵਲ ਜਾ ਰਹੇ ਸਨ ।
(ਸ) ਅਗਲੇ ਪਿੰਡ ਵਿਚ ਇਕ ਲੜਕੀ ਦਾ ਵਿਆਹ ਸੀ ।
(ਹ) ਕਿਰਸਾਣ ਦੀ ਪੱਕੀ ਫ਼ਸਲ ਨੂੰ ਅੱਗ ਲੱਗੀ ਹੋਈ ਸੀ ।

ਪ੍ਰਸ਼ਨ 7.
ਬੁੱਧੂ ਆਪਣੇ ਨਾਨਕੇ ਪਹੁੰਚਿਆ । ਰਾਤ ਨੂੰ ਉਸ ਨੇ ਆਪਣੀ ਨਾਨੀ ਨੂੰ ਆਪ ਬੀਤੀ ਸੁਣਾਈ । ਤਦ ਨਾਨੀ ਨੇ ਸਮਝਾਇਆ, “ਜੇਕਰ ਤੂੰ ਅਨਪੜ੍ਹ ਰਿਹਾ, ਤਾਂ ਹੀ ਬੁੱਧੂ ਬਣ ਗਿਆ । ਪੜ੍ਹਾਈ ਕਰ ਕੇ ਤੂੰ ਹੁਸ਼ਿਆਰ ਹੋ ਜਾਣਾ ਸੀ । ਫਿਰ ਤੂੰ ਬਿਨਾਂ ਮਤਲਬ ਨਹੀਂ ਸੀ ਬੋਲਣਾ । ਪੜ੍ਹੇ-ਲਿਖੇ ਮੁੰਡੇ-ਕੁੜੀਆਂ ਫ਼ਜ਼ੂਲ ਨਹੀਂ ਬੋਲਦੇ । ਜੇ ਬੋਲਣ ਦੀ ਲੋੜ ਹੋਵੇ, ਤਾਂ ਸੋਚਸਮਝ ਕੇ ਬੋਲਦੇ ਹਨ ’
ਉਪਰੋਕਤ ਪੈਰੇ ਨੂੰ ਪੜ੍ਹ ਕੇ ਹੇਠ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਲਿਖੋ-

1. ਬੁੱਧੂ ਕਿੱਥੇ ਪਹੁੰਚਿਆ ?
2. ਬੁੱਧੂ ਨੇ ਕਿਸ ਨੂੰ ਆਪ ਬੀਤੀ ਸੁਣਾਈ ?
3. ਬੁੱਧੂ ਕਿਉਂ ਹੁਸ਼ਿਆਰ ਨਹੀਂ ਸੀ ਬਣਿਆ ?
4. ਕੌਣ ਫ਼ਜ਼ਲ ਨਹੀਂ ਬੋਲਦੇ ?
5. ਪੜੇ-ਲਿਖੇ ਮੁੰਡੇ-ਕੁੜੀਆਂ ਲੋੜ ਪੈਣ ਤੇ ਕਿਸ ਤਰ੍ਹਾਂ ਬੋਲਦੇ ਹਨ ?

ਉੱਤਰ:

1. ਨਾਨਕਿਆਂ ਦੇ ਘਰ ।
2. ਆਪਣੀ ਨਾਨੀ ਨੂੰ ।
3. ਅਨਪੜ ਰਹਿਣ ਕਰਕੇ
4. ਪੜ੍ਹੇ-ਲਿਖੇ ਮੁੰਡੇ-ਕੁੜੀਆਂ ।
5. ਸੋਚ-ਸਮਝ ਕੇ ।

ਪ੍ਰਸ਼ਨ 8.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਨੂੰ ਵਾਕਾਂ ਵਿਚ ਵਰਤੋ
ਨਿਕੰਮਾ, ਸ਼ਿਕਾਰੀ, ਆਪ-ਬੀਤੀ, ਹੁਸ਼ਿਆਰ, ਫ਼ਜੂਲ, ਬਜ਼ੁਰਗ, ਬੀੜ ।
ਉੱਤਰ:

1. ਨਿਕੰਮਾ ਕੋਈ ਕੰਮ ਨਾ ਕਰ ਸਕਣ ਵਾਲਾ)–ਇਹ ਆਦਮੀ ਬਿਲਕੁਲ ਨਿਕੰਮਾ ਹੈ । ਇਸਨੂੰ ਕੋਈ ਕੰਮ ਨਹੀਂ ਆਉਂਦਾ ।
2. ਸ਼ਿਕਾਰੀ (ਸ਼ਿਕਾਰ ਕਰਨ ਵਾਲਾ)-ਜੰਗਲ ਵਿਚ ਸ਼ਿਕਾਰੀ ਸ਼ਿਕਾਰ ਖੇਡ ਰਿਹਾ ਹੈ ।
3. ਆਪ-ਬੀਤੀ ਆਪਣੇ ਨਾਲ ਬੀਤੀ ਗੱਲ-ਬੁੱਧੂ ਨੇ ਸਾਰੀ ਆਪ-ਬੀਤੀ ਆਪਣੀ ਨਾਨੀ ਨੂੰ ਸੁਣਾਈ ।
4. ਹੁਸ਼ਿਆਰ ਤੇਜ਼ ਦਿਮਾਗ਼ ਵਾਲਾ, ਚੁਕੰਨਾ)-ਤੂੰ ਜ਼ਰਾ ਹੁਸ਼ਿਆਰ ਹੋ ਕੇ ਘਰ ਦੀ ਰਾਖੀ ਕਰੋ ।
5. ਫ਼ਜੂਲ (ਵਿਅਰਥ)-ਫ਼ਜੂਲ ਗੱਲਾਂ ਕਰ ਕੇ ਸਮਾਂ ਬਰਬਾਦ ਨਾ ਕਰੋ ।…
6. ਬਜ਼ੁਰਗ ਵਡੇਰੀ ਉਮਰ ਦਾ ਆਦਮੀ-ਹਮੇਸ਼ਾ ਬਜ਼ੁਰਗਾਂ ਦਾ ਆਦਰ-ਸਤਿਕਾਰ ਕਰੋ ।
7. ਬੀੜ (ਜੰਗਲ)-ਪੰਜਾਬ ਵਿਚ ਛਤ ਬੀੜ ਵਿਖੇ ਬਹੁਤ ਵੱਡਾ ਚਿੜੀਆ-ਘਰ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਦੇ ਅਰਥ ਲਿਖੋ ਤੇ ਉਨ੍ਹਾਂ ਦੀ ਵਾਕਾਂ ਵਿਚ ਵਰਤੋਂ ਕਰੋ
ਨਾਨਕੇ, ਦੋਹਤਾ, ਬੀੜ, ਮੜੀਆਂ ।
ਉੱਤਰ:

1. ਨਾਨਕੇ ਮਾਂ ਦੇ ਪੇਕੇ-ਘਰ ਨੂੰ ਨਾਨਕੇ ਕਹਿੰਦੇ ਹਨ)-ਮੈਂ ਅੱਜ ਆਪਣੇ ਨਾਨਕੇ-ਘਰ ਜਾਣਾ ਹੈ ।
2. ਦੋਹਤਾ (ਧੀ ਦੇ ਪੁੱਤਰ ਨੂੰ ਦੋਹਤਾ ਕਹਿੰਦੇ ਹਨ-ਨਾਨਕਿਆਂ ਦੇ ਘਰ ਦੋਹਤੇ ਨੂੰ ਆਮ ਕਰਕੇ ਖੂਬ ਪਿਆਰ ਮਿਲਦਾ ਹੈ ।
3. ਬੀੜ (ਜੰਗਲ)-ਅਸੀਂ ਛੱਤ ਬੀੜ ਵਿਚ ਬਣੇ ਚਿੜੀਆ-ਘਰ ਨੂੰ ਵੇਖਣ ਗਏ ।
4. ਮੜੀਆਂ ਮੁਰਦੇ ਦਾ ਦਾਹ-ਸਸਕਾਰ ਕਰਨ ਲਈ ਬਣਾਈ ਥਾਂ)-ਮੁਰਦੇ ਦਾ ਮੜ੍ਹੀਆਂ ਵਿਚ ਲਿਜਾ ਕੇ ਅੰਤਮ-ਸਸਕਾਰ ਕਰ ਦਿੱਤਾ ਗਿਆ ।

ਪ੍ਰਸ਼ਨ 10.
ਬੁੱਧੂ ਦੇ ਸਫ਼ਰ ਦੌਰਾਨ ਉਸਨੂੰ ਕੌਣ-ਕੌਣ ਮਿਲਿਆ ? ਹੇਠਾਂ ਦਿੱਤੇ ਗੋਲ-ਚੱਕਰਾਂ ਵਿਚ ਲਿਖੋ ।

ਉੱਤਰ:

ਪ੍ਰਸ਼ਨ 11.
ਛੁੱਟੀਆਂ ਵਿਚ ਤੁਸੀਂ ਆਪਣੇ ਨਾਨਕੇ ਜਾਂ ਕਿਸੇ ਰਿਸ਼ਤੇਦਾਰੀ ਵਿਚ ਗਏ ਹੋ, ਤਾਂ ਰਸਤੇ ਵਿਚ ਜਾਂ ਉੱਥੇ ਰਹਿੰਦਿਆਂ ਜੋ ਕੁੱਝ ਤੁਸੀਂ ਦੇਖਿਆ ਜਾਂ ਕੀਤਾ, ਉਸ ਸੰਬੰਧੀ ਪੰਜ-ਛੇ ਸਤਰਾਂ ਲਿਖੋ ।
ਉੱਤਰ:
ਬੀਤੀਆਂ ਗਰਮੀਆਂ ਦੀਆਂ ਛੁੱਟੀਆਂ ਵਿਚ ਮੈਂ ਆਪਣੇ ਪਿਤਾ ਜੀ ਦੇ ਸਕੂਟਰ ਦੇ ਪਿੱਛੇ ਬੈਠ ਕੇ ਆਪਣੇ ਨਾਨਕਿਆਂ ਦੇ ਪਿੰਡ ਗਿਆ । ਮੇਰੇ ਨਾਨਕਿਆਂ ਦੀ ਬਹੁਤ ਸਾਰੀ ਜ਼ਮੀਨ ਸੀ । ਉਨ੍ਹਾਂ ਦਿਨਾਂ ਵਿਚ ਕਣਕ ਦੀ ਵਾਢੀ ਖ਼ਤਮ ਹੋ ਚੁੱਕੀ ਸੀ । ਖੇਤਾਂ ਵਿਚ ਕਿਧਰੇ-ਕਿਧਰੇ ਪਸ਼ੂਆਂ ਦੇ ਹਰੇ ਚਾਰੇ ਦੇ ਖੇਤ ਖੜ੍ਹੇ ਸਨ ਤੇ ਕਿਧਰੇ-ਕਿਧਰੇ ਹਰੇ-ਭਰੇ ਕਮਾਦ ਦੇ ਖੇਤ ਸਨ । ਗਰਮੀ · ਜ਼ਿਆਦਾ ਹੋਣ ਕਰਕੇ ਖੇਤਾਂ ਨੂੰ ਪਾਣੀ ਦੇਣ ਲਈ ਟਿਊਬਵੈੱਲ ਚਲਦਾ ਰਹਿੰਦਾ ਸੀ । ਖੇਤਾਂ ਨੂੰ ਪਾਣੀ ਦੇਣ ਦਾ ਕੰਮ ਯੂ.ਪੀ. ਦਾ ਭਈਆ ਕਰਦਾ ਸੀ । ਮੇਰੇ ਮਾਮੇ ਦਾ ਵੱਡਾ ਮੁੰਡਾ ਟਰੈਕਟਰ ਨਾਲ ਖੇਤਾਂ ਨੂੰ ਵਾਹੁੰਦਾ ਤੇ ਅਗਲੀ ਫ਼ਸਲ ਲਈ ਤਿਆਰ ਕਰ ਰਿਹਾ ਸੀ । ਉਹ ਦੱਸਦਾ ਸੀ ਕਿ ਕੁੱਝ ਖੇਤਾਂ ਵਿਚ ਝੋਨਾ, ਕੁੱਝ ਵਿਚ ਮੱਕੀ, ਕੁੱਝ ਵਿਚ ਦਾਲਾਂ, ਕੁੱਝ ਵਿੱਚ ਚੜ੍ਹੀ ਤੇ ਬਾਜਰਾ ਬੀਜਿਆ ਜਾਵੇਗਾ । ਨਾਨਕਿਆਂ ਦੇ ਘਰ ਦੋ ਮੱਝਾਂ ਸਨ, ਜੋ ਦੁੱਧ ਦਿੰਦੀਆਂ ਸਨ । ਮੈਨੂੰ ਹਰ ਰੋਜ਼ ਤਾਜ਼ਾ ਦੁੱਧ ਪੀਣ ਲਈ ਮਿਲਦਾ । ਨਾਨਕਿਆਂ ਦੇ ਇਕ ਖੇਤ ਵਿਚ ਖ਼ਰਬੂਜ਼ੇ ਪੱਕੇ ਹੋਏ ਸਨ । ਮੈਂ ਤੇ ਮੇਰੇ ਮਾਮੇ ਦਾ ਛੋਟਾ ਮੁੰਡਾ ਤੇ ਕੁੜੀ ਹਰ ਰੋਜ਼ ਰੱਜ-ਰੱਜ ਕੇ ਖ਼ਰਬੂਜੇ ਖਾਂਦੇ ਸਾਂ । ਇਸ ਪ੍ਰਕਾਰ ਦਸ ਦਿਨ ਉੱਥੇ ਗੁਜ਼ਾਰ ਕੇ ਮੈਂ ਘਰ ਪਰਤ ਆਇਆ ।

Punjab State Board PSEB 4th Class Punjabi Book Solutions Chapter 5 ਵੀਰੂ ਤੇ ਮੰਗੂ Textbook Exercise Questions and Answers.

PSEB Solutions for Class 4 Punjabi Chapter 5 ਵੀਰੂ ਤੇ ਮੰਗੂ

ਪਾਠ-ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ-ਉੱਤਰ

ਪ੍ਰਸ਼ਨ 1.
ਮੇਮਣਿਆਂ ਨੂੰ ਘਾਹ-ਪੱਤਾ ਕਿਹੋ-ਜਿਹਾ ਲੱਗਦਾ ਸੀ ?
ਉੱਤਰ:
ਮੇਮਣਿਆਂ ਨੂੰ ਘਾਹ-ਪੱਤਾ ਕੁਸੈਲਾ ਲੱਗਦਾ ਸੀ ।

ਪ੍ਰਸ਼ਨ 2.
ਭਾਗ ਹਰ ਰੋਜ਼ ਹੀ ਰੁੱਖਾਂ ਦੀਆਂ ਲਗਰਾਂ ਵੱਢ ਕੇ ਮੇਮਣਿਆਂ ਨੂੰ ਕਿਉਂ ਪਾਉਂਦਾ ਸੀ ?
ਉੱਤਰ:
ਭਾਗ ਹਰ ਰੋਜ਼ ਹੀ ਰੁੱਖਾਂ ਦੀਆਂ ਲਗਰਾਂ ਵੱਢ ਕੇ ਮੇਮਣਿਆਂ ਨੂੰ ਪਾਉਂਦਾ ਸੀ, ਤਾਂ ਜੋ ਉਹ ਲਗਰਾਂ ਖਾ ਕੇ ਢਿੱਡ ਭਰ ਲੈਣ ਤੇ ਆਪਣੀ ਮਾਂ ਦੇ ਦੁੱਧ ਦੀ ਝਾਕ ਨਾ ਰੱਖਣ ।

ਪ੍ਰਸ਼ਨ 3.
ਵੀਰੂ ਨੇ ਰੋਣ-ਹਾਕਾ ਮੂੰਹ ਬਣਾ ਕੇ ਮੰਗੂ : ਨੂੰ ਕੀ ਕਿਹਾ ?
ਉੱਤਰ:
ਵੀਰੂ ਨੇ ਰੋਣ-ਹਾਕਾ ਮੂੰਹ ਬਣਾ ਕੇ ਮੰਗੂ ਨੂੰ ਕਿਹਾ ਕਿ ਜੇਕਰ ਉਨ੍ਹਾਂ ਦਾ ਆਜੜੀ ਭਰਾ ਹਰ ਰੋਜ਼ ਇਸੇ ਤਰ੍ਹਾਂ ਰੁੱਖ ਛਾਂਗਦਾ ਤੇ ਵੱਢਦਾ ਰਿਹਾ, ਤਾਂ ਸਾਰੇ ਰੁੱਖ ਮੁੱਕ ਜਾਣਗੇ । ਫਿਰ ਮੀਂਹ ਪੈਣੋਂ ਹਟ ਜਾਵੇਗਾ ਤੇ ਧਰਤੀ ਬੰਜਰ ਹੋ ਜਾਵੇਗੀ ।

ਪ੍ਰਸ਼ਨ 4.
ਸ਼ਹਿਰ ਤੋਂ ਆਏ ਬੰਦੇ ਨੇ ਕੀ ਆਖਿਆ ?
ਉੱਤਰ:
ਸ਼ਹਿਰ ਤੋਂ ਆਏ ਬੰਦੇ ਨੇ ਆਖਿਆ ਕਿ ਜੇਕਰ ਇਸੇ ਤਰ੍ਹਾਂ ਹੀ ਰੁੱਖ ਵੱਢੇ ਜਾਂਦੇ ਰਹੇ, ਤਾਂ ਪਾਣੀ ਦੀ ਘਾਟ ਹੋ ਜਾਵੇਗੀ ਤੇ ਸਾਹ ਲੈਣ ਲਈ ਹਵਾ ਵੀ ਠੀਕ ਨਹੀਂ ਰਹੇਗੀ ।

ਪ੍ਰਸ਼ਨ 5.
ਬੈਕਟਾਂ ਵਿੱਚੋਂ ਠੀਕ ਸ਼ਬਦ ਚੁਣ ਕੇ ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ-
(ਦਾਤ, ਘਾਹ-ਪੱਤਾ, ਖੇਤ, ਘਾਹ, ਮਾਂ ।)
(ਉ) ਵੀਰੂ ਤੇ ਮੰਗੂ …………. ਦਾ ਦੁੱਧ ਪੀਣ ਲਈ ਮੌਕਾ ਲੱਭਦੇ ਰਹਿੰਦੇ ।
(ਅ) ਹੁਣ ਤਾਂ …………. ਦੀ ਤਿੜ੍ਹ ਵੀ ਭਾਲੀ ਨਹੀਂ ਲੱਭਦੀ ।
(ਈ) ਆਪਾਂ ਤਾਂ …………. ਖਾ ਕੇ ਗੁਜ਼ਾਰਾ ਕਰ ਲਵਾਂਗੇ ।
(ਸ) ਭਾਗ ਨੇ ਛੋਟੇ-ਛੋਟੇ ਮੇਮਣਿਆਂ ਲਈ …….. ਨਾਲ ਕਿੱਕਰ ਛਾਂਗੀ ਸੀ ।
(ਹ) ਸ਼ਹਿਰ ਤੋਂ ਇਕ ਬੰਦਾ …………. ਦੇਖਣ ਆਇਆ ਸੀ ।
ਉੱਤਰ:
(ੳ) ਵੀਰੂ ਤੇ ਮੰਗੂ ਮਾਂ ਦਾ ਦੁੱਧ ਪੀਣ ਲਈ ਮੌਕਾ ਲੱਭਦੇ ਰਹਿੰਦੇ ।
(ਅ) ਹੁਣ ਤਾਂ ਘਾਹ ਦੀ ਤਿੜ੍ਹ ਵੀ ਭਾਲੀ ਨਹੀਂ ਲੱਭਦੀ ।.
(ਈ ਆਪਾਂ ਤਾਂ ਘਾਹ-ਪੱਤਾ ਖਾ ਕੇ ਗੁਜ਼ਾਰਾ ਕਰ ਲਵਾਂਗੇ ।
(ਸ) ਭਾਗ ਨੇ ਛੋਟੇ-ਛੋਟੇ ਮੇਮਣਿਆਂ ਲਈ ਦਾਤ ਨਾਲ ਕਿੱਕਰ ਝਾਂਗੀ ਸੀ ।
(ਹ) ਸ਼ਹਿਰ ਤੋਂ ਇਕ ਬੰਦਾ ਖੇਤ ਦੇਖਣ ਆਇਆ ਸੀ ।

ਪ੍ਰਸ਼ਨ 6.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦਾਂ ਨੂੰ ਵਾਕਾਂ ਵਿਚ ਵਰਤੋ” ਕੁਸੈਲਾ, ਹਿੰਮਤ, ਗੁਜ਼ਾਰਾ, ਬੰਜਰ, ਆਲੇ-ਦੁਆਲੇ, ਝਾਕ, ਆਜੜੀ, ਮੇਮਣਾ |’
ਉੱਤਰ:

1. ਕੁਸੈਲਾ (ਕੌੜਾ)-ਛੋਟੇ ਮੇਮਣਿਆਂ ਨੂੰ ਘਾਹ-ਪੱਤਾ ਕੁਸੈਲਾ ਲਗਦਾ ।
2. ਹਿੰਮਤ (ਦਲੇਰੀ)-ਤੇਰੇ ਵਿਚ ਹਿੰਮਤ ਹੈ, ਤਾਂ ਮੇਰਾ ਮੁਕਾਬਲਾ ਕਰ ।
3. ਗੁਜ਼ਾਰਾ (ਨਿਰਬਾਹ, ਖ਼ਰਚ ਪੂਰਾ ਹੋਣਾ)-ਇੰਨੇ ਥੋੜੇ ਪੈਸਿਆਂ ਨਾਲ ਘਰ ਦਾ ਗੁਜ਼ਾਰਾ ਨਹੀਂ ਹੁੰਦਾ ।
4. ਬੰਜਰ (ਜਿਸ ਜ਼ਮੀਨ ਵਿਚ ਫ਼ਸਲ ਪੈਦਾ ਨਾ ਹੋਵੇ)-ਰਾਜਸਥਾਨ ਦੀ ਬਹੁਤੀ ਧਰਤੀ ਰੇਗਿਸਤਾਨੀ ਤੇ ਬੰਜਰ ਹੈ ।
5. ਆਲੇ-ਦੁਆਲੇ (ਚੁਫ਼ੇਰੇ)-ਸਾਡੇ ਮਕਾਨ ਦੇ ਆਲੇਦੁਆਲੇ ਪੰਜ-ਪੰਜ ਫੁੱਟ ਉੱਚੀ ਕੰਧ ਹੈ ।
6. ਝਾਕ (ਧਿਆਨ, ਉਮੀਦ)-ਬਿੱਲੀ ਦੁੱਧ ਦੇ ਪਤੀਲੇ . ਵਲ ਝਾਕ ਲਾਈ ਬੈਠੀ ਸੀ ।
7. ਆਜੜੀ (ਭੇਡਾਂ-ਬੱਕਰੀਆਂ ਚਾਰਨ ਵਾਲਾ)ਆਜੜੀ ਭੇਡਾਂ ਚਾਰ ਰਿਹਾ ਹੈ ।
8. ਮੇਮਣਾ ਬੱਕਰੀ ਦਾ ਬੱਚਾ)-ਮੇਮਣਾ ਜੰਮਦਾ ਹੀ ਛਾਲਾਂ ਮਾਰਨ ਲੱਗਾ

ਪ੍ਰਸ਼ਨ 7.
ਪੜੋ, ਸਮਝੋ ਤੇ ਲਿਖੋ-

ਉੱਤਰ:

ਪ੍ਰਸ਼ਨ 8.
ਹੇਠ ਲਿਖੇ ਸ਼ਬਦ ਕਿਸ ਨੇ, ਕਿਸ ਨੂੰ ਕਹੇ
(ਉ) ‘‘ਪੁੱਤਰ, ਤੂੰ ਵੱਡਾ ਹੋ ਗਿਆ, ਹੁਣ ਘਾਹਪੱਤਾ ਚੁਗਿਆ ਕਰ ।
(ਅ) “ਤੂੰ ਵੀ ਹਿੰਮਤ ਕਰ ਲੈ।”
(ਇ) ‘‘ਭਲਾ ਇਹ ‘ਵਾਜਾਂ ਕੌਣ ਮਾਰਦੈ ।’
(ਸ) ‘‘ਅਸੀਂ ਨਹੀਂ ਖਾਣੀ ਚੁੰਗ, ਭਾਗ ਆਜੜੀ ਹਰ ਰੋਜ਼ ਕੋਈ ਨਾ ਕੋਈ ਰੁੱਖ ਵੱਢ ਦਿੰਦੈ ।”
ਉੱਤਰ:
(ੳ) ਇਹ ਸ਼ਬਦ ਮਾਂ ਨੇ ਵੀਰੂ ਨੂੰ ਕਹੇ ।
(ਅ) ਇਹ ਸ਼ਬਦ ਵੀਰੂ ਨੇ ਮੰਗੂ ਨੂੰ ਕਹੇ ।
(ਈ) ਇਹ ਸ਼ਬਦ ਮੰਗੂ ਨੇ ਵੀਰ ਨੂੰ ਕਹੇ ।
(ਸ) ਇਹ ਸ਼ਬਦ ਵੀਰੂ ਨੇ ਮੰਗੂ ਨੂੰ ਕਹੇ ।

ਪ੍ਰਸ਼ਨ 9.
ਹੇਠ ਲਿਖੀਆਂ ਸਤਰਾਂ ਬੋਲ ਕੇ ਦੂਜੇ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਲਿਖਾਓ-

1. ਮੇਰੀ ਜੀਭ ਕੌੜੀ ਹੋ ਗਈ ।
2. ਆਜੜੀ ਬੱਕਰੀਆਂ ਚਾਰ ਰਿਹਾ ਸੀ ।
3. ਚਲ ਆਪਾਂ ਘਾਹ ਚੁਗੀਏ ।
4. ਇਹ ਜਗੀਰਾ ਕਿਰਸਾਣ ਹੈ ।
5. ਵੀਰੂ ਨੇ ਖੇਤਾਂ ਵਲ ਨਜ਼ਰ ਘੁਮਾਈ,
6. ਮੀਂਹ ਘੱਟ ਪੈਣ ਲਗ ਪਏ ਸਨ ।
7. ਵੀਰੂ ਨੇ ਰੋਣਹਾਕਾ ਮੂੰਹ ਬਣਾਇਆ ।

ਉੱਤਰ:
ਨੋਟ-ਵਿਦਿਆਰਥੀ ਆਪੇ ਹੀ ਕਰਨ ।

ਪ੍ਰਸ਼ਨ 10.
“ਮੇਰਾ ਪਿੰਡ ਮੇਰਾ ਸ਼ਹਿਰ’ ਵਿਸ਼ੇ ਉੱਤੇ ਇਕ ਲੇਖ ਲਿਖੋ ।
ਉੱਤਰ:
(ਨੋਟ-ਇਹ ਲੇਖ ਲਿਖਣ ਲਈ ਦੇਖੋ ਅਗਲੇ ਸਫ਼ਿਆਂ ਵਿਚ “ਲੇਖ-ਰਚਨਾ’ ਵਾਲਾ ਭਾਗ ।)