Bhagya

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 10 Circles Ex 10.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 10 Circles Ex 10.4

Question 1.
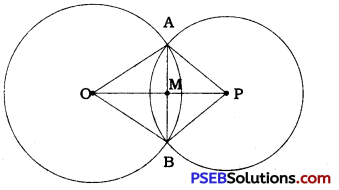
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Answer:

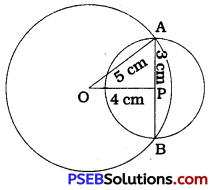
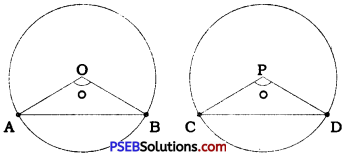
The circle with centre O and radius 5 cm intersects the circle with centre P and radius 3 cm at points A and B.
Hence, AB is their common chord.
Then, OP = 4 cm (Given),
OA = 5 cm and PA = 3 cm.
In ∆ OAP, OA² = 5² = 25 and
OP² + AP² = 4² + 3² = 16 + 9 = 25
Thus, in ∆ OAP, OA² = OP² + AP²
∴ ∆ OAP is a right triangle in which ∠OPA is a right angle and OA is the hypotenuse.
Thus, in the circle with centre O, OP is perpendicular from centre O to chord AB.
∴ OP bisects AB.
AB = 2PA = 2 × 3 = 6 cm
Thus, the length of the common chord is 6 cm.

Question 2.
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Answer:

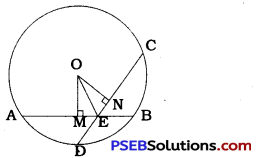
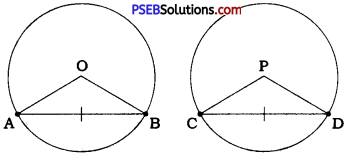
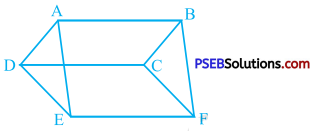
In the circle with centre O, equal chords AB and CD intersect at E.
Draw OM ⊥ AB and ON ⊥ CD.
∴ AM = BM = \(\frac{1}{2}\)AB and CN = DN = \(\frac{1}{2}\)CD.
But, AB = CD
∴AM = BM = CN = DN …………….. (1)
Chords AB and CD, being equal, are equidistant from the centre.
∴ OM = ON
In ∆ OME and ∆ ONE,
∠OME = ∠ONE (Right angles)
OE = OE (Common)
OM = ON
By RHS rule, ∆ OME ≅ ∆ ONE
∴ME = EN (CPCT) ……………… (2)
From (1) and (2),
AM + ME = CN + NE
∴ AE = CE
Similarly, BM – ME = DN – NE
∴ BE = DE
Thus, if two equal chords of a circle intersect within the circle, the segments of one chord are equal to corresponding segments of the other chord.

Question 3.
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Answer:
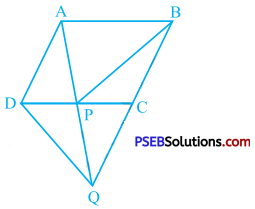
As the data of example 2 and example 3 are same, we use the proof of example 2 up to the required stage and do not repeat it here.
In example 2, we proved that,
∆ OME ≅ ∆ ONE ,
∴ ∠ OEM = ∠ OEN
∴ ∠ OEA = ∠ OEC
Thus, the line joining the point of intersection of two equal chords of a circle to the centre makes equal angles with the chords.

Question 4.
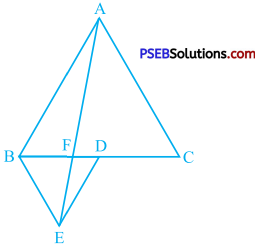
If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see the given figure).

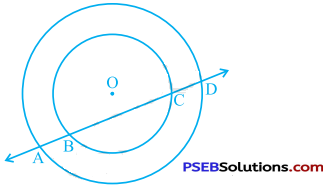
Answer:

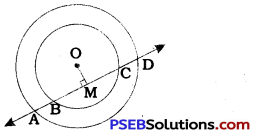
From centre O, draw perpendicular OM to line AD.
In the outer circle, OM is the perpendicular drawn from centre O to chord AD.
Hence, M is the midpoint of AD.
∴ MA = MD …………… (1)
In the inner circle, OM is the perpendicular drawn from centre O to chord BC.
Hence, M is the midpoint of BC.
∴ MB = MC ………….. (2)
Subtracting (2) from (1),
MA – MB = MD – MC
∴ AB = CD

Question 5.
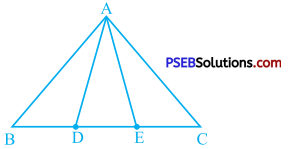
Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5 m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6 m each, what is the distance between Reshma and Mandip?
Answer:

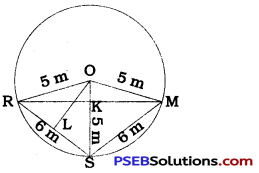
Here, OR = OM = OS = 5 m (Radius of the circle) and RS = SM = 6 m.
In quadrilateral ORSM, OR = OM = 5 m and RS = SM = 6 m.
∴ Quadrilateral ORSM is a kite.
∴ It diagonal OS bisects the diagonal RM at right angles.
∴ ∠RKO = 90° ………………. (1)
OK is perpendicular from centre O to chord RM.
Hence, K is the midpoint of RM.
∴ RM = 2RK ………………… (2)
From centre O, draw perpendicular OL to chord RS.
∴ RL = \(\frac{1}{2}\)RS = \(\frac{1}{2}\) × 6 = 3 m
In ∆ RLO, ∠ L = 90°
∴ RO² = OL² + RL²
∴ 5² = OL² + 3²
∴ 25 = OL² + 9
∴ OL² = 16
∴ OL = 4 m
Now, area of ∆ ROS = \(\frac{1}{2}\) × RS × OL
= \(\frac{1}{2}\) × OS × RK [by (1)]
∴RS × OL = OS × RK
∴ 6 × 4 = 5 × RK
∴ 24 = 5 × RK
∴ RK = \(\frac{24}{5}\) = 4.8 m
Then, RM = 2RK [by (2)]
∴ RM = 2 × 4.8
∴ RM = 9.6 m
Thus, the distance between Reshma and Mandip is 9.6 m.

Question 6.
A circular park of radius 20 m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk with each other. Find the length of the string of each phone.
Answer:

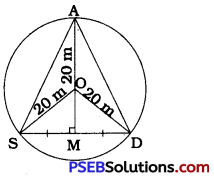
Here, the circle with centre O represents the park and the points A, S and D represent the positions of Ankur, Syed and David respectively. Since Ankur, Syed and David are sitting at equal distances from the others, ∆ ASD is an equilateral triangle.

Then, drawing the perpendicular bisector of SD from its midpoint M, it will pass through O as well as A.
Suppose, SM = x m
∴ SD = 2SM = 2xm
Area of equilateral ∆ ASD = \(\frac{\sqrt{3}}{4}\) (side)²
∴ Area of equilateral ∆ ASD = \(\frac{\sqrt{3}}{4}\) × (2x)²
∴ Area of equilateral ∆ ASD = √3x² …………. (1)
In ∆ OMS, ∠M = 90°
∴ OM² = OS² – SM² = (20)² – (x)² = 400 – x²
∴ OM = \(\sqrt{400-x^{2}}\)
Now, area of ∆ OSD = \(\frac{1}{2}\) × SD × OM
∴ Area of ∆ OSD = \(\frac{1}{2}\) × 2x × \(\sqrt{400-x^{2}}\)
∴ Area of ∆ OSD = x\(\sqrt{400-x^{2}}\) …………….. (2)
Here, ∆ OAS, ∆ OSD and ∆ ODA are congruent triangles.
Area of ∆ ASD = Area of ∆ OAS + Area of ∆ OSD + Area of ∆ ODA
∴ Area of ∆ ASD = 3 × Area of ∆ OSD
∴ √3 ∙ x<sup2 = 3 × x\(\sqrt{400-x^{2}}\)
∴x = √3 ∙ \(\sqrt{400-x^{2}}\)
∴ x² = 3(400 – x²2)
∴ x²= 1200 – 3x²
∴ 4x² = 1200
∴x² = 300
∴x= 10 √3
SD = 2x = 2 × 10 √3 = 20 √3 m
Thus, the length of the string of each phone is 20 √3m.

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 12 Algebraic Expressions Ex 12.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.2

1. Fill in the blanks :

(i) 5y + 7y = ……………..
(ii) 3xy + 2xy = ……………..
(iii) 12a² – 7a² = ……………..
(iv) 8mn² – 3mn² = ……………..
Solution:
(i) 12y
(ii) 5xy
(iii) 5a²
(iv) 5mn²

2. Add the following algebraic expressions 

(a) 3xy², 7xy²
Solution:
Given terms are like terms. Their coefficients are 3 and 7.
Required sum is given as :
3xy² + 7xy² = (3 + 7) xy²
= 10xy²

(b) 7x, – 3x, 2x
Solution:
7x + (- 3x) + 2x = (7 – 3 + 2) x
= 6x

(c) 12p²q, 3p²q, – 5p²q
Solution:
(12p²q) + (3p²q) + (- 5p²q)
= (12 + 3 – 5) p²q
= 10p²q

(d) 3x², – 8x², – 5x², 13x²
Solution:
3x² + (- 8x)² + (- 5x)² + 13x²
= (3 – 8 – 5 + 13) x²
= 3x²

3. Add the following algebraic expressions.

(a) x + y and 2x – 3y
Solution:
(a) Horizontal method:
(x + y) + (2x – 3y)
= x + 2x + y – 3y
= 3x – 2y

Column method:

(b) 5a + 7b and 3a – 2b
Solution:
Horizontal method:
(5a + 7b) + (3a – 2b)
= 5a + 3a + 7a – 2b
= 8a + 5b.

Column method:

(c) 3m + 2n, 7m – 8n, 2m – n
Solution:
Horizontal method:
(3m + 2n) + (7m – 8n) + (2m – n)
= 3m + 7m + 2m + 2n – 8n – n
= 12m – 7n

Column method:

(d) 3x² + 2x – 7 and 5x² – 7x + 8
Solution:
Horizontal method:
(3x² + 2x – 7) + (5x² – 7x + 8)
= 3x² + 5x² + 2x – 7x – 1 + 8
= 8x² – 5x + 1

Column method:

(e) m² + 2n² – p², – 3m² + n² + 2p² and 4m² – 3n² + 5p²
Solution:
Horizontal method:
(m² + 2n² – p²) + (- 3m² + n² + 2p²) + (4m² – 3n² + 5p²)
= m² – 3m² + 4m² + 2n² + n² – 3n² – p² + 2p² + 5p²
= 2m² + 0n² + 6p²

Column method:

(f) 3xy + 7x² – 2y², 2xy + y² and 2x² + y²
Solution:
Horizontal method:
(3xy + 7x² – 2y²) + (2xy + y²) + (2x² + y²)
= 3xy + 2xy + 7x² + 2x² – 2y² + y² + y²
= 5xy + 9x² + 0y²

Column method:

4. Simplify the following algebraic expressions by combining like terms.

(a) -5ax + 3xy + 2xy – 8ax
Solution:
– 5ax + 3xy + 2xy – 8ax
= – 5ax – 8ax + 3xy + 2xy
= – 13ax + 5xy.

(b) 3m – 2n + 5m – 3m + 8n
Solution:
3m – 2n + 5m – 3m + 8n
= 3m + 5m – 3m – 2n + 8n
= 5m + 6 n.

(c) 3pq – 15r² – 3l²m² + 2r² + 2l²m² – 5pq
Solution:
3pq – 15r² – 3l²m² + 2r² + 2l²m² – 5pq
= 3pq – 5pq – 15r² + 2r² – 3l²m² + 2l²m²
= – 2pq – 13r² – 2l²m².

(d) 4x³ + 7x² – 3x + 2 – 2x³ – 2x² + 7x – 3
Solution:
4x³ + 7x² – 3x + 2 – 2x³ – 2x² + 7x – 3
= 4x³ – 2x³ + 7x² – 2x² – 3x + 7x + 2 – 3
= 2x³ + 5x² + 4x – 1.

5. Subtract the algebraic expressions.

(a) – 3x² from 7x²
Solution:
7x² – (- 3x²) = 7x² + 3x² = 10x²

(b) – 3ab from 10ab
Solution:
10ab – (- 3ab) = 10ab + 3ab = 13 ab

(c) a + b from a – b
Solution:
(a – b) – (a+ b)
= a – b – a – b
= -2b

(d) 15m + 10n from 2m – 16n
Solution:
2m – 6n – (15m + 10n)
= 2m – 15m – 6n – 10n
= – 13m – 16n

(e) 2x + 8y – 3z from – 3x + 2y + z
Solution:
– 3x + 2y + z – (2x + 8y – 3z)
= – 3x + 2y + z – 2x – 8y + 3z
= – 5x – 6y + 4z

(f) 18m² + 3n² – 2mn – 7 from 3m² – 2n² + 8mn – 8m + 4
Solution:
(3m² – 2n² + 8mn – 8m + 4) – (18m² + 3n² – 2mn – 7)
= 3m² – 2n² + 8mn – 8m + 4 – 18m² – 3n² + 2mn + 7
= 3m² – 18m² – 2n² – 3n² + 8mn + 2mn – 8m + 4 + 7
= – 15m² – 5n² + 10mn – 8m + 11

6. What should be subtracted from l – 2m + 5n to get 2l – 3m + 4n ?
Solution:
(l – 2m + 5n) – (2l – 3m + 4n)
= l – 2l – 2m + 3m + 5n – 4n
= -l + m + n.
Hence, -l + m + n should be subtracted.

7. What should be added to 3x² + 2xy – y² to obtain x² – 7xy + 3y² ?
Solution:
(x² – 7xy + 3y²) – (3x² + 2xy – y²)
= x² – 3x² – 7xy – 2xy + 3y² + y²
= – 2x² – 9xy + 4y².

8. Subtract 3a² + 2b² – 8ab + 8 from the sum of a² – b² + 7ab + 3 and 2a² + 4b² – 18ab + 7
Solution:
First add a² – b² + 7ab + 3 and 2a² + 4b² – 18ab + 7
(a² – b² + 7ab + 3) + (2a² + 4b² – 18ab + 7)
= a² + 2a² – b² + 4b² + 7ab – 18ab + 3 + 7
= 3a² + 3b² – 11ab + 10 …… (1)
Now we subtract 3a² + 2b² – 8ab + 8 from (1)
3a² + 3b² – 11ab + 10 – (3a² + 2b² – 8ab + 8)
= 3a² – 3a² + 3b² – 2b² – 11ab + 8ab + 10 – 8
= 0a² + b² – 3ab + 2
= b² – 3ab + 2

9. How much x² + 3xy + y² is less than 2x² + 5xy – y2 ?
Solution:
(2x² + 5xy – y²) – (x² + 3xy + y²)
= 2x² – x² + 5xy – 3xy – y² – y²
= x² + 2xy – 0y²
Hence, x² + 3xy + y² is less than 2x² + 5xy – y² by x² + 2xy – 2y².

10. Multiple Choice Questions :

Question (i).
The algebraic expression for “Number 5 added to three times the product of numbers m and n” is.
(a) 5 + 3mn
(b) 3 + 5mn
(c) (5 + 3) mn
Answer:
(a) 5 + 3mn

Question (ii).
The sum of algebraic expressions 3x + 11 and 2x – 7 is
(a) 5x + 4
(b) x + 4
(c) 5x – 18
Answer:
(a) 5x + 4

Question (iii).
Subtraction of a + b from 2a + 3b.
(a) a + 2b
(b) – a – 2b
(c) 3a + 4b
(d) a + b
Answer:
(a) a + 2b

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 10 Circles Ex 10.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 10 Circles Ex 10.3

Question 1.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Answer:

Thus, given a pair of circles, the maximum number of common points they have is 2.

Question 2.
Suppose you are given a circle. Give a construction to find its centre.
Answer:

• In the given circle, draw chords AB and BC with one endpoint B in common.
• Draw l-the perpendicular bisector of AB and m-the perpendicular bisector of BC.
• Let l and m intersect at O.
• Then, O is the centre of the given circle.

Note: Here, any two chords without an end-point in common can be drawn.

Question 3.
If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
Answer:

Here, two circles with centre O and P intersect each other at points A and B.
AB and OP intersect at M.
In ∆ OAP and ∆ OBR
OA = OB (Radii of the circle with centre O)
PA = PB (Radii of the circle with centre P).
OP = OP (Common)
∴ ∆ OAP ≅ ∆ OBP (SSS rule)
∴ ∠ AOP = ∠ BOP (CPCT)
∴ ∠ AOM = ∠BOM
Now, in ∆ AOM and ∆ BOM,
AO = BO (Radii of the circle)
∠ AOM = ∠ BOM
OM = OM (Common)
∴ ∆ AOM = ∆ BOM (SAS rule)
∴ AM = BM and ∠ AMO = ∠ BMO (CPCT)
But, ∠AMO + ∠BMO = 180° (Linear pair)
∴ ∠ AMO = ∠ BMO = \(\frac{180^{\circ}}{2}\) = 90°
Thus, line OM is the perpendicular bisector of AB.
Hence, line OP is the perpendicular bisector of AB.
Thus, the centres O and P of the circle intersecting in points A and B lie on the perpendicular bisector of common chord AB.

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 10 Circles Ex 10.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 10 Circles Ex 10.2

Question 1.
Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
Answer:

Two circles with centres O and P are congruent. Moreover, chord AB of the circle with centre
O and chord CD of the circle with centre P are congruent.
In ∆ OAB and ∆ PCD,
OA = PC and OB = PD (Radii of congruent circles)
And, AB = CD (Given)
∴ ∆ OAB ≅ ∆ PCD (SSS rule)
∴ ∠AOB = ∠ CPD
Thus, equal chords of congruent circles subtend equal angles at their centres.

Question 2.
Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
Answer:

Two circles with centres O and P are congruent. Moreover, ∠ AOB subtended by chord AB of the circle with centre O and ∠CPD subtended by chord CD of the circle with centre P at their respective centres are equal.
In ∆ OAB and ∆ PCD,
OA = PC and OB = PD (Radii of congruent circles)
And, ∠AOB = ∠CPD (Given)
∴ ∆ OAB ≅ ∆ PCD (SAS rule)
∴ AB = CD
Thus, if chords of congruent circles subtend equal angles at their centres, then the chords are equal.

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 10 Circles Ex 10.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 10 Circles Ex 10.1

Question 1.
Fill in the blanks :
(i) The centre of a circle lies in ……………………….. of the circle, (exterior/interior)
Answer:
interior

(ii) A point, whose distance from the centre of a circle is greater than its radius lies in ………………….. of the circle, (exterior/interior)
Answer:
exterior

(iii) The longest chord of a circle is a ………………………. of the circle.
Answer:
diameter

(iv) An arc is a ……………….. when its ends are the ends of a diameter.
Answer:
semicircle

(v) Segment of a circle is the region between an arc and …………………………… of the circle.
Answer:
a chord

(vi) A circle divides the plane, on which it lies, in ………………………….. parts.
Answer:
three

Question 2.
Write True or False. Give reasons for your answers.
(i ) Line segment joining the centre to any point on the circle is a radius of the circle.
Answer:
The given statement is true, because according to the definition of a radius, a line segment joining the centre to any point on the circle is a radius of the circle.

(ii) A circle has only finite number of equal chords.
Answer:
The given statement is false, because a circle has infinitely many equal chords, e.g., all the diameters of a circle are chords and they are all equal and uncountable.

(iii) If a circle is divided into three equal arcs, each is a major arc.
Answer:
The given statement is false, because if a circle is divided into three equal parts, each part is a minor arc.

(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
Answer:
The given statement is true, because a chord of a circle which is twice as long as its radius passes through the centre of the circle and a chord passing through the centre is called a diameter of the circle.

(v) Sector is the region between the chord and its corresponding arc.
Answer:
The given statement is false, because the region between a chord an corresponding arc is called a segment, not a sector.

(vi) A circle is a plane figure.
Answer:
The given statement is true, because circle is a collection of all the points in a plane which are at a fixed distance from a fixed point in the plane.

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 6 Decimals Ex 6.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 6 Decimals Ex 6.2

1. Convert the following decimal numbers into fractions and reduce it to lowest form.

Question (i)
1.4
Solution:
1.4 = \(\frac{14}{10}=\frac{14 \div 2}{10 \div 2}\)
(H.C.F. of 14 and 10 is 2)
= \(\frac {7}{5}\)

Question (ii)
2.25
Solution:
2.25 = \(\frac{225}{100}=\frac{225 \div 25}{100 \div 25}\)
(H.C.F. of 225 and 100 is 25)
= \(\frac {9}{4}\)

Question (iii)
18.6
Solution:
18.6 = \(\frac{186}{10}=\frac{186 \div 2}{10 \div 2}\)
(H.C.F. of 186 and 10 is 2)
= \(\frac {93}{5}\)

Question (iv)
4.04
Solution:
4.04 = \(\frac{404}{100}=\frac{404 \div 4}{100 \div 4}\)
(H.C.F. of 404 and 100 is 4)
= \(\frac {101}{25}\)

Question (v)
21.6
Solution:
21.6 = \(\frac{216}{10}=\frac{216 \div 2}{10 \div 2}\)
(H.C.F. of 216 and 10 is 2)
= \(\frac {108}{5}\)

2. Convert the following fractions into decimal numbers:

Question (i)
\(\frac {7}{100}\)
Solution:
\(\frac {7}{100}\) = 0.07
(Here denominator is 100)

Question (ii)
\(\frac {12}{10}\)
Solution:
\(\frac {12}{10}\) = 1.2
(Here denominator is 10)

Question (iii)
\(\frac {215}{100}\)
Solution:
\(\frac {215}{100}\) = 2.15
(Here denominator is 100)

Question (iv)
\(\frac {18}{1000}\)
Solution:
\(\frac {18}{1000}\) = 0.018
(Here denominator is 1000)

Question (v)
\(\frac {245}{10}\)
Solution:
\(\frac {245}{10}\) = 24.5
(Here denominator is 10)

3. Convert the following fractions into decimal numbers by equivalent fraction method:

Question (i)
\(\frac {5}{2}\)
Solution:
Here denominator is 2.
Convert into equivalent fraction with denominator 10 by multiplying it by 5.
∴ \(\frac{5}{2}=\frac{5 \times 5}{2 \times 5}=\frac{25}{10}\) = 2.5

Question (ii)
\(\frac {3}{4}\)
Solution:
Here denominator is 4.
Convert into equivalent fraction with denominator 100 by multiplying it by 25.
∴ \(\frac{3}{4}=\frac{3 \times 25}{4 \times 25}=\frac{75}{100}\) = 0.75

Question (iii)
\(\frac {28}{5}\)
Solution:
Here denominator is 5.
Convert into equivalent fraction with denominator 10 by multiplying it by 2.
∴ \(\frac{28}{5}=\frac{28 \times 2}{5 \times 2}=\frac{56}{10}\) = 5.6

Question (iv)
\(\frac {135}{20}\)
Solution:
Here denominator is 20.
Convert into equivalent fraction with denominator 100 by multiplying it by 5.
∴ \(\frac{135}{20}=\frac{135 \times 5}{20 \times 5}=\frac{675}{100}\)
= 6.75

Question (v)
\(\frac {17}{4}\)
Here denominator is 4.
Convert into equivalent fraction with denominator 100 by multiplying it by 25.
∴ \(\frac{17}{4}=\frac{17 \times 25}{4 \times 25}=\frac{425}{100}\)
= 4.25

4. Convert the following fractions into decimals by long division method:

Question (i)
\(\frac {17}{2}\)
Solution:

= 8.5

Question (ii)
\(\frac {33}{4}\)
Solution:

= 8.25

Question (iii)
\(\frac {76}{5}\)
Solution:

= 15.2

Question (iv)
\(\frac {24}{25}\)
Solution:

= 0.96

Question (v)
\(\frac {5}{8}\)
Solution:

= 0.625

5. Represent the following decimals on number line:

Question (i)
(i) 0.7
(ii) 1.6
(iii) 3.7
(iv) 6.3
(v) 5.4
Solution:

6. Write three decimal numbers between:

Question (i)
1.2 and 1.6
Solution:
Three decimal numbers between 1.2 and 1.6 are:
1.3, 1.4, 1.5

Question (ii)
2.8 and 3.2
Solution:
Three decimal numbers between 2.8 and 3.2 are:
2.9, 3, 3.1

Question (iii)
5 and 5.5.
Solution:
Three decimal numbers between 5 and 5.5 are:
5.1, 5.2, 5.3, 5.4.

7. Which number is greater:

Question (i)
0.4 or 0.7
Solution:

Since, 7 > 4
So, 0.7 > 0.4

Question (ii)
2.6 or 2.5
Solution:

Since, 6 > 5
So, 2.6 > 2.5

Question (iii)
1.23 or 1.32
Solution:

Since, 3 > 2
So, 1.32 > 1.23

Question (iv)
12.3 or 12.4
Solution:

Since, 4 > 3
So, 12.4 > 12.3

Question (v)
18.35 or 18.3
Solution:

Since, 5 > 0
So, 18.35 > 18.30

Question (vi)
12 or 1.2
Solution:

Since, 12 > 1
So, 12 > 1.2

Question (vii)
5.06 or 5.061
Solution:

Since, 1 > 0
So, 5.061 > 5.060

Question (viii)
2.34 or 23.3
Solution:

Since, 23 > 2
So, 23.3 > 2.34

Question (ix)
13.08 or 13.078
Solution:

Since, 8 > 7
So, 13.08 > 13.078

Question (x)
2.3 or 2.03.
Solution:

Since, 3 > 0
So, 2.3 > 2.03

8. Arrange the decimal numbers in ascending order:

Question (i)
2.5, 2, 1.8, 1.9
Solution:
Ascending order is :
1.8, 1.9, 2, 2.5

Question (ii)
3.4, 4.3, 3.1, 1.3
Solution:
Ascending order is :
1.3, 3.1, 3.4, 4.3

Question (iii)
1.24, 1.2, 1.42, 1.8.
Solution:
Ascending order is :
1.2, 1.24, 1.42, 1.8.

9. Arrange the decimal numbers in descending order:

Question (i)
4.1, 4.01, 4.12, 4.2
Solution:
Descending order is :
4.2, 4.12, 4.1, 4.01

Question (ii)
1.3, 1.03, 1.003, 13
Solution:
Descending order is :
13, 1.3, 1.03, 1.003

Question (iii)
8.02, 8.2, 8.1, 8.002.
Solution:
Descending order is :
8.2, 8.1, 8.02, 8.002.

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 9 Areas of Parallelograms and Triangles MCQ Questions with Answers.

PSEB 9th Class Maths Chapter 9 Areas of Parallelograms and Triangles MCQ Questions

Multiple Choice Questions and Answer

Answer each question by selecting the proper alternative from those given below each question to make the statement true:

Question 1.
Area of a parallelogram = ………………….
A. \(\frac{1}{2}\) × base × corresponding altitude
B. \(\frac{1}{2}\) × the product of diagonals
C. base × corresponding altitude
D. \(\frac{1}{2}\) × the product of adjacent sides.
Answer:
C. base × corresponding altitude

Question 2.
Area of a triangle = ……………………
A. base × corresponding altitude
B. base + corresponding altitude
C. \(\frac{1}{2}\) × base × corresponding altitude
D. 2 × base × corresponding altitude
Answer:
C. \(\frac{1}{2}\) × base × corresponding altitude

Question 3.
ABCD is a rectangle. If AB = 10 cm and ar (ABCD) = 150 cm², then BC = ………………….. cm.
A. 7.5
B. 15
C. 30
D. 12
Answer:
B. 15

Question 4.
ABCD is a square. If ar (ABCD) = 36 cm², then AB = ………………… cm.
A. 18
B. 9
C. 6
D. 12
Answer:
C. 6

Question 5.
In ∆ ABC, BC = 10 cm and the length of altitude AD is 5 cm. Then, ar (ABC) = …………………. cm².
A. 50
B. 100
C. 25
D. 15
Answer:
C. 25

Question 6.
In ∆ ABC, AD is an altitude. If BC = 8 cm and ar (ABC) = 40 cm², then AD = …………………. cm.
A. 5
B. 10
C. 15
D. 20
Answer:
B. 10

Question 7.
In ∆ PQR, QM is an altitude and PR is the hypotenuse. If PR = 12 cm and QM = 6 cm, then ar (PQR) = ……………………. cm².
A. 18
B. 72
C. 36
D. 24
Answer:
C. 36

Question 8.
In ∆ XYZ, XZ is the hypotenuse. If XY = 8cm and YZ = 12 cm, then ar (XYZ) = ……………….. cm².
A. 20
B. 40
C. 96
D. 48
Answer:
D. 48

Question 9.
In parallelogram ABCD, AM is an altitude corresponding to base BC. If BC = 8 cm and AM = 6 cm, then ar (ABCD) = …………………. cm².
A. 48
B. 24
C. 12
D. 96
Answer:
A. 48

Question 10.
In parallelogram PQRS, QR = 10 cm and ar (PQRS) = 120 cm². Then, the length of altitude PM corresponding to base QR is ……………………… cm.
A. 6
B. 12
C. 18
D. 24
Answer:
B. 12

Question 11.
For parallelogram ABCD, ar (ABCD) = 48 cm².
Then, ar (ABC) = …………………….. cm².
A. 96
B. 48
C. 24
D. 12
Answer:
C. 24

Question 12.
ABCD is a rhombus. If AC = 6 cm and BD = 9 cm, then ar (ABCD) = ………………….. cm².
A. 15
B. 7.5
C. 54
D. 27
Answer:
D. 27

Question 13.
PQRS is a rhombus. If ar (PQRS) = 40 cm² and PR = 8 cm, then QS = ………………….. cm.
A. 20
B. 10
C. 25
D. 40
Answer:
B. 10

Question 14.
In ∆ PQR, ∠Q = 90°, PQ = 5 cm and PR = 13 cm.
Then, ar (PQR) = …………………….. cm².
A. 15
B. 30
C. 45
D. 60
Answer:
B. 30

Question 15.
In ∆ ABC, P Q and R are the midpoints of AB, BC and CA respectively. If ar (ABC) = 32 cm²,
then ar (PQR) = ………………………. cm².
A. 128
B. 16
C. 8
D. 64
Answer:
C. 8

Question 16.
In ∆ ABC, P, Q and R are the midpoints of AB, BC and CA respectively. If ar (ABC) = 32 cm², then ar (PBCR) = ………………….. cm².
A. 10
B. 20
C. 30
D. 40
Answer:
C. 30

Question 17.
In ∆ ABC, P, Q and R are the midpoints of AB, BC and CA respectively. If ar (PBQR) = 36 cm², then ar (ABC) = ……………………….. cm².
A. 18
B. 36
C. 54
D. 72
Answer:
D. 72

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.4

Question 1.
Parallelogram ABCD and rectangle ABEF are on the, same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.

Rectangle ABEF is a parallelogram too.
Now, parallelograms ABCD and ABEF are on the same base AB and they have equal areas. Hence, they are between the same parallels FC and AB.
In ∆ AFD, ∠F, being an angle of rectangle ABEF, is a right angle and so, AD is the hypotenuse.
∴ AD > AF
∴ AD + AB > AF + AB
∴ 2 (AD + AB) > 2 (AF + AB)
∴ Perimeter of parallelogram ABCD > Perimeter of rectangle ABEF

Question 2.
In the given figure, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you now answer the question that you have left in the ‘Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
[Remark : Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide AABC into n triangles of equal areas.]

Answer:
Here, in ∆ ABE, D is a point on BE such that BD = DE.
So, in ∆ ABE, D is the midpoint of BE and AD is a median.
∴ ar (ABD) = ar (ADE) ……………… (1)
Similarly, in A ADC, E is the midpoint of DC and AE is a median.
∴ ar (ADE) = ar (AEC) ……………. (2)
From (1) and (2),
ar (ABD) = ar (ADE) = ar (AEC)
Thus, in ∆ ABC, by joining the points of trisection of BC, i.e., D and E to vertex A, the triangle is divided into ∆ ABD, ∆ ADE and ∆ AEC which have the same area.

Now, the answer to the question which was left unanswered in the ‘Introduction’ is ‘Yes’. The manner in which Budhia divided her field, the area of all the three parts are equal.

Question 3.
In the given figure, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).

Answer:
Opposite sides of a parallelogram are equal.
∴ In parallelogram ABCD, AD = BC, in parallelogram DCFE, DE = CF and in parallelogram ABFE, AE = BF.
Now, in ∆ ADE and ∆ BCE
AD = BC, DE = CF and AE = BE
∴ By SSS rule, ∆ ADE = ∆ BCF
∴ ar (ADE) = ar (BCF)

Question 4.
In the given figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at E show that ar (BPC) = ar (DPQ).
[Hint: Join AC.]

Answer:
Join AC.
In parallelogram ABCD, BC || AD and BC = AD.
BC is produced to point Q such that AD = CQ.
Thus, AD = CQ and AD || CQ.
∴ Quadrilateral ACQD is a parallelogram.
Diagonals of a parallelogram divide it into four triangles of equal areas.
∴ ar (DPQ) = ar (DPA) = ar (APC) = ar (CPQ)
∴ ar (DPQ) = ar (APC) ……………. (1)
Now, ∆ APC and ∆ BPC are on the same base PC and between the same parallels PC and AB.
∴ ar (APC) = ar (BPC) ………….. (2)
From (1) and (2),
ar (BPC) = ar (DPQ)

Question 5.
In the given figure, ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that
(i) ar (BDE) = \(\frac{1}{4}\)ar (ABC)
(ii) ar (BDE) = \(\frac{1}{2}\)ar (BAE)
(iii) ar (ABC) = 2ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v ) ar (BFE) = 2ar (FED)
(vi) ar (FED) = \(\frac{1}{8}\)ar (AFC)
[Hint: Join EC and AD. Show that BE || AC and DE || AB, etc.]

Answer:
Join EC and AD.
In equilateral ∆ ABC, ∠ ACB = 60°
In equilateral ∆ BDE, ∠ DBE = 60°
∴ ∠ CBE = 60°
Thus, ∠ ACB = ∠ CBE
But, ∠ ACB and ∠ CBE are alternate angles formed by transversal BC of AC and BE and they are equal.
∴BE || AC .
Similarly, ∠ ABD = ∠ BDE = 60°
∴ DE || AB
Now, in ∆ ABC, D is the midpoint of BC.
Hence, AD is a median of ∆ ABC.
∴ ar (ADB) = ar (ADC) = \(\frac{1}{2}\)ar (ABC)
∆ ABC and AAEC are on the same base AC and between the same parallels AC and BE.
∴ ar (ABC) = ar (AEC)
∴ ar (ABC) = ar (ADC) + ar (EDC) + ar (AED) …………….. (1)
In ∆ EBC, ED is a median.
∴ ar (EDC) = ar (BDE) = \(\frac{1}{2}\)ar (EBC) ………………… (2)
∆ AED and ∆ BDE are on the same base DE and between the same parallels AB and DE.
∴ ar (AED) = ar (BDE) …………… (3)
From (1), (2) and (3),
ar (ABC) = \(\frac{1}{2}\)ar (ABC) + ar (BDE) + ar (BDE)
∴ ar (ABC) – \(\frac{1}{2}\) ar (ABC) = 2ar (BDE)
∴\(\frac{1}{2}\)ar (ABC) = 2ar (BDE)
∴ ar (BDE) = \(\frac{1}{4}\)ar (ABC) ….. Result (i)
∆ BAE and ∆ BCE are on the same base BE and between the same parallels BE and AC.
∴ ar (BAE) = ar (BCE) ……………. (4)
In ∆ BEC, ED is a median.
∴ ar (BDE) = \(\frac{1}{2}\)ar (BCE)
∴ ar (BDE) = \(\frac{1}{2}\)ar (BAE) [by (4)] ……. Result (ii)
The diagonals of trapezium ABED intersect at F.
∴ ar (AFD) = ar (BFE) ……………… (5)
The diagonals of trapezium ABEC intersect at F.
∴ ar (ABF) = ar (EFC) ………………….. (6)
In ∆ ABC, AD is a median. s
∴ ar (ABC) = 2ar (ADB) S
∴ ar (ABC) = 2[ar (ABF) + ar (AFD)l
∴ ar (ABC) = 2[ar (EFC) + ar (BFE)] [by (5) and (6)]
∴ ar (ABC) = 2ar (BEC) … Result (iii)
In trapezium ABED, AB || ED and diagonals intersect at F.
∴ ar (BFE) = ar (AFD) …….. Result (iv)
By result (i),
ar (BDE) = \(\frac{1}{4}\)ar (ABC)
∴ ar (BDE) = \(\frac{1}{4}\) 2ar (ABD)
∴ ar (BDE) = \(\frac{1}{2}\)ar (ABD)
∆ BDE and ∆ ABD have the common base s BD.
∴ Altitude on BD in ∆ BDE = \(\frac{1}{2}\) × altitude on BD in ∆ ABD.
Now, the altitude on base BD in ∆ BDE is the same as the altitude on base BF in ∆ BEF and the altitude on base BD in ∆ ABD is the same as the altitude on base FD in ∆ AFD.
∴ Altitude on base BF in ∆ BEF
= \(\frac{1}{2}\) × altitude on base FD in ∆ AFD.
But, ar (BFE) = ar (AFD) …Result (iv)]
∴ BF = 2 × FD
Now, in ∆ BFE and ∆ FED, the altitudes corresponding to base BF and FD respectively are the same.
∴ ar (BFE) = 2ar (FED) … Result (v)
Suppose, in ∆ ABD, the altitude on base BD = h.
∴ In ∆ AFC, the altitude on base FC = h.
Also, in ∆ BDE, the altitude on base BD = \(\frac{h}{2}\)
∴ In A FED, the altitude on base FD = \(\frac{h}{2}\).
Now, ar (FED) = \(\frac{1}{2}\) × FD × \(\frac{h}{2}\) = \(\frac{h \times \mathrm{FD}}{4}\).
∴ FD = \(\frac{4 {ar}(\mathrm{FED})}{h}\) ………….. (7)
and ar (AFC) = \(\frac{1}{2}\) × FC × h = \(\frac{h}{2}\) × FC
= \(\frac{h}{2}\) (CD + FD)
= \(\frac{h}{2}\) (BD + FD) [∵ BD = CD]
= \(\frac{h}{2}\) (BF + FD + FD)
= \(\frac{h}{2}\) (2FD + FD + FD) [∵ BF = 2FD]
= \(\frac{h}{2}\) × 4FD
∴ ar (AFC) = 2 × h × FD
= 2 × h × \(\frac{4 {ar}(\mathrm{FED})}{h}\) [by (7)]
∴ ar (AFC) = 8 ar (FED)
∴ ar (FED) = \(\frac{1}{8}\) ar (AFC) … Result (vi)

Question 6.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at E Show that
ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
[(Hint: From A and C, draw perpendiculars to BD.]
Answer:

Draw AM ⊥ BD and CN ⊥ BD, where M and N are points on BD.
∴ ar (APB) × ar (CPD)
= (\(\frac{1}{2}\) × PB × AM) × (\(\frac{1}{2}\) × PD × CN)
= (\(\frac{1}{2}\) × PB × CN) × (\(\frac{1}{2}\) × PD × AM)
Thus, ar (APB) × ar (CPD) = ar (APD) × ar (BPC)

Question 7.
P and Q are respectively the midpoints of sides AB and BC of a triangle ABC and R is the midpoint of AR show that
(i) ar (PRQ) = \(\frac{1}{2}\) ar (ARC)
(ii) ar (RQC) = \(\frac{3}{8}\) ar (ABC)
(iii) ar (PBQ) = ar (ARC)
Answer:

In ∆ ABC, AQ and CP are medians. In ∆ APC, CR is a median, In ∆ APQ, QR is a median. In ∆ PBC, PQ is a median, In ∆ RBC, RQ is a median.

(i) ar (PRQ) = ar(ARQ) }
= \(\frac{1}{2}\)ar (APQ)
= \(\frac{1}{2}\)ar (BPQ)
= \(\frac{1}{2}\)ar(PQC)
= \(\frac{1}{2}\) ∙ \(\frac{1}{2}\)ar (PBC)
= \(\frac{1}{4}\)ar (PBC)
= \(\frac{1}{4}\) ∙ \(\frac{1}{2}\)ar (ABC)
= \(\frac{1}{8}\)ar (ABC)
\(\frac{1}{2}\)ar (ARC) = \(\frac{1}{2}\) ∙ \(\frac{1}{2}\)ar(APC)
= \(\frac{1}{4}\)ar (APC)
= \(\frac{1}{4}\) ∙ \(\frac{1}{2}\)ar (ABC)
= \(\frac{1}{8}\)ar (ABC)
∴ar (PRQ) = \(\frac{1}{2}\)ar (ARC)

(ii) ar(RQC) = ar(RBQ)
= ar (PBQ) + ar (PRQ)
= \(\frac{1}{2}\)ar (PBC) + \(\frac{1}{8}\)ar (ABC)
= \(\frac{1}{2}\) ∙ \(\frac{1}{2}\)ar (ABC) + \(\frac{1}{8}\)ar (ABC)
= \(\frac{1}{4}\)ar (ABC) + \(\frac{1}{8}\)ar (ABC)
= \(\frac{3}{8}\)ar (ABC)

(iii) ar (PBQ) = \(\frac{1}{2}\)ar (PBC) = \(\frac{1}{2}\) ∙ \(\frac{1}{2}\)ar (ABC)
= \(\frac{1}{4}\)ar (ABC)
ar (ARC) = \(\frac{1}{2}\)ar (APC) = \(\frac{1}{2}\) ∙ \(\frac{1}{2}\)ar (ABC)
= \(\frac{1}{4}\)ar (ABC)
∴ ar (PBQ) = ar (ARC)

Question 8.
In the given figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN „ are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:
(i) ∆ MBC S ∆ ABD
(ii) ar (BYXD) = 2ar (MBC)
(iii) ar (BYXD) = ar (ABMN)
(iv) ∆ FCB ≅ ∆ ACE
( v ) ar (CYXE) = 2ar (FCB)
(vi) ar (CYXE) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler j! proof of this theorem in Class X.

Answer:
(i) ∠ ABM = ∠ CBD = 90°
∴ ∠ABM + ∠ABC = ∠CBD + ∠ABC
∴ ∠ MBC = ∠ ABD
In ∆ MBC and ∆ ABD,
MB = AB, ∠ MBC = ∠ ABD and BC = BD
∴ By SAS rule, ∆ MBC ≅ ∆ ABD

(ii) ar (BYXD) = 2ar (ABD)
∴ ar (BYXD) = 2ar (MBC) [∆ MBC ≅ ∆ ABD]

(iii) ar (BYXD) = 2ar (ABD)
ar (ABMN) = 2ar (MBC)
But, ar (MBC) = ar (ABD)
∴ ar (BYXD) = ar (ABMN)

(iv) ∠ FCA = ∠ ECB = 90°
∴ ∠FCA + ∠ACB = ∠ECB + ∠ACB
∴ ∠FCB = ∠ACE
In ∆ FCB and ∆ ACE,
FC = AC, ∠ FCB = ∠ACE and CB = CE
∴By SAS rule, ∆ FCB ≅ ∆ ACE

(v) ar (CYXE) = 2ar (ACE)
∴ar (CYXE) = 2ar (FCB) [∵ ∆ FCB ≅ ∆ ACE]

(vi) ar (CYXE) = 2ar (FCB)
and ar (ACFG) = 2ar (FCB)
∴ ar (CYXE) = ar (ACFG)

(vii) ar (BCED) = ar (CYXE) + ar (BYXD)
∴ ar (BCED) = ar (ACFG) + ar (ABMN) [By result (iii) and (vi)]
∴ ar (BCED) = ar (ABMN) + ar (ACFG)

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 12 Algebraic Expressions Ex 12.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1

1. Generate algebraic expressions for the following :

(i) The sum of a and b.
(ii) The number z multiplied by itself.
(iii) The product of x and y added to the product of m and n.
(iv) The quotient of p by 5 is multiplied by q.
(v) One half of z added to twice the number t.
(vi) Sum of squares of the number x and z.
(vii) Sum of the numbers x and z is subtracted from their product.
Solution:
(i) a + b
(ii) z²
(iii) xy + mn
(iv) \(\frac{p}{5} q\)
(v) \(2 t+\frac{z}{2}\)
(vi) x² + z²
(vii) xy – (x + y)

2. Separate constant terms and variable terms from the following :
7, xy, \(\frac{3 x^{2}}{2}, \frac{72}{3} z, \frac{-8 z}{3 x^{2}}\)
Solution:
Constant Terms 7, \(\frac {72}{3}\)
Variable Terms xy, \(\frac{3 x^{2}}{2}, \frac{72}{3} z, \frac{-8 z}{3 x^{2}}\)

3. Write the terms and factors for each of the following algebraic expression.
(a) 2x² + 3yz
(b) 15x²y + 3xy²
(c) -7xyz²
(d) 100pq + 10p²q²
(e) xy + 3x²y²
(f) -7x²yz + 3xy²z + 2xyz²
Solution:

Expression	Terms	Factors
(a) 2x2 + 3xy	2x2 3xy	2, x, x 3, x, y
(b) 15x2y + 3xy2	15x2y 3xy2	15, x, x, y 3, x, y, y
(c) -7xyz2	-7xyz2	-7, x, y, z, z
(d) 100pq + 10p2q2	100pq 10p2q2	100, p, q 10, p, p, q, q
(e) xy + 3x2y2	Xy 3x2y2	X, y 3, x, x, y, y
(f) -7x2yz + 3xy2z + 2 xyz2	-7x2yz 3xy2z 2xyz2	-7, x, x, y, z 3, x, y, y, z 2, x, y, z, z

4. Classify the following algebraic expression into monomial, binomial and trinomial.
(a) 7x + 3y
(b) 5 + 2x2y²z
(c) ax + by² + cz²
(d) 3x²y²
(e) 1 + x
(f) 10
(g) \(\frac {3}{2}\)p + \(\frac {7}{6}\)q
Solution:
(a) Binomial
(b) Binomial
(c) Trinomial
(d) Monomial
(e) Binomial
(f) Monomial
(g) Binomial.

5. Write numerical coefficient of each of the following algebraic expression.
(a) 2x
(b) \(\frac {-3}{2}\)xyz
(c) \(\frac {7}{2}\)x²p
(d) -p²q²
(e) -5mn²
Solution:
(a) 2
(b) \(\frac {-3}{2}\)
(c) \(\frac {7}{2}\)
(d) -1
(e) -5

6. State whether the given pairs of terms is of like or unlike terms.
(a) – 3y, \(\frac {7}{8}\)y
(b) – 32, – 32x
(c) 3x²y, 3xy²
(d) 14mn², 14mn²q
(e) 8pq, 32pq²
(f) 10, 15
Solution:
(a) Like
(b) Unlike
(c) unlike
(d) unlike
(e) unlike
(f) like

7. In the following algebraic expressions write the coefficient of :
(a) x in x²y
(b) xyz in 15x²yz
(c) 3pq² in 3p²q²r²
(d) m² in m² + n²
(e) xy in x²y² + 2x + 3
Solution:
(a) xy
(b) 15x
(c) pr²
(d) 1
(e) xy

8. Identify the terms and their factors in the following algebraic expressions by tree diagrams
(a) 12xy + 7x²
(b) p²q² + 3mn² – pqr
(c) 2x²y² + xyz² + zy
(d) \(\frac {3}{2}\)x³ + 2x²y² – 7y³
Solution:
(a)

(b)

(c)

(d)

9. Multiple Choice Questions :

Question (i).
An expression with only one term is called a
(a) Monomial
(b) Binomial
(c) Trinomial
(d) None of these
Answer:
(a) Monomial

Question (ii).
The coefficient of x in 8 – x + y is
(a) -1
(b) 1
(c) 8
(d) 0
Answer:
(a) -1

Question (iii).
Which of the following are like terms ?
(a) 7x, 12y
(b) 15x, 12x
(c) 3xy, 3x
(d) 2y, -2yx
Answer:
(c) 3xy, 3x

Question (iv).
Terms are added to form
(a) Expressions
(b) Variables
(c) Constants
(d) Factors
Answer:
(a) Expressions

Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 6 Decimals Ex 6.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 6 Maths Chapter 6 Decimals Ex 6.1

1. Write each of the following in figures:

Question (i)
Seventy-two point one four.
Solution:
Seventy-two point one four = 72.14

Question (ii)
Two hundred fifty-seven point zero eight
Solution:
Two hundred fifty-seven point zero eight = 257.08

Question (iii)
Eight point two five-six.
Solution:
Eight point two five six = 8.256

Question (iv)
Forty-five and twenty-three hundredths.
Solution:
Forty five and twenty three hundredths
= 45 + \(\frac {23}{100}\)
= 45.23

Question (v)
Six hundred twenty-one and two hundred fifty-three thousandths
Solution:
Six hundred twenty-one and two hundred fifty-three thousandths
= 621 + \(\frac {253}{1000}\)
= 621.253

Question (vi)
Twelve and eight thousandths.
Solution:
Twelve and eight thousandths
= 12 + \(\frac {8}{1000}\)
= 12.008

2. Write the following decimal numbers in words:

Question (i)
12.52
Solution:
12.52 = Twelve point five two or twelve and fifty-two hundredths.

Question (ii)
7.148
Solution:
7.148 = Seven point one four eight or seven and one hundred forty-eight thousandths.

Question (iii)
0.24
Solution:
0.24 = Zero Point two four or twenty-four hundredths.

Question (iv)
5.018
Solution:
5.018 = Five-point zero one eight or five and eighteen thousandths.

Question (v)
.009.
Solution:
.009 = Point zero zero nine or nine thousandths.

3. Write the following decimals in the place value table:

Question (i)
(i) 21.569
(ii) 0.64
(iii) 3.51
(iv) 14.087
(v) 3.002.
Solution:

Number	Thousands	Hundreds	Tens	Ones	Tenths	Hundredths	Thousandths
1. 21.569	–	–	2	1	5	6	9
2. 0.64	–	–	–	0	6	4	–
3. 3.51	–	–	–	3	5	1	–
4. 14.087	–	–	1	4	0	8	7
5. 3.002	–	–	–	3	0	0	2

4. Write the following as decimals:

Question (i)
40 + \(\frac {2}{10}\)
Solution:
40 + \(\frac {2}{10}\) = 40.2

Question (ii)
700 + 5 + \(\frac {3}{10}\) + \(\frac {4}{100}\)
Solution:
700 + 5 + \(\frac {3}{10}\) + \(\frac {4}{100}\) = 705.34

Question (iii)
100 + \(\frac {5}{100}\) + \(\frac {3}{1000}\)
Solution:
100 + \(\frac {5}{100}\) + \(\frac {3}{1000}\) = 10.053

Question (iv)
100 + \(\frac {7}{10}\) + \(\frac {4}{1000}\)
Solution:
100 + \(\frac {7}{10}\) + \(\frac {4}{1000}\) = 0.704

Question (v)
\(\frac {5}{1000}\)
Solution:
\(\frac {5}{1000}\) = 0.005

5. Write the decimals shown in the following place value table:

Question (i)

Thousands	Hundreds	Tens	Ones	Tenth	Hundredths	Thousandths
–	5	2	4	1	2	–
2	0	3	4	2	1	–
–	–	6	1	0	2	3
–	–	–	4	0	0	1
–	1	0	0	0	3

Solution:
(i) 524.12
(ii) 2034.21
(iii) 61.023
(iv) 4.001
(v) 100.03

6. Expand the following decimals.

Question (i)
2.5
Solution:
2.5 = 2 + 0.5
= 2 + \(\frac {5}{10}\)

Question (ii)
18.43
Solution:
18.43 = 10 + 8 + 0.4 + 0.03
= 10 + 8 + \(\frac {4}{10}\) + \(\frac {3}{100}\)

Question (iii)
4.05
Solution:
4.05 = 4 + 0.05
= 4 + \(\frac {5}{100}\)

Question (iv)
13.123
Solution:
13.123 = 10 + 3 + 0.1 + 0.02 + 0.003
= 10 + 3 + \(\frac {1}{10}\) + \(\frac {2}{100}\) + \(\frac {3}{1000}\)

Question (v)
245.456
Solution:
245.456 = 200 + 40 + 5 + 0.4 + 0.05 + 0.006
= 200 + 40 + 5 + \(\frac {4}{10}\) + \(\frac {5}{100}\) + \(\frac {6}{1000}\)

Question (vi)
20.057
Solution:
20.057 = 20 + 0.05 + 0.007
= 20 + \(\frac {5}{100}\) + \(\frac {7}{1000}\)