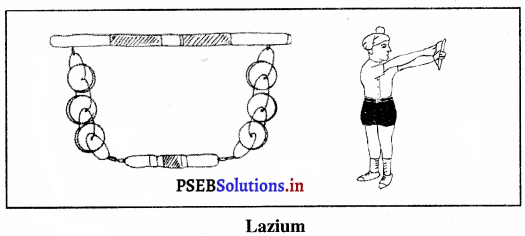
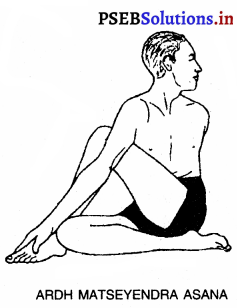
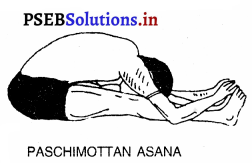
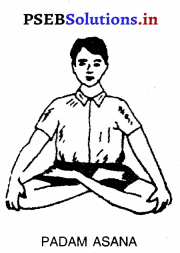
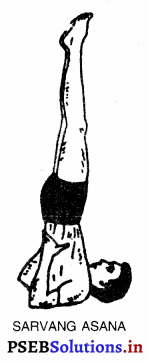
Punjab State Board PSEB 10th Class Social Science Book Solutions Geography Chapter 4 ਕੁਦਰਤੀ ਬਨਸਪਤੀ, ਜੀਵ-ਜੰਤੂ ਅਤੇ ਮਿੱਟੀਆਂ Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Social Science Geography Chapter 4 ਕੁਦਰਤੀ ਬਨਸਪਤੀ, ਜੀਵ-ਜੰਤੂ ਅਤੇ ਮਿੱਟੀਆਂ
SST Guide for Class 10 PSEB ਕੁਦਰਤੀ ਬਨਸਪਤੀ, ਜੀਵ-ਜੰਤੂ ਅਤੇ ਮਿੱਟੀਆਂ Textbook Questions and Answers
ਅਭਿਆਸ ਦੇ ਪ੍ਰਸ਼ਨ
I. ਹੇਠਾਂ ਲਿਖੇ ਹਰੇਕ ਪ੍ਰਸ਼ਨ ਦਾ ਸੰਖੇਪ ਉੱਤਰ ਇਕ ਸ਼ਬਦ ਜਾਂ ਇਕ ਵਾਕ ਵਿਚ ਦਿਓ-
(ਉ) ਕੁਦਰਤੀ ਬਨਸਪਤੀ
ਪ੍ਰਸ਼ਨ 1.
ਸਾਡੇ ਦੇਸ਼ ਵਿਚ ਮੌਜੂਦ ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਦੇ ਵਿਦੇਸ਼ੀ ਜਾਤਾਂ ਦੇ ਨਾਂ ਤੇ ਮਾਤਰਾ ਦੱਸੋ ।
ਉੱਤਰ-
ਦੇਸ਼ ਵਿਚ ਮੌਜੂਦ ਵਿਦੇਸ਼ੀ ਬਨਸਪਤੀ ਜਾਤਾਂ ਨੂੰ ਬੋਰੀਅਲ (Boreal) ਅਤੇ ਪੋਲੀਓ ਊਸ਼ਣ-ਖੰਡੀ (PaleoTropical) ਦੇ ਨਾਂ ਨਾਲ ਸੱਦਦੇ ਹਨ | ਭਾਰਤ ਦੀ ਬਨਸਪਤੀ ਵਿਚ ਵਿਦੇਸ਼ੀ ਬਨਸਪਤੀ ਦੀ ਮਾਤਰਾ 40% ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਬੰਗਾਲ ਦੀ ਦਹਿਸ਼ਤ ਕਿਸ ਬਨਸਪਤੀ ਕਿਸਮ ਨੂੰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਜਲ ਹਾਈਆਸਿੰਥ (Water Hyacinth) ਨਾਂ ਦੇ ਪੌਦੇ ਨੂੰ ‘ਬੰਗਾਲ ਦੀ ਦਹਿਸ਼ਤ’ (Terror of Bengal) ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਸਾਡੇ ਦੇਸ਼ ਵਿਚ ਸੰਸਾਰ ਦੇ ਮੁਕਾਬਲੇ ਕਿੰਨੇ ਪ੍ਰਤੀਸ਼ਤ ਭੂਮੀ ਜੰਗਲਾਂ ਨਾਲ ਢੱਕੀ ਹੋਈ ਹੈ ?
ਉੱਤਰ-
ਵਿਸ਼ਵ ਵਿਚ 29.5% ਭੂਮੀ ਜੰਗਲਾਂ ਨਾਲ ਢੱਕੀ ਹੋਈ ਹੈ । ਪਰੰਤੂ ਸਾਡੇ ਦੇਸ਼ ਵਿਚ ਭੂਮੀ ਦਾ ਸਿਰਫ਼ 22.7% ਹਿੱਸਾ ਜੰਗਲਾਂ ਨਾਲ ਢੱਕਿਆ ਹੋਇਆ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਦੇਸ਼ ਦੇ ਸਭ ਤੋਂ ਵੱਧ ਤੇ ਘੱਟ ਜੰਗਲੀ ਖੇਤਰ ਕਿਸ ਰਾਜ ਤੇ ਸੰਘੀ ਖੇਤਰ ਵਿਚ ਮਿਲਦੇ ਹਨ ?
ਉੱਤਰ-
ਸਭ ਤੋਂ ਵੱਧ ਜੰਗਲੀ ਖੇਤਰ-ਰਾਜ ਤਿਪੁਰਾ (59.6%).
ਸੰਘੀ ਖੇਤਰ-ਅੰਡੇਮਾਨ ਨਿਕੋਬਾਰ ਦੀਪ ਸਮੂਹ (94.6%)
ਸਭ ਤੋਂ ਘੱਟ ਜੰਗਲੀ ਖੇਤਰ-ਰਾਜ-ਪੰਜਾਬ (2.3%)
ਸੰਘੀ ਖੇਤਰ-ਦਿੱਲੀ (2.1%) ।
ਪ੍ਰਸ਼ਨ 5.
ਰਾਜ ਵਣ (State Forests) ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਰਾਜੇ ਵਣ (State Forests) ਉਹ ਵਣ ਹਨ ਜਿਸ ਤੇ ਕਿਸੇ ਰਾਜ ਸਰਕਾਰ ਦਾ ਏਕਾਧਿਕਾਰ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 6.
ਊਸ਼ਣ ਸਦਾਬਹਾਰ ਬਨਸਪਤੀ ਵਿਚ ਉੱਗਣ ਵਾਲੇ ਦਰੱਖ਼ਤਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਊਸ਼ਣ ਸਦਾਬਹਾਰ ਬਨਸਪਤੀ ਖੇਤਰ ਵਿਚ ਮਿਲਣ ਵਾਲੇ ਦਰੱਖ਼ਤਾਂ ਵਿਚ ਮਹੋਗਨੀ, ਬਾਂਸ, ਰਬੜ, ਨਾਰੀਅਲ, ਤਾੜ, ਰੋਜ਼ਵੁੱਡ, ਲੋਹਕਾਠ, ਬੈਂਤ, ਨਾਗਕੇਸਰ, ਚਪਲਾਂਸ, ਅੰਬ, ਮੈਚੀਲਸ ਅਤੇ ਕਦੰਬ ਆਦਿ ਮੁੱਖ ਹਨ ।
ਪ੍ਰਸ਼ਨ 7.
ਅਰਧ-ਖੁਸ਼ਕ ਪੱਤਝੜੀ ਬਨਸਪਤੀ ਦਾ ਵਿਨਾਸ਼ ਕਿਹੜੇ-ਕਿਹੜੇ ਤੱਤ ਕਰਦੇ ਹਨ ?
ਉੱਤਰ-
ਅਰਧ-ਖੁਸ਼ਕ ਪੱਤਝੜੀ ਬਨਸਪਤੀ ਦੇ ਵਿਨਾਸ਼ ਦਾ ਮੁੱਖ ਕਾਰਨ ਖੇਤੀ ਖੇਤਰ ਦਾ ਵਿਸਥਾਰ ਹੈ । ਜਿੱਥੇ ਕਿਤੇ ਖੇਤੀ ਯੋਗ ਭੂਮੀ ਮਿਲਦੀ ਹੈ ਉੱਥੇ ਇਸ ਬਨਸਪਤੀ ਨੂੰ ਭਾਰੀ ਮਾਤਰਾ ਵਿਚ ਕੱਟ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 8.
ਖ਼ੁਸ਼ਕ ਬਨਸਪਤੀ ਵਿਚ ਮਿਲਣ ਵਾਲੇ ਦਰੱਖ਼ਤਾਂ ਦੇ ਨਾਂ ਅਤੇ ਖੇਤਰ ਦੱਸੋ ।
ਉੱਤਰ-
ਖੁਸ਼ਕ ਬਨਸਪਤੀ ਵਿਚ ਮਿਲਣ ਵਾਲੇ ਦਰੱਖ਼ਤ, ਮੁੱਖ ਤੌਰ ‘ਤੇ ਕਿੱਕਰ, ਫਲਾਹੀ, ਜੰਡ, ਤਮਾਰਿਕਸ਼, ਰਾਮ ਬਾਂਸ, ਬੇਰ, ਨਿੰਮ, ਥੋਹਰ (ਕੈਕਟਸ) ਅਤੇ ਮੁੰਜ ਘਾਹ ਆਦਿ ਸ਼ਾਮਲ ਹਨ । ਇਹ ਬਨਸਪਤੀ ਮੁੱਖ ਰੂਪ ਨਾਲ ਪੱਛਮੀ ਰਾਜਸਥਾਨ, ਪੱਛਮੀ ਹਰਿਆਣਾ ਅਤੇ ਗੁਜਰਾਤ ਦੇ ਪੱਛਮੀ ਭਾਗਾਂ ਵਿਚ ਮਿਲਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 9.
ਜਵਾਰੀ ਬਨਸਪਤੀ ਦੇ ਦੂਸਰੇ ਨਾਂ ਕੀ ਹਨ ?
ਉੱਤਰ-
ਜਵਾਰੀ ਬਨਸਪਤੀ ਨੂੰ ਮੈਂਗਰੋਵ, ਦਲਦਲੀ (Swamps) ਸਮੁੰਦਰੀ ਕਿਨਾਰੇ ਵਾਲੀ ਜਾਂ ਸੁੰਦਰ ਵਣ (Sundervan) ਆਦਿ ਨਾਂਵਾਂ ਨਾਲ ਸੱਦਦੇ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 10.
ਪੂਰਬੀ ਹਿਮਾਲਿਆ ਵਿਚ 2500 ਮੀਟਰ ਤੋਂ ਵੱਧ ਉਚਾਈ ‘ਤੇ ਮਿਲਣ ਵਾਲੇ ਦਰੱਖਤਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਪੂਰਬੀ ਹਿਮਾਲਿਆ ਖੇਤਰ ਵਿਚ 2500 ਮੀਟਰ ਤੋਂ ਵੱਧ ਉਚਾਈ ‘ਤੇ ਮਿਲਣ ਵਾਲੇ ਦਰੱਖਤਾਂ ਵਿਚ ਮੁੱਖ ਤੌਰ ‘ਤੇ ਸਿਲਵਰ ਫਰ, ਪਾਈਨ, ਸਪਰੂਸ, ਦੇਵਦਾਰ, ਨੀਲਾ ਪਾਈਨ ਆਦਿ ਹਨ ।
ਪ੍ਰਸ਼ਨ 11.
ਦੱਖਣ ਦੀ ਪਠਾਰ ਵਿਚ ਪਰਬਤੀ ਬਨਸਪਤੀ ਕਿਹੜੇ-ਕਿਹੜੇ ਸਥਾਨਾਂ ‘ਤੇ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਦੱਖਣ ਦੀ ਪਠਾਰ ਵਿਚ ਪਰਬਤੀ ਬਨਸਪਤੀ ਬਸਤਰ, ਪੰਚਮੜੀ, ਮਹਾਂਬਲੇਸ਼ਰ, ਨੀਲਗਿਰੀ, ਪਲਨੀ, ਸ਼ਿਵਰਾਇ ਆਦਿ ਅਨਾਮਲਾਈ ਦੇ ਪਹਾੜੀ ਖੇਤਰਾਂ ਵਿਚ ਮਿਲਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 12.
ਕਿਹੜੇ-ਕਿਹੜੇ ਦਰੱਖ਼ਤਾਂ ਤੋਂ ਸਿਹਤਵਰਧਕ ਦਵਾਈਆਂ ਤਿਆਰ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਖੈਰ, ਸਿਨਕੋਨਾ, ਨਿੰਮ, ਸਰਪਗੰਧਾ ਝਾੜੀ, ਬੋਹੜ, ਆਂਵਲਾ ਆਦਿ ਦਰੱਖ਼ਤਾਂ ਤੋਂ ਸਾਨੂੰ ਸਿਹਤਵਰਧਕ ਦਵਾਈਆਂ ਪ੍ਰਾਪਤ ਹੁੰਦੀਆਂ ਹਨ ।
ਪ੍ਰਸ਼ਨ 13.
ਚਮੜਾ ਰੰਗਣ ਲਈ ਕਿਹੜੇ ਦਰੱਖ਼ਤਾਂ ਦੀ ਸਹਾਇਤਾ ਲਈ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਚਮੜਾ ਰੰਗਣ ਲਈ ਬਨਸਪਤੀ ਟੈਨਿਨ, ਮੈਂਗਰੋਵ, ਅਖਰੋਟ ਅਤੇ ਕਿੱਕਰ ਆਦਿ ਦੇ ਦਰੱਖ਼ਤਾਂ ਤੋਂ ਸਮੱਗਰੀ ਪ੍ਰਾਪਤ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।
(ਅ) ਜੀਵ-ਜੰਤੂ
ਪ੍ਰਸ਼ਨ 1.
ਜੀਵ-ਜੰਤੂ ਕਿੰਨੀ ਕਿਸਮ ਦੇ ਹੋ ਸਕਦੇ ਹਨ ?
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਜੀਵ-ਜੰਤੂਆਂ ਦੀਆਂ 76 ਹਜ਼ਾਰ ਜਾਤਾਂ ਮਿਲਦੀਆਂ ਹਨ ।
ਪ੍ਰਸ਼ਨ 2.
ਹਾਥੀ ਕਿਸ ਤਰ੍ਹਾਂ ਦੇ ਖੇਤਰਾਂ ਵਿਚ ਰਹਿਣਾ ਪਸੰਦ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-
ਹਾਥੀ ਵਧੇਰੇ ਵਰਖਾ ਅਤੇ ਸੰਘਣੇ ਜੰਗਲ ਵਾਲੇ ਖੇਤਰ ਵਿਚ ਰਹਿਣਾ ਪਸੰਦ ਕਰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
ਭਾਰਤ ਵਿਚ ਹਿਰਨਾਂ ਦੀਆਂ ਕਿਹੜੀਆਂ-ਕਿਹੜੀਆਂ ਕਿਸਮਾਂ ਮਿਲਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਮਿਲਣ ਵਾਲੀਆਂ ਹਿਰਨਾਂ ਦੀਆਂ ਜਾਤਾਂ ਚਾਰ-ਸਿੰਗਾ, ਕਾਲਾ ਹਿਰਨ, ਚਿਕਾਰਾ ਅਤੇ ਆਮ ਹਿਰਨ ਮੁੱਖ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 4.
ਦੇਸ਼ ਵਿਚ ਸ਼ੇਰ ਕਿਹੜੇ ਸਥਾਨਾਂ ‘ਤੇ ਵਧੇਰੇ ਮਿਲਦਾ ਹੈ ?
ਉੱਤਰ-
ਭਾਰਤੀ ਸ਼ੇਰ ਦਾ ਕੁਦਰਤੀ ਨਿਵਾਸ ਸਥਾਨ ਗੁਜਰਾਤ ਵਿੱਚ ਸੌਰਾਸ਼ਟਰ ਦੇ ਗਿਰ ਵਨ ਹਨ ।
ਪ੍ਰਸ਼ਨ 5.
ਹਿਮਾਲਿਆ ਵਿਚ ਮਿਲਣ ਵਾਲੇ ਜੀਵਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਹਿਮਾਲਿਆ ਵਿਚ ਜੰਗਲੀ ਭੇਡ, ਪਹਾੜੀ ਬੱਕਰੀ, ਸਾਕਿਨ (ਇਕ ਲੰਮੇ ਸਿੰਗਾਂ ਵਾਲੀ ਜੰਗਲੀ ਬੱਕਰੀ) ਅਤੇ ਟੈਪੀਰ ਆਦਿ ਜੀਵ-ਜੰਤੂ ਪਾਏ ਜਾਂਦੇ ਹਨ ਜਦਕਿ ਉੱਚੇ ਪਹਾੜੀ ਖੇਤਰਾਂ ਵਿਚ ਪਾਂਡਾ ਅਤੇ ਹਿਮਤੇਂਦੂਆ ਨਾਂ ਦੇ ਜੰਤੂ ਮਿਲਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 6.
ਸਾਡੇ ਦੇਸ਼ ਦੇ ਰਾਸ਼ਟਰੀ ਪਸ਼ੂ ਅਤੇ ਪੰਛੀ ਦਾ ਕੀ ਨਾਂ ਹੈ ?
ਉੱਤਰ-
ਸਾਡੇ ਦੇਸ਼ ਦਾ ਰਾਸ਼ਟਰੀ ਪਸ਼ੂ ਸ਼ੇਰ ਅਤੇ ਰਾਸ਼ਟਰੀ ਪੰਛੀ ਮੋਰ ਹੈ ।
ਪ੍ਰਸ਼ਨ 7.
ਦੇਸ਼ ਵਿਚ ਕਿਹੜੇ-ਕਿਹੜੇ ਜੀਵਾਂ ਦੇ ਖ਼ਤਮ ਹੋ ਜਾਣ ਦਾ ਡਰ ਹੈ ?
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਬਘਿਆੜ, ਗੈਂਡਾ, ਸੋਨ ਚਿੜੀ, ਸ਼ੇਰ ਆਦਿ ਜੀਵਾਂ ਦੇ ਖ਼ਤਮ ਹੋ ਜਾਣ ਦਾ ਡਰ ਹੈ ।
(ੲ) ਮਿੱਟੀਆਂ
ਪ੍ਰਸ਼ਨ 1.
ਮਿੱਟੀ ਦੀ ਪਰਿਭਾਸ਼ਾ ਦਿਓ ।
ਉੱਤਰ-
ਧਰਤੀ ਦੇ ਧਰਾਤਲ ਤੇ ਮਿਲਦੇ ਹਲਕੇ, ਢਿੱਲੇ ਅਤੇ ਅਸੰਗਠਿਤ ਚੱਟਾਨੀ ਰੇ ਅਤੇ ਬਰੀਕ ਜੀਵ-ਅੰਸ਼ ਦੇ ਸੰਯੁਕਤ ਮਿਸ਼ਰਨ ਨੂੰ ਮਿੱਟੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਮਿੱਟੀ ਕਿਵੇਂ ਬਣਦੀ ਹੈ ?
ਉੱਤਰ-
ਮਿੱਟੀ ਮੌਸਮੀ ਕਿਰਿਆਵਾਂ ਦੁਆਰਾ ਚੱਟਾਨਾਂ ਦੀ ਟੁੱਟ-ਭੱਜ ਨਾਲ ਬਣਦੀ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਮਿੱਟੀ ਦੇ ਮੂਲ ਪਦਾਰਥ ਕਿਹੜੇ-ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਮਿੱਟੀ ਦੇ ਮੂਲ ਤੱਤ ਹਨ-
- ਮੁੱਢਲੀ ਚੱਟਾਨ
- ਪੌਣ-ਪਾਣੀ
- ਖੇਤਰੀ ਢਲਾਣ
- ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਅਤੇ
- ਮਿਆਦ ।
ਪ੍ਰਸ਼ਨ 4.
ਕਾਲੀ ਮਿੱਟੀ ਵਿਚ ਕਿਹੜੇ-ਕਿਹੜੇ ਰਸਾਇਣਿਕ ਤੱਤ ਮਿਲਦੇ ਹਨ ?
ਉੱਤਰ-
ਕਾਲੀ ਮਿੱਟੀ ਵਿਚ ਮੁੱਖ ਤੌਰ ‘ਤੇ ਲੋਹਾ, ਪੋਟਾਸ਼, ਐਲੂਮੀਨੀਅਮ, ਚੂਨਾ ਅਤੇ ਮੈਗਨੀਸ਼ੀਅਮ ਆਦਿ ਤੱਤ ਪਾਏ ਜਾਂਦੇ ਹਨ ।
ਪਸ਼ਨ 5.
ਲੈਟਰਾਈਟ ਮਿੱਟੀ ਦੇਸ਼ ਦੇ ਕਿਹੜੇ-ਕਿਹੜੇ ਭਾਗਾਂ ਵਿਚ ਮਿਲਦੀ ਹੈ ?
ਉੱਤਰ-
ਲੈਟਰਾਈਟ ਮਿੱਟੀ ਵਿੰਧਿਆਚਲ, ਸਤਪੁੜਾ ਦੇ ਨਾਲ ਲਗਦੇ ਮੱਧ ਪ੍ਰਦੇਸ਼, ਉੜੀਸਾ, ਪੱਛਮੀ ਬੰਗਾਲ ਦੀਆਂ ਬੈਸਾਲਟਿਕ ਪਰਬਤ ਚੋਟੀਆਂ, ਦੱਖਣੀ ਮਹਾਂਰਾਸ਼ਟਰ, ਕਰਨਾਟਕ ਦੀਆਂ ਪੱਛਮੀ ਘਾਟ ਦੀਆਂ ਪਹਾੜੀਆਂ, ਕੇਰਲ ਵਿਚ ਮਾਲਾਬਾਰ ਅਤੇ ਸ਼ਿਲਾਂਗ ਦੇ ਪਠਾਰ ਦੇ ਉੱਤਰੀ ਅਤੇ ਪੂਰਬੀ ਭਾਗ ਵਿਚ ਮਿਲਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 6.
‘ਭੂੜ’ ਮਿੱਟੀਆਂ ਕਿੱਥੇ ਮਿਲਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਪੰਜਾਬ ਅਤੇ ਹਰਿਆਣਾ ਦੇ ਸਰਹੱਦੀ ਜ਼ਿਲ੍ਹਿਆਂ ਵਿਚ ।.
ਪ੍ਰਸ਼ਨ 7.
ਨਮਕੀਨ ਮਿੱਟੀਆਂ ਦੇਸ਼ ਦੇ ਵੱਖੋ-ਵੱਖਰੇ ਭਾਗਾਂ ਵਿਚ ਕਿਹੜੇ ਨਾਂਵਾਂ ਨਾਲ ਜਾਣੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਨਮਕੀਨ ਮਿੱਟੀ ਨੂੰ ਉੱਤਰ ਪ੍ਰਦੇਸ਼ ਵਿਚ ਔਸੜ ਜਾਂ ਰੇਹ’ ਅਤੇ ਪੰਜਾਬ ਵਿਚ ‘ਕੱਲਰ ਜਾਂ ਥੁੜ੍ਹ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 8.
ਚਾਹ ਵਾਲੀਆਂ ਮਿੱਟੀਆਂ ਦੇਸ਼ ਦੇ ਕਿਹੜੇ ਭਾਗਾਂ ਵਿਚ ਹੁੰਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਚਾਹ ਉਤਪਾਦਨ ਲਈ ਢੁੱਕਵੀਂ ਮਿੱਟੀ ਅਸਾਮ, ਹਿਮਾਚਲ ਪ੍ਰਦੇਸ਼ ਲਾਹੌਲ ਸਪਿਤੀ, ਕਿਨੌਰ), ਪੱਛਮੀ ਬੰਗਾਲ, ਦਾਰਜੀਲਿੰਗ, ਉਤਰਾਂਚਲ ਅਤੇ ਦੱਖਣ ਵਿਚ ਨੀਲਗਿਰੀ ਦੇ ਪਰਬਤੀ ਖੇਤਰਾਂ ਵਿਚ ਮਿਲਦੀ ਹੈ ।
ਸ਼ਨ 9.
ਮਿੱਟੀ ਦੇ ਕਟਾਅ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਭੌਤਿਕ ਤੱਤਾਂ ਦੁਆਰਾ ਧਰਾਤਲ ਦੀ ਉੱਪਰੀ ਪਰਤ ਦਾ ਹਟਾ ਦਿੱਤਾ ਜਾਣਾ ਮਿੱਟੀ ਦਾ ਕਟਾਓ ਅਖਵਾਉਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 10.
ਮਾਰੂਥਲ ਦੇ ਵਧਣ ਨੂੰ ਰੋਕਣ ਲਈ ਕਿਹੜੇ ਉਪਾਅ ਕੀਤੇ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਮਾਰੂਥਲ ਵਿਚ ਪੌਣਾਂ ਦੀ ਗਤੀ ਨੂੰ ਘੱਟ ਕਰਨ ਲਈ ਦਰੱਖ਼ਤਾਂ ਦੀਆਂ ਕਤਾਰਾਂ ਲਗਾਉਣੀਆਂ ਅਤੇ ਘਾਹ ਉਗਾਉਣਾ ।
II. ਹੇਠ ਲਿਖੇ ਹਰੇਕ ਪ੍ਰਸ਼ਨ ਦਾ ਉੱਤਰ ਲਗਪਗ 50-60 ਸ਼ਬਦਾਂ ਵਿਚ ਦਿਓ-
(ਉ) ਕੁਦਰਤੀ ਬਨਸਪਤੀ-
ਪ੍ਰਸ਼ਨ 1.
ਬਾਹਰੀ ਬਨਸਪਤੀ ਸਾਡੇ ਲਈ ਸਮੱਸਿਆ ਕਿਉਂ ਬਣ ਗਈ ਹੈ ? ਉਦਾਹਰਨਾਂ ਨਾਲ ਸਪੱਸ਼ਟ ਕਰੋ ।
ਉੱਤਰ-
ਭਾਰਤੀ ਬਨਸਪਤੀ ਦਾ 40 ਪ੍ਰਤੀਸ਼ਤ ਹਿੱਸਾ ਵਿਦੇਸ਼ੀ ਜਾਤਾਂ ਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਨੂੰ ਬੋਰੀਅਲ ਅਤੇ ਪੋਲੀਓ-ਊਸ਼ਣ ਖੰਡੀ ਜਾਤਾਂ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਹਨਾਂ ਵਿਚੋਂ ਵਧੇਰੇ ਪੌਦੇ ਸਜਾਵਟ ਲਈ ਡੈਕੋਰੇਟਿਵ ਪਲਾਂਟ) ਹਨ । ਸਾਡੇ ਦੇਸ਼ ਵਿਚ ਆਈ ਇਸ ਵਿਦੇਸ਼ੀ ਬਨਸਪਤੀ ਨਾਲ ਹੇਠ ਲਿਖੀਆਂ ਸ਼ਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਗਈਆਂ ਹਨ-
- ਇੱਥੋਂ ਦੇ ਗਰਮ ਖੁਸ਼ਕ ਮੌਸਮ ਦੇ ਕਾਰਨ ਦੇਸ਼ ਦੀਆਂ ਨਦੀਆਂ, ਤਲਾਬਾਂ, ਨਹਿਰਾਂ ਆਦਿ ਵਿਚ ਇਹਨਾਂ ਪੌਦਿਆਂ ਦੀ ਸੰਖਿਆ ਇੰਨੀ ਵੱਧ ਗਈ ਹੈ ਕਿ ਇਹਨਾਂ ਨੂੰ ਵਧਣ-ਫੁਲਣ ਤੋਂ ਰੋਕ ਸਕਣਾ ਅਸੰਭਵ ਜਿਹਾ ਹੋ ਗਿਆ ਹੈ ।
- ਇਹ ਵਿਦੇਸ਼ੀ ਪੌਦੇ ਸਥਾਨਕ ਲਾਭਕਾਰੀ ਬਨਸਪਤੀ ਦੇ ਵਿਕਾਸ ਵਿੱਚ ਰੁਕਾਵਟ ਬਣ ਗਏ ਹਨ । ਇਹ ਉਪਯੋਗੀ ਭੂਮੀ ਨੂੰ ਘੱਟ ਕਰਨ ਅਤੇ ਖ਼ਤਰਨਾਕ ਰੋਗਾਂ ਨੂੰ ਫੈਲਾਉਣ ਵਿਚ ਵੀ ਆਪਣਾ ਪ੍ਰਭਾਵ ਦਿਖਾ ਰਹੇ ਹਨ ।
- ਜਲ ਹਾਇਆਸਿੰਥ (Water Hyacinth) ਪੌਦੇ ਦੇ ਜਲ ਸੋਮਿਆਂ ਵਿਚ ਫੈਲ ਜਾਣ ਦੇ ਕਾਰਨ ਇਸ ਨੂੰ ‘ਬੰਗਾਲ ਦਾ ਡਰ’ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ “ਲੇਨਟਾਨਾ” ਨਾਂ ਦੇ ਪੌਦੇ ਨੇ ਦੇਸ਼ ਦੀਆਂ ਹਰੀਆਂ-ਭਰੀਆਂ ਚਰਾਗਾਹਾਂ ਅਤੇ ਵਣਾਂ ਵਿਚ ਤੇਜ਼ੀ ਨਾਲ ਫੈਲ ਕੇ ਆਪਣਾ ਪ੍ਰਭਾਵ ਜਮਾ ਲਿਆ ਹੈ ।
- ਪਾਰਥੇਨਿਯਮ ਘਾਹ ਜਾਂ ਕਾਂਗਰਸੀ ਘਾਹ ਨੇ ਵੀ ਤੇਜ਼ੀ ਨਾਲ ਦੇਸ਼ ਅੰਦਰ ਫੈਲ ਕੇ ਲੋਕਾਂ ਵਿਚ ਸਾਹ ਅਤੇ ਚਮੜੀ ਦੇ ਰੋਗਾਂ ਵਿਚ ਭਾਰੀ ਮਾਤਰਾ ਵਿਚ ਵਾਧਾ ਕੀਤਾ ਹੈ ।
- ਖਾਧ-ਅੰਨਾਂ ਦੀ ਕਮੀ ਦੇ ਦੌਰਾਨ ਆਯਾਤ ਕੀਤੀ ਗਈ ਕਣਕ ਦੇ ਦਾਣਿਆਂ ਨਾਲ ਆਏ ਅਣ-ਲੋੜੀਂਦੇ ਬੀਜ ਵੀ ਤੇਜ਼ੀ ਨਾਲ ਫੈਲੇ ਹਨ । ਉਹਨਾਂ ਨੂੰ ਖ਼ਤਮ ਕਰਨ ਲਈ ਵਿਦੇਸ਼ੀ ਦਵਾਈਆਂ ‘ਤੇ ਕਾਫ਼ੀ ਪੈਸਾ ਬਰਬਾਦ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਵਿਦੇਸ਼ੀ ਪੌਦਿਆਂ ਤੋਂ ਸਾਨੂੰ ਕੀ ਨੁਕਸਾਨ ਹੋ ਸਕਦੇ ਹਨ ?
ਉੱਤਰ-
ਵਿਦੇਸ਼ੀ ਪੌਦਿਆਂ ਤੋਂ ਸਾਨੂੰ ਹੇਠ ਲਿਖੇ ਨੁਕਸਾਨ ਹੋ ਸਕਦੇ ਹਨ-
- ਸਾਡੀ ਸਥਾਨਕ ਲਾਭਕਾਰੀ ਬਨਸਪਤੀ ਬਰਬਾਦ ਹੋ ਸਕਦੀ ਹੈ ।
- ਵਿਦੇਸ਼ੀ ਬਨਸਪਤੀ ਨੂੰ ਖ਼ਤਮ ਕਰਨ ਵਿਚ ਸਾਡਾ ਬਹੁਤ ਸਾਰਾ ਪੈਸਾ ਖ਼ਰਚ ਹੋਵੇਗਾ ।
- ਵਿਦੇਸ਼ੀ ਬਨਸਪਤੀ ਨਾਲ ਸਾਹ ਅਤੇ ਚਮੜੀ ਸੰਬੰਧੀ ਖ਼ਤਰਨਾਕ ਰੋਗ ਫੈਲ ਸਕਦੇ ਹਨ ।
- ਸਾਡੇ ਜਲ ਭੰਡਾਰ ਵਿਦੇਸ਼ੀ ਬਨਸਪਤੀ ਨਾਲ ਦੂਸ਼ਿਤ ਹੋ ਸਕਦੇ ਹਨ ।
- ਸਾਡੀ ਉਪਯੋਗੀ ਭੂਮੀ ਘੱਟ ਹੋ ਸਕਦੀ ਹੈ, ਚਰਾਂਦਾਂ ਵਿਚ ਕਮੀ ਆ ਸਕਦੀ ਹੈ ਅਤੇ ਵਣ ਖੇਤਰ ਬਰਬਾਦ ਹੋ ਸਕਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 3.
ਸਾਡੀ ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਦੇ ਅਸਲ ਵਿਚ ਕੁਦਰਤੀ ਨਾ ਰਹਿਣ ਦੇ ਕੀ ਕਾਰਨ ਹਨ ?
ਉੱਤਰ-
ਸਾਡੀ ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਅਸਲ ਵਿਚ ਕੁਦਰਤੀ ਨਹੀਂ ਰਹੀ । ਇਹ ਸਿਰਫ਼ ਦੇਸ਼ ਦੇ ਕੁੱਝ ਹੀ ਹਿੱਸਿਆਂ ਵਿਚ ਮਿਲਦੀ ਹੈ । ਦੂਜੇ ਹਿੱਸਿਆਂ ਵਿਚ ਇਸ ਦਾ ਬਹੁਤਾ ਭਾਗ ਜਾਂ ਤਾਂ ਬਰਬਾਦ ਹੋ ਗਿਆ ਹੈ ਜਾਂ ਫਿਰ ਬਰਬਾਦ ਹੋ ਰਿਹਾ ਹੈ । ਇਸ ਦੇ ਹੇਠ ਲਿਖੇ ਕਾਰਨ ਹਨ-
- ਤੇਜ਼ੀ ਨਾਲ ਵਧਦੀ ਹੋਈ ਸਾਡੀ ਵਸੋਂ ।
- ਰਵਾਇਤੀ ਖੇਤੀ ਵਿਕਾਸ ਦਾ ਰਿਵਾਜ ।
- ਚਰਾਂਦਾਂ ਦਾ ਵਿਨਾਸ਼ ਅਤੇ ਬਹੁਤ ਜ਼ਿਆਦਾ ਚਰਾਈ ।
- ਬਾਲਣ ਅਤੇ ਇਮਾਰਤੀ ਲੱਕੜੀ ਲਈ ਵਣਾਂ ਦਾ ਅੰਨ੍ਹੇਵਾਹ ਕਟਾਓ ।
- ਵਿਦੇਸ਼ੀ ਪੌਦਿਆਂ ਦੀ ਵਧਦੀ ਹੋਈ ਸੰਖਿਆ ।
![]()
ਪ੍ਰਸ਼ਨ 4.
ਪੱਤਝੜੀ ਜਾਂ ਮਾਨਸੂਨੀ ਬਨਸਪਤੀ ‘ਤੇ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਉਹ ਬਨਸਪਤੀ ਜੋ ਗਰਮੀ ਰੁੱਤ ਦੇ ਸ਼ੁਰੂ ਹੋਣ ਤੋਂ ਪਹਿਲਾਂ ਵਧੇਰੇ ਵਾਸ਼ਪੀਕਰਨ ਨੂੰ ਰੋਕਣ ਲਈ ਆਪਣੇ ਪੱਤੇ ਸੁੱਟ ਦਿੰਦੀ ਹੈ ਪੱਤਝੜੀ ਜਾਂ ਮਾਨਸੂਨੀ ਬਨਸਪਤੀ ਕਹਾਉਂਦੀ ਹੈ । ਬਨਸਪਤੀ ਨੂੰ ਵਰਖਾ ਦੇ ਆਧਾਰ ‘ਤੇ ਸਿੱਲ੍ਹਾ ਅਤੇ ਅਰਧਖ਼ੁਸ਼ਕ ਦੋ ਉਪ-ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
- ਜਿਲ੍ਹੇ ਪੱਤਝੜੀ ਵਣ – ਇਸ ਤਰ੍ਹਾਂ ਦੀ ਬਨਸਪਤੀ ਉਹਨਾਂ ਚਾਰ ਵੱਡੇ ਖੇਤਰਾਂ ਵਿਚ ਮਿਲਦੀ ਹੈ ਜਿੱਥੇ ਸਾਲਾਨਾ ਵਰਖਾ 100 ਤੋਂ 200 ਸੈਂ: ਮੀ: ਤਕ ਹੈ । ਇਹਨਾਂ ਖੇਤਰਾਂ ਵਿਚ ਦਰੱਖਤ ਘੱਟ ਸੰਘਣੇ ਹੁੰਦੇ ਹਨ ਪਰ ਇਹਨਾਂ ਦੀ ਲੰਬਾਈ 30 ਮੀਟਰ ਤਕ ਪਹੁੰਚ ਜਾਂਦੀ ਹੈ । ਸਾਲ, ਟਾਹਲੀ, ਸਾਗੋਨ, ਟੀਕ, ਚੰਦਨ, ਜਾਮਣ, ਅਮਲਤਾਸ਼, ਹਲਦੂ, ਮਹੂਆ, ਸ਼ਾਰਬੂ, ਏਬੋਨੀ, ਸ਼ਹਿਤੂਤ ਇਹਨਾਂ ਵਣਾਂ ਦੇ ਮੁੱਖ ਦਰੱਖਤ ਹਨ ।
- ਖੁਸ਼ਕ ਪੱਤਝੜੀ ਬਨਸਪਤੀ-ਇਸ ਤਰ੍ਹਾਂ ਦੀ ਬਨਸਪਤੀ 50 ਤੋਂ 100 ਸੈਂ: ਮੀ: ਤੋਂ ਘੱਟ ਵਰਖਾ ਵਾਲੇ ਖੇਤਰਾਂ ਵਿਚ ਮਿਲਦੀ ਹੈ । ਇਸ ਦੀ ਲੰਬੀ ਪੱਟੀ ਪੰਜਾਬ ਤੋਂ ਸ਼ੁਰੂ ਹੋ ਕੇ ਦੱਖਣੀ ਪਠਾਰ ਦੇ ਮੱਧਵਰਤੀ ਹਿੱਸੇ ਦੇ ਆਸ-ਪਾਸ ਦੇ ਖੇਤਰਾਂ ਤਕ ਫੈਲੀ ਹੋਈ ਹੈ । ਟਾਹਲੀ, ਕਿੱਕਰ, ਫਲਾਹੀ, ਬੋਹੜ, ਹਲਦੁ ਇੱਥੋਂ ਦੇ ਮੁੱਖ ਦਰੱਖਤੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 5.
ਪੂਰਬੀ ਹਿਮਾਲਿਆ ਖੇਤਰਾਂ ਵਿਚ ਕਿਸ ਤਰ੍ਹਾਂ ਦੀ ਬਨਸਪਤੀ ਮਿਲਦੀ ਹੈ ?
ਉੱਤਰ-
ਪੂਰਬੀ ਹਿਮਾਲਾ ਖੇਤਰ ਵਿਚ 4000 ਕਿਸਮ ਦੇ ਫੁੱਲ ਅਤੇ 250 ਕਿਸਮ ਦੀ ਫਰਨ ਮਿਲਦੀ ਹੈ । ਇੱਥੋਂ ਦੀ ਬਨਸਪਤੀ ਤੇ ਉਚਾਈ ਦੇ ਵਧਣ ਨਾਲ ਤਾਪਮਾਨ ਅਤੇ ਵਰਖਾ ਵਿਚ ਆਏ ਅੰਤਰ ਦਾ ਡੂੰਘਾ ਅਸਰ ਪੈਂਦਾ ਹੈ ।
- ਇੱਥੇ 1200 ਮੀਟਰ ਦੀ ਉਚਾਈ ਤਕ ਪੱਤਝੜੀ ਬਨਸਪਤੀ ਦੇ ਮਿਸ਼ਰਤੇ ਦਰੱਖ਼ਤ ਵਧੇਰੇ ਮਿਲਦੇ ਹਨ ।
- ਇੱਥੇ 1200 ਤੋਂ ਲੈ ਕੇ 2000 ਮੀਟਰ ਦੀ ਉਚਾਈ ਤਕ ਸੰਘਣੇ ਸਦਾਬਹਾਰ ਵਣ ਮਿਲਦੇ ਹਨ । ਸਾਲ ਅਤੇ ਮੈਂਗਨੋਲੀਆ ਇਹਨਾਂ ਵਣਾਂ ਦੇ ਮੁੱਖ ਦਰੱਖ਼ਤ ਹਨ । ਇਹਨਾਂ ਵਿਚ ਦਾਲਚੀਨੀ, ਅਸੁਰਾ, ਚਿਨੋਲੀ ਤੇ ਵਿਲੇਨੀਆ ਦੇ ਦਰੱਖ਼ਤ ਵੀ ਮਿਲਦੇ ਹਨ ।
- ਇੱਥੇ 2000 ਤੋਂ 2500 ਮੀਟਰ ਦੀ ਉਚਾਈ ਤਕ ਤਾਪਮਾਨ ਘੱਟ ਹੋ ਜਾਣ ਦੇ ਕਾਰਨ ਸ਼ੀਤ-ਊਸ਼ਣ ਪ੍ਰਕਾਰ (Temperate type) ਦੀ ਬਨਸਪਤੀ ਮਿਲਦੀ ਹੈ । ਇਸ ਵਿਚ ਓਕ, ਚੈਸਟਨਟ, ਲਾਰੇਲ, ਬਰਚ, ਮੈਪਲ ਅਤੇ ਓਲਚਰ ਜਿਹੇ ਚੌੜੇ ਪੱਤਿਆਂ ਵਾਲੇ ਰੁੱਖ ਮਿਲਦੇ ਹਨ ।
- ਇੱਥੇ 2500 ਤੋਂ ਲੈ ਕੇ 3500 ਮੀਟਰ ਤਕ ਤਿੱਖੇ ਪੱਤੇ ਵਾਲੇ ਕੋਣਧਾਰੀ ਅਤੇ ਸ਼ੰਕੂਧਾਰੀ ਰੁੱਖ ਦਿਖਾਈ ਦਿੰਦੇ ਹਨ । ਇਹਨਾਂ ਵਿਚ ਸਿਲਵਰ ਫਰ, ਪਾਈਨ, ਸਪਰੂਸ, ਦੇਵਦਾਰ, ਰੋਡੋਡੇਂਡਰਾਨ, ਨੀਲਾ ਪਾਈਨ ਜਿਹੇ ਘੱਟ ਉਚਾਈ ਵਾਲੇ ਰੁੱਖ ਮਿਲਦੇ ਹਨ ।
ਇਸ ਤੋਂ ਵੱਧ ਉਚਾਈ ਤੇ ਛੋਟੀ-ਛੋਟੀ ਕੁਦਰਤੀ ਘਾਹ ਅਤੇ ਫੁੱਲ ਆਦਿ ਦੇ ਪੌਦੇ ਵੀ ਉੱਗਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 6.
ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਉਦਯੋਗਾਂ ਲਈ ਕਿਸ ਤਰ੍ਹਾਂ ਜੀਵਨ ਦਾਨ ਦਾ ਕੰਮ ਕਰਦੀ ਹੈ ?
ਉੱਤਰ-
ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਕਈ ਤਰ੍ਹਾਂ ਨਾਲ ਉਦਯੋਗਾਂ ਦਾ ਆਧਾਰ ਹੈ । ਵਣਾਂ ‘ਤੇ ਆਧਾਰਿਤ ਕੁੱਝ ਮਹੱਤਵਪੂਰਨ ਉਦਯੋਗ ਹੇਠ ਲਿਖੇ ਹਨ
- ਮਾਚਿਸ ਉਦਯੋਗ – ਵਣਾਂ ਤੋਂ ਪ੍ਰਾਪਤ ਨਰਮ ਲੱਕੜੀ ਮਾਚਿਸ ਬਨਾਉਣ ਦੇ ਕੰਮ ਆਉਂਦੀ ਹੈ ।
- ਲਾਖ ਉਦਯੋਗ – ਲਾਖ ਇਕ ਤਰ੍ਹਾਂ ਦੇ ਕੀੜੇ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ । ਇਸ ਨੂੰ ਰਿਕਾਰਡ, ਬੂਟ ਪਾਲਿਸ਼, ਬਿਜਲੀ ਦਾ ਸਾਮਾਨ ਆਦਿ ਬਨਾਉਣ ਵਿਚ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ।
- ਕਾਗਜ਼ ਉਦਯੋਗ – ਕਾਗਜ਼ ਉਦਯੋਗ ਵਿਚ ਬਾਂਸ, ਸਫੈਦਾ ਅਤੇ ਕਈ ਤਰ੍ਹਾਂ ਦੀ ਘਾਹ ਵਰਤੀ ਜਾਂਦੀ ਹੈ । ਬਾਂਸ ਤਰਾਈ ਖੇਤਰ ਵਿਚ ਬਹੁਤ ਮਿਲਦਾ ਹੈ ।
- ਵਾਰਨਿਸ਼ ਅਤੇ ਰੰਗ – ਵਾਰਨਿਸ਼ ਅਤੇ ਰੰਗ ਗੰਦੇ ਬਰੋਜ਼ੇ ਤੋਂ ਤਿਆਰ ਹੁੰਦੇ ਹਨ ਜੋ ਵਣਾਂ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
- ਦਵਾਈ ਨਿਰਮਾਣ – ਵਣਾਂ ਤੋਂ ਪ੍ਰਾਪਤ ਕੁੱਝ ਰੁੱਖਾਂ ਤੋਂ ਉਪਯੋਗੀ ਦਵਾਈਆਂ ਵੀ ਬਣਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ।ਉਦਾਹਰਨ ਵਜੋਂ ਸਿਨਕੋਨਾ ਤੋਂ ਕੁਨੀਨ ਬਣਦੀ ਹੈ ।
- ਹੋਰ ਉਦਯੋਗ – ਵਣਾਂ ਤੇ ਪੈਂਨਸਿਲ, ਡੱਬੇ ਬਣਾਉਣਾ, ਰਬੜ, ਤਾਰਪੀਨ, ਚੰਦਨ ਦਾ ਤੇਲ, ਫਰਨੀਚਰ ਅਤੇ ਖੇਡਾਂ ਦਾ ਸਾਮਾਨ ਬਣਾਉਣ ਦੇ ਉਦਯੋਗ ਵੀ ਆਧਾਰਿਤ ਹਨ ।
ਪ੍ਰਸ਼ਨ 7.
ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਦੇ ਦੇਸ਼ ਅੰਦਰ ਅੰਧਾ-ਧੁੰਦ ਕਟਾਅ ਦੇ ਕੀ ਸਿੱਟੇ ਨਿਕਲੇ ਹਨ ?
ਉੱਤਰ-
ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਦਾ ਸਾਡੇ ਜੀਵਨ ਵਿਚ ਬਹੁਤ ਮਹੱਤਵ ਹੈ ਪਰ ਪਿਛਲੇ ਕੁੱਝ ਸਾਲਾਂ ਵਿਚ ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਦੀ ਅੰਧਾ-ਧੁੰਦ ਕਟਾਈ ਕੀਤੀ ਗਈ ਹੈ । ਇਸ ਕਟਾਈ ਤੋਂ ਸਾਨੂੰ ਹੇਠ ਲਿਖੀਆਂ ਹਾਨੀਆਂ ਹਨ-
- ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਦੀ ਕਟਾਈ ਨਾਲ ਵਾਤਾਵਰਨ ਦਾ ਸੰਤੁਲਨ ਵਿਗੜ ਗਿਆ ਹੈ ।
- ਪਹਾੜੀ ਢਲਾਣਾਂ ਅਤੇ ਮੈਦਾਨੀ ਖੇਤਰਾਂ ਦੇ ਬਨਸਪਤੀ ਰਹਿਤ ਹੋਣ ਦੇ ਕਾਰਨ ਹੜ ਅਤੇ ਭੋਂ-ਖੋਰ ਦੀਆਂ ਸਮੱਸਿਆਵਾਂ ਪੈਦਾ ਹੋ ਗਈਆਂ ਹਨ ।
- ਪੰਜਾਬ ਦੇ ਉੱਤਰੀ ਭਾਗਾਂ ਵਿਚ ਸ਼ਿਵਾਲਿਕ ਪਰਬਤ ਮਾਲਾ ਦੇ ਹੇਠਲੇ ਹਿੱਸੇ ਵਿੱਚ ਵਗਣ ਵਾਲੇ ਬਰਸਾਤੀ ਨਾਲਿਆਂ ਦੇ ਖੇਤਰ ਵਿਚ ਵਣ ਕਟਾਅ ਨਾਲ ਭੁਮੀ ਕਟਾਅ ਦੀ ਸਮੱਸਿਆ ਦੇ ਕਾਰਨ ਬੰਜਰ ਜ਼ਮੀਨ ਵਿਚ ਵਾਧਾ ਹੋਇਆ ਹੈ । ਮੈਦਾਨੀ ਖੇਤਰਾਂ ਦਾ ਪਾਣੀ ਦਾ ਪੱਧਰ ਵੀ ਪ੍ਰਭਾਵਿਤ ਹੋਇਆ ਹੈ, ਜਿਸ ਨਾਲ ਖੇਤੀ ਨੂੰ ਸਿੰਜਾਈ ਦੀ ਸਮੱਸਿਆ ਨਾਲ ਘੁਲਣਾ ਪੈ ਰਿਹਾ ਹੈ ।
![]()
(ਅ) ਜੀਵ-ਜੰਤੂ-
ਪ੍ਰਸ਼ਨ 1.
ਦੇਸ਼ ਵਿਚ ਜੀਵ-ਜੰਤੂਆਂ ਦੀ ਸਾਂਭ ਤੇ ਸੰਭਾਲ ਲਈ ਕੀ ਉਪਰਾਲੇ ਕੀਤੇ ਜਾ ਰਹੇ ਹਨ ?
ਉੱਤਰ-
- 1972 ਵਿਚ ਭਾਰਤੀ ਵਣ ਜੀਵਨ ਸੁਰੱਖਿਆ ਕਾਨੂੰਨ ਬਣਾਇਆ ਗਿਆ । ਇਸ ਦੇ ਅਧੀਨ ਦੇਸ਼ ਦੇ ਵੱਖ-ਵੱਖ ਹਿੱਸਿਆਂ ਵਿਚ 83835 ਵਰਗ ਕਿਲੋਮੀਟਰ ਖੇਤਰ ਦੇਸ਼ ਦਾ 27 ਪ੍ਰਤੀਸ਼ਤ ਅਤੇ ਕੁੱਲ ਵਣ ਖੇਤਰ ਦਾ 12 ਪ੍ਰਤੀਸ਼ਤ ਹਿੱਸਾ) ਨੂੰ ਰਾਸ਼ਟਰੀ ਪਾਰਕ ਅਤੇ ਵਣ-ਪਾਣੀ ਚਿੜੀਆਘਰ ਐਲਾਨਿਆ ਗਿਆ ਹੈ ।
- ਖ਼ਤਮ ਹੋ ਰਹੇ ਵਣ ਜੀਵਾਂ ਵਲ ਖ਼ਾਸ ਧਿਆਨ ਦਿੱਤਾ ਜਾਣ ਲੱਗਾ ਹੈ ।
- ਪਸ਼ੂ ਪੰਛੀਆਂ ਦੀ ਗਣਨਾ ਦਾ ਕੰਮ ਰਾਸ਼ਟਰੀ ਪੱਧਰ ‘ਤੇ ਸ਼ੁਰੂ ਕੀਤਾ ਗਿਆ ਹੈ ।
- ਦੇਸ਼ ਦੇ ਵੱਖ-ਵੱਖ ਹਿੱਸਿਆਂ ਵਿਚ ਇਸ ਸਮੇਂ ਬਆੜਾਂ ਦੇ 16 ਰੱਖਿਅਤ ਖੇਤਰ ਹਨ ।
- ਆਸਾਮ ਵਿਚ ਗੈਂਡੇ ਦੇ ਸੰਰੱਖਿਅਣ ਦੀ ਇਕ ਖ਼ਾਸ ਯੋਜਨਾ ਚਲਾਈ ਜਾ ਰਹੀ ਹੈ ।
ਸੱਚ ਤਾਂ ਇਹ ਹੈ ਕਿ ਦੇਸ਼ ਵਿਚ ਹੁਣ ਤਕ 18 ਜੀਵ ਸੁਰੱਖਿਅਤ ਖੇਤਰ (Biosphere Reserve) ਸਥਾਪਿਤ ਕੀਤੇ ਜਾ ਚੁੱਕੇ ਹਨ | ਯੋਜਨਾ ਦੇ ਅਧੀਨ ਸਭ ਤੋਂ ਪਹਿਲਾ ਜੀਵ ਸੰਰੱਖਿਅਣ ਖੇਤਰ ਨੀਲਗਿਰੀ ਵਿਚ ਬਣਾਇਆ ਗਿਆ ਸੀ । ਇਸ ਯੋਜਨਾ ਅਧੀਨ ਹਰੇਕ ਜੰਤੂ ਦਾ ਸੰਰੱਖਿਅਣ ਜ਼ਰੂਰੀ ਹੈ । ਇਹ ਕੁਦਰਤੀ ਅਮਾਨਤ (Natural Heritage) ਆਉਣ ਵਾਲੀਆਂ ਪੀੜ੍ਹੀਆਂ ਲਈ ਹੈ ।
(ੲ) ਮਿੱਟੀਆਂ-
ਪ੍ਰਸ਼ਨ 1.
ਮਿੱਟੀਆਂ ਦੇ ਜਨਮ ਵਿਚ ਮੁੱਢਲੀ ਚੱਟਾਨ ਦਾ ਕੀ ਯੋਗਦਾਨ ਹੈ ?
ਉੱਤਰ-
ਦੇਸ਼ ਵਿਚ ਮੁੱਢਲੀਆਂ ਚੱਟਾਨਾਂ ਵਿਚ ਉੱਤਰੀ ਮੈਦਾਨਾਂ ਦੀਆਂ ਮੋੜਦਾਰ ਚੱਟਾਨਾਂ ਅਤੇ ਪਠਾਰੀ ਭਾਗ ਦੀਆਂ ਲਾਵਾ ਨਿਰਮਿਤ ਚੱਟਾਨਾਂ ਆਉਂਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਵਿਚ ਵੱਖ-ਵੱਖ ਖਣਿਜ ਹੁੰਦੇ ਹਨ । ਇਸ ਲਈ ਇਹਨਾਂ ਤੋਂ ਚੰਗੀ ਕਿਸਮ ਦੀ ਮਿੱਟੀ ਬਣਦੀ ਹੈ ।
ਮੁੱਢਲੀਆਂ ਚੱਟਾਨਾਂ ਤੋਂ ਬਣਨ ਵਾਲੀ ਮਿੱਟੀ ਦਾ ਰੰਗ, ਸੰਗਠਨ, ਬਣਾਵਟ ਆਦਿ ਇਸ ਗੱਲ ‘ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ਕਿ ਚੱਟਾਨਾਂ ਕਿੰਨੇ ਸਮੇਂ ਤੋਂ ਅਤੇ ਕਿਸ ਤਰ੍ਹਾਂ ਦੀ ਜਲਵਾਯੂ ਤੋਂ ਪ੍ਰਭਾਵਿਤ ਹੋ ਰਹੀਆਂ ਹਨ । ਪੱਛਮੀ ਬੰਗਾਲ ਵਰਗੇ ਦੇਸ਼ ਵਿਚ ਜਲਵਾਯੂ ਵਿਚ ਰਸਾਇਣਿਕ ਕਿਰਿਆਵਾਂ ਦੇ ਪ੍ਰਭਾਵ ਅਤੇ ਜੀਵਾਂਸ਼ ਦੇ ਕਾਰਨ ਮਿੱਟੀ ਬਹੁਤ ਵਿਕਸਿਤ ਹੁੰਦੀ ਹੈ । ਪਰ ਰਾਜਸਥਾਨ ਵਰਗੇ ਖ਼ੁਸ਼ਕ ਖੇਤਰ ਵਿਚ ਬਨਸਪਤੀ ਦੀ ਕਮੀ ਦੇ ਕਾਰਨ ਮਿੱਟੀ ਦੀ ਉਪਜਾਊ ਸ਼ਕਤੀ ਘੱਟ ਹੋ ਜਾਂਦੀ ਹੈ । ਇਸੇ ਤਰ੍ਹਾਂ ਵਧੇਰੇ ਵਰਖਾ ਅਤੇ ਤੇਜ਼ ਪੌਣਾਂ ਵਾਲੇ ਖੇਤਰਾਂ ਵਿਚ ਮਿੱਟੀ ਦਾ ਕਟਾਅ ਜ਼ਿਆਦਾ ਹੁੰਦਾ ਹੈ । ਸਿੱਟੇ ਵਜੋਂ ਮਿੱਟੀ ਦਾ ਉਪਜਾਊਪਨ ਘੱਟ ਹੋ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਮਿੱਟੀ ਦੀ ਉਪਜਾਊ ਸ਼ਕਤੀ ਨੂੰ ਵਧਾਉਣ ਲਈ ਕੀ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਮਿੱਟੀ ਬਹੁਤ ਕੀਮਤੀ ਸੰਸਾਧਨ ਹੈ । ਇਸ ਦਾ ਸੰਰੱਖਿਅਣ ਅਤੇ ਇਸ ਦੇ ਉਪਜਾਊਪਨ ਨੂੰ ਬਣਾਈ ਰੱਖਣ ਲਈ ਅੱਜ ਸਾਡੀ ਸਭ ਦੀ ਨੈਤਿਕ ਜ਼ਿੰਮੇਵਾਰੀ ਹੈ ।
- ਪੰਜਾਬ, ਹਰਿਆਣਾ, ਰਾਜਸਥਾਨ, ਗੁਜਰਾਤ ਵਿਚ ਪੌਣਾਂ ਦੀ ਰਫ਼ਤਾਰ ਨੂੰ ਘੱਟ ਕਰਨ ਲਈ ਰੁੱਖਾਂ ਦੀਆਂ ਕਤਾਰਾਂ ਲਗਾਉਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ । ਨਾਲ ਹੀ ਰੇਤਲੇ ਟਿੱਲਿਆਂ ‘ਤੇ ਘਾਹ ਉਗਾਈ ਜਾਣੀ ਚਾਹੀਦੀ ਹੈ ।
- ਪਰਬਤੀ ਖੇਤਰਾਂ ਵਿਚ ਪੌੜੀਦਾਰ ਖੇਤ, ਢਾਲ ਦੇ ਉਲਟ ਦਿਸ਼ਾ ਵਿਚ ਬੰਨ੍ਹ (Contour Bending) ਬਣਾਉਣਾ ਅਤੇ ਛੋਟੇ-ਛੋਟੇ ਜਲ-ਭੰਡਾਰ ਬਣਾਏ ਜਾਣੇ ਚਾਹੀਦੇ ਹਨ ।
- ਮੈਦਾਨੀ ਭਾਗਾਂ ਵਿਚ ਭੂਮੀ ਤੇ ਬਨਸਪਤੀ ਉਗਾਉਣੀ ਚਾਹੀਦੀ ਹੈ ।
- ਇਸ ਤੋਂ ਇਲਾਵਾ ਫ਼ਸਲ ਚੱਕਰ, ਢਾਲ ਦੇ ਉਲਟ ਖੇਤਾਂ ਨੂੰ ਵਾਹੁਣਾ ਅਤੇ ਗੋਹੇ ਦੀ ਖਾਦ ਦੀ ਵਰਤੋਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ । ਇਸ ਨਾਲ ਮਿੱਟੀ ਦੇ ਉਪਜਾਊਪਨ ਵਿਚ ਵਾਧਾ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
ਪੀਟ ਤੇ ਦਲਦਲੀ ਮਿੱਟੀ ‘ਤੇ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਪੀਟ ਤੇ ਦਲਦਲੀ ਮਿੱਟੀ ਸਿਰਫ਼ 150 ਵਰਗ ਕਿਲੋਮੀਟਰ ਦੇ ਖੇਤਰ ਵਿਚ ਮਿਲਦੀ ਹੈ । ਇਸ ਦਾ ਵਿਸਥਾਰ ਸੁੰਦਰਵਣ ਡੈਲਟਾ, ਉੜੀਸਾ ਦੇ ਤਟਵਰਤੀ ਖੇਤਰ, ਤਾਮਿਲਨਾਡੂ ਦੇ ਦੱਖਣ-ਪੂਰਬੀ ਤਟਵਰਤੀ ਹਿੱਸੇ, ਮੱਧਵਰਤੀ ਬਿਹਾਰ ਅਤੇ ਉਤਰਾਖੰਡ ਦੇ ਅਲਮੋੜਾ ਵਿਚ ਹੈ । ਜੈਵਿਕ ਪਦਾਰਥਾਂ ਦੀ ਬਹੁਲਤਾ ਦੇ ਕਾਰਨ ਇਸ ਦਾ ਰੰਗ ਕਾਲਾ ਅਤੇ ਸੁਭਾਅ ਤੇਜ਼ਾਬੀ ਹੁੰਦਾ ਹੈ । ਇਸ ਰੰਗ ਦੇ ਕਾਰਨ ਇਸ ਨੂੰ ਕੇਰਲ ਵਿਚ ‘ਕਾਰੀ ਮਿੱਟੀ (Kari Soil) ਦੇ ਨਾਂ ਨਾਲ ਵੀ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ । ਜੈਵਿਕ ਪਦਾਰਥਾਂ ਦੀ ਬਹੁਲਤਾ ਦੇ ਕਾਰਨ ਇਹ ਮਿੱਟੀ ਨੀਲੇ ਰੰਗ ਵਾਲੀ ਮਿੱਟੀ ਵੀ ਬਣ ਜਾਂਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਮਿੱਟੀ ਦਾ ਕਟਾਅ ਕਿੰਨੀ ਤਰ੍ਹਾਂ ਦਾ ਹੁੰਦਾ ਹੈ ?
ਉੱਤਰ-
ਧਰਾਤਲ ਉੱਪਰ ਮਿਲਣ ਵਾਲੀ ਮਿੱਟੀ ਦੀ ਤਹਿ ਦਾ ਭੌਤਿਕ ਅਤੇ ਗ਼ੈਰ-ਭੌਤਿਕ ਤੱਤਾਂ ਦੁਆਰਾ ਟੁੱਟਣਾ ਜਾਂ ਹਟਣਾ ਮਿੱਟੀ ਦਾ ਕਟਾਅ ਕਹਾਉਂਦਾ ਹੈ । ਇਹ ਕਟਾਅ ਤਿੰਨ ਤਰ੍ਹਾਂ ਦਾ ਹੋ ਸਕਦਾ ਹੈ –
- ਤਹਿਦਾਰ ਕਟਾਅ – ਇਸ ਤਰ੍ਹਾਂ ਦੇ ਕਟਾਅ ਵਿਚ ਪੌਣਾਂ ਦੇ ਚੱਲਣ ਅਤੇ ਨਦੀ ਜਲ ਦੇ ਲੰਬੇ ਸਮੇਂ ਤਕ ਵਗਣ ਦੇ ਬਾਅਦ ਧਰਾਤਲ ਦੀ ਉੱਪਰਲੀ ਤਹਿ ਵਹਿ ਜਾਂਦੀ ਹੈ ਜਾਂ ਉਡਾ ਕੇ ਲੈ ਜਾਂਦੀ ਹੈ ।
- ਨਾਲੀਦਾਰ ਕਟਾਓ – ਮੋਹਲੇਧਾਰ ਵਰਖਾ ਦੇ ਸਮੇਂ ਜ਼ਿਆਦਾ ਪਾਣੀ ਦੀਆਂ ਘੱਟ ਚੌੜਾਈ ਵਾਲੀਆਂ ਨਾਲੀਆਂ ਵਗਣ ਲੱਗਦੀਆਂ ਹਨ । ਇਸ ਨਾਲ ਧਰਾਤਲ ‘ਤੇ ਲੰਬੀਆਂ-ਲੰਬੀਆਂ ਖਾਈਆਂ ਬਣ ਜਾਂਦੀਆਂ ਹਨ । ਇਸ ਨੂੰ ਨਾਲੀਦਾਰ ਕਟਾਅ ਕਹਿੰਦੇ ਹਨ ।
- ਟੋਏਦਾਰ ਕਟਾਅ – ਪੌਣਾਂ ਜਾਂ ਜਲ ਧਰਾਤਲ ਦੇ ਖ਼ਾਸ ਸਥਾਨਾਂ ‘ਤੇ ਮਿੱਟੀ ਦੇ ਉੱਡਣ ਜਾਂ ਘੁਲਣ ਦੇ ਬਾਅਦ ਡੂੰਘੇ ਟੋਏ ਬਣਾ ਦਿੱਤੇ ਹਨ । ਹੌਲੀ-ਹੌਲੀ ਇਹ ਟੋਏ ਬਹੁਤ ਵੱਡੇ ਹੋ ਜਾਂਦੇ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਮਿੱਟੀ ਦੇ ਕਟਾਅ ਲਈ ਕਿਹੜੇ-ਕਿਹੜੇ ਕਾਰਕ ਜ਼ਿੰਮੇਵਾਰ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਮਿੱਟੀ ਦਾ ਕਟਾਅ ਮੁੱਖ ਤੌਰ ‘ਤੇ ਦੋ ਕਾਰਕਾਂ ਨਾਲ ਹੁੰਦਾ ਹੈ-ਭੌਤਿਕ ਕਿਰਿਆਵਾਂ ਦੁਆਰਾ ਅਤੇ ਮਨੁੱਖੀ ਕਿਰਿਆਵਾਂ ਦੁਆਰਾ । ਅਜੋਕੇ ਸਮੇਂ ਵਿਚ ਮਨੁੱਖੀ ਕਿਰਿਆਵਾਂ ਦੁਆਰਾ ਮਿੱਟੀਆਂ ਦੇ ਕਟਾਅ ਦੀ ਪ੍ਰਕਿਰਿਆ ਵੱਧਦੀ ਜਾ ਰਹੀ ਹੈ ।
ਭੌਤਿਕ ਤੱਤਾਂ ਵਿਚ ਉੱਚਾ ਤਾਪਮਾਨ, ਬਰਫ਼ੀਲੇ ਤੂਫਾਨ, ਤੇਜ਼ ਹਵਾਵਾਂ, ਮੋਹਲੇਧਾਰ ਵਰਖਾ, ਤਿੱਖੀਆਂ ਢਲਾਣਾਂ ਦੀ ਗਣਨਾ ਹੁੰਦੀ ਹੈ । ਇਹ ਮਿੱਟੀ ਦੇ ਕਟਾਅ ਦੇ ਮੁੱਖ ਕਾਰਕ ਹਨ । ਮਨੁੱਖੀ ਕਿਰਿਆਵਾਂ ਵਿਚ ਜੰਗਲਾਂ ਦੀ ਕਟਾਈ, ਪਸ਼ੂਆਂ ਦੀ ਬੇਰੋਕ-ਟੋਕ ਚਰਾਈ, ਸਥਾਨਾਂਤਰੀ ਖੇਤੀ, ਖੇਤੀ ਦੀ ਦੋਸ਼ਪੂਰਨ ਪੱਧਤੀ, ਖਾਣਾਂ ਦੀ ਖੁਦਾਈ ਆਦਿ ਤੱਤ ਆਉਂਦੇ ਹਨ ।
III. ਹੇਠ ਲਿਖੇ ਹਰੇਕ ਪ੍ਰਸ਼ਨ ਦਾ ਉੱਤਰ ਲਗਪਗ 125-130 ਸ਼ਬਦਾਂ ਵਿਚ ਦਿਓ-
ਪ੍ਰਸ਼ਨ 1.
ਭਾਰਤ ਵਿਚ ਵੱਖੋ-ਵੱਖਰੇ ਆਧਾਰਾਂ ਰਾਹੀਂ ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਦੇ ਵਰਗੀਕਰਨ ਦਾ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਭਾਰਤੀ ਬਨਸਪਤੀ ਦਾ ਕਈ ਆਧਾਰਾਂ ‘ਤੇ ਵਰਗੀਕਰਨ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਮੁੱਖ ਆਧਾਰ ਹੇਠਾਂ ਲਿਖੇ ਹਨ-
1. ਪਹੁੰਚ ਦੇ ਆਧਾਰ ‘ਤੇ – ਇਸ ਦ੍ਰਿਸ਼ਟੀ ਤੋਂ ਵਣ ਦੋ ਪ੍ਰਕਾਰ ਦੇ ਹਨ-ਛੂਤੇ ਅਤੇ ਅਛੂਤੇ ।
ਦੇਸ਼ ਵਿਚ 18% ਵਣ ਖੇਤਰ ਅਜਿਹੇ ਹਨ ਜੋ ਕਿ ਹਿਮਾਲਾ ਦੀਆਂ ਉੱਚੀਆਂ ਢਲਾਣਾਂ ’ਤੇ ਸਥਿਤ ਹਨ । ਇਸ ਕਾਰਨ ਇਹ ਮਨੁੱਖੀ ਪਹੁੰਚ ਤੋਂ ਬਾਹਰ ਹਨ ਅਰਥਾਤ ਅਛੂਤੇ ਹਨ | ਅਸੀਂ ਸਿਰਫ਼ 82% ਵਣ ਖੇਤਰ ਦਾ ਹੀ ਪ੍ਰਯੋਗ ਕਰ ਸਕਦੇ ਹਾਂ |
2. ਪੱਤੀਆਂ ਦੇ ਆਧਾਰ `ਤੇ – ਦੇਸ਼ ਵਿਚ ਕੁੱਲ ਉਪਲੱਬਧ ਵਣਾਂ ਦੇ 5% ਖੇਤਰ ਨੁਕੀਲੀ ਪੱਤੀਆਂ ਵਾਲੇ ਹਨ । ਇਹ ਬਹੁਮੁੱਲੇ ਸ਼ੰਕੁਧਾਰੀ ਵਣ ਹਿਮਾਲਾ ਦੀਆਂ ਉਬੜ-ਖਾਬੜ ਢਲਾਣਾਂ ‘ਤੇ ਸਥਿਤ ਹੋਣ ਕਰਕੇ ਆਵਾਜਾਈ ਦੀਆਂ ਸਹੂਲਤਾਂ ਦੀ ਘਾਟ ਕਾਰਨ ਅਛੂਤੇ ਹੀ ਰਹਿ ਜਾਂਦੇ ਹਨ । ਇਸਦੇ ਉਲਟ ਅਸੀਂ ਚੌੜੇ ਪੱਤੀ ਵਾਲੇ ਸਾਲ ਤੇ ਟੀਕ ਜਿਹੇ 95% ਵਣਾਂ ਦਾ ਹੀ ਪ੍ਰਯੋਗ ਕਰ ਸਕਦੇ ਹਾਂ ।
3. ਪ੍ਰਸ਼ਾਸਨਿਕ ਜਾਂ ਪ੍ਰਬੰਧਕੀ ਆਧਾਰ ‘ਤੇ – ਵਣਾਂ ਦੇ ਪ੍ਰਬੰਧਨ ਨੂੰ ਧਿਆਨ ਵਿਚ ਰੱਖਦੇ ਹੋਏ ਇਨ੍ਹਾਂ ਨੂੰ ਤਿੰਨ ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਗਿਆ ਹੈ । ਇਸ ਦੇ ਅਨੁਸਾਰ 95% (717 ਲੱਖ ਹੈਕਟੇਅਰ ਵਣ ਖੇਤਰ ਰਾਜ ਦੇ ਅਧੀਨ ਹੈ । ਇਨ੍ਹਾਂ ‘ਤੇ ਰਾਜ ਸਰਕਾਰ ਦਾ ਪੁਰਾ ਏਕਾਧਿਕਾਰ ਹੁੰਦਾ ਹੈ ! ਦੁਸਰੇ ਪ੍ਰਕਾਰ ਦੇ ਵਣ ਸਥਾਨਿਕ ਨਗਰਪਾਲਿਕਾ ਜਾਂ ਜ਼ਿਲ੍ਹਾ ਪਰਿਸ਼ਦ ਦੀ ਦੇਖ ਰੇਖ ਦੇ ਅਧੀਨ ਆਉਂਦੇ ਹਨ । ਇਹ ਸਮੂਹਿਕ ਵਣ ਵੀ ਕਹਾਉਂਦੇ ਹਨ ।
4. ਵਣ ਕਾਨੂੰਨ ਦੇ ਆਧਾਰ ‘ਤੇ – ਕਾਨੂੰਨੀ ਨਿਯੰਤਰਣ ਤੇ ਸੁਰੱਖਿਆ ਦੇ ਪੱਖ ਤੋਂ ਤਿੰਨ ਵਰਗਾਂ ਸੁਰੱਖਿਅਤ ਵਣ, ਸੰਰਖਣ ਵਣ ਤੇ ਅਵਰਗੀਕ੍ਰਿਤ ਵਣਾਂ (ਅਣ-ਵੰਡੇ ਵਣ ਵਿੱਚ 52% ਵਣ ਖੇਤਰ ਆਉਂਦਾ ਹੈ । ਦੇਸ਼ ਵਿਚ ਭੁਮੀ ਦੇ ਕਟਾਅ ਨੂੰ ਰੋਕਣ, ਵਾਤਾਵਰਨ ਦੀ ਸੰਭਾਲ ਅਤੇ ਲੱਕੜੀ ਦੀ ਪੂਰਤੀ ਲਈ 52% (394 ਲੱਖ ਹੈਕਟੇਅਰ ਵਣ ਖੇਤਰ ਸੁਰੱਖਿਅਤ ਰੱਖਿਆ ਗਿਆ ਹੈ । ਇਨ੍ਹਾਂ ਵਣਾਂ ਵਿਚ ਪਸ਼ੂਆਂ ਨੂੰ ਚਰਾਉਣਾ ਅਤੇ ਲੱਕੜੀ ਕੱਟਣਾ ਮਨ੍ਹਾਂ ਹੈ । ਦੁਸਰੇ 32% (233 ਲੱਖ ਹੈਕਟੇਅਰ ਹਿੱਸਾ ਰਾਖਵਾਂ ਵਣ ਖੇਤਰ ਹੈ । ਸਰਕਾਰੀ ਕਾਨੂੰਨ ਅਨੁਸਾਰ ਇਨ੍ਹਾਂ ਨੂੰ ਨਸ਼ਟ ਨਹੀਂ ਕੀਤਾ ਜਾ ਸਕਦਾ । ਪਰ ਇੱਥੇ ਪਸ਼ੂ ਚਰਾਉਣਾ, ਲੱਕੜੀ ਕੱਟਣਾ ਆਦਿ ਸਹੂਲਤਾਂ ਮਿਲ ਜਾਂਦੀਆਂ ਹਨ । ਅਣ-ਵੰਡੇ ਵਣ ਜੋ 16% ਹਨ । ਇਹਨਾਂ ਵਿਚ ਵੀ ਲੋਕਾਂ ਨੂੰ ਸਹੂਲਤਾਂ ਪ੍ਰਾਪਤ ਹਨ ।
5. ਭੂਗੋਲਿਕ ਤੱਤਾਂ ਦੇ ਆਧਾਰ ‘ਤੇ – ਭੂਗੋਲਿਕ ਤੱਤਾਂ ਦੇ ਆਧਾਰ ‘ਤੇ ਦੇਸ਼ ਦੀ ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਨੂੰ ਹੇਠ ਲਿਖੇ ਖੰਡਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ
- ਊਸ਼ਣ ਸਦਾਬਹਾਰ ਬਨਸਪਤੀ
- ਪੱਤਝੜੀ ਜਾਂ ਮਾਨਸੂਨੀ ਬਨਸਪਤੀ
- ਖੁਸ਼ਕ ਬਨਸਪਤੀ
- ਜਵਾਰੀ ਬਨਸਪਤੀ
- ਪਰਬਤੀ ਬਨਸਪਤੀ ।
ਪ੍ਰਸ਼ਨ 2.
ਦੇਸ਼ ਵਿਚ ਭੂਗੋਲਿਕ ਤੱਤਾਂ ‘ਤੇ ਆਧਾਰਿਤ ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਦਾ ਵਰਗੀਕਰਨ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਭੂਗੋਲਿਕ ਤੱਤਾਂ ਦੇ ਆਧਾਰ ‘ਤੇ ਭਾਰਤ ਦੀ ਬਨਸਪਤੀ ਨੂੰ ਹੇਠ ਲਿਖੇ ਪੰਜ ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ-
1. ਊਸ਼ਣ ਸਦਾਬਹਾਰ ਵਣ – ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਵਣ ਮੁੱਖ ਰੂਪ ਨਾਲ ਜ਼ਿਆਦਾ ਵਰਖਾ (200 ਸੈਂਟੀਮੀਟਰ ਤੋਂ ਜ਼ਿਆਦਾ ਵਾਲੇ ਭਾਗਾਂ ਵਿਚ ਮਿਲਦੇ ਹਨ । ਇਸ ਲਈ ਇਨ੍ਹਾਂ ਨੂੰ ਬਰਸਾਤੀ ਵਣ ਵੀ ਕਹਿੰਦੇ ਹਨ । ਇਹ ਵਣ ਜ਼ਿਆਦਾਤਰ ਪੂਰਬੀ ਹਿਮਾਲਾ ਦੇ ਤਰਾਈ ਦੇਸ਼, ਪੱਛਮੀ ਘਾਟ, ਪੱਛਮੀ ਅੰਡੇਮਾਨ, ਅਸਮ, ਬੰਗਾਲ ਅਤੇ ਉੜੀਸਾ ਦੇ ਕੁੱਝ ਭਾਗਾਂ ਵਿਚ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਵਣਾਂ ਵਿਚ ਪਾਏ ਜਾਣ ਵਾਲੇ ਮੁੱਖ ਗ੍ਰਿਛ ਮਹੋਗਨੀ, ਤਾੜ, ਬਾਂਸ, ਬੈਂਤ, ਰਬੜ, ਚਪਲਾਂਸ, ਮੈਰੀਲਸ ਅਤੇ ਕਦੰਬ ਹਨ ।
2. ਪੱਤਝੜੀ ਜਾਂ ਮਾਨਸੂਨੀ ਵਣ – ਪੱਤਝੜੀ ਜਾਂ ਮਾਨਸੂਨੀ ਵਣ ਭਾਰਤ ਦੇ ਉਹਨਾਂ ਦੇਸ਼ਾਂ ਵਿਚ ਮਿਲਦੇ ਹਨ ਜਿੱਥੇ 100 ਤੋਂ 200 ਸੈਂਟੀਮੀਟਰ ਤਕ ਸਾਲਾਨਾ ਵਰਖਾ ਹੁੰਦੀ ਹੈ । ਭਾਰਤ ਵਿਚ ਇਹ ਵਣ ਮੁੱਖ ਰੂਪ ਨਾਲ ਹਿਮਾਲਿਆ ਦੇ ਹੇਠਲੇ ਭਾਗ, ਛੋਟਾ ਨਾਗਪੁਰ, ਗੰਗਾ ਦੀ ਘਾਟੀ, ਪੱਛਮੀ ਘਾਟ ਦੀਆਂ ਪੁਰਬੀ ਢਲਾਣਾਂ ਅਤੇ ਤਾਮਿਲਨਾਡੂ ਖੇਤਰ ਵਿਚ ਮਿਲਦੇ ਹਨ | ਇਨ੍ਹਾਂ ਵਣਾਂ ਵਿਚ ਮਿਲਣ ਵਾਲੇ ਮੁੱਖ ਦਰੱਖਤ ਸਾਗਵਾਨ, ਸਾਲ, ਸ਼ੀਸ਼ਮ, ਅੰਬ, ਚੰਦਨ, ਮਹੂਆ, ਏਬੋਨੀ, ਸ਼ਹਿਤੂਤ ਅਤੇ ਸੋਮਲ ਹਨ । ਗਰਮੀਆਂ ਵਿਚ ਇਹ ਦਰੱਖਤ ਆਪਣੀਆਂ ਪੱਤੀਆਂ ਡੇਗ ਦਿੰਦੇ ਹਨ ਇਸ ਲਈ ਇਹਨਾਂ ਨੂੰ ਪੱਤਝੜੀ ਵਣ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
3. ਮਾਰੂਥਲੀ ਵਣ – ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਵਣ ਉਹਨਾਂ ਖੇਤਰਾਂ ਵਿਚ ਪਾਏ ਜਾਂਦੇ ਹਨ ਜਿੱਥੇ ਸਾਲਾਨਾ ਵਰਖਾ ਦਾ ਮੱਧਮਾਨ 20 ਤੋਂ 60 ਸੈਂਟੀਮੀਟਰ ਤਕ ਹੁੰਦਾ ਹੈ । ਭਾਰਤ ਵਿਚ ਇਹ ਵਣ ਰਾਜਸਥਾਨ, ਪੱਛਮੀ ਹਰਿਆਣਾ, ਦੱਖਣੀ-ਪੱਛਮੀ ਪੰਜਾਬ ਅਤੇ ਗੁਜਰਾਤ ਵਿਚ ਮਿਲਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਵਣਾਂ ਵਿਚ ਰਾਮਬਾਂਸ, ਖੈਰ, ਪਿੱਪਲ ਅਤੇ ਖਜੂਰ ਦੇ ਦਰੱਖਤ ਮੁੱਖ ਹਨ ।
4. ਜਵਾਰੀ ਵਣ – ਜਵਾਰੀ ਵਣ ਨਦੀਆਂ ਦੇ ਡੈਲਟਿਆਂ ਵਿਚ ਪਾਏ ਜਾਂਦੇ ਹਨ। ਇੱਥੋਂ ਦੀ ਮਿੱਟੀ ਦੀ ਉਪਜਾਊ ਹੁੰਦੀ ਹੈ ਅਤੇ ਪਾਣੀ ਵੀ ਜ਼ਿਆਦਾ ਮਾਤਰਾ ਵਿਚ ਮਿਲ ਜਾਂਦਾ ਹੈ । ਭਾਰਤ ਵਿਚ ਇਸ ਪ੍ਰਕਾਰ ਦੇ ਵਣ ਮਹਾਂਨਦੀ, ਗੋਦਾਵਰੀ, ਕ੍ਰਿਸ਼ਨਾ, ਕਾਵੇਰੀ ਆਦਿ ਦੇ ਡੈਲਟਾਈ ਦੇਸ਼ਾਂ ਵਿਚ ਮਿਲਦੇ ਹਨ । ਇੱਥੋਂ ਦੀ ਬਨਸਪਤੀ ਨੂੰ ਮੈਂਗਰੋਵ ਜਾਂ ਸੁੰਦਰ ਵਣ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਕੁੱਝ ਖੇਤਰਾਂ ਵਿਚ ਤਾੜ, ਕੈਂਸ, ਨਾਰੀਅਲ ਆਦਿ ਦੇ ਦਰੱਖਤ ਮਿਲਦੇ ਹਨ ।
5. ਪਰਬਤੀ ਬਨਸਪਤੀ-ਇਸ ਪ੍ਰਕਾਰ ਦੀ ਬਨਸਪਤੀ ਹਿਮਾਲਿਆ ਦੇ ਪਰਬਤੀ ਖੇਤਰਾਂ ਅਤੇ ਦੱਖਣ ਵਿਚ ਨੀਲਗਿਰੀ ਦੀਆਂ ਪਹਾੜੀਆਂ ‘ਤੇ ਮਿਲਦੀ ਹੈ । ਇਸ ਬਨਸਪਤੀ ਵਿਚ ਵਰਖਾ ਦੀ ਮਾਤਰਾ ਅਤੇ ਉਚਾਈ ਤੇ ਸਦਾਬਹਾਰ ਵਣ ਮਿਲਦੇ ਹਨ ਤਾਂ ਜ਼ਿਆਦਾ ਉਚਾਈ ‘ਤੇ ਸਿਰਫ਼ ਘਾਹ ਅਤੇ ਕੁੱਝ ਫੁੱਲਦਾਰ ਪੌਦੇ ਹੀ ਮਿਲਦੇ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਕੁਦਰਤੀ ਬਨਸਪਤੀ (ਵਣਾਂ ਦਾ ਦੇਸ਼ ਨੂੰ ਕੀ ਲਾਭ ਹੈ ?
ਉੱਤਰ-
ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਤੋਂ ਸਾਨੂੰ ਕਈ ਸਿੱਧੇ ਅਤੇ ਅਸਿੱਧੇ ਲਾਭ ਹੁੰਦੇ ਹਨ-
ਸਿੱਧੇ ਲਾਭ – ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਤੋਂ ਹੋਣ ਵਾਲੇ ਸਿੱਧੇ ਲਾਭਾਂ ਦਾ ਵਰਣਨ ਇਸ ਪ੍ਰਕਾਰ ਹੈ-
- ਵਣਾਂ ਤੋਂ ਸਾਨੂੰ ਕਈ ਪ੍ਰਕਾਰ ਦੀ ਲੱਕੜੀ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ਜਿਸ ਦਾ ਪ੍ਰਯੋਗ ਇਮਾਰਤਾਂ, ਫ਼ਰਨੀਚਰ, ਲੱਕੜ ਦਾ ਕੋਲਾ ਆਦਿ ਬਣਾਉਣ ਵਿਚ ਹੁੰਦਾ ਹੈ । ਇਸ ਦਾ ਪ੍ਰਯੋਗ ਬਾਲਣ ਦੇ ਰੂਪ ਵਿਚ ਵੀ ਹੁੰਦਾ ਹੈ ।
- ਖੈਰ, ਸਿਨਕੋਨਾ, ਕੁਨੀਨ, ਬਹੇੜਾ ਅਤੇ ਆਂਵਲੇ ਤੋਂ ਕਈ ਪ੍ਰਕਾਰ ਦੀਆਂ ਦਵਾਈਆਂ ਤਿਆਰ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ।
- ਮੈਂਗਰੋਵ, ਕੰਚ, ਗੈਂਬੀਅਰ, ਹਰੜ, ਬਹੇੜਾ, ਆਂਵਲਾ ਅਤੇ ਕਿੱਕਰ ਆਦਿ ਦੇ ਪੱਤੇ, ਛਿਲਕੇ ਤੇ ਫਲਾਂ ਨੂੰ ਸੁਕਾ ਕੇ ਚਮੜਾ ਰੰਗਣ ਦਾ ਪਦਾਰਥ ਤਿਆਰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
- ਪਾਲਸ਼ ਤੇ ਪਿੱਪਲ ਤੋਂ ਲਾਖ, ਸ਼ਹਿਤੂਤ ਤੋਂ ਰੇਸ਼ਮ, ਚੰਦਨ ਤੋਂ ਤੰਗ ਤੇ ਤੇਲ ਅਤੇ ਸਾਲ ਤੋਂ ਧੂਪ ਤੇ ਬਿਰੋਜ਼ਾ ਤਿਆਰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
ਅਸਿੱਧੇ ਲਾਭ – ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਤੋਂ ਸਾਨੂੰ ਹੇਠ ਲਿਖੇ ਅਸਿੱਧੇ ਲਾਭ ਹੁੰਦੇ ਹਨ-
- ਵਣ ਜਲਵਾਯੂ ‘ਤੇ ਕੰਟਰੋਲ ਰੱਖਦੇ ਹਨ । ਸੰਘਣੇ ਵਣ ਗਰਮੀਆਂ ਵਿਚ ਤਾਪਮਾਨ ਨੂੰ ਵਧਣ ਤੋਂ ਰੋਕਦੇ ਹਨ ਅਤੇ ਸਰਦੀਆਂ ਵਿਚ ਤਾਪਮਾਨ ਨੂੰ ਵਧਾ ਦਿੰਦੇ ਹਨ ।
- ਸੰਘਣੀ ਬਨਸਪਤੀ ਦੀਆਂ ਜੜਾਂ ਵਗਦੇ ਪਾਣੀ ਦੀ ਰਫ਼ਤਾਰ ਨੂੰ ਘੱਟ ਕਰਨ ਵਿਚ ਮੱਦਦ ਕਰਦੀਆਂ ਹਨ । ਇਸ ਨਾਲ ਹੜਾਂ ਦੀ ਕਰੋਪੀ ਘੱਟ ਜਾਂਦੀ ਹੈ । ਦੁਸਰੇ ਜੜ੍ਹਾਂ ਰਾਹੀਂ ਰੋਕਿਆ ਗਿਆ ਪਾਣੀ ਜ਼ਮੀਨ ਅੰਦਰ ਸਮਾ ਜਾਣ ਕਰਕੇ ਇਕ ਤਾਂ ਜਲ-ਸਤਰ ਉੱਚਾ ਹੋ ਜਾਂਦਾ ਹੈ ਤੇ ਦੂਸਰੇ ਪਾਸੇ ਧਰਾਤਲ ਤੇ ਪਾਣੀ ਦੀ ਮਾਤਰਾ ਘੱਟ ਜਾਣ ਕਰਕੇ ਪਾਣੀ ਨਦੀਆਂ ਵਿਚ ਆਸਾਨੀ ਨਾਲ ਵਹਿੰਦਾ ਰਹਿੰਦਾ ਹੈ ।
- ਦਰੱਖਤਾਂ ਦੀਆਂ ਜੜ੍ਹਾਂ ਮਿੱਟੀ ਦੀ ਜਕੜਨ ਨੂੰ ਮਜ਼ਬੂਤ ਰੱਖਦੀਆਂ ਹਨ ਅਤੇ ਮਿੱਟੀ ਦੇ ਕਟਾਅ ਨੂੰ ਰੋਕਦੀਆਂ ਹਨ ।
- ਬਨਸਪਤੀ ਦੇ ਸੁੱਕ ਕੇ ਡਿੱਗਣ ਨਾਲ ਜੀਵਾਂਸ਼ (Humus) ਦੇ ਰੂਪ ਵਿਚ ਮਿੱਟੀ ਨੂੰ ਹਰੀ ਖਾਦ ਮਿਲਦੀ ਹੈ ।
- ਹਰੀ ਭਰੀ ਬਨਸਪਤੀ ਬਹੁਤ ਹੀ ਮਨਮੋਹਕ ਦ੍ਰਿਸ਼ ਪੇਸ਼ ਕਰਦੀ ਹੈ । ਇਸ ਤੋਂ ਆਕਰਸ਼ਿਤ ਹੋ ਕੇ ਲੋਕ ਸੰਘਣੇ ਵਣ ਖੇਤਰਾਂ ਵਿਚ ਯਾਤਰਾ, ਸ਼ਿਕਾਰ ਅਤੇ ਮਾਨਸਿਕ ਸ਼ਾਂਤੀ ਲਈ ਜਾਂਦੇ ਹਨ । ਕਈ ਵਿਦੇਸ਼ੀ ਸੈਲਾਨੀ ਵੀ ਵਣ ਖੇਤਰਾਂ ਵਿੱਚ ਬਣੇ ਸੈਰਗਾਹ ਕੇਂਦਰ ‘ਤੇ ਆਉਂਦੇ ਹਨ । ਇਸ ਨਾਲ ਸਰਕਾਰ ਨੂੰ ਵਿਦੇਸ਼ੀ ਮੁਦਰਾ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ।
- ਸੰਘਣੇ ਵਣ ਅਨੇਕਾਂ ਉਦਯੋਗਾਂ ਦਾ ਆਧਾਰ ਹਨ । ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਕਾਗਜ਼, ਦੀਆ-ਸਲਾਈ, ਰੇਸ਼ਮ, ਖੇਡਾਂ ਦਾ ਸਾਮਾਨ, ਪਲਾਈ ਵੁੱਡ, ਗੂੰਦ, ਬਰੋਜ਼ਾ ਆਦਿ ਮੁੱਖ ਉਦਯੋਗ ਹਨ ।
ਪ੍ਰਸ਼ਨ 4.
ਮਿੱਟੀ ਦੀ ਬਣਤਰ ਕਿਹੜੇ-ਕਿਹੜੇ ਤੱਤਾਂ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ ?
ਉੱਤਰ-
ਮਿੱਟੀ ਦੀ ਬਣਤਰ ਹੇਠ ਲਿਖੇ ਪੰਜ ਤੱਤਾਂ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ-
1. ਮੁੱਢਲੀ ਚੱਟਾਨ – ਦੇਸ਼ ਦੇ ਉੱਤਰੀ ਮੈਦਾਨਾਂ ਦੀਆਂ ਤਹਿਦਾਰ ਚੱਟਾਨਾਂ ਵੱਖਰੇ-ਵੱਖਰੇ ਖਣਿਜਾਂ ਦੀ ਬਣੀ ਹੋਣ ਕਰਕੇ ਸਭ ਤੋਂ ਵਧੀਆ ਕਿਸਮ ਦੀ ਮਿੱਟੀ ਪ੍ਰਦਾਨ ਕਰਦੀਆਂ ਹਨ ਉੱਥੇ ਦੂਸਰੇ ਪਾਸੇ ਦੇਸ਼ ਦੇ ਪਠਾਰੀ ਭਾਗ ਦੀਆਂ ਲਾਵੇ ਤੋਂ ਬਣੀਆਂ ਚੱਟਾਨਾਂ ਜ਼ੋਨਲ ਮਿੱਟੀਆਂ ਨੂੰ ਜਨਮ ਦਿੰਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਵਿਚ ਕਈ ਪ੍ਰਕਾਰ ਦੇ ਖਣਿਜ ਪਦਾਰਥ ਮਿਲਦੇ ਹਨ, ਜਿਸ ਦੇ ਕਾਰਨ ਇਹ ਮਿੱਟੀਆਂ ਉਪਜਾਉ ਹੁੰਦੀਆਂ ਹਨ ।
2. ਜਲਵਾਯੂ – ਮੁੱਢਲੀਆਂ ਚੱਟਾਨਾਂ ਤੋਂ ਬਣਨ ਵਾਲੀ ਮਿੱਟੀ ਦਾ ਰੰਗ, ਗਠਨ, ਬਨਾਵਟ ਆਦਿ ਇਸ ਗੱਲ ‘ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ਕਿ ਚੱਟਾਨ ਕਿੰਨੇ ਸਮੇਂ ਅਤੇ ਕਿਸ ਤਰ੍ਹਾਂ ਦੀ ਜਲਵਾਯੂ ਦੁਆਰਾ ਪ੍ਰਭਾਵਿਤ ਹੋ ਰਹੀ ਹੈ । ਪੱਛਮੀ ਬੰਗਾਲ ਵਰਗੇ ਦੇਸ਼ ਵਿਚ ਜਲਵਾਯੂ ਰਸਾਇਣਿਕ ਕਿਰਿਆਵਾਂ ਦੇ ਪ੍ਰਭਾਵ ਤੇ ਮਲ੍ਹੜ ਦੀ ਹੋਂਦ ਕਾਰਨ ਮਿੱਟੀ ਜ਼ਿਆਦਾ ਵਿਕਸਿਤ ਹੁੰਦੀ ਹੈ । ਇਸ ਦੇ ਉਲਟ ਰਾਜਸਥਾਨ ਵਰਗੇ ਖ਼ੁਸ਼ਕ ਖੇਤਰ ਵਿਚ ਬਨਸਪਤੀ ਦੀ ਕਮੀ ਦੇ ਕਾਰਨ ਮਿੱਟੀ ਦੀ ਉਪਜਾਊ ਸ਼ਕਤੀ ਘੱਟ ਹੁੰਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਜ਼ਿਆਦਾ ਵਰਖਾ ਤੇ ਤੇਜ਼ ਪੌਣਾਂ ਵਾਲੇ ਖੇਤਰਾਂ ਵਿਚ ਮਿੱਟੀ ਦਾ ਕਟਾਅ ਜ਼ਿਆਦਾ ਹੋਣ ਨਾਲ ਮਿੱਟੀ ਦੀ ਉਪਜਾਊ ਸ਼ਕਤੀ ਘੱਟ ਹੋ ਜਾਂਦੀ ਹੈ ।
3. ਢਲਾਣ – ਜਲਵਾਯੂ ਤੋਂ ਬਿਨਾਂ ਖੇਤਰੀ ਢਲਾਨ ਵੀ ਮਿੱਟੀ ਦੇ ਵਿਕਾਸ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀ ਹੈ । ਦੇਸ਼ ਦੇ ਤਿੱਖੀਆਂ ਢਲਾਣਾਂ ਵਾਲੇ ਪਹਾੜੀ ਖੇਤਰਾਂ ਵਿਚ ਪਾਣੀ ਦੇ ਤੇਜ਼ ਵਹਾਅ ਅਤੇ ਗੁਰੂਤਾ ਖਿੱਚ ਸ਼ਕਤੀ ਦੇ ਕਾਰਨ ਮਿੱਟੀ ਖਿਸਕਦੀ ਰਹਿੰਦੀ ਹੈ । ਇਹੋ ਕਾਰਨ ਹੈ ਪਰਬਤੀ ਖੇਤਰਾਂ ਦੀਆਂ ਢਲਾਣਾਂ ਦੀ ਬਜਾਏ ਗੰਗਾ, ਸਿੰਧੂ ਅਤੇ ਬ੍ਰਹਮਪੁੱਤਰ ਵਰਗੀਆਂ ਨਦੀਆਂ ਦੀਆਂ ਘਾਟੀਆਂ ਵਿਚ ਮਿੱਟੀ ਜ਼ਿਆਦਾ ਉਪਜਾਉ ਹੁੰਦੀ ਹੈ ।
4. ਕੁਦਰਤੀ ਬਨਸਪਤੀ – ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਜੈਵਿਕ ਚੂਰੇ ਦੀ ਪੂਰਤੀ ਕਰਕੇ ਮਿੱਟੀ ਦਾ ਵਿਕਾਸ ਕਰਨ ਵਾਲਾ ਮੁੱਖ ਤੱਤ ਹੈ । ਪਰ ਸਾਡੇ ਦੇਸ਼ ਦੀ ਜ਼ਿਆਦਾਤਰ ਭੂਮੀ ਖੇਤੀ ਦੇ ਅਧੀਨ ਹੋਣ ਦੇ ਕਾਰਨ ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਦੀ ਘਾਟ ਹੈ। ਦੇਸ਼ ਦੀਆਂ ਲਾਵੇ ਵਾਲੀਆਂ ਮਿੱਟੀਆਂ ਵਿਚ ਅਤੇ ਸੁਰੱਖਿਅਤ ਵਣ ਖੇਤਰ ਦੀ ਮਿੱਟੀ ਵਿਚ 5-10% ਤਕ ਜੈਵਿਕ ਅੰਸ਼ ਮਿਲਦਾ ਹੈ ।
5. ਸਮਾਂ – ਇਨ੍ਹਾਂ ਸਾਰੇ ਤੱਤਾਂ ਤੋਂ ਬਿਨਾਂ ਮਿੱਟੀ ਦੇ ਵਿਕਾਸ ਵਿਚ ਸਮੇਂ ਦਾ ਵੀ ਆਪਣਾ ਮਹੱਤਵ ਹੁੰਦਾ ਹੈ । ਮਿੱਟੀਆਂ ਵਿਚ ਹਰੇਕ ਸਾਲ ਮਲ੍ਹੜ ਤੇ ਜੀਵਾਂਸ਼ ਪ੍ਰਾਪਤ ਹੋ ਜਾਂਦੀ ਹੈ ਅਤੇ ਲੱਖਾਂ ਸਾਲਾਂ ਦੀ ਨਿਰਵਿਘਨ ਕਿਰਿਆ ਦੁਆਰਾ ਹੀ ਵਧੀਆ ਮਿੱਟੀ ਦਾ ਨਿਰਮਾਣ ਹੁੰਦਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਭਾਰਤ ਵਿਚ ਮਿਲਣ ਵਾਲੀਆਂ ਮਿੱਟੀਆਂ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਕਿਸਮਾਂ ਦਾ ਵਿਸ਼ੇਸ਼ਤਾਈਆਂ ਸਮੇਤ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਕਈ ਪ੍ਰਕਾਰ ਦੀਆਂ ਮਿੱਟੀਆਂ ਮਿਲਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਦੇ ਗੁਣਾਂ ਦੇ ਆਧਾਰ ‘ਤੇ ਇਨ੍ਹਾਂ ਨੂੰ ਅੱਠ , ਵਰਗਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ-
1. ਜਲੋਢ ਮਿੱਟੀ (Alluvial Soil) – ਭਾਰਤ ਵਿਚ ਜਲੋਢ ਮਿੱਟੀ ਉੱਤਰੀ ਮੈਦਾਨ, ਰਾਜਸਥਾਨ, ਗੁਜਰਾਤ ਅਤੇ ਦੱਖਣ ਦੇ ਤਟੀ ਮੈਦਾਨਾਂ ਵਿਚ ਆਮ ਮਿਲਦੀ ਹੈ । ਇਨ੍ਹਾਂ ਬਾਰੀਕ ਕਣਾਂ ਨੂੰ ਜਲੋਢ ਕਹਿੰਦੇ ਹਨ । ਇਸ ਵਿਚ ਰੇਤ, ਗਾਰ ਮਿਲੀ ਹੁੰਦੀ ਹੈ । ਜਲੋਢ ਮਿੱਟੀ ਦੋ ਪ੍ਰਕਾਰ ਦੀ ਹੁੰਦੀ ਹੈ-ਬਾਂਗਰ ਅਤੇ ਖਾਦਰ ।
ਜਲੋਢ ਮਿੱਟੀਆਂ ਆਮ ਤੌਰ ‘ਤੇ ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਉਪਜਾਊ ਹੁੰਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਮਿੱਟੀਆਂ ਵਿਚ, ਪੋਟਾਸ਼, ਫਾਸਫੋਰਿਕ ਐਸਿਡ ਅਤੇ ਚੂਨਾ ਕਾਫ਼ੀ ਮਾਤਰਾ ਵਿਚ ਹੁੰਦਾ ਹੈ । ਪਰ ਇਨ੍ਹਾਂ ਵਿਚ ਨਾਈਟਰੋਜਨ ਅਤੇ ਜੈਵਿਕ ਪਦਾਰਥਾਂ ਦੀ ਕਮੀ ਹੁੰਦੀ ਹੈ ।
2. ਕਾਲੀ ਜਾਂ ਰੇਗੁਰ ਮਿੱਟੀ (Black Soil) – ਇਸ ਮਿੱਟੀ ਦਾ ਨਿਰਮਾਣ ਲਾਵੇ ਦੇ ਪ੍ਰਵਾਹ ਤੋਂ ਹੋਇਆ ਹੈ । ਇਹ ਮਿੱਟੀ ਕਪਾਹ ਦੀ ਫ਼ਸਲ ਲਈ ਬਹੁਤ ਲਾਭਦਾਇਕ ਹੈ । ਇਸ ਲਈ ਇਸ ਨੂੰ ਕਪਾਹ ਵਾਲੀ ਮਿੱਟੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਮਿੱਟੀ ਦਾ ਸਥਾਨਿਕ ਨਾਂ ‘ਰੇਗੁਰ’ ਹੈ । ਇਹ ਦੱਖਣ ਟੈਪ ਪ੍ਰਦੇਸ਼ ਦੀ ਪਮੁੱਖ ਮਿੱਟੀ ਹੈ । ਇਹ ਪੱਛਮ ਵਿਚ ਮੁੰਬਈ ਤੋਂ ਲੈ ਕੇ ਪੁਰਬ ਵਿਚ ਅਮਰਕੰਟਕ ਪਠਾਰ, ਉੱਤਰ ਵਿੱਚ ਗਨਾ (ਮੱਧ ਪ੍ਰਦੇਸ਼ ਅਤੇ ਦੱਖਣ ਵਿਚ ਬੈਲਗਾਮ ਤਕ ਤ੍ਰਿਭੁਜਾਂ ਆਕਾਰ ਖੇਤਰ ਵਿਚ ਫੈਲੀ ਹੋਈ ਹੈ ।
ਕਾਲੀ ਮਿੱਟੀ ਨਮੀ ਨੂੰ ਜ਼ਿਆਦਾ ਸਮੇਂ ਤਕ ਧਾਰਨ ਕਰ ਸਕਦੀ ਹੈ । ਇਸ ਮਿੱਟੀ ਵਿਚ ਲੌਹ, ਪੋਟਾਸ਼, ਚੂਨਾ, ਐਲੂਮੀਨੀਅਮ ਅਤੇ ਮੈਗਨੀਸ਼ੀਅਮ ਦੀ ਮਾਤਰਾ ਵਧੇਰੇ ਹੁੰਦੀ ਹੈ, ਪਰ ਨਾਈਟ੍ਰੋਜਨ, ਫਾਸਫੋਰਸ ਅਤੇ ਜੀਵਾਂਸ਼ ਦੀ ਮਾਤਰਾ ਘੱਟ ਹੁੰਦੀ ਹੈ ।
3. ਲਾਲ ਮਿੱਟੀ (Red Soil) – ਇਸ ਮਿੱਟੀ ਦਾ ਲਾਲ ਰੰਗ ਲੋਹੇ ਦੇ ਰਵੇਦਾਰ ਅਤੇ ਪਰਿਵਰਤਿਤ ਚੱਟਾਨਾਂ ਵਿਚ ਬਦਲ ਜਾਣ ਕਾਰਨ ਹੁੰਦਾ ਹੈ । ਇਸ ਦਾ ਵਿਸਥਾਰ ਤਾਮਿਲਨਾਡੂ, ਕਰਨਾਟਕ, ਆਂਧਰਾ ਪ੍ਰਦੇਸ਼, ਉੜੀਸਾ, ਦੱਖਣੀ ਬਿਹਾਰ, ਝਾਰਖੰਡ, ਪੂਰਬੀ ਮੱਧ ਪ੍ਰਦੇਸ਼, ਛਤੀਸਗੜ੍ਹ ਅਤੇ ਉੱਤਰੀ-ਪੂਰਬੀ ਪਰਬਤੀ ਰਾਜਾਂ ਵਿਚ ਹੈ । ਲਾਲ ਮਿੱਟੀ ਵਿਚ ਨਾਈਟ੍ਰੋਜਨ ਅਤੇ ਚੂਨੇ ਦੀ ਕਮੀ, ਪਰ ਮੈਗਨੀਸ਼ੀਅਮ, ਐਲੂਮੀਨੀਅਮ ਤੇ ਲੋਹੇ ਦੀ ਮਾਤਰਾ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ ।
4. ਲੈਟਰਾਈਟ ਮਿੱਟੀ (Laterite Soil) – ਇਸ ਮਿੱਟੀ ਵਿਚ ਨਾਈਟ੍ਰੋਜਨ, ਚਨਾ ਅਤੇ ਪੋਟਾਸ਼ ਦੀ ਕਮੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਲੋਹੇ ਅਤੇ ਐਲੂਮੀਨੀਅਮ ਆਕਸਾਈਡ ਦੀ ਜ਼ਿਆਦਾ ਮਾਤਰਾ ਹੋਣ ਦੇ ਕਾਰਨ ਇਸ ਦਾ ਸੁਭਾਅ ਤੇਜ਼ਾਬੀ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਦਾ ਵਿਸਥਾਰ ਵਿੰਧੀਆਚਲ, ਸਤਪੁੜਾ ਦੇ ਨਾਲ ਲੱਗਦੇ ਮੱਧ ਪ੍ਰਦੇਸ਼, ਉੜੀਸਾ, ਪੱਛਮੀ ਬੰਗਾਲ ਦੀਆਂ ਬਸਾਲਟਿਕ ਪਰਬਤੀ ਚੋਟੀਆਂ, ਦੱਖਣੀ ਮਹਾਂਰਾਸ਼ਟਰ ਅਤੇ ਉੱਤਰ-ਪੂਰਬ ਵਿਚ ਸ਼ਿਲਾਂਗ ਦੇ ਪਠਾਰ ਦੇ ਉੱਤਰੀ ਅਤੇ ਪੂਰਬੀ ਭਾਗ ਵਿਚ ਹੈ ।
5. ਮਾਰੂਥਲੀ ਮਿੱਟੀ (Desert Soil) – ਇਸ ਮਿੱਟੀ ਦਾ ਵਿਸਥਾਰ ਪੱਛਮ ਵਿਚ ਸਿੰਧੂ ਨਦੀ ਤੋਂ ਲੈ ਕੇ ਪੂਰਬ ਵਿਚ ਅਰਾਵਲੀ ਪਰਬਤ ਤਕ ਰਾਜਸਥਾਨ, ਦੱਖਣੀ ਪੰਜਾਬ ਤੇ ਦੱਖਣੀ ਹਰਿਆਣਾ ਵਿਚ ਮਿਲਦਾ ਹੈ । ਇਸ ਵਿਚ ਘੁਲਣਸ਼ੀਲ ਨਮਕ ਦੀ ਮਾਤਰਾ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ | ਪਰ ਇਸ ਮਿੱਟੀ ਵਿਚ ਨਾਈਟਰੋਜਨ ਮੜ ਦੀ ਬਹੁਤ ਘਾਟ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ 92% ਰੇਤ ਤੇ 8% ਚੀਕਣੀ ਮਿੱਟੀ ਦਾ ਅੰਸ਼ ਹੁੰਦਾ ਹੈ । ਇਸ ਵਿਚ ਸਿੰਜਾਈ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਬਾਜਰਾ, ਜਵਾਰ, ਕਪਾਹ, ਗੰਨਾ, ਕਣਕ ਅਤੇ ਸਬਜ਼ੀਆਂ ਆਦਿ ਉਗਾਈਆਂ ਜਾ ਰਹੀਆਂ ਹਨ ।
6. ਖਾਰੀ ਤੇ ਤੇਜ਼ਾਬੀ ਮਿੱਟੀ (Saline & Alkaline Soil) – ਇਹ ਉੱਤਰ ਪ੍ਰਦੇਸ਼, ਰਾਜਸਥਾਨ, ਹਰਿਆਣਾ ਤੇ ਪੰਜਾਬ ਦੇ ਦੱਖਣੀ ਭਾਗਾਂ ਵਿਚ ਛੋਟੇ-ਛੋਟੇ ਟੁਕੜਿਆਂ ਵਿਚ ਮਿਲਦੀ ਹੈ ।
ਖਾਰੀਆਂ ਮਿੱਟੀਆਂ ਵਿਚ ਸੋਡੀਅਮ ਭਰਪੂਰ ਮਾਤਰਾ ਵਿਚ ਮਿਲਦਾ ਹੈ, ਤੇਜ਼ਾਬੀ ਮਿੱਟੀ ਵਿਚ ਕੈਲਸ਼ੀਅਮ ਤੇ ਨਾਈਟਰੋਜਨ ਦੀ ਕਮੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਨਮਕੀਨ ਮਿੱਟੀ ਨੂੰ ਉੱਤਰ ਪ੍ਰਦੇਸ਼ ਵਿਚ “ਔਸੜ ਜਾਂ ‘ਰੇਹ”, ਪੰਜਾਬ ਵਿਚ ‘ਕੱਲਰ` ਜਾਂ “ਬੁੜ ਅਤੇ ਹੋਰ ਭਾਗਾਂ ਵਿਚ ‘ਰੱਕੜ’, ‘ਕਾਰਲ’ ਅਤੇ ‘ਛੋਪਾਂ ਮਿੱਟੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
7. ਪੀਟ ਅਤੇ ਦਲਦਲੀ ਮਿੱਟੀ (Peat & Marshy Soils) – ਇਸ ਦਾ ਵਿਸਥਾਰ ਸੁੰਦਰ ਵਣ ਦੇ ਡੈਲਟਾ, ਉੜੀਸਾ ਦੇ ਤਟਵਰਤੀ ਖੇਤਰ, ਤਾਮਿਲਨਾਡੂ ਦੇ ਦੱਖਣ-ਪੂਰਬੀ ਤਟਵਰਤੀ ਭਾਗ, ਮੱਧਵਰਤੀ ਬਿਹਾਰ ਅਤੇ ਉਤਰਾਖੰਡ ਦੇ ਅਲਮੋੜਾ ਵਿਚ ਹੈ । ਇਸ ਦਾ ਰੰਗ ਜੈਵਿਕ ਪਦਾਰਥਾਂ ਦੀ ਅਧਿਕਤਾ ਦੇ ਕਾਰਨ ਕਾਲਾ ਤੇ ਤੇਜ਼ਾਬੀ ਸੁਭਾਅ ਵਾਲਾ ਹੁੰਦਾ ਹੈ । ਜੈਵਿਕ ਪਦਾਰਥਾਂ ਦੀ ਅਧਿਕਤਾ ਦੇ ਕਾਰਨ ਇਹ ਨੀਲੇ ਰੰਗ ਵਾਲੀ ਮਿੱਟੀ ਵੀ ਬਣ ਜਾਂਦੀ ਹੈ ।
8. ਪਰਬਤੀ ਮਿੱਟੀ (Mountain Soils) – ਇਸ ਮਿੱਟੀ ਵਿਚ ਰੇਤ, ਪੱਥਰ ਅਤੇ ਬਜਰੀ ਦੀ ਮਾਤਰਾ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਚੂਨਾ ਘੱਟ ਅਤੇ ਲੋਹੇ ਦੀ ਮਾਤਰਾ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ । ਇਹ ਚਾਹ ਦੀ ਖੇਤੀ ਲਈ ਬਹੁਤ ਅਨੁਕੂਲ ਹੁੰਦੀ ਹੈ । ਇਸ ਦਾ ਵਿਸਥਾਰ ਅਸਾਮ, ਲੱਦਾਖ, ਲਾਹੌਲ ਸਪੀਤੀ, ਕਿਨੌਰ, ਦਾਰਜੀਲਿੰਗ, ਦੇਹਰਾਦੂਨ, ਅਲਮੋੜਾ, ਗੜ੍ਹਵਾਲ ਤੇ ਦੱਖਣ ਵਿਚ ਨੀਲਗਿਰੀ ਦੇ ਪਰਬਤੀ ਖੇਤਰ ਵਿਚ ਹੈ ।
ਪ੍ਰਸ਼ਨ 6.
ਮਿੱਟੀ ਦਾ ਕਟਾਅ ਕੀ ਹੈ ਤੇ ਕਿਉਂ ਹੁੰਦਾ ਹੈ ? ਇਸ ਦੀ ਖੇਤਰੀ ਵੰਡ ਕੀ ਹੈ ? ਇਸ ਦੀ ਸੰਭਾਲ ਕਿਵੇਂ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ?
ਉੱਤਰ-
ਧਰਾਤਲ ‘ਤੇ ਮਿਲਣ ਵਾਲੀ 15 ਤੋਂ 30 ਸੈਂਟੀਮੀਟਰ ਮੋਟੀ ਤਹਿ ਦਾ ਭੌਤਿਕ ਤੇ ਗੈਰ-ਭੌਤਿਕ ਤੱਤਾਂ ਦੁਆਰਾ ਆਪਣੇ ਮੂਲ ਸਥਾਨ ਤੋਂ ਟੁੱਟ ਜਾਣਾ ਜਾਂ ਹਟ ਜਾਣਾ, ਮਿੱਟੀ ਦਾ ਕਟਾਅ ਕਹਾਉਂਦਾ ਹੈ ।
ਖੇਤਰੀ ਵੰਡ – ਮਿੱਟੀ ਦੇ ਕਟਾਅ ਦਾ ਦੇਸ਼ ਦੇ ਅੱਗੇ ਲਿਖੇ ਭਾਗਾਂ ‘ਤੇ ਪ੍ਰਭਾਵ ਪਿਆ ਹੈ-
- ਬਾਹਰੀ ਹਿਮਾਲਿਆ (ਸ਼ਿਵਾਲਿਕ) ਖੇਤਰਾਂ ਵਿਚ ਕੁਦਰਤੀ ਬਨਸਪਤੀ ਦਾ ਬਹੁਤ ਜ਼ਿਆਦਾ ਕਟਾਅ ਹੋਇਆ ਹੈ । ਇਸ ਨੇ ਉਪਜਾਊ ਭੂਮੀ ਨੂੰ ਪਾਣੀ ਤੇ ਗਾਰੇ ਨਾਲ ਲੱਦ ਕੇ ਖੇਤੀਬਾੜੀ ਤੋਂ ਬੇਕਾਰ ਕਰ ਦਿੱਤਾ ਹੈ ।
- ਪੰਜਾਬ ਦੇ ਹੁਸ਼ਿਆਰਪੁਰ, ਰੋਪੜ ਜ਼ਿਲ੍ਹੇ, ਯਮੁਨਾ, ਚੰਬਲ, ਮਾਹੀ ਤੇ ਸਾਬਰਮਤੀ ਨਦੀਆਂ ਦੇ ਕੈਚਮੈਂਟ ਖੇਤਰਾਂ ਵਿਚ ਨਾਲਿਆਂ ਤੇ ‘ਚੋਆਂ ਨੇ ਬਨਸਪਤੀ ਦੀ ਕਮੀ ਦੇ ਕਾਰਨ ਭੂਮੀ ਨੂੰ ਬੰਜਰ ਬਣਾ ਦਿੱਤਾ ਹੈ ।
- ਦੱਖਣੀ ਪੰਜਾਬ, ਹਰਿਆਣਾ ਤੇ ਪੂਰਬੀ ਰਾਜਸਥਾਨ, ਪੱਛਮੀ ਉੱਤਰ ਪ੍ਰਦੇਸ਼ ਤੇ ਉੱਤਰ ਪੂਰਬੀ ਗੁਜਰਾਤ ਦੇ ਖੁਸ਼ਕ ਖੇਤਰਾਂ ਵਿਚ ਪੌਣਾਂ ਦੁਆਰਾ ਕਟਾਅ ਹੋਇਆ ਹੈ ।
- ਦੇਸ਼ ਦੇ ਉੱਤਰ-ਪੂਰਬੀ ਰਾਜਾਂ ਵਿਚ ਪੱਛਮੀ ਬੰਗਾਲ ਸਮੇਤ ਭਾਰੀ ਵਰਖਾ, ਹੜ੍ਹ ਤੇ ਨਦੀ-ਕਿਨਾਰਿਆਂ ਦੀ ਕਟਾਈ ਨਾਲ ਸੈਂਕੜੇ ਟਨ ਮਿੱਟੀ ਬੰਗਾਲ ਦੀ ਖਾੜੀ ਵਿਚ ਚਲੀ ਜਾਂਦੀ ਹੈ ।
- ਦੱਖਣ ਤੇ ਦੱਖਣ ਪੂਰਬੀ ਭਾਰਤ ਵਿਚ ਮਿੱਟੀ ਦਾ ਕਟਾਅ ਤੇਜ਼ ਢਲਾਨਾਂ, ਭਾਰੀ ਵਰਖਾ ਤੇ ਖੇਤੀਬਾੜੀ ਦੇ ਦੋਸ਼ਪੂਰਨ ਢੰਗਾਂ ਦੀ ਵਰਤੋਂ ਕਰਕੇ ਹੁੰਦਾ ਹੈ ।
ਮਿੱਟੀ ਦੀ ਸੰਭਾਲ – ਮਿੱਟੀ ਦੀ ਸੰਭਾਲ ਲਈ ਹੇਠ ਲਿਖੇ ਉਪਾਅ ਕੀਤੇ ਜਾ ਰਹੇ ਹਨ-
- ਪੰਜਾਬ, ਹਰਿਆਣਾ, ਰਾਜਸਥਾਨ, ਗੁਜਰਾਤ ਵਿਚ ਪੌਣਾਂ ਦੇ ਵੇਗ ਨੂੰ ਘੱਟ ਕਰਨ ਲਈ ਦਰੱਖਤਾਂ ਦੀਆਂ ਕਤਾਰਾਂ ਲਾਈਆਂ ਜਾ ਰਹੀਆਂ ਹਨ ।
- ਰੇਤਲੇ ਟਿੱਲਿਆਂ ਤੇ ਘਾਹ ਉਗਾਈ ਜਾ ਰਹੀ ਹੈ ।
- ਪਰਬਤੀ ਖੇਤਰਾਂ ਵਿਚ ਪੌੜੀਦਾਰ ਖੇਤ, ਢਲਾਣ ਦੇ ਉਲਟ ਦਿਸ਼ਾ ਵਿਚ ਵੱਟਾਂ ਬਣਾ ਕੇ ਛੋਟੇ-ਛੋਟੇ ਜਲ-ਭੰਡਾਰ ਬਣਾਏ ਜਾਂਦੇ ਹਨ ।
- ਮੈਦਾਨੀ ਭਾਗਾਂ ਵਿਚ ਭੁਮੀ ਤੇ ਬਨਸਪਤੀ ਉਗਾ ਕੇ ਫ਼ਸਲ ਚੱਕਰ, ਢਲਾਨ ਦੇ ਉਲਟ ਖੇਤਾਂ ਦੀ ਵਾਹੀ ਅਤੇ ਦੇਸੀ ਖਾਦ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ ਮਿੱਟੀ ਦੀ ਉਪਜਾਊ ਸ਼ਕਤੀ ਵਧਾਈ ਜਾ ਸਕਦੀ ਹੈ ।
- ਝਾਰਖੰਡ ਸਰਕਾਰ ਨੇ ਛੋਟਾ ਨਾਗਪੁਰ ਦੇ ਪਠਾਰੀ ਭਾਗ ਵਿਚ ਸਥਾਨਾਂਤਰੀ ਖੇਤੀਬਾੜੀ ਦੇ ਕਠੋਰ ਨਿਯਮ ਬਣਾਏ ਹਨ ।
![]()
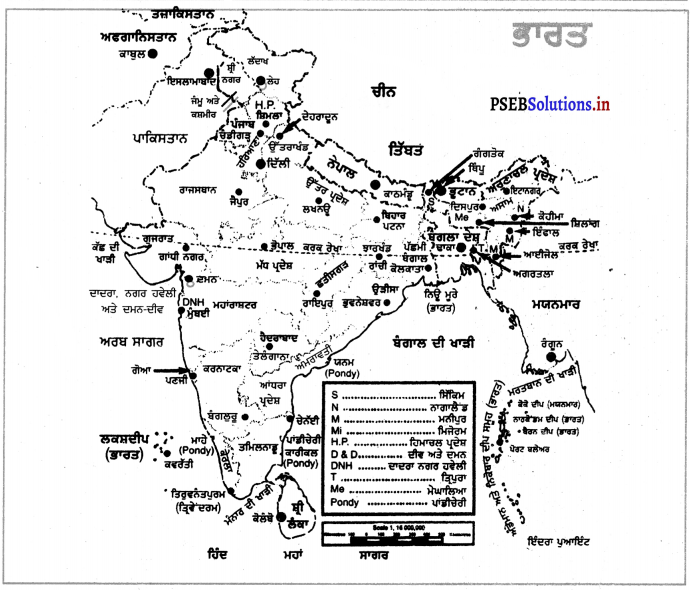
IV ਭਾਰਤ ਦੇ ਨਕਸ਼ੇ ਵਿਚ ਭਰੋ-
1. ਖੁਸ਼ਕ ਬਨਸਪਤੀ ਖੇਤਰ
2. ਸੈਗਰੋਣ ਬਨਸਪਤੀ ਖੇਤਰ
3. ਕਾਲੀ ਮਿੱਟੀ ਤੇ ਜਲੋਢ ਮਿੱਟੀ ਖੇਤਰ ।
PSEB 10th Class Social Science Guide ਕੁਦਰਤੀ ਬਨਸਪਤੀ, ਜੀਵ-ਜੰਤੂ ਅਤੇ ਮਿੱਟੀਆਂ Important Questions and Answers
ਵਸਤੂਨਿਸ਼ਠ ਪ੍ਰਸ਼ਨ (Objective Type Questions)
I. ਉੱਤਰ ਇਕ ਲਾਈਨ ਜਾਂ ਇਕ ਸ਼ਬਦ ਵਿਚ-
ਪ੍ਰਸ਼ਨ 1.
ਭਾਰਤ ਵਿਚ ਕਈ ਪ੍ਰਕਾਰ ਦੀ ਬਨਸਪਤੀ ਪਾਏ ਜਾਣ ਦਾ ਕੀ ਕਾਰਨ ਹੈ ?
ਉੱਤਰ-
ਭਾਰਤ ਦੀ ਕੁਦਰਤੀ ਦਸ਼ਾ, ਇਸ ਦੀ ਜਲਵਾਯੂ ਅਤੇ ਇਸ ਦੀ ਮਿੱਟੀ ਵਿਚ ਭਿੰਨਤਾ ਦੇ ਕਾਰਨ ਇੱਥੇ ਕਈ ਪ੍ਰਕਾਰ ਦੀ ਬਨਸਪਤੀ ਪਾਈ ਜਾਂਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਗਰਮ ਸਦਾਬਹਾਰ ਜੰਗਲ ਭਾਰਤ ਦੇ ਕਿਨ੍ਹਾਂ ਭਾਗਾਂ ਵਿਚ ਪਾਏ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਗਰਮ ਸਦਾਬਹਾਰ ਜੰਗਲ ਭਾਰਤ ਦੇ ਪੱਛਮੀ ਤੱਟ, ਪੱਛਮੀ ਘਾਟ, ਅਸਾਮ, ਨਾਗਾਲੈਂਡ, ਤ੍ਰਿਪੁਰਾ ਅਤੇ ਪੱਛਮੀ ਬੰਗਾਲ ਵਿਚ ਪਾਏ ਜਾਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 3.
ਮਾਨਸੂਨੀ ਜੰਗਲ ਭਾਰਤ ਦੇ ਕਿਨ੍ਹਾਂ ਹਿੱਸਿਆਂ ਵਿਚ ਪਾਏ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਮਹਾਂਰਾਸ਼ਟਰ, ਤਾਮਿਲਨਾਡੂ, ਮੱਧ ਪ੍ਰਦੇਸ਼, ਬਿਹਾਰ, ਉੜੀਸਾ, ਉੱਤਰ ਪ੍ਰਦੇਸ਼, ਪੰਜਾਬ ਆਦਿ ਰਾਜਾਂ ਵਿਚ ਮਾਨਸੂਨੀ ਜੰਗਲ ਪਾਏ ਜਾਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 4.
ਮਾਨਸੂਨੀ ਜੰਗਲਾਂ ਵਿਚ ਪਾਏ ਜਾਣ ਵਾਲੇ ਚਾਰ ਮੁੱਖ ਰੁੱਖਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਸਾਲ, ਸਾਗਵਾਨ, ਟਾਹਲੀ ਅਤੇ ਐਬੋਨੀ ।
ਪ੍ਰਸ਼ਨ 5.
ਡੈਲਟਾਈ ਜੰਗਲਾਂ ਵਿਚ ਪਾਏ ਜਾਣ ਵਾਲੇ ਇਕ ਪ੍ਰਮੁੱਖ ਰੁੱਖ ਦਾ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਸੁੰਦਰੀ।
![]()
ਪ੍ਰਸ਼ਨ 6.
ਫ਼ਰਨੀਚਰ, ਸਮੁੰਦਰੀ ਜਹਾਜ਼ ਅਤੇ ਰੇਲਾਂ ਦੇ ਡੱਬਿਆਂ ਲਈ ਕਿਹੜੀ ਲੱਕੜੀ ਸਭ ਤੋਂ ਚੰਗੀ ਰਹਿੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਇਨ੍ਹਾਂ ਦੇ ਲਈ ਸਾਗਵਾਨ ਦੀ ਲੱਕੜੀ ਸਭ ਤੋਂ ਚੰਗੀ ਰਹਿੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 7.
ਊਸ਼ਣ ਸਦਾਬਹਾਰ ਵਰਖਾ ਵਾਲੇ ਵਣਾਂ ਦੀ ਇਕ ਮਹੱਤਵਪੂਰਨ ਵਿਸ਼ੇਸ਼ਤਾ ਦੱਸੋ ।
ਉੱਤਰ-
ਊਸ਼ਣ ਸਦਾਬਹਾਰ ਵਰਖਾ ਵਾਲੇ ਵਣ ਹਮੇਸ਼ਾ ਹਰੇ ਰਹਿੰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 8.
ਊਸ਼ਣ ਸਦਾਬਹਾਰ ਵਰਖਾ ਵਣਾਂ ਦੇ ਵਪਾਰਿਕ ਉਪਯੋਗ ਵਿਚ ਕਿਉਂ ਕਠਿਨਾਈ ਆਉਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਊਸ਼ਣ ਸਦਾਬਹਾਰ ਵਰਖਾ ਵਾਲੇ ਵਣਾਂ ਵਿਚ ਨਾਲ-ਨਾਲ ਜੁੜੇ ਹੋਏ ਅਨੇਕਾਂ ਜਾਤੀਆਂ ਦੇ ਦਰੱਖਤ ਮਿਲਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 9.
ਊਸ਼ਣ ਸਦਾਬਹਾਰ ਵਣ ਕਿਹੜੀ ਜਲਵਾਯੂ ਪ੍ਰਦੇਸ਼ ਦੇ ਖਾਸ ਵਣ ਹਨ ?
ਉੱਤਰ-
ਉਸ਼ਣ ਸਦਾਬਹਾਰ ਵਣ ਮਾਨਸੂਨੀ ਪ੍ਰਦੇਸ਼ ਦੇ ਖ਼ਾਸ ਵਣ ਹਨ |
ਪ੍ਰਸ਼ਨ 10.
ਮਾਨਸੂਨੀ ਵਣਾਂ ਦੇ ਕਿਹੜੇ-ਕਿਹੜੇ ਦੋ ਉਪ ਵਰਗ ਹਨ ?
ਉੱਤਰ-
ਮਾਨਸੂਨੀ ਵਣਾਂ ਦੇ ਦੋ ਉਪ ਵਰਗ ਹਨ-
- ਅਰਧ ਖੁਸ਼ਕ ਪੱਤਝੜੀ ਬਨਸਪਤੀ
- ਸ਼ਕ ਪੱਤਝੜੀ ਬਨਸਪਤੀ ।
ਪ੍ਰਸ਼ਨ 11.
(i) ਮੈਂਗਰੋਵ ਦੇ ਦਰੱਖਤ ਕਿੱਥੇ ਮਿਲਦੇ ਹਨ ?
(i) ਇਨ੍ਹਾਂ ਦੀਆਂ ਮੁੱਖ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਕੀ ਹਨ ?
ਉੱਤਰ-
(i) ਮੈਂਗਰੋਵ ਦੇ ਦਰੱਖਤ ਤਟ ਦੇ ਨਾਲ-ਨਾਲ ਅਤੇ ਨਦੀਆਂ ਦੇ ਜਵਾਰੀ ਖੇਤਰ ਵਿਚ ਮਿਲਦੇ ਹਨ ।
(ii) ਇਨ੍ਹਾਂ ਬ੍ਰਿਛਾਂ ਦੀ ਮੁੱਖ ਵਿਸ਼ੇਸ਼ਤਾ ਇਹ ਹੈ ਕਿ ਇਹ ਖਾਰੇ ਪਾਣੀ ਤੇ ਤਾਜ਼ੇ ਪਾਣੀ ਦੋਹਾਂ ਵਿਚ ਹੀ ਉੱਗ ਸਕਦੇ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 12.
ਮਾਰੂਥਲਾਂ ਵਿਚ ਦਰੱਖਤਾਂ ਦੀਆਂ ਜੜ੍ਹਾਂ ਲੰਮੀਆਂ ਕਿਉਂ ਹੁੰਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਕੁਦਰਤ ਨੇ ਉਨ੍ਹਾਂ ਨੂੰ ਲੰਮੀਆਂ ਜੜ੍ਹਾਂ ਇਸ ਲਈ ਪ੍ਰਦਾਨ ਕੀਤੀਆਂ ਹਨ ਤਾਂ ਜੋ ਇਹ ਡੂੰਘਾਈ ਤੋਂ ਨਮੀ ਪ੍ਰਾਪਤ ਕਰ ਸਕਣ ।
ਪ੍ਰਸ਼ਨ 13.
ਕੀ ਕਾਰਨ ਹੈ ਕਿ ਵਣਾਂ ਨਾਲ ਹੜ੍ਹ ਦੀ ਭਿਆਨਕਤਾ ਘੱਟ ਹੋ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਵਣਾਂ ਦੀ ਰੋਕ ਦੇ ਕਾਰਨ ਹੜ੍ਹਾਂ ਦਾ ਵਹਾਅ ਹੌਲਾ ਹੋ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 14.
ਮਾਰੂਥਲੀ ਮਿੱਟੀ ਦੇ ਉਪਜਾਊ ਹੋਣ ‘ਤੇ ਵੀ ਇਸ ਵਿਚ ਖੇਤੀ ਘੱਟ ਹੁੰਦੀ ਹੈ, ਕਿਉਂ ?
ਉੱਤਰ-
ਵਰਖਾ ਦੀ ਕਮੀ ਕਾਰਨ ਇਸ ਮਿੱਟੀ ਵਿਚ ਨਾਈਟਰੋਜਨ ਅਤੇ ਮੱਲ੍ਹੜ ਦੀ ਘਾਟ ਰਹਿੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 15.
ਜਲੋਢ ਮਿੱਟੀ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਜਲੋਢ ਮਿੱਟੀ ਤੋਂ ਸਾਡਾ ਭਾਵ ਅਜਿਹੀ ਮਿੱਟੀ ਤੋਂ ਹੈ ਜਿਸ ਦਾ ਨਿਰਮਾਣ ਨਦੀਆਂ ਦੁਆਰਾ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 16.
ਜਲੋਢ ਮਿੱਟੀ ਦੀਆਂ ਚਾਰ ਕਿਸਮਾਂ ਕਿਹੜੀਆਂ-ਕਿਹੜੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਜਲੋਢ ਮਿੱਟੀ ਦੀਆਂ ਚਾਰ ਕਿਸਮਾਂ ਹਨ-ਬਾਂਗਰ ਮਿੱਟੀ, ਖਾਦਰ ਮਿੱਟੀ, ਡੈਲਟਾਈ ਮਿੱਟੀ ਅਤੇ ਤਟਵਰਤੀ ਜਲੋਢ ਮਿੱਟੀ ।
ਪ੍ਰਸ਼ਨ 17.
ਕਾਲੀ ਮਿੱਟੀ ਦਾ ਕੋਈ ਇਕ ਗੁਣ ਦੱਸੋ ।
ਉੱਤਰ-
ਕਾਲੀ ਮਿੱਟੀ ਵਿਚ ਨਮੀ ਸੋਖਣ ਦੀ ਸਮਰੱਥਾ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ । ਇਹ ਕਪਾਹ ਦੀ ਖੇਤੀ ਲਈ ਉੱਤਮ ਮੰਨੀ ਜਾਂਦੀ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 18.
ਕਾਲੀ ਮਿੱਟੀ ਕਿਹੜੀ ਉਪਜ ਲਈ ਆਦਰਸ਼ ਮੰਨੀ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਕਪਾਹ ।
ਪ੍ਰਸ਼ਨ 19.
ਲੈਟਰਾਈਟ ਮਿੱਟੀ ਵਿਚ ਕਿਹੜੇ ਤੱਤਾਂ ਦੀ ਮਾਤਰਾ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਲੈਟਰਾਈਟ ਮਿੱਟੀ ਵਿਚ ਲੋਹਾ ਅਤੇ ਐਲੂਮੀਨੀਅਮ ਦੀ ਮਾਤਰਾ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 20.
ਭਾਰਤ ਵਿਚ ਪਾਈ ਜਾਣ ਵਾਲੀ ਸੰਪੂਰਨ ਬਨਸਪਤੀ ਜਾਤੀ ਦਾ ਕਿੰਨੇ ਪ੍ਰਤੀਸ਼ਤ ਭਾਗ ਵਿਦੇਸ਼ੀ ਜਾਤੀਆਂ ਦਾ ਹੈ ?
ਉੱਤਰ-
40%.
ਪ੍ਰਸ਼ਨ 21.
ਕਿਸ ਵਿਦੇਸ਼ੀ ਬਨਸਪਤੀ ਨੇ ਲੋਕਾਂ ਵਿਚ ਚਮੜੀ ਅਤੇ ਸਾਹ ਸੰਬੰਧੀ ਰੋਗਾਂ ਵਿਚ ਵਾਧਾ ਕੀਤਾ ਹੈ ?
ਉੱਤਰ-
ਪਾਰਥੇਨਿਅਮ ਜਾਂ ਕਾਂਗਰਸੀ ਘਾਹ ।
ਪ੍ਰਸ਼ਨ 22.
ਭਾਰਤ ਵਿਚ ਪਹਿਲੀ ਵਾਰ ਵਣ ਨੀਤੀ (ਰਾਸ਼ਟਰੀ ਵਣ ਨੀਤੀ ਦਾ ਐਲਾਨ ਕਦੋਂ ਕੀਤਾ ਗਿਆ ਸੀ ?
ਉੱਤਰ-
1951 ਵਿਚ ।
ਪ੍ਰਸ਼ਨ 23.
ਭਾਰਤ ਵਿਚ ਪ੍ਰਤੀ ਵਿਅਕਤੀ ਵਣ ਖੇਤਰ ਕਿੰਨਾ ਹੈ ?
ਉੱਤਰ-
0.14 ਹੈਕਟੇਅਰ ।
![]()
ਪ੍ਰਸ਼ਨ 24.
ਕਿਹੜੇ ਕੇਂਦਰ ਸ਼ਾਸਿਤ ਦੇਸ਼ ਵਿਚ ਸਭ ਤੋਂ ਵਧੇਰੇ ਵਣ ਖੇਤਰ ਹੈ ?
ਉੱਤਰ-
ਅੰਡਮਾਨ ਤੇ ਨਿਕੋਬਾਰ ਦੀਪ ਸਮੂਹ ।
ਪ੍ਰਸ਼ਨ 25.
ਕੇਂਦਰੀ ਸ਼ਾਸਿਤ ਦੇਸ਼ਾਂ ਵਿਚ ਸਭ ਤੋਂ ਘੱਟ ਵਣ ਖੇਤਰ ਕਿਸ ਦੇਸ਼ ਦਾ ਹੈ ?
ਉੱਤਰ-
ਰਾਸ਼ਟਰੀ ਰਾਜਧਾਨੀ ਖੇਤਰ ਦਿੱਲੀ ਦਾ ।
ਪ੍ਰਸ਼ਨ 26.
ਅਸੀਂ ਆਪਣੇ ਕਿੰਨੇ ਪ੍ਰਤੀਸ਼ਤ ਵਣ ਖੇਤਰ ਦੀ ਵਰਤੋਂ ਕਰ ਪਾਉਂਦੇ ਹਾਂ ?
ਉੱਤਰ-
82 ਪ੍ਰਤੀਸ਼ਤ ਦੀ ।
ਪ੍ਰਸ਼ਨ 27.
ਕਿੱਕਰ ਅਤੇ ਬਬੂਲ ਕਿਸ ਤਰ੍ਹਾਂ ਦੀ ਬਨਸਪਤੀ ਦੇ ਰੁੱਖ ਹਨ ?
ਉੱਤਰ-
ਮਾਰੂਥਲੀ ਜਾਂ ਖ਼ੁਸ਼ਕ ਬਨਸਪਤੀ ।
ਪ੍ਰਸ਼ਨ 28.
ਥਣਧਾਰੀਆਂ ਵਿਚ ਰਾਜਸੀ ਠਾਠ-ਬਾਠ ਵਾਲਾ ਸ਼ਾਕਾਹਾਰੀ ਪਸ਼ੂ ਕਿਸਨੂੰ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਹਾਥੀ ।
![]()
ਪ੍ਰਸ਼ਨ 29.
ਥਾਰ-ਮਾਰੂਥਲ ਦਾ ਸਾਧਾਰਨ ਪਸ਼ੂ ਕਿਹੜਾ ਹੈ ?
ਉੱਤਰ-
ਊਠ ।
ਪ੍ਰਸ਼ਨ 30.
ਭਾਰਤ ਵਿਚ ਜੰਗਲੀ ਗਧੇ ਕਿੱਥੇ ਪਾਏ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਕੱਛ ਦੇ ਰਣ ਵਿਚ ।
ਪ੍ਰਸ਼ਨ 31.
ਭਾਰਤ ਵਿਚ ਇਕ ਸਿੰਗ ਵਾਲਾ ਡਾ ਕਿੱਥੇ ਮਿਲਦਾ ਹੈ ?
ਉੱਤਰ-
ਆਸਾਮ ਅਤੇ ਪੱਛਮੀ ਬੰਗਾਲ ਦੇ ਉੱਤਰੀ ਭਾਗਾਂ ਵਿਚ ।
ਪ੍ਰਸ਼ਨ 32.
ਜੰਗਲੀ ਜੀਵਾਂ ਵਿਚ ਸਭ ਤੋਂ ਸ਼ਕਤੀਸ਼ਾਲੀ ਪਸ਼ੂ ਕਿਹੜਾ ਹੈ ?
ਉੱਤਰ-
ਸ਼ੋਰ ।
ਪ੍ਰਸ਼ਨ 33.
ਸਿੱਧ ਬੰਗਾਲੀ ਸ਼ੇਰ ਜਾਂ ਬੰਗਾਲ ਟਾਈਗਰ ਦਾ ਕੁਦਰਤੀ ਆਵਾਸ ਕਿਹੜਾ ਹੈ ?
ਉੱਤਰ-
ਗੰਗਾ ਡੈਲਟਾ ਦੇ ਸੁੰਦਰ ਵਣ ।
ਪ੍ਰਸ਼ਨ 34.
ਗੁਜਰਾਤ ਵਿਚ ਸੌਰਾਸ਼ਟਰ ਦੇ ਗਿਰ ਵਣ ਕਿਹੜੇ ਵਿਸ਼ੇਸ਼ ਪਸ਼ੂ ਦਾ ਕੁਦਰਤੀ ਆਵਾਸ ਹਨ ?
ਉੱਤਰ-
ਭਾਰਤੀ ਸਿੰਘ ਦਾ ।
ਪ੍ਰਸ਼ਨ 35.
ਹਿਮਾਲਿਆ ਦੇ ਉੱਚ ਖੇਤਰਾਂ ਵਿਚ ਪਾਏ ਜਾਣ ਵਾਲੇ ਦੋ ਜਾਨਵਰਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ?
ਉੱਤਰ-
ਲਮਚਿੱਤਾ ਅਤੇ ਹਿਮ ਤੇਂਦੁਆ ।
![]()
ਪ੍ਰਸ਼ਨ 36.
ਭਾਰਤ ਦਾ ਸਭ ਤੋਂ ਪਹਿਲਾ ਵਣ ਰਾਖਵਾਂ ਖੇਤਰ ਕਦੋਂ ਅਤੇ ਕਿੱਥੇ ਬਣਾਇਆ ਗਿਆ ਸੀ ?
ਉੱਤਰ-
ਭਾਰਤ ਦਾ ਪਹਿਲਾ ਵਣ ਰਾਖਵਾਂ ਖੇਤਰ 1986 ਵਿਚ ਨੀਲਗਿਰੀ ਵਿਚ ਬਣਾਇਆ ਗਿਆ ਸੀ ।
ਪ੍ਰਸ਼ਨ 37.
ਦਰਿਆਈ ਜਲੋੜ ਮਿੱਟੀ ਨੂੰ ਕਿਹੜੇ-ਕਿਹੜੇ ਦੋ ਉਪਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਖਾਦਰ ਅਤੇ ਬਾਂਗਰ ।
ਪ੍ਰਸ਼ਨ 38.
ਅਗਨੀ ਚੱਟਾਨਾਂ ਦੇ ਟੁੱਟਣ ਨਾਲ ਬਣੀ ਮਿੱਟੀ ਕੀ ਅਖਵਾਉਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਕਾਲੀ ਮਿੱਟੀ ।
ਪ੍ਰਸ਼ਨ 39.
ਕੇਂਦਰੀ ਮਿੱਟੀ ਰੱਖਿਆ ਬੋਰਡ ਦੀ ਸਥਾਪਨਾ ਕਦੋਂ ਹੋਈ ?
ਉੱਤਰ-
1953 ਵਿਚ ।
ਪ੍ਰਸ਼ਨ 40.
ਕਿਸ ਤਰ੍ਹਾਂ ਦੇ ਵਣਾਂ ਨੂੰ ਬਰਸਾਤੀ ਵਣ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਊਸ਼ਣ ਸਦਾਬਹਾਰ ਵਣਾਂ ਨੂੰ ।
ਪ੍ਰਸ਼ਨ 41.
ਭਾਰਤ ਦੇ ਦੋ ਖ਼ਤਮ ਹੋ ਰਹੇ ਜੰਗਲੀ ਜੀਵਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਦੋ ਖ਼ਤਮ ਹੋ ਰਹੇ ਜੰਗਲੀ ਜੀਵ ਬਘਿਆੜ ਅਤੇ ਗੈਂਡਾ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 42.
(i) ਰਾਸ਼ਟਰੀ ਚਿੜੀਆਘਰ ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ?
(ii) ਇਸ ਦੇ ਦੋ ਉਦਾਹਰਨ ਭਾਰਤ ਵਿਚੋਂ ਦਿਓ ।
ਉੱਤਰ-
(i) ਰਾਸ਼ਟਰੀ ਚਿੜੀਆਘਰ ਤੋਂ ਭਾਵ ਉਨ੍ਹਾਂ ਸੁਰੱਖਿਅਤ ਥਾਵਾਂ ਤੋਂ ਹੈ ਜਿੱਥੇ ਜਾਨਵਰਾਂ ਨੂੰ ਉਨ੍ਹਾਂ ਦੀਆਂ ਨਸਲਾਂ ਸੁਰੱਖਿਅਤ ਰੱਖਣ ਲਈ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ ।
(ii) ਕਾਰਬੇਟ ਨੈਸ਼ਨਲ ਪਾਰਕ ।
II. ਖ਼ਾਲੀ ਥਾਂਵਾਂ ਭਰੋ-
1. ਫ਼ਰਨੀਚਰ ਸਮੁੰਦਰੀ ਜਹਾਜ਼ ਅਤੇ ਰੇਲ ਦੇ ਡੱਬੇ ਬਣਾਉਣ ਲਈ ………………………… ਦੀ ਲੱਕੜੀ ਸਭ ਤੋਂ ਚੰਗੀ ਰਹਿੰਦੀ ਹੈ ।
ਉੱਤਰ-
ਸਾਗਵਾਨ
2. …………………………. ਵਰਖਾ ਵਣ ਸਦਾ ਹਰੇ-ਭਰੇ ਰਹਿੰਦੇ ਹਨ।
ਉੱਤਰ-
ਊਸ਼ਣ ਕਟੀਬੰਧੀ
3. ਭਾਰਤ ਵਿਚ ਮਿਲਣ ਵਾਲੀ ਸੰਪੂਰਨ ਬਨਸਪਤੀ ਜਾਤੀ ਦਾ …………………………….. ਪ੍ਰਤੀਸ਼ਤ ਭਾਗ ਵਿਦੇਸ਼ੀ ਜਾਤਾਂ ਦਾ ਹੈ ।
ਉੱਤਰ-
40
4. ਵਿਦੇਸ਼ੀ ਬਨਸਪਤੀ ਦੀ ……………………….. ਘਾਹ ਨੇ ਲੋਕਾਂ ਵਿਚ ਚਮੜੀ ਅਤੇ ਸਾਹ ਸੰਬੰਧੀ ਬੀਮਾਰੀਆਂ ਵਿਚ ਵਾਧਾ ਕੀਤਾ ਹੈ ।
ਉੱਤਰ-
ਕਾਂਗਰਸੀ
5. ਬਾਰ ਮਾਰੂਥਲ ਦਾ ਆਮ ਪਸ਼ੁ ……………………….. ਹੈ ।
ਉੱਤਰ-
ਊਠ
![]()
6. ਭਾਰਤ ਵਿਚ ਜੰਗਲੀ ਗਧੇ ………………………….. ਵਿਚ ਮਿਲਦੇ ਹਨ ।
ਉੱਤਰ-
ਰਣ ਦੇ ਕੱਛ
7. ਜੰਗਲੀ ਜੀਵਾਂ ਵਿਚ ……………………….. ਸਭ ਤੋਂ ਤਾਕਤਵਰ ਪਸ਼ੂ ਹੈ ।
ਉੱਤਰ-
ਸ਼ੇਰ
8. ਭਾਰਤ ਦਾ ਪਹਿਲਾ ਵਣ ਰਿਜ਼ਰਵ ਖੇਤਰ ……………………….. ਵਿਚ ਬਣਾਇਆ ਗਿਆ ।
ਉੱਤਰ-
ਨੀਲਗਿਰੀ
9. ਅਗਨੀ ਚੱਟਾਨਾਂ ਦੇ ਟੁੱਟਣ ਨਾਲ ਬਣੀ ਮਿੱਟੀ ………………………. ਮਿੱਟੀ ਕਹਾਉਂਦੀ ਹੈ ।
ਉੱਤਰ-
ਕਾਲੀ
10. ਕੇਂਦਰੀ ਮਿੱਟੀ ਰੱਖਿਆ ਬੋਰਡ ਦੀ ਸਥਾਪਨਾ …………… ਈ: ਵਿਚ ਕੀਤੀ ਗਈ ।
ਉੱਤਰ-
1953
![]()
II. ਬਹੁਵਿਕਲਪੀ ਪ੍ਰਸ਼ਨ-
ਪ੍ਰਸ਼ਨ 1.
ਡੈਲਟਾਈ ਵਣਾਂ ਵਿਚ ਮਿਲਣ ਵਾਲਾ ਮੁੱਖ ਰੁੱਖ ਹੈ-
(A) ਸਾਲ
(B) ਟਾਹਲੀ
(C) ਸੁੰਦਰੀ
(D) ਸਾਗਵਾਨ ।
ਉੱਤਰ-
(C) ਸੁੰਦਰੀ
ਪ੍ਰਸ਼ਨ 2.
ਕਾਲੀ ਮਿੱਟੀ ਕਿਸ ਉਪਜ ਲਈ ਉੱਤਮ ਮੰਨੀ ਜਾਂਦੀ ਹੈ ?
(A) ਕਪਾਹ
(B) ਕਣਕ
(C) ਚੌਲ
(D) ਗੰਨਾ |
ਉੱਤਰ-
(A) ਕਪਾਹ
ਪ੍ਰਸ਼ਨ 3.
ਕਿਸ ਮਿੱਟੀ ਵਿਚ ਲੋਹੇ ਅਤੇ ਐਲੂਮੀਨੀਅਮ ਦੀ ਮਾਤਰਾ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ ?
(A) ਕਾਲੀ ਮਿੱਟੀ
(B) ਲੈਟਰਾਈਟ ਮਿੱਟੀ
(C) ਮਾਰੂਥਲੀ ਮਿੱਟੀ
(D) ਜਲੌੜ ਮਿੱਟੀ ।
ਉੱਤਰ-
(B) ਲੈਟਰਾਈਟ ਮਿੱਟੀ
ਪ੍ਰਸ਼ਨ 4.
ਭਾਰਤ ਵਿਚ ਪਹਿਲੀ ਵਾਰ ਵਣ ਨੀਤੀ (ਰਾਸ਼ਟਰੀ ਵਣ ਨੀਤੀ) ਦੀ ਘੋਸ਼ਣਾ ਕੀਤੀ ਗਈ-
(A) 1947 ਈ: ਵਿਚ
(B) 1950 ਈ: ਵਿਚ
(C) 1937 ਈ: ਵਿਚ
(D) 1951 ਈ: ਵਿਚ ।
ਉੱਤਰ-
(D) 1951 ਈ: ਵਿਚ ।
ਪ੍ਰਸ਼ਨ 5.
ਭਾਰਤ ਵਿਚ ਪ੍ਰਤੀ ਵਿਅਕਤੀ ਵਣ ਖੇਤਰ ਹੈ-
(A) 0.14 ਹੈਕਟੇਅਰ
(B) 1.4 ਹੈਕਟੇਅਰ
(C) 14.0 ਹੈਕਟੇਅਰ
(D) 4.1 ਹੈਕਟੇਅਰ ।
ਉੱਤਰ-
(A) 0.14 ਹੈਕਟੇਅਰ
ਪ੍ਰਸ਼ਨ 6.
ਕਿਸ ਕੇਂਦਰ ਸ਼ਾਸਿਤ ਪ੍ਰਦੇਸ਼ ਵਿਚ ਸਭ ਤੋਂ ਵੱਧ ਵਣ ਖੇਤਰ ਹੈ- :
(A) ਚੰਡੀਗੜ੍ਹ ਵਿਚ
(B) ਅੰਡੇਮਾਨ ਅਤੇ ਨਿਕੋਬਾਰ ਦੀਪ ਸਮੂਹ
(C) ਦਾਦਰ ਅਤੇ ਨਗਰ ਹਵੇਲੀ ਵਿਚ
(D) ਪਾਂਡੀਚੇਰੀ ਵਿਚ ।
ਉੱਤਰ-
(B) ਅੰਡੇਮਾਨ ਅਤੇ ਨਿਕੋਬਾਰ ਦੀਪ ਸਮੂਹ
![]()
ਪ੍ਰਸ਼ਨ 7.
ਹੇਠ ਲਿਖੇ ਕੇਂਦਰ ਸ਼ਾਸਿਤ ਪ੍ਰਦੇਸ਼ ਵਿਚ ਸਭ ਤੋਂ ਘਟ ਵਣ ਖੇਤਰ ਹੈ-
(A) ਚੰਡੀਗੜ੍ਹ
(B) ਲਕਸ਼ਦੀਪ
(C) ਦਿੱਲੀ
(D) ਦਮਨ-ਦੀਵ ।
ਉੱਤਰ-
(C) ਦਿੱਲੀ
ਪ੍ਰਸ਼ਨ 8.
ਥਣਧਾਰੀਆਂ ਵਿਚ ਰਾਜਸੀ-ਠਾਠ ਵਾਲਾ ਸ਼ਾਕਾਹਾਰੀ ਪਸ਼ੂ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ-
(A) ਬਾਂਦਰ
(B) ਹਾਥੀ
(C) ਲੰਗੂਰ
(D) ਮੱਝ ।
ਉੱਤਰ-
(B) ਹਾਥੀ
ਪ੍ਰਸ਼ਨ 9.
ਭਾਰਤ ਵਿਚ ਇਕ ਸਿੰਝ ਵਾਲਾ ਗੈਂਡਾ ਮਿਲਦਾ ਹੈ-
(A) ਤਾਮਿਲਨਾਡੂ ਵਿਚ
(B) ਅਸਾਮ ਅਤੇ ਉੱਤਰ ਪ੍ਰਦੇਸ਼ ਵਿਚ
(C) ਅਸਾਮ ਅਤੇ ਪੱਛਮੀ ਬੰਗਾਲ ਵਿਚ
(D) ਉੱਤਰਾਖੰਡ ਅਤੇ ਉੱਤਰ ਪ੍ਰਦੇਸ਼ ਵਿਚ ।
ਉੱਤਰ-
(C) ਅਸਾਮ ਅਤੇ ਪੱਛਮੀ ਬੰਗਾਲ ਵਿਚ
ਪ੍ਰਸ਼ਨ 10.
ਭਾਰਤ ਵਿਚ ਪਹਿਲਾ ਵਣ ਰਿਜ਼ਰਵ ਖੇਤਰ ਬਣਾਇਆ ਗਿਆ
(A) 1986 ਈ: ਵਿਚ
(B) 1976 ਈ: ਵਿਚ
(C) 1971 ਈ: ਵਿਚ
(D) 1981 ਈ: ਵਿਚ ।
ਉੱਤਰ-
(A) 1986 ਈ: ਵਿਚ
IV. ਸਹੀ-ਗਲਤ ਕਥਨ-
ਪ੍ਰਸ਼ਨ-ਸਹੀ ਕਥਨਾਂ ‘ਤੇ (√) ਅਤੇ ਗ਼ਲਤ ਕਥਨਾਂ ਉੱਪਰ (×) ਦਾ ਨਿਸ਼ਾਨ ਲਗਾਓ :
1. ਸੁੰਦਰਵਣ ਦਾ ਜੀਵ ਸੁਰੱਖਿਅਤ ਦਾ ਖੇਤਰ ਮੱਧ ਪ੍ਰਦੇਸ਼ ਵਿਚ ਸਥਿਤ ਹੈ ।
2. ਰਾਸ਼ਟਰੀ ਵਣ ਨੀਤੀ 1951 ਦੇ ਅਨੁਸਾਰ ਦੇਸ਼ ਦੇ ਕੁੱਲ ਖੇਤਰਫਲ ਦੇ ਇਕ ਤਿਹਾਈ (33.3 ਪ੍ਰਤੀਸ਼ਤ) ਭਾਗ ਉੱਤੇ ਵਣ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।
3. ਬਬੂਲ, ਕਿੱਕਰ ਆਦਿ ਦਰੱਖ਼ਤ ਅਰਧ-ਪੱਤਝੜੀ ਜੰਗਲਾਂ ਦੇ ਦਰੱਖ਼ਤ ਹਨ ।
4. ਸੰਘਣੇ ਵਣ ਗਰਮੀਆਂ ਵਿਚ ਤਾਪਮਾਨ ਨੂੰ ਵੱਧਣ ਤੋਂ ਰੋਕਦੇ ਹਨ ।
5. ਪਰਬਤੀ ਮਿੱਟੀ ਚਾਹ ਉਤਪੰਨ ਦੇ ਅਨੁਕੂਲ ਹੁੰਦੀ ਹੈ ।
ਉੱਤਰ-
1. ×
2. √
3. ×
4. √
5. √
![]()
V. ਸਹੀ-ਮਿਲਾਨ ਕਰੋ-
| 1. ਜਲ ਹਾਏਸਿੰਥ (Water-Hyacinth) | ਸੁੰਦਰਵਣ |
| 2. ਭਾਰਤ ਵਿਚ ਸਭ ਤੋਂ ਵੱਧ ਜੰਗਲ ਦਾ ਖੇਤਰਫਲ | ਪੰਜਾਬ ਅਤੇ ਹਰਿਆਣਾ |
| 3. ਜਵਾਰੀ ਬਨਸਪਤੀ | ਬੰਗਾਲ ਦਾ ਡਰ |
| 4. ਭੂੜ ਮਿੱਟੀ | ਤ੍ਰਿਪੁਰਾ । |
ਉੱਤਰ-
| 1. ਜਲ ਹਾਏਸਿੰਥ (Water-Hyacinth) | ਬੰਗਾਲ ਦਾ ਡਰ |
| 2. ਭਾਰਤ ਵਿਚ ਸਭ ਤੋਂ ਵੱਧ ਜੰਗਲ ਦਾ ਖੇਤਰਫਲ | ਤ੍ਰਿਪੁਰਾ |
| 3. ਜਵਾਰੀ ਬਨਸਪਤੀ | ਸੁੰਦਰਵਣ |
| 4. ਭੂੜ ਮਿੱਟੀ | ਪੰਜਾਬ ਅਤੇ ਹਰਿਆਣਾ। |
ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Short Answer Type Questions)
ਪ੍ਰਸ਼ਨ 1.
ਖੁਸ਼ਕ ਪੱਤਝੜੀ ਬਨਸਪਤੀ ‘ਤੇ ਸੰਖੇਪ ਨੋਟ ਲਿਖੋ ।
ਉੱਤਰ-
ਇਸ ਕਿਸਮ ਦੀ ਬਨਸਪਤੀ 50 ਤੋਂ 100 ਸੈ: ਮੀ: ਘੱਟ ਵਰਖਾ ਵਾਲੇ ਖੇਤਰਾਂ ਵਿਚ ਮਿਲਦੀ ਹੈ ।
ਖੇਤਰ-ਇਸ ਦੀ ਇਕ ਲੰਬੀ ਪੱਟੀ ਪੰਜਾਬ ਤੋਂ ਲੈ ਕੇ ਹਰਿਆਣਾ, ਦੱਖਣ-ਪੱਛਮੀ ਉੱਤਰ ਪ੍ਰਦੇਸ਼, ਪੂਰਬੀ ਰਾਜਸਥਾਨ, ਕਾਠੀਆਵਾੜ, ਦੱਖਣ ਦੇ ਪਠਾਰ ਦੇ ਮੱਧਵਰਤੀ ਭਾਗ ਦੇ ਆਸ-ਪਾਸ ਦੇ ਖੇਤਰਾਂ ਵਿਚ ਫੈਲੀ ਹੋਈ ਹੈ ।
ਮੁੱਖ ਰੁੱਖ – ਇਸ ਬਨਸਪਤੀ ਵਿਚ ਟਾਹਲੀ, ਕਿੱਕਰ, ਫਲਾਹੀ, ਬੋਹੜ, ਹਲਦੁ ਵਰਗੇ ਰੁੱਖ ਭਾਰੀ ਮਾਤਰਾ ਵਿਚ ਮਿਲਦੇ ਹਨ । ਇਸ ਵਿਚ ਚੰਦਨ, ਮਹੂਆ, ਸੀਰਸ ਅਤੇ ਸਾਗਵਾਨ ਵਰਗੇ ਕੀਮਤੀ ਰੁੱਖ ਵੀ ਮਿਲਦੇ ਹਨ । ਇਹ ਰੁੱਖ ਅਕਸਰ ਗਰਮੀਆਂ ਸ਼ੁਰੂ ਹੁੰਦੇ ਹੀ ਆਪਣੇ ਪੱਤੇ ਸੁੱਟ ਦਿੰਦੇ ਹਨ ।
ਘਾਹ – ਇਨ੍ਹਾਂ ਖੇਤਰਾਂ ਵਿਚ ਦੂਰ-ਦੂਰ ਕੰਡੇਦਾਰ ਝਾੜੀਆਂ ਅਤੇ ਕਈ ਤਰ੍ਹਾਂ ਦੀ ਘਾਹ ਨਜ਼ਰ ਆਉਂਦੀ ਹੈ, ਜੋ ਕਿ ਘਾਹ ਦੇ ਮੈਦਾਨ ਵਾਂਗ ਦਿੱਸਦੀ ਹੈ । ਇਸ ਘਾਹੇ ਨੂੰ ਮੁੰਜ, ਕਾਂਸ ਅਤੇ ਸਬਾਈ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਹੇਠ ਲਿਖਿਆਂ ‘ਤੇ ਸੰਖੇਪ ਟਿੱਪਣੀਆਂ ਲਿਖੋ
(i) ਜੰਗਲੀ ਜੀਵਾਂ ਦੀ ਸੰਭਾਲ,
(ii) ਮਿੱਟੀ ਦੀ ਸੰਭਾਲ ।
ਉੱਤਰ-
(i) ਜੰਗਲੀ ਜੀਵਾਂ ਦੀ ਸੰਭਾਲ – ਭਾਰਤ ਵਿਚ ਵੱਖ-ਵੱਖ ਤਰ੍ਹਾਂ ਦੇ ਜੰਗਲੀ ਜੀਵ ਮਿਲਦੇ ਹਨ । ਉਨ੍ਹਾਂ ਦੀ ਸਹੀ ਦੇਖਭਾਲ ਨਾ ਹੋਣ ਨਾਲ ਜੀਵਾਂ ਦੀਆਂ ਕਈ ਜਾਤਾਂ ਜਾਂ ਤਾਂ ਖ਼ਤਮ ਹੋ ਗਈਆਂ ਹਨ ਜਾਂ ਖ਼ਤਮ ਹੋਣ ਵਾਲੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਜੀਵਾਂ ਦੇ ਮਹੱਤਵ ਨੂੰ ਦੇਖਦੇ ਹੋਏ ਹੁਣ ਇਨ੍ਹਾਂ ਦੀ ਸੁਰੱਖਿਆ ਅਤੇ ਸੰਭਾਲ ਦੇ ਉਪਾਅ ਕੀਤੇ ਜਾ ਰਹੇ ਹਨ । ਨੀਲਗਿਰੀ ਵਿਚ ਭਾਰਤ ਦਾ ਪਹਿਲਾ ਜੀਵ-ਰਾਖਵਾਂ ਖੇਤਰ ਸਥਾਪਿਤ ਕੀਤਾ ਗਿਆ । ਇਹ ਕਰਨਾਟਕ, ਤਾਮਿਲਨਾਡੂ ਅਤੇ ਕੇਰਲ ਦੇ ਸੀਮਾਵਰਤੀ ਖੇਤਰਾਂ ਵਿਚ ਫੈਲਿਆ ਹੋਇਆ ਹੈ । ਇਸ ਦੀ ਸਥਾਪਨਾ 1986 ਵਿਚ ਕੀਤੀ ਗਈ ਸੀ ਨੀਲਗਿਰੀ ਤੋਂ ਬਾਅਦ 1988 ਈ: ਵਿਚ ਉੱਤਰਾਖੰਡ (ਮੌਜੂਦਾ) ਵਿਚ ਨੰਦਾ ਦੇਵੀ ਦਾ ਜੀਵ-ਰਾਖਵਾਂ ਖੇਤਰ ਬਣਾਇਆ ਗਿਆ । ਉਸੇ ਸਾਲ ਮੇਘਾਲਿਆ ਵਿਚ ਤੀਜਾ ਖੇਤਰ ਸਥਾਪਿਤ ਕੀਤਾ ਗਿਆ । ਇਕ ਹੋਰ ਜੀਵ-ਰਾਖਵਾਂ ਖੇਤਰ ਅੰਡੇਮਾਨ ਅਤੇ ਨਿਕੋਬਾਰ ਦੀਪ ਸਮੂਹ ਵਿਚ ਸਥਾਪਿਤ ਕੀਤਾ ਗਿਆ ਹੈ । ਇਨ੍ਹਾਂ ਜੀਵ ਰਾਖਵਾਂ ਖੇਤਰਾਂ ਤੋਂ ਇਲਾਵਾ ਭਾਰਤ ਸਰਕਾਰ ਦੁਆਰਾ ਅਰੁਣਾਚਲ ਪ੍ਰਦੇਸ਼, ਤਾਮਿਲਨਾਡੂ, ਰਾਜਸਥਾਨ, ਗੁਜਰਾਤ ਅਤੇ ਅਸਾਮ ਵਿਚ ਵੀ ਜੀਵ-ਰਾਖਵੇਂ ਖੇਤਰ ਸਥਾਪਿਤ ਕੀਤੇ ਗਏ ਹਨ ।
(ii) ਮਿੱਟੀ ਦੀ ਸੰਭਾਲ – ਭਾਰਤ ਵਿਚ ਵੱਖ-ਵੱਖ ਤਰ੍ਹਾਂ ਦੀਆਂ ਮਿੱਟੀਆਂ ਮਿਲਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਮਿੱਟੀਆਂ ਵਿਚ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਫ਼ਸਲਾਂ ਉਗਾਈਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ ਦੇਸ਼ ਵਿਚ ਮਿਲਦੀਆਂ ਉਪਜਾਊ ਮਿੱਟੀਆਂ ਦੇ ਕਾਰਨ ਹੀ ਭਾਰਤ ਖੇਤੀ ਉਤਪਾਦਾਂ ਵਿਚ ਆਤਮ-ਨਿਰਭਰ ਹੋ ਸਕਿਆ ਹੈ | ਪਰ ਮਿੱਟੀ ਦਾ ਉਪਜਾਊਪਨ ਬਣਾਈ ਰੱਖਣ ਲਈ ਇਹ ਜ਼ਰੂਰੀ ਹੈ ਕਿ ਵਿਗਿਆਨਿਕ ਤਰੀਕੇ ਅਪਣਾਏ ਜਾਣ | ਸਾਨੂੰ ਮਿੱਟੀਆਂ ਦੀ ਸਹੀ ਸੰਭਾਲ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਖੁਰਨ ਤੋਂ ਬਚਾਉਣਾ ਚਾਹੀਦਾ ਹੈ । ਮਿੱਟੀ ਦੀ ਉਪਜਾਊਪਨ ਬਣਾਈ ਰੱਖਣ ਲਈ ਰਸਾਇਣਿਕ ਖਾਦਾਂ ਦੇ ਨਾਲ-ਨਾਲ ਜੈਵਿਕ ਖਾਦਾਂ ਦੀ ਸਹਾਇਤਾ ਵੀ ਲੈਣੀ ਚਾਹੀਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਸਪੱਸ਼ਟ ਹੈ ਕਿ ਭੂਮੀ ਦੀ ਉਤਪਾਦਕਤਾ ਨੂੰ ਲਗਾਤਾਰ ਬਣਾਈ ਰੱਖਣ ਲਈ ਮਿੱਟੀ ਦੀ ਸੰਭਾਲ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
ਰੇਗੁਰ ਅਤੇ ਲੈਟਰਾਈਟ ਮਿੱਟੀ ਵਿਚ ਅੰਤਰ ਸਪੱਸ਼ਟ ਕਰੋ ।
ਉੱਤਰ-
ਰੇਗੁਰ ਮਿੱਟੀ ਅਤੇ ਲੈਟਰਾਈਟ ਮਿੱਟੀ ਵਿਚ ਹੇਠ ਲਿਖੇ ਅੰਤਰ ਹਨ-

![]()
ਪ੍ਰਸ਼ਨ 4.
ਸਾਡੀ ਮਿੱਟੀ ਦੀ ਉਪਜਾਊ ਸ਼ਕਤੀ ਘੱਟ ਹੁੰਦੀ ਜਾ ਰਹੀ ਹੈ । ਇਸ ਨੂੰ ਦੂਰ ਕਰਨ ਲਈ ਤੁਸੀਂ ਕੀ ਸੁਝਾਅ ਦਿਉਗੇ ?
ਉੱਤਰ-
ਭਾਰਤ ਦੀ ਮਿੱਟੀ ਦੀ ਉਪਜਾਊ ਸ਼ਕਤੀ ਨੂੰ ਵਧਾਉਣ ਲਈ ਹੇਠ ਲਿਖੇ ਸੁਝਾਅ ਦਿੱਤੇ ਜਾ ਸਕਦੇ ਹਨ-
- ਰਸਾਇਣਿਕ ਖਾਦਾਂ ਦੀ ਵਰਤੋਂ – ਸਾਡੇ ਦੇਸ਼ ਦੇ ਕਿਸਾਨ ਵਧੇਰੇ ਕਰਕੇ ਗੋਹੇ ਦੀ ਖਾਦ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹਨ ਜਿਸ ਨਾਲ ਉਪਜ ਘੱਟ ਹੁੰਦੀ ਹੈ । ਰਸਾਇਣਿਕ ਖਾਦ ਦੀ ਵਰਤੋਂ ਕਰਨ ਨਾਲ ਜ਼ਰੂਰੀ ਤੱਤਾਂ ਦੀ ਕਮੀ ਨੂੰ ਪੂਰਾ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਇਸ ਲਈ ਕਿਸਾਨਾਂ ਨੂੰ ਗੋਹੇ ਦੀ ਖਾਦ ਦੇ ਨਾਲ-ਨਾਲ ਰਸਾਇਣਿਕ ਖਾਦਾਂ ਦੀ ਵੀ ਵਰਤੋਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ।
- ਜ਼ਮੀਨ ਨੂੰ ਖਾਲੀ ਛੱਡਣਾ – ਜੇਕਰ ਜ਼ਮੀਨ ਨੂੰ ਕੁੱਝ ਸਮੇਂ ਲਈ ਖ਼ਾਲੀ ਛੱਡ ਦਿੱਤਾ ਜਾਵੇ ਤਾਂ ਉਹ ਉਪਜਾਊ ਸ਼ਕਤੀ ਵਿਚ ਆਈ ਕਮੀ ਨੂੰ ਪੂਰਾ ਕਰ ਲੈਂਦੀ ਹੈ । ਇਸ ਲਈ ਜ਼ਮੀਨ ਨੂੰ ਕੁੱਝ ਸਮੇਂ ਲਈ ਖ਼ਾਲੀ ਛੱਡ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ ।
- ਫ਼ਸਲਾਂ ਦਾ ਵੇਰ-ਬਦਲ – ਪੌਦੇ ਆਪਣਾ ਭੋਜਨ ਧਰਤੀ ਤੋਂ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਨ । ਹਰੇਕ ਪੌਦਾ ਤੁਮੀ ਤੋਂ ਅਲੱਗ-ਅਲੱਗ ਪ੍ਰਕਾਰ ਦਾ ਤੱਤ ਪ੍ਰਾਪਤ ਕਰਦਾ ਹੈ । ਜੇਕਰ ਇਕ ਫ਼ਸਲ ਨੂੰ ਵਾਰ-ਵਾਰ ਬੀਜਿਆ ਜਾਵੇ ਤਾਂ ਭੂਮੀ ਵਿਚ ਇਕੋ ਖ਼ਾਸ ਤੱਤ ਦੀ ਕਮੀ ਹੋ ਜਾਂਦੀ ਹੈ । ਇਸ ਲਈ ਫ਼ਸਲਾਂ ਨੂੰ ਅਦਲ-ਬਦਲ ਕੇ ਬੀਜਣਾ ਚਾਹੀਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 5.
ਭਾਰਤ ਵਿਚ ਮਿਲਣ ਵਾਲੀ ਕਾਲੀ ਅਤੇ ਲਾਲ ਮਿੱਟੀ ਦੀ ਤੁਲਨਾ ਕਰੋ ।
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਮਿਲਣ ਵਾਲੀ ਕਾਲੀ ਅਤੇ ਲਾਲ ਮਿੱਟੀ ਦੀ ਤੁਲਨਾ ਇਸ ਤਰ੍ਹਾਂ ਹੈ-

ਪ੍ਰਸ਼ਨ 6.
ਜਲੋਢ ਮਿੱਟੀ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਇਹ ਭਾਰਤ ਵਿਚ ਕਿਹੜੇ-ਕਿਹੜੇ ਭਾਗਾਂ ਵਿਚ ਮਿਲਦੀ ਹੈ ? ਇਸ ਮਿੱਟੀ ਦੇ ਗੁਣ ਅਤੇ ਲੱਛਣਾਂ ਦਾ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਨਦੀਆਂ ਆਪਣੇ ਨਾਲ ਲਿਆਂਦੀ ਹੋਈ ਮਿੱਟੀ ਅਤੇ ਗਾਰ ਦੇ ਬਰੀਕ ਕਣਾਂ ਨੂੰ ਮੈਦਾਨ ਵਿਚ ਵਿਛਾ ਦਿੰਦੀਆਂ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਨਾਲ ਜੋ ਮਿੱਟੀ ਬਣਦੀ ਹੈ ਉਸ ਨੂੰ ਜਲੋਢ ਮਿੱਟੀ ਕਹਿੰਦੇ ਹਨ । ਜਲੋਢ ਮਿੱਟੀ ਬਹੁਤ ਉਪਜਾਊ ਹੁੰਦੀ ਹੈ ।
ਜਲੋ ਮਿੱਟੀ ਦੇ ਖੇਤਰ – ਭਾਰਤ ਵਿਚ ਜਲੋਢ ਮਿੱਟੀ ਗੰਗਾ-ਸਤਲੁਜ ਦੇ ਮੈਦਾਨ, ਮਹਾਂਨਦੀ, ਕ੍ਰਿਸ਼ਨਾ ਅਤੇ ਕਾਵੇਰੀ ਨਦੀਆਂ ਦੇ ਡੈਲਟਿਆਂ, ਮਪੁੱਤਰ ਦੀ ਘਾਟੀ ਅਤੇ ਪੂਰਬੀ ਤੇ ਪੱਛਮੀ ਤਟੀ ਮੈਦਾਨਾਂ ਵਿਚ ਮਿਲਦੀ ਹੈ ।
ਗੁਣ ਅਤੇ ਲੱਛਣ-
- ਇਹ ਮਿੱਟੀ ਬਹੁਤ ਉਪਜਾਊ ਹੁੰਦੀ ਹੈ ।
- ਇਹ ਮਿੱਟੀ ਸਖ਼ਤ ਨਹੀਂ ਹੁੰਦੀ । ਇਸ ਲਈ ਇਸ ਵਿਚ ਆਸਾਨੀ ਨਾਲ ਹਲ ਚਲਾਇਆ ਜਾ ਸਕਦਾ ਹੈ । ਵਰਖਾ ਘੱਟ ਹੋਣ ‘ਤੇ ਇਸ ਮਿੱਟੀ ਵਿਚ ਨਾਈਟਰੋਜਨ ਅਤੇ ਮਲ ਦੀ ਮਾਤਰਾ ਘੱਟ ਹੋ ਜਾਂਦੀ ਹੈ ਅਤੇ ਪੋਟਾਸ਼ ’ਤੇ ਫਾਸਫੋਰਸ ਦੀ ਮਾਤਰਾ ਵੱਧ ਜਾਂਦੀ ਹੈ । ਤਦ ਇਹ ਖੇਤੀ ਯੋਗ ਨਹੀਂ ਰਹਿੰਦੀ ।
ਪ੍ਰਸ਼ਨ 7.
ਜਲੋਢ ਮਿੱਟੀ ਕਿੰਨੇ ਤਰ੍ਹਾਂ ਦੀ ਹੁੰਦੀ ਹੈ ? ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਜਲੋਢ ਮਿੱਟੀ ਵਿਚ ਵਰਖਾ ਦੀ ਭਿੰਨਤਾ ਦੇ ਕਾਰਨ ਖਾਰ, ਰੇਤ ਅਤੇ ਚੀਕਾ ਦੀ ਮਾਤਰਾ ਅਲੱਗ-ਅਲੱਗ ਹੁੰਦੀ ਹੈ । ਇਸ ਆਧਾਰ ‘ਤੇ ਇਸ ਨੂੰ ਚਾਰ ਹਿੱਸਿਆਂ ਵਿਚ ਵੰਡਿਆ ਜਾ ਸਕਦਾ ਹੈ-
- ਬਾਂਗਰ ਮਿੱਟੀ – ਇਹ ਪਾਚੀਨ ਜਲੋਢ ਮਿੱਟੀ ਹੈ । ਇੱਥੇ ਅਜਿਹੀ ਮਿੱਟੀ ਮਿਲਦੀ ਹੈ ਜਿੱਥੇ ਹੜ੍ਹ ਦਾ ਪਾਣੀ ਨਹੀਂ ਪਹੁੰਚਦਾ । ਇਸ ਵਿਚ ਰੇਤ ਅਤੇ ਚੀਕਾ ਦੀ ਮਾਤਰਾ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਕਿਤੇ-ਕਿਤੇ ਕੰਕਰ ਅਤੇ ਚੂਨੇ ਦੀਆਂ ਡਲੀਆਂ ਵੀ ਮਿਲਦੀਆਂ ਹਨ ।
- ਖਾਦਰ ਮਿੱਟੀ – ਇਸ ਨੂੰ ਨਵੀਨ ਜਲੋਢ ਵੀ ਕਹਿੰਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਦੀ ਮਿੱਟੀ ਦੇ ਖੇਤਰ ਨਦੀਆਂ ਦੇ ਨੇੜੇ ਮਿਲਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਵਿਚ ਹੜ੍ਹ ਦਾ ਪਾਣੀ ਹਰ ਸਾਲ ਪਹੁੰਚ ਜਾਂਦਾ ਹੈ ਜਿਸ ਨਾਲ ਨਵੀਂ ਜਲੋਢ ਦਾ ਜਮਾਓ ਹੁੰਦਾ ਰਹਿੰਦਾ ਹੈ ।
- ਡੈਲਟਾਈ ਮਿੱਟੀ – ਇਸ ਨੂੰ ਸਭ ਤੋਂ ਨਵੀਂ ਕਛਾਰੀ ਮਿੱਟੀ ਵੀ ਕਹਿੰਦੇ ਹਨ । ਇਹ ਨਦੀਆਂ ਦੇ ਡੈਲਟਿਆਂ ਦੇ ਨੇੜੇ-ਤੇੜੇ ਮਿਲਦੀ ਹੈ । ਇਸ ਵਿਚ ਚੀਕਾ ਦੀ ਮਾਤਰਾ ਜ਼ਿਆਦਾ ਹੁੰਦੀ ਹੈ ।
- ਤਟਵਰਤੀ ਜਲੋਦ ਮਿੱਟੀ – ਇਸ ਪ੍ਰਕਾਰ ਦੀ ਮਿੱਟੀ ਦਾ ਨਿਰਮਾਣ ਤਟਾਂ ਦੇ ਨਾਲ ਸਮੁੰਦਰੀ ਲਹਿਰਾਂ ਦੇ ਨਿਖੇਪ ਨਾਲ ਪ੍ਰਾਪਤ ਚੂਰੇ ਤੋਂ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 8.
ਜੰਗਲੀ ਜੀਵਾਂ ਦੀ ਰੱਖਿਆ ਕਰਨਾ ਹਰੇਕ ਨਾਗਰਿਕ ਦਾ ਕਰਤੱਵ ਕਿਉਂ ਹੈ ?
ਉੱਤਰ-
ਸਾਡੇ ਵਣਾਂ ਵਿਚ ਬਹੁਤ ਸਾਰੇ ਮਹੱਤਵਪੂਰਨ ਪਸ਼ੂ-ਪੰਛੀ ਮਿਲਦੇ ਹਨ । ਪਰ ਅਫ਼ਸੋਸ ਦੀ ਗੱਲ ਇਹ ਹੈ ਕਿ ਪੰਛੀਆਂ ਅਤੇ ਜਾਨਵਰਾਂ ਦੀਆਂ ਅਨੇਕਾਂ ਜਾਤਾਂ ਸਾਡੇ ਦੇਸ਼ ਵਿਚੋਂ ਲੁਪਤ ਹੋ ਚੁੱਕੀਆਂ ਹਨ । ਇਸ ਲਈ ਜੰਗਲੀ ਜੀਵਾਂ ਦੀ ਰੱਖਿਆ ਕਰਨਾ ਸਾਡੇ ਲਈ ਬਹੁਤ ਹੀ ਜ਼ਰੂਰੀ ਹੈ । ਮਨੁੱਖ ਨੇ ਆਪਣੇ ਨਿੱਜੀ ਲਾਭ ਲਈ ਵਣਾਂ ਨੂੰ ਕੱਟ ਕੇ ਅਤੇ ਜਾਨਵਰਾਂ ਦਾ ਸ਼ਿਕਾਰ ਕਰਕੇ ਇਕ ਦੁੱਖ ਵਾਲੀ ਸਥਿਤੀ ਪੈਦਾ ਕਰ ਦਿੱਤੀ ਹੈ । ਅੱਜ ਗੈਂਡਾ, ਚੀਤਾ, ਬਾਂਦਰ, ਸ਼ੇਰ ਅਤੇ ਸਾਰੰਗ ਨਾਂ ਦੇ ਪਸ਼ੂ-ਪੰਛੀ ਬਹੁਤ ਘੱਟ ਗਿਣਤੀ ਵਿਚ ਮਿਲਦੇ ਹਨ । ਇਸ ਲਈ ਹਰੇਕ ਨਾਗਰਿਕ ਦਾ ਇਹ ਕਰਤੱਵ ਹੈ ਕਿ ਉਹ ਜੰਗਲੀ ਜੀਵਾਂ ਦੀ ਰੱਖਿਆ ਕਰੇ ।
ਪ੍ਰਸ਼ਨ 9.
ਕਿਸਾਨ ਦੇ ਲਈ ਪਸ਼ੂ ਧਨ/ਪਸ਼ੂ ਪਾਲਣ ।
ਉੱਤਰ-
ਸਾਡੇ ਦੇਸ਼ ਵਿਚ ਵਿਸ਼ਾਲ ਪਸ਼ੂ ਧਨ ਪਾਇਆ ਜਾਂਦਾ ਹੈ, ਜਿਨ੍ਹਾਂ ਨੂੰ ਕਿਸਾਨ ਆਪਣੇ ਖੇਤਾਂ ‘ਤੇ ਪਾਲਦੇ ਹਨ । ਪਸ਼ੂਆਂ ਤੋਂ ਕਿਸਾਨ ਨੂੰ ਗੋਹਾ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ਜੋ ਮਿੱਟੀ ਦੇ ਉਪਜਾਊਪਨ ਨੂੰ ਬਣਾਈ ਰੱਖਣ ਵਿਚ ਉਨ੍ਹਾਂ ਦੀ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ । ਪਹਿਲਾਂ ਕਿਸਾਨ ਗੋਹੇ ਨੂੰ ਬਾਲਣ ਦੇ ਰੂਪ ਵਿਚ ਵਰਤਦੇ ਸਨ । ਪਰ ਹੁਣ ਪ੍ਰਤੀਸ਼ੀਲ ਕਿਸਾਨ ਗੋਹੇ ਦੀ ਬਾਲਣ ਅਤੇ ਖਾਦ ਦੋਹਾਂ ਰੂਪਾਂ ਵਿਚ ਵਰਤੋਂ ਕਰਦੇ ਹਨ । ਖੇਤ ਵਿਚ ਗੋਹੇ ਨੂੰ ਖਾਦ ਦੇ ਰੂਪ ਵਿਚ ਵਰਤੋਂ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਉਹ ਉਸ ਤੋਂ ਗੈਸ ਬਣਾਉਂਦੇ ਹਨ, ਜਿਸ ‘ਤੇ ਉਹ ਖਾਣਾ ਬਣਾਉਂਦੇ ਹਨ ਅਤੇ ਰੌਸ਼ਨੀ ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਨ । ਪਸ਼ੂਆਂ ਦੀਆਂ ਖੱਲਾਂ ਵੱਡੇ ਪੈਮਾਨੇ ‘ਤੇ ਨਿਰਯਾਤ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਪਸ਼ੂਆਂ ਤੋਂ ਉਨ੍ਹਾਂ ਨੂੰ ਉੱਨ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ । ਸੱਚ ਤਾਂ ਇਹ ਹੈ ਕਿ ਪਸ਼ੂਧਨ ਭਾਰਤੀ ਕਿਸਾਨ ਦੇ ਲਈ ਅਤਿਰਿਕਤ ਆਮਦਨ ਦਾ ਸਾਧਨ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 10.
ਮਿੱਟੀ ਦੇ ਮੁੱਖ ਪੰਜ ਉਪਯੋਗ ਦੱਸੋ ।
ਉੱਤਰ-
ਮਿੱਟੀ ਇਕ ਬਹੁਤ ਹੀ ਕੀਮਤੀ ਕੁਦਰਤੀ ਤੋਹਫ਼ਾ ਹੈ । ਇਸ ਤੋਂ ਸਾਨੂੰ ਵੱਖ-ਵੱਖ ਉਤਪਾਦ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ । ਇਸ ਦੇ ਮੁੱਖ ਪੰਜ ਉਪਯੋਗ ਹੇਠ ਲਿਖੇ ਹਨ-
- ਇਸ ਤੋਂ ਕਣਕ, ਚੌਲ, ਬਾਜਰਾ, ਜਵਾਰ ਆਦਿ ਅਨਾਜ ਪ੍ਰਾਪਤ ਹੁੰਦਾ ਹੈ ।
- ਇਸ ਵਿਚ ਪਸ਼ੂਆਂ ਦੇ ਲਈ ਘਾਹ ਅਤੇ ਪੱਠੇ ਉੱਗਦੇ ਹਨ ।
- ਇਸ ਤੋਂ ਕਪਾਹ, ਪਟਸਨ, ਸੀਸਲ ਆਦਿ ਰੇਸ਼ੇਦਾਰ ਪਦਾਰਥ ਮਿਲਦੇ ਹਨ ।
- ਇਸ ਤੋਂ ਸਾਨੂੰ ਦਾਲਾਂ ਮਿਲਦੀਆਂ ਹਨ ।
- ਇਸ ਤੋਂ ਉਪਯੋਗੀ ਲੱਕੜੀ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ।
ਵੱਡੇ ਉੱਤਰ ਵਾਲਾ ਪ੍ਰਸ਼ਨ (Long Answer Type Question)
ਪ੍ਰਸ਼ਨ 1.
ਭਾਰਤ ਵਿਚ ਮਿਲਦੇ ਜੰਗਲੀ ਜੀਵਾਂ ਦਾ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਬਨਸਪਤੀ ਦੀ ਤਰ੍ਹਾਂ ਹੀ ਸਾਡੇ ਦੇਸ਼ ਦੇ ਜੀਵ-ਜੰਤੂਆਂ ਵਿਚ ਵੀ ਬਹੁਤ ਵਿਭਿੰਨਤਾ ਹੈ । ਭਾਰਤ ਵਿਚ ਇਨ੍ਹਾਂ ਦੀਆਂ 76,000 ਜਾਤੀਆਂ ਮਿਲਦੀਆਂ ਹਨ । ਦੇਸ਼ ਦੇ ਤਾਜ਼ੇ ਅਤੇ ਖਾਰੇ ਪਾਣੀ ਵਿਚ 2500 ਜਾਤਾਂ ਦੀਆਂ ਮੱਛੀਆਂ ਮਿਲਦੀਆਂ ਹਨ । ਇਸੇ ਤਰ੍ਹਾਂ ਇੱਥੇ ਪੰਛੀਆਂ ਦੀਆਂ ਵੀ 2000 ਜਾਤੀਆਂ ਮਿਲਦੀਆਂ ਹਨ। ਮੁੱਖ ਤੌਰ ‘ਤੇ ਭਾਰਤ ਦੇ ਜੰਗਲੀ ਜੀਵਾਂ ਦਾ ਵਰਣਨ ਇਸ ਤਰ੍ਹਾਂ ਹੈ-
- ਹਾਥੀ – ਹਾਥੀ ਰਾਜਸੀ ਠਾਠ-ਬਾਠ ਵਾਲਾ ਪਸ਼ੂ ਹੈ । ਇਹ ਗਰਮ ਜਿਲ੍ਹੇ ਵਣਾਂ ਦਾ ਪਸ਼ੂ ਹੈ । ਇਹ ਅਸਮ, ਕੇਰਲਾ ਅਤੇ ਕਰਨਾਟਕ ਦੇ ਜੰਗਲਾਂ ਵਿਚ ਮਿਲਦਾ ਹੈ । ਇਨ੍ਹਾਂ ਥਾਂਵਾਂ ‘ਤੇ ਭਾਰੀ ਵਰਖਾ ਦੇ ਕਾਰਨ ਬਹੁਤ ਸੰਘਣੇ ਜੰਗਲ ਮਿਲਦੇ ਹਨ ।
- ਉਠ – ਉਠ ਗਰਮ ਅਤੇ ਖ਼ੁਸ਼ਕ ਮਾਰੂਥਲਾਂ ਵਿਚ ਮਿਲਦਾ ਹੈ ।
- ਜੰਗਲੀ ਖੋਤਾ ਜੰਗਲੀ ਖੋਤੇ ਕੱਛ ਦੇ ਰਣ ਵਿਚ ਮਿਲਦੇ ਹਨ ।
- ਇਕ ਸਿੰਗ ਵਾਲਾ ਗੈਂਡਾ – ਇਕ ਸਿੰਗ ਵਾਲੇ ਗੈਂਡੇ ਅਸਮ ਅਤੇ ਪੱਛਮੀ ਬੰਗਾਲ ਦੇ ਉੱਤਰੀ ਭਾਗਾਂ ਦੇ ਦਲਦਲੀ ਖੇਤਰਾਂ ਵਿਚ ਮਿਲਦੇ ਹਨ ।
- ਬਾਂਦਰ – ਭਾਰਤ ਵਿਚ ਬਾਂਦਰਾਂ ਦੀਆਂ ਅਨੇਕਾਂ ਜਾਤਾਂ ਮਿਲਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਲੰਗੂਰ ਆਮ ਮਿਲਦਾ ਹੈ । ਪੂਛ ਵਾਲਾ ਬਾਂਦਰ (ਕਾਕ) ਬੜਾ ਹੀ ਵਚਿੱਤਰ ਜੀਵ ਹੈ । ਇਸ ਦੇ ਮੂੰਹ ਦੇ ਚਾਰੇ ਪਾਸੇ ਵਾਲ ਉੱਗੇ ਹੁੰਦੇ ਹਨ ਜੋ ਇਕ ਪ੍ਰਭਾਮੰਡਲ ਦੀ ਤਰ੍ਹਾਂ ਦਿਸਦਾ ਹੈ ।
- ਹਿਰਨ – ਭਾਰਤ ਵਿਚ ਹਿਰਨਾਂ ਦੀਆਂ ਅਨੇਕਾਂ ਜਾਤਾਂ ਮਿਲਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਵਿਚ ਚੌਗਿੰਗਾ, ਕਾਲਾ ਹਿਰਨ, ਚਿੰਕਾਰਾ ਅਤੇ ਆਮ ਹਿਰਨ ਮੁੱਖ ਹਨ । ਇੱਥੇ ਹਿਰਨਾਂ ਦੀਆਂ ਕੁੱਝ ਹੋਰ ਵੀ ਜਾਤਾਂ ਮਿਲਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਵਿਚ ਕਸ਼ਮੀਰੀ ਬਾਰਾਂਸਿੰਗਾ, ਦਲਦਲੀ ਹਿਰਨ, ਧੱਬੇਦਾਰ ਹਿਰਨ, ਕਸਤੂਰੀ ਹਿਰਨ ਅਤੇ ਮੂਸ਼ਕ ਹਿਰਨ ਮੁੱਖ ਹਨ ।
- ਸ਼ਿਕਾਰੀ ਜੰਤੂ – ਸ਼ਿਕਾਰੀ ਜੰਤੂਆਂ ਵਿਚ ਭਾਰਤੀ ਸ਼ੇਰ ਦਾ ਖ਼ਾਸ ਥਾਂ ਹੈ । ਅਫ਼ਰੀਕਾ ਤੋਂ ਇਲਾਵਾ ਇਹ ਸਿਰਫ਼ ਭਾਰਤ ਵਿਚ ਹੀ ਮਿਲਦਾ ਹੈ । ਇਸ ਦਾ ਕੁਦਰਤੀ ਆਵਾਸ ਗੁਜਰਾਤ ਵਿਚ ਸੌਰਾਸ਼ਟਰ ਦੇ ਗਿਰ ਜੰਗਲਾਂ ਵਿਚ ਹੈ । ਹੋਰ ਸ਼ਿਕਾਰੀ ਪਸ਼ੂਆਂ ਵਿਚ ਸ਼ੇਰ, ਚੀਤਾ, ਲੱਮਚਿੱਤਾ (ਕਲਾਊਡਿਡ ਲਿਓਪਾਰਡ ਅਤੇ ਬਰਫ਼ ਦਾ ਚੀਤਾ ਮੁੱਖ ਹਨ ।
- ਹੋਰ ਜੀਵ-ਜੰਤੂ-ਹਿਮਾਲਾ ਦੀਆਂ ਲੜੀਆਂ ਵਿਚ ਵੀ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਜੀਵ-ਜੰਤੂ ਰਹਿੰਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਵਿਚ ਜੰਗਲੀ ਭੇਡਾਂ ਅਤੇ ਪਹਾੜੀ ਬੱਕਰੀਆਂ ਖ਼ਾਸ ਤੌਰ ‘ਤੇ ਵਰਣਨ ਯੋਗ ਹਨ | ਭਾਰਤੀ ਜੰਤੂਆਂ ਵਿਚ ਭਾਰਤੀ ਮੋਰ, ਭਾਰਤੀ ਸੰਢਾ ਅਤੇ ਨੀਲ ਗਾਂ ਮੁੱਖ ਹਨ । ਭਾਰਤ ਸਰਕਾਰ ਕੁੱਝ ਜਾਤਾਂ ਦੇ ਜੀਵ ਜੰਤੂਆਂ ਦੀ ਸੰਭਾਲ ਲਈ ਖ਼ਾਸ ਯਤਨ ਕਰ ਰਹੀ ਹੈ ।