Punjab State Board PSEB 10th Class Home Science Book Solutions Chapter 4 ਡਿਜ਼ਾਈਨ ਦੇ ਮੂਲ ਅੰਸ਼ ਅਤੇ ਸਿਧਾਂਤ Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Home Science Chapter 4 ਡਿਜ਼ਾਈਨ ਦੇ ਮੂਲ ਅੰਸ਼ ਅਤੇ ਸਿਧਾਂਤ
Home Science Guide for Class 10 PSEB ਡਿਜ਼ਾਈਨ ਦੇ ਮੂਲ ਅੰਸ਼ ਅਤੇ ਸਿਧਾਂਤ Textbook Questions and Answers
ਅਭਿਆਸ
ਵਸਤੂਨਿਸ਼ਠ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਡਿਜ਼ਾਈਨ ਦੇ ਮੂਲ ਅੰਸ਼ ਕਿਹੜੇ-ਕਿਹੜੇ ਹਨ, ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਜਦੋਂ ਵੀ ਕੋਈ ਚੀਜ਼ ਬਣਾਈ ਜਾਂਦੀ ਹੈ ਤਾਂ ਉਸ ਦਾ ਨਮੂਨਾ ਭਾਵ ਡਿਜ਼ਾਈਨ ਬਣਦਾ ਹੈ ਭਾਵੇਂ ਇਹ ਚੀਜ਼ ਕੁਰਸੀ, ਮੇਜ਼ ਹੋਵੇ ਜਾਂ ਮਕਾਨ । ਇਕ ਚੰਗਾ ਡਿਜ਼ਾਈਨ ਬਣਾਉਣ ਲਈ ਇਸ ਦੇ ਮੂਲ ਤੱਤਾਂ ਦਾ ਗਿਆਨ ਅਤੇ ਕਲਾ ਦੇ ਮੂਲ ਸਿਧਾਂਤਾਂ ਦੀ ਜਾਣਕਾਰੀ ਹੋਣੀ ਜ਼ਰੂਰੀ ਹੈ । ਇਹਨਾਂ ਮੂਲ ਸਿਧਾਂਤਾਂ ਵਿਚ ਰੇਖਾਵਾਂ, ਰੂਪ ਤੇ ਆਕਾਰ, ਰੰਗ ਅਤੇ ਬਣਤਰ (Texture) ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 2.
ਡਿਜ਼ਾਈਨ ਵਿਚ ਇਕਸੁਰਤਾ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਡਿਜ਼ਾਈਨ ਬਣਾਉਣ ਲਈ ਲਾਈਨਾਂ, ਆਕਾਰ, ਰੰਗ ਅਤੇ ਰਚਨਾ ਦੀ ਜ਼ਰੂਰਤ ਪੈਂਦੀ ਹੈ । ਇਕੋ ਤਰ੍ਹਾਂ ਦੀਆਂ ਦੋ ਚੀਜ਼ਾਂ ਜਿਵੇਂ ਇਕੋ ਰੰਗ, ਇਕ ਤਰ੍ਹਾਂ ਦੀਆਂ ਲਾਈਨਾਂ ਜਾਂ ਆਕਾਰ ਨਾਲ ਡਿਜ਼ਾਈਨ ਵਿਚ ਇਕਸੁਰਤਾ ਲਿਆਂਦੀ ਜਾ ਸਕਦੀ ਹੈ । ਪਰ ਜੇਕਰ ਹਰ ਇਕ ਚੀਜ਼ ਅਲੱਗ ਤਰ੍ਹਾਂ ਦੀ ਹੋਵੇ, ਤਾਂ ਉਹ ਪਰੇਸ਼ਾਨੀ ਦਾ ਅਹਿਸਾਸ ਦਵਾਉਂਦੀ ਹੈ । ਜਦੋਂ | ਡਿਜ਼ਾਈਨ ਦੇ ਸਾਰੇ ਅੰਸ਼ਾਂ ਵਿਚ ਇਕਸੁਰਤਾ ਹੋਵੇਗੀ ਤਾਂ ਉਹ ਇਕ ਸਮੁੱਚਾ ਡਿਜ਼ਾਈਨ ਜਾਪੇਗਾ ਨਾ ਕਿ ਅੱਡ-ਅੱਡ ਅੰਸ਼ਾਂ ਦਾ ਬੇਤੁਕਾ ਜੋੜ, ਅਜਿਹੇ ਡਿਜ਼ਾਈਨ ਨੂੰ ਚੰਗਾ ਸਮਝਿਆ ਜਾਵੇਗਾ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਡਿਜ਼ਾਈਨ ਵਿਚ ਸੰਤੁਲਨ ਕਿੰਨੇ ਪ੍ਰਕਾਰ ਦਾ ਹੋ ਸਕਦਾ ਹੈ ਅਤੇ ਕਿਹੜਾ-ਕਿਹੜਾ ?
ਉੱਤਰ-
ਡਿਜ਼ਾਈਨ ਵਿਚ ਸੰਤੁਲਨ ਦੋ ਤਰ੍ਹਾਂ ਦਾ ਹੁੰਦਾ ਹੈ-
1. ਉਪਚਾਰਿਕ ਸੰਤੁਲਨ (Formal Balance) – ਉਪਚਾਰਿਕ | ਸੰਤੁਲਨ ਨੂੰ ਸਮਿਟਰੀਕਲ ਸੰਤੁਲਨ ਦੇ ਨਾਂ ਨਾਲ ਵੀ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ । ਜਦੋਂ ਕਿ ਇਕ ਕੇਂਦਰ ਬਿੰਦੂ ਦੇ ਸਾਰੇ ਪਾਸੇ ਦੀਆਂ ਚੀਜ਼ਾਂ ਹਰ ਪੱਖੋਂ ਇਕੋ ਜਿਹੀਆਂ ਹੋਣ ਤਾਂ ਇਸ ਨੂੰ ਉਪਚਾਰਿਕ ਸੰਤੁਲਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
2. ਅਣਉਪਚਾਰਿਕ ਸੰਤੁਲਨ (Informal Balance) – ਜਦੋਂ ਵਸਤਾਂ ਇਸ ਪ੍ਰਕਾਰ ਰੱਖੀਆਂ ਜਾਣ ਕਿ ਵੱਡੀ ਵਸਤੁ ਕੇਂਦਰ ਬਿੰਦੂ ਦੇ ਕੋਲ ਹੋਵੇ ਅਤੇ ਛੋਟੀ ਵਸਤੂ ਨੂੰ ਕੇਂਦਰ ਬਿੰਦੂ ਤੋਂ ਥੋੜਾ ਦੂਰ ਰੱਖਿਆ ਜਾਵੇ ਤਾਂ ਇਸ ਨੂੰ ਅਣਉਪਚਾਰਿਕ ਸੰਤੁਲਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਹ ਸੰਤੁਲਨ ਬਣਾਉਣਾ ਥੋੜਾ ਔਖਾ ਹੈ ਜੋ ਠੀਕ ਅਣਉਪਚਾਰਿਕ ਸੰਤੁਲਨ ਬਣ ਜਾਵੇ ਤਾਂ ਉਪਚਾਰਿਕ ਸੰਤੁਲਨ ਨਾਲੋਂ ਬਹੁਤ ਸੋਹਣਾ ਲਗਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਡਿਜ਼ਾਈਨ ਵਿਚ ਬਲ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਬਲ ਤੋਂ ਭਾਵ ਕਿਸੇ ਇਕ ਰੁਚੀਕਰ ਬਿੰਦੂ ਉੱਤੇ ਜ਼ਿਆਦਾ ਬਲ ਦੇਣਾ ਭਾਵ ਉਸ ਨੂੰ ਵੱਧ ਆਕਰਸ਼ਿਤ ਬਣਾਉਣਾ ਅਤੇ ਅਰੁਚੀਕਰ ਵਸਤਾਂ ‘ਤੇ ਘੱਟ ਬਲ ਦੇਣਾ ਹੈ । ਜਦੋਂ ਡਿਜ਼ਾਈਨ ਪੁਰਾ ਸੰਤੁਲਿਤ ਹੋਵੇ, ਉਸ ਵਿਚ ਪੂਰਨ ਅਨੁਰੂਪਤਾ ਹੋਵੇ ਪਰ ਫਿਰ ਵੀ ਫਿੱਕਾ ਅਤੇ ਅਰੁਚੀਕਰ ਲੱਗੇ ਤਾਂ ਮਤਲਬ ਕਿ ਉਸ ਡਿਜ਼ਾਈਨ ਵਿਚ ਕੋਈ ਵਿਸ਼ੇਸ਼ ਬਿੰਦੂ ਨਹੀਂ ਹੈ ਜਿੱਥੇ ਧਿਆਨ ਕੇਂਦਰਿਤ ਹੋ ਸਕੇ । ਅਜਿਹੇ ਡਿਜ਼ਾਈਨ ਵਿਚ ਬਲ ਦੀ ਕਮੀ ਹੈ । ਬਲ ਕਲਾ ਦਾ ਇਕ ਸਿਧਾਂਤ ਹੈ ਕਿ ਕਮਰੇ ਵਿਚ ਵੜਦਿਆਂ ਜਿੱਥੇ ਤੁਹਾਡਾ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਧਿਆਨ ਜਾਵੇ ਅਤੇ ਫਿਰ ਮਹੱਤਵ ਦੇ ਕ੍ਰਮ ਅਨੁਸਾਰ ਨਿਗਾਹ ਟਿਕਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 5.
ਡਿਜ਼ਾਈਨ ਵਿਚ ਅਨੁਪਾਤ ਹੋਣਾ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹੈ ?
ਉੱਤਰ-
ਡਿਜ਼ਾਈਨ ਵਿਚ ਅਨੁਪਾਤ ਤੋਂ ਭਾਵ ਕਮਰਾ ਅਤੇ ਉਸ ਵਿਚਲੇ ਸਾਮਾਨ ਦਾ ਆਪਸ ਵਿਚ ਸੰਬੰਧ ਹੈ । ਜੇ ਕਮਰਾ ਵੱਡਾ ਹੈ ਤਾਂ ਉਸ ਵਿਚਲਾ ਸਾਮਾਨ ਫਰਨੀਚਰ ਵੀ ਵੱਡਾ ਹੀ ਚੰਗਾ ਲੱਗਦਾ ਹੈ, ਪਰ ਵੱਡਾ ਫਰਨੀਚਰ ਛੋਟੇ ਕਮਰੇ ਵਿਚ ਰੱਖਿਆ ਜਾਵੇ ਤਾਂ ਭੈੜਾ ਲੱਗਦਾ ਹੈ । ਇਕ ਵੱਡੇ ਕਮਰੇ ਵਿਚ ਗੁੜੇ ਰੰਗ ਦੇ ਵੱਡੇ ਡਿਜ਼ਾਈਨ ਵਾਲੇ ਪਰਦੇ ਅਤੇ ਭਾਰਾ ਤੇ ਵੱਡਾ ਫਰਨੀਚਰ ਹੀ ਵਰਤਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਸ ਦੇ ਉਲਟ ਛੋਟੇ ਕਮਰੇ ਵਿਚ ਫਿੱਕੇ ਰੰਗ ਦੇ ਪਰਦੇ ਅਤੇ ਹਲਕਾ ਫਰਨੀਚਰ ਜਿਵੇਂ ਬੈਂਤ, ਐਲੂਮੀਨੀਅਮ ਜਾਂ ਲੱਕੜ ਦਾ ਵੀ ਸਾਦੇ ਡਿਜ਼ਾਈਨ ਵਾਲਾ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ਜਿਸ ਨਾਲ ਕਮਰਾ ਖੁੱਲ੍ਹਾ-ਖੁੱਲਾ ਲੱਗਦਾ ਹੈ | ਸੋ ਘਰ ਦੀ ਬਣਤਰ ਜਾਂ ਨਮੂਨਾ ਅਤੇ ਉਸ ਵਿਚ ਰੱਖਿਆ ਸਾਮਾਨ ਘਰ ਦੇ ਕਮਰਿਆਂ ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਹੀ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂ ਹੀ ਘਰ ਸੋਹਣਾ ਦਿਖੇਗਾ ਨਹੀਂ ਤਾਂ ਘਰ ਅਤੇ ਚੀਜ਼ਾਂ ‘ਤੇ ਲਾਇਆ ਧਨ ਵੀ ਬੇਕਾਰ ਹੀ ਲੱਗਦਾ ਹੈ ਜੇ ਸਾਮਾਨ ਘਰ ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਨਾ ਹੋਵੇ ਤਾਂ ।
ਪ੍ਰਸ਼ਨ 6.
ਡਿਜ਼ਾਈਨ ਵਿਚ ਲੈਅ ਕਿਵੇਂ ਪੈਦਾ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ?
ਉੱਤਰ-
ਕਿਸੇ ਵੀ ਡਿਜ਼ਾਈਨ ਵਿਚ ਲੈਅ ਹੇਠ ਲਿਖੇ ਤਰੀਕਿਆਂ ਨਾਲ ਪੈਦਾ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ-
- ਦੁਹਰਾਉਣ ਨਾਲ (Repetition) – ਡਿਜ਼ਾਈਨ ਵਿਚ ਲੈਅ ਪੈਦਾ ਕਰਨ ਲਈ ਰੰਗ, ਰੇਖਾਵਾਂ ਜਾਂ ਆਕਾਰ ਨੂੰ ਦੁਹਰਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਨਾਲ ਉਸ ਚੀਜ਼ ਜਾਂ ਥਾਂ ਦੇ ਵੱਖ-ਵੱਖ ਹਿੱਸਿਆਂ ਵਿਚ ਤਾਲ-ਮੇਲ ਪੈਦਾ ਹੁੰਦਾ ਹੈ ।
- ਦਰਜਾਬੰਦੀ (Gradation) – ਜਦੋਂ ਵੱਖ-ਵੱਖ ਚੀਜ਼ਾਂ ਨੂੰ ਆਕਾਰ ਦੇ ਹਿਸਾਬ ਨਾਲ ਇਕ ਲੜੀ ਵਿਚ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਵੀ ਲੈਅ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ।
- ਪ੍ਰਤੀਕੂਲਤਾ (Opposition) – ਡਿਜ਼ਾਈਨ ਵਿਚ ਲੈਅ ਪ੍ਰਤੀਕੂਲਤਾ ਨਾਲ ਵੀ ਲਿਆਈ ਜਾਂਦੀ ਹੈ ਤਾਂ ਜੋ ਰੇਖਾਵਾਂ ਇਕ-ਦੂਜੇ ਨਾਲ ਸਹੀ ਕੋਣਾਂ ‘ਤੇ ਆਉਣ | ਵਰਗਾਕਾਰ ਅਤੇ ਆਇਤਾਕਾਰ ਫ਼ਰਨੀਚਰ ਇਸ ਦੀ ਇਕ ਉਦਾਹਰਨ ਹੈ ।
- ਰੇਡੀਏਸ਼ਨ (Radiation) – ਜਦੋਂ ਰੇਖਾਵਾਂ ਇਕ ਕੇਂਦਰੀ ਬਿੰਦੂ ਤੋਂ ਬਾਹਰ ਨੂੰ ਆਉਣ ਤਾਂ ਇਸ ਨੂੰ ਰੇਡੀਏਸ਼ਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
- ਸਮਾਨਾਂਤਰ (Parallel) – ਇਕ ਸਮਾਨਾਂਤਰ ਰੇਖਾਵਾਂ ਦੇ ਸਥਾਨ ਲੈਂਦੀ ਹੈ ਅਤੇ ਆਕਿਰਤੀਆਂ ਬਣਾਉਂਦੀ ਹੋਈ ਦੂਜੇ ਸਾਹਮਣੇ ਹੁੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 7.
ਪ੍ਰਾਥਮਿਕ ਜਾਂ ਪਹਿਲੇ ਦਰਜੇ ਦੇ ਰੰਗ ਕਿਹੜੇ ਹਨ ?
ਜਾਂ
ਮੱਢਲੇ ਰੰਗਾਂ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਪਾਥਮਿਕ ਜਾਂ ਪਹਿਲੇ ਦਰਜੇ ਦੇ ਰੰਗ-ਪੀਲਾ, ਨੀਲਾ ਅਤੇ ਲਾਲ ਹਨ । ਇਹ ਤਿੰਨੋਂ ਰੰਗ ਹੋਰ ਰੰਗਾਂ ਨੂੰ ਮਿਲਾ ਕੇ ਨਹੀਂ ਬਣਦੇ। ਇਸ ਲਈ ਇਨ੍ਹਾਂ ਨੂੰ ਪ੍ਰਾਥਮਿਕ ਜਾਂ ਪਹਿਲੇ ਦਰਜੇ ਦੇ ਰੰਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 8.
ਉਦਾਸੀਨ ਰੰਗ ਕਿਹੜੇ-ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਕਾਲਾ, ਸਲੇਟੀ, ਚਿੱਟਾ ਉਦਾਸੀਨ ਰੰਗ ਹਨ । ਇਹਨਾਂ ਨੂੰ ਕਿਸੇ ਵੀ ਰੰਗ ਨਾਲ ਮਿਲਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 9.
ਵਿਰੋਧੀ ਰੰਗ ਯੋਜਨਾ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
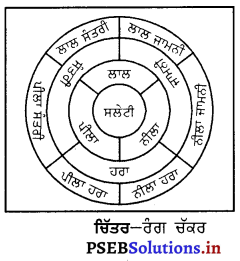
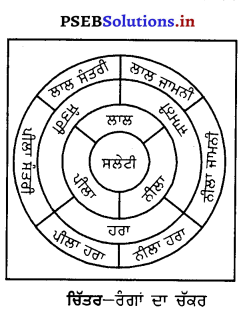
ਵਿਰੋਧੀ ਰੰਗ ਯੋਜਨਾ ਵਿਚ ਇਕ-ਦੂਜੇ ਦੇ ਉਲਟ ਰੰਗ ਵਰਤੇ ਜਾਂਦੇ ਹਨ । ਜਿਵੇਂ ਰੰਗ ਚੱਕਰ ਵਿਚ ਵਿਖਾਇਆ ਗਿਆ ਹੈ । ਜਿਵੇਂ ਲਾਲ ਤੇ ਹਰਾ, ਪੀਲਾ ਅਤੇ ਜਾਮਨੀ ਜਾਂ ਸੰਤਰੀ ਅਤੇ ਨੀਲਾ ਆਦਿ।
ਪ੍ਰਸ਼ਨ 10.
ਸੰਬੰਧਿਤ ਵਿਉਂਤ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਜਦੋਂ ਰੰਗਾਂ ਦੇ ਚੱਕਰ ਦੇ ਨਾਲ ਲੱਗਦੇ ਰੰਗਾਂ ਦੀ ਚੋਣ ਕੀਤੀ ਜਾਵੇ ਤਾਂ ਇਸ ਨੂੰ ਸੰਬੰਧਿਤ ਵਿਉਂਤ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਵਿਉਂਤ ਵਿਚ ਵੱਧ ਤੋਂ ਵੱਧ ਤਿੰਨ ਰੰਗ ਵਰਤੇ ਜਾਂਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਨੀਲਾ, ਹਰਾ-ਨੀਲਾ ਅਤੇ ਨੀਲਾ-ਜਾਮਨੀ । ਇਸ ਦੀ ਇਕਸਾਰਤਾ ਨੂੰ ਤੋੜਨ ਲਈ ਵੀ ਰੰਗ ਚੱਕਰ ਦੇ ਦੂਸਰੇ ਪਾਸੇ ਦੇ ਰੰਗ, ਜਿਵੇਂ ਕਿ ਸੰਤਰੀ ਜਾਂ ਸੰਤਰੀ-ਪੀਲਾ ਛੋਟੀਆਂ ਚੀਜ਼ਾਂ ਲਈ ਵਰਤੇ ਜਾ ਸਕਦੇ ਹਨ ।
ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 11.
ਡਿਜ਼ਾਈਨ ਦੇ ਮੂਲ ਅੰਸ਼ ਕਿਹੜੇ ਹਨ ? ਰੂਪ ਅਤੇ ਆਕਾਰ ਕਿਵੇਂ ਡਿਜ਼ਾਈਨ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ ? :
ਉੱਤਰ-
ਕੋਈ ਵੀ ਮਕਾਨ ਜਾਂ ਚੀਜ਼ ਬਣਾਉਣ ਲਈ ਪਹਿਲਾਂ ਉਸ ਦਾ ਡਿਜ਼ਾਈਨ ਤਿਆਰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਹਰ ਡਿਜ਼ਾਈਨ ਤਿਆਰ ਕਰਨ ਲਈ ਉਸ ਦੇ ਮੂਲ ਤੱਤਾਂ ਦਾ ਪਤਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ, ਜਿਵੇਂ-
- ਰੇਖਾਵਾਂ-ਸਿੱਧੀਆਂ ਰੇਖਾਵਾਂ, ਲੇਟਵੀਆਂ ਰੇਖਾਵਾਂ, ਤਿਰਛੀਆਂ ਰੇਖਾਵਾਂ ਅਤੇ ਗੋਲ ਰੇਖਾਵਾਂ ।
- ਰੂਪ ਅਤੇ ਆਕਾਰ
- ਰੰਗ
- ਬਣਤਰ ।
ਰੂਪ ਅਤੇ ਆਕਾਰ (Shape and Size) – ਰੂਪ ਅਤੇ ਆਕਾਰ ਦਾ ਆਪਸ ਵਿਚ ਡੂੰਘਾ ਸੰਬੰਧ ਹੈ, ਰੇਖਾਵਾਂ ਨੂੰ ਮਿਲਾ ਕੇ ਹੀ ਕਿਸੇ ਚੀਜ਼ ਨੂੰ ਰੂਪ ਅਤੇ ਆਕਾਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਰੇਖਾਵਾਂ ਆਪਣੇ ਆਪ ਵਿਚ ਇਕ ਇਕਾਈ ਹਨ ਜਿਨ੍ਹਾਂ ਦੇ ਮਿਲਾਪ ਨਾਲ ਕੋਈ ਚੀਜ਼ ਬਣਾਈ ਜਾਂਦੀ ਹੈ । ਘਰ ਦੀ ਇਮਾਰਤ ਜਾਂ ਉਸ ਦੀ ਅੰਦਰੂਨੀ ਸਜਾਵਟ ਵਿਚ ਰੂਪ ਅਤੇ ਆਕਾਰ ਨਜ਼ਰ ਆਉਂਦਾ ਹੈ । ਅੱਜ-ਕੱਲ੍ਹ ਕਮਰਿਆਂ ਨੂੰ ਵੱਡਾ ਵਿਖਾਉਣ ਲਈ ਵੱਡੀਆਂਵੱਡੀਆਂ ਖਿੜਕੀਆਂ ਰੱਖੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ਤਾਂ ਕਿ ਅੰਦਰ ਅਤੇ ਬਾਹਰ ਮਿਲਦੇ ਨਜ਼ਰ ਆਉ । ਕਮਰੇ ਦਾ ਆਕਾਰ, ਉਸ ਦੀ ਛੱਤ ਦੀ ਉਚਾਈ ਅਤੇ ਉਸ ਵਿਚਲੇ ਦਰਵਾਜ਼ਿਆਂ ਅਤੇ ਖਿੜਕੀਆਂ ਕਮਰੇ ਵਿਚ ਰੱਖਣ ਵਾਲੇ ਫ਼ਰਨੀਚਰ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ | ਕਮਰੇ ਵਿਚਲਾ ਫ਼ਰਨੀਚਰ, ਪਰਦੇ, ਕਾਲੀਨ ਅਤੇ ਹੋਰ ਸਾਮਾਨ ਸਾਰੇ ਕਮਰੇ ਨੂੰ ਛੋਟਾ ਕਰਦੇ ਹਨ ।
ਜੇਕਰ ਕਿਸੇ ਕਮਰੇ ਨੂੰ ਉਸ ਦੇ ਕੰਮ ਦੇ ਮੁਤਾਬਕ ਵੰਡ ਦਿੱਤਾ ਜਾਏ, ਜਿਵੇਂ ਕਿ ਇਕ ਹਿੱਸਾ ਬੈਠਣ ਦਾ, ਇਕ ਖਾਣਾ ਖਾਣ ਦਾ ਅਤੇ ਇਕ ਪੜ੍ਹਨ ਦਾ ਤਾਂ ਉਹ ਕਮਰਾ ਛੋਟਾ ਲਗਣ ਲੱਗ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਕਮਰੇ ਨੂੰ ਵੱਡਾ ਦਿਖਾਉਣਾ ਚਾਹੁੰਦੇ ਹੋ ਤਾਂ ਇਸ ਦੇ ਘੱਟ ਤੋਂ ਘੱਟ ਹਿੱਸੇ ਕਰੋ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਕਮਰੇ ਨੂੰ ਵੱਡਾ ਦਿਖਾਉਣ ਲਈ ਛੋਟਾ ਅਤੇ ਹਲਕਾ ਫਰਨੀਚਰ, ਘੱਟ ਸਜਾਵਟ ਦਾ ਸਾਮਾਨ ਅਤੇ ਹਲਕੇ ਰੰਗ ਵਰਤੋ | ਪਤਲੀਆਂ ਲੱਤਾਂ ਵਾਲੇ ਫ਼ਰਨੀਚਰ ਨਾਲ ਕਮਰਾ ਵੱਡਾ ਲੱਗਦਾ ਹੈ ਕਿਉਂਕਿ ਇਸ ਨਾਲ ਫ਼ਰਨੀਚਰ ਦੇ ਹੇਠਾਂ ਫਰਸ਼ ਦਾ ਜ਼ਿਆਦਾ ਹਿੱਸਾ ਦਿਖਾਈ ਦਿੰਦਾ ਰਹਿੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 12.
ਲਾਈਨਾਂ ਕਿਹੋ ਜਿਹੀਆਂ ਹੋ ਸਕਦੀਆਂ ਹਨ ਅਤੇ ਡਿਜ਼ਾਈਨ ਨੂੰ ਕਿਵੇਂ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਹਰ ਡਿਜ਼ਾਈਨ ਵਿਚ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਲਾਈਨਾਂ ਹੁੰਦੀਆਂ ਹਨ ਪਰ ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਕੁੱਝ ਜ਼ਿਆਦਾ ਉੱਭਰੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ਜਿਸ ਨਾਲ ਡਿਜ਼ਾਈਨ ਵਿਚ ਭਿੰਨਤਾ ਆਉਂਦੀ ਹੈ । ਰੇਖਾਵਾਂ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ਜਿਵੇਂ ਸਿੱਧੀਆਂ, ਲੇਟਵੀਆਂ, ਤਿਰਛੀਆਂ, ਗੋਲ ਅਤੇ ਕੋਣ ।
ਕਿਸੇ ਵੀ ਫਰਨੀਚਰ ਦੇ ਡਿਜ਼ਾਈਨ ਜਾਂ ਸਜਾਵਟ ਦੇ ਸਾਮਾਨ ਦੇ ਡਿਜ਼ਾਈਨ, ਤਸਵੀਰਾਂ ਨੂੰ ਕੰਧਾਂ ‘ਤੇ ਲਾਉਣ ਦੇ ਢੰਗ ਜਾਂ ਕਮਰੇ ਵਿਚ ਫਰਨੀਚਰ ਰੱਖਣ ਦੇ ਡਿਜ਼ਾਈਨ ਵਿਚ ਰੇਖਾਵਾਂ ਆਪਣਾ ਪ੍ਰਭਾਵ ਵਿਖਾਉਂਦੀਆਂ ਹਨ । ਪਰ ਇਹਨਾਂ ਲਾਈਨਾਂ ਦਾ ਪ੍ਰਭਾਵ ਉਹੀ ਪੈਣਾ ਚਾਹੀਦਾ ਹੈ ਜੋ ਤੁਸੀਂ ਚਾਹੁੰਦੇ ਹੋ । ਜੇ ਤੁਸੀਂ ਕਮਰੇ ਨੂੰ ਅਰਾਮਦਾਇਕ ਬਣਾਉਣਾ ਚਾਹੁੰਦੇ ਹੋ, ਤਾਂ ਲੇਟਵੀਆਂ ਲਾਈਨਾਂ ਦੀ ਵਰਤੋਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਜੇ ਕਮਰੇ ਦੀ ਛੱਤ ਨੂੰ ਉੱਚਾ ਵਿਖਾਉਣਾ ਹੈ ਤਾਂ ਸਿੱਧੀਆਂ ਲੰਮੀਆਂ ਲਾਈਨਾਂ ਵਾਲੇ ਪਰਦਿਆਂ ਦੀ ਵਰਤੋਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ । ਗੋਲ ਰੇਖਾਵਾਂ ਪ੍ਰਸੰਨਤਾ ਅਤੇ ਜਸ਼ਨ ਨੂੰ ਪ੍ਰਗਟਾਉਂਦੀਆਂ ਹਨ ਜਦ ਕਿ ਕੋਣ ਵਾਲੀਆਂ ਰੇਖਾਵਾਂ ਉਤੇਜਿਤ ਕਰਨ ਵਾਲੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 13.
ਪਰੈੱਗ ਦੀ ਰੰਗ ਪ੍ਰਣਾਲੀ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਪਰੇਂਗ ਦੇ ਅਨੁਸਾਰ ਸਾਰੇ ਰੰਗ ਮੁੱਢਲੇ ਤਿੰਨ ਰੰਗਾਂ-ਪੀਲਾ, ਨੀਲਾ ਅਤੇ ਲਾਲ ਤੋਂ ਬਣਦੇ ਹਨ । ਇਹ ਤਿੰਨ ਰੰਗ ਹੋਰ ਰੰਗਾਂ ਨੂੰ ਮਿਲਾ ਕੇ ਨਹੀਂ ਬਣਾਏ ਜਾ ਸਕਦੇ । ਇਸ ਲਈ ਇਹਨਾਂ ਨੂੰ ਪ੍ਰਾਥਮਿਕ (ਪਹਿਲੇ) ਦਰਜੇ ਦੇ ਰੰਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਜਦੋਂ ਦੋ ਪ੍ਰਾਥਮਿਕ ਰੰਗਾਂ ਨੂੰ ਇਕੋ ਜਿੰਨੀ ਮਾਤਰਾ ਵਿਚ ਮਿਲਾਇਆ ਜਾਏ ਤਾਂ ਤਿੰਨ ਦੂਜੇ ਦਰਜੇ ਦੇ ਰੰਗ ਬਣਦੇ ਹਨ । ਜਿਵੇਂ ਕਿ-
ਪੀਲਾ + ਨੀਲਾ = ਹਰਾ,
ਨੀਲਾ + ਲਾਲ = ਜਾਮਨੀ,
ਲਾਲ + ਪੀਲਾ = ਸੰਤਰੀ ।
ਇਨ੍ਹਾਂ ਛੇ ਰੰਗਾਂ ਨੂੰ ਅਧਾਰ ਰੰਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਕ ਪਾਥਮਿਕ ਅਤੇ ਉਸ ਦੇ ਨਾਲ ਲੱਗਦੇ ਇਕ ਦੂਸਰੇ ਦਰਜੇ ਦੇ ਰੰਗ ਨੂੰ ਮਿਲਾ ਕੇ ਜੋ ਰੰਗ ਬਣਦੇ ਹਨ ਉਨ੍ਹਾਂ ਨੂੰ ਤੀਸਰੇ ਦਰਜੇ ਦੇ ਰੰਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਜਿਵੇਂ ਕਿ-
ਪੀਲਾ + ਹ = ਪੀਲਾ ਹਰਾ,
ਨੀਲਾ + ਹ = ਨੀਲਾ ਹਰਾ,
ਨੀਲਾ + ਜਾਮਨੀ = ਨੀਲਾ ਜਾਮਨੀ,
ਲਾਲ + ਜਾਮਨੀ = ਲਾਲ ਜਾਮਨੀ,
ਲਾਲ + ਸੰਤਰੀ = ਲਾਲ ਸੰਤਰੀ,
ਪੀਲਾ + ਸੰਤਰੀ = ਪੀਲਾ ਸੰਤਰੀ ।
ਇਸ ਪ੍ਰਕਾਰ ਤਿੰਨ (3) ਪ੍ਰਾਥਮਿਕ, ਤਿੰਨ (3) ਦੂਸਰੇ ਦਰਜੇ ਦੇ ਅਤੇ ਛੇ (6) ਤੀਸਰੇ ਦਰਜੇ ਦੇ ਰੰਗ ਹੁੰਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਰੰਗਾਂ ਦਾ ਆਪਸੀ ਅਨੁਪਾਤ ਵਧਾ-ਘਟਾ ਕੇ ਅਨੇਕਾਂ ਰੰਗ ਬਣਾਏ ਜਾ ਸਕਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਰੰਗਾਂ ਵਿਚ ਚਿੱਟਾ ਰੰਗ ਮਿਲਾਉਣ ਨਾਲ ਰੰਗਾਂ ਦੀ ਭਾਅ (ਹਲਕਾ ਰੰਗ) ਬਣਦੀ ਹੈ, ਜਿਵੇਂ ਕਿ-
ਲਾਲ + ਚਿੱਟਾ = ਗੁਲਾਬੀ,
ਨੀਲਾ + ਚਿੱਟਾ = ਅਸਮਾਨੀ ।
ਗੁਲਾਬੀ ਅਤੇ ਅਸਮਾਨੀ, ਲਾਲ ਅਤੇ ਨੀਲੇ ਰੰਗ ਦੀ ਭਾਅ ਹਨ ।
ਕਿਸੇ ਵੀ ਰੰਗ ਵਿਚ ਕਾਲਾ ਰੰਗ ਮਿਲਾਉਣ ਨਾਲ ਉਸ ਰੰਗ ਵਿਚ ਗਹਿਰਾਈ ਆ ਜਾਂਦੀ ਹੈ, ਜਿਵੇਂ ਕਿ-
ਲਾਲ + ਕਾਲਾ = ਲਾਖਾ ।
ਕਾਲਾ, ਸਲੇਟੀ (ਗਰੇ) ਅਤੇ ਚਿੱਟੇ ਨੂੰ ਉਦਾਸੀਨ (neutral) ਰੰਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਇਨ੍ਹਾਂ ਨੂੰ ਕਿਸੇ ਵੀ ਰੰਗ ਨਾਲ ਮਿਲਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 14.
ਘਰਾਂ ਵਿਚ ਰੰਗਾਂ ਸੰਬੰਧੀ ਕਿਹੋ ਜਿਹੀ ਵਿਉਂਤ ਬਣਾਈ ਜਾ ਸਕਦੀ ਹੈ ?
ਉੱਤਰ-
ਘਰਾਂ ਵਿਚ ਆਮ ਤੌਰ ‘ਤੇ ਰੰਗਾਂ ਨਾਲ ਤਿੰਨ ਤਰ੍ਹਾਂ ਦੀ ਵਿਉਂਤ ਬਣਾਈ ਜਾ ਸਕਦੀ ਹੈ-
- ਇਕ ਰੰਗ ਦੀ ਵਿਉਂਤ – ਇਸ ਵਿਉਂਤ ਵਿਚ ਇਕ ਹੀ ਰੰਗ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ਭਾਵ ਕਿ ਇਕ ਰੰਗ ਦੇ ਵੱਖ-ਵੱਖ ਭਾਅ/ਗੂੜੇ/ਫਿੱਕੇ ਰੰਗ ਵਰਤੇ ਜਾਂਦੇ ਹਨ । ਜਿਵੇਂ ਨੀਲਾ ਜਾਂ ਲਾਲ ਦੇ ਗੁੜੇ ਤੇ ਹਲਕੇ ਭਾਅ ਵਾਲੇ ਰੰਗ ਵਰਤੇ ਜਾ ਸਕਦੇ ਹਨ । ਇਸੇ ਰੰਗ ਵਿਚ ਪ੍ਰਿੰਟ ਵੀ ਵਰਤਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਰੰਗ ਦੀ ਇਕਸਾਰਤਾ ਨੂੰ ਤੋੜਨ ਲਈ ਕੁਸ਼ਨ ਕਵਰ ਜਾਂ ਲੈਂਪ ਸ਼ੇਡ ਆਦਿ ਪੀਲੇ, ‘ ਹਰੇ ਜਾਂ ਭੂਰੇ ਰੰਗ ਦੇ ਵਰਤੇ ਜਾ ਸਕਦੇ ਹਨ ।
- ਵਿਰੋਧੀ ਰੰਗ ਯੋਜਨਾ – ਇਹ ਰੰਗ ਯੋਜਨਾ ਕਾਫ਼ੀ ਪ੍ਰਚਲਿਤ ਹੈ । ਇਸ ਵਿਚ ਰੰਗ ਚੱਕਰ ਦੇ ਆਹਮੋ-ਸਾਹਮਣੇ ਵਾਲੇ ਰੰਗ ਵਰਤੇ ਜਾਂਦੇ ਹਨ, ਜਿਵੇਂ-ਪੀਲਾ ਤੇ ਜਾਮਨੀ ਜਾਂ ਲਾਲ ਤੇ ਹਰਾ ਜਾਂ ਸੰਤਰੀ ਤੇ ਨੀਲਾ ਆਦਿ ।
- ਸੰਬੰਧਿਤ ਰੰਗ ਵਿਉਂਤ – ਜਦੋਂ ਰੰਗ ਚੱਕਰ ਦੇ ਨਾਲ-ਨਾਲ ਦੇ ਰੰਗ ਵਰਤੇ ਜਾਣ ਤਾਂ ਇਸਨੂੰ ਸੰਬੰਧਿਤ ਵਿਉਂਤ ਕਹਿੰਦੇ ਹਨ । ਇਸ ਵਿਚ ਵੱਧ ਤੋਂ ਵੱਧ ਤਿੰਨ ਰੰਗ ਵਰਤੇ ਜਾਂਦੇ ਹਨ । ਜਿਵੇਂ ਕਿ ਨੀਲਾ, ਹਰਾ ਨੀਲਾ ਅਤੇ ਜਾਮਨੀ ਨੀਲਾ ਪਰ ਰੰਗ ਦੀ ਇਕਸਾਰਤਾ ਨੂੰ ਤੋੜਨ ਲਈ ਰੰਗ ਚੱਕਰ ਦੇ ਦੂਜੇ ਪਾਸੇ ਦੇ ਰੰਗ ਜਿਵੇਂ ਕਿ ਸੰਤਰੀ ਅਤੇ ਸੰਤਰੀ ਪੀਲਾ ਕੁੱਝ ਛੋਟੀਆਂ ਚੀਜ਼ਾਂ ਜਿਵੇਂ ਕੁਸ਼ਨ ਜਾਂ ਲੈਪ ਸ਼ੇਡ ਲਈ ਵਰਤਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 15.
ਉਪਚਾਰਿਕ ਅਤੇ ਅਣਉਪਚਾਰਿਕ ਸੰਤੁਲਨ ਵਿਚ ਕੀ ਅੰਤਰ ਹੈ ਅਤੇ ਕਿਵੇਂ ਪੈਦਾ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਉਪਚਾਰਿਕ ਸੰਤੁਲਨ ਨੂੰ ਸਮਿਟਰੀਕਲ ਭਾਵ ਬਰਾਬਰ ਦਾ ਸੰਤੁਲਨ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਜਦੋਂ ਕਿਸੇ ਡਿਜ਼ਾਈਨ ਜਾਂ ਕਿਸੇ ਕਮਰੇ ਵਿਚ ਰੇਖਾ, ਰੰਗ ਅਤੇ ਸਥਾਨ ਇਕੋ ਜਿਹੇ ਹੋਣ ਜਾਂ ਇਕੋ ਜਿਹੇ ਲੱਗਣ ਦੋਹਾਂ ਪਾਸਿਆਂ ਵਿਚੋਂ ਕੋਈ ਵੀ ਪਾਸਾ ਕਾਲਪਨਿਕ ਬਿੰਦੁ ਪ੍ਰਤੀਤ ਹੋਵੇ ਤਾਂ ਪੂਰਾ ਉਪਚਾਰਿਕ ਸੰਤੁਲਨ ਹੁੰਦਾ ਹੈ । ਇਹ ਸੰਤੁਲਨ ਸ਼ਾਂਤੀ ਦੀ ਭਾਵਨਾ ਪੈਦਾ ਕਰਦਾ ਹੈ । ਪਰ ਕਦੇ-ਕਦੇ ਥਕਾਉ ( monotonous) ਵੀ ਹੋ ਜਾਂਦਾ ਹੈ ।
ਇਹ ਸੰਤੁਲਨ ਨੂੰ ਸੀ-ਸਾਅ (See-Saw) ਝਲੇ ਦੇ ਰੂਪ ਵਿਚ ਸਪੱਸ਼ਟ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਜਿਸ ਵਿਚ ਇਕੋ ਜਿਹੇ ਭਾਰ ਦੇ ਦੋ ਬੱਚੇ ਕੇਂਦਰ ਤੋਂ ਬਰਾਬਰ ਦੂਰੀ ‘ਤੇ ਬੈਠੇ ਹੋਣ ਤਾਂ ਇਹ ਉਪਚਾਰਿਕ ਸੰਤੁਲਨ ਦੀ ਇਕ ਉਦਾਹਰਨ ਹੈ । ਜਿਵੇਂ ਖਾਣੇ ਵਾਲੇ ਮੇਜ਼ ਦੇ ਆਸ ਪਾਸਇਕੋ ਹੀ ਡਿਜ਼ਾਈਨ ਦੀਆਂ ਕੁਰਸੀਆਂ ਇਕੋ ਜਿੰਨੇ ਫਾਸਲੇ ‘ਤੇ ਰੱਖਣ ਨਾਲ ।
ਅਣਉਪਚਾਰਿਕ ਸੰਤੁਲਨ, ਅਸਮਿਟਰੀਕਲ ਸੰਤੁਲਨ ਦੇ ਨਾਂ ਨਾਲ ਵੀ ਜਾਣਿਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਸੰਤੁਲਨ ਚੀਜ਼ਾਂ ਦੀ ਬਨਾਵਟ ਤੋਂ ਇਲਾਵਾ ਉਨ੍ਹਾਂ ਦੇ ਰੰਗ, ਨਮੂਨੇ ਅਤੇ ਕੇਂਦਰ ਬਿੰਦੂ ਤੋਂ ਦੁਰ ਜਾਂ ਨੇੜੇ ਰੱਖ ਕੇ ਵੀ ਪੈਦਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਹ ਸੰਤੁਲਨ ਪੈਦਾ ਕਰਨਾ ਮੁਸ਼ਕਿਲ ਹੈ ਪਰ ਜੇ ਠੀਕ ਹੋਵੇ ਤਾਂ ਉਪਚਾਰਿਕ ਸੰਤੁਲਨ ਨਾਲੋਂ ਵਧੀਆ ਲੱਗਦਾ ਹੈ, ਨਾਲ ਹੀ ਕੁਦਰਤੀ ਦਿਖਦਾ ਹੈ ।
![]()
ਨਿਬੰਧਾਤਮਕ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 16.
ਡਿਜ਼ਾਈਨ ਦੇ ਮੂਲ ਸਿਧਾਂਤ ਕਿਹੜੇ ਹਨ ? ਇਨ੍ਹਾਂ ਬਾਰੇ ਪਤਾ ਹੋਣਾ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹੈ ?
ਉੱਤਰ-
ਜਦੋਂ ਵੀ ਕੋਈ ਚੀਜ਼ ਬਣਾਈ ਜਾਂਦੀ ਹੈ, ਚਾਹੇ ਮਕਾਨ ਹੋਵੇ, ਫ਼ਰਨੀਚਰ ਜਾਂ ਘਰ ਦਾ ਹੋਰ ਸਮਾਨ ਤਾਂ ਉਸ ਦਾ ਇਕ ਨਮੂਨਾ ਤਿਆਰ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਜਿਸ ਨੂੰ ਡਿਜ਼ਾਈਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਡਿਜ਼ਾਈਨ ਵਿਚ ਇਹ ਧਿਆਨ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ ਕਿ ਨਮੂਨੇ ਵਿਚਲੇ ਤੱਤਾਂ ਦਾ ਇਕ-ਦੂਜੇ ਨਾਲ ਤਾਲ-ਮੇਲ ਹੋਵੇ । ਜਿਵੇਂ ਕਿ ਘਰ ਵਿਚ ਇਕ ਕਮਰੇ ਦਾ ਦੂਜੇ ਕਮਰੇ ਨਾਲ ਕੰਧਾਂ, ਛੱਤਾਂ, ਖਿੜਕੀਆਂ ਅਤੇ ਦਰਵਾਜ਼ਿਆਂ ਦਾ ਆਪਸ ਵਿਚ। ਇਸੇ ਤਰ੍ਹਾਂ ਫ਼ਰਨੀਚਰ ਵਿਚ ਆਕਾਰ, ਰੇਖਾ, ਰੰਗ ਆਦਿ ਜਿਵੇਂ ਕਿ ਲੱਕੜ ਦਾ ਰੰਗ, ਕੱਪੜੇ ਦਾ ਰੰਗ, ਬੈਂਤ ਦਾ ਰੰਗ ਅਤੇ | ਉਸ ਦੀ ਬੁਣਾਈ ਆਦਿ ਆਪਸ ਵਿਚ ਮਿਲਦੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ | ਜੇ ਇਕ ਕਮਰੇ ਵਿਚਲਾ ਸਾਰਾ ਸਾਮਾਨ ਆਪਸ ਵਿਚ ਮੇਲ ਖਾਂਦਾ ਹੋਵੇ ਤਾਂ ਹੀ ਵਧੀਆ ਡਿਜ਼ਾਈਨ ਹੋਵੇਗਾ ਜੋ ਕਿ ਵੇਖਣ ਵਿਚ ਸੁੰਦਰ ਲਗਦਾ ਹੈ । ਇਸ ਲਈ ਇਕ ਚੰਗਾ ਡਿਜ਼ਾਈਨ ਬਣਾਉਣ ਲਈ ਉਸ ਦੇ ਮੂਲ ਸਿਧਾਂਤਾਂ ਦੀ ਜਾਣਕਾਰੀ ਹੋਣੀ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ । ਇਹ ਮੂਲ ਸਿਧਾਂਤ ਹੇਠ ਲਿਖੇ ਹਨ-
- ਇਕਸੁਰਤਾ (Harmony)
- ਅਨੁਪਾਤ (Proportion)
- ਸੰਤੁਲਨ (Balance)
- ਲੈਅ (Rhythm)
- ਬਲ (Emphasis) ।
1. ਇਕਸੁਰਤਾ (Harmony) – ਕਿਸੇ ਵੀ ਡਿਜ਼ਾਈਨ ਵਿਚ ਇਕੋ ਤਰ੍ਹਾਂ ਦੀਆਂ ਚੀਜ਼ਾਂ ਜਿਵੇਂ ਕਿ ਰੰਗ, ਇਕੋ ਤਰ੍ਹਾਂ ਦੀਆਂ ਲਾਈਨਾਂ, ਆਕਾਰ ਜਾਂ ਰਚਨਾ ਦਾ ਪ੍ਰਯੋਗ ਕਰਕੇ ਇਕਸੁਰਤਾ ਲਿਆਈ ਜਾ ਸਕਦੀ ਹੈ । ਪਰ ਜੇ ਇਕ ਕਮਰੇ ਵਿਚ ਸਾਰੀਆਂ ਚੀਜ਼ਾਂ ਇਕ ਹੀ ਰੰਗ, ਆਕਾਰ ਜਾਂ ਰਚਨਾ ਦੀਆਂ ਹੋਣ ਤਾਂ ਵੀ ਉਹ ਚੰਗਾ ਨਹੀਂ ਲੱਗਦਾ । ਇਸ ਲਈ ਭਿੰਨ-ਭਿੰਨ ਤਰ੍ਹਾਂ ਦੀਆਂ ਚੀਜ਼ਾਂ ਨੂੰ ਵਰਤਣਾ ਜ਼ਰੂਰੀ ਹੈ । ਪਰ ਜੇਕਰ ਹਰ ਇਕ ਚੀਜ਼ ਹੀ ਅਲੱਗ ਤਰ੍ਹਾਂ ਦੀ ਹੋਵੇ ਤਾਂ ਵੀ | ਉਹ ਪਰੇਸ਼ਾਨੀ ਦਾ ਅਹਿਸਾਸ ਦੁਆਉਂਦੀ ਹੈ । ਜਦੋਂ ਡਿਜ਼ਾਈਨ ਦੇ ਸਾਰੇ ਅੰਸ਼ਾਂ ਵਿਚ ਇਕਸੁਰਤਾ ਹੋਵੇ ਤਾਂ ਕਿ ਉਹ ਇਕ ਸਮੁੱਚਾ ਡਿਜ਼ਾਈਨ ਜਾਪੇ ਨਾ ਕਿ ਅੱਡ-ਅੱਡ ਅੰਸ਼ਾਂ ਦਾ ਬੇਤੁਕਾ ਜੋੜ ਤਾਂ ਉਸ ਨੂੰ ਚੰਗਾ ਡਿਜ਼ਾਈਨ ਸਮਝਿਆ ਜਾਂਦਾ ਹੈ । ਕਈ ਵਾਰ ਭਿੰਨ ਰੇਖਾਵਾਂ ਜਾਂ ਰੰਗਾਂ ਦੇ ਪ੍ਰਯੋਗ ਨਾਲ ਵੀ ਚੰਗਾ ਡਿਜ਼ਾਈਨ ਬਣਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।
2. ਅਨੁਪਾਤ (Proportion) ਕਿਸੇ ਵੀ ਕਮਰੇ ਵਿਚ ਪਈਆਂ ਚੀਜ਼ਾਂ ਕਮਰੇ ਦੇ ਖੇਤਰਫਲ ਦੇ ਅਨੁਸਾਰ ਹੋਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ | ਸਾਰੀਆਂ ਚੀਜ਼ਾਂ ਦਾ ਆਪਸ ਵਿਚ ਅਤੇ ਕਮਰੇ ਦੇ ਅਨੁਸਾਰ ਅਨੁਪਾਤ ਠੀਕ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਇਕ ਵੱਡੇ ਕਮਰੇ ਵਿਚ ਭਾਰਾ ਫ਼ਰਨੀਚਰ ਜਾਂ ਗੂੜ੍ਹੇ ਰੰਗ ਜਾਂ ਵੱਡੇ ਡਿਜ਼ਾਈਨ ਦੇ ਪਰਦੇ ਜਾਂ ਕਾਲੀਨ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ । ਪਰ ਜੇਕਰ ਕਮਰਾ ਛੋਟਾ ਹੋਵੇ ਤਾਂ ਉਸ ਵਿਚ ਹਲਕੇ ਰੰਦਾ, ਛੋਟਾ ਡਿਜ਼ਾਈਨ ਡਿਜ਼ਾਈਨ ਦੇ ਮੂਲ ਅੰਸ਼ ਅਤੇ ਸਿਧਾਂਤ ਅਤੇ ਹਲਕਾ ਫ਼ਰਨੀਚਰ ਪ੍ਰਯੋਗ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ । ਵੱਡੇ ਕਮਰੇ ਵਿਚ ਛੋਟਾ ਜਾਂ ਹਲਕਾ ਫ਼ਰਨੀਚਰ, ਜਿਵੇਂ ਕਿ ਲੱਕੜੀ, ਬੈਂਤ ਦੀਆਂ ਕੁਰਸੀਆਂ ਜਾਂ ਬਾਂਸ ਦਾ ਫ਼ਰਨੀਚਰ ਜਾਂ ਐਲੂਮੀਨੀਅਮ ਦੀਆਂ ਕੁਰਸੀਆਂ ਰੱਖਣ ਨਾਲ ਕਮਰਾ ਹੋਰ ਵੀ ਵੱਡਾ ਅਤੇ ਖ਼ਾਲੀ ਲੱਗੇਗਾ ।
3. ਸੰਤੁਲਨ (Balance) – ਇਹ ਸਿਧਾਂਤ ਡਿਜ਼ਾਈਨ ਵਿਚ ਉਸ ਦੇ ਹਿੱਸਿਆਂ ਦੀ ਸੰਤੋਸ਼ਜਨਕ ਵਿਵਸਥਾ ਦੁਆਰਾ ਪੂਰਨ ਸਥਿਰਤਾ ਲਿਆਉਂਦਾ ਹੈ । ਇਸ ਦੇ ਆਕਾਰਾਂ, ਰੰਗਾਂ ਅਤੇ ਬਣਤਰ ਨੂੰ ਇਕ ਕੇਂਦਰ ਬਿੰਦੂ ਦੇ ਚਾਰੇ-ਪਾਸੇ ਇਕ ਪ੍ਰਕਾਰ ਦਾ ਸਮੂਹ ਬਣਾ ਕੇ ਪ੍ਰਾਪਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ਤਾਂ ਕਿ ਕੇਂਦਰ ਦੇ ਹਰ ਪਾਸੇ ਇਕੋ ਜਿਹਾ ਆਕਰਸ਼ਣ ਰਹੇ । ਸੰਤੁਲਨ ਦੋ ਤਰ੍ਹਾਂ ਦਾ ਹੁੰਦਾ ਹੈ (ਉ) ਉਪਚਾਰਿਕ ਸੰਤੁਲਨ ਅਤੇ (ਅ) ਅਣ-ਉਪਚਾਰਿਕ ਸੰਤੁਲਨ ।
(ਉ) ਉਪਚਾਰਿਕ (ਨਿਸਚਿਤ) ਸੰਤੁਲਨ – ਜਦੋਂ ਇਕ ਕੇਂਦਰ-ਬਿੰਦੁ ਦੇ ਸਾਰੇ ਪਾਸੇ ਦੀਆਂ ਚੀਜ਼ਾਂ ਹਰ ਲਿਹਾਜ਼ ਨਾਲ ਇਕੋ ਜਿਹੀਆਂ ਹੋਣ ਜਿਵੇਂ ਕਿ ਖਾਣੇ ਵਾਲੇ ਮੇਜ਼ ਦੇ ਆਸ-ਪਾਸ ਇਕੋ ਹੀ ਤਰ੍ਹਾਂ ਦੀਆਂ ਕੁਰਸੀਆਂ, ਮੇਜ਼ ਦੇ ਦੁਆਲੇ ਇਕੋ ਜਿਹੇ ਫ਼ਾਸਲੇ ‘ਤੇ ਜਾਂ ਇਕ ਵੱਡੇ ਸੋਫ਼ੇ ਦੇ ਆਸ-ਪਾਸ ਦੋ ਛੋਟੇ ਸੋਫ਼ੇ ਜਾਂ ਤਿਪਾਈਆਂ ਦਾ ਹੋਣਾ | ਪਰ ਇਸ ਤਰ੍ਹਾਂ ਨਾਲ ਸਜਾਇਆ ਬੈਠਣ ਵਾਲਾ ਕਮਰਾ ਕੁੱਝ ਖਵਾ ਪ੍ਰਤੀਤ ਹੁੰਦਾ ਹੈ ਪਰ ਵੱਡਾ ਕਮਰਾ ਚੰਗਾ ਲੱਗਦਾ ਹੈ ।
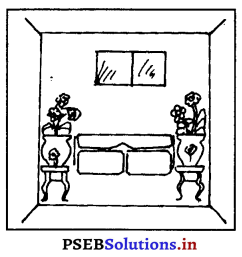
(ਅ) ਅਣਉਪਚਾਰਿਕ (ਅਨਿਸਚਿਤ ਸੰਤੁਲਨ ਨਿਸਚਿਤ ਸੰਤੁਲਨ ਨੂੰ ਸੁਧਾਰਨ ਲਈ ਸੰਤੁਲਨ ਚੀਜ਼ਾਂ ਦੀ ਬਨਾਵਟ ਤੋਂ ਇਲਾਵਾ ਉਨ੍ਹਾਂ ਦੇ ਰੰਗ ਜਾਂ ਨਮੂਨੇ ਨਾਲ ਜਾਂ ਚੀਜ਼ਾਂ ਨੂੰ ਕੇਂਦਰ ਬਿੰਦੂ ਤੋਂ ਨੇੜੇ ਜਾਂ ਦੂਰ ਰੱਖ ਕੇ ਵੀ ਪੈਦਾ ਕੀਤਾ ਜਾ ਸਕਦਾ । ਹੈ । ਅਨਿਸਚਿਤ ਸੰਤੁਲਨ ਕਰਨਾ ਜ਼ਿਆਦਾ ਮੁਸ਼ਕਿਲ ਹੈ ਪਰ ਜੇ ਕਰ ਚੰਗੀ ਤਰ੍ਹਾਂ ਕੀਤਾ ਜਾਏ ਤਾਂ ਇਹ ਨਿਸ਼ਚਿਤ ਸੰਤੁਲਨ ਤੋਂ ਵਧੇਰੇ ਚੰਗਾ। ਲੱਗਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਦਾ ਸੰਤੁਲਨ ਕੁਦਰਤੀ ਲਗਦਾ ਹੈ ਅਤੇ ਇਸ ਵਿਚ ਰਚਨਾਤਮਕ ਕਲਾ ਦਾ ਪ੍ਰਦਰਸ਼ਨ ਵੀ ਹੁੰਦਾ ਹੈ ।
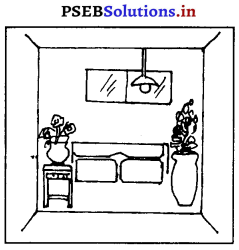
4. ਲੈਅ (Rhythm) – ਜਦੋਂ ਤੁਸੀਂ ਕਿਸੇ ਕਮਰੇ ਦੇ ਅੰਦਰ ਜਾਂਦੇ ਹੋ ਤਾਂ ਤੁਹਾਡੀ ਨਜ਼ਰ ਇਕ ਥਾਂ ਤੋਂ ਦੂਸਰੀ ਥਾਂ ਤਕ ਜਾਂਦੀ ਹੈ । ਜਦੋਂ ਕੋਈ ਡਿਜ਼ਾਈਨ ਦੇ ਅੱਡ-ਅੱਡ ਅੰਸ਼ਾਂ ਵਿਚ ਜ਼ਿਆਦਾ ਭਿੰਨਤਾ ਨਾ ਹੋਵੇ ਅਤੇ ਸਾਡੀ ਨਜ਼ਰ ਇਕ ਥਾਂ ਤੋਂ ਦੂਸਰੀ ਥਾਂ ‘ਤੇ ਆਸਾਨੀ ਨਾਲ ਘੁੰਮੇ ਤਾਂ ਉਸ ਡਿਜ਼ਾਈਨ ਵਿਚ ਲੈਅ ਹੁੰਦੀ ਹੈ । ਲੈਅ ਕਈ ਪ੍ਰਕਾਰ ਨਾਲ ਪ੍ਰਾਪਤ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ।
(ੳ) ਇਕੋ ਤਰ੍ਹਾਂ ਦੀਆਂ ਰੇਖਾਵਾਂ – ਇਕੋ ਹੀ ਕਮਰੇ ਵਿਚ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਰੇਖਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ਪਰ ਉਨ੍ਹਾਂ ਵਿਚੋਂ ਇਕ ਤਰ੍ਹਾਂ ਦੀਆਂ ਰੇਖਾਵਾਂ ਨੂੰ ਜ਼ਿਆਦਾ ਮਹੱਤਵ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ, ਇਹ ਦੇਖਣ ਨੂੰ ਜ਼ਿਆਦਾ ਅਰਾਮਦਾਇਕ ਪ੍ਰਤੀਤ ਹੁੰਦੀਆਂ ਹਨ ।
(ਅ) ਤੀਲਿਪੀ (Repetition) ਜਾਂ ਦੁਹਰਾਉਣਾ-ਰੰਗ, ਰੇਖਾ, ਰਚਨਾ ਜਾਂ ਆਕਾਰ ਨੂੰ ਬਾਰ-ਬਾਰ ਦੁਹਰਾਉਣ ਨਾਲ ਵੀ ਲੈਅ ਪੈਦਾ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ । ਇਕ ਆਕਾਰ ਦੀਆਂ | ਚੀਜ਼ਾਂ ਨਾਲ ਵੀ ਲੈਅ ਉਤਪੰਨ ਹੁੰਦੀ ਹੈ ਜਿਵੇਂ ਕਿ ਅੱਡ-ਅੱਡ ਤਰ੍ਹਾਂ ਦੀਆਂ ਤਸਵੀਰਾਂ ਨੂੰ ਇਕੋ ਜਿਹੇ ਫਰੇਮ ਵਿਚ ਜੜਵਾ ਕੇ ਇਕ ਕੇਂਦਰ ਬਿੰਦੂ ਦੇ ਆਸ-ਪਾਸ ਲਗਾਉਣਾ ।
5. ਬਲ (Emphasis) – ਬਲ ਤੋਂ ਭਾਵ ਕਿਸੇ ਇਕ ਰੁਚੀਕਰ ਬਿੰਦੁ ਉੱਤੇ ਜ਼ਿਆਦਾ ਬਲ ਦੇਣਾ ਭਾਵ ਉਸ ਨੂੰ ਵੱਧ ਆਕਰਸ਼ਿਤ ਬਣਾਉਣਾ ਅਤੇ ਅਰੁਚੀਕਰ ਵਸਤਾਂ ‘ਤੇ ਘੱਟ ਬਲ ਦੇਣਾ । ਜਦੋਂ ਕੋਈ ਡਿਜ਼ਾਈਨ ਪੂਰਾ ਸੰਤੁਲਿਤ ਹੋਵੇ, ਉਸ ਵਿਚ ਪੂਰਨ ਅਨੁਰੂਪਤਾ ਹੋਵੇ ਪਰ ਫਿਰ ਵੀ ਫਿੱਕਾ ਅਤੇ ਅਰੁਚੀਕਰ ਲੱਗੇ ।ਉਸ ਡਿਜ਼ਾਈਨ ਵਿਚ ਕੋਈ ਵਿਸ਼ੇਸ਼ ਬਿੰਦੂ ਨਹੀਂ ਹੈ।
ਜਿੱਥੇ ਧਿਆਨ ਕੇਂਦਰਿਤ ਹੋ ਸਕੇ ਅਜਿਹੇ ਡਿਜ਼ਾਈਨ ਵਿਚ ਬਲ ਦੀ ਕਮੀ ਹੈ । ਬਲ ਕਲਾ ਦਾ । ਇਕ ਸਿਧਾਂਤ ਹੈ ਕਿ ਕਮਰੇ ਅੰਦਰ ਵੜਦਿਆਂ ਜਿੱਥੇ ਤੁਹਾਡਾ ਸਭ ਤੋਂ ਪਹਿਲਾਂ ਧਿਆਨ ਜਾਵੇ ਅਤੇ ਫਿਰ ਮਹੱਤਵ ਦੇ ਕ੍ਰਮ ਅਨੁਸਾਰ ਹੋਰ ਕਿਤੇ ਟਿਕਦਾ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 17.
ਡਿਜ਼ਾਈਨ ਦੇ ਮੂਲ ਅੰਸ਼ ਕਿਹੜੇ ਹਨ ? ਇਹ ਡਿਜ਼ਾਈਨ ਨੂੰ ਕਿਵੇਂ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ ?
ਉੱਤਰ-
ਜਦੋਂ ਵੀ ਕੋਈ ਚੀਜ਼ ਬਣਾਈ ਜਾਂਦੀ ਹੈ ਤਾਂ ਉਸ ਦਾ ਇਕ ਨਮੂਨਾ ਜਾਂ ਡਿਜ਼ਾਈਨ ਬਣਦਾ ਹੈ । ਇਹ ਚੀਜ਼ ਭਾਵੇਂ ਕੁਰਸੀ ਮੇਜ਼ ਹੋਵੇ ਜਾਂ ਮਕਾਨ ਜਾਂ ਕੋਈ ਸ਼ਹਿਰ । ਕੋਈ ਵੀ ਚੀਜ਼ ਬਣਾਈ ਜਾਵੇ ਉਸ ਦੇ ਅਲੱਗ-ਅਲੱਗ ਹਿੱਸਿਆਂ ਦਾ ਆਪਸ ਵਿਚ ਤਾਲ-ਮੇਲ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ, ਜਿਵੇਂ ਕਿ ਕੁਰਸੀ ਦੀ ਲੱਕੜੀ, ਉਸ ਦੀ ਪਾਲਸ਼ ਦਾ ਰੰਗ, ਉਸ ਦੀ ਰਚਨਾ, ਉਸ ਤੇ ਬੈਂਤ ਦੀ ਬਣਾਈ ਜਾਂ ਉਸ ਉੱਤੇ ਚੜੇ ਕੱਪੜੇ ਦਾ ਰੰਗ, ਨਮਨਾ ਜਾਂ ਬਣਤਰ ਸਾਰੇ ਮਿਲ ਕੇ ਇਕ ਡਿਜ਼ਾਈਨ ਬਣਾਉਂਦੇ ਹਨ | ਘਰ ਵਿਚ ਵੱਖ-ਵੱਖ ਕਮਰੇ ਮਿਲ ਕੇ ਇਕ ਡਿਜ਼ਾਈਨ ਬਣਾਉਂਦੇ ਹਨ । ਇਸੇ ਤਰ੍ਹਾਂ ਇਕ ਕਮਰੇ ਵਿਚ ਵੱਖ-ਵੱਖ ਤਰ੍ਹਾਂ ਦਾ ਸਾਮਾਨ ਰੱਖ ਕੇ ਇਕ ਡਿਜ਼ਾਈਨ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਇਕ ਕਮਰੇ ਦੀਆਂ ਸਾਰੀਆਂ ਚੀਜ਼ਾਂ ਦਾ ਆਪਸੀ ਤਾਲ ਮੇਲ ਠੀਕ ਹੋਵੇ ਤਾਂ ਹੀ ਇਕ ਚੰਗਾ ਡਿਜ਼ਾਈਨ ਬਣੇਗਾ । ਰੇਖਾ, ਆਕਾਰ, ਰੰਗ, ਰੂਪ ਅਤੇ ਬਣਤਰ ਦੀ ਵਿਵਸਥਾ ਨਾਲ ਹੀ ਕੋਈ ਡਿਜ਼ਾਈਨ ਬਣਦਾ ਹੈ । ਇਸ ਲਈ ਚੰਗਾ ਡਿਜ਼ਾਈਨ ਬਣਾਉਣ ਲਈ ਇਸ ਦੇ ਮੂਲ ਤੱਤਾਂ ਦਾ ਗਿਆਨ ਅਤੇ ਇਹਨਾਂ ਨੂੰ ਸੁਹਜਵਾਦੀ ਅਤੇ ਕਲਾਤਮਿਕ ਢੰਗ ਨਾਲ ਸ਼ਾਮਲ ਕਰਨਾ ਹੈ ।
ਡਿਜ਼ਾਈਨ ਦੇ ਮੂਲ ਅੰਸ਼ (Elements of Design)-
1. ਰੇਖਾਵਾਂ (Lines)-
ਹਰ ਇਕ ਡਿਜ਼ਾਈਨ ਵਿਚ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਰੇਖਾਵਾਂ ਸ਼ਾਮਲ ਹੁੰਦੀਆਂ ਹਨ ਪਰ ਇਨ੍ਹਾਂ ਵਿਚੋਂ ਕੁੱਝ ਰੇਖਾਵਾਂ ਜ਼ਿਆਦਾ ਉਭਰੀਆਂ ਹੋਈਆਂ ਹੁੰਦੀਆਂ ਹਨ ਜਿਸ ਨਾਲ ਉਸ ਡਿਜ਼ਾਈਨ ਵਿਚ ਵਿਭਿੰਨਤਾ ਆਉਂਦੀ ਹੈ । ਰੇਖਾਵਾਂ ਸਾਡੀਆਂ ਭਾਵਨਾਵਾਂ ਨੂੰ ਵੀ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀਆਂ ਹਨ । ਇਸ ਲਈ ਇਨ੍ਹਾਂ ਨੂੰ ਚੁਣਨ ਵੇਲੇ ਸਾਵਧਾਨੀ ਵਰਤਣੀ ਚਾਹੀਦੀ ਹੈ । ਰੇਖਾਵਾਂ ਕਈ ਪ੍ਰਕਾਰ ਦੀਆਂ ਹੋ ਸਕਦੀਆਂ ਹਨ ।
(ੳ) ਸਿੱਧੀਆਂ ਰੇਖਾਵਾਂ – ਸਿੱਧੀਆਂ ਰੇਖਾਵਾਂ ਦਿਤਾ ਅਤੇ ਸਾਦਗੀ ਦੀਆਂ ਪ੍ਰਤੀਕ ਹੁੰਦੀਆਂ ਹਨ । ਸਿੱਧੀਆਂ ਰੇਖਾਵਾਂ ਦਾ ਜ਼ਿਆਦਾ ਪ੍ਰਯੋਗ ਗਿਰਜਾ ਘਰਾਂ ਵਿਚ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਘਰ ਦੀ ਸਜਾਵਟ ਵਿਚ ਜੇਕਰ ਕਮਰੇ ਦੀ ਛੱਤ ਨੀਵੀਂ ਹੋਵੇ ਤਾਂ ਦਰਵਾਜ਼ੇ ਅਤੇ ਖਿੜਕੀਆਂ ‘ਤੇ ਸਿੱਧੀਆਂ ਰੇਖਾਵਾਂ ਵਾਲੇ ਪਰਦੇ ਲਾ ਕੇ ਜ਼ਿਆਦਾ ਉਚਾਈ ਦਾ ਅਹਿਸਾਸ ਦਵਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।
(ਅ) ਲੇਟਵੀਆਂ ਰੇਖਾਵਾਂ-ਇਹ ਰੇਖਾਵਾਂ ਸ਼ਾਂਤੀ ਅਤੇ ਅਰਾਮ ਦੀਆਂ ਪ੍ਰਤੀਕ ਹੁੰਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਨੂੰ ਥਕਾਵਟ ਦੂਰ ਕਰਨ ਵਾਲੀਆਂ ਸਮਝਿਆ ਜਾਂਦਾ ਹੈ । ਇਹ ਕਿਸੇ ਚੀਜ਼ ਦੇ ਅਕਾਰ ਨੂੰ ਛੋਟਾ ਦਿਖਾਉਣ ਦਾ ਭਰਮ ਪੈਦਾ ਕਰਦੀਆਂ ਹਨ । ਇਸ ਲਈ ਜਿਨ੍ਹਾਂ ਕਮਰਿਆਂ ਦੀ ਛੱਤ ਜ਼ਿਆਦਾ ਉੱਚੀ ਹੋਵੇ ਉਨ੍ਹਾਂ ਦੇ ਦਰਵਾਜ਼ਿਆਂ ਤੇ ਖਿੜਕੀਆਂ ਦੇ ਪਰਦਿਆਂ ਵਿਚ ਲੇਟਵੀਆਂ ਰੇਖਾਵਾਂ ਵਰਤੀਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ ।
(ੲ) ਤਿਰਛੀਆਂ ਰੇਖਾਵਾਂ – ਤਿਰਛੀਆਂ ਰੇਖਾਵਾਂ ਦਾ ਪ੍ਰਭਾਵ ਉਨ੍ਹਾਂ ਦੇ ਕੋਣ ਨਾਲ ਪ੍ਰਭਾਵਿਤ ਹੁੰਦਾ ਹੈ । ਜੇਕਰ ਇਹ ਸਿੱਧੀ ਰੇਖਾ ਦੇ ਨੇੜੇ ਹੋਵੇ ਤਾਂ ਦ੍ਰਿੜ੍ਹ ਅਤੇ ਜੇਕਰ ਲੇਟਵੀਂ ਰੇਖਾ ਦੇ ਨੇੜੇ ਹੋਵੇ ਤਾਂ ਸ਼ਾਂਤੀ ਦੀਆਂ ਪ੍ਰਤੀਕ ਹੁੰਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਰੇਖਾਵਾਂ ਦੇ ਜ਼ਿਆਦਾ ਪ੍ਰਯੋਗ ਨਾਲ ਅਨੁਸ਼ਾਸਨ ਦੀ ਘਾਟ ਲੱਗਦੀ ਹੈ, ਬਨਾਵਟੀਪਨ ਲੱਗਦਾ ਹੈ ਅਤੇ ਦੇਖਣ ਵਿਚ ਜ਼ਿਆਦਾ ਸੋਹਣਾ ਨਹੀਂ ਲੱਗਦਾ ।
(ਸ) ਗੋਲ ਰੇਖਾਵਾਂ – ਗੋਲ ਰੇਖਾਵਾਂ ਸਾਡੀਆਂ ਭਾਵਨਾਵਾਂ ਨੂੰ ਦਰਸਾਉਣ ਵਿਚ ਮਦਦ ਕਰਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਵਿਚ ਕਈ ਵੰਨਗੀਆਂ ਹੋ ਸਕਦੀਆਂ ਹਨ | ਪੁਰੀ ਗੋਲਾਈ ਵਾਲੀਆਂ ਲਾਈਨਾਂ ਪ੍ਰਸੰਨਤਾ ਅਤੇ ਜਸ਼ਨ ਦਾ ਅਹਿਸਾਸ ਦਿਵਾਉਂਦੀਆਂ ਹਨ ਜਿਵੇਂ ਕਿ ਕਿਸੇ ਖ਼ੁਸ਼ੀ ਦੇ ਅਵਸਰ ‘ਤੇ ਗੁਬਾਰੇ ਤੇ ਕਿਸੇ ਤਰ੍ਹਾਂ ਦੇ ਗਲੋਬ ਦਾ ਵਰਤਣਾ, ਬੱਚਿਆਂ ਦੀਆਂ ਟੋਪੀਆਂ ‘ਤੇ ਗੋਲ ਫੰਦੇ ਜਾਂ ਜੌਕਰਾਂ ਦੀਆਂ ਟੋਪੀਆਂ ‘ਤੇ ਪੋਲਕਾ ਡਿਜ਼ਾਈਨ ਆਦਿ ਦਾ ਇਸਤੇਮਾਲ ਕਰਨਾ | ਘੱਟ ਗੋਲਾਈ ਵਾਲੀਆਂ ਰੇਖਾਵਾਂ ਜਿਵੇਂ ਕਿ “S” ਸੁੰਦਰਤਾ ਅਤੇ ਨਿਖਾਰ ਦੀਆਂ ਪ੍ਰਤੀਕ ਹੁੰਦੀਆਂ ਹਨ ।
(ਹ) ਕੋਣ – ਕੋਣ ਵਾਲੀਆਂ ਰੇਖਾਵਾਂ ਵੀ ਕਈ ਪ੍ਰਕਾਰ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ਜਿਨ੍ਹਾਂ ਦਾ ਅਸਰ ਵੀ ਅੱਡ-ਅੱਡ ਹੁੰਦਾ ਹੈ । ਇਹ ਦ੍ਰਿੜ, ਅਸ਼ਾਂਤ ਜਾਂ ਹਲਚਲ ਪੈਦਾ ਕਰਨ ਵਾਲੀਆਂ ਹੋ ਸਕਦੀਆਂ ਹਨ । ਇਹ ਉਤੇਜਿਤ ਕਰਨ ਵਾਲੀਆਂ ਵੀ ਹੋ ਸਕਦੀਆਂ ਹਨ ।
ਦੀਵਾਰ ‘ਤੇ ਲਗਾਈਆਂ ਗਈਆਂ ਇਕੋ ਜਿਹੀਆਂ ਤਸਵੀਰਾਂ ਸਿੱਧੀਆਂ, ਲੇਟਵੀਆਂ ਜਾਂ ਤਿਰਛੀ ਰੇਖਾ ਵਿਚ ਲਾਉਣ ‘ਤੇ ਵੱਖ-ਵੱਖ ਪ੍ਰਭਾਵ ਦਿੰਦੀਆਂ ਹਨ ।
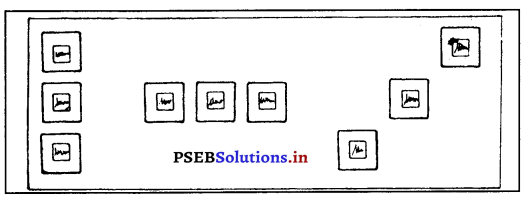
ਕਿਸੇ ਵੀ ਫ਼ਰਨੀਚਰ ਦੇ ਡਿਜ਼ਾਈਨ ਜਾਂ ਸਜਾਵਟ ਦੇ ਹੋਰ ਸਾਮਾਨ ਦੇ ਡਿਜ਼ਾਈਨ ਵਿਚ ਜਾਂ ਜਿਸ ਤਰੀਕੇ ਨਾਲ ਇਹ ਚੀਜ਼ਾਂ ਕਿਸੇ ਵੀ ਕਮਰੇ ਵਿਚ ਰੱਖੀਆਂ ਜਾਂਦੀਆਂ ਹਨ, ਉਨ੍ਹਾਂ ਵਿਚ ਰੇਖਾਵਾਂ ਦਾ ਇਸ ਤਰੀਕੇ ਨਾਲ ਪ੍ਰਯੋਗ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂ ਕਿ ਉਹ ਹੀ ਪ੍ਰਭਾਵ ਪੈਦਾ ਹੋਵੇ ਜੋ ਤੁਸੀਂ ਚਾਹੁੰਦੇ ਹੋ । ਜਿਸ ਕਮਰੇ ਨੂੰ ਤੁਸੀਂ ਅਰਾਮਦਾਇਕ ਬਣਾਉਣਾ ਚਾਹੁੰਦੇ ਹੋ ਉਸ ਵਿਚ ਲੇਟਵੀਆਂ ਰੇਖਾਵਾਂ ਦਾ ਜ਼ਿਆਦਾ ਪ੍ਰਯੋਗ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
2. ਰੂਪ ਅਤੇ ਆਕਾਰ (Shape and Size) – ਰੂਪ ਅਤੇ ਆਕਾਰ ਦਾ ਆਪਸ ਵਿਚ ਡੂੰਘਾ ਸੰਬੰਧ ਹੈ, ਰੇਖਾਵਾਂ ਨੂੰ ਮਿਲਾ ਕੇ ਹੀ ਕਿਸੇ ਚੀਜ਼ ਨੂੰ ਰੂਪ ਅਤੇ ਆਕਾਰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਰੇਖਾਵਾਂ । ਆਪਣੇ ਆਪ ਵਿਚ ਇਕ ਇਕਾਈ ਹਨ ਜਿਨ੍ਹਾਂ ਦੇ ਮਿਲਾਪ ਨਾਲ ਕੋਈ ਚੀਜ਼ ਬਣਾਈ ਜਾਂਦੀ ਹੈ । ਘਰ ਦੀ ਇਮਾਰਤ ਜਾਂ ਉਸ ਦੀ ਅੰਦਰੂਨੀ ਸਜਾਵਟ ਵਿਚ ਰੂਪ ਅਤੇ ਆਕਾਰ ਨਜ਼ਰ । ਆਉਂਦਾ ਹੈ । ਅੱਜ-ਕਲ੍ਹ ਕਮਰਿਆਂ ਨੂੰ ਵੱਡਾ ਵਿਖਾਉਣ ਲਈ ਵੱਡੀਆਂ-ਵੱਡੀਆਂ ਖਿੜਕੀਆਂ ਰੱਖੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ਤਾਂ ਕਿ ਅੰਦਰ ਅਤੇ ਬਾਹਰ ਮਿਲਦੇ ਨਜ਼ਰ ਆਉਣ । ਕਮਰੇ ਦਾ । ਅਕਾਰ, ਉਸ ਦੇ ਛੱਡ ਦੀ ਉਚਾਈ ਅਤੇ ਉਸ ਵਿਚਲੇ ਦਰਵਾਜ਼ਿਆਂ ਅਤੇ ਖਿੜਕੀਆਂ ਕਮਰੇ ਵਿਚ ਰੱਖਣ ਵਾਲੇ ਫ਼ਰਨੀਚਰ ਨੂੰ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ । ਕਮਰੇ ਵਿਚਲਾ ਫ਼ਰਨੀਚਰ, ਪਰਦੇ, । ਕਾਲੀਨ ਅਤੇ ਹੋਰ ਸਾਮਾਨ ਸਾਰੇ ਕਮਰੇ ਨੂੰ ਛੋਟਾ ਕਰਦੇ ਹਨ । ਜੇਕਰ ਕਿਸੇ ਕਮਰੇ ਨੂੰ ਉਸ ਦੇ । ਕੰਮ ਦੇ ਮੁਤਾਬਿਕ ਵੰਡ ਦਿੱਤਾ ਜਾਏ ਜਿਵੇਂ ਕਿ ਇਕ ਹਿੱਸਾ ਬੈਠਣ ਦਾ, ਇਕ ਖਾਣਾ-ਖਾਣ ਦਾ | ਅਤੇ ਇਕ ਪੜ੍ਹਨ ਦਾ ਤਾਂ ਉਹ ਕਮਰਾ ਛੋਟਾ ਲੱਗਣ ਲੱਗ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਕਮਰੇ ਨੂੰ ਵੱਡਾ ਦਿਖਾਉਣਾ ਚਾਹੁੰਦੇ ਹੋ ਤਾਂ ਇਸ ਦੇ ਘੱਟ ਤੋਂ ਘੱਟ ਹਿੱਸੇ ਕਰੋ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਕਮਰੇ ਨੂੰ ਵੱਡਾ ਦਿਖਾਉਣ ਲਈ ਛੋਟਾ ਅਤੇ ਹਲਕਾ ਫ਼ਰਨੀਚਰ, ਘੱਟ ਸਜਾਵਟ ਦਾ ਸਮਾਨ ਅਤੇ ਹਲਕੇ ਰੰਗ ਵਰਤੋ । ਪਤਲੀਆਂ ਲੱਤਾਂ ਵਾਲੇ ਫ਼ਰਨੀਚਰ ਨਾਲ ਕਮਰਾ ਵੱਡਾ ਲੱਗਦਾ ਹੈ ਕਿਉਂਕਿ ਇਸ ਨਾਲ ਫ਼ਰਨੀਚਰ ਦੇ ਹੇਠਾਂ ਫਰਸ਼ ਦਾ ਜ਼ਿਆਦਾ ਹਿੱਸਾ ਦਿਖਾਈ ਦਿੰਦਾ ਰਹਿੰਦਾ ਹੈ ।
3. ਰੰਗ (Colour) – ਅੱਜ-ਕਲ੍ਹ ਆਦਮੀ ਨੇ ਰੰਗਾਂ ਦੀ ਮਹੱਤਤਾ ਨੂੰ ਪਛਾਣਿਆ ਹੈ । ਰੰਗਾਂ ਦਾ ਅਸਰ ਸਾਡੀਆਂ ਭਾਵਨਾਵਾਂ ਅਤੇ ਸਾਡੇ ਕੰਮ ਕਰਨ ਦੇ ਤਰੀਕੇ ‘ਤੇ ਪੈਂਦਾ ਹੈ । ਅੱਜ ਤੋਂ ਕੁੱਝ ਸਾਲ ਪਹਿਲਾਂ ਕਾਰਾਂ ਦਾ ਰੰਗ ਸਿਰਫ਼ ਚਿੱਟਾ, ਕਾਲਾ, ਗਰੇਅ ਆਦਿ ਹੀ ਹੁੰਦੇ ਸਨ । ਇਸੇ ਤਰ੍ਹਾਂ ਟਾਈਪ ਰਾਈਟਰ, ਟੈਲੀਫੋਨ ਅਤੇ ਸਿਲਾਈ ਮਸ਼ੀਨ ਕਾਲੇ ਰੰਗ ਦੀ ਅਤੇ ਫਰਿਜ਼ ਅਤੇ ਕੁਕਿੰਗ ਰੇਂਜ ਸਿਰਫ਼ ਚਿੱਟੇ ਹੀ ਹੁੰਦੇ ਸਨ | ਪਰ ਅੱਜ-ਕਲ੍ਹ ਇਹ ਸਾਰੀਆਂ ਚੀਜ਼ਾਂ ਵੱਖਵੱਖ ਰੰਗਾਂ ਵਿਚ ਮਿਲਣ ਲੱਗ ਪਈਆਂ ਹਨ | ਖਾਣਾ-ਖਾਣ ਵਾਲੀਆਂ ਪਲੇਟਾਂ ਆਦਿ ਦੇ ਰੰਗ ਦਾ ਅਸਰ ਸਾਡੀ ਭੁੱਖ ‘ਤੇ ਪੈਂਦਾ ਹੈ । ਖਾਣ ਵਾਲੀਆਂ ਚੀਜ਼ਾਂ ਦਾ ਰੰਗ ਜੇਕਰ ਮਨ ਭਾਉਂਦਾ ਹੋਵੇ ਤਾਂ ਭੁੱਖ ਜ਼ਿਆਦਾ ਲੱਗਦੀ ਹੈ ਅਤੇ ਖਾਣਾ ਹਜ਼ਮ ਵੀ ਜਲਦੀ ਹੋ ਜਾਂਦਾ ਹੈ ।
ਪਰੌਂਗ ਦੇ ਅਨੁਸਾਰ ਸਾਰੇ ਰੰਗ ਮੁੱਢਲੇ ਤਿੰਨ ਰੰਗਾਂ-ਪੀਲਾ, ਨੀਲਾ ਅਤੇ ਲਾਲ ਤੋਂ ਬਣਦੇ ਹਨ । ਇਹ ਤਿੰਨ ਰੰਗ ਹੋਰ ਰੰਗਾਂ ਨੂੰ ਮਿਲਾ ਕੇ ਨਹੀਂ ਬਣਾਏ ਜਾ ਸਕਦੇ । ਇਸ ਲਈ ਇਹਨਾਂ ਨੂੰ ਪ੍ਰਾਥਮਿਕ (ਪਹਿਲੇ) ਦਰਜੇ ਦੇ ਰੰਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਜਦੋਂ ਦੋ ਪ੍ਰਾਥਮਿਕ ਰੰਗਾਂ ਨੂੰ ਇਕੋ ਜਿੰਨੀ ਮਾਤਰਾ ਵਿਚ ਮਿਲਾਇਆ ਜਾਏ ਤਾਂ ਤਿੰਨ ਦੂਜੇ ਦਰਜੇ ਦੇ ਰੰਗ ਬਣਦੇ ਹਨ, ਜਿਵੇਂ ਕਿ-
ਪੀਲਾ + ਨੀਲਾ = ਹਰਾ,
ਨੀਲਾ ਅਤੇ ਲਾਲ = ਜਾਮਨੀ,
ਲਾਲ + ਪੀਲਾ = ਸੰਤਰੀ
ਇਨ੍ਹਾਂ ਛੇ ਰੰਗਾਂ ਨੂੰ ਆਧਾਰ ਰੰਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਕ ਪ੍ਰਾਥਮਿਕ ਅਤੇ ਉਸ ਦੇ ਨਾਲ ਲੱਗਦੇ ਇਕ ਦੂਸਰੇ ਦਰਜੇ ਦੇ ਰੰਗ ਨੂੰ ਮਿਲਾ ਕੇ ਜੋ ਰੰਗ ਬਣਦੇ ਹਨ, ਉਨ੍ਹਾਂ ਨੂੰ ਤੀਸਰੇ ਦਰਜੇ ਦੇ ਰੰਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ, ਜਿਵੇਂ ਕਿ-
ਪੀਲਾ + ਹ = ਪੀਲਾ ਹਰਾ,
ਨੀਲਾ + ਹ = ਨੀਲਾ ਹਰਾ,
ਨੀਲਾ + ਜਾਮਨੀ = ਨੀਲਾ ਜਾਮਨੀ,
ਲਾਲ + ਜਾਮਨੀ = ਲਾਲ ਜਾਮਨੀ,
ਲਾਲ + ਸੰਤਰੀ = ਲਾਲ ਸੰਤਰੀ,
ਪੀਲਾ + ਸੰਤਰੀ = ਪੀਲਾ ਸੰਤਰੀ ।
ਇਸ ਪ੍ਰਕਾਰ ਤਿੰਨ ਪ੍ਰਾਥਮਿਕ, ਤਿੰਨ ਦੂਸਰੇ ਦਰਜੇ ਦੇ ਅਤੇ ਛੇ ਤੀਸਰੇ ਦਰਜੇ ਦੇ ਰੰਗ ਹੁੰਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਰੰਗਾਂ ਦਾ ਆਪਸੀ ਅਨੁਪਾਤ ਵਧਾ-ਘਟਾ ਕੇ ਅਨੇਕਾਂ ਰੰਗ ਬਣਾਏ ਜਾ ਸਕਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਰੰਗਾਂ ਵਿਚ ਚਿੱਟਾ ਰੰਗ ਮਿਲਾਉਣ ਨਾਲ ਰੰਗਾਂ ਦੀ ਭਾਅ (ਹਲਕਾ ਰੰਗ) ਬਣਦੀ ਹੈ, ਜਿਵੇਂ ਕ-
ਲਾਲ + ਚਿੱਟਾ = ਗੁਲਾਬੀ,
ਨੀਲਾ + ਚਿੱਟਾ = ਅਸਮਾਨੀ ।
ਗੁਲਾਬੀ ਅਤੇ ਅਸਮਾਨੀ ਲਾਲ ਅਤੇ ਨੀਲੇ ਰੰਗ ਦੀ ਭਾਅ ਹਨ ।
ਕਿਸੇ ਵੀ ਰੰਗ ਵਿਚ ਕਾਲਾ ਰੰਗ ਮਿਲਾਉਣ ਨਾਲ ਉਸ ਰੰਗ ਵਿਚ ਗਹਿਰਾਈ ਆ ਜਾਂਦੀ ਹੈ, ਜਿਵੇਂ ਕਿ-
ਲਾਲ + ਕਾਲਾ = ਲਾਖਾ |
ਕਾਲਾ, ਸਲੇਟੀ (ਗਰੇ) ਅਤੇ ਚਿੱਟੇ ਨੂੰ ਉਦਾਸੀਨ (neutral) ਰੰਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਇਨ੍ਹਾਂ ਨੂੰ ਕਿਸੇ ਵੀ ਰੰਗ ਨਾਲ ਮਿਲਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।
ਜੇਕਰ ਰੰਗਾਂ ਦੇ ਚੱਕਰ ਨੂੰ ਦੇਖਿਆ ਜਾਏ ਤਾਂ ਇਸ ਦੇ ਅੱਧੇ ਹਿੱਸੇ ਦੇ ਰੰਗ ਠੰਢੇ ਹਨ ਜਿਵੇਂ ਕਿ ਹਰਾ ਅਤੇ ਨੀਲਾ, ਇਹ ਜ਼ਿਆਦਾ ਅਰਾਮਦਾਇਕ ਹੁੰਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਨੂੰ ਪਿੱਛੇ ਹਟਣ ਵਾਲੇ (receding) ਰੰਗ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿਉਂਕਿ ਇਹ ਪਿੱਛੇ ਵਲ ਨੂੰ ਜਾਂਦੇ ਪ੍ਰਤੀਤ ਹੁੰਦੇ ਹਨ । ਜਿਸ ਕਾਰਨ ਕਮਰਾ ਵੱਡਾ ਲੱਗਦਾ ਹੈ ।
ਚੱਕਰ ਦੇ ਦੂਜੇ ਪਾਸੇ ਦੇ ਰੰਗ ਲਾਲ, ਸੰਤਰੀ ਅਤੇ ਪੀਲਾ ਗਰਮ ਰੰਗ ਅਖਵਾਉਂਦੇ ਹਨ । ਇਹ ਰੰਗ ਭੜਕੀਲੇ ਅਤੇ ਉਤੇਜਿਤ ਕਰਨ ਵਾਲੇ ਹੁੰਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਦੀ ਜੇਕਰ ਜ਼ਿਆਦਾ ਵਰਤੋਂ ਕੀਤੀ ਜਾਏ ਤਾਂ ਭੁੰਜਲਾਹਟ ਪੈਦਾ ਕਰਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਨੂੰ ਸਲੇਟੀ ਅਗਾਂਹ ਵਧੂ (advancing) ਰੰਗ ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਕਿਉਂਕਿ ਇਨ੍ਹਾਂ ਦੀ ਵਰਤੋਂ ਨਾਲ ਚੀਜ਼ਾਂ ਅੱਗੇ-ਅੱਗੇ ਨਜ਼ਰ ਆਉਂਦੀਆਂ ਹਨ ਅਤੇ ਕਮਰੇ ਦਾ ਆਕਾਰ ਛੋਟਾ ਲਗਦਾ ਹੈ । ਜਾਮਨੀ ਰੰਗ ਵਿਚ ਜੇਕਰ ਲਾਲ ਜ਼ਿਆਦਾ ਹੋਵੇ ਤਾਂ ਗਰਮ ਅਤੇ ਜੇਕਰ ਨੀਲਾ ਜ਼ਿਆਦਾ ਹੋਵੇ ਤਾਂ ਠੰਢਾ ਹੋਵੇਗਾ ।
ਘਰਾਂ ਵਿਚ ਆਮ ਤੌਰ ‘ਤੇ ਤਿੰਨ ਤਰ੍ਹਾਂ ਨਾਲ ਰੰਗਾਂ ਦੀ ਵਿਉਂਤ ਬਣਾਈ ਜਾ ਸਕਦੀ ਹੈ –
(ੳ) ਇਕ ਰੰਗ – ਇਸ ਤਰ੍ਹਾਂ ਦੀ ਵਿਉਂਤ ਵਿਚ ਇਕੋ ਹੀ ਰੰਗ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ । ਪਰ ਇਸ ਦਾ ਮਤਲਬ ਇਹ ਨਹੀਂ ਕਿ ਇਕੋ ਹੀ ਥਾਨ ਨਾਲੋਂ ਪਰਦੇ, ਕੁਸ਼ਨ ਕਵਰ ਅਤੇ ਸੋਫ਼ਿਆਂ ਦੇ ਕੱਪੜੇ ਆਦਿ ਬਣਾਏ ਜਾਣ । ਅੱਡ-ਅੱਡ ਚੀਜ਼ਾਂ ਲਈ ਇਕ ਹੀ ਰੰਗ ਜਿਵੇਂ ਕਿ ਨੀਲਾ ਜਾਂ ਹਰਾ ਦੇ ਗਹਿਰੇ ਜਾਂ ਹਲਕੇ ਭੈਅ ਵਾਲੇ ਰੰਗ ਵਰਤੇ ਜਾ ਸਕਦੇ ਹਨ । ਕਿਸੇ ਚੀਜ਼ ਵਿਚ ਪ੍ਰਿੰਟ ਵੀ ਵਰਤਿਆ ਜਾ ਸਕਦਾ ਹੈ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਛੋਟੀਆਂ ਚੀਜ਼ਾਂ ਵਿਚ ਜਿਵੇਂ ਕਿ ਕੁਸ਼ਨ ਕਵਰ ਜਾਂ ਲੈਂਪ ਸ਼ੇਡ ਆਦਿ ਵਿਚ ਲਾਲ, ਸੰਤਰੀ ਜਾਂ ਪੀਲਾ ਵਰਤੇ ਜਾ ਸਕਦੇ ਹਨ ਤਾਂ ਜੋ ਇਕਸਾਰਤਾ ਨੂੰ ਤੋੜਿਆ ਜਾ ਸਕੇ ।
(ਅ) ਆਪਸ ਵਿਚ ਟਕਰਾਉਣ ਵਾਲੇ ਰੰਗ ਵਿਰੋਧੀ ਰੰਗ ਯੋਜਨਾ) (Contrasting Colours) – ਇਸ ਪ੍ਰਕਾਰ ਦੀ ਰੰਗ ਵਿਉਂਤ ਕਾਫ਼ੀ ਪ੍ਰਚਲਿਤ ਹੈ । ਰੰਗ ਦੇ ਚੱਕਰ ਦੇ ਦੋ ਸਾਹਮਣੇ ਵਾਲੇ ਰੰਗ ਵਰਤੇ ਜਾਂਦੇ ਹਨ ਜਿਵੇਂ ਕਿ ਸੰਤਰੀ ਅਤੇ ਨੀਲਾ ਜਾਂ ਪੀਲਾ ਅਤੇ ਜਾਮਨੀ ਜਾਂ ਲਾਲ ਅਤੇ ਹਰਾ ।
(ੲ) ਸੰਬੰਧਿਤ ਵਿਉਂਤ – ਜਦੋਂ ਰੰਗਾਂ ਦੇ ਚੱਕਰ ਦੇ ਨਾਲ-ਨਾਲ ਲੱਗਦੇ ਰੰਗਾਂ ਦੀ ਚੋਣ ਕੀਤੀ ਜਾਏ ਤਾਂ ਇਸ ਨੂੰ ਸੰਬੰਧਿਤ ਵਿਉਂਤ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਵਿਚ ਜ਼ਿਆਦਾ ਤੋਂ ਜ਼ਿਆਦਾ ਤਿੰਨ ਰੰਗ ਵਰਤੇ ਜਾਂਦੇ ਹਨ, ਜਿਵੇਂ ਕਿ-ਨੀਲਾ, ਹਰਾ-ਨੀਲਾ ਅਤੇ ਨੀਲਾ-ਜਾਮਨੀ । ਇਸ ਦੀ ਇਕਸਾਰਤਾ (monotony) ਨੂੰ ਤੋੜਨ ਲਈ ਵੀ ਰੰਗ ਚੱਕਰ ਦੇ ਦੂਸਰੇ ਪਾਸੇ ਦੇ ਰੰਗ ਜਿਵੇਂ ਕਿ ਸੰਤਰੀ ਜਾਂ ਸੰਤਰੀ-ਪੀਲਾ ਵੀ ਕੁੱਝ ਛੋਟੀਆਂ ਚੀਜ਼ਾਂ ਲਈ ਵਰਤੇ ਜਾ ਸਕਦੇ ਹਨ ।
4. ਰਚਨਾ/ਬਣਤਰ (Texture) – ਕੁੱਝ ਚੀਜ਼ਾਂ ਪੱਧਰੀਆਂ ਜਾਂ ਮੁਲਾਇਮ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਕੁੱਝ ਖੁਰਦਰੀਆਂ, ਕੁੱਝ ਸਖ਼ਤ ਤੇ ਕੁੱਝ ਨਰਮ, ਕੁੱਝ ਚਮਕਦਾਰ ਅਤੇ ਕੁੱਝ ਮੱਧਮ ਹੁੰਦੇ (ਤੇਜ਼ ਹੀਨ) ।ਜਿਸ ਤਰ੍ਹਾਂ ਲਾਈਨਾਂ, ਆਕਾਰ ਅਤੇ ਰੰਗ ਕਿਸੇ ਭਾਵਨਾ ਜਾਂ ਪ੍ਰਵਿਰਤੀ ਦੇ ਪ੍ਰਤੀਕ ਹੁੰਦੇ ਹਨ । ਇਸੇ ਪ੍ਰਕਾਰ ਖੁਰਦਰੀ ਚੀਜ਼ ਵੀ ਦੇਖਣ ਨੂੰ ਸਖ਼ਤ ਖਰਵੀ ਅਤੇ ਮਜ਼ਬੂਤ ਲਗਦੀ ਹੈ । ਜਿਨ੍ਹਾਂ ਚੀਜ਼ਾਂ ਦੀ ਰਚਨਾ ਕੋਮਲ ਜਾਂ ਨਾਜ਼ੁਕ ਹੋਵੇ, ਉਹ ਜ਼ਿਆਦਾ ਸ਼ਾਨਦਾਰ ਅਤੇ ਵਿਵਸਥਿਤ ਲੱਗਦੀਆਂ ਹਨ । ਜਿਸ ਕਮਰੇ ਵਿਚ ਜ਼ਰੀ ਜਾਂ ਸ਼ਨੀਲ ਵਰਤੀ ਗਈ ਹੋਵੇ ਉੱਥੇ ਜੇਕਰ ਨਾਲ ਹੀ ਪਿੱਤਲ ਦੇ ਲੈਂਪ ਸ਼ੇਡ ਜਾਂ ਲੋਹੇ ਜਾਂ ਚੀਨੀ ਮਿੱਟੀ ਦੇ ਫੁਲਦਾਨ ਜਾਂ ਸੁਆਹਦਾਨੀ ਰੱਖੀ ਜਾਏ ਤਾਂ ਚੰਗੀ ਨਹੀਂ ਲੱਗੇਗੀ । ਅਖਰੋਟ ਦੀ ਲੱਕੜੀ ਦੇ ਨਾਲ ਟਾਹਲੀ ਦੀ ਲੱਕੜੀ ਦਾ ਫ਼ਰਨੀਚਰ ਵੀ ਭੈੜਾ ਲੱਗੇਗਾ। ਲਾਲ, ਸੁਨਹਿਰੀ, ਜਾਮਨੀ, ਨੀਲਾ ਅਤੇ ਹਰਾ ਰੰਗ ਜ਼ਿਆਦਾ ਭੜਕੀਲੇ ਲਗਦੇ ਹਨ ਪਰ (ਬਰਾਉਨ) ਭੂਰਾ, ਬਦਾਮੀ, ਮੋਤੀਆ, ਹਲਕਾ ਨੀਲਾ ਅਤੇ ਮੱਧਮ ਤੇਜ਼ ਰੰਗ ਹਨ । ਰੰਗਾਂ ਤੋਂ ਇਲਾਵਾ ਕੱਪੜੇ ਦੀ ਬਣਤਰ ਦਾ ਵੀ ਕਮਰੇ ਤੇ ਅਸਰ ਪੈਂਦਾ ਹੈ, ਜਿਵੇਂ ਕਿ ਹਲਕੇ ਨੀਲੇ ਰੰਗ ਦੀ ਸਿਲਕ ਜਾਂ ਸਾਟਨ ਜ਼ਿਆਦਾ ਚਮਕਦਾਰ ਲੱਗੇਗੀ ਜਦੋਂ ਕਿ ਉਸੇ ਰੰਗ ਦੀ ਕੇਸਮੈਂਟ ਜਾਂ ਖੱਦਰ ਘੱਟ ਚਮਕੀਲੀ ਹੋਵੇਗੀ ।
![]()
ਪ੍ਰਸ਼ਨ 18.
ਰੰਗ ਡਿਜ਼ਾਈਨ ਦਾ ਮਹੱਤਵਪੂਰਨ ਅੰਸ਼ ਹੈ । ਕਿਵੇਂ ?
ਉੱਤਰ-
ਹਰ ਡਿਜ਼ਾਈਨ ਦੇ ਮੂਲ ਅੰਸ਼ਾਂ ਰੇਖਾਵਾਂ, ਆਕਾਰ, ਬਣਤਰ ਤੋਂ ਇਲਾਵਾ ਰੰਗ ਵੀ ਇਕ ਮਹੱਤਵਪੂਰਨ ਅੰਸ਼ ਹੈ । ਰੰਗ, ਮਨੁੱਖ ਦੀ ਮਾਨਸਿਕਤਾ ਨੂੰ ਵੀ ਪ੍ਰਭਾਵਿਤ ਕਰਦੇ ਹਨ । ਰੰਗ ਉਤੇਜਿਤ ਅਤੇ ਹਲਕੇ ਵੀ ਹੋ ਸਕਦੇ ਹਨ । ਸਾਰੇ ਰੰਗ ਪ੍ਰਕਾਸ਼ ਤੋਂ ਉਤਪੰਨ ਹੁੰਦੇ ਹਨ । ਰੰਗਾਂ ਦੀਆਂ ਆਪਣੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਈਆਂ ਹਨ ਜਿਨ੍ਹਾਂ ਦੇ ਅਧਾਰ ‘ਤੇ ਇਨ੍ਹਾਂ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਇਹ ਹੇਠਾਂ ਦਿੱਤੀ ਹੈ-
ਪੀਲਾ – ਗਰਮ, ਧੁੱਪ ਵਾਲਾ, ਚਮਕਦਾਰ, ਖੁਸ਼ੀ ਦੇਣ ਵਾਲਾ (Cheerful
ਲਾਲ – ਗਰਮ, ਉਤੇਜਨਸ਼ੀਲ (Stimulating), ਸਾਹਸੀ, ਤੇਜਸਵੀ ।
ਸੰਤਰੀ – ਸਜੀਵ, ਰੁਚੀਕਰ, ਖ਼ੁਸ਼ੀ ਦੇਣ ਵਾਲਾ, ਗਰਮ ।
ਹਰਾ – ਠੰਢਾ, ਸ਼ਾਂਤ, ਚਮਕ ਅਤੇ ਆਰਾਮਦਾਇਕ ।
ਨੀਲਾ – ਸਾਰੇ ਰੰਗਾਂ ਤੋਂ ਜ਼ਿਆਦਾ ਠੰਢਾ,, ਕਠੋਰ, ਸ਼ਾਂਤੀਪੂਰਨ, ਨਿਸ਼ਚੇਸ਼ਠ ਜਾਂ ਸਥਿਰ ।
ਬੈਂਗਣੀ-ਭੜਕੀਲਾ, ਸ਼ਾਹੀ, ਓਜਸਵੀ, ਪ੍ਰਭਾਵਸ਼ਾਲੀ, ਕਿਰਿਆਸ਼ੀਲ ।
ਸਫ਼ੈਦ – ਸ਼ੁੱਧ, ਸ਼ਵੇਤ, ਠੰਢਾ ।
ਕਾਲਾ – ਨਿਸਤਬਧਤਾ, ਮ੍ਰਿਤਕ, ਗੰਭੀਰ, ਗੋਰਮ ।
ਕਿਸੇ ਵੀ ਫਰਨੀਚਰ ਦੇ ਡਿਜ਼ਾਈਨ ਜਾਂ ਸਜਾਵਟ ਦੇ ਹੋਰ ਸਾਮਾਨ ਦੇ ਡਿਜ਼ਾਈਨ ਵਿਚ ਰੰਗ ਦੀ ਅਹਿਮ ਭੂਮਿਕਾ ਹੈ । ਫਰਨੀਚਰ ਦਾ ਰੰਗ ਕਮਰੇ ਦੇ ਰੰਗ ਅਤੇ ਬਾਕੀ ਸਾਮਾਨ ਦੇ ਰੰਗ ਅਨੁਸਾਰ ਹਲਕਾ ਜਾਂ ਗਾੜਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਰੰਗ ਦੀ ਵਰਤੋਂ ਕਮਰੇ ਦੇ ਆਕਾਰ, ਫੈਸ਼ਨ, ਮੌਸਮ ਅਤੇ ਕਮਰੇ ਦੀ ਵਰਤੋਂ ‘ਤੇ ਅਧਾਰਿਤ ਹੈ । ਜਿਨ੍ਹਾਂ ਕਮਰਿਆਂ ਵਿਚ ਜ਼ਿਆਦਾ ਸਮਾਂ ਬਤੀਤ ਕਰਨਾ ਹੋਵੇ, ਉੱਥੋਂ ਦੀ ਰੰਗ ਯੋਜਨਾ ਸ਼ਾਂਤੀਪੂਰਨ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਇਸ ਯੋਜਨਾ ਲਈ ਹਲਕੇ ਰੰਗਾਂ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਮੌਸਮ ਦਾ ਵੀ ਰੰਗਾਂ ‘ਤੇ ਬਹੁਤ ਪ੍ਰਭਾਵ ਹੁੰਦਾ ਹੈ । ਗਰਮੀ ਦੇ ਮੌਸਮ ਵਿਚ ਹਲਕੇ ਅਤੇ ਠੰਢੇ ਰੰਗ ਚੰਗੇ ਲਗਦੇ ਹਨ ਜਦ ਕਿ ਸਰਦੀਆਂ ਵਿਚ ਗੂੜੇ ਅਤੇ ਗਰਮ ਰੰਗ ਠੀਕ ਹੁੰਦੇ ਹਨ ।
ਕਿਸੇ ਘਰ, ਫਰਨੀਚਰ ਜਾਂ ਹੋਰ ਸਾਮਾਨ ਦਾ ਡਿਜ਼ਾਈਨ ਤਿਆਰ ਕਰਦੇ ਸਮੇਂ, ਬਾਕੀ ਸਮਾਨ ਦੇ ਅਨੁਸਾਰ ਰੰਗ ਦੀ ਚੋਣ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।
PSEB 10th Class Home Science Guide ਡਿਜ਼ਾਈਨ ਦੇ ਮੂਲ ਅੰਸ਼ ਅਤੇ ਸਿਧਾਂਤ Important Questions and Answers
ਹੋਰ ਮਹੱਤਵਪੂਰਨ ਪ੍ਰਸ਼ਨ
ਬਹੁਤ ਛੋਟੇ ਪੁੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਡਿਜ਼ਾਈਨ ਦੇ ਮੂਲ ਅੰਸ਼ ਦੱਸੋ ।
ਉੱਤਰ-
ਰੇਖਾਵਾਂ, ਰੂਪ ਤੇ ਆਕਾਰ, ਰੰਗ, ਬਣਤਰ ।
ਪ੍ਰਸ਼ਨ 2.
ਡਿਜ਼ਾਈਨ ਦੇ ਮੂਲ ਸਿਧਾਂਤ ਹਨ ।
ਉੱਤਰ-
ਪੰਜ ।
ਪ੍ਰਸ਼ਨ 3.
ਡਿਜ਼ਾਈਨ ਦੇ ਪੰਜ ਮੂਲ ਸਿਧਾਂਤ ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਇਕਸੁਰਤਾ, ਅਨੁਪਾਤ, ਸੰਤੁਲਨ, ਲੈਅ ਅਤੇ ਬਲ ।
ਪ੍ਰਸ਼ਨ 4.
ਪਹਿਲੇ ਦਰਜੇ ਦੇ ਜਾਂ ਮੁੱਢਲੇ ਰੰਗ (ਪਰਾਥਮਿਕ ਰੰਗ ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਲਾਲ, ਪੀਲਾ ਅਤੇ ਨੀਲਾ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਮੁੱਢਲੇ ਰੰਗ ਕਿੰਨੇ ਹਨ ?
ਉੱਤਰ-
ਤਿੰਨ ।
ਪ੍ਰਸ਼ਨ 6.
ਦੋ ਮੁੱਢਲੇ ਰੰਗ ਮਿਲਾ ਕੇ ਜਿਹੜੇ ਰੰਗ ਬਣਦੇ ਹਨ, ਉਹਨਾਂ ਨੂੰ ਕੀ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਦੂਸਰੇ ਦਰਜੇ ਦੇ ਰੰਗ ।
ਪ੍ਰਸ਼ਨ 7.
ਦੂਸਰੇ ਦਰਜੇ ਦੇ ਕਿੰਨੇ ਰੰਗ ਹਨ ?
ਉੱਤਰ-
ਤਿੰਨ ।
ਪ੍ਰਸ਼ਨ 8.
ਤੀਸਰੇ ਦਰਜੇ ਦੇ ਕਿੰਨੇ ਰੰਗ ਹਨ ?
ਉੱਤਰ-
ਛੇ ।
ਪ੍ਰਸ਼ਨ 9.
ਰੰਗ ਯੋਜਨਾਵਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਸੰਬੰਧਿਤ ਰੰਗ ਯੋਜਨਾ, ਵਿਰੋਧੀ ਰੰਗ ਯੋਜਨਾ, ਇਕ ਰੰਗ ਯੋਜਨਾ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 10.
ਠੰਢੇ ਰੰਗਾਂ ਦੀ ਉਦਾਹਰਨ ਦਿਓ ।
ਜਾਂ
ਠੰਢੇ ਰੰਗ ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਹਰਾ, ਨੀਲਾ, ਸਫੈਦ ।
![]()
ਪ੍ਰਸ਼ਨ 11.
ਗਰਮ ਰੰਗ ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਲਾਲ, ਕਾਲਾ, ਪੀਲਾ ।
ਪ੍ਰਸ਼ਨ 12.
ਸੰਤੁਲਨ ਕਿੰਨੇ ਪ੍ਰਕਾਰ ਦਾ ਹੈ, ਨਾਂ ਦੱਸੋ ।
ਜਾਂ
ਸੰਤੁਲਨ ਦੀਆਂ ਕਿਸਮਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਉਪਚਾਰਿਕ ਸੰਤੁਲਨ, ਅਣਉਪਚਾਰਿਕ ਸੰਤੁਲਨ ।
ਪ੍ਰਸ਼ਨ 13.
ਜਦੋਂ ਰੇਖਾਵਾਂ ਇਕ ਕੇਂਦਰੀ ਬਿੰਦੂ ਤੋਂ ਬਾਹਰ ਆਉਣ, ਤਾਂ ਇਸ ਨੂੰ ਕੀ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਰੇਡੀਏਸ਼ਨ ।
ਪ੍ਰਸ਼ਨ 14.
ਲਾਲ + ਪੀਲਾ = ?
ਉੱਤਰ-
ਸੰਤਰੀ ।
ਪ੍ਰਸ਼ਨ 15.
ਨੀਲਾ + ਲਾਲ = ?
ਉੱਤਰ-
ਜਾਮਨੀ ।
![]()
ਪ੍ਰਸ਼ਨ 16.
ਕਿਹੜੇ ਛੇ ਰੰਗਾਂ ਨੂੰ ਆਧਾਰ ਰੰਗ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਲਾਲ, ਪੀਲਾ, ਨੀਲਾ, ਸੰਤਰੀ, ਜਾਮਨੀ ਅਤੇ ਹਰਾ ।
ਪ੍ਰਸ਼ਨ 17.
ਲਾਖਾ ਰੰਗ ਕਿਵੇਂ ਪੈਦਾ ਕਰੋਗੇ ?
ਉੱਤਰ-
ਲਾਲ + ਕਾਲਾ = ਲਾਖਾ ।
ਪ੍ਰਸ਼ਨ 18.
ਉਦਾਸੀਨ ਰੰਗ ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਕਾਲਾ, ਸਲੇਟੀ ।
ਪ੍ਰਸ਼ਨ 19.
ਵਿਰੋਧੀ ਰੰਗ ਯੋਜਨਾ ਵਿੱਚ ਕੋਈ ਉਦਾਹਰਨ ਦਿਓ ।
ਉੱਤਰ-
ਪੀਲਾ ਤੇ ਜਾਮਨੀ, ਲਾਲ ਤੇ ਹਰਾ ।
ਪ੍ਰਸ਼ਨ 20.
ਸਿੱਧੀਆਂ ਰੇਖਾਵਾਂ ਕਿਸ ਦੀਆਂ ਪ੍ਰਤੀਕ ਹਨ ?
ਉੱਤਰ-
ਦ੍ਰਿੜ੍ਹਤਾ ਅਤੇ ਸਾਦਗੀ ਦਾ ।
![]()
ਪ੍ਰਸ਼ਨ 21.
ਪ੍ਰਸੰਨਤਾ ਤੇ ਜਸ਼ਨ ਦਾ ਅਹਿਸਾਸ ਕਰਵਾਉਣ ਵਾਲੀਆਂ ਕਿਹੜੀਆਂ ਰੇਖਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਪੂਰੀ ਗੋਲਾਈ ਵਾਲੀਆਂ ਰੇਖਾਵਾਂ ।
ਪ੍ਰਸ਼ਨ 22.
ਸਫ਼ੈਦ ਰੰਗ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਸ਼ੁੱਧ, ਠੰਢਾ ।
ਪ੍ਰਸ਼ਨ 23.
ਲਾਲ ਰੰਗ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਗਰਮ, ਸਾਹਸੀ, ਤੇਜਸਵੀ ।
ਪ੍ਰਸ਼ਨ 24.
ਬੈਂਗਣੀ ਰੰਗ ਦੇ ਗੁਣ ਦੱਸੋ ।
ਉੱਤਰ-
ਭੜਕੀਲਾ, ਸ਼ਾਹੀ, ਉਜਸਵੀ ਕਿਰਿਆਸ਼ੀਲ :
ਪ੍ਰਸ਼ਨ 25.
ਕਾਲਾ ਅਤੇ ਸਲੇਟੀ ਕਿਹੜੇ ਰੰਗ ਹਨ ?
ਉੱਤਰ-
ਉਦਾਸੀਨ ਰੰਗ ।
ਪ੍ਰਸ਼ਨ 26.
ਲਾਲ, ਪੀਲਾ ਅਤੇ ਨੀਲਾ ਕਿਹੜੇ ਰੰਗ ਹਨ ?
ਉੱਤਰ-
ਮੁੱਢਲੇ ਰੰਗ ।
![]()
ਪ੍ਰਸ਼ਨ 27.
ਡਿਜ਼ਾਈਨ ਵਿੱਚ ਇਕਸੁਰਤਾ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਦੇਖੋ ਉਪਰੋਕਤ ਪ੍ਰਸ਼ਨਾਂ ਵਿਚ ।
ਪ੍ਰਸ਼ਨ 28.
ਕਿਸੇ ਦੋ ਡਿਜ਼ਾਈਨ ਦੇ ਤੱਤਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਰੇਖਾਵਾਂ, ਰੰਗ ।
ਪ੍ਰਸ਼ਨ 29.
ਦੂਜੇ ਦਰਜੇ ਦੇ ਰੰਗ ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਹਰਾ, ਜਾਮਨੀ, ਸੰਤਰੀ ।
ਪ੍ਰਸ਼ਨ 30.
ਤੀਸਰੇ ਦਰਜੇ ਦੇ ਰੰਗ ਕਿਹੜੇ-ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਪੀਲਾ-ਹਰਾ, ਨੀਲਾ-ਹਰਾ, ਨੀਲਾ-ਜਾਮਨੀ, ਲਾਲ-ਜਾਮਨੀ, ਲਾਲ-ਸੰਤਰੀ, ਪੀਲਾਸੰਤਰੀ ।
ਛੋਟੇ ਉੱਡਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਡਿਜ਼ਾਈਨ ਵਿਚ ਲੈਅ ਤੋਂ ਤੁਸੀਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਉੱਤਰ-
ਡਿਜ਼ਾਈਨ ਵਿਚ ਲੈਅ ਤੋਂ ਭਾਵ ਕਿ ਜਦੋਂ ਤੁਸੀਂ ਕਿਸੇ ਕਮਰੇ ਵਿਚ ਜਾਉ ਤਾਂ ਤੁਹਾਡੀ ਨਜ਼ਰ ਪਹਿਲਾਂ ਇਕ ਥਾਂ ‘ਤੇ ਜਾਂਦੀ ਹੈ ਅਤੇ ਫਿਰ ਹੌਲੀ-ਹੌਲੀ ਬਾਕੀ ਚੀਜ਼ਾਂ ਤੇ ਜਾਂਦੀ ਹੈ । ਇਹ ਨਜ਼ਰ ਦੀ ਗਤੀ ਜੇ ਲੈਅ ਵਿਚ ਹੋਵੇ ਤਾਂ ਡਿਜ਼ਾਈਨ ਲੈਅ ਵਿਚ ਹੈ ਕਿਉਂਕਿ ਇਕ ਖ਼ਾਲੀ ਕਮਰੇ ਵਿਚ ਕੋਈ ਗਤੀ ਨਹੀਂ ਹੁੰਦੀ । ਡਿਜ਼ਾਈਨ ਵਿਚ ਲੈਅ, ਰੰਗ, ਆਕਾਰ ਜਾਂ ਰੇਖਾ ਦੇ ਕਿਸੇ ਵੀ ਕੂਮ ਵਿਚ ਆਪਸ ਵਿਚ ਜੁੜੇ ਹੋਏ ਉਸ ਮਾਰਗ ਤੋਂ ਹੈ ਜਿਸ ਨੂੰ ਅੱਖਾਂ ਇਕ ਗਤੀ ਵਿਚ ਵੇਖਦੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ।
ਪ੍ਰਸ਼ਨ 2.
ਆਧਾਰ ਰੰਗ ਕਿਹੜੇ-ਕਿਹੜੇ ਹਨ ?
ਜਾਂ
ਦੂਜੇ ਦਰਜੇ ਦੇ ਰੰਗ ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਜਦੋਂ ਦੋ ਪ੍ਰਾਥਮਿਕ ਰੰਗਾਂ ਨੂੰ ਇਕੋ ਜਿੰਨੀ ਮਾਤਰਾ ਵਿਚ ਮਿਲਾਇਆ ਜਾਏ ਤਾਂ ਤਿੰਨ ਦੂਜੇ ਦਰਜੇ ਦੇ ਰੰਗ ਬਣਦੇ ਹਨ , ਜਿਵੇਂ-
ਲਾਲ + ਪੀਲਾ = ਸੰਤਰੀ
ਪੀਲਾ + ਨੀਲਾ = ਹਰਾ
ਨੀਲਾ + ਲਾਲ = ਜਾਮਨੀ
ਸੋ ਇਨ੍ਹਾਂ ਛੇ ਰੰਗਾਂ ਲਾਲ, ਪੀਲਾ, ਨੀਲਾ, ਸੰਤਰੀ, ਜਾਮਨੀ ਅਤੇ ਹਰਾ) ਨੂੰ ਆਧਾਰ ਰੰਗ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
![]()
ਵਸਤੂਨਿਸ਼ਠ ਪ੍ਰਸ਼ਨ
I. ਖ਼ਾਲੀ ਸਥਾਨ ਭਰੋ-
1. ਡਿਜ਼ਾਈਨ ਦੇ ਮੂਲ ਸਿਧਾਂਤ ………………… ਹਨ ।
2. ਲਾਲ, ਪੀਲਾ ਅਤੇ ਨੀਲਾ ਰੰਗ …………………. ਰੰਗ ਹਨ ।
3. ਸਿੱਧੀਆਂ ਰੇਖਾਵਾਂ ………………. ਦੀਆਂ ਪ੍ਰਤੀਕ ਹਨ ।
4. ਦੋ ਪ੍ਰਾਥਮਿਕ ਰੰਗਾਂ ਨੂੰ ਮਿਲਾ ਕੇ ………………….. ਦੇ ਰੰਗ ਬਣਦੇ ਹਨ ।
5. ਪੀਲਾ + ਨੀਲਾ = …………………….. ਰੰਗ ।
ਉੱਤਰ-
1. ਪੰਜ,
2. ਮੁੱਢਲੇ,
3. ਦ੍ਰਿੜ੍ਹਤਾ ਅਤੇ ਸਾਦਗੀ,
4. ਦੂਜੇ ਦਰਜੇ,
5. ਹਰਾ ।
II. ਠੀਕ / ਗਲਤ ਦੱਸੋ-
1. ਪੀਲਾ, ਨੀਲਾ ਅਤੇ ਲਾਲ ਪਹਿਲੇ ਦਰਜੇ ਦੇ ਰੰਗ ਹਨ ।
ਉੱਤਰ-
ਠੀਕ
2. ਨੀਲਾ ਰੰਗ + ਚਿੱਟਾ ਰੰਗ = ਗੁਲਾਬੀ ।
ਉੱਤਰ-
ਗ਼ਲਤ
3. ਦੂਸਰੇ ਦਰਜੇ ਦੇ ਛੇ ਰੰਗ ਹਨ ।
ਉੱਤਰ-
ਗ਼ਲਤ
4. ਇਕਸੁਰਤਾ, ਅਨੁਪਾਤ, ਸੰਤੁਲਨ, ਲੈਅ ਅਤੇ ਬਲ ਡਿਜ਼ਾਇਨ ਦੇ ਮੂਲ ਸਿਧਾਂਤ ਹਨ ।
ਉੱਤਰ-
ਠੀਕ
![]()
5. ਕਾਲਾ ਅਤੇ ਸਲੇਟੀ, ਉਦਾਸੀਨ ਰੰਗ ਹੈ ।
ਉੱਤਰ-
ਠੀਕ
6. ਸਫ਼ੈਦ ਰੰਗ ਸ਼ੁੱਧ ਅਤੇ ਠੰਢਾ ਹੁੰਦਾ ਹੈ ।
ਉੱਤਰ-
ਠੀਕ
III. ਬਹੁਵਿਕਲਪੀ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਲਾਲ + ਕਾਲਾ = ………………
(ਉ) ਲਾਖਾ
(ਅ) ਸਲੇਟੀ
(ੲ) ਜਾਮਨੀ
(ਸ) ਸੰਤਰੀ ।
ਉੱਤਰ-
(ਉ) ਲਾਖਾ
ਪ੍ਰਸ਼ਨ 2.
ਪੀਲਾ + ਨੀਲਾ = …………………
(ਉ) ਜਾਮਨੀ
(ਅ) ਹਰਾ
(ੲ) ਸੰਤਰੀ
(ਸ) ਗੁਲਾਬੀ ।
ਉੱਤਰ-
(ਅ) ਹਰਾ
ਪ੍ਰਸ਼ਨ 3.
ਦੂਸਰੇ ਦਰਜੇ ਦੇ ਕਿੰਨੇ ਰੰਗ ਹਨ ?
(ਉ) ਦੋ
(ਅ) ਤਿੰਨ
(ੲ) ਪੰਜ
(ਸ) ਛੇ ।
ਉੱਤਰ-
(ਅ) ਤਿੰਨ
![]()
ਪ੍ਰਸ਼ਨ 4.
ਹੇਠ ਵਿਚੋਂ ਗਰਮ ਰੰਗ ਹਨ ?
(ਉ) ਲਾਲ
(ਅ) ਕਾਲਾ
(ੲ) ਪੀਲਾ
(ਸ) ਸਾਰੇ ।
ਉੱਤਰ-
(ਸ) ਸਾਰੇ ।