Bhagya

Punjab State Board PSEB 5th Class Hindi Book Solutions Chapter 3 नगर की सुंदरता Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Hindi Chapter 3 नगर की सुंदरता

Hindi Guide for Class 5 PSEB नगर की सुंदरता Textbook Questions and Answers

I. बताओ

प्रश्न 1.
महाराज कृष्णदेव क्या करना चाहते थे?
उत्तर:
महाराज कृष्णदेव विजयनगर को अत्यधिक साफ़-सुथरा और सुन्दर बनाना चाहते थे।

प्रश्न 2.
सैलानियों का समूह क्यों उमड़ आया ?
उत्तर:
सैलानियों का समूह विजयनगर की सन्दरता को देखने के लिए उमड आया।

प्रश्न 3.
राजा के पूछने पर तेनालीराम क्यों चुप रहे?
उत्तर;
तेनालीराम राजा के किए गए कार्यों से खुश नहीं थे इसीलिए वह चुप रहे।

प्रश्न 4.
कृष्णदेव ने कमी सिद्ध न कर पाने पर क्या शर्त बतायी ?
उत्तर:
कमी सिद्ध न कर पाने पर कृष्णदेव ने तेनालीराम को मृत्यु दण्ड की शर्त बतायी।

प्रश्न 5.
जय-जयकार करने वाले लोम कौन थे ?
उत्तर:
जय-जयकार करने वाले लोग मंत्रियों के चमचे थे।

प्रश्न 6.
बस्ती के लोगों की कैसी दशा थी ?
उत्तर:
बस्ती के लोगों की दशा अच्छी नहीं थी। वे लोग तरह-तरह की बीमारियों से ग्रस्त थे।

प्रश्न 7.
प्रजा के सुन्दर जीवन के लिए राजा ने क्या आदेश दिया ?
उत्तर:
प्रजा. के सुन्दर जीवन के लिए राजा ने बस्ती को साफ़ करवाने, बीमारों का इलाज करवाने और बढ़े हुए करों को वापिस लेने का आदेश दिया।

प्रश्न 8.
इस कहानी से क्या सन्देश मिलता है ?
उत्तर:
यह कहानी सन्देश देती है कि श्रेष्ठ राजा वह है जो प्रजा के हितों का ध्यान रखे। असली सुन्दरता प्रजा के खिले हुए चेहरे हैं।

II. विलोम शब्द लिखो

(i) राजा : रंक
(ii) दुःखी : ……………
(iii) सुन्दर : ……………
(iv) अन्धेरा : ……………
(v) विजय : ……………
(vi) गन्दगी : ……………
(vii) सम्मान : ……………
(viii) उपस्थित : ……………
उत्तर:
विलोम शब्द
(i) राजा = रंक।
(ii) दुःखी = सुखी।
(iii) सुन्दर = कुरूप।
(iv) अन्धेरा = उजाला।
(v) विजय = पराजय।
(vi) गन्दगी = सफ़ाई।
(vii) सम्मान = अपमान।
(viii) उपस्थित = अनुपस्थित।

III. समानार्थक शब्द लिखें

(i) राजा = नरेश।
(ii) जीवन = ……………।
(iii) खुशी = ……………।
(iv) सैलानी = ……………।
(v) मृत्यु = ……………।
(vi) प्रश्न = ……………।
उत्तर:
समानार्थक शब्द:
(i) राजा = नरेश।
(ii) जीवन = ज़िन्दगी।
(iii) खशी = प्रसन्नता।
(iv) सैलानी = पर्यटक।
(v) मृत्यु = मरण।
(vi) प्रश्न = सवाल।

IV. संज्ञा शब्द छाँटकर लिखो

1. मुझे लगता है ये विजयनगर की सुन्दरता से खुश नहीं है।
2. तेनालीराम ने अपनी चुप्पी तोड़ते हुए कहा।
3. महाराज की खुशी का ठिकाना न रहा।
4. प्रजा में कोई उत्साह नहीं दिखाई दिया।
उत्तर:
संज्ञा शब्द:
(1) (i) विजयनगर-(व्यक्तिवाचक संज्ञा)
(ii) सुन्दरता-(भाववाचक संज्ञा)।

(2) (i) तेनालीराम-(व्यक्तिवाचक संज्ञा)।
(ii) चुप्पी-(भाववाचक संज्ञा)

(3) (i) महाराज-(जातिवाचक संज्ञा)
(ii) खुशी-(भाववाचक संज्ञा)।

(4) (i) प्रजा-(जातिवाचक संज्ञा)
(ii) उत्साह-(भाववाचक संज्ञा)।

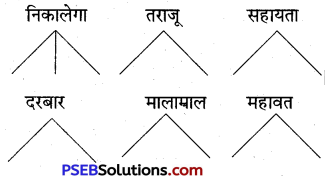
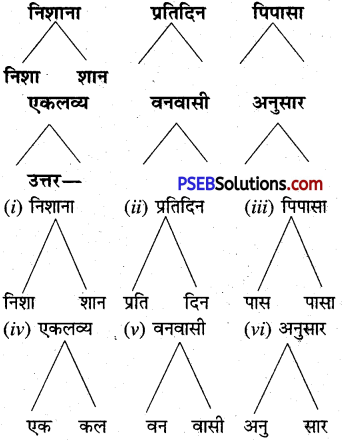
V. दिए गए शब्दों से नए शब्द बनाइए

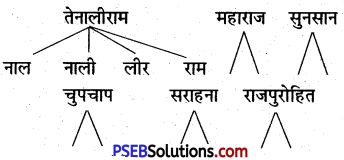
उत्तर:
(i) तेनालीराम-(i) नाल (ii) नाली (iii) लीर (iv) राम।
(ii) महाराज-(i) महा (ii) राज।
(iii) सुनसान-(i) सुन (ii) सान।
(iv) चुपचाप-(i) चुप (ii) चाप।
(v) सराहना-(i) सर (ii) राह।
(vi) राजपुरोहित-(i) राज (ii) पुर (iii) हित (iv) पुरोहित (v) रोहित।

VI. निम्नलिखित मुहावरों को वाक्यों में प्रयोग करो

मुहावरा – अर्थ – वाक्य
1. उमड़ पड़ना – जोश में आ जाना – ……………
2. दिल रो पड़ना – अफसोस होना – …………..
3. खुशी का ठिकाना न रहना – बहुत खुश होना – …………..
4. एक स्वर में कहना – मिलकर कहना – ………….
5. चुप्पी तोड़ना – मौन तोड़ना, बोलना – …………….
उत्तर:
(i) उमड़ पड़ना – जोश में आ जाना – नेता के आते ही जनता उन्हें देखने के लिए उमड़ पड़ी।
(ii) दिल रो पड़ना – अफसोस होना – भिखारी की दयनीय दशा देखकर मेरा दिल रो पड़ा।
(iii) खुशी का ठिकाना न रहना – बहुत खुश होना – परीक्षा में प्रथम आने का समाचार पाते ही मेरी ख़ुशी का ठिकाना न रहा।
(iv) एक स्वर में कहना – मिलकर कहना – सभी विद्यार्थियों ने मिलकर एक स्वर में कहा-हम नशावृति से दूर रहेंगे।
(v) चुप्पी तोड़ना – मौन तोड़ना, बोलना – सभा में सभी चुपचाप, शान्त भाव से बैठे थे। संन्यासी जी ने चुप्पी तोड़ते हुए बोलना आरम्भ किया।

VII. निम्नलिखित के विराम चिह्न लगाएँ

1. महाराज तेनालीराम चुपचाप बैठे हैं।
2. कैसी कमी महाराज ने हैरानी से पूछा
3. लेकिन तुम गुमसुम क्यों हो
4. काश मंत्री लोग प्रजा की सुविधाओं पर ध्यान देते
उत्तर:
विराम चिह्न
(i) “महाराज! तेनालीराम चुपचाप बैठे हैं।”
(ii) “कैसी कमी ?” महाराज ने हैरानी से पूछा।
(iii) लेकिन तुम गुमसुम क्यों हो ?
(iv) काश! मंत्री लोग प्रजा की सुविधाओं पर ध्यान देते।

VIII. निम्नलिखित शब्दों में अन्तर समझें और वाक्यों में प्रयोग करें

1. चमचा : चम्मच
चमचा.: चापलूसी करने वाला

2. अमल : नशा
अमल : काम, क्रिया, व्यवहार

3. चक्कर : मोड़, घुमाव
चक्कर : उलझन

4. नक्शा : रंगरूप, बनावट
नक्शा : मानचित्र।
उत्तर:
(1) (i) चमचा = चम्मच → कृपया मुझे एक चमचा देना।
(ii) चमचा = चापलूसी करने वाला → मुकेश तो साहब का चमचा है।

(2) (i) अमल = नशा → दिनेश को शराब का अमल लग गया है।
(ii) अमल = पालन करना, व्यवहार → मैं आपके विचारों पर अमल करूंगा।

(3) (i) चक्कर = मोड़, घुमाव → पहाड़ी रास्ता चक्करदार है।
(ii) चक्कर = उलझन → मैं इस चक्कर में नहीं पड़ना चाहता।

(4) (i) नक्शा = रंगरूप, बनावट → उसके नाक-नक्श बहुत तीखे हैं।
(ii) नक्शा = मानचित्र → मुझे पंजाब का नक्शा देना।

IX. कुछ करने को

किसी बस्ती में अपने अभिभावक / अध्यापक के साथ जाकर वहाँ के लोगों की दशा और बस्ती की दशा पर अपने विचार लिखें। आप उसके सुधार के लिए क्या करेंगे ?
उत्तर:
विद्यार्थी स्वयं प्रयास करें।

बहुवैकल्पिक प्रश्न

पूछे गए प्रश्नों के सही विकल्प पर (✓) निशान लगाएं

प्रश्न 1.
विजयनगर के राजा कौन थे ?
(क) कृष्णदेव
(ख) विजय देव
(ग) विजय सिंह
(घ) कृष्ण सिंह।
उत्तर:
(क) कृष्णदेव

प्रश्न 2.
महाराज कृष्णदेव विजयनगर को कैसा बनाना चाहते थे.?
(क) सुरमय
(ख) सुशील
(ग) सुन्दर
(घ) सुनहरा।
उत्तर:
(ग) सुन्दर

प्रश्न 3.
विजय को देखने के लिए कौन आए ?
(क) राजा
(ख) सैलानी
(ग) मंत्री
(घ) प्रजा।
उत्तर:
(ख) सैलानी

प्रश्न 4.
मंत्री और चमचे राजा की क्या करते थे ?
(क) जय-जयकार
(ख) नमस्ते
(ग) दुहाई
(घ) बुराई।
उत्तर:
(क) जय-जयकार

प्रश्न 5.
एक श्रेष्ठ राजा किसके हितों का ध्यान रखता
(क) प्रजा
(ख) धनी
(ग) पैसे वाले
(घ) लुटेरों।
उत्तर:
(क) प्रजा

नगर की सुंदरता Summary

नगर की सुंदरता पाठ का सार

महाराज कृष्णदेव विजयनगर को साफ़-सुथरा और सुन्दर बनाना चाहते थे। उन्होंने अपने मन्त्री को अपनी इच्छा बताई। महाराज की आज्ञा का पालन करते हुए मन्त्री विजयनगर को सजाने-सँवारने में लग गया। कुछ ही दिनों में विजयनगर की सुन्दरता की चर्चा दूर-दूर तक होने लगी। दूर-दूर से लोग उसकी सुन्दरता को देखने के लिए आने लगे। इससे महाराज बहुत ही खुश हुए। उन्होंने विजयनगर की सुन्दरता के बारे में दरबारियों की राय माँगी तो सभी दरबारियों ने एक ही स्वर में कहा कि विजयनगर की सुन्दरता में हमें कोई कमी नहीं दिखाई। देती। सभी ने विजयनगर की प्रशंसा की, लेकिन तेनालीराम चुपचाप बैठा रहा। उसे चुप बैठे देखकर महाराज ने कहा, “तेनालीराम, चारों ओर विजयनगर की प्रशंसा हो रही है, लेकिन तुम गुमसुम क्यों हो ?” तेनालीराम ने कहा कि महाराज विजयनगर की सुन्दरता में कुछ कमी रह गई है।

महाराज के पूछे जाने पर कि क्या कमी रह गई है, तेनालीराम ने इसके उत्तर में कहा कि उस कमी को देखने के लिए आपको मेरे साथ नगर का भ्रमण करना पड़ेगा। महाराज ने कहा कि यदि तुम कमी को सिद्ध नहीं कर पाए तो तुम्हें मृत्यु दण्ड दिया जाएगा। तेनालीराम महाराज को लेकर एक बस्ती की ओर गये। बस्ती में पहुँचने पर मंत्रियों के चमचे तो महाराज की जय-जयकार करने लगे, लेकिन प्रजा में कोई उत्साह नहीं था। आगे बढ़ने पर महाराज ने अँधेरा ही अँधेरा देखा, वहाँ का माहौल बहुत-ही गन्दा था, लोग तरह-तरह की बीमारियों से पीड़ित थे। प्रजा को दुखी देखकर महाराज का दिल रो पड़ा। उन्होंने दुखी होकर तेनालीराम की ओर देखा। तेनालीराम ने बताया कि नगर को सुन्दर बनाने के प्रयास में प्रजा की अनदेखी हुई है। महाराज ने तुरन्त आदेश दिया कि प्रजा के सुन्दर जीवन के बिना विजयनगर की सारी सुन्दरता बेकार है। अत: नगर की गन्दी बस्तियों को साफ़ किया जाए, बीमारों का इलाज करवाया जाए और बढ़े हुए करों को वापिस ले लिया जाए। महाराज के आदेश को तुरन्त अमल में लाया गया। नगर को सुन्दर बनाने का अभियान चल पड़ा। तेनालीराम का भी बहुत मान-सम्मान होने लगा।

कठिन शब्दों के अर्थ:

अत्यधिक = बहुत ज्यादा। इच्छा = लालसा। अवगत = जानकारी। आदेश = आज्ञा। बखान = प्रशंसा। सैलानियों = पर्यटकों। समूह = झुण्ड, जत्था। उपस्थित = मौजूद, हाज़िर। सराहना = प्रशंसा, तारीफ। आश्चर्यचकित = हैरान। भ्रमण = सैर। घृणा = नफ़रत।

Punjab State Board PSEB 5th Class Hindi Book Solutions Chapter 4 हम सुमन एक उपवन के Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Hindi Chapter 4 हम सुमन एक उपवन के

Hindi Guide for Class 5 PSEB हम सुमन एक उपवन के Textbook Questions and Answers

I. बताओ

प्रश्न 1.
उपवन के फूलों को क्या-क्या समान चीजें प्राप्त होती हैं ?
उत्तर:
उपवन के फूलों को एक-सी धरती, मिट्टी, धूप, जल, सूर्य की किरणें, चाँद की चाँदनी, भँवरों का गुंजन आदि सब कुछ एक समान रूप में प्राप्त होती हैं।

प्रश्न 2.
उपवन की शोभा किनसे बनती है ?
उत्तर:
उपवन की शोभा फूलों से बनती है।

प्रश्न 3.
फूलों ने हँसकर जीना किससे सीखा है ?
उत्तर:
फलों ने हँसकर जीना काँटों से सीखा है।।

प्रश्न 4.
‘एक सूत्र में बँधकर हमने, हार गले का बनना सीखा’, इस काव्य पंक्ति का क्या अर्थ है ?
उत्तर:
इस पंक्ति का अर्थ है कि अलग-अलग होते हुए भी हम सब एक ही धागे से बँधकर हार के रूप में गले की शोभा बने हुए हैं।

प्रश्न 5.
फूल अपनी सुगन्ध किसे देता है ?
उत्तर:
फूल अपनी सुगन्ध सबको देता है।

II. इन प्रश्नों के उत्तर चार-पाँच पंक्तियों में लिखो

प्रश्न 1.
कवि ने फूल के द्वारा क्या सन्देश दिया है? पाँच वाक्यों में लिखो।
उत्तर:
कवि ने फूल के द्वारा सन्देश दिया है कि जिस प्रकार फूल अलग-अलग रंगों के होते हैं, अलग-अलग क्यारियों में पलते हैं, लेकिन सभी मिलकर उपवन की शोभा बढ़ाते हैं, इसी प्रकार अलग-अलग जातियों, प्रान्तों में रहते हुए सभी लोग भारत देश की शोभा बढ़ाते हैं।

फूलों के समान ही सभी मनुष्यों को परस्पर मिलजुल कर रहना चाहिए। फूलों के समान ही मनुष्यों को अपने अच्छे कर्मों, सद्व्यवहार और सदाचरण की महक चारों ओर बिखरानी चाहिए।

प्रश्न 2.
प्रकृति जैसे मिट्टी, वायु, सूरज, चाँद, भँवरे अपने गुण देने में कोई भेदभाव नहीं करते। वे निस्वार्थ भाव से देते हैं। इसी प्रकार पाँच उन प्राकृतिक वस्तुओं के नाम लिखो जो सबको समान भाव से देते रहते हैं।
उत्तर:
सर्दी, गर्मी, वर्षा, फल, फूल, नदियों का कल-कल करता बहता जल आदि ऐसे प्राकृतिक उपहार हैं जो सभी प्राणियों को समान भाव से मिलते हैं।

III. सरलार्थ करो

काँटों से खिलकर हम सबने,
हँस-हँस कर है जीना सीखा,
एक सूत्र में बँधकर हमने,
हार गले का बनना सीखा।
सबके लिए सुगन्ध हमारी
हम शृंगार धनी-निर्धन के।
उत्तर::
यह पद्यांश ‘हम सुमन एक उपवन के’ नामक कविता से लिया गया है। इसमें कवि कहता है कि हम सभी देशवासियों ने मुसीबतों तथा कठिनाइयों का डटकर सामना करना सीखा है। हमें रास्ते के काँटों की कोई परवाह नहीं है। हम सभी एक ही धागे में बँधे हुए हैं। हमने एक हार बनकर भारत माँ की शोभा बढ़ायी है। हम सब एक हैं। हमारी खुशब सभी के लिए समान है। हम अमीरग़रीब सभी की शोभा हैं। हम किसी से कोई भेदभाव नहीं रखते।

IV. वाक्यों में प्रयोग करो

(i) उर की कली खिलना = खुश होना
(ii) गले का हार बनना = अतिप्रिय, सदा साथ लगे रहना।
उत्तर:
(i) उर की कली खिलना = खुश होनाअपने जन्म दिन पर चाचा जी से सुन्दर घड़ी पाकर मेरे तो उर की कली खिल गई।
(ii) गले का हार बनना = अतिप्रिय-अपने अच्छे कार्यों से मन्त्री तो राजा के गले का हार बन गया।।

V. समानार्थक शब्द लिखो

(i) सुमन = प्रसून
(ii) उपवन = ……………
(iii) धरती = …………
(iv) जल = …………
(v) पवन = ………..
(vi) सूरज = …………
(vii) चाँद = ……………
(viii) भ्रमर = ………………..
(ix) गगन = ………..
उत्तर:
समानार्थक शब्द
(i) सुमन = प्रसून, पुष्प।
(ii) उपवन = बाग़, बगीचा।
(ii) धरती = धरा, पृथ्वी।
(iv) जल = पानी, नीर।
(v) पवन = हवा, वायु।
(vi) सूरज = सूर्य, रवि।
(vii) चाँद = राकेश, चन्द्र।
(vii) भ्रमर = भंवरा, अलि।
(ix) गगन = आकाश, आसमान।

VI. विपरीत शब्द मिलाओ

(i) धरती – दुर्गन्ध।
(ii) धूप – अन्धेरी
(iii) चाँदनी – निर्धन
(iv) सुगन्ध – छाया
(v) धनी – आकाश।
उत्तर:
विपरीतार्थक शब्द:
(i) धरती – आकाश।
(ii) धूप – छाया।
(iii) चाँदनी – अन्धेरी।
(iv) सुगन्ध – दुर्गन्ध।
(v) धनी – निर्धन।

VII. नए शब्द बनाओ

(i) सूत्र = त् + रत्र ………… , ……………
(ii) श्रृंगार = श् + ऋ = शृ, श्रृंग ……………., ……………
उत्तर:
(i) त्र = पुत्र, पत्र।
(ii) शृ = शृंगाल।

अध्यापन संकेत : अध्यापक इस कविता को पढ़ाते हुए बच्चों को बताए ‘कि देखो कवि की कल्पना का चमत्कार। एक फूल के माध्यम से एक ओर तो प्रकृति की नि:स्वार्थ देन की ओर संकेत किया है तो दूसरी ओर देश की एकता का सन्देश है। अलग-अलग प्रांतों, भाषा, वेशभूषा, त्योहार, संस्कृति के होते भी हम सब एक हैं। हमारा एक माली, ईश्वर है जो हमें सुख-दुःख में जीना सिखाता है।

बहुवैकल्पिक प्रश्न

पूछे गए प्रश्नों के सही विकल्प पर (✓) निशान लगाएं

प्रश्न 1.
कवि ने मनुष्यों को किसके समान माना है ?
(क) फूल
(ख) धूल
(ग) भूल
(घ) मूल।
उत्तर:
(क) फूल

प्रश्न 2.
सारा संसार किससे सींचा जाता है ?
(क) फूल
(ख) धूल
(ग) जल
(घ) बादल।
उत्तर:
(ग) जल

प्रश्न 3.
सबसे मिलकर किसकी शोभा बढ़ती है ?
(क) घर की
(ख) उपवन की
(ग) बाहर की
(घ) धरती की।
उत्तर:
(ख) उपवन की

प्रश्न 4.
फूलों ने हंसकर जीना किससे सीखा है ?
(क) कांटों से
(ख) बातों से
(ग) उपवन से
(घ) लोगों से।
उत्तर:
(क) कांटों से

प्रश्न 5.
फूल अपनी सुगंध किसे देता है ?
(क) राजा को
(ख) रानी को
(ग) भंवरे को
(घ) सबको।
उत्तर:
(घ) सबको।

हम सुमन एक उपवन के Summary

हम सुमन एक उपवन के पाठ का सार

कवि हम सब मनुष्यों को फूल के समान मान कर कहता है कि यह धरती हम सबकी है जिस पर हमने जन्म लिया है। इस पर रहते हुए समान रूप से धूप-पानी हमने प्राप्त किया है। हवा के झूलों में हम झूले हैं। सूर्य और चाँद ने हमारे प्रति एक-सा अच्छा व्यवहार किया है। हमें भंवरों-सी मीठी आवाज़ प्राप्त हुई है। चाहे हमारे रूप-रंग अलग-अलग हैं पर हम सब धरती रूपी इस उपवन की शोभा हैं। इस आसमान के नीचे रहने वाले हम सब का ईश्वर रूपी माली एक ही है। कष्टों में रहकर भी हमने हंस-हंस कर जीना सीखा है। हम चाहे अमीर हों या गरीब हमने एक साथ मिल-जुल कर रहना सीखा है।

पद्यांशों के सरलार्थ

1. हम सब सुमन एक उपवन के।
एक हमारी धरती सबकी।
जिसकी मिट्टी में जनमे हम,
मिली एक ही धूप हमें है।
सींचे गए एक जल से हम।
पले हुए हैं झूल-झूलकर ।
पलनों में हम एक पवन के।

शब्दार्थ:
सुमन = फूल। उपवन = बगीचा, बाग़। पलना = बच्चों का झूला। पवन = हवा।

सरलार्थ:
यह पद्यांश ‘हम सुमन एक उपवन के’ कविता से लिया गया है। इसमें कवि कहता है कि हम सभी देशवासी एक ही बाग़ में खिले फूलों के समान हैं। एक ही धरती पर रहते हैं। इस धरती की मिट्टी में हमारा जन्म हुआ है। हम सब को एकजैसी धूप मिली है। हम सब ने एक ही जैसा जल पिया है। हम सभी एक ही वायु के पलनों में झूल झूल कर बड़े हुए हैं। हम सब को एक ही जैसी वायु मिली है। कहने का भाव है कि हम सब एक हैं।

भावार्थ:
कवि का मानना है कि हम सब एक समान हैं।

2. सूरज एक हमारा,
जिसकी किरणें उर की कली खिलाती,
एक हमारा चाँद,
चाँदनी जिसकी हम सबको नहलाती।
मिले एक से स्वर हमको हैं
भ्रमरों के मीठे गुंजन के।

शब्दार्थ:
सूरज = सूर्य। उर = हृदय। स्वर = आवाज़। भ्रमर = भौरे। गुंजन = गूंज, भँवरे की आवाज़।

सरलार्थ:
यह पद्यांश ‘हम सुमन एक उपवन के’ नामक कविता से लिया गया है। इसमें कवि कहता है कि हम सब का एक ही सूरज है। उसकी किरणों से हमारे मन की कली खिल उठती है। हम सब का चाँद भी एक ही है। हम सभी उसकी शीतल चाँदनी का आनन्द लेते हैं। भंवरों के मीठे-मीठे गीतों की तरह हम सब को एक जैसी आवाजें मिली हुई हैं।

भावार्थ:
ईश्वर ने हमें एक-सी सुख-सुविधाएं – और बोलने की शक्ति दी है।

3. रंग-रंग के रूप हमारे
अलग-अलग है क्यारी-क्यारी,
लेकिन हम सबसे मिलकर ही है
उपवन की शोभा सारी।
एक हमारा माली,
हम सब रहते नीचे एक गगन के।

शब्दार्थ;
रूप = आकृति। शोभा = सुन्दरता।। गगन = आकाश।

सरलार्थ:
यह पद्यांश ‘हम सुमन एक उपवन के’ नामक कविता से लिया गया है। इसमें कवि कहता है कि भारतवर्ष एक बाग़ की तरह है। हम सब भारतीय हैं, इस बाग़ के भिन्न-भिन्न फूल हैं। हमारे रंग-रूप भले ही अलग-अलग हैं फिर भी हम सब एक हैं। हमारे प्रदेश बाग़ की अलग-अलग क्यारियों की तरह हैं। परन्तु हम सब मिलकर ही इस भारत रूपी बाग़ की सारी शोभा बढ़ाते हैं। हमारा माली एक ही है और हम एक ही आकाश के नीचे मिलकर रहते हैं। भाव यह है कि अलग-अलग होते हुए भी हम सब एक हैं।

भावार्थ:
कवि का मानना है कि चाहे हम सबके रूप-रंग अलग-अलग हैं पर हमारा ईश्वर रूपी माली एक ही है।

4. कांटों में खिलकर हम सबने
हँस-हँस कर है जीना सीखा,
एक सूत्र में बंधकर हमने
हार गले का बनना सीखा।
सबके लिए सुगंध हमारी
हम श्रृंगार धनी-निर्धन के।

शब्दार्थ:
सूत्र = धागा, डोरी। सुगन्ध = खुशबू। श्रृंगार = सजावट। निर्धन = ग़रीब धनी = अमीर।

सरलार्थ:
यह पद्यांश ‘हम सुमन एक उपवन के’ नामक कविता से लिया गया है। इसमें कवि कहता है कि हम सभी देशवासियों ने मुसीबतों तथा कठिनाइयों का डटकर सामना करना सीखा है। हमें रास्ते के काँटों की कोई परवाह नहीं है। हम सभी एक ही धागे में बँधे हुए हैं। हमने एक हार बनकर भारत माँ की शोभा बढ़ायी है। हम सब एक हैं। हमारी खुशब सभी के लिए समान है। हम अमीरग़रीब सभी की शोभा हैं। हम किसी से कोई भेदभाव नहीं रखते।

भावार्थ;
हम सबने कष्टों को झेलते हुए एक साथ मिल-जुल कर जीना सीखा है।

Punjab State Board PSEB 5th Class Hindi Book Solutions Chapter 5 हमारा स्वास्थ्य Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Hindi Chapter 5 हमारा स्वास्थ्य

Hindi Guide for Class 5 PSEB हमारा स्वास्थ्य Textbook Questions and Answers

I. पढ़ो, समझो और लिखो

स्वस्थ = अस्वस्थ।
दूषित = स्वच्छ
योग्य = …………..
स्फूर्ति = …………
निश्चित = …………
उचित = …………..
पर्याप्त = ………….
सकारात्मक = ………….
उत्तर:
विपरीतार्थक शब्द:
(i) स्वस्थ = अस्वस्थ।
(ii) दूषित = स्वच्छ।
(iii) योग्य = अयोग्य।
(iv) स्फूर्ति = आलस्य।
(v) निश्चित = अनिश्चित।
(vi) उचित = अनुचित।
(vii) पर्याप्त = अपर्याप्त।
(viii) सकारात्मक = नकारात्मक।

II. पढ़ो और समझो

स्वस्थ = स्वास्थ्य
सन्तुलित = सन्तुलन
आवश्यक = आवश्यकता
नियमित = नियम
स्वच्छ = स्वच्छता
गरम = गरमी
उत्तर:
विद्यार्थी इन्हें पढ़ें और समझें।

III. नित्य कर्म की सूची दी गई है इसे सही क्रम दो

सफ़ाई करना, दातुन करना, सोना, स्नान करना, सैर करना, शौच जाना, पढ़ना, व्यायाम करना।
उत्तर:

1. शौच जाना
2. दातुन करना
3. सैर करना
4. व्यायाम करना
5. स्नान करना
6. सफ़ाई करना
7. पढ़ना
8. सोना।

IV. वाक्य परे करो

1. हमें बिना धुले …………………. नहीं पहनने चाहिएं।
2. शौच के बाद हाथ…………………. से अवश्य धोने चाहिएं।
3. ……………… अपने आप में सन्तुलित आहार है।
4. फल व ……………… बिना धोए न खाएं।।
5. घर में …………………. लगाकर, फिनायल डालकर पोंछा लगाना चाहिए।
6. स्वच्छता तन की, मन की, की और बाहर की भी।
उत्तर:
1. कपड़े
2. साबुन
3. दूध
4. सब्जियाँ
5. झाडू
6. घर।

V. बताओ

प्रश्न 1.
दुनिया में सबसे पहला सुख कौन-सा है?
उत्तर:
दुनिया में सबसे पहला सुख ‘नीरोगी काया’ है।

प्रश्न 2.
पाऊडर के छिड़काव से त्वचा पर क्या दुष्प्रभाव पड़ता है?
उत्तर:
पाऊडर आदि बाहरी तत्वों के छिड़काव से त्वचा के रोमछिद्र बन्द हो जाते हैं।

प्रश्न 3.
दिन में कितने गिलास और कैसा पानी पीना चाहिए ?
उत्तर:
दिन में आठ-दस गिलास शुद्ध पानी पीना चाहिए।

प्रश्न 4.
पेट के रोगी को कैसा पानी पीना चाहिए?
उत्तर:
पेट के रोगी को पानी उबालकर पीना चाहिए।

प्रश्न 5.
सकारात्मक सोच कैसे पैदा होती है ?
उत्तर:
महापुरुषों की जीवनियाँ इत्यादि पढ़ने से मन मस्तिष्क में सकारात्मक सोच पैदा होती है।

प्रश्न 6.
गन्दे पानी से कौन-कौन से रोग होते हैं ?
उत्तर:
गन्दे पानी से मलेरिया और हैज़ा जैसे रोग होते हैं।

प्रश्न 7.
साफ़ ठहरे पानी से कौन-कौन से रोग फैलने का डर होता है ?
उत्तर:
साफ़ ठहरे पानी से डेंगू के फैलने का डर होता है।

VI. चार-पाँच पंक्तियों में उत्तर लिखो

प्रश्न 1.
स्वस्थ व्यक्ति के क्या लक्षण हैं ?
उत्तर:
स्वस्थ व्यक्ति के चेहरे पर रौनक तथा चमक होती है। वह हर काम को स्फूर्ति से करता है। उसे भूख और प्यास भी लगी है। मन में हर समय उल्लास और उमंग रहती है। आलस्य पास में नहीं फटकता। रात को नींद भी अच्छी आती है।

प्रश्न 2.
शरीर की सफाई कैसे रखनी चाहिए ?
उत्तर:
शरीर की सफाई भी अत्यावश्यक है। शरीर की स्वच्छता के लिए हमें शरीर के सभी अंगों को साफ़ रखना चाहिए। नित्य प्रति स्नान करना चाहिए। स्नान करते समय साबुन का प्रयोग करना चाहिए। शौच के बाद हाथ साबुन से अवश्य धोने चाहिएं। दाँत नित्य प्रति साफ़ करने चाहिएं।

प्रश्न 3.
सन्तुलित आहार में क्या-क्या होना चाहिए?
उत्तर:
स्वस्थ रहने के लिए हमें सन्तुलित आहार लेना चाहिए। सन्तुलित आहार में चोकर वाले आटे की रोटी, हरी सब्जियाँ, दालें, फल, दूध, दही, पनीर और अंकुरित अनाज आदि शामिल हैं। सुबह और शाम दूध अवश्य पीना चाहिए। इससे शरीर में ऊर्जा उत्पन्न होती है।

प्रश्न 4.
शुद्ध जल ही क्यों पीना चाहिए ?
उत्तर:
सुन्दर स्वास्थ्य के लिए पानी का उपयोग भी महत्त्वपूर्ण है। प्रत्येक मनुष्य को दिन में आठ से दस गिलास पानी पीना चाहिए। पानी हमेशा शुद्ध ही पीना चाहिए। ऐसा न करने से पेट सम्बन्धी विकार पैदा हो जाते हैं। पानी को फिल्टर करके अथवा उबालकर शुद्ध किया जा सकता है।

प्रश्न 5.
प्रत्येक वस्तु यथास्थान पर न होने से क्या होता है?
उत्तर:
सभी वस्तुएँ यथास्थान पर होनी चाहिएं। ऐसा न करने से एक तो अस्त-व्यस्त सामान से मन की एकाग्रता पर बुरा प्रभाव पड़ता है, साथ ही ज़रूरत के समय वस्तु न मिलने से घर में कलह का कारण बनता है।

प्रश्न 6.
स्वस्थ तन में स्वस्थ मन निवास करता है’, स्पष्ट करें।
उत्तर:
यह कथन बिल्कुल सत्य है कि स्वस्थ तन में स्वस्थ मन निवास करता है। यदि हमारा शरीर स्वस्थ है तो काम में हमारा मन लगेगा। मन प्रसन्न रहेगा। मन में हर समय ताज़गी और स्फूर्ति रहेगी। मन में आलस्य नहीं होगा। स्वभाव में चिड़चिड़ापन नहीं होगा। अतः यह सत्य ही है कि स्वस्थ तन में स्वस्थ मन निवास करता है।।

VII. (i) नीचे लिखे शब्दों को बोलकर सही ढंग से लिखो

शरीर, आवश्यक, शुद्ध, शर्त, हमेशा, रोशनी सफ़ाई, उल्लास, पसीना, सन्देह, सब्जी, सुखी
नोट:-पहली पंक्ति में बार-बार आई ध्वनि है ‘श’
दूसरी पंक्ति में बार-बार आई ध्वनि है ‘स’
(विद्यार्थी इनके सही उच्चारण करते हुए अपनी उत्तर-पुस्तिका में लिखें।)

(ii) अब इन्हें पढ़ो

(iii) श्रुतलेख

स्वास्थ्य, मस्तिष्क, उमंग, स्फूर्ति, पर्याप्त, हृष्ट-पुष्ट। त्वचा, शुद्धता, तत्पर, पौष्टिक, सन्तुलित, योगाभ्यास।
उत्तर:
विद्यार्थी अपनी उत्तर-पुस्तिकाओं में इन्हें लिखने का अभ्यास करें।

रचनात्मक.

प्रश्न 1.
अपनी छोटी बहन/भाई को पत्र लिखकर यह बताएँ कि स्वास्थ्य अच्छा कैसे रखा जा सकता है ?
उत्तर:
अपनी छोटी बहन को पत्र लिखो कि अच्छा स्वास्थ्य कैसे रखा जा सकता है।

25 लारेंस रोड,
अमृतसर।
27 मार्च, 20…..

प्रिय बहन विमला,
स्नेहपूर्ण नमस्ते।

मैंने तुम्हें पहले भी लिखा था कि अच्छा स्वास्थ्य सुखमय जीवन का आधार है। तुम अक्सर बीमार रहती हो। मैं तुम्हें स्वास्थ्य अच्छा रखने के लिए कुछ सूत्र या ढंग बताता हूँ-
(क) सुबह सूर्य निकलने से पहले जाग जाना चाहिए। फिर नित्य कर्म के बाद भ्रमण और व्यायाम करना चाहिए।
(ख) भोजन पौष्टिक और सन्तुलित होना चाहिए। दूध, दही, फल, सब्जियाँ आदि स्वास्थ्य के लिए बहुत उपयोगी हैं। स्वच्छ जल का प्रयोग करना चाहिए।
(ग) अच्छे स्वास्थ्य के लिए सफ़ाई भी ज़रूरी है।

मुझे पूर्ण विश्वास है कि तुम मेरे उक्त सुझावों को मान कर स्वास्थ्य में सुधार करने का प्रयास करोगी। यदि तुम इन सुझावों पर न चली तो बाद में पछताना पड़ेगा।
पूज्य माता जी और पिता जी को प्रणाम।

तुम्हारा बड़ा भाई,
प्रदीप।

यह भी करो-

1. शरीर, कपड़े घर, आस-पड़ोस की नियमित सफाई।
2. प्रतिदिन व्यायाम एवं सैर।
3. खाने-पीने की वस्तुओं को ढक कर रखो।
4. शारीरिक अंगों की हमेशा सफ़ाई रखो।

बहुवैकल्पिक प्रश्न

पूछे गए प्रश्नों के सही विकल्प पर (✓) निशान लगाएं

प्रश्न 1.
दुनिया में सबसे पहला सुख किसे माना जाता
(क) नीरोगी काया
(ख) धन
(ग) बड़ा घर
(घ) अधिक धन।
उत्तर:
(क) नीरोगी काया

प्रश्न 2.
अच्छे स्वास्थ्य के लिए हमें कैसा आहार खाना चाहिए ?
(क) अच्छा
(ख) बढ़िया
(ग) संतुलित
(घ) बादाम।
उत्तर:
(ग) संतुलित

प्रश्न 3.
अपने आप में संतुलित आहार क्या है ?
(क) दूध
(ख) लस्सी
(ग) फल
(घ) केला।
उत्तर:
(क) दूध

प्रश्न 4.
हमें अपने दाँत कब साफ करने चाहिएं ?
(क) एक बार
(ख) नित्य
(ग) कभी-कभी
(घ) दिन में।
उत्तर:
(ख) नित्य

प्रश्न 5.
स्वस्थ व्यक्ति के चेहरे पर क्या होती है ?
(क) चमक
(ख) रौब
(ग) साहस
(घ) स्वच्छता।
उत्तर:
(क) चमक

हमारा स्वास्थ्य Summary

हमारा स्वास्थ्य पाठ का सार

दुनिया में सबसे पहला सुख नीरोगी काया है। यदि हम स्वस्थ हैं तो सब कुछ अच्छा लगता है, सारे काम फुर्ती से हो जाते हैं, लेकिन यदि स्वास्थ्य ठीक न हो तो कुछ भी अच्छा नहीं लगता, स्वभाव में चिड़चिड़ापन आ जाता है। तन और मन को स्वस्थ रखने के लिए स्वच्छ रहने की आवश्यकता है।

अपने शरीर की सफाई के लिए हमें शरीर के सभी अंगों को साफ़ रखना चाहिए। रोज़ाना नहाना चाहिए। नहाते समय अपनी त्वचा के अनुसार साबुन का प्रयोग करना चाहिए। इससे शरीर की मैल भी धुलती है और शरीर के रोम-छिद्र भी खुलते हैं। शौच के बाद हाथ साबुन से अवश्य धोने चाहिएं। हाथ-मुँह पोंछने के लिए अपना ही तौलिया प्रयोग करना चाहिए। किसी दूसरे के तौलिये का प्रयोग नहीं करना चाहिए। तन के साथ-साथ कपड़ों की सफ़ाई भी आवश्यक है। हमेशा साफ़-सुथरे और इस्त्री किए हुए कपड़े ही पहनने चाहिएं।

अच्छे स्वास्थ्य के लिए हमें सन्तुलित आहार खाना चाहिए। हरी सब्जियाँ, दालें, फल, दही, पनीर तथा अंकुरित अनाज नियमित रूप से खाना चाहिए। इन सबसे हमारे शरीर में ऊर्जा आती है। दूध अपने आप में सन्तुलित आहार है। इसका सेवन सुबहशाम अवश्य करना चाहिए। खाने की वस्तुएँ ढकी हुई होनी चाहिए। फल और सब्जियों को प्रयोग में लाने से पहले धो अवश्य लेना चाहिए। पानी भी साफ़-सुथरा ही पीना चाहिए। जहाँ तक हो सके पानी को छानकर या उबालकर पीना चाहिए। हमें दिन में आठ-दस गिलास पानी अवश्य पीना चाहिए। इससे चेहरे और आँखों में चमक आती है।

शरीर को स्वस्थ रखने के लिए व्यायाम करना आवश्यक है। इससे शरीर भी स्वस्थ रहता है और मन भी स्वस्थ रहता है। व्यायाम हमें खुली हवा में करना चाहिए। मन में सकारात्मक सोच रखनी चाहिए। सकारात्मक सोच के लिए अच्छी प्रेरणादायक तथा महापुरुषों की जीवनियाँ पढ़नी चाहिएं। तन और मन की सफ़ाई के साथ-साथ घर की सफ़ाई भी आवश्यक है। घर को झाड़ लगाकर फ़िनायल डालकर पोंछा लगाना चाहिए। सभी चीजें अपने-अपने स्थान पर रखी रहनी चाहिएं। अस्तव्यस्त चीजें हों तो मन की एकाग्रता पर भी असर पड़ता है और आवश्यकता पड़ने पर समय पर वस्तु न मिलने से घर में झगड़ा भी होता है। घर का कूड़ा-कर्कट ढक्कनदार डिब्बे में ही डालना चाहिए। गड्ढों में और नालियों में पानी इकट्ठा नहीं होने देना चाहिए। कूलर, बाल्टियों और डिब्बों में, पानी की टंकियों में पानी इकट्ठा नहीं होने देना चाहिए। इन सब बातों को अपनाते हुए हम अपने आपको सदा स्वस्थ रख सकते हैं। कहा भी गया है-तन्दुरुस्ती हज़ार नियामत है।

कठिन शब्दों के अर्थ:

नीरोगी = स्वस्थ। काया = शरीर। रौनक = लाली, चमक। उमंग = खुशी। उल्लास = प्रसन्नता। स्फूर्ति = चुस्ती, फुर्ती के साथ। आलस्य = सुस्ती। विपरीत = उल्ट।। स्वभाव = आदत। मस्तिष्क = बुद्धि। आवश्यक = ज़रूरी। स्वच्छता = सफ़ाई। त्वचा = चमड़ी। छिद्र = छेद। रोम = रोएँ। स्नान = नहाना। शौच = पाखाना। सन्तुलित = नपा-तुला, ऐसा भोजन जिसमें सभी तत्व विद्यमान हों। ऊर्जा = शक्ति, ताकत। भय = डर। हैंड पम्प = हाथ से चलाया जाने वाला नल। खासतौर = विशेषकर। नियमित = नियम से। हृष्ट-पुष्ट = मज़बूत। सकारात्मक = प्रगतिवादी। स्मरण शक्ति = याद रखने की क्षमता, याददाशत। पौष्टिक = ताकत देने वाली। अस्त-व्यस्त = बिखरा हुआ, इधर-उधर फैला हुआ। एकाग्रता = स्थिर मन। कलह = क्लेश। प्रभाव = असर। जाले = मकड़ी के जाले। एकत्रित = इकट्ठा। मलेरिया = मच्छरों से फैलने वाला रोग। हैज़ा = मक्खियों से फैलने वाला रोग। दिनचर्या = दैनिक कार्य। प्रसन्नचित्त = प्रसन्न मन। कठिन परिस्थितियों = मुश्किल समय। धैर्य = धीरज। तत्पर = तैयार।

Punjab State Board PSEB 5th Class Hindi Book Solutions Chapter 6 हाथी कैसे तोला गया Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Hindi Chapter 6 हाथी कैसे तोला गया

Hindi Guide for Class 5 PSEB हाथी कैसे तोला गया Textbook Questions and Answers

I. बताओ

प्रश्न 1.
राजा को अपना हाथी क्यों प्रिय था ?
उत्तर:
राजा का हाथी अनेक युद्धों में अपनी बहादुरी तथा साहस दिखा चुका था। इसीलिए राजा को अपना हाथी प्रिय था।

प्रश्न 2.
राजा ने कितना सोना निर्धन लोगों में बाँटने का निश्चय किया ?
उत्तर:
राजा ने हाथी के भार के बराबर का सोना निर्धन लोगों में बाँटने का निश्चय किया।

प्रश्न 3.
किस व्यक्ति ने हाथी तोलने का दावा किया?
उत्तर:
एक निर्धन मछुए ने हाथी तोलने का दावा किया।

प्रश्न 4.
मछुए ने राजा से नाव बनाने के लिए कितने दिन का समय माँगा ?
उत्तर:
मछुए ने राजा से नाव बनाने के लिए सौ दिन का समय माँगा।

प्रश्न 5.
मछुए की शर्त क्या थी ?
उत्तर:
मछुए की शर्त थी कि पहले राजा के कर्मचारी एक बड़ी नाव बनाने में मछुए की मदद करें।

II. इन प्रश्नों के उत्तर चार या पाँच वाक्यों में लिखो

प्रश्न 1.
मछुए ने हाथी को कैसे तोला? अपने शब्दों में लिखो।
उत्तर:
मछुए ने हाथी को तोलने से पूर्व एक नाव बनवाई। कई लोगों की सहायता से नाव को समुद्र में उतारा गया। हाथी को उस नाव पर चढ़ाया गया। नाव जितनी पानी में डूब गई वहाँ पर निशान लगा दिया गया। फिर हाथी को नाव से उतार लिया गया। अब नाव में सोना डाला जाने लगा। डालतेडालते जब सोना उसी निशान तक पहुँच गया जहाँ तक हाथी के भार का निशान था। इस प्रकार सोना तोला गया।

प्रश्न 2.
आजकल हाथी. को कैसे तोला जा सकता है ?
उत्तर:
आजकल हाथी को तोलने के लिए बड़ीबड़ी मशीनें हैं। मशीनों पर हाथी को खड़ा करके उसे तोला जा सकता है।

प्रश्न 3.
इस कहानी से आपको क्या शिक्षा मिलती है ?
उत्तर:
इस कहानी से यह शिक्षा मिलती है कि बुद्धि के बल पर प्रत्येक कार्य किया जा सकता है। बुद्धि का प्रयोग करके असम्भव कार्य को भी सफलतापूर्वक सम्भव बनाया जा सकता है। अतः बुद्धि बल, श्रेष्ठ बल है।

III. वाक्य पढ़ो और बताओ कि यह कहानी के अनुसार सही हैं या ग़लत

(i) हाथी राजा को बहुत प्रिय था।
(ii) सभी राजदरबार के लोग हाथी तोलने का उपाय खोज कर लाए।
(iii) मछुआ समुद्र के किनारे रहता था।
(iv) राजा के आदमी दिन-रात नाव बनाने में लगे रहे।
(v) मछुए ने नाव को अकेले समुद्र में धकेला।
(vi) धीरे-धीरे कदम रखते हुए हाथी नाव पर चढ़ गया।
(vii) हाथी के बराबर सोना तुल गया-मछुए ने कहा।
उत्तर:
(i) ✓
(ii) ✗
(iii) ✓
(iv) ✓
(v) ✗
(vi) ✓
(vii) ✓

IV. विपरीत शब्दों का मिलान करो

दिन – डरपोक
बूढ़ा – सम्पन्न
साहसी – रात
निर्धन – जवान
इनाम – रंक
एक – दण्ड
राजा – अनेक
उत्तर:
दिन – रात।
बूढ़ा – जवान।
साहसी – डरपोक।
निर्धन – सम्पन्न।
इनाम – दण्ड।
एक – अनेक।
राजा – रंक।

V. पढ़ो, समझो और लिखो

राज-दरबार = राजा का दरबार
प्रजा-जन = प्रजा के जन
अनाज-भण्डार = ………….
धन-दौलत = धन और दौलत
दिन-रात = …………..
प्रश्न-उत्तर = …………
उत्तर;
राज-दरबार = राजा का दरबार।
प्रजा-जन = प्रजा के जन (लोग)।
अनाज-भण्डार = अनाज के भण्डार।
धन-दौलत = धन और दौलत।
दिन-रात = दिन और रात।
प्रश्न-उत्तर = प्रश्न और उत्तर

VI. हाथी के चित्र में से उपयुक्त समानार्थक शब्द चुनकर लिखो

(i) राजा = नृप, ………….
(ii) हाथी = ………….. , …………..
(iii) पानी = ………….. , …………..
(iv) समुद्र = ………….. , …………..
(v) नाव = ………….. , …………..
(vi) सोना = ………….. , …………..
उत्तर:
पर्यायवाची/समानार्थक शब्द
(i) राजा = नृप, नरेश।
(ii) हाथी = गज, नाग।
(ii) पानी = अम्बू, नीर।
(iv) समुद्र = जलधि, वारिधि।
(v) नाव = नैया, नौका।
(vi) सोना = कनक, स्वर्ण।

VII. विराम चिह्न लगाओ

(i) कई दिन बीत गए पर राज्य में किसी भी व्यक्ति ने कोई उपाय नहीं सुझाया
(ii) परन्तु नाव हाथी कैसे तोलेगी महाराज ने प्रश्न किया
उत्तर:
(i) कई दिन बीत गए, पर राज्य में किसी भी व्यक्ति ने कोई उपाय नहीं सुझाया।
(ii) परन्तु नाव हाथी कैसे तोलेगी ?’ महाराज ने प्रश्न किया।

VIII. उपयुक्त अक्षर लगाकर पाठ में आए शब्द को पूरा करो.

1. मूल्य ___ न
2. उ. ___ य
3. सा ___ स
4. म ___ आ
5. क ___ चारी
6. श ___ ती
7. ___ हाज
8. ___ त।
उत्तर:
1. मूल्यवान
2. उदय।
3. साहस
4. मछुआ।
5. कर्मचारी
6. शहतीर।
7. महाराज।
8. शर्त।

IX. शब्द में से कम-से-कम दो शब्द ढूँढकर लिखो

उत्तर:
(1) निकालेगा-(i) निकाल, (ii) काले, (iii) कागा (iv) लेगा।
(2) तराजू-(i) तर (ii) राजू।
(3) सहायता-(i) हाय (ii) सह (iii) सहाय।
(4) दरबार-(i) दर (i) बार (iii) दरबा।
(5) मालामाल-(i) माल (ii) माला।
(6) महावत-(i) महा (i) हाव।

प्रयोगात्मक व्याकरण

राजा ने अपने मंत्रियों से कहा कि तुम में से जो भी हाथी को तोलने का उपाय बताएगा उसे मैं इनाम दूंगा। एक कर्मचारी ने राजा से कहा कि समुद्र के किनारे एक मछुआ रहता है। वह हाथी को तोलने का दावा करता है।

उपर्युक्त पंक्तियों में राजा, मन्त्री और मछुआ शब्द संज्ञा हैं। यहाँ राजा ने अपने लिए ‘मैं’, मन्त्रियों के लिए ‘तुम’ और ‘उसे’ तथा मछुए के लिए ‘वह’ शब्द का प्रयोग किया है। ये शब्द संज्ञा के स्थान पर आने के कारण सर्वनाम हैं।

अत: संज्ञा शब्दों के स्थान पर प्रयोग में आने वाले शब्द सर्वनाम कहलाते हैं। जैसे मैं, हम, आप, तुम, तू, वह, वे आदि। अन्य सर्वनाम शब्द :-उन्हें, उस, उसका, मेरा, हमारा, तेरा, तुम्हारा, अपना, स्वयं
आदि।

X. रेखांकित शब्दों के स्थान पर उचित सर्वनाम का प्रयोग करके वाक्य दोबारा लिखें।

प्रश्न 1.
हाथी को कैसे तोला जाए कि हाथी तोल के बराबर सोना तुल जाए।
उत्तर:
हाथी को कैसे तोला जाए कि उसके तोल के बराबर सोना तुल जाए।

प्रश्न 2.
राजा के पास एक हाथी था। राजा हाथी को बहुत प्यार करता था।
उत्तर:
राजा के पास एक हाथी था। वह उसको बहुत प्यार करता था।

प्रश्न 3.
एक राजा था। प्रजा राजा को बहुत चाहती थी।
उत्तर:
एक राजा था। प्रजा उसे बहुत चाहती थी।

प्रश्न 4.
मछुए ने कहा कि मछुआ हाथी को तोलूँगा।
उत्तर:
मछुए ने कहा कि मैं हाथी को तोलूँगा।

प्रश्न 5.
मछुए ने कहा कि राजा के सेवकों को सोना लाने की आज्ञा दें।
उत्तर:
मछुए ने कहा कि राजा अपने सेवकों को सोना लाने की आज्ञा दें।

बहुवैकल्पिक प्रश्न

पूछे गए प्रश्नों के सही विकल्प पर (✓) निशान लगाएं-

प्रश्न 1.
राजा के पास क्या था ?
(क) हाथी
(ख) सेना
(ग) वजीर
(घ) मंत्री।
उत्तर:
(क) हाथी

प्रश्न 2.
राजा को सबसे प्रिय क्या था ?
(क) सेना
(ख) धन-दौलत
(ग) मंत्री
(घ) हाथी।
उत्तर:
(घ) हाथी।

प्रश्न 3.
हाथी तोलने का दावा किसने किया ?
(क) मंत्री ने
(ख) सेनानायक ने
(ग) मछुए ने
(घ) रानी ने।
उत्तर:
(ग) मछुए ने

प्रश्न 4.
दुनिया में किसके बल पर प्रत्येक कार्य किया जा सकता है ?
(क) बुद्धि के
(ख) मन के
(ग) धन के
(घ) बल के।
उत्तर:
(क) बुद्धि के

हाथी कैसे तोला गया Summary

हाथी कैसे तोला गया पाठ का सार

बहुत समय पहले की बात है कि हमारे देश में एक राजा राज्य करता था। प्रजा उसे बहुत चाहती थी। उसके पास एक हाथी था, जिसे वह बहुत प्यार करता था। एक बार उसके राज्य में सूखा पड़ा। बहुत समय तक वर्षा न होने के कारण अनाज पैदा न हुआ और लोग दुःखी रहने लगे। राजा ने लोगों के लिए अनाज के भण्डार खोल दिए। उसने ग़रीबों की सहायता के लिए अपने प्रिय हाथी के भार के बराबर सोना तोल कर ग़रीबों में बाँटने का निश्चय किया। पर एक उलझन यह थी कि इतने बड़े हाथी का भार कैसे तोला जाए ? उन दिनों भार तोलने की इतनी बड़ी मशीनें नहीं थीं। तब राजा ने प्रजा में यह घोषणा करवाई कि जो मनुष्य हाथी को तोलने का तरीका बतलाएगा, उसे वह सोने से भरी दस थैलियाँ इनाम में देगा।

बहुत-से लोगों ने सोचा लेकिन हाथी को तोलने का कोई उपाय न सूझा। अन्त में एक सेवक ने आकर बताया कि एक मछुआ हाथी को तोलने के लिए तैयार है। राजा अपने सेवकों के साथ हाथी को लेकर मछुआरे के पास गया। मछुआरे ने कहा कि पहले एक बड़ी नाव बनाई जाए। मछुआरे तथा राजा के सेवकों ने मिलकर सौ दिन मेहनत करके एक नाव तैयार की। उस नाव को समुद्र में उतारा गया। हाथी को नाव पर चढ़ाया गया। नाव का बहुत-सा भाग पानी में डूब गया। जहाँ तक नाव पानी में डूबी मछुआरे ने वहाँ निशान लगा लिया। फिर हाथी को नाव से उतार कर सोना भर दिया गया। जब निशान वाले स्थान तक नाव पानी में डूब गई तब मछुए ने कहा यही हाथी के भार के बराबर सोना है। मछुए की सूझ-बूझ देखकर सब हैरान हुए। सभी ने उसकी प्रशंसा की। राजा ने उसे पुरस्कार दिया।

कठिन शब्दों के अर्थ:

अत्यधिक = बहुत ज़्यादा। मूल्यवान् = कीमती। अचम्भित = हैरान। अंकश = लोहे की छोटी नुकीली छड, हाथी को काब में रखने का शस्त्र। कर्मचारी = काम करने वाला। विधि = तरीका। लश्कर = सेना। महावत = हाथी को हाँकने वाला। सहस्त्र = हज़ार। दृश्य = नज़ारा। चिह्न = निशान। असमर्थ = लाचार।

Punjab State Board PSEB 5th Class Hindi Book Solutions Chapter 7 वैशाखी आई रे Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Hindi Chapter 7 वैशाखी आई रे

Hindi Guide for Class 5 PSEB वैशाखी आई रे Textbook Questions and Answers

I. बताओ

प्रश्न 1.
पंजाब में फ़सलों की कटाई से जुड़ा कौन-सा त्योहार मनाया जाता है ?
उत्तर:
पंजाब में फ़सलों की कटाई से जुड़ा त्योहार वैशाखी मनाया जाता है।

प्रश्न 2.
जलियाँवाले बाग़ में किसने गोलियाँ चलाई थीं ?
उत्तर:
जलियाँवाले बाग़ में जरनल डायर ने गोलियाँ चलाई थीं।

प्रश्न 3.
आनन्दपुर साहिब में गुरु गोबिन्द सिंह जी ने किसकी स्थापना की थी ?
उत्तर:
आनन्दपुर साहिब में गुरु गोबिन्द सिंह जी ने खालसा पंथ की स्थापना की थी।

प्रश्न 4.
वैशाखी पर किसान अपनी खुशी कैसे प्रकट करता है ?
उत्तर:
वैशाखी पर किसान भंगड़ा करके, गहनों, कपड़ों आदि की खरीदारी करके अपनी खुशी प्रकट करता है।

प्रश्न 5.
पंजाब में वैशाखी पर कौन-सा गीत गाया जाता है ?
उत्तर:
पंजाब में वैशाखी पर गाया जाने वाला गीत है ‘कनकां दी मुक गई राखी ओ जट्टा आई वैशाखी।’

II. अपने अध्यापक से

(1) जलियाँवाले बाग़ की घटना सुनो।
(2) धर्म की रक्षा के लिए गुरु गोबिन्द सिंह जी द्वारा स्थापित ‘खालसा पंथ’ की जानकारी प्राप्त करो।
(3) सिक्ख धर्म के दस गुरुओं के नाम लिखो और उनके बारे में जानकारी प्राप्त करो।
उत्तर:
1 और 2 के लिए विद्यार्थी अपने कक्षा अध्यापक से जानकारी प्राप्त करें।

(3) सिक्ख धर्म के दस गुरुओं के नाम इस प्रकार हैं-

• श्री गुरु नानक देव जी
• श्री गुरु अंगद देव जी
• श्री गुरु अमरदास जी
• श्री गुरु रामदास जी
• श्री गुरु अर्जन देव जी
• श्री गुरु हरिगोबिन्द जी
• श्री गुरु हरिराय जी
• श्री गुरु हरिकृष्ण जी
• श्री गुरु तेग़ बहादुर जी
• श्री गुरु गोबिन्द सिंह जी।

III. सरलार्थ करो

पंथ खालसा सिरजन हेतु
बना आनन्दपुर सांखी
अमृत छकाकर, सिंह सजाकर
जन-जन की चेतना जगाई रे
वैशाखी आई रे …………..
उत्तर:
कवि कहता है कि हम कैसे भूल सकते हैं सन् सोलह सौ निनयानवें का वैशाखी वाला वह दिन, जब कलगीधर दशम गुरु श्री गुरु गोबिन्द सिंह जी ने धर्म की रक्षा के लिए आनन्दपुर साहिब में खालसा पंथ की सृजना की थी। आनन्दपुर साहिब इस बात का प्रत्यक्ष साक्षी है जब अमृत पिलाकर पाँच ‘सिंह’ सजाकर जन-जन में एक नई चेतना जगाई थी।

IV. वैशाखी पर लगने वाले मेले का आनन्द लें। अपनी डायरी में लिखें आपने वैशाखी का त्योहार कैसे मनाया ?

कवि कहता है कि वैशाखी का त्योहार आया है और अपने साथ हज़ारों पुरानी यादों को भी लाया है। वैशाखी का यह त्योहार हमें जलियाँवाले बाग़ की उस मिट्टी की याद दिलाता है जहाँ अपने प्यारे भारत देश की आजादी की माँग करने वाले हज़ारों लोग शहीद कर दिए गए। याद आता है वह शहीदी कुआँ जहाँ जनरल डायर की गोलियों से बचने के लिए हज़ारों लोग कुएँ में कूद कर जान गँवा बैठे। वैशाखी वाले दिन याद आता है जब बच्चों, बूढ़ों और जवानों ने देश को आजाद करवाने के लिए अपने सीने पर गोलियाँ खाई थीं।

V. (क) योग्यता विस्तार

जलियाँवाला बाग़-जलियाँवाला बाग़ अमृतसर में स्थित है। 13 अप्रैल, सन् 1919 को इस बाग़ में एक सभा का आयोजन किया गया था। जब लोग, अपने नेताओं के विचार सुन रहे थे, तभी एक अंग्रेज़ अफसर जनरल डायर अपनी सशस्त्र सेना के साथ बाग़ में दाखिल हुआ और उसने फौज को गोलियाँ चलाने का आदेश दिया। उन्होंने चीखते-चिल्लाते, भागते हए, दीवारों पर चढ़ते हए, कूदते हए, निहत्थे लोगों को निशाना बनाया। देश की स्वाधीनता के लिए हज़ारों की संख्या में लोग शहीद हुए। उन शहीदों के बलिदान ने देश को आजादी दिलाई।

खूनी कुआँ – जलियाँवाला बाग़ में स्थित एक कुआँ है जिसे खुनी कुआँ कहा जाता है। जब जनरल डायर ने जलियाँवाला बाग़ में सभा में बैठे लोगों पर गोलियां चलाईं तो लोग जान बचाने के लिए इस कुएँ में कूद गए और मर गए। कहते हैं कि कुओं लाशों से भर गया था। इसलिए इसे खूनी कुआँ कहा जाता है।

खालसा पंथ – सिक्खों के दसवें गुरु गोबिन्द सिंह जी ने आनन्दपुर साहिब में सन् 1699 में वैशाखी के दिन एक विशाल दीवान का आयोजन किया था। गुरु जी ने धर्म की रक्षा के लिए ‘पाँच प्यारों’ का चुनाव किया था। यह पाँच प्यारे अलग-अलग धर्मों और प्रदेशों के थे। लाहौर का भाई दयाराम, हस्तिनापुर का भाई धर्मराय, द्वारिका का भाई मोहकम चन्द, बिदर का भाई साहिब चन्द और पुरी का भाई हिम्मत राय। गुरु जी ने इन्हें ‘पाँच प्यारों’ के नाम से पुकारा।

(ख) योग्यता विस्तार

जैसे पंजाब में किसान और कृषि से जुड़ा त्योहार वैशाखी मनाया जाता है, उसी प्रकार दक्षिण भारत के तमिलनाडु और आन्ध्र प्रदेश में जनवरी माह में मकर संक्राति के अवसर पर कृषि से सम्बन्धित पोंगल त्योहार मनाया जाता है। जैसे पंजाब में किसान गेहूँ की फ़सल की कटाई शुरू करते हैं, उसी प्रकार तमिलनाडु में (धान) की फ़सल की कटाई शुरू होती है। वैशाखी से भारतीय सम्वत् शुरू होता है, इसे नव वर्ष के रूप में मनाया जाता है।

बहुवैकल्पिक प्रश्न

पूछे गए प्रश्नों के सही विकल्प पर (✓) निशान लगाएं

प्रश्न 1.
वैशाखी हमें किसकी याद दिलाती है ?
(क) वीरों की
(ख) देशभक्तों की
(ग) जलियाँवाला बाग की
(घ) अंग्रेजों की।
उत्तर:
(ग) जलियाँवाला बाग की

प्रश्न 2.
गुरु गोबिन्द सिंह जी ने किस पंथ की स्थापना की ?
(क) खालसा
(ख) चालीसा
(ग) वीर
(घ) वीरांगना।
उत्तर:
(क) खालसा

प्रश्न 3.
खालसा पंथ की स्थापना किस दिन हुई थी ?
(क) होली
(ख) दीवाली
(ग) वैशाखी
(घ) लोहड़ी।
उत्तर:
(ग) वैशाखी

प्रश्न 4.
आज़ादी हमारा क्या है ?
(क) सपना
(ख) अधिकार
(ग) अपना
(घ) धन।
उत्तर:
(ख) अधिकार

प्रश्न 5.
वैशाखी त्योहार किसकी कटाई से जुड़ा है ?
(क) पेड़ों
(ख) फसलों
(ग) सड़कों
(घ) वनों।
उत्तर:
(ख) फसलों

प्रश्न 6.
जलियाँवाला बाग में किसने गोलियां चलाई थीं ?
(क) जनरल डायर
(ख) जनरल हायर
(ग) जनरल फेयर
(घ) मेयर।
उत्तर:
(क) जनरल डायर

वैशाखी आई रे Summary

वैशाखी आई रे पाठ का सार

हर वर्ष वैशाखी आती है। वह अपने साथ अनेक यादें लेकर आती है। यह हमें जलियांवाला बाग की याद दिलाती है। अंग्रेज अधिकारी डायर के जुल्म और खूनी कुएँ की यादें इसी से जुड़ी हुई हैं। आज़ादी के अधिकार को पाने के लिए इसी दिन बच्चों, युवकों और बूढ़ों ने अपने सीने पर गोलियां खाई थीं। इसी दिन ही तो गुरु गोबिन्द सिंह जी ने खालसा पंथ की स्थापना की थी। वैशाखी का दिन ही तो है | जब किसान अपनी पकी फसलों की कटाई कंबाइनों से करने लगते हैं। इस खुशी में भंगड़े, गिद्दे, मेलों, नए कपड़ों और गहनों की खरीद की धूम-सी मच जाती है।

पद्यांशों के सरलार्थ

1. वैशाखी आई रे, वैशाखी आई रे
यादें हज़ारों साथ लाई रे ……….
वैशाखी है याद दिलाती
जलियाँवाला बाग़ की माटी
आज़ादी अधिकार हमारा हमें
अपना देश है प्यारा,
खूनी कुआँ जो है कहलाता
डायर का वह जुल्म बताता
बच्चे, बूढ़े और युवकों ने
सीने पे गोली खाई रे
वैशाखी आई रे ……….॥

कठिन शब्दों के अर्थ :
माटी = मिट्टी। अधिकार = हक। जुल्म = अत्याचार।

प्रसंग:
प्रस्तुत पंक्तियाँ हमारी पाठ्य-पुस्तक में संकलित कविता ‘वैशाखी आई रे’ से ली गई हैं। इस कविता में कवि ने वैशाखी पर्व के आगमन का स्वागत करते हुए इसकी ऐतिहासिक महत्ता को भी बताने का प्रयास किया है।

सरलार्थ:
कवि कहता है कि वैशाखी का त्योहार आया है और अपने साथ हज़ारों पुरानी यादों को भी लाया है। वैशाखी का यह त्योहार हमें जलियाँवाले बाग़ की उस मिट्टी की याद दिलाता है जहाँ अपने प्यारे भारत देश की आजादी की माँग करने वाले हज़ारों लोग शहीद कर दिए गए। याद आता है वह शहीदी कुआँ जहाँ जनरल डायर की गोलियों से बचने के लिए हज़ारों लोग कुएँ में कूद कर जान गँवा बैठे। वैशाखी वाले दिन याद आता है जब बच्चों, बूढ़ों और जवानों ने देश को आजाद करवाने के लिए अपने सीने पर गोलियाँ खाई थीं।

भावार्थ:
कवि ने उपरोक्त पद में उल्लासमय त्योहार वैशाखी के अवसर पर उसकी ऐतिहासिक महत्ता को भी दर्शाया है।

2. कैसे भुलाएं सन सोलह सौ
निनानवें की वो वैशाखी
कलगीधर दशमेश पिता ने
करने को जब धर्म की राखी
पंथ खालसा सिरजन हेतु
बना आनन्दपुर साखी
अमृत छकाकर सिंह सजाकर
जन-जन की चेतना जगाई रे
वैशाखी आई रे ………..

कठिन शब्दों के अर्थ:
कलगीधर = कलगी धारण करने वाले। दशमेश = दशम (दसवें) गुरु। सिरजन = सृजना, रचना, स्थापना। राखी = रक्षा। हेतु = लिए। साखी = साक्षी, गवाह, प्रमाण।। छकाकर = पिलाकर।

प्रसंग:
प्रस्तुत पंक्तियाँ हमारी पाठ्य-पुस्तक में संकलित कविता ‘वैशाखी आई रे’ से ली गई हैं। इस कविता में कवि ने वैशाखी पर्व के आगमन का स्वागत करते हुए इसकी ऐतिहासिक महत्ता को भी बताया है।

सरलार्थ:
कवि कहता है कि हम कैसे भूल सकते हैं सन् सोलह सौ निनयानवें का वैशाखी वाला वह दिन, जब कलगीधर दशम गुरु श्री गुरु गोबिन्द सिंह जी ने धर्म की रक्षा के लिए आनन्दपुर साहिब में खालसा पंथ की सृजना की थी। आनन्दपुर साहिब इस बात का प्रत्यक्ष साक्षी है जब अमृत पिलाकर पाँच ‘सिंह’ सजाकर जन-जन में एक नई चेतना जगाई थी।

भावार्थ:
वैशाखी पर्व की ऐतिहासिक महत्ता बताते हए खालसा पंथ की स्थापना के बारे में बताया है।

3. खत्म हई फ़सलों की राखी
देख ले जट्टा आई वैशाखी
कंबाइनों से फ़सल कटी है
मण्डी में वह आन बिकी है
धूम मची है अब मेलों की
भंगड़े गिददे और खेलों की
कपड़े लत्ते और गहनों की
खरीदारी ने धम मचाई रे
वैशाखी आई रे …………….

कठिन शब्दों के अर्थ:
खत्म = समाप्त। राखी = रक्षा। कंबाइनों = फ़सल काटने वाली मशीन। धूम मचाना = रौनक होना।

प्रसंग:
प्रस्तुत पंक्तियाँ हमारी पाठ्य-पुस्तक में संकलित कविता ‘वैशाखी आई रे’ से ली गई हैं। इस कविता में कवि ने वैशाखी पर्व का स्वागत करते हुए कहा है।

सरलार्थ:
वैशाखी आने का स्वागत करते हुए कवि कहता है कि अब फ़सलों की राखी (रखवाली) समाप्त हुई ओ जट्टा (किसान भाई) वैशाखी आई है। कंबाइनों से फ़सल कट गई है और सारी फ़सल मंडी में आकर बिकने लगी है। मेलों की धूम मच गई है। भंगड़े, गिद्दे और खेलों की धूम मच गई है। कपड़ों की तथा गहनों की खरीदारी ने धूम मचा दी है। चारों तरफ खुशियों का माहौल है। वैशाखी का त्योहार आया है। .

भावार्थ:
वैशाखी के त्योहार में होने वाले मेलों, उत्सवों, खेलों व रौनक मेले का वर्णन किया है।

Punjab State Board PSEB 5th Class Hindi Book Solutions Chapter 8 भाखड़ा बाँध Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Hindi Chapter 8 भाखड़ा बाँध

Hindi Guide for Class 5 PSEB भाखड़ा बाँध Textbook Questions and Answers

I. बताओ

प्रश्न 1.
बाँध किसे कहते हैं ?
उत्तर:
बाँध वह निर्माण है जिसके द्वारा नदियों के पानी को बाँध कर अथवा इकट्ठा करके आवश्यकता के समय उपयोग में लाया जाता है।

प्रश्न 2.
भाखड़ा बाँध किस नदी पर बनाया गया है?
उत्तर;
भाखड़ा बाँध सतलुज नदी पर बनाया गया है।

प्रश्न 3.
भाखड़ा बाँध की ऊँचाई कितनी है ?
उत्तर:
भाखड़ा बाँध की ऊँचाई 226 मीटर है।

प्रश्न 4.
‘गोबिन्द सागर’ झील का नाम किस गुरु के नाम पर रखा गया है ?
उत्तर:
गोबिन्द सागर झील का नाम दशम गुरु श्री गुरु गोबिन्द सिंह जी के नाम पर रखा गया है।

प्रश्न 5.
किस नहर पर और कहाँ दो बिजली घर बनाए गए हैं ?
उत्तर:
सतलुज नहर पर गंगूवाल और कोटला नामक स्थानों पर दो बिजलीघर बनाए गए हैं।

प्रश्न 6.
भाखड़ा बाँध से किस-किस राज्य को सिंचाई के लिए पानी मिलता है?
उत्तर:
भाखड़ा बाँध से पंजाब, हरियाणा और राजस्थान को सिंचाई के लिए पानी मिलता है।

प्रश्न 7.
पंडित जवाहर लाल नेहरू ने इसे कब राष्ट्र को समर्पित किया था ?
उत्तर:
पंडित जवाहर लाल नेहरू ने इसे 22 अक्तूबर, सन् 1963 को राष्ट्र को समर्पित किया था।

II. इन प्रश्नों के उत्तर चार-पाँच वाक्यों में लिखो

प्रश्न 1.
कैसा स्थान बाँध बनाने के लिए उपयुक्त समझा जाता है ?
उत्तर:
दो पहाड़ों के बीच का संकरा रास्ता, जहाँ नदी के पानी को आसानी से इकट्ठा किया जा सके, बाँध बनाने के लिए उपयुक्त स्थान समझा जाता है।

प्रश्न 2.
गोबिन्द सागर झील की सुन्दरता का वर्णन करो।
उत्तर:
तीन ओर से पहाड़ों से घिरी हरी-भरी घाटियाँ. ऊँचे-ऊँचे वक्षों की पंक्तियाँ और बीच में लहराता हुआ जल गोबिन्द सागर झील की सुन्दरता का अनुपम दृश्य उपस्थित करता है। दर्शकों का मन तो इस प्राकृतिक सौन्दर्य की छटा को देखकर मुग्ध हो उठता है।

प्रश्न 3.
भाखड़ा बाँध के निर्माण से पंजाब के पड़ोसी राज्यों को क्या-क्या लाभ हुए हैं ?
उत्तर:
भाखड़ा बाँध के निर्माण से पंजाब के साथ-साथ पड़ोसी राज्यों हरियाणा और राजस्थान को भी खूब लाभ मिला है। इन्हें सिंचाई के लिए पानी मिलता है जिस कारण इन राज्यों की उपज भी दोगुनी हो गई है। पहले जहाँ इन स्थानों में भूमि रेतीली और बंजर नज़र आती थी अब वहाँ फ़सलें लहलहाती नज़र आ रही हैं।

III. वाक्य पूरे करो-

(i) भाखड़ा बाँध …………. पहला बाँध है।
(ii) यह आनन्दपुर साहिब से . सतलुज नदी पर बनाया गया है।
(iii) भाखड़ा बाँध ………………. में से एक है।
(iv) भाखड़ा बाँध बनने से ………….. दृष्टिगोचर होते हैं।
(v) भाखड़ा बाँध …………………… गौरव है।
उत्तर:
(i) स्वतन्त्र भारत में बनाया गया
(ii) लगभग तीस किलोमीटर की दूरी पर
(iii) एशिया के सबसे ऊँचे बाँधों
(iv) पंजाब और हरियाणा में चारों ओर लहलहाते खेत
(v) हमारे देश का।

IV. वाक्यों में प्रयोग करो

स्वर्गीय, प्राकृतिक, तीर्थ, आधुनिक, सौन्दर्य, दृष्टिगोचर, सोना उगलना।
उत्तर:
स्वर्गीय-स्वर्गीय पं० जवाहर लाल नेहरू भारत के प्रथम प्रधानमन्त्री थे।
प्राकृतिक-शिमला का प्राकृतिक सौन्दर्य अनूठा है।
तीर्थ-अमृतसर पंजाब का एक प्रमुख तीर्थ स्थल है।
आधुनिक-भाखड़ा बाँध को पं० नेहरू ने आधुनिक तीर्थ स्थल कहा।
सौन्दर्य-पहाड़ों में प्रकृति का सौन्दर्य दर्शनीय है।
दृष्टिगोचर-पंजाब के खेतों में हरियाली ही हरियाली दृष्टिगोचर होती है।
सोना उगलना-पंजाब की उपजाऊ धरती सोना उगलती है।

V. पढ़ो, समझो और लिखो

(i) बहना = बहाव
(ii) चुनना = ……….
(iii) दबना = ………..
(iv) सींचना = सिंचाई
(v) चढ़ना = ……….
(vi) पढ़ना = …………
उत्तर:
(i) बहना = बहाव।
(ii) चुनना = चुनाव।
(iii) दबना = दबाव।।
(iv) सींचना = सिंचाई।
(v) चढ़ना = चढाई।
(vi) पढ़ना = पढ़ाई।

VI. शुद्ध शब्द पर गोला लगाओ:

(i) उदोयोग – उद्योग – उदयोग
(ii) समरीध – समृद्ध – समृद्ध
(iii) समरपित – समर्पित – समीत
(iv) द्रिष्टि – दरिष्टि – दृष्टि
(v) उपस्थित – उपस्थीत – उपस्थिति
उत्तर:
शुद्ध शब्द
(i) उद्योग!
(ii) समृद्ध।
(iii) समर्पित।
(iv) दृष्टि।
(v) उपस्थित।

VII. अनेक शब्दों के स्थान पर एक शब्द लिखो.

(i) किसी देश का सबसे बड़ा मन्त्री = प्रधानमन्त्री
(ii) नदी के पानी को बाँधना/रोकना = ……………..
(iii) सुख सुविधाओं से परिपूर्ण = ……………..
(iv) ज़मीन के नीचे खोदकर बनाई हुई नाली = ……………..
(v) सैलानियों के घूमने-फिरने का स्थान = ……………..
(vi) वह भूमि जो खेती योग्य न हो = ……………..
(vii) वह भूमि जिस पर भरपूर फ़सल हो = ……………..
(viii) पशुओं के चरने की जगह = ……………..
(ix) मृत्यु को प्राप्त = ……………..
उत्तर:
(i) किसी देश का सबसे बड़ा मन्त्री = प्रधानमन्त्री।
(ii) नदी के पानी को बांधना/रोकना = बाँध।
(iii) सुख-सुविधाओं से परिपूर्ण = समृद्ध।
(iv) जमीन के नीचे खोदकर बनाई हुई नाली = सुरंग।
(v) सैलानियों के घूमने-फिरने का स्थान = पर्यटन स्थल।
(vi) वह भूमि जो खेती योग्य न हो = बंजर।
(vii) वह भूमि जिस पर भरपूर फसल हो = ऊसर/ उपजाऊ।
(viii) पशुओं के चरने की जगह = चारागाह।
(ix) मृत्यु को प्राप्त = मृत।

VIII. निम्नलिखित गद्यांश में आए संज्ञा शब्दों पर गोला तथा सर्वनाम शब्दों को रेखांकित करें

भाखड़ा बाँध पर काम करने वाले मजदूरों तथा इंजीनियरों की सुविधा के लिए विशेष रूप से एक बस्ती बनाई गई है। यह बस्ती नया नंगल के नाम से प्रसिद्ध है। यह स्थान भाखड़ा से तेरह किलोमीटर की दूरी पर है और बाँध के सबसे समीप पड़ता है। इसी स्थान पर सतलुज नदी पर एक छोटा बाँध और बनाया गया है। इससे एकनिहर निकाली गई है, जिस पर दो बिजली घर गंगुवाल तथा कोटला नामक स्थानों पर बनाए गए हैं।

IX. पढ़ो, समझो और लिखो

(क) ‘समर्पित’ शब्द में मूल शब्द समर्पण है। उसमें ‘इत’ शब्दांश जोड़ कर समर्पित शब्द बना है। इसी प्रकार नए शब्द बनाएँ-
(i) समर्पण + इत = समर्पित
(ii) प्रवाह + इत = ……………..
(iii) सम्मान + इत = …………….
(iv) एकत्र + इत = …………….
(v) निर्माण + इत = …………..
(vi) अनुमान + इत = …………
उत्तर:
इत’ प्रत्यय लगाकर बनाए गए शब्द
(i) समर्पण + इत = समर्पित।
(ii) प्रवाह + इत = प्रवाहित।
(iii) सम्मान + इत = सम्मानित।
(iv) एकत्र + इत = एकत्रित।
(v) निर्माण + इत = निर्माणित।
(vi) अनुमान + इत = अनुमानित।

प्रयोगात्मक व्याकरण

(ख) विशेषण-
उदाहरण-

1. हरी भरी घाटियाँ तथा ऊँचे-ऊँचे वृक्ष दिखाई दे रहे थे।
2. हज़ारों मजदूरों की मेहनत रंग लाई।
3. रेतीली भूमि में भी फ़सलें लहलहाने लगी हैं।।
4. यह ऊँचा है।

उपर्युक्त वाक्यों में ‘हरी भरी’ शब्द घाटियों (संज्ञा) की ‘ऊँचे-ऊँचे’ शब्द वृक्ष (संज्ञा) की, ‘हज़ारों’ शब्द मज़दूरों (संज्ञा) की, ‘रेतीली’ शब्द भूमि (संज्ञा) की तथा ‘ऊँचा’ शब्द ‘यह’ सर्वनाम की विशेषता बता रहा है।

परिभाषा-संज्ञा या सर्वनाम की विशेषता बताने वाले शब्दों को विशेषण कहते हैं।

निम्नलिखित में से विशेषण शब्द छाँटिए।
1. अनेक यात्री भाखड़ा बाँध की सैर करने आते हैं।
2. इसके लिए दो सुरंगें खोदी गईं।
3. अब बंजर भूमि सोना उगलने लगी है।
4. कँटीली झाड़ियाँ नजर आ रही हैं।
5. प्रथम प्रधानमन्त्री जवाहरलाल नेहरू का सपना साकार हुआ।
उत्तर:
विशेषण शब्द
(1) अनेक।
(2) दो।
(3) बंजर।
(4) कँटीली
(5) प्रथम।

बहुवैकल्पिक प्रश्न

पूछे गए प्रश्नों के सही विकल्प पर (✓) निशान लगाएं

प्रश्न 1.
भाखड़ा बाँध की ऊँचाई कितनी है ?
(क) 255 मीटर
(ख) 226 मीटर
(ग) 227 मीटर
(घ) 228 मीटर।
उत्तर:
(ख) 226 मीटर

प्रश्न 2.
भाखड़ा बाँध किस नदी पर बनाया गया है ?
(क) गंगा
(ख) यमुना
(ग) सतलुज
(घ) गोदावरी।
उत्तर:
(ग) सतलुज

प्रश्न 3.
भाखड़ा बाँध से किस राज्य को सिंचाई के लिएं पानी मिलता है ?
(क) पंजाब
(ख) हरियाणा
(ग) राजस्थान
(घ) तीनों को।
उत्तर:
(घ) तीनों को।

प्रश्न 4.
भाखड़ा बाँध का उद्घाटन कब हुआ ?
(क) 22 अक्तूबर 1963
(ख) 22 अक्तूबर 1964
(ग) 22 अक्तूबर 1965
(घ) 22 अक्तूबर 1966.
उत्तर:
(ख) 22 अक्तूबर 1964

प्रश्न 5.
आनंदपुर साहिब से भाखड़ा बाँध की दूरी लगभग कितने कि०मी० है ?
(क) 20
(ख) 25
(ग) 30
(घ) 35
उत्तर:
(ग) 30

प्रश्न 6.
भाखड़ा बाँध हमारे देश का क्या है ?
(क) गौरव
(ख) बाँध
(ग) सागर
(घ) सब कुछ।
उत्तर:
(क) गौरव

प्रश्न 7.
भाखड़ा बाँध के लिए बनाई झील का क्या नाम है ?
(क) गोबिन्द सागर
(ख) गोबिन्द झील
(ग) गोबिन्द नदी
(घ) गोबिन्द बिन्दू।
उत्तर:
(क) गोबिन्द सागर

भाखड़ा बाँध Summary

भाखड़ा बाँध पाठ का सार

भारत का आधुनिक तीर्थ भाखड़ा बाँध हमारे देश की स्वतन्त्रता प्राप्ति के बाद बनाया गया सबसे पहला बाँध है। नदियों के पानी को इकट्ठा कर बाँध की सहायता से उपयोग में लाया जाता है। भाखड़ा बाँध चण्डीगढ़ से एक सौ पन्द्रह किलोमीटर दूर है। इसे आनन्दपुर से लगभग तीस किलोमीटर दूर सतलुज पर बनाया गया है। यहाँ सतलुज दो पहाड़ों के बीच में से गुज़रती है। बाँध बनाने से पहले दो सुरंगें खोदकर नदी का पानी इनसे निकाला गया था। यह बाँध एशिया के सबसे ऊँचे बाँधों में से एक है जिस की ऊँचाई 226 मीटर है। यह कुतुब मीनार से तीन गुणा ऊंचा है। इसके लिए बनाई गई झील का नाम गुरु गोबिन्द सिंह जी के नाम पर गोबिन्द सागर’ रखा गया है। इससे एक नहर निकालकर उस पर दो बिजली घर बनाए गए हैं। इससे सिंचाई के लिए। पानी प्राप्त होता है। इससे पंजाब, हरियाणा और राजस्थान में फसलें लहलहाने लगी हैं। इससे प्राप्त बिजली का उपयोग उद्योगों के विकास के लिए किया गया है। यह बाँध हमारे देश का गौरव है।

कठिन शब्दों के अर्थ:

स्वतन्त्र = आज़ाद। आधुनिक = आजकल का, नवीन। निर्माण = बनाना, रचना। सम्पन्न = धनी, उन्नतिशील। आवश्यकता = ज़रूरत। उद्योग-धन्धे = ऐसे धन्धे जिनके द्वारा कुछ उत्पादन किया जा सके। संकरे = तंग। उपयुक्त = उचित, ठीक। प्रवाह = बहाव। अनुपम = जिसकी कोई उपमा न हो। दर्शक = देखने वाला। प्राकृतिक = कुदरती। सौन्दर्य = सुन्दरता। मुग्ध = प्रसन्न। पर्यटन स्थल = घूमने का स्थान। दृष्टिगोचर = नज़र आना। चरागाह = पशुओं के चराने के लिए बने घास के मैदान। अधिकांश = ज़्यादा भाग। विकास = उन्नति। समृद्ध = खुशहाल, सम्पन्न। सहस्त्रों = हज़ारों। अथक = जो कभी न थके। गौरव = बड़प्पन। स्वर्गीय = जिसकी मृत्यु हो चुकी हो। समर्पित = समर्पण करना, सौंप देना।

Punjab State Board PSEB 5th Class Hindi Book Solutions Chapter 9 गलती छिपाने की सजा Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Hindi Chapter 9 गलती छिपाने की सजा

Hindi Guide for Class 5 PSEB गलती छिपाने की सजा Textbook Questions and Answers

I. बताओ

प्रश्न 1.
अपनी ग़लती स्वीकार कर लेने में क्या समझदारी है ?
उत्तर:
अपनी ग़लती स्वीकार कर लेने में समझदारी है क्योंकि इससे सबका विश्वास बना रहता है।

प्रश्न 2.
कुश के पापा से बचपन में ग़लती से क्या टूट गया था ?
उत्तर:
बचपन में कुश के पापा से इटली से मँगवाई गई काँच की ट्रे टूट गई थी।

प्रश्न 3.
उन्होंने अपनी ग़लती छिपाने की क्या कोशिश की थी ?
उत्तर:
उन्होंने अपनी ग़लती छिपाने के लिए ट्रे के टुकड़े उठाकर कूड़ेदान में फेंक दिए और घर में किसी को बताया नहीं।

प्रश्न 4.
कुश की बुआ उसके पापा को बचपन में क्यों ब्लैकमेल करती थी ?
उत्तर:
कुश के पापा ने बचपन में ट्रे के टूटने की ख़बर किसी को नहीं दी थी लेकिन उसकी बहन ने उसे ऐसा करते हुए देख लिया था। वह इसी बात का फ़ायदा उठा कर उसे ब्लैकमेल करती थी।

प्रश्न 5.
कश के पापा ने अपनी बहन की ब्लैकमेलिंग से कैसे छुटकारा पाया ?
उत्तर:
अपनी बहन की ब्लैकमेलिंग से परेशान होकर कुश के पापा ने अपने दादा जी को ट्रे वाली सारी बात बता दी और अपनी बहन की ब्लैकमेलिंग से छुटकारा पाया।

प्रश्न 6.
कुश के पापा अपने बचपन की बात के द्वारा कुश को क्या सिखाना चाहते थे ?
उत्तर:
कुश के पापा अपने बचपन की बात के द्वारा कुश को सिखाना चाहते थे कि जीवन में ग़लती सबसे हो ही जाती है, लेकिन उस ग़लती को छिपाना नहीं चाहिए बल्कि सबको विश्वास में लेकर अपनी ग़लती मान लेनी चाहिए। इससे सबका विश्वास बना रहता है और कोई भी उस ग़लती की आड़ में उसे ब्लैकमेल नहीं कर पाता।

प्रश्न 7.
कुश ने अपने पापा से अपनी कौन-सी ग़लती स्वीकार की और क्यों ?
उत्तर:
कुश ने फ्रिज़ में से आईसक्रीम चोरी से निकाल कर खाने की ग़लती अपने पापा के सामने स्वीकार की।

II. निम्नलिखित मुहावरों के वाक्य बनायें

मुहावरा	अर्थ	वाक्य
(i) राहत की साँस लेना	चैन मिलना	चोरी का सारा सामान ठिकाने लगा कर चोरों ने राहत की साँस ली।
(ii) आँखें तरेरना	क्रोध से देखना	सेठ ने गुस्से में आँखें तरेर कर नौकर को देखा तो नौकर सकपका गया।
(iii) खून का चूंट पीकर रह जाना	अत्यधिक क्रोध का आवेश सह लेना	मैं बेबसी में खून का चूंट पीकर रह गया।
(iv) आनाकानी करना	किसी काम को करने से हिचकिचाना	मैंने रमेश से अपनी पुस्तक माँगी तो वह देने में आनाकानी करने लगा।
(v) दब्बू बनना	डरपोक बनना	पिता जी के अत्यधिक आक्रोश के चलते मोहन दब्बू बन कर रह गया।
(vi) तंग आना	परेशान होना	मैं तुम्हारी हरकतों से तंग आ गया हूँ।
(vii) पानी सिर के ऊपर से निकल जाना	किसी बात की हद हो जाना	पानी सिर के ऊपर से निकलता देख मंटू ने सारी बात अपने पिता को सच-सच बता दी।
(viii) हाथ बंटाना	सहायता करना	हमें अपने माता-पिता के कामों में हाथ बँटाना चाहिए।
(ix) उधेड़बुन में बैठे रहना	चिन्ता में रहना, फिक्र करना	दिन रात मैं इसी उधेड़बुन में लगा रहा कि यह कार्य कैसे पूरा कर सकूँगा।
(x) आसमान से धरती पर आ गिरना	कल्पना लोक से निकल कर यथार्थ में आना	कल्पना की दुनिया में विचरने वाली सुनीता का सच्चाई से जब सामना हुआ तो मानों वह आसमान से धरती पर आ गिरी।
(xi) दादागिरी सहन करना	किसी का जुल्म सहना	“मोहन ! मैं तुम्हारी दादागिरी अब और सहन नहीं करूँगा।”
(xii) सिर झुकाकर खड़ा हो जाना	शर्म से गर्दन झुकाकर खड़े हो जाना	चोरी पकड़े जाने पर नौकर सेठ के सामने सिर झुकाकर खड़ा हो गया।

III. इस पाठ में अंग्रेजी और फ़ारसी के शब्दों का प्रयोग भी हुआ है। कम-से-कम पाँच ऐसे शब्दों को चुनकर लिखें

अंग्रेजी के शब्द – फ़ारसी के शब्द
स्कूल – ग़लतफहमी
ब्लैकमेलिंग – ग़लती
ट्रे शॉट – हादसा। खुद
गैलरी – आईसक्रीम
रोज़मर्रा – जुल्म।

IV. (क) लिंग बदलो-

पापा – …………
दादा – ………….
सहेली – ……………
बहन – …………
तुम्हारा ….तुम्हारी…
अपना – …………….
बुआ – ……………
उत्तर:
पापा = माँ।
दादा = दादी।
सहेली = सखा।
बहन = बहनोई।
तुम्हारा = तुम्हारी।
अपना = अपनी।
बुआ = फूफा।.

(ख) वचन बदलो

तुम्हारा – तुम्हारे
अपना – ……………
यह . ………….
वह . ………….
उत्तर:
एकवचन = बहुवचन
तुम्हारा = तुम्हारे
अपना = अपने।
यह = ये।
वह = वे।

V. निम्नलिखित प्रत्येक समूह में से सबसे जो अलग हो उस पर गोला लगायें।

1. बाल, बल्ला, शाट, खुश
2. दादा, बहन, बुआ, दादागिरी
3. रोज़मर्रा, कभी-कभी, दिनभर, विश्वास
4. गुस्सा, प्रेम, मुस्कान, स्कूल
5. हाथ, कान, आँख, आईसक्रीम।
उत्तर:
1. खुश
2. दादागिरी
3. विश्वास
4. स्कूल
5. आईसक्रीम

VI. अन्तर समझो और वाक्य बनाओ

1. मुद्रा : मुख, हाथ, गर्दन आदि
विशेष भाव सूचक स्थिति
………………..
मुद्रा : रुपया/सिक्का
उत्तर:
मुद्रा – उसकी मुख मुद्रा पर चिन्ता की रेखाएँ स्पष्ट थीं।
मुद्रा – अमेरिका की मुद्रा डालर है।

2. वहन : भार ढोना, निर्वाह करना
…………………..
बहन : माँ-बाप की बेटी
उत्तर:
वहन-मैं अब आपका भार वहन नहीं कर सकता।
बहन-मेरी बड़ी बहन मेरा बहुत ध्यान रखती है।

3. साँस : श्वास, दम
………………….
सास : पत्नी या पति की माता
उत्तर:
साँस-जब तक साँस तब तक आस।
सास-मेरी सास बहुत बुद्धिमान स्त्री है।।

4. बाल : केश, बालक
………………..
बॉल : गेंद
उत्तर:
बाल-मैंने बाल कटवा लिए हैं।
बॉल-मुझे क्रिकेट की बॉल चाहिए।

प्रयोगात्मक व्याकरण

I. पढ़ो, समझो और लिखो

1. वर्तमान काल : हमारी माँ नहीं है इसलिए यह ज़िम्मेदारी ऊषा बहन को वहन करनी पड़ती है।
भूतकाल : हमारी माँ नहीं थी इसलिए यह जिम्मेवारी ऊषा बहन को वहन करनी पड़ती थी।
भविष्यकाल : हमारी माँ नहीं होगी इसलिए यह जिम्मेवारी ऊषा बहन को वहन करनी पड़ेगी।

2. वर्तमान काल : ……………..
भूतकाल : मुझे दादा जी ने नसीहत दी।
भविष्यकाल : ………………
उत्तर:
वर्तमान काल : मुझे दादा जी नसीहत देते हैं।
भूतकाल : मुझे दादा जी ने नसीहत दी।
विष्यकाल : मुझे दादा जी नसीहत देंगे।

3. वर्तमान काल : ………………
भूतकाल : …………….
भविष्यकाल : मैं स्कूल में पढुंगा।
उत्तर:
वर्तमान काल : मैं स्कूल में पढ़ता हूँ।
भूतकाल : मैं स्कूल में पढ़ता था।
भविष्यकाल : मैं स्कूल में पढुंगा।

II. क्या आप ने कभी अपनी ग़लती के लिए क्षमा माँगी है ? चार-पाँच वाक्यों में लिखें।

मनुष्य से जीवन में गल्तियाँ हो ही जाती हैं। मैंने भी जीवन में एक छोटी-सी ग़लती की थी। मैंने अपने दोस्तों के कहने पर पापा की जेब से बीस रुपए चुरा लिए थे और दोस्तों के साथ कैंटीन में खूब खाया-पिया। लेकिन अन्दर ही अन्दर मन के भीतर से यह आवाज़ बार-बार आ रही थी कि मन्न तूने यह अच्छा नहीं किया। मुझसे रहा न गया मैंने रात को पिता जी से अपनी ग़लती मानते हुए सारी बात सच-सच बता दी। पिता जी सुनने के बाद कुछ पल शाँत रहे फिर मुझे गले से लगाकर समझाया कि इस तरह किसी के बहकावे में नहीं आया करते वरना तुम्हारा जीवन नष्ट हो जाएगा। उस दिन के बाद से मैं कभी किसी के बहकावे में नहीं आता।

बहुवैकल्पिक प्रश्न

पूछे गए प्रश्नों के सही विकल्प पर (✓) निशान लगाएं.

प्रश्न 1.
कुश के पापा से बचपन में क्या टूट गई थी ?
(क) इटली की कांच की ट्रे
(ख) इटली की मीनार
(ग) इटली का जग
(घ) इटली का खिलौना।
उत्तर:
(क) इटली की कांच की ट्रे

प्रश्न 2.
कुश के पापा को कौन ब्लैकमेल करती थी ?
(क) कुश की मां
(ख) कुश की बुआ
(ग) कुश की दादी
(घ) कुश की चाची।
उत्तर:
(ख) कुश की बुआ

प्रश्न 3.
कुश के पापा ने अपनी बहन की ब्लैकमेलिंग को रोकने के लिए किसे सारी बात बताई ?
(क) दादा जी को
(ख) पापा जी को
(ग) माँ को
(घ) मामा जी को।
उत्तर:
(क) दादा जी को

गलती छिपाने की सजा Summary

गलती छिपाने की सजा पाठ का सार

पिता जी ने अपने बेटे को समझाते हुए कहा कि देखो बेटा गलतियाँ तो सबसे होती हैं, लेकिन अपनी ग़लती को मान लेना सबसे बड़ी समझदारी है और इसे छिपाने की चेष्टा कई बार बड़ी महँगी पड़ सकती है। कुश ने हैरान होकर पूछा, “बड़ी महँगी कैसे ? पापा।”

पिता ने उसे समझाते हुए कहा कि एक बार जब मैं स्कूल में पढ़ता था तो क्रिकेट खेलने का बहुत शौक था। एक दिन इसी से मेरे द्वारा काँच की वह ट्रे टूट गई जिसे मेरे दादा जी ने इटली से मँगवाया था। मैं घबरा गया और चुपचाप ट्रे के टुकड़े उठाकर कूड़ेदान में फेंक आया और संतोष किया कि किसी ने मुझे देखा नहीं, नहीं तो मुसीबत हो जाती। लेकिन मेरी छोटी बहन ऊषा ने मुझे ऐसा करते हुए देख लिया था लेकिन उसने भी किसी से कुछ नहीं कहा।। लेकिन अब जब भी दादा जी उसे किसी भी काम जैसे बर्तन धोने, झाड़ पोंछा लगाने के लिए कहते तो वह झट से मेरा नाम ले लेती और यदि मैं मना करता तो मुझे धमकाती कि मैं बता दूँ दादा जी को, ट्रे वाली बात। मैं डर के मारे चुपचाप सारे काम करने लगता। ऐसा करते-करते ऊषा की हिम्मत बहुत बढ़ गई। वह धमकी दे-देकर मुझसे सारे काम करवा लेती थी।

एक दिन परेशान होकर मैं दादा जी के पास पहुँचा और सिर झुका कर सारी बात बता दी और सज़ा के लिए इन्तज़ार करने लगा। लेकिन सारी बात सुनकर दादा जी ने हँसते हुए कहा कि मुझे पहले ही इस बात का पता था लेकिन तुमने अपनी ग़लती को छिपाया और ऊषा की ब्लैकमेलिंग का शिकार होते रहे दादा जी ने मुझे समझाया कि ग़लती छिपाने की कितनी बड़ी सज़ा मिल सकती है।

कहानी सुनते ही कुश झट से अपने कान पकड़ते हुए बोल पड़ा कि पापा जी फ्रिज में रखी हुई आईसक्रीम मैंने खाई थी, लव ने नहीं। वह तो अभी इतना छोटा है कि फ्रिज़ भी नहीं खोल सकता।

कठिन शब्दों के अर्थ:

स्वीकार = मान। चेष्टा = कोशिश। उधेड़बुन = असमंजस, फैसला न कर पाने की स्थिति मुद्रा = अवस्था। सकुचाते = शर्माते हुए। आलीशान = बहुत सुन्दर, महँगी। अप्रत्याशित 1 = अचानक। हादसा = घटना। अवशेष = टुकडे। राहत = चैन। लफड़ा = मुसीबत। गलतफहमी = भ्रम, झूठा विश्वास। वहन = उठाना। संकल्प = प्रण। आँखें तरेरना = गुस्सा दिखाना। खून के छूट पीकर रह जाना = मज़बूरी में मन मार कर रह जाना। रोज़मर्रा = प्रतिदिन। आनाकानी करना = इन्कार करना। कुटिल = फीकी। दब्बू बनकर = डरकर। कबूल करना = मान लेना। अविश्वास = विश्वास न होना। स्नेहपूर्वक = प्रेम से भरकर। रहस्योद्घाटन = भेद खोलना। क्षमा = माफ़। ब्लैकमेलिंग = ठगी करना। नसीहत = समझाना। तपाक = जल्दी।

Punjab State Board PSEB 5th Class Hindi Book Solutions Chapter 10 फूल और काँटा Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Hindi Chapter 10 फूल और काँटा

Hindi Guide for Class 5 PSEB फूल और काँटा Textbook Questions and Answers

I. बताओ

प्रश्न 1.
फूल और काँटे को कौन-सी समान परिस्थितियाँ मिलती हैं ?
उत्तर:
फूल और काँटे को एक ही पौधा पालता है, चाँद की रोशनी, वर्षा का पानी और हवाएँ एक समान प्राप्त होती हैं।

प्रश्न 2.
फूल किस प्रकार सुख देता है ?
उत्तर:
फूल अपनी सुगन्धि, सुन्दरता तथा रस से दूसरों को सुख देता है।

प्रश्न 3.
काँटा किस प्रकार दुःख देता है ?
उत्तर:
काँटा दूसरों की उँगलियों में चुभ कर और उनके सुन्दर कपड़े फाड़कर दुःख देता है।

प्रश्न 4.
देवता के शीश पर किसे चढ़ाया जाता है?
उत्तर;
देवता के शीश पर फूल को चढ़ाया जाता है।

प्रश्न 5.
कवि ने इस कविता में कुल का क्या महत्त्व बताया है ?
उत्तर:
इस कविता में कवि ने कुल का नहीं बल्कि अच्छे कर्म का महत्त्व बताया है।

II. इन प्रश्नों के उत्तर चार-पाँच पंक्तियों में लिखो

प्रश्न 1.
इस कविता से आपको क्या शिक्षा मिलती है ? अपने शब्दों में लिखो।
उत्तर:

1. हमें सभी से प्यार करना चाहिए।
2. हमें किसी को दुःख नहीं पहुँचाना चाहिए।
3. हमें दूसरों का भला करना चाहिए।
4. हमें अपने अन्दर अच्छाइयाँ (गुण) पैदा करनी चाहिएं।

प्रश्न 2.
समान कुल में जन्म लेने और समान परिस्थितियाँ मिलने पर भी व्यक्तियों का व्यवहार अलग-अलग होता है। क्यों ? उदाहरण देकर लिखो।
उत्तर:
(1) रावण और विभीषण एक ही खानदान में पले थे, परन्तु रावण ने पराई स्त्री का धोखे से हरण किया। इसके विपरीत विभीषण ने उसे छुड़ाने में भगवान् राम का साथ दिया।

(2) राम और लक्ष्मण दोनों भाई थे। एक ही पिता के आश्रय तले पालन-पोषण होने पर भी दोनों के व्यवहार में बहुत अन्तर था। राम धीर-गम्भीर और शान्त स्वभाव के थे जबकि लक्ष्मण उग्र और अधीर स्वभाव के थे।

III. काव्य-पंक्ति पूरी करो

(1) एक ही पौधा …………….
(2) मेह उन पर है ……………..।
(3) प्यार डूबी ……………।
(4) जब किसी में ……………।
उत्तर:
(1) उन्हें है पालता
(2) बरसता एक सा
(3) तितलियों के पर कतर
(4) हो बड़प्पन की कसर।

IV. सरलार्थ करो

है खटकता एक सबकी आँख में,
दूसरा है सोहता सुर-सीस पर।।
किस तरह कुल की बड़ाई काम दे,
जब किसी में हो बड़प्पन की कसर।

प्रसंग:
प्रस्तुत पद्यांश हमारी पाठ्य-पुस्तक में संकलित ‘हरिऔध’ जी द्वारा लिखित कविता ‘फूल और काँटा’ में से लिया गया है। प्रस्तुत पद्यांश में समान परिस्थितियाँ होते हुए भी फूल और काँटे के भाग्य में अन्तर को स्पष्ट किया है।

सरलार्थ:
कवि फूल और काँटे की तुलना करते हुए लिखता है कि इनमें से एक (काँटा) सभी को बुरा लगता है। दूसरा (फूल) देवता के सिर पर शोभा देता है। इस प्रकार किसी बड़े खानदान में पैदा होने का कोई लाभ नहीं, जब तक कि उसमें स्वयं बड़ों जैसे गुण न हों।

V. वाक्य बनाओ

(i) कली का जी खिलना = प्रसन्न होना ………….
(ii) आँख में खटकना = बुरा लगना ……………
उत्तर:
(i) कली का जी खिलना = भँवरे के मंडराने से कली का जी खिल उठा।
(ii) आँख में खटकना = काँटा सबकी आँख में खटकता है।

VI. विपरीत शब्दों का मिलान करो

(क)

श्याम	दुर्गन्ध
सुगन्ध	असुर
सुर	घृणा
एक	अनेक
प्यार	श्वेत।

उत्तर:
श्याम – श्वेत।
सुगन्ध – दुर्गन्ध।
सुर – असुर।
एक – अनेक।
प्यार – घृणा।

(ख) फूल के चित्र में से समानार्थक शब्द ढूँढकर लिखो

(i) फूल = पुष्प …………..
(ii) चाँद = ……………
(iii) हवा = ……………
(iv) वर्षा = …………..
(v) देवता = …………..
(vi) भौंरा = …………..
(vii) चाँदनी = …………..
उत्तर:
(i) फूल = पुष्प, सुमन।
(ii) चाँद = शशि, राकेश।
(iii) हवा = समीर, मारुत।
(iv) वर्षा = मेह, बारिश।
(v) देवता = देव, सुर।
(vi) भौंरा = अलि, भ्रमर।
(vii) चाँदनी = ज्योत्स्ना, चंद्रिका।

(ग) बहुवचन रूप लिखो-

उँगली = उँगलियाँ
काँटा = काँटे
हवा = हवाएँ
कली = ……..
भौंरा = ……………
कविता = …………
तितली = …………..
निराला = ………….
लता = …………..
उत्तर:
उँगली = उँगलियाँ।
कली = कलियाँ।
तितली = तितलियाँ।
काँटा = काँटे।
भौंरा = भौंरे।
निराला = निराले।
हवा = हवाएँ।
कविता = कविताएँ।
लता = लताएँ।

कविता में ‘श्याम-तन’ ‘वर-वसन’ ‘सुर-शीश’ शब्द युग्म के रूप में प्रयोग हुए हैं। इनमें पहला शब्द दूसरे शब्द की विशेषता बताता है। जिसकी विशेषता बताई जाये, उसे विशेष्य और जो शब्द विशेषता बताए उसे विशेषण कहते हैं। इन शब्द-युग्मों में से विशेषण और विशेष्य अलग-अलग कर लिखो।
उत्तर:
विशेषण – विशेष्य
(i) श्याम – तन।
(ii) वर – वसन।
(iii) सुर – शीश।

बहुवैकल्पिक प्रश्न

पूछे गए प्रश्नों के सही विकल्प पर (✓) निशान लगाएं

प्रश्न 1.
फूल और कांटे के जीवन में क्या समानता
(क) एक पौधे द्वारा पालना
(ख) दो पौधों द्वारा पालना
(ग) अलग-अलग
(घ) एक रस।
उत्तर:
(क) एक पौधे द्वारा पालना

प्रश्न 2.
फूल हमें क्या देता है ?
(क) सुगंध
(ख) सुन्दरता
(ग) रस
(घ) सभी।
उत्तर:
(घ) सभी।

प्रश्न 3.
कांटा हमें क्या देता है ?
(क) चुभन
(ख) कपड़े फाड़ना।
(ग) पीड़ा
(घ) सभी।
उत्तर:
(घ) सभी।

प्रश्न 4.
देवता के शीश पर किसे चढ़ाया जाता है ?
(क) फूल
(ख) कांटा
(ग) चावल
(घ) आटा।
उत्तर:
(क) फूल

प्रश्न 5.
कुल से बढ़कर किसका महत्त्व ज्यादा है?
(क) अच्छे कर्म का
(ख) अच्छे धर्म का
(ग) अच्छे सौंदर्य का
(घ) अच्छी ऊंचाई का।
उत्तर:
(क) अच्छे कर्म का

फूल और काँटा Summary

फूल और काँटा पाठ का सार

कवि फूल और काँटे के विषय में कहता है कि दोनों एक ही पौधे पर लगते हैं। चाँद की चाँदनी उन पर एक-सी ही पड़ती है, वर्षा एक साथ ही बरसती है और हवा भी एक समान प्राप्त होती है पर फिर भी दोनों में कितना बड़ा अन्तर होता है। काँटा चुभ कर किसी को कष्ट देता है, कपड़े फाड़ता है, भंवरों| तितलियों को बींध डालता है तो फूल सबको प्रसन्नता देता है। अपनी सुगन्ध से सबको हर्षित करता है। काँटा सबको बुरा लगता है तो फूल देवताओं के शीश पर शोभा देता है। प्रत्येक जीव अपने कार्यों से ही श्रेष्ठता प्राप्त करता है न कि परिवार के नाम से।

पद्यांशों के सरलार्थ

1. हैं जन्म लेते जगह में एक ही,
एक ही पौधा उन्हें है पालता।
रात में उन पर चमकता चाँद भी,
एक-सी ही चाँदनी है डालता॥

कठिन शब्दों के अर्थ:
जगह = स्थान। पालता = पालन करना। चाँदनी = चाँद की रोशनी।

प्रसंग:
प्रस्तुत पद्यांश हमारी पाठ्य-पुस्तक में संकलित ‘हरिऔध’ जी द्वारा लिखित कविता ‘फूल और काँटा’ में से लिया गया है। प्रस्तुत कविता में समान परिस्थितियाँ होते हुए भी फूल और काँटे के भाग्य में अन्तर को स्पष्ट किया गया है।

सरलार्थ:
कवि फूल और काँटे का वर्णन करते हुए लिखता है कि ये दोनों एक ही जगह पर जन्म (पैदा होते हैं) लेते हैं। एक ही पौधा उन्हें पालतापोसता है। रात के समय चाँद उन पर एक समान चमकता है और उन दोनों पर एक-जैसी रोशनी डालता है।

भावार्थ:
फूल हो या काँटा-प्रकृति उन्हें अपने समान व्यवहार से ही पालती-पोसती है।

2. मेह उन पर है बरसता एक-सा,
एक-सी उन पर हवाएँ हैं बहीं।
पर सदा ही यह दिखाता है हमें,
ढंग उनके एक से होते नहीं।

कठिन शब्दों के अर्थ:
मेह = वर्षा। बहीं = बहती हैं। ढंग = तरीका।

प्रसंग:
प्रस्तुत पद्यांश हमारी पाठ्य-पुस्तक में संकलित ‘हरिऔध’ जी द्वारा लिखित कविता ‘फूल और काँटा’ में से लिया गया है। प्रस्तुत कविता में समान परिस्थितियाँ होते हुए भी फूल और काँटे के | भाग्य में अन्तर को स्पष्ट किया गया है।

सरलार्थ:
फूल और काँटे दोनों पर एक समान वर्षा बरसती है। उन पर हवाएँ भी एक-सी बहती हैं। लेकिन हमें हमेशा ही यह दिखाई देता है कि उन दोनों, फूल और काँटे के तरीके एक समान नहीं होते।

भावार्थ:
प्रकृति का व्यवहार सभी के लिए एक समान ही होता है-चाहे कोई अच्छा हो या बुरा।

3. छेद कर काँटा किसी की उंगलियाँ,
फाड़ देता है किसी का वर वसन।
प्यार में डबी तितलियों के पर कतर,
भौंर का है बेध देता श्याम तन॥

कठिन शब्दों के अर्थ:
छेदकर = बेधकर। वर वसन = सुन्दर कपड़े। कतर = काट देना। पर = पंख। श्याम = काला। बेध देता = जख्मी कर देता है।

प्रसंग:
प्रस्तुत पद्यांश हमारी पाठ्य-पुस्तक में संकलित ‘हरिऔध’ जी द्वारा लिखित कविता ‘फूल और काँटा’ में से लिया गया है। इन पंक्तियों में कवि ने काँटे के स्वभाव के बारे में बताया है।

सरलार्थ:
पौधे पर लगा काँटा किसी आदमी की उंगलियाँ छेदकर अथवा उंगलियों में चुभ कर दुःख पहुँचाता है। काँटा किसी के सुन्दर कपड़ों को फाड़ देता है। वह फूलों के प्यार में डूबी प्यार करने वाली तितलियों के पंख काट देता है। वह भंवरों के काले शरीर को ज़ख्मी कर देता है।

भावार्थ:
बुरों का व्यवहार सबके लिए बुरा ही होता है।

4. फूल लेकर तितलियों को गोद में,
भौंर को अपना अनूठा रस पिला।
निज सुगन्धित औ’ निराले ढंग से,
है सदा देता कली का जी खिला॥

कठिन शब्दों के अर्थ:
अनूठा = निराला, बहुत अच्छा।

प्रसंग:
प्रस्तुत पद्यांश हमारी पाठ्य-पुस्तक में संकलित ‘हरिऔध’ जी द्वारा लिखित कविता ‘फूल और काँटा’ में से लिया गया है। इन पंक्तियों में कवि ने फूल के कोमल स्वभाव के बारे में बताया है।

सरलार्थ:
फूल तितलियों को अपनी गोद में ले प्यार करता है और भंवरे को अपना मीठा रस पिलाता है। फूल अपनी खुशबू और अपने अच्छे ढंग से हमेशा कली के दिल को प्रसन्न कर देता है। कहने का भाव यह है कि फूल सबको सुख पहुँचाता है।

भावार्थ:
अच्छे स्वभाव वाले सभी के प्रति अच्छा व्यवहार ही करते हैं।

5. है खटकता एक सब की आँख में,
दूसरा है सोहता सुर-सीस पर।
किस तरह कुल की बड़ाई काम दे,
जब किसी में हो बड़प्पन की कसर॥

कठिन शब्दों के अर्थ:
खटकता = बुरा लगता है। सोहता = शोभा देता है। सुर = देवता। कुल = खानदान। बड़प्पन = श्रेष्ठता।

प्रसंग:
प्रस्तुत पद्यांश ‘फूल और काँटा’ नामक कविता से लिया गया है, जिसमें कवि ने स्पष्ट किया है कि हमारे कार्य और गुण ही हमें बड़ा बनाते हैं न कि हमारा परिवार।

सरलार्थ:
कवि फूल और काँटे की तुलना करते हुए लिखता है कि इनमें से एक (काँटा) सभी को बुरा लगता है। दूसरा (फूल) देवता के सिर पर शोभा देता है। इस प्रकार किसी बड़े खानदान में पैदा होने का कोई लाभ नहीं, जब तक कि उसमें स्वयं बड़ों जैसे गुण न हों।

भावार्थ:
प्रत्येक प्राणी अपने गुणों से बड़ा बनता है न कि अपने परिवार की श्रेष्ठता से।

Punjab State Board PSEB 5th Class Hindi Book Solutions Chapter 11 क्राँतिजोत : सावित्रीबाई फुले Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Hindi Chapter 11 क्राँतिजोत : सावित्रीबाई फुले

Hindi Guide for Class 5 PSEB क्राँतिजोत : सावित्रीबाई फुले Textbook Questions and Answers

I. बताओ

प्रश्न 1.
सावित्रीबाई फुले का जन्म कब और कहाँ हुआ?
उत्तर:
सावित्रीबाई फुले का जन्म 3 जनवरी, सन् 1831 को महाराष्ट्र के सतारा जिले के नैगाँव, तहसील खण्डाला में हुआ।

प्रश्न 2.
सावित्रीबाई फुले के माता-पिता व पति का क्या नाम था?
उत्तर:
सावित्रीबाई फुले की माता का नाम लक्ष्मी और पिता का नाम खंदोजी नैवसे तथा पति का नाम ज्योतिबा राव फुले था।

प्रश्न 3.
सबसे पहले सावित्रीबाई फुले ने लड़कियों के स्कूल की स्थापना कब की?
उत्तर:
सावित्रीबाई फुले ने सन् 1848 में सबसे पहले लड़कियों के स्कूल की स्थापना की।

प्रश्न 4.
ब्रिटिश सरकार ने उन्हें व उनके पति को कब सम्मानित किया?
उत्तर:
ब्रिटिश सरकार ने सावित्री और उनके पति को सन 1852 में सम्मानित किया।

प्रश्न 5.
सावित्रीबाई फुले की मृत्यु कब और |किस बीमारी की चपेट में आने से हुई?
उत्तर:
सावित्रीबाई फुले की मृत्यु 10 मार्च, सन् 1897 में प्लेग के कारण हुई।

प्रश्न 6.
सावित्रीबाई फुले को पढ़ने व पढ़ाई के कार्य में किन समस्याओं का सामना करना पड़ा?
उत्तर:
सावित्रीबाई को पढ़ने के लिए घर में ही काफ़ी विरोध का सामना करना पड़ा था, लेकिन वह अडिग अपने लक्ष्य-पथ पर चलती रही। पढ़ाई के कार्य में चलते हुए भी उन्हें लोगों का विरोध सहना पड़ता। लोग उन्हें कई कुछ भला-बुरा कहते और उसके कपड़ों पर कीचड़ आदि फेंकते। लेकिन सावित्री बाई इन बातों से घबराई नहीं और अपने रास्ते पर चलती रही।

प्रश्न 7.
भारत सरकार ने सावित्रीबाई फुले का डाक टिकट कब जारी किया?
उत्तर:
भारत सरकार ने 10 मार्च, सन् 1998 को उनके नाम का डाक टिकट जारी किया।

II. शुद्ध शब्द पर गोला लगाओ

1. तहसील/तहिसील/तहसिल
2. अध्यापीका/अध्यिापिका/अध्यापिका
3. सावित्री/सावितरी/सावीत्री
4. महतवपूर्ण/महत्त्वपूर्ण/महत्वपूरण
5. सथापना/स्थापना/स्थाप्ना
6. समानित/सम्मानित/सम्मानीत
7. प्रेरणादायक/प्रेरणादाइक/प्ररेनादायक
8. सरानीय/सराहनीय/सराहनिय
9. प्रकाशित/प्ररकाशित/प्रकासित
उत्तर:
1. तहसील
2. अध्यापिका
3. सावित्री
4. महत्त्वपूर्ण
5. स्थापना
6. सम्मानित
7. प्रेरणादायक
8. सराहनीय
9. प्रकाशित।

III. समान अर्थ वाले शब्द ढूँढ़कर लिखो

कल्याण, अंधेरा, लगातार, इरादा, पहली, हौसला, स्वयं, शिक्षिका, खेमा।
प्रथम – ……………
शिविर – ……………
धैर्य – ……………
अंधकार – ……………
अध्यापिका -. …………..
निश्चय – ……………
उद्धार – ……………
निरन्तर – ……………
खुद – ……………
उत्तर:
प्रथम – पहली
शिविर – खेमा
धैर्य – हौसला
अंधकार – अंधेरा
अध्यापिका – शिक्षिका
उद्धार – कल्याण
निश्चय – इरादा
निरन्तर – लगातार
खुद – स्वयं

IV. बहुवचन रूप लिखो

स्त्री = स्त्रियाँ
बच्चा = बच्चे
लड़की = ……………
कपड़ा = ……………
बेटी = …………..
बेटा = ……………
उत्तर:
स्त्री = स्त्रियाँ
बच्चा = बच्चे
लड़की = लड़कियाँ
बेटी = बेटियाँ
बेटा = बेटे
कपड़ा = कपड़े

पढ़ो, समझो और लिखो-

शिक्षक = शिक्षिका
औरत = मर्द
कवि = कवयित्री
विधवा = सधवा।

बहुवैकल्पिक प्रश्न

पूछे गए प्रश्नों के सही विकल्प पर (✓) निशान लगाएं

प्रश्न 1.
सावित्रीबाई फुले का जन्म कब हुआ ?
(क) 3 जनवरी 1831 को
(ख) 3 जनवरी 1852 को
(ग) 3 जनवरी 1833 को
(घ) 3 जनवरी 1834 को।
उत्तर:
(क) 3 जनवरी 1831 को

प्रश्न 2.
सावित्रीबाई का जन्म कहां हुआ ?
(क) पंजाब में
(ख) महाराष्ट्र में
(ग) हरियाणा में
(घ) राजस्थान में।
उत्तर:
(ख) महाराष्ट्र में

प्रश्न 3.
सावित्रीबाई का विवाह किसके साथ हुआ ?
(क) ज्योतिबा राव
(ख) ज्योति प्रसाद
(ग) ज्योति सिंह
(घ) ज्योति भारती।
उत्तर:
(क) ज्योतिबा राव

प्रश्न 4.
ज्योतिबा राव किसके पक्षधर थे ?
(क) धर्म के
(ख) सम्प्रदाय के
(ग) स्त्री-शिक्षा के
(घ) स्त्री-प्रथा
उत्तर:
(ग) स्त्री-शिक्षा के

प्रश्न 5.
सावित्रीबाई ने पति के साथ मिलकर पुणे में लड़कियों के लिए स्कूल कब खोला ?
(क) 1845 ई० में
(ख) 1846 ई० में
(ग) 1847 ई० में
(घ) 1848 ई० में।
उत्तर:
(घ) 1848 ई० में।

प्रश्न 6.
भारत सरकार ने सावित्रीबाई के नाम पर क्या जारी किया ?
(क) डाक टिकट
(ख) डाक पार्सल
(ग) डाक गाड़ी
(घ) डाकपाल।
उत्तर:
(क) डाक टिकट

क्राँतिजोत : सावित्रीबाई फुले Summary

क्राँतिजोत : सावित्रीबाई फुले पाठ का सार

सावित्रीबाई फुले का जन्म 3 जनवरी, सन् 1831 को महाराष्ट्र के सतारा जिले के नैगाँव, तहसील खण्डाला में हुआ। इनके पिता जी का नाम खंदोजी नैवसे तथा माता का नाम लक्ष्मी था। 9 वर्ष की आयु में ही इनका विवाह ज्योतिबा राव फुले के साथ हुआ। ज्योतिबा राव स्त्री-शिक्षा के पक्षधर थे। उन्होंने औरतों को पढ़ाने का बीड़ा उठाया क्योंकि वे समझते थे कि स्त्री शिक्षा से ही समाज में फैले अज्ञानअन्धकार को दूर किया जा सकता है। इसलिए सबसे पहले उन्होंने सावित्री फुले को पढ़ाने का निश्चय किया। ज्योतिबा ने खाली समय में सवित्रीबाई को पढ़ाना शुरू किया। हालांकि परिवार में इस बात का बहुत विरोध भी हुआ, लेकिन ज्योतिबा अपने रास्ते पर चलते रहे। पढ़ाई के कार्यों में भी सावित्री को बहुत-सी समस्याओं का सामना करना पड़ा। मार्ग में चलते हुए लोग न जाने उन्हें क्या-क्या कहते, कपड़ों पर कीचड़ आदि फेंकते, लेकिन सावित्री बाई इन सब की परवाह न करते हुए अपने लक्ष्य पर अडिग चलती रही और लड़कियों को पढ़ाती रही।

सन् 1848 में उन्होंने अपने पति के साथ मिलकर पुणे में लड़कियों के लिए एक स्कूल खोला। इस स्कूल की पहली मुख्याध्यापिका सावित्रीबाई बनी। इसी प्रकार उन्होंने अपने पति के साथ मिलकर और भी कई स्कूल खोले। इनके इन कार्यों से प्रसन्न होकर ब्रिटिश सरकार ने सन् 1852 में उन्हें और ज्योतिबा राव. को सम्मानित किया।

ज्योतिबा राव ने ग़रीबों, अनाथों और विधवाओं की भलाई के लिए जो भी कार्य किए, सावित्री जी ने उन्हें अपना पूरा सहयोग दिया। उन्होंने एक ग़रीब औरत को सहारा दिया, उसे अपनी बेटी के समान -घर पर रखा। सावित्रीबाई ने उसके बेटे का पालनपोषण किया और उसे पढ़ा-लिखाकर डॉक्टर बनाया। ज्योतिबा के निधन के पश्चात् इन्होंने उनके द्वारा स्थापित सत्यशोधक मंडल का दायित्व स्वयं सम्भाल लिया।

प्लेग फैलने पर सावित्रीबाई ने प्लेग-पीड़ितों की खूब सेवा की। उन्होंने उनके लिए शिविर लगवाए तथा उनके भोजन का प्रबन्ध किया। इसी प्रकार एक प्लेग पीड़ित बालिका की सेवा करते हुए वह स्वयं
भी इसका शिकार हो गई और इसी बीमारी के चलते 10 मार्च, सन् 1897 को उन्होंने प्राण त्याग दिए। निश्चय ही महिलाओं की मुक्ति के लिए सावित्री जी का योगदान सराहनीय है। भारत सरकार ने 10 मार्च, | सन् 1998 को उनके नाम पर डाक-टिकट जारी किया।

कठिन शब्दों के अर्थ:

अधिकार = हक। अन्याय = न्याय न होना। ताल्लुक = सम्बन्ध। उद्धार = कल्याण। अन्धकार = अन्धेरा। दृढ़ निश्चय = पक्का इरादा। विद्या = शिक्षा। बीड़ा उठाया = दायित्व लिया। निश्चय = इरादा। निरन्तर = लगातार। समस्याएँ = मुश्किलें। अडोल = बिना डगमगाए, स्थिर। अडिग = स्थिर। डगमगाई = लड़खड़ाई, डोली। धैर्य = हौंसला। कथनी = कहना। आश्रय = सहारा। लालन-पालन = पालना-पोसना, परवरिश। बखूबी = बड़ी अच्छी तरह। फर्ज = कर्त्तव्य। निधन = मृत्यु। दायित्व = ज़िम्मेदारी। खुद = स्वयं। सराहनीय = प्रशंसा के योग्य।

Punjab State Board PSEB 5th Class Hindi Book Solutions Chapter 12 श्रद्धा और अभ्यास Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Hindi Chapter 12 श्रद्धा और अभ्यास

Hindi Guide for Class 5 PSEB श्रद्धा और अभ्यास Textbook Questions and Answers

I. बताओ

प्रश्न 1.
पाँच पाँडवों के नाम लिखो।
उत्तर:
पाँच पाँडवों के नाम हैं-युधिष्ठिर, भीम, अर्जुन, नकुल और सहदेव।

प्रश्न 2.
कौरव-पांडव के गुरु कौन थे?
उत्तर:
कौरव-पांडव के गुरु द्रोणाचार्य थे।

प्रश्न 3.
गुरु शिष्यों को कौन-सी विद्या सिखा रहे थे?
उत्तर;
गुरु द्रोणाचार्य अपने शिष्यों को धनुर्विद्या सिखा रहे थे।

प्रश्न 4.
अर्जुन किस विद्या में निपुण था?
उत्तर;
अर्जुन धनुर्विद्या में निपुण था।

प्रश्न 5.
बनवासी बालक क्या कर रहा था?
उत्तर:
बनवासी बालक धनुर्विद्या का अभ्यास कर रहा था।

प्रश्न 6.
आश्रम में कुत्ते को देखकर सभी क्यों चकित हो गए?
उत्तर:
कुत्ते का मुँह बाणों से भरा हुआ था। यह देखकर आश्रम में सभी चकित हो गए।

प्रश्न 7.
गुरु द्रोणाचार्य प्रतिमा देखकर क्यों हैरान हो गए?
उत्तर:
गुरु द्रोणाचार्य प्रतिमा देखकर हैरान इसलिए हो गए क्योंकि वह प्रतिमा उन्हीं की थी।

प्रश्न 8.
एकलव्य का गुरु कौन था?
उत्तर:
एकलव्य ने गुरु द्रोणाचार्य को अपना गुरु माना था।

प्रश्न 9.
श्रद्धा और अभ्यास का एकलव्य पर क्या प्रभाव पड़ा?
उत्तर:
श्रद्धा और अभ्यास के बल पर एकलव्य धनुर्विद्या में कुशल हो गया।

प्रश्न 10.
इस कहानी से हमें क्या शिक्षा मिलती है?
उत्तर:
इस कहानी से हमें शिक्षा मिलती है कि श्रद्धा, विश्वास, लगन और परिश्रम से कोई भी कार्य कठिन नहीं रह सकता।

II. वाक्य पूरे करो

1. अर्जुन का निशाना अन्य ………………. से सर्वश्रेष्ठ था।
2. ………… उन्हें धनुष विद्या सिखा रहे थे।
3. अचानक एक …………… वहाँ आया।
4. कुत्ते का मुँह ……………. से भरा था।
5. वह बालक ………………. था।
6. मैंने मन से आपको ……………….. मान लिया था।
7. बालक सभी को ………………… के सम्मुख ले गया।
उत्तर:
(1) शिष्यों
(2) गुरु द्रोणाचार्य
(3) कुत्ता
(4) बाणों
(5) एकलव्य
(6) गुरु
(7) मूर्ति।

III. बनवासी शब्द वन + वासी शब्द जोड़ कर बना है नीचे कुछ शब्द जोड़ दिए गए हैं इनसे शब्द बनाओ और अर्थ लिखो

शब्दजोड़ – शब्द – अर्थ
(i) वन + चर …………… , …………….
(ii) वन + राज …………… , …………….
(iii)वन + मानुष …………… , …………….
(iv) वन + माली ………………… , वनमाला धारण करने वाला, कृष्ण
(v) वन + रोपण …………… , …………….
(vi) वन + पाल ………….., वन की रक्षा करने वाला सरकारी कर्मचारी
उत्तर:
(i) वन + चर = वनचर-वन में घूमनेफिरने वाला।
(ii) वन + राज = वनराज-वन (जंगल) में राज करने वाला।
(iii) वन + मानुष = वनमानुष-जंगली।
(iv) वन + माली = वनमाली-पौधों की देखभाल करने वाला/वनमाला धारण करने वाला, कृष्ण।
(v) वन + रोपण = वनरोपण-वन (पौधों) का लगाना।
(vi) वन + पाल = वनपाल-वन (पौधों) का पालन-पोषण, देख-रेख करने वाला/वन की रक्षा करने वाला सरकारी कर्मचारी।

IV. निम्न मुहावरों का वाक्यों में प्रयोग करो.

मुहावरा = अर्थ
1. गद्गद् होना = प्रसन्न होना
वाक्य – पुत्र का परीक्षा-परिणाम देखते ही माँ गद्गद् हो गई।

2. एकटक देखना = लगातार देखना
वाक्य – बच्चा चन्द्रमा की ओर एकटक देखता रहा।

3. मुँह से शब्द न निकलना = चुप्पी साध लेना
वाक्य – पुलिस के सामने रघु के मुँह से शब्द तक नहीं निकला।

4. चकित होना = हैरान होना
वाक्य – अरे, मैं तो तुम्हारा यह रूप देखकर चकित रह गया हूँ।

5. एक पंथ दो काज = एक कार्य करते समय दूसरा कार्य भी हो जाना
वाक्य – इधर आकर खरीदारी हो गई और तुम्हें भी मिल लिया। यह तो एक पंथ दो काज हो गए।

6. मन में बसना = प्रिय लगना, पसंद आना
वाक्य – प्रत्येक बच्चा अपने माँ-बाप के मन में बसता है।

7. आश्चर्य का ठिकाना न रहना = बहुत हैरान
होना वाक्य – तीन फुट ऊँचे पेड़ को आमों से लदा देख मेरे आश्चर्य का ठिकाना न रहा।

8. नतमस्तक होना = नम्र बनना
वाक्य – अपने गुरु जी को देखते ही मैं नतमस्तक हो गया।

इनको भी जानो

(1) महान विद्वान् वरदराज जिसे गुरु ने मूढ़ समझ आश्रम से निकाल दिया था, परन्तु अभ्यास के बल पर एक दिन विद्वान् बन गया तभी तो कहा है-
करत करत अभ्यास के जड़मति होत सुजान।
रसरी आवत जात ते सिल पर परत निसान॥

(2) राजा ब्रूस की कहानी अपने अध्यापक से सुनें और उससे शिक्षा लेते हुए अपने जीवन के उद्देश्य की ओर बढ़ें।

VI. निम्नलिखित शब्दों के एक से अधिक शब्द बनाएँ.

प्रयोगात्मक व्याकरण

I. (क) क्रिया
(1) गुरु द्रोणाचार्य अपने शिष्यों को धनुर्विद्या की शिक्षा दे रहे थे।
(2) मैं आपकी प्रतिमा के सम्मुख प्रतिदिन -अभ्यास करता हूँ।
(3) गुरु शिष्यों से तीर चलवाते थे।
(4) अचानक एक कुत्ता आश्रम में आया।
(5) गुरु के प्रति ऐसी श्रद्धा देख कर सभी चकित

उपर्युक्त वाक्यों में ‘दे रहे थे’, ‘करता हूँ’, से काम का करना, ‘चलवाते थे’, से काम करवाना तथा ‘आया’ और थे में काम का होना प्रकट हो रहा हैं।

परिभाषा-वाक्य में जिस पद से किसी काम का ‘करना’, ‘करवाना’ या ‘होना’ प्रकट हो, उसे क्रिया कहते हैं।

(ख) निम्नलिखित वाक्यों में से क्रिया शब्दों को छाँटिए

(1) बालक गुरु द्रोण को श्रद्धा से देख रहा था।
(2) उसकी आवाज़ तक नहीं निकल रही थी।
(3) उसने मिट्टी की एक मूर्ति बनायी।
(4) वह एकटक गुरु को निहारता रहा।
(5) मेरे गुरु आप हैं।
(6) मेरी एकाग्रता भंग हो रही थी।
उत्तर:
(1) देख रहा था।
(2) निकल रही थी।
(3) बनायी।
(4) निहारता रहा।
(5) हैं। (होना)
(6) भंग हो रही थी।

बहुवैकल्पिक प्रश्न

पूछे गए प्रश्नों के सही विकल्प पर (✓) निशान लगाएं

प्रश्न 1.
महाभारत किन-किन के बीच हुआ ?
(क) कौरव-पांडवों के
(ख) कौरव-यक्षों के
(ग) पांडव-सेना के
(घ) कौरव-दिल्ली।
उत्तर:
(क) कौरव-पांडवों के

प्रश्न 2.
कौरव-पांडवों को किसने शिक्षा दी ?
(क) गुरु द्रोणाचार्य
(ख) गुरु वशिष्ट
(ग) गुरु परशुराम
(घ) गुरु आचार्य।
उत्तर:
(क) गुरु द्रोणाचार्य

प्रश्न 3.
अर्जुन किस विद्या में निपुण थे ?
(क) गदा विद्या
(ख) धनुर्विद्या
(ग) तलवार विद्या
(घ) पास विद्या।
उत्तर:
(ख) धनुर्विद्या

प्रश्न 4.
कुत्ते का मुँह वाणों से किसने भर दिया ?
(क) एकलव्य ने
(ख) एकत्नय ने
(ग) एकरस ने
(घ) एक लता ने।
उत्तर:
(क) एकलव्य ने

प्रश्न 5.
एकलव्य के गुरु कौन थे ?
(क) गुरु वशिष्ट
(ख) गुरु अर्जुन देव
(ग) गुरु द्रोणाचार्य
(घ) गुरु वशिष्ट।
उत्तर:
(ग) गुरु द्रोणाचार्य

श्रद्धा और अभ्यास Summary

श्रद्धा और अभ्यास पाठ का सार

महाभारत के समय की बात है। पाँचों पाण्डव और कौरव पत्र दुर्योधन तथा दुशासन आदि गुरु द्रोणाचार्य के पास दूर जंगल में उनके आश्रम में शिक्षा ग्रहण करते थे। एक दिन जब वे सभी गुरु द्रोणाचार्य के साथ धनुर्विद्या प्राप्त कर रहे थे तो एक बनवासी बड़ी श्रद्धा से उन्हें देख रहा था। बनवासी बालक ने अर्जुन की धनुर्विद्या देखकर प्रण किया कि वह भी अर्जुन की तरह महान् धनुर्धर बनेगा। वह चुपचाप अपनी कुटिया में लौट आया। उसने मिट्टी की एक मूर्ति बनाई और वह रोज़ उस मूर्ति को प्रणाम करता और फिर धनुष चलाने का अभ्यास करता।

समय बीतता गया फिर एक दिन द्रोणाचार्य अपने आश्रम में शिष्यों को शिक्षा दे रहे थे कि अचानक एक कुत्ता आश्रम में आया जिसका मुँह बाणों से भरा हुआ था और उसकी आवाज़ भी नहीं निकल रही थी। सभी यह देखकर हैरान रह गए। सभी के मन में उस धनुर्धारी को देखने की इच्छा हुई। सभी उसे देखने के लिए जंगल में निकल पड़े। कुछ दूरी पर जाकर उन्होंने देखा कि एक बालक अपने अभ्यास में लीन था। वह इतना मग्न था कि उसे इनके आने का पता भी नहीं चला। द्रोणाचार्य ने उस बालक से पूछा कि तुम कौन हो? बालक गुरु द्रोणाचार्य को सामने देखकर मुंह से कुछ न बोल सका बस उन्हें . एकटक देखता रह गया। गुरु ने फिर पूछा कि बालक तुम कौन हो? तुम्हारा गुरु कौन है? उस कुत्ते को तुमने दंड क्यों दिया? बालक ने उन्हें प्रणाम किया और कहा कि गुरुवर मैं एक साधारण बनवासी हूँ। मेरे गुरु आप हैं। गुरु द्रोणाचार्य ने हैरान होते हुए कहा कि मैंने तो तुम्हें शिक्षा नहीं दी है? फिर मैं कैसे तुम्हारा गुरु हआ? बालक ने उत्तर दिया कि मैंने आपको मन में अपना गुरु मानकर आपकी एक प्रतिमा बनाई और उसी के सामने मैं अभ्यास करता हूँ। कुत्ते के बारे में पूछने पर उसने बताया कि यह कुत्ता भौंक-भौंक कर मेरे कार्य में बाधा उत्पन्न कर रहा था इसलिए मैंने उसका मुँह ही बन्द कर दिया।

गुरु के प्रति ऐसी श्रद्धा और अपने काम के प्रति इतनी लगन देखकर सभी हैरान थे। यह बालक था एकलव्य जो अपने अभ्यास और श्रद्धा के बल पर महान् बना। सच है कि श्रद्धा, विश्वास और लगन तथा परिश्रम से कोई भी कार्य कठिन नहीं रह जाता।

कठिन शब्दों के अर्थ:

काल = समय। आश्रम = साधु, संन्यासियों के रहने का स्थान। धनुर्विद्या = धनुष चलाने की शिक्षा। सर्वोत्तम = सबसे अच्छा। गद्गद् = खुश। बनवासी = जंगल में वास (रहने) करने वाला। कुटिया = झोंपड़ी। एकांत = जहाँ कोई न हो, अकेले में। सानिध्य = पास। सम्मुख = सामने। प्रमाण = सबूत। प्रबल = तेज़। तल्लीन = मग्न। एकाग्रता = एकचित्त होना, एक केन्द्र पर मन लगना। धन्य = आनन्दित। एकटक = बिना पलक झपके, लगातार। निहारता = देखता। दण्ड = सजा। दण्डवत = लेट कर प्रणाम करना। जिज्ञासा = जानने की इच्छा। प्रतिमा = मूर्ति। समर्पण = त्याग। चकित = हैरान। परिश्रम = मेहनत।