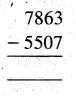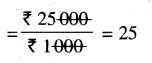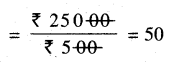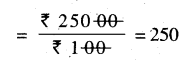Bhagya

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 3 HCF and LCM Ex 3.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 3 HCF and LCM Ex 3.2

Question 1.
Write the Prime numbers from the following :

Solution:
(a) 5, 7, 3
(b) 2, 11, 13
(c) 5
(d) 41, 23, 17, 19
(e) 41, 37, 47.

Question 2.
Write the composite numbers from the following :

Solution:
(a) 14, 9, 6
(b) 21, 12, 18
(c) 32, 15
(d) 10, 25, 9
(e) 24, 49, 50.

Question 3.
Find HCF of following numbers using Prime factorisation.
(a) 18, 27
(b) 21, 63
(c) 80, 100
(d) 42, 98.
Solution:

Prime factorisation of 18 = 2 × 3 × 3
Prime factorisation of 27 = 3 × 3 × 3
Common Prime Factors = 3 and 3
∴ HCF of 18 and 27 = 3 × 3 = 9

Prime factorisation of 21 = 3 × 7
Prime factorisation of 63 = 3 × 3 × 7
Common Prime Factors = 3 and 7
∴ HCF of 21 and 63 = 3 × 7 = 21

Prime factorisation of 80 = 2 × 2 × 2 × 2 × 5
Prime factorisation of 100 = 2 × 2 × 5 × 5
Common Prime Factors = 2, 2 and 5
HCF of 80 and 100 = 2 × 2 × 5 = 20

Prime factorisation of 42 = 2 × 3 × 7
Prime factorisation of 98 = 2 × 7 × 7
Common Prime Factors = 2 and 7
HCF of 42 and 98 = 2 × 7 = 14

Question 4.
Find HCF of following numbers using Prime factorisation :
(a) 30, 50, 70
(b) 24, 32, 40
(b) 36, 60, 72
(d) 25, 30, 35.
Solution:

Prime factorisation of 30 = 2 × 3 × 5
Prime factorisation of 50 = 2 × 5 × 5
Prime factorisation of 70 = 2 × 5 × 7
Common Prime Factors = 2 and 5
∴ HCF of 30, 50 and 70 = 2 × 5 = 10

Prime factorisation of 24 = 2 × 2 × 2 × 3
Prime factorisation of 32 = 2 × 2 × 2 × 2 × 2
Prime factorisation of 40 = 2 × 2 × 2 × 5
Common Prime Factors = 2, 2 and 2
∴ HCF of 24, 32 and 40 = 2 × 2 × 2 = 8

Prime factorisation of 36 = 2 × 2 × 3 × 3
Prime factorisation of 60 = 2 × 2 × 3 × 5
Prime factorisation of 72 = 2 × 2 × 2 × 3 × 3
Common Prime Factors = 2, 2 and 3
∴ HCF of 36, 60 and 72 = 2 × 2 × 3 = 12

Prime factorisation of 25 = 5 × 5
Prime factorisation of 30 = 2 × 3 × 5
Prime factorisation of 35 = 5 × 7
Common Prime Factor = 5
∴ HCF of 25, 30, 35 = 5

Question 5.
Find HCF of following numbers using Prime factorisation :
(a) 42, 84
(b) 45, 90
(c) 16, 64, 80
(d) 45, 90, 105.
Solution:

Prime factorisation of 42 = 2 × 3 × 7
Prime factorisation of 84 = 2 × 2 × 3 × 7
Common Prime Factors = 2, 3 and 7
∴ HCF of 42, 84 = 2 × 3 × 7 = 42

Prime factorisation of 45 = 3 × 3 × 5
Prime factorisation of 90 = 2 × 3 × 3 × 5
Common Prime Factors = 3, 3 and 5
HCF of 45, 90 = 3 × 3 × 5 = 45

Prime factorisation of 16 = 2 × 2 × 2 × 2
Prime factorisation of 64 = 2 × 2 × 2 × 2 × 2 × 2
Prime factorisation of 80 = 2 × 2 × 2 × 2 × 5
Common Prime Factors = 2, 2, 2 and 2
∴ HCF of 16, 64, 80 = 2 × 2 × 2 × 2 = 16

Prime factorisation of 45 = 3 × 3 × 5
Prime factorisation of 90 = 2 × 3 × 3 × 5
Prime factorisation of 105 = 3 × 5 × 7
Common Prime Factors = 3 and 5
∴ HCF of 45, 90 and 105 = 3 × 5 = 15

Question 6.
Find HCF of following numbers using Division method :
(a) 48, 60
(b) 120, 140
(c) 12, 18, 64
(d) 60, 96, 128
Solution:
(a)

∴ HCF of 120 and 140 = 20
(c) First find HCF of any two numbers say 12 and 18.

∴ HCF of 12, 18 and 64 = 2

(d) First find HCF of any two numbers say 60 and 96.

∴ HCF of 60 and 96 = 12
Now find HCF of 12 and 128

∴ HCF of 60, 96, 128 = 4

Question 7.
Find the largest number which divides 60, 75 and 90 without leaving any remainder.
Solution:
The largest number which divides 60, 75 and 90 without leaving any remainder = HCF of 60, 75 and 90
First find HCF of any two numbers say 60 and 75.

∴ HCF of 60 and 75 = 15
Now, find HCF of 15 and 90

The greatest number which divides 60, 75 and 90 = 15

Question 8.
There are three drums that contain 36l, 45l, and 72l milk respectively. Find the largest vessel which can measure milk of all the three drums completely.
Solution:

The capacity of the largest vessel that can measure milk of all the three drums completely = 9 l.

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 6 Measurement Ex 6.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 6 Measurement Ex 6.2

1. Find the weight.

Question 1.

Question 2.

Solution:
2 kg 250g = 2.250 kg

Question 3.

Solution:
1 kg 50 g = 1.50 kg

Question 4.

Solution:
2 kg 150 g = 2.150 kg

Question 2.
Tick ( ✓) the required weights for the following :

Solution:

3. Fill in the blanks :

Question 1.
2.850 kg = ……………….. kg …………… g
Solution:
2.850 kg = 2 kg 850 g

Question 2.
15.790 g = …………… g ……………….. mg
Solution:
15.790 g = 15 g 790 mg

Question 3.
……………….. kg = 12 kg 625 g
Solution:
12.625 kg = 12 kg 625 g

Question 4.
……………….. kg = 7 kg 75 g
Solution:
7.075 kg = 7 kg 75 g

Question 5.
……………….. g = 10 g 800 mg
Solution:
10.800 g = 10 g 800 mg

4. Convert :

Question 1.
3.275 g into mg
Solution:
3.275 g = 3.275 × 1000 mg = 3275 mg

Question 2.
8050 g into kg
Solution:
8050 g = \(\frac{8050}{1000}\) kg= 8.050 kg

Question 3.
4.2 kg into g
Solution:
4.2 kg = 4.2 × 1000 g = 4200 g

Question 4.
865 mg into g
Solution:
865 mg = \(\frac{865}{1000}\) g = 0.865 g

Question 5.
520 g into kg
Solution:
520 g = \(\frac{520}{1000}\) kg = 0.520 kg

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 6 Measurement Ex 6.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 6 Measurement Ex 6.1

1. Find the length:

Question 1.

Question 2.

Solution:
11 cm 0 cm = 11 cm

Question 3.

Solution:
4 cm 2 mm = 4.2 cm

Question 4.

Solution:
5 cm 8 mm = 5.8 cm

2. Measure the length of line segments in cm and draw on your notebooks.

Question 1.

Solution:
3.6 cm

Question 2.

Solution:
4.4 cm

Question 3.

Solution:
1.9 cm

Question 4.

Solution:
6 cm

Question 5.

Solution:
2.7 cm

Question 6.

Solution:
4.5 cm

3. Fill in the blanks:

Question 1.
3.45 m = …………….. m ……………….. cm
Solution:
3 m 45 cm

Question 2.
5.75 m = ……………. m ……………. cm
Solution:
5 m 75 cm

Question 3.
10.850 km = ………………. km …………….. m
Solution:
10 km 850 m

Question 4.
………………….. m = 4 m 25 cm
Solution:
4.25 m

Question 5.
……………… km = 7 km 375 m
Solution:
7.375 km

4. Convert the following:

Question 1.
4.5 cm into mm
Solution:
4.5 cm = 4.5 × 10 mm = 45 mm

Question 2.
270 m into km
Solution:
270 m = \(\frac{270}{1000}\) km = 0.270 km

Question 3.
5.82 km into m
Solution:
5.82 = 5.82 × 1000 m = 5820 m

Question 4.
0.65 m into cm
Solution:
0.65 = 0.65 × 100 cm = 65 cm

Question 5.
18 mm into m
Solution:
18 mm = \(\frac{18}{1000}\) m = 0.018 m

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 3 HCF and LCM Ex 3.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 3 HCF and LCM Ex 3.1

Question 1.
Write the first five multiples of the following numbers :
(a) 5
(b) 9
(c) 10
(d) 12
(e) 16
(f) 17
Solution:
(a) Multiples of 5 = 5, 10, 15, 20, 25
(b) Multiples of 9 = 9, 18, 27, 36, 45
(c) Multiples of 10 = 10, 20, 30, 40, 50
(d) Multiples of 12 = 12, 24, 36, 48, 60
(e) Multiples of 16 = 16, 32,48, 64, 80
(f) Multiples of 17 = 17, 34, 51, 68, 85

Question 2.
Find the factors of the given numbers :

Solution:
(a) 1, 5
(b) 1, 2, 4, 8
(c) 1, 2, 7, 14
(d) 1, 2, 3, 4, 6, 12
(e) 1, 5, 25
(f) 1, 2, 3, 4, 6, 9, 12, 18, 36

Question 3.
Write the factors of the following numbers :
(a) 18
(b) 24
(c) 35
(d) 36
(e) 45
(f) 21
Solution:
(a) 1, 2, 3, 6, 9, 18
(b) 1, 2, 3, 4, 6, 8, 12, 24
(c) 1, 5, 7, 35
(d) 1, 2, 3, 4, 6, 9, 12, 18, 36
(e) 1, 3, 5, 9, 15, 45
(f) 1, 3, 7, 21.

Question 4.
Find out the even numbers from the following :

Solution:
(a) 12, 34, 16, 28
(b) 48, 72, 90
(c) 450, 568, 664, 98
(d) 456, 968, 604, 888
(e) 136, 446, 1278
(f) 168, 5864.

Question 5.

Solution:
(a) 11, 23, 19, 35
(b) 45, 69, 97
(c) 451, 215, 789, 983
(d) 237, 739
(e) 631, 135, 249, 1279, 2851
(f) 49, 765, 1729, 9261, 6859.

Question 6.
Fill in the blanks :
(a) If 4 × 9 = 36 then factors of 36 are …….. and ………
(b) If 8 × 7 = 56 then factors of 56 are ……… and ……….
(c) If 3 × 5 × 6 = 90 then factors of 90 are ……., ……. and …….
(d) If 8 × 10 = 80, the multiple of 8 and 10 is ……….
(e) If 2 × 3 × 5 = 30, then 30, is the multiple of …….., ………. and ……..
Solution:
(a) 4, 9
(b) 8, 7
(c) 3, 5, 6
(d) 80
(e) 2, 3, 5.

Question 7.
Write True or False:

(a) 24 is a factor of 24. ____
(b) 2 is a factor of every number. ____
(c) 24 is an even number. ____
(d) 136 is an odd number. ____
(e) There are infinite multiples of a number. ____
(f) 36 is a multiple of 5 and 7. ____
(g) Sum of two even numbers is an odd number. ____
(h) Smallest even number is 0. ____
(i) 152 is an odd number. ____
(j) There are five single digit even numbers. ____
Solution:
(a) True
(b) False
(c) True
(d) False
(e) True
(f) False
(g) False
(h) False
(i) False
(j) False

Question 8.
Observe the Factorisation Pattern and complete :

Solution:

Question 9.
Look at the pattern and solve:

Solution:

Question 10.
Understand and complete the following:

Answer:

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 7 Geometry MCQ Questions and Answers.

PSEB 5th Class Maths Chapter 7 Geometry MCQ Questions

Multiple Choice Questions

Question 1.
Name the angle marked on the cover of book.

(a) Right angle
(b) Acute angle
(c) Obtuse angle
(d) Straight angle.
Answer:
(a) Right angle

Question 2.
The angle of 90° is called :
(a) Right angle
(b) Obtuse angle
(c) Acute angle
(d) Straight angle.
Answer:
(a) Right angle

Question 3.
The angle greater than 90° is called:
(a) Acute angle
(b) Right angle
(c) Obtuse angle
(d) Straight angle.
Answer:
(c) Obtuse angle

Question 4.
Make the axis of symmetry of the given figure.

Answer:

Question 5.

In the given figure angles have been marked. Write them in their columns in the table

Answer:
Obtuse angle : 4, 5, 6, 7 ;
Right angle : 2 ;
Acute angle : 1, 3, 8

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 7 Geometry Ex 7.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 7 Geometry Ex 7.5

Question 1.
Give an examples of the following from the surroundings:

Solution:

Question 2.
Which of the following can form cubes ? Draw them on paper and find answers :


Solution:
(a), (c), (d), (f).

3. Name the figures made from the following nets:

Question 1.

Solution:
cube

Question 2.

Solution:
Cuboid

Question 3.

Solution:
Cone

Question 4.

Solution:
Cylinder

Question 4.
Match the following figures with their nets :

Solution:
(a) – (iv)
(b) – (i)
(c) – (ii)
(d) – (iii).

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 7 Geometry Ex 7.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 7 Geometry Ex 7.4

Question 1.
Pick out 2-D and 3-D shapes from the following : Encircle 2-D shapes and draw on 3-D shapes :

Solution:
2-D shapes:

3-D shapes:
Battery. Cylinder, Football, Almirah and Tree.

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 7 Geometry Ex 7.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 7 Geometry Ex 7.3

Question 1.
Circle the symmetrical figures of the following :

Solution:
Symmetrical figure : Aeroplane.

Question 2.
Draw symmetry line in the following :

Solution:

3. Draw line of symmetry of the following:

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 4.
Complete the figure, if dotted line is a line of symmetry :

Solution:

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 2 Fundamental Operations on Numbers MCQ Questions and Answers.

PSEB 5th Class Maths Chapter 2 Fundamental Operations on Numbers MCQ Questions

Tick (✓) the right answer :

Question 1.
65432 + 34568
(a) 99999
(b) 100000
(c) 10000
(d) 99998.
Answer:
(b) 100000

Question 2.
35406 + 2580 + 43251 = 43251
+ ____ + 35406
(a) 35406
(b) 43251
(c) 2580
(d) 81237
Answer:
(c) 2580

Question 3.
99999 + 0
(a) 99990
(b) 99900
(c) 100000
(d) 99999
Answer:
(d) 99999

Question 4.
100000 – 1 = ___
(a) 10000
(b) 0
(c) 99999
(d) 100000.
Answer:
(c) 99999

Question 5.
Simar has ₹ 5832 and his sister Prabhjot has ₹ 3565. How much amount does Simar have more than his sister ?
(a) ₹ 2267
(b) ₹ 9397
(c) ₹ 2276
(d) ₹ 9973.
Answer:
(a) ₹ 2267

Question 6.
Surjeet has ₹ 50000 in her bank account and her hasband Charan Singh has ₹ 35682 in hisr account. What is total amount in both the accounts ?
(a) ₹ 14318
(b) ₹ 95682
(c) ₹ 85682
(d) ₹ 15318.
Answer:
(c) ₹ 85682

Question 7.
The population of a town is 12078. Out of that the number of men is 4872, women is 4729 and the rest are children. How many children are in the town ?
(a) 2477
(b) 20578
(c) 9601
(d) 8206.
Answer:
(a) 2477

Question 8.
98540 – ___ = 98539
(a) 0
(b) 1
(c) 98540
(d) 98539
Answer:
(b) 1

Question 9.
9999 + ___ = 100000
(a) 1
(b) 0
(c) 90001
(d) 9001.
Answer:
(c) 90001

Question 10.
1000 – __ = 999
(a) 1
(b) 0
(c) 90001
(d) 9001
Answer:
(a) 1

Question 11.
Find the difference between 5-digit smallest number and 4-digit largest number.
(a) 10000
(b) 9999
(c) 1
(d) 0
Answer:
(c) 1

Question 12.
Find the sum of the greatest and smallest 5-digit number using digits 2, 0, 4, 6, 7 ?
(a) 98687
(b) 96887
(c) 55953
(d) 76420.
Answer:
(b) 96887

Question 13.
1500 × 30 × 0 =
(a) 45000
(b) 30
(c) 0
(d) 450.
Answer:
(c) 0

Question 14.
7500 × 40 = 40 × ____
(a) 400
(b) 4000
(c) 750
(d) 7500.
Answer:
(d) 7500.

Question 15.
___ ÷ 100 = 1000
(a) 100
(b) 100000
(c) 10000
(d) 10.
Answer:
(b) 100000

Question 16.
The cost of a book ₹ 79. What is the cost of 12 books ?
(a) ₹ 948
(b) ₹ 938
(c) ₹ 790
(d) ₹ 793.
Answer:
(a) ₹ 948

Question 17.
Geeta has ₹ 175 with her. If she gives ₹ 25 to each child. How many children will get the money ?
(a) 6
(b) 9
(c) 1
(d) 8
Answer:
(c) 1

Question 18.
700 × ___ = 2800 × 1
(a) 5
(b) 6
(c) 4
(d) 3
Answer:
(c) 4

Question 19.
9999 ÷ 1 =
(a) 999
(b) 1
(c) 111
(d) 9999
Answer:
(d) 9999

Question 20.
8899 ÷ 8899 = ____
(a) 0
(b) 1
(c) 2
(d) 8899.
Answer:
(b) 1

Question 21.
99 × 99 = ____
(a) 99
(b) 9801
(c) 9901
(d) 1.
Answer:
(b) 9801

Question 22.
If price of 15 notebooks is ₹ 90. What is the price of one notebook ?
(a) ₹ 3
(b) ₹ 5
(c) ₹ 6
(d) ₹ 6.
Answer:
(c) ₹ 6

Question 23.
The Product of two numbers is 256. If one number is 256 then find the other number.
(a) 1
(b) 2
(c) 0
(d) 256.
Answer:
(a) 1

Question 24.
If 894 × 100 = 89400 then 894 × 10 = ____
(a) 894
(b) 89400
(c) 8940
(d) 8941.
Answer:
(c) 8940

Question 25.
26 ÷ 2 × 4 + 4 – 40 = ___
(a) 64
(b) 8
(c) 4
(d) 16.
Answer:
(d) 16.

Question 26.
A car has four wheels and auto has 3 wheels. Number of wheels of 2 cars and one auto is :

(a) 11
(b) 10
(c) 7
(d) 8.
Answer:
(a) 11

Question 27.
1500 × 30 × 0 = …….
(a) 1530
(b) 0
(c) 1
(d) 1230.
Answer:
(b) 0

Question.
Find the difference of the largest and the smallest number that can be formed by using the digits 5,1, 8, 6 and 7.
Solution:
The largest 5 digit number that can be formed by using the digits 5, 1, 8, 6 and 7 = 87651
The smallest 5 digit number that can be formed by using the digits 5, 1, 8, 6 and 7 = 15678
Their difference =

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 7 Geometry Ex 7.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 7 Geometry Ex 7.2

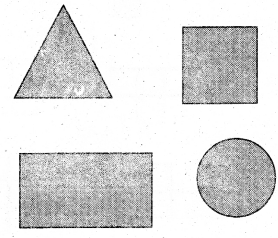
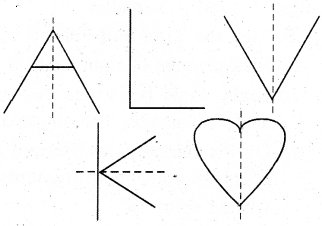
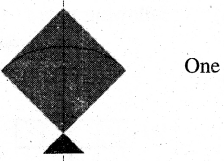
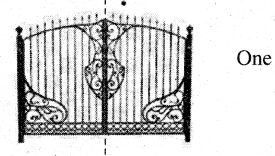
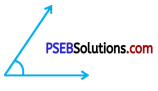
1. Measure the following angles using protractor:

Question 1.

Solution:
70°

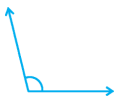
Question 2.

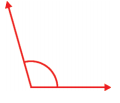
Solution:
105°

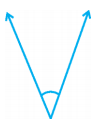
Question 3.

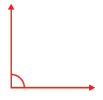
Solution:
90°

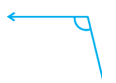
Question 4.

Solution:
130°

Question 5.

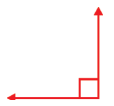
Solution:
90°

Question 6.

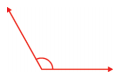
Solution:
115°

Question 7.

Solution:
20°

Question 8.

Solution:
50°

Question 9.

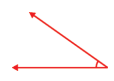
Solution:
35°

Question 10.

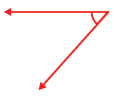
Solution:
50°

2. Draw the following angles by using a protractor:

Question 1.
15°
Solution:

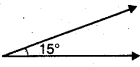
Question 2.
40°
Solution:

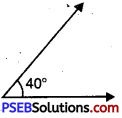
Question 3.
42°
Solution:

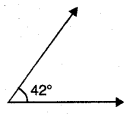
Question 4.
53°
Solution:

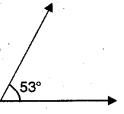
Question 5.
65°
Solution:

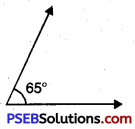
Question 6.
75°
Solution:

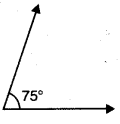
Question 7.
90°
Solution:

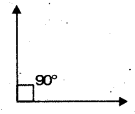
Question 8.
110°
Solution:

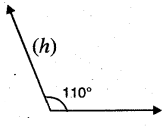
Question 9.
117°
Solution:

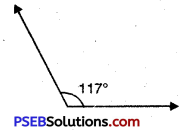
Question 10.
135°
Solution:

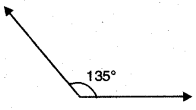
Question 11.
157°
Solution:

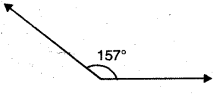
Question 12.
180°
Solution:

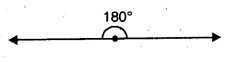
3. Pick out the acute angle, obtuse angle and right angle from the following :

Question 1.
35°
Solution:
Acute angle

Question 2.
89°
Solution:
Acute angle

Question 3.
120°
Solution:
Obtuse angle

Question 4.
100°
Solution:
Obtuse angle

Question 5.
96°
Solution:
Obtuse angle

Question 6.
74°
Solution:
Acute angle

Question 7.
62°
Solution:
Acute angle

Question 8.
166°.
Solution:
Obtuse angle.

4. Fill in the blanks :

Question 1.
An angle between 0° and 90° is called ………………
Solution:
Acute angle

Question 2.
175° angle is ……………… angle.
Solution:
Obtuse

Question 3.
The hands of a clock make an angle of ……………….. at 3 a.m.
Solution:
right angle

Question 4.
Measurements of an angle between North and South direction is ………………….
Solution:
180°

Question 5.
An acute angle is ……………….. than right angle.
Sol.
smaller.

5. Tick the True and False :

Question 1.
Measurement of right angle is 90°.
Solution:
True

Question 2.
Right angle is greater than acute angle but smaller than obtuse angle.
Solution:
True

Question 3.
On the Internal and External scale of protractor, measurements are written up to 90°.
Solution:
False

Question 4.
85° is a right angle.
Solution:
False

Question 5.
115° is an obtuse angle.
Solution:
True

Question 6.
90° is an acute angle.
Solution:
False