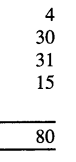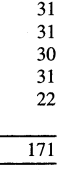Punjab State Board PSEB 4th Class Maths Book Solutions Chapter 2 Fundamental Operations on Numbers MCQ Questions and Answers.
PSEB 4th Class Maths Chapter 2 Fundamental Operations on Numbers MCQ Questions
Question 1.
573 + 227 = ____________
(a) 798
(b) 799
(c) 800
(d) 801.
Answer:
(c) 800
Question 2.
__________ + 336 = 868
(a) 632
(b) 528
(c) 532
(d) 1204.
Answer:
(c) 532

Question 3.
700 – 125 = ____________
(a) 475
(b) 575
(c) 675
(d) 825.
Answer:
(b) 575
Question 4.
801 – __________ = 602
(a) 201
(b) 1403
(c) 100
(d) 199.
Answer:
(d) 199
Question 5.
53 × 8 = 8 × __________
(a) 3
(b) 53
(c) 40
(d) 159
Answer:
(b) 53
Question 6.
716 × ________ = 716
(a) 0
(b) 1
(c) 716
(d) 2
Answer:
(b) 1

Question 7.
573 × 0 = _________
(a) 573
(b) 1
(c) 0
(d) 57
Answer:
(c) 0
Question 8.
_________ × 1 = 600
(a) 1
(b) 200
(c) 600
(d) 300
Answer:
(c) 600
Question 9.
7 × 1000 = ___________
(a) 7
(b) 1000
(c) 7000
(d) 700
Answer:
(c) 7000
Question 10.
53 × 30 = __________
(a) 159
(b) 1590
(c) 83
(d) 1690
Answer:
(b) 1590

Question 11.
128 ÷ 16 = __________
(a) 9
(b) 10
(c) 12
(d) 8
Answer:
(d) 8
Question 12.
126 ÷ 14 = 9, which is divisor?
(a) 14
(b) 9
(c) 126
(d) 0
Answer:
(a) 14
Question 13.
15 × 12 + 8 = __________
(a) 168
(b) 198
(c) 178
(d) 188
Answer:
(d) 188
Question 14.
1509 ÷ 1 = ___________
(a) 1
(b) 1509
(c) 3
(d) 0
Answer:
(b) 1509

Question 15.
In a school there are 22 students in 1st, 25 students in 2nd, 23 students in 3rd, 27 students in 4th and 23 students In 5th class. Find out total number of students in the school.
(a) 120
(b) 130
(c) 145
(d) 160
Answer:
(a) 120
Question 16.
Which number must be added in 779 to get the smallest number of 4 digit ?
(a) 231
(b) 220
(c) 321
(d) 221
Answer:
(d) 221
Question 17.
How many hours are there in the month of May ?
(a) 31
(b) 744
(c) 24
(d) 720
Answer:
(b) 744
Question 18.
Find the difference between 4 digits greatest number and the smallest number by using digits 2,0, 4 and 6.
(a) 3747
(b) 6174
(c) 2046
(d) 4374.
Answer:
(d) 4374

Question 19.
Find the product of 3 digits smallest number and 2 digits greatest number.
(a) 9900
(b) 10,000
(c) 290
(d) 9700.
Answer:
(a) 9900
Question 20.
After distributing 178 toffees among 15 children equally, find the number of toffees left.
(a) 13
(b) 14
(c) 12
(d) 11
Answer:
(a) 13
Question 21.
19 × 300 = _________
(a) 57000
(b) 5700
(c) 2200
(d) 319
Answer:
(b) 5700

Question 22.
225 × ___________ = 2250
(a) 1
(b) 10
(c) 100
(d) 0
Answer:
(b) 10
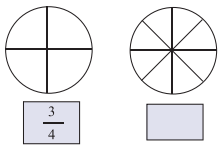
Brain Teaser
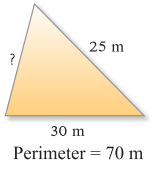
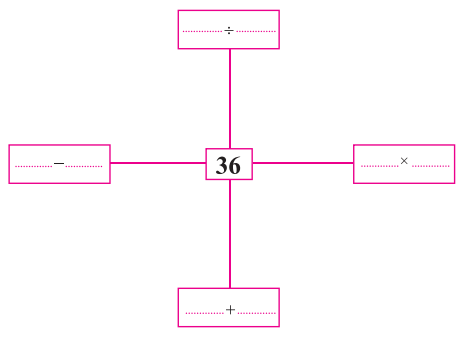
Question 1.
Fill in the blank boxes replacing sign of ?
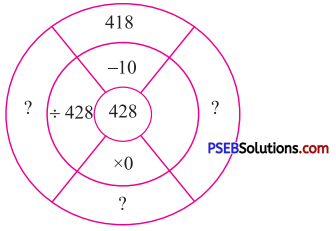
Solution:
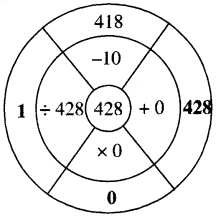
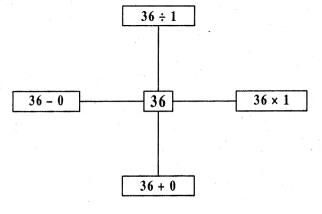
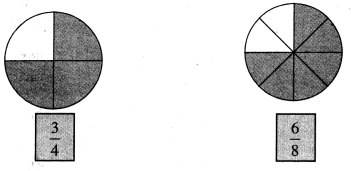
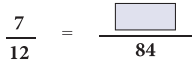
Question 2.
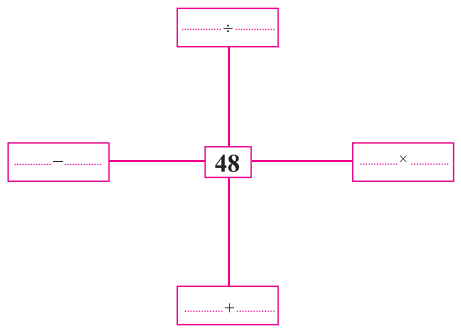
Solution:
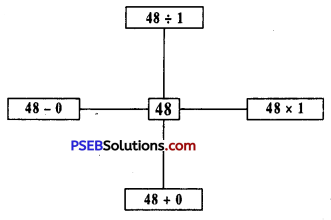
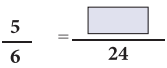
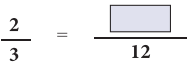
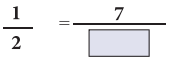
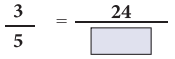
Question 3.
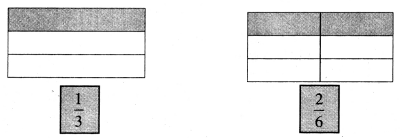
Solution:

![]()
![]()

![]()
![]()
![]()
![]()

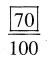
![]()
![]()
![]()

![]()
![]()