Bhagya

Punjab State Board PSEB 10th Class Physical Education Book Solutions Chapter 4 ਏਸ਼ੀਅਨ ਅਤੇ ਉਲੰਪਿਕ ਖੇਡਾਂ Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 10 Physical Education Chapter 4 ਏਸ਼ੀਅਨ ਅਤੇ ਉਲੰਪਿਕ ਖੇਡਾਂ

Physical Education Guide for Class 10 PSEB ਏਸ਼ੀਅਨ ਅਤੇ ਉਲੰਪਿਕ ਖੇਡਾਂ Textbook Questions and Answers

ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Very Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਓਲੰਪਿਕ ਖੇਡਾਂ ਦਾ ਨਾਂ ਓਲੰਪਿਕ ਕਿਉਂ ਪਿਆ ? (Why Olympic games are called Olympic ?)
ਉੱਤਰ-
ਪਾਚੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਓਲੰਪੀਆ ਨਾਮੀ ਨਗਰ ਵਿਚ ਆਰੰਭ ਹੋਈਆਂ ਸਨ, ਇਸ ਕਰਕੇ ਇਹਨਾਂ ਖੇਡਾਂ ਦਾ ਨਾਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਪਿਆ ।

ਪ੍ਰਸ਼ਨ 2.
ਪ੍ਰਾਚੀਨ ਖੇਡਾਂ ਕਦੋਂ ਸ਼ੁਰੂ ਹੋਈਆਂ ?(When Ancient Olympic games started ?)
ਉੱਤਰ-
ਪ੍ਰਾਚੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ 776 ਈ: ਪੂ: ਵਿਚ ਯੂਨਾਨ ਵਿਚ ਸ਼ੁਰੂ ਹੋਈਆਂ ।

ਪ੍ਰਸ਼ਨ 3.
ਓਲੰਪਿਕ ਝੰਡੇ ਵਿਚ ਕਿੰਨੇ ਰਿੰਗ ਹੁੰਦੇ ਹਨ ? (How many rings are these in Olympic Flag ?)
ਉੱਤਰ-
ਪੰਜ ਰਿੰਗ ।

ਪ੍ਰਸ਼ਨ 4.
ਪ੍ਰਾਚੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦੇ ਵਿਜੇਤਾਵਾਂ ਨੂੰ ਕੀ ਇਨਾਮ ਮਿਲਦਾ ਸੀ ? (What prizes are given to the winner of Ancient Olympic ?)
ਉੱਤਰ-
ਵਿਜੇਤਾਵਾਂ ਨੂੰ ਜੀਅਸ ਦੇਵਤਾ ਦੇ ਮੰਦਰ ਵਿਚ ਲਿਜਾ ਕੇ ਜੈਤੁਨ ਰੁੱਖ ਦੀਆਂ ਟਹਿਣੀਆਂ ਅਤੇ ਪੱਤੇ ਭੇਟ ਕੀਤੇ ਜਾਂਦੇ ਸਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਪਾਚੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦੇ ਕੋਈ ਦੋ ਨਿਯਮ ਲਿਖੋ । (Write any two rules of Ancient Olympic.)
ਉੱਤਰ-

1. ਇਹਨਾਂ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲੇ ਸਭ ਖਿਡਾਰੀ ਯੂਨਾਨ ਦੇ ਨਾਗਰਿਕ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।
2. ਕੋਈ ਵੀ ਕਿੱਤਾਕਾਰ (Professional) ਖਿਡਾਰੀ ਇਹਨਾਂ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਨਹੀਂ ਲੈ ਸਕਦਾ ਸੀ ।

ਪ੍ਰਸ਼ਨ 6.
ਨਵੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਕਿਸ ਨੇ ਸ਼ੁਰੂ ਕਰਵਾਈਆਂ ? (Who was the founder of Modern Olympic Games ?)
ਉੱਤਰ-
ਬੈਰਨ ਪਾਇਰ ਡੀ. ਕਬਰਟਿਨ ਨੇ ।

ਪ੍ਰਸ਼ਨ 7.
ਨਵੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਕਿੱਥੇ ਅਤੇ ਕਦੋਂ ਸ਼ੁਰੂ ਹੋਈਆਂ ? (When and where Modern Olympic were started ?)
ਉੱਤਰ-
ਨਵੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ 1896 ਈ: ਨੂੰ ਏਥਨਜ਼ ਵਿਚ ਸ਼ੁਰੂ ਹੋਈਆਂ ।

ਪ੍ਰਸ਼ਨ 8.
ਨਵੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦੇ ਕੋਈ ਦੋ ਨਿਯਮ ਲਿਖ । (Write any two rules of Modern Olympic Games.)
ਉੱਤਰ-

1. ਇਸ ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲੇ ਖਿਡਾਰੀ ਤੇ ਉਮਰ, ਜਾਤੀ, ਧਰਮ ਆਦਿ ਦਾ ਪਤੀਬੰਧ ਨਹੀਂ ਹੈ ।
2. ਕੋਈ ਵੀ ਵਿਵਸਾਇਕ ਖਿਡਾਰੀ (Professional Player) ਓਲੰਪਿਕ ਖੇਡ ਵਿਚ ਭਾਗ ਨਹੀਂ ਲੈ ਸਕਦਾ ।

ਪ੍ਰਸ਼ਨ 9.
ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਕਿਸ ਦੇ ਯਤਨ ਨਾਲ ਸ਼ੁਰੂ ਹੋਈਆਂ ? (Who has originated Asian Games ?)
ਉੱਤਰ-
ਮਹਾਰਾਜਾ ਪਟਿਆਲਾ ਸਰਦਾਰ ਯਾਦਵਿੰਦਰ ਸਿੰਘ ਅਤੇ ਜੀ. ਡੀ. ਸੋਂਧੀ ਦੇ ਯਤਨਾਂ ਨਾਲ ਇਹ ਖੇਡਾਂ ਸ਼ੁਰੂ ਹੋਈਆਂ ।

ਪ੍ਰਸ਼ਨ 10.
ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਕਦੋਂ ਅਤੇ ਕਿੱਥੇ ਸ਼ੁਰੂ ਹੋਈਆਂ ? (When and where Asian Games were started ?)
ਉੱਤਰ-
ਪਹਿਲੀਆਂ ਏਸ਼ਿਆਈ ਖੇਡਾਂ 1951 ਨੂੰ ਨਵੀਂ ਦਿੱਲੀ ਦੇ ਨੈਸ਼ਨਲ ਸਟੇਡੀਅਮ ਵਿਚ ਹੋਈਆਂ ।

ਪ੍ਰਸ਼ਨ 11.
ਓਲੰਪਿਕ ਖੇਡਾਂ ਕਿੰਨੇ ਚਿਰ ਬਾਅਦ ਹੁੰਦੀਆਂ ਹਨ ? (After how many years Olympic games were held ?)
ਉੱਤਰ-
ਚਾਰ ਸਾਲ ਬਾਅਦ ।

ਪ੍ਰਸ਼ਨ 12.
ਪੰਜਵੀਆਂ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਕਿੱਥੇ ਹੋਈਆਂ ? (Where were the fifth Asian games were held ?)
ਉੱਤਰ-
ਇਹ ਖੇਡਾਂ 1966 ਵਿਚ ਜਕਾਰਤਾ (ਇੰਡੋਨੇਸ਼ੀਆ) ਵਿੱਚ ਹੋਈਆਂ ।

ਪ੍ਰਸ਼ਨ 13.
ਮਿਲਖਾ ਸਿੰਘ ਨੇ ਕਿਹੜੇ ਓਲੰਪਿਕ ਵਿਚ 400 ਮੀਟਰ ਦੀ ਦੌੜ ਵਿਚ ਚੌਥਾ ਸਥਾਨ ਹਾਸਿਲ ਕੀਤਾ ਸੀ ?(In which Olympic Mr. Milkha Singh got 4th position in 400 mt. race ?)
ਉੱਤਰ-
1984 ਓਲੰਪਿਕ ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 14.
ਭਾਰਤ ਨੇ ਪਹਿਲੀ ਵਾਰ ਓਲੰਪਿਕ ਵਿਚ ਭਾਗ ਕਦੋਂ ਲਿਆ ਸੀ ? (In which year India participated in Olympic first time ?)
ਉੱਤਰ-
1920 ਦੇ ਓਲੰਪਿਕ ਵਿਚ ।

ਪ੍ਰਸ਼ਨ 15.
2008 ਬੀਜਿੰਗ ਉਲੰਪਿਕ ਖੇਡਾਂ ਵਿੱਚ ਕਿਸ ਭਾਰਤੀ ਖਿਡਾਰੀ ਨੇ ਸਵਰਨ ਪਦਕ ਜਿੱਤਿਆ ?
ਉੱਤਰ-
ਸ੍ਰੀ ਅਭੀਨਵ ਬਿੰਦਰਾ ਨੇ 2008 ਬੀਜਿੰਗ ਉਲੰਪਿਕ ਗੇਮ ਵਿੱਚ ਸੋਨੇ ਦਾ ਤਗਮਾ ਜਿੱਤਿਆ ।

ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਓਲੰਪਿਕ ਝੰਡੇ ਸੰਬੰਧੀ ਸੰਖੇਪ ਜਾਣਕਾਰੀ ਦਿਓ : (Give brief description about Olympic Flag.)
ਉੱਤਰ-
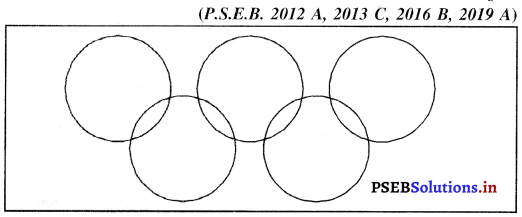
ਓਲੰਪਿਕ ਝੰਡਾ 1919 ਈ: ਵਿਚ ਇੱਟਵਰਪ (Antwerp) ਵਿਚ ਹੋਣ ਵਾਲੀਆਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਲਹਿਰਾਇਆ ਗਿਆ । ਇਸ ਝੰਡੇ ਦੀ ਰਚਨਾ ਕੁਬਰਟਿਨ ਨੇ ਕੀਤੀ ਸੀ । ਇਸ ਝੰਡੇ ਵਿਚ ਪੰਜ ਰੰਗਾਂ-ਲਾਲ, ਹਰਾ, ਪੀਲਾ, ਨੀਲਾ ਅਤੇ ਕਾਲਾ ਨਾਲ ਪੰਜ ਚੱਕਰ ਆਪਸ ਵਿਚ ਜੋੜ ਕੇ ਬਣਾਏ ਗਏ ਹਨ । ਇਹ ਪੰਜ ਚੱਕਰ ਯੂਰਪ, ਆਸਟਰੇਲੀਆ, ਏਸ਼ੀਆ, ਅਫ਼ਰੀਕਾ ਅਤੇ ਅਮਰੀਕਾ-ਪੰਜ ਮਹਾਂਦੀਪਾਂ ਦੀ ਪ੍ਰਤੀਨਿਧਤਾ ਕਰਦੇ ਹਨ । ਇਹਨਾਂ ਚੱਕਰਾਂ ਦਾ ਆਪਸ ਵਿਚ ਜੁੜੇ ਹੋਣਾ ਇਹਨਾਂ ਪੰਜ ਮਹਾਂਦੀਪਾਂ ਦੀ ਮਿੱਤਰਤਾ ਅਤੇ ਸਦਭਾਵਨਾ ਦਾ ਪ੍ਰਤੀਕ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਓਲੰਪਿਕ ਖੇਡਾਂ ਕਦੋਂ ਤੇ ਕਿਹੜੇ-ਕਿਹੜੇ ਦੇਸ਼ ਵਿਚ ਹੋਈਆਂ ? (When and where Olympic Games are organised ?)
ਉੱਤਰ-
ਪਹਿਲੀਆਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦੇ ਸਥਾਨ ਤੇ ਤਾਰੀਖਾਂ

• 1896 – ਏਥਨਜ਼
• 1900 – ਪੈਰਿਸ
• 1904 – ਸੇਂਟ ਲੂਈਸ
  1906* – ਏਥਨਜ਼
• 1908 – ਲੰਦਨ
• 1916 – ਸਟਾਕਹੋਮ .
• 1918 – ਬਰਲਿਨ
• 1920 – ਅੰਦੀਪ
• 1924 – ਪੈਰਿਸ
• 1928 – ਐਮਸਟਰਡਮ
• 1932 – ਲਾਸ ਏਂਜਲਸ
• 1936 – ਬਰਲਿਨ
• 1940 – ਟੋਕੀਓ (ਉਸ ਸਮੇਂ ਹੇਲਸਿੰਕੀ)
• 1944 – ਲੰਦਨ

*1904 ਦੀਆਂ ਖੇਡਾਂ ਆਧੁਨਿਕ ਖੇਡਾਂ ਦੀ 10ਵੀਂ ਵਰ੍ਹੇ ਗੰਢ ਆਉਣ ਲਈ ਕਰਾਈਆਂ ਗਈਆਂ ਪਰ ਉਨ੍ਹਾਂ ਦੀ ਗਿਣਤੀ ਨਹੀਂ ਕੀਤੀ ਗਈ ਕਿਉਂਕਿ ਇਹ ਖੇਡਾਂ 1904-1908 ਦੇ ਉਲੰਪਿਕ ਦੇ ਪਹਿਲੇ ਵਰੇ ਵਿਚ ਨਹੀਂ ਸਨ ਕਰਵਾਈਆਂ ਗਈਆਂ ।

• 1960 – ਰੋਮ
• 1964 – ਟੋਕੀਓ
• 1968 – ਮੈਕਸੀਕੋ ਸ਼ਹਿਰ
• 1972 – ਮਿਉਨਿਖ
• 1976 – ਮਾਂਟਰੀਆਲ
• 1980 – ਮਾਸਕੋ
• 1984 – ਲਾਸ ਏਂਜਲਸ
• 1988 – ਸਿਉਲ
• 1992 – ਬਾਰਸੀਲੋਨਾ
• 1996 – ਅਟਲਾਂਟੀਕਾ
• 2000 – ਸਿਡਨੀ
• 2004 – ਐਥਨ
• 2008 – ਚੀਨ
• 2012 – ਲੰਡਨ
• 2016 – ਰਿਓ
• 2020 – ਟੋਕੀਓ (ਜਾਪਾਨ)

ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Long Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਪ੍ਰਾਚੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਕਿੱਥੇ, ਕਦੋਂ ਤੇ ਕਿਉਂ ਸ਼ੁਰੂ ਹੋਈਆਂ ? [ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ – 1] (When, where and why Ancient Olympic was organised ?)
ਉੱਤਰ-
ਇਤਿਹਾਸ (History) – ਪ੍ਰਾਚੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ 776 ਈ: ਪੂ: ਵਿਚ ਯੂਨਾਨ ਦੇ ਉਲੰਪੀਆ ਨਾਮੀ ਨਗਰ ਵਿਚ ਆਰੰਭ ਹੋਈਆਂ । ਇਹਨਾਂ ਖੇਡਾਂ ਨੂੰ ਆਰੰਭ ਕਰਨ ਦਾ ਸਿਹਰਾ ਇਫਿਟਸ ਅਤੇ ਕਲਾਉਸਥੈਨੀਥ ਨੂੰ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇਹ ਅਗਸਤ ਅਤੇ ਸਤੰਬਰ ਮਹੀਨੇ ਦੀ ਪੁੰਨਿਆਂ ਦੀ ਰਾਤ ਨੂੰ ਆਰੰਭ ਹੋਈਆਂ । ਪਹਿਲੀਆਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦੇ ਜੇਤੂ ਦਾ | ਨਾਂ ਕੋਰਬਸ ਸੀ । ਇਹ ਖੇਡਾਂ ਹਰ ਸਾਲ ਦੇ ਬਾਅਦ ਪ੍ਰਬੰਧਿਤ ਕੀਤੀਆਂ ਜਾਂਦੀਆਂ ਸਨ । 394 ਈ: ਪੂ: ਵਿਚ ਰੋਮ ਸਮਰਾਟ ਥੀਓਡੀਸੀਅਜ ਦੇ ਹੁਕਮ ਨਾਲ ਇਹ ਖੇਡਾਂ ਬੰਦ ਹੋ ਗਈਆਂ । ਉਲੰਪੀਆ ਨਗਰ ਏਲਿਸ ਨਦੀ ਦੇ ਤੱਟ ‘ਤੇ ਵਸਿਆ ਹੋਇਆ ਸੀ । ਇਹ ਏਲਿਜ ਰਾਜ ਦਾ
**ਇੱਥੇ ਸਿਰਫ ਘੋੜ-ਸਵਾਰੀ ਦੀਆਂ ਹੀ ਖੇਡਾਂ ਕਰਵਾਈਆਂ ਗਈਆਂ ਸਨ ।

ਪਵਿੱਤਰ ਨਗਰ ਸੀ 1100 ਈ: ਪੂ: ਵਿਚ ਇਹਨਾਂ ਖੇਡਾਂ ਲਈ ਵਿਸ਼ੇਸ਼ ਜਗਾ ਬਣ ਗਈ ਜਿਸ ਦੀ ਪੂਜਾ ਮੰਦਰ ਦੀ ਤਰ੍ਹਾਂ ਹੋਣ ਲੱਗੀ । ਉਲੰਪਿਕ ਖੇਡਾਂ ਦੇ ਸ਼ੁਰੂ ਹੋਣ ਤੇ ਸਾਰੇ ਯੂਨਾਨ
ਵਿਚ ਲੜਾਈਆਂ ਬੰਦ ਹੋ ਜਾਂਦੀਆਂ ਸਨ । ਉਲੰਪੀਆ ਨਗਰ ਵਿਚ ਕੋਈ ਵੀ ਸ਼ਸਤਰਾਂ ਦੇ ਨਾਲ | ਪ੍ਰਵੇਸ਼ ਨਹੀਂ ਕਰ ਸਕਦਾ ਸੀ । ਇਹ ਖੇਡਾਂ ਯੂਨਾਨੀ ਦੇਵਤਾ ਜੀਅਸ ਦੇ ਨਾਲ ਸੰਬੰਧਿਤ ਹਨ ।

ਖੇਡਾਂ (Sports) – ਪ੍ਰਾਚੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਪਹਿਲਾਂ ਦੌੜ (Race) ਹੀ ਹੁੰਦੀ ਸੀ । ਇਹ ਲਗਪਗ 100 ਗਜ਼ ਲੰਬੀਆਂ ਸਨ । 724 ਈ: ਪੂ: ਵਿਚ 400 | ਗਜ਼ ਦੀ ਦੌੜ ਦਾ ਵਾਧਾ ਕੀਤਾ ਗਿਆ । ਪੰਦਰਵੀਆਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਤਿੰਨ ਮੀਲ ਦੀ ਦੌੜ ਦਾ ਵਾਧਾ ਕੀਤਾ ਗਿਆ । 18ਵੀਂ ਓਲੰਪਿਕਸ ਵਿਚ ਪੈਂਟਾਥਲੋਨ (Pentathlon) ਸ਼ੁਰੂ | ਕੀਤੀ ਗਈ । ਇਸ ਵਿਚ ਲੰਮੀ ਛਾਲ, ਦੋ ਸੌ ਗਜ਼ ਦੀ ਦੌੜ, ਨੇਜ਼ਾ ਸੁੱਟਣਾ ਅਤੇ ਕੁਸ਼ਤੀਆਂ | ਪੰਜ ਖੇਡਾਂ ਰੱਖੀਆਂ ਗਈਆਂ । 25ਵੀਂ ਓਲੰਪਿਕਸ ਵਿਚ ਰੱਥ ਦੌੜ (Chariot Race) ਅਤੇ |30ਵੀਂ ਓਲੰਪਿਕਸ ਵਿਚ ਮੁੱਕੇਬਾਜ਼ੀ, ਪਾਣੀ ਦੀਆਂ ਖੇਡਾਂ, ਕੁਸ਼ਤੀਆਂ ਅਤੇ ਪੈਕਪ੍ਰੀਅਮ ਆਦਿ ਖੇਡਾਂ ਸ਼ਾਮਲ ਕੀਤੀਆਂ ਗਈਆਂ । ਇਹ ਖੇਡਾਂ ਤਿੰਨ ਤੋਂ ਪੰਜ ਦਿਨ ਤਕ ਚਲਦੀਆਂ ਸਨ । | ਪਹਿਲਾਂ ਇਸਤਰੀਆਂ ਇਹਨਾਂ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਨਹੀਂ ਲੈ ਸਕਦੀਆਂ ਸਨ ਪਰ ਬਾਅਦ ਵਿਚ ਇਸਤਰੀਆਂ ਲਈ ਵੀ ਦਰਵਾਜ਼ੇ ਖੋਲ੍ਹ ਦਿੱਤੇ ਗਏ ।

ਇਨਾਮ (Rewards) – ਇਹਨਾਂ ਖੇਡਾਂ ਦੇ ਜੇਤੂਆਂ ਨੂੰ ਖੂਬ ਸਨਮਾਨਿਤ ਕੀਤਾ ਜਾਂਦਾ ਸੀ । ਉਹਨਾਂ ਨੂੰ ਜੀਅਸ ਦੇਵਤਾ ਦੇ ਮੰਦਰ ਵਿਚ ਲੈ ਜਾ ਕੇ ਜੈਤਨ ਰੁੱਖ ਦੀਆਂ ਟਹਿਣੀਆਂ ਅਤੇ ਪੱਤੇ ਭੇਂਟ ਕੀਤੇ ਜਾਂਦੇ ਸਨ । ਲੋਕ ਉਹਨਾਂ ਦੀ ਜਿੱਤ ਦੇ ਜੇਤੂ | ਗੀਤ ਗਾਉਂਦੇ ਸਨ । ਜੇਤੂਆਂ ਦੇ ਨਾਂ ਤੇ ਖੇਡਾਂ ਦੇ ਨਾਂ ਰੱਖੇ ਜਾਂਦੇ ਸਨ । ਜੇਤੂਆਂ ਦੇ ਸਾਥੀ ਵਾਜਾ | ਵਜਾ ਕੇ ਉਹਨਾਂ ਦੇ ਘਰ ਛੱਡ ਆਉਂਦੇ ਸਨ । ਜੇਤੂ ਖਿਡਾਰੀਆਂ ਤੇ ਦੇਸ਼ ਮਾਣ ਕਰਦਾ ਜਾਂ ਸਭ ਯੂਨਾਨੀ ਇਹਨਾਂ ਖੇਡਾਂ ਵਿਚ ਜਿੱਤ ਪ੍ਰਾਪਤ ਕਰਨ ਦੀ ਹਾਰਦਿਕ ਕਾਮਨਾ ਕਰਦੇ ਸਨ ।

ਸਮਾਪਤੀ (End) – ਸਮੇਂ ਦੀ ਗਤੀ ਦੇ ਨਾਲ ਇਹ ਖੇਡਾਂ ਲੋਕਪ੍ਰਿਯ ਹੁੰਦੀਆਂ ਗਈਆਂ ਅਤੇ ਹੋਰ ਦੇਸ਼ਾਂ ਅਤੇ ਰਾਸ਼ਟਰਾਂ ਨੇ ਵੀ ਭਾਗ ਲੈਣਾ ਆਰੰਭ ਕਰ ਦਿੱਤਾ । ਰੋਮਨਾਂ ਦੁਆਰਾ ਯੂਨਾਨ ਦੀ ਜਿੱਤ ਦੇ ਬਾਅਦ ਇਹਨਾਂ ਖੇਡਾਂ ਦੀ ਲੋਕਪ੍ਰਿਯਤਾ ਨੂੰ ਠੇਸ ਪੁੱਜੀ । ਕਈ ਕਿੱਤਾਕਾਰ (Professional) ਖਿਡਾਰੀ ਇਹਨਾਂ ਵਿਚ ਭਾਗ ਲੈਣ ਲੱਗੇ । ਇਸ | ਨਾਲ ਖੇਡਾਂ ਵਿਚ ਕਈ ਬੁਰਾਈਆਂ ਘਰ ਕਰ ਗਈਆਂ । ਰੋਮਨ ਸਮਰਾਟ ਥੀਓਜੀਸੀਅਸ ਦੇ | ਆਦੇਸ਼ ਨਾਲ 394 ਈ: ਪੂ: ਵਿਚ ਇਹ ਖੇਡਾਂ ਬੰਦ ਕਰ ਦਿੱਤੀਆਂ ਗਈਆਂ । 395 ਈ: ਪੂ: ਵਿਚ ਜੀਅਸ ਦੇਵਤਾ ਦਾ ਬੁੱਤ ਵੀ ਤੋੜ ਦਿੱਤਾ ਗਿਆ । ਓਲੰਪਿਕ ਨਗਰ ਦੀ ਰੌਣਕ ਖ਼ਤਮ | ਹੋ ਗਈ । ਰੋਮਨ ਸਮਰਾਟ ਥੀਓਡੀਸੀਅਸ ਦੁਜੇ ਨੇ ਸਟੇਡੀਅਮ ਵੀ ਨਸ਼ਟ ਕਰਵਾ ਦਿੱਤੇ । ਇਸ ਤਰ੍ਹਾਂ ਕੁੱਝ ਸਮੇਂ ਤਕ ਓਲੰਪਿਕ ਖੇਡਾਂ ਅਤੇ ਓਲੰਪਿਕ ਨਗਰ ਦੇ ਚਿੰਨ੍ਹ ਹੀ ਮਿਟ ਗਏ ।’

ਪ੍ਰਸ਼ਨ 2.
ਪਾਚੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦੇ ਕੀ ਨਿਯਮ ਸਨ ਅਤੇ ਕਿਹੜੀਆਂ-ਕਿਹੜੀਆਂ ਖੇਡਾਂ ਕਰਵਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ? [ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ-2] (What were the main Rules of the Ancient Olympic Games ? Which were the different games organised ?)
ਉੱਤਰ-
ਪ੍ਰਾਚੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦੇ ਨਿਯਮ (Rules of Ancient Olympics) – ਪ੍ਰਾਚੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਲੈਣ ਲਈ ਹੇਠ ਲਿਖੇ ਨਿਯਮਾਂ ਦਾ ਪਾਲਣ ਕਰਨਾ ਬਹੁਤ ਜ਼ਰੂਰੀ ਸੀ-

• ਇਹਨਾਂ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲੇ ਸਭ ਖਿਡਾਰੀ ਯੂਨਾਨ ਦੇ ਨਾਗਰਿਕ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।
• ਖਿਡਾਰੀ ਲਈ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਲੈਣ ਤੋਂ ਪਹਿਲਾਂ ਕਿਸੇ ਵੀ ਦੇਖ-ਰੇਖ ਵਿਚ 10 ਮਹੀਨਿਆਂ ਤਕ ਟਰੇਨਿੰਗ ਲੈਣਾ ਜ਼ਰੂਰੀ ਸੀ । ਉਸ ਨੂੰ ਅਖ਼ੀਰਲਾ ਇਕ ਮਹੀਨਾ ਉਲੰਪੀਆ ਵਿਚ ਬਤੀਤ ਕਰਨਾ ਪੈਂਦਾ ਸੀ ।
• ਕੋਈ ਵੀ ਕਿੱਤਾਕਾਰ (Professional) ਖਿਡਾਰੀ ਇਹਨਾਂ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਨਹੀਂ ਲੈ ਸਕਦਾ ਸੀ ।
• ਆਰੰਭ ਵਿਚ ਔਰਤਾਂ ਨੂੰ ਨਾ ਤਾਂ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਲੈਣ ਅਤੇ ਨਾ ਹੀ ਇਹਨਾਂ ਨੂੰ ਵੇਖਣ ਦੀ ਆਗਿਆ ਸੀ ।
• ਖਿਡਾਰੀਆਂ ਨੂੰ ਖੇਡਾਂ ਵਿਚ ਠੀਕ ਢੰਗ ਨਾਲ ਭਾਗ ਲੈਣ ਦੀ ਸਹੁੰ ਲੈਣੀ ਪੈਂਦੀ ਸੀ ।
• ਖਿਡਾਰੀਆਂ ਤੇ ਕਿਸੇ ਕਿਸਮ ਦੇ ਅਪਰਾਧ ਦਾ ਅਰੋਪ ਨਹੀਂ ਹੋਣਾ ਚਾਹੀਦਾ ।
• ਪਹਿਲਾ ਅਤੇ ਅੰਤਿਮ ਦਿਨ ਧਾਰਮਿਕ ਰੀਤੀਆਂ ਅਤੇ ਬਲੀਆਂ ਲਈ ਨਿਸਚਿਤ ਸੀ ।

ਖੇਡਾਂ (Sports) – ਪ੍ਰਾਚੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਪਹਿਲਾਂ ਤਾਂ ਕੇਵਲ ਇਕ ਦੌੜ ਸ਼ਾਮਲ ਸੀ, ਪਰ ਹੌਲੀ-ਹੌਲੀ ਇਸ ਵਿਚ ਹੋਰ ਖੇਡਾਂ ਸ਼ਾਮਲ ਹੋ ਗਈਆਂ । ਇਹ ਦੌੜ ਲਗਪਗ 100 ਗਜ਼ ਲੰਬੀ ਸੀ । 724 ਈ: ਪੂ: ਵਿਚ ਪ੍ਰਬੰਧਿਤ 14ਵੀਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ 400 ਗਜ਼ ਦੀ ਦੌੜ ਵਿਚ ਪੈਂਟਾਥਲੋਨ ਆਰੰਭ ਕੀਤੀ ਗਈ । ਇਸ ਵਿਚ ਲੰਮੀ ਛਾਲ, ਨੇਜ਼ਾ ਬਾਜ਼ੀ, 200 ਗਜ਼ ਦੌੜ ਅਤੇ 15ਵੀਂ ਓਲੰਪਿਕਸ ਵਿਚ 3 ਮੀਲ ਦੀ ਦੌੜ ਸ਼ਾਮਲ ਕੀਤੀ ਗਈ । 18ਵੀਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਪੈਂਟਾਥਲੋਨ ਆਰੰਭ ਕੀਤੀ ਗਈ । ਇਸ ਵਿਚ ਲੰਮੀ ਛਾਲ, ਨੇਜ਼ਾਬਾਜ਼ੀ, 200 ਗਜ਼ ਦੌੜ, ਡਿਸਕਸ ਥਰੋ ਅਤੇ ਕੁਸ਼ਤੀਆਂ ਪੰਜ ਖੇਡਾਂ ਆਉਂਦੀਆਂ ਸਨ । 23ਵੀਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਅਤੇ 25ਵੀਂ ਓਲੰਪਿਕਸ ਵਿਚ 3 ਮੀਲ ਦੀ ਦੌੜ ਸ਼ਾਮਲ ਕੀਤੀ ਗਈ । 28ਵੀਂ ਓਲੰਪਿਕਸ ਖੇਡਾਂ ਵਿਚ ਰਥ ਦੌੜ ਅਤੇ 30ਵੀਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਪਾਣੀ ਦੀਆਂ ਖੇਡਾਂ ਨੂੰ ਥਾਂ ਦਿੱਤੀ ਗਈ । ਇਹ ਖੱਡਾਂ 3 ਤੋਂ 5 ਦਿਨ ਤਕ ਚਲਦੀਆਂ ਸਨ । ਪਹਿਲਾਂ ਇਸਤਰੀਆਂ ਇਹਨਾਂ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਨਹੀਂ ਲੈ ਸਕਦੀਆਂ ਸਨ, ਪਰ ਬਾਅਦ ਵਿਚ ਉਹਨਾਂ ਨੂੰ ਆਗਿਆ ਦੇ ਦਿੱਤੀ ਗਈ ।

ਪ੍ਰਸ਼ਨ 3.
ਨਵੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਕਿਸ ਨੇ ਸ਼ੁਰੂ ਕਰਵਾਈਆਂ ਅਤੇ ਉਸ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? [ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ] (Who has started Modern Olympic Games ? What do you know about him ?)
ਉੱਤਰ-
14ਵੀਂ ਸਦੀ ਤਕ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦੇ ਮਹੱਤਵ ਵਲ ਕਿਸੇ ਨੇ ਜ਼ਰਾ ਧਿਆਨ ਨਾ, ਦਿੱਤਾ | ਪਰ ਇਹਨਾਂ ਖੇਡਾਂ ਦਾ ਪੁਨਰ-ਜਨਮ ਲਿਖਿਆ ਹੋਇਆ ਸੀ । 1829 ਈ: ਵਿਚ ਜਾਪਾਨੀ ਅਤੇ ਫ਼ਰਾਂਸੀਸੀ ਵਿਗਿਆਨਕਾਂ ਨੇ ਓਲੰਪੀਆ ਦੀ ਖੁਦਾਈ ਦਾ ਕੰਮ ਆਰੰਭ ਕੀਤਾ । ਸਾਲਾਂ ਦੇ ਯਤਨਾਂ ਦੇ ਬਾਅਦ ਉਹਨਾਂ ਦੇ ਹੱਥ ਸਫ਼ਲਤਾ ਲੱਗੀ । ਇਹਨਾਂ ਖੁਦਾਈਆਂ ਨਾਲ ਉਲੰਪੀਆ ਦੇ ਮੰਦਰ ਅਤੇ ਸਟੇਡੀਅਮ ਪ੍ਰਾਪਤ ਹੋਏ । | ਬੈਰਨ ਦਿ ਕਿਊਬਰਟਿਨ ਨੂੰ ਨਵੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦਾ ਜਨਮ ਦਾਤਾ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਉਹਨਾਂ ਦਾ ਜਨਮ 1863 ਈ: ਵਿਚ ਫ਼ਰਾਂਸ ਵਿਚ ਹੋਇਆ । ਉਹ ਫ਼ਰਾਂਸ ਦੇ ਸਿੱਖਿਆ ਵਿਭਾਗ ਵਿਚ ਕੰਮ ਕਰਦੇ ਸਨ । ਉਹਨਾਂ ਦੀ ਸਰੀਰਕ ਸਿੱਖਿਆ ਵਿਚ ਵਿਸ਼ੇਸ਼ ਰੁਚੀ ਸੀ । 1854 ਈ: ਵਿਚ ਉਹ ਇੰਗਲੈਂਡ ਦੇ ਦੌਰੇ ‘ਤੇ ਗਏ । ਉਹ ਇੰਗਲੈਂਡ ਦੇ ਸਿੱਖਿਅਕ ਢਾਂਚੇ ਤੋਂ ਬਹੁਤ ਪ੍ਰਭਾਵਿਤ ਹੋਏ ।

ਕਿਉਬਰਟਿਨ ਬਰਤਾਨੀਆ ਅਤੇ ਅਮਰੀਕਾ ਗਏ । ਉੱਥੇ ਉਹਨਾਂ ਨੇ ਲੋਕਾਂ ਨੂੰ ਆਪਣੀਆਂ ਯੋਜਨਾਵਾਂ ਤੋਂ ਜਾਣੂ ਕਰਵਾਇਆ । ਇਸ ਤੇ ਹੋਰ ਖੇਡ ਪ੍ਰੇਮੀਆਂ ਨੇ ਉਹਨਾਂ ਨੂੰ ਸਹਾਇਤਾ ਦੇਣ ਦਾ ਸਮਰਥਨ ਕੀਤਾ । ਕਿਉਬਰਟਿਨ ਖੇਡਾਂ ਦੇ ਮਾਧਿਅਮ ਨਾਲ ਸਿਹਤ, ਸੁੰਦਰਤਾ, ਮਨੋਰੰਜਨ ਅਤੇ ਸਹਿਯੋਗ ਵਿਚ ਵਾਧਾ ਕਰਨਾ ਚਾਹੁੰਦੇ ਸਨ । ਉਹਨਾਂ ਨੇ ਭਿੰਨ-ਭਿੰਨ ਦੇਸ਼ਾਂ ਦਾ ਦੌਰਾ ਕੀਤਾ ਅਤੇ ਉੱਥੋਂ ਦੇ ਲੋਕਾਂ ਨੂੰ ਆਪਣੇ ਵਿਚਾਰ ਦੀ ਜਾਣਕਾਰੀ ਦਿੱਤੀ । ਉਹਨਾਂ ਨੇ ਫ਼ਰਾਂਸ ਵਿਚ ਫ਼ਰਾਂਸੀਸੀ ਖੇਡ ਸੰਘ ਦੀ ਆਧਾਰਸ਼ਿਲਾ ਰੱਖੀ । 16 ਜੂਨ, 1894 ਈ: ਨੂੰ ਇਕ ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਕਾਂਗਰਸ ਦੇ ਸਾਹਮਣੇ ਓਲੰਪਿਕ ਯੋਜਨਾ ਰੱਖੀ ਗਈ । ਇਸ ਦਾ ਸਭ ਨੇ ਸਮਰਥਨ ਕੀਤਾ । ਫਲਸਰੂਪ 5 ਅਪਰੈਲ, 1896 ਈ: ਤਕ ਪਹਿਲੀਆਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦਾ ਪ੍ਰਬੰਧ ਕੀਤਾ ਗਿਆ । ਇਹਨਾਂ ਖੇਡਾਂ ਦੇ ਲਈ ਕਿਊਬਰਟਿਨ ਨੇ ਇਕ ਮਹਾਨ ਆਦਰਸ਼ ਪੇਸ਼ ਕੀਤਾ । ਉਹ ਆਦਰਸ਼ ਹੈ(P.S..B. 2004 C, 2005 C) ‘‘ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਮਹੱਤਵਪੂਰਨ ਗੱਲ ਜਿੱਤ ਪ੍ਰਾਪਤ ਕਰਨਾ ਨਹੀਂ, ਸਗੋਂ ਉਹਨਾਂ ਵਿਚ ਭਾਗ ਲੈਣਾ ਹੈ । ਜਿਵੇਂ ਕਿ ਜੀਵਨ ਵਿਚ ਇਕ ਮਹੱਤਵਪੂਰਨ ਗੱਲ ਜਿੱਤ ਨਹੀਂ, ਸਗੋਂ ਸੰਘਰਸ਼ ਹੈ । ਜ਼ਰੂਰੀ ਗੱਲ ਜਿੱਤਣਾ ਨਹੀਂ, ਸਗੋਂ ਚੰਗੀ ਤਰ੍ਹਾਂ ਮੁਕਾਬਲਾ ਕਰਨਾ ਹੈ ।” (“The important thing in Olympics is not to win but to take part. As the important thing in life is not triumph but the struggle. The essential thing is not to have conquered but to have fought well.”’)

ਪ੍ਰਸ਼ਨ 4.
ਨਵੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦੇ ਮਾਟੋ, ਸਹੁੰ ਅਤੇ ਝੰਡੇ ਬਾਰੇ ਲਿਖੋ । [ਅਭਿਆਸ-ਪ੍ਰਸ਼ਨ-4] (What is Olympic Motto, Olympic Flag and Olympic Oath of Modern Olympic Games ?)
ਉੱਤਰ –
ਓਲੰਪਿਕ ਮਾਟੋ (Olmypic Motto) – ਓਲੰਪਿਕ ਮਾਟੋ ਤਿੰਨ ਸ਼ਬਦਾਂ ਨਾਲ ਬਣਿਆ ਹੈ । ਇਹ ਤਿੰਨ ਸ਼ਬਦ ਹਨ –
ਸੀਟਿਅਸ (Citius) ਦਾ ਅਰਥ ਹੈ ਬਹੁਤ ਤੇਜ਼,
ਆਲਟੀਅਸ (Altius) ਦਾ ਅਰਥ ਹੈ ਬਹੁਤ ਉੱਚਾ,
ਫਰਟਿਅਸ (Fortius) ਦਾ ਅਰਥ ਹੈ ਬਹੁਤ ਜ਼ੋਰ ਨਾਲ ।
ਇਹ ਤਿੰਨ ਸ਼ਬਦ ਹੀ ਖਿਡਾਰੀ ਦੇ ਨਿਸ਼ਾਨੇ ਨੂੰ ਸੂਚਿਤ ਕਰਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਦਾ ਭਾਵ ਹੈਬਹੁਤੇ ਤੇਜ਼ ਭੱਜਣਾ, ਬਹੁਤ ਉੱਚੀ ਛਾਲ ਲਗਾਉਣਾ ਅਤੇ ਬਹੁਤ ਜ਼ੋਰ ਨਾਲ ਡਿਸਕਸ ਜਾਂ ਗੋਲਾ ਸੁੱਟਣਾ ।

ਓਲੰਪਿਕ ਸਹੁੰ (Olympic Oath) – ਓਲੰਪਿਕ ਸੁਗੰਧ ਇਸ ਤਰ੍ਹਾਂ ਹੈ| ਇਹ ਰੀਤ 1920 ਵਿਚ ਅੰਤਦੀਪ ਵਿਖੇ ਸ਼ੁਰੂ ਹੋਈ । 1984 ਦੀਆਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦੇ ਚਾਰਟਰ ਰੁਪ 63 ਵਿਚ ਕਿਹਾ ਗਿਆ ਕਿ ਮੇਜ਼ਬਾਨ ਰਾਸ਼ਟਰ ਦਾ ਇਕ ਖਿਡਾਰੀ ਆਪਣੇ ਖੱਬੇ ਹੱਥ ਵਿਚ ਓਲੰਪਿਕ ਝੰਡੇ ਦਾ ਕੋਨਾ ਫੜ ਕੇ ਅਤੇ ਆਪਣਾ ਸੱਜਾ ਹੱਥ ਖੜ੍ਹਾ ਕਰਕੇ ਹੇਠ ਲਿਖੀ ਸਹੁੰ ਚੁੱਕੇ :
“ਸਾਰੇ ਖਿਡਾਰੀਆਂ ਵੱਲੋਂ ਮੈਂ ਵਚਨ ਲੈਂਦਾ ਹਾਂ ਕਿ ਅਸੀਂ ਇਨ੍ਹਾਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਉਨ੍ਹਾਂ ਨਿਯਮਾਂ ਦਾ ਆਦਰ ਕਰਦਿਆਂ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਪਾਬੰਦ ਰਹਿੰਦਿਆਂ ਜੋ ਕਿ ਇਸ ਦੀ ਨਿਗਰਾਨੀ ਕਰਦੇ ਹਨ ਖਿਡਾਰੀ ਦੀ ਸੱਚੀ ਭਾਵਨਾ ਨਾਲ ਖੇਡਾਂ ਦੇ ਗੌਰਵ ਅਤੇ ਸਾਰੀਆਂ ਟੀਮਾਂ ਦੇ ਸਨਮਾਨ ਲਈ ਭਾਗ ਲਵਾਂਗੇ ।

ਓਲੰਪਿਕ ਝੰਡਾ
(Olympic Flag).

ਓਲੰਪਿਕ ਝੰਡਾ 1919 ਈ: ਵਿਚ ਏਟਵਰਪ (Antwerp) ਵਿਚ ਹੋਣ ਵਾਲੀਆਂ ਉਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਲਹਿਰਾਇਆ ਗਿਆ । ਇਸ ਝੰਡੇ ਦੀ ਰਚਨਾ, ਕੁਬਰਟਿਨ ਨੇ ਕੀਤੀ ਸੀ । ਇਸ ਝੰਡੇ ਵਿਚ ਪੰਜ ਰੰਗਾਂ ਲਾਲ, ਹਰਾ, ਪੀਲਾ, ਨੀਲਾ ਅਤੇ ਕਾਲਾ-ਨਾਲ ਪੰਜ ਚੱਕਰ ਆਪਸ ਵਿਚ ਜੋੜ ਕੇ ਬਣਾਏ ਗਏ ਹਨ । ਇਹ ਪੰਜ ਚੱਕਰ ਯੂਰਪ, ਆਸਟਰੇਲੀਆ, ਏਸ਼ੀਆ, ਅਫਰੀਕਾ ਅਤੇ ਅਮਰੀਕਾ-ਪੰਜ ਮਹਾਂਦੀਪਾਂ ਦੀ ਪ੍ਰਤੀਨਿਧਤਾ ਕਰਦੇ ਹਨ । ਇਹਨਾਂ ਚੱਕਰਾਂ ਦਾ ਆਪਸ ਵਿਚ ਜੁੜੇ ਹੋਣਾ ਇਹਨਾਂ ਪੰਜ ਮਹਾਂਦੀਪਾਂ ਦੀ ਮਿੱਤਰਤਾ ਅਤੇ ਸਦਭਾਵਨਾ ਦਾ ਪ੍ਰਤੀਕ ਹੈ ।

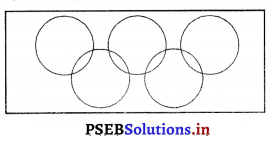
ਪ੍ਰਸ਼ਨ 5.
ਨਵੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦੇ ਕੀ ਨਿਯਮ ਹਨ ? [ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ]- 5] (What are the main Rules of Modern Olympic ?)
ਉੱਤਰ-
ਨਵੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦੇ ਨਿਯਮ (Rules of new Olympics ) – ਪਹਿਲਾਂ ਤਾਂ ਖੇਡਾਂ ਦੇ ਨਿਯਮ ਬਹੁਤ ਹੀ ਸਾਧਾਰਨ ਸਨ ਕੋਈ ਵੀ ਵਿਅਕਤੀ ਇਹਨਾਂ ਵਿਚ ਭਾਗ ਲੈ | ਸਕਦਾ ਸੀ ।1908 ਈ: ਵਿਚ ਓਲੰਪਿਕ ਖੇਡਾਂ ਲੰਡਨ ਵਿਚ ਆਯੋਜਿਤ ਕੀਤੀਆਂ ਗਈਆਂ ਅਤੇ ਨਿਯਮਾਂ ਦਾ ਨਿਰਮਾਣ ਕੀਤਾ ਗਿਆ । ਇਹ ਨਿਯਮ ਇਸ ਪ੍ਰਕਾਰ ਹਨ-

(1) ਹਰੇਕ ਦੇਸ਼ ਜੋ ਉਲੰਪਿਕ ਖੇਡਾਂ ਦਾ ਮੈਂਬਰ ਹੈ ਆਪਣੇ ਕਿਸੇ ਵੀ ਦੇਸ਼ ਵਾਸੀ ਨੂੰ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਲੈਣ ਲਈ ਭੇਜ ਸਕਦਾ ਹੈ ।

(2) ਕੋਈ ਵੀ ਵਿਵਸਾਇਕ ਖਿਡਾਰੀ (Professional Player) ਇਸ ਵਿਚ ਭਾਗ ਨਹੀਂ ਲੈ ਸਕਦਾ । ਇਸ ਗੱਲ ਦੀ ਪੁਸ਼ਟੀ ਉਸ ਦੀ ਰਾਸ਼ਟਰੀ ਕਮੇਟੀ ਕਰਦੀ ਹੈ । ਇਸ ਵਿਸ਼ੇ ਵਿਚ ਖਿਡਾਰੀ ਨੂੰ ਵੀ ਲਿਖ ਕੇ ਦੇਣਾ ਪੈਂਦਾ ਹੈ ।

(3) ਇਸ ਵਿਚ ਭਾਗ ਲੈਣ ਵਾਲੇ ਖਿਡਾਰੀ ’ਤੇ ਉਮਰ, ਜਾਤੀ, ਧਰਮ ਆਦਿ ਦਾ ਪ੍ਰਤੀਬਿੰਧ ਨਹੀਂ ਹੈ ।

(4) ਕੋਈ ਵੀ ਖਿਡਾਰੀ ਨਸ਼ੇ ਦੀ ਹਾਲਤ ਵਿਚ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਨਹੀਂ ਲੈ ਸਕਦਾ ।

(5) ਖਿਡਾਰੀ ਦੇ ਲਿੰਗ ਦੀ ਜਾਂਚ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।

(6) ਕਿਸੇ ਇਕ ਦੇਸ਼ ਵਲੋਂ ਭਾਗ ਲੈਣ ਵਾਲਾ ਖਿਡਾਰੀ ਕਿਸੇ ਦੂਸਰੇ ਰਾਸ਼ਟਰ ਵਲੋਂ ਭਾਗ ਨਹੀਂ ਲੈ ਸਕਦਾ ।

(7) ਜੇ ਕੋਈ ਨਵਾਂ ਦੇਸ਼ ਹੋਂਦ ਵਿਚ ਆਇਆ ਹੋਵੇ ਤਾਂ ਉਹ ਆਪਣਾ ਖਿਡਾਰੀ ਭੇਜ ਸਕਦਾ ਹੈ । ਇਹਨਾਂ ਖੇਡਾਂ ਦਾ ਪ੍ਰਬੰਧ ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਓਲੰਪਿਕ ਕਮੇਟੀ ਦੁਆਰਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਕਮੇਟੀ ਵਿਚ ਹਰੇਕ ਦੇਸ਼ ਦਾ ਇਕ ਮੈਂਬਰ ਹੁੰਦਾ ਹੈ, ਪਰ ਜਿਸ ਦੇਸ਼ ਵਿਚ ਓਲੰਪਿਕ ਕਮੇਟੀਆਂ ਸਥਾਪਿਤ ਹੋਣ ਜਾਂ ਜਿੱਥੇ ਖੇਡਾਂ ਦਾ ਪ੍ਰਬੰਧ ਚੰਗੀ ਤਰ੍ਹਾਂ ਹੋਵੇ, ਉਸ ਦੇ ਦੋ ਮੈਂਬਰ ਹੋ ਸਕਦੇ ਹਨ । ਇਸ ਕਮੇਟੀ ਦੇ ਅੱਠ ਮੈਂਬਰ ਸਾਲ ਲਈ ਆਪਣੇ ਪ੍ਰਧਾਨ ਦੀ ਚੋਣ ਕਰਦੇ ਹਨ । ਇਸ ਤੋਂ ਇਲਾਵਾ ਚਾਰ ਸਾਲ ਲਈ ਦੋ ਉਪ-ਪ੍ਰਧਾਨਾਂ ਦੀ ਚੋਣ ਕਰਦੇ ਹਨ । ਪੰਜ ਹੋਰ ਮੈਂਬਰ ਵੀ ਇਸ ਕਮੇਟੀ ਦੇ ਮੈਂਬਰ ਚੁਣਦੇ ਹਨ । ਇਹ ਕਮੇਟੀ ਨਿਯਮ ਅਨੁਸਾਰ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦਾ ਪ੍ਰਬੰਧ ਰਕਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਓਲੰਪਿਕ ਕਮੇਟੀ ਬਾਰੇ ਲਿਖੋ । (Write about International Olympic Committee.)
ਉੱਤਰ-
ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਓਲੰਪਿਕ ਕਮੇਟੀ (International Olympic Committee) – ਓਲੰਪਿਕ ਖੇਡਾਂ ਦੇ ਪ੍ਰਬੰਧ ਲਈ ਇਕ ਕਮੇਟੀ ਬਣਾਈ ਗਈ ਜਿਸ ਦਾ ਨਾਂ ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਓਲੰਪਿਕ ਕਮੇਟੀ (International Olympic Committee) ਰੱਖਿਆ ਗਿਆ । ਇਸ ਵਿਚ ਹਰੇਕ ਦੇਸ਼ ਦਾ ਇਕ-ਇਕ ਪ੍ਰਤੀਨਿਧ ਲਿਆ ਗਿਆ । ਇਸ ਕਮੇਟੀ ਦਾ ਮੁੱਖ ਦਫਤਰ Compague Mon Zeps Lausanne (Switzerland) ਵਿਚ ਹੈ । ਇਸ ਕਮੇਟੀ ਦਾ ਇਕ ਪ੍ਰਧਾਨ ਚੁਣਿਆ ਜਾਂਦਾ ਹੈ, ਦੋ ਮੀਤ ਪ੍ਰਧਾਨ ਅਤੇ ਕਾਰਜਪਾਲਿਕਾ (Executive) ਦੇ ਮੈਂਬਰ ਚੁਣੇ ਜਾਂਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਕਮੇਟੀ ਹਰ ਚਾਰ ਸਾਲ ਮਗਰੋਂ ਹੋਣ ਵਾਲੇ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦੇ ਸਥਾਨ ਅਤੇ ਸਮੇਂ ਆਦਿ ਦਾ ਫ਼ੈਸਲਾ ਕਰਦੀ ਹੈ । ਫੈਸਲੇ ਤੋਂ ਮਗਰੋਂ ਉਸ ਦੇਸ਼ ਦੀ ਰਾਸ਼ਟਰੀ ਓਲੰਪਿਕ ਕਮੇਟੀ ਵੱਖ-ਵੱਖ ਖੇਡਾਂ ਦੀ ਤਿਆਰੀ ਸ਼ੁਰੂ ਕਰ ਦਿੰਦੀ ਹੈ ।

ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਓਲੰਪਿਕ ਕਮੇਟੀ ਇਹ ਖੇਡਾਂ ਲਗਾਤਾਰ ਕਰਵਾਉਣ ਲਈ ਹਮੇਸ਼ਾ ਤਿਆਰ ਰਹਿੰਦੀ ਹੈ । ਇਸ ਕਮੇਟੀ ਦੀ ਲਗਾਤਾਰ ਕੋਸ਼ਿਸ਼ ਹੁੰਦੀ ਹੈ ਕਿ ਕਿਉਬਰਟਿਨ ਦੇ ਫ਼ੈਸਲੇ ਅਨੁਸਾਰ ਸਾਰੇ ਸੰਸਾਰ ਵਿਚ ਪਿਆਰ ਅਤੇ ਸ਼ਾਂਤੀ ਦਾ ਸੰਦੇਸ਼ ਪਹੁੰਚਾਵੇ । ਖੇਡਾਂ ਵਿਚ ਖੇਡ ਦੀ ਭਾਵਨਾ ਨਾਲ ਹੀ ਮੁਕਾਬਲੇ ਕਰਵਾਏ ਜਾਣ ਅਤੇ ਉਨ੍ਹਾਂ ਵਿਚ ਕਿੱਤੇ ਆਦਿ ਦਾ ਕੋਈ ਸਥਾਨ ਨਾ ਹੋਵੇ ।

ਖੇਡਾਂ ਸੰਸਾਰ ਵਿਚ ਸ਼ਾਂਤੀ ਅਤੇ ਮਿੱਤਰਤਾ ਨੂੰ ਵਧਾਉਣ ਵਿਚ ਸਹਾਇਕ ਹੁੰਦੀਆਂ ਹਨ । ਓਲੰਪਿਕ ਕਮੇਟੀ ਵਿਚ ਹਰ ਇਕ ਦੇਸ਼ ਦਾ ਇਕ ਨੁਮਾਇੰਦਾ ਹੁੰਦਾ ਹੈ, ਪਰ ਜਿਸ ਦੇਸ਼ ਵਿਚ ਓਲੰਪਿਕ ਖੇਡਾਂ ਹੋਈਆਂ ਹੋਣ ਜਾਂ ਓਲੰਪਿਕ ਲਹਿਰ ਨੂੰ ਅੱਗੇ ਚਲਾਉਣ ਵਿਚ ਸਹਾਇਤਾ ਕੀਤੀ ਹੋਵੇ, ਉਸ ਦੇਸ਼ ਦੇ ਦੋ ਮੈਂਬਰ ਹੁੰਦੇ ਹਨ । ਇਹ ਕਮੇਟੀ ਆਪਣਾ ਪ੍ਰਧਾਨ ਆਪ ਚੁਣਦੀ ਹੈ ਜੋ ਪੰਜ ਸਾਲ ਤਕ ਰਹਿੰਦਾ ਹੈ । ਦੁਬਾਰਾ ਚੁਣੇ ਜਾਣ ‘ਤੇ ਚਾਰ ਸਾਲ ਤੱਕ ਫਿਰ ਪ੍ਰਧਾਨ ਰਹਿ ਸਕਦਾ ਹੈ । ਇਸ ਵਿਚ ਦੋ ਉਪ ਪ੍ਰਧਾਨ ਹੁੰਦੇ ਹਨ, ਜੋ ਕੇਵਲ ਚਾਰ ਸਾਲ ਤਕ ਕੰਮ ਕਰਦੇ ਹਨ । ਇਹ ਉਪ ਪ੍ਰਧਾਨ ਦੁਬਾਰਾ ਚੋਣ ਲੜ ਸਕਦੇ ਹਨ । ਉਪ ਪ੍ਰਧਾਨ ਅਤੇ ਪੰਜ ਐਗਜ਼ੈਕਟਿਵ ਦੇ ਮੈਂਬਰ ਚਾਰ ਸਾਲ ਮਗਰੋਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਨੂੰ ਕਰਵਾਉਣ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦੇ ਹਨ । ਮੁੱਖ ਕਾਰਜਪਾਲਿਕਾ ਦਾ ਮੁੱਖ ਸੈਕਰੇਟਰੀ ਹੁੰਦਾ ਹੈ ਜੋ ਬੋਰਡ ਦੁਆਰਾ ਚੁਣਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਆਪਣੇ ਪ੍ਰਧਾਨ ਦੇ ਹੁਕਮ ਅਨੁਸਾਰ ਕੰਮ ਕਰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਭਾਰਤੀ ਖਿਡਾਰੀਆਂ ਨੇ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਕੀ ਸਥਾਨ ਪ੍ਰਾਪਤ ਕੀਤਾ ਹੈ ? (Discuss the main achievements of Indian Players in Olympic ?)
ਉੱਤਰ-
ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਭਾਰਤੀ ਖਿਡਾਰੀਆਂ ਦੀਆਂ ਸਫ਼ਲਤਾਵਾਂ (Achievements of Indian Players in Olmypic) – ਨਵੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦਾ ਆਰੰਭ 1896 ਈ: ਵਿਚ ਹੋਇਆ । ਇਸ ਕੰਮ ਵਿਚ ਫ਼ਰਾਂਸ ਦੇ ਬੈਰਨ ਦਿ ਕਿਉਬਰਟਿਨ ਨੇ ਪਸ਼ੰਸਾ ਯੋਗ ਭੂਮਿਕਾ ਨਿਭਾਈ ਸੀ । ਇਸੇ ਕਾਰਨ ਉਸ ਨੂੰ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦਾ ਜਨਮਦਾਤਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । (P.S.E.B. 2007 C) ਭਾਰਤ ਨੇ ਇਹਨਾਂ ਖੇਡਾਂ ਵਿਚ 1900 ਈ: ਵਿਚ ਪਹਿਲੀ ਵਾਰ ਭਾਗ ਲਿਆ । ਭਾਰਤੀ ਖਿਡਾਰੀ ਨਾਰਮਨ ਨੇ 200 ਮੀਟਰ ਦੀ ਦੌੜ ਵਿਚ ਦੂਸਰਾ ਸਥਾਨ ਪ੍ਰਾਪਤ ਕਰ ਕੇ ਚਾਂਦੀ ਦਾ ਤਮਗਾ ਪ੍ਰਾਪਤ ਕੀਤਾ 1920 ਈ: ਦੀਆਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਭਾਰਤ ਵਲੋਂ ਛੇ , ਖਿਡਾਰੀਆਂ ਨੇ ਐਥਲੈਟਿਕਸ ਅਤੇ ਕੁਸ਼ਤੀਆਂ ਵਿਚ ਭਾਗ ਲਿਆ । 1924 ਈ: ਵਿਚ ਪੈਰਿਸ ਵਿਚ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦਾ ਪ੍ਰਬੰਧ ਹੋਇਆ । ਇਹਨਾਂ ਵਿਚ ਅੱਠ ਭਾਰਤੀ ਖਿਡਾਰੀਆਂ ਨੇ ਭਾਗ ਲਿਆ ਸੀ । ਸ੍ਰੀ ਜੀ. ਡੀ. ਸੋਂਧੀ, ਐਚ. ਸੀ. ਬੈਂਕ ਅਤੇ ਏ.ਜੀ. ਲਾਰੇਨ ਨੇ ਓਲੰਪਿਕ ਲਹਿਰ ਨੂੰ ਦੇਸ਼ ਵਿਚ ਲੋਕ-ਪਿਯ ਕਰਨ ਦੇ ਲਈ ਮਹੱਤਵਪੂਰਨ ਯੋਗਦਾਨ ਦਿੱਤਾ । (P.S.E.B. 2004 B) 1927 ਈ: ਵਿਚ ਇੰਡੀਅਨ ਓਲੰਪਿਕ ਐਸੋਸੀਏਸ਼ਨ ਦੀ ਸਥਾਪਨਾ ਹੋਈ ।

1928 ਈ: ਵਿਚ ਭਾਰਤੀ ਹਾਕੀ ਟੀਮ ਨੇ ਪਹਿਲੀ ਵਾਰ ਐਮਸਟਰਡਮ (P.S.E.B. 2005 C) ਵਿਚ ਪ੍ਰਬੰਧਿਤ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਲਿਆ । ਇਸ ਨੇ ਸੋਨੇ ਦਾ ਤਮਗਾ ਜਿੱਤਿਆ । 1928 ਈ: ਤੋਂ 1956 ਈ: ਤਕ ਭਾਰਤ ਹਾਕੀ ਜਗਤ ਵਿਚ ਛਾਇਆ ਰਿਹਾ । 1952 ਈ: ਵਿਚ ਕੇ. ਡੀ. ਯਾਦਵ ਨੇ ਕੁਸ਼ਤੀ ਦੇ ਮੁਕਾਬਲੇ ਵਿਚ ਭਾਗ ਲਿਆ ਅਤੇ ਤਾਂਬੇ ਦਾ ਤਮਗਾ ਜਿੱਤਿਆ । 1956 ਈ: ਵਿਚ ਮੈਲਬੋਰਨ ਵਿਚ ਪ੍ਰਬੰਧਿਤ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਭਾਰਤ ਦੀ ਫੁੱਟਬਾਲ ਟੀਮ ਨੇ ਪਹਿਲੀ ਵਾਰ ਭਾਗ ਲਿਆ । ਇਸ ਟੀਮ ਨੇ ਚੌਥਾ ਸਥਾਨ ਪ੍ਰਾਪਤ ਕੀਤਾ 1960 ਈ: ਵਿਚ ਰੋਮ ਵਿਚ ਹੋਈਆਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਭਾਰਤੀ ਹਾਕੀ ਟੀਮ ਨੇ ਦੂਸਰਾ ਸਥਾਨ ਪ੍ਰਾਪਤ ਕੀਤਾ । ਇਸੇ ਸਾਲ ਮਿਲਖਾ ਸਿੰਘ ਨੇ 400 ਮੀਟਰ ਦੌੜ ਵਿਚ ਚੌਥਾ ਸਥਾਨ ਪ੍ਰਾਪਤ ਕੀਤਾ ।

1954 ਈ: ਵਿਚ ਟੋਕਿਓ ਵਿਚ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦਾ ਪ੍ਰਬੰਧ ਹੋਇਆ। ਇਸ ਵਿਚ ਭਾਰਤੀ ਹਾਕੀ ਟੀਮ ਫੇਰ ਤੋਂ ਪਹਿਲਾਂ ਸਥਾਨ ਪ੍ਰਾਪਤ ਕਰਨ ਵਿਚ ਸਫਲ ਹੋਈ । 1968, 1972 ਅਤੇ 1976 ਵਿਚ ਪ੍ਰਬੰਧਿਤ ਹੋਣ ਵਾਲੀਆਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਭਾਰਤੀ ਹਾਕੀ ਟੀਮ ਪਹਿਲਾ ਸਥਾਨ | ਪਾ ਕੇ ਸੋਨੇ ਦਾ ਤਮਗਾ ਜਿੱਤਣ ਵਿਚ ਅਸਫਲ ਰਹੀ ।1976 ਵਿਚ ਓਲੰਪਿਕ ਖੇਡਾਂ ਮਾਂਟਰੀਆਲ ਵਿਚ ਹੋਈਆਂ । ਇਸ ਵਿਚ ਸ਼ਿਵਨਾਥ ਨੇ ਮੈਰਾਥਨ ਦੌੜ ਵਿਚ ਗਿਆਰਵਾਂ ਅਤੇ ਸ੍ਰੀ ਰਾਮ ਨੇ 800 ਮੀਟਰ ਦੌੜ ਵਿਚ ਸੱਤਵਾਂ ਸਥਾਨ ਪ੍ਰਾਪਤ ਕੀਤਾ । 1980 ਵਿਚ ਮਾਸਕੋ ਵਿਚ ਹੋਈਆਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਭਾਰਤੀ ਹਾਕੀ ਟੀਮ ਨੇ ਸੋਨੇ ਦਾ ਤਮਗਾ ਜਿੱਤਣ ਵਿਚ ਸਫਲਤਾ ਪ੍ਰਾਪਤ ਕੀਤੀ । ਇਹਨਾਂ ਖੇਡਾਂ ਵਿਚ ਭਾਰਤੀ ਟੀਮ ਨੇ ਐਥਲੈਟਿਕਸ, ਕੁਸ਼ਤੀਆਂ, ਬਾਕਸਿੰਗ, ਬਾਸਕਟ ਬਾਲ, ਨਿਸ਼ਾਨੇਬਾਜ਼ੀ ਅਤੇ ਵਾਲੀਬਾਲ ਵਿਚ ਤਾਂ ਭਾਗ ਲਿਆ ਸੀ, ਪਰ ਇਹਨਾਂ ਵਿਚ ਉਸ ਨੂੰ ਕੋਈ ਵਿਸ਼ੇਸ਼ ਸਫਲਤਾ ਹੱਥ ਨਹੀਂ ਲੱਗੀ । ਪਰ 1984 ਵਿਚ ਲਾਂਸ ਏਂਜਲਸ ਵਿਚ ਹੋਈਆਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਭਾਰਤੀ ਖਿਡਾਰੀਆਂ ਦਾ ਪ੍ਰਦਰਸ਼ਨ ਬਹੁਤ ਨਿਰਾਸ਼ਾਜਨਕ ਰਿਹਾ ।

ਉੱਪਰ ਦੱਸੇ ਖਿਡਾਰੀਆਂ ਦੇ ਇਲਾਵਾ ਕਈ ਹੋਰ ਭਾਰਤੀ ਖਿਡਾਰੀਆਂ ਨੇ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਵੀ ਆਪਣੀ ਉੱਤਮ ਖੇਡ ਦਾ ਪ੍ਰਦਰਸ਼ਨ ਕਰ ਕੇ ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਖੇਤਰ ਵਿਚ ਬਹੁਤ ਨਾਂ ਕਮਾਇਆ |

1996 ਦੀਆਂ ਉਲੰਪਿਕ ਖੇਡਾਂ ਜੋ ਕਿ ਐਟਲਾਂਟਾ ਵਿੱਚ ਹੋਈਆਂ। ਲਾਨ ਟੈਨਿਸ ਦੇ ਖਿਡਾਰੀ ਲਿਏਂਡਰ ਪੇਅਸ ਨੇ ਤਾਂਬੇ ਦਾ ਤਮਗਾ ਜਿਤਿਆ ਸੀ। ਇਸ ਤੋਂ ਬਾਅਦ ਸੰਨ 2000 ਵਿਚ ਕਰਨਮ ਮਲੇਸ਼ਵਰੀ ਨੇ ਵੇਟਲਿਫਟਿੰਗ ਦੇ 69 ਕਿਲੋ ਵਜ਼ਨ ਵਰਗ ਵਿਚ ਕਾਂਸੀ ਦਾ ਤਮਗਾ ਹਾਸਿਲ ਕੀਤਾ। ਇਸ ਵਿਚ ਮੁੱਕੇਬਾਜ਼ ਗੁਰਚਰਨ ਸਿੰਘ, ਦੌੜਾਕ ਲੜਕੀ ਕੇ. ਐਸ. ਸ਼ੀਲਾ ਕੌਲ ਅਤੇ ਨਿਸ਼ਾਨੇਬਾਜ਼ ਅੰਜਲੀ ਵੇਦ ਪਾਠਕ ਨੇ ਨਾਮਣਾ ਖੱਟਿਆ। 2004 ਦੀਆਂ ਉਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਭਾਰਤ ਦੇ ਸ੍ਰੀ ਰਾਜਵਰਧਨ ਸਿੰਘ ਰਾਠੌਰ ਨੇ ਸ਼ੂਟਿੰਗ ਵਿਚ ਚਾਂਦੀ ਦਾ ਤਮਗਾ ਜਿੱਤਿਆ ਅਤੇ ਐਥਲੀਟ ਅੰਜੂ ਬੌਬੀ ਜਾਰਜ ਨੇ ਲੰਬੀ ਛਾਲ ਵਿਚ 6ਵਾਂ ਸਥਾਨ ਹਾਸਿਲ ਕੀਤਾ।

2008 ਦੀਆਂ ਉਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਭਾਰਤੀਆਂ ਦਾ ਪ੍ਰਦਰਸ਼ਨ

ਨਾਂ – ਤਮਗਾ – ਖੇਡ

1. ਅਭਿਨਵ ਬਿੰਦਰਾ – ਸੋਨੇ ਦਾ – ਸ਼ੂਟਿੰਗ
2. ਸੁਸ਼ੀਲ ਕੁਮਾਰ – ਤਾਂਬੇ ਦਾ – ਕੁਸ਼ਤੀ
3. ਵਿਜੇਂਦਰ ਕੁਮਾਰ – ਤਾਂਬੇ ਦਾ – ਬਾਕਸਿੰਗ

2012 ਦੀਆਂ ਉਲੰਪਿਕ ਖੇਡਾਂ
ਨਾਂ – ਤਮਗਾ – ਖੇਡ

1. ਸੁਸ਼ੀਲ ਕੁਮਾਰ – ਚਾਂਦੀ ਦਾ – ਕੁਸ਼ਤੀ
2. ਵਿਜੈ ਕੁਮਾਰ – ਚਾਂਦੀ ਦਾ – ਸ਼ੂਟਿੰਗ
3. ਮੈਰੀ ਕੋਮ – ਤਾਂਬੇ ਦਾ – ਬਾਕਸਿੰਗ
4. ਸਾਹਿਨਾ ਨੇਹਵਾਲ – ਤਾਂਬੇ ਦਾ – ਬੈਡਮਿੰਟਨ
5. ਗਗਨ ਨਾਰੰਗ – ਤਾਂਬੇ ਦਾ – ਸ਼ੂਟਿੰਗ
6. ਯੋਗੇਸ਼ਵਰ ਦੱਤ – ਤਾਂਬੇ ਦਾ – ਕੁਸ਼ਤੀ

2016 ਦੀਆਂ ਉਲੰਪਿਕ ਖੇਡਾਂ |
ਨਾਂ – ਤਮਗਾ – ਖੇਡ

1. ਪੀ.ਵੀ. ਸਿੰਧੂ – ਚਾਂਦੀ ਦਾ – ਬੈਡਮਿੰਟਨ
2. ਸਾਕਸ਼ੀ ਮਲਿਕ – ਤਾਂਬੇ ਦਾ – ਕੁਸ਼ਤੀ

ਪ੍ਰਸ਼ਨ 8.
ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਕਦੋਂ ਅਤੇ ਕਿਉਂ ਸ਼ੁਰੂ ਹੋਈਆਂ ? ਇਹ ਖੇਡਾਂ ਸ਼ੁਰੂ ਕਰਨ ਵਿਚ ਭਾਰਤ ਦਾ ਕੀ ਯੋਗਦਾਨ ਹੈ ? [ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ] (When and where Asian Games were Started ? Write the contribution of India to start Asian Games.)
ਉੱਤਰ-
ਏਸ਼ਿਆਈ ਖੇਡਾਂ (Asian Gemes) – 14ਵੀਂ ਓਲੰਪਿਕ ਖੇਡਾਂ ਦਾ 1948 ਈ: ਵਿਚ ਲੰਡਨ ਵਿਚ ਪ੍ਰਬੰਧ ਕੀਤਾ ਗਿਆ । ਉਸ ਸਮੇਂ ਸ੍ਰੀ ਜੀ. ਡੀ. ਸੋਂਧੀ ਨੇ ਇਹ ਵਿਚਾਰ ਕੀਤਾ ਕਿ ਜਦੋਂ ਭਾਰਤੀ ਜਾਂ ਏਸ਼ਿਆਈ ਖਿਡਾਰੀ ਯੂਰਪੀ ਦੇਸ਼ਾਂ ਵਿਚ ਪ੍ਰਬੰਧਿਤ ਖੇਡਾਂ ਦੇ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਭਾਗ ਲੈਣ ਜਾਂਦੇ ਹਨ ਤਾਂ ਉਹ ਖੇਡ ਦਾ ਚੰਗਾ ਪ੍ਰਦਰਸ਼ਨ ਨਹੀਂ ਕਰ ਪਾਉਂਦੇ । ਇਸ ਲਈ ਜੇ ਏਸ਼ਿਆਈ ਦੇਸ਼ਾਂ ਦੇ ਖਿਡਾਰੀ ਆਪਸ ਵਿਚ ਮੁਕਾਬਲਾ ਕਰ ਲੈਣ ਤਾਂ ਇਕ ਤਾਂ ਉਹਨਾਂ ਵਿਚ ਮੁਕਾਬਲਾ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਵਧੇਗੀ ਅਤੇ ਦੂਸਰੇ ਖੇਡ ਦਾ ਪੱਧਰ ਉੱਨਤ ਹੋਵੇਗਾ । ਇਸ | ਵਿਚਾਰ ਨੂੰ ਕਾਰਜ ਰੂਪ ਦੇਣ ਲਈ ਉਹਨਾਂ ਨੇ 8 ਅਗਸਤ, 1948 ਈ: ਨੂੰ ਲੰਡਨ ਦੇ ਮਾਊਂਟ ਰਾਇਲ ਹੋਟਲ ਵਿਖੇ ਏਸ਼ਿਆਈ ਦੇਸ਼ਾਂ ਦੀ ਇਕ ਸਭਾ ਬੁਲਾਈ । ਇਸ ਸਭਾ ਵਿਚ ਕੋਰੀਆ, ਬਰਮਾ (ਮਿਆਂਮਾਰ), ਚੀਨ, ਸ੍ਰੀ ਲੰਕਾ ਆਦਿ ਦੇਸ਼ਾਂ ਦੇ ਪ੍ਰਤੀਨਿਧੀਆਂ ਨੇ ਭਾਗ ਲਿਆ । ਇਸ ਸਭਾ ਦੇ ਸਭ ਮੈਂਬਰਾਂ ਨੇ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਦੇ ਮੁਕਾਬਲੇ ਕਰਵਾਉਣ ਦੇ ਸੁਝਾਅ ਦਾ ਸਮਰਥਨ ਕੀਤਾ ।

ਮਹਾਰਾਜਾ ਪਟਿਆਲਾ ਸ੍ਰੀ ਯਾਦਵਿੰਦਰ ਸਿੰਘ ਨੇ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਦੇ ਆਰੰਭ ਕਰਨ ਵਿਚ | ਵਿਸ਼ੇਸ਼ ਮਹੱਤਵਪੂਰਨ ਭੂਮਿਕਾ ਨਿਭਾਈ । ਉਹਨਾਂ ਨੇ ਫਰਵਰੀ, 1949 ਵਿਚ ਦਿੱਲੀ ਵਿਚ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਲਈ ਏਸ਼ਿਆਈ ਦੇਸ਼ਾਂ ਦੀ ਸਭਾ ਬੁਲਾਈ । ਇਸ ਸਭਾ ਵਿਚ ਭਾਰਤ, ਅਫ਼ਗਾਨਿਸਤਾਨ, ਸ੍ਰੀ ਲੰਕਾ, ਬਰਮਾ (ਮਿਆਂਮਾਰ), ਪਾਕਿਸਤਾਨ, ਇੰਡੋਨੇਸ਼ੀਆ, ਨੇਪਾਲ, ਫਿਲਿਪਾਈਨ ਅਤੇ ਥਾਈਲੈਂਡ ਆਦਿ ਦੇਸ਼ਾਂ ਦੇ ਪ੍ਰਤੀਨਿਧੀਆਂ ਨੇ ਭਾਗ ਲਿਆ । ਇਸ ਸਭਾ ਵਿਚ | ਏਸ਼ੀਆ ਐਥਲੈਟਿਕਸ ਫੈਡਰੇਸ਼ਨ ਨੂੰ ਏਸ਼ੀਅਨ ਖੇਡ ਫੈਡਰੇਸ਼ਨ ਦਾ ਨਾਂ ਦਿੱਤਾ ਗਿਆ ਸੀ । ਇਸ ਦੇ ਸੰਵਿਧਾਨ ਦਾ ਨਿਰਮਾਣ ਕੀਤਾ ਗਿਆ । ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਨੂੰ ਹਰ ਚਾਰ ਸਾਲ ਬਾਅਦ ਆਯੋਜਿਤ ਕਰਨ ਦਾ ਨਿਸ਼ਚਾ ਕੀਤਾ ਗਿਆ । ਪਹਿਲੀਆਂ ਏਸ਼ਿਆਈ ਖੇਡਾਂ 4 ਮਾਰਚ ਤੋਂ 11 ਮਾਰਚ, 1951 ਤਕ ਦਿੱਲੀ ਦੇ ਨੈਸ਼ਨਲ ਸਟੇਡੀਅਮ ਵਿਚ ਹੋਣੀਆਂ ਨਿਸ਼ਚਿਤ ਹੋਈਆਂ ਸਨ । 1982 ਅਤੇ 1986 ਵਿਚ ਇਹ ਦਿੱਲੀ ਅਤੇ ਸਿਓਲ ਵਿਚ ਹੋਈਆਂ ।

ਪ੍ਰਸ਼ਨ 9.
ਕਿਨ੍ਹਾਂ-ਕਿਨ੍ਹਾਂ ਭਾਰਤੀ ਖਿਡਾਰੀਆਂ ਨੇ ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਪੱਧਰ ਤੇ ਨਾਮਣੇ ਪ੍ਰਾਪਤ ਕੀਤੇ ਹਨ ?
(Write about the outstanding players of India who won Laurels in International Competition ?)
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ਅਜਿਹੇ ਖਿਡਾਰੀ ਹੋਏ ਹਨ ਜਿਨ੍ਹਾਂ ਨੇ ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਖੇਡਾਂ ਵਿਚ ਆਪਣੇ ਸਰਵ-ਉੱਤਮ ਪ੍ਰਦਰਸ਼ਨ ਦੁਆਰਾ ਭਾਰਤ ਦੇ ਨਾਂ ਨੂੰ ਰੌਸ਼ਨ ਕੀਤਾ । ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਪੱਧਰ ‘ਤੇ ਨਾਂ ਕਮਾਉਣ ਵਾਲੇ ਭਾਰਤੀ ਖਿਡਾਰੀਆਂ ਦਾ ਵਰਣਨ ਹੇਠ ਦਿੱਤਾ ਗਿਆ ਹੈ-
(1) ਲੈਰੀ ਮਿੰਟੋ ਨੇ 1951 ਵਿਚ ਹੋਈਆਂ ਪਹਿਲੀਆਂ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਵਿਚ 100 ਮੀਟਰ ਦੌੜ ਵਿਚ ਪਹਿਲੀ ਥਾਂ ਪ੍ਰਾਪਤ ਕਰਕੇ ਸੋਨੇ ਦਾ ਤਮਗਾ ਜਿੱਤਿਆ ।

(2) 1954 ਵਿਚ ਮਨੀਲਾ ਵਿਚ ਪਬੰਧਿਤ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਵਿਚ ਸੋਹਨ ਸਿੰਘ ਨੇ 800 ਮੀਟਰ ਦੌੜ, ਅਜੀਤ ਸਿੰਘ ਨੇ ਉੱਚੀ ਛਾਲ, ਪਦੱਮਣ ਸਿੰਘ ਨੇ ਡਿਸਕਸ ਥਰੋ ਅਤੇ ਗੋਲਾ | ਸੁੱਟਣ ਵਿਚ ਸੋਨੇ ਦੇ ਤਮਗੇ ਜਿੱਤੇ । ਇਹਨਾਂ ਦੇ ਇਲਾਵਾ ਜੋਗਿੰਦਰ ਸਿੰਘ ਨੇ ਚਾਂਦੀ ਅਤੇ ਐੱਮ. ਗੋਬਿਆਨ ਨੇ 100 ਮੀਟਰ ਦੌੜ ਅਤੇ ਕਾਲੂ ਰਾਮ ਨੇ 3000 ਅਤੇ 5000 ਮੀਟਰ ਦੌੜ ਵਿਚ ਤੀਸਰਾ ਸਥਾਨ ਪ੍ਰਾਪਤ ਕਰਕੇ ਕਾਂਸੇ ਦੇ ਤਮਗੇ ਜਿੱਤੇ ।

(3) 1958 ਵਿਚ ਹੋਈਆਂ ਪ੍ਰਬੰਧਿਤ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਵਿਚ ਫਲਾਇੰਗ ਸਿੱਖ (Flying Sikh) ਮਿਲਖਾ ਸਿੰਘ ਨੇ 200 ਮੀਟਰ ਅਤੇ 400 ਮੀਟਰ ਦੌੜ ਵਿਚ, ਮਹਿੰਦਰ ਸਿੰਘ ਨੇ ਹਾਪ ਸਟੈਪ ਐਂਡ ਜੰਪ ਵਿਚ, ਬਲਕਾਰ ਸਿੰਘ ਨੇ ਜੈਵਲਿਨ ਸੁੱਟਣ ਵਿਚ, ਦੁੱਮਣ ਸਿੰਘ ਨੇ ਗੋਲਾ ਸੁੱਟਣ ਵਿਚ, ਐੱਚ. ਚਾਂਦ ਨੇ 100 ਮੀਟਰ ਹਰਡਲਜ਼ ਵਿਚ ਅਤੇ ਜਗਜੀਤ ਸਿੰਘ ਨੇ 400 | ਮੀਟਰ ਹਰਡਲਜ਼ ਵਿਚ ਸੋਨੇ ਦਾ ਤਮਗਾ ਪ੍ਰਾਪਤ ਕੀਤਾ । ਇਹਨਾਂ ਤੋਂ ਇਲਾਵਾ ਸਵੀਟਾ ਡਿਸੂਜਾ ਨੇ 200 ਮੀਟਰ ਦੌੜ ਜਿੱਤ ਕੇ ਨਵਾਂ ਰਿਕਾਰਡ ਕਾਇਮ ਕੀਤਾ । ਐਲਿਜਾਬੇਥ ਡੈਵਨ ਪੋਰਟ ਨੇ 46.07 ਮੀਟਰ ਦੂਰ ਜੈਵਲਿਨ ਸੁੱਟ ਕੇ ਦੂਸਰਾ ਸਥਾਨ ਪ੍ਰਾਪਤ ਕੀਤਾ ।

(4) 1966 ਵਿਚ ਹੋਈਆਂ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਵਿਚ ਅਜਮੇਰ ਸਿੰਘ ਨੇ 400 ਮੀਟਰ ਅਤੇ ਬੀ.ਐਸ. ਬਰੂਆ ਨੇ 800 ਮੀਟਰ ਦੌੜ ਵਿਚ ਸੋਨੇ ਦਾ ਤਮਗਾ ਪ੍ਰਾਪਤ ਕੀਤਾ । ਪ੍ਰਵੀਨ ਨੇ ਡਿਸਕਸ ਥਰੋ, ਜੋਗਿੰਦਰ ਸਿੰਘ ਨੇ ਗੋਲਾ ਸੁੱਟਣ ਅਤੇ ਭੀਮ ਸਿੰਘ ਨੇ ਉੱਚੀ ਛਾਲ ਵਿਚ ਸੋਨੇ ਦੇ ਤਮਗੇ ਜਿੱਤੇ ।

(5) 1970 ਵਿਚ ਬੈਂਕਾਕ ਵਿਚ ਪ੍ਰਬੰਧਿਤ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਵਿਚ ਕੰਵਲਜੀਤ ਸੰਧੂ ਨੇ 400 | ਮੀਟਰ ਦੌੜ ਵਿਚ, ਮਹਿੰਦਰ ਸਿੰਘ ਨੇ ਹਾਪ ਸਟੈਪ ਐਂਡ ਜੰਪ ਵਿਚ ਅਤੇ ਜੋਗਿੰਦਰ ਸਿੰਘ ਨੇ ਗੋਲਾ ਸੁੱਟਣ ਵਿਚ ਸੋਨੇ ਦੇ ਤਮਗੇ ਪ੍ਰਾਪਤ ਕੀਤੇ । ਇਹਨਾਂ ਤੋਂ ਇਲਾਵਾ ਐਡਵਰਡ ਸ਼ਕੇਰਾ ਨੇ 500 ਮੀਟਰ ਵਿਚ, ਸ੍ਰੀ ਰਾਮ ਨੇ 800 ਮੀਟਰ ਵਿਚ, ਲਾਭ ਸਿੰਘ ਨੇ ਲੰਮੀ ਛਾਲ, ਹਾਪ ਸਟੈਪ ਅਤੇ ਜੰਮ ਵਿਚ ਚਾਂਦੀ ਦੇ ਤਮਗੇ ਪ੍ਰਾਪਤ ਕੀਤੇ । ਮਨਜੀਤ ਵਾਲੀਆ ਨੇ 800 ਮੀਟਰ ਹਰਡਲਜ਼, ਸੁੱਚਾ ਸਿੰਘ ਨੇ 400 ਮੀਟਰ ਵਿਚ ਅਤੇ ਗੁਰਮੇਜ਼ ਸਿੰਘ ਨੇ 3000 ਮੀਟਰ ਵਿਚ ਤਾਂਬੇ ਦਾ ਤਮਗਾ ਪ੍ਰਾਪਤ ਕੀਤਾ ।

(6) 1974 ਵਿਚ ਤਹਿਰਾਨ ਵਿਚ ਹੋਈਆਂ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਵਿਚ ਸ਼ਿਵਨਾਥ ਨੇ 500 ਮੀਟਰ ਵਿਚ ਨਵਾਂ ਰਿਕਾਰਡ ਸਥਾਪਿਤ ਕੀਤਾ । ਕੰਵਲਜੀਤ ਸੰਧੂ ਨੇ 56.5 ਸੈਕਿੰਡ ਵਿਚ 400 ਮੀਟਰ ਦੀ ਦੌੜ ਜਿੱਤ ਕੇ ਭਾਰਤੀ ਇਸਤਰੀ ਵਜੋਂ ਸੋਨੇ ਦਾ ਤਮਗਾ ਜਿੱਤਿਆ । ਇਹਨਾਂ ਹੀ ਖੇਡਾਂ ਵਿਚ ਟੀ. ਸੀ. ਯੋਗਨਨ ਨੇ ਲੰਮੀ ਛਾਲ ਵਿਚ ਅਤੇ ਵੀ. ਐਸ. ਚੌਹਾਨ ਨੇ 1500 ਮੀਟਰ ਦੌੜ ਵਿਚ ਸੋਨੇ ਦਾ ਤਮਗਾ ਪ੍ਰਾਪਤ ਕੀਤਾ । ਨਿਰਮਲ ਸਿੰਘ ਨੇ ਹੈਮਰ ਸੁੱਟਣ ਵਿਚ ਚਾਂਦੀ ਦਾ ਅਤੇ ਲੈਹਿੰਬਰ ਸਿੰਘ ਨੇ 400 ਮੀਟਰ ਹਰਡਲ ਵਿਚ ਤਾਂਬੇ ਦਾ ਤਮਗਾ ਪ੍ਰਾਪਤ ਕੀਤਾ ।

(7) 1978 ਦੀਆਂ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਵਿਚ ਹਰੀ ਚੰਦ ਨੇ 100 ਮੀਟਰ ਦੌੜ ਵਿਚ ਸੋਨੇ ਦਾ ਤਮਗਾ ਪ੍ਰਾਪਤ ਕੀਤਾ । ਗੀਤਾ ਜੁਤਸ਼ੀ ਨੇ 1500 ਮੀਟਰ ਵਿਚ ਚਾਂਦੀ ਅਤੇ 800 ਮੀਟਰ ਦੌੜ ਵਿਚ ਸੋਨੇ ਦੇ ਤਮਗੇ ਪ੍ਰਾਪਤ ਕੀਤੇ ।

1982 ਦੀਆਂ ਨੌਵੀਆਂ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਜੋ ਦਿੱਲੀ ਵਿਖੇ ਹੋਈਆਂ ਸਨ । ਬਹਾਦਰ ਸਿੰਘ ਨੇ ਗੋਲਾ ਸੁੱਟਣ ਵਿਚ ਨਵਾਂ ਰਿਕਾਰਡ ਕਾਇਮ ਕੀਤਾ, ਗੀਤਾ ਜੁਤਸ਼ੀ ਨੇ 800, 1500 ਮੀਟਰ ਦੌੜ ਵਿਚ ਦੁਸਰਾ ਸਥਾਨ, ਵਾਲਸੰਮਾ ਨੇ 400 ਮੀਟਰ ਹਰਡਲ ਦੌੜ ਵਿਚ ਪਹਿਲਾ ਸਥਾਨ, 800 ਮੀਟਰ ਵਿਚ ਬਰੋਮੀਓ ਨੇ ਪਹਿਲਾ ਸਥਾਨ ਅਤੇ ਚਾਂਦ ਰਾਮ ਨੇ 200 ਕਿਲੋਮੀਟਰ ਵਾਕ ਵਿਚ ਪਹਿਲਾ ਸਥਾਨ ਪ੍ਰਾਪਤ ਕੀਤਾ । ਹਾਕੀ ਵਿਚ ਲੜਕੀਆਂ ਨੇ ਸੋਨੇ ਦਾ ਤਮਗਾ ਅਤੇ ਮੁੰਡਿਆਂ ਨੇ ਚਾਂਦੀ ਦਾ ਤਮਗਾ ਜਿੱਤਿਆ । ਕੁਸ਼ਤੀਆਂ ਵਿਚ ਸਤਪਾਲ ਸਿੰਘ ਨੇ ਸੋਨੇ ਦਾ ਤਮਗਾ ਅਤੇ ਕਰਤਾਰ ਸਿੰਘ ਨੇ ਚਾਂਦੀ ਦਾ ਤਮਗਾ ਜਿੱਤਿਆ ।

ਕੌਰ ਸਿੰਘ ਨੇ ਬਾਕਸਿੰਗ ਵਿਚ ਸੋਨੇ ਦਾ ਤਮਗਾ ਜਿੱਤਿਆ | ਭਾਰਤ ਦੀ ਘੋੜਿਆਂ ਦੀ ਟੀਮ ਨੇ ਸੋਨੇ ਦੇ ਤਮਗੇ ਜਿੱਤੇ ਅਤੇ ਭਾਰਤ ਦੀ ਗੋਲਫ ਦੀ ਟੀਮ ਨੇ ਸੋਨੇ ਦੇ ਤਮਗੇ ਜਿੱਤੇ ।

ਪ੍ਰਸ਼ਨ 10.
ਨਵੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਕਿਹੜੀਆਂ-ਕਿਹੜੀਆਂ ਖੇਡ ਘਟਨਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ ? (ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ – 6) (Name the main sports events which are organised in Modern Olympic ?)
ਉੱਤਰ-
ਨਵੀਨ ਓਲੰਪਿਕ ਖੇਡਾਂ ਵਿਚ ਹੇਠ ਲਿਖੀਆਂ ਖੇਡ ਘਟਨਾਵਾਂ ਹੁੰਦੀਆਂ ਹਨ-

1. ਤੀਰ ਅੰਦਾਜ਼ੀ (Archery)
2. ਐਥਲੈਟਿਕਸ (Athletics)
3. ਬਾਸਕਟਬਾਲ (Basket ball)
4. ਬਾਕਸਿੰਗ (Boxing)
5. ਕੈਨੋਇੰਗ (Canoeing)
6. ਸਾਈਕਲਿੰਗ (Cycling)
7. ਈਕਵੀਸਟਰੇਟ (Equestrin)
8. ਫੁੱਟਬਾਲ (Foot Ball)
9. ਜਿਮਨਾਸਟਿਕ (Gymnastics)
10. ਹੈਂਡ ਬਾਲ (Hand Ball)
11. ਹਾਕੀ (Hockey)
12. ਜੂਡੋ (Judo)
13. ਨਿਸ਼ਾਨੇ ਬਾਜ਼ੀ (Shooting)
14. ਰੋਇੰਗ (Rowing)
15. ਤੈਰਾਕੀ ਤੇ (Swimming and ਡੁਬਕੀ ਲਾਉਣਾ Diving)
16. ਤਲਵਾਰ ਬਾਜ਼ੀ (Fencing)
17. ਵਾਲੀਬਾਲ (Volley Ball)
18. ਵਾਟਰ ਪੋਲੋ (Water Polo)
19. ਭਾਰ ਉਠਾਉਣਾ (Weight Lifting)
20. ਕੁਸ਼ਤੀ (Wrestling)
21. ਯਾਟ-ਕਿਸ਼ਤੀ ਦੌੜ (Yachting)

ਪ੍ਰਸ਼ਨ 11.
11ਵੀਂ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਵਿਚ ਭਾਰਤੀਆਂ ਨੇ ਕਿਹੜੇ-ਕਿਹੜੇ ਇਨਾਮ ਪ੍ਰਾਪਤ ਕੀਤੇ ਹਨ ? [ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ – 9] (Mention the achievements of Indian sportsman in eleventh Asian Games.)
ਉੱਤਰ-
ਗਿਆਰਵੀਆਂ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਬੀਜਿੰਗ (ਚੀਨ) ਵਿਚ ਸੰਨ 1990 ਵਿਚ 22-9-1990 ਤੋਂ 7-10-1990 ਤਕ ਹੋਈਆਂ ਸਨ । ਇਸ ਵਿਚ ਭਾਰਤੀਆਂ ਨੇ ਹੇਠ ਲਿਖੇ ਮੁਕਾਬਲਿਆਂ ਵਿਚ ਇਨਾਮ ਪ੍ਰਾਪਤ ਕੀਤੇ ਸਨਖੇਡ ਸੋਨਾ-

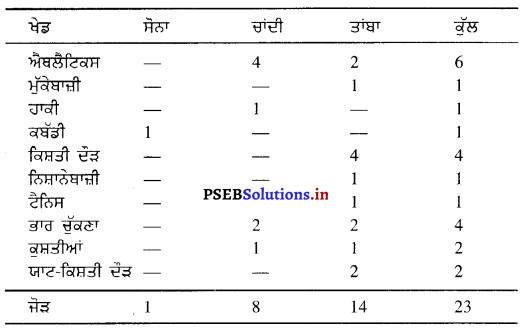
ਪ੍ਰਸ਼ਨ 12.
ਸਾਲ 1982 ਦੀਆਂ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਕਿਸ ਦੇਸ਼ ਵਿਚ ਹੋਈਆਂ ਸਨ ? (In which country were the 1982 Asian games were held ?)
ਉੱਤਰ-
ਭਾਰਤ ਵਿਚ ।
ਏਸ਼ਿਆਈ ਖੇਡਾਂ

ਨੰਬਰ – ਸੰਨ – ਸਥਾਨ
1. – 1951 – ਦਿੱਲੀ (ਭਾਰਤ)
2. – 1954 – ਮਨੀਲਾ (ਫਿਲਪੀਨ)
3. – 1958 – ਟੋਕੀਓ (ਜਾਪਾਨ)
4. – 1962 – ਜਕਾਰਤਾ (ਇੰਡੋਨੇਸ਼ੀਆ) (ਥਾਈ ਦੇਸ਼ਾਂ ਦੇ ਮਿਲਵਰਤਨ ਨਾ ਮਿਲਣ ਕਾਰਨ ਇਹਨਾਂ ਨੂੰ ਏਸ਼ਿਆਈ ਖੇਡਾਂ ਦੀ ਮਾਨਤਾ ਨਾ ਮਿਲ ਸਕੀ।)
5. – 1966 – ਬੈਂਕਾਕ (ਥਾਈਲੈਂਡ)
6. – 1970 – ਬੈਂਕਾਕ (ਥਾਈਲੈਂਡ)
7. – 1974 – ਤਹਿਰਾਨ (ਈਰਾਨ)
8. – 1978 – ਬੈਂਕਾਕ (ਥਾਈਲੈਂਡ)
9. – 1982 – ਦਿੱਲੀ (ਭਾਰਤ)
10. – 1986 – ਮਿਓਲ (ਦੱਖਣੀ ਕੋਰੀਆ)
11. – 1990 – ਬੀਜਿੰਗ (ਚੀਨ)
12. – 1994 – ਹੀਰੋਸ਼ੀਮਾ (ਜਾਪਾਨ)
13. – 1998 – ਬੈਂਕਾਕ (ਥਾਈਲੈਂਡ)
14. – 2002 – ਪੁਸਾਜ (ਸਾਊਥ ਕੋਰੀਆ)
15. – 2006 – ਦੋਹਾ (ਕਤਰ)
16. – 2010 – ਗੋਗਘੋ (ਚੀਨ)
17. – 2014 – ਇੰਮੀਐਨ (ਸਾਊਥ ਕੋਰੀਆ)
18. – 2018 – ਜਕਾਰਤਾ (ਇੰਡੋਨੇਸ਼ੀਆ)
19. – 2022 – ਹੈਮਪਾਡ ਚੀਨ ਵਿਚ ਹੋਣਗੀਆਂ

Punjab State Board PSEB 10th Class Physical Education Book Solutions Chapter 3 ਯੋਗ Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 10 Physical Education Chapter 3 ਯੋਗ

Physical Education Guide for Class 10 PSEB ਯੋਗ Textbook Questions and Answers

ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Very Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਭਾਰਤੀ ਕਸਰਤ ਦੀ ਪ੍ਰਾਚੀਨ ਵਿਧੀ ਕਿਹੜੀ ਹੈ ? (Which is the oldest method of Indian Exercises ?)
ਉੱਤਰ-
ਯੋਗ-ਆਸਣ |

ਪ੍ਰਸ਼ਨ 2.
ਸ਼ੀਸ਼ ਆਸਣ ਹਰ ਰੋਜ਼ ਕਿੰਨੇ ਸਮੇਂ ਲਈ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ? (How much time Searsh Asana may be performed daily ?)
ਉੱਤਰ-
ਦੋ ਮਿੰਟ ।

ਪ੍ਰਸ਼ਨ 3.
ਸ਼ੀਸ਼ ਆਸਣ ਦੇ ਕੋਈ ਦੋ ਲਾਭ ਲਿਖੋ । (Mention any two advantages of Searsh Asana.)
ਉੱਤਰ-

1. ਸ਼ੀਸ਼ ਆਸਣ ਨਾਲ ਯਾਦਦਾਸ਼ਤ ਤੇਜ਼ ਹੁੰਦੀ ਹੈ ।
2. ਮੋਟਾਪਾ ਦੂਰ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਵਜਰ ਆਸਣ ਦੇ ਕੋਈ ਦੋ ਲਾਭ ਲਿਖੋ । (Mention any two advantages of Vazur Asana.)
ਉੱਤਰ-

1. ਵਜਰ ਆਸਣ ਨਾਲ ਸੁਪਨ-ਦੋਸ਼ ਦੂਰ ਹੁੰਦਾ ਹੈ ।
2. ਇਸ ਨਾਲ ਸ਼ੂਗਰ ਦੀ ਬਿਮਾਰੀ ਦੂਰ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਪਦਮ ਆਸਣ ਦੇ ਦੋ ਲਾਭ ਲਿਖੋ । (Mention any two advantages of Padam Asana.)
ਉੱਤਰ-

1. ਕਮਰ ਦਰਦ ਦੂਰ ਹੁੰਦਾ ਹੈ ।
2. ਵਾਰ-ਵਾਰ ਪੇਸ਼ਾਬ ਆਉਣਾ ਬੰਦ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਭੁਜੰਗ ਆਸਣ ਦੇ ਕੋਈ ਦੋ ਲਾਭ ਲਿਖੋ । (Describe any two advantages of Bhujung Asana.)
ਉੱਤਰ-

1. ਕਬਜ਼ ਦੂਰ ਹੋ ਜਾਂਦੀ ਹੈ ।
2. ਧਾਤੁ ਰੋਗ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਧਨੁਰ ਆਸਣ ਦੇ ਕੋਈ ਦੋ ਲਾਭ ਲਿਖੋ । (Mention any two advantages of Dhanura Asana.)
ਉੱਤਰ-

1. ਗਠੀਏ ਦੀ ਬਿਮਾਰੀ ਦੂਰ ਹੋ ਜਾਂਦੀ ਹੈ ।
2. ਇਸਤਰੀਆਂ ਦੇ ਯੋਨ ਸੰਬੰਧੀ ਨੁਕਸ ਅਤੇ ਮਾਸਿਕ ਧਰਮ ਸੰਬੰਧੀ ਰੋਗ ਦੂਰ ਹੋ ਜਾਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 8.
ਹਰਨੀਆਂ ਅਤੇ ਨਲਾਂ ਦੇ ਰੋਗਾਂ ਨੂੰ ਠੀਕ ਕਰਨ ਲਈ ਕਿਹੜਾ ਆਸਣ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ ? (Name the Asana which prevent Hernia Disease.)
ਉੱਤਰ-
ਚੱਕਰ ਆਸਣ ।

ਪ੍ਰਸ਼ਨ 9.
ਆਤਮਾ ਨੂੰ ਪਰਮਾਤਮਾ ਨਾਲ ਮਿਲਾਉਣ ਦਾ ਮਹੱਤਵਪੂਰਨ ਢੰਗ ਕਿਹੜਾ ਹੈ ? (Which is the means of uniting soul with God ?)
ਉੱਤਰ-
ਯੋਗ ।

ਪ੍ਰਸ਼ਨ 10.
ਮਾਨਸਿਕ ਇਕਾਗਰਤਾ ਦੇ ਲਈ ਕਿਹੜਾ ਆਸਣ ਸਭ ਤੋਂ ਚੰਗਾ ਹੈ ? (Which is the best Asana for mental concentration ?)
ਉੱਤਰ-
ਪਦਮ ਆਸਣ ।

ਪ੍ਰਸ਼ਨ 11.
ਥਕਾਵਟ ਕਿੰਨੇ ਤਰ੍ਹਾਂ ਦੀ ਹੁੰਦੀ ਹੈ ?(Mention the types of Fatigue.)
ਉੱਤਰ-
ਥਕਾਵਟ ਦੋ ਤਰ੍ਹਾਂ ਦੀ ਹੁੰਦੀ ਹੈ-

1. ਮਾਨਸਿਕ
2. ਸਰੀਰਕ ।

ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ : (Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਯੋਗ ਕੀ ਹੈ ? ਇਸ ਦੇ ਕੀ ਲਾਭ ਹਨ ? [ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ – 1]
(What is Yoga ? Discuss its uses.)
ਉੱਤਰ-
ਯੋਗ (Yoga) – ਭਾਰਤ ਦੀ ਸਭ ਤੋਂ ਪੁਰਾਣੀ ਕਸਰਤ ਕਰਨ ਦੀ ਵਿਧੀ ਯੋਗ ਹੈ । ਪੁਰਾਣੇ ਜ਼ਮਾਨੇ ਵਿਚ ਸਾਧੂ-ਸੰਤ, ਮਹਾਤਮਾ ਲੋਕ ਇਸ ਦਾ ਅਭਿਆਸ ਕਰਦੇ ਸਨ ਅਤੇ ਆਪਣਾ ਸਰੀਰ ਤੰਦਰੁਸਤ ਰੱਖਦੇ ਸਨ । ਇਸ ਨੂੰ ਅਸੀਂ ਆਮ ਤੌਰ ‘ਤੇ ਤਪੱਸਿਆ ਕਰਨ ਵਾਸਤੇ ਵੀ ਵਰਤ ਸਕਦੇ ਹਾਂ । ਯੋਗ ਹਰ ਇਕ ਵਿਅਕਤੀ ਲਈ ਜ਼ਰੂਰੀ ਹੈ ।

ਯੋਗ ਦੇ ਸਾਨੂੰ ਹੇਠ ਦਿੱਤੇ ਲਾਭ ਹਨ-

1. ਯੋਗ ਆਸਣ ਦੇ ਰਾਹੀਂ ਮਨੁੱਖ ਦਾ ਸਰੀਰ ਤੰਦਰੁਸਤ ਰਹਿੰਦਾ ਹੈ ।
2. ਇਸ ਦੇ ਰਾਹੀਂ ਬਹੁਤ ਸਾਰੀਆਂ ਬਿਮਾਰੀਆਂ ਦੂਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
3. ਮਾਨਸਿਕ ਕਮਜ਼ੋਰੀ ਦੂਰ ਹੋ ਜਾਂਦੀ ਹੈ ।
4. ਸਰੀਰ ਸ਼ਕਤੀਸ਼ਾਲੀ ਬਣ ਜਾਂਦਾ ਹੈ ।
5. ਮਨੁੱਖ ਛੇਤੀ ਘਬਰਾਹਟ ਵਿਚ ਨਹੀਂ ਆਉਂਦਾ ।
6. ਚਿੰਤਾ ਅਤੇ ਪਰੇਸ਼ਾਨੀਆਂ ਦੂਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
7. ਮਨੁੱਖ ਦਾ ਸਰੀਰ ਸੋਹਣਾ ਅਤੇ ਤਾਕਤਵਰ ਬਣ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਯੋਗ ਆਤਮਾ ਤੇ ਪਰਮਾਤਮਾ ਵਿਚ ਮੇਲ ਕਰਾਉਣ ਦਾ ਮਹੱਤਵਪੂਰਨ ਸਾਧਨ ਹੈ । ਕਿਵੇਂ ? (Yoga is the means of uniting soul with God. How ?)
ਉੱਤਰ-
ਪੁਰਾਣੇ ਜ਼ਮਾਨੇ ਦੇ ਸਾਧੂ-ਸੰਤਾਂ ਦੀਆਂ ਗੱਲਾਂ ਅਸੀਂ ਅੱਜ ਤਕ ਸੁਣਦੇ ਆ ਰਹੇ ਹਾਂ । | ਉਨ੍ਹਾਂ ਦੇ ਵਿਚਾਰ ਅਨੁਸਾਰ ਜੇਕਰ ਕਿਸੇ ਵਿਅਕਤੀ ਨੇ ਆਤਮਾ ਤੇ ਪਰਮਾਤਮਾ ਨਾਲ ਮੇਲ ਕਰਨਾ
ਹੈ ਤਾਂ ਉਸ ਦਾ ਸਾਧਨ ਸਰੀਰ ਹੈ ।ਉਹ ਹੀ ਵਿਅਕਤੀ ਆਤਮਾ ਤੇ ਪਰਮਾਤਮਾ ਨੂੰ ਮਿਲ ਸਕਦਾ ਹੈ ਜਾਂ ਦਰਸ਼ਨ ਕਰ ਸਕਦਾ ਹੈ ਜਿਹੜਾ ਸਰੀਰਕ ਰੂਪ ਵਿਚ ਤੰਦਰੁਸਤ ਹੋਵੇ ।

ਅਸੀਂ ਯੋਗ ਸਾਧਨ ਦੇ ਰਾਹੀਂ ਸਰੀਰ ਨੂੰ ਠੀਕ ਰੱਖ ਸਕਦੇ ਹਾਂ | ਬਹੁਤ ਸਾਰੀਆਂ ਬਿਮਾਰੀਆਂ ਆਪਣੇ ਆਪ ਹੀ ਦੂਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ । ਇਸ ਲਈ ਸਾਬਿਤ ਹੁੰਦਾ ਹੈ ਕਿ ਯੋਗ ਆਤਮਾ ਤੇ ਪਰਮਾਤਮਾ ਦਾ ਮੇਲ ਕਰਾਉਣ ਦਾ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਸਾਧਨ ਹੈ । ਇਸ ਲਈ ਸਾਨੂੰ ਯੋਗ ਦੀ ਵਰਤੋਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ।

ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Long Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਕੋਈ ਪੰਜ ਆਸਣਾਂ ਦੀ ਵਿਧੀ ਅਤੇ ਲਾਭ ਦੱਸੋ । (Discuss the methods of any five Asanas and give their uses.)
ਜਾਂ
ਆਸਣਾਂ ਦੇ ਲਾਭ ਦੱਸੋ ।
[ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ – 6]
(Discuss the advantages of Asanas.)
ਉੱਤਰ-
1. ਸਵ ਆਸਣ (Sha Asana)-

ਸਥਿਤੀ (Position) – ਪਿੱਠ ਦੇ ਭਾਰ ਲੇਟ ਕੇ ਸਰੀਰ ਨੂੰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਢਿੱਲਾ ਛੱਡ ਦਿਓ ।
ਵਿਧੀ (Technique) –

• ਪਿੱਠ ਦੇ ਭਾਰ ਲੇਟ ਕੇ ਸਰੀਰ ਨੂੰ ਢਿੱਲਾ ਛੱਡੋ ।
• ਹੌਲੀ-ਹੌਲੀ ਲੰਮੇ ਸਾਹ ਲਵੋ ।
• ਲੰਮੇ ਪੈ ਕੇ ਸਰੀਰ ਦੇ ਪੂਰੇ ਅੰਗਾਂ ਨੂੰ ਆਰਾਮ ਦਿਓ ।
• ਦੋਹਾਂ ਪੈਰਾਂ ਨੂੰ 12 ਫੁੱਟ ਦੀ ਦੂਰੀ ਤੇ ਰੱਖੋ ।
• ਦੋਹਾਂ ਹੱਥਾਂ ਦੀਆਂ ਹਥੇਲੀਆਂ ਨੂੰ ਅਸਮਾਨ ਵਲ ਕਰਕੇ ਸਰੀਰ ਤੋਂ ਇਕ ਗਿੱਠ ਦੀ ਦੁਰੀ ਤੇ ਰੱਖੋ ।
• ਅੱਖਾਂ ਬੰਦ ਕਰਕੇ ਅੰਤਰ-ਧਿਆਨ ਹੋ ਜਾਉ ।
• ਸਰੀਰ ਨੂੰ ਆਰਾਮ ਦੀ ਹਾਲਤ ਵਿਚ ਰੱਖੋ ।

ਲਾਭ (Advantages)-

• ਸਰੀਰ ਦੀ ਥਕਾਵਟ ਨੂੰ ਦੂਰ ਕਰਦਾ ਹੈ ।
• ਮਾਨਸਿਕ ਤਣਾਅ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਹਾਈ-ਬਲੱਡ ਪ੍ਰੈਸ਼ਰ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਦਿਲ ਅਤੇ ਦਿਮਾਗ਼ ਵਿਚ ਤਾਜ਼ਗੀ ਆਉਂਦੀ ਹੈ ।
• ਸਰੀਰ ਨੂੰ ਤਾਕਤ ਮਿਲ ਜਾਂਦੀ ਹੈ ।

2. ਪਸ਼ਚਿਮੋਤਾਨ ਆਸਣ (Paschimotan Asana)-
ਸਥਿਤੀ – ਸਾਰੇ ਸਰੀਰ ਨੂੰ ਫੈਲਾ ਕੇ ਮੋੜਨਾ ।

Paschimotan Asana ਵਿਧੀ (Technique) –

• ਲੱਤਾਂ ਨੂੰ ਅੱਗੇ ਵੱਲ ਵਧਾ ਕੇ ਜ਼ਮੀਨ ਉੱਪਰ ਬੈਠ ਜਾਉ ।
• ਦੋਹਾਂ ਹੱਥਾਂ ਨਾਲ ਪੈਰਾਂ ਦੇ ਅੰਗੂਠੇ ਫੜੋ ।
• ਹੌਲੀ-ਹੌਲੀ ਸਾਹ ਛੱਡਦੇ ਹੋਏ ਨੱਕ ਗੋਡਿਆਂ ਨੂੰ ਲਾਉਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰੋ ।
• ਹੌਲੀ-ਹੌਲੀ ਸਿਰ ਉੱਪਰ ਚੁੱਕੋ ਅਤੇ ਪਹਿਲੀ ਵਾਲੀ ਹਾਲਤ ਵਿਚ ਆ ਜਾਉ ।
• ਇਹ ਆਸਣ 10 ਤੋਂ 15 ਵਾਰੀ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।

ਲਾਭ (Advantages)

• ਇਹ ਆਸਣ ਪੇਟ ਗੈਸ ਦੀ ਬਿਮਾਰੀ ਦੂਰ ਕਰਦਾ ਹੈ ।
• ਨਾੜਾਂ ਸਾਫ਼ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਲੱਤਾਂ ਤੇ ਬਾਹਾਂ ਮਜ਼ਬੂਤ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਸਰੀਰ ਦੀ ਵਧੀ ਹੋਈ ਚਰਬੀ ਘੱਟ ਜਾਂਦੀ ਹੈ ।
• ਪੇਟ ਦੀਆਂ ਬਹੁਤ ਸਾਰੀਆਂ ਬਿਮਾਰੀਆਂ ਦੂਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਸਰੀਰ ਹਲਕਾਪਨ ਮਹਿਸੂਸ ਕਰਦਾ ਹੈ ।
• ਲੱਤਾਂ ਟੇਢੀਆਂ ਨਹੀਂ ਹੁੰਦੀਆਂ ਹਨ !

3. ਧਨੁਰ ਆਸਣ (Dhanura Asana)-
ਸਥਿਤੀ – ਇਸ ਆਸਣ ਦੇ ਵਿਚ ਸਰੀਰ ਦੀ ਹਾਲਤ ਕਮਾਨ ਦੀ ਤਰ੍ਹਾਂ ਹੁੰਦੀ ਹੈ ।

Dhanura Asana feut (Technique)-

• ਇਸ ਆਸਣ ਨੂੰ ਕਰਨ ਦੇ ਲਈ ਪੇਟ ਦੇ ਭਾਰ ਲੇਟ ਜਾਓ ।
• ਪੈਰਾਂ ਨੂੰ ਪਿੱਠ ਵੱਲ ਕਰੋ ।
• ਹੱਥਾਂ ਨਾਲ ਗਿੱਟਿਆਂ ਨੂੰ ਪਕੜੋ ।
• ਜਿੱਥੋਂ ਤਕ ਹੋ ਸਕੇ ਲੰਮਾ ਸਾਹ ਲੈ ਕੇ ਸਰੀਰ ਅਤੇ ਛਾਤੀ ਨੂੰ ਉੱਪਰ ਚੁੱਕ ਕੇ ਸਰੀਰ ਦਾ ਆਕਾਰ ਧਨੁੱਖ ਵਾਂਗ ਕਰ ਲਵੋ ।
• ਜਿੰਨੀ ਦੇਰ ਆਸਾਨੀ ਨਾਲ ਰੱਖ ਸਕੋ, ਰੱਖੋ ਅਤੇ ਫਿਰ ਸਾਹ ਨੂੰ ਹੌਲੀ-ਹੌਲੀ ਛੱਡਦੇ ਹੋਏ ਸਰੀਰ ਨੂੰ ਢਿੱਲਾ ਛੱਡ ਦਿਉ ਅਤੇ ਪਹਿਲੀ ਹਾਲਤ ਵਿਚ ਲੈ ਆਉ ।

ਲਾਭ (Advantages)-

• ਆਂਦਰਾਂ ਨੂੰ ਤਾਕਤ ਮਿਲਦੀ ਹੈ।
• ਪਾਚਨ ਸ਼ਕਤੀ ਵਿਚ ਵਾਧਾ ਹੁੰਦਾ ਹੈ ।
• ਮੋਟਾਪਾ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਗਠੀਆ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਦੂਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਔਰਤਾਂ ਦੇ ਯੋਨੀ-ਵਿਕਾਰ ਅਤੇ ਮਾਸਕ-ਧਰਮ ਸੰਬੰਧੀ ਰੋਗਾਂ ਨੂੰ ਦੂਰ ਕਰਦਾ ਹੈ।
• ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਮਜ਼ਬੂਤ ਹੋ ਜਾਂਦੀ ਹੈ ।
• ਮਾਸਪੇਸ਼ੀਆਂ ਲਚਕੀਲੀਆਂ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।

4. ਪਦਮ ਆਸਣ (Padam Asana)
ਸਥਿਤੀ {Position) – ਇਸ ਆਸਣ ਵਿਚ ਸਰੀਰ ਦੀ ਸਥਿਤੀ ਕਮਲ ਦੇ ਸਮਾਨ ਹੁੰਦੀ ਹੈ ।

ਵਿਧੀ (Technique) –

• ਪਦਮ ਆਸਣ ਕਰਨ ਲਈ ਪਹਿਲਾਂ ਚੌਕੜੀ ਮਾਰ ਕੇ ਬੈਠੇ ।
• ਸੱਜਾ ਪਰ ਖੱਬੇ ਪੈਰ ਤੇ ਇਸ ਤਰ੍ਹਾਂ ਰੱਖੋ ਕਿ ਸੱਜੇ ਪੈਰ ਦੀ ਅੱਡੀ ਖੱਬੇ ਪੱਟ ਦੀ ਹੱਡੀ ਨੂੰ ਛੁਹੇ । ਇਸ ਤੋਂ ਬਾਅਦ ਪੱਬੇ ਪੈਰ ਨੂੰ ਚੁੱਕ ਕੇ ਸੱਜੇ ਪੱਟ ਦੇ ਪਰ ਸੇ ਤਰ੍ਹਾਂ ਰੱਖੇ ।
• ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਸਿੱਧੀ ਰੱਖੋ ।
• ਬਾਹਾਂ ਨੂੰ ਤਾਨ ਕੇ ਹੱਥਾਂ ਨੂੰ ਗੋਡਿਆਂ ‘ਤੇ ਰੱਖੋ ।

ਲਾਭ (Advantages) –

• ਇਸ ਆਸਣ ਨਾਲ ਮਨ ਸਥਿਰ ਰਹਿੰਦਾ ਹੈ ।
• ਇਸ ਆਸਣ ਨਾਲ ਕਮਰ ਦਾ ਦਰਦ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਇਸ ਆਸਣ ਨਾਲ ਦਿਲ ਅਤੇ ਪੇਟ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਦੂਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਪਾਚਨ-ਸ਼ਕਤੀ ਵੱਧ ਜਾਂਦੀ ਹੈ ।
• ਵਾਰ-ਵਾਰ ਪੇਸ਼ਾਬ ਆਉਣ ਦਾ ਰੋਗ ਨਹੀਂ ਹੋ ਸਕਦਾ ।
• ਬਹੁਤ ਸਾਰੀਆਂ ਅੰਦਰੂਨੀ ਬਿਮਾਰੀਆਂ ਦੂਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਬਾਹਾਂ ਤੇ ਲੱਤਾਂ ਮਜ਼ਬੂਤ ਹੁੰਦੀਆਂ ਹਨ ।
• ਖੂਨ ਦਾ ਸੰਚਾਰ ਤੇਜ਼ ਹੁੰਦਾ ਹੈ ।
• ਸਰੀਰ ਸਿਹਤਮੰਦ ਰਹਿੰਦਾ ਹੈ ।

5. ਹਲ ਆਸਣ ਦੀ ਸਥਿਤੀ (Position of Hal Asana)-
ਵਿਧੀ (Technique) – ਆਪਣੇ ਪੈਰ ਫੈਲਾ ਕੇ ਪਿੱਠ ਦੇ ਬਲ ਜ਼ਮੀਨ ਉੱਤੇ ਲੰਮੇ ਪੈ ਜਾਓ । ਹੱਥਾਂ ਦੀਆਂ ਤਲੀਆਂ ਨੂੰ ਕੂਲ੍ਹਿਆਂ ਦੀ ਬਗਲ ਵਿਚ ਜਮਾ ਦਿਓ | ਕਮਰ ਦੇ ਹੇਠਲੇ ਭਾਗ ਨੂੰ ਦੋਹਾਂ ਪੈਰਾਂ ਨੂੰ ਜ਼ਮੀਨ ਤੋਂ ਹੌਲੀ ਜਿਹੀ ਉੱਪਰ ਚੁੱਕੋ ਅਤੇ ਇੰਨਾ ਉੱਪਰ ਲੈ ਜਾਓ ਕਿ ਦੋਹਾਂ ਪੈਰਾਂ ਦੇ ਅੰਗੂਠੇ ਸਿਰ ਦੇ ਪਿੱਛੇ ਜ਼ਮੀਨ ਨਾਲ ਲੱਗ ਜਾਣ । ਜਦੋਂ ਤਕ

ਸੰਭਵ ਹੋਵੇ, ਇਸ ਸਥਿਤੀ ਵਿਚ ਰਹੋ । ਪੈਰਾਂ ਨੂੰ ਹੌਲੀ ਜਿਹੀ ਉਸ ਸਥਾਨ ਤੇ ਵਾਪਸ ਲੈ ਜਾਓ ਜਿੱਥੋਂ ਸ਼ੁਰੂ ਕੀਤਾ ਸੀ ।
ਨੋਟ-

• ਇਹ ਆਸਣ ਹਰ ਉਮਰ ਦੀ ਔਰਤ ਤੇ ਮਰਦ ਲਈ ਲਾਭਦਾਇਕ ਹੈ ।
• ਇਹ ਆਸਣ ਦਿਲ ਦੇ ਰੋਗੀਆਂ ਜਾਂ ਉੱਚੇ ਜਾਂ ਨੀਵੇਂ ਰਕਤ-ਚਾਪ ਵਾਲਿਆਂ ਲਈ ਮਨ੍ਹਾਂ ਹੈ ।
• ਇਸ ਆਸਣ ਨੂੰ ਝਟਕੇ ਨਾਲ ਨਹੀਂ ਕਰਨਾ ਚਾਹੀਦਾ ।

ਲਾਭ (Advantages) –

• ਇਹ ਆਸਣ ਸਾਰੇ ਸਰੀਰ ਵਿਚ ਖੂਨ ਦੇ ਦੌਰੇ ਨੂੰ ਨਿਯਮਿਤ ਕਰਦਾ ਹੈ । ਫਲਸਰੂਪ ਚਮੜੀ ਸੰਬੰਧੀ ਰੋਗ ਜਲਦੀ ਦੂਰ ਹੋ ਜਾਂਦੇ ਹਨ ।
• ਮੋਟਾਪਾ ਦੂਰ ਕਰਨ ਲਈ ਇਹ ਆਸਣ ਸਰਵਸ੍ਰੇਸ਼ਠ ਹੈ । ਕਮਰ ਅਤੇ ਕੂਲਿਆਂ ਨੂੰ ਪਤਲਾ ਕਰਦਾ ਹੈ ।
• ਪੇਟ ਦੀ ਸਥੂਲਤਾ ਨੂੰ ਆਸਾਨੀ ਨਾਲ ਘੱਟ ਕਰਦਾ ਹੈ ।
• ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਲਚਕੀਲੀ ਹੁੰਦੀ ਹੈ । ਸਰੀਰ ਸੁੰਦਰ ਅਤੇ ਨਿਰੋਗ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਇਹ ਆਸਣ ਸਰੀਰ ਦੀ ਬਦਬੂ ਨੂੰ ਦੂਰ ਕਰਦਾ ਹੈ । ਸਰੀਰ ਨੂੰ ਸੁੰਦਰ ਬਣਾਉਂਦਾ ਹੈ ।
• ਚਿਹਰਾ ਖ਼ੁਸ਼ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਅੱਖਾਂ ਵਿਚ ਤੇਜ਼ੀ ਆ ਜਾਂਦੀ ਹੈ ।

6. ਸਰਵਾਂਗ ਆਸਣ ਦੀ ਸਥਿਤੀ (Position of Sarvang Asana) – ਇਸ ਆਸਣ ਵਿਚ ਸਾਰੇ ਸਰੀਰ ਦੀ ਸਥਿਤੀ ਅਰਧ-ਹਲ ਦੀ ਤਰ੍ਹਾਂ ਹੋ ਜਾਂਦੀ ਹੈ ।
ਵਿਪੀ (Technique) –

• ਇਸ ਆਸਣ ਦੇ ਲਈ ਸਰੀਰ ਨੂੰ ਸਿੱਧਾ ਕਰਕੇ ਪਿੱਠ ਦੇ ਭਾਰ ਸਿੱਧੇ ਲੰਮੇ ਪੈ ਜਾਓ ।
• ਹੱਥਾਂ ਨੂੰ ਪੇਟ ਦੇ ਬਰਾਬਰ ਸਿੱਧਾ ਕਰੋ ।
• ਦੋਹਾਂ ਪੈਰਾਂ ਨੂੰ ਇੱਕੋ ਵੇਲੇ ਉੱਪਰ ਚੁੱਕ ਕੇ ਤਲੀਆਂ ਤੋਂ ਪਿੱਠ ਨੂੰ ਸਹਾਰਾ ਦਿੰਦੇ ਹੋਏ ਕੂਹਣੀਆਂ ਨੂੰ ਜ਼ਮੀਨ ‘ਤੇ ਟਿਕਾਓ ।
• ਸਾਰੇ ਸਰੀਰ ਨੂੰ ਸਿੱਧਾ ਰੱਖੋ।
• ਸਾਰੇ ਸਰੀਰ ਦਾ ਭਾਰ ਮੋਢਿਆਂ ਅਤੇ ਧੌਣ ‘ਤੇ ਰਹੇ ।
• ਨੋਡੀ ਨੂੰ ਛਾਤੀ ਨਾਲ ਛੂਹੋ ।
• ਕੁੱਝ ਦੇਰ ਇਸੇ ਸਥਿਤੀ ਵਿਚ ਰਹਿਣ ਦੇ ਬਾਅਦ ਫਿਰ ਪਹਿਲਾਂ ਵਾਲੀ ਸਥਿਤੀ ਵਿਚ ਜਾਓ ।

ਲਾਭ (Advantages)-

• ਸਰੀਰ ਵਿਚ ਫੁਰਤੀ ਆਉਂਦੀ ਹੈ ।
• ਸਰੀਰ ਤਾਕਤਵਰ ਬਣ ਜਾਂਦਾ ਹੈ ।
• ਮੋਟਾਪਾ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਬਾਹਾਂ ਅਤੇ ਪੈਰ ਮਜ਼ਬੂਤ ਹੋ ਜਾਂਦੇ ਹਨ ।
• ਲੱਤਾਂ ਵਿੰਗੀਆਂ ਨਹੀਂ ਹੁੰਦੀਆਂ ।

7. ਭੁਜੰਗ ਆਸਣ (Bhujang Asana) – ਇਸ ਵਿਚ ਪਿੱਠ ਭਾਰ ਲੇਟ ਕੇ ਧੜ ਨੂੰ ਢਿੱਲਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
ਭੁਜੰਗ ਆਸਣ ਦੀ ਵਿਧੀ (Technique of Bhujang Asana) – ਇਸ ਨੂੰ ਸਰਪ ਆਸਣ ਵੀ ਕਹਿੰਦੇ ਹਨ । ਇਸ ਵਿਚ ਸਰੀਰ ਦੀ ਸਥਿਤੀ ਸੱਪ ਦੇ ਆਕਾਰ ਵਰਗੀ ਹੁੰਦੀ ਹੈ | ਸਰਪ ਆਸਣ ਕਰਨ ਲਈ ਧਰਤੀ ‘ਤੇ ਪੇਟ ਦੇ ਬਲ ਲੇਟੋ । ਦੋਵੇਂ ਹੱਥ ਮੋਢਿਆਂ ਦੇ ਬਰਾਬਰ ਰੱਖੋ | ਹੌਲੀ-ਹੌਲੀ ਲੱਤਾਂ ਨੂੰ ਅਕੜਾਉਂਦੇ ਹੋਏ ਹਥੇਲੀਆਂ ਦੇ ਬਲ ਛਾਤੀ ਨੂੰ ਇੰਨਾ ਉੱਪਰ ਚੁੱਕੋ ਕਿ ਬਾਹਵਾਂ ਬਿਲਕੁਲ ਸਿੱਧੀਆਂ ਹੋ ਜਾਣ । ਪੰਜਿਆਂ ਨੂੰ ਅੰਦਰ ਵਲ ਨੂੰ ਕਰੋ ਅਤੇ ਸਿਰ ਨੂੰ ਹੌਲੀ-ਹੌਲੀ ਪਿੱਛੇ ਵਲ ਨੂੰ ਲਟਕਾਓ । ਹੌਲੀ-ਹੌਲੀ ਪਹਿਲਾਂ ਵਾਲੀ ਸਥਿਤੀ ਵਿਚ ਆ ਜਾਓ । ਇਸ ਆਸਣ ਨੂੰ ਤਿੰਨ ਤੋਂ ਪੰਜ ਵਾਰੀ ਕਰੋ ।

ਲਾਭ (Advantages)-

• ਭੁਜੰਗ ਆਸਣ ਨਾਲ ਪਾਚਨ ਸ਼ਕਤੀ ਵਧਦੀ ਹੈ ।
• ਜਿਗਰ ਅਤੇ ਤਿੱਲੀ ਦੇ ਰੋਗਾਂ ਤੋਂ ਛੁਟਕਾਰਾ ਮਿਲਦਾ ਹੈ ।
• ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਅਤੇ ਪੱਠੇ ਮਜ਼ਬੂਤ ਬਣਦੇ ਹਨ ।
• ਕਬਜ਼ ਦੂਰ ਹੁੰਦੀ ਹੈ ।
• ਵਧਿਆ ਹੋਇਆ ਪੇਟ ਅੰਦਰ ਨੂੰ ਧਸਦਾ ਹੈ ।
• ਫੇਫੜੇ ਸ਼ਕਤੀਸ਼ਾਲੀ ਹੁੰਦੇ ਹਨ ।

8. ਸ਼ਲਭ ਆਸਣ (Shlab Asana) – ਇਸ ਆਸਣ ਵਿਚ ਪਿੱਠ ਦੇ ਭਾਰ ਲੇਟ ਕੇ ਗਲ ਨੂੰ ਪਿੱਛੇ ਫੈਲਾਇਆ ਜਾਂਦਾ ਹੈ ।

ਵਿਧੀ (Technique) – ਪੇਟ ਦੇ ਬਲ ਲੇਟ ਕੇ ਗਰਦਨ ਨੂੰ ਪਿੱਛੇ ਫੈਲਾਉਣ ਲਈ ਦੋਵੇਂ ਹਥੇਲੀਆਂ ਸਰੀਰ ਦੇ ਨਾਲ ਜ਼ਮੀਨ ਤੇ ਟਿਕਾ ਲਵੋ । ਪੈਰਾਂ ਨੂੰ ਉੱਪਰ ਕਰਕੇ ਲੱਤਾਂ ਉੱਚੀਆਂ ਚੁੱਕੋ । ਧੁੰਨੀ ਤੋਂ ਹੇਠਲਾ ਭਾਗ ਜ਼ੋਰ ਲਗਾ ਕੇ ਜਿੰਨਾ ਉੱਚਾ ਚੁੱਕ ਸਕਦੇ ਹੋ, ਚੁੱਕੋ ।

ਲਾਭ (Advantages)-

• ਇਹ ਆਸਣ ਕਰਨ ਨਾਲ ਸ਼ੂਗਰ ਦੀ ਬਿਮਾਰੀ ਦੂਰ ਹੋ ਜਾਂਦੀ ਹੈ ।
• ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਲਚਕੀਲੀ ਹੋ ਜਾਂਦੀ ਹੈ ।
• ਇਸ ਨਾਲ ਲਹੂ ਦਾ ਦੌਰਾ ਠੀਕ ਤੇ ਵੱਧ ਜਾਂਦਾ ਹੈ ।
• ਸ਼ਲਭ ਆਸਣ ਕਰਨ ਨਾਲ ਧਰਨ ਆਪਣੀ ਜਗ੍ਹਾ ‘ਤੇ ਰਹਿੰਦਾ ਹੈ ।
• ਪਾਚਨ-ਕਿਰਿਆ ਤੇ ਸਾਰੇ ਦੋਸ਼ ਦੂਰ ਹੋ ਜਾਂਦੇ ਹਨ ।
• ਮਾਨਸਿਕ ਤਣਾਅ ਦੂਰ ਹੁੰਦਾ ਹੈ ਅਤੇ ਯਾਦਦਾਸ਼ਤ ਵੱਧ ਜਾਂਦੀ ਹੈ ।

9, ਅਰਧ-ਮੱਤੀਸਿਏਂਦਰ ਆਸਣ (Ardh Matseyndra Asana) – ਇਸ ਵਿਚ ਬੈਠਣ ਦੀ ਸਥਿਤੀ ਵਿਚ ਧੜ ਨੂੰ ਪਾਸਿਆਂ ਵੱਲ ਧੱਸਿਆ ਜਾਂਦਾ ਹੈ ।

ਵਿਧੀ (Technique) – ਜ਼ਮੀਨ ‘ਤੇ ਬੈਠ ਕੇ ਖੱਬੇ ਪੈਰ ਦੀ ਅੱਡੀ ਨੂੰ ਸੱਜੇ ਪੱਟ ਵੱਲ ਲੈ ਜਾਓ ਜਿਸ ਨਾਲ ਅੱਡੀ ਦਾ ਹਿੱਸਾ ਗੁਦਾ ਦੇ ਨਾਲ ਲੱਗ ਜਾਏ । ਸੱਜੇ ਪੈਰ ਨੂੰ ਜ਼ਮੀਨ ਤੇ ਖੱਬੇ ਪੈਰ ਨੂੰ ਗੋਡੇ ਦੇ ਨੇੜੇ ਰੱਖੋ । ਫਿਰ ਖੱਬੀ ਬਾਂਹ ਛਾਤੀ ਨੇੜੇ ਲੈ ਜਾਓ, ਸੱਜੇ ਪੈਰ ਦੇ ਗੋਡੇ ਹੇਠਾਂ ਆਪਣੇ ਪੱਟ ਤੇ ਰੱਖੋ । ਪਿੱਛੇ ਨੂੰ ਸੱਜੇ ਹੱਥ ਨੂੰ ਕਮਰ ਨਾਲ ਲਪੇਟਦੇ ਹੋਏ ਧੁਨੀ ਨੂੰ ਛੂਹਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰੋ । ਇਸ ਮਗਰੋਂ ਪੈਰ ਬਦਲ ਕੇ ਸਾਰੀ ਕਿਰਿਆ ਦੁਹਰਾਓ ॥

ਲਾਭ (Advantages)-

• ਇਹ ਆਸਣ ਕਰਨ ਨਾਲ ਸਰੀਰ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਲਚਕੀਲੀਆਂ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਜੋੜਾਂ ਵਿਚ ਲਚਕ ਆ ਜਾਂਦੀ ਹੈ | ਸਰੀਰ ਵਿਚ ਤਾਕਤ ਵੱਧ ਜਾਂਦੀ ਹੈ ।
• ਇਹ ਸਾਹ ਰੋਗ ਅਤੇ ਸ਼ੂਗਰ ਦੀ ਬਿਮਾਰੀ ਠੀਕ ਕਰਦਾ ਹੈ ਅਤੇ ਹਰਨੀਆਂ ਦਾ ਰੋਗ ਵੀ ਠੀਕ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਪੇਸ਼ਾਬ, ਜਿਗਰ ਆਦਿ ਦੇ ਰੋਗ ਠੀਕ ਹੋ ਜਾਂਦੇ ਹਨ ।
• ਇਹ ਆਸਣ ਕਰਨ ਨਾਲ ਮੋਟਾਪਾ ਘੱਟ ਜਾਂਦਾ ਹੈ ।
• ਇਹ ਆਸਣ ਛੋਟੀਆਂ ਅਤੇ ਵੱਡੀਆਂ ਆਂਦਰਾਂ ਦੇ ਰੋਗਾਂ ਤੋਂ ਬਚਾਅ ਲਈ ਬੜਾ ਲਾਭਦਾਇਕ ਹੁੰਦਾ ਹੈ ।

10. ਮਯੂਰ ਆਸਣ (Mayur Asana) – ਇਸ ਵਿਚ ਸਰੀਰ ਨੂੰ ਖਤਿਜ ਰੂਪ ਵਿਚ ਕੂਹਣੀਆਂ ਤੇ ਸੰਤੁਲਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਹਥੇਲੀਆਂ ਧਰਤੀ ‘ਤੇ ਟਿਕੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ।

ਵਿਧੀ (Technique) – ਮਯੂਰ ਆਸਣ ਕਰਨ ਲਈ ਪੇਟ ਦੇ ਭਾਰ ਲੇਟ ਕੇ ਦੋਵੇਂ ਪੈਰ ਇਕੱਠੇ ਕਰੋ ਅਤੇ ਦੋਵੇਂ ਕੂਹਣੀਆਂ ਧੁਨੀ ਦੇ ਹੇਠਾਂ ਰੱਖੋ !ਇਸ ਤਰ੍ਹਾਂ ਕਰਨ ਨਾਲ ਸਰੀਰ ਦਾ ਸਾਰਾ ਭਾਰ ਕੂਹਣੀਆਂ ‘ਤੇ ਪਾਉਂਦੇ ਹੋਏ ਪੈਰ ਅਤੇ ਗੋਡੇ ਜ਼ਮੀਨ ਤੋਂ ਉੱਪਰ ਚੁੱਕੋ ।

Mayur Asana ਵਿਧੀ (Technique) – ਪਦਮ ਆਸਣ ਲਗਾ ਕੇ ਸਿਰ ਨੂੰ ਇੰਨਾ ਪਿੱਛੇ ਲੈ ਜਾਓ ਜਿਸ ਨਾਲ ਸਿਰ ਦਾ ਅਗਲਾ ਭਾਗ ਜ਼ਮੀਨ ‘ਤੇ ਲੱਗ ਜਾਵੇ ਅਤੇ ਪਿੱਠ ਦੇ ਭਾਗ ਨੂੰ ਜ਼ਮੀਨ ਤੋਂ ਉੱਪਰ ਚੱਕੋ ! ਦੋਹਾਂ ਹੱਥਾਂ ਨਾਲ ਪੈਰਾਂ ਦੇ ਦੋਵੇਂ ਅੰਗਠੇ ਫੜੋ ।

ਲਾਭ (Advantages)-

• ਇਹ ਆਸਣ ਚਿਹਰੇ ਅਤੇ ਚਮੜੀ ਨੂੰ ਚਮਕਦਾਰ ਬਣਾਉਂਦਾ ਹੈ । ਇਸ ਨਾਲ ਚਮੜੀ ਦੇ ਰੋਗ ਦੂਰ ਹੋ ਜਾਂਦੇ ਹਨ ।
• ਇਹ ਆਸਣ ਟਾਂਸਿਲ, ਸ਼ੂਗਰ, ਗੋਡੇ ਅਤੇ ਕਮਰ ਦਰਦ ਲਈ ਲਾਭਦਾਇਕ ਹੈ । ਇਸ ਨਾਲ ਸਾਫ਼ ਲਹੁ ਬਣਦਾ ਹੈ ਅਤੇ ਦੌਰਾ ਕਰਦਾ ਹੈ ।
• ਇਸ ਆਸਣ ਨਾਲ ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਵਿਚ ਲਚਕ ਵੱਧਦੀ ਹੈ । ਕਬਜ਼ ਦੂਰ ਹੁੰਦੀ ਹੈ । ਭੁੱਖ ਲੱਗਣ ਲੱਗਦੀ ਹੈ । ਗੈਸ ਦੂਰ ਕਰਕੇ ਭੋਜਨ ਪਚਨ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ ।
• ਇਹ ਆਸਣ ਫੇਫੜਿਆਂ ਲਈ ਵੀ ਲਾਹੇਵੰਦ ਹੈ । ਸਾਹ ਨਾਲ ਸੰਬੰਧ ਰੱਖਣ ਵਾਲੀਆਂ | ਬਿਮਾਰੀਆਂ ਜਿਵੇਂ ਖਾਂਸੀ, ਦਮਾ, ਸਾਹ-ਨਲੀ ਦੀ ਬਿਮਾਰੀ ਆਦਿ ਤੋਂ ਛੁਟਕਾਰਾ ਮਿਲ ਜਾਂਦਾ ਹੈ । ਅੱਖਾਂ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਵੀ ਦੂਰ ਹੁੰਦੀਆਂ ਹਨ ।
• ਇਸ ਆਸਣ ਨਾਲ ਲੱਤਾਂ ਅਤੇ ਬਾਹਵਾਂ ਮਜ਼ਬੂਤ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਮਾਨਸਿਕ ਕਮਜ਼ੋਰੀ ਦੂਰ ਹੁੰਦੀ ਹੈ ।

11. ਵਜਰ ਆਸਣ (Vajur Asana)-
ਸਥਿਤੀ ਪੈਰਾਂ ਨੂੰ ਪਿੱਛੇ ਵਲ ਕਰ ਕੇ ਬੈਠਣਾ ਅਤੇ ਹੱਥਾਂ ਨੂੰ ਗੋਡਿਆਂ ‘ਤੇ ਰੱਖਣਾ ਇਸ ਆਸਣ ਦੀ ਸਥਿਤੀ ਹੈ ।

ਵਿਧੀ (Technique)-

• ਗੋਡੇ ਉਲਟੇ ਕਰ ਕੇ ਪੈਰ ਪਿੱਛੇ ਨੂੰ ਕਰਕੇ ਪੈਰਾਂ ਦੀਆਂ ਤਲੀਆਂ ਦੇ ਭਾਰ ਬੈਠ ਜਾਓ !
• ਹੋਨਾਂ ਪੈਰਾਂ ਦੇ ਅੰਗੂਠੇ ਇਕ-ਦੂਜੇ ਵਲ ਹੋਣ ।
• ਦੋਵੇਂ ਗੋਡੇ ਮਿਲੇ ਹੋਣ ਤੇ ਕਮਰ ਤੇ ਪਿੱਠ ਇਕ-ਦਮ ਸਿੱਧੀਆਂ ਹੋਣ ।
• ਦੋਵੇਂ ਹੱਥ ਦੱਬ ਕੇ ਗੋਡਿਆਂ ਕੋਲ ਰੱਖੋ ।
• ਸਾਹ ਦੀ ਗਤੀ ਲੰਮੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।
• ਇਹ ਆਸਣ ਹਰ ਰੋਜ਼ 3 ਮਿੰਟ ਤੋਂ ਲੈ ਕੇ 20 ਮਿੰਟ ਤਕ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।

ਲਾਭ (Advantages) –

• ਸਰੀਰ ਵਿਚ ਚੁਸਤੀ ਆਉਂਦੀ ਹੈ ।
• ਸਰੀਰ ਦਾ ਮੋਟਾਪਨ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਸਰੀਰ ਤੰਦਰੁਸਤ ਰਹਿੰਦਾ ਹੈ ।
• ਮਾਸ-ਪੇਸ਼ੀਆਂ ਮਜ਼ਬੂਤ ਹੁੰਦੀਆਂ ਹਨ ।
• ਇਸ ਨਾਲ ਸੁਪਨਦੋਸ਼ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਪੈਰਾਂ ਦਾ ਦਰਦ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਮਾਨਸਿਕ ਤੌਰ ‘ਤੇ ਸ਼ਾਂਤੀ ਮਿਲਦੀ ਹੈ।
• ਇਨਸਾਨ ਬੇ-ਫ਼ਿਕਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਇਸ ਦੇ ਰਾਹੀਂ ਸ਼ੂਗਰ ਦਾ ਰੋਗ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਪਾਚਨ ਸ਼ਕਤੀ ਠੀਕ ਰਹਿੰਦੀ ਹੈ ।

12. ਸ਼ੀਰਸ਼ ਆਸਣ (Searesh Asana) – ਸਥਿਤੀ-ਸਿਰ ਹੇਠਾਂ ਅਤੇ ਪੈਰ ਉੱਪਰ ਵੱਲ ਕਰਨਾ ।

ਵਿਧੀ (Technique) –

• ਕੰਬਲ ਜਾਂ ਦਰੀ ਵਿਛਾ ਕੇ ਗੋਡਿਆਂ ਦੇ ਭਾਰ ਬੈਠ ਜਾਉ ।
• ਦੋਵੇਂ ਹੱਥਾਂ ਦੀਆਂ ਉਂਗਲੀਆਂ ਕੱਸ ਕੇ ਬੰਨ੍ਹ ਦਿਉ ਅਤੇ ਦੋਵੇਂ ਹੱਥਾਂ ਨੂੰ ਕੋਣਾਕਾਰ ਬਣਾ ਕੇ ਕੰਬਲ ਜਾਂ ਦਰੀ ਉੱਤੇ ਰੱਖੋ ।
• ਸਿਰ ਦੇ ਉੱਪਰ ਵਾਲਾ ਹਿੱਸਾ ਹੱਥ ਦੇ ਵਿਚ ਇਸ ਤਰ੍ਹਾਂ ਜ਼ਮੀਨ ਉੱਪਰ ਰੱਖੋ ਕਿ ਦੋਵੇਂ ਅੰਗੂਠੇ ਸਿਰ ਦੇ ਪਿਛਲੇ ਹਿੱਸੇ ਨੂੰ ਦਬਾਉਣ ।
• ਲੱਤਾਂ ਨੂੰ ਹੌਲੀ-ਹੌਲੀ ਅੰਦਰ ਵਲ ਮੋੜਦੇ ਹੋਏ ਸਿਰ ਅਤੇ ਦੋਵੇਂ ਹੱਥਾਂ ਦੇ ਸਹਾਰੇ ਧੜ ਅਸਮਾਨ ਵਲ ਸਿੱਧਾ ਚੱਕੋ ।
• ਪੈਰਾਂ ਨੂੰ ਹੌਲੀ-ਹੌਲੀ ਉੱਪਰ ਚੁੱਕੋ । ਪਹਿਲਾਂ ਇਕ ਲੱਤ ਸਿੱਧੀ ਕਰੋ, ਫਿਰ ਦੂਜੀ ।
• ਸਰੀਰ ਨੂੰ ਬਿਲਕੁਲ ਸਿੱਧਾ ਰੱਖੋ ।
• ਸਰੀਰ ਦਾ ਭਾਰ ਬਾਹਵਾਂ ਤੇ ਸਿਰ ਉੱਪਰ ਬਰਾਬਰ ਰੱਖੋ ।
• ਦੀਵਾਰ ਜਾਂ ਸਾਥੀ ਦਾ ਸਹਾਰਾ ਲਵੋ ।

ਲਾਭ (Advantages) –

• ਭੁੱਖ ਬਹੁਤ ਹੀ ਜ਼ਿਆਦਾ ਲੱਗਦੀ ਹੈ ।
• ਯਾਦ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਵੱਧ ਜਾਂਦੀ ਹੈ ।
• ਮੋਟਾਪਾ ਦੂਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਜਿਗਰ ਅਤੇ ਤਿੱਲੀ ਠੀਕ ਪ੍ਰਕਾਰ ਨਾਲ ਕੰਮ ਕਰਦੀ ਹੈ ।
• ਪਿਸ਼ਾਬ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਦੂਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਬਵਾਸੀਰ ਦੀ ਬਿਮਾਰੀ ਦੂਰ ਹੋ ਜਾਂਦੀ ਹੈ ।
• ਇਸ ਆਸਣ ਨੂੰ ਹਰ ਰੋਜ਼ ਕਰਨ ਦੇ ਨਾਲ ਕਈ ਪ੍ਰਕਾਰ ਦੀਆਂ ਮਾਨਸਿਕ ਬਿਮਾਰੀਆਂ ਦੂਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ । | ਸਾਵਧਾਨੀਆਂ (Precautions)-ਇਹ ਆਸਣ ਉੱਚ ਰਕਤ-ਚਾਪ ਵਾਲੇ ਨੂੰ ਨਹੀਂ ਕਰਨਾ ਚਾਹੀਦਾ ।

13. ਚੱਕਰ ਆਸਣ (Chakar Asana)-
ਸਥਿਤੀ – ਗੋਲ ਚੱਕਰ ਵਾਂਗ ਸਰੀਰ ਕਰਨਾ ।

ਵਿਧੀ (Technique)-

• ਪਿੱਠ ਦੇ ਭਾਰ ਸਿੱਧੇ ਲੇਟ ਕੇ ਗੋਡਿਆਂ ਨੂੰ ਮੋੜ ਕੇ, ਪੈਰਾਂ ਤੇ ਤਲੀਆਂ ਨੂੰ ਜ਼ਮੀਨ ਨਾਲ ਜਮਾ ਲਵੋ ਅਤੇ ਪੈਰਾਂ ਵਿਚ ਇਕ ਤੋਂ ਡੇਢ ਫੁੱਟ ਦਾ ਫ਼ਾਸਲਾ ਰੱਖੋ ।
• ਹੱਥਾਂ ਨੂੰ ਪਿੱਛੇ ਵੱਲ ਜ਼ਮੀਨ ‘ਤੇ ਰੱਖੋ । ਹਥੇਲੀਆਂ ਅਤੇ ਉਂਗਲੀਆਂ ਨੂੰ ਪੱਕੀ ਤਰ੍ਹਾਂ ਜ਼ਮੀਨ ਨਾਲ ਜਮਾ ਕੇ ਰੱਖੋ ।
• ਹੁਣ ਹੱਥਾਂ ਅਤੇ ਪੈਰਾਂ ਦਾ ਸਹਾਰਾ ਲੈ ਕੇ ਪੂਰੇ ਸਰੀਰ ਨੂੰ ਕਮਾਨੀ ਜਾਂ ਚੱਕਰ ਵਾਂਗ ਬਣਾਓ ॥
• ਸਾਰੇ ਸਰੀਰ ਦੀ ਸ਼ਕਲ ਗੋਲਦਾਰ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।
• ਅੱਖਾਂ ਬੰਦ ਰੱਖਣੀਆਂ ਚਾਹੀਦੀਆਂ ਹਨ ਤਾਂ ਜੋ ਸਾਹ ਦੀ ਗਤੀ ਤੇਜ਼ ਹੋ ਸਕੇ ।

ਲਾਭ (Advantages) –

• ਸਰੀਰ ਦੀਆਂ ਸਾਰੀਆਂ ਕਮਜ਼ੋਰੀਆਂ ਦੂਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਸਰੀਰ ਦੇ ਸਾਰੇ ਅੰਗਾਂ ਨੂੰ ਲਚਕੀਲਾ ਬਣਾ ਦਿੰਦਾ ਹੈ ।
• ਹਰਨੀਆਂ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਦੂਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਪਾਚਨ ਸ਼ਕਤੀ ਵਧਾਉਂਦਾ ਹੈ ।
• ਪੇਟ ਦੀ ਗੈਸ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਦੂਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਰੀੜ ਦੀ ਹੱਡੀ ਮਜ਼ਬੂਤ ਹੋ ਜਾਂਦੀ ਹੈ ।
• ਲੱਤਾਂ ਤੇ ਬਾਂਹਾਂ ਵਿਚ ਤਾਕਤ ਆਉਂਦੀ ਹੈ ।
• ਗੁਰਦੇ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਦੂਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਕਮਰ ਦਰਦ ਦੂਰ ਹੋ ਜਾਂਦੀ ਹੈ ।
• ਸਰੀਰ ਹਲਕਾਪਣ ਮਹਿਸੂਸ ਕਰਦਾ ਹੈ ।

14. ਗਰੁੜ ਆਸਣ (Garur Asana)-
ਸਥਿਤੀ – ਗਰੁੜ ਆਸਣ (Garur Asana) ਵਿਚ ਸਰੀਰ ਦੀ ਸਥਿਤੀ ਗਰੁੜ ਪੰਛੀ ਵਾਂਗ ਹੁੰਦੀ ਹੈ ।

ਵਿਧੀ (Technique)-

• ਸਿੱਧੇ ਖੜੇ ਹੋ ਕੇ ਖੱਬੇ ਪੈਰ ਨੂੰ ਚੁੱਕ ਕੇ ਸੱਜੀ ਲੱਤ ਦੁਆਲੇ ਵੇਲ ਵਾਂਗ ਲਪੇਟ ਦਿਓ ।
• ਖੱਬਾ ਪੱਟ ਸੱਜੇ ਪੱਟ ਦੇ ਉੱਪਰ ਆ ਜਾਵੇਗਾ ਅਤੇ ਖੱਬੀ ਪਿੰਡਲੀ ਸੱਜੀ ਪਿੰਡਲੀ ਨੂੰ ਢੱਕ ਲਵੇਗੀ ।
• ਸਰੀਰ ਦਾ ਪੂਰਾ ਭਾਰ ਇਕ ਪੈਰ ‘ਤੇ ਕਰ ਦਿਓ ।
• ਖੱਬੀ ਬਾਂਹ ਨੂੰ ਸੱਜੀ ਬਾਂਹ ਦੇ ਉੱਤੇ ਲਪੇਟ ਕੇ ਉੱਪਰ ਚੁੱਕ ਕੇ ਦੋਹਾਂ ਹਥੇਲੀਆਂ ਨਾਲ ਨਮਸਕਾਰ ਵਾਂਗ ਹੱਥ ਜੋੜ ਦਿਓ ।
• ਫਿਰ ਸੱਜੀ ਲੱਤ ਨੂੰ ਥੋੜਾ ਝੁਕਾ ਕੇ ਸਰੀਰ ਨੂੰ ਬੈਠਣ ਦੀ ਸਥਿਤੀ ਵਿਚ ਲਿਆਉ । ਇਸ ਨਾਲ ਸਰੀਰ ਦੀਆਂ ਨਾੜੀਆਂ ਖਿੱਚੀਆਂ ਜਾਣਗੀਆਂ । ਉਸ ਤੋਂ ਬਾਅਦ ਸਰੀਰ ਫਿਰ ਸਿੱਧਾ ਕਰ ਲਉ ॥ ਸਾਵਧਾਨ ਦੀ ਸਥਿਤੀ ਵਿਚ ਆ ਜਾਉ ।
• ਹੁਣ ਹੱਥ-ਪੈਰਾਂ ਨੂੰ ਬਦਲ ਕੇ ਆਸਣ ਦੀ ਸਥਿਤੀ ਦੁਹਰਾਉ । ਨੋਟ-ਇਹ ਆਸਣ ਹਰ ਇਕ ਲੱਤ ਉੱਤੇ ਇਕ ਤੋਂ ਪੰਜ ਮਿੰਟ ਤੱਕ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।

ਲਾਭ (Advantages)-

• ਸਰੀਰ ਦੇ ਸਾਰੇ ਅੰਗਾਂ ਵਿਚ ਤਾਕਤ ਆਉਂਦੀ ਹੈ ।
• ਸਰੀਰ ਤੰਦਰੁਸਤ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਬਾਂਹਾਂ ਸ਼ਕਤੀਸ਼ਾਲੀ ਬਣ ਜਾਂਦੀਆਂ ਹਨ ।
• ਹਰਨੀਆਂ ਦੇ ਰੋਗ ਤੋਂ ਮਨੁੱਖ ਬਚ ਸਕਦਾ ਹੈ ।
• ਲੱਤਾਂ ਵਿਚ ਸ਼ਕਤੀ ਆਉਂਦੀ ਹੈ ।
• ਸਰੀਰ ਹਲਕਾ| ਪਣ ਮਹਿਸੂਸ ਕਰਦਾ ਹੈ ।
• ਖੂਨ ਦੀ ਰਫ਼ਤਾਰ ਤੇਜ਼ ਹੋ ਜਾਂਦੀ ਹੈ ।
• ਗਰੁੜ ਆਸਣ ਰਾਹੀਂ ਮਨੁੱਖ ਬਹੁਤ ਸਾਰੀਆਂ ਬਿਮਾਰੀਆਂ ਤੋਂ ਬਚ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਪਾਤੰਜਲੀ ਰਿਸ਼ੀ ਦੇ ਅਸ਼ਟਾਂਗ ਯੋਗ ਅਨੁਸਾਰ ਕਿਹੜੇ-ਕਿਹੜੇ ਅੱਠ ਅੰਗ ਹਨ ? ਉਨ੍ਹਾਂ ਬਾਰੇ ਲਿਖੋ ।
(What are the Eight components of Ashtang Yoga according to Patanjali Rishi. Write about them.)
ਉੱਤਰ-
ਅਸ਼ਟਾਂਗ ਯੋਗ (Ashtang Yoga) – ਅਸ਼ਟਾਂਗ ਯੋਗ ਦੇ ਅੱਠ ਅੰਗ ਹਨ, ਇਸੇ ਕਰਕੇ ਇਸ ਦਾ ਨਾਂ ਅਸ਼ਟਾਂਗ ਯੋਗ ਹੈ ।
ਯੋਗ ਅਭਿਆਸ ਦੀਆਂ ਪਾਤੰਜਲੀ ਰਿਸ਼ੀ ਅਨੁਸਾਰ ਹੇਠ ਲਿਖੀਆਂ ਅੱਠ ਅਵਸਥਾਵਾਂ ਮੰਨੀਆਂ ਗਈਆਂ ਹਨ-

1. ਯਮ (Yama, Forbearance)
2. ਨਿਯਮ (Niyama, Observance)
3. ਆਸਣ (Asana, Posture)
4. ਪ੍ਰਾਣਾਯਾਮ (Pranayama, Regulation of breathing)
5. ਪ੍ਰਤਿਆਹਾਰ (Pratyahara, Abstraction)
6. ਧਾਰਨਾ (Dharana, Concentration)
7. ਬਿਆਨ (Dhyana, Meditation)
8. ਸਮਾਧੀ (Samadhi, Trance)

ਯੋਗ ਦੀਆਂ ਇਨ੍ਹਾਂ ਉੱਪਰ ਵਰਣਿਤ ਅੱਠ ਅਵਸਥਾਵਾਂ ਵਿਚੋਂ ਪਹਿਲੀਆਂ ਪੰਜ ਅਵਸਥਾਵਾਂ ਦਾ ਸੰਬੰਧ ਬਾਹਰਲੀਆਂ ਯੋਗਿਕ ਕਿਰਿਆਵਾਂ ਨਾਲ ਹੈ । ਬਾਕੀ ਦੀਆਂ ਤਿੰਨ ਅਵਸਥਾਵਾਂ ਦਾ ਸੰਬੰਧ ਅੰਦਰੁਨੀ ਯੋਗਿਕ ਕਿਰਿਆਵਾਂ ਨਾਲ ਹੈ । ਇਹ ਸਾਰੀਆਂ ਅਵਸਥਾਵਾਂ ਹੇਠ ਵੰਡੀਆਂ ਹੋਈਆਂ ਹਨ, ਜਿਵੇਂ-
1. ਯਮ (Yama, Forbearance) – ਯਮ ਦੇ ਹੇਠ ਦਿੱਤੇ ਪੰਜ ਅੰਗ ਹਨ-

• ਅਹਿੰਸਾ (Ahimsa, Non-Violence)
• ਸਤਿਅ (Satya, Truth)
• ਅਸਤੇਯ (Asteya, Conquest of the senses of mind)
• ਅਪਰੀਗ੍ਰਹਿ (Aprigrahha, Non-receiving)
• ਬ੍ਰਹਮਚਰੀਆ (Brahamcharaya, Celibacy)

2. ਨਿਮਯ (Niyama, Observance) – ਇਸ ਦੇ ਪੰਜ ਅੰਗ ਹਨ-

• ਤਪ (Tapa, Penance)
• ਸਵਧਿਆਏ (Swadhyay, Self-study)
• ਈਸ਼ਵਰ ਪਧਾਨ (Iswar Pridhan, God Consciousness)

3. ਆਸਣ (Asiana, Posture) – ਆਸਣਾਂ ਦੀ ਸੰਖਿਆ ਜਿੰਨੇ ਪਸ਼ੂ-ਪੰਛੀ ਹਨ, ਉੱਨੀ ਹੈ | ਆਸਣ ਸਰੀਰਕ ਸਮਰੱਥਾ, ਸ਼ਕਤੀ ਦੇ ਅਨੁਸਾਰ, ਨਿੱਤ-ਪ੍ਰਤੀ ਹਵਾ ਦੇ ਬਾਹਰ ਕੱਢਣ, ਸਾਹ ਰੋਕਣ ਅਤੇ ਫਿਰ ਸਾਹ ਲੈਣ ਦੇ ਨਾਲ ਕਰਨੇ ਚਾਹੀਦੇ ਹਨ ।

4. ਪ੍ਰਾਣਾਯਾਮ (Pranayama, Regulation of breathing) – ਪ੍ਰਾਣਾਯਾਮ ਉਪਾਸ਼ਨਾ ਦਾ ਭਾਗ ਹੈ । ਇਸ ਦੇ ਤਿੰਨ ਹਿੱਸੇ ਹਨ-\

• ਪੂਰਕ  (Purak, Inhalation)
• ਰੋਚਕ (Rechak, Exhalation)
• ਕੁੰਭਕ (Kunabhak, Holding of Breath) – ਕਈ ਆਸਣ ਲਗਾ ਕੇ ਸਾਹ ਲੈ ਕੇ ਫਿਰ ਰੋਕ ਕੇ ਬਾਹਰ ਕੱਢਣ ਨੂੰ ਪ੍ਰਾਣਾਯਾਮ ਕਹਿੰਦੇ ਹਨ ।
• ਪ੍ਰਤਿਆਹਾਰ (Pratyahara, Abstraction) – ਪ੍ਰਤਿਆਹਾਰ ਤੋਂ ਭਾਵ ਵਾਪਸ ਲਿਆਉਣਾ ਅਤੇ ਦੁਨਿਆਵੀ ਖ਼ੁਸ਼ੀਆਂ ਤੋਂ ਆਪਣੇ ਮਨ ਨੂੰ ਮੋੜਨਾ ਹੈ ।
• ਧਾਰਨਾ (Dharna, Concentration) – ਆਪਣੀਆਂ ਇੰਦਰੀਆਂ ਨੂੰ ਕਾਬੂ ਵਿਚ ਰੱਖਣ ਨੂੰ ਧਾਰਨਾ ਆਖਦੇ ਹਨ ਜੋ ਕਿ ਬਹੁਤ ਹੀ ਮੁਸ਼ਕਿਲ ਹੈ ।
• ਧਿਆਨ (Dhyana, Meditation) – ਜਦੋਂ ਮਨ ਕਾਬੂ ਹੋ ਜਾਂਦਾ ਹੈ ਤਾਂ ਧਿਆਨ ਲੱਗਣਾ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਅਵਸਥਾ ਵਿਚ ਮਨ ਅਤੇ ਸਰੀਰ ਵਗਦੀ ਨਦੀ ਵਾਂਗ ਹੋ ਜਾਂਦੇ ਹਨ ਜਿਸ ਵਿਚ ਪਾਣੀ ਦੀ ਲਹਿਰ ਦਾ ਕੋਈ ਅਸਰ ਨਹੀਂ ਹੁੰਦਾ ।
• ਸਮਾਧੀ (Smadhi, Trance) – ਜਿਹੜੇ ਚਿੱਤ ਦੀ ਅਵਸਥਾ ਧਾਰਨਾ ਤੋਂ ਸ਼ੁਰੂ ਹੁੰਦੀ ਹੈ, ਉਹ ਸਮਾਧੀ ਵਿਚ ਖ਼ਤਮ ਹੋ ਜਾਂਦੀ ਹੈ । ਇਨ੍ਹਾਂ ਸਾਰੀਆਂ ਅਵਸਥਾਵਾਂ ਦਾ ਡੂੰਘਾ ਸੰਬੰਧ ਹੈ ।

ਯੋਗ ਵਿਗਿਆਨ ਦੁਨੀਆਂ ਨੂੰ ਭਾਰਤ ਦੀ ਇਕ ਵੱਡੀ ਦੇਣ ਹੈ | ਅੱਜ-ਕਲ੍ਹ ਇਹ ਦੇਸ਼ ਵਿਦੇਸ਼ ਵਿਚ ਹਰਮਨ ਪਿਆਰਾ ਹੋਇਆ ਹੈ । ਇਸ ਦੀ ਉਪਯੋਗਤਾ ਦਾ ਸਿੱਕਾ ਸਾਰੇ ਡਾਕਟਰ ਅਤੇ ਸਰੀਰਕ ਅਧਿਆਪਕ ਮੰਨਦੇ ਹਨ | ਯੋਗ-ਆਸਣ ਕਸਰਤ ਵਿਧੀ ਰੂਪ ਨਾਲ ਵਿਗਿਆਨਿਕ ਅਤੇ ਸਰੀਰਕ ਬਣਤਰ ਦੇ ਅਨਕਲ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਯੋਗ ਦੇ ਮੁੱਖ ਸਿਧਾਂਤ ਕਿਹੜੇ-ਕਿਹੜੇ ਹਨ ? [ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ-3] (Write the main Principles of Yoga.)
ਉੱਤਰ-
ਯੋਗ ਦੇ ਮੁੱਖ ਸਿਧਾਂਤ (Main Principles of Yoga) – ਯੋਗ ਕਰਦੇ ਸਮੇਂ ਕੁੱਝ ਸਿਧਾਂਤਾਂ ਦੀ ਪਾਲਣਾ ਜ਼ਰੂਰੀ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ । ਇਨ੍ਹਾਂ ਸਿਧਾਂਤਾਂ ਦਾ ਵਰਣਨ ਇਸ ਤਰ੍ਹਾਂ ਹੈ-

• ਯੋਗ ਆਸਣਾਂ ਦਾ ਅਭਿਆਸ ਸਵੇਰ ਵੇਲੇ ਸ਼ੌਚ ਆਦਿ ਤੋਂ ਫਾਰਗ ਹੋ ਕੇ ਕਰੋ । ਇਸ਼ਨਾਨ ਕਰਕੇ ਯੋਗ ਆਸਣ ਕੀਤੇ ਜਾਣ ਤਾਂ ਹੋਰ ਵੀ ਚੰਗਾ ਹੋਵੇਗਾ । ਇਸ਼ਨਾਨ ਕਰਨ ਨਾਲ ਸਰੀਰ ਹਲਕਾ ਹੁੰਦਾ ਹੈ, ਲਚਕ ਆਉਂਦੀ ਹੈ ਅਤੇ ਆਸਣ ਚੰਗੇ ਢੰਗ ਨਾਲ ਹੁੰਦੇ ਹਨ । ਉਂਝ ਸ਼ਾਮ ਨੂੰ ਵੀ ਜਦੋਂ ਪੇਟ ਖ਼ਾਲੀ ਹੋਵੇ ਤਾਂ ਆਸਣ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ ।
• ਆਸਣ ਕਰਨ ਦੀ ਥਾਂ ਸ਼ਾਂਤ ਅਤੇ ਸਾਫ਼-ਸੁਥਰੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਕਿਸੇ ਬਗੀਚੀ ਵਿਚ ਆਸਣ ਕੀਤੇ ਜਾਣ ਤਾਂ ਬਹੁਤ ਚੰਗਾ ਹੈ ।
• ਜਿਸ ਥਾਂ ‘ਤੇ ਆਸਣ ਕਰੋ, ਉਹ ਸਮਤਲ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਦਰੀ ਜਾਂ ਕੰਬਲ ਵਿਛਾ ਕੇ ਆਸਣ ਕਰਨੇ ਚਾਹੀਦੇ ਹਨ ਤਾਂ ਕਿ ਜ਼ਮੀਨ ਦੀ ਚੁੰਬਕੀ ਸ਼ਕਤੀ ਤੁਹਾਡੇ ਧਿਆਨ ਨੂੰ ਨਾ ਤੋੜੇ ਅਤੇ ਹੇਠੋਂ ਕੋਈ ਚੀਜ਼ ਨਾ ਚੁੱਭੇ ।
• ਯੋਗ ਆਸਣ ਕਰਦੇ ਹੋਏ ਗੱਲਬਾਤ ਬਿਲਕੁਲ ਨਾ ਕਰੋ, ਆਪਣੇ ਧਿਆਨ ਨੂੰ ਸਾਹ ਅਤੇ ਜਿਸ ਅੰਗ ‘ਤੇ ਜ਼ੋਰ ਪੈ ਰਿਹਾ ਹੈ, ਉਸ ‘ਤੇ ਲਾਓ ! ਜਿੰਨਾ ਤੁਸੀਂ ਇਕ-ਸੁਰ ਹੋ ਕੇ ਆਸਣ ਕਰੋਗੇ, ਉੱਨਾ ਹੀ ਵੱਧ ਸਰੀਰਕ ਲਾਭ ਮਿਲੇਗਾ | ਆਸਣ ਸ਼ੁਰੂ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਸ਼ਵਆਸਣ ਕਰਕੇ ਸਾਹ, ਸਰੀਰ ਅਤੇ ਮਨ ਨੂੰ ਸ਼ਾਂਤ ਕਰ ਦਿਓ ।
• ਯੋਗ ਆਸਣ ਅਹਿੰਸਕ ਕਿਰਿਆ ਹੈ । ਇਸ ਨੂੰ ਕਰਦੇ ਹੋਏ ਝਟਕੇ ਨਹੀਂ ਲੱਗਣੇ ਚਾਹੀਦੈ । ਹਰ ਆਸਣ ਨੂੰ ਸਰੀਰ ਤਾਣ ਕੇ ਅਤੇ ਖਿੱਚ ਕੇ ਹੌਲੀ-ਹੌਲੀ ਕਰੋ । ਉਸ ਦੇ ਬਾਅਦ ਕੁੱਝ ਪਲ ਆਪਣੇ ਸਰੀਰ ਨੂੰ ਨਿਢਾਲ ਕਰੋ । ਜਦੋਂ ਤੁਹਾਡਾ ਸਾਹ ਸੁਭਾਵਿਕ ਸਥਿਤੀ ਵਿਚ ਆ ਜਾਵੇ, ਉਦੋਂ ਦੂਸਰਾ ਆਸਣ ਕਰੋ ।
• ਯੋਗ ਆਸਣਾਂ ਦਾ ਅਭਿਆਸ ਹੌਲੀ-ਹੌਲੀ ਵਧਾਓ । ਆਸਣ ਦੀ ਪੂਰਨ ਸਥਿਤੀ ਤਕ ਜਾਣ ਦਾ ਹਰ ਰੋਜ਼ ਅਭਿਆਸ ਕਰੋ | ਹੌਲੀ-ਹੌਲੀ ਤੁਹਾਡੇ ਬੰਦ ਖੁੱਲ੍ਹਣਗੇ ਅਤੇ ਸਰੀਰ ਵਿਚ ਲਚਕ ਪੈਦਾ ਹੋਵੇਗੀ ।
• ਰੁੱਤ ਦੇ ਅਨੁਸਾਰ ਆਸਣਾਂ ਦਾ ਘੱਟ ਤੋਂ ਘੱਟ ਕੱਪੜੇ ਪਹਿਨ ਕੇ ਅਭਿਆਸ ਕਰੋ ।
• ਯੋਗ ਆਸਣਾਂ ਦਾ ਅਭਿਆਸ ਸਭ ਵਰਗਾਂ ਦੇ ਬੱਚੇ, ਬੁੱਢੇ, ਮਰਦ-ਔਰਤ ਕਰ ਸਕਦੇ ਹਨ | ਦਸ ਸਾਲ ਤੋਂ ਲੈ ਕੇ 80-85 ਸਾਲ ਤਕ ਦੇ ਵਿਅਕਤੀ ਯੋਗ ਅਭਿਆਸ ਕਰ ਸਕਦੇ ਹਨ | ਆਸਣਾਂ ਦਾ ਅਭਿਆਸ ਵਿਧੀ ਪੂਰਵਕ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।
• ਯੋਗ ਆਸਣ ਕਰਨ ਵਾਲੇ ਵਿਅਕਤੀ ਨੂੰ ਆਪਣਾ ਭੋਜਨ ਹਲਕਾ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ । ਭੋਜਨ ਚੰਗਾ ਪਚਣ ਵਾਲਾ, ਸਾਤਵਿਕ ਅਤੇ ਕੁਦਰਤੀ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਜਿੰਨਾ ਹਲਕਾ ਭੋਜਨ ਹੋਵੇਗਾ, ਉੱਨੀ ਉਸਦੀ ਕਾਰਜ-ਸ਼ਕਤੀ ਵੱਧ ਜਾਵੇਗੀ ।
• ਕਠਿਨ ਰੋਗਾਂ ਅਤੇ ਬੁਖ਼ਾਰ ਨਾਲ ਪੀੜਿਤ ਵਿਅਕਤੀ ਨੂੰ ਆਸਣ, ਪ੍ਰਾਣਾਯਾਮ ਦਾ ਅਭਿਆਸ ਨਹੀਂ ਕਰਨਾ ਚਾਹੀਦਾ ।
• ਸ਼ੁਰੂ ਵਿਚ ਇਕ ਹੀ ਦਿਨ ਬਹੁਤ ਸਾਰੇ ਆਸਣ ਨਾ ਕਰੋ | ਹਰੇਕ ਆਸਣ ਨੂੰ ਮਨੋਯੋਗ ਨਾਲ ਅੱਖਾਂ ਬੰਦ ਕਰਕੇ ਹੌਲੀ-ਹੌਲੀ ਕਰੋ । ਸਰਵਾਂਗ ਆਸਣ ਅਤੇ ਸ਼ੀਰਸ਼ ਆਸਣ ਹੌਲੀ-ਹੌਲੀ ਵਧਾ ਕੇ ਦਸ ਮਿੰਟ ਤਕ ਕਰ ਸਕਦੇ ਹੋ | ਆਸਣ ਦੀ ਪਹਿਲੀ ਸਥਿਤੀ ਵਿਚ ਅਤੇ ਆਖ਼ਰੀ ਸਥਿਤੀ ਵਿਚ ਵਾਪਸ ਜਲਦੀ ਨਾ ਆਓ ।
• ਆਸਣਾਂ ਦਾ ਅਭਿਆਸ-ਕ੍ਰਮ ਇਸ ਤਰ੍ਹਾਂ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ਕਿ ਆਸਣ ਦੇ ਬਾਅਦ ਉਸ ਦਾ ਉਪ-ਆਸਣ (ਕਾਉਂਟਰ ਪੋਜ਼) ਕਰ ਸਕੋ । ਜਿਵੇਂ ਪਸ਼ਚਮੋਤਾਨ ਆਸਣ ਅਤੇ ਉਸ ਦਾ ਉਪ-ਆਸਣ, ਕੋਣਾਸਨ, ਸਰਵਾਂਗ ਆਸਣ ਦੇ ਬਾਅਦ ਮਤੱਸਿਆ ਆਸਣ ਆਦਿ ।
• ਯੋਗ ਆਸਣਾਂ ਦੀ ਸਮਾਪਤੀ ਦੇ ਬਾਅਦ ਕੁੱਝ ਸਮੇਂ ਲਈ ਸ਼ਵ-ਆਸਣ ਜ਼ਰੂਰ ਕਰੋ । ਆਸਣਾਂ ਦਾ ਲਾਭ ਤਦ ਹੀ ਮਿਲੇਗਾ ਜਦੋਂ ਤੁਸੀਂ ਸ਼ਵ-ਆਸਣ ਕਰਕੇ ਆਪਣੇ ਸਰੀਰ ਨੂੰ ਥੋੜਾ ਆਰਾਮ ਦਿਓ । ਸ਼ਵ-ਆਸਣ ਆਪਣੇ ਆਪ ਵਿਚ ਪੂਰਨ ਆਸਣ ਹੈ ਅਤੇ ਇਸ ਨਾਲ ਸਰੀਰ ਵਿਚ ਅਨੋਖੀ ਸ਼ਕਤੀ ਦਾ ਸੰਚਾਰ ਹੁੰਦਾ ਹੈ ।
• ਯੋਗ ਆਸਣ ਪ੍ਰਾਣਾਯਾਮ ਦਾ ਕਾਰਜਕ੍ਰਮ ਖ਼ਤਮ ਕਰਨ ਦੇ ਬਾਅਦ ਘੱਟੋ-ਘੱਟ ਅੱਧੇ . ਘੰਟੇ ਤਕ ਕੁੱਝ ਨਾ ਖਾਓ 1. ‘ਲਾ ,
• ਹਵਾ ਨੂੰ ਬਾਹਰ ਕੱਢਣ ਦੇ ਬਾਅਦ ਸਾਹ ਕਿਰਿਆ ਰੋਕਣ ਦਾ ਅਭਿਆਸ ਕਰੋ । (16) ਯੋਗ ਅਭਿਆਸ ਹਰ ਰੋਜ਼ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
“ਯੋਗ ਤੰਦਰੁਸਤੀ ਦਾ ਸਾਧਨ ਹੈ ।` ਇਸ ਬਾਰੇ ਆਪਣੇ ਵਿਚਾਰ ਪ੍ਰਗਟ ਕਰੋ । [ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ – 4]
(“Yoga is means of Good Health.” Write.)
ਉੱਤਰ-
ਯੋਗ ਦਾ ਸਭ ਤੋਂ ਵੱਡਾ ਉਦੇਸ਼ ਇਹ ਹੈ ਕਿ ਵਿਅਕਤੀ ਨੂੰ ਸਰੀਰਕ ਅਤੇ ਮਾਨਸਿਕ ਤੌਰ ‘ਤੇ ਦਿੜ ਅਤੇ ਚੇਤੰਨ ਅਤੇ ਵਿਚਾਰ ਵਿਚ ਵਾਧਾ ਕਰਨਾ । ਇਸ ਦੀਆਂ ਵਿਸ਼ੇਸ਼ਤਾਵਾਂ ਇਸ ਪ੍ਰਕਾਰ ਹਨ-

• ਯੋਗ ਨਾਲ ਮਨੁੱਖ ਦੀਆਂ ਸਰੀਰਕ ਅਤੇ ਮਾਨਸਿਕ ਬੁਨਿਆਦੀ ਸ਼ਕਤੀਆਂ ਵਿਕਸਿਤ ਹੁੰਦੀਆਂ ਹਨ | ਪ੍ਰਾਣਾਯਾਮ ਦੁਆਰਾ ਫੇਫੜਿਆਂ ਵਿਚ ਬਹੁਤ ਸਾਰੀ ਹਵਾ ਚਲੀ ਜਾਂਦੀ ਹੈ ਜਿਸ ਨਾਲ ਫੇਫੜਿਆਂ ਦੀ ਕਸਰਤ ਹੁੰਦੀ ਹੈ । ਇਸ ਨਾਲ ਫੇਫੜਿਆਂ ਦੇ ਬਹੁਤ ਸਾਰੇ ਰੋਗ ਦੂਰ ਹੁੰਦੇ ਹਨ ।
• ਯੋਗ ਅਭਿਆਸ ਕਰਨ ਨਾਲ ਸਰੀਰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਸਵਸਥ ਰਹਿੰਦਾ ਹੈ । ਧੋਤੀ ਕਿਰਿਆ ਅਤੇ ਵਸਤੀ ਕਿਰਿਆ ਕ੍ਰਮਵਾਰ ਜਿਗਰ ਅਤੇ ਅੰਤੜੀਆਂ ਨੂੰ ਸਾਫ਼ ਰੱਖਦੀ ਹੈ । ਸਾਫ਼ ਸਰੀਰ ਸਦਾ ਹੀ ਨਿਰੋਗ ਰਹਿੰਦਾ ਹੈ ।
• ਯੋਗ ਕਰਨ ਨਾਲ ਸਰੀਰ ਮਜ਼ਬੂਤ ਬਣਦਾ ਹੈ ।
• ਯੋਗ ਅਭਿਆਸ ਕਰਨ ਨਾਲ ਸਰੀਰਕ ਅੰਗ ਲਚਕਦਾਰ ਬਣਦੇ ਹਨ, ਜਿਵੇਂ ਹਲ ਆਸਣ ਅਤੇ ਧਨੁਰ ਆਸਣ ਨਾਲ ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਦੀ ਲਚਕ ਵਧਦੀ ਹੈ ।
• ਯੋਗ ਆਸਣ ਕਰਨ ਨਾਲ ਸਰੀਰ ਦੀਆਂ ਸਭ ਪ੍ਰਣਾਲੀਆਂ ਠੀਕ ਤਰ੍ਹਾਂ ਕੰਮ ਕਰਨ ਲੱਗਦੀਆਂ ਹਨ ।
• ਯੋਗ ਅਭਿਆਸ ਮਨੁੱਖ ਦੇ ਸਰੀਰ ਨੂੰ ਚੰਗੀ ਸਥਿਤੀ (Posture) ਵਿਚ ਰੱਖਦਾ ਹੈ ਜਿਸ ਨਾਲ ਉਸ ਦੇ ਵਿਅਕਤਿੱਤਵ ਵਿਚ ਨਿਖਾਰ ਆਉਂਦਾ ਹੈ । ਉਦਾਹਰਨ ਦੇ ਤੌਰ ‘ਤੇ ਬ੍ਰਿਖ ਆਸਣ ਕਰਨ ਨਾਲ ਗੋਡੇ ਨਹੀਂ ਭਿੜਦੇ ਅਤੇ ਪਦਮ ਆਸਣ ਕਰਨ ਨਾਲ ਨਾ ਹੀ ਪੇਟ ਅੱਗੇ ਵੱਲ ਨਿਕਲਦਾ ਹੈ ਅਤੇ ਨਾ ਹੀ ਮੋਢਿਆਂ ਵਿਚ ਕੁੱਬਾਪਨ ਆਉਂਦਾ ਹੈ ।
• ਯੋਗ ਆਸਣ ਕਰਨ ਨਾਲ ਮਾਨਸਿਕ ਅਨੁਸ਼ਾਸਨ ਆਉਂਦਾ ਹੈ | ਯਮ ਅਤੇ ਨਿਯਮ ਦੁਆਰਾ ਮਨੁੱਖੀ ਵਿਕਾਰਾਂ ਅਤੇ ਅਨੁਚਿਤ ਇੱਛਾਵਾਂ ‘ਤੇ ਕੰਟਰੋਲ ਸਥਾਪਿਤ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਮਿਲਦੀ ਹੈ !
• ਉੱਚਿਤ ਆਸਣ ਕਰਨ ਨਾਲ ਕਈ ਕਿਸਮ ਦੇ ਰੋਗ ਦੂਰ ਹੋ ਜਾਂਦੇ ਹਨ ਅਤੇ ਕਈ ਰੋਗਾਂ ਦੀ ਰੋਕਥਾਮ ਹੋ ਜਾਂਦੀ ਹੈ । ਵੱਜਰ ਆਸਣ ਅਤੇ ਮੱਤਸਿਏਂਦਰ ਆਸਣ ਗਰ (Diabetes) ਰੋਗ ਨੂੰ ਠੀਕ ਕਰਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਪ੍ਰਾਣਾਯਾਮ ਫੇਫੜਿਆਂ ਨੂੰ ਰੋਗ ਨਹੀਂ ਲੱਗਣ ਦਿੰਦਾ ।
• ਯੋਗ ਆਸਣ ਸਰੀਰਕ ਅਤੇ ਮਾਨਸਿਕ ਥਕਾਵਟ ਨੂੰ ਦੂਰ ਕਰਨ ਵਿਚ ਸਹਾਇਤਾ ਪ੍ਰਦਾਨ ਕਰਦੇ ਹਨ । ਸ਼ਵ-ਅਸਣ ਮਨੁੱਖ ਦੀ ਬਕਸਵਟ ਨੂੰ ਦੂਰ ਕਰਨ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ |
• *ਯੋਗ ਕਰਨ ਨਾਲ ਬੁੱਧੀ ਤੇਜ਼ ਹੁੰਦੀ ਹੈ ਅਤੇ ਯਾਦ-ਸ਼ਕਤੀ ਵਧਦੀ ਹੈ । ਇਸ ਗੱਲ ਲਈ ਸ਼ੀਰਸ਼ ਆਸਣ ਬਹੁਤ ਹੀ ਉਪਯੋਗੀ ਹੈ ।
• ਯੋਗ ਅਭਿਆਸ ਕਰਨ ਨਾਲ ਮਨੁੱਖ ਦੇ ਸਰੀਰ ਵਿਚ ਤਾਲ (Rhythm) ਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਨਾਲ ਸਰੀਰ ਦੀ ਸ਼ਕਤੀ ਸੰਜਮ ਨਾਲ ਖ਼ਰਚ ਹੁੰਦੀ ਹੈ ।
• ਯੋਗ ਆਸਣ ਸੰਤੁਲਨ ਅਤੇ ਪ੍ਰਸੰਨਤਾ ਪ੍ਰਾਪਤੀ ਦਾ ਸਰਵ-ਉੱਤਮ ਆਸਣ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਹੋਰ ਕਸਰਤਾਂ ਜਿਵੇਂ ਸੈਰ, ਡੰਡ-ਬੈਠਕ, ਮਗਦਰ, ਮੱਲ-ਯੁੱਧ, ਪੱਛਮੀ ਦੇਸ਼ਾਂ ਦੀਆਂ ਖੇਡਾਂ ਆਦਿ ਵਿਚ ਕੀ ਦੋਸ਼ ਹੈ ਅਤੇ ਯੋਗ ਆਸਣਾਂ ਵਿਚ ਅਜਿਹੀ ਕੀ ਵਿਸ਼ੇਸ਼ਤਾ ਹੈ ਜੋ ਉਸ ਨੂੰ ਹੀ ਜੀਵਨ ਦਾ ਅੰਗ ਬਣਾਇਆ ਜਾਵੇ ?
(What are the disadvantages of western exercises like astroll, Dand bethak, Wrestling, Mugdhar etc. Why Yoga is important for our life ?)
ਉੱਤਰ-
1. ਹੋਰ ਜਿੰਨੀਆਂ ਵੀ ਕਸਰਤਾਂ ਹਨ, ਉਹ ਮੁੱਖ ਤੌਰ ‘ਤੇ ਮਾਸਪੇਸ਼ੀਆਂ ‘ਤੇ ਹੀ | ਅਸਰ ਪਾਉਂਦੀਆਂ ਹਨ, ਜਿਸ ਨਾਲ ਬਾਹਰੀ ਸਰੀਰ ਹੀ ਬਲਵਾਨ ਨਜ਼ਰ ਆਉਂਦਾ ਹੈ, ਅੰਦਰ ਕੰਮ ਕਰਨ ਵਾਲੇ ਜੰਤਰਾਂ ‘ਤੇ ਉੱਨਾ ਪ੍ਰਭਾਵ ਨਹੀਂ ਪੈਂਦਾ ਜਿਸ ਨਾਲ ਵਿਅਕਤੀ ਜ਼ਿਆਦਾ ਦੇਰ ਤਕ ਸਿਹਤਮੰਦ ਨਹੀਂ ਰਹਿ ਸਕਦਾ ਜਦੋਂ ਕਿ ਯੋਗ-ਆਸਣਾਂ ਨਾਲ ਵਿਅਕਤੀ ਦੀ ਉਮਰ ਲੰਬੀ ਹੁੰਦੀ ਹੈ, ਵਿਕਾਰਾਂ ਨੂੰ ਸਰੀਰ ਤੋਂ ਬਾਹਰ ਕਰਨ ਦੀ ਅਨੋਖੀ ਸ਼ਕਤੀ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ਅਤੇ ਸਰੀਰ ਦੇ ਖੰਡ ਬਣਦੇ ਵੱਧ ਅਤੇ ਟੁੱਟਦੇ ਘੱਟ ਹਨ ।

2. ਹੋਰ ਕਸਰਤਾਂ ਅਤੇ ਖੇਡਾਂ ਲਈ ਸਥਾਨ ਅਤੇ ਸਾਧਨਾਂ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ । ਖੇਡ ਤਾਂ | ਸਾਥੀਆਂ ਦੇ ਬਿਨਾਂ ਖੇਡੀ ਹੀ ਨਹੀਂ ਜਾ ਸਕਦੀ, ਜਦੋਂ ਕਿ ਯੋਗ ਆਸਣ ਇਕੱਲੇ ਹੀ ਦਰੀ ਜਾਂ ਚਾਦਰ ਤੇ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ ।

3. ਦੁਸਰੀਆਂ ਕਸਰਤਾਂ ਦਾ ਪ੍ਰਭਾਵ ਮਨ ਅਤੇ ਇੰਦਰੀਆਂ ‘ਤੇ ਬਹੁਤ ਘੱਟ ਪੈਂਦਾ ਹੈ ਜਦੋਂ ਕਿ ਆਸਣਾਂ ਨਾਲ ਮਾਨਸਿਕ ਸ਼ਕਤੀ ਵੱਧਦੀ ਹੈ ਅਤੇ ਇੰਦਰੀਆਂ ਨੂੰ ਕਾਬੂ ਵਿਚ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਆਉਂਦੀ ਹੈ ।

4. ਦੁਸਰੀਆਂ ਕਸਰਤਾਂ ਵਿਚ ਵਧੇਰੇ ਖ਼ੁਰਾਕ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ ਜਿਸ ਦੇ ਲਈ ਵਧੇਰੇ ਖ਼ਰਚ ਕਰਨਾ ਪੈਂਦਾ ਹੈ ਜਦੋਂ ਕਿ ਯੋਗ ਆਸਣਾਂ ਵਿਚ ਬਹੁਤ ਘੱਟ ਭੋਜਨ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ।

5. ਯੋਗ ਆਸਣਾਂ ਵਿਚ ਸਰੀਰ ਦੀ ਰੋਗ ਨਾਸ਼ਕ ਸ਼ਕਤੀ ਦਾ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ ਜਿਸ ਨਾਲ | ਸਰੀਰ ਕਿਸੇ ਵੀ ਵਿਜਾਤੀ ਦਵ ਨੂੰ ਅੰਦਰ ਰੁਕਣ ਨਹੀਂ ਦਿੰਦਾ, ਫੌਰਨ ਬਾਹਰ ਕੱਢਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰਦਾ ਹੈ ਜਿਸ ਨਾਲ ਤੁਸੀਂ ਰੋਗ ਮੁਕਤ ਹੁੰਦੇ ਹੋ ।

6. ਯੋਗ ਆਸਣਾਂ ਨਾਲ ਸਰੀਰ ਵਿਚ ਲਚਕ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ਜਿਸ ਨਾਲ ਸਰੀਰ ਫੁਰਤੀਲਾ ਰਹਿੰਦਾ ਹੈ, ਸਰੀਰ ਦੇ ਹਰ ਅੰਗ ਵਿਚ ਖੂਨ ਦਾ ਸੰਚਾਰ ਠੀਕ ਹੁੰਦਾ ਹੈ, ਵੱਧ ਉਮਰ ਵਿਚ ਵੀ ਵਿਅਕਤੀ ਜਵਾਨ ਲੱਗਦਾ ਹੈ ਅਤੇ ਕੰਮ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਬਣੀ ਰਹਿੰਦੀ ਹੈ । ਹੋਰ ਕਸਰਤਾਂ ਨਾਲ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਵਿਚ ਸਖ਼ਤੀ ਆ ਜਾਂਦੀ ਹੈ, ਸਰੀਰ ਸਖ਼ਤ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਬੁਢਾਪਾ ਜਲਦੀ ਆ ਜਾਂਦਾ ਹੈ ।

7. ਜਿਸ ਤਰ੍ਹਾਂ ਨਾਲੀ ਦੀ ਗੰਦਗੀ ਨੂੰ ਝਾੜੂ ਲਾ ਕੇ, ਪਾਣੀ ਸੁੱਟ ਕੇ ਸਾਫ਼ ਕਰਦੇ ਹਨ, ਉਸੇ ਤਰਾਂ ਵੱਖ-ਵੱਖ ਆਸਣਾਂ ਨਾਲ ਖ਼ੂਨ ਦੀਆਂ ਨਲੀਆਂ ਅਤੇ ਕੋਸ਼ਿਕਾਵਾਂ ਨੂੰ ਸਾਫ਼ ਕਰਦੇ ਹਨ ਤਾਂ ਕਿ ਉਨ੍ਹਾਂ ਵਿਚ ਰਵਾਨਗੀ ਰਹੇ ਅਤੇ ਸਰੀਰ ਰੋਗ ਮੁਕਤ ਹੋਵੇ । ਇਹ ਸਿਰਫ਼ ਯੋਗ ਆਸਣ ਕਿਰਿਆਵਾਂ ਨਾਲ ਹੀ ਹੋ ਸਕਦਾ ਹੈ, ਹੋਰ ਕਸਰਤਾਂ ਵਿਚ ਨਹੀਂ । ਹੋਰ ਕਸਰਤਾਂ ਨਾਲ ਤਾਂ ਦਿਲ ਦੀ ਗਤੀ ਤੇਜ਼ ਹੋ ਜਾਂਦੀ ਹੈ ਅਤੇ ਖੂਨ ਪੂਰੀ ਤਰ੍ਹਾਂ ਸ਼ੁੱਧ ਨਹੀਂ ਹੋ ਸਕਦਾ ।

8. ਫੇਫੜਿਆਂ ਦੇ ਰਾਹੀਂ ਸਾਡੇ ਖੂਨ ਦੀ ਸ਼ੁੱਧੀ ਹੁੰਦੀ ਹੈ । ਯੋਗ ਆਸਣਾਂ ਅਤੇ ਪ੍ਰਾਣਾਯਾਮ ਰਾਹੀਂ ਅਸੀਂ ਆਪਣੇ ਫੇਫੜਿਆਂ ਦੇ ਫੈਲਣ ਤੇ ਸੁੰਗੜਨ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਵਧਾਉਂਦੇ ਹਾਂ ਜਿਸ ਨਾਲ ਵੱਧ ਤੋਂ ਵੱਧ ਆਕਸੀਜਨ ਮਿਲੀ ਹੋਈ ਹਵਾ ਫੇਫੜਿਆਂ ਵਿਚ ਭਰ ਸਕਣ ਅਤੇ ਖੂਨ ਦੀ ਸ਼ੁੱਧੀ ਕਰ ਸਕਣ | ਸਾਰੀਆਂ ਕਸਰਤਾਂ ਵਿਚ ਫੇਫੜੇ ਜਲਦੀ-ਜਲਦੀ ਸਾਹ ਲੈਂਦੇ ਹਨ ਜਿਸ ਨਾਲ ਪਾਣ ਹਵਾ ਫੇਫੜਿਆਂ ਦੇ ਆਖ਼ਰੀ ਸਿਰੇ ਤੱਕ ਨਹੀਂ ਪਹੁੰਚ ਸਕਦੀ ਜਿਸ ਦਾ ਸਿੱਟਾ ਹੁੰਦਾ ਹੈ ਵਿਕਾਰ ਤੇ ਵਿਕਾਰ ਰੋਗ ਦਾ ਕਾਰਨ ਹੈ ।

9. ਵਰਤਮਾਨ ਸਮੇਂ ਵਿਚ ਗਲਤ ਰਹਿਣ-ਸਹਿਣ ਅਤੇ ਗੈਰ-ਕੁਦਰਤੀ ਭੋਜਨ ਦੇ ਕਾਰਨ ਪਾਚਨ ਪ੍ਰਣਾਲੀ ਦੇ ਯੰਤਰਾਂ ਦਾ ਕੰਮ ਸੁਚਾਰੂ ਰੂਪ ਨਾਲ ਨਹੀਂ ਚੱਲ ਸਕਦਾ । ਉਨ੍ਹਾਂ ਨੂੰ ਕਿਰਿਆਸ਼ੀਲ ਰੱਖਣ ਵਿਚ ਯੋਗ ਆਸਣ ਬਹੁਤ ਸਹਾਇਕ ਸਿੱਧ ਹੁੰਦੇ ਹਨ ਜਦੋਂ ਕਿ ਦੂਸਰੀਆਂ ਕਸਰਤਾਂ ਨਾਲ ਪਾਚਨ ਕਿਰਿਆ ਵਿਗੜ ਜਾਂਦੀ ਹੈ ।

9. ਵਰਤਮਾਨ ਸਮੇਂ ਵਿਚ ਗਲਤ ਰਹਿਣ-ਸਹਿਣ ਅਤੇ ਗੈਰ-ਕੁਦਰਤੀ ਭੋਜਨ ਦੇ ਕਾਰਨ ਪਾਚਨ ਪ੍ਰਣਾਲੀ ਦੇ ਯੰਤਰਾਂ ਦਾ ਕੰਮ ਸੁਚਾਰੂ ਰੂਪ ਨਾਲ ਨਹੀਂ ਚੱਲ ਸਕਦਾ । ਉਨ੍ਹਾਂ ਨੂੰ ਕਿਰਿਆਸ਼ੀਲ ਰੱਖਣ ਵਿਚ ਯੋਗ ਆਸਣ ਬਹੁਤ ਸਹਾਇਕ ਸਿੱਧ ਹੁੰਦੇ ਹਨ ਜਦੋਂ ਕਿ ਦੂਸਰੀਆਂ ਕਸਰਤਾਂ ਨਾਲ ਪਾਚਨ ਕਿਰਿਆ ਵਿਗੜ ਜਾਂਦੀ ਹੈ ।

10. ਰੀੜ੍ਹ ਦੀ ਹੱਡੀ ਤੇ ਸਾਡੀ ਜਵਾਨੀ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਸਾਰਾ ਖੂਨ ਸੰਚਾਰ ਅਤੇ ਨਾੜੀ ਸੰਚਾਲਨ ਇਸੇ ਵਿਚੋਂ ਹੋ ਕੇ ਸਰੀਰ ਵਿਚ ਫੈਲਦਾ ਹੈ । ਜਿੰਨੀ ਲਚਕ ਰੀੜ ਦੀ ਹੱਡੀ ਵਿਚ ਰਹੇਗੀ, ਉੱਨਾ ਹੀ ਸਰੀਰ ਸਿਹਤਮੰਦ ਹੋਵੇਗਾ, ਉਮਰ ਲੰਬੀ ਹੋਵੇਗੀ, ਮਾਨਸਿਕ ਸੰਤੁਲਨ ਬਣਿਆ ਰਹੇਗਾ । ਇਹ ਸਿਰਫ਼ ਯੋਗ-ਆਸਣਾਂ ਨਾਲ ਹੀ ਸੰਭਵ ਹੈ ।

11. ਦੁਸਰੀਆਂ ਕਸਰਤਾਂ ਨਾਲ ਤੁਹਾਨੂੰ ਥਕਾਵਟ ਹੋਵੇਗੀ, ਬਹੁਤ ਜ਼ਿਆਦਾ ਸ਼ਕਤੀ ਖ਼ਰਚ ਕਰਨੀ ਪਵੇਗੀ ਜਦੋਂ ਕਿ ਯੋਗ ਆਸਣਾਂ ਨਾਲ ਸ਼ਕਤੀ ਪ੍ਰਾਪਤ ਹੋ ਜਾਂਦੀ ਹੈ ਕਿਉਂਕਿ ਯੋਗ ਆਸਣ ਹੌਲੀ-ਹੌਲੀ ਅਤੇ ਆਰਾਮ ਦੇ ਲਈ ਕੀਤੇ ਜਾਂਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਨੂੰ ਅਹਿੰਸਕ ਅਤੇ ਸ਼ਾਂਤੀਪਿਅ ਕਿਰਿਆਵਾਂ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।

12. ਹੋਰ ਕਸਰਤਾਂ ਨਾਲ ਮਨੁੱਖ ਦੇ ਚਰਿੱਤਰ ‘ਤੇ ਕੋਈ ਖ਼ਾਸ ਪ੍ਰਭਾਵ ਨਹੀਂ ਪੈਂਦਾ । ਯੋਗ ਆਸਣ ਸਿਹਤ ਦੇ ਨਾਲ-ਨਾਲ ਚਰਿੱਤਰਵਾਨ ਵੀ ਬਣਾਉਂਦੇ ਹਨ | ਯੌਗਿਕ ਕਿਰਿਆ ਨਾਲ ਮਾਨਸਿਕ ਅਤੇ ਨੈਤਿਕ ਸ਼ਕਤੀ ਦਾ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ । ਮਨ ਸਥਿਰ ਰਹਿੰਦਾ ਹੈ, ਮਨ ਦੇ ਸਥਿਰ ਰਹਿਣ ਨਾਲ ਬੁੱਧੀ ਦਾ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ । ਸਤਵਗੁਣ ਦੀ ਪ੍ਰਧਾਨਤਾ ਹੁੰਦੀ ਹੈ ਅਤੇ ਸਤਵਗੁਣ ਨਾਲ ਮਾਨਸਿਕ ਸ਼ਕਤੀ ਦਾ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ । ਇਹ ਸਾਰੇ ਲਾਭ ਸਿਰਫ਼ ਯੋਗ ਆਸਣ ਅਤੇ ਪ੍ਰਾਣਾਯਾਮ ਤੋਂ ਹੀ ਪ੍ਰਾਪਤ ਹੋ ਸਕਦੇ ਹਨ ।

13. ਸਾਡੇ ਸਰੀਰ ਵਿਚ ਕਈ ਗ੍ਰੰਥੀਆਂ ਹਨ ਜੋ ਸਾਨੂੰ ਸਿਹਤਮੰਦ ਅਤੇ ਨਿਰੋਗ ਰੱਖਣ ਵਿਚ ਮਹੱਤਵਪੂਰਨ ਕੰਮ ਕਰਦੀਆਂ ਹਨ । ਇਨ੍ਹਾਂ ਗ੍ਰੰਥੀਆਂ ਦਾ ਰਸ ਖੂਨ ਵਿਚ ਮਿਲ ਜਾਂਦਾ ਹੈ ਜਿਸ ਨਾਲ ਮਨੁੱਖ ਸਿਹਤਮੰਦ ਅਤੇ ਸ਼ਕਤੀਸ਼ਾਲੀ ਬਣਦਾ ਹੈ । ਗਲੇ ਦੀ ਥਾਇਰਾਈਡ ਅਤੇ ਪੈਰਾਥਾਈਰਾਈਡ ਗ੍ਰੰਥੀਆਂ ਵਿਚੋਂ ਨਿਕਲਣ ਵਾਲਾ ਰਸ ਕਾਫ਼ੀ ਮਾਤਰਾ ਵਿਚ ਨਾ ਹੋਣ ਨਾਲ | ਬੱਚਿਆਂ ਦਾ ਪੂਰਨ ਵਿਕਾਸ ਨਹੀਂ ਹੋ ਸਕਦਾ ਅਤੇ ਗੱਭਰੂਆਂ ਦੇ ਸਮੇਂ ਤੋਂ ਪਹਿਲਾਂ ਹੀ ਵਾਲ ਡਿੱਗਣ ਲੱਗਦੇ ਹਨ ਅਤੇ ਸਰੀਰ ਵਿਚ ਖੁਸ਼ੀ ਨਹੀਂ ਰਹਿੰਦੀ | ਸਰੀਰ ਦੀਆਂ ਭਿੰਨ-ਭਿੰਨ ਗ੍ਰੰਥੀਆਂ ਸੁਚੇਤ ਕਰਕੇ ਕਾਫ਼ੀ ਮਾਤਰਾ ਵਿਚ ਰਸ ਦੇਣ ਦੇ ਯੋਗ ਬਣਾਉਣ ਲਈ ਯੋਗ ਆਸਣ ਪ੍ਰਣਾਲੀ ਬਹੁਤ ਚੰਗੀ ਹੈ । ਹੋਰ ਕਸਰਤਾਂ ਦਾ ਪ੍ਰਭਾਵ ਇਸ ਦਿਸ਼ਾ ਵਿਚ ਨਾਂਹ ਵਾਲਾ ਹੈ ।

14. ਸਰੀਰ ਦੇ ਰੋਗਾਂ ਨੂੰ ਦੂਰ ਕਰਨ ਵਿਚ ਪ੍ਰਾਣਾਯਾਮ ਅਤੇ ਸ਼ਟਕਰਮ ਰਾਮ-ਬਾਣ ਦਾ ਕੰਮ ਕਰਦੇ ਹਨ । ਜਦੋਂ ਵਿਜਾਤੀ ਦ੍ਰਵਾਂ ਦੇ ਵੱਧ ਜਾਣ ਨਾਲ ਸਰੀਰ ਦੇ ਅੰਗ ਉਨ੍ਹਾਂ ਨੂੰ ਬਾਹਰ ਕੱਢਣ ਵਿਚ ਸਮਰੱਥ ਨਹੀਂ ਹੁੰਦੇ ਤਾਂ ਰੋਗ ਦਾ ਆਰੰਭ ਹੁੰਦਾ ਹੈ । ਇਨ੍ਹਾਂ ਵਿਜਾਤੀ ਵਾਂ ਨੂੰ ਬਾਹਰ ਕੱਢਣ ਦੇ ਲਈ ਇਨ੍ਹਾਂ ਕਿਰਿਆਵਾਂ ਦਾ ਸਹਾਰਾ ਲਿਆ ਜਾ ਸਕਦਾ ਹੈ ਅਤੇ ਆਪਣੇ ਆਪ ਨੂੰ ਤੰਦਰੁਸਤ ਅਤੇ ਸ਼ਕਤੀਸ਼ਾਲੀ ਬਣਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ।

15. ਸਰੀਰਕ, ਮਾਨਸਿਕ, ਬੌਧਿਕ ਅਤੇ ਆਤਮਿਕ ਵਿਕਾਸ ਦੇ ਲਈ ਯੋਗ ਪ੍ਰਣਾਲੀ ਸਭ ਤੋਂ ਚੰਗੀ ਪ੍ਰਣਾਲੀ ਹੈ । ਇਸ ਦਾ ਮੁਕਾਬਲਾ ਹੋਰ ਕੋਈ ਪ੍ਰਣਾਲੀ ਨਹੀਂ ਕਰ ਸਕਦੀ ।

Punjab State Board PSEB 10th Class Physical Education Book Solutions Chapter 2 ਸੰਤੁਲਿਤ ਭੋਜਨTextbook Exercise Questions, and Answers.

PSEB Solutions for Class 10 Physical Education Chapter 2 ਸੰਤੁਲਿਤ ਭੋਜਨ

Physical Education Guide for Class 10 PSEB ਸੰਤੁਲਿਤ ਭੋਜਨ ਪ੍ਰਭਾਵTextbook Questions and Answers

ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Very Short Answer Type Questions) 

ਪ੍ਰਸ਼ਨ 1.
ਪੋਟੀਨ ਕਿੰਨੇ ਪ੍ਰਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ, ਉਹਨਾਂ ਦੇ ਨਾਂ ਲਿਖੋ । (Name the types of Protein.)
ਉੱਤਰ-
ਪ੍ਰੋਟੀਨ ਦੋ ਪ੍ਰਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ-ਪਸ਼ੂ ਪ੍ਰੋਟੀਨ ਅਤੇ ਬਨਸਪਤੀ ਪ੍ਰੋਟੀਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਕੀ ਹਨ ? (What is Carbohydrates ?)
ਉੱਤਰ-
ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਕਾਰਬਨ, ਹਾਈਡਰੋਜਨ ਅਤੇ ਆਕਸੀਜਨ ਦਾ ਮਿਸ਼ਰਨ ਹਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਵਿਟਾਮਿਨ ਕਿੰਨੀ ਪ੍ਰਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ ? (Mention the types of Vitamins ?)
ਉੱਤਰ-
ਵਿਟਾਮਿਨ ਛੇ ਪ੍ਰਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ ‘ਏ’, ‘ਬੀ’, ‘ਸੀ’, ‘ਡੀ’, ‘ਈ’ ਅਤੇ ‘ਕੇ’ ।

ਪ੍ਰਸ਼ਨ 4.
ਕਿਹੜੇ ਵਿਟਾਮਿਨ ਪਾਣੀ ਵਿਚ ਘੁਲਣਸ਼ੀਲ ਨਹੀਂ ਹੁੰਦੇ ? (Which Vitamins are not soluble in water ?)
ਉੱਤਰ-
ਵਿਟਾਮਿਨ ‘ਸੀ’, ‘ਡੀ’ ਅਤੇ ‘ਕੇ’|

ਪ੍ਰਸ਼ਨ 5.
ਛੋਟੇ ਬੱਚੇ ਲਈ ਕਿਹੜਾ ਦੁੱਧ ਚੰਗਾ ਹੁੰਦਾ ਹੈ ? (Which milk is better for a child ?)
ਉੱਤਰ-
ਮਾਂ ਦਾ ਦੁੱਧ ।

ਪ੍ਰਸ਼ਨ 6.
ਸਾਡੇ ਰੋਜ਼ਾਨਾ ਦੇ ਭੋਜਨ ਵਿਚ ਪ੍ਰੋਟੀਨ ਦੀ ਮਾਤਰਾ ਕਿੰਨੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ? (How much proteins we should take in our daily meals ?)
ਉੱਤਰ-
700 ਤੋਂ 100 ਗ੍ਰਾਮ ।

ਪ੍ਰਸ਼ਨ 7.
ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਕਿਹੜੇ ਦੋ ਰੂਪਾਂ ਵਿਚ ਮਿਲਦੇ ਹਨ ? (Name the Isomers of Carbohydrates ?)
ਉੱਤਰ-
ਸਟਾਰਚ ਅਤੇ ਸ਼ੱਕਰ ।

ਪ੍ਰਸ਼ਨ 8.
ਪ੍ਰੋਟੀਨ ਕਿਹੜੇ ਤੱਤਾਂ ਦਾ ਮਿਸ਼ਰਨ ਹਨ ? (Of what elements protein is a mixture ?)
ਉੱਤਰ-
ਕਾਰਬਨ, ਨਾਈਟਰੋਜਨ, ਹਾਈਡਰੋਜਨ ਤੇ ਗੰਧਕ |

ਪ੍ਰਸ਼ਨ 9.
ਜੀਵਨ ਤੱਤ ਕਿਨ੍ਹਾਂ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ? (Which thing is known as life saving ?)
ਉੱਤਰ-
ਵਿਟਾਮਿਨਾਂ ਨੂੰ ।

ਪ੍ਰਸ਼ਨ 10.
ਸਾਡੇ ਭੋਜਨ ਵਿਚ ਚਰਬੀ ਦੀ ਮਾਤਰਾ ਕਿੰਨੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ? (How much Fat one should take daily ?)
ਉੱਤਰ-
50 ਤੋਂ 70 ਗ੍ਰਾਮ ।

ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਭੋਜਨ ਦੇ ਕਿਹੜੇ-ਕਿਹੜੇ ਮੁੱਖ ਕੰਮ ਹਨ ? (What are the functions of food ?)
ਉੱਤਰ-
ਅਸੀਂ ਜਿਹੜਾ ਭੋਜਨ ਖਾਂਦੇ ਹਾਂ ਉਹ ਪਚਣ ਤੋਂ ਬਾਅਦ ਸਰੀਰ ਵਿਚ ਕਈ ਕੰਮ ਕਰਦਾ ਹੈ । ਉਹਨਾਂ ਕੰਮਾਂ ਦਾ ਵੇਰਵਾ ਹੇਠ ਦਿੱਤਾ ਗਿਆ ਹੈ
1. ਸਰੀਰਕ ਵਾਧੇ ਵਿਚ ਸਹਾਇਤਾ-ਭੋਜਨ ਸਰੀਰ ਦੇ ਵਾਧੇ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ । ਇਸ ਨਾਲ ਸਰੀਰ ਦੇ ਵੱਖ-ਵੱਖ ਅੰਗਾਂ ਦਾ ਨਿਰਮਾਣ ਅਤੇ ਵਾਧਾ ਹੁੰਦਾ ਹੈ ।

2. ਸਰੀਰ ਨੂੰ ਸ਼ਕਤੀ-ਭੋਜਨ ਸਰੀਰ ਨੂੰ ਸ਼ਕਤੀ ਦਿੰਦਾ ਹੈ ਸਾਡਾ ਸਰੀਰ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਕਿਰਿਆਵਾਂ ਕਰਦਾ ਹੈ । ਇਹਨਾਂ ਕਿਰਿਆਵਾਂ ਲਈ ਲੋੜੀਂਦੀ ਸ਼ਕਤੀ ਭੋਜਨ ਤੋਂ ਹੀ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ।

3. ਸਰੀਰ ਵਿਚ ਗਰਮੀ ਪੈਦਾ ਕਰਨਾ-ਭੋਜਨ ਸਰੀਰ ਵਿਚ ਗਰਮੀ ਪੈਦਾ ਕਰਦਾ ਹੈ । ਜਦੋਂ ਖਾਧਾ ਹੋਇਆ ਭੋਜਨ ਹਜ਼ਮ ਹੋ ਕੇ ਸਾਹ ਰਾਹੀਂ ਆਈ ਆਕਸੀਜਨ ਵਿਚ ਮਿਲ ਕੇ ਖੂਨ ਵਿਚ ਉਬਲਦਾ ਹੈ ਤਾਂ ਗਰਮੀ ਪੈਦਾ ਹੁੰਦੀ ਹੈ । ਇਹ ਗਰਮੀ ਸਰੀਰ ਲਈ ਬਹੁਤ ਹੀ ਜ਼ਰੂਰੀ ਹੈ । ਇਸ ਦੇ ਬਿਨਾਂ ਅਸੀਂ ਜਿਉਂਦੇ ਨਹੀਂ ਰਹਿ ਸਕਦੇ ।

4. ਨਵੇਂ ਸੈੱਲਾਂ ਦਾ ਬਣਾਉਣਾ ਅਤੇ ਟੁੱਟੇ-ਭੱਜੇ ਸੈੱਲਾਂ ਦੀ ਮੁਰੰਮਤ ਕਰਨਾ-ਭੋਜਨ ਟੁੱਟੇ-ਭੱਜੇ ਸੈੱਲਾਂ ਦੀ ਮੁਰੰਮਤ ਕਰਦਾ ਹੈ, ਭੋਜਨ ਨਾਲ ਨਵੇਂ ਸੈੱਲ ਵੀ ਬਣਦੇ ਹਨ । ਸਰੀਰ ਵਿਚ ਚਲ ਰਹੀਆਂ ਕਿਰਿਆਵਾਂ ਦੇ ਕਾਰਨ ਕੁੱਝ ਕੀਟਾਣੂ ਨਸ਼ਟ ਹੋ ਜਾਂਦੇ ਹਨ ਤੇ ਕੁੱਝ ਟੁੱਟ ਜਾਂਦੇ ਹਨ । ਭੋਜਨ ਦਾ ਸਭ ਤੋਂ ਵੱਡਾ ਕੰਮ ਟੁੱਟੇ-ਫੁੱਟੇ ਸੈੱਲਾਂ ਦੀ ਮੁਰੰਮਤ ਕਰਨਾ ਹੁੰਦਾ ਹੈ । ਨਸ਼ਟ ਹੋਏ ਸੈੱਲਾਂ ਦੀ ਥਾਂ ਨਵੇਂ ਸੈੱਲ ਵੀ ਭੋਜਨ ਹੀ ਤਿਆਰ ਕਰਦੇ ਹਨ ।

5. ਬਿਮਾਰੀਆਂ ਤੋਂ ਰੱਖਿਆ-ਭੋਜਨ ਸਰੀਰ ਨੂੰ ਬਿਮਾਰੀਆਂ ਤੋਂ ਬਚਾਉਂਦਾ ਹੈ । ਭੋਜਨ ਖਾਣ ਨਾਲ ਸ਼ਕਤੀ ਪੈਦਾ ਹੁੰਦੀ ਹੈ । ਇਹ ਸ਼ਕਤੀ ਸਾਨੂੰ ਬਿਮਾਰੀਆਂ ਦਾ ਮੁਕਾਬਲਾ ਕਰਨ ਦੇ ਯੋਗ ਬਣਾ ਦਿੰਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਅਸੀਂ ਕਈ ਤਰ੍ਹਾਂ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਤੋਂ ਬਚ ਸਕਦੇ ਹਾਂ ! ਉੱਪਰ ਦੱਸੇ ਸਾਰੇ ਕੰਮ ਭੋਜਨ ਦੇ ਮੁੱਖ ਕੰਮ ਹੁੰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਭੋਜਨ ਕੀ ਹੁੰਦਾ ਹੈ ? ਅਸੀਂ ਭੋਜਨ ਕਿਉਂ ਕਰਦੇ ਹਾਂ ? (What is Food ? Why we take it ?).
ਉੱਤਰ-
ਭੋਜਨ ਕੀ ਹੁੰਦਾ ਹੈ ? (What is Food ?)-ਭੋਜਨ ਇਕ ਅਜਿਹੀ ਵਸਤੁ ਦਾ ਨਾਂ ਹੈ ਜੋ ਸਾਡੇ ਸਰੀਰ ਵਿਚ ਜਾ ਕੇ ਲਹੂ ਪੈਦਾ ਕਰਦਾ ਹੈ, ਨਵੇਂ ਸੈੱਲਾਂ ਦਾ ਨਿਰਮਾਣ ਕਰਦਾ ਹੈ, ਅੰਦਰਲੀ ਟੁੱਟ-ਭੱਜ ਦੀ ਮੁਰੰਮਤ ਕਰਦਾ ਹੈ ਅਤੇ ਸਰੀਰ ਵਿਚ ਗਰਮੀ ਅਤੇ ਸ਼ਕਤੀ ਪੈਦਾ ਕਰਦਾ ਹੈ ।

ਇਸ ਦੇ ਹੇਠ ਲਿਖੇ ਕੰਮ ਹਨ –
1. ਹਾਨੀ ਪੂਰਤੀ ਜਾਂ ਨਵੇਂ ਸੈੱਲਾਂ ਦਾ ਬਣਾਉਣਾ (Formation of new cells) ਮਨੁੱਖੀ ਸਰੀਰ ਦੇ ਹਰ ਸਮੇਂ ਕਿਰਿਆਵਾਂ ਕਰਨ ਨਾਲ ਸਰੀਰ ਦੇ ਸੈੱਲ (Cells) ਟੁੱਟਦੇ-ਭੱਜਦੇ ਰਹਿੰਦੇ ਹਨ । ਉੱਚਿਤ ਭੋਜਨ ਦੁਆਰਾ ਸਰੀਰ ਦੇ ਪੁਰਾਣੇ ਸੈੱਲਾਂ ਦੀ ਮੁਰੰਮਤ ਹੁੰਦੀ ਹੈ ਅਤੇ ਨਵੇਂ ਸੈੱਲਾਂ ਦਾ ਨਿਰਮਾਣ ਹੁੰਦਾ ਹੈ ।

2. ਭੋਜਨ ਸਰੀਰ ਨੂੰ ਸ਼ਕਤੀ ਦਿੰਦਾ ਹੈ (Food supplies energy to body)-ਰੋਜ਼ਾਨਾ ਜੀਵਨ ਦੇ ਕੰਮਾਂ ਨੂੰ ਕਰਨ ਲਈ ਸਰੀਰ ਨੂੰ ਸ਼ਕਤੀ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ । ਭੋਜਨ ਦੇ ਜਲਣ (Combustion) ਨਾਲ ਤਾਪ ਪੈਦਾ ਹੁੰਦਾ ਹੈ ਜਿਸ ਨਾਲ ਸਰੀਰ ਵਿਚ ਕੰਮ ਕਰਨ ਲਈ ਸ਼ਕਤੀ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ।

3. ਭੋਜਨ ਸਰੀਰ ਨੂੰ ਗਰਮੀ ਦਿੰਦਾ ਹੈ (Food supplies heat to body)-ਭੋਜਨ ਰਾਹੀਂ ਸਰੀਰ ਨੂੰ ਗਰਮੀ ਮਿਲਦੀ ਹੈ । ਜੇਕਰ ਸਰੀਰ ਵਿਚ ਗਰਮੀ ਦੀ ਮਾਤਰਾ ਘੱਟ ਹੋ ਜਾਂਦੀ ਹੈ ਤਾਂ ਜੀਵਨ ਅਸੰਭਵ ਹੋ ਜਾਂਦਾ ਹੈ ।

4. ਭੋਜਨ ਸਰੀਰ ਦੇ ਵਾਧੇ ਵਿਚ ਸਹਾਇਕ ਹੁੰਦਾ ਹੈ (Food helps growth of body)-ਭੋਜਨ ਰਾਹੀਂ ਸਰੀਰ ਦੇ ਅੰਗਾਂ ਵਿਚ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ । ਜੇ ਕਿਸੇ ਬੱਚੇ ਨੂੰ ਭੋਜਨ ਨਾ ਮਿਲੇ ਜਾਂ ਉੱਚਿਤ ਮਾਤਰਾ ਵਿਚ ਨਾ ਮਿਲੇ ਤਾਂ ਉਸ ਦੇ ਸਰੀਰ ਦੇ ਅੰਗਾਂ ਦਾ ਉੱਚਿਤ ਵਿਕਾਸ ਨਹੀਂ ਹੋ ਸਕਦਾ ।

ਪ੍ਰਸ਼ਨ 3.
ਵਿਟਾਮਿਨ ਕੀ ਹੁੰਦੇ ਹਨ ? ਇਹ ਸਾਡੇ ਸਰੀਰ ਲਈ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹੁੰਦੇ ਹਨ ? (What are Vitamins ? Why these are needed for our body ?)
ਉੱਤਰ-
ਵਿਟਾਮਿਨ (Vitamins)-ਵਿਟਾਮਿਨ ਅਜਿਹੇ ਰਸਾਇਣਿਕ ਪਦਾਰਥ ਹਨ ਜਿਨ੍ਹਾਂ ਦੀ ਸਾਡੇ ਸਰੀਰ ਦੇ ਵਿਕਾਸ ਲਈ ਲੋੜ ਹੁੰਦੀ ਹੈ । ਹੁਣ ਤਕ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਵਿਟਾਮਿਨਾਂ ਦੀ ਖੋਜ ਕੀਤੀ ਜਾ ਚੁੱਕੀ ਹੈ ਪਰ ਮੁੱਖ ਵਿਟਾਮਿਨ ਛੇ ਹੀ ਮੰਨੇ ਜਾਂਦੇ ਹਨ ਜੋ ਇਸ ਪ੍ਰਕਾਰ ਹਨ : ‘ਏ’, ‘ਬੀ’, ‘ਸੀ’, ‘ਡੀ’, ‘ਬੀ’ ਅਤੇ ‘ਕੇ’ । ਇਹਨਾਂ ਵਿਚੋਂ ਵਿਟਾਮਿਨ ‘ਬੀ’ ਤੇ ‘ਸੀ ਪਾਣੀ ਵਿਚ ਘੁਲਣਸ਼ੀਲ ਹਨ ਤੇ ਬਾਕੀ ਵਿਟਾਮਿਨ ‘ਏ’ ‘ਡੀ’ ਤੇ ‘ਕੇ ਚਰਬੀ ਵਿਚ ਘੁਲਣਸ਼ੀਲ ਹੁੰਦੇ ਹਨ । ਵਿਟਾਮਿਨ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਖ਼ੁਰਾਕ ਪਦਾਰਥਾਂ ਵਿਚ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਭੋਜਨ ਵਿਚ ਵਿਟਾਮਿਨਾਂ ਦੀ ਉੱਚਿਤ ਮਾਤਰਾ ਦਾ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ । ਭੋਜਨ ਦੀ ਜੀਵਨ ਲਈ ਬਹੁਤ ਜ਼ਿਆਦਾ ਮਹੱਤਤਾ ਨੂੰ ਅਨੁਭਵ ਕਰਦੇ ਹੋਏ ਇਹਨਾਂ ਨੂੰ ਜੀਵਨ-ਦਾਤਾ ਵੀ ਆਖਿਆ ਜਾਂਦਾ ਹੈ । ਵਿਟਾਮਿਨ ਡੀ ਧੁੱਪ ਤੋਂ ਮਿਲਦਾ ਹੈ । ਵਿਟਾਮਿਨ ਦੀ ਸਰੀਰ ਲਈ ਜ਼ਰੂਰਤ (Need of Vitamins) –

ਵਿਟਾਮਿਨ ਦੀ ਸਾਡੇ ਸਰੀਰ ਲਈ ਜ਼ਰੂਰਤ ਅੱਗੇ ਲਿਖੇ ਤੱਤਾਂ ਤੋਂ ਬਿਲਕੁਲ ਸਪੱਸ਼ਟ ਹੋ ਜਾਂਦੀ ਹੈ –

• ਵਿਟਾਮਿਨ ਸਾਡੀ ਸਿਹਤ ਨੂੰ ਠੀਕ ਰੱਖਦੇ ਹਨ ।
• ਇਹ ਸਾਡੇ ਸਰੀਰਕ ਵਾਧੇ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦੇ ਹਨ ।
• ਇਹ ਸਾਡੀ ਪਾਚਨ ਸ਼ਕਤੀ ਵਧਾਉਂਦੇ ਹਨ ।
• ਇਹ ਸਾਡਾ ਖੂਨ ਸਾਫ ਕਰਦੇ ਹਨ ਅਤੇ ਖੂਨ ਦੀ ਮਾਤਰਾ ਵਿਚ ਵਾਧਾ ਕਰਦੇ ਹਨ ।
• ਇਹ ਹੱਡੀਆਂ ਅਤੇ ਦੰਦਾਂ ਨੂੰ ਮਜ਼ਬੂਤ ਬਣਾਉਂਦੇ ਹਨ ।
• ਇਹ ਸਾਨੂੰ ਬਿਮਾਰੀਆਂ ਦਾ ਮੁਕਾਬਲਾ ਕਰਨ ਦੇ ਯੋਗ ਬਣਾਉਂਦੇ ਹਨ ।
• ਵਿਟਾਮਿਨ ਰਾਹੀਂ ਚਮੜੀ ਦੇ ਰੋਗ ਦੂਰ ਹੋ ਜਾਂਦੇ ਹਨ ।
• ਵਿਟਾਮਿਨ ਸਰੀਰ ਦੀ ਸ਼ਕਤੀ ਵਿਚ ਵਾਧਾ ਕਰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਮੁੱਖ ਭੋਜਨ ਪਦਾਰਥ ਅਤੇ ਉਹਨਾਂ ਦੇ ਗੁਣਾਂ ਦਾ ਵਰਣਨ ਕਰੋ | (Discuss the main constituents of food and give their advantages.)
ਉੱਤਰ-
ਅਨਾਜ, ਦਾਲਾਂ, ਸਬਜ਼ੀਆਂ, ਫਲ, ਸੁੱਕੇ ਮੇਵੇ, ਦੁੱਧ, ਮੀਟ, ਮੱਛੀ ਆਦਿ ਮੁੱਖ ਭੋਜਨ ਪਦਾਰਥ ਹਨ । ਇਹਨਾਂ ਦੇ ਗੁਣ ਹੇਠਾਂ ਦਿੱਤੇ ਗਏ ਹਨ

1. ਅਨਾਜ (Cereals-ਕਣਕ, ਚੌਲ, ਛੋਲੇ, ਜੌ, ਮੱਕੀ ਤੇ ਬਾਜਰਾ ਆਦਿ ਅਨਾਜ ਆਮ ਖਾਧੇ ਜਾਂਦੇ ਹਨ ।

ਗੁਣ (Advantages)-ਅਨਾਜ ਦੇ ਗੁਣ ਹੇਠ ਲਿਖੇ ਦਿੱਤੇ ਗਏ ਹਨ –

• ਇਹਨਾਂ ਨਾਲ ਸਾਡੇ ਸਰੀਰ ਦਾ ਨਿਰਮਾਣ ਹੁੰਦਾ ਹੈ ।
• ਇਹ ਸਰੀਰ ਨੂੰ ਸ਼ਕਤੀ ਵੀ ਪ੍ਰਦਾਨ ਕਰਦੇ ਹਨ ।
• ਇਹਨਾਂ ਵਿਚ ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਬਹੁਤ ਹੁੰਦੇ ਹਨ ।
• ਇਹਨਾਂ ਦੇ ਬਾਹਰਲਿਆਂ ਛਿਲਕਿਆਂ ਵਿਚ ਲੋਹਾ, ਚੂਨਾ, ਵਿਟਾਮਿਨ ਅਤੇ ਪ੍ਰੋਟੀਨ ਹੁੰਦੇ ਹਨ ।

2. ਦਾਲਾਂ (Pulses) -ਸੋਇਆਬੀਨ, ਮਾਂਹ, ਮਸਰ, ਅਰਹਰ, ਸੁੱਕੇ ਮਟਰ, ਰਾਜਮਾਂਹ ਆਦਿ ਦੀ ਗਿਣਤੀ ਮੁੱਖ ਦਾਲਾਂ ਵਿਚ ਹੁੰਦੀ ਹੈ ।
ਗੁਣ (Advantages)-ਦਾਲਾਂ ਦੇ ਹੇਠ ਲਿਖੇ ਗੁਣ ਹਨ –

• ਇਹਨਾਂ ਦੀ ਵਰਤੋਂ ਕਰਨ ਨਾਲ ਸਰੀਰ ਨੂੰ ਸ਼ਕਤੀ ਮਿਲਦੀ ਹੈ ।
• ਭੁੱਖ ਵਧਦੀ ਹੈ ।
• ਪਾਚਨ ਸ਼ਕਤੀ ਤੇਜ਼ ਹੁੰਦੀ ਹੈ ।

ਇਹਨਾਂ ਵਿਚ ਵਿਟਾਮਿਨ ਏ, ਬੀ ਤੇ ਸੀ ਬਹੁਤ ਹੁੰਦੇ ਹਨ । ਇਸ ਤੋਂ ਬਿਨਾਂ ਇਹਨਾਂ ਵਿਚ ਪ੍ਰੋਟੀਨ, ਖਣਿਜ ਲੂਣ, ਲੋਹਾ ਤੇ ਫਾਸਫੋਰਸ ਵੀ ਮਿਲਦੇ ਹਨ !

3. ਸਬਜ਼ੀਆਂ (Vegitables)-ਬੰਦ ਗੋਭੀ, ਪਾਲਕ, ਸਰੋਂ ਦਾ ਸਾਗ, ਮੇਥੀ, ਗਾਜਰ, ਮੂਲੀ, ਸਲਾਦ, ਚੁਕੰਦਰ, ਟਮਾਟਰ, ਆਲੂ, ਮਟਰ, ਕਰੇਲਾ, ਬੈਂਗਣ, ਭਿੰਡੀ, ਫੁੱਲਗੋਭੀ ਅਤੇ ਸ਼ਲਗਮ ਆਦਿ ਮੁੱਖ ਸਬਜ਼ੀਆਂ ਹਨ ।

ਗੁਣ (Advantages)-ਸਬਜ਼ੀਆਂ ਦੇ ਗੁਣ ਇਸ ਪ੍ਰਕਾਰ ਹਨ-

• ਇਹ ਸਰੀਰ ਦੀ ਰੱਖਿਆ ਕਰਦੀਆਂ ਹਨ ।
• ਇਹ ਸਰੀਰ ਨੂੰ ਤੰਦਰੁਸਤ ਬਣਾਈ ਰੱਖਦੀਆਂ ਹਨ ।
• ਇਹ ਲਹੂ ਸਾਫ਼ ਕਰਦੀਆਂ ਹਨ ।
• ਇਹ ਸਰੀਰ ਨੂੰ ਕਮਜ਼ੋਰ ਨਹੀਂ ਹੋਣ ਦਿੰਦੀਆਂ ।

4, ਫਲ (Fruit)-ਅੰਗੂਰ, ਅਮਰੂਦ, ਔਲਾ, ਨਾਰੰਗੀ, ਸੰਤਰਾ, ਮਾਲਟਾ, ਅਨਾਰ, ਮੁਸੰਮੀ, ਨਿੰਬੂ, ਅੰਬ, ਕੇਲਾ, ਸੇਬ, ਨਾਸ਼ਪਤੀ ਅਤੇ ਆਲੂ-ਬੁਖਾਰਾ ਆਦਿ ਫਲਾਂ ਦੀ ਜ਼ਿਆਦਾ ਵਰਤੋਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ।

ਗੁਣ (Advantages)-ਫਲਾਂ ਦੇ ਗੁਣ ਇਸ ਪ੍ਰਕਾਰ ਹਨ-

• ਇਹ ਸਰੀਰ ਦੀ ਸਫ਼ਾਈ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦੇ ਹਨ ।
• ਇਹਨਾਂ ਵਿਚ ਲੋਹਾ, ਲੂਣ ਅਤੇ ਸਾਰੇ ਵਿਟਾਮਿਨ ਹੁੰਦੇ ਹਨ ।
• ਇਹ ਸਰੀਰ ਨੂੰ ਰੋਗਾਂ ਤੋਂ ਬਚਾਉਂਦੇ ਹਨ ।

5. ਸੁੱਕੇ ਮੇਵੇ (Dry Fruits)-ਬਦਾਮ, ਅਖਰੋਟ, ਪਿਸਤਾ, ਕਾਜੂ, ਖਜੂਰ ਤੇ ਮੂੰਗਫਲੀ ਆਦਿ ਸੁੱਕੇ ਮੇਵੇ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਵਿਚ ਕਾਰਬੋਹਾਈਡਰੇਟਸ, ਪ੍ਰੋਟੀਨ ਅਤੇ ਚਰਬੀ ਹੁੰਦੀ ਹੈ ।
ਗੁਣ-

• ਇਹ ਸਰੀਰਕ ਵਾਧੇ ਵਿਚ ਸਹਾਇਕ ਹੁੰਦੇ ਹਨ ।
• ਇਹ ਦਿਮਾਗੀ ਤਾਕਤ ਨੂੰ ਵਧਾਉਂਦੇ ਹਨ ।

6. ਦੁੱਧ ਅਤੇ ਉਸ ਤੋਂ ਬਣਨ ਵਾਲੇ ਪਦਾਰਥ (Milk)-ਮੱਖਣ, ਘਿਓ, ਦਹੀਂ, ਪਨੀਰ ਤੇ ਲੱਸੀ ਆਦਿ ਦੁੱਧ ਤੋਂ ਤਿਆਰ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਵਿਚ ਭੋਜਨ ਦੇ ਸਾਰੇ ਤੱਤ ਹੁੰਦੇ ਹਨ । ਇਹ ਸਰੀਰ ਵਿਚ ਗਰਮੀ ਤੇ ਸ਼ਕਤੀ ਪੈਦਾ ਕਰਦੇ ਹਨ । ਇਹ ਸਰੀਰ ਦਾ ਵਾਧਾ ਕਰਦੇ ਹਨ ਅਤੇ ਟੁੱਟੇ-ਭੱਜੇ ਤੰਤੂਆਂ ਦੀ ਮੁਰੰਮਤ ਵੀ ਕਰਦੇ ਹਨ । ਇਹ ਸਾਫ਼ ਖ਼ੂਨ ਵੀ ਤਿਆਰ ਕਰਦੇ ਹਨ ।

7. ਮੀਟ, ਮੱਛੀ ਤੇ ਆਂਡੇ ਆਦਿ (Meat, Fish and Eggs)-ਮੀਟ, ਮੱਛੀ ਤੇ ਆਂਡਿਆਂ ਦੀ ਵਰਤੋਂ ਵੀ ਆਮ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਇਹਨਾਂ ਵਿਚ ਪ੍ਰੋਟੀਨ, ਚਰਬੀ, ਕੈਲਸ਼ੀਅਮ, ਲੋਹਾ ਅਤੇ ਵਿਟਾਮਿਨ ‘ਏ’ ‘ਬੀ’ ਤੇ ‘ਡੀ’ ਬਹੁਤ ਮਾਤਰਾ ਵਿਚ ਹੁੰਦੇ ਹਨ । ਇਹ ਸਰੀਰ ਦੇ ਵਾਧੇ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦੇ ਹਨ ਅਤੇ ਇਸ ਨੂੰ ਕਈ ਰੋਗਾਂ ਤੋਂ ਬਚਾਉਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 5.
ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਅਤੇ ਚਰਬੀ ਸਾਡੇ ਲਈ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹਨ ? (Why Carbohydrates and fats are necessary for us ?) .
ਉੱਤਰ-
ਕਾਰਬੋਹਾਈਡਰੇਟਸ (Carbohydrates)-ਇਹ ਸਾਨੂੰ ਸ਼ੱਕਰ ਦੇ ਰੂਪ ਵਿਚ ਮਿਲਣ ਵਾਲੇ ਅਤੇ ਸਟਾਰਚ ਦੇ ਰੂਪ ਵਿਚ ਮਿਲਣ ਵਾਲੇ ਤੱਤਾਂ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ, ਜਿਵੇਂਅੰਬ, ਗੰਨੇ ਦਾ ਰਸ, ਗੁੜ, ਸ਼ੱਕਰ, ਅੰਗੂਰ, ਖਜੂਰ, ਗਾਜਰ, ਸੁੱਕੇ ਮੇਵੇ ਅਤੇ ਕਣਕ, ਮੱਕੀ, ਜੋਂ, ਜੁਆਰ, ਸ਼ਕਰਕੰਦੀ, ਅਖਰੋਟ ਤੇ ਕੇਲੇ ਆਦਿ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ ।
ਜ਼ਰੂਰਤ (Need)-

• ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਸਾਡੇ ਸਰੀਰ ਨੂੰ ਗਰਮੀ ਤੇ ਸ਼ਕਤੀ ਦਿੰਦੇ ਹਨ ।
• ਇਹ ਸਰੀਰ ਵਿਚ ਚਰਬੀ ਪੈਦਾ ਕਰਦੇ ਹਨ ।
• ਇਹ ਚਰਬੀ ਨਾਲੋਂ ਸਸਤੇ ਹੁੰਦੇ ਹਨ ।
• ਗ਼ਰੀਬ ਤੇ ਘੱਟ ਆਮਦਨੀ ਵਾਲੇ ਲੋਕ ਵੀ ਇਸ ਦੀ ਵਰਤੋਂ ਕਰ ਸਕਦੇ ਹਨ ।

ਚਿਕਨਾਈ (Fat) -ਇਹ ਸਾਨੂੰ ਬਨਸਪਤੀ ਅਤੇ ਪਸ਼ੂਆਂ ਤੋਂ ਪ੍ਰਾਪਤ ਹੋਣ ਵਾਲੀ ਚਰਬੀ ਤੋਂ ਮਿਲਦੀ ਹੈ । ਸਬਜ਼ੀਆਂ, ਸੁੱਕੇ ਮੇਵਿਆਂ, ਫਲਾਂ, ਅਖਰੋਟ, ਬਦਾਮ, ਮੂੰਗਫਲੀ, ਬੀਜਾਂ ਦੇ ਤੇਲ ਅਤੇ ਘਿਉ, ਦੁੱਧ, ਮੱਖਣ, ਮੱਛੀ ਦਾ ਤੇਲ, ਆਂਡੇ ਆਦਿ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ।
ਜ਼ਰੂਰਤ (Need)-

• ਚਰਬੀ ਸਰੀਰ ਵਿਚ ਸ਼ਕਤੀ ਪੈਦਾ ਕਰਦੀ ਹੈ ।
• ਇਸ ਦੇ ਰਾਹੀਂ ਸਰੀਰ ਵਿਚ ਗਰਮੀ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ।
• ਇਹ ਸਰੀਰ ਵਿਚ ਬਾਲਣ ਦਾ ਕੰਮ ਕਰਦੀ ਹੈ ।
• ਚਰਬੀ ਰਾਹੀਂ ਸਰੀਰ ਮੋਟਾ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਵੱਖ-ਵੱਖ ਖਣਿਜ ਲੂਣ ਸਾਡੇ ਸਰੀਰ ਲਈ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹਨ ? (Why the different Mineral Salts are useful for our body ?)
ਉੱਤਰ-
ਸਾਡੇ ਸਰੀਰ ਵਿਚ ਕੈਲਸ਼ੀਅਮ, ਫਾਸਫੋਰਸ, ਸੋਡੀਅਮ, ਲੋਹਾ, ਮੈਗਨੀਸ਼ੀਅਮ, ਪੋਟਾਸ਼ੀਅਮ, ਆਇਉਡੀਨ, ਕਲੋਰੀਨ ਅਤੇ ਗੰਧਕ ਜਿਹੇ ਤੱਤਾਂ ਦੀ ਬਹੁਤ ਜ਼ਰੂਰਤ ਹੈ । ਸਾਡੇ ਭੋਜਨ ਵਿਚ ਇਹਨਾਂ ਖਣਿਜ ਲੂਣਾਂ ਦਾ ਹੋਣਾ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ । ਇਹ ਖਣਿਜ ਲੂਣ ਸਾਡੀ ਤੰਦਰੁਸਤੀ ਲਈ ਬਹੁਤ ਹੀ ਜ਼ਰੂਰੀ ਹੈ ।

ਇਹਨਾਂ ਖਣਿਜ ਲੂਣਾਂ ਅਤੇ ਸਾਡੇ ਸਰੀਰ ਲਈ ਇਹਨਾਂ ਦੀ ਉਪਯੋਗਿਤਾ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਹੇਠਾਂ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ –
1. ਕੈਲਸ਼ੀਅਮ ਅਤੇ ਫ਼ਾਸਫ਼ੋਰਸ (Calcium and Phosphorus)-ਇਹ ਖਣਿਜ ਲੂਣ, ਦੁੱਧ, ਦਹੀਂ, ਪਨੀਰ, ਆਂਡੇ, ਮੱਛੀ, ਮੀਟ, ਹਰੀਆਂ ਸਬਜ਼ੀਆਂ, ਤਾਜ਼ੇ ਫਲ, ਦਲੀਏ, ਦਾਲਾਂ ਅਤੇ ਬਦਾਮਾਂ ਵਿਚ ਬਹੁਤ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਨਾਲ ਸਰੀਰ ਦਾ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ, ਦੰਦ ਅਤੇ ਹੱਡੀਆਂ ਦਾ ਨਿਰਮਾਣ ਹੁੰਦਾ ਹੈ । ਇਹ ਦਿਲ ਤੇ ਦਿਮਾਗ਼ ਲਈ ਲਾਭਦਾਇਕ ਹੁੰਦੇ ਹਨ ।

2. ਲੋਹਾ (Iron)-ਲੋਹਾ ਹਰੀਆਂ ਸਬਜ਼ੀਆਂ, ਫਲਾਂ, ਅਨਾਜਾਂ, ਆਂਡਿਆਂ ਤੇ ਮੀਟ ਵਿਚ ਜ਼ਿਆਦਾ ਹੁੰਦਾ ਹੈ । ਇਹ ਨਵਾਂ ਖ਼ੂਨ ਪੈਦਾ ਕਰਦਾ ਹੈ ਤੇ ਭੁੱਖ ਵਧਾਉਂਦਾ ਹੈ । ਇਹ ਖੂਨ ਸਾਫ਼ ਕਰਦਾ ਹੈ ।

3. ਸੋਡੀਅਮ (Sodium-ਇਹ ਆਮ ਤੌਰ’ ਤੇ ਭਿੰਡੀ, ਅੰਜੀਰ, ਨਾਰੀਅਲ, ਆਲੂ-ਬੁਖਾਰਾ, ਲਸਣ, ਮੂਲੀ, ਗਾਜਰ ਅਤੇ ਸ਼ਲਗਮ ਆਦਿ ਵਿਚ ਮਿਲਦਾ ਹੈ । ਇਹ ਮਿਹਦੇ ਤੇ ਗੁਰਦੇ ਦੇ ਕਈ ਤਰ੍ਹਾਂ ਦੇ ਰੋਗਾਂ ਨੂੰ ਰੋਕਦਾ ਹੈ ।

4. ਪੋਟਾਸ਼ੀਅਮ (Potasium-ਇਹ ਨਾਸ਼ਪਾਤੀ, ਆਲੂ-ਬੁਖਾਰਾ, ਨਾਰੀਅਲ, ਨਿੰਬੂ, ਅੰਜੀਰ, ਬੰਦ ਗੋਭੀ, ਕਰੇਲੇ, ਮੂਲੀ, ਸ਼ਲਗਮ ਆਦਿ ਵਿਚ ਮਿਲਦਾ ਹੈ । ਇਹ ਜਿਗਰ ਤੇ ਦਿਲ ਨੂੰ ਤਾਕਤ ਦਿੰਦਾ ਹੈ ਤੇ ਕਬਜ਼ ਦੂਰ ਕਰਦਾ ਹੈ ।

5. ਆਇਓਡੀਨ (Iodean)-ਇਹ ਸਮੁੰਦਰੀ ਮੱਛੀ, ਸਮੁੰਦਰੀ ਲੂਣ, ਪਿਆਜ਼, ਲਸਣ, ਟਮਾਟਰ, ਸੇਬ, ਪਾਲਕ, ਗਾਜਰ ਅਤੇ ਦੁੱਧ ਆਦਿ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ।
ਇਸ ਨਾਲ ਸਰੀਰ ਦਾ ਭਾਰ ਤੇ ਤਾਕਤ ਵਧਦੀ ਹੈ । ਇਸ ਦੀ ਕਮੀ ਨਾਲ ਗਿਲੜ ਦਾ ਰੋਗ ਹੋ ਜਾਂਦਾ ਹੈ ।

6. ਮੈਗਨੀਸ਼ੀਅਮ (Magnesium)-ਇਹ ਨਾਰੰਗੀ, ਸੰਤਰਾ, ਅੰਜੀਰ, ਆਲੂ-ਬੁਖਾਰਾ, ਕਣਕ, ਟਮਾਟਰ ਅਤੇ ਪਾਲਕ ਆਦਿ ਵਿਚ ਬਹੁਤ ਮਿਲਦਾ ਹੈ । ਇਹ ਚਮੜੀ ਦੇ ਰੋਗ ਰੋਕਦਾ ਹੈ ਅਤੇ ਪੱਠਿਆਂ ਨੂੰ ਮਜ਼ਬੂਤ ਬਣਾਉਂਦਾ ਹੈ ।

7. ਗੰਧਕ (Sulphur)-ਇਹ ਪਿਆਜ਼, ਮੂਲੀ, ਬੰਦ-ਗੋਭੀ ਆਦਿ ਵਿਚ ਬਹੁਤ ਹੁੰਦੀ ਹੈ । ਇਹ ਨਹੁੰਆਂ ਅਤੇ ਵਾਲਾਂ ਨੂੰ ਵਧਾਉਂਦੀ ਹੈ । ਚਮੜੀ ਨੂੰ ਸਾਫ਼ ਰੱਖਦੀ ਹੈ।

8. ਕਲੋਰੀਨ (Chlorine-ਇਹ ਪਿਆਜ਼, ਪਾਲਕ, ਮੂਲੀ, ਗਾਜਰ, ਬੰਦ ਗੋਭੀ ਅਤੇ ਟਮਾਟਰ ਵਿਚ ਬਹੁਤ ਹੁੰਦੀ ਹੈ । ਇਹ ਸਰੀਰ ਵਿਚੋਂ ਗੰਦੇ ਪਦਾਰਥ ਬਾਹਰ ਕੱਢਦੀ ਹੈ । ਇਹ ਸਰੀਰ ਦੀ ਸਫ਼ਾਈ ਕਰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 7.
ਹੇਠ ਲਿਖਿਆਂ ‘ਤੇ ਨੋਟ ਲਿਖੋ
(ੳ) ਸੰਤੁਲਿਤ ਭੋਜਨ ਅਤੇ ਪ੍ਰੋਟੀਨ
(ੲ) ਕੈਲਸ਼ੀਅਮ
(ਸ) ਫ਼ਾਸਫੋਰਸ
(ਹ) ਵਿਟਾਮਿਨਾਂ ਦੀ ਕਮੀ ।
(ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ-4) (Write down a brief note on the following
(a) Balance diet
(b) Proteins
(c) Calcium
(d) Phosphorus
(e) Lack of Vitamins.)
ਉੱਤਰ-
(ੳ) ਸੰਤੁਲਿਤ ਭੋਜਨ (Balance diet) -ਜਿਸ ਭੋਜਨ ਵਿਚ ਬਹੁਤ ਸਾਰੇ ਤੱਤ ਉੱਚਿਤ ਮਾਤਰਾ ਵਿਚ ਹੋਣ ਅਤੇ ਜਿਹੜਾ ਸਰੀਰ ਦੀਆਂ ਸਾਰੀਆਂ ਲੋੜਾਂ ਦੀ ਪੂਰਤੀ ਕਰਨ ਦੇ ਯੋਗ ਹੋਵੇ, ਉਸ ਨੂੰ ਸੰਤੁਲਿਤ ਭੋਜਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਸੰਤੁਲਿਤ ਭੋਜਨ ਵਿਚ ਪ੍ਰੋਟੀਨ, ਕਾਰਬੋਹਾਈਡਰੇਟਸ, ਚਰਬੀ, ਖਣਿਜ ਲੂਣ, ਵਿਟਾਮਿਨ ਤੇ ਪਾਣੀ ਉੱਚਿਤ ਮਾਤਰਾ ਵਿਚ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ । ਸਰੀਰ ਦੇ ਪੂਰੇ ਵਿਕਾਸ ਲਈ, ਉਸ ਨੂੰ ਰੋਗਾਂ ਤੋਂ ਬਚਾਉਣ ਲਈ ਅਤੇ ਚੰਗੀ ਸਿਹਤ ਵਾਸਤੇ ਸਾਨੂੰ ਸੰਤੁਲਿਤ ਭੋਜਨ ਦੀ ਵਰਤੋਂ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ । ਕੋਈ ਵੀ ਇਕੱਲਾ ਭੋਜਨ ਪਦਾਰਥ ਸੰਤੁਲਿਤ ਭੋਜਨ ਨਹੀਂ । ਸਿਰਫ਼ ਦੁੱਧ ਹੀ ਇਕ ਅਜਿਹਾ ਪਦਾਰਥ ਹੈ ਜਿਸ ਵਿਚ ਸਾਰੇ ਪੌਸ਼ਟਿਕ ਤੱਤ ਮਿਲਦੇ ਹਨ ।

(ਅ) ਪ੍ਰੋਟੀਨ (Protein) -ਪ੍ਰੋਟੀਨ, ਕਾਰਬਨ, ਹਾਈਡਰੋਜਨ, ਆਕਸੀਜਨ ਅਤੇ ਗੰਧਕ ਤੇ ਰਸਾਇਣਿਕ ਮਿਸ਼ਰਨ ਤੋਂ ਬਣਦੇ ਹਨ । ਇਹ ਦੋ ਤਰ੍ਹਾਂ ਤੇ ਹੁੰਦੇ ਹਨ-ਪਸ਼ੂ ਪ੍ਰੋਟੀਨ ਅਤੇ ਬਨਸਪਤੀ ਪ੍ਰੋਟੀਨ | ਪਸ਼ੂ ਪ੍ਰੋਟੀਨ ਮੀਟ, ਮੱਛੀ, ਆਂਡੇ, ਦੁੱਧ ਅਤੇ ਪਨੀਰ ਆਦਿ ਤੋਂ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਹਨ | ਬਨਸਪਤੀ ਪ੍ਰੋਟੀਨ ਦਾਲਾਂ, ਮਟਰ, ਫੁੱਲ ਗੋਭੀ, ਸੋਇਆਬੀਨ, ਛੋਲੇ, ਪਾਲਕ, ਹਰੀ ਮਿਰਚ, ਪਿਆਜ਼ ਅਤੇ ਸੁੱਕੇ ਮੇਵਿਆਂ ਵਿਚ ਮਿਲਦੇ ਹਨ । ਪ੍ਰੋਟੀਨ ਸਰੀਰ ਵਿਚ ਸ਼ਕਤੀ ਪੈਦਾ ਕਰਦੇ ਹਨ । ਇਹ ਹੱਡੀਆਂ ਦੇ ਨਿਰਮਾਣ ਤੇ ਭੋਜਨ ਪਚਾਉਣ ਵਿਚ ਮਦਦ ਕਰਦੇ ਹਨ । ਇਹਨਾਂ ਦੀ ਘੱਟ ਵਰਤੋਂ ਨਾਲ ਸਰੀਰ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦਾ ਹੈ ।

(ੲ) ਕੈਲਸ਼ੀਅਮ (Calcium)-ਕੈਲਸ਼ੀਅਮ ਦੁੱਧ, ਦਹੀਂ, ਪਨੀਰ, ਆਂਡੇ, ਮੱਛੀ, ਮੀਟ, ਹਰੀਆਂ ਸਬਜ਼ੀਆਂ, ਤਾਜ਼ੇ ਫਲਾਂ, ਲੂਣ, ਦਲੀਏ, ਦਾਲਾਂ ਅਤੇ ਬਦਾਮਾਂ ਵਿਚ ਬਹੁਤ ਹੁੰਦਾ ਹੈ । ਇਸ ਨਾਲ ਸਰੀਰ ਦਾ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ । ਦੰਦਾਂ ਤੇ ਹੱਡੀਆਂ ਲਈ ਇਹ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੈ । ਇਹ ਦਿਲ ਤੇ ਦਿਮਾਗ਼ ਲਈ ਬਹੁਤ ਲਾਭਦਾਇਕ ਹੁੰਦਾ ਹੈ । ਇਸ ਦੀ ਘਾਟ ਨਾਲ ਹੱਡੀਆਂ ਵਿੰਗੀਆਂ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਦੰਦ ਵੀ ਡਿੱਗ ਜਾਂਦੇ ਹਨ ।

(ਸ) ਫ਼ਾਸਫੋਰਸ (Phosphorus)-ਫ਼ਾਸਫੋਰਸ ਜ਼ਿਆਦਾਤਰ ਦੁੱਧ, ਦਹੀਂ, ਪਨੀਰ, ਆਂਡੇ, ਮੱਛੀ, ਮੀਟ, ਹਰੀਆਂ ਸਬਜ਼ੀਆਂ ਤੇ ਤਾਜ਼ੇ ਫਲਾਂ ਵਿਚ ਹੁੰਦੀ ਹੈ । ਇਸ ਨਾਲ ਵੀ ਹੱਡੀਆਂ ਤੇ ਦੰਦ ਮਜ਼ਬੂਤ ਹੁੰਦੇ ਹਨ । ਇਸ ਦੀ ਘਾਟ ਨਾਲ ਹੱਡੀਆਂ ਵਿੰਗੀਆਂ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।

(ਹ) ਵਿਟਾਮਿਨਾਂ ਦੀ ਕਮੀ (Lack of Vitamins)-ਮੁੱਖ ਵਿਟਾਮਿਨ ਛੇ ਹਨ-ਏ, ਬੀ, ਸੀ, ਡੀ, ਈ ਅਤੇ ਕੇ ! ਇਹਨਾਂ ਵਿਟਾਮਿਨਾਂ ਦੀ ਕਮੀ ਨਾਲ ਸਰੀਰ ਵਿਚ ਕਈ ਪ੍ਰਕਾਰ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਉਤਪੰਨ ਹੁੰਦੀਆਂ ਹਨ । ਇਸ ਦਾ ਵੇਰਵਾ ਹੇਠਾਂ ਕੂਮ ਅਨੁਸਾਰ ਦਿੱਤਾ ਗਿਆ ਹੈ –

1. ਵਿਟਾਮਿਨ ਏ (Vitamin A)

• ਇਸਦੀ ਕਮੀ ਦੇ ਕਾਰਨ ਅੰਧਰਾਤਾ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਗਲੇ ਅਤੇ ਨੱਕ ਦੇ ਰੋਗ ਲੱਗ ਜਾਂਦੇ ਹਨ ।
• ਫੇਫੜੇ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੇ ਹਨ ।
• ਚਮੜੀ ਦੇ ਰੋਗ ਲੱਗ ਜਾਂਦੇ ਹਨ ।
• ਛੂਤ ਦੇ ਰੋਗ ਲੱਗ ਜਾਂਦੇ ਹਨ ।

2. ਵਿਟਾਮਿਨ ਬੀ (Vitamin B)

• ਭੁੱਖ ਦਾ ਨਾ ਲੱਗਣਾ |
• ਚਮੜੀ ਦੇ ਰੋਗਾਂ ਦਾ ਪੈਦਾ ਹੋਣਾ ।
• ਵਾਲਾਂ ਦਾ ਝੜਨਾ ।
• ਜੀਭ ਦੇ ਛਾਲਿਆਂ ਦਾ ਪੈ ਜਾਣਾ ।
• ਖੂਨ ਦਾ ਘੱਟ ਹੋਣਾ ।

3. ਵਿਟਾਮਿਨ ਸੀ (Vitamin C)

• ਹੱਡੀਆਂ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਜ਼ਖ਼ਮਾਂ ਦਾ ਛੇਤੀ ਨਾ ਭਰਨਾ ।
• ਅੱਖਾਂ ਵਿਚ ਮੋਤੀਆ ਉਤਰ ਆਉਣਾ ।
• ਹੱਥ-ਪੈਰ ਸੁੱਜਣ ਲੱਗ ਪੈਂਦੇ ਹਨ ।
• ਇਸ ਦੀ ਘਾਟ ਦੇ ਕਾਰਨ ਸਕਰਵੀ ਦਾ ਰੋਗ ਲੱਗ ਜਾਂਦਾ ਹੈ ।

4. ਵਿਟਾਮਿਨ ਡੀ (Vitamin D)

• ਹੱਡੀਆਂ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਮਿਰਗੀ ਤੇ ਸੋਕੜੇ ਦਾ ਰੋਗ ਵੱਧ ਜਾਂਦਾ ਹੈ ।
• ਹੱਡੀਆਂ ਟੇਢੀਆਂ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਮਾਸ-ਪੇਸ਼ੀਆਂ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।

5. ਵਿਟਾਮਿਨ ਈ (vitamin E)

• ਇਸ ਦੀ ਘਾਟ ਕਾਰਨ ਨਾਮਰਦੀ ਅਤੇ ਬਾਂਝਪਨ ਦੇ ਰੋਗ ਲੱਗ ਜਾਂਦੇ ਹਨ ।
• ਫੋੜੇ ਫਿਨਸੀਆਂ ਨਿਕਲ ਆਉਂਦੇ ਹਨ ।
• ਸਰੀਰ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦਾ ਹੈ ।

6. ਵਿਟਾਮਿਨ ਕੇ (Vitamin K)

• ਚਮੜੀ ਦੇ ਰੋਗ ਲੱਗ ਜਾਂਦੇ ਹਨ ।
• ਜ਼ਖ਼ਮਾਂ ਵਿਚ ਵਗਦਾ ਖੂਨ ਛੇਤੀ ਬੰਦ ਨਹੀਂ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਪ੍ਰੋਟੀਨ, ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਅਤੇ ਚਿਕਨਾਈ ਦੀ ਪ੍ਰਾਪਤੀ ਦੇ ਕੀ ਸਾਧਨ ਹਨ ਅਤੇ ਇਹਨਾਂ ਦੀ ਉੱਚਿਤ ਮਾਤਰਾ ਕਿੰਨੀ ਲੈਣੀ ਚਾਹੀਦੀ ਹੈ ?[ ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ-2] (What are the main sources of Proteins, Carbohydrates and Fats. How much quantities we should take of these ?)
ਉੱਤਰ-
(ਉ) ਪ੍ਰੋਟੀਨ (Proteins)- ਪ੍ਰੋਟੀਨ, ਕਾਰਬਨ, ਹਾਈਡਰੋਜਨ, ਆਕਸੀਜਨ, ਨਾਈਟਰੋਜਨ, ਗੰਧਕ ਅਤੇ ਫਾਸਫੋਰਸ ਦੇ ਰਸਾਇਣਿਕ ਮੇਲ ਨਾਲ ਬਣਿਆ ਮਿਸ਼ਰਿਤ ਪਦਾਰਥ ਹੈ । ਪ੍ਰੋਟੀਨ ਦੋ ਪ੍ਰਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ-ਬਨਸਪਤੀ ਪ੍ਰੋਟੀਨ ਅਤੇ ਪਸ਼ੂ ਪ੍ਰੋਟੀਨ ਬਨਸਪਤੀ ਪ੍ਰੋਟੀਨ ਸੋਇਆਬੀਨ, ਮੂੰਗਫਲੀ, ਬਾਦਾਮ, ਅਖਰੋਟ, ਕਣਕ, ਬਾਜਰਾ, ਮੱਕੀ ਆਦਿ ਵਿਚ ਪਾਈ ਜਾਂਦੀ ਹੈ । ਪਸ਼ੂ ਪ੍ਰੋਟੀਨ ਮਾਸ, ਮੱਛੀ, ਆਂਡਾ, ਦੁੱਧ, ਪਨੀਰ ਆਦਿ ਵਿਚ ਪਾਈ ਜਾਂਦੀ ਹੈ। ਇਕ ਸਾਧਾਰਨ ਵਿਅਕਤੀ ਨੂੰ ਪ੍ਰਤੀ-ਦਿਨ 70 ਤੋਂ 100 ਗਰਾਮ ਤਕ ਪ੍ਰੋਟੀਨ ਦੀ ਮਾਤਰਾ ਲੈਣੀ ਚਾਹੀਦੀ ਹੈ ।

(ਅ) ਕਾਰਬੋਹਾਈਡਰੇਟਸ (Carbohydrates) ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਸਰੀਰ ਨੂੰ ਗਰਮੀ ਅਤੇ ਸ਼ਕਤੀ ਪ੍ਰਦਾਨ ਕਰਦੇ ਹਨ | ਭਾਰਤੀਆਂ ਦੇ ਭੋਜਨ ਵਿਚ 70-80% ਤਕ ਇਹੀ ਤੱਤ ਪਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਕ ਸਾਧਾਰਨ ਵਿਅਕਤੀ ਦੇ ਰੋਜ਼ਾਨਾ ਭੋਜਨ ਵਿਚ 400 ਤੋਂ 700 ਗਰਾਮ ਤਕ ਕਾਰਬੋਹਾਈਡਰੇਟ ਦੀ ਮਾਤਰਾ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।

(ਈ) ਚਰਬੀ ਜਾਂ ਚਿਕਨਾਈ (Fat) -ਚਰਬੀ ਸਰੀਰ ਨੂੰ ਸ਼ਕਤੀ ਦਿੰਦੀ ਹੈ। ਚਰਬੀ ਦੋ ਤਰ੍ਹਾਂ ਦੀ ਹੁੰਦੀ ਹੈ-ਬਨਸਪਤੀ ਚਰਬੀ ਤੇ ਪਸ਼ੂ ਚਰਬੀ | ਬਨਸਪਤੀ ਚਰਬੀ ਸਰੋਂ, ਮੁੰਗਫਲੀ, ਅਖਰੋਟ ਆਦਿ ਵਿਚ ਪਾਈ ਜਾਂਦੀ ਹੈ । ਓ, ਮੱਖਣ, ਦੁੱਧ, ਮੱਛੀ, ਮਾਸ, ਆਂਡੇ ਆਦਿ ਪਸ਼ੂ ਬਨਸਪਤੀ ਦੇ ਮੁੱਖ ਸੋਮੇ ਹਨ । ਇਕ ਸਾਧਾਰਨ ਵਿਅਕਤੀ ਦੇ ਭੋਜਨ ਵਿਚ ਪ੍ਰਤੀ ਦਿਨ ਲਗਭਗ 50 ਤੋਂ 75 ਗਰਾਮ ਤਕ ਚਰਬੀ ਦੀ ਮਾਤਰਾ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 9.
ਫੋਕਟ ਸਾਡੇ ਸਰੀਰ ਲਈ ਬੜੇ ਹੀ ਲਾਭਦਾਇਕ ਹਨ, ਕਿਵੇਂ ? (Waste Product are useful for us. How ?) ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ-
ਉੱਤਰ-
ਫੋਕਟ- ਸਰੀਰਕ ਵਾਧੇ ਤੇ ਵਿਕਾਸ ਲਈ ਅਸੀਂ ਸੰਤੁਲਿਤ ਭੋਜਨ ਖਾਂਦੇ ਹਾਂ ਜਿਨ੍ਹਾਂ ਵਿਚ ਭੋਜਨ ਦੇ ਸਾਰੇ ਤੱਤ ਠੀਕ ਮਾਤਰਾ ਵਿਚ ਹੋਣ ਜਿਵੇਂ ਕਿ ਪ੍ਰੋਟੀਨ, ਕਾਰਬੋਹਾਈਡਰੇਟਸ, ਥੰਧਿਆਈ, ਖਣਿਜ ਲੂਣ, ਪਾਣੀ ਤੇ ਵਿਟਾਮਿਨਜ਼ | ਪਰ ਜੇ ਇਹ ਸਾਰੇ ਤੱਤ ਨਿਰੋਲ ਹੀ ਲਏ ਜਾਣ ਤਾਂ ਇਹਨਾਂ ਦਾ ਫਾਇਦਾ ਨਹੀਂ ਹੋ ਸਕਦਾ | ਸਰੀਰ ਵਿਚੋਂ ਜਿਸ ਗੰਦਗੀ ਨੇ ਬਾਹਰ ਨਿਕਲਣਾ ਹੈ, ਉਹ ਵੀ ਨਹੀਂ ਨਿਕਲ ਸਕੇਗੀ, ਮਿਹਦੇ ਤੇ ਅੰਤੜੀਆਂ ਦੀਆਂ ਅੰਦਰਲੀਆਂ ਝੱਲੀਆਂ ਨਾਲ ਜੰਮ ਜਾਵੇਗੀ ।

ਇਸ ਲਈ ਇਹਨਾਂ ਸਾਰੇ ਤੱਤਾਂ ਨੂੰ ਜਾਂ ਇਕੱਲੇ ਨੂੰ ਨਿਰੋਲ ਕਿਸਮ ਨਹੀਂ ਕਿਹਾ ਜਾ ਸਕਦਾ ਅਤੇ ਕੱਚੀਆਂ ਸਬਜ਼ੀਆਂ ਜਿਵੇਂ ਕਿ ਮੂਲੀ, ਸ਼ਲਗਮ, ਗਾਜਰ, ਟਮਾਟਰ, ਖੀਰਾ, ਸਲਾਦ, ਛਿਲਕੇ ਵਾਲੇ ਅਨਾਜ ਜਿਵੇਂ ਕਣਕ, ਛੋਲਿਆਂ ਦਾ ਆਟਾ, ਖਾਣ ਵੇਲੇ ਆਟਾ ਛਾਣ ਕੇ ਛਿਲਕੇ ਸੁੱਟਣੇ ਨਹੀਂ ਚਾਹੀਦੇ । ਮਿਹਦੇ ਤੇ ਅੰਤੜੀਆਂ ਵਿਚ ਜਾ ਕੇ ਇਹ ਛਿੱਲੜ ਸਫ਼ਾਈ ਵਾਲੇ ਬੁਰਸ਼ ਦੀ ਤਰ੍ਹਾਂ ਕੰਮ ਦਿੰਦੇ ਹਨ । ਸਰੀਰ ਤਾਜ਼ਾ ਦਮ ਰਹਿੰਦਾ ਹੈ । ਇਸ ਲਈ ਖਾਣ ਵਾਲੀਆਂ ਚੀਜ਼ਾਂ ਨਾਲ ਰੇਸ਼ੇ ਹੋਣੇ ਜ਼ਰੂਰੀ ਹਨ ।

ਪ੍ਰਸ਼ਨ 10.
ਕੈਲੋਰੀ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਭੋਜਨ ਦਾ ਤੱਤ ਨਾਪਣ ਦੀ ਸਭ ਤੋਂ ਛੋਟੀ ਇਕਾਈ ਨੂੰ ਕੈਲੋਰੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ।

ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Long Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਵਿਟਾਮਿਨ ਕਿੰਨੀ ਤਰ੍ਹਾਂ ਦੇ ਹੁੰਦੇ ਹਨ ? ਇਹਨਾਂ ਦੇ ਮੁੱਖ ਕੰਮ ਦੱਸੋ । ਇਹ ਕਿਹੜੇ-ਕਿਹੜੇ ਭੋਜਨ ਪਦਾਰਥਾਂ ਵਿਚ ਮਿਲਦੇ ਹਨ ? (Give the types of Vitamins ? Describe their main functions and sources.)
ਜਾ
ਹੇਠ ਲਿਖੇ ਵਿਟਾਮਿਨਾਂ ਦੀ ਪ੍ਰਾਪਤੀ ਦੇ ਸੋਮੇ ਅਤੇ ਲਾਭ ਦੱਸੋ । ਵਿਟਾਮਿਨ ਏ, ਬੀ, ਸੀ, ਡੀ ਅਤੇ ਕੇ । (ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ-6) (Write down the sources of the following Vitamins and their uses. Vitamins A, B, C, D and K.)
ਉੱਤਰ-
ਵਿਟਾਮਿਨ (Vitamins)-ਹੁਣ ਤਕ ਬਹੁਤ ਸਾਰੇ ਵਿਟਾਮਿਨਾਂ ਦੀ ਖੋਜ ਹੋ ਚੁੱਕੀ ਹੈ, ਪਰ ਪ੍ਰਸਿੱਧ ਵਿਟਾਮਿਨ ਏ, ਬੀ, ਸੀ, ਡੀ, ਈ ਅਤੇ ਕੇ ਹੀ ਮੰਨੇ ਜਾਂਦੇ ਹਨ।
ਇਹਨਾਂ ਵਿਚੋਂ ਹਰ ਵਿਟਾਮਿਨ ਦਾ ਮੁੱਖ ਕੰਮ ਅਤੇ ਇਹ ਕਿਹੜੇ ਭੌਜਨ ਪਦਾਰਥਾਂ ਵਿਚੋਂ ਮਿਲਦਾ ਹੈ, ਵਰਣਨ ਹੇਠਾਂ ਦਿੱਤਾ ਗਿਆ ਹੈ

1. ਵਿਟਾਮਿਨ ਏ (Vitamin A)ਵਿਟਾਮਿਨ ‘ਏ’ ਦੇ ਕੰਮ ਹੇਠ ਲਿਖੇ ਹਨ-

• ਇਸ ਨਾਲ ਅੱਖਾਂ ਦੀ ਰੌਸ਼ਨੀ ਵਧਦੀ ਹੈ |
• ਭੁੱਖ ਵਧਦੀ ਹੈ ।
• ਪਾਚਨ ਸ਼ਕਤੀ ਠੀਕ ਰਹਿੰਦੀ ਹੈ ।
• ਇਹ ਵਿਟਾਮਿਨ ਸਰੀਰ ਨੂੰ ਵਧਾਉਣ ਤੇ ਮਜ਼ਬੂਤ ਕਰਨ ਵਿਚ ਮੱਦਦੇ ਦਿੰਦਾ ਹੈ ।

ਘਾਟ ਨਾਲ ਹਾਨੀਆਂ (Abuses)-

• ਇਸ ਦੀ ਘਾਟ ਦੇ ਕਾਰਨ ਅੰਧਰਾਤਾ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਚਮੜੀ ਖੁਸ਼ਕ ਹੋ ਜਾਂਦੀ ਹੈ ।
• ਗਲਾ, ਨੱਕ ਤੇ ਅੱਖਾਂ ਤੇ ਚਮੜੀ ਨੂੰ ਹਰ ਛੂਤ ਦੀ ਬਿਮਾਰੀ ਛੇਤੀ ਲੱਗਦੀ ਹੈ |
• ਸਰੀਰ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦਾ ਹੈ ਤੇ ਵਾਧਾ ਰੁਕ ਜਾਂਦਾ ਹੈ ।
• ਫੇਫੜੇ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੇ ਹਨ ।

ਪ੍ਰਾਪਤੀ ਸੋਮਾ (Sources) -ਇਹ ਜ਼ਿਆਦਾ ਦੁੱਧ, ਦਹੀਂ, ਮੱਖਣ, ਪਨੀਰ, ਆਂਡੇ, ਮੱਛੀ, ਤਾਜ਼ੀਆਂ ਸਬਜ਼ੀਆਂ ਤੇ ਪੱਤਿਆਂ ਜਿਵੇਂ-ਪਾਲਕ, ਗਾਜਰ, ਬੰਦ-ਗੋਭੀ, ਟਮਾਟਰ, ਕੇਲਾ, ਸੰਤਰਾ, ਅੰਬ, ਪਪੀਤਾ, ਅਨਾਨਾਸ ਆਦਿ ਵਿਚੋਂ ਮਿਲਦਾ ਹੈ ।

2. ਵਿਟਾਮਿਨ ਬੀ (Vitamin B) ਵਿਟਾਮਿਨ ‘ਬੀ’ ਦੇ ਕੰਮ ਹੇਠ ਲਿਖੇ ਹਨ

• ਇਸ ਵਿਟਾਮਿਨ ਨਾਲ ਨਾੜੀ ਸਿਸਟਮ (Nervous System) ਠੀਕ ਰਹਿੰਦਾ ਹੈ ।
• ਇਹ ਨਾੜੀਆਂ, ਪੱਠਿਆਂ, ਦਿਲ ਤੇ ਦਿਮਾਗ਼ ਨੂੰ ਸ਼ਕਤੀ ਦਿੰਦਾ ਹੈ ।
• ਭੁੱਖ ਤੇਜ਼ ਕਰਦਾ ਹੈ ।
• ਚਮੜੀ ਦੇ ਰੋਗਾਂ ਤੋਂ ਰੱਖਿਆ ਕਰਦਾ ਹੈ।

ਘਾਟ ਨਾਲ ਹਾਨੀਆਂ (Abuses)-

• ਭੁੱਖ ਘੱਟ ਲੱਗਦੀ ਹੈ ।
• ਬੱਚਿਆਂ ਦਾ ਵਾਧਾ ਰੁਕ ਜਾਂਦਾ ਹੈ ।
• ਬੇਰੀ-ਬੇਰੀ ਰੋਗ ਤੇ ਚਮੜੀ ਦੇ ਕਈ ਰੋਗ ਲੱਗ ਜਾਂਦੇ ਹਨ ।
• ਜੀਭ ‘ਤੇ ਛਾਲੇ ਪੈ ਜਾਂਦੇ ਹਨ ।
• ਵਾਲ ਡਿੱਗਣ ਲੱਗ ਪੈਂਦੇ ਹਨ ।

ਪ੍ਰਾਪਤੀ ਸੋਮਾ (Sources) – ਇਹ ਦੁੱਧ, ਦਹੀਂ, ਮੱਖਣ, ਪਨੀਰ, ਸਾਬਤ ਦਾਲਾਂ, ਅਨਾਜ, ਸੋਇਆਬੀਨ, ਮਟਰ, ਆਂਡੇ, ਹਰੀਆਂ ਸਬਜ਼ੀਆਂ ਤੇ ਪੱਤਿਆਂ ਜਿਵੇਂ ਬੰਦੇ-ਗੋਭੀ, ਪਿਆਜ, ਪਾਲਕ, ਟਮਾਟਰ, ਸ਼ਲਗਮ ਤੇ ਸਲਾਦ ਆਦਿ ਵਿਚ ਹੁੰਦਾ ਹੈ ।

3. ਵਿਟਾਮਿਨ ‘ਸੀ’ (Vitamin C) ਵਿਟਾਮਿਨ ‘ਸੀ’ ਦੇ ਕੰਮ ਹੇਠ ਲਿਖੇ ਹਨ

• ਇਹ ਵਿਟਾਮਿਨ ਲਹੂ ਨੂੰ ਸਾਫ਼ ਰੱਖਦਾ ਹੈ ।
• ਦੰਦਾਂ ਨੂੰ ਮਜ਼ਬੂਤ ਰੱਖਦਾ ਹੈ ।
• ਜ਼ਖ਼ਮਾਂ ਤੇ ਟੁੱਟੀਆਂ ਹੱਡੀਆਂ ਨੂੰ ਵੀ ਜਲਦੀ ਠੀਕ ਕਰਦਾ ਹੈ ।
• ਸਰੀਰ ਨੂੰ ਛੂਤ ਦੀਆਂ ਬਿਮਾਰੀਆਂ ਤੋਂ ਬਚਾਉਂਦਾ ਹੈ ।
• ਗਲੇ ਨੂੰ ਠੀਕ ਰੱਖਦਾ ਹੈ ।
• ਜ਼ੁਕਾਮ ਤੋਂ ਬਚਾਉਂਦਾ ਹੈ ।

ਘਾਟ ਨਾਲ ਹਾਨੀਆਂ (Abuses)

• ਦੰਦਾਂ ਨੂੰ ਪਾਇਓਰੀਆ ਰੋਗ ਲੱਗ ਜਾਂਦਾ ਹੈ ।
• ਹੱਡੀਆਂ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਜ਼ਖ਼ਮ ਜਲਦੀ ਠੀਕ ਨਹੀਂ ਹੋ ਸਕਦੇ ।
• ਅਨੀਮੀਆ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਲਹੂ ਵਹਿਣਾ ਜਲਦੀ ਬੰਦ ਨਹੀਂ ਹੁੰਦਾ ।

ਪ੍ਰਾਪਤੀ ਸੋਮਾ (Sources) ਇਹ ਆਮ ਤੌਰ ‘ਤੇ ਰਸਦਾਰ ਖੱਟੇ ਫਲਾਂ ਵਿਚ ਹੁੰਦਾ ਹੈ, ਜਿਵੇਂ- ਸੰਤਰਾ, ਮਾਲਟਾ, ਮੁਸੰਮੀ, ਅੰਗੂਰ, ਅਨਾਰ, ਨਿੰਬੂ, ਅਮਰੂਦ ਅਤੇ ਔਲਾ ਆਦਿ । ਇਸ ਤੋਂ ਬਿਨਾਂ ਹਰੀਆਂ ਸਬਜ਼ੀਆਂ, ਟਮਾਟਰ, ਬੰਦਗੋਭੀ, ਗਾਜਰ, ਪਾਲਕ, ਸ਼ਲਗਮ ਆਦਿ ਵਿਚ ਵੀ ਮਿਲਦਾ ਹੈ ।

4. ਵਿਟਾਮਿਨ ‘ਡੀ’ (Vitamin D) –
ਵਿਟਾਮਿਨ ‘ਡੀ ਦੇ ਕੰਮ ਹੇਠ ਲਿਖੇ ਹਨ –

• ਇਹ ਵਿਟਾਮਿਨ ਹੱਡੀਆਂ ਤੇ ਦੰਦ ਬਣਾਉਂਦਾ ਹੈ ।
• ਉਹਨਾਂ ਨੂੰ ਮਜ਼ਬੂਤ ਵੀ ਕਰਦਾ ਹੈ ।
• ਬੱਚਿਆਂ ਨੂੰ ਸਰੀਰਕ ਵਾਧੇ ਲਈ ਇਸ ਦੀ ਬਹੁਤ ਜ਼ਰੂਰਤ ਹੈ ।

ਧਰਪਤੀ ਸੋਸਾ (Sources) – ਇਹ ਦੁੱਧ, ਆਂਡੇ ਦੀ ਜ਼ਰਦੀ, ਮੱਖਣ, ਘਿਓ, ਮੱਛੀ ਦੇ ਤੇਲ ਆਦਿ ਵਿਚ ਬਹੁਤ ਹੁੰਦਾ ਹੈ । ਵਿਟਾਮਿਨ ਸੂਰਜ ਦੀਆਂ ਕਿਰਨਾਂ ਦੇ ਪ੍ਰਭਾਵ ਨਾਲ ਆਪਣੇ ਆਪ ਹੀ ਬਣਦਾ ਰਹਿੰਦਾ ਹੈ ।

ਘਾਟ ਨਾਲ ਹਾਨੀਆਂ (Abuses)

• ਹੱਡੀਆਂ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।
• ਦੰਦ ਠੀਕ ਸਮੇਂ ਤੇ ਨਹੀਂ ਨਿਕਲਦੇ ।
• ਮਿਰਗੀ, ਹਿਸਟੀਰੀਆ ਤੇ ਸੋਕਾ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਮਾਸ-ਪੇਸ਼ੀਆਂ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ।

5. ਵਿਟਾਮਿਨ ‘ਈ (Vitamin E) – ਵਿਟਾਮਿਨ ‘ਈ’ ਦੇ ਕੰਮ ਹੇਠ ਲਿਖੇ ਹਨ

• ਇਹ ਵਿਟਾਮਿਨ ਔਰਤਾਂ ਅਤੇ ਮਰਦਾਂ ਵਿਚ ਸੰਤਾਨ ਪੈਦਾ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਨੂੰ ਵਧਾਉਂਦਾ ਹੈ ।
• ਇਹ ਨਾਮਰਦੀ ਤੇ ਬਾਂਝਪਣ ਨੂੰ ਰੋਕਦਾ ਹੈ ।

ਘਾਟ ਨਾਲ ਹਾਨੀਆਂ (Abuses)

• ਫਿਨਸੀਆਂ ਨਿਕਲਦੀਆਂ ਹਨ ।
• ਬਾਂਝਪਣ ਰੋਗ ਹੋ ਜਾਂਦਾ ਹੈ |

ਪ੍ਰਾਪਤੀ ਸੋਮਾ (Sources)-ਇਹ ਬੰਦਗੋਭੀ, ਗਾਜਰ, ਸਲਾਦ, ਮਟਰ, ਪਿਆਜ਼, ਟਮਾਟਰ, ਫੁੱਲ ਗੋਭੀ ਵਿਚ ਹੁੰਦਾ ਹੈ । ਇਸ ਤੋਂ ਬਿਨਾਂ ਸ਼ਹਿਦ, ਕਣਕ, ਚੌਲ, ਬੀਜਾਂ ਦੇ ਤੇਲ, ਆਂਡੇ ਦੀ ਜ਼ਰਦੀ, ਬਾਦਾਮ, ਪਿਸਤੇ, ਛੋਲਿਆਂ ਦੀ ਦਾਲ ਤੇ ਦਲੀਏ ਵਿਚ ਬਹੁਤ ਜ਼ਿਆਦਾ ਹੁੰਦਾ ਹੈ ।

6. ਵਿਟਾਮਿਨ ਕੇ (Vitamin K)-
ਵਿਟਾਮਿਨ ‘ਕੇ’ ਦੇ ਕੰਮ ਹੇਠ ਲਿਖੇ ਹਨ –

• ਇਹ ਵਿਟਾਮਿਨ ਜ਼ਖ਼ਮਾਂ ਵਿਚੋਂ ਰਿਸਦੇ ਖੂਨ ਨੂੰ ਰੋਕਦਾ ਹੈ :
• ਉਸ ਦੇ ਜਮਾਓ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ ।
• ਇਹ ਚਮੜੀ ਤੇ ਰੋਗਾਂ ਤੋਂ ਰੱਖਿਆ ਕਰਦਾ ਹੈ ।

ਘਾਟ ਨਾਲ ਹਾਨੀਆਂ (Abuses)-

• ਲਹੁ ਜੰਮਣ ਦੀ ਕਿਰਿਆ ਵਿਚ ਰੋਕ ਪੈਂਦੀ ਹੈ ।
• ਚਮੜੀ ਦੇ ਰੋਗ ਲੱਗ ਜਾਂਦੇ ਹਨ ।

ਪਤੀ ਸੋਮਾ (Sources)-ਇਹ ਜ਼ਿਆਦਾਤਰ ਬੰਦਗੋਭੀ, ਪਾਲਕ, ਮੱਛੀ, ਸੋਇਆਬੀਨ, ਟਮਾਟਰ ਤੇ ਆਂਡੇ ਦੀ ਜ਼ਰਦੀ ਆਦਿ ਵਿਚ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਸੰਤੁਲਿਤ ਭੋਜਨ ਦੇ ਵੱਖ-ਵੱਖ ਤੱਤ ਕਿਹੜੇ ਹਨ ? (ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ-1) (What are the various constituents of Balanced Diet ?)
ਉੱਤਰ-
ਸੰਤੁਲਿਤ ਭੋਜਨ (Balanced Diet)-ਸੰਤੁਲਿਤ ਭੋਜਨ ਉਹ ਭੋਜਨ ਹੈ ਜਿਸ ਵਿਚ ਸਰੀਰ ਲਈ ਸਭ ਜ਼ਰੂਰੀ ਤੱਤ ਉੱਚਿਤ ਮਾਤਰਾ ਵਿਚ ਸ਼ਾਮਲ ਹਨ, ਜਿਵੇਂ-ਪ੍ਰੋਟੀਨ, ਚਰਬੀ, ਕਾਰਬੋਹਾਈਡਰੇਟਸ, ਖਣਿਜ ਲੂਣ, ਵਿਟਾਮਿਨ, ਪਾਣੀ ਆਦਿ । ਇਹਨਾਂ ਤੱਤਾਂ ਦੀ ਮਾਤਰਾ ਵਿਅਕਤੀ ਦੀ ਉਮਰ, ਸਿਹਤ ਅਤੇ ਕਾਰਜ ‘ਤੇ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਸੰਤੁਲਿਤ ਭੋਜਨ ਦੇ ਤੱਤ (Constituents of Balanced Diet)-ਸੰਤੁਲਿਤ ਭੋਜਨ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਤੱਤਾਂ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਇਸ ਤਰ੍ਹਾਂ ਹੈ
1. ਪ੍ਰੋਟੀਨ (Proteins) -ਪ੍ਰੋਟੀਨ ਕਾਰਬਨ, ਹਾਈਡਰੋਜਨ, ਆਕਸੀਜਨ, ਨਾਈਟਰੋਜਨ, ਗੰਧਕ ਅਤੇ ਫਾਸਫੋਰਸ ਦੇ ਰਸਾਇਣਿਕ ਮੇਲ ਨਾਲ ਬਣਿਆ ਇਕ ਮਿਸ਼ਚਿਤ ਪਦਾਰਥ ਹੈ। ਪ੍ਰੋਟੀਨ ਦੋ ਤਰ੍ਹਾਂ ਦੇ ਹੁੰਦੇ ਹਨ-ਬਨਸਪਤੀ ਪ੍ਰੋਟੀਨ ਅਤੇ ਪਸੂ ਪ੍ਰੋਟੀਨ |

ਪ੍ਰਾਪਤੀ ਦੇ ਸੋਮੇ (Sources)-

• ਬਨਸਪਤੀ ਪ੍ਰੋਟੀਨ–ਇਹ ਸੋਇਆਬੀਨ, ਮੂੰਗਫਲੀ, ਕਾਜੂ, ਪਿਸਤਾ, ਅਖਰੋਟ, ਕਣਕ, ਬਾਜਰਾ, ਮੱਛੀ ਆਦਿ ਵਿਚ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ।
• ਪਸ਼ੂ ਪ੍ਰੋਟੀਨ -ਇਹ ਮਾਸ, ਮੱਛੀ, ਕਲੇਜੀ, ਆਂਡਾ, ਪਨੀਰ ਆਦਿ ਵਿਚ ਪਾਇਆ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰੋਟੀਨ ਦੇ ਲਾਭ (Advantages)-

• ਇਸ ਨਾਲ ਸਰੀਰਕ ਵਾਧਾ ਅਤੇ ਵਿਕਾਸ ਹੁੰਦਾ ਹੈ ।
• ਇਹ ਸਰੀਰ ਦੇ ਟੁੱਟੇ-ਫੁੱਟੇ ਸੈੱਲਾਂ ਦੀ ਮੁਰੰਮਤ ਕਰਦੇ ਹਨ |
• ਇਹ ਸਰੀਰ ਦਾ ਤਾਪਮਾਨ ਠੀਕ ਰੱਖਦੇ ਹਨ ।
• ਜਦੋਂ ਸਰੀਰ ਵਿਚ ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਜਾਂ ਚਰਬੀ ਦੀ ਮਾਤਰਾ ਘੱਟ ਹੋ ਜਾਂਦੀ ਹੈ ਤਾਂ ਸ਼ਕਤੀ ਪੈਦਾ ਕਰਨ ਦਾ ਕੰਮ ਵੀ ਪ੍ਰੋਟੀਨ ਹੀ ਕਰਦੇ ਹਨ ।

ਪ੍ਰੋਟੀਨ ਦੀ ਘਾਟ ਨਾਲ ਹਾਨੀਆਂ (Abuses) –
ਪ੍ਰੋਟੀਨ ਦੀ ਘਾਟ ਨਾਲ ਹੇਠ ਲਿਖੇ ਰੋਗ ਲੱਗ ਜਾਂਦੇ ਹਨ

1. ਕਵਾਸ਼ੀਓਰਕਰ (Kwashiorkar)-ਪ੍ਰੋਟੀਨ ਦੀ ਘਾਟ ਨਾਲ ਇਕ ਸਾਲ ਤੋਂ ਲੈ ਕੇ ਤਿੰਨ ਸਾਲ ਤਕ ਦੀ ਉਮਰ ਦੇ ਬੱਚਿਆਂ ਨੂੰ ਇਹ ਰੋਗ ਹੋ ਜਾਂਦਾ ਹੈ ।ਪਹਿਲਾਂ ਬੱਚੇ ਦੀਆਂ ਲੱਤਾਂ ਸੁੱਕ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਫੇਰ ਉਸ ਦੇ ਮੂੰਹ ਅਤੇ ਸਾਰੇ ਸਰੀਰ ਵਿਚ ਸੋਜ ਹੋ ਜਾਂਦੀ ਹੈ । ਚਮੜੀ ਖੁਰਦਰੀ ਅਤੇ ਲਾਲ ਹੋ ਜਾਂਦੀ ਹੈ । ਬੱਚਾ ਚਿੜਚਿੜਾ ਹੋ ਜਾਂਦਾ ਹੈ |
2. ਸੋਕਾ-ਪ੍ਰੋਟੀਨ ਦੀ ਘਾਟ ਨਾਲ ਬੱਚਿਆਂ ਨੂੰ ਸੋਕਾ ਨਾਮੀ ਰੋਗ ਲੱਗ ਜਾਂਦਾ ਹੈ । ਬੱਚਾ ਪਤਲਾ ਅਤੇ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦਾ ਹੈ। ਉਸਦੇ ਮਾਸ ਦੇ ਹੇਠਾਂ ਹੱਡੀਆਂ ਨਜ਼ਰ ਆਉਂਦੀਆਂ ਹਨ ।

3. ਭੁੱਖ ਨਾਲ ਸੋਜਾ (litige oedenaa)-ਭੁੱਖੇ ਰਹਿਣ ਨਾਲ ਪ੍ਰੋਟੀਨ ਦੀ ਕਮੀ ਕਾਰਨ ਮਨੁੱਖ ਦੇ ਸਰੀਰ ਵਿਚ ਘੱਟ ਖ਼ੁਰਾਕ ਪਹੁੰਚਦੀ ਹੈ, ਸੈੱਲਾਂ ਵਿਚ ਪਾਣੀ ਵਧੇਰੇ ਇਕੱਠਾ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਸਰੀਰ ਸੁੱਜਿਆ ਹੋਇਆ ਨਜ਼ਰ ਆਉਂਦਾ ਹੈ ।

4. ਪਲੈਗਰਾ (Pellagra) – ਇਸ ਰੋਗ ਦੇ ਕਾਰਨ ਚਮੜੀ ਖੁਰਦਰੀ ਅਤੇ ਖੁਸ਼ਕ ਹੋ ਜਾਂਦੀ ਹੈ ।

5. ਜਿਗਰ ਦੀ ਖ਼ਰਾਬੀ-ਪ੍ਰੋਟੀਨ ਦੀ ਘਾਟ ਨਾਲ ਜਿਗਰ ਖ਼ਰਾਬ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰੋਟੀਨ ਦੀ ਜ਼ਿਆਦਤੀ ਨਾਲ ਹਾਨੀਆਂ (Abuses)-ਪ੍ਰੋਟੀਨ ਦੀ ਜ਼ਿਆਦਾ ਮਾਤਰਾ ਲੈਣ ਨਾਲ ਗੁਰਦਿਆਂ ਦੀਆਂ ਕਈ ਬਿਮਾਰੀਆਂ ਲੱਗ ਜਾਂਦੀਆਂ ਹਨ ।
ਖੂਨ ਦੀਆਂ ਨਾੜੀਆਂ ਵਿਚ ਵੀ ਫ਼ਰਕ ਆਉਂਦਾ ਹੈ ਅਤੇ ਜੋੜਾਂ ਦੇ ਦਰਦ ਵੀ ਹੋ ਜਾਂਦੇ ਹਨ ।

ਪ੍ਰੋਟੀਨ ਦੀ ਉੱਚਿਤ ਮਾਤਰਾ (Proper Quantity)-ਇਕ ਸਾਲ ਤੋਂ ਲੈ ਕੇ ਛੇ ਸਾਲ ਤਕ ਦੀ ਉਮਰ ਦੇ ਬੱਚਿਆਂ ਨੂੰ ਪ੍ਰੋਟੀਨ ਦੀ ਬਹੁਤ ਜ਼ਿਆਦਾ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ । ਇਕ ਸਾਧਾਰਨ ਵਿਅਕਤੀ ਨੂੰ ਪ੍ਰਤੀਦਿਨ 10 ਤੋਂ 100 ਗ੍ਰਾਮ ਤਕ ਪ੍ਰੋਟੀਨ ਦੀ ਮਾਤਰਾ ਲੈਣੀ ਚਾਹੀਦੀ ਹੈ ।

2. ਕਾਰਬੋਹਾਈਡਰੇਟਸ (Carbohydrates)-ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਸਰੀਰ ਨੂੰ ਸ਼ਕਤੀ ਅਤੇ ਗਰਮੀ ਪ੍ਰਦਾਨ ਕਰਦੇ ਹਨ | ਭਾਰਤੀਆਂ ਦੇ ਭੋਜਨ ਦਾ 70-80% ਭਾਗ ਇਸ ਤੱਤ ਨਾਲ ਪੂਰਾ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਾਪਤੀ ਦੇ ਸੋਮੇ (Sources)-ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਕਣਕ, ਚਾਵਲ, ਜਵਾਰ (ਜੋਂ, ਮੱਕੀ, ਬਾਜਰਾ, ਗੁੜ, ਖੰਡ, ਸ਼ਕਰਕੰਦੀ, ਆਲੂ ਆਦਿ ਵਸਤੂਆਂ ਵਿਚ ਪਾਏ ਜਾਂਦੇ ਹਨ ।

ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਦੇ ਲਾਭ (Advantages)-

• ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਨਾਲ ਸਰੀਰ ਨੂੰ ਸ਼ਕਤੀ ਅਤੇ ਗਰਮੀ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ ।
• ਉਹ ਚਰਬੀ ਪਚਾਉਣ ਵਿਚ ਮਦਦ ਕਰਦੇ ਹਨ ।
• ਇਸ ਨਾਲ ਜਿਗਰ ਅਤੇ ਅੰਤੜੀਆਂ ਦੀ ਸਫ਼ਾਈ ਹੁੰਦੀ ਹੈ ।

ਘਾਟ ਅਤੇ ਹਾਨੀਆਂ (Abuses)-

• ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਦੀ ਉੱਚਿਤ ਮਾਤਰਾ ਨਾ ਮਿਲਣ ਨਾਲ ਖੂਨ ਵਿਚ ਐਲਕਲੀਨ ਘੱਟ ਹੋ ਜਾਂਦੀ ਹੈ ਅਤੇ ਤੇਜ਼ਾਬੀ ਮਾਦਾ (Acidity) ਵੱਧ ਜਾਂਦਾ ਹੈ ।ਇਸ ਦਸ਼ਾ ਵਿਚ ਵਿਅਕਤੀ ਬੇਹੋਸ਼ ਹੋ ਸਕਦਾ ਹੈ | ਅਜਿਹੀ ਦਸ਼ਾ ਵਿਚ ਜ਼ਿਆਦਾ ਭੁੱਖੇ ਰਹਿਣ ਨਾਲ ਸ਼ੱਕਰ (Diabetes) ਰੋਗ ਹੋ ਸਕਦਾ ਹੈ ।
• ਅੰਤੜੀਆਂ ਦੀ ਪੂਰੀ ਤਰ੍ਹਾਂ ਸਫ਼ਾਈ ਨਹੀਂ ਹੁੰਦੀ ।
• ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਤੇ ਘੱਟ ਖਾਣ ਨਾਲ ਸਰੀਰ ਦੀ ਚਰਬੀ ਵੀ ਠੀਕ ਤਰ੍ਹਾਂ ਨਾਲ ਹਜ਼ਮ ਨਹੀਂ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ।
• ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਦੇ ਘੱਟ ਖਾਣ ਨਾਲ ਜਿਗਰ ਵਿਚ ਤੇਜ਼ਾਬੀ ਤੱਤਾਂ ਦਾ ਵਾਧਾ ਹੋ ਜਾਂਦਾ ਹੈ ਜਿਸ ਨਾਲ ਸਰੀਰ ਨੂੰ ਹਾਨੀ ਪੁੱਜਦੀ ਹੈ ।
• ਇਸ ਦੀ ਵਧੇਰੇ ਘਾਟ ਨਾਲ ਸਰੀਰ ਬਹੁਤ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਵਿਅਕਤੀ ਦੀ ਮੌਤ ਹੋ ਸਕਦੀ ਹੈ ।

ਜ਼ਿਆਦਤੀ ਨਾਲ ਹਾਨੀਆਂ (Abuses)-

• ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਦੀ ਜ਼ਿਆਦਤੀ ਨਾਲ ਸਰੀਰ ਵਿਚ ਮੋਟਾਪਾ ਆ ਜਾਂਦਾ ਹੈ :
• ਉੱਚਾ ਰਕਤਚਾਪ |
• ਸ਼ੱਕਰ ਅਤੇ ਜੋੜਾਂ ਦੇ ਦਰਦ ਆਦਿ ਰੋਗ ਲੱਗ ਜਾਂਦੇ ਹਨ ।

ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਦੀ ਉੱਚਿਤ ਮਾਤਰਾ (Proper Qualtity) – ਸਾਡੇ ਭੋਜਨ ਵਿਚ 50-80% ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਤੱਤ ਹੁੰਦੇ ਹਨ । ਸੰਤੁਲਿਤ ਭੋਜਨ ਦਾ 50-6% ਭਾਰ ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਦਾ ਹੀ ਹੁੰਦਾ ਹੈ | ਇਹ ਸਾਧਾਰਨ ਵਿਅਕਤੀ ਦੇ ਭੋਜਨ ਵਿਚ ਪ੍ਰਤੀਦਿਨ 400 ਤੋਂ 70 ਗਰਾਮ ਕਾਰਬੋਹਾਈਡਰੇਟਸ ਦੀ ਮਾਤਰਾ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।

3. ਚਰਬੀ ਜਾਂ ਚਿਕਨਾਈ (Fats) – ਚਰਬੀ ਜਾਂ ਚਿਕਨਾਈ ਦੋ ਤਰ੍ਹਾਂ ਦੀ ਹੁੰਦੀ ਹੈ । ਬਨਸਪਤੀ ਚਰਬੀ ਤੇ ਪਸ਼ੂ ਚਰਬੀ ।
ਪ੍ਰਾਪਤੀ ਦੇ ਸੋਮੇ (Sources)-

• ਬਨਸਪਤੀ ਚਰਬੀ-ਸਰੋਂ, ਮੁੰਗਫਲੀ ਅਤੇ ਨਾਰੀਅਲ ਦਾ ਤੇਲ, ਅਖ਼ਰੋਟ, ਬਾਦਾਮ, ਮੂੰਗਫਲੀ, ਸੋਇਆਬੀਨ ਆਦਿ ਵਿਚ ਪਾਈ ਜਾਂਦੀ ਹੈ ।
• ਪਸ਼ੂ ਚਰਬੀ–ਇਹ ਘਿਓ, ਮੱਖਣ, ਦੁੱਧ, ਮਾਸ, ਮੱਛੀ, ਆਂਡਿਆਂ ਆਦਿ ਵਿਚ ਪਾਈ ਜਾਂਦੀ ਹੈ !

ਚਰਬੀ ਦੇ ਲਾਭ (Advantages)-

• ਇਸ ਨਾਲ ਸਰੀਰ ਵਿਚ ਸ਼ਕਤੀ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ।
• ਇਹ ਸਰੀਰ ਦੇ ਤਾਪਮਾਨ ਨੂੰ ਸਥਿਰ ਰੱਖਦੀ ਹੈ ।
• ਸਰੀਰ ਦੇ ਸਭ ਅੰਗਾਂ ਦੀ ਬਾਹਰੀ ਚੋਟ ਤੋਂ ਰੱਖਿਆ ਕਰਦੀ ਹੈ ।
• ਇਹ ਵਿਟਾਮਿਨ ਏ, ਡੀ ਅਤੇ ਕੇ ਨੂੰ ਸਰੀਰਕ ਜ਼ਰੂਰਤ ਦੇ ਅਨੁਸਾਰ ਸੰਭਾਲ ਕੇ ਰੱਖ ਸਕਦੀ ਹੈ ।

ਘਾਟ ਨਾਲ ਹਾਨੀਆਂ (Disadvantages)-ਚਰਬੀ ਦੀ ਘਾਟ ਨਾਲ ਕਈ ਹਾਨੀਆਂ ਹੁੰਦੀਆਂ ਹਨ

• ਚਮੜੀ (Skin) ਖ਼ੁਸ਼ਕ ਹੋ ਜਾਂਦੀ ਹੈ ।
• ਵਿਟਾਮਿਨ ਏ, ਡੀ, ਈ ਅਤੇ ਕੇ ਦੀ ਘਾਟ ਹੋ ਜਾਂਦੀ ਹੈ |
• ਚਰਬੀ ਤੇਜ਼ਾਬਾਂ ਦੀ ਘਾਟ ਨਾਲ ਚਮੜੀ ਖੁਸ਼ਕ ਹੋ ਜਾਂਦੀ ਹੈ ।

ਜ਼ਿਆਦਤੀ ਨਾਲ ਹਾਨੀਆਂ (Abuses)-ਭੋਜਨ ਵਿਚ ਚਰਬੀ ਦੀ ਵਧੇਰੇ ਮਾਤਰਾ ਵੀ ਹਾਨੀਕਾਰਕ ਹੁੰਦੀ ਹੈ

• ਸਰੀਰ ਵਿਚ ਮੋਟਾਪਾ ਆ ਜਾਂਦਾ ਹੈ ।
• ਦਿਲ ਦਾ ਰੋਗ ਲੱਗ ਜਾਂਦਾ ਹੈ ।
• ਹਾਜ਼ਮਾ ਖ਼ਰਾਬ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਸ਼ੱਕਰ (Diabetes) ਰੋਗ ਲੱਗ ਜਾਂਦਾ ਹੈ ।
• ਪੇਟ ਵਿਚ ਪੱਥਰੀ (Stone) ਬਣ ਜਾਂਦੀ ਹੈ ।

ਚਰਬੀ ਦੀ ਉੱਚਿਤ ਮਾਤਰਾ (Proper Quantity)-ਇਕ ਸਾਧਾਰਨ ਵਿਅਕਤੀ ਦੇ ਝੋਜਨ ਵਿਚ ਪ੍ਰਤੀ-ਦਿਨ ਲਗਪਗ 50 ਗਰਾਮ ਤੋਂ 75 ਗਰਾਮ ਚਰਬੀ ਦੀ ਮਾਤਰਾ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।

4. ਖਣਿਜ ਲੂਣ (Mineral Salts)-ਸਾਡੇ ਸਰੀਰ ਵਿਚ ਖਣਿਜ ਲੂਣ 4% ਹੁੰਦੇ ਹਨ । ਫਾਸਫੋਰਸ, ਕੈਲਸ਼ੀਅਮ, ਸੋਡੀਅਮ, ਕਲੋਰੀਨ, ਪੋਟਾਸ਼ੀਅਮ, ਮੈਗਨੀਸ਼ੀਅਮ, ਮੈਂਗਨੀਜ਼, ਆਇਓਡੀਨ ਅਤੇ ਕੈਲਸ਼ੀਅਮ ਜ਼ਿੰਕ ਆਦਿ ਮੁੱਖ ਖਣਿਜ ਲੂਣ ਹਨ ।

ਪ੍ਰਾਪਤੀ ਦੇ ਸੋਮੇ (Sources)-ਇਹ ਖਣਿਜ ਹਰੇ ਪੱਤਿਆਂ ਵਾਲੇ ਸਾਗ ਅਤੇ ਹਰੇ ਫਲਾਂ, ਮਾਸ, ਮੱਛੀ, ਦੁੱਧ ਆਦਿ ਵਿਚ ਕਾਫ਼ੀ ਮਾਤਰਾ ਵਿਚ ਪਾਏ ਜਾਂਦੇ ਹਨ । ਦੁੱਧ ਵਿਚ ਲੋਹੇ ਦੀ ਮਾਤਰਾ ਘੱਟ ਹੈ, ਪਰ ਹੋਰ ਸਭ ਖਣਿਜ ਲੂਣ ਪ੍ਰਾਪਤ ਹੋ ਜਾਂਦੇ ਹਨ ।

ਲਾਭ (Advantages)

• ਇਹ ਦੰਦਾਂ ਅਤੇ ਹੱਡੀਆਂ ਨੂੰ ਮਜ਼ਬੂਤ ਬਣਾਉਂਦੇ ਹਨ ।
• ਇਹ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਦੇ ਤੰਤੂਆਂ (Muscular Tissues) ਦਾ ਵਿਕਾਸ ਕਰਦੇ ਹਨ ।
• ਇਹ ਖੂਨ ਦੇ ਰੰਗ ਨੂੰ ਲਾਲ ਬਣਾਉਂਦੇ ਹਨ ।
• ਕੈਲਸ਼ੀਅਮ ਖ਼ੂਨ ਦੇ ਜਮਾ ਵਿਚ ਯੋਗਦਾਨ ਦਿੰਦੇ ਹਨ ।
• ਖਣਿਜ ਲੂਣ ਸਰੀਰ ਦੇ ਸਭ ਕੰਮਾਂ ਨੂੰ ਠੀਕ ਤਰ੍ਹਾਂ ਚਲਾਉਂਦੇ ਹਨ ।

ਪਾਣੀ ਦੀ ਘਾਟ ਨਾਲ ਹਾਨੀਆਂ (Disadvantages) –

• ਕੈਲਸ਼ੀਅਮ ਦੀ ਘਾਟ ਨਾਲ ਹੱਡੀਆਂ ਅਤੇ ਦੰਦ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦੇ ਹਨ ।
• ਸਰੀਰ ਹਰੇਕ ਰੋਗ ਦਾ ਜਲਦੀ ਸ਼ਿਕਾਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਆਇਓਡੀਨ ਦੀ ਘਾਟ ਨਾਲ ਗਿੱਲ੍ਹੜ ਨਾਮੀ ਰੋਗ ਹੋ ਜਾਂਦਾ ਹੈ ।

5. ਪਾਣੀ (Water) -ਸਾਡੇ ਸਰੀਰ ਦਾ ਪੁਤ ਭਾਗ ਪਾਣੀ ਦਾ ਹੁੰਦਾ ਹੈ । ਇਹ ਆਕਸੀਜਨ ਅਤੇ ਹਾਈਡਰੋਜਨ ਦੇ ਮੇਲ ਨਾਲ ਬਣਦਾ ਹੈ ।
ਇਸ ਦਾ ਸਰੀਰ ਦੇ ਲਈ ਉੱਨਾ ਹੀ ਮਹੱਤਵ ਹੈ ਜਿੰਨਾ ਕਿ ਹਵਾ ਦਾ ।

ਸੋਮੇ (Sources)-ਪਾਣੀ ਸਾਨੂੰ ਕਈ ਕਿਸਮ ਦੇ ਭੋਜਨ ਦੇ ਤੱਤਾਂ ਦੁੱਧ, ਫਲ ਅਤੇ ਸਬਜ਼ੀਆਂ ਵਿਚ ਸ਼ੁੱਧ ਰੂਪ ਵਿਚ ਮਿਲਦਾ ਹੈ ।

ਪਾਣੀ ਦੇ ਲਾਭ (Advantages) –

• ਪਾਣੀ ਸੈੱਲਾਂ ਦੇ ਨਿਰਮਾਣ ਵਿਚ ਸਹਾਇਤਾ ਦਿੰਦਾ ਹੈ ।
• ਇਹ ਸੈਂਲਾਂ ਤਕ ਖ਼ੁਰਾਕ ਪਹੁੰਚਾਉਂਦਾ ਹੈ । ਇਹ ਸਰੀਰ ਵਿਚੋਂ ਗੰਦੇ ਪਦਾਰਥਾਂ ਦਾ ਨਿਕਾਸ ਕਰਦਾ ਹੈ ।
• ਇਹ ਭੋਜਨ ਨੂੰ ਪਚਾਉਣ ਵਿਚ ਮਦਦ ਕਰਦਾ ਹੈ ।
• ਇਹ ਸਾਡੇ ਸਰੀਰ ਦੀ ਗਰਮੀ ਨੂੰ ਨਿਯਮਬੱਧ ਕਰਦਾ ਹੈ ।
• ਪਾਣੀ ਦੁਆਰਾ ਭੋਜਨ ਦੇ ਤੱਤ ਖੂਨ ਵਿਚ ਮਿਲਦੇ ਹਨ ।
• ਇਹ ਸਰੀਰ ਦੇ ਜੋੜਾਂ ਅਤੇ ਅੰਗਾਂ ਨੂੰ ਨਰਮ ਰੱਖਦਾ ਹੈ ।
• ਪਾਣੀ ਦੇ ਸਹਾਰੇ ਸਰੀਰ ਵਿਚ ਖੂਨ ਦਾ ਚੱਕਰ ਚਲਦਾ ਹੈ ।

ਪਾਣੀ ਦੀ ਘਾਟ ਨਾਲ ਹਾਨੀਆਂ (Disadvantages) ਪਾਣੀ ਘੱਟ ਪੀਣ ਨਾਲ ਬਹੁਤ ਸਾਰੀਆਂ ਹਾਨੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ।

• ਪਾਣੀ ਘੱਟ ਪੀਣ ਨਾਲ ਖਾਧਾ ਹੋਇਆ ਭੋਜਨ ਚੰਗੀ ਤਰ੍ਹਾਂ ਨਹੀਂ ਪਚਦਾ ।
• ਜਿਗਰ ਭਾਰਾ ਰਹਿੰਦਾ ਹੈ ।
• ਕਬਜ਼ ਹੋ ਜਾਂਦੀ ਹੈ ।
• ਸਿਰ ਹਮੇਸ਼ਾਂ ਥੱਕਿਆ ਜਿਹਾ ਮਹਿਸੂਸ ਹੁੰਦਾ ਹੈ ।
• ਸਰੀਰ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਚਿਹਰਾ ਪੀਲਾ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਸਰੀਰ ਵਿਚੋਂ ਗੰਦੇ ਪਦਾਰਥਾਂ ਦਾ ਘੱਟ ਨਿਕਾਸ ਹੁੰਦਾ ਹੈ ।
• ਜੋੜਾਂ ਦਾ ਦਰਦ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਗੁਰਦਿਆਂ ਵਿਚ ਪੱਥਰੀ ਬਣ ਜਾਂਦੀ ਹੈ ।

ਪਾਣੀ ਦੀ ਜ਼ਿਆਦਤੀ ਨਾਲ ਹਾਨੀਆਂ (Abuses) -ਪਾਣੀ ਹਮੇਸ਼ਾ ਉੱਚਿਤ ਮਾਤਰਾ ਵਿਚ ਹੀ ਪੀਣਾ ਚਾਹੀਦਾ ਹੈ। ਜ਼ਿਆਦਾ ਪਾਣੀ ਪੀਣ ਨਾਲ ਜਿਗਰ ਭਰਿਆ ਰਹਿੰਦਾ ਹੈ ਅਤੇ ਭੁੱਖ ਘੱਟ ਲੱਗਦੀ ਹੈ । ਭੋਜਨ ਕਰਦੇ ਸਮੇਂ ਨਾਲ-ਨਾਲ ਪਾਣੀ ਪੀਣ ਨਾਲ ਭੋਜਨ ਜਲਦੀ ਹਜ਼ਮ ਨਹੀਂ ਹੁੰਦਾ |

ਪਾਣੀ ਦੀ ਉੱਚਿਤ ਮਾਤਰਾ (Proper Quantity) -ਪਾਣੀ ਦੀ ਮਾਤਰਾ ਵਿਚ ਰੁੱਤ, ਕਸਰਤ ਜਾਂ ਖ਼ੁਰਾਕ ਦੇ ਅਨੁਸਾਰ ਪਰਿਵਰਤਨ ਹੁੰਦਾ ਰਹਿੰਦਾ ਹੈ ।
ਸਾਧਾਰਨ ਤੌਰ ‘ਤੇ ਦਿਨ ਵਿਚ 5-6 ਗਲਾਸ ਪਾਣੀ ਪੀਣਾ ਚਾਹੀਦਾ ਹੈ ।

6. ਵਿਟਾਮਿਨ (Vitamin) -ਭੋਜਨ ਵਿਚ ਵਿਟਾਮਿਨਾਂ ਦੀ ਉੱਚਿਤ ਮਾਤਰਾ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਇਨ੍ਹਾਂ ਦਾ ਮਨੁੱਖੀ ਸਰੀਰ ਦੇ ਲਈ ਵਿਸ਼ੇਸ਼ ਮਹੱਤਵ ਹੈ । ਇਨ੍ਹਾਂ ਬਿਨਾਂ ਸਰੀਰ ਦਾ ਕੋਈ ਕੰਮ ਨਹੀਂ ਹੋ ਸਕਦਾ । ਵਿਟਾਮਿਨਾਂ ਤੋਂ ਰਹਿਤ ਭੋਜਨ ਸੰਤੁਲਿਤ ਭੋਜਨ ਨਹੀਂ ਕਿਹਾ ਜਾ ਸਕਦਾ । ਵਿਟਾਮਿਨ ਆਮ ਤੌਰ ‘ਤੇ ਤਾਜ਼ੇ ਫਲ, ਹਰੀਆਂ ਸਬਜ਼ੀਆਂ ਅਤੇ ਆਂਡਿਆਂ ਵਿਚ ਮਿਲਦੇ ਹਨ । ਇਹ 6 ਤਰ੍ਹਾਂ ਦੇ ਹੁੰਦੇ ਹਨ-ਵਿਟਾਮਿਨ ਏ, ਬੀ, ਸੀ, ਡੀ, ਈ ਅਤੇ ਕੇ ।

ਲਾਭ (Advantages)-

• ਇਹ ਪਾਚਨ ਸ਼ਕਤੀ ਨੂੰ ਵਧਾਉਂਦੇ ਹਨ ।
• ਭਿੰਨ-ਭਿੰਨ ਰੋਗਾਂ ਨੂੰ ਰੋਕਦੇ ਹਨ ।
• ਸਾਡੇ ਸਰੀਰ ਦੀ ਚਮੜੀ ਦੇ ਰੋਗਾਂ ਤੋਂ ਰੱਖਿਆ ਕਰਦੇ ਹਨ ।
• ਸਾਡੀਆਂ ਹੱਡੀਆਂ ਨੂੰ ਮਜ਼ਬੂਤ ਬਣਾਉਂਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 3.
ਖਣਿਜ ਲੂਣ ਅਤੇ ਵਿਟਾਮਿਨਾਂ ਦੇ ਲਾਭ ਦੱਸੋ । [ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ-4] (Describe the advantages of Mineral Salt and Vitamins.)
ਉੱਤਰ-
ਖਣਿਜ ਲੂਣਾਂ ਦੇ ਲਾਭ (Advantages of Mineral Salts)- ਮਨੁੱਖੀ ਸਰੀਰ ਵਿਚ ਪ੍ਰੋਟੀਨ, ਕਾਰਬੋਹਾਈਡਰੇਟਸ, ਚਰਬੀ ਅਤੇ ਪਾਣੀ ਦੀ ਮਾਤਰਾ 96% ਹੁੰਦੀ ਹੈ ਅਤੇ ਬਾਕੀ 4% ਖਣਿਜ ਲੂਣ ਹੁੰਦੇ ਹਨ । ਕੈਲਸ਼ੀਅਮ, ਫਾਸਫੋਰਸ, ਸੋਡੀਅਮ, ਕਲੋਰੀਨ, ਸਲਫਰ, ਆਇਰਨ, ਆਇਓਡੀਨ ਆਦਿ ਪ੍ਰਮੁੱਖ ਲੂਣ ਹਨ |

ਖਣਿਜ ਲੂਣਾਂ ਦੇ ਅੱਗੇ ਲਿਖੇ ਲਾਭ ਹਨ –

• ਇਹ ਦੰਦਾਂ ਅਤੇ ਹੱਡੀਆਂ ਦਾ ਵਾਧਾ ਕਰਦੇ ਹਨ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਮਜ਼ਬੂਤ ਬਣਾਉਂਦੇ ਹਨ ।
• ਇਹ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਦੇ ਟਿਸ਼ੂਆਂ (Muscular Tissues) ਦਾ ਵਾਧਾ ਕਰਦੇ ਹਨ |
• ਇਹ ਖੂਨ ਦਾ ਰੰਗ ਲਾਲ ਬਣਾਉਂਦੇ ਹਨ ।
• ਕੈਲਸ਼ੀਅਮ ਖ਼ੂਨ ਦੇ ਜਮਾਅ ਵਿਚ ਯੋਗਦਾਨ ਦਿੰਦੇ ਹਨ ।
• ਇਹ ਸਰੀਰ ਦਾ ਸਾਰਾ ਕੰਮ ਠੀਕ ਢੰਗ ਨਾਲ ਚਲਾਉਣ ਲਈ ਜ਼ਰੂਰੀ ਹਨ ।

ਵਿਟਾਮਿਨਾਂ ਦੇ ਲਾਭ (Advantages of vitamins)-ਵਿਟਾਮਿਨ ਭੋਜਨ ਦੇ ਮਹੱਤਵਪੂਰਨ ਤੱਤ ਹਨ । ਇਹ ਸੰਖਿਆ ਵਿਚ ਛੇ ਹਨ-ਵਿਟਾਮਿਨ ਏ, ਬੀ, ਸੀ, ਡੀ, ਈ ਅਤੇ ਕੇ । ਇਨ੍ਹਾਂ ਦੇ ਮਵਾਰ ਲਾਭ ਇਸ ਤਰ੍ਹਾਂ ਹਨ –
ਵਿਟਾਮਿਨ ‘ਏ’ ਦੇ ਲਾਭ (Advantages of Vitamin A) –

• ਇਹ ਅੱਖਾਂ ਦੀ ਰੋਸ਼ਨੀ ਤੇਜ਼ ਕਰਦਾ ਹੈ ।
• ਇਹ ਅੱਖਾਂ, ਜਿਗਰ ਅਤੇ ਅੰਤੜੀਆਂ ਦੀਆਂ ਝਿੱਲੀਆਂ ਨੂੰ ਮਜ਼ਬੂਤ ਬਣਾਉਂਦਾ ਹੈ ।
• ਛੂਤ ਦੇ ਰੋਗ ਤੋਂ ਰੱਖਿਆ ਕਰਦਾ ਹੈ ।
• ਇਹ ਸਰੀਰ ਨੂੰ ਵਧਾਉਣ ਅਤੇ ਵਿਕਾਸ ਕਰਨ ਵਿਚ ਸਹਾਇਤਾ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ ।
• ਇਹ ਭੁੱਖ ਵਧਾਉਂਦਾ ਹੈ ਅਤੇ ਪਾਚਨ ਕਿਰਿਆ ਨੂੰ ਠੀਕ ਰੱਖਦਾ ਹੈ ।

ਵਿਟਾਮਿਨ ‘‘ਬੀ’ ਦੇ ਲਾਭ (Advantages of Vitamin B)-

• ਇਹ ਦਿਮਾਗ਼ ਨੂੰ ਸ਼ਕਤੀ ਪ੍ਰਦਾਨ ਕਰਦਾ ਹੈ ।
• ਇਹ ਹੱਡੀਆਂ ਨੂੰ ਮਜ਼ਬੂਤ ਬਣਾਉਂਦਾ ਹੈ ।
• ਇਸ ਨਾਲ ਪਾਚਨ ਸ਼ਕਤੀ ਠੀਕ ਹੁੰਦੀ ਹੈ ਅਤੇ ਭੁੱਖ ਲੱਗਦੀ ਹੈ ।
• ਇਹ ਚਮੜੀ ਨੂੰ ਠੀਕ ਰੱਖਦਾ ਹੈ ।

ਵਿਟਾਮਿਨ ‘ਸੀ’ ਦੇ ਲਾਭ (Advantages of Vitamin C)-

• ਸਰੀਰ ਦੀ ਛੂਤ ਦੇ ਰੋਗ ਤੋਂ ਰੱਖਿਆ ਕਰਦਾ ਹੈ ।
• ਦੰਦਾਂ ਅਤੇ ਮਸੂੜਿਆਂ ਨੂੰ ਮਜ਼ਬੂਤ ਬਣਾਉਂਦਾ ਹੈ ।
• ਜ਼ੁਕਾਮ ਨੂੰ ਰੋਕਦਾ ਹੈ |
• ਜ਼ਖ਼ਮਾਂ ਨੂੰ ਭਰਨ ਅਤੇ ਟੁੱਟੀਆਂ ਹੱਡੀਆਂ ਨੂੰ ਠੀਕ ਕਰਨ ਵਿਚ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ ।

ਵਿਟਾਮਿਨ ‘ਡੀ’ ਦੇ ਲਾਭ (Advantages of Vitamin D)-ਹੱਡੀਆਂ ਨੂੰ ਮਜ਼ਬੂਤ ਕਰਦਾ ਹੈ । ਵਿਟਾਮਿਨ ‘ਈਂ’ ਦੇ ਲਾਭ (Advantages of Vitamin E)-ਇਹ ਜਨਣ ਸ਼ਕਤੀ ਨੂੰ ਵਧਾਉਂਦਾ ਹੈ । ਵਿਟਾਮਿਨ ‘ ਕੇ` ` ਦੇ ਲਾਭ (Advantages of Vitamin K)-ਇਹ ਖੂਨ ਨੂੰ ਜੰਮਣ ਦੀ ਕਿਰਿਆ ਵਿਚ ਸਹਾਇਤਾ ਪਹੁੰਚਾਉਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਇਕ ਆਮ ਖਿਡਾਰੀ ਲਈ ਉੱਚਿਤ ਖ਼ੁਰਾਕ ਦੀ ਮਾਤਰਾ ਦੱਸੋ । [ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ-5]. (Describe the balance diet of an ordinary sports person.)
ਉੱਤਰ-
ਇਕ ਆਮ ਸਾਧਾਰਨ ਖਿਡਾਰੀ ਲਈ ਉੱਚਿਤ ਖ਼ੁਰਾਕ ਦੀ ਮਾਤਰਾ ਹੇਠਾਂ ਦਿੱਤੀ ਜਾਂਦੀ ਹੈ –

Punjab State Board PSEB 10th Class Physical Education Book Solutions Chapter 1 ਕਸਰਤ ਦੇ ਸਾਹ ਕਿਰਿਆ, ਲਹੂ ਚੱਕਰ, ਮਾਸ-ਪੇਸ਼ੀਆਂ ਅਤੇ ਮਲ-ਨਿਕਾਸ ਉੱਤੇ ਪ੍ਰਭਾਵ Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 10 Physical Education Chapter 1 ਕਸਰਤ ਦੇ ਸਾਹ ਕਿਰਿਆ, ਲਹੂ ਚੱਕਰ, ਮਾਸ-ਪੇਸ਼ੀਆਂ ਅਤੇ ਮਲ-ਨਿਕਾਸ ਉੱਤੇ ਪ੍ਰਭਾਵ

Physical Education Guide for Class 10 PSEB ਕਸਰਤ ਦੇ ਸਾਹ ਕਿਰਿਆ, ਲਹੂ ਚੱਕਰ, ਮਾਸ-ਪੇਸ਼ੀਆਂ ਅਤੇ ਮਲ-ਨਿਕਾਸ ਉੱਤੇ ਪ੍ਰਭਾਵTextbook Questions and Answers

ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Very Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਮਾਸ-ਪੇਸ਼ੀਆਂ ਜਾਂ ਪੱਠੇ ਕੀ ਹਨ ? (Describe Muscles.)
ਉੱਤਰ-
ਮਾਸ-ਪੇਸ਼ੀਆਂ ਮਾਸ ਸੁਤਰ ਸੈੱਲਾਂ ਦਾ ਸੁਮੇਲ ਹਨ । ਹਰੇਕ ਮਾਸ-ਪੇਸ਼ੀ ਹੱਡੀ ਨਾਲ ਜੁੜੀ ਹੋਣ ਕਰਕੇ ਇਹਨਾਂ ਵਿਚੋਂ ਸੁੰਗੜਨ ਤੇ ਭਿੰਨ-ਭਿੰਨ ਅੰਗ ਕੰਮ ਕਰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਮਾਸ-ਪੇਸ਼ੀਆਂ ਦੀਆਂ ਕਿਸਮਾਂ ਦੇ ਨਾਂ ਲਿਖੋ । (Name the types of Muscles.)
ਉੱਤਰ –

• ਸਵੈ-ਇੱਛਤ ਮਾਸ-ਪੇਸ਼ੀਆਂ (Voluntary Muscles)
• ਅਣਇੱਛਤ ਮਾਸ-ਪੇਸ਼ੀਆਂ (Involuntary Muscles)
• ਦਿਲ ਦੀਆਂ ਮਾਸ-ਪੇਸ਼ੀਆਂ (Cardiac Muscles) ।

ਪ੍ਰਸ਼ਨ 3.
ਮਲ-ਤਿਆਗ ਪ੍ਰਣਾਲੀ ਕੀ ਹੈ ? (What is Excretory System ?)
ਉੱਤਰ-
ਮਲ-ਤਿਆਗ ਪ੍ਰਣਾਲੀ ਉਸ ਪ੍ਰਬੰਧ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ਜਿਸ ਦੁਆਰਾ ਸਰੀਰ ਵਿਚੋਂ ਫਾਲਤੂ ਅਤੇ ਹਾਨੀਕਾਰਕ ਪਦਾਰਥਾਂ ਦਾ ਨਿਕਾਸ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਮਲ-ਤਿਆਗ ਪ੍ਰਣਾਲੀ ਦੇ ਮੁੱਖ ਅੰਗਾਂ ਦੇ ਨਾਂ ਲਿਖੋ । (Name the organs of Excretory System.)
ਉੱਤਰ-

• ਫੇਫੜੇ
• ਗੁਰਦੇ
• ਚਮੜੀ
• ਅੰਤੜੀਆਂ ।

ਪ੍ਰਸ਼ਨ 5.
ਮਾਸ-ਪੇਸ਼ੀਆਂ ਦੇ ਕੋਈ ਦੋ ਕੰਮ ਲਿਖੋ । (Give two functions of Muscles.)
ਉੱਤਰ-

1. ਇਹ ਸਰੀਰ ਨੂੰ ਰੂਪ ਪ੍ਰਦਾਨ ਕਰਦੀਆਂ ਹਨ ।
2. ਇਹਨਾਂ ਦੀ ਮੱਦਦ ਨਾਲ ਵਿਅਕਤੀ ਚਲਦਾ-ਫਿਰਦਾ, ਕੁੱਦਦਾ-ਟੱਪਦਾ ਅਤੇ ਸਾਹ ਆਦਿ ਲੈਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 6.
ਸਵੈ-ਇੱਛਤ ਮਾਸ-ਪੇਸ਼ੀਆਂ (Voluntary Muscles) ਕੀ ਹਨ ? (What is Voluntary Muscles ?)
ਉੱਤਰ-
ਸਵੈ-ਇੱਛਤ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਉਹ ਹਨ ਜੋ ਵਿਅਕਤੀ ਦੀ ਇੱਛਾ ਅਨੁਸਾਰ ਕੰਮ ਕਰਦੀਆਂ ਹਨ ।

ਪਸ਼ਨ 7.
ਅਣ-ਇੱਛਤ ਮਾਸ-ਪੇਸ਼ੀਆਂ (Involuntary Muscles) ਕੀ ਹਨ ? (What is Involuntary Muscles ?)
ਉੱਤਰ-
ਇਹ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਵਿਅਕਤੀ ਦੇ ਵਸ ਵਿਚ ਨਹੀਂ ਹੁੰਦੀਆਂ । ਇਹ ਵਿਅਕਤੀ ਦੀ ਇੱਛਾ ਦੇ ਬਿਨਾਂ ਕੰਮ ਕਰਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 8.
ਦਿਲ ਦੀਆਂ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਵੀ ਹੁੰਦੀਆਂ ਹਨ ? (What is Cordiac Muscles ?)
ਉੱਤਰ-
ਇਹ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਅਣ-ਇੱਛਤ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਵਰਗੀਆਂ ਹੁੰਦੀਆਂ ਹਨ । ਪਰ ਇਹ ਲਗਾਤਾਰ ਕੰਮ ਕਰਨ ਨਾਲ ਵੀ ਥੱਕਦੀਆਂ ਨਹੀਂ ।

ਪ੍ਰਸ਼ਨ 9.
ਸਰੀਰ ਵਿਚ ਕਿੰਨੇ ਗੁਰਦੇ ਹੁੰਦੇ ਹਨ ? (How many kidneys are there in our body ?)
ਉੱਤਰ-
ਦੋ ।

ਪ੍ਰਸ਼ਨ 10.
ਵਿਅਕਤੀ ਦੇ ਸਰੀਰ ਵਿਚ ਫੇਫੜਿਆਂ ਦੀ ਗਿਣਤੀ ਦੱਸੋ । (How many lungs a person possesses ?)
ਉੱਤਰ-
ਦੋ ।

ਪ੍ਰਸ਼ਨ 11. ਨਬਜ਼ ਕੀ ਹੈ ? (What is Pulse ?)
ਉੱਤਰ-
ਨਬਜ਼ ਦਰ ਦਾ ਭਾਵ ਦਿਲ ਦੀ ਧੜਕਣ ਹੈ । ਇਹ ਦਰ 72 ਤੋਂ 80 ਇਕ ਮਿੰਟ ਵਿਚ ਹੋ ਸਕਦੀ ਹੈ । ਦਿਲ ਦੀ ਧੜਕਣ ਵੀ ਨਬਜ਼ ਦੀ ਦਰ ਦੇ ਬਰਾਬਰ ਹੁੰਦੀ ਹੈ।

ਪ੍ਰਸ਼ਨ 12.
ਲਹੂ ਦਾ ਕੰਮ ਲਿਖੋ । (Write the function of the blood.)
ਉੱਤਰ-
ਲਹੂ ਸਰੀਰ ਨੂੰ ਆਕਸੀਜਨ ਸਪਲਾਈ ਕਰਦਾ ਹੈ ਅਤੇ ਵਿਅਰਥ ਪਦਾਰਥਾਂ ਨੂੰ ਸਰੀਰ ਵਿਚੋਂ ਮਲ-ਤਿਆਗ ਪ੍ਰਣਾਲੀ ਨਾਲ ਬਾਹਰ ਕੱਢਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 13.
ਨੱਕ ਰਾਹੀਂ ਸਾਹ ਲੈਣ ਦੇ ਕੀ ਲਾਭ ਹਨ ? (What are the uses of nose breathing ?)
ਉੱਤਰ-
ਨੱਕ ਰਾਹੀਂ ਸਾਹ ਲੈਣ ਨਾਲ ਹਵਾ ਸ਼ੁੱਧ ਅਤੇ ਗਰਮ ਹੋ ਕੇ ਸਰੀਰ ਵਿਚ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 14.
ਸਾਹ ਲੈਂਦੇ ਸਮੇਂ ਅਸੀਂ ਕਿਹੜੀ ਗੈਸ ਅੰਦਰ ਲੈ ਜਾਂਦੇ ਹਾਂ ? (Which gas do we take while breathing ?)
ਉੱਤਰ-
ਆਕਸੀਜਨ ।

ਪ੍ਰਸ਼ਨ 15.
ਸਰੀਰਕ ਥਕਾਵਟ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? (What do you mean by physical fatigue ?)
ਉੱਤਰ-
ਇਸ ਵਿਚ ਸਰੀਰ ਥੱਕ ਜਾਂਦਾ ਹੈ ਅਤੇ ਕੰਮ ਕਰਨ ਨੂੰ ਮਨ ਨਹੀਂ ਕਰਦਾ । ਮਾਨਸਿਕ ਥਕਾਵਟ ਮਨ ਦੀ ਥਕਾਵਟ ਹੈ ।

ਪ੍ਰਸ਼ਨ 16.
ਮਾਨਸਿਕ ਥਕਾਵਟ ਦੇ ਮੁੱਖ ਕਾਰਣ ਕੀ ਹਨ ?
ਉੱਤਰ-

• ਭੋਜਨ ਵਿਚ ਪੌਸ਼ਟਿਕ ਪਦਾਰਥਾਂ ਦੀ ਘਾਟ
• ਠੀਕ ਤਰ੍ਹਾਂ ਨੀਂਦ ਨਾ ਲੈਣਾ ।
• ਵਿਅਕਤੀ ਦੀ ਸਮਰੱਥਾ ਤੋਂ ਜ਼ਿਆਦਾ ਕੰਮ ਦਾ ਬੋਝ
• ਰੋਗ
• ਇਕਾਗਰਤਾ ਦੀ ਘਾਟ ।

ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Short Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਸਾਹ ਕਿਰਿਆ ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ? (What is Respiration ?)
ਉੱਤਰ-
ਸਾਹ ਕਿਰਿਆ ਦੋ ਕਿਰਿਆਵਾਂ ਦਾ ਮੇਲ ਹੈ : ਸਾਹ ਅੰਦਰ ਲੈ ਜਾਣ ਦੀ ਕਿਰਿਆ ਜਿਸ ਨੂੰ ਉੱਛਵਾਸ ਕਿਰਿਆ (Inspiration) ਕਹਿੰਦੇ ਹਨ ਅਤੇ ਸਾਹ ਬਾਹਰ ਕੱਢਣ ਦੀ ਕਿਰਿਆ ਜਿਸ ਨੂੰ ਨਿਰਸੁਆਹ ਕਿਰਿਆ (Expiration) ਕਹਿੰਦੇ ਹਨ | ਸਾਹ ਕਿਰਿਆ ਦਾ ਮਨੁੱਖੀ ਜੀਵਨ ਲਈ ਵਿਸ਼ੇਸ਼ ਮਹੱਤਵ ਹੈ । ਆਮ ਅਰੋਗੀ ਵਿਅਕਤੀ ਪ੍ਰਤੀ ਮਿੰਟ 20 ਤੋਂ 22 ਵਾਰ ਸਾਹ ਲੈਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਲਹੂ ਕਿਸ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ? (What is Blood ?)
ਉੱਤਰ-
ਲਹੁ ਇਕ ਕਿਸਮ ਦਾ ਤਰਲ ਪਦਾਰਥ ਹੈ । ਇਹ ਸਰੀਰ ਵਿਚ ਸ਼ਿਰਾਵਾਂ (Veins) ਅਤੇ ਧਮਨੀਆਂ ਵਿਚ ਦਿਨ-ਰਾਤ ਚੱਲਦਾ ਹੈ । ਇਹ ਗਾੜੇ ਰੰਗ ਦਾ ਨਮਕੀਨ ਪਦਾਰਥ ਹੈ । ਇਹ ਵਿਅਕਤੀ ਵਿਚ ਉਸ ਦੇ ਸਰੀਰ ਦੇ ਜਾਂ 5 ਭਾਗ ਦੇ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਲਹੂ ਦੇ ਭਾਗਾਂ ਬਾਰੇ ਤੁਸੀਂ ਕੀ ਜਾਣਦੇ ਹੋ ? (What do you know about the composition of Blood ?)
ਉੱਤਰ-
ਲਹੂ ਵਿਚ ਹੇਠ ਲਿਖੇ ਪਦਾਰਥ ਹੁੰਦੇ ਹਨ

• ਪਲਾਜ਼ਮਾ (Plasma),
• ਲਾਲ ਲਹੂ ਕਣ (Red Corpuscles),
• ਚਿੱਟੇ ਲਹੂ | ਕਣ (White Corpuscles),
• ਪਲੇਟਲੇਟਸ (Platelets) ।

ਪਲਾਜ਼ਮਾ ਪੀਲੇ ਰੰਗ ਦਾ ਨਮਕੀਨ ਪਦਾਰਥ ਹੈ । ਇਸ ਵਿਚ ਲਾਲ ਅਤੇ ਚਿੱਟੇ ਲਹੂ ਕਣ ਤੈਰਦੇ ਹਨ । ਲਾਲ ਲਹੂ ਕਣ ਗੋਲ ਅਤੇ ਦੋਨੋਂ ਪਾਸੇ ਚਿੰਬੜੇ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਦੀ ਉਮਰ 15 ਦਿਨ ਹੁੰਦੀ ਹੈ । ਚਿੱਟੇ ਲਹੂ ਕਣ ਸਰੀਰ ਦੀ ਰੋਗਾਂ ਦੇ ਹਮਲਿਆਂ ਤੋਂ ਰੱਖਿਆ ਕਰਦੇ ਹਨ । ਇਹ ਰੰਗਹੀਨ ਅਤੇ ਬੇਡੌਲ ਆਕਾਰ ਕਣਾਂ ਦੇ ਹੁੰਦੇ ਹਨ । ਪਲੇਟਲੇਟਸ ਦਾ ਆਕਾਰ \(\frac{1}{2}\) ਜਾਂ \(\frac{1}{3}\) ਨੂੰ ਹੁੰਦਾ ਹੈ । ਇਹ ਲਹੂ ਨੂੰ ਵਗਣ ਤੋਂ ਰੋਕਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 4.
ਹੂ ਦਾ ਦਬਾਅ ਕੀ ਹੁੰਦਾ ਹੈ ? (What is Blood Pressure ?)
ਉੱਤਰ-
ਸ਼ਿਰਾਵਾਂ, ਧਮਨੀਆਂ ਅਤੇ ਰੱਤ ਵਾਲਾਂ ਦੀ ਮਦਦ ਨਾਲ ਖੂਨ ਸਰੀਰ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਅੰਗਾਂ ਵਿਚ ਦੌਰਾ ਕਰਦਾ ਹੈ । ਸ਼ਿਰਾਵਾਂ ਵਿਚ ਸ਼ੁੱਧ ਅਤੇ ਧਮਨੀਆਂ ਵਿਚ ਅਧ ਲਹੂ ਕਣ ਚੱਕਰ ਲਗਾਉਂਦੇ ਹਨ । ਇਸ ਦੌਰੇ ਵਿਚ ਖੂਨ ਨਾਲੀਆਂ ਦੀਆਂ ਕੰਧਾਂ ਨਾਲ ਟਕਰਾਉਂਦਾ ਹੈ, ਜਿਸ ਨਾਲ ਦਬਾਅ ਵਧਦਾ ਹੈ । ਇਹ ਦਬਾਅ ਘੱਟ ਹੁੰਦਾ ਹੈ ਤਾਂ ਲਹੁ ਅੱਗੇ ਵਧਦਾ ਹੈ । ਖੂਨ ਦੀ ਇਸ ਵਧਣ ਅਤੇ ਘੱਟ ਹੋਣ ਦੀ ਕਿਰਿਆ ਨੂੰ ਲਹੂ ਦਾ ਦਬਾਅ (Blood Pressure) ਕਹਿੰਦੇ ਹਨ । ਇਸ ਦਬਾਅ ਨੂੰ ਮਾਪਨ ਲਈ ਸਫੀਰਾਨੋ ਮੈਨੋਮੀਟਰ (sphygne manometer) ਯੰਤਰ ਦੀ ਵਰਤੋਂ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਮਾਸ-ਪੇਸ਼ੀਆਂ ਦੇ ਕੰਮ ਦੱਸੋ । (Describe the functions of Muscles.)
ਉੱਤਰ-
ਮਾਸ-ਪੇਸ਼ੀਆਂ ਹੱਡੀਆਂ ਨਾਲ ਜੁੜੀਆਂ ਹੁੰਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਦੇ ਮੁੱਖ ਕੰਮ ਇਸ ਤਰ੍ਹਾਂ ਹਨ

• ਇਹ ਸਰੀਰ ਨੂੰ ਰੂਪ ਪ੍ਰਦਾਨ ਕਰਦੀਆਂ ਹਨ ।
• ਇਹ ਸਰੀਰ ਨੂੰ ਗਤੀ ਵਿਚ ਸਹਾਇਤਾ ਪ੍ਰਦਾਨ ਕਰਦੀਆਂ ਹਨ ।
• ਇਹਨਾਂ ਦੀ ਮਦਦ ਨਾਲ ਵਿਅਕਤੀ ਤੁਰਦਾ-ਫਿਰਦਾ, ਟੱਪਦਾ ਅਤੇ ਸਾਹ ਆਦਿ ਲੈਂਦਾ ਹੈ ।
• ਮਾਸ-ਪੇਸ਼ੀਆਂ ਛਾਤੀ ਦੇ ਪੱਠਿਆਂ ਨੂੰ ਫੈਲਣ ਵਿਚ ਮਦਦ ਕਰਦੀਆਂ ਹਨ ।
• ਇਹਨਾਂ ਰਾਹੀਂ ਸਰੀਰ ਸਮੁੱਚਾ ਵਿਕਾਸ ਕਰਦਾ ਹੈ ।
• ਮਾਸ-ਪੇਸ਼ੀਆਂ ਹੱਡੀਆਂ ਨੂੰ ਮਜ਼ਬੂਤ ਰੱਖਦੀਆਂ ਹਨ ।
• ਜੋੜਾਂ ਦਾ ਵਿਕਾਸ ਕਰਨ ਵਿਚ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਸਹਾਇਤਾ ਕਰਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਮਾਸ-ਪੇਸ਼ੀਆਂ ਕਿੰਨੀ ਕਿਸਮ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ? (Mention the types of Muscles.)
ਉੱਤਰ-
ਮਾਸ-ਪੇਸ਼ੀਆਂ ਤਿੰਨ ਕਿਸਮ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ (There are three types of the muscles )
1. ਸਵੈ-ਇੱਛਤ ਮਾਸ-ਪੇਸ਼ੀਆਂ (Voluntary Muscles)-ਸਵੈ-ਇੱਛਤ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਉਹ ਹਨ ਜੋ ਵਿਅਕਤੀ ਦੀ ਇੱਛਾ ਅਨੁਸਾਰ ਚੱਲਦੀਆਂ ਹਨ । ਉਹਨਾਂ ਨੂੰ ਜਿਵੇਂ ਸੂਚਨਾ ਮਿਲਦੀ ਹੈ ਉਸੇ ਤਰ੍ਹਾਂ ਹੀ ਕੰਮ ਕਰਦੀਆਂ ਹਨ । ਇਹ ਸਰੀਰ ਨੂੰ ਗਤੀ ਪ੍ਰਦਾਨ ਕਰਦੀਆਂ ਹਨ । ਇਹ ਸਰੀਰ ਨੂੰ ਸੰਭਾਲ ਕੇ ਰੱਖਦੀਆਂ ਹਨ ਅਤੇ ਇਸ ਵਿਚ ਗਰਮੀ ਪੈਦਾ ਕਰਦੀਆਂ ਹਨ । ਇਹ ਲੱਤਾਂ ਅਤੇ ਬਾਹਾਂ ਵਿਚ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ।

2. ਅਣ-ਇੱਛਤ ਮਾਸ-ਪੇਸ਼ੀਆਂ (Involuntary Muscles)-ਇਹ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਵਿਅਕਤੀ ਦੇ ਵਸ ਵਿਚ ਨਹੀਂ ਹੁੰਦੀਆਂ । ਇਹ ਵਿਅਕਤੀ ਦੀ ਇੱਛਾ ਦੇ ਬਿਨਾਂ ਕੰਮ ਕਰਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ । ਇਹ ਵਿਅਕਤੀ ਦੇ ਸੁੱਤਿਆਂ ਵੀ ਕੰਮ ਕਰਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ । ਇਹ ਦਿਲ, ਜਿਗਰ ਅਤੇ ਅੰਤੜੀਆਂ ਵਿਚ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ।

3. ਦਿਲ ਦੀਆਂ ਮਾਸ-ਪੇਸ਼ੀਆਂ (Cardiac Musclesਇਹ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਅਣ-ਇੱਛਤ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਵਰਗੀਆਂ ਹੁੰਦੀਆਂ ਹਨ, ਪਰ ਇਹ ਲਗਾਤਾਰ ਕੰਮ ਕਰਨ ਨਾਲ ਵੀ ਥੱਕਦੀਆਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 7.
ਚਮੜੀ ਦੇ ਬਾਰੇ ਵਿਚ ਸੰਖੇਪ ਜਾਣਕਾਰੀ ਦਿਓ । (Describe briefly about Skin.)
ਉੱਤਰ-
ਚਮੜੀ ਇਕ ਕਿਸਮ ਦਾ ਪਰਦਾ ਹੈ ਜੋ ਅੰਦਰੂਨੀ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਅਤੇ ਅੰਗਾਂ ਨੂੰ ਢੱਕ ਕੇ ਰੱਖਦਾ ਹੈ । ਇਹ ਦੋ ਕਿਸਮ ਦੀ ਹੈ-ਬਾਹਰੀ ਜਾਂ ਉੱਪਰਲੀ(Epidermis) ਅਤੇ ਹੇਠਲੀ ਜਾਂ ਅੰਦਰੂਨੀ (Endodermis) । ਉੱਪਰਲੀ ਚਮੜੀ ਵਿਚ ਛੋਟੇ-ਛੋਟੇ ਮੁਸਾਮ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਰਾਹੀਂ ਪਸੀਨਾ ਸਰੀਰ ਵਿਚੋਂ ਬਾਹਰ ਨਿਕਲਦਾ ਹੈ । ਅੰਦਰੂਨੀ ਜਾਂ ਹੇਠਲੀ ਚਮੜੀ ਵਿਚ ਚਰਬੀ ਹੁੰਦੀ ਹੈ ਜੋ ਸਰੀਰ ਵਿਚ ਗਰਮੀ ਪੈਦਾ ਕਰਨ ਵਿਚ ਸਹਾਇਤਾ ਪ੍ਰਦਾਨ ਕਰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
ਗੁਰਦਿਆਂ ਦੇ ਕੰਮ ਦੱਸੋ । (Describe the functions of the Kidneys.)
ਉੱਤਰ-
ਗੁਰਦੇ ਢਿੱਡ ਦੇ ਪਿੱਛੇ ਵਲ ਹੁੰਦੇ ਹਨ । ਇਹ ਸੰਖਿਆ ਵਿਚ ਦੋ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਦਾ ਆਕਾਰ ਸੇਮ ਦੇ ਬੀਜ ਵਰਗਾ ਹੁੰਦਾ ਹੈ ।
ਕੰਮ-

1. ਇਹਨਾਂ ਦੁਆਰਾ ਪੇਸ਼ਾਬ ਵਿਚ ਯੂਰੀਆ, ਯੂਰਿਕ ਐਸਿਡ, ਖਣਿਜ ਲੂਣ, ਪੇਸ਼ਾਬ ਦੇ ਰੂਪ ਵਿਚ ਸਰੀਰ ਤੋਂ ਬਾਹਰ ਆਉਂਦੇ ਹਨ ।
2. ਇਹ ਖੂਨ ਵਿਚ ਪਾਣੀ ਦੀ ਮਾਤਰਾ ਨੂੰ ਸਮਾਨ ਰੱਖਦੇ ਹਨ ।
3. ਇਸ ਦੇ ਫਲਸਰੂਪ ਸਰੀਰ ਵਿਚ ਐਸਿਡ ਅਤੇ ਖਾਰ ਦੀ ਮਾਤਰਾ ਵਿਚ ਸਮਾਨਤਾ ਰਹਿੰਦੀ ਹੈ |

ਪ੍ਰਸ਼ਨ 9.
ਫੇਫੜਿਆਂ ਦੀ ਸ਼ਕਤੀ ਕੀ ਹੈ ? ਇਸ ਬਾਰੇ ਲਿਖੋ । [ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ-2] (What is Vital Capacity ? Write briefly.)
ਉੱਤਰ-
ਫੇਫੜਿਆਂ ਦੀ ਸ਼ਕਤੀ (Capacity of Lungs or Vital Capacity)-ਉਹ ਕਿਰਿਆ ਜਿਸ ਦੁਆਰਾ ਡੂੰਘੇ ਸਾਹ ਲੈਣ ਨਾਲ ਹਵਾ ਦੀ ਮਾਤਰਾ ਅੰਦਰ ਲਿਜਾਈ ਜਾਂਦੀ ਹੈ ਅਤੇ ਫੇਰ ਜ਼ੋਰ ਨਾਲ ਬਾਹਰ ਕੱਢੀ ਜਾਂਦੀ ਹੈ, ਉਸ ਨੂੰ ਫੇਫੜਿਆਂ ਦੀ ਸ਼ਕਤੀ (Vital Capacity) ਕਹਿੰਦੇ ਹਨ ।

ਸਾਧਾਰਨ ਤੌਰ ‘ਤੇ ਅਸੀਂ ਲਗਪਗ 500 ਸੀ.ਸੀ. ਹਵਾ ਲੈ ਜਾਂਦੇ ਹਾਂ ਅਤੇ ਲਗਪਗ 1500 ਸੀ. ਸੀ. ਹੋਰ ਹਵਾ ਕੱਢ ਸਕਦੇ ਹਾਂ । ਇੰਨਾ ਕਰਨ ਤੇ ਵੀ ਸਾਡੇ ਫੇਫੜੇ ਹਵਾ ਤੋਂ ਰਹਿਤ ਨਹੀਂ ਹੋ ਜਾਂਦੇ । ਤਦ ਵੀ ਲਗਪਗ 500 ਸੀ. ਸੀ. ਹਵਾ ਇਹਨਾਂ ਵਿਚ ਰਹਿ ਜਾਂਦੀ ਹੈ । ਫੇਫੜਿਆਂ ਦੀ ਇਸ ਸ਼ਕਤੀ ਜਾਂ ਸਮਰੱਥਾ ਨੂੰ ਮਾਪਣ ਲਈ ਸਪਾਇਰੋ ਮੀਟਰ ਯੰਤਰ ਦਾ ਪ੍ਰਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 10.
ਥਕਾਵਟ ਕੀ ਹੈ ? (What is Fatigue ?)
ਉੱਤਰ-
ਥਕਾਵਟ (Fatigue)-ਮਾਸਪੇਸ਼ੀਆਂ ਵਿਚ ਕੰਮ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਦੀ ਘਾਟ ਥਕਾਵਟ ਅਖਵਾਉਂਦੀ ਹੈ ਜਦੋਂ ਸਾਡੇ ਸਰੀਰ ਦੀਆਂ ਮਾਸਪੇਸ਼ੀਆਂ ਲਗਾਤਾਰ ਕੰਮ ਕਰਦੀਆਂ ਹਨ ਤਾਂ ਉਨ੍ਹਾਂ ਵਿਚ ਲੈਕਟਿਨ ਐਸਿਡ ਇਕੱਠਾ ਹੋ ਜਾਂਦਾ ਹੈ ਜਿਸ ਨਾਲ ਸਰੀਰ ਥੱਕ ਜਾਂਦਾ ਹੈ । ਥਕਾਵਟ ਜ਼ਿਆਦਾ ਦੇਰ ਖੇਡਣ, ਤੁਰਨ ਜਾਂ ਜ਼ੋਰ ਵਾਲੇ ਕੰਮ ਕਾਰਨ ਹੁੰਦੀ ਹੈ । ਇਹ ਨੀਂਦ, ਆਰਾਮ, ਮਾਲਸ਼ ਤੇ ਮਨੋਰੰਜਨ ਕਿਰਿਆ ਨਾਲ ਦੂਰ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ।

ਪ੍ਰਸ਼ਨ 11.
ਥਕਾਵਟ ਕਿੰਨੇ ਪ੍ਰਕਾਰ ਦੀ ਹੁੰਦੀ ਹੈ ? (What are the kinds of Fatigue ?)
ਉੱਤਰ-
ਥਕਾਵਟ ਦੋ ਤਰ੍ਹਾਂ ਦੀ ਹੁੰਦੀ ਹੈ –

• ਸਰੀਰਕੇ
• ਮਾਨਸਿਕ ।

ਪ੍ਰਸ਼ਨ 12.
ਲਹੂ ਗੇੜ ਪ੍ਰਣਾਲੀ ਦੇ ਅੰਗਾਂ ਦੇ ਨਾਂ ਲਿਖੋ । (Name the organs of blood circulation.)
ਉੱਤਰ-

• ਦਿਲ
• ਆਰਟਰੀਮ ਸ਼ਿਰਾਵਾਂ
• ਧਮਨੀਆਂ ।

ਪ੍ਰਸ਼ਨ 13.
ਨਬਜ਼ ਕੀ ਹੈ ? (What is pulse ?)
ਉੱਤਰ-
ਲਹੂ ਦੀ ਤੇਜ਼ ਗਤੀ ਕਾਰਨ ਲਹੂ ਦੀਆਂ ਧਮਨੀਆਂ ਦੀਆਂ ਦੀਵਾਰਾਂ ਵੱਧਦੀਆਂ ਅਤੇ ਘੱਟਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ । ਇਸ ਕਿਰਿਆ ਨੂੰ ਨਬਜ਼ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਜੋ ਆਮ ਵਿਅਕਤੀ ਵਿਚ 76 ਤੋਂ 80 ਵਾਰੀ ਪ੍ਰਤੀ ਮਿੰਟ ਹੁੰਦੀ ਹੈ । ਨਬਜ਼ ਨੂੰ ਇਕ ਹੱਥ ਨਾਲ ਦੂਸਰੀ ਬਾਜੂ ਤੋਂ ਉਂਗਲਾਂ ਦਾ ਦਬਾਅ ਪਾ ਕੇ ਦੇਖਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
ਖਿਡਾਰੀਆਂ ਦੀ ਨਬਜ਼ ਇਕ ਮਿੰਟ ਵਿਚ 60 ਤੋਂ ਘੱਟ ਵੀ ਹੋ ਸਕਦੀ ਹੈ ।

ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ (Long Answer Type Questions)

ਪ੍ਰਸ਼ਨ 1.
ਲਹੂ ਦੇ ਵੱਖ-ਵੱਖ ਅੰਸ਼ਾਂ ਦਾ ਵਰਣਨ ਕਰੋ । ਲਹੂ ਦੇ ਮੁੱਖ ਕੰਮ ਕੀ ਹਨ ? (What is composition of Blood ? Discuss its functions.)
ਉੱਤਰ-
ਲਹੂ ਅਤੇ ਉਸ ਦੇ ਅੰਸ਼ (Blood and its Parts)-ਰਕਤ ਜਾਂ ਲਹੂ ਇਕ ਪ੍ਰਕਾਰ ਦਾ ਤਰਲ ਪਦਾਰਥ ਹੈ ਜਿਸ ਦਾ ਨਿਰਮਾਣ ਖਾਣ ਅਤੇ ਪੀਣ ਵਾਲੇ ਪਦਾਰਥਾਂ ਰਾਹੀਂ ਹੁੰਦਾ ਹੈ । ਲਹੂ ਸਾਡੇ ਸਰੀਰ ਵਿਚ ਇਕ ਮਹੱਤਵਪੂਰਨ ਪਦਾਰਥ ਹੈ । ਇਹ ਆਦਮੀ ਦੇ ਸਰੀਰ ਵਿਚ ਉਸ ਦੇ ਸਰੀਰ ਦੇ ਭਾਰ ਦਾ ਬਾਵਾਂ \(\left(\frac{1}{12}\right)\) ਨੇ ਹਿੱਸਾ ਹੁੰਦਾ ਹੈ । ਆਮ ਤੌਰ ‘ਤੇ ਇਕ ਨੌਜਵਾਨ ਦੇ ਸਰੀਰ ਵਿਚ ਖੂਨ ਦੀ ਮਾਤਰਾ 12-13 ਪਿੰਟ (Pint) ਤਕ ਹੁੰਦੀ ਹੈ । ਕਈ | ਹਾਲਤਾਂ ਵਿਚ ਇਹ ਮਾਤਰਾ ਘੱਟ ਜਾਂ ਵੱਧ ਵੀ ਹੋ ਸਕਦੀ ਹੈ । ਤਰਲ (liquid) ਪਦਾਰਥ ਨਿਕਲਦਾ ਹੈ । ਇਸ ਤਰਲ ਪਦਾਰਥ ਦਾ ਨਾਂ ਹੀ ‘ਲਹੁ’ ਹੈ । ਦੇਖਣ ਨੂੰ ਤਾਂ ਇਹ ਲਾਲ ਰੰਗ ਦਾ ਮਾਲੂਮ ਹੁੰਦਾ ਹੈ, ਪਰ ਅਸਲ ਵਿਚ ਅਜਿਹਾ ਨਹੀਂ । ਜੇ ਅਸੀਂ ਇਸ ਤਰਲ ਪਦਾਰਥ ਅਰਥਾਤ ਲਹੂ ਨੂੰ ਖੁਰਦਬੀਨ (Microscope) ਵਿਚ ਦੇਖੀਏ ਤਾਂ ਸਾਨੂੰ ਪਤਾ ਲੱਗੇਗਾ ਕਿ ਲਹੂ ਵਿਚ ਬਹੁਤ ਛੋਟੇ-ਛੋਟੇ ਕਣ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਕਣਾਂ ਦਾ ਰੰਗ ਚਿੱਟਾ ਤੇ ਲਾਲ ਹੁੰਦਾ ਹੈ ।

ਇਹਨਾਂ ਨੂੰ ਲਾਲ ਲਹੂ ਕਣ (Red Corpuscles) ਅਤੇ ਚਿੱਟੇ ਲਹੂ ਕਣ (White Corpuscles) ਕਹਿੰਦੇ ਹਨ । ਇਹ ਇਕ ਕਿਸਮ ਦੇ ਹਲਕੇ ਪੀਲੇ ਤਰਲ (Yellow Liquid) ਵਿਚ ਤੈਰਦੇ ਹਨ, ਜਿਸ ਨੂੰ ਪਲਾਜ਼ਮਾ (Plasma) ਕਹਿੰਦੇ ਹਨ । ਲਹੂ ਵਿਚ ਮੁੱਖ ਤੌਰ ‘ਤੇ ਜੋ ਪਦਾਰਥ ਹਨ ਉਹਨਾਂ ਨੂੰ ਹੇਠ ਦਿੱਤੇ ਗਏ ਚਾਰਟ ਦੁਆਰਾ ਇਸ ਤਰ੍ਹਾਂ ਪ੍ਰਗਟ ਕੀਤਾ ਜਾਂਦਾ ਹੈ-

(i) ਪਲਾਜ਼ਮਾ (Plasma) – ਇਹ ਲਹੂ ਦੇ ਹਲਕੇ ਪੀਲੇ ਰੰਗ ਦਾ ਪਾਰਦਰਸ਼ਕ (Transparent) ਪਦਾਰਥ ਹੁੰਦਾ ਹੈ । ਇਸ ਵਿਚ ਲਾਲ ਅਤੇ ਚਿੱਟੇ ਲਹੂ ਦੇ ਕਣ ਤੈਰਦੇ ਹਨ । ਇਸ ਵਿਚ 90% ਪਾਣੀ ਤੇ 10% ਠੋਸ ਪਦਾਰਥ ਘੁਲੇ ਹੁੰਦੇ ਹਨ । ਇਹ ਠੋਸ ਪਦਾਰਥ ਪ੍ਰੋਟੀਨ, ਖਣਿਜ ਲੂਣ ਤੇ ਚਰਬੀ (Fat) ਹੁੰਦੇ ਹਨ | ਪਲਾਜ਼ਮਾ

(Plasma) ਲਹੂ ਦੇ ਦਬਾਅ (Pressure) ਨੂੰ ਠੀਕ ਰੱਖਦਾ ਹੈ ਤੇ ਲਾਲ ਅਤੇ ਚਿੱਟੇ ਲਹੂ ਕਣਾਂ ਨੂੰ ਲਿਜਾਣ ਵਿਚ ਮਦਦ ਦਿੰਦਾ ਹੈ । ਇਸ ਦੀ ਪ੍ਰੋਟੀਨ ਲਹੁ ਨੂੰ ਵਹਿਣ ਤੋਂ ਰੋਕਣ ਵਿਚ ਮਦਦ ਦਿੰਦੀ ਹੈ ।

(ii) ਲਾਲ ਲਹੂ ਕਣ (Red Corpuscles) – ਆਦਮੀ ਦੇ ਲਾਲ ਲਹੂ ਕਣ ਗੋਲ ਤੇ ਦੋਹਾਂ ਪਾਸਿਆਂ ਤੋਂ ਚਿਪਕੇ ਹੁੰਦੇ ਹਨ । ਆਦਮੀ ਦੇ ਇਕ ਘਣ ਮਿਲੀ ਮੀਟਰ ਲਹੂ ਵਿਚ ਇਹਨਾਂ ਦੀ ਗਿਣਤੀ ਲਗਪਗ 50,00,000 ਹੁੰਦੀ ਹੈ । ਇਹ ਇੰਨੇ ਛੋਟੇ ਹੁੰਦੇ ਹਨ ਕਿ ਜੇਕਰ ਕੰਢੇ ਨਾਲ ਮਿਲਾ ਕੇ ਰੱਖੇ ਜਾਣ ਤਾਂ 2.5 ਵਰਗ ਸੈਂਟੀਮੀਟਰ ਥਾਂ ਵਿਚ ਲਗਪਗ 1 ਕਰੋੜ ਆ ਜਾਣਗੇ । ਇਹਨਾਂ ਦੀ ਬਾਹਰਲੀ ਪਰਤ ਇਕ ਲਚਕੀਲੇ ਠੋਸ ਦੇ ਰੂਪ ਵਿਚ ਹੁੰਦੀ ਹੈ ਜਿਸ ਦੇ ਅੰਦਰ ਪੀਲੇ ਰੰਗ ਦਾ ਲੋਹੇ ਦਾ ਇਕ ਰੰਗ (Pigment) ਹੁੰਦਾ ਹੈ ਜਿਸ ਨੂੰ ਹਿਮੋਗਲੋਬਿਨ (Haemoglobin). ਕਹਿੰਦੇ ਹਨ ਜੋ ਕਿ ਲੋਹੇ ਅਤੇ ਪ੍ਰੋਟੀਨ ਵਸਤਾਂ ਨਾਲ ਮਿਲ ਕੇ ਬਣਦਾ ਹੈ । ਹਿਮੋਗਲੋਬਿਨ ਆਕਸੀਜਨ ਨੂੰ ਚੂਸ ਲੈਂਦਾ ਹੈ ਜਿਸ ਕਾਰਨ ਇਸ ਦਾ ਰੰਗ ਚਮਕਦਾਰ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਹ ਆਕਸੀ-ਹਿਮੋਗਲੋਬਿਨ (Oxy Haemoglobin) ਵਿਚ ਬਦਲ ਜਾਂਦਾ ਹੈ । ਇਸ ਪਦਾਰਥ ਦੇ ਕਾਰਨ ਖੂਨ ਫੇਫੜਿਆਂ ਵਿਚੋਂ ਆਕਸੀਜਨ ਚੂਸ ਕੇ ਸਰੀਰ ਦੇ ਹਰ ਹਿੱਸੇ ਤਕ ਪਹੁੰਚਾਉਂਦਾ ਹੈ । ਲੜਕੀਆਂ ਵਿਚ ਲਾਲ ਲਹੂ ਕਣ ਲੜਕਿਆਂ ਨਾਲੋਂ ਘੱਟ ਹੁੰਦੇ ਹਨ । ਜ਼ਿਆਦਾ ਕਸਰਤ ਕਰਨ ਤੇ ਉਚਾਈ (Heights) ਉੱਤੇ ਲਾਲ ਕਣਾਂ ਦੀ ਗਿਣਤੀ ਵੱਧ ਜਾਂਦੀ ਹੈ ।

(iii) ਚਿੱਟੇ ਲਹੂ ਕਣ (White Corpuscles) – ਸਰੀਰ ਦੀ ਤੁਲਨਾ ਇਕ ਰਾਜ ਨਾਲ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ । ਜਿਸ ਤਰ੍ਹਾਂ ਰਾਜ ਦੀ ਰੱਖਿਆ ਲਈ ਫ਼ੌਜ ਦਾ ਪ੍ਰਬੰਧ ਹੁੰਦਾ ਹੈ, ਉਸੇ ਤਰ੍ਹਾਂ ਸਰੀਰ ਰੂਪੀ ਰਾਜ ਦੇ ਲਈ ਲਹੂ ਕਣ ਰੂਪੀ ਫ਼ੌਜ ਦਾ ਪ੍ਰਬੰਧ ਹੁੰਦਾ ਹੈ । ਚਿੱਟੇ ਲਹੂ ਕਣਾਂ ਦੀ ਗਿਣਤੀ ਲਾਲ ਲਹੂ ਕਣਾਂ ਨਾਲੋਂ ਘੱਟ ਹੁੰਦੀ ਹੈ | ਸਰੀਰ ਵਿਚ ਲਗਪਗ 600 ਲਾਲ ਲਹੂ ਕਣਾਂ ਮਗਰੋਂ ਕੇਵਲ ਇਕ ਚਿੱਟਾ ਲਹੂ ਕਣ ਹੁੰਦਾ ਹੈ । ਇਕ ਘਣ ਕਿਲੋ ਲਹੂ ਵਿਚ ਚਿੱਟੇ ਲਹੂ ਕਣਾਂ ਦੀ ਗਿਣਤੀ ਲਗਪਗ 8000 ਤੋਂ 10000 ਦੇ ਲਗਪਗ ਹੁੰਦੀ ਹੈ । ਇਹ ਰੰਗਹੀਣ ਤੇ ਬੇਡੌਲ (irregular) ਆਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਦੀ ਮਦਦ ਨਾਲ ਸਰੀਰ ਰੋਗਾਂ ਦਾ ਟਾਕਰਾ ਕਰਦਾ ਹੈ । ਇਹਨਾਂ ਦਾ ਕੰਮ ਰੋਗਾਂ ਦੇ ਜੀਵਾਣੂਆਂ (germs) ਨੂੰ ਘੇਰ ਕੇ ਉਹਨਾਂ ਦਾ ਖ਼ਾਤਮਾ ਕਰਨਾ ਹੈ | ਸਰੀਰ ਵਿਚ ਸੱਟ ਆਦਿ ਲੱਗਣ ਕਾਰਨ ਇਹੀ ਜ਼ਖ਼ਮਾਂ ਨੂੰ ਭਰਨ ਵਿਚ ਸਹਾਇਕ ਹੁੰਦੇ ਹਨ ।

(iv) ਪਲੇਟਲੇਟਸ (Platelets) -ਆਦਮੀ ਦੇ ਹੁ ਵਿਚ ਲਾਲ ਤੇ ਚਿੱਟੇ ਕਣਾਂ ਤੋਂ ਬਿਨਾਂ ਇਕ ਤੀਜੀ ਕਿਸਮ ਦੇ ਲਹੂ ਕਣ ਵੀ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਨੂੰ ਪਲੇਟਲੇਟਸ (Platelets) ਕਹਿੰਦੇ ਹਨ । ਇਹ ਲਾਲ ਅਤੇ ਚਿੱਟੇ ਲਹੂ ਕਣਾਂ ਤੋਂ ਬਿਲਕੁਲ ਵੱਖਰੇ ਹਨ । ਇਹ ਲਾਲ ਲਹੂ ਕਣਾਂ \(\frac{1}{2}\) ਜਾਂ \(\frac{1}{3}\) ਹੁੰਦੇ ਹਨ । ਲਹੂ ਦੇ ਇਕ ਘਣ ਮਿਲੀਮੀਟਰ ਵਿਚ ਇਹਨਾਂ ਦੀ ਸੰਖਿਆ ਲਗਪਗ 3 ਲੱਖ ਹੁੰਦੀ ਹੈ । ਇਹ ਚਿੱਟੇ ਤੇ ਬੇਡੌਲ (irregular) ਆਕਾਰ ਦੇ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਦਾ ਮੁੱਖ ਕੰਮ ਲਹੂ ਨੂੰ ਵਹਿਣ ਤੋਂ ਰੋਕਣਾ ਹੈ ।

ਲਹੂ ਦੇ ਕੰਮ (Functions of Blood)-ਖੂਨ ਦੇ ਕੰਮ ਹੇਠ ਲਿਖੇ ਹੁੰਦੇ ਹਨ –

• ਲਹੂ ਸਾਡੇ ਭੋਜਨ ਦੇ ਪਚੇ ਹੋਏ ਹਿੱਸੇ ਨੂੰ ਸਰੀਰ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਅੰਗਾਂ ਤਕ ਪਹੁੰਚਾਉਣ ਦਾ ਕੰਮ ਕਰਦਾ ਹੈ ।
• ਹੁ ਹੀ ਸਰੀਰ ਵਿਚੋਂ ਜ਼ਹਿਰੀਲੇ ਤੇ ਵਿਅਰਥ ਪਦਾਰਥ ਨੂੰ ਬਾਹਰ ਕੱਢਣ ਵਿਚ ਮਦਦ ਕਰਦਾ ਹੈ । ਇਹ ਇਹਨਾਂ ਪਦਾਰਥਾਂ ਨੂੰ ਆਪਣੇ ਅੰਦਰ ਘੋਲ ਕੇ ਗੁਰਦੇ ਵਿਚ ਲੈ ਜਾਂਦਾ ਹੈ, ਜਿੱਥੇ ਉਹ ਪੇਸ਼ਾਬ (Urine) ਦੇ ਰੂਪ ਵਿਚ ਬਾਹਰ ਨਿਕਲਦੇ ਹਨ ।
• ਲਹੂ ਵਿਚ ਮੌਜੂਦ ਲਾਲ ਲਹੂ ਕਣ (Red Corpuscles) ਫੇਫੜਿਆਂ ਵਿਚੋਂ ਆਕਸੀਜਨ ਚੂਸ ਕੇ ਸਰੀਰ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਭਾਗਾਂ ਵਿਚ ਲਿਜਾਂਦੇ ਹਨ ।
• ਲਾਲ ਲਹੂ ਕਣ ਹੀ ਆਕਸੀਜਨ ਕਿਰਿਆ ਤੋਂ ਮਗਰੋਂ ਬਣੀ ਕਾਰਬਨ-ਡਾਈਆਕਸਾਈਡ (Carbon Dioxide) ਨੂੰ ਫੇਫੜਿਆਂ ਵਿਚ ਲਿਆ ਕੇ ਬਾਹਰ ਕੱਢਣ ਦਾ ਕੰਮ ਕਰਦੇ ਹਨ ।
• ਲਹੂ ਦੇ ਚਿੱਟੇ ਲਹੂ ਕਣ (White Corpuscles) ਸਰੀਰ ਦੀ ਜਰਮਾਂ ਜਾਂ ਕੀਟਾਣੂਆਂ ਤੋਂ ਰੱਖਿਆ ਕਰਦੇ ਹਨ ।
• ਲਹੂ ਪਲੇਟਲੇਟਸ ਸੱਟ ਲੱਗਣ ਵੇਲੇ ਲਹੁ ਨੂੰ ਸਰੀਰ ਤੋਂ ਬਾਹਰ ਵਹਿ ਜਾਣ ਤੋਂ ਰੋਕਦੇ ਹਨ ।
• ਲਹੁ ਹਾਰਮੋਨਜ਼ (Hormones) ਨੂੰ ਇਕ ਥਾਂ ਤੋਂ ਦੂਜੀ ਥਾਂ ਲਿਜਾਣ ਦਾ ਕੰਮ ਕਰਦਾ ਹੈ ।
• ਲਹੁ ਰਾਹੀਂ ਸਰੀਰ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਅੰਗ ਆਪਸ ਵਿਚ ਮਿਲੇ ਰਹਿੰਦੇ ਹਨ ਅਤੇ ਸੁੱਕ ਕੇ ਨਸ਼ਟ ਹੋਣ ਤੋਂ ਬਚੇ ਰਹਿੰਦੇ ਹਨ ।
• ਹੂ ਰਾਹੀਂ ਹੀ ਸਰੀਰ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਅੰਗਾਂ ਦਾ ਤਾਪਮਾਨ ਇੱਕੋ ਜਿਹਾ ਰਹਿੰਦਾ ਹੈ ।

ਸੰਖੇਪ ਵਿਚ ਅਸੀਂ ਇਹ ਆਖਾਂਗੇ ਕਿ ਖ਼ੂਨ ਜੀਵਨ ਪ੍ਰਦਾਨ ਕਰਨ ਵਾਲਾ ਹੈ । ਜੇਕਰ ਕਿਸੇ ਅੰਗ ਵਿਚ ਖੂਨ ਦਾ ਪ੍ਰਵਾਹ ਨਾ ਹੋਵੇ ਤਾਂ ਉਹ ਅੰਗ ਪੀਲਾ ਪੈ ਜਾਂਦਾ ਹੈ ਅਤੇ ਕਮਜ਼ੋਰ ਹੋ ਜਾਂਦਾ ਹੈ । ਵਧੇਰੇ ਸਮੇਂ ਤਕ ਇਸ ਕੂਮ ਦੇ ਬੰਦ ਰਹਿਣ ਨਾਲ ਉਹ ਅੰਗ ਮਰ ਵੀ ਸਕਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 2.
ਸਾਹ-ਪ੍ਰਣਾਲੀ ਦੇ ਅੰਗਾਂ ਦੇ ਨਾਂ ਲਿਖੋ । ਸਾਹ-ਪ੍ਰਣਾਲੀ ਉੱਤੇ ਕਸਰਤਾਂ ਦੇ ਪ੍ਰਭਾਵ ਲਿਖੋ । (Mention the main organs of Respiration. Discuss the effects of Exercises on Respiratory System.)
ਉੱਤਰ-
ਸਾਹ ਲੈਣ ਅਤੇ ਛੱਡਣ ਦੀ ਕਿਰਿਆ ਨੂੰ ਸਾਹ-ਕਿਰਿਆ (Respiration) ਕਹਿੰਦੇ ਹਨ । ਇਸ ਕਿਰਿਆ ਦੁਆਰਾ ਮਨੁੱਖ ਹਵਾ ਦੇ ਨਾਲ ਆਕਸੀਜਨ ਫੇਫੜਿਆਂ ਵਿਚ ਲੈ ਜਾਂਦਾ ਹੈ ਅਤੇ ਹਵਾ ਦੇ ਨਾਲ ਸਰੀਰ ਵਿਚ ਪੈਦਾ ਹੋਈ ਕਾਰਬਨ-ਡਾਈਆਕਸਾਈਡ ਬਾਹਰ ਕੱਢ ਦਿੰਦਾ ਹੈ । ਸਾਹ-ਕਿਰਿਆ ਵਿਚ ਕਈ ਅੰਗ ਜਿਵੇਂ ਨੱਕ, ਸਾਹ ਨਲੀ ਅਤੇ ਫੇਫੜੇ ਆਦਿ ਕੰਮ ਕਰਦੇ ਹਨ ।

ਸਾਹ-ਪ੍ਰਣਾਲੀ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਅੰਗ ਹੇਠ ਲਿਖੇ ਹਨ

• ਨੱਕ (Nose)
• ਗਨਿਕਾ ਜਾਂ ਸੰਘ (Pharynx)
• ਸੁਰ-ਯੰਤਰ ਜਾਂ ਕੰਠ (Larynx)
• ਸੁਆਸ ਨਲੀ ਜਾਂ ਟੱਟੂਆ (Wind-Pipe or Trachea)
• ਸੁਆਸ ਨਲੀਆਂ (Bronchial Tubes).
• ਫੇਫੜੇ (Lungs) ।

1. ਨੱਕ (Nose-ਇਸ ਦੀ ਥਾਂ ਦੋਨਾਂ ਅੱਖਾਂ ਦੇ ਵਿਚਕਾਰ ਹੈ | ਸਾਹ ਲੈਣ ਦੀ ਕਿਰਿਆ ਨੱਕ ਤੋਂ ਆਰੰਭ ਹੁੰਦੀ ਹੈ । ਨੱਕ ਵਿਚ ਦੋ ਛੇਕ ਹੁੰਦੇ ਹਨ । ਇਨ੍ਹਾਂ ਨੂੰ ਨਾਸਾਂ (Nostrils) ਕਹਿੰਦੇ ਹਨ | ਨਾਸਾਂ ਦੇ ਅੰਦਰਲੇ ਹਿੱਸੇ ਵਿਚ ਛੋਟੇ-ਛੋਟੇ ਵਾਲ ਹੁੰਦੇ ਹਨ । ਇਹ ਹਵਾ ਨੂੰ ਸ਼ੁੱਧ ਕਰਕੇ ਅੰਦਰ ਜਾਣ ਦਿੰਦੇ ਹਨ । ਇਹਨਾਂ ਦੀ ਦੀਵਾਰ ਇਕ ਝਿੱਲੀ ਦੀ ਬਣੀ ਹੁੰਦੀ ਹੈ ਜਿਸ ਨਾਲ ਖ਼ਾਸ ਵ ਬਣਦਾ ਹੈ । ਇਹ ਤ੍ਰ ਹਵਾ ਦੇ ਕੀਟਾਣੂਆਂ ਨੂੰ ਨਸ਼ਟ ਕਰਦਾ ਹੈ ਅਤੇ ਹਵਾ ਨੂੰ ਠੰਢਾ ਰੱਖਦਾ ਹੈ । ਇਸ ਦੇ ਪਿਛਲੇ ਹਿੱਸੇ ਵਿਚ ਸੁੰਘਣ ਦੀਆਂ ਗਿਆਨ-ਇੰਦਰੀਆਂ ਹੁੰਦੀਆਂ ਹਨ । ਇਹ ਹਿੱਸਾ ਦੋ ਛੇਕਾਂ ਦੁਆਰਾ ਕੰਨ ਵਿਚ ਖੁੱਲ੍ਹਦਾ ਹੈ । ਨਾਸਾਂ ਵਿਚ ਲੱਗੇ ਹੋਏ ਵਾਲਾਂ ਵਿਚੋਂ ਜਦੋਂ ਹਵਾ ਨਿਕਲਦੀ ਹੈ, ਉਸ ਵਿਚੋਂ ਠੋਸ ਕਣ ਉੱਥੇ ਹੀ ਰਹਿ ਜਾਂਦੇ ਹਨ । ਦੂਸਰੇ ਨੱਕ ਦੀ ਖਿੱਲੀ ਦੇ ਸੰਪਰਕ ਵਿਚ ਆ ਕੇ ਹਵਾ ਗਰਮ ਹੋ ਜਾਂਦੀ ਹੈ ਜਿਸ ਨਾਲ ਫੇਫੜਿਆਂ ਆਦਿ ਵਿਚ ਠੰਢ ਲੱਗਣ ਦਾ ਡਰ ਨਹੀਂ ਰਹਿੰਦਾ । ਇਸ ਦੇ ਉਲਟ ਮੂੰਹ ਰਾਹੀਂ ਸਾਹ ਲੈਣ ਨਾਲ ਨਾ ਤਾਂ ਹਵਾ ਛਣ ਕੇ ਹੀ ਅੰਦਰ ਜਾਂਦੀ ਹੈ ਤੇ ਨਾ ਹੀ ਗਰਮ ਹੋ ਕੇ । ਇਸ ਲਈ ਇਹ ਜ਼ਰੂਰੀ ਹੈ ਕਿ ਸਾਹ ਨੱਕ ਰਾਹੀਂ ਲਿਆ ਜਾਵੇ, ਮੂੰਹ ਰਾਹੀਂ ਨਹੀਂ ।

2. ਸ਼ਨਿਕਾ (Pharynx) ਜਾਂ ਸੰਘ-ਇਹ ਅੰਗ (Organ) ਗਲੇ ਦੀਆਂ ਗਿਲਟੀਆਂ (Tonsils) ਦੇ ਪਿੱਛੇ ਸਥਿਤ ਹੈ । ਇਸ ਦਾ ਆਕਾਰ ਕੀਪ (Funnel) ਵਰਗਾ ਹੁੰਦਾ ਹੈ । ਇਹ ਛੋਟੀਆਂ-ਛੋਟੀਆਂ ਹੱਡੀਆਂ ਨਾਲ ਮਿਲ ਕੇ ਬਣੀ ਹੋਈ ਇਕ ਲੱਛੇਦਾਰ ਨਲੀ ਹੈ ਜੋ ਨੱਕ ਦੇ ਉੱਪਰਲੇ ਹਿੱਸੇ ਤੋਂ ਸ਼ੁਰੂ ਹੋ ਕੇ ਜੀਭ ਦੀ ਜੜ੍ਹ ਤਕ ਜਾਂਦੀ ਹੈ । ਇਸ ਪ੍ਰਕਾਰ ਕੰਠ-ਸੰਘ ਜਾਂ ਨਿਕਾ ਉਹ ਸਥਾਨ ਹੈ ਜਿੱਥੇ ਹਵਾ ਅਤੇ ਭੋਜਨ ਦੀਆਂ ਨਾਲੀਆਂ ਮਿਲਦੀਆਂ ਹਨ । ਭੋਜਨ ਦੀ ਨਾਲੀ ਹਵਾ ਦੀ ਨਾਲੀ ਤੋਂ ਪਿੱਛੋਂ ਹੁੰਦੀ ਹੈ । ਹਵਾ ਦੀ ਨਾਲੀ ਤੇ ਇਕ ਢੱਕਣ ਹੁੰਦਾ ਹੈ ਜਿਸ ਨੂੰ ਕੰਠ ਵਿਧਾਨ (Epiglottis) ਕਹਿੰਦੇ ਹਨ । ਇਹ ਢੱਕਣ ਭੋਜਨ ਨੂੰ ਨਿਕਲਦੇ ਸਮੇਂ ਹਵਾ ਨਾਲੀ ਨੂੰ ਬੰਦ ਕਰ ਦਿੰਦਾ ਹੈ, ਜਿਸ ਪ੍ਰਕਾਰ ਇਹ ਭੋਜਨ ਨੂੰ ਹਵਾ ਨਾਲੀ ਵਿਚ ਜਾਣ ਤੋਂ ਰੋਕਦਾ ਹੈ ।

3. ਸੁਰ-ਯੰਤਰ ਜਾਂ ਕੰਠ (Larynx)-ਇਹ ਹਵਾ ਨਲੀ ਦਾ ਉੱਪਰਲਾ ਮੋਟਾ ਅਤੇ ਚੌੜਾ ਬਕਸੇ ਜਿਹਾ ਹਿੱਸਾ ਹੈ । ਇਸੇ ਵਿਚੋਂ ਆਵਾਜ਼ ਪੈਦਾ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਇਸ ਨੂੰ ਸੁਰ ਵਾਲਾ ਡੱਬਾ (Sound Box) ਵੀ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਇੱਥੋਂ ਹੋ ਕੇ ਹਵਾ ਸਾਹ-ਨਲੀ ਜਾਂ ਟੱਟੂਆ (Trachea) ਵਿਚ ਪਹੁੰਚਦੀ ਹੈ । ਸੁਰ-ਯੰਤਰ ਦੇ ਮੂੰਹ ‘ਤੇ ਹੱਡੀਆਂ (Cartilages) ਦਾ ਇਕ ਢੱਕਣ ਰਹਿੰਦਾ ਹੈ, ਜਿਸ ਨੂੰ ਉਪ-ਜੀਵ ਕਹਿੰਦੇ ਹਨ । ਇਹ ਢੱਕਣ ਅਕਸਰ ਸਿੱਧਾ ਖੜਾ ਰਹਿੰਦਾ ਹੈ ਤਾਂ ਜੋ ਹਵਾ ਆਸਾਨੀ ਨਾਲ ਦਾਖ਼ਲ ਹੋ ਸਕੇ |

4. ਸੁਆਸ ਨਲੀ ਜਾਂ ਟੱਟੂਆ (Wind-Pipe or Trachea)-ਸੁਆਸ ਨਲੀ 4″ ਲੰਬੀ ਅਤੇ \(\frac{3 “}{4}\) ਵਿਆਸ ਦੀ ਇਕ ਨਾਲੀ ਹੈ ।
ਇਹ ਸ਼ਰ-ਯੰਤਰ ਦੇ ਥੱਲੇ ਤੋਂ ਆਰੰਭ ਹੋ ਕੇ ਛਾਤੀ ਦੇ ਅੰਦਰ ਹੇਠਾਂ ਵੱਲ ਜਾਂਦੀ ਹੈ । ਇਹ ਉਪ-ਹੱਡੀਆਂ ਦੇ ਅਧੂਰੇ ਛੱਲਿਆਂ ਨਾਲ ਮਿਲ ਕੇ ਬਣਦੀ ਹੈ, ਜੋ ਪਿੱਛੇ ਵੱਲੋਂ ਜੁੜੇ ਨਹੀਂ ਹੁੰਦੇ, ਕਿਉਂਕਿ ਟੱਟੂਏ ਦੇ ਪਿੱਛੇ ਦਾ ਹਿੱਸਾ ਚਪਟਾ ਹੁੰਦਾ ਹੈ । ਛੱਲਿਆਂ ਦੀ ਗਿਣਤੀ 16 ਤੋਂ 20 ਤਕ ਹੁੰਦੀ ਹੈ । ਇਸ ਦੀ ਅੰਦਰਲੀ ਤਹਿ ਤੱਕ ਦੀ ਤਿੱਲੀ ਦੇ ਵਾਂਗ ਹੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਵੀ ਹਵਾ ਛਾਨਣ ਲਈ ਛੋਟੇ-ਛੋਟੇ ਵਾਲ ਹੁੰਦੇ ਹਨ । ਹੇਠਲੇ ਸਿਰੇ ਤੇ ਇਹ ਨਲੀ ਦੋ ਹਿੱਸਿਆਂ ਵਿਚ ਵੰਡੀ ਜਾਂਦੀ ਹੈ ।
ਜਿਸ ਦਾ ਇਕ ਹਿੱਸਾ ਸੱਜੇ ਪਾਸੇ ਦੇ ਫੇਫੜੇ ਵਿਚ ਚਲਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਦੂਸਰਾ ਖੱਬੇ ਪਾਸੇ ਦੇ ਫੇਫੜੇ ਵਿਚ । ਇਸ ਵਿਚੋਂ ਹਰੇਕ ਹਿੱਸੇ ਨੂੰ ਹਵਾ ਦੀ ਨਾਲੀ (Bronchi) ਕਹਿੰਦੇ ਹਨ | ਅੱਗੇ ਚੱਲ ਕੇ ਇਹ ਨਾਲੀ ਵਾਲ ਸੂਖ਼ਮ ਹਿੱਸਿਆਂ ਵਿਚ ਵੰਡੀ ਜਾਂਦੀ ਹੈ ।

5. ਹਵਾ ਨਾਲੀਆਂ (Bronchial Tubes-ਹਰੇਕ ਹਵਾ ਨਾਲ ਫੇਫੜੇ ਵਿਚ ਦਾਖ਼ਲ ਹੋਣ ਦੇ ਬਾਅਦ ਦੋ ਨਾਲੀਆਂ ਜਿਨ੍ਹਾਂ ਨੂੰ ਹਵਾ ਨਾਲੀਆਂ (Bronchial Tubes) ਕਹਿੰਦੇ ਹਨ, ਵਿਚ ਵੰਡੀ ਜਾਂਦੀ ਹੈ । ਫਿਰ ਇਹ ਕਈ ਹਿੱਸਿਆਂ ਵਿਚ ਵੰਡੀ ਜਾ ਕੇ ਛੋਟੀਆਂ-ਛੋਟੀਆਂ ਸੂਖ਼ਮ ਨਾਲੀਆਂ ਵਿਚ ਵੰਡੀ ਜਾਂਦੀ ਹੈ ਜੋ ਅੰਤ ਵਿਚ ਛੋਟੀਆਂ-ਛੋਟੀਆਂ ਹਵਾ ਗੁਥਲੀਆਂ (Air Sacs) ਵਿਚ ਖੁੱਲ੍ਹਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਵਿਚ ਗੈਸਾਂ ਦੀ ਅਦਲਾ-ਬਦਲੀ (Exchange of Gases) ਹੁੰਦੀ ਹੈ ।

6. ਫੇਫੜੇ (Lungs-ਫੇਫੜੇ ਸਾਹ ਦੀ ਕਿਰਿਆ ਦੇ ਸਭ ਤੋਂ ਮਹੱਤਵਪੂਰਨ ਅੰਗ ਹਨ । ਇਹ ਸਪੰਜ ਵਾਂਗ ਲਚਕੀਲੇ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਦਾ ਰੰਗ ਕੁੱਝ ਨੀਲਾਹਟ ਵਾਲਾ ਭੂਰਾ ਹੁੰਦਾ ਹੈ । ਇਹ ਛਾਤੀ ਵਿਚ ਦਿਲ ਵੱਲ ਸਥਿਤ ਹੁੰਦੇ ਹਨ । ਫੇਫੜੇ ਗਿਣਤੀ ਵਿਚ ਦੋ ਹੁੰਦੇ ਹਨ-ਸੱਜਾ ਫੇਫੜਾ ਅਤੇ ਖੱਬਾ ਫੇਫੜਾ । ਸੱਜਾ ਫੇਫੜਾ ਖੱਬੇ ਨਾਲੋਂ ਕੁੱਝ ਵੱਡਾ ਹੁੰਦਾ ਹੈ ਅਤੇ ਭਾਰਾ ਵੀ । ਇਹ ਚਾਰ ਹਿੱਸਿਆਂ (Lobes) ਵਿਚ ਵੰਡਿਆ ਹੁੰਦਾ ਹੈ । ਖੱਬਾ ਫੇਫੜਾ ਸਿਰਫ਼ ਦੋ ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਹੁੰਦਾ ਹੈ । ਹਰੇਕ ਫੇਫੜਾ ਇਕ ਦੋਹਰੀ ਖੁੱਲੀ ਦੇ ਥੈਲੇ ਵਿਚ ਸੁਰੱਖਿਅਤ ਰਹਿੰਦਾ ਹੈ । ਇਸ ਥੈਲੇ ਨੂੰ ਪਲਰਾ (Pleura) ਕਹਿੰਦੇ ਹਨ । ਵਿਚਕਾਰ ਇਕ ਤਰਲ ਪਦਾਰਥ ਹੁੰਦਾ ਹੈ ਜੋ ਫੇਫੜਿਆਂ ਦੀ ਸੱਟ, ਰਗੜ ਅਤੇ ਧੱਕੇ ਆਦਿ ਤੋਂ ਰੱਖਿਆ ਕਰਦਾ ਹੈ ।

ਫੇਫੜਿਆਂ ਵਿਚ ਪਹੁੰਚ ਕੇ ਛੋਟੀਆਂ-ਛੋਟੀਆਂ ਰੱਤ ਰਵਾਲਾਂ ਅੰਤ ਵਿਚ ਫੁੱਲੇ ਹੋਏ ਹਵਾ ਦੇ ਥੈਲਿਆਂ ਦਾ ਰੂਪ ਧਾਰਨ ਕਰ ਲੈਂਦੀਆਂ ਹਨ । ਇਹ ਥੈਲੇ ਫੇਫੜਿਆਂ ਵਿਚ ਅੰਗੂਰਾਂ ਦੇ ਗੁੱਛੇ ਵਾਂਗ ਦਿਖਾਈ ਦਿੰਦੇ ਹਨ । ਇਹਨਾਂ ਹਵਾ ਦੇ ਥੈਲਿਆਂ ਦੇ ਕਾਰਨ ਫੇਫੜਿਆਂ ਦੀ ਬਣਤਰ ਸਪੰਜ ਜਿਹੀ ਹੋ ਗਈ ਹੈ । ਫੇਫੜਿਆਂ ਦੇ ਵਧਣ-ਫੁੱਲਣ ਲਈ ਸ਼ੁੱਧ ਖੂਨ ਦੀਆਂ ਅਨੇਕਾਂ ਨਾਲੀਆਂ ਅਤੇ ਨਾੜੀਆਂ ਆਦਿ ਵੀ ਫੇਫੜਿਆਂ ਵਿਚ ਫੈਲੀਆਂ ਹੋਈਆਂ ਹਨ । ਫੇਫੜੇ ਅਸ਼ੁੱਧ ਖੂਨ ਨੂੰ ਸਾਫ਼ ਕਰਦੇ ਹਨ | ਫੇਫੜਿਆਂ ਦੀ ਸ਼ਕਤੀ ਸਪੈਰੋਮੀਟਰ ਦੇ ਨਾਲ ਮਾਪੀ ਜਾਂਦੀ ਹੈ । ਫੇਫੜਿਆਂ ਦੀ ਸਮਰੱਥਾ, ਇਹਨਾਂ ਵਿਚ ਹਵਾ ਭਰਨ ਦੀ ਤਾਕਤ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ।

ਸਾਹ-ਪ੍ਰਣਾਲੀ ਤੇ ਕਸਰਤ ਦਾ ਪ੍ਰਭਾਵ (Effect of Exercise on Respiration) –
ਕਸਰਤ ਸਾਹ ਪ੍ਰਣਾਲੀ ‘ਤੇ ਵਿਸ਼ੇਸ਼ ਪ੍ਰਭਾਵ ਪਾਉਂਦੀ ਹੈ ਜਿਸ ਦਾ ਸੰਖੇਪ ਵਰਣਨ ਇਸ ਤਰ੍ਹਾਂ ਹੈ –

• ਕਸਰਤ ਕਰਨ ਨਾਲ ਸਰੀਰ ਵਿਚ ਹਿਲ-ਜੁਲ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ਜਿਸ ਨਾਲ ਜ਼ਹਿਰੀਲੇ ਪਦਾਰਥ ਪਸੀਨਾ, ਮਲ-ਤਿਆਗ ਅਤੇ ਪੇਸ਼ਾਬ ਦੇ ਰਸਤੇ ਸਰੀਰ ਵਿਚੋਂ ਬਾਹਰ ਨਿਕਲ ਜਾਂਦੇ ਹਨ । ਇਸ ਨਾਲ ਸਰੀਰ ਰੋਗਾਂ ਤੋਂ ਮੁਕਤ ਰਹਿੰਦਾ ਹੈ ।
• ਕਸਰਤ ਕਰਨ ਨਾਲ ਫੇਫੜਿਆਂ ਵਿਚ ਹਵਾ ਭਰਨ ਦੀ ਸ਼ਕਤੀ ਵਿਚ ਵਾਧਾ ਹੁੰਦਾ ਹੈ ਜਿਸ ਦੇ ਫਲਸਰੂਪ ਫੇਫੜਿਆਂ ਵਿਚ ਵਧੇਰੇ ਲਚਕ ਆਉਂਦੀ ਅਤੇ ਇਹ ਕਈ ਰੋਗਾਂ ਤੋਂ ਬਚੇ ਰਹਿੰਦੇ ਹਨ ।
• ਕਸਰਤ ਕਰਨ ਨਾਲ ਸਰੀਰ ਵਿਚ ਖੂਨ ਵੱਧ ਮਾਤਰਾ ਵਿਚ ਸਾਫ਼ ਹੁੰਦਾ ਹੈ । ਇਸ ਦੇ ਫਲਸਰੂਪ ਸਰੀਰ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਸੈੱਲਾਂ ਵਿਚ ਸੁਆਸ ਕਿਰਿਆ ਦੁਆਰਾ ਖੂਨ ਵੱਧ ਮਾਤਰਾ ਵਿਚ ਪੁੱਜਦਾ ਹੈ ।
• ਕਸਰਤ ਕਰਨ ਨਾਲ ਸਰੀਰ ਵਿਚੋਂ ਫਜੂਲ ਪਦਾਰਥਾਂ ਦਾ ਨਿਕਾਸ ਹੋ ਜਾਂਦਾ ਹੈ ਜਿਸ ਨਾਲ ਸਰੀਰ ਵਿਚ ਕੰਮ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਵੱਧ ਪੈਦਾ ਹੁੰਦੀ ਹੈ ।
• ਕਸਰਤ ਕਰਨ ਨਾਲ ਸਰੀਰ ਦੇ ਸਭ ਸੈੱਲਾਂ ਨੂੰ ਵੱਧ ਮਾਤਰਾ ਵਿਚ ਆਕਸੀਜਨ ਮਿਲਦੀ ਹੈ । ਇਸ ਦੇ ਫਲਸਰੂਪ ਸਰੀਰ ਤੰਦਰੁਸਤ ਅਤੇ ਸ਼ਕਤੀਸ਼ਾਲੀ ਬਣਦਾ ਹੈ ।
• ਇਸ ਰਾਹੀਂ ਜ਼ੋਰ ਦਾ ਕੰਮ ਕਰਨ ਨਾਲ ਵਿਅਕਤੀ ਦੀ ਜੀਵਨ ਧਾਰਾ ਵਧ ਜਾਂਦੀ ਹੈ ।
• ਇਸ ਰਾਹੀਂ ਵਿਕਾਸ ਵੱਧ ਤੋਂ ਵੱਧ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ।
• ਇਸ ਰਾਹੀਂ ਗੈਸਾਂ ਦੀ ਅਦਲਾ-ਬਦਲੀ ਤੇਜ਼ੀ ਨਾਲ ਤੇ ਠੀਕ ਹੁੰਦੀ ਹੈ ।
• ਇਸ ਰਾਹੀਂ ਸਰੀਰ ਦੀ ਮੁਕਾਬਲਾ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਵਧ ਜਾਂਦੀ ਹੈ ।
• ਕਸਰਤ ਕਰਨ ਨਾਲ ਕਾਰਬਨ-ਡਾਈਆਕਸਾਈਡ ਦੇ ਬਾਹਰ ਨਿਕਲਣ ਅਤੇ ਆਕਸੀਜਨ ਦੇ ਅੰਦਰ ਪ੍ਰਵੇਸ਼ ਕਰਨ ਦੀ ਮਾਤਰਾ ਵਿਚ ਵਾਧਾ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਲਹੂ-ਪ੍ਰਣਾਲੀ ਉੱਤੇ ਕਸਰਤ ਦੇ ਪ੍ਰਭਾਵ ਲਿਖੋ । [ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ-3] (Write down the effects of exercises on Circulatory System.)
ਉੱਤਰ-
ਲਹੁ ਇਕ ਕਿਸਮ ਦਾ ਤਰਲ ਪਦਾਰਥ (Liquid) ਹੈ । ਇਸ ਦਾ ਨਿਰਮਾਣ ਉਸ ਭੋਜਨ ਅਤੇ ਪੀਣ ਵਾਲੇ ਪਦਾਰਥ ਤੋਂ ਹੁੰਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਨੂੰ ਅਸੀਂ ਆਪਣੇ ਸਰੀਰ ਵਿਚ ਪਹੁੰਚਾਉਂਦੇ ਹਨ | ਮਨੁੱਖੀ ਸਰੀਰ ਵਿਚ ਖੂਨ ਉਸ ਦੇ ਕੁੱਲ ਭਾਰ ਦਾ \(\frac{1}{12}\) ਜਾਂ \(\frac{1}{14}\) ਚ ਭਾਗ ਹੁੰਦਾ ਹੈ । ਲਹੂ ਵਿਚ ਅਣਗਿਣਤ ਛੋਟੇ-ਛੋਟੇ ਲਾਲ ਅਤੇ ਚਿੱਟੇ ਕਣ ਹੁੰਦੇ ਹਨ ਜੋ ਪਲਾਜ਼ਮਾ ਨਾਮੀ ਹਲਕੇ ਪੀਲੇ ਰੰਗ ਦੇ ਦ੍ਰਵ ਵਿਚ ਤੈਰਦੇ ਰਹਿੰਦੇ ਹਨ । ਲਹੂ ਸਾਡੇ ਸਰੀਰ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਅੰਗਾਂ ਵਿਚ ਦਿਨ-ਰਾਤ ਦੌਰਾ ਕਰਦਾ ਹੈ । ਲਹੂ ਦੀ ਗਤੀ ਨੂੰ ਲਹੂ ਪਰਿਵਹਨ (Blood Circulation) ਕਹਿੰਦੇ ਹਨ । ਲਹੂ ਪਰਿਵਹਨ ਵਿਚ ਸਰੀਰ ਦੇ ਜੋ ਅੰਗ ਭਾਗ ਲੈਂਦੇ ਹਨ, ਉਹਨਾਂ ਦੇ ਸਮੂਹ ਨੂੰ ਲਹੂ-ਪ੍ਰਣਾਲੀ (Circulatory System) ਕਹਿੰਦੇ ਹਨ ।

ਲਹੂ-ਪ੍ਰਣਾਲੀ ਉੱਤੇ ਕਸਰਤ ਦੇ ਪ੍ਰਭਾਵ (Effects of Exercise on Circulatory System)-
ਲਹੂ-ਪ੍ਰਣਾਲੀ ‘ਤੇ ਕਸਰਤ ਦੇ ਹੇਠ ਲਿਖੇ ਪ੍ਰਭਾਵ ਪੈਂਦੇ ਹਨ

• ਕਸਰਤ ਕਰਦੇ ਸਮੇਂ ਦਿਲ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਨੂੰ ਜ਼ਰੂਰਤ ਅਨੁਸਾਰ ਵਧੇਰੇ ਲਹੂ ਦਿੰਦਾ ਹੈ ਜਿਸ ਦੇ ਫਲਸਰੂਪ ਛੋਟੀਆਂ ਲਹੂ ਦੀਆਂ ਨਾਲੀਆਂ ਅਤੇ ਤੰਤੂਆਂ ਦੇ ਤਣਾਓ ਵਿਚ ਵਾਧਾ ਹੁੰਦਾ ਹੈ ।
• ਕਸਰਤ ਕਰਨ ਵਾਲਿਆਂ ਦੇ ਸਰੀਰ ਵਿਚ ਸ਼ੁੱਧ ਅਤੇ ਅਸ਼ੁੱਧ ਲਹੂ ਦੀ ਅਦਲਾ-ਬਦਲੀ ਛੇਤੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਦੇ ਫਲਸਰੂਪ ਸਰੀਰ ਵਿਚ ਪੌਸ਼ਟਿਕ ਪਦਾਰਥ ਅਤੇ ਆਕਸੀਜਨ ਦੀ ਮਾਤਰਾ ਵਧੇਰੇ ਮਿਲਦੀ ਹੈ ਅਤੇ ਸਰੀਰ ਵਿਚੋਂ ਕਾਰਬਨ-ਡਾਈਆਕਸਾਈਡ ਆਦਿ ਫਜ਼ੂਲ ਅਤੇ ਹਾਨੀਕਾਰਕ ਪਦਾਰਥਾਂ ਦਾ ਪਸੀਨੇ ਤੇ ਪੇਸ਼ਾਬ ਦੇ ਰੂਪ ਵਿਚ ਨਿਕਾਸ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਨਾਲ ਸਰੀਰ ਰਿਸ਼ਟ-ਪੁਸ਼ਟ ਅਤੇ ਨਿਰੋਗ ਰਹਿੰਦਾ ਹੈ ।
• ਕਸਰਤ ਕਰਨ ਵਾਲੇ ਵਿਅਕਤੀ ਦਾ ਲਹੁ ਦਬਾਅ ਵੱਧ ਨਹੀਂ ਹੁੰਦਾ । ਉਸ ਦੀਆਂ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਸੁੰਗੜਦੀਆਂ ਅਤੇ ਫੈਲਦੀਆਂ ਹਨ । ਨਤੀਜੇ ਦੇ ਤੌਰ ‘ਤੇ ਲਹੁ ਜਲਦੀ ਸਾਫ਼ ਹੋ ਜਾਂਦਾ ਹੈ ।
• ਕਸਰਤ ਕਰਦੇ ਸਮੇਂ ਸਰੀਰ ਦਾ ਹਰੇਕ ਅੰਗ ਕੰਮ ਕਰਦਾ ਹੈ । ਇਸ ਕਾਰਨ ਉਹਨਾਂ ਨੂੰ ਆਕਸੀਜਨ ਦੀ ਵੱਧ ਜ਼ਰੂਰਤ ਪੈਂਦੀ ਹੈ | ਕਸਰਤ ਕਰਨ ਵਾਲੇ ਵਿਅਕਤੀ ਦੇ ਲਹੂ ਦੀ ਗਤੀ ਸਾਧਾਰਨ ਵਿਅਕਤੀ ਤੋਂ ਦੋ ਗੁਣਾ ਵੱਧ ਹੁੰਦੀ ਹੈ ।
• ਇਸ ਰਾਹੀਂ ਦਿਲ ਦੀ ਕਾਰਜ-ਸ਼ਕਤੀ ਵਧ ਜਾਂਦੀ ਹੈ ਜੋ ਲੋੜ ਦੇ ਅਨੁਸਾਰ ਹੋਣ ਦੀ ਸਮਰੱਥਾ ਰੱਖਦੀ ਹੈ ।
• ਇਸ ਰਾਹੀਂ ਲਹੂ ਦਾ ਪ੍ਰਵਾਹ ਵਧ ਜਾਂਦਾ ਹੈ ।
• ਇਸ ਨਾਲ ਹਾਜ਼ਮਾ ਠੀਕ ਰਹਿੰਦਾ ਹੈ ।
• ਕਸਰਤ ਨਾਲ ਅਸੀਂ ਚੰਗਾ ਲਹੂ ਤਿਆਰ ਕਰ ਸਕਦੇ ਹਾਂ ਜੋ ਸਾਡੇ ਜੀਵਨ ਦਾ ਆਧਾਰ ਹੈ ।
• ਕਸਰਤ ਕਰਨ ਨਾਲ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਮਜ਼ਬੂਤ ਹੁੰਦੀਆਂ ਹਨ | ਇਸ ਦੇ ਫਲਸਰੂਪ ਆਰਾਮ ਦੀ ਹਾਲਤ ਵਿਚ ਦਿਲ ਦੀ ਧੜਕਣ ਠੀਕ ਚੱਲਦੀ ਹੈ ਪਰ ਖੂਨ ਦੀ ਗਤੀ ਤੇਜ਼ ਹੁੰਦੀ ਹੈ ।
• ਕਸਰਤ ਕਰਨ ਵਾਲੇ ਮਨੁੱਖ ਨੂੰ ਆਕਸੀਜਨ ਦੀ ਵਧੇਰੇ ਮਾਤਰਾ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਆਕਸੀਜਨ ਦੀ ਖਪਤ ਵਿਚ ਵਾਧਾ ਹੁੰਦਾ ਹੈ ਅਤੇ ਲਹੂ ਵਿਚ ਇਸ ਦੀ ਮਾਤਰਾ ਵਧਦੀ ਹੈ । ਇਸ ਵਧੀ ਹੋਈ ਆਕਸੀਜਨ ਕਾਰਨ ਲੈਕਟਿਕ ਐਸਿਡ ਵਿਚ ਵਾਧਾ ਨਹੀਂ ਹੁੰਦਾ । ਇਸ ਲਈ ਖਿਡਾਰੀ ਅਤੇ ਐਥਲੀਟ ਬਿਨਾਂ ਥਕਾਵਟ ਮਹਿਸੂਸ ਕੀਤੇ ਕਾਫ਼ੀ ਸਮੇਂ ਤਕ ਖੇਡਾਂ ਵਿਚ ਭਾਗ ਲੈ ਸਕਦੇ ਹਨ ।
• ਕਸਰਤ ਕਰਦੇ ਸਮੇਂ ਲਹੂ ਨਾਲੀਆਂ ਦੇ ਮੂੰਹ ਖੁੱਲ੍ਹਦੇ ਅਤੇ ਬੰਦ ਹੁੰਦੇ ਰਹਿੰਦੇ ਹਨ । ਭਾਰੀ ਕਸਰਤ ਅਤੇ ਦੌੜਦੇ ਸਮੇਂ ਆਕਸੀਜਨ ਵੱਧ ਮਾਤਰਾ ਵਿਚ ਅੰਦਰ ਜਾਂਦੀ ਰਹਿੰਦੀ ਹੈ । ਭਾਰੀ ਕਸਰਤ ਅਤੇ ਦੌੜਦੇ ਸਮੇਂ ਆਕਸੀਜਨ 3500 ਘਣ ਮਿਲੀਲਿਟਰ ਤਕ ਅੰਦਰ ਚਲੀ ਜਾਂਦੀ ਹੈ ਜਦੋਂ ਕਿ ਸਾਧਾਰਨ ਕਸਰਤ ਕਰਨ ਵਾਲਿਆਂ ਵਿਚ ਆਕਸੀਜਨ ਦੀ ਇਹ ਮਾਤਰਾ ਕੇਵਲ 5000 ਤੋਂ 8000 ਘਣ ਮਿਲੀਲਿਟਰ ਤਕ ਹੁੰਦੀ ਹੈ ।
• ਕਸਰਤ ਕਰਨ ਵਾਲੇ ਵਿਅਕਤੀ ਦੀਆਂ ਸ਼ਿਰਾਵਾਂ (Veins) ਤੇ ਧਮਨੀਆਂ (Arteries) ਨੂੰ ਵੱਧ ਕੰਮ ਕਰਨਾ ਪੈਂਦਾ ਹੈ । ਫਲਸਰੂਪ ਇਹਨਾਂ ਦੀਆਂ ਕੰਧਾਂ ਮਜ਼ਬੂਤ ਹੋ ਜਾਂਦੀਆਂ ਹਨ । ਕਸਰਤ ਕਰਨ ਵਾਲੇ ਵਿਅਕਤੀ ਦੀ ਦਿਲ ਲਹੂ ਸਟਰੋਕ (Stroke Volume) ਆਮ ਵਿਅਕਤੀ ਤੋਂ ਵੱਧ ਹੁੰਦੀ ਹੈ ।

ਪ੍ਰਸ਼ਨ 4.
ਮਾਸ-ਪੇਸ਼ੀਆਂ ਕੀ ਹਨ ? ਇਹ ਕਿੰਨੀ ਪ੍ਰਕਾਰ ਦੀਆਂ ਹਨ ? ਇਹਨਾਂ ਉੱਤੇ ਕਸਰਤਾਂ ਦੇ ਪ੍ਰਭਾਵ ਲਿਖੋ । [ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ-4] (What are Muscles ? Give its types. Write down the effects of exercises on Muscular System.)
ਉੱਤਰ-
ਮਾਸ-ਪੇਸ਼ੀਆਂ (Muscles)ਮਨੁੱਖੀ ਸਰੀਰ ਦਾ ਸਰਵ-ਉੱਤਮ ਗੁਣ ਇਸ ਦੀ ਗਤੀ ਜਾਂ ਚਲਣਾ-ਫਿਰਨਾ ਹੈ । ਮਨੁੱਖ ਦੇ ਘੁੰਮਣਫਿਰਨ ਵਿਚ ਹੱਡੀਆਂ ਧੁਰੀ ਦੀ ਭੂਮਿਕਾ ਨਿਭਾਉਂਦੀਆਂ ਹਨ । ਹੱਡੀਆਂ ਦੇ ਨਾਲ ਮਾਸਪੇਸ਼ੀਆਂ ਜੁੜੀਆਂ ਹੁੰਦੀਆਂ ਹਨ । ਇਹ ਭਿੰਨਭਿੰਨ ਕਿਸਮ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਮਾਸਪੇਸ਼ੀਆਂ ਵਿਚ ਮਾਸ ਸੁਤਰ ਸੈੱਲਾਂ ਦਾ ਸੁਮੇਲ ਹੈ ॥ ਹਰੇਕ ਮਾਸ-ਪੇਸ਼ੀ ਹੱਡੀ ਦੇ ਨਾਲ ਜੁੜੀ ਹੁੰਦੀ ਹੈ । ਮਾਸ-ਪੇਸ਼ੀ ਦੇ ਸੁੰਗੜਨ ਨਾਲ ਹੱਡੀਆਂ ਵਿਚ ਵੀ ਖਿਚਾਅ ਉਤਪੰਨ ਹੁੰਦਾ ਹੈ ਅਤੇ ਭਿੰਨ-ਭਿੰਨ ਅੰਗ ਕੰਮ ਕਰਦੇ ਹਨ । ਮਾਸ-ਪੇਸ਼ੀਆਂ ਵਿਚ 75% ਪਾਣੀ, 18% ਪ੍ਰੋਟੀਨ ਅਤੇ ਬਾਕੀ ਚਰਬੀ ਅਤੇ ਲਣ ਆਦਿ ਹੁੰਦੇ ਹਨ | ਖੂਨ ਅਤੇ ਸੁਖਮਣਾ ਨਾੜੀਆਂ ਇਹਨਾਂ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਨੂੰ ਸੂਚਨਾ ਪਹੁੰਚਾਉਣ ਦਾ ਕੰਮ ਕਰਦੀਆਂ ਹਨ |

ਮਾਸ-ਪੇਸ਼ੀਆਂ ਦੀਆਂ ਕਿਸਮਾਂ (Types of Muscles)-ਮਾਸ-ਪੇਸ਼ੀਆਂ ਹੇਠ ਲਿਖੀਆਂ ਦੋ ਕਿਸਮਾਂ ਦੀਆਂ ਹੁੰਦੀਆਂ ਹਨ

1. ਸਵੈਇੱਛਿਤ ਮਾਸ-ਪੇਸ਼ੀਆਂ (Voluntary Muscles)
2. ਅਣਇੱਛਿਤ ਮਾਸ-ਪੇਸ਼ੀਆਂ (Involuntary Muscles) ।

1. ਸਵੈਇੱਛਿਤ ਮਾਸ-ਪੇਸ਼ੀਆਂ (Voluntary Muscles) – ਸਵੈਇੱਛਿਤ ਮਾਸਪੇਸ਼ੀਆਂ ਉਹ ਹਨ ਜੋ ਵਿਅਕਤੀ ਦੀ ਇੱਛਾ ਅਨੁਸਾਰ ਕੰਮ ਕਰਦੀਆਂ ਹਨ ।
ਇਹ ਹੱਡੀਆਂ ਦੇ ਪਿੰਜਰ ਦੇ ਉੱਪਰ ਲੱਗੀਆਂ ਹੁੰਦੀਆਂ ਹਨ । ਇਹ ਲੱਤਾਂ ਅਤੇ ਬਾਹਾਂ ਵਿਚ

ਮਿਲਦੀਆਂ ਹਨ । ਇਹ ਪ੍ਰਾਪਤ ਸੂਚਨਾ ਦੇ ਅਨੁਸਾਰ ਕੰਮ ਕਰਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ । ਇਹ ਸਰੀਰ ਨੂੰ ਗਤੀ ਪ੍ਰਦਾਨ ਕਰਦੀਆਂ ਹਨ, ਸਰੀਰਕ ਢਾਂਚੇ ਨੂੰ ਸੰਭਾਲ ਕੇ ਰੱਖਦੀਆਂ ਹਨ ਅਤੇ ਸਰੀਰ ਵਿਚ ਗਰਮੀ ਪੈਦਾ ਕਰਦੀਆਂ ਹਨ ।

2. ਅਣਇੱਛਿਤ ਮਾਸ-ਪੇਸ਼ੀਆਂ (Involuntary Muscles)-ਅਣਇੱਛਿਤ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਉਹ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਹਨ ਜੋ ਵਿਅਕਤੀ ਦੇ ਵੱਸ ਵਿਚ ਨਹੀਂ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਉਸ ਦੀ ਇੱਛਾ ਦੇ ਬਿਨਾਂ ਹੀ ਕੰਮ ਕਰਦੀਆਂ ਹਨ । ਇਹ ਦਿਲ, ਜਿਗਰ ਅਤੇ ਅੰਤੜੀਆਂ ਆਦਿ ਵਿਚ ਪਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਇਹ ਵਿਅਕਤੀ ਦੇ ਸੌਂਦੇ ਹੋਏ ਵੀ ਕੰਮ ਕਰਦੀਆਂ ਰਹਿੰਦੀਆਂ ਹਨ । ਇਹ ਲਹੂ ਚੱਕਰ ਅਤੇ ਪਾਚਨ ਕਿਰਿਆ ਵਿਚ ਸਹਾਇਤਾ ਪਹੁੰਚਾਉਂਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਦੇ ਲੱਛਣ ਸੁੰਗੜਨਾ, ਫੈਲਣਾ ਅਤੇ ਲਚਕ ਆਦਿ ਹੈ ।

ਮਾਸ-ਪੇਸ਼ੀਆਂ ਉੱਤੇ ਕਸਰਤ ਦੇ ਪ੍ਰਭਾਵ (Effects of Exercise on Muscles)-

ਕਸਰਤ ਦੇ ਮਾਸ-ਪੇਸ਼ੀਆਂ ‘ਤੇ ਹੇਠ ਲਿਖੇ ਪ੍ਰਭਾਵ ਪੈਂਦੇ ਹਨ –

• ਕਸਰਤ ਕੋਰਨ ਵਾਲੇ ਵਿਅਕਤੀਆਂ ਦੀਆਂ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਵੱਧ ਕੰਮ ਕਰਦੀਆਂ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਇਹਨਾਂ ਨੂੰ ਆਕਸੀਜਨ ਦੁਆਰਾ ਪੌਸ਼ਟਿਕ ਖ਼ੁਰਾਕ ਵਧੇਰੇ ਮਾਤ੍ਰਾ ਵਿਚ ਪ੍ਰਾਪਤ ਹੁੰਦੀ ਹੈ । ਇਸ ਨਾਲ ਇਹ ਵੱਧ ਪੁਸ਼ਟ ਅਤੇ ਮਜ਼ਬੂਤ ਬਣ ਜਾਂਦੀਆਂ ਹਨ |
• ਹਰ ਰੋਜ਼ ਕਸਰਤ ਕਰਨ ਨਾਲ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਦਾ ਤਾਲਮੇਲ ਵੱਧਦਾ ਹੈ । ਇਹਨਾਂ ਵਿਚ ਕਸਰਤ ਕਾਰਨ ਵੱਧ ਸ਼ਕਤੀ ਆਉਂਦੀ ਹੈ । ਫਲਸਰੂਪ ਵਿਅਕਤੀ ਲੰਮੀ ਮਿਆਦ ਤਕ ਕੰਮ ਕਰਕੇ ਵੀ ਥਕਾਵਟ ਮਹਿਸੂਸ ਨਹੀਂ ਕਰਦਾ ।
• ਕਸਰਤ ਕਰਨ ਨਾਲ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਨੂੰ ਵੱਧ ਕੰਮ ਕਰਨਾ ਪੈਂਦਾ ਹੈ | ਕਸਰਤ ਕਰਨ ਵਾਲੇ ਵਿਅਕਤੀ ਦੇ ਅੰਦਰ ਆਕਸੀਜਨ ਦੀ ਖਪਤ ਵੀ ਵੱਧ ਜਾਂਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਵਿਚ ਤੇਜ਼ੀ ਨਾਲ ਖੂਨ ਪਹੁੰਚਦਾ ਰਹਿੰਦਾ ਹੈ ।
• ਕਸਰਤ ਕਰਨ ਨਾਲ ਸਰੀਰ ਵਿਚ ਹਿਲ-ਜੁਲ ਹੁੰਦੀ ਰਹਿੰਦੀ ਹੈ । ਇਸ ਨਾਲ ਕਈ ਫਾਲਤੂ ਪਦਾਰਥਾਂ ਦਾ ਸਰੀਰ ਵਿਚੋਂ ਨਿਕਾਸ ਹੋ ਜਾਂਦਾ ਹੈ ਅਤੇ ਸਰੀਰ ਦਾ ਤਾਪਮਾਨ ਅਕਸਰ ਸਮਾਨ ਹੀ ਰਹਿੰਦਾ ਹੈ |
• ਕਸਰਤ ਕਰਨ ਨਾਲ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਨੂੰ ਗਲਾਈਕੋਜਿਨ, ਫਾਸਫੋਰਾਟਿਨ ਅਤੇ ਪੋਟਾਸ਼ੀਅਮ ਆਦਿ ਰਸਾਇਣਿਕ ਪਦਾਰਥ ਪ੍ਰਾਪਤ ਹੁੰਦੇ ਰਹਿੰਦੇ ਹਨ । ਇਹ ਰਸਾਇਣਿਕ ਪਦਾਰਥ ਖੂਨ ਦੀ ਗਤੀ ਵਿਚ ਵਾਧਾ ਕਰਦੇ ਹਨ ।
• ਕਸਰਤ ਕਰਨ ਨਾਲ ਸਰੀਰ ਦੀਆਂ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਵਿਚ ਲਚਕ ਅਤੇ ਫੁਰਤੀ ਆਉਂਦੀ ਹੈ । ਇਸ ਨਾਲ ਸਾਡਾ ਸਰੀਰ ਨਿਰੋਲ ਅਤੇ ਮਜ਼ਬੂਤ ਰਹਿੰਦਾ ਹੈ ।
• ਕਸਰਤ ਕਰਨ ਨਾਲ ਛਾਤੀ ਦੀਆਂ ਹੱਡੀਆਂ ਦੇ ਪੱਠਿਆਂ ਦੀ ਫੈਲਣ ਦੀ ਸਮਰੱਥਾ ਵੱਧ ਹੁੰਦੀ ਹੈ ।
• ਇਸ ਰਾਹੀਂ ਪੱਠਿਆਂ ਨੂੰ ਵਰਤੋਂ ਦੇ ਯੋਗ ਰੱਖਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
• ਇਸ ਰਾਹੀਂ ਸਾਡੀਆਂ ਹੱਡੀਆਂ ਸਖ਼ਤ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਵਧੇਰੇ ਸਮੇਂ ਤਕ ਕੰਮ ਕਰ ਸਕਦੀਆਂ ਹਨ ।
• ਵਿਸਰਾਮ ਅਵਸਥਾ ਵਿਚ ਵਿਅਕਤੀ ਦਾ ਇਕ ਲਹੂ ਚੱਕਰ ਪੂਰਾ ਹੋਣ ਲਈ 21 ਸੈਕਿੰਡ ਲੱਗਦੇ ਹਨ ਪਰ ਕਸਰਤ ਕਰਨ ਨਾਲ ਇਹ 8-15 ਜਾਂ 10 ਸੈਕਿੰਡ ਵਿਚ ਪੂਰਾ ਹੋ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 5.
ਮਲ-ਤਿਆਗ ਪ੍ਰਣਾਲੀ ਦੇ ਅੰਗਾਂ ਨੂੰ ਮੁੱਖ ਰੱਖਦੇ ਹੋਏ ਕਸਰਤ ਦੇ ਪ੍ਰਭਾਵ ਬਿਆਨ ਕਰੋ । [ਅਭਿਆਸ ਦਾ ਪ੍ਰਸ਼ਨ-5] (Discuss the main organs of Excretory System. Give the effects of exercises on Excretory System.)
ਉੱਤਰ-
ਮਲ-ਤਿਆਗ ਪ੍ਰਣਾਲੀ (Excretory System) ਉਸ ਪ੍ਰਬੰਧ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ਜਿਸ ਦੁਆਰਾ ਸਰੀਰ ਵਿਚੋਂ ਫਾਲਤੂ ਅਤੇ ਹਾਨੀਕਾਰਕ ਪਦਾਰਥਾਂ ਦਾ ਨਿਕਾਸ ਹੁੰਦਾ ਹੈ । ਜੇ ਇਹ ਫਜ਼ੂਲ ਅਤੇ ਹਾਨੀਕਾਰਕ ਪਦਾਰਥ ਸਰੀਰ ਵਿਚ ਹੀ ਜਮਾਂ ਰਹਿਣ ਤਾਂ ਸਰੀਰ ਅਨੇਕਾਂ ਰੋਗਾਂ ਦਾ ਸ਼ਿਕਾਰ ਹੋ ਸਕਦਾ ਹੈ । ਇਹਨਾਂ ਬਾਹਰ ਆਉਣ ਵਾਲੇ ਪਦਾਰਥਾਂ ਵਿਚ ਯੂਰੀਆ, ਕਾਰਬਨ-ਡਾਈਆਕਸਾਈਡ, ਪਸੀਨਾ ਅਤੇ ਪਾਣੀ ਪ੍ਰਮੁੱਖ ਹਨ । ਇਹਨਾਂ ਪਦਾਰਥਾਂ ਦਾ ਨਿਕਾਸ ਫੇਫੜਿਆਂ, ਗੁਰਦਿਆਂ, ਚਮੜੀ (Skin) ਅਤੇ ਅੰਤੜੀਆਂ ਰਾਹੀਂ ਹੁੰਦਾ ਹੈ ।

ਕਸਰਤ ਦੇ ਪ੍ਰਭਾਵ (Effects of Exercise) -ਕਸਰਤ ਮਲ-ਤਿਆਗ ਪ੍ਰਣਾਲੀ ਨੂੰ ਹੇਠ ਲਿਖੇ ਢੰਗ ਨਾਲ ਪ੍ਰਭਾਵਿਤ ਕਰਦੀ ਹੈ

• ਕਸਰਤ ਕਰਨ ਨਾਲ ਸਰੀਰ ਵਿਚ ਹਿਲ-ਜੁਲ ਹੁੰਦੀ ਹੈ ਜਿਸ ਦੇ ਕਾਰਨ ਖੂਨ ਦੀ ਗਤੀ ਤੇਜ਼ ਹੋ ਜਾਂਦੀ ਹੈ | ਸਰੀਰ ਵਿਚ ਗੈਸਾਂ ਦੀ ਅਦਲਾ-ਬਦਲੀ (Exchange of gases) ਦੇ ਕਾਰਨ ਪੌਸ਼ਟਿਕ ਪਦਾਰਥ ਹਜ਼ਮ ਹੋ ਜਾਂਦੇ ਹਨ ਅਤੇ ਫਾਲਤੂ ਪਦਾਰਥਾਂ ਦਾ ਨਿਕਾਸ ਹੋ ਜਾਂਦਾ ਹੈ, ਜਿਸ ਨਾਲ ਸਰੀਰ ਦਾ ਤਾਪਮਾਨ ਸਥਿਰ ਰਹਿੰਦਾ ਹੈ ।
• ਕਸਰਤ ਦੇ ਕਾਰਨ ਸਰੀਰ ਦੀਆਂ ਵੱਖ-ਵੱਖ ਮਾਸ-ਪੇਸ਼ੀਆਂ ਨੂੰ ਕੰਮ ਕਰਨਾ ਪੈਂਦਾ ਹੈ । ਇਸ ਨਾਲ ਸਰੀਰ ਵਿਚ ਟੁੱਟ-ਫੁੱਟ ਹੁੰਦੀ ਰਹਿੰਦੀ ਹੈ ਜਿਸ ਨਾਲ ਚਮੜੀ ਵਿਚੋਂ ਗੰਦਗੀ ਦਾ ਨਿਕਾਸ ਹੁੰਦਾ ਰਹਿੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਸਰੀਰ ਚਮੜੀ ਦੇ ਰੋਗਾਂ ਤੋਂ ਮੁਕਤ ਰਹਿੰਦਾ ਹੈ ।
• ਕਸਰਤ ਕਰਨ ਨਾਲ ਸਰੀਰ ਵਿਚੋਂ ਗੈਰ-ਜ਼ਰੂਰੀ ਪਦਾਰਥਾਂ ਦੇ ਰੂਪ ਵਿਚ ਜ਼ਹਿਰੀਲੀਆਂ ਵਸਤੂਆਂ ਦਾ ਸਰੀਰ ਤੋਂ ਬਾਹਰ ਨਿਕਾਸ ਹੁੰਦਾ ਰਹਿੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਜ਼ਹਿਰੀਲੇ ਕੀਟਾਣੂ ਸਰੀਰ ਵਿਚ ਇਕੱਠੇ ਨਹੀਂ ਹੁੰਦੇ ਅਤੇ ਸਰੀਰ ਵਿਚ ਇਹਨਾਂ ਜ਼ਹਿਰੀਲੇ ਕੀਟਾਣੂਆਂ ਦੇ ਵਿਰੁੱਧ ਸੰਘਰਸ਼ ਕਰਨ ਦੀ ਸ਼ਕਤੀ ਵਧਦੀ ਹੈ ।
• ਕਸਰਤ ਕਰਨ ਨਾਲ ਗੁਰਦੇ ਫਾਲਤੂ ਪਦਾਰਥਾਂ ਨੂੰ ਛਾਣ ਕੇ ਪੇਸ਼ਾਬ ਦੇ ਰੂਪ ਵਿਚ ਬਾਹਰ ਕੱਢਦੇ ਹਨ । ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਇਕ ਛਾਣਨੀ ਦਾ ਕੰਮ ਕਰਦੇ ਹਨ ।

ਪ੍ਰਸ਼ਨ 6.
ਹੇਠ ਲਿਖਿਆਂ ‘ਤੇ ਨੋਟ ਲਿਖੋ –
(ਉ) ਚਮੜੀ ਦੇ ਕੰਮ
(ਅ) ਗੁਰਦੇ .
(ੲ) ਦਿਲ
(ਸ) ਸ਼ਿਰਾਵਾਂ ਤੇ ਧਮਨੀਆਂ (ਅਭਿਆਸ ਪ੍ਰਸ਼ਨ 6) (Write a note on the following )
(a) Functions of Skin
(b) Kidney
(c) Heart
(d) Arteries and Veines.)
ਉੱਤਰ-
(ਉ) ਚਮੜੀ ਦੇ ਕੰਮ (Functions of Skin)-ਚਮੜੀ ਇਕ ਪ੍ਰਕਾਰ ਦਾ ਪਰਦਾ ਹੈ ਜੋ ਸਰੀਰ ਦੇ ਅੰਦਰੂਨੀ ਭਾਗਾਂ ਅਤੇ ਮਾਸਪੇਸ਼ੀਆਂ ਨੂੰ ਢੱਕ ਕੇ ਰੱਖਦਾ ਹੈ ।
ਚਮੜੀ ਦੋ ਕਿਸਮ ਦੀ ਹੁੰਦੀ ਹੈ-ਉੱਪਰਲੀ ਜਾਂ ਬਾਹਰੀ (Epidermis) ਅਤੇ ਹੇਠਲੀ ਅੰਦਰੂਨੀ (Endodermis) । ਉੱਪਰਲੀ ਚਮੜੀ ਸਖ਼ਤ ਅਤੇ ਨਰਮ ਹੁੰਦੀ ਹੈ। ਇਸ ਵਿਚ ਛੋਟੇ-ਛੋਟੇ ਮੁਸਾਮ ਹੁੰਦੇ ਹਨ ਜਿਨ੍ਹਾਂ ਨਾਲ ਪਸੀਨਾ ਸਰੀਰ ਵਿਚੋਂ ਬਾਹਰ ਨਿਕਲਦਾ ਰਹਿੰਦਾ ਹੈ । ਹੇਠਲੀ ਜਾਂ ਅੰਦਰੂਨੀ ਚਮੜੀ ਬੰਧਕ ਟਿਸ਼ੂਆਂ (Connective tissues) ਦੀ ਬਣੀ ਹੁੰਦੀ ਹੈ । ਇਸ ਵਿਚ ਚਰਬੀ ਹੁੰਦੀ ਹੈ ਜੋ ਗਰਮੀ ਪੈਦਾ ਕਰਨ ਵਿਚ ਸਹਾਇਤਾ ਪ੍ਰਦਾਨ ਕਰਦੀ ਹੈ । ਇਸ ਵਿਚ ਦੋ ਤਰ੍ਹਾਂ ਦੀਆਂ ਪਸੀਨਾ ਅਤੇ ਚਿਕਨਾਹਟ ਦੀਆਂ ਗੰਥੀਆਂ ਹੁੰਦੀਆਂ ਹਨ ਜੋ ਸਰੀਰ ਦੇ ਤਾਪਮਾਨ ਨੂੰ ਇਕ ਸਮਾਨ ਰੱਖਣ ਵਿਚ ਮਦਦ ਦਿੰਦੀਆਂ ਹਨ ।

(ਅ) ਗੁਰਦੇ (Kidneys) – ਗੁਰਦੇ ਸੰਖਿਆ ਵਿਚ ਦੋ ਹੁੰਦੇ ਹਨ । ਇਹ ਢਿੱਡ ਵੱਲ ਸਥਿਤ ਹੁੰਦੇ ਹਨ । ਇਹਨਾਂ ਦਾ ਆਕਾਰ ਸੇਮ ਦੇ ਬੀਜ ਵਰਗਾ ਹੁੰਦਾ ਹੈ ।
ਇਹ ਪੇਸ਼ਾਬ ਦਾ ਸਰੀਰ ਤੋਂ ਨਿਕਾਸ ਕਰਨ ਵਿਚ ਮਦਦ ਦਿੰਦੇ ਹਨ । ਇਹ ਸਰੀਰ ਵਿਚ ਖੂਨ ਅਤੇ ਪਾਣੀ ਦੀ ਮਾਤਰਾ ਇਕ ਸਮਾਨ ਰੱਖਦੇ ਹਨ ।

ਗੁਰਦਿਆਂ ਦੁਆਰਾ ਸਰੀਰ ਵਿਚੋਂ ਯੂਰੀਆ, ਯੂਰਿਕ ਐਸਿਡ, ਖਣਿਜ ਲੂਣ ਪੇਸ਼ਾਬ ਦੇ ਰੂਪ ਵਿਚ ਨਿਕਲਦੇ ਰਹਿੰਦੇ ਹਨ ।

(ੲ) ਦਿਲ (Heart) ਇਹ ਸਰੀਰ ਦਾ ਸਭ ਤੋਂ ਵਾਲਾ ਭਾਗ ਕੋਮਲ ਅਤੇ ਲਹੂ ਚੱਕਰ ਦਾ ਪ੍ਰਮੁੱਖ ਅੰਗ ਹੈ । ਇਹ ਛਾਤੀ ਦੇ ਖੱਬੇ ਪਾਸੇ ਸਥਿਤ ਤਿੰਨ ਤਖਤੇ ਹੈ । ਇਸ ਦਾ ਆਕਾਰ ਬੰਦ ਮੁੱਠੀ ਵਰਗਾ ਹੁੰਦਾ ਹੈ । ਇਹ ਲੰਬਾਈ ਵਲੋਂ ਦੋ ਤਖ਼ਤੇ ਦੋ ਭਾਗਾਂ ਵਿਚ ਵੰਡਿਆ ਹੁੰਦਾ ਹੈ । ਖੱਬਾ ਹੇਠਲਾ ਹਰੇਕ ਭਾਗ ਅੱਗੇ ਦੋ ਭਾਗਾਂ ਵਿਚ ਭਾਰਾ ਸੱਜਾ ਹੇਠਲਾ ਵੰਡਿਆ ਹੁੰਦਾ ਹੈ ।

ਉੱਪਰਲਾ ਭਾਗ ਅਤੇ ਹੇਠਲਾ ਭਾਗ ਉੱਪਰਲੇ ਭਾਗ ਨੂੰ ਉੱਪਰਲਾ ਖਾਨਾ (Auricle) ਅਤੇ ਹੇਠਲੇ ਨੂੰ ਹੇਠਲਾ ਖਾਨਾ (Ventricle) ਕਹਿੰਦੇ ਹਨ । ਸਰੀਰ ਵਿਚੋਂ ਸ਼ੁੱਧ ਖੂਨ ਭਿੰਨ-ਭਿੰਨ ਅੰਗਾਂ ਅਤੇ ਸ਼ਿਰਾਵਾਂ ਦੇ ਮਾਧਿਅਮ ਰਾਹੀਂ ਦਿਲ ਦੇ ਸੱਜੇ ਉੱਪਰਲੇ ਖਾਨੇ (Auricle) ਵਿਚ ਪੁੱਜਦਾ ਹੈ ਅਤੇ ਉੱਪਰੋਂ ਤਿੰਨਪਦੀ ਦੁਆਰ (Triscuspid Valve) ਦੁਆਰਾ ਹੇਠਲੇ ਖਾਨੇ (Ventricle) ਵਿਚ ਪੁੱਜਦਾ ਹੈ । ਇੱਥੋਂ ਉੱਪਰ ਵਾਪਸ ਨਹੀਂ ਜਾ ਸਕਦਾ । ਸੱਜੇ ਹੇਠਲੇ ਖਾਨੇ ਤੋਂ ਖੂਨ ਫੇਫੜਿਆਂ ਵਾਲੀ ਧਮਨੀ (Pulmonary Artery) ਤੋਂ ਫੇਫੜਿਆਂ ਵਿਚ ਸ਼ੁੱਧ ਹੋਣ ਦੇ ਲਈ ਜਾਂਦਾ ਹੈ ਅਤੇ ਵਾਪਸੀ ਵਿਚ ਆਕਸੀਜਨ ਨਾਲ ਮਿਸ਼ਰਤ ਸ਼ੁੱਧ ਖੂਨ ਦਿਲ ਦੇ ਖੱਬੇ ਉੱਪਰਲੇ ਖ਼ਾਨੇ ਵਿਚ ਪੁੱਜ ਜਾਂਦਾ ਹੈ । ਇਹ ਹੇਠਲੇ ਖ਼ਾਨੇ ਵਿਚ ਦੁਪਦੀ (Bricuspid) ਦੁਆਰਾ ਪੁੱਜਦਾ ਹੈ । | ਹੇਠਲੇ ਖਾਨੇ ਵਿਚੋਂ ਮਹਾਂਧਮਨੀ (Aorta) ਦੇ ਦੁਆਰਾ ਸਰੀਰ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਅੰਗਾਂ ਵਿਚ ਪੁੱਜਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਲਹੂ ਚੱਕਰ ਦਾ ਇਕ ਚੱਕਰ ਲਗਾਤਾਰ ਕੰਮ ਕਰਦਾ ਰਹਿੰਦਾ ਹੈ ।

(ਸ) ਸ਼ਿਰਾਵਾਂ ਤੇ ਧਮਨੀਆਂ (Veins and Arteries) -ਜੋ ਨਾਲੀਆਂ ਖੂਨ ਨੂੰ ਫੇਫੜਿਆਂ ਅਤੇ ਸਰੀਰ ਦੇ ਹੋਰਾਂ ਭਾਗਾਂ ਤੋਂ ਫੇਫੜਿਆਂ ਵੱਲ ਲੈ ਜਾਂਦੀਆਂ ਭਾਗ ਹਨ, ਉਹਨਾਂ ਨੂੰ ਸ਼ਿਰਾਵਾਂ (Veins) ਕਹਿੰਦੇ ਹਨ । ਇਹਨਾਂ ਦੀਆਂ ਕੰਧਾਂ ਦੀ ਬਨਾਵਟ ਤਾਂ ਧਮਨੀਆਂ ਵਰਗੀ ਹੀ ਹੁੰਦੀ ਹੈ, ਪਰ ਇਹਨਾਂ ਵਿਚ ਲਚੀਲੇ ਟਿਸ਼ੂਆਂ ਅਤੇ ਮਾਸਦਾਰ ਪੇਸ਼ੀਆਂ ਦੀ ਤਹਿ ਬਹੁਤ ਬਰੀਕ ਹੁੰਦੀ ਹੈ । ਪਲਮੋਨਰੀ ਸ਼ਿਰਾ ਨੂੰ ਛੱਡ ਕੇ ਬਾਕੀ ਸਭ ਸ਼ਿਰਾਵਾਂ ਨੂੰ ਅਸ਼ੁੱਧ ਖੂਨ ਨੂੰ ਹੀ ਦਿਲ ਵਿਚੋਂ ਲਿਆਉਂਦੀਆਂ ਹਨ । ਧਮਨੀਆਂ -ਇਹ ਸ਼ੁੱਧ ਖੂਨ ਨੂੰ ਦਿਲ ਤੋਂ ਸਰੀਰ ਦੇ ਭਿੰਨ-ਭਿੰਨ ਭਾਗਾਂ ਤੱਕ ਪਹੁੰਚਾਉਂਦੀਆਂ ਹਨ । ਇਹ ਲਚਕਦਾਰ ਅਤੇ ਮੋਟੀ ਕੰਧ ਦੀਆਂ ਬਣੀਆਂ ਹੁੰਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਵਿਚ ਸਾਫ਼ ਖ਼ੂਨ ਵਗਦਾ ਹੈ, ਪਰ ਫੇਫੜੇ ਵਿਚ ਖੂਨ

ਲੈ ਜਾਣ ਵਾਲੀ ਧਮਨੀ ਵਿਚ ਗੰਦਾ ਖੂਨ ਵਗਦਾ ਹੈ । ਇਸ ਖੂਨ ਨੂੰ ਲੈ ਜਾਣ ਵਾਲੀ ਧਮਨੀ ਨੂੰ ਪਲਮੋਨਰੀ ਧਮਨੀ (Pulmonary Artery) ਕਹਿੰਦੇ ਹਨ |
ਧਮਨੀਆਂ ਵਿਚ ਸਭ ਤੋਂ ਪ੍ਰਮੁੱਖ ਧਮਨੀ ਨੂੰ ਮੂਲ ਧਮਨੀ ਜਾਂ ਮਹਾਂਧਮਨੀ (Aorta) ਕਹਿੰਦੇ ਹਨ |

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 3Matrices Ex 3.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.1

Question 1.
In the matrix A = \(=\left[\begin{array}{cccc}
2 & 5 & 19 & -7 \\
35 & -2 & \frac{5}{2} & 12 \\
\sqrt{3} & 1 & -5 & 17
\end{array}\right]\), write:
(i) The order of the matrix
(ii) The number of elements,
(iii) The elements a₁₃, a₂₁, a₃₃, a₂₄, a₂₃.
Solution.
(i) In the given matrix, the number of rows is 3 and the number of columns is 4. Therefore, the order of the matrix is 3 × 4.
(ii) Since, the order of the matrix is 3 × 4, so there are 3 × 4 = 12 elements in it.
(iii) a₁₃ = 19, a₂₁ = 35, a₃₃= – 5, a₂₄ = 12, a₂₃ = \(\frac{5}{2}\).

Question 2.
If a matrix has 24 elements, what are the possible orders it can have? What, if it has 13 elements?
Solution.
We know that if a matrix is of the order m × n, it has mn elements. Thus, to find all the possible orders of a matrix having 24 elements, we have to find all the ordered pairs of natural numhers whose product is 24.
The ordered pairs are: (1, 24), (24,1), (2,12), (12, 2), (3, 8), (8, 3), (4, 6) and (6, 4).
Hence, the possible orders of a matrix having 24 elements are 1 × 24,24 × 1, 2 × 12,12 × 2, 3 × 8, 8 × 3, 4 × 6, and 6 × 4 (1, 13) and (13, 1) are the ordered pairs of natural numbers whose product is 13.
Hence, the possible orders of a matrix having 13 elements are 1 x 13 and 13×1.

Question 3.
If a matrix has 18 elements, what are the possible orders it can have? What, if it has 5 elements?
Solution.
We know that if a matrix is of the order m × n, it has mn elements. Thus, to find all the possible orders of a matrix having 18 elements, we have to find all the ordered pairs of natural numbers whose product is 18.
The ordered pairs are: (1, 18), (18, 1), (2, 9), (9, 2), (3, 6), and (6, 3)
Hence, the possible orders of a matrix having 18 elements are 1 × 18, 18 × 1, 2 × 9, 9 × 2, 3 × 6 and 6 × 3.
(1, 5)and (5, 1)are ordered pairs of natural numbers whose product is 5.
Hence, the possible orders of a matrix having 5 elements are 1 × 5 and 5 × 1.

Question 4.
Construct 2 × 2 matrix, A = [a_ij] whose elements are given by
(i) a_ij = \(\frac{(i+j)^{2}}{2}\)

(ii) a_ij = \(\frac{i}{j}\)

(iii) a_ij = \(\frac{(i+2 j)^{2}}{2}\)
Solution.
(i) The order of the given matrix is 2 × 2, so A = \(\left[\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right]_{2 \times 2}\)
where a_ij = \(\frac{(i+2 j)^{2}}{2}\).
To find a₁₁, put i = 1 and j = 1
∴ a₁₁ = \(\frac{(1+1)^{2}}{2}\) = 2 Similarly

a₁₂ = \(\frac{(1+2)^{2}}{2}=\frac{9}{2}\)

a₂₁ = \(\frac{(2+1)^{2}}{2}=\frac{9}{2}\) and

a₂₂ = \(\frac{(2+2)^{2}}{2}\) = 8

(ii) Here, A = \(\left[\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right]_{2 \times 2}\), where a_ij = \(\frac{i}{j}\).
∴ a₁₁ = \(\frac{1}{1}\) = 1,

a₁₂ = \(\frac{1}{2}\),

a₂₁ = \(\frac{2}{1}\) = 2 and

a₂₂ = \(\frac{2}{1}\) = 1

Hence, the required matrix is A = \(\left[\begin{array}{cc}
1 & 1 / 2 \\
2 & 1
\end{array}\right]_{2 \times 2}\)

(iii) Here, A = \(\left[\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right]_{2 \times 2}\), where a_ij = \(\frac{(i+2 j)^{2}}{2}\)
∴ a₁₁ = \(\frac{(1+2)^{2}}{2}=\frac{9}{2}\)

a₁₂ = \(\frac{(1+4)^{2}}{2}=\frac{25}{2}\)

a₂₁ = \(\frac{(2+2)^{2}}{2}\) = 8

a₂₂ = \(\frac{(2+4)^{2}}{2}\) = 18.

Hence, the required matrix is A = \(\left[\begin{array}{cc}
9 / 2 & 25 / 2 \\
8 & 18
\end{array}\right]_{2 \times 2}\).

Question 5.
Construct a 3 × 4 matrix, whose elements are given by:
(i) a_ij = \(\frac{4}{4}\) |- 3i + j|
(ii) a_ij = 2i – j
Solution.
In general, a 3 × 4 matrix is given by A = \(\left[\begin{array}{llll}
a_{11} & a_{12} & a_{13} & a_{14} \\
a_{21} & a_{22} & a_{23} & a_{24} \\
a_{31} & a_{32} & a_{33} & a_{34}
\end{array}\right]\)

(i) (i) a_ij = \(\frac{1}{2}\) |- 3i + j|, i = 1, 2, 3, 4 and j =1, 2, 3, 4
a₁₁ = \(\frac{1}{2}\) |- 3 × 1 + 1|
= \(\frac{1}{2}\) |- 3 + 1|
= \(\frac{1}{2}\) |- 2|
= \(\frac{21}{2}\) = 1

a₂₁ = \(\frac{1}{2}\) |- 3 × 2 + 1|
= \(\frac{1}{2}\) |- 6 + 1|
= \(\frac{1}{2}\) |- 5|
= \(\frac{5}{2}\)

a₃₁ = \(\frac{1}{2}\) |- 3 × 3 + 1|
= \(\frac{1}{2}\) |- 9 + 1|
= \(\frac{1}{2}\) |- 8|
= \(\frac{8}{2}\) = 4

a₁₂ = \(\frac{1}{2}\) |- 3 × 1 + 2|
= \(\frac{1}{2}\) |- 3 + 2|
= \(\frac{1}{2}\) |- 1|
= \(\frac{1}{2}\)

a₂₂ = \(\frac{1}{2}\) |- 3 × 2 + 2|
= \(\frac{1}{2}\) |- 6 + 2|
= \(\frac{1}{2}\) |- 4|
= \(\frac{4}{2}\) = 2

a₃₂ = \(\frac{1}{2}\) |- 3 × 3 + 2|
= \(\frac{1}{2}\) |- 9 + 2|
= \(\frac{1}{2}\) |- 7|
= \(\frac{7}{2}\)

a₁₃ = \(\frac{1}{2}\) |- 3 × 1 + 3|
= \(\frac{1}{2}\) |- 3 + 3| = 0

a₂₃ = \(\frac{1}{2}\) |- 3 × 2 + 3|
= \(\frac{1}{2}\) |- 6 + 3|
= \(\frac{1}{2}\) |- 3|
= \(\frac{3}{2}\)

a₃₃ = \(\frac{1}{2}\) |- 3 × 3 + 3|
= \(\frac{1}{2}\) |- 9 + 3|
= \(\frac{1}{2}\) |- 6|
= \(\frac{6}{2}\) = 3

a₁₄ = \(\frac{1}{2}\) |- 3 × 1 + 4|
= \(\frac{1}{2}\) |- 3 + 4|
= \(\frac{1}{2}\) |1|
= \(\frac{1}{2}\)

a₂₄ = \(\frac{1}{2}\) |- 3 × 2 + 4|
= \(\frac{1}{2}\) | – 6 + 4|
= \(\frac{1}{2}\) |- 2|
= \(\frac{2}{2}\) = 1

a₃₄ = \(\frac{1}{2}\) |- 3 × 3 + 4|
= \(\frac{1}{2}\) |- 9 + 4|
= \(\frac{1}{2}\) |- 5|
= \(\frac{5}{2}\)

Therfore, the required matrix is A = \(\left[\begin{array}{cccc}
1 & \frac{1}{2} & 0 & \frac{1}{2} \\
\frac{5}{2} & =2 & \frac{3}{2} & 1 \\
4 & \frac{7}{2} & 3 & \frac{5}{2}
\end{array}\right]_{3 \times 4}\)

(ii) a_ij = 2i – j, i = 1, 2, 3, 4 and j = 1, 2, 3, 4
a₁₁ = 2 × 1 – 1 = 2 – 1 = 1
a₁₂ = 2 × 2 – 1 = 4 – 1 = 3
a₁₃ = 2 × 3 – 1 = 6 – 1 = 5

a₂₁ = 2 × 1 – 2 = 2 – 2 = 0
a₂₂ = 2 × 2 – 2 = 4 – 2 = 2
a₂₃ = 2 × 3 – 2 = 6 – 2 = 4

a₃₁ = 2 × 1 – 3 = 2 – 3 = – 1
a₃₂ = 2 × 2 – 3 = 4 – 3 = 1
a₃₃ = 2 × 3 – 3 = 6 – 3 = 3

a₄₁ = 2 × 1 – 4 = 2 – 4 = – 2
a₄₂ = 2 × 2 – 4 = 4 – 4 = 0
a₄₃ = 2 × 3 – 4 = 6 – 4 = 0

Therfore, the required matrix is A = \(\left[\begin{array}{cccc}
1 & 0 & -1 & -2 \\
3 & 2 & 1 & 0 \\
5 & 4 & 3 & 2
\end{array}\right]_{3 \times 4}\).

Question 6.
Find the values of x, y, and z from the following equations:
(i) \(\left[\begin{array}{ll}
\mathbf{4} & \mathbf{3} \\
\boldsymbol{x} & 5
\end{array}\right]=\left[\begin{array}{ll}
\boldsymbol{y} & \boldsymbol{z} \\
\mathbf{1} & \mathbf{5}
\end{array}\right]\)

(ii) \(\left[\begin{array}{cc}
x+y & 2 \\
5+z & x y
\end{array}\right]=\left[\begin{array}{ll}
6 & 2 \\
5 & 8
\end{array}\right]\)

(iii) \(\left[\begin{array}{c}
x+y+z \\
x+z \\
y+z
\end{array}\right]=\left[\begin{array}{l}
9 \\
5 \\
7
\end{array}\right]\)
Solution.
(i) \(\left[\begin{array}{ll}
\mathbf{4} & \mathbf{3} \\
\boldsymbol{x} & 5
\end{array}\right]=\left[\begin{array}{ll}
\boldsymbol{y} & \boldsymbol{z} \\
\mathbf{1} & \mathbf{5}
\end{array}\right]\)
As the given matrices are equal, their corresponding elements are also equal.
Comparing the corresponding eleme nts, we get x = 1, y = 4, and z = 3

(ii) \(\left[\begin{array}{cc}
x+y & 2 \\
5+z & x y
\end{array}\right]=\left[\begin{array}{ll}
6 & 2 \\
5 & 8
\end{array}\right]\)
As the given matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get x + y = 6, xy = 8, 5 + z = 5
Now, 5 + z = 5
⇒ z = 0
We know that,
(x – y)² = (x + y)² – 4xy
⇒ (x – y)² = 36 – 32 = 4
⇒ x – y = ±2
Now, when x – y – 2 and x + y = 6, we get x = 4 and y = 2
When x – y = – 2 and x + y = 6, we get x = 2 and y = 4
∴ x = 4, y = 2, and z = 0 or x = 2, y = 4, and z = 0.

(iii) \(\left[\begin{array}{c}
x+y+z \\
x+z \\
y+z
\end{array}\right]=\left[\begin{array}{l}
9 \\
5 \\
7
\end{array}\right]\)
As the two matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get
x + y + z = 9 ………..(i)
x + z = 5 ………….(ii)
y + z = 7
From Eqs. (i) and (ii), we have
y = 9 – 5
⇒ y = 4
Then, from Eq. (iii), we have:
4 + z = 7
⇒ z = 3
Now, x + z = 5
⇒ x = 5 – 3 = 2
∴ x – 2, y = 4 and z = 3.

Question 7.
Find the value of a, b, c and d from the following equation:
\(\left[\begin{array}{cc}
a-b & 2 a+c \\
2 a-b & 3 c+d
\end{array}\right]=\left[\begin{array}{cc}
-1 & 5 \\
0 & 13
\end{array}\right]\)
Solution.
We have,
\(\left[\begin{array}{cc}
a-b & 2 a+c \\
2 a-b & 3 c+d
\end{array}\right]=\left[\begin{array}{cc}
-1 & 5 \\
0 & 13
\end{array}\right]\)
As the two matrices are equal, their corresponding elements are also equal.
Comparing the corresponding elements, we get
a – b = – 1 ……………(i)
2a – b = 0 …………….(ii)
2a + c = 5 …………..(iii)
3c + d = 13 ………..(iv)
From Eq. (ii), we have
b = 2a
Then, from Eq. (i), we have
a – 2a = – 1
⇒ a -1
⇒ b = 2
Now, from Eq. (iii), we have
2 x 1 + c = 5
⇒ c = 5 – 2 = 3
From Eq. (iv) we have
3 × 3 + d = 13
⇒ 9 + d = 13
⇒ d = 13 – 9 = 4
Hence, a = 1, b = 2, c = 3 and d = 4.

Question 8.
A = [a_ij]_{m × n} is a square matrix, if
(A) m < n (B) m > n
(C) m = n
(D) None of these
Solution.
It is known that a given matrix is said to be a square matrix, if the number of rows is equal to the number of columns.
Therefore, A = [a_ij]_{m × n} is a square matrix, if m – n.
Hence, the correct answer is (C).

Question 9.
Which of the given values of x and y make the following pair of matrices equal?
\(\left[\begin{array}{cc}
3 x+7 & 5 \\
y+1 & 2-3 x
\end{array}\right]=\left[\begin{array}{cc}
0 & y-2 \\
8 & 4
\end{array}\right]\)
(A) x = \(\frac{-1}{3}\), y = 7

(B) Not possible to find

(C) y = 7, x = \(\frac{-2}{3}\)

(D) x = \(\frac{-1}{3}\), y = \(\frac{-2}{3}\)
Solution.
It is given that \(\left[\begin{array}{cc}
3 x+7 & 5 \\
y+1 & 2-3 x
\end{array}\right]=\left[\begin{array}{cc}
0 & y-2 \\
8 & 4
\end{array}\right]\)
On equating the corresponding elements, we get
3x + y = 0
⇒ x = – 3
5 = y – 2
⇒ y = 7
y + 1 = 8
⇒ y = 7
2 – 3x = 4
⇒ x = \(\frac{-2}{3}\)

We find that on comparing the corresponding elements of the two matrices, we get two different values of x, which is not possible.
Hence, it is not possible to find the values of x and y for which the given matrices are equal.
Hence, the correct answer is (B).

Q. 10.
The number of all possible matrices of order 3 x 3 with each entry 0 or 1 is
(A) 27
(B) 18
(C) 81
(D) 512
Solution.
The given matrix of the order 3 × 3 has 9 elements and each of these elements can be either 0 or 1.
Now, each of the 9 elements can be filled in two possible ways.
Therefore, by the multiplication principle, the required number of possible matrices is 2⁹ = 512.
Hence, the correct answer is (D).

Punjab State Board PSEB 11th Class Chemistry Book Solutions Chapter 1 Some Basic Concepts of Chemistry Important Questions and Answers.

PSEB 11th Class Chemistry Important Questions Chapter 1 Some Basic Concepts of Chemistry

Very Short Answer Type Questions

Question 1.
A liquid has a volume of 49.0 cm³ and a mass of 57.642 g. Find out the density of this liquid in SI unit.
Answer:
Density = \(\frac{\text { Mass }(\mathrm{kg})}{\text { Volume }\left(\mathrm{m}^{3}\right)}\)
Mass = 57.642 g = 57.642 x 10^-3 kg
Volume = 49.0 cm³ = 49.0 x (10^-3)³ = 49.0 x 10^-6 m³
∴ Density = \(\frac{57.642 \times 10^{-3}}{49.0 \times 10^{-6}}\) = 1.176 x 10³ kg/m³

Question 2.
Convert the following temperatures into degree Fahrenheit,
(i) 25°C, physiological (human body) temperature.
(ii) 35°C, the room temperature.
Answer:
(i) Given
C = 25 °C
°F = \(\frac{9}{5}\) °C + 32 = \(\frac{9}{5}\) x 25 + 32 = 45 + 32 = 77°F

(ii) Given, C = 35 °C
°F = \(\frac{9}{5}\) °C + 32 = \(\frac{9}{5}\) x 35 + 32 = 63 + 32 = 95°F

Question 3.
What is the mass (in grams) of a copper block whose dimensions are 5.0 inch x 6.0 inch and whose density is 8.96 g/cm³? Given that 1 inch = 2.54 cm
Answer:
Here, unit conversion factors are 1 = \(\frac{2.54 \mathrm{~cm}}{1 \text { inch }}=\frac{1 \text { inch }}{2.54 \mathrm{~cm}}\)
Hence, required mass (in g) = 5.0 inch x 6.0 inch x 4.0 inch
\(\) = 1.76 x 10⁴ g.

Question 4.
If 6.3 g of NaHCO₃ are added to 15.0 g of CH₃COOH solution, the residue is found to weigh 18.0 g. What is the mass of CO₂ released in the reaction?
Answer:

Sum of the masses of reactants = 6.3 + 15 = 21.3 g
Sum of the masses of products = x + 18
21.3 = x +18; x = 21.3 – 18 = 3.3 g
Thus, the mass of the C02 released is 3.3 g.

Question 5.
Why is the law of Gay Lussac’s not obeyed if any reactant or product is not a gas?
Answer:
If any reactant or product is a liquid or solid, the volume occupied by them is extremely small as compared to the gas and hence, the law is not obeyed.

Question 6.
Calculate the normality of solution containing 62.3 g of hydrated copper sulphate (CuSO₄ . 5H₂O) in 500 mL of solution.
Answer:
Mass of solute = 62.3 g
Equivalent mass of oxalic acid = \(\frac{249.5}{2}\) = 124.75 g
Gram equivalents of oxalic acid = \(\frac{62.3}{124.75}\) = 0.5
Volume of solution = 500 mL
Normality = \(\frac{0.5}{500}\) x 1000 = 1N

Question 7.
What is the difference between molality and molarity?
Answer:
Molality : It is defined as the number of moles of solute dissolved in 1 kg of solvent. It is independent of temperature. ,
Molarity : It is defined as the number of moles of solute dissolved in 1 L of solution. It depends upon temperature because, volume of solution °c temperature.

Question 8.
How is the term material different from matter?
Answer:
Anything which has mass and occupies space is called matter. However, material corresponds to the matter which has specific use.

Question 9.
Why are the atomic masses of most of the elements fractional?
Answer:
It is because most of the elements occur in nature as a mixture of isotopes and their atomic masses are the average relative atomic masses of the isotopes depending on their abundance.

Question 10.
Volume of a solution changes with change in temperature, then, will the molality of the solution be affected by temperature? Give reason for your answer.
Answer:
No, molality of solution does not change with temperature since mass remains unaffected with temperature.

Short Answer Type Questions

Question 1.
Express the following in the scientific notation.
(i) 0.000968
(ii) 157428
(iii) 90,000
(iv) (5.7 x 10⁶) x (4.2 x 10^-2)
(v) (6.8 x 10^-9) + (1.4 x 10^-6)
(vi) (456 x 10³ + 2.62 x 10²)
(vii) (9.87 x 10^-3 – 2.26 x 10^-4)
Answer:
(i) 0.000968 = 9.68 x 10^-4
(ii) 157428 = 1.57428 x 10⁵
(iii) 90,000 = 9 x 10⁴

(iv) (5.7 x 10⁶)x (4.2 x 10^-2) = (5.7 x 4.2)(10^6-2)
= 23.94 x 10⁴ =2.394 x 10⁵
(v) (6.8 x 10^-9) ÷ (1.4 x 10^-6) = x (10^-9-(-6)) = 4.857 x 10^-3
(vi) (4.56 x 10³ + 2.62 x 10²)= 45.6 x 10² + 2.62 x 10²
=(45.6 +2.62) x 10²
= 48.22 x 10²
= 4.822 x 10³
(vii) (9.87 x 10^-3 – 2.26 x 10^-4) = 9.87 x 10^-3 – 0.226 x 10^-3
= (9.87 – 0.226) x 10^-3 = 9.644 x 10^-3

Question 2.
The percentage composition of elements in NH3, H20, and N20 3 is given below. –
NH₃ → 82.35% N and 17.65% H
H₂O → 88.90% O and 11.10% H
N₂O₃ → 6a 15% O and 36.85% N
Show that these data are in accordance with the law of reciprocal proportion.
Answer:
(i) In NH₃, 1 part of H reacts with = \(\) = 4.67 part of N
(ii) In H₂O, 1 part of H reacts with = \(\) = 8.01 part of O
Thus, the ratio N : O :: 4.67 : 8.01 = 1 :1.72
(iii) In N₂O₃, N and O reacts with each other in the ratio N : O :: 36.85: 63.15 = 1 :1.71.
Thus, the two ratios are the same. Hence, it illustrates the law of reciprocal proportions.

Question 3.
A solution contains 25% water, 25% ethanol and 50% acetic acid by mass. Calculate the mole fraction of each component.
Answer:
Let the total mass of solution = 100 g
Mass of water = 25 g, Mass of ethanol = 25 g
Mass of acetic acid = 50 g
Moles of water = \(\frac{25}{18}\) = 1.388 (∵ Molar mass of H₂O= 18)
Moles of ethanol = \(\frac{25}{46}\) = 0.543 (∵ Molar mass of C₂H₅OH = 18)
Moles of acetic acid = \(\frac{50}{60}\) = 0.833 (∵ Molar mass of CH₃COOH = 18)
Total number of moles = 1.388 + 0.543 + 0.833 = 2.764
Mole fraction of water = \(\frac{1.388}{2.764}\) = 0.502
Mole fraction of ethanol = \(\frac{0.543}{2.764}\) = 0.196
Mole fraction of acetic acid = \(\frac{0.833}{2.764}\) = 0.302

Question 4.
Calculate the molality of a solution containing 20.7 g potassium carbonate dissolved in 500 mL of solution (assume density of solution = 1 g mL^-2).
Mass of K₂CO₃ = 20.7 g
Molar mass of K₂CO₃ = 2 x 39 + 12 + 3 x 16 = 138 mol^-1
Moles of K₂CO₃ = \(\frac{20.7}{138}\) = 0.15 .
Mass of solution = (500 mL) x (1 g mL^-1) = 500 g
Amount of water = 500 – 20.7 = 479.3 g
Molality = \(\frac{Moles of solute}
{Mass of solvent in gram}\) x 100
= \(\frac{0.15}{479.3}\) x 1000 = 0.313 mx`

Question 5.
45.4 L of dinitrogen reacted with 22.7 L of dioxygen and 45.4 L of nitrous oxide was formed. The reaction is given below 2N₂(g) + O₂(g) → 2N₂O(g)
Which law is being obeyed in this experiment? Write the statement of the law. [NCERT Exemplar]
Answer:

Hence, the ratio between the volumes of the reactants and the product in the given question is simple i.e., 2:1:2. It proves the Gay-Lussac’s law of gaseous volumes.
Gay-Lussac’s law of gaseous volumes : The law of combining volume states that when gases react together to form other gases, and when all volumes are measured at the same temperature and pressure, the ratio between the volumes of the gaseous reactants and products can be expressed in simple whole numbers.

Long Answer Type Questions

Question 1.
Copper oxide was prepared by the following methods.
(i) In first case, 1.75 g of the metal was dissolved in nitric acid and igniting the residual copper nitrate yielded 2.19 g of copper oxide.
(ii) In the second case, 1.14 g of metal dissolved in nitric acid were precipitated as copper hydroxide by adding caustic alkali solution. The precipitated copper hydroxide after washing, drying and heating yielded 1.43 g of copper oxide.
(iii) In the third case, 1.46 g of copper when strongly heated in a current of air yielded 1.83 g of copper oxide. Show that the given data illustrate the law of definite composition.
Answer:
Step I and II In the first experiment,
2.19 g of copper oxide contained 1.75 g of Cu.
∴ 100 g of copper oxide contained Cu
i.e., %ofCu = 79.91

In the second experiment,
1.43 g of copper oxide contained 1.14 g copper.
∴ 100 g of copper oxide contained Cu = \(\frac{1.14}{1.43}\) x 100 = 79.72 g,
i.e„ % of Cu = 79.72

In the third experiment,
1.83 g of copper oxide contained 1.46 g of copper
∴ 100 g of copper oxide contained Cu = \(\frac{1.46}{1.83}\) x 100 = 79.78g.
i.e., % of Cu = 79.78
Step III The percentage of copper in copper oxide derived from all the three experiments is nearly the same. Hence, the above data illustrate the law of definite composition.

Question 2.
Three oxides of nitrogen contained 63.6%, 46.7% and 30.4% nitrogen respectively. Show that these figures illustrate the law of multiple proportions.
Answer:
In case first,
Step I The oxide of nitrogen contains 63.6% N ‘ i.e., 63.6 g of N reacts with (100 – 63.6) g of O = 36.4 g of O.
Step II ∴ 1 g of N will react with \(\frac{36.4}{63.6}\) g of O = 0.57 g of O.

In case second,
Step I The oxide of nitrogen contains 46.7% N
i.e., 46.7 g of N reacts with (100 – 46.7) g of O = 53.3 g of O.

In case third,
Step I The oxide of nitrogen contains 30.4% N
i.e., 30.4 g of N reacts with (100 – 30.4) g of O = 69.6 g of O.
Step II ∴ 1 g of N will react with \(\frac{69.6}{30.4}\) of O = 2.26 g of O

Step III This means the ratio of the masses of oxygen which combine with 1 g of nitrogen is 0.57 : 1.14 : 2.26, i.e., 1: 2 : 4 is obviously in accordance with the law of multiple proportions.

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 2 Inverse Trigonometric Functions Miscellaneous Exercise Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions Miscellaneous Exercise

Find the value of the following :

Question 1.
cos^-1 (cos \(\frac{13 \pi}{6}\)).
Solution.
We know that cos^-1(cos x) = x if x ∈ [0, π], which is the principal value of cos^-1 x.
Here, \(\frac{13 \pi}{6}\) ∉ [0, π].
Now, cos^-1 (cos \(\frac{13 \pi}{6}\)) can be written as
cos^-1 (cos \(\frac{13 \pi}{6}\)) = cos^-1 [cos (2π + \(\frac{pi}{6}\))]
= cos^-1 [cos (\(\frac{pi}{6}\))],
where \(\frac{pi}{6}\) ∈ [0, π]
[∵ cos(2π + x) = cos x]
∴ cos^-1 (cos \(\frac{13 \pi}{6}\)) = cos^-1 [cos (\(\frac{pi}{6}\))]
= \(\frac{pi}{6}\).

Question 2.
tan^-1 (tan \(\frac{7 \pi}{6}\))
Solution.
We know that tan^-1(tan x) = x if x ∈ (\(-\frac{\pi}{2}, \frac{\pi}{2}\)) which is the principal value of cos^-1 x.
Here, \(\frac{7 \pi}{6}\) ∉ (\(-\frac{\pi}{2}, \frac{\pi}{2}\))
Now, tan^-1 (tan \(\frac{7 \pi}{6}\)) can be written as
tan^-1 (tan \(\frac{7 \pi}{6}\)) = tan^-1 (tan (π + \(\frac{\pi}{6}\)))
= tan^-1 [tan (\(\frac{\pi}{6}\))]
where \(\frac{pi}{6}\) ∈ (\(-\frac{\pi}{2}, \frac{\pi}{2}\))
[∵ tan(π + x) = tan x]
∴ tan^-1 (tan \(\frac{7 \pi}{6}\)) = tan^-1 [tan (\(\frac{\pi}{6}\))]
= \(\frac{pi}{6}\)

Prove that

Question 3.
2 sin^-1 \(\frac{3}{5}\) = tan^-1 \(\frac{24}{7}\).
Solution.
Let sin^-1 \(\frac{3}{5}\) = x.
Then, sin x = \(\frac{3}{5}\)
⇒ cos x = \(\sqrt{1-\left(\frac{3}{5}\right)^{2}}=\sqrt{1-\frac{9}{25}}=\sqrt{\frac{25-9}{25}}=\sqrt{\frac{16}{25}}=\frac{4}{5}\)
∴ tan x = \(\frac{3 / 5}{4 / 5}=\frac{3}{4}\)
∴ x = tan^-1 \(\frac{3}{4}\)
⇒ sin^-1 \(\frac{3}{5}\) = tan^-1 \(\frac{3}{4}\)
Now, we have
L.H.S = 2 sin^-1 \(\frac{3}{5}\) = 2 tan^-1 \(\frac{3}{4}\)
= tan^-1 \(\left(\frac{2 \times \frac{3}{4}}{1-\left(\frac{3}{4}\right)^{2}}\right)\)

[∵ 2 tan^-1 x = tan^-1 \(\frac{2 x}{1-x^{2}}\)]

= tan^-1 \(\left(\frac{\frac{3}{2}}{\frac{16-9}{16}}\right)\)

= tan^-1 \(\left(\frac{3}{2} \times \frac{16}{7}\right)\)

= tan^-1 \(\frac{24}{7}\)

= R.H.S.
Hence proved.

Question 4.
sin^-1 \(\frac{8}{17}\) + sin^-1 \(\frac{3}{5}\) = tan^-1 \(\frac{77}{36}\)
solution.
Let sin^-1 \(\frac{8}{17}\) = x.
Then, sin x = \(\frac{8}{17}\)
⇒ cos x = \(\sqrt{1-\left(\frac{8}{17}\right)^{2}}=\sqrt{\frac{225}{289}}=\frac{15}{17}\)
∴ tan x = \(\frac{8 / 17}{15 / 17}=\frac{8}{15}\)
⇒ x = tan^-1 \(\frac{8}{15}\)
∴ sin^-1 \(\frac{8}{17}\) = tan^-1 \(\frac{8}{15}\) …………..(i)

Now, let sin^-1 \(\frac{3}{5}\) = y.
Then, sin y = \(\frac{3}{5}\)
⇒ cos y = \(\sqrt{1-\left(\frac{3}{5}\right)^{2}}=\sqrt{\frac{16}{25}}=\frac{4}{5}\)
∴ tan y = \(\frac{3 / 5}{4 / 5}=\frac{3}{4}\)
⇒ y = tan^-1 \(\frac{3}{4}\)
∴ sin^-1 \(\frac{3}{5}\) = tan^-1 \(\frac{3}{4}\) …………..(ii)

Now, we have
L.H.S = sin^-1 \(\frac{8}{17}\) + sin^-1 \(\frac{3}{5}\)
[Using Eqs. (i) and (ii)]
= tan^-1 \(\frac{8}{15}\) + tan^-1 \(\frac{3}{4}\)
= tan^-1 \(\frac{\frac{8}{15}+\frac{3}{4}}{1-\frac{8}{15} \times \frac{3}{4}}\)
= tan^-1 \(\left(\frac{32+45}{60-24}\right)\)
[tan^-1 x + tan^-1 y = tan^-1 \(\left(\frac{x+y}{1-x y}\right)\)]
= tan^-1 \(\frac{77}{36}\)
= R.H.S
Hence proved.

Question 5.
cos^-1 \(\frac{4}{5}\) + cos^-1 \(\frac{12}{13}\) = cos^-1 \(\frac{33}{65}\)
Solution.
Let cos^-1 \(\frac{4}{5}\) = x
Then, cos x = \(\frac{4}{5}\)
⇒ sin x = \(\sqrt{1-\left(\frac{4}{5}\right)^{2}}=\sqrt{\frac{9}{25}}=\frac{3}{5}\)
∴ tan x = \(\frac{3 / 5}{4 / 5}=\frac{3}{4}\) …………(i)

⇒ x = tan^-1 \(\frac{3}{4}\)
Now, let cos^-1 \(\frac{12}{13}\) = y.
Then cos y = \(\frac{12}{13}\)
⇒ sin y = \(\sqrt{1-\left(\frac{12}{13}\right)^{2}}=\sqrt{\frac{25}{169}}=\frac{5}{13}\)
∴ tan y = \(\frac{5 / 13}{12 / 13}=\frac{5}{12}\)
⇒ y = tan^-1 \(\frac{5}{12}\)
∴ cos^-1 \(\frac{12}{13}\) = tan^-1 \(\frac{5}{12}\) ……………(ii)

Let cos^-1 \(\frac{33}{65}\) = z.
Then, cos z = \(\frac{33}{65}\)
⇒ sin z = \(\sqrt{1-\left(\frac{33}{65}\right)^{2}}=\sqrt{\frac{3136}{4225}}=\frac{56}{65}\)
∴ tan z = \(\frac{56 / 65}{33 / 65}=\frac{56}{33}\)
⇒ z = tan^-1 \(\frac{56}{33}\)
∴ cos^-1 \(\frac{33}{65}\) = tan^-1 \(\frac{56}{33}\) …………..(iii)

Now, we have
L.H.S = cos^-1 \(\frac{4}{5}\) + cos^-1 \(\frac{12}{13}\)
= \(\frac{3 / 5}{4 / 5}=\frac{3}{4}\) + tan^-1 \(\frac{5}{12}\)
[∵ Usin Eqs. (i) and (ii)]
= tan^-1 \(\frac{\frac{3}{4}+\frac{5}{12}}{1-\frac{3}{4} \cdot \frac{5}{12}}\)
[∵ tan^-1 x + tan^-1 y = tan^-1 \(\left(\frac{x+y}{1-x y}\right)\)]
= tan^-1 \(\frac{36+20}{48-15}\)
= tan^-1 \(\frac{56}{33}\)
= cos^-1 \(\frac{33}{65}\) = R.H.S.
Hence proved.

Question 6.
cos^-1 \(\frac{12}{13}\) + sin^-1 \(\frac{3}{5}\) = sin^-1 \(\frac{56}{65}\)
Solution.
Let sin^-1 \(\frac{3}{5}\) = x.
Then, sin x = \(\frac{3}{5}\)
⇒ cos x= \(\sqrt{1-\left(\frac{3}{5}\right)^{2}}=\sqrt{\frac{16}{25}}=\frac{4}{5}\)
∴ tan x = \(\frac{3 / 5}{4 / 5}=\frac{3}{4}\)
⇒ x = tan^-1 \(\frac{3}{4}\)
∴ sin^-1 \(\frac{3}{5}\) = tan^-1 \(\frac{3}{4}\) …………(i)

Now, let cos^-1 \(\frac{12}{13}\) = y.
Then, cos y = \(\frac{12}{13}\)
⇒ sin y = \(\sqrt{1-\left(\frac{12}{13}\right)^{2}}=\sqrt{\frac{25}{169}}=\frac{5}{13}\)
∴ tan y = \(\frac{5 / 13}{12 / 13}=\frac{5}{12}\)
⇒ y = tan^-1 \(\frac{5}{12}\)
∴ cos^-1 \(\frac{12}{13}\) = tan^-1 \(\frac{5}{12}\) ………………(ii)

Let sin^-1 \(\frac{56}{65}\) = z.
Then, sin z = \(\frac{56}{65}\)
⇒ cos z = \(\sqrt{1-\left(\frac{56}{65}\right)^{2}}=\sqrt{\frac{1089}{4225}}=\frac{33}{65}\)
∴ tan z = \(\frac{56 / 65}{33 / 65}=\frac{56}{33}\)
⇒ z = tan^-1 \(\frac{56}{33}\)
∴ sin^-1 \(\frac{56}{65}\) = tan^-1 \(\frac{56}{33}\) …………….(iii)

Now, we have
L.H.S. = cos^-1 \(\frac{12}{13}\) + sin^-1 \(\frac{3}{5}\)
= tan^-1 \(\frac{3}{4}\) + tan^-1 \(\frac{5}{12}\)
[Using Eqs. (i) and (ii)]
= tan^-1 \(\frac{\frac{5}{12}+\frac{3}{4}}{1-\frac{5}{12} \cdot \frac{3}{4}}\)

[∵ tan^-1 x + tan^-1 y = tan^-1 \(\left(\frac{x+y}{1-x y}\right)\)]
= tan^-1 \(\frac{20+36}{48-15}\)
= tan^-1 \(\frac{56}{33}\)
= sin^-1 \(\frac{56}{65}\).
Hence proved.

Question 7.
tan^-1 \(\frac{63}{16}\) = sin^-1 \(\frac{5}{13}\) + cos ^-1 \(\frac{3}{5}\)
Solution.
Let sin^-1 \(\frac{5}{13}\) = x
Then, sin x = \(\frac{5}{13}\)
⇒ cos x = \(\sqrt{1-\left(\frac{5}{13}\right)^{2}}=\sqrt{\frac{144}{169}}=\frac{12}{13}\)
∴ tan x = \(\frac{5 / 13}{12 / 13}=\frac{5}{12}\)
⇒ x = tan^-1 \(\frac{5}{12}\)
∴ sin^-1 \(\frac{5}{13}\) = tan^-1 \(\frac{5}{12}\) ………….(i)

Let cos^-1 \(\frac{3}{5}\) = y.
Then, cos y = \(\frac{3}{5}\)
⇒ sin y = \(\sqrt{1-\left(\frac{3}{5}\right)^{2}}=\sqrt{\frac{16}{25}}=\frac{4}{5}\)
∴ tan y = \(\sqrt{1-\left(\frac{3}{5}\right)^{2}}=\sqrt{\frac{16}{25}}=\frac{4}{5}\)
⇒ y = tan^-1 \(\frac{4}{5}\)
∴ cos^-1 \(\frac{3}{5}\) = tan^-1 \(\frac{4}{5}\) ………………(ii)

Using Eqs. (i) and (ii), we have
R.H.S = sin^-1 \(\frac{5}{13}\) + cos^-1 \(\frac{3}{5}\)
= tan^-1 \(\frac{5}{12}\) + tan^-1 \(\frac{4}{5}\)
[∵ tan^-1 x + tan^-1 y = tan^-1 \(\left(\frac{x+y}{1-x y}\right)\)]
= tan^-1 \(\left(\frac{\frac{5}{12}+\frac{4}{3}}{1-\frac{5}{12} \times \frac{4}{3}}\right)\)

= tan^-1 \(\left(\frac{15+48}{36-20}\right)\)

= tan^-1 \(\frac{63}{16}\) = L.H.S.
Hence proved.

Question 8.
tan^-1 \(\frac{1}{5}\) + tan^-1 \(\frac{1}{7}\) + tan^-1 \(\frac{1}{3}\) + tan^-1 \(\frac{1}{8}\) = \(\frac{\pi}{4}\)
Solution.
tan^-1 \(\frac{1}{5}\) + tan^-1 \(\frac{1}{7}\) + tan^-1 \(\frac{1}{3}\) + tan^-1 \(\frac{1}{8}\)

Question 9.
tan^-1 √x = \(\frac{1}{2}\) cos^-1 \(\left(\frac{1-x}{1+x}\right)\), x ∈ [0, 1]
Solution.
Let x = tan² θ.
Then, √x = tan θ
⇒ θ = tan^-1 √x
∴ \(\frac{1-x}{1+x}=\frac{1-\tan ^{2} \theta}{1+\tan ^{2} \theta}\) = cos 2θ
[∵ cos 2θ = \(\frac{1-\tan ^{2} \theta}{1+\tan ^{2} \theta}\)]
Now, we have
R.H.S = \(\frac{1}{2}\) cos^-1 \(\left(\frac{1-x}{1+x}\right)\)
= \(\frac{1}{2}\) cos^-1 2θ = θ
= tan^-1 √x = L.H.S
Hence Proved.

Question 10.
cot^-1 \(\left(\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right)=\frac{x}{2}\), x ∈ (0, \(\frac{\pi}{4}\))
Solution.
Consider, \(\left(\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right)\)

= \(\frac{(\sqrt{1+\sin x}+\sqrt{1-\sin x})^{2}}{(\sqrt{1+\sin x})^{2}-(\sqrt{1-\sin x})^{2}}\) (By rationalising)

= \(\frac{(1+\sin x)+(1-\sin x)+2 \sqrt{(1+\sin x)(1-\sin x)}}{1+\sin x-1+\sin x}\)

= \(\frac{2\left(1+\sqrt{\left.1-\sin ^{2} x\right)}\right.}{2 \sin x}=\frac{1+\cos x}{\sin x}=\frac{2 \cos ^{2} \frac{x}{2}}{2 \sin \frac{x}{2} \cos \frac{x}{2}}\)

= cot \(\frac{x}{2}\)

L.H.S = cot^-1 \(\left(\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right)\)

= cot^-1 (cot \(\frac{x}{2}\))
= \(\frac{x}{2}\) = R.H.S

Question 11.
tan^-1 \(\left(\frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt{1+x}+\sqrt{1-x}}\right)\) = \(\frac{\pi}{4}-\frac{1}{2} \cos ^{-1} x\), \(-\frac{1}{\sqrt{2}}\) ≤ x ≤ 1.
[Hint: put x = cos 2θ]
Solution.
Put x = cos 2θ, so that θ = \(\frac{1}{2}\) cos^-1 x.
Then, we have

Question 12.
\(\frac{9 \pi}{8}-\frac{9}{4} \sin ^{-1} \frac{1}{3}=\frac{9}{4} \sin ^{-1} \frac{2 \sqrt{2}}{3}\)
Solution.
L.H.S = \(\frac{9 \pi}{8}-\frac{9}{4} \sin ^{-1} \frac{1}{3}\)

= \(\frac{9}{4}\left(\frac{\pi}{2}-\sin ^{-1} \frac{1}{3}\right)\)

= \(=\frac{9}{4}\left(\cos ^{-1} \frac{1}{3}\right)\) [∵ sin^-1 x + cos^-1 x = \(\frac{\pi}{2}\)]

= \(\frac{9}{4}\left(\sin ^{-1} \sqrt{1-\left(\frac{1}{3}\right)^{2}}\right)\)
[∵ cos^-1 x = sin^-1 \(\sqrt{1-x^{2}}\)]

= \(\frac{9}{4} \sin ^{-1} \sqrt{\frac{8}{9}}\)

= \(\frac{9}{4} \sin ^{-1} \frac{2 \sqrt{2}}{3}\)

= R.H.S
Hence proved.

Direction (13 – 17): Solve the following equations.

Question 13.
2 tan^-1 (cos x) = tan^-1 (2cosec x)
Solution.
We have, 2 tan^-1 (cos x) = tan^-1 (2 cosec x)
⇒ tan^-1 \(\left(\frac{2 \cos x}{1-\cos ^{2} x}\right)\) = tan^-1 (2 cosec x)

[∵ 2 tan^-1 x = tan^-1 \(\frac{(2 x)}{1-x^{2}}\)]

⇒ \(\left(\frac{2 \cos x}{1-\cos ^{2} x}\right)\) = 2 cosec x

⇒ \(\frac{2 \cos x}{\sin ^{2} x}=\frac{2}{\sin x}\)

⇒cos x = sin x

⇒ tan x = 1 = tan \(\frac{\pi}{4}\).

Question 14.
tan^-1 \(\frac{1-x}{1+x}\) = \(\frac{1}{2}\) tan^-1 x, (x > 0)
Solution.
We have, sin^-1 (1 – x) – 2 sin^-1 x = \(\frac{\pi}{2}\)
⇒ – 2 sin^-1 x = \(\frac{\pi}{2}\) – sin^-1 (1 – x)
⇒ – 2 sin^-1 x = cos^-1 (1 – x) ………….(i)
Let sin^-1 x = θ
⇒ sin θ = x
⇒ cos θ = \(\sqrt{1-x^{2}}\)
∴ θ = cos^-1 \(\sqrt{1-x^{2}}\)
∴ sin^-1 x = cos^-1 \(\sqrt{1-x^{2}}\)
Therefore, from Eq. (i), we have
– 2 cos^-1 (\(\sqrt{1-x^{2}}\) ) = cos^-1 (1 – x)
Put x = sin y. Then, we have
– 2 cos^-1 (\(\)) = cos^-1 (1 – sin y)
⇒ – 2 cos^-1 (cos y) = cos^-1 (1 – sin y)
⇒ – 2y = cos^-1 (1 – sin y)
⇒ 1 – sin y = cos(- 2y) = cos 2y
⇒ 1 – sin y = 1 – 2 sin2 y
⇒ 2 sin² y – sin y = 0
⇒ sin y(2 sin y – 1) = 0
sin y = 0 or \(\frac{1}{2}\)
∴ x = 0 or x = \(\frac{1}{2}\)
But, when x = \(\frac{1}{2}\), it can be observed that
We have, tan^-1 \(\frac{1-x}{1+x}\) = \(\frac{1}{2}\) tan^-1 x
⇒ tan^-1 1 – tan^-1 x = \(\frac{1}{2}\) tan^-1 x
[∵ tan^-1 x – tan^-1 y = tan^-1 \(\frac{(x-y)}{1+x y}\)]
[∵ tan^-1 (1) = \(\frac{\pi}{4}\)]
⇒ \(\frac{\pi}{4}\) = \(\frac{3}{2}\) tan^-1 x
⇒ tan^-1 x = \(\frac{\pi}{6}\)
⇒ x = tan \(\frac{\pi}{6}\)
∴ x = \(\frac{1}{\sqrt{3}}\).

Question 15.
sin(tan^-1 x), |x| < 1 is equal to
(A) \(\frac{x}{\sqrt{1-x^{2}}}\)

(B) \(\frac{1}{\sqrt{1-x^{2}}}\)

(C) \(\frac{1}{\sqrt{1+x^{2}}}\)

(D) \(\frac{x}{\sqrt{1+x^{2}}}\)
Solution.
Let tan^-1 x = y.
Then, tan y = x
⇒ sin y = \(\frac{x}{\sqrt{1+x^{2}}}\)
∴ y = sin^-1 (\(\frac{x}{\sqrt{1+x^{2}}}\))
⇒ tan^-1 x = sin^-1 (\(\frac{x}{\sqrt{1+x^{2}}}\))
Now, sin(tan^-1 x) = sin(sin^-1 (\(\frac{x}{\sqrt{1+x^{2}}}\)))
= \(\frac{x}{\sqrt{1+x^{2}}}\)
The correct answer is (D).

Question 16.
sin^-1 (1 – x) – 2 sin^-1 x = \(\frac{\pi}{2}\), then x is equal to
(A) 0, \(\frac{1}{2}\)
(B) 1, \(\frac{1}{2}\)
(C) 0
(D) \(\frac{1}{2}\)
Solution.
Given, sin^-1 (1 – x) – 2 sin^-1 x = \(\frac{\pi}{2}\)
putting \(\frac{\pi}{2}\) = sin^-1 (1 – x) + cos^-1 (1 – x)
or sin^-1 (1 – x) – 2 sin^-1 (1 – x) = sin^-1 (1 – x) + cos^-1 (1 – x)
⇒ – 2 sin^-1 x = cos^-1 (1 – x)
Let sin^-1 x = α
∴ sin α = x
∴ – 2 sin^-1 x = – 2 α = cos^-1 (1 – x)
or cos 2α = 1 – x [∵ cos(- θ) = cos θ]
∴ 1 – 2 sin² α = (1 – x)
Putting sin α = x
⇒ 1 – 2x² = 1 – x
or 2x² – x = 0
x(2x – 1) = 0
∴ x = 0, \(\frac{1}{2}\)
But x = \(\frac{1}{2}\) does not satisfy the equation.
∴ x = 0
Hence, the correct answer is (C).

Question 17.
tan^-1 \(\left(\frac{x}{y}\right)\) – tan^-1 \(\frac{x-y}{x+y}\) is equal to
(A) \(\frac{\pi}{2}\)

(B) \(\frac{\pi}{3}\)

(C) \(\frac{\pi}{4}\)

(D) \(\frac{3 \pi}{4}\)
Solution.
We have tan^-1 \(\left(\frac{x}{y}\right)\) – tan^-1 \(\frac{x-y}{x+y}\)

Punjab State Board PSEB 11th Class Chemistry Book Solutions Chapter 1 Some Basic Concepts of Chemistry Exercise Questions and Answers.

PSEB Solutions for Class 11 Chemistry Chapter 1 Some Basic Concepts of Chemistry

PSEB 11th Class Chemistry Guide Some Basic Concepts of Chemistry InText Questions and Answers

Question 1.
Calculate the molecular mass of the following:
(i) H₂O (ii)CO₂ (iii) CH₄
Answer:
(i) H₂O
The molecular mass of water (H20)
= (2 x Atomic mass of hydrogen) + (1 x Atomic mass of oxygen)
= [2(1.008 u) +1(16.00 u)]
= 2.016u +16.00u = 18.016 u=18.02u

(ii) CO₂
The molecular mass of carbon dioxide (CO₂)
= (1 x Atomic mass of carbon) + (2 x Atomic mass of oxygen)
= [1(12.011u) + 2(16.00u)]
= 12.011u + 32.00u = 44.01u

(iii) CH₄
The molecular mass of methane (CH₄)
= (1 x Atomic mass of carbon) + (4 x Atomic mass of hydrogen)
– [1(12.011u) + 4(1.008u)]
= 12.011u + 4.032u = 16.043u

Question 2.
Calculate the mass per cent of different elements present in sodium sulphate (Na₂SO₄).
Answer:
The molecular formula of sodium sulphate is Na₂SO₄
Molar mass of Na₂SO₄ = 2 x Atomic mass of Na + 1 x Atomic mass of S + 4 x Atomic mass of O
= [(2 x 23.0) + (1 x 32.066) + (4 x 16.00)]
= 46.0 + 32.066 + 64.00 = 142.066 g
Mass per cent of sodium

Question 3.
Determine the empirical formula of an oxide of iron which has 69.9% iron and 30.1% dioxygen by mass.
Answer:

Question 4.
Calculate the amount of carbon dioxide that could be produced when
(i) 1 mol of carbon is burnt in air
(ii) 1 mole of carbon is burnt in 16g of dioxygen
(iii) 2 moles of carbon are burnt in 16g of dioxygen
Answer:

∵ 32.0g of O₂ produce 44.0 g of CO₂
∵ 16.0 g of O₂ produce = \(\frac{44}{32}\) x 16 = 22.0 g of CO₂
Amount of CO₂produced = 22.0g
(iii) Amount of CO₂produced when 2 moles (= 24 g) of C are burnt in 16.0g (limited amount ) of O₂ = 22.0g

Question 5.
Calculate the mass of sodium acetate (CH₃COONa) required to make 500mL of 0.375 molar aqueous solution. Molar mass of sodium acetate is 82.0.245 g mol^-1.
Answer:
0.375M aqueous solution of sodium acetate = 1000mL of solution containing 0.375 moles of sodium actate
∴ Number of moles of sodium acetate in 500 mL.
= \(\frac{0.375}{1000}\) x 500 = 0.1875 mole.
Molar mass of sodium acetate = 82.0245 g mol^-1
∴ Required mass of sodium acetate
= 82.0245 g mol^-1 x 0.1875 mole
= 15.38 g

Question 6.
Calculate the concentration of nitric acid in moles per litre in a sample which has a density, 1.41 gmLT1 and the mass per cent of nitric acid in it being 69%.
Answer:
Mass percent of nitric acid in the sample = 69%
Thus, 100 g of sample contains 69 g of nitric acid
Molar mass of nitric acid (HNO₃)
= {1 +14 + 3(16)} g mol^-1
= 1 +14 + 48 = 63 g mol^-1
∴ Number of moles in 69 g of HNO₃

Question 7.
How much copper can be obtained from 100 g of copper sulphate (CuSO₄)?
Answer:
1 mole of CuSO₄ contains 1 mole of copper.
Molar mass of CuSO₄
= (63.5) + (32.00) + 4(16.00)
= 63.5 + 32.00 + 64.00 = 159.5 g mol^-1
159.5 g of CuSO₄ contains = 63.5 g of copper
=> 100 g of CuSO₄ contains = \(\frac{63.5 \times 100 \mathrm{~g}}{159.5}\) = 39.81g
∴ Mass of copper that can be obtained from 100 g of CuSO₄ = 39.81 g

Question 8.
Determine the molecular formula of an oxide of iron in which the mass per cent of iron and oxygen are 69.9 and 30.1 respectively.
Answer:

Question 9.
Calculate the atomic mass (average) of chlorine using the following data:

	% Natural Abundance	Molar Mass
35cl	75.77	34.9689
37Cl	24.23	36.9659

Answer:
The average atomic mass of chlorine

= 26.4959 + 8.9568 = 35.4527
∴ The average atomic mass of chlorine = 35.4527

Question 10.
In three moles of ethane (C₂H₆), calculate the following:
(i) Number of moles of carbon atoms.
(ii) Number of moles of hydrogen atoms.
(iii) Number of molecules of ethane.
Answer:
(i) 1 mole of C₂H₆ contains 2 moles of carbon atoms.
∴ 3 moles of C₂H₆ will contain = 2 x 3 = 6 moles of carbon atoms
(ii) 1 mole of C₂H₆ contains 6 moles of hydrogen atoms.
∴ 3 moles of C₂H₆ will contain =3 x 6 = 18 moles of hydrogen atoms
(iii) 1 mole of C₂H₆ contains 6.022 x 10²³ molecules of ethane.
∴ 3 moles of C₂H₆ will contain = 3 x 6.022 x 10²³
= 18.066 x 10²³ molecules of ethane

Question 11.
What is the concentration of sugar (C₁₂H₂₂O₁₁) in mol L^-1 if 20 g of sugar are dissolved in enough water to make a final volume up to 2 L?
Answer:
Molar mass of sugar (C₁₂H₂₂O₁₁)
= 12 x 12 + 22 x 1 +11 x 16 = 342 g mol^-1
Molar concentration = \(\frac{\text { Moles of solute }}{\text { Volume of solution in L }}=\frac{0.0585}{2 \mathrm{~L}}\)
= 0.0293 mol L^-1 = 0.0293 M

Question 12.
If the density of methanol is 0.793 kg L^-1, what is its volume needed for making 2.5 L of its 0.25 M solution?
Answer:
Final volume, V₂ = 2.5 L
Final molarity, M₂ = 0.25 M
Density of methanol = 0.793 kg L^-1
Molarity of initial solution M₁ = ?
Initial volume, V₁ = ?
Molar mass of methanol (CH₃OH) = (1 x 12) + (4 x 1) + (1 x 16)
= 32 g mol^-1 = 0.032 kg mol^-1
Molarity of methanol solution, M₁ = \(\frac{0.793 \mathrm{~kg} \mathrm{~L}^{-1}}{0.032 \mathrm{~kg} \mathrm{~mol}^{-1}}\) = 24.78 mol L^-1
Applying,
M₁V₁ = M₂V₂
(24.78 mol L^-1)V₁ = (2.5L) (0.25mol L^-1)
V₁ = 0.02522 L
V₁ = 25.22 mL

Question 13.
Pressure is determined as force per unit area of the surface. The SI unit of pressure, pascal is as shown below :
1 Pa= IN m^-2
If mass of air at sea level is 1034 g cm-2, calculate the pressure in pascal.
Answer:
Pressure is defined as force acting per unit area of the surface.
i.e, P = F/A

= 101332.0 Nm^-2 [1N = 1kg ms^-2]
∴ Pressure = 1.01332 x 10 ⁵

Question 14.
What is the SI unit of mass? How is it defined?
Answer:
The SI unit of mass is kilogram (kg).
1 kilogram is defined as the mass equal to the mass of the international prototype of kilogram.

Question 15.
Match the following prefixes with their multiples :

	Prefixes	Multiples
(i)	micro	106
(ii)	deca	109
(iii)	mega	10-6
(iv)	giga	10-15
(v)	femto	10

Answer:

	Prefixes	Multiples
(i)	micro	10-6
(ii)	deca	10
(iii)	mega	106
(iv)	giga	109
(v)	femto	10-15

Question 16.
What do you mean by significant figures?
Answer:
The number of significant figures in a given data is the number of all certain digits plus one uncretain digit.
For example, if 15.6 mL is the result of an experiment, then 15 is certain while 6 is uncertain, and the total number of significant figures are 3.

Question 17.
A sample of drinking water was found to he severely contaminated with chloroform, CHC13, supposed to he carcinogenic in nature. The level of contamination was 15 ppm (by mass).
(i) Express this in per cent by mass.
(ii) Determine the molarity of chloroform in the water sample.
Answer:
(i) ∵ 10⁶ g of solution contains 15 g of CHCl₃
∴ 1 g of solution contains = \(\frac{15}{10^{6}}\) g of CHCl_{3
100 g of solution contains = \(\frac{15}{10^{6}}\) x 10² = 15 x 10^-4 g of CHCl3
∴ Percent by mass = 0.0015%}

(ii) Molar mass of CHCl₃ = 12 +1 + 3 x 35.5 = 119.5 g mol^-1
0.0015% means 15 x 10^-4 g chloroform is present in 100 g sample.
Molarity = \(\frac{W \times 1000}{m \times \text { Volume of sample }}\)
[For water density = 1 g cm^-3; so mass = volume]
= \(\frac{15 \times 10^{-4} \times 1000}{119.5 \times 100}\)
= 1.25 x 10^-4 M

Question 18.
Express the following in the scientific notation :
(i) 0.0048
(ii) 234000
(iii) 8008
(iv) 500.0
(v) 6.0012
Answer:
(i) 0.0048 = 4.8 x 10^-3
(ii) 234000 = 2.34 x 10⁵
(iii) 8008 = 8.008 x 10³
(iv) 500.0 = 5.00 x 10²
(v) 6.0012 = 6.0012 x 10⁰

Question 19.
How many significant figures are present in the following?
(i) 0.0025
(ii) 208
(iii) 5005
(iv) 126000
(v) 500.0
(vi) 2.0034
Answer:
(i) 0.0025
There are 2 significant figures,
(ii) 208
There are 3 significant figures.
(iii) 5005
There are 4 significant figures.
(iv) 126000
There are 3 significant figures.
(v) 500.0
There are 4 significant figures.
(vi) 2.0034
There are 5 significant figures.

Question 20.
Round up the following upto three significant figures :
(i) 34.216 (ii) 10.4107
(iii) 0.04597 (iv) 2808
Answer:
(i) 34.2
(ii) 10.4
(iii) 0.0460
(iv) 2810

Question 21.
The following data are obtained when dinitrogen and dioxygen react together to form different compounds :

	Mass of dinitrogen	Mass of dioxygen
(i)	14 g	16 g
(ii)	14 g	32 g
(iii)	28 g	32 g
(iv)	28 g	80 g

(a) Which law of chemical combination is obeyed by the above experimental data? Give its statement.
(b) Fill in the blanks in the following conversions :
(i) 1 km = ………mm = ………pm
(ii) 1 mg = ………kg = ………ng
(iii) 1 mL = ………L = ………dm³
Answer:
On fixing the mass of dinitrogen as 14 g, then the masses of dioxygen which combines with the fixed mass (= 14 g) of dinitrogen will be 16, 32, 16, 40 which are in the simple whole number ratio of 1 : 2 : 1 : 2.5 or 2 : 4 : 2 : 5.

(a) Law of multiple proportions : This law was proposed by Dalton in 1803. According to this law, if tvo elements can combine to form two or more than two compounds, the masses of one element that combine with a fixed mass of the other element are in the ratio of small whole numbers.

Question 22.
If the speed of light is 3.0 x 10⁸ms^-1, calculate the distance covered by light in 2.00 ns.
Answer:
According to the question,
Time taken to cover the distance = 2.00 ns
2ns = 2.00 x 10^-9s [∵ 1ns = 10^-9s]
Speed of light = 3.0 x 10⁸ms^-1
Distance travelled by light in 2.00 ns
= Speed of light x Time taken
= (3.0 x 10⁸ms^-1)(2.00 x 10^-9s) = 6.00 x 10^-1 m = 0.6 m

Question 23.
In a reaction A + B₂ → AB₂
Identify the limiting reagent, if any, in the following reaction mixtures.
(i) 300 atoms of A + 200 molecules of B
(ii) 2 mol A + 3 mol B
(iii) 100 atoms of A + 100 molecules of B
(iv) 5 mol A + 2.5 mol B
(v) 2.5 mol A + 5 mol B
Answer:
(i) According to the given reaction, 1 atom of A reacts with 1 molecule of B.
Thus, 300 atoms of A will react with 200 molecules of B thereby, leaving 100 atoms of A unused. Hence, B is the limiting reagent.
(ii) According to the given reaction, 1 mol of A reacts with 1 mol of B. Thus, 2 mol of A will react with 2 mol of B. As a result, 1 mol of B will not be consumed. Hence, A is the limiting reagent.
(iii) According to the given reaction, 1 atom of A combines with 1 molecule of B. Thus, all 100 atoms of A will combine with all 100 molecules of B. Hence, the mixture is stoichiometric where no limiting reagent is present.
(iv) 1 mol of atom A combines with 1 mol of molecule B. Thus, 2.5 mol of B will combine only 2.5 mol of A. As a result, 2.5 mol of A will be left as such. Hence, B is the limiting reagent.
(v) 1 mol of atom A combines with 1 mql of molecule B. Thus, 2.5 mol of A will combine only 2.5 mol of B and the remaining 2.5 mol of B will be left as such. Hence, A is the limiting reagent.

Question 24.
Dinitrogen and dihydrogen react with each other to produce ammonia according to the following chemical equation: N2(g)+H2(g) → 2NH₃(g)
(i) Calculate the mass of ammonia produced if 2.00 x 10³ g dinitrogen reacts with 1.00 x 10³ g of dihydrogen.
(ii) Will any of the two reactants remain unreacted?
(iii) If yes, which one and what would be its mass?
On balancing the given chemical equation,
Answer:

⇒ 28 g N₂ reacts with 6 g H₂; 1 g N₂ reacts with \(\frac{6}{28}\) g H₂;
2.0 x 10³ g of N2 will react with \(\frac{2000 \times 6}{28}\) = 428.6 g of H₂.
Hence, N₂ is the limiting reagent.
∵ 28 g N2 produces 34 g NH3 34
∴ 1 g N2 produces \(\frac{34}{28}\) g NH₃
2.00 x 10³ f N₂ will produce = \(\frac{34 g}{28 g}\) x 2000g = 2428.57 g NH₃
(ii) N₂ is the limiting reagent and H₂ is the excess reagent. Hence, H₂ will remain unreacted.
(iii) Mass of H₂ remain unreacted = 1.00 x 10³ g – 428.6 g = 571.43 g

Question 25.
How are 0.50 mol Na₂CO₃ and 0.50 M Na₂CO₃ different?
Answer:
Molar mass of Na₂CO₃ = (2 x 23) +12.00 + (3 x 16) = 106 g mol^-1
Now, 1 mol Na₂CO₃ means 106 g Na₂CO₃
∴ 0.5 mol Na₂CO₃ = x °-5 mo1 Na₂C0₃ = 53 g Na₂C0₃
⇒ 0.50 M Na₂CO₃ = 0.50 mol/L Na₂CO₃
Hence, 0.50 mol Na₂CO₃ means 53 g Na₂CO₃ is present in 1 L of the solution.

Question 26.
If ten volumes of dihydrogen gas reacts with five volumes of dioxygen gas, how many volumes of water vapour would be produced?
Answer:
Reaction of dihydrogen with dioxygen can be written as:

Now, 2 volumes of dihydrogen react with 1 volume of O₂ to produce 2 volumes of water vapour.
Hence, 10 volumes of dihydrogen will react with 5 volumes of dioxygen to produce 10 volumes of water vapour.

Question 27.
Convert the following into basic units :
(i) 28.7 pm
(ii) 15.15 pm
(iii) 25365 mg
Answer:
(i) 28.7 pm :
∵ 1 pm = 10^-12 m
∴ 28.7pm = 28.7 x 10^-12 m = 2.87 x 10^-11 m

(ii) 15.15pm
∵ 1 pm =10 12 m
∴ 15.15 pm = 15.15 x 10^-12 m = 1.515 x 10^-11 m

(iii) 25365 mg :
1 mg = 10^-3 g
25365 mg = 2.5365 x 10⁴ x 10^-3 g
= 2.5365 x 10¹ g
Since,
1 g = 10^-3 kg
2.5365 x 10¹ g = 2.5365 x 10¹ x 10^-3 kg.
∴ 25365 mg = 2.5365 x 10^-2 kg

Question 28.
Which one of the following will have largest number of atoms?
(i) 1 g Au(s)
(ii) 1 g Na(s)
(iii) 1g Li (s)
(iv) 1 g of Cl₂(g)
Answer:
(i) 1 g Au (s) = \(\frac{1}{197}\) mol atoms of Au (s)
= \(\frac{6.022 \times 10^{23}}{197}\) mol atoms of Au (s)
= 3.06 x 10²¹ atoms of Au (s)

(ii) 1 g Na (s) = \(\frac{1}{23}\) mol atoms of Na (s)
= \(\frac{6.022 \times 10^{23}}{23}\) atoms of Na (s)
= 0.262 x 10²³ atoms of Na (s)
= 26.2 x 10²¹ atoms of Na (s)

(iii) 1 g Li (s) = \(\frac{1}{7}\) mol atoms of Li (s)
= \(\frac{6.022 \times 10^{23}}{23}\) atoms of Li (s)
= 86.0 x 1021 atoms of Li (s)

(iv) 1 gCl₂ (g) = \(\frac{1}{71}\) mol molecules of Cl₂ (g)
= \(\frac{6.022 \times 10^{23}}{71}\) molecules of Cl? (g)
= 0.0848 x 10²³ molecules of Cl₂ (g)
= 8.48 x 10²¹ molecules of Cl₂ (g)
(one molecule of Cl₂ contains two atoms of Cl)
Number of atoms of Cl = 2 x 8.48 x 10²¹ = 16.96 x 10²¹ atoms of Cl
Hence, 1 g of Li (s) has largest number of atoms.

Question 29.
Calculate the molarity of a solution of ethanol in water in which the mole fraction of ethanol is 0.040 (assume the density of water to be one).
Answer:
Mole fraction of ethanol (C₂H₅OH)

Number of moles present in 1L water;
ⁿH₂O = \(\)
ⁿH₂O = 55.55 moles
Substituting the value of ⁿH₂O in eq (i).
\(\frac{n_{\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}}}{n_{\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{OH}}+55.55}\) = 0.040
ⁿC₂H₅OH – 0.040ⁿC₂H₅OH = 2.222mol
0.96 ⁿC₂H₅OH = 2.222 mol ⁿC₂H₅OH = \(\frac{2.222}{0.96}\) mol.
ⁿC₂H₅OH = 2.314 mol
∴ Molarity of solution = \(\frac{2.314 \mathrm{~mol}}{1 \mathrm{~L}}\) = 2.314M

Question 30.
What will be the mass of one 12C atom in g?
Answer:
1 mol of carbon atoms = 6.022 x 10²³ atoms of carbon = 12 g of carbon
∴ Mass of one ¹²C atom = \(\frac{\text { Atomic mass of } \mathrm{C}}{\text { Avogadro’s number }}=\frac{12 \mathrm{~g}}{6.022 \times 10^{23}}\)
= 1.993 x 10^-23 g

Question 31.
How many significant figures should be present in the answer of the following calculations?
(i) \(\frac{0.02856 \times 298.15 \times 0.112}{0.5785}\)
(ii) 5 x 5.364
(iii) 0.0125 + 0.7864 + 0.0215
Answer:
\(\frac{0.02856 \times 298.15 \times 0.112}{0.5785}\)
Least precise number of calculation = 0.112
Number of significant figures in the answer = Number of significant figures in the least precise number = 3 /*
(ii) 5 x 5.364
Least precise number of calculation = 5.364
Number of significant figures in the answer = Number of significant figures in 5.364 = 4
(iii) 0.0125 + 0.7864 + 0.0215
Since the least number of decimal places in each term is four, the number of significant figures in the answer is also 4.

Question 32.
Use the data given in the following table to calculate the molar mass of naturally occurring argon isotopes :

Isotope	Isotopic molar mass	Abundance
36 Ar	35.96755 g mol-1	0.337%
38 Ar	37.96272 g mol-1	0.063%
40 Ar	39.9624 g mol-1	99.600%

Answer:
Molar mass of argon

= 0.121 + 0.024 + 39.802 g mol^-1 = 39.947 g mol^-1

Question 33.
Calculate the number of atoms in each of the following
(i) 52 moles of Ar (ii) 52 u of He (iii) 52 g of He.
Answer:
(i) ∵ 1 mol of Ar = 6.022 x 10²³ atoms of Ar
∴ 52 moles of Ar = 52 x 6.022 x 10²³ atoms of Ar
= 3.131 x 10²⁵ atoms

(ii) ∵ 1 atom of He = 4 u of He
Or, 4 u of He = 1 atom of He
∴ 1 u of He = 1/4 atom of He
∴ 52 u of He = 52/4 atoms of He = 13 atoms

(iii) ∵ 4 g of He = 6.022 x 10²³ atoms
6022 1023 52
∴ 52 g of He = \(\frac{6.022 \times 10^{23} \times 52}{4}\) = 7.8286 x 10²⁴ atoms

Question 34.
A welding fuel gas contains carbon and hydrogen only. Burning a small sample of it in oxygen gives 3.38 g carbon dioxide, 0.690 g of water and no other products. A volume of 10.0 L (measured at STP) of this welding gas is found to weigh 11.6 g. Calculate (i) empirical formula, (ii) molar mass of the gas, and (iii) molecular formula.
Answer:
(i) 44 g CO₂ = 12 g carbon
3.38 g CO₂ = 12/44 x 3.38g = 0.9218 g carbon
18 g H₂O = 2g hydrogen
0.690 g H₂O = 2/18 x 0.690 g = 0.0767 g hydrogen
Total mass of compound = 0.9218+0.0767 = 0.9985 g (because compound contains only carbon and hydrogen)
% of C in the compound = \(\frac{0.9218}{0.9985}\) x 100 = 92.32
% of H in the compound = \(\frac{0.0767}{0.9985}\) x 100 = 7.68
Calculation for Empirical Formula

Hence, empirical formula = CH
(ii) Calculation for molar mass of the gas
10.0 L of the given gas at STP weigh = 11.6 g
∴ 22.4 L of the given gas at STP will weigh = \(\frac{11.6 \times 22.4}{10}\) = 25.984 g
Molar mass = 25.984 = 26 g mol^-1
(iii) Empirical formula mass (CH) =12 + 1 = 13
∴ n = \(\frac{\text { Molecular mass }}{\text { Empirical formula mass }}=\frac{26}{13}\) = 2
Hence, molecular formula = n x CH = 2 x CH = C₂H₂

Question 35.
Calcium carbonate reacts with aqueous HC1 to give CaCl₂ and CO₂ according to the reaction,
CaC0₃(s) + 2 HCl(aq) -» CaCl₂(aq) + C0₂(g) + H₂O(l) What mass of CaC0₃ is required to react completely with 25 mL of 0.75 M HC1?
Answer:
The given reaction is
CaC0₃(s) + 2HCl(aq) → CaCl₂(aq) + C0₂(g) + H₂0(l)
Let us find out the weight of HCl present in 25 mL of 0.75 M HCl
1000 mL of 1.0 M HCl contains = 36.5 g
25 mL of 0.75 M HCl contains = \(\frac{36.5}{1000}\) x 25 x 0.75
= 0.6844 g of HCl
According to the equation;
73 g of HCl [2(1 + 35.5)] reacts with 100.0 g of CaC0₃
0.6844 g of HCl reacts with = \(\frac{100}{73}\) x 0.6844 = 0.94 g of CaC0₃

Question 36.
Chlorine is prepared in the laboratory by treating manganese dioxide (MnO₂) with aqueous hydrochloric acid according to the reaction
4HCl(oq) + MnO₂(s) > 2H₂O(l) + MnCl₂(aq) + Cl₂(g)
How many grams of HCl react with 5.0 g of manganese dioxide?
Answer:

According to the balanced chemical equation,
∵ 87 g of MnO₂ react with 4 x 36.5 g HCl
∴ 5 g of MnO₂ will react \(\frac{4 \times 36.5 \times 5}{87}\) = 8.39 g HCl

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 2 Inverse Trigonometric Functions Ex 2.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions Ex 2.2

Direction (1 – 4): Prove the following.

Question 1.
3 sin^-1 x = sin^-1 (3x – 4x³), x ∈ [- \(\frac{1}{2}\), \(\frac{1}{2}\)]
Solution.
Let x = sin θ. Then, sin^-1 x = θ.
We have,
R.H.S. = sin^-1 (3x – 4x³) = sin^-1(3 sin θ – 4 sin³ θ)
= sin^-1 (sin 3θ) = 3θ = 3 sin^-1 x
= L.H.S.
Hence proved.

Question 2.
3 cos^-1 x = cos^-1 (4x³ – 3x), x ∈ [\(\frac{1}{2}\), 1]
Solution.
Let x = cos θ. Then, cos^-1 x = θ.
We have, R.H.S. = cos^-1 (4x³ – 3x)
= cos^-1 (4cos 3θ – 3 cos θ)
= cos^-1 (cos 3θ) = 3θ = 3 cos^-1 x
= L.H.S.
Hence proved.

Question 3.
tan^-1 \(\frac{2}{11}\) + tan^-1 \(\frac{7}{24}\) = tan^-1 \(\frac{1}{2}\).
Solution.
Given, tan^-1 \(\frac{2}{11}\) + tan^-1 \(\frac{7}{24}\) = tan^-1 \(\frac{1}{2}\)

Question 4.
2 tan^-1 \(\frac{1}{2}\) + tan^-1 \(\frac{1}{7}\) = tan^-1 \(\frac{31}{17}\)
Solution.
Given, 2 tan^-1 \(\frac{1}{2}\) + tan^-1 \(\frac{1}{7}\) = tan^-1 \(\frac{31}{17}\)
L.H.S. = 2 tan^-1 \(\frac{1}{2}\) + tan^-1 \(\frac{1}{7}\)
= \(\tan ^{-1}\left[\frac{2 \cdot \frac{1}{2}}{1-\left(\frac{1}{2}\right)^{2}}\right]+\tan ^{-1}\left(\frac{1}{7}\right)\) [∵ 2 tan^-1 x = tan^-1 (\(\frac{2 x}{1-x^{2}}\))]

Direction (5 – 10):- Write the following functions in the simplest form:

Question 5.
tan^-1 \(\frac{\sqrt{1+x^{2}}-1}{x}\), x ≠ 0.
Solution.
We have, tan^-1 \(\frac{\sqrt{1+x^{2}}-1}{x}\)
put x = tan θ
⇒ θ = tan^-1 x

Question 6.
tan^-1 \(\frac{1}{\sqrt{x^{2}-1}}\), |x| > 1
Solution.
Let x = sec θ, then θ = sec^-1 x
∴ tan^-1 \(\frac{1}{\sqrt{x^{2}-1}}\) = tan^-1 \(\left(\frac{1}{\sqrt{\sec ^{2} \theta-1}}\right)\)
= tan^-1 \(\left(\frac{1}{\sqrt{\tan ^{2} \theta}}\right)\) [∵ sec² θ – 1 = tan² θ]
= tan^-1 \(\left(\frac{1}{\tan \theta}\right)\)
= tan^-1 (cot θ)
= tan^-1 [tan (\(\frac{\pi}{2}\) – θ)] [∵ tan (\(\frac{\pi}{2}\) – θ) = cot θ]
= \(\frac{\pi}{2}\) – θ
= \(\frac{\pi}{2}\) – sec^-1 x.

Question 7.
tan^-1 \(\left(\sqrt{\frac{1-\cos x}{1+\cos x}}\right)\), x < π.
Solution.
We have, tan^-1 \(\left(\sqrt{\frac{1-\cos x}{1+\cos x}}\right)\)
= tan^-1 \(\left(\sqrt{\frac{2 \sin ^{2} \frac{x}{2}}{2 \cos ^{2} \frac{x}{2}}}\right)\)
= tan^-1 (tan \(\left(\frac{\sin \frac{x}{2}}{\cos \frac{x}{2}}\right)\))
= tan^-1 (tan \(\frac{x}{2}\))
= \(\frac{x}{2}\)

Question 8.
tan^-1 (\(\frac{\cos x-\sin x}{\cos x+\sin x}\)), 0 < x < π.
Solution.

Question 9.
tan^-1 \(\frac{x}{\sqrt{a^{2}-x^{2}}}\), |x| < a.
Solution.
We have, tan^-1 \(\frac{x}{\sqrt{a^{2}-x^{2}}}\)
Let x = a sin θ
⇒ \(\frac{x}{a}\) = sin θ
⇒ θ = sin^-1 (\(\frac{x}{a}\))
∴ tan^-1 \(\frac{x}{\sqrt{a^{2}-x^{2}}}\) = tan^-1 \(\left(\frac{a \sin \theta}{\sqrt{a^{2}-a^{2} \sin ^{2} \theta}}\right)\)
= tan^-1 \(\left(\frac{a \sin \theta}{a \sqrt{1-\sin ^{2} \theta}}\right)\)
= tan^-1 \(\left(\frac{a \sin \theta}{a \cos \theta}\right)\)
= tan^-1 (tan θ)
= θ = sin^-1 \(\frac{x}{a}\).

Question 10.
tan^-1 \(\left(\frac{3 a^{2} x-x^{3}}{a^{3}-3 a x^{2}}\right)\), a > 0; \(\frac{-a}{\sqrt{3}} \leq x \leq \frac{a}{\sqrt{3}}\).
Solution.
We have, tan^-1 \(\left(\frac{3 a^{2} x-x^{3}}{a^{3}-3 a x^{2}}\right)\), a > 0; \(\frac{-a}{\sqrt{3}} \leq x \leq \frac{a}{\sqrt{3}}\)
Let x = a tan θ
⇒ \(\frac{x}{a}\) = tan θ
⇒ θ = tan^-1 \(\frac{x}{a}\)

∴ tan^-1 \(\left(\frac{3 a^{2} x-x^{3}}{a^{3}-3 a x^{2}}\right)\), a > 0; \(\frac{-a}{\sqrt{3}} \leq x \leq \frac{a}{\sqrt{3}}\) = tan^-1 \(\left(\frac{3 a^{2} \cdot(a \tan \theta)-a^{3} \tan ^{3} \theta}{a^{3}-3 a \cdot\left(a^{2} \tan ^{2} \theta\right)}\right)\)

= tan ^-1 \(\left(\frac{3 a^{3} \tan \theta-a^{3} \tan ^{3} \theta}{a^{3}-3 a^{3} \tan ^{2} \theta}\right)\)

= tan^-1 \(\left(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\right)\)

= tan^-1 (tan 3θ) [∵ tan 3θ = \(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\)]

= 3θ = 3 tan^-1 \(\frac{x}{a}\).

Direction (11 – 15) : Find the value of each of the following.

Question 11.
tan^-1 [2 cos(2 sin^-1 \(\frac{1}{2}\))].
Solution.
Let sin^-1 \(\frac{1}{2}\) = x
Then, sin x = \(\frac{1}{2}\) = sin (\(\frac{\pi}{6}\)))
Now, tan^-1 [2 cos(2 sin^-1 \(\frac{1}{2}\))] = tan^-1 [2 cos(2 × \(\frac{\pi}{6}\))]
= tan^-1 [2 cos \(\frac{\pi}{3}\)]
= tan^-1 [2 × \(\frac{1}{2}\)] [∵ cos (\(\frac{\pi}{3}\)) = \(\frac{1}{2}\))
= tan^-1 1 = \(\frac{\pi}{4}\)

Question 12.
cot(tan^-1 a + cot^-1 a).
Solution.
We have, cot(tan^-1 a + cot^-1 a)
= cot (\(\frac{\pi}{2}\))
= 0 [∵ tan^-1 x + cot^-1 x = \(\frac{\pi}{2}\)].

Question 13.
tan \(\frac{1}{2}\) [sin^-1 \(\frac{2 x}{1+x^{2}}\) + cos^-1 \(\frac{1-y^{2}}{1+y^{2}}\)], |x| < 1, y > 0 and xy < 1.
Solution.
Let x = tan θ.
Then, θ = tan^-1 x.
∴ sin^-1 \(\frac{2 x}{1+x^{2}}\) = sin^-1 \(\left(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\right)\)
= sin^-1 (sin 2θ) = 2θ = 2 tan^-1 x
Again, let y = tan φ.
Then, φ = tan^-1 y
∴ cos^-1 \(\frac{1-y^{2}}{1+y^{2}}\) = cos^-1 \(\left(\frac{1-\tan ^{2} \varphi}{1+\tan ^{2} \varphi}\right)\)
= cos^-1 (cos 2φ) = 2φ = 2 tan^-1 y
Now, tan \(\frac{1}{2}\) [sin^-1 \(\frac{2 x}{1+x^{2}}\) + cos^-1 \(\frac{1-y^{2}}{1+y^{2}}\)]
= tan \(\frac{1}{2}\) [2 tan^-1 x + tan^-1 y]
= tan [tan^-1 x + tan^-1 y]
= tan[tan^-1 \(\left(\frac{x+y}{1-x y}\right)\)]
[∵ tan^-1 x + tan^-1 y = tan^-1 \(\left(\frac{x+y}{1-x y}\right)\)]
= \(\frac{x+y}{1-x y}\)

Question 14.
If sin(sin^-1 \(\frac{1}{5}\) + cos^-1 x) = 1, then find the value of x.
Solution.
Given, sin(sin^-1 \(\frac{1}{5}\) + cos^-1 x) = 1
⇒ sin^-1 \(\frac{1}{5}\) + cos^-1 x = sin^-1 (1)
[∵ sin θ = x ⇒ θ = sin^-1 x]
⇒ sin^-1 \(\frac{1}{5}\) + cos^-1 x = sin^-1 (sin \(\frac{\pi}{2}\))
[∵ sin (\(\frac{\pi}{2}\)) = 1]
⇒ sin^-1 \(\frac{1}{5}\) + cos^-1 x = \(\frac{\pi}{2}\)
⇒ sin^-1 \(\frac{1}{5}\) = \(\frac{\pi}{2}\) – cos^-1 x
sin^-1 \(\frac{1}{5}\) = sin^-1 x
[∵ sin^-1 x + cos^-1 x = \(\frac{\pi}{2}\)]
⇒ \(\frac{1}{5}\) = x
Hence, the value of x is \(\frac{1}{5}\).

Question 15.
If tan^-1 \(\frac{x-1}{x-2}\) + tan^-1 \(\frac{x+1}{x+2}=\frac{\pi}{4}\), then find the value of x.
Solution.
We have, tan^-1 \(\frac{x-1}{x-2}\) + tan^-1 \(\frac{x+1}{x+2}=\frac{\pi}{4}\)

⇒

Direction (16 – 18): Find the value of each expression.

Question 16.
sin^-1 (sin \(\frac{2 \pi}{3}\))
Solution.
We have, sin^-1 (sin \(\frac{2 \pi}{3}\))
We know that sin^-1(sin x) = x , if x ∈ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\)) which is the principal value branch of sin^-1 x.
Here, \(\frac{2 \pi}{3}\) ∉ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\)
Now, sin^-1 (sin \(\frac{2 \pi}{3}\)) can be written as
sin^-1 (sin \(\frac{2 \pi}{3}\)) = \(\sin ^{-1}\left[\sin \left(\pi-\frac{\pi}{3}\right)\right]=\sin ^{-1}\left(\sin \frac{\pi}{3}\right)\) where \(\frac{\pi}{3}\) ∈ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\))
∴ sin^-1 (sin \(\frac{2 \pi}{3}\)) = sin^-1 (sin \(\frac{\pi}{3}\)) = \(\frac{\pi}{3}\).

Question 17.
tan^-1 (tan \(\frac{3 \pi}{4}\))
Solution.
We have, tan^-1 (tan \(\frac{3 \pi}{4}\))
We know that tan^-1 (tan x) = x, if x ∈ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\)), which is the principal value branch of tan^-1 x.
Here, \(\frac{3 \pi}{4}\) ∉ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\))
Now, tan^-1 (tan \(\frac{3 \pi}{4}\)) can be written as
tan^-1 (tan \(\frac{3 \pi}{4}\)) = tan^-1 [tan(π – \(\frac{\pi}{4}\))]
= tan^-1 [- tan \(\frac{\pi}{4}\)]
= tan^-1 [tan (- \(\frac{\pi}{4}\))]
where – \(\frac{\pi}{4}\) ∈ (- \(\frac{\pi}{2}\), \(\frac{\pi}{2}\))
[∵ – tan θ = tan(- θ)]
∴ tan^-1 (tan \(\frac{3 \pi}{4}\)) = tan^-1 [tan (- \(\frac{\pi}{4}\))]
= – \(\frac{\pi}{4}\)

Question 18.
tan (sin^-1 \(\frac{3}{5}\) + cot^-1 \(\frac{3}{2}\))
Solution.
Let sin^-1 \(\frac{3}{5}\) = x.
Then, sin x = \(\frac{3}{5}\)
⇒ cos x = \(\sqrt{1-\sin ^{2} x}\) = \(\frac{4}{5}\)
⇒ sec x = \(\frac{5}{4}\)
∴ tan x = \(\sqrt{\sec ^{2} x-1}=\sqrt{\frac{25}{16}-1}=\frac{3}{4}\)
∴ x = tan^-1 \(\frac{3}{4}\)
∴ sin^-1 \(\frac{3}{5}\) = tan^-1 \(\frac{3}{4}\) ………..(i)
Now, cot^-1 \(\frac{3}{2}\) = tan^-1 \(\frac{2}{3}\)
[∵ tan^-1 \(\frac{1}{x}\) = cot^-1 x] ……………(ii)
Hence, tan (sin^-1 \(\frac{3}{5}\) + cot^-1 \(\frac{3}{2}\))
= tan (tan^-1 \(\frac{3}{4}\) + tan^-1 \(\frac{2}{3}\))
= \(\tan \left(\tan ^{-1} \frac{\frac{3}{4}+\frac{2}{3}}{1-\frac{3}{4} \cdot \frac{2}{3}}\right)\)
[∵ tan^-1 x + tan^-1 y = tan^-1 \(\left(\frac{x+y}{1-x y}\right)\)]
= tan (tan^-1 \(\frac{9+8}{12-6}\))
= tan (tan^-1 \(\frac{17}{6}\))
= \(\frac{17}{6}\).

Question 19.
cos^-1 (cos \(\frac{7 \pi}{6}\)) is equal to
(A) \(\frac{7 \pi}{6}\)

(B) \(\frac{5 \pi}{6}\)

(C) \(\frac{\pi}{3}\)

(D) \(\frac{\pi}{6}\)

Solution.
We know that cos^-1 (cos x) = x if x ∈ [0, x], which is the principal value branch of cos^-1 x.
Here, \(\frac{7 \pi}{6}\) ∉ x ∈ [0, π]
Now, cos^-1 (cos \(\frac{7 \pi}{6}\)) can be written as
cos^-1 (cos \(\frac{7 \pi}{6}\)) = cos^-1 [cos(2π – \(\frac{5 \pi}{6}\))]

= cos^-1 [cos \(\frac{5 \pi}{6}\)], where \(\frac{5 \pi}{6}\) ∈ [0, π]
[∵ cos(2π – x) = cos x]
∴ cos^-1 (cos \(\frac{7 \pi}{6}\)) = cos^-1 (cos \(\frac{5 \pi}{6}\))
= \(\frac{5 \pi}{6}\)
The correct option is (B).

Question 20.
sin[\(\frac{\pi}{3}\) – sin^-1 (- \(\frac{1}{2}\))] is equal to
(A) \(\frac{1}{2}\)

(B) \(\frac{1}{3}\)

(C) \(\frac{1}{4}\)

(D) 1
Solution.
Let sin^-1 (- \(\frac{1}{2}\)) = x.
Then, sin x = – \(\frac{1}{2}\) = – sin \(\frac{\pi}{6}\) = sin(-\(\frac{\pi}{6}\))
We know that the range of the principal value of sin^-1 x is (- \(\frac{\pi}{2}\), –\(\frac{\pi}{2}\))
∴ sin^-1 (- \(\frac{1}{2}\)) = – \(\frac{\pi}{6}\)
Now, sin[\(\frac{\pi}{6}\) – sin^-1 (- \(\frac{1}{2}\))] = sin \(\left[\frac{\pi}{3}-\left(-\frac{\pi}{6}\right)\right]\)
= sin \(\left(\frac{\pi}{3}+\frac{\pi}{6}\right)\)
= sin (\(\frac{3 \pi}{6}\))
= sin (\(\frac{\pi}{2}\)) = 1
The correct option is (D).

Question 21.
tan^-1 (- √3) – cot^-1 (- √3) is equal to
(A) π
(B) – \(\frac{\pi}{2}\)
(C) 0
(D) 2√3
Solution.
Let tan^-1 √3 = x
⇒ tan x = √3 = tan \(\frac{\pi}{3}\)
∴ tan^-1 √3 = \(\frac{\pi}{3}\)
Again, let cos^-1(- √3) = x
⇒ cot x = – √3 = – cot \(\frac{\pi}{6}\)
= cot (π – \(\frac{\pi}{6}\))
= cot \(\frac{5 \pi}{6}\)
∴ cot^-1 (- √3) = \(\frac{5 \pi}{6}\)
Now, tan^-1 (- √3) – cot^-1 (- √3) = \(\frac{\pi}{3}\) – \(\frac{5 \pi}{6}\)
= \(\frac{2 \pi-5 \pi}{6}=\frac{-3 \pi}{6}=-\frac{\pi}{2}\)
Hence, correct option is (B).

Punjab State Board PSEB 11th Class Political Science Book Solutions Chapter 21 संविधान की मुख्य विशेषताएं Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Political Science Chapter 21 संविधान की मुख्य विशेषताएं

दीर्घ उत्तरीय प्रश्न-

प्रश्न 1.
भारतीय संविधान की मुख्य विशेषताओं का वर्णन करो।
(Describe the chief features of the Indian Constitution.)
अथवा
भारतीय संविधान की मुख्य विशेषताओं का वर्णन करो।
(Discuss the salient features of the Indian Constitution.)
उत्तर- भारत का संविधान एक संविधान सभा ने बनाया और इस संविधान को 26 जनवरी, 1950 को लागू किया गया। इस संविधान की अपनी कुछ विशेषतायें हैं जो कि निम्नलिखित हैं-

1. लिखित तथा विस्तृत संविधान (Written and Detailed Constitution)-अमेरिका, स्विट्ज़रलैंड, साम्यवादी चीन, फ्रांस और जापान के संविधानों की तरह भारत का संविधान भी लिखित तथा विस्तृत है। संविधानसभा ने भारत का संविधान 2 वर्ष, 11 महीने तथा 18 दिनों में बनाया और इस संविधान को 26 जनवरी, 1950 को लागू किया। भारतीय संविधान लिखित होने के साथ-साथ अन्य देशों के संविधानों के मुकाबले में बहुत विस्तृत संविधान है। हमारे संविधान में 395 अनुच्छेद तथा 12 अनुसूचियां हैं और इन्हें 22 भागों में बांटा गया है।
सर आइवर जेनिंग्स (Sir Ivor Jennings) का कहना है कि, “भारतीय संविधान संसार में सबसे लम्बा एवं विस्तृत संविधान है।”

2. प्रस्तावना (Preamble)—प्रत्येक अच्छे संविधान की तरह भारत के संविधान में भी प्रस्तावना दी गई है। इस प्रस्तावना में संविधान के मुख्य लक्ष्यों, विचारधाराओं तथा राज्य के उत्तरदायित्वों का वर्णन किया गया है।

3. सम्पूर्ण प्रभुत्व-सम्पन्न, समाजवादी, धर्म-निरपेक्ष, लोकतन्त्रात्मक गणराज्य की स्थापना (Creation of a Sovereign, Socialist, Secular, Democratic Republic)-भारतीय संविधान ने भारत को सम्पूर्ण प्रभुत्व सम्पन्न, समाजवादी, धर्म-निरपेक्ष, लोकतन्त्रात्मक गणराज्य घोषित किया है। इसका अर्थ है कि अब भारत पूर्ण रूप से स्वतन्त्र तथा सर्वोच्च सत्ताधारी है और किसी अन्य सत्ता के अधीन नहीं है। भारत का लक्ष्य समाजवादी समाज की स्थापना करना है और भारत धर्म-निरपेक्ष राज्य है। यहां पर लोकतन्त्रीय गणराज्य की स्थापना की गई है। राष्ट्रपति का चुनाव एक निर्वाचक-मण्डल द्वारा 5 वर्ष की अवधि के लिए होता है।

4. जनता का अपना संविधान (People’s own Constitution)-भारत के संविधान की एक महत्त्वपूर्ण विशेषता यह है कि वह जनता का अपना संविधान है और इसे जनता ने स्वयं अपनी इच्छा से अपने ऊपर लागू किया है। यद्यपि हमारे संविधान में आयरलैण्ड के संविधान की तरह कोई अनुच्छेद ऐसा नहीं है जिससे यह स्पष्ट होता हो कि भारतीय संविधान को जनता ने स्वयं बनाया है तथापि इस बात की पुष्टि संविधान की प्रस्तावना करती है-
“हम भारत के लोग, भारत में एक सम्पूर्ण प्रभुत्व-सम्पन्न समाजवादी, धर्मनिरपेक्ष, लोकतन्त्रात्मक गणराज्य स्थापित करते हैं। अपनी इस संविधान सभा में 26 नवम्बर, 1949 ई० को इस संविधान को अपनाते हैं।”

5. अनेक स्रोतों से तैयार किया हुआ संविधान (A Unique Constitution Derived from many Sources) हमारे संविधान की यह भी एक विशेषता है कि इसमें अन्य देशों के संविधान के अच्छे सिद्धान्तों तथा गुणों को सम्मिलित किया गया है। हमारे संविधान निर्माताओं का उद्देश्य एक अच्छा संविधान बनाना था, इसलिए उनको जिस देश के संविधान में कोई अच्छी बात दिखाई दी, उसको उन्होंने संविधान में शामिल कर लिया। संसदीय शासन प्रणाली को इंग्लैण्ड के संविधान से लिया गया है। संघीय प्रणाली अमेरिका तथा राज्य के नीति निर्देशक सिद्धान्त आयरलैण्ड के संविधान से लिए गए हैं। इस प्रकार भारत का संविधान, अनेक संविधानों के गुणों का सार है।

6. संविधान की सर्वोच्चता (Supremacy of the Constitution)-भारतीय संविधान की एक अन्य विशेषता यह है कि यह देश का सर्वोच्च कानून है। कोई कानून या आदेश इसके विरुद्ध जारी नहीं किया जा सकता है। सरकार के सभी अंगों को संविधान के अनुसार कार्य करना पड़ता है। यदि संसद् कोई ऐसा कानून पास करती है जो संविधान के विरुद्ध हो या राष्ट्रपति आदेश जारी करता है जो संविधान के साथ मेल नहीं खाता तो न्यायपालिका ऐसे कानून और आदेश को अवैध घोषित कर सकती है, अतः संविधान सर्वोच्च है।

7. धर्म निरपेक्ष (Secular State)-भारत के संविधान के अनुसार भारत एक धर्म-निरपेक्ष राज्य है। 42वें संशोधन द्वारा प्रस्तावना में धर्म-निरपेक्ष शब्द जोड़ कर स्पष्ट रूप से भारत को धर्म-निरपेक्ष राज्य घोषित किया गया है। धर्मनिरपेक्ष राज्य का अर्थ है कि राज्य का अपना कोई धर्म नहीं है और राज्य की दृष्टि में सभी धर्म समान हैं। नागरिकों को धार्मिक स्वतन्त्रता प्राप्त है और वे अपनी इच्छानुसार किसी भी धर्म को अपना सकते हैं, अपनी इच्छानुसार अपने इष्ट देव की पूजा कर सकते हैं, अपने धर्म का प्रचार कर सकते हैं। अनुच्छेद 25 से 28 तक में धार्मिक स्वन्त्रता प्रदान की गई है।

8. लचीला तथा कठोर संविधान (Flexible and Rigid Constitution)—भारत का संविधान लचीला भी है और कठोर भी। संविधान के कुछ भाग में संशोधन करना बड़ा सरल है जिसमें संसद् साधारण बहुमत से उसमें संशोधन कर सकती है। संविधान के कुछ अनुच्छेद ऐसे हैं, जिनमें संशोधन करना बड़ा ही कठोर है जैसे राष्ट्रपति के निर्वाचन की विधि, सर्वोच्च तथा उच्च न्यायालयों के अधिकार क्षेत्र तथा शक्तियां, संघ तथा राज्यों में शक्ति विभाजन, संसद् में राज्यों का प्रतिनिधित्व आदि विषयों में संशोधन करने के लिए यह आवश्यक है कि ऐसा प्रस्ताव संसद् के दोनों सदनों के दो-तिहाई बहुमत से पास होने के अतिरिक्त कम-से-कम आधे राज्यों के विधानमण्डलों द्वारा भी पास होना चाहिए। संविधान के शेष उपबन्धों को संशोधित करने के लिए संसद् का दो-तिहाई बहुमत आवश्यक है।

9. संघात्मक संविधान परन्तु एकात्मक प्रणाली की ओर झुकाव (Federal Constitution with Unitary Bias) यद्यपि हमारे संविधान में किसी अनुच्छेद द्वारा ‘संघ’ शब्द का प्रयोग नहीं किया गया, फिर भी मूल रूप में भारतीय संविधान भारत में संघात्मक सरकार की स्थापना करता है। संविधान की धारा 1 में कहा गया है कि “भारत राज्यों का एक संघ है।” (India is a Union of States) इस समय भारत में 29 राज्य और 7 संघीय क्षेत्र हैं जिसमें राष्ट्रीय राजधानी क्षेत्र दिल्ली भी शामिल है। इसमें संघात्मक शासन व्यवस्था की सभी बातें पाई जाती हैं-

• भारत का संविधान लिखित तथा कठोर है।
• भारत का संविधान सर्वोच्च कानून है।
• केन्द्र और राज्यों में शक्तियों का बंटवारा करने के लिए तीन सूचियों का वर्णन किया गया है।
• न्यायपालिका को सर्वोच्च स्थान प्राप्त है। केन्द्र और राज्यों के झगड़ों तथा राज्यों के परस्पर झगड़ों का निर्णय सर्वोच्च न्यायालय द्वारा किया जाता है।
• संसद् के दो सदन हैं-लोकसभा तथा राज्यसभा। लोकसभा सारे देश का प्रतिनिधित्व करती है जबकि राज्यसभा राज्यों का प्रतिनिधित्व करती है।

इस प्रकार भारत के संविधान में संघात्मक सरकार की सभी विशेषताएं पाई जाती हैं, परन्तु इसके बावजूद भी हमारे संविधान का झुकाव एकात्मक स्वरूप की ओर है। यह प्रायः कहा जाता है कि “भारतीय संविधान आकार में संघात्मक है और भावना में एकात्मक है।” (“Indian Constitution is federal in form but unitary in spirit.”) व्हीयर (Wheare) का कहना है कि, “भारतीय संविधान ने अर्ध-संघीय शासन प्रणाली की व्यवस्था की है।” निम्नलिखित कारणों के कारण संविधान का झुकाव एकात्मक स्वरूप की ओर है-

• केन्द्र के पास राज्यों की अपेक्षा अधिक शक्तियां हैं । केन्द्रीय-सूची में 97 विषय हैं, जबकि राज्य-सूची में 66 विषय हैं।
• समवर्ती-सूची में 47 विषय हैं। केन्द्र और राज्यों को इस सूची में दिए गए विषयों पर कानून बनाने का अधिकार है यदि इन विषयों पर केन्द्र और राज्य सरकारें दोनों कानून बनाती हैं तो केन्द्र का ही कानून लागू होता है।
• अवशेष शक्तियां केन्द्रीय सरकार के पास हैं।
• यदि राज्यसभा दो-तिहाई बहुमत से यह प्रस्ताव पास कर दे कि राज्य-सूची में दिया गया कोई विषय राष्ट्रीय महत्त्व का है तो संसद् उस पर एक वर्ष के लिए कानून पास कर सकती है।
• संकटकाल में संविधान का संघात्मक स्वरूप एकात्मक स्वरूप में बदल जाता है।
• संसद् राज्यों की सीमाओं में परिवर्तन कर सकती है।
• राज्यों को अपना संविधान बनाने का अधिकार नहीं है।
• नागरिकों को केवल भारत की नागरिकता प्राप्त है।
• राज्य वित्तीय सहायता के लिए केन्द्र पर निर्भर करते हैं।
• सारे देश के लिए आर्थिक और सामाजिक योजनाएं बनाने का अधिकार केन्द्रीय सरकार के पास है।
• संविधान में संशोधन की विधि बहुत कठोर नहीं है।
  यद्यपि भारत के संविधान में संघात्मक सरकार की सभी विशेषताएं पाई जाती हैं, परन्तु इसके बावजूद भी हमारे संविधान का झुकाव एकात्मक स्वरूप की ओर है।

10. संसदीय सरकार (Parliamentary form of Government) भारतीय संविधान ने भारत में संसदीय शासन प्रणाली की व्यवस्था की है। राष्ट्रपति राज्य का अध्यक्ष है, परन्तु उसकी शक्तियां नाम-मात्र हैं, वास्तविक नहीं। राष्ट्रपति अपनी शक्तियों का प्रयोग मन्त्रिपरिषद् की सलाह से ही करता है और मन्त्रिपरिषद् का संसद् के साथ घनिष्ठ सम्बन्ध है। मन्त्री संसद् सदस्यों में से लिए जाते हैं और वे अपने कार्यों के लिए संसद् के निम्न सदन और लोकसभा के प्रति उत्तरदायी हैं। लोकसभा अविश्वास प्रस्ताव पास करके मन्त्रिपरिषद् को जब चाहे अपदस्थ कर सकती है अर्थात् मन्त्रिपरिषद् लोकसभा के प्रसाद-पर्यन्त ही अपने पद पर रह सकती है।

11. द्वि-सदनीय विधानमण्डल (Bicameral Legislature)-हमारे संविधान की एक अन्य विशेषता यह है कि इसके द्वारा केन्द्र में द्वि-सदनीय विधानमण्डल की स्थापना की गई है। संसद् के निम्न सदन को लोकसभा (Lok Sabha) तथा ऊपरि सदन को राज्यसभा (Rajya Sabha) कहा जाता है। लोकसभा की कुल अधिकतम संख्या 552 हो सकती है परन्तु आजकल 545 सदस्य हैं। राज्यसभा की अधिकतम संख्या 250 हो सकती है परन्तु आजकल 245 सदस्य हैं। लोकसभा की शक्तियां और अधिकार राज्यसभा की शक्तियों और अधिकारों से अधिक हैं।

12. मौलिक अधिकार (Fundamental Rights)-भारतीय संविधान की एक महत्त्वपूर्ण विशेषता यह है कि संविधान के तीसरे भाग में भारतीयों को 6 मौलिक अधिकार प्रदान किए गए हैं। ये अधिकार हैं-(i) समानता का अधिकार, (ii) स्वतन्त्रता का अधिकार, (iii) शोषण के विरुद्ध अधिकार, (iv) धार्मिक स्वतन्त्रता का अधिकार, (1) सांस्कृतिक तथा शिक्षा सम्बन्धी अधिकार तथा (vi) संवैधानिक उपचारों का अधिकार। इसके द्वारा नागरिकों को जाति, धर्म, रंग, जन्म, लिंग आदि के आधार पर बने भेदभाव के बिना समान घोषित किया गया है और उन्हें कई प्रकार की स्वतन्त्रताएं प्रदान की गई हैं जैसा कि भाषण देने, अपने विचार प्रकट करने, घूमने-फिरने, सभा व समुदाय बनाने, कोई भी व्यवसाय करने का अधिकार। धार्मिक स्वतन्त्रता के साथ ही उन्हें अपनी इच्छानुसार शिक्षा ग्रहण करने तथा अपनी भाषा व संस्कृति की रक्षा व विकास करने का अधिकार भी दिया गया है।

नागरिकों को शोषण के विरुद्ध भी अधिकार दिया गया है। कोई भी सरकार इन अधिकारों का उल्लंघन नहीं कर सकती तथा उच्च न्यायालयों व सर्वोच्च न्यायालय को इनकी रक्षा के लिए पर्याप्त अधिकार व शक्तियां प्रदान की गई हैं। न्यायालय किसी भी कानून या सरकारी आदेश को जो इन अधिकारों के विरुद्ध हो, रद्द कर सकते हैं और प्रत्येक नागरिक को यह अधिकार है कि वह अपने इन अधिकारों की रक्षा के लिए उच्च तथा सर्वोच्च न्यायालय का द्वार खटखटा सकता है। अब तक मौलिक अधिकारों का उल्लंघन करने वाले बहुत से कानून अवैध घोषित किए जा चुके हैं। इन अधिकारों को लागू करना सरकार का कर्तव्य है। 1967 में गोलकनाथ केस के फैसले में सर्वोच्च न्यायालय ने संसद् को मौलिक अधिकारों में संशोधन करने के अधिकार से वंचित कर दिया था, परन्तु संविधान के 24वें संशोधन के अनुसार संसद् को पुन: यह अधिकार देने की व्यवस्था की गई है तथा सर्वोच्च न्यायालय ने अपने पूर्व निर्णय (गोलकनाथ के केस में) को रद्द करते हुए संसद् के इस अधिकार को वैध घोषित कर दिया है।

13. मौलिक कर्त्तव्य (Fundamental Duties)_42वें संशोधन द्वारा संविधान में ‘मौलिक कर्त्तव्यों’ के नाम पर चतुर्थ भाग-ए (Part IV-A) शामिल किया गया है। इसमें नागरिकों के 11 कर्तव्यों का वर्णन किया गया है जो कि इस प्रकार हैं-

• संविधान का पालन करना तथा उसके आदर्शों, संस्थाओं, राष्ट्रीय झण्डे और राष्ट्रीय गान का सम्मान करना।
• स्वतन्त्रता संग्राम को प्रेरित करने वाले उच्च आदर्शों को बनाए रखना और उनका पालन करना।
• भारत की प्रभुसत्ता, एकता और अखण्डता में विश्वास रखना तथा उसकी रक्षा करना।
• देश की सुरक्षा करना और आवश्यकता पड़ने पर राष्ट्रीय सेवा करना।
• भारत के सभी लोगों में मेल-मिलाप और बन्धुत्व की भावना का विकास करना तथा ऐसी रीतियों को त्यागना जो त्रियों की प्रतिष्ठा के विरुद्ध हों।
• राष्ट्र की मिली-जुली संस्कृति की सम्पन्न परम्परा का आदर करना और उसे सुरक्षित रखना।
• प्राकृतिक वातावरण को सुरक्षित रखना और उसे उन्नत करना तथा सभी जीवित प्राणियों के प्रति दया की भावना रखना।
• दृष्टिकोण में वैज्ञानिकता, मानवता, जिज्ञासा और सुधार की भावना को विकसित करना।
• सार्वजनिक सम्पत्ति को सुरक्षित रखना और हिंसा से बचना।
• व्यक्तिगत तथा सामूहिक क्रिया-कलापों के सभी क्षेत्रों में ऊंचा उठाने का प्रयत्न करना।
• छ: साल से 14 साल की आयु के बच्चे के माता-पिता या अभिभावक अथवा संरक्षक द्वारा अपने बच्चे को शिक्षा दिलाने के लिए अवसर उपलब्ध कराना।

14. राज्यनीति के निर्देशक सिद्धान्त (Directive Principles of State Policy) भारतीय संविधान की एक महत्त्वपूर्ण विशेषता यह है कि संविधान के चौथे भाग में अनुच्छेद 36 से 51 तक राज्यनीति के निर्देशक सिद्धान्तों का वर्णन किया गया है। राज्यनीति के निर्देशक सिद्धान्तों का अभिप्राय यह है कि केन्द्रीय तथा राज्य सरकारों के लिए संविधान में कुछ आदर्श रखे गए हैं ताकि उनके अनुसार अपनी नीति का निर्माण करके जनता की भलाई के लिए कुछ कर सके। यदि इन सिद्धान्तों को लागू किया जाए तो भारत का सामाजिक, राजनीतिक तथा आर्थिक विकास बहुत शीघ्र हो सकता है।

15. स्वतन्त्र न्यायपालिका (Independent Judiciary)-भारत के संविधान में स्वतन्त्र न्यायपालिका की व्यवस्था की गई है। भारत के संविधान में उन सभी बातों का वर्णन किया गया है जो स्वतन्त्र न्यायपालिका के लिए आवश्यक हैं। सर्वोच्च न्यायलय तथा राज्यों के उच्च न्यायालयों के न्यायाधीशों की नियुक्ति राष्ट्रपति सम्बन्धित अधिकारियों की सलाह से करता है। राष्ट्रपति इन न्यायाधीशों को अपनी इच्छा से नहीं हटा सकता। सर्वोच्च न्यायालय तथा उच्च न्यायालयों के न्यायाधीशों को संसद् महाभियोग द्वारा ही हटा सकती है। इस प्रकार न्यायाधीशों की नौकरी सुरक्षित की गई। न्यायाधीशों का कार्यकाल भी निश्चित आयु पर आधारित है। सर्वोच्च न्यायलय का न्यायाधीश 65 वर्ष तथा राज्यों के उच्च न्यायालयों के न्यायाधीश 62 वर्ष की आयु में रिटायर होते हैं। न्यायाधीशों को बहुत अच्छा वेतन दिया जाता है तथा रिटायर होने के पश्चात् पेंशन भी दी जाती है।

सर्वोच्च न्यायालय के मुख्य न्यायाधीश को 2,80,000 रुपए मासिक वेतन तथा अन्य न्यायाधीशों को 2,50,000 हज़ार रुपए मासिक वेतन मिलता है जबकि उच्च न्यायालय के मुख्य न्यायाधीशों को 2,50,000 और अन्य न्यायाधीशों को 2,25,000 रुपए मासिक वेतन मिलता है। न्यायाधीशों के वेतन और भत्ते उनके कार्यकाल में कम नहीं किए जा सकते। ऐसी व्यवस्था इसलिए की गई है ताकि न्यायाधीश सरकार के विरुद्ध बिना किसी डर के निर्णय दे सकें। सर्वोच्च न्यायालय के न्यायाधीशों तथा उच्च न्यायालयों के न्यायाधीशों की योग्यताओं का वर्णन संविधान में किया गया है। सर्वोच्च न्यायालय के न्यायाधीश रिटायर होने के पश्चात् किसी न्यायालय में वकालत नहीं कर सकते और उच्च न्यायालय के न्यायाधीश उस न्यायालय में वकालत नहीं कर सकते जहां से वे रिटायर हुए हों।

16. न्यायिक पुनर्निरीक्षण (Judicial Review)-न्यायिक पुनर्निरीक्षण का अर्थ है कि सर्वोच्च न्यायालय तथा उच्च न्यायालय संसद् द्वारा बनाए गए कानूनों तथा राज्य विधानमण्डलों के बनाए हुए कानून की संवैधानिक जांचपड़ताल कर सकती है और यदि कानून संविधान के विरुद्ध हो तो उसे अवैध घोषित कर सकती है। सर्वोच्च न्यायालय द्वारा असंवैधानिक घोषित किया गया कोई भी कानून, अध्यादेश, आदेश या सन्धि अवैध मानी जाती है और सरकार उसे लागू नहीं कर सकती। सर्वोच्च न्यायालय ने अपने इस अधिकार का इस्तेमाल कई बार किया है।

17. इकहरी नागरिकता (Single Citizenship) भारत में नागरिकों को एक ही नागरिकता प्राप्त है। सभी नागरिक चाहे वे किसी राज्य के हों, भारत के नागरिक हैं। नागरिकों को अपने राज्य की नागरिकता प्राप्त नहीं है।
18. वयस्क मताधिकार (Adult Franchise)-भारत के संविधान की एक अन्य विशेषता व्यस्क मताधिकार है। 61वें संशोधन एक्ट के अनुसार प्रत्येक नागरिक को जिसकी आयु 18 वर्ष अथवा इससे अधिक हो बिना किसी भेदभाव के वोट डालने का अधिकार प्राप्त है।

19. संयुक्त चुनाव प्रणाली (Joint Electorate System)-साम्प्रदायिक चुनाव प्रणाली को समाप्त करके संयुक्त चुनाव प्रणाली की व्यवस्था की गई है। अब सभी सम्प्रदाय मिलजुल कर अपने प्रतिनिधियों का चुनाव करते हैं।

20. कानून का शासन (Rule of Law)-भारत के संविधान की यह विशेषता है कि इसके द्वारा कानून के शासन की स्थापना की गई है। कानून के सम्मुख सभी नागरिक समान हैं, कोई व्यक्ति कानून से ऊपर नहीं है। अमीर-गरीब, पढ़े-लिखे तथा अनपढ़, शक्तिशाली तथा कमज़ोर सभी देश के कानून के सामने समान हैं कानून से कोई ऊंचा नहीं है।

21. अल्पसंख्यकों, अनुसूचित व पिछड़ी जातियों तथा कबीलों का संरक्षण (Protection of Minorities, Scheduled and Backward Classes and Tribes)—भारत के संविधान की अन्य विशेषता यह है कि इसमें एक ओर तो समानता की घोषण की गई है और दूसरी ओर इसमें अल्पसंख्यकों, अनुसूचित व पिछड़ी हुई जातियों तथा कबीलों के हितों के संरक्षण के लिए विशेष धाराओं की व्यवस्था की गई है। संसद् तथा राज्यों के विधानमण्डलों में अनुसूचित तथा पिछड़ी जातियों के लिए कुछ स्थान सुरक्षित रखे जाते हैं। 95वें संशोधन द्वारा इस अवधि को 2020 ई० तक कर दिया गया है।

22. कल्याणकारी राज्य (Welfare State) भारत को कल्याणकारी राज्य घोषित किया गया है। उद्देश्य प्रस्ताव, संविधान की प्रस्तावना, मौलिक अधिकार तथा राज्य के निर्देशक सिद्धान्तों को पढ़ कर यह स्पष्ट हो जाता है कि संविधान निर्माताओं का उद्देश्य भारत में एक ऐसा कल्याणकारी राज्य स्थापित करना था जिसमें व्यक्ति के लिए आर्थिक, राजनीतिक तथा सामाजिक सुरक्षा की व्यवस्था की जा सके।

23. विश्व शान्ति तथा अन्तर्राष्ट्रीय सुरक्षा का समर्थक (Advocate of World Peace and International Security) भारतीय संविधान विश्व शान्ति का प्रबल समर्थक है। राज्यनीति के निर्देशक सिद्धान्तों में स्पष्ट लिखा गया है कि भारत राष्ट्रों के बीच न्याय तथा समानतापूर्ण सम्बन्ध स्थापित करने की चेष्टा करेगा, अन्तर्राष्ट्रीय शान्ति तथा सुरक्षा बनाये रखने के लिए विधि तथा सन्धि बन्धनों के प्रति आदर का निर्माण करेगा और अन्तर्राष्ट्रीय विवादों को मध्यस्थता के द्वारा हल करने का प्रयत्न करेगा। व्यवहार में भी भारत सरकार ने अन्तर्राष्ट्रीय शान्ति को बनाये रखने के लिए अनेक प्रयास किये हैं।

24. एक सरकारी भाषा (One Official Language) भारत में अनेक भाषाएं बोली जाती हैं, इसलिए संविधान में 22 भाषाओं को मान्यता दी गई है। हिन्दी को देवनागरी लिपि में संघ सरकार की सरकारी (Official) भाषा घोषित किया गया है।

25. छुआछूत की समाप्ति (Abolition of Untouchability)-भारतीय संविधान की यह विशेषता है कि इसके अनुच्छेद 17 द्वारा छुआछूत को समाप्त कर दिया गया है। जो व्यक्ति छुआछूत की समाप्ति के विरुद्ध बोलता है उसे कानून के अनुसार दण्ड दिया जा सकता है।

निष्कर्ष (Conclusion)-उपर्युक्त विशेषताओं के आधार पर यह निष्कर्ष निकाला जा सकता है कि यह संविधानों में एक अनूठा संविधान है। न्यायाधीश पी० वी० मुखर्जी के अनुसार, “यद्यपि हमारे संविधान ने विश्व के संवैधानिक प्रयोगों से बहुत-सी बातों को लिया है, केवल यही नहीं बल्कि अपने चरित्र और समन्वय में यह अनूठा संविधान है।” संविधान निर्माताओं का उद्देश्य कोई मौलिक या अद्वितीय संविधान बनाना नहीं था बल्कि वे एक अच्छा तथा कार्यसाधक संविधान बनाना चाहते थे।

प्रश्न 2.
भारतीय संविधान में संशोधन करने के विभिन्न तरीकों का वर्णन करें।
(Describe the various methods of amending the Indian Constitution.)
उत्तर-
प्रत्येक राज्य का संविधान एक निश्चित समय पर तैयार किया जाता है, परन्तु समय के अनुसार देश की सामाजिक, राजनीतिक एवं आर्थिक परिस्थितियां बदलती रहती हैं। एक अच्छा संविधान वही होता है जिसे परिस्थितियों के अनुकूल परिवर्तित किया जा सके। इसलिए प्रत्येक लिखित संविधान में संशोधन की प्रक्रिया का स्पष्ट उल्लेख कर दिया जाता है। ___ संविधान को संशोधित करने की प्रक्रिया का वर्णन अनुच्छेद 368 में किया गया है। अनुच्छेद के अनुसार संविधान में संशोधन करने के लिए दो विधियों का वर्णन किया गया है, परन्तु भारतीय संविधान में निम्नलिखित तीन विधियों द्वारा संशोधन किया गया है-

1. संसद् द्वारा साधारण बहुमत से संशोधन ;
2. संसद् द्वारा दो तिहाई बहुमत से संशोधन ;
3. संसद् के विशेष बहुमत तथा कम-से-कम आधे राज्यों के विधानमण्डलों की स्वीकृति से संशोधन।

1.संसद द्वारा साधारण बहुमत से संशोधन (Amendment by the Parliament by a Simple Majority)संविधान की कुछ धाराएं ऐसी हैं जिन्हें भारतीय संसद् उसी प्रकार से और उतनी ही आसानी से बदल सकती है जितना कि ब्रिटिश संसद् ब्रिटिश संविधान को अर्थात् संसद् साधारण बहुमत से संविधान के कुछ भाग में संशोधन कर सकती है। इसमें मुख्य विषय सम्मिलित हैं-नए राज्यों का निर्माण, राज्यों की सीमाओं में परिवर्तन करना, नागरिकता की प्राप्ति और समाप्ति, सर्वोच्च न्यायालय का क्षेत्राधिकार बढ़ना इत्यादि।

2. संसद् द्वारा दो-तिहाई बहुमत से संशोधन (Amendment by the Parliament by a two-third Majority) संविधान की कुछ धाराएं ऐसी हैं जिन्हें संसद् दो-तिहाई बहुमत से संशोधन कर सकती है। संविधान के अनुच्छेद 368 में स्पष्ट कहा गया है कि संविधान में संशोधन का प्रस्ताव संसद् के किसी भी सदन में पेश किया जा सकता है। दोनों सदनों में सदन की कुल संख्या के बहुमत तथा उपस्थित व मत देने वाले सदस्यों के दो-तिहाई बहुमत से पास होने के बाद वह संशोधन प्रस्ताव राष्ट्रपति की स्वीकृति के लिए भेजा जाएगा और स्वीकृति मिलने पर ही संविधान इस प्रस्ताव की धाराओं के अनुसार संशोधित समझा जायेगा लोकसभा और राज्यसभा को संवैधानिक संशोधन के क्षेत्र में बिल्कुल बराबर की शक्तियां प्राप्त हैं।

3. संसद के विशेष बहुमत तथा राज्य विधानपालिका के अनुसमर्थन द्वारा संशोधन (Amendment by the special majority of Parliament and ratification by State Legislature) संविधान की कुछ धाराएं ऐसी भी हैं जिन्हें और भी कठोर बनाया गया है और जिसमें संसद् स्वतन्त्रतापूर्वक परिवर्तन नहीं कर सकती। संविधान के कुछ भाग में संसद् के दोनों सदनों के दो तिहाई बहुमत और आधे राज्यों के विधानमण्डलों के समर्थन से ही संशोधन किया जा सकता है। जिन विषयों में इस विधि से संशोधन किया जा सकता है उनमें मुख्य हैं-राष्ट्रपति का चुनाव और चुनाव विधि, केन्द्र और राज्यों के वैधानिक सम्बन्ध, संघीय सरकार और राज्य सरकारों की कार्यपालिका सम्बन्धी शक्तियों की सीमा इत्यादि।

संशोधन प्रक्रिया की आलोचना (Criticism of the Procedure of Amendment)-
भारतीय संविधान की संशोधन प्रक्रिया की आलोचना निम्नलिखित आधारों पर की जाती है-

• राज्य को संशोधन प्रस्ताव पेश करने का अधिकार नहीं-संविधान में संशोधन का प्रस्ताव केवल केन्द्रीय संसद् द्वारा ही पेश किया जा सकता है। राज्यों को संशोधन का समर्थन करते हुए ही अपनी राय देने का अधिकार है।
• सभी धाराओं में संशोधन करने के लिए राज्यों की आवश्यकता नहीं-संविधान की कुछ धाराओं पर ही आधे राज्यों के विधानमण्डलों के समर्थन की आवश्यकता है। संविधान का एक बहुत बड़ा भाग संसद् स्वयं ही संशोधित कर सकती है।
• राज्यों के अनुसमर्थन के लिए समय निश्चित नहीं-संविधान में इस बात का उल्लेख नहीं है कि किसी संशोधन प्रस्ताव पर राज्य के विधानमण्डल कितने समय के अन्दर अपना निर्णय दे सकते हैं।
• दोनों में मतभेद-भारतीय संविधान इस बारे में भी मौन है कि यदि संसद् के दोनों सदनों में किसी संशोधन प्रस्ताव पर मतभेद उत्पन्न हो जाए तो उसे कैसे सुलझाया जाएगा। ऐसी दशा में संशोधन प्रस्ताव रद्द समझा जाएगा या यह प्रस्ताव दोनों सदनों की संयुक्त बैठक में रखा जाएगा।
• संशोधन प्रस्ताव पर राष्ट्रपति की स्वीकृति-संविधान में इस बात का उल्लेख नहीं है कि क्या राष्ट्रपति को संशोधन के प्रस्ताव पर निषेधाधिकार (Veto-Power) प्राप्त है या नहीं। संविधान के 24वें संशोधन के अनुसार इस बात के विषय में जो सन्देह थे वे दूर कर दिए गए हैं। इस संशोधन के अनुसार संशोधन बिल पर राष्ट्रपति अपने हस्ताक्षर नहीं रोक सकता।
• जनमत संग्रह की व्यवस्था नहीं है-हमारे संविधान में कोई ऐसी व्यवस्था नहीं कि जिसके अनुसार जनता की इच्छा किसी अमुक प्रस्तावित संशोधन बिल पर ली जा सके अर्थात् संविधान में संशोधन जनता को पूछे बिना ही संसद् कर सकती है। आलोचकों का कहना है कि ऐसी व्यवस्था अन्यायपूर्ण एवं अलोकतन्त्रीय है।

निष्कर्ष (Conclusion)-उपर्युक्त दोषों के होते हुए भी भारतीय संविधान के बारे में हम इतना अवश्य कह सकते हैं कि यह एक ऐसा प्रलेख है जो काफ़ी सोच-विचार के बाद तैयार किया गया है और जिसे न तो इतनी आसानी से बदला जा सकता है कि यह सत्तारूढ़ दल के हाथों में खिलौना-मात्र बन कर रह जाए और न ही इतना कठोर है कि समय के अनुसार बदलती हुई आवश्यकताओं के अनुसार इसमें परिवर्तन न किया जा सके और यह अतीत की एक वस्तु बन कर रह जाए। हमारा संविधान न तो अमेरिकन संविधान की भान्ति कठोर है और न ही ब्रिटिश संविधान की तरह लचीला। प्रो० ह्वीयर (Wheare) ने ठीक ही कहा है कि, “भारतीय संविधान अधिक कठोर तथा अधिक लचीलापन के मध्य एक अच्छा सन्तुलन स्थापित करता है।”

लघु उत्तरीय प्रश्न

प्रश्न 1.
संविधान का क्या अर्थ है ?
उत्तर-
संविधान ऐसे नियमों तथा सिद्धान्तों का समूह है, जिसके अनुसार शासन के विभिन्न अंगों का संगठन किया जाता है, उसको शक्तियां प्रदान की जाती हैं, उनके आपसी सम्बन्धों को नियमित किया जाता है तथा नागरिकों और राज्य के बीच सम्बन्ध स्थापित किये जाते हैं। इन नियमों के समूह को ही संविधान कहा जाता है।
पिनॉक (Pennock) और स्मिथ (Smith) के अनुसार, “संविधान केवल प्रक्रिया एवं तथ्यों का ही मामला नहीं बल्कि राजनीतिक शक्तियों के संगठनों का प्रभावशाली नियन्त्रण भी है एवं प्रतिनिधित्व, प्राचीन परम्पराओं तथा भविष्य की आशाओं का प्रतीक है।”

प्रश्न 2.
हमें संविधान की आवश्यकता क्यों होती है ?
उत्तर–
प्रत्येक राज्य में संविधान का होना आवश्यक है। संविधान के बिना राज्य का शासन नहीं चल सकता। इसीलिए संविधान के बिना एक राज्य-राज्य न होकर अराजकता का शासन होता है। संविधान का होना आवश्यक है ताकि शासन के विभिन्न अंगों की शक्तियां तथा कार्य निश्चित किए जा सकें। संविधान का होना आवश्यक है ताकि देश का शासन सिद्धान्तों तथा नियमों के अनुसार चलाया जा सके।

प्रश्न 3.
भारतीय संविधान का निर्माण किस द्वारा किया गया है ?
उत्तर-
भारत का संविधान एक संविधान सभा द्वारा बनाया गया है। भारत के लिए संविधान सभा की मांग सबसे पहले 1922 में महात्मा गांधी ने, 1935 में कांग्रेस ने और 1940 में मुस्लिम लीग ने भी अलग से संविधान सभा की मांग की थी। दूसरे विश्वयुद्ध के दौरान संविधान सभा के गठन की मांग तेज़ हो गई। ब्रिटिश सरकार ने भारतीय नेताओं की इस मांग को ध्यान में रखते हुए 15 मार्च, 1946 को कैबिनेट मिशन की स्थापना है। कैबिनेट मिशन ने अपनी योजनाओं में संविधान सभा की रचना के बारे में खुला वर्णन किया है। संविधान सभा में कुल 389 सदस्यों की व्यवस्था की गई। संविधान सभा की पहली बैठक 9 दिसम्बर, 1946 को बुलाई गई और काफी मेहनत और विचार-विमर्श के बाद 26 नवम्बर, 1949 को संविधान बन कर तैयार हो गया। 26 नवम्बर, 1949 को संविधान सभा के प्रधान ने मसौदे पर हस्ताक्षर कर दिए। 26 जनवरी, 1950 को यह संविधान लागू कर दिया गया।

प्रश्न 4.
भारतीय संविधान की किन्हीं चार विशेषताओं का वर्णन करो।
उत्तर-
भारतीय संविधान की मुख्य विशेषताएं निम्नलिखित हैं-

• लिखित एवं विस्तृत संविधान-भारत के संविधान की प्रथम विशेषता यह है कि यह लिखित एवं विस्तृत है। इसमें 395 अनुच्छेद तथा 12 अनुसूचियां हैं और इन्हें 22 भागों में बांटा गया है। इसे 2 वर्ष, 11 महीने तथा 18 दिनों के समय में बनाया गया।
• प्रस्तावना-प्रत्येक अच्छे संविधान की तरह भारतीय संविधान में भी प्रस्तावना दी गई है। इस प्रस्तावना में संविधान के मुख्य लक्ष्यों, विचारधाराओं तथा राज्य के उद्देश्यों का वर्णन किया गया है।
• सम्पूर्ण प्रभुत्व सम्पन्न, समाजवादी, धर्म-निरपेक्ष लोकतन्त्रात्मक गणराज्य की स्थापना- इसका अर्थ यह है कि भारत पूर्ण रूप से प्रभुता सम्पन्न है। इसका उद्देश्य समाजवादी समाज की स्थापना करना है। भारत धर्म-निरपेक्ष और लोकतन्त्रात्मक गणराज्य है।
• भारतीय संविधान की एक अन्य विशेषता वयस्क मताधिकार है।

प्रश्न 5.
धर्म-निरपेक्ष राज्य किसे कहते हैं ? क्या भारत एक धर्म-निरपेक्ष राज्य है ? व्याख्या करो।
उत्तर-
धर्म-निरपेक्ष राज्य वह राज्य है जिसका कोई राज्य धर्म नहीं होता। राज्य धार्मिक मामलों में हस्तक्षेप नहीं करता। राज्य न तो धार्मिक और न ही अधार्मिक और न ही धर्म-विरोधी होता है। धर्म के आधार पर नागरिकों के साथ भेद-भाव नहीं किया जाता। सभी धर्म के लोगों को समान रूप से बिना किसी भेद-भाव के अधिकार दिए जाते हैं।

42वें संशोधन द्वारा प्रस्तावना में धर्म-निरपेक्ष शब्द जोड़ कर भारत को स्पष्ट रूप से धर्म-निरपेक्ष राज्य घोषित किया गया है। राज्य का अपना कोई धर्म नहीं है और न ही राज्य धर्म को महत्त्व देता है। सभी धर्म समान हैं। किसी धर्म को विशेषाधिकार प्राप्त नहीं है। सरकारी स्कूलों और कॉलेजों में धार्मिक शिक्षा नहीं दी जा सकती है। प्रत्येक व्यक्ति अपनी इच्छानुसार किसी भी धर्म का पालन कर सकता है। सभी धर्मों को प्रचार एवं उन्नति के लिए समान अधिकार प्रदान किए गए हैं। साम्प्रदायिक चुनाव प्रणाली का अन्त कर दिया गया है।

प्रश्न 6.
भारतीय संविधान की सफलता के लिए चार उत्तरदायी तत्त्वों का वर्णन करें।
उत्तर-
भारतीय संविधान की सफलता के मुख्य कारण निम्नलिखित हैं-

• देश की परिस्थतियों के अनुकूल–भारतीय संविधान की सफलता का महत्त्वपूर्ण कारण यह है कि संविधान निर्माताओं ने देश की परिस्थितियों को ध्यान में रखकर संविधान बनाया।
• लिखित तथा विस्तृत संविधान-लिखित तथा विस्तृत संविधान के कारण जनता के प्रतिनिधियों, शासकों तथा सरकारी कर्मचारियों को शासन चलाते हुए पथ-प्रदर्शन के लिए इधर-उधर भटकना नहीं पड़ता बल्कि हर प्रकार की सलाह और मार्गदर्शन संविधान से ही मिल जाता है।
• विश्व के संविधान की अच्छी बातों को ग्रहण करना-भारतीय संविधान में अन्य देशों के संविधानों के अच्छे सिद्धान्तों तथा गुणों को सम्मिलित किया गया है।
• भारतीय संविधान सभी धर्मों, समुदायों एवं वर्गों को साथ लेकर चलता है।

प्रश्न 7.
भारतीय संविधान 26 जनवरी, 1950 को ही क्यों लागू किया गया ?
अथवा
26 जनवरी का क्या महत्त्व है ?
उत्तर-
भारत का संविधान 26 जनवरी, 1950 को लागू किया गया। 26 जनवरी का दिन भारत के इतिहास में एक विशेष महत्त्व रखता है। दिसम्बर, 1929 में कांग्रेस ने पण्डित जवाहर लाल नेहरू की अध्यक्षता में हुए लाहौर अधिवेशन में भारत के लिए पूर्ण स्वतन्त्रता की मांग का प्रस्ताव पास किया और 26 जनवरी, 1930 का दिन स्वतन्त्रता दिवस के रूप में निश्चित किया गया और इस दिन सभी भारतीयों ने देश को स्वतन्त्र कराने का प्रण लिया। इसके पश्चात् हर वर्ष 26 जनवरी का दिन स्वतन्त्रता दिवस के रूप में मनाया जाता रहा। इसलिए यद्यपि संविधान 26 नवम्बर, 1949 को तैयार हो गया था परन्तु इसको 26 जनवरी, 1950 को लागू किया गया।

प्रश्न 8.
भारतीय संविधान के विस्तृत होने के क्या कारण हैं ?
उत्तर-
भारतीय संविधान लिखित होने के साथ ही विश्व के अन्य देशों के संविधानों के मुकाबले बहुत विस्तृत है। हमारे संविधान में 395 अनुच्छेद, 12 अनुसूचियां हैं जिन्हें 22 भागों में बांटा गया है। भारतीय संविधान निम्नलिखित तथ्यों के कारण विशाल है-

• भारत में केन्द्र और राज्यों के लिए एक ही संयुक्त संविधान की व्यवस्था की गई है। प्रान्तों के लिए कोई पृथक् संविधान नहीं है।
• संविधान के तृतीय भाग में मौलिक अधिकारों की विस्तृत व्याख्या की गई है।
• संविधान के चौथे भाग में राजनीति के निर्देशक सिद्धान्त शामिल किए गए हैं।
• संविधान के 18वें भाग में अनुच्छेद 352 से लेकर 360 तक राष्ट्रपति की संकटकालीन शक्तियों की व्यवस्था की गई है।

प्रश्न 9.
भारतीय संविधान में संशोधन करने के विभिन्न तरीकों का संक्षिप्त वर्णन करें।
उत्तर-
अनुच्छेद 368 के अन्तर्गत संविधान में संशोधन करने के लिए दो विधियों का वर्णन किया है। परन्तु भारतीय संविधान में निम्नलिखित तीन विधियों द्वारा संशोधन किया जा सकता है-

1. संसद् द्वारा साधारण बहुमत से संशोधन-संविधान की कुछ धाराएं ऐसी हैं जिन्हें भारतीय संसद् उसी प्रकार से और उतनी ही आसानी से बदल सकती है जितना कि ब्रिटिश संविधान को अर्थात् उनमें साधारण बहुमत से संशोधन किया जा सकता है।
2. संसद् द्वारा दो-तिहाई बहुमत से संशोधन-संविधान की कुछ धाराएं ऐसी हैं जिनमें संसद् दो-तिहाई बहुमत से संशोधन कर सकती है। दोनों सदनों के सदस्यों की कुल संख्या के बहुमत तथा उपस्थित और मत देने वाले दो तिहाई सदस्यों की स्वीकृति के पश्चात् संशोधन प्रस्ताव राष्ट्रपति के पास भेजा जाता है तथा राष्ट्रपति द्वारा स्वीकृति मिलने के पश्चात् ही उन धाराओं को संशोधित किया जाता है।
3. संसद् के विशेष बहुमत तथा आधे राज्य विधानमण्डलों के अनुसमर्थन द्वारा संशोधन-संविधान की कुछ धाराएं ऐसी भी हैं जिन्हें और भी कठोर बनाया गया है और जिनमें संसद् स्वतन्त्रतापूर्वक परिवर्तन नहीं कर सकती। संविधान के कुछ भाग में संसद् के दो-तिहाई बहुमत और आधे राज्यों के विधानमण्डलों के समर्थन से ही संशोधन किया जा सकता है।

प्रश्न 10.
भारतीय संविधान में संशोधन प्रक्रिया के किन्हीं चार आधारों पर आलोचना करें।
उत्तर-
भारतीय संविधान की संशोधन प्रक्रिया की आलोचना निम्नलिखित आधारों पर की जाती है-

1. राज्य को संशोधन प्रस्ताव पेश करने का अधिकार नहीं-संविधान में संशोधन का प्रस्ताव केवल केन्द्रीय संसद् द्वारा ही पेश किया जा सकता है। राज्यों को संशोधन का समर्थन करते हुए ही अपनी राय देने का अधिकार है।
2. सभी धाराओं में संशोधन करने के लिए राज्यों की आवश्यकता नहीं-संविधान की कुछ धाराओं पर ही आधे राज्यों के विधानमण्डलों के समर्थन की आवश्यकता है। संविधान का एक बहुत बड़ा भाग संसद् स्वयं ही संशोधित कर सकती है।
3. राज्यों के अनुसमर्थन के लिए समय निश्चित नहीं-संविधान में इस बात का उल्लेख नहीं है कि किसी संशोधन प्रस्ताव पर राज्य के विधानमण्डल कितने समय के अन्दर अपना निर्णय दे सकते हैं।
4. दोनों में मतभेद-भारतीय संविधान इस बारे में भी मौन है कि यदि संसद् के दोनों सदनों में किसी संशोधन प्रस्ताव पर मतभेद उत्पन्न हो जाए तो उसे कैसे सुलझाया जाएगा। ऐसी दशा में संशोधन प्रस्ताव रद्द समझा जाएगा या यह प्रस्ताव दोनों सदनों की संयुक्त बैठक में रखा जाएगा।

प्रश्न 11.
भारतीय संविधान की संशोधन प्रक्रिया की विशषताएं बताएं।
उत्तर-

• संविधान के प्रत्येक भाग में संशोधन किया जा सकता है। केशवानन्द भारती और मिनर्वा मिल्स के मुकद्दमे में सर्वोच्च न्यायालय ने यह निर्णय दिया कि संसद् संविधान के बुनियादी ढांचे में परिवर्तन नहीं कर सकती।
• भारतीय संविधान लचीला और कठोर भी है।
• संवैधानिक संशोधन बिल संसद् के किसी भी सदन में पेश किया जा सकता है।
• राज्य विधान मण्डल को संशोधन का प्रस्ताव पेश करने का कोई अधिकार नहीं है।
• संवैधानिक संशोधन सम्बन्धी दोनों सदनों की शक्तियां बराबर हैं।
• संवैधानिक संशोधन को न्यायालय में चुनौती दी जा सकती है।

प्रश्न 12.
“भारतीय संविधान लचीला और कठोर भी है।” व्याख्या कीजिए।
उत्तर-
भारतीय संविधान की एक महत्त्वपूर्ण विशेषता यह है कि यह न तो पूर्णतः लचीला है और न ही पूर्णतः कठोर है। लचीला संविधान उसे कहा जाता है जिसमें संशोधन उतनी ही सरलता से किया जा सकता है जितनी सरलता से कोई कानून बनाया जा सकता है। भारतीय संविधान की कुछ धाराओं को, जैसे कि राज्यों के नाम बदलना, उनकी सीमाओं में परिवर्तन करना, राज्यों में विधान परिषद् को बनाना या उसे समाप्त करना आदि को संसद् के दोनों सदनों द्वारा उपस्थित सदस्यों के साधारण बहुमत से बदला जा सकता है। इस तरह भारतीय संविधान लचीला है। संविधान की कुछ धाराओं को बदलने के लिए संसद् के दोनों सदनों का दो-तिहाई बहुमत आवश्यक है। इस प्रक्रिया के अनुसार संविधान कुछ कठोर हो गया है, परन्तु संघात्मक प्रणाली की आवश्यकताओं को देखते हुए इस अवस्था को भी लचीला कहा जा सकता है।
परन्तु कुछ महत्त्वपूर्ण धाराओं को बदलने के लिए संसद् को दो-तिहाई बहुमत के बाद कम-से-कम आधे राज्यों के विधानमण्डलों द्वारा संशोधन प्रस्ताव पर समर्थन प्राप्त होना आवश्यक है। यह तरीका बड़ा कठोर है और इसको देखते हुए संविधान को कठोर कहा गया है।

अति लघु उत्तरीय प्रश्न

प्रश्न 1.
भारतीय संविधान की किन्हीं दो विशेषताओं का वर्णन करो।
उत्तर-

1. लिखित एवं विस्तृत संविधान-भारत के संविधान की प्रथम विशेषता यह है कि यह लिखित एवं विस्तृत है। इसमें 395 अनुच्छेद तथा 12 अनुसूचियां हैं और इन्हें 22 भागों में बांटा गया है। इसे 2 वर्ष, 11 महीने तथा 18 दियं के समय में बनाया गया।
2. प्रस्तावना-प्रत्येक अच्छे संविधान की तरह भारतीय संविधान में भी प्रस्तावना दी गई है। इस प्रस्तावना में संविधान के मुख्य लक्ष्यों, विचारधाराओं तथा राज्य के उद्देश्यों का वर्णन किया गया है।

प्रश्न 2.
26 जनवरी का क्या महत्त्व है ?
उत्तर-
भारत का संविधान 26 जनवरी, 1950 को लागू किया गया। 26 जनवरी का दिन भारत के इतिहास में एक विशेष महत्त्व रखता है। दिसम्बर, 1929 में कांग्रेस ने पण्डित जवाहर लाल नेहरू की अध्यक्षता में हुए लाहौर अधिवेशन में भारत के लिए पूर्ण स्वतन्त्रता की मांग का प्रस्ताव पास किया और 26 जनवरी, 1930 का दिन स्वतन्त्रता दिवस के रूप में निश्चित किया गया और इस दिन सभी भारतीयों ने देश को स्वतन्त्र कराने का प्रण लिया। इसके पश्चाता हर वर्ष 26 जनवरी का दिन स्वतन्त्रता दिवस के रूप में मनाया जाता रहा। इसलिए यद्यपि संविधान 26 नवम्बर, 1949 को तैयार हो गया था परन्तु इसको 26 जनवरी, 1950 को लागू किया गया।

प्रश्न 3.
भारतीय संविधान के विस्तृत होने के दो कारण लिखें।
उत्तर-

1. भारत में केन्द्र और राज्यों के लिए एक ही संयुक्त संविधान की व्यवस्था की गई है। प्रान्तों के लिए कोई पृथक् संविधान नहीं है।
2. संविधान के तृतीय भाग में मौलिक अधिकारों की विस्तृत व्याख्या की गई है।

वस्तुनिष्ठ प्रश्न

प्रश्न I. एक शब्द/वाक्य वाले प्रश्न-उत्तर-

प्रश्न 1. वर्तमान भारतीय संविधान में कुल कितनी अनुसूचियां हैं ?
उत्तर-वर्तमान भारतीय संविधान में कुल 12 अनुसूचियां हैं।

प्रश्न 2. वर्तमान संविधान में कुल कितने अनुच्छेद हैं ?
उत्तर-वर्तमान भारतीय संविधान में कुल 395 अनुच्छेद हैं।

प्रश्न 3. भारतीय संविधान के मौलिक ढांचे की धारणा का विकास किस मुकद्दमें में हुआ ?
उत्तर-भारतीय संविधान के मौलिक ढांचे की धारणा का विकास 23 अप्रैल, 1973 को स्वामी केशवानंद भारती के मुकद्दमें में हुआ।

प्रश्न 4. भारतीय संघ में कितने राज्य एवं संघीय क्षेत्र शामिल हैं ?
उत्तर-29 राज्य एवं 7 संघीय क्षेत्र।

प्रश्न 5. भारत में कौन-सी शासन प्रणाली है?
उत्तर-भारत में संसदीय शासन प्रणाली है।

प्रश्न 6. भारत में कितने वर्ष के आयु के नागरिक को वोट डालने का अधिकार है?
उत्तर-18 वर्ष।

प्रश्न 7. भारत की राष्ट्र भाषा क्या है?
उत्तर-भारत की राष्ट्र भाषा हिंदी है।

प्रश्न 8. भारत गणतन्त्र कब बना?
उत्तर-भारत गणतन्त्र 26 जनवरी, 1950 को बना।

प्रश्न 9. संविधान के किस अनुच्छेद में संशोधन विधि का वर्णन किया गया है?
उत्तर-अनुच्छेद 368 में।

प्रश्न II. खाली स्थान भरें-

1. 91वां संवैधानिक संशोधन ……….. में किया गया।
2. 61वें संशोधन द्वारा मताधिकार की आयु 21 वर्ष से घटाकर ………. कर दी गई।
3. 1985 में दल-बदल रोकने के लिए संविधान में ………….. संशोधन किया गया।
4. भारतीय संविधान …………. है।
5. संशोधन विधि का वर्णन संविधान के अनुच्छेद ……….. में किया गया।
उत्तर-

1. 2003
2. 18 वर्ष
3. 52वां
4. लिखित
5. 368.

प्रश्न III. निम्नलिखित में से सही एवं ग़लत का चुनाव करें।

1. जीवंत संविधान उसे कहा जाता है, जिसमें समयानुसार परिवर्तन नहीं होते।
2. भारतीय संविधान एक जीवंत संविधान है।
3. भारतीय संविधान विकसित एवं अलिखित है।
4. राजनीतिक दल-बदल की बुराई को दूर करने के लिए 1980 में 42वां संशोधन पास किया गया।
उत्तर-

1. ग़लत
2. सही
3. ग़लत
4. ग़लत !

प्रश्न IV. बहुविकल्पीय प्रश्न

प्रश्न 1.
भारत में वोट डालने का अधिकार—
(क) 18 वर्ष के नागरिक को प्राप्त है
(ख) 21 वर्ष के नागरिक को प्राप्त है
(ग) 25 वर्ष के नागरिक को प्राप्त है
(घ) 20 वर्ष के नागरिक को प्राप्त है।
उत्तर-
(क) 18 वर्ष के नागरिक को प्राप्त है

प्रश्न 2.
भारत की राष्ट्र भाषा
(क) हिंदी
(ख) तमिल
(ग) उर्दू
(घ) अंग्रेजी।
उत्तर-
(क) हिंदी

प्रश्न 3.
भारत का संविधान-
(क) संसार के सभी संविधानों से छोटा है
(ख) संसार में सबसे अधिक लंबा तथा विस्तृत है
(ग) जापान के संविधान से बड़ा और अमेरिका के संविधान से छोटा है
(घ) सोवियत संघ के संविधान से छोटा है।
उत्तर-
(ख) संसार में सबसे अधिक लंबा तथा विस्तृत है

प्रश्न 4.
निम्नलिखित में से कौन-सा वाक्य ग़लत सूचना देता है ?
(क) 1935 का एक्ट भारतीय संविधान का महत्त्वपूर्ण स्रोत है
(ख) संसदीय शासन प्रणाली ब्रिटिश शासन की देन है
(ग) अमेरिकन संविधान का भारत पर प्रभाव पड़ा है
(घ) पाकिस्तानी संविधान का भारत पर प्रभाव पड़ा है।
उत्तर-
(घ) पाकिस्तानी संविधान का भारत पर प्रभाव पड़ा है।