Punjab State Board PSEB 11th Class Physics Important Questions Chapter 10 Mechanical Properties of Fluids Important Questions and Answers.
PSEB 11th Class Physics Important Questions Chapter 10 Mechanical Properties of Fluids
Very Short Answer Type Questions
Question 1.
Three vessels have same base area and different neck area. Equal volume of liquid is poured into them, which will possess more pressure at the base?
Answer:
If the volumes are same, then height of the liquid will be highest in which the cross-section area is least at the top. So, the vessel having least cross-section area at the top possess more pressure at the base (∵ P = ρgh).
Question 2.
What is the use of barometer?
Answer:
Barometer is used to measure the atmospheric pressure.
Question 3.
What is the use of open tube manometer?
Answer:
Open tube manometer is used for measuring pressure difference.
Question 4.
‘What is the gauge pressure?
Solution:
The difference between absolute pressure and atmospheric pressure is known as gauge pressure.
As, Pabsolute = Pa+ ρgh
So, Pabsolute – Pa = ρgh
i.e., Pgauge = ρgh
Here ρ is the density of a fluid of depth h.
![]()
Question 5.
If a wet piece of wood bums, then water droplets appear on the other end, why?
Answer:
When a piece of the wet wood bums, then steam formed and water appear in the form of droplets due to surface tension on the other end.
Question 6.
Why soap bubble bursts after some time?
Answer:
Soap bubble bursts after some time because the pressure inside it become more than the outside pressure.
Question 7.
Can two streamlines cross each other? Why?
Answer:
Two streamlines can never cross each other because if they cross them at the point of intersection there will be two possible direction of flow of fluid which is impossible for streamlines.
Question 8.
A hot liquid moves faster than a cold liquid. Why?
Answer:
The viscosity of liquid decreases with the increase in temperature. Therefore, viscosity of hot liquid is less than that of cold liquid. Due to this hot liquid moves faster than the cold liquid.
Question 9.
Is viscosity a vector? (NCERT Exemplar)
Answer:
Viscosity is a property of liquid it does not have any direction, hence it is a scalar quantity.
Question 10.
Is surface tension a vector? (NCERT Exemplar)
Answer:
No, surface tension is a scalar quantity.
Surface tension = \(\frac{\text { Work done }}{\text { Surface area }} \) , where work done and surface area both Surface area are scalar quantities.
Short Answer Type Questions
Question 1.
A large force is needed to normally separate two glass plates having a thin layer of water between them. Why?
Answer:
The thin layer of water between the glass plates forms a concave surface all around. This decreases the pressure on the inner side of the liquid film. Thus, a large amount of force is required to pull them apart against the atmospheric pressure.
Question 2.
Two soap bubbles in vacuum having radii 3 cm and 4 cm respectively coalesce under isothermal conditions to form a single bubble. What is the radius of the new bubble?
Solution:
Surface energy of first bubble = Surface area x Surface tension
= 2 x 4 πr21T = 8πr21T
Surface energy of second bubble = 8πr22T
Let r be the radius of the coalesced bubbles.
∴ Surface energy of new bubble = 8πr2 T
According to the law of conservation of energy,
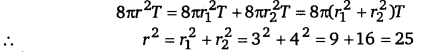
∴ r = 5 cm
Question 3.
A balloon with hydrogen in it rises up but a balloon with air comes down. Why?
Answer:
The density of hydrogen is less than air. So, the buoyant force on the balloon will be more than its weight in case of the hydrogen. So, in this case the balloon rises up. In case of air, the weight of balloon is more than the buoyant force acting on it, so balloon will come down.
![]()
Question 4.
It is easier to spray water in which some soap is dissolved. Explain why?
Answer:
When the liquid is sprayed, it is broken into small drops. The surface area increases and hence the surface energy is also increased. Therefore, work has to be done to supply the additional energy. Since surface energy is numerically equal to the surface tension, so when soap is dissolved in water, the surface tension of the solution decreases and hence less energy is spent to spray it.
Question 5.
Why are the wings of an aeroplane rounded outwards while flattened inwards?
Answer:
The special design of the wings increases velocity at the upper surface and decreases velocity at the lower surface. So, according to Bernoulli’s theorem, the pressure on the upper side is less than the pressure on the lower side. This difference of pressure provides lift.
Question 6.
The surface tension and vapour pressure of water at 20°C is 7.28 x 10-2 Nm-1 and 233x 103 Pa, respectively. What is the radius of the smallest spherical water droplet which can form without evaporating at 20°C?
Answer:
Given, surface tension of water (S) = 7.28 x 10-2 N/m
Vapour pressure (p) = 2.33 x 103 Pa
The drop will evaporate if the water pressure is greater than the vapour pressure.
Let a water droplet or radius R can be formed without évaporating.
Vapour pressure = Excess pressure in drop.
∴ p = \(\frac{2 S}{R}\) or R= \(\frac{2 S}{p}=\frac{2 \times 7.28 \times 10^{-2}}{2.33 \times 10^{3}}\)
= 6.25 x 10-5 m
Long Answer Type Questions
Question 1.
if a sphere of radius r falls under gravity through a liquid of viscosity q, its average acceleration is half that of in starting of the motion. Then, show that the time taken by it to attain the term mal velocity is independent of the liquid density.
Solution:
Let the density of sphere’s material is ρ and that of liquid is σ.
When the sphere just enters in the liquid.
Downward force on the sphere, F = weight of the sphere – weight of the fluid displaced by it.
F= \(\frac{4}{3} \pi r^{3}\) ρg – \(\frac{4}{3} \pi r^{3}\)σg
∵ Mass = Volume xDensity = \(\frac{4}{3} \pi r^{3}\) (ρ-σ)g
∴ Acceleration of the sphere at this instant.
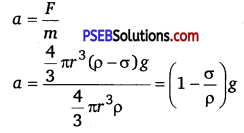
When the sphere approches to terminal velocity, its acceleration becomes zero.
∴ Average acceleration of the sphere = \(\frac{a+0}{2}\)
= \(\frac{\left(1-\frac{\sigma}{\rho}\right) g}{2}=\left(1-\frac{\sigma}{\rho}\right) \frac{g}{2}\)
If time t taken by the sphere to attain the terminal velocity As we know that,
Terminal velocity, ν = \(\frac{2}{3} \frac{r^{2}}{\eta}(\rho-\sigma) g\)
∵ The sphere falls from rest,
∴ u=O
Using ν=u+at
Putting values in above eqdation, we get

Thus, t is independent of the liquid density.
![]()
Question 2.
(a) Derive the expression for excess of pressure inside:
(i) a liquid drop.
(ii) a liquid bubble.
(iii) an air bubble.
(b) Derive the relation between the surface tension and the surface energy
Solution:
(a) (i) Let r = radius of a spherical liquid drop of centre O.
T = surface teñsion of the liquid.
Let pi and p0 be the values of pressure inside and outside the drop.
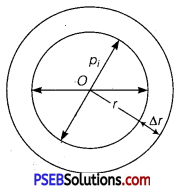
∴ Excess of pressure inside the liquid drop = pi -p0
Let Δr be the increase in its radius due to excess of pressure. It has one free surface outside it.
∴ increase in surface area of the liquid drop
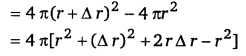
= 8πr Δr …………………………… (i)
(∵ Δr is small ∴ Δr2 is neglected.)
∴ increase in surface energy of the drop is
W = surface tension x increase in area
=T x8πr Δr …………………………………… (ii)
Also W = Force due to excess of pressure x displacement
W = Excess of pressure x area of drop x increase in radius
= (pi -p0 )4πr2 Δr ………………………………… (iii)
From eqs. (ii) and (iii), we get
(pi -p0 ) x 4 πr2 Δr = T x8πr A r Δr
or pi -p0 = \(\frac{2 T}{r}\)
(ii) In a liquid bubble : A liquid bubble has air both inside and outside it and therefore it has two free surfaces.
r,Δr, T = ? as above
Thus increase in its surface area
= 2 [ 4 π(r+Δr)2 – 4 πr²]
= 2 x 8 πrΔr
= 16πrΔr
∴ W = T x 16πrΔr, …………………… (iv)
Also W= (pi -p0 ) x 4πr² x Δr ………………………. (v)
∴ From (iv) and (v), we get
(pi -p0 ) x 4πr² x Δr = T. 16πrΔr
or pi -p0 = \(\frac{4 T}{r}\)
(iii) Inside an air bubble: Air bubble is formed inside liquid, thus air bubble has one free surface inside it and liquid is outside.
If r = radius of the air bubble.
Δr = increase in its radius due to excess of pressure (pi -p0 ) inside it.
T = surface tension of the liquid in which bubble is formed, increase in surface area = 8 πrΔr
∴ W = T x 8 πrΔr
Also W = (pi -p0)x 4 πr²Δr
∴ (pi -p0) x 4 πr²Δr = T x 8 πrΔr
or pi -p0 = \(\frac{2 T}{r}\)
(b) Let ABCD be a rectangular frame of wire. Let LM be a slidable cross-piece. Now dip the wireframe in the soap solution so that a film is formed over the frame. Due to surface tension, the film has a tendency to shrink and thereby, the cross-piece LM will be pulled in inward direction which can be kept in its position by applying an equal and opposite force F on it.
∴ F = T × 2l
where T = surface tension and l = length of LM.
It has been taken 21 as the film has two free surfaces.
Let x = small distance by which LM moves to L’M’.
∴ 2l × x = increase in the area of the film
if W = work done in increasing the area by 2l × x,
then W = F × x = (T × 2l) × x
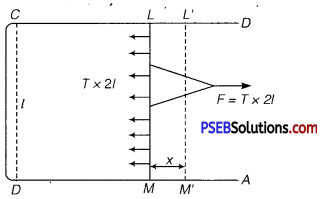
If U be the surface energy, then by definition
U = \(\frac{\text { Work done in increasing the surface area }}{\text { increase in surface area }} \)
= \(\frac{T \times 2 l \times x}{2 l \times x}\)
U = T
Thus, U is numerically equal to the surface energy.