Punjab State Board PSEB 11th Class Physics Important Questions Chapter 5 Laws of Motion Important Questions and Answers.
PSEB 11th Class Physics Important Questions Chapter 5 Laws of Motion
very short answer type questions
Question 1.
Bodies of larger mass need greater initial effort to put them in motion. Why?
Answer:
According to the Newton’s second law of motion, F = ma, for given acceleration a, if m is large, F should be more i. e., greater force will be required to put a larger mass in motion.
Question 2.
The distance travelled by a moving body is directly proportional to time. Is any external force acting on it?
Solution:
When S ∝ t, so acceleration = 0. Therefore, no external force is acting on the body.
Question 3.
A body is acted upon by a number of external forces. Can it remain at rest?
Answer:
Yes, if the external forces acting on the body can be represented in magnitude and direction by the sides of a closed polygon taken in the same order.
![]()
Question 4.
If force is acting on a moving body perpendicular to the direction of motion, then what will be its effect on the speed and direction of the body?
Answer:
No change in speed, but change in direction is possible. Forces acting on a body in circular motion is an example.
Question 5.
An impulse is applied to a moving object with a force at an angle of 20° w.r.t. velocity vector, what is the angle between the impulse vector and change in momentum vector?
Answer:
Impulse and change in momentum are along the same direction. Therefore, angle between these two vectors is zero degree.
Question 6.
A body is moving in a circular path such that its speed always remains constant. Should there be a force acting on the body?
Answer:
When a body is moving along a circular path, speed always remains constant and a centripetal force is acting on the body.
Question 7.
The mountain road is generally made winding upwards rather than going straight up. Why?
Solution:
When we go up a mountain, the opposing force of friction
F = μR = μ mg cosθ.
where θ is angle of slope with horizontal. To avoid skidding, F should be large.
∴ cosθ should be large and hence, θ must be small.
Therefore, mountain roads are generally made winding upwards. The road straight up would have large slope.
Short answer type questions
Question 1.
A body of mass 500 g tied to a string of length 1 m is revolved in the vertical circle with a constant speed. Find the minimum speed at which there will not be any slack on the string. Take g = 10ms-2
Solution:
The tension T in the string will provide the necessary centripetäl force
\(\frac{m v^{2}}{r}\) i.e., T = \(\frac{m v^{2}}{r}\)
Here, m = 500g = \(\frac{1}{2}\)kg; r = 1m
T = \(\frac{1}{2}\)υ2N ……………. (i)
There will not be slack 1f T ≥ weight of the body
i.e., T ≥ mg or \(\frac{1}{2}\)υ2 ≥\(\frac{1}{2}\) × 10
υ2 ≥ 10 or υ ≥ \(\sqrt{10}\) ms-1
So the minimum speed = \(\sqrt{10}\) ms-1 = 3.162 ms-1
![]()
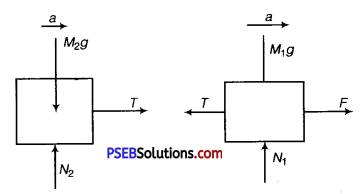
Question 2.
A light, inextensible string as shown in figure connects two blocks of mass M1 and M2. A force F as shown acts upon M1. Find acceleration of the system and tension in string.

Solution:
Here as the string is inextensible, acceleration of two blocks will be same. Also, string is massless so tension throughout the string will be same. Contact force will be normal force only. Let acceleration of each block is a, tension in string is T and contact force between M1 and surface is N1 and contact force between M2 and surface is N2
Applying Newton’s second law for the blocks;
For M1, F – T = M1 a ……………. (i)
M1 g – N1 = 0 …………….. (ii)
For M2, T = M2 ……………… (iii)
M2g – N = 0 ……………… (iv)
Solving equations (i) and (iii), we get
a = \(\frac{F}{M_{1}+M_{2}}\)
and T = \(\frac{M_{2} F}{M_{1}+M_{2}}\)
Question 3.
A block of mass m is held against a rough vertical wall by pressing it with a finger. If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g, calculate the minimum force required to be applied by finger to hold the block against the wall? (NCERT Exemplar)
Solution:
Given, mass of the block = m
Coefficient of friction between the block and the wall = μ
Let a force F be applied on the block to hold the block against the wall.
The normal reaction of mass be N and force of friction acting upward be f.
In equilibrium, vertical and horizontal forces should be balanced separately.
f = mg …………….. (i)
∴ and F = N …………… (ii)
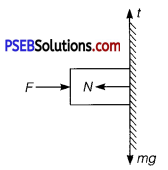
But force of friction (f) = μN
= μF [using eq. (ii) ] ………….. (iii)
From eqs. (i) and (iii), we get
μF = mg
or F = \(\frac{m g}{\mu}\)
![]()
Question 4.
A bird is sitting on the floor of a closed glass cage and the cage is in the hand of a girl. Will the girl experience any change in the weight of the cage when the bird (i) starts flying in the cage with a constant velocity, (ii) flies upwards with acceleration and (iii) flies downwards with acceleration?
Solution:
In a closed glass cage, air inside is bound with the cage. Therefore,
(i) there would be no change in weight of the cage if the bird flies with a constant velocity.
(ii) the cage becomes heavier, when bird flies upwards with an acceleration.
(iii) the cage appears lighter, when bird flies downwards with an acceleration.
Question 5.
When walking on ice, one should take short steps rather than long steps. Why?
Solution:
Let R represent the reaction offered by the ground. The vertical component R cosθ will balance the weight of the person and the horizontal component R sinθ will help the person to walk forward.
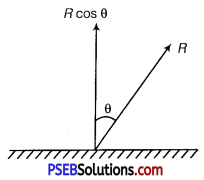
Now, normal reaction = R cosθ
Friction force = R sinθ
Coefficient of friction, μ = \(\frac{R \sin \theta}{R \cos \theta}\) = tanθ
In a long step, θ is more. So tanθ is more. But μ has a fixed value. So, there is danger of slipping in a long step.
Question 6.
A body of mass m is suspended by two strings making angles α and β with the horizontal as shown in fig. Calculate the tensions in the two strings.
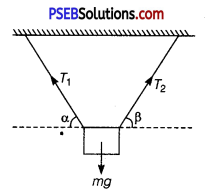
Solution:
Considering components of tensions T1 and T2 along the horizontal and vertical directions,
We have
-T1cosα + T2cosβ = 0
or T1cosα = T2cosβ …………… (i)
and T1 sinα + T2 sinβ = mg
From eq. (i) T2 = \(\frac{T_{1} \cos \alpha}{\cos \beta}\) and substituting it in eq. (ii), we get

![]()
Question 7.
State the law of conservation of momentum. Establish the same for a ‘n’ body system.
Solution:
When no external force acts on a system the momentum will remain conserved. Consider a system of a n bodies of masses m1 ,m2 ,m3 , ………… ,mn. If p1 , p2 , P3 , ………. ,Pn are the momentum associated then the rate of change of momentum with the system,
\(\frac{d p}{d t}=\frac{d p_{1}}{d t}+\frac{d p_{2}}{d t}+\frac{d p_{3}}{d t}\) + ………. + \(\frac{d p_{n}}{d t}=\frac{d}{d t}\) = (p+1 +p2 +p3+ ………. +pn )
If no external force acts, \(\frac{d p}{d t}\) = 0
∴ p = constant, i.e., P1 + p2 + P3 +………… +Pn = constant.
Question 8.
A block slides down from top of a smooth inclined plane of elevation θ fixed in an elevator going up with an acceleration a0. The base of incline has length L. Find the time taken by the block to reach the bottom.
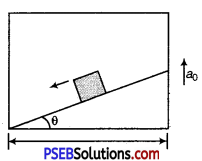
Solution:
The free body force diagram is shown. The forces are
(i) N normal to the plane (ii) mg acting vertically down (iii) ma0 (pseudo-force).
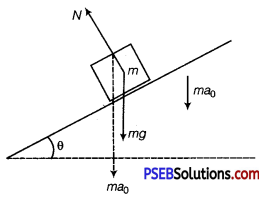
If a is the acceleration of the body with respect to incline, taking components of forces parallel to the incline mg sinθ + ma0 sinθ = ma
a = (g + a0)sinθ
This is the acceleration with respect to elevator.
The distance travelled is \(\frac{L}{\cos \theta}\) If t is the time for reaching the bottom of
incline, using equation of motion, s = ut + \(\frac{1}{2}\)at2, we get
\(\frac{L}{\cos \theta}\) = 0 + \(\frac{1}{2}\)(g + a0)sinθ.t2
t = [latex]\frac{2 L}{\left(g+a_{0}\right) \sin \theta \cos \theta}[/latex]1/2
Long answer type questions
Question 1.
Figure shows (x – t), (y – t) diagram of a particle moving in 2-dimensions.
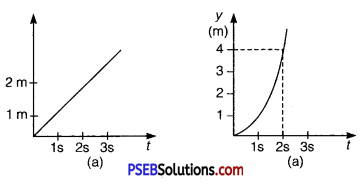
If the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle. (NCERT Exemplar)
Given, mass of the particle (m) = 500 g = 0.5 kg
x – t graph of the particle is a straight line.
Hence, particle is moving with a uniform velocity along x-axis, i. e., its acceleration along x-axis is zero and hence, force acting along x-axis is zero.
y – t graph of particle is a parabola. Therefore, particle is in accelerated motion along y – axis.
At t = 0, uy = 0
Along y – axis, at t = 2s, y = 4m
Using equation of motion, y = uyt + \(\frac{1}{2}\) ayt2
4 = 0 × 2 + \(\frac{1}{2}\) × ay × (2)2
or ay = 2 m/s2
∴ Force acting along y – axis (fy) = may = 0.5 × 2 = 1.0 N (along y – axis)
![]()
Question 2.
When a body slides down from rest along a smooth inclined plane making an angle of 45° with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the coefficient of friction between the body and the rough plane. (NCERT Exemplar)
Solution:
On smooth inclined plane Acceleration of a body sliding down a smooth inclined plane, a = g sinθ
Here, θ = 45°
a = gsin45°= \(\frac{g}{\sqrt{2}}\)
Let the travelled distance be s.
Using the equation of motion, s = ut + \(\frac{1}{2}\) at2 ,
We get
s = 0 .t + \(\frac{1}{2} \frac{g}{\sqrt{2}}\)T2
or s = \(\frac{g T^{2}}{2 \sqrt{2}}\) ………… (i)
On rough inclined plane
Acceleration of the body,
a = g (sinθ – μ cosθ)
= g (sin 45° – μ cos 45°)
= \(\frac{g(1-\mu)}{\sqrt{2}}\) [as sin 45°= cos 45° = \(\frac{1}{\sqrt{2}}\)]
Again using equation of motion,
