Punjab State Board PSEB 11th Class Physics Important Questions Chapter 4 Motion in a Plane Important Questions and Answers.
PSEB 11th Class Physics Important Questions Chapter 4 Motion in a Plane
Very short answer type questions
Question 1.
When do we say two vectors are orthogonal?
Solution:
If the dot product of two vectors is zero, then the vectors are orthogonal.
Question 2.
What is the property of two vectors \(\overrightarrow{\boldsymbol{A}}\) and \(\overrightarrow{\boldsymbol{B}}\) such that \(\overrightarrow{\boldsymbol{B}}+\overrightarrow{\boldsymbol{A}}=\overrightarrow{\boldsymbol{C}}\) and \(\overrightarrow{\boldsymbol{A}}+\overrightarrow{\boldsymbol{B}}=\overrightarrow{\boldsymbol{C}}\)?
Solution:
The two vectors are parallel and acting in the same direction i. e., θ = 0 °.
![]()
Question 3.
What are the minimum number of forces which are numerically equal whose vector sum can be zero?
Answer:
Two only, provided that they are acting in opposite directions.
Question 4.
Under what condition the three vectors cannot give zero resultant?
Answer:
When the three vectors are not lying in one plane, they cannot produce zero resultant.
Question 5.
Can the scalar product of two vectors be negative?
Solution:
Yes, it will be negative if the angle between the two vectors lies between 90° to 270°.
Question 6.
Can the walking on a road be an example of resolution of vectors?
Answer:
Yes, when a man walks on the road, he presses the road along an oblique direction. The horizontal component of the reaction helps the man to walk on the road.
Question 7.
A particle cannot accelerate if its velocity is constant, why?
Answer:
When the particle is moving with a constant velocity, there is no change – in velocity with time and hence, its acceleration is zero.
![]()
Question 8.
A football is kicked into the air vertically upwards. What is its (i) acceleration and (ii) velocity at the highest point?
(NCERT Exemplar)
Answer:

(i) Acceleration at the highest point = -g
(ii) Velocity at the highest point = 0.
Question 9.
Why does a tennis ball bounce higher on bills than in plains?
Answer:
Maximum height attained by a projectile ∝ 1/ g. As the value of g is less on hills than on plains, so a tennis ball bounces higher on hills than on plains.
Short answer type quetions
Question 1.
Explain the property of two vectors \(\overrightarrow{\boldsymbol{A}}\) and \(\overrightarrow{\boldsymbol{B}}\) if \(|\overrightarrow{\boldsymbol{A}}+\overrightarrow{\boldsymbol{B}}|=|\overrightarrow{\boldsymbol{A}}-\overrightarrow{\boldsymbol{B}}|\).
Solution:
As we know that
\(|\vec{A}+\vec{B}|=\sqrt{A^{2}+B^{2}+2 A B \cos \theta}\)
and \(|\vec{A}-\vec{B}|=\sqrt{A^{2}+B^{2}-2 A B \cos \theta}\)
But as per question, we have
\(\sqrt{A^{2}+B^{2}+2 A B \cos \theta}=\sqrt{A^{2}+B^{2}-2 A B \cos \theta}\)
Squaring both sides, we have (4 AB cos θ) = 0
⇒ cosθ = 0 or θ = 90°
Hence, the two vectors \(\vec{A}\) and \(\vec{B}\) are perpendicular to each other.
Question 2.
The sum and difference of two vectors are perpendicular to each other. Prove that the vectors are equal in magnitude.
Solution:
As the vectors \(\vec{A}+\vec{B}\) and \(\vec{A}-\vec{B}\) are perpendicular to each other, therefore
\((\vec{A}+\vec{B}) \cdot(\vec{A}-\vec{B})\) = 0
\(\vec{A} \cdot \vec{A}-\vec{A} \cdot \vec{B}+\vec{B} \cdot \vec{A}-\vec{B} \cdot \vec{B}\) = 0
or A2 – B2 = 0 [∵ \(\vec{A} \cdot \vec{B}=\vec{B} \cdot \vec{A}\)]
⇒ A = B
![]()
Question 3.
The dot product of two vectors vanishes when vectors are orthogonal and has maximum value when vectors are parallel to each other. Explain.
Solution:
We know that \(\vec{A} \cdot \vec{B}\) = AB cos θ, when vectors are orthogonal, then, θ = 90°.
So, \(\vec{A} \cdot \vec{B}\) = AB cos 90 ° = 0, when vectors are parallel, then, θ = 0°
So, \(\vec{A} \cdot \vec{B}\) = AB cos ° = AB (maximum)
Question 4.
Can a flight of a bird, an example of composition of vectors. Why?
Answer:

Yes, the flight of a bird is an example of composition of vectors as the bird flies, it strikes the air with its wings W, W along WO. According to Newton’s third law of motion, air strikes the wings in opposite directions with the same force in reaction. The reactions are \(\overrightarrow{O A}\) and \(\overrightarrow{O B}\). From law of parallelogram vectors, \(\overrightarrow{O C}\) is the resultant of \(\overrightarrow{O A}\) and \(\overrightarrow{O B}\). This resultant upwards force \(\overrightarrow{O C}\) is responsible for the flight of the bird.
Question 5.
How does the knowledge of projectile help, a player in the baseball game?
Answer:
In the baseball game, a player has to throw a ball so that it goes a certain distance in the minimum time. The time would depend on velocity of ball and angle of throw with the horizontal. Thus, while playing a baseball game, die speed and angle of projection have to be adjusted suitable so that the ball covers the desired distance in minimum time. So, a player has to see the distance and air resistance while playing with a baseball game.
Question 6.
A skilled gun man always keeps his gun slightly tilted above the line of sight while shooting. Why?
Answer:
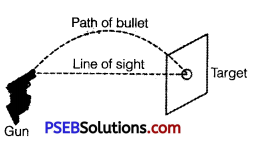
When a bullet is fired from a gun with its barrel directed towards the target, it starts falling downwards on account of acceleration due to gravity.
Due to which the bullet hits below the target. Just to avoid it, the barrel of the gun is lined up little above the target, so that the bullet after traveling in parabolic path hits the distant target.
![]()
Question 7.
Establish a relation between angular velocity and time period.
Answer:
We know that angular velocity A0
ω = \(\frac{\Delta \theta}{\Delta t}\)
For motion with uniform angular velocity, in one complete revolution A0 = 2JI radian and At = T s, hence
ω = \(\frac{2 \pi}{T}\) or T = \(\frac{2 \pi}{\omega}\).
Question 8.
A fighter plane is flying horizontally at an altitude of 1.5 km with speed 720 km/h. At what angle of sight (w.r.t. horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target? (NCERT Exemplar)
Answer:
Consider the adjacent diagram. Let a fighter plane, when it be at position P, drops a bomb to hit a target T.
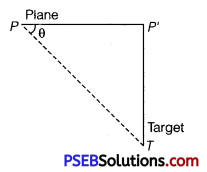
Let < P’PT= θ
Speed of the plane = 720 km/h
= 720 × \(\frac{5}{18}\) m/s = 200m/s
Altitude of the plane (PT) = 1.5km = 1500 m
If bomb hits the target after time t, then horizontal distance travelled by the bomb.
PP’ = u × t = 200t
Vertical distance travelled by the bomb,
P’T = \(\frac{1}{2}\)gt2 ⇒ 1500 = \(\frac{1}{2}\) × 9.8t2
⇒ t2 = \(\frac{1500}{49}\) ⇒ t = \($\sqrt{\frac{1500}{49}}$\) = 17.49s
Using value oft in Eq. (i),
PP’ = 200 × 17.49 m
Now,
tanθ = \($\frac{P^{\prime} T}{P^{\prime} P}=\frac{1500}{200 \times 17.49}$\) 0.49287 = tan23°12′
θ = 23°12′
Note Angle is with respect to target. As seen by observer in the plane motion of the bomb will be vertically downward below tbe plane.
Long answer type questions
Question 1.
An airline passenger late for a flight walks on an airport moving sidewalk at a speed of 5.00 km/h relative to the sidewalk, in the direction of its motion. The sidewalk is moving at 3.00 km/h relative to the ground and has a total length of 135 m.
(i) What is the passenger’s speed relative to the ground?
(ii) How long does it take him to reach the end of the sidewalk?
(iii) How much of the sidewalk has he covered by the time he reaches Hie end?
Solution:
The situation is sketched in figure. We assign a letter to each body in relative motion, P passenger, S sidewalk, G ground. The relative velocities υ ps and υ SG are given
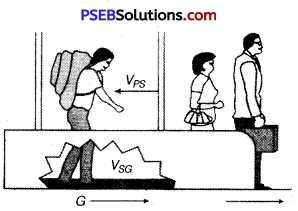
υPS = 5.00 km/h, to the right
υSG = 3.00 km/h, to the right
(i) Here, we must find the magnitude of the vector υPG, given the magnitude and direction of two other vectors. We find the velocity υPG by using the relation
υPG = υPS + υSG
Here, the vectors are parallel, and so the vector addition is quite simple (see figure). We add vectors by adding magnitudes.
υPG = υPS +υSG
= 5.00 km/h + 3.00 km/h
= 8.00 km/h
= 8 × \(\frac{5}{18}\) m/s = \(\frac{40}{18}\) = 2.22 m/s
(ii) The length of the sidewalk is 135 m, and so this is the distance Δ xG the passenger travels relative to the ground. So, our problem is to find Δt when ΔxG =135 m. The rate at which this distance along the ground is covered by the passenger is υPG, where
υPG = \(\frac{\Delta x_{G}}{\Delta t}\)
Therefore, Δ t = \(\frac{\Delta x_{G}}{v_{P G}}\) = \(\frac{135 \mathrm{~m}}{2.22 \mathrm{~m} / \mathrm{s}}\) = 60.8 s
(iii) The problem here is to determine how much of the sidewalk’s surface the passenger moves over. If he was standing still and not walking along the surface, he would cover none of it. Because he is moving relative to the surface at velocity υPS, he does move some distance Δ xs relative to the surface. The problem is to find Δ XS when Δt = 60.8 s, since we found in part (ii) that this is the time interval during which he is on the moving sidewalk. His velocity relative to the sidewalk is υPS = ΔxS / Δt, and so
ΔXS = υPS = Δt = (5.00 km/h) × (60.8s)
= \(\frac{25}{18}\) × 60.8 (∵ 1 km/h = \(\frac{5}{18}\) m/s)
= 84.4 m
![]()
Question 2.
A hunter aims his gun and fires a bullet directlyiafoi monkey in a tree. At the instant, the bullet leaves the barrebdi,;the gun, the monkey drops. Will the bullet hit the monkey? Substantiate your answer with proper reasoning.
Solution:
Let the monkey stationed at A, be fired with a gun fromO with a velocityu at an angle 0 with the horizontal direction OX.
Draw AC, perpendicular to OX. Let the bullet cross the vertical line AC at B after time t and coordinates of B (x, y) be w.r.t. origin O as shown in figure.
∴ t = \(\frac{O C}{u \cos \theta}=\frac{x}{u \cos \theta}\) ………….. (i)
In ∆ OAC, AC = OC tanO = x tanθ ……………. (ii)
Clearly, CB = y = the vertical distance travelled by the bullet in time t. Taking motion of the bullet from O to B along Y-axis, we have y0 = 0, y = y,Uy = usin0, ay = -g,t = t
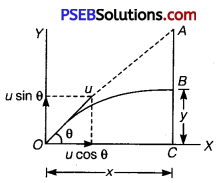

It means the bullet will pass through the point B on vertical line AC at a vertical distance \(\frac {1}{2}\)gt2 below point A.
The distance through which the monkey falls vertically in time t = \(\frac {1}{2}\)gt2
= AB. It means the bullet and monkey will pass through the point B simultaneously.
Therefore, the bullet will hit the monkey.