PSEB 10th Class Maths Solutions Chapter 2 Polynomials Ex 2.3

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 2 Polynomials Ex 2.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 2 Polynomials Ex 2.3

Question 1.
Apply the division algorithm to find the quotient and remainder on dividing p (x) by g (x) as given below:
(i) p (x) = x³ – 3x² + 5x – 3, g (x) = x² – 2 (Pb. 2018 Set I, II, III)
(ii) p (x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
(iii) p (x) = x⁴ – 5x + 6, g (x) = 2 – x² [Pb. 2017 Set-B]
Solution:
(i) Given that p (x) = x³ – 3x² + 5x – 3 and g (x) = x² – 2,

By division algorithm,
x³ – 3x² + 5x – 3 = (x – 3) (x² – 2) + (7x – 9)
Hence, quotient = x – 3 and remainder = 7x – 9

(ii) Given that p (x) = x⁴ – 3x² + 4x + 5
or p (x) = x⁴ + 0x³ – 3x² + 4x + 5
and g (x) = x² + 1 – x
or g (x) = x² – x + 1

By Division Algorithm,
x⁴ – 3x² + 4x + 5 = (x² + x – 3) (x² – x + 1) + 8
Hence, Quotient = x² + x – 3 and remainder = 8

(iii) Given that p (x) = x⁴ – 5x + 6
or p (x) = x⁴ + 0x³ + 0x² – 5x + 6
and g (x) = 2 – x²
or g (x) = – x² + 2

By division algorithtm,
x⁴ – 5x + 6 = (- x² – 2) (- x² + 2) + (- 5x + 10)
Hence, quotient = -x² – 2.
remainder = – 5x + 10

Question 2.
Check whether the first polynomial is a factor of the second polynomial by applying the division algorithm:
(i) t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12
(ii) x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2
(iii) x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1
Solution:

∵ remainder is zero
∵ By division algorithm,
t² – 3 is factor of 2t⁴ + 3t³ – 2t² – 9t – 12

(ii)

∵ remainder is zero
∴ By division algorithm, x² + 3x + 1 is a factor of 3x⁴ + 5x³ – 7x² + 2x + 2

(iii)

∵ remainder is not zero.
∴ By division algorithm, x³ – 3x + 1 is not a factor of x⁵ – 4x³ + x² + 3x + 1.

Question 3.
Obtain all other zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are \(\sqrt{\frac{5}{3}}\) and – \(\sqrt{\frac{5}{3}}\).
Solution:
Given that two zeroes are \(\sqrt{\frac{5}{3}}\) and –\(\sqrt{\frac{5}{3}}\)
∴ (x – \(\sqrt{\frac{5}{3}}\)) [x – (-\(\sqrt{\frac{5}{3}}\))] are factors of given polynomial or
(x – \(\sqrt{\frac{5}{3}}\)) (x + \(\sqrt{\frac{5}{3}}\)) are factors of given polynomial.
or x² – \(\frac{5}{3}\) is a factor of given polynomial.
Now, apply division algorithm to given polynomial and x² – \(\frac{5}{3}\)

∴ 3x⁴ + 6x³ – 2x² – 10x – 5
= (x² – \(\frac{5}{3}\)) (3x² + 6x + 3)
= (x² – \(\frac{5}{3}\)) (3) [x² + 2x + 1]
= 3 (x² – \(\frac{5}{3}\)) [x² + 2x + 1]
[S = 2, P = 1]
= 3 (x² – \(\frac{5}{3}\)) [x(x + 1) + 1 (x + 1)]
= 3 (x² – \(\frac{5}{3}\)) (x + 1) (x + 1)
Now, other zeroes of polynomials are given by
x + 1 = 0 ; x = -1 or
x + 1 = 0 ; x = -1
The zeroes of the given fourth degree polynomial are :
\(\sqrt{\frac{5}{3}}\), –\(\sqrt{\frac{5}{3}}\), -1, -1.

Question 4.
On dividing x³ – 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and – 2x + 4 respectively find g(x).
Solution.
Compare given data with division algorithm, we have
p(x)= g (x). q(x) + r (x) or
p(x) – r(x) = g(x).q(x)
or g(x) . q (x) = p(x) – r(x)
or g(x) = \(\frac{p(x)-r(x)}{q(x)}\)
By putting various values, we get:
g(x) = \(\frac{\left(x^{3}-3 x^{2}+x+2\right)-(-2 x+4)}{x-2}\)

g(x) = \(\frac{x^{3}-3 x^{2}+x+2+2 x-4}{x-2}\)

g(x) = \(\frac{x^{3}-3 x^{2}+3 x-2}{x-2}\) …………….(1)

Now,

∴ \(\frac{x^{3}-3 x^{2}+3 x-2}{x-2}\) = x² – x + 1
From (1) and (2), we get:
g(x) = x² – x + 1

Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the dhriskm algorithm and
(i) deg p (x) = deg q (x)
(ii) deg r (x) = 0
(iii) deg q (x) = deg r (x)
Solution:
(i) Let p(x) = 5x² – 5x +10; g(x) = 5 q(x) = x² – x + 2; r(x) = 0

∴ By division algorithm,
5x² – 5x + 10 = 5(x² – x + 2) + 0
or p(x) = g(x) q(x) + r(x)
Also, deg p(x) = deg q(x) = 2

(ii) Let p(x) = 7x³ – 42x + 53
g(x) = x³ – 6x + 7
q(x) = 7; r(x) = 4

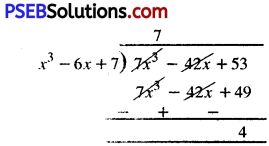
∴ By division algorithm,
7x³ -42x + 53 = 7(x³ – 6x+ 7)+ 4
or p(x) = q(x) g(x) + r(x)
Also, deg q(x) = 0 = deg r(x)

(iii) Let p(x) = 4x³ + x² + 3x + 6;
g(x) = x² + 3x + 1;
q(x) = 4x – 11;
r(x) = 32x + 17

∴ By division algorithm,
4x³ + x² + 3x + 6 = (4x – 11) (x² + 3x + 1) + (32x + 17)
or p(x) = q(x) . g(x) + r(x)
Also, deg q(x) = deg r(x)