Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
Question 1.
Form the pair of linear equations in the following problems, and find their solutions graphically.
(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
(ii) 5 pencils and 7 pens together cost ₹ 50, whereas 7 pencils and 5 pens together cost ₹ 46. Find the cost of one
pencil and that of one pen.
Solution:
(i) Let the number of boys in the Quiz = X
and the number of girls in the Quiz = y
Total number of students took part in Quiz = 10
x + y = 10
or x + y – 10 = 0
According to Question,
y = x + 4
or x = y – 4
Now, draw the graph of linear equations
x + y = 10
and x – y + 4 = 0
x + y = 10
or x = 10 – y
Putting y = 0 in (1), we get :
x = 10 – 0 = 10
Putting y = 7 in(1), we get:
x = 10 – 7 = 3
Putting y = 10 in (1) we get:
X = 10 – 10 = 0

Plotting the points A (10, 0), B (3, 7), C (0, 10) and drawing a line joining them we get the graph of the equation x + y = 10
![]()
Now x – y + 4 = 0
or x = y – 4
Putting y = 0 in (2), we get:
x = 0 – 4 = -4
Putting y = 7 in (2), we get:
x = 7 – 4 = 3
Putting y = 4 in (2), we get:
x = 4 – 4 = 0

Plotting the points D (-4, 0), B (3, 7), E (0, 4) and drawing a line joining them, we get the graph of the equation x – y + 4 = 0
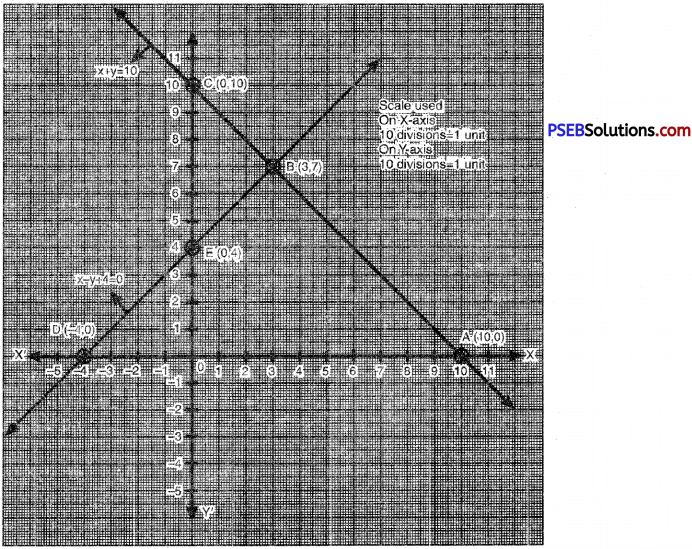
From the graph it is clear that both the linear equations meets at a point B (3, 7).
∴ Point B (3, 7) is the graphic solution.
Hence, number of boys in the Quiz = 3
Number of girls in the Quiz = 7
![]()
(ii) Let cost of one pencil = ₹ x
and cost of one pen = ₹ y
According to 1st condition,
5x + 7y = 50
According to 2nd condition,
7x + 5y = 46
∴ Pairs of linear equations is
5x + 7y = 50
7x + 5y = 46
Now, draw the graph of these linear equations.
5x + 7y = 50
or 5x = 50 – 7y
x = \(\frac{50-7 y}{5}\) ………………..(1)
Putting y = 0 in (1), we get :
x = \(\frac{50-7 \times 0}{5}=\frac{50}{5}\)
Putting y = 5 in (1), we get:
x = \(\frac{50-7 \times 5}{5}=\frac{50-35}{5}\)
= \(\frac{15}{5}\) = 3
Putting y = 7 in (1), we get :
x = \(\frac{50-7 \times 7}{5}=\frac{50-49}{5}\)
= \(\frac{1}{5}\) = 0.2
Table:
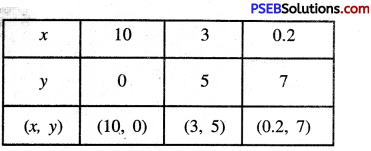
Plotting the points A (10, 0), B (3, 5), C (0.2, 7) and drawing a line joining them, we get the graph of the equation
5x + 7y = 50
Now 7x + 5y = 46
0r 7x = 46 – 5y
or x = \(\frac{46-5 y}{7}\) …………….(2)
Putting y = 0 in (2), we get:
x = \(\frac{46-5 \times 0}{7}=\frac{46}{7}\) = 6.5
Putting y = 5 in (2), we get:
x = \(\frac{46-5 \times 5}{7}=\frac{46-25}{7}\)
= \(\frac{21}{7}\) = 3
Putting y = – 4 in (2), we get:
x = \(\frac{46-5 \times(-4)}{7}=\frac{46+20}{7}\)
= \(\frac{66}{7}\) = 9.5
Table:
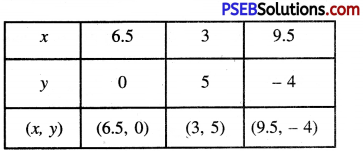
Plotting the points E (6.5, 0), B (3, 5), F (9.5. -4) and drawing a line joining them, we get the graph of the equation.
7x + 5y = 46
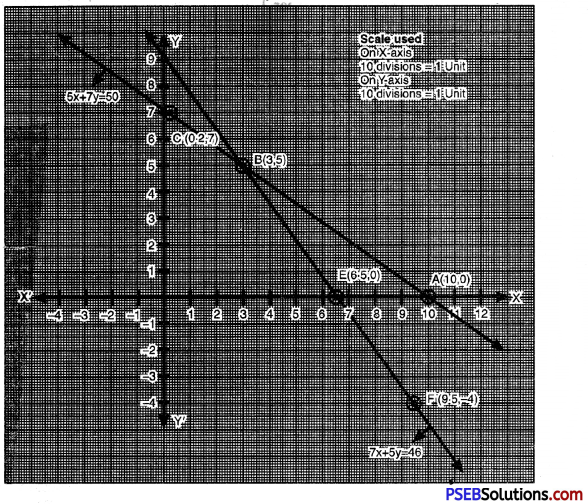
From the graph, it is clear that both the linear equations meets at a point B (3, 5).
∴ point B (3, 5) is the graphic solution.
Hence, cost of one pencil = ₹ 3
Cost of one pen = ₹ 5
![]()
Question 2.
On comparing the ratios \(\frac{a_{1}}{a_{2}}\), \(\frac{b_{1}}{b_{2}}\) and \(\frac{c_{1}}{c_{2}}\) and find out whether the lines representing the following pairs of linear
equations intersect at point, are parallel or coincident :
(i) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
(iii) 6x – 3y + 10 = 0
2x – y + 9 = 0
Solution:
(i) Given pairs of linear equation
5x – 4y + 8 = 0
and 7x + 6y – 9 = 0
Here a1 = 5, b1 = – 4, c1 = 8
a2 = 7, b2 = 6, c2 = -9
Now,
\(\frac{a_{1}}{a_{2}}\) = \(\frac{5}{7}\);
\(\frac{b_{1}}{b_{2}}\) = \(-\frac{4}{6}\);
\(\frac{c_{1}}{c_{2}}\) = \(\frac{8}{-9}\)
∵ \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
Hence, given pairs of linear equation intersect at a point.
(ii) Given pairs of linear equation is
9x + 3y + 12 = 0
and 18x + 6y + 24 = 0
Here, a1 = 9, b1 = 3, c1 = 12
a2 = 18, b2 = 6, c2 = 24
Now \(\frac{a_{1}}{a_{2}}=\frac{9}{18}=\frac{1}{2}\);
\(\frac{b_{1}}{b_{2}}=\frac{3}{6}=\frac{1}{2}\);
\(\frac{c_{1}}{c_{2}}=\frac{12}{24}=\frac{1}{2}\)
Hence, given pairs of linear equation intersect at a point.
![]()
(iii) Given pairs of linear equation is
6x – 3y + 10 = 0
and 2x – y + 9 = 0
Here a1 = 6, b1 = – 3, c1 = 10
a2 = 2, b2 = -1, c2 = 9
Now,
\(\frac{a_{1}}{a_{2}}\) = \(\frac{6}{2}\) = 3;
\(\frac{b_{1}}{b_{2}}\) = \(\frac{-3}{-1}\) = 3;
\(\frac{c_{1}}{c_{2}}\) = \(\frac{10}{9}\)
∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
Hence, given pairs of linear equations are parallel to each other.
![]()
Question 3.
On comparing the ratios \(\frac{a_{1}}{a_{2}}\), \(\frac{b_{1}}{b_{2}}\) and \(\frac{c_{1}}{c_{2}}\). find out whether the following pair of linear equations are consistent, or inconsistent.
(i) 3x + 2y = 5; 2x – 3y = 7
(ii) 2x – 3y =8; 4x – 6y = 9
(iii) \(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7; 9x – 10y = 14
(iv) 5x – 3y = 11; -10x + 6y = -22
(v) \(\frac{4}{3}\)x + 2y = 8; 2x +3y = 12
Solution:
(i) Given pair of linear equation is
3x + 2y = 5
and 2x – 3y = 7
or 3x + 2y – 5 = 0
and 2x – 3y – 7 = 0
Here a1 = 3, b1 = 2, c1 = -5
a2 = 2, b2 = -3, c2 = -7
Now
\(\frac{a_{1}}{a_{2}}\) = \(\frac{3}{2}\);
\(\frac{b_{1}}{b_{2}}\) = \(\frac{2}{-3}\);
\(\frac{c_{1}}{c_{2}}\) = \(\frac{-5}{-7}\) = \(\frac{5}{7}\)
∴ \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
Hence, given pairs of linear equations are consistent.
(ii) Given pair of linear equation is:
2x – 3y = 8
and 4x – 6y = 9
Or 2x – 3y – 8 = 0
4x – 6y – 9 = 0
Here a1 = 2, a1 = -3, c1 = -8
a2 = 4, b2 = -6, c 2 = -9
Now
\(\frac{a_{1}}{a_{2}}\) = \(\frac{2}{4}\) = \(\frac{1}{2}\);
\(\frac{b_{1}}{b_{2}}\) = \(\frac{-3}{-6}\) = \(\frac{1}{2}\);
\(\frac{c_{1}}{c_{2}}\) = \(\frac{-8}{-9}\) = \(\frac{8}{9}\)
∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
Hence, given pairs of linear equations are inconsistent.
![]()
(iii) Given pair of linear equation is:
\(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7;
and 9x – 10y = 14
Or \(\frac{3}{2}\)x + \(\frac{5}{3}\)y – 7 = 0
and 9x – 10y – 14 = 0
Here a1 = \(\frac{3}{2}\), b1 = \(\frac{5}{3}\), c1 = -7
a2 = 9, b2 = -10, c2 = -14

Hence, given pairs of linear equations are consistent.
![]()
(iv) Given pair of linear equations is
5x – 3y= 11
and -10x + 6y = -22
Or 5x – 3y – 11 = 0
and -10x + 6y + 22 = 0
Here a1 = 5, b1 = -3, c1 = -11
a2 = -10, b2 = 6, c2 = 22
Hence given pair of linear equations is consistent.
(v) Given pair of linear equations is
\(\frac{4}{3}\)x + 2y = 8 and 2x + 3y = 12
or \(\frac{4}{3}\)x + 2y – 8 = 0
and 2x + 3y – 12 = 0
Here a1 = \(\frac{4}{3}\), b1 = 2, c1 = -8
a2 = 2, b2 = 2, c2 = -12
Now,
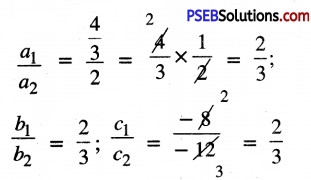
∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
Hence, given pairs of linear equations are consistent.
![]()
Question 4.
Which of the following pairs of linear equations are consistent / inconsistent? If consistent, obtain the solution graphically.
(i) x + y = 5, 2x + 2y = 10
(ii) x – y = 8, 3x – 3y = 16
(iii) 2x + y – 6 = 0,4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0,4x – 4y – 5= 0
Solution:
(1) Given pair of linear equations is
x + y = 5
and 2x + 2y = 10
Or x + y – 5 = 0
2x + 2y – 10 = 0
Here a1 = 1, b1 = 1, c1 = -5
a2 = 2, b2 = 2, c2 = -10
Now
\(\frac{a_{1}}{a_{2}}\) = \(\frac{1}{2}\);
\(\frac{b_{1}}{b_{2}}\) = \(\frac{1}{2}\);
\(\frac{c_{1}}{c_{2}}\) = \(\frac{-5}{-10}\) = \(\frac{1}{2}\)
∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
Hence, given pairs of linear equations are consistent.
Draw the graph of these equations
![]()
x + y = 5
x = 5 – y ………….(1)
Putting y = 0 in (1), we get:
x = 5 – 0 = 5
Putting y = 3 in (1), we get
x = 5 – 3 = 2
Putting y = 5 in (1), we get
x = 5 – 5 = 0
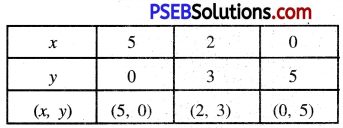
Plotting the points A (5, 0), B (2, 3), C (0, 5) and drawing a line joining them, we ge the graph of the equation x + y = 5
2x + 2y = 10 Or 2 (x + y) = 10
Or x + y = 5
Or x = 5 – y
Putting y = 0 in (1), we get :
x = 5 – 0 = 5
Putting y = 2 in (2), we get :
x = 5 – 2 = 3
Putting y = 5 in (2), we get:
x = 5 – 5 = 0
Putting y = 2 in (2), we get :
x = 5 – 2 = 3
Putting y = 5 in (2), we get:
x = 5 – 5 = 0
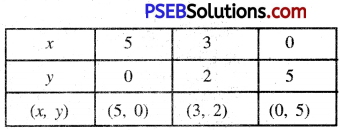
Plotting the points A (5, 0), D (3, 2), C (0, 5) and drawing a line joining them, we get the graph of the equation 2x + 2y = 10

The graphs of two equations are coincident. Hence system of equations has infinitely many solutions i.e. consistent.
![]()
(ii) Given pair of linear equations is :
x – y = 8
and 3x – 3y = 16
Or
x – y – 8 = 0
and 3x – 3y – 16 = 0
Here a1 = 1, b1 = -1, c1 = -8
a2 = 3, b2 = -3, c2 = -16
Now,
\(\frac{a_{1}}{a_{2}}\) = \(\frac{1}{3}\);
\(\frac{b_{1}}{b_{2}}\) = \(\frac{-1}{-3}\); = \(\frac{1}{3}\)
\(\frac{c_{1}}{c_{2}}\) = \(\frac{-8}{-16}\) = \(\frac{1}{2}\)
∵ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
Hence, given pairs of linear equations are inconsistent solution.
(iii) Given pailt of linear equations is :
2x + y – 6 = 0
and 4x – 2y – 4 = 0
Here a1 = 2, b1 = 1, c1 = -6
a2 = 4, b2 = -2, c2 = -4
Now
\(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\);
\(\frac{b_{1}}{b_{2}}=\frac{1}{-2}\);
\(\frac{c_{1}}{c_{2}}=\frac{-6}{-4}=\frac{3}{2}\)
∴ given pair of system is consistent.
Draw the graph of these linear equations
2x + y – 6 = 0
Or 2x = 6 – y
Or x = \(\frac{6-y}{2}\) ………….(1)
Putting y = 0 in (1), we get:
x = \(\frac{6-0}{2}=\frac{6}{2}\) = 3
putting y = 2 in (1), we get:
x = \(\frac{6-2}{2}=\frac{4}{2}\) = 2
Putting y = -2 in (1), we get:
x = \(\frac{6-(-2)}{2}=\frac{6+2}{2}=\frac{8}{2}\) = 4
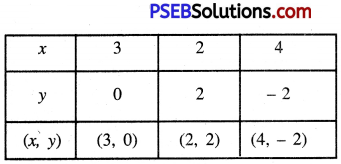
Plotting the points A (3, 0), B (2, 2), C (4, -2) and drawing a line joining them, we get the graph of the equation.
2x + y – 6 = 0
Now 4x – 2y – 4= 0
or 2[2x – y – 2] = 0
or 2x – y – 2 = 0
or 2x = y + 2
or x = \(\frac{y+2}{2}\) …………..(2)
Putting y = 0 in (2), we get:
x = \(\frac{0+2}{2}=\frac{2}{2}\) = 1
Putting y = 2 in (2), we get :
\(\frac{2+2}{2}=\frac{4}{2}\) = 2
Putting y = – 2 in (2), we get:
x = \(\frac{-2+2}{2}=\frac{0}{2}\) = 0
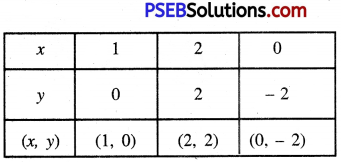
Plotting the points D (1, 0), B (2, 2), E (0, -2) and drawing a line joining them, we get the graph of the equation
4x – 2y – 4 = 0
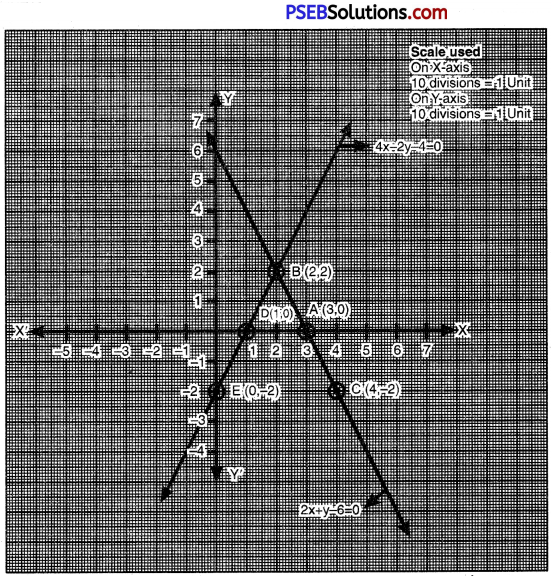
From the graph, it is clear that given system of equations meets at a point B (2, 2).
Hence, given pair of linear equations have unique solution.
![]()
(iv) Given pair of linear equations is :
2x – 2y – 2 = 0
and 4x – 4y – 5 = 0
Here a1 = 2, b1 = -2, c1 = -2
a2 = 4, b2 = -4, c2 = -5
Now,
\(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\);
\(\frac{b_{1}}{b_{2}}=\frac{-2}{-4}=\frac{1}{2}\);
\(\frac{c_{1}}{c_{2}}=\frac{-2}{-5}=\frac{2}{5}\)∵ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
Hence, given pair of system have inconsistent solution.
Question 5.
Half the perimeter of a rectangular garden, whose length is 4 m more than its width is 36 m Find the dimensions of the garden.
Solution:
Let length of garden = x m
Width of garden =y m
Perimeter of garden = 2 [x + y] m
Half perimeter of garden = (x + y) m
According to 1st condition x = y +4
According to 2nd condition
x + y = 36
∴ Pair of linear equations is
x = y + 4
and x + y = 36
x = y + 4 ………………(1)
Putting y = 0 in (1), we get :
x = 0 + 4 = 4
Putting y = – 4 in (1), we get:
x = -4 + 4 = 0
Putting y = 16 in (1), we get :
x = 16 + 4 = 20

Plotting the points A (4, 0) B (0, -4), C (20, 16) and drawing a line joining them.
we get the graph of the equation.
x = y + 4
Now x + y = 36
x = 36 – y
Putting y = 12 in (2), we get:
x = 36 – 12 = 24
Putting y = 24 in (2), we get :
x = 36 – 24 = 12
Putting y = 16 in (2), we get:
x = 36 – 16 = 20

Plotting the points D (24, 12), E (12, 24) C(20, 16) and drawing a line joining them, we get the raph of the equation.
x + y = 36
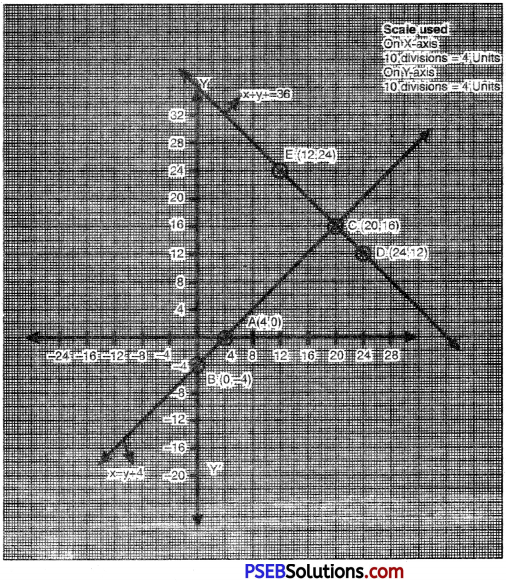
From the graph. it is clear that pair of linear equations meet at a point C (20, 16).
∴ C (20, 16) i.e. x = 20 and y = 16 is the solution of linear equations.
Hence, length of garden = 20 m
Width of garden = 16 m
![]()
Another Method:
Let width of garden = x m
Lengh of garden = (x + 4) m
Perimeter of garden = 2 [Length + Width]
= 2 [x + x + 4] m
= 2[2x + 4]m
∴ Half perimeter of garden = (2x +4) m
According to Question,
2x + 4 = 36
or 2x = 36 – 4
or 2x = 32
or x = \(\frac{32}{16}\) = 2 m
Hence, width of garden = 16 m
and length of garden = (16 + 4)m = 20 m
Question 6.
Given the Linear equation 2x + 3y – 8 = 0, write another linear equadon in two variables such that the geometiical representation of the pair so formed is:
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines
Solution:
Case I. For Intersecting Unes
Given linear equation is:
2x + 3y – 8 = 0
There are many another linear equations in two variahes which satisfies the condition of intersecing lines i.e.
\(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
One of which is as follow:
3x – 2y – 6 = 0
Now, draw the graph of linear equations (1) and (2).
2x + 3y – 8 = 0
2x = 8 – 3y
Putting y = 0 in (1), we get;
x = \(\frac{8-3 \times 0}{2}=\frac{8}{2}\) = 4
Putting y = -2 in (1), we get:
x = \(\frac{8-3(-2)}{2}=\frac{14}{2}\) = 7
Piating y = 2 in (1) we get:
x = \(\frac{8-3 \times 2}{2}=\frac{8-6}{2}=\frac{2}{2}=1\)

Plotting the points A (4, 0), B (7, -2), C (1, 2) and drawing a line joining them, we get the graph of the equation
2x + 3y – 8 = 0
Now 3x – 2y – 6 = 0
3x = 6 + 2y
or x = \(\frac{6+2 y}{3}\)
Putting y = 0 in (1), we get:
x = \(\frac{6+2 \times 0}{3}=\frac{6}{3}\) = 2
Putting y = – 3 in (1), we get :
x = \(\frac{6+2(-3)}{3}\) = \(\frac{6-6}{3}\) = 0
Putting y = 3 in (2), we get :
x = \(\frac{6+2 \times 3}{3}=\frac{6+6}{3}=\frac{12}{3}\) = 4
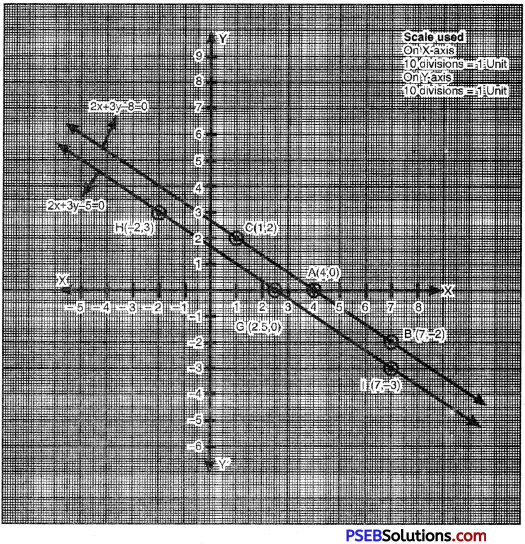
From the graph it is clear that linear equations intersect at a point G.
![]()
Case II:
For Parallel Lines
Given linear equation is
2x + 3y – 8 = 0 ……………(1)
There are many other linear equation in two variables which satisfies the condition of parallel lines i.e.
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
One of which is as follow :
2x + 3 – 5 = 0
Now, draw the graph of linear equations (1) and (3)
Table for linear equation 2x + 3y – 8 = 0 is follow:

Consider, 2x + 3y – 5 = 0
or 2x = 5 – 3y
or x = \(\frac{5-3 y}{2}\) …………..(3)
Putting y = 0 in (3), we get :
x =\(\frac{5-3 \times 0}{2}=\frac{5}{2}\) = 2.5
Putting y = 3 in (3), we get:
x = \(\frac{5-3 \times 3}{2}=\frac{5-9}{2}=\frac{-4}{2}\) = -2
Putting y = 3 in (3), we get:
x = \(\frac{5-3(-3)}{2}=\frac{5+9}{2}=\frac{14}{2}\) = 7

Plotting the points G (2.5, 0), H (-2, 3), I (7, -3) and drawing a line joining them,
we get the graph of the equation
2 + 3y – 5 = 0.
Case III. For Coincident Lines
Given linear equation is
2x + 3y – 8 = 0
There are many other linear equations ¡n two variables which satisfies the condition of coincident lines i.e.
\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
One of which is as follow :
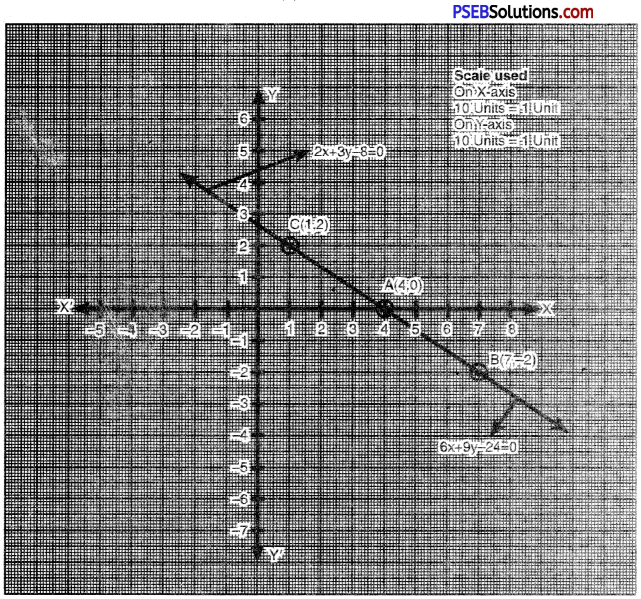
6x+ 9y – 24 = 0
Now, draw the graph of linear equations (1) and (4).
Consider linear equation (4)
6x + 9y – 24 = o
or 3[2x + 3 – 8] = 0
or 2x + 3y – 8 = 0
∴ The points of both are same and line of both equations are same.
![]()
Question 7.
Drab tht graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed b these lines and the x-axis and shade the triangular region. (Pb. 2018 Set I, II, III)
Solution:
Consider the pair of linear equation
x – y + 1 =0
and 3x + 2y – 12 = 0
x – y + 1 = 0
or x = y – 1
Putting y = 0 in (1), we get:
x = 0 – 1 = -1
Puning y = 3 in (1) we get:
x = 3 – 1 = 2
Putting y = 1 in (1) , we get:
x = 1 – 1 = 0

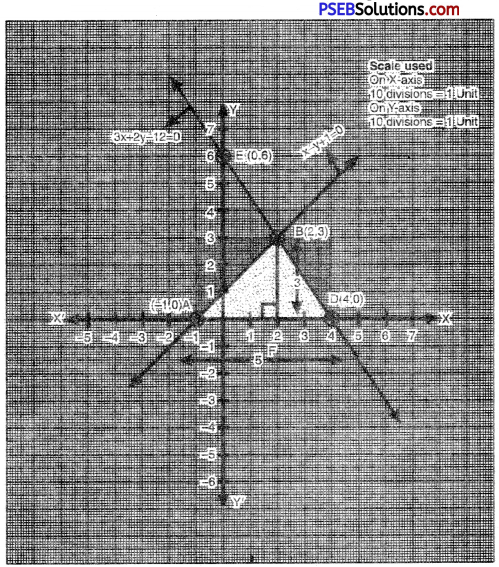
PloningthepointsA(-1, 0), B(2, 3), C(0, 1) and drawing a line ioining them. we get the graph of the equation x – y + 1 = 0
3x + 2y – 12 = 0
or 3x = 12 – 2y
or x = \(\frac{12-2 y}{3}\) …………..(2)
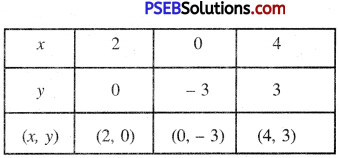
Putting y = 0 in (2), we get:
x = \(\frac{12-2 \times 0}{3}=\frac{12}{3}\) = 4
Putting y = 3 in (2), we get:
x = \(\frac{12-2 \times 3}{3}=\frac{12-6}{3}=\frac{6}{3}\) = 2
Putting y = 6 in (2), we get:
x = \(\frac{12-2 \times 6}{3}=\frac{12-12}{3}=0\)
Table:

Plotting the points D(4, 0) B (2, 3), E (0, 6) and drawing a line oinin them, we get the graph of the equation 3x – 2y – 12 = 0
![]()
The vertices of the triangle formed by pair of linear equations and the x-axis are shaded in the graph. The triangle so formed is ∆ABD.Coordinates of the vertices of ∆ABD are
A(-1, 0), B(2, 3) and D(4, 0).
Now, length of Base AD = AO + OD = 1 + 4 = 5 units
Length of perpendicular BF = 3 units
∴ Area of ∆ABD = \(\frac{1}{2}\) × Base × altitude
= \(\frac{1}{2}\) × AD × BF
= (\(\frac{1}{2}\) × 5 × 3) sq. units
= \(\frac{15}{2}\) = 7.5 sq. units