Class 8

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 10 Visualising Solid Shapes Ex 10.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.1

1. For each of the given solid, the two views are given. Match for each solid the corresponding top and front views: The first one is done for you.


Solution:
(a) → (iii) → (iv)
(b) → (i) → (v), (c) → (iv) → (ii)
(d) → (v) → (iii), (e) → (ii) → (i)

2. For each of the given solid, the three views are given. Identify for each solid the corresponding top, front and side views.


Solution:
(a)

Object	(i)	(ii)	(iii)
View	Front view	Side view	Top view

(b)

Object	(i)	(ii)	(iii)
View	Side view	Front view	Top view

(c)

Object	(i)	(ii)	(iii)
View	Front view	Side view	Top view

(d)

Object	(i)	(ii)	(iii)
View	Front view	Side view	Top view

3. For each given solid, identify the top view, front view and side view:


Solution:
(a)

Object	(i)	(ii)	(iii)
View	Top view	Front view	Side view

(b)

Object	(i)	(ii)	(iii)
View	Side view	Front view	Top view

(c)

Object	(i)	(ii)	(iii)
View	Top view	Side view	Front view

(d)

Object	(i)	(ii)	(iii)
View	Side view	Front view	Top view

(e)

Object	(i)	(ii)	(iii)
View	Front view	Top view	Side view

4. Draw the front view, side view and top view of the given objects:

Solution:

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 11 Mensuration InText Questions and Answers.

PSEB 8th Class Maths Solutions Chapter 11 Mensuration InText Questions

From Textbook : [Textbook Page No. 170]

Can you write an expression for the perimeter of each of the above shapes?
Solution:
1. Rectangle → a × b
2. Square → a × a
3. Triangle → \(\frac {1}{2}\) × b × h
4. Parallelogram → b × h
5. Circle → πb²

Yes, perimeter of above shapes are as follows:
1. Perimeter of rectangle = 2 (length + breadth)
2. Perimeter of square = 4 × (side)
3. Perimeter of triangle = sum of lengths of three sides
4. Perimeter of parallelogram = 2 × (sum of adjacent sides)
5. Perimeter (circumference) of circle = 2πr

Try These : [Textbook Page No. 170]

(a) Match the following figures with their respective areas in the box.

Solution:

Area of square
= l × l = 7 × 7

(b) Write the perimeter of each shape.
Solution:
Perimeter of given shapes:
1. Perimeter of this figure can’t be found as breadth is not given [7 cm is the height, not breadth].

2. Perimeter of semicircle = πr + 2r
= \(\frac {22}{7}\) × 7 + 2 × 7
= 22 + 14
= 36 cm

3. Perimeter of triangle = sum of lengths of three sides
= 14 + 11 + 19 = 34cm

4. Perimeter of rectangle = 2(l + b)
= 2 (14 + 7)
= 2 × 21
= 42cm

5. Perimeter of square = 4l
= 4 × 7 = 28cm

Try These : [Textbook Page No. 172]

1. Nazma’s sister also has a trapezium-shaped plot. Divide it into three parts as shown in figure. Show that the area of trapezium WXYZ = \(\frac {a + b}{2}\).

Solution:
Area of ∆ PWZ = \(\frac {1}{2}\) × base × height
= \(\frac {1}{2}\) × c × h
= \(\frac {1}{2}\)ch
Area of rectangle PQYZ = length × breadth
= b × h = bh
Area of ∆ QXY = \(\frac {1}{2}\) × base × height
= \(\frac {1}{2}\) × d × h
= \(\frac {1}{2}\)dh
Now, Area of trapezium WXYZ
Area of ∆ PWZ + Area of rectangle PQYZ + Area of ∆ QXY
= \(\frac {1}{2}\) ch + bh + \(\frac {1}{2}\)dh
= \(\frac {1}{2}\) ch + \(\frac {1}{2}\)dh + bh
= \(\frac {1}{2}\) (c + d)h + bh
= \(\frac {1}{2}\)(a – b)h + bh (∵ c + d = a – b)
= [\(\frac {1}{2}\)(a – b) + b]h
= [\(\frac {a – b}{2}\) + b] h
= \(\frac {a-b+2b}{2}\) h
= \(\frac {h (a + b)}{2}\)
Thus, area of trapezium WXYZ = \(\frac{h(a+b)}{2}\)

2. If h = 10 cm, c = 6 cm, b = 12 cm, d = 4 cm, find the values of each of its parts separetely and add to find the area WXYZ. Verify it by putting the values of h, a and b in the expression \(\frac{h(a+b)}{2}\).
Solution:
h = 10 cm, c = 6 cm, b = 12 cm, d = 4 cm.
Area of ∆ PWZ = \(\frac {1}{2}\) × c × h
= (\(\frac {1}{2}\) × 6 × 10)cm²
= 30 cm²
Area of ∆ QXY = \(\frac {1}{2}\) × d × h
= (\(\frac {1}{2}\) × 4 × 10)cm²
= 20 cm²
Area of rectangle PQYZ
= length × breadth
= 12 × 10
= 120 cm²
∴ Area of trapezium WXYZ = Area of ∆ PWZ + Area of ∆ QXY + Area of rectangle PQYZ
= (30 + 20 + 120) cm²
= 170 cm²
Now, Area of trapezium WXYZ
= \(\frac{h(a+b)}{2}\)
= \(\frac{10(22+12)}{2}\)
= \(\frac{10(34)}{2}\)
= 170cm²
∵ a = c + b + d
= 6 + 12 + 4
= 22 cm
Thus, area of trapezium verified.

Try These : [Textbook Page No. 173]

1. Find the area of the following trapeziums:

Solution:
(i) Area of given trapezium = \(\frac {1}{2}\) × (9 + 7) × 3
= \(\frac {1}{2}\) × 16 × 3 cm² = 24 cm²
(ii) Area of given trapezium = \(\frac {1}{2}\) × (10 + 5) × 6
= \(\frac {1}{2}\) × 15 × 6 cm² = 45 cm²

Try These : [Textbook Page No. 174]

1. We know that parallelogram is also a quadrilateral.

Let us also split such a quadrilateral into two triangles, find their areas and hence that of the parallelogram. Does this agree with the formula that you know already?
Solution:
Let XYZW be a given quadrilateral, which is a parallelogram.

Join the diagonal WY of the parallelogram XYZW. It divides the parallelogram into two triangles ∆WXY and ∆YZW.
Then, area of parallelogram WXYZ
= Area of ∆ WXY + Area of ∆ YZW
= (\(\frac {1}{2}\) × xy × h) + (\(\frac {1}{2}\) × wz × h)
= (\(\frac {1}{2}\) × b × h) + (\(\frac {1}{2}\) × b × h)
= \(\frac {1}{2}\) bh + \(\frac {1}{2}\) bh
= bh sq units
Area of parallelogram = base × height
= b × h
= bh sq units
As we have studied that, a parallelogram is a special case of a trapezium, where parallel sides are equal.
∴ Area of trapezium XYZW
= \(\frac {1}{2}\) × (b + b) × h
= (\(\frac {1}{2}\) × 2b × h) sq. units
= bh sq units
Thus, the above relation prooves the formula which already we know.

Think, Discuss and Write: [Textbook Page No. 175]

1. A parallelogram is divided into two congruent triangles by drawing a diagonal across it. Can we divide a trapezium into two congruent triangles?
Solution:
No, by dividing trapezium by diagonal two congruent triangles cannot be obtained.

Let us understand from given figures. Here, by drawing diagonals of a quadrilateral ABCD (which is a trapezium) congruent triangles are not obtained.

Try These : [Textbook Page No. 175]

1. Find the area of these quadrilaterals:

Solution:
(i) h₁ = 3 cm, h₂ = 5 cm
d = length of diagonal AC = 6 cm
∴ Area of quadrilateral ABCD
= \(\frac {1}{2}\)d(h₁ + h₂)
= \(\frac {1}{2}\) × 6 × (3 + 5)
= 3 × 8 cm²
= 24 cm²

(ii) d₁ = 7 cm, d₂ = 6 cm
∴ Area of rhombus ABCD
= \(\frac {1}{2}\) × d₁ × d₂
= \(\frac {1}{2}\) × 7 × 6
= 7 × 3 cm²
= 21 cm²

(iii) [Note : Here, given figure is a parallelogram. It’s diagonals divides it into two congruent triangles. From this figure, we can see that base of the triangle is 8 cm and height is 2 cm.]
∴ Area of parallelogram
= 2 (area of ∆ ADC)
= 2 × (\(\frac {1}{2}\) × b × h)
= 2 × (\(\frac {1}{2}\) × 8 × 2) cm²
= 2 × 8
= 16 cm²

Try These : [Textbook Page No. 176]

(i) Divide the following polygons into parts (triangles and trapezium) to find out its area.

Solution:
(a)

Let’s draw perpendicular on diagonal \(\overline{\mathrm{FI}}\).
Here, GA ⊥ FI, EB ⊥ FI and HC ⊥ FI are drawn.
Area of polygon EFGHI = Area of ∆ GFA + Area of the trapezium ACHG + Area of ∆ HCI + Area of ∆ BIE + Area of ∆ FBE
= [\(\frac {1}{2}\) × FA × GA] + [\(\frac {1}{2}\) (AG + CH) × AC] + [\(\frac {1}{2}\) × CI × HC] + [\(\frac {1}{2}\) × BI × BE] + [\(\frac {1}{2}\) × FB × BE]
[Note : We can also use Area of ∆ EFI in place of Area of ∆ BIE + Area of ∆ FBE]

(b)

Let’s draw perpendicular on diagonal \(\overline{\mathrm{NQ}}\).
\(\overline{\mathrm{OE}}\) ⊥ \(\overline{\mathrm{NQ}}\), \(\overline{\mathrm{MF}}\) ⊥ \(\overline{\mathrm{NQ}}\), \(\overline{\mathrm{PG}}\) ⊥ \(\overline{\mathrm{NQ}}\) and \(\overline{\mathrm{RH}}\) ⊥ \(\overline{\mathrm{NQ}}\) are drawn.
Area of polygon MNOPQR = Area of ∆ NEO + Area of trapezium EGPO + Area of ∆ GQP + Area of ∆ HQR + Area of trapezium MRHF + Area of ∆ NFM
= [\(\frac {22}{7}\) × NE × OE] + [\(\frac {22}{7}\) × (OE + PG) × EG] + [\(\frac {22}{7}\) × GQ × PG] + [\(\frac {22}{7}\) × HQ × HR] + [\(\frac {22}{7}\) × (FM + HR) × FH] + [\(\frac {22}{7}\) × NF × FM]

(ii) Polygon ABODE is divided into parts as shown in figure.

Find its area if AD = 8 cm, AH = 6 cm,
AG = 4 cm, AF = 3 cm and perpendiculars BF = 2 cm, CH = 3 cm, EG = 2.5 cm.
Area of polygon ABODE = area of ∆ AFB + ….
Area of ∆ AFB = \(\frac {1}{2}\) × AF × BF
= \(\frac {1}{2}\) × 3 × 2 = ………..
Area of trapezium FBCH
= FH × \(\frac{(BF + CH)}{2}\)
= 3 × \(\frac{(2+3)}{2}\) [FH = AH – AF]
Area of ∆ CHD = \(\frac {1}{2}\) × HD × CH= …………;
Area of ∆ ADE = \(\frac {1}{2}\) × AD × GE = ………….
So the area of polygon ABCDE = …………
Solution:

Here, AD = 8 cm,
AH = 6 cm,
HD = 2 cm,
AG = 4 cm,
GD = 4 cm,
AF = 3 cm and
GF = 1 cm
Area of polygon ABCDE = Area of ∆ AFB + Area of trapezium FBCH + Area of ∆ CHD + Area of ∆ ADE
Now,
Area of ∆ AFB = \(\frac {1}{2}\) × AF × BF
= \(\frac {1}{2}\) × 3 × 2 = 3 cm2 … (i)
Area of trapezium FBCH
= \(\frac {1}{2}\) × (BF × CH) × FH
= \(\frac {1}{2}\) × (2 + 3) × 3 [∵ FH = AH – AF]
= \(\frac {1}{2}\) × 5 × 3 = \(\frac {15}{2}\)
= 7.5 cm² … (ii)
Area of ∆ CHD = \(\frac {1}{2}\) × HD × CH
= \(\frac {1}{2}\) × (AD – AH) × CH
[∵ HD = AD – AH]
= \(\frac {1}{2}\) × (8 – 6) × 3
= \(\frac {1}{2}\) × 2 × 3
= 3 cm² … (iii)
Area of ∆ ADE = \(\frac {1}{2}\) × AD × GE
= \(\frac {1}{2}\) × 8 × 2.5
= 4 × 2.5
= 10 cm² ………. (iv )
∴ Area of polygon ABCDE = Area of [(i) + (ii) + (iii) + (iv)]
= (3 + 7.5 + 3 + 10) cm²
= 23.5 cm²

(iii) Find the area of polygon MNOPQR if MP = 9 cm, MD = 7 cm, MC = 6 cm, MB = 4 cm, MA = 2 cm NA, OC, QD and RB are perpendiculars to diagonal MP.

Solution:

Here,
MP = 9 cm,
MD = 7 cm
∴ DP = MP – MD
= (9 – 7) cm
= 2 cm
MC = 6 cm ∴ CP = 3 cm
MB = 4 cm ∴ BP = 5 cm
MA = 2 cm ∴ AC = MC – MA
= (6 – 2) cm = 4 cm
MB + BD = MD
∴ BD = (7 – 4) cm
= 3 cm
Area of ∆ MAN = \(\frac {1}{2}\) × MA × AN
= \(\frac {1}{2}\) × 2 × 2.5
= 2.5 cm² ……. (i)
Area of trapezium ACON
= \(\frac {1}{2}\) × (AN + OC) × AC
= \(\frac {1}{2}\) × (2.5 + 3) × 4
= \(\frac {1}{2}\) × 4 × 5.5
= 2 × 5.5
= 11 cm² … (ii)
Area of ∆ CPO = \(\frac {1}{2}\) × CP × CO
= \(\frac {1}{2}\) × 3 × 3
= \(\frac {9}{2}\) = 4.5 cm² … (iii)
Area of ∆ MBR = \(\frac {1}{2}\) × MB × BR
= \(\frac {1}{2}\) × 4 × 2.5
= 2 × 2.5
= 5 cm² … (iv )
Area of trapezium BRQD
= \(\frac {1}{2}\) × (BR + DQ) × BD
= \(\frac {1}{2}\) × (2.5 + 2) × 3
= \(\frac {1}{2}\) × 4.5 × 3
= 6.75 cm² ………. (v)
Area of ∆ DQP = \(\frac {1}{2}\) × DP × DQ
= \(\frac {1}{2}\) × 2 × 2
= 2 cm² … ( vi )
∴ Area of polygon MNOPQR = Area of [(i) + (ii) + (iii) + (iv) + (v) + (vi)]
= (2.5 + 11 + 4.5 + 5 + 6.75 + 2) cm²
= 31.75 cm²

Think, Discuss and Write : [Textbook Page No. 180]

1. Why is it incorrect to call the solid shown here a cylinder?
Solution:

It is incorrect to call given solid as a cylinder because, a cylinder has two identical circular faces, parallel to each other. The radii of both the faces are the same.

Try These :[Textbook Page No. 181]

1. Find the total surface area of the following cuboids:

Solution:
(i) Here, length (i) = 6 cm,
breadth (b) = 4 cm and
height (h) = 2 cm.
Total surface area of a cuboid = 2 (lb + bh + hl)
= 2(6 × 4 + 4 × 2 + 2 × 6)
= 2(24 + 8 + 12)
= 2 (44)
= 88 cm²

(ii) Here, length (l) = 4 cm,
breadth (b) = 4 cm and
height (h) = 10 cm.
Total surface area of a cuboid = 2 (lb + bh + hl)
= 2 (4 × 4 + 4 × 10 + 10 × 4)
= 2 (16 + 40 + 40)
= 2(96) = 192 cm²

Think, Discuss and Write :[Textbook Page No. 181]

1. Can we say that the total surface area of cuboid = lateral surface area + 2 × area of base?
Solution:
Yes, the total surface area of cuboid = lateral surface area + 2 × area of base [Note: Area of base and area of top of a cuboid, both are same.]

2. If we interchange the lengths of the base and the height of a cuboid to get another cuboid, will its lateral surface area change?

Solution:
(a) Lateral surface area of cuboid (i)
= 2(l + b) × h
(b) Lateral surface area of cuboid (ii)
= 2 (h + b) × l
Thus, it is clear that by interchanging the lengths of the base and the height of a cuboid, its lateral surface area will change.

Try These : [Textbook Page No. 182]

1. Find the surface area of cube A and lateral surface area of cube B.

Solution:
For cube A:
Side = 10 cm
Surface area of cube A = 6 × (side)²
= 6 × (10)²
= 6 × 100
= 600 cm²

For cube B:
Side = 8 cm
Lateral surface area of a cube B
= 4 × (side)²
= 4 × (8)²
= 4 × 64
= 256 cm²

Think, Discuss and Write : [Textbook Page No. 183]

Question (i)
Two cubes each with side b are joined to form a cuboid. What is the surface area of this cuboid? Is it 12b²? Is the surface area of cuboid formed by joining three such cubes, 18b²? Why?

Solution:
(a) By joining two cubes end-to-end with side b, a cuboid shape formed.
For cuboid:
length = b + b = 2b, breadth = b and height = b
Total surface area of this cuboid = 2 (lb + bh + lh)
= 2 [(2b × b) + (b × b) + (2b × b)]
= 2 (2b² + b² + 2b²)
= 2 (5b²)
= 10b²
So surface area of the cuboid formed by joining two cubes is not equal to 12b²), it is 10b²).

(b) By joining three cubes end-to-end with side b, a cuboid shape forms.
For cuboid:
length = b + b + b = 3b, breadth = b and height = b
Total surface area of this cuboid = 2 (lb + bh + lh)
= 2 [(3b × b) + (b × b) + (3b × b)]
= 2 (3b² + b² + 3b²)
= 2(7b²) = 14b²
So the surface area of cuboid formed by joining three such cubes is not equal to 18b², it is 14b².

(ii) How will you arrange 12 cubes of equal length to form a cuboid of smallest surface area?
Solution:
Let us arrange 12 cubes of equal length say b to form a cuboid in different situations.
(a)

Here, length = 12b, breadth = b and height = b
Total surface area of a cuboid = 2 (lb + bh + lh)
= 2 [(12b × b) + (b × b) + (12b × b)]
= 2 (12b² + b² + 12b²)
= 2 (25b²) – 50b²

(b)

Here, length = 3b, breadth = 2b and height = 2b
Total surface area of a cuboid
= 2 (lb+ bh+ lh)
= 2 [(3b × 2b) + (2b × 2b) + (2b × 3b)]
= 2 (6b² + 4b² + 6b²)
= 2 (16b²) = 32b²

(c)

Here, length = 6b, breadth = 2b and height = b
Total surface area of a cuboid
= 2 (lb + bh + lh)
= 2 [(6b × 2b) + (2b × b) + (b × 6b)]
= 2 (12b² + 2b² + 6b²)
= 2 (20b²)
= 40b²
Hence, from above results we can conclude that, if we arrange 12 cubes of equal length according to situation (b), we get smallest surface area.

(iii) After the surface area of a cube is painted, the cube is cut into 64 smaller cubes of same dimensions. How many have no face painted? 1 face painted? 2 faces painted? 3 faces painted?
Solution:
1. 8 cubes, which have no face painted. (∵ Middle 4 × 2)
2. 24 cubes, which have 1 face painted. (∵ on each surface 4 × 6)
3. 24 cubes, which have 2 faces painted. (∵ on each surface 4 × 6)
4. 8 cubes, which have 3 faces painted. (∵ on each surface 2 × 4)

Try These : [Textbook Page No. 184]

1. Find total surface area of the following cylinders:

Solution:
(i) Radius of cylinder r = 14 cm
Height of cylinder h = 8 cm
Total surface area of a cylinder = 2πr (r + h)
= 2 × \(\frac {22}{7}\) × 14(14 + 8)
= 2 × 22 × 2 × 22
= 44 × 44
= 1936 cm²

(ii) Radius of cylinder r = \(\frac{\text { diameter }}{2}=\frac{2}{2}\) = 14 cm
Height of cylinder h = 2 cm
Total surface area of a cylinder = 2πr (r + h)
= 2 × \(\frac {22}{7}\) × 1(1 + 2)
= 2 × \(\frac {22}{7}\) × 1 × 3
= \(\frac {132}{7}\)
= 18\(\frac {6}{7}\) m²

Think, Discuss and Write: [Textbook Page No. 184]

1. Note that lateral surface area of a cylinder is the circumference of base × height of cylinder. Can we write lateral surface area of a cuboid as perimeter of base × height of cuboid?
Solution:

Let l be the height, b be the breadth and h be the height of cuboid.
∴ Lateral surface area of a cuboid = Area of 4 walls of the cuboid
= (l × h) + (l × h) + (b × h) + (b × h)
= 2 lh + 2 bh
= 2(1 + b) × h
= Perimeter of base × height
Yes, we can write lateral surface area of a cuboid as perimeter of base × height of cuboid.

Try These : [Textbook Page No. 188]

1. Find the volume of the following cuboids:

Solution:
(i) For given cuboid:
length (l) = 8 cm, breadth (b) = 3 cm s and height (h) = 2 cm
Volume of a cuboid
= Area of base × height
= (l × b) × h
= (8 × 3) × 2
= 24 × 2 = 48 cm³
OR
Volume of cuboid = l × b × h
= (8 × 3 × 2) cm³
= 48 cm³

(ii) Area of base of cuboid = 24 m³
height (h) = 3 cm = \(\frac {3}{100}\) m
Volume of cuboid
= Area of base × height
= 24 × \(\frac {3}{100}\) = 0.72 m³

Try These: [Textbook Page No. 189]

1. Find the volume of the following cubes
(a) With a side 4 cm
Solution:
For given cube : side = 4 cm
∴ Volume of the cube = (side)³
= (4)³ = 4 × 4 × 4
= 64 cm³

(b) With a side 1.5m
Solution:
For given cube : side = 1.5 m
∴ Volume of the cube = (side)³
= (1.5)³ = 1.5 × 1.5 × 1.5
= \(\frac{15}{10} \times \frac{15}{10} \times \frac{15}{10}=\frac{3375}{1000}\)
= 3.375 m³

Think, Discuss and Write: [Textbook Page No. 189]

1. A company sells biscuits. For packing purpose they are using cuboidal boxes:
box A → 3 cm × 8 cm × 20 cm,
box B → 4 cm × 12 cm × 10 cm. What size of the box will be economical for the company? Why? Can you suggest any other size (dimensions) which has the same volume but is more economical than these?
Solution:
For box A:
Given dimension = 3 cm × 8 cm × 20 cm
length = 20 cm, breadth = 8 cm and height = 3 cm
∴ Volume of the box A = l × b × h
= 20 × 8 × 3
= 480 cm³
Total surface area of the box A
= 2 (lb + bh + lh)
= 2 [(20 × 8) + (8 × 3) + (20 × 3)]
= 2 (160 + 24 + 60 )
= 2 (244)
= 488 cm³

For box B:
Given dimension = 4 cm × 12 cm × 10 cm
length = 12 cm, breadth = 10 cm and height = 4 cm
∴ Volume of the box B = l × b × h
= 12 × 10 × 4
= 480 cm³
Total surface area of the box B
= 2 (lb + bh + lh)
= 2 [(12 × 10) + (10 × 4) + (12 × 4)]
= 2(120 + 40 + 48 )
= 2(208)
= 416 cm³
From above results, we can conclude that both boxes have same volume, but surface area of box B is less than that of box A.
∴ Box B is more economical than box A.
Now, let another box of size be 8 cm × 6 cm × 10 cm.
∴ length = 8 cm, breadth = 6 cm and height =10 cm
Volume = l × b × h
= 8 × 6 × 10 = 480 cm³
It’s surface area = 2 (lb + bh + Ih)
= 2 [(8 × 6) + (6 × 10) + (8 × 10)]
= 2 (48 + 60 + 80)
= 2 (188) = 376 cm²
Surface area of this box is less than that of box B.
∴ This box is more economical for company.

Try These: [Textbook Page No. 189]

1. Find the volume of the following cylinders:

Solution:
(i) For given cylinder :
radius (r) = 7 cm, height (h) = 10 cm
Volume of the cylinder = πr²h
= \(\frac {22}{7}\) × 7² × 10
= \(\frac {22}{7}\) × 7 × 7 × 10
= 22 × 70
= 1540cm³

(ii) For given cylinder:
base area 250 m², height (h) = 2m
Volume of the cylinder
= base area × height
= 250 × 2
= 500 m³

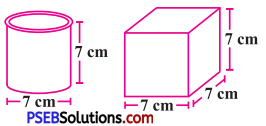
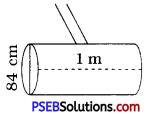
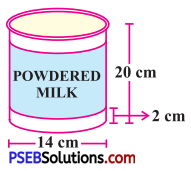
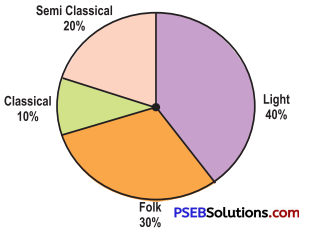
Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 6 Squares and Square Roots Ex 6.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.4

1. Find the square root of each of the following numbers by Division method.

Question (i).
2304
Solution:

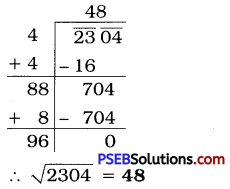
Question (ii).
4489
Solution:

Question (iii).
3481
Solution:

Question (iv).
529
Solution:

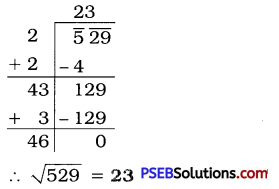
Question (v).
3249
Solution:

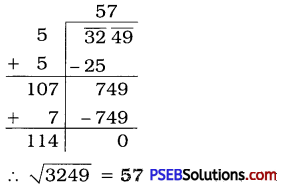
Question (vi).
1369
Solution:

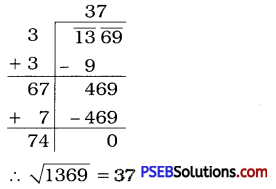
Question (vii).
5776
Solution:

Question (viii).
7921
Solution:

Question (ix).
576
Solution:

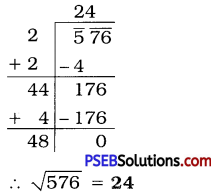
Question (x).
1024
Solution:

Question (xi).
3136
Solution:

Question (xii).
900
Solution:

2. Find the number of digits in the square root of each of the following numbers (without any calculation).

Question (i).
64
Solution:
Here, number of digits, n = 2
(Which is an even number.)
∴ Number of digits in the square root of 64 = \(\frac{n}{2}=\frac{2}{2}\) = 1

Question (ii).
144
Solution:
Here, number of digits, n = 3
(Which is an odd number.)
∴ Number of digits in the square root of 144 = \(\frac{n+1}{2}=\frac{3+1}{2}\)
= \(\frac {4}{2}\)
= 2

Question (iii).
4489
Solution:
Here, number of digits, n = 4
(Which is an even number.)
∴ Number of digits in the square root of 4489 = \(\frac{n}{2}=\frac{4}{2}\)
= 2

Question (iv).
27225
Solution:
Here, number of digits, n = 5
(Which is an odd number.)
∴ Number of digits in the square root of 27225 = \(\frac{n+1}{2}=\frac{5+1}{2}\)
= \(\frac {6}{2}\)
= 3

Question (v).
390625
Solution:
Here, number of digits, n = 6
(Which is an even number.)
∴ Number of digits in the square root of 390625 = \(\frac{n}{2}=\frac{6}{2}\)
= 3

3. Find the square root of the following decimal numbers.

Question (i).
2.56
Solution:

Here, number of decimal places are two.
∴ The number of decimal places in square root should be one.

Question (ii).
7.29
Solution:

Here, number of decimal places are two.
∴ The number of decimal places in square root should be one.

Question (iii).
51.84
Solution:

Here, number of 51.84 decimal places are two.
∴ The number of decimal places in square root should be one.

Question (iv).
42.25
Solution:

Question (v).
31.36
Solution:

4. Find the least number which must be subtracted from each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.

Question (i).
402
Solution:

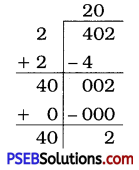
Here, the remainder is 2. It shows that 20² is less than 402 by 2.
So, to get a perfect square, 2 must be subtracted from given number.
∴ Required perfect square number = 402 – 2 = 400
\(\sqrt{400}\) = 20

Question (ii).
1989
Solution:

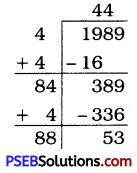
Here, the remainder is 53. It shows that 44² is less than 1989 by 53.
So, to get a perfect square, 53 must be subtracted from the given number.
∴ Required perfect square number = 1989 – 53 = 1936
\(\sqrt{1936}\) = 44

Question (iii).
3250
Solution:

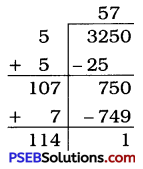
Here, the remainder is 1. It shows that 57² is less them 3250 by 1.
So, to get a perfect square, 1 must be subtracted from the given number.
∴ Required perfect square number = 3250 – 1 = 3249
\(\sqrt{3249}\) = 57

Question (iv).
825
Solution:

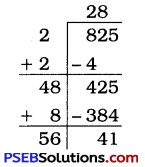
Here, the remainder is 41. It shows that 28² is less than 825 by 41.
So, to get a perfect square, 41 must be subtracted from the given number.
∴ Required perfect square number = 825 – 41 = 784
\(\sqrt{784}\) = 28

Question (v).
4000
Solution:

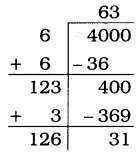
Here, the remainder is 31. It shows that 63² is less than 4000 by 31.
So, to get a perfect square, 31 must be subtracted from the given number.
∴ Required perfect square number = 4000 – 31 = 3969
\(\sqrt{3969}\) = 63

5. Find the least number which must be added to each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.

Question (i).
525
Solution:

Here, the remainder is 41.
525 > 22²,
and the number next to 22 is 23.
23² = 529.
∴ The required number to be added
= 23² – 525
= 529 – 525 = 4
Now, 525 + 4 = 529
\(\sqrt{529}\) = 23
Thus, 4 is the least number which must be added to 525 to get a perfect square.

Question (ii).
1750
Solution:

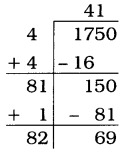
Here, the remainder is 69.
1750 > 41²,
and the number next to 41 is 42.
42² = 1764.
∴ The required number to be added = 42² – 1750
= 1764 – 1750
= 14
Now, 1750 + 14 = 1764
\(\sqrt{1764}\) = 42
Thus, 14 is the least number which must be added to 1750 to get a perfect square.

Question (iii).
252
Solution:

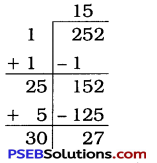
Here, the remainder is 27.
252 > 15²,
and the number next to 15 is 16.
16² = 256.
∴ The required number to be added = 16² – 252
= 256 – 252
= 4
Now, 252 + 4 = 256
\(\sqrt{256}\) = 16
Thus, 4 is the least number which must be added to 252 to get a perfect square.

Question (iv).
1825
Solution:

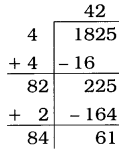
Here, the remainder is 61.
1825 > 42²,
and the number next to 42 is 43.
43² = 1849.
∴ The required number to be added 43² – 1825
= 1849 – 1825
= 24
Now, 1825 + 24 = 1849
\(\sqrt{1849}\) = 43
Thus, 24 is the least number which must be added to 1825 to get a perfect square.

Question (v).
6412
Solution:

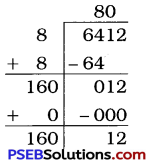
Here, the remainder is 12.
6412 > 80²,
and the number next to 80 is 81.
81² = 6561.
∴ The required number to be added = 81² – 6412
= 6561 – 6412
= 149
Now, 6412 + 149 = 6561
\(\sqrt{6561}\) = 81
Thus, 149 is the least number which must be added to 6412 to get a perfect square.

6. Find the length of the side of a square whose area is 441 m².
Solution:
Let the side of a square be x m.
Area of a square = x × x = x²
Area of a square = 441 (given)

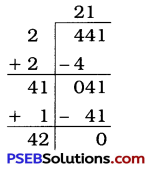
∴x² = 441
∴ x = \(\sqrt{441}\)
∴ x = 21
Thus, the length of the side of the square is 21 m.

7. In a right triangle ABC, ∠B = 90° :
(a) If AB = 6 cm, BC = 8 cm, find AC.
(b) If AC = 13 cm, BC = 5 cm, find AB.
Solution:
[Note: In a right triangle, the longest side is called the hypotenuse. The square of the hypotenuse is equal to the sum of the squares of the remaining two sides.]
Let us use this theorem here.
(a) Here, ∠B = 90°, AB = 6 cm, BC = 8 cm
In ΔABC, AC is hypotenuse.

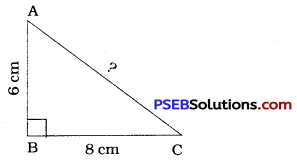
AC² = AB² + BC²
= (6)² + (8)²
= 36 + 64
=100
∴ AC = \(\sqrt{100}\)
= 10cm

(b) Here, ∠B= 90°, AC = 13cm, BC = 5cm
In ΔABC, AC Is hypotenuse.


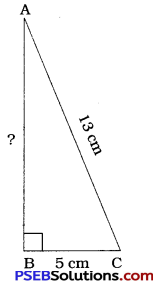
AC² = AB² + BC²
∴ (13)² = AB² + (5)²
∴ 169 = AB² + 25
∴ AB² = 169 – 25
= 144
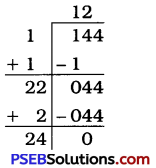
∴ AB = \(\sqrt{144}\)
= 12 cm

8. A gardener has 1000 plants. He wants to plant these in such a way that the number of rows and the number of columns remain same. Find the minimum number of plants he needs more for this.
Solution:
Total number of plants = 1000
The number of plants in a row = The number of plants in a column
Let the number of plants planted in a row be x.
So, the number of plants planted in a column is x.
∴ Total plants = x × x = x²
∴ x² > 1000
∴ x > \(\sqrt{1000}\)
Here, the remainder is 39.
(31)² < 1000
The next square number would be 32.
32² = 1024
∴ The number of plants required to be added = 1024 – 1000
= 24
Thus, 24 more plants needed.

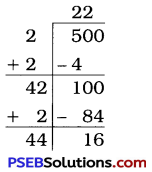
9. There are 500 children in a school. For a P.T. drill they have to stand in such a manner that the number of rows is equal to number of columns. How many children would be left out in this arrangement?
Solution:
Total number of children in a school = 500
The number of rows = The number of columns
Let the number of children in a row be x.
So, the number of children in a column is x.
Total number of children = x × x = x².
∴ x² < 500
∴ x < \(\sqrt{500}\)
Here, the remainder is 16.
500 > 22²
∴ 500 > 484
500 – 484 = 16
Thus, 16 children would be left out in this arrangement.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 6 Squares and Square Roots Ex 6.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.3

1. What could be the possible ‘one’s’ digits of the square root of each of the following numbers ?

Question (i).
9801
Solution:
The possible digit at one’s place of the square root of 9801 can be either 1 or 9.
(∵ 1 × 1 = 1 and 9 × 9 = 81)

Question (ii).
99856
Solution:
The possible digit at one’s place of the square root of 99856 can be either 4 or 6.
(∵ 4 × 4= 16 and 6 × 6 = 36)

Question (iii).
998001
Solution:
The possible digit at one’s place of the square root of 998001 can be either 1 or 9.
(∵ 1 × 1 = 1 and 9 × 9 = 81)

Question (iv).
657666025
Solution:
The possible digit at one’s place of the square root of 657666025 can be 5.
(∵ 5 × 5 = 25)

2. Without doing any calculation, find the numbers which are surely not perfect squares:
[Note : The ending digit of perfect square is 0, 1, 4, 5, 6 or 9.
∴ A number having end digit 2, 3, 7 or 8 can never be a perfect square.

Question (i).
153
Solution:
153
Here, the end digit is 3.
∴ 153 cannot be a perfect square.

Question (ii).
257
Solution:
257
Here, the end digit is 7.
∴ 257 cannot be a perfect square.

Question (iii).
408
Solution:
408
Here, the end digit is 8.
∴ 408 cannot be a perfect square.

Question (iv).
441
Solution:
441
Here, the end digit is 1.
∴ 441 can be a perfect square.

3. Find the square roots of 100 and 169 by the method of repeated subtraction.

Question (i).
100
Solution:
100 – 1 = 99   99 – 3 = 96
96 – 5 = 91   91 – 7 = 84
84 – 9 = 75   75 – 11 = 64
64 – 13 = 51   51 – 15 = 36
36 – 17 = 19   19 – 19 = 0
∴ 100 is a perfect square.
∴ \(\sqrt{100}\) = 10

Question (ii).
169
Solution:
169 – 1 = 168   168 – 3 = 165
165-5 = 160   160 – 7 = 153
153-9 = 144   144 – 11 = 133
133-13 = 120   120 – 15 = 105
105-17 = 88   88 – 19 = 69
69-21 = 48   48 – 23 = 25
25 – 25 = 0
∴ 169 is a perfect square.
∴ \(\sqrt{169}\) = 13

4. Find the square roots of the following numbers by the Prime Factorisation Method:

Question (i).
729
Solution:
729
\(\begin{array}{l|r}
3 & 729 \\
\hline 3 & 243 \\
\hline 3 & 81 \\
\hline 3 & 27 \\
\hline 3 & 9 \\
\hline 3 & 3 \\
\hline & 1
\end{array}\)
729 = 3 × 3 × 3 × 3 × 3 × 3
= 3² × 3² × 3²
∴ \(\sqrt{729}\) = 3 × 3 × 3
= 27

Question (ii).
400
Solution:
400
\(\begin{array}{l|r}
2 & 400 \\
\hline 2 & 200 \\
\hline 2 & 100 \\
\hline 2 & 50 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
400 = 2 × 2 × 2 × 2 × 5 × 5
= 2² × 2² × 5²
∴ \(\sqrt{400}\) = 2 × 2 × 5
= 20

Question (iii).
1764
Solution:
1764
\(\begin{array}{l|r}
2 & 1764 \\
\hline 2 & 882 \\
\hline 3 & 441 \\
\hline 3 & 147 \\
\hline 7 & 49 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)
1764 = 2 × 2 × 3 × 3 × 7 × 7
= 2² × 3² × 7²
∴ \(\sqrt{1764}\) = 2 × 3 × 7
= 42

Question (iv).
4096
Solution:
4096
\(\begin{array}{l|r}
2 & 4096 \\
\hline 2 & 2048 \\
\hline 2 & 1024 \\
\hline 2 & 512 \\
\hline 2 & 256 \\
\hline 2 & 128 \\
\hline 2 & 64 \\
\hline 2 & 32 \\
\hline 2 & 16 \\
\hline 2 & 8 \\
\hline 2 & 4 \\
\hline 2 & 2 \\
\hline & 1
\end{array}\)
4096 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 2² × 2² × 2² × 2² × 2² × 2²
∴ \(\sqrt{4096}\) = 2 × 2 × 2 × 2 × 2 × 2
= 64

Question (v).
7744
Solution:
7744
\(\begin{array}{r|r}
2 & 7744 \\
\hline 2 & 3872 \\
\hline 2 & 1936 \\
\hline 2 & 968 \\
\hline 2 & 484 \\
\hline 2 & 242 \\
\hline 11 & 121 \\
\hline 11 & 11 \\
\hline & 1
\end{array}\)
7744 = 2 × 2 × 2 × 2 × 2 × 2 × 11 × 11
= 2² × 2² × 2² × 11²
∴ \(\sqrt{7744}\) = 2 × 2 × 2 × 11
= 88

Question (vi).
9604
Solution:
9604
\(\begin{array}{l|r}
2 & 9604 \\
\hline 2 & 4802 \\
\hline 7 & 2401 \\
\hline 7 & 343 \\
\hline 7 & 49 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)
9604 = 2 × 2 × 7 × 7 × 7 × 7
= 2² × 7² × 7²
∴ \(\sqrt{9604}\) =2 × 7 × 7
= 98

Question (vii).
5929
Solution:
5929
\(\begin{array}{r|r}
7 & 5929 \\
\hline 7 & 847 \\
\hline 11 & 121 \\
\hline 11 & 11 \\
\hline & 1
\end{array}\)
5929 = 7 × 7 × 11 × 11
= 7² × 11²
∴ \(\sqrt{5929}\) = 7 × 11
= 77

Question (viii).
9216
Solution:
9216
\(\begin{array}{r|r}
2 & 9216 \\
\hline 2 & 4608 \\
\hline 2 & 2304 \\
\hline 2 & 1152 \\
\hline 2 & 576 \\
\hline 2 & 288 \\
\hline 2 & 144 \\
\hline 2 & 72 \\
\hline 2 & 36 \\
\hline 2 & 18 \\
\hline 3 & 9 \\
\hline 3 & 3 \\
\hline & 1
\end{array}\)
9216 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3
= 2² × 2² × 2² × 2² × 2² × 3²
∴ \(\sqrt{9216}\) = 2 × 2 × 2 × 2 × 2 × 3
= 96

Question (ix).
529
Solution:
529
\(\begin{array}{l|r}
23 & 529 \\
\hline 23 & 23 \\
\hline & 1
\end{array}\)
529 = 23 × 23
= 23²
∴ \(\sqrt{529}\) = 23

Question (x).
8100
Solution:
8100
\(\begin{array}{l|r}
2 & 8100 \\
\hline 2 & 4050 \\
\hline 3 & 2025 \\
\hline 3 & 675 \\
\hline 3 & 225 \\
\hline 3 & 75 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
8100 = 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5
= 2² × 3² × 3² × 5²
∴ \(\sqrt{8100}\) = 2 × 3 × 3 × 5
= 90

5. For each of the following numbers, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained:

Question (i).
252
Solution:
252
\(\begin{array}{l|r}
2 & 252 \\
\hline 2 & 126 \\
\hline 3 & 63 \\
\hline 3 & 21 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)
252 = 2 × 2 × 3 × 3 × 7
The prime factor 7 is unpaired.
∴ [252] × 7 = [2 × 2 × 3 × 3 × 7] × 7
1764 = 2 × 2 × 3 × 3 × 7 × 7
= 2² × 3² × 7²
∴ \(\sqrt{1764}\) = 2 × 3 × 7 = 42
Thus, 252 should be multiplied by smallest whole number 7 to get a perfect square.

Question (ii).
180
Solution:
180
\(\begin{array}{l|r}
2 & 180 \\
\hline 2 & 90 \\
\hline 3 & 45 \\
\hline 3 & 15 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
180 = 2 × 2 × 3 × 3 × 5
Here, the prime factor 5 is unpaired.
∴ [180] × 5 = [2 × 2 × 3 × 3 × 5] × 5
∴ 900 = 2 × 2 × 3 × 3 × 5 × 5
= 2² × 3² × 5²
∴ \(\sqrt{900}\) = 2 × 3 × 5 = 30
Thus, 180 should be multiplied by smallest whole number 5 to get a perfect square.

Question (iii).
1008
Solution:
1008
\(\begin{array}{l|r}
2 & 1008 \\
\hline 2 & 504 \\
\hline 2 & 252 \\
\hline 2 & 126 \\
\hline 3 & 63 \\
\hline 3 & 21 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)
1008 = 2 × 2 × 2 × 2 × 3 × 3 × 7
Here, the prime factor 7 is unpaired.
∴ [1008] × 7 = [2 × 2 × 2 × 2 × 3 × 3 × 7] × 7
∴ 7056 = 2 × 2 × 2 × 2 × 3 × 3 × 7 × 7
= 2² × 2² × 3² × 7²
∴ \(\sqrt{7056}\) = 2 × 2 × 3 × 7 = 84
Thus, 1008 should be multiplied by smallest whole number 7 to get a perfect square.

Question (iv).
2028
Solution:
2028
\(\begin{array}{r|r}
2 & 2028 \\
\hline 2 & 1014 \\
\hline 3 & 507 \\
\hline 13 & 169 \\
\hline 13 & 13 \\
\hline & 1
\end{array}\)
2028 = 2 × 2 × 3 × 13 × 13
Here, the prime factor 3 is unpaired.
∴ [2028] × 3 = [2 × 2 × 3 × 13 × 13] × 3
∴ 6084 = 2 × 2 × 3 × 3 × 13 × 13
= 2² × 3² × 13²
∴ \(\sqrt{6084}\) = 2 × 3 × 13 = 78
Thus, 2028 should be multiplied by smallest whole number 3 to get a perfect square.

Question (v).
1458
Solution:
1458
\(\begin{array}{l|r}
2 & 1458 \\
\hline 3 & 729 \\
\hline 3 & 243 \\
\hline 3 & 81 \\
\hline 3 & 27 \\
\hline 3 & 9 \\
\hline 3 & 3 \\
\hline & 1
\end{array}\)
1458 = 2 × 3 × 3 × 3 × 3 × 3 × 3
Here, the prime factor 2 is unpaired.
∴ [1458] × 2 = [2 × 3 × 3 × 3 × 3 × 3 × 3] × 2
∴ 2916 = 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
= 2² × 3² × 3² × 3²
∴ \(\sqrt{2916}\) = 2 × 3 × 3 × 3 = 54
Thus, 1458 should be multiplied by smallest whole number 2 to get a perfect square.

Question (vi).
768
Solution:
768
\(\begin{array}{l|r}
2 & 768 \\
\hline 2 & 384 \\
\hline 2 & 192 \\
\hline 2 & 96 \\
\hline 2 & 48 \\
\hline 2 & 24 \\
\hline 2 & 12 \\
\hline 2 & 6 \\
\hline 3 & 3 \\
\hline & 1
\end{array}\)
768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3
Here, the prime factor 3 is unpaired.
∴ [768] × 3 = [2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3] × 3
∴ 2304 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3
= 2² × 2² × 2² × 2² × 3²
∴ \(\sqrt{2304}\) = 2 × 2 × 2 × 2 × 3 = 48
Thus, 768 should be multiplied by smallest whole number 3 to get a perfect square.

6. For each of the following numbers, find the smallest whole number by which it should be divided so as to get a perfect square. Also find the square root of the square number so obtained:

Question (i).
252
Solution:
252
\(\begin{array}{r|r}
2 & 252 \\
\hline 2 & 126 \\
\hline 3 & 63 \\
\hline 3 & 21 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)
252 = 2 × 2 × 3 × 3 × 7
Here, the prime factor 7 is unpaired. So, given number should be divided by 7.
∴ [252] ÷ 7 = [2 × 2 × 3 × 3 × 7] ÷ 7
∴ 36 = 2 × 2 × 3 × 3
= 2² × 3²
∴ \(\sqrt{36}\) = 2 × 3 = 6
Thus, 252 should be divided by smallest whole number 7 to get a perfect square number.

Question (ii).
2925
Solution:
2925
\(\begin{array}{r|r}
3 & 2925 \\
\hline 3 & 975 \\
\hline 5 & 325 \\
\hline 5 & 65 \\
\hline 13 & 13 \\
\hline & 1
\end{array}\)
2925 = 3 × 3 × 5 × 5 × 13
Here, the prime factor 13 is unpaired. So, given number should be divided by 13.
∴ [2925] ÷ 13 = [3 × 3 × 5 × 5 × 13] ÷ 13
∴ 225 = 3 × 3 × 5 × 5
= 3² × 5²
∴ \(\sqrt{225}\) = 3 × 5 = 15
Thus, 2925 should be divided by smallest whole number 13 to get a perfect square number.

Question (iii).
396
Solution:
396
\(\begin{array}{r|r}
2 & 396 \\
\hline 2 & 198 \\
\hline 3 & 99 \\
\hline 3 & 33 \\
\hline 11 & 11 \\
\hline & 1
\end{array}\)
396 = 2 × 2 × 3 × 3 × 11
Here, the prime factor 11 is unpaired. So, given number should be divided by 11.
∴ [396] ÷ 11 = [2 × 2 × 3 × 3 × 11] ÷ 11
∴ 36 = 2 × 2 × 3 × 3
= 2² × 3²
∴ \(\sqrt{36}\) = 2 × 3 = 6
Thus, 396 should be divided by smallest whole number 11 to get a perfect square number.

Question (iv).
2645
Solution:
2645
\(\begin{array}{r|r}
5 & 2645 \\
\hline 23 & 529 \\
\hline 23 & 23 \\
\hline & 1
\end{array}\)
2645 = 5 × 23 × 23
Here, the prime factor 5 is unpaired. So, given number should be divided by 5.
∴ [2645] ÷ 5 = [5 × 23 × 23] ÷ 5
∴ 529 = 23 × 23 = 23²
∴ \(\sqrt{529}\) = 23
Thus, 2645 should be divided by smallest whole number 5 to get a perfect square number.

Question (v).
2800
Solution:
2800
\(\begin{array}{l|r}
2 & 2800 \\
\hline 2 & 1400 \\
\hline 2 & 700 \\
\hline 2 & 350 \\
\hline 5 & 175 \\
\hline 5 & 35 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)
2800 = 2 × 2 × 2 × 2 × 5 × 5 × 7
Here, the prime number 7 is unpaired. So, given number should be divided by 7.
∴ [2800] ÷ 7 = [2 × 2 × 2 × 2 × 5 × 5 × 7] ÷ 7
∴ 400 = 2 × 2 × 2 × 2 × 5 × 5
= 2² × 2² × 5²
∴ \(\sqrt{400}\) = 2 × 2 × 5 = 20
Thus, 2800 should be divided by smallest whole number 7 to get a perfect square number.

Question (vi).
1620
Solution:
1620
\(\begin{array}{l|r}
2 & 1620 \\
\hline 2 & 810 \\
\hline 3 & 405 \\
\hline 3 & 135 \\
\hline 3 & 45 \\
\hline 3 & 15 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
1620 = 2 × 2 × 3 × 3 × 3 × 3 × 5
Here, the prime factor 5 is unpaired. So, given number should be divided by 5.
∴ [1620] ÷ 5 = [2 × 2 × 3 × 3 × 3 × 3 × 5] ÷ 5
∴ 324 = 2 × 2 × 3 × 3 × 3 × 3
= 2² × 3² × 3²
∴ \(\sqrt{324}\) = 2 × 3 × 3 = 18
Thus, 1620 should be divided by 5 to get a perfect square number.

7. The students of Class VIII of a school donated ₹ 2401 in all, for Prime Minister’s National Relief Fund. Each student donated as many rupees as the number of students in the class. Find the number of students in the class.
Solution:
Let the number of students be x.
Amount each student donated = Number of students in the class.
So, amount donated by each student = ₹ x
Total amount donated by class = ₹ x × x = x²
\(\begin{array}{l|r}
7 & 2401 \\
\hline 7 & 343 \\
\hline 7 & 49 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)
∴ x² = 2401
∴ \(\sqrt{x^{2}}=\sqrt{2401}\)
∴ x = \(\sqrt{7 \times 7 \times 7 \times 7}\)
= \(\sqrt{7^{2} \times 7^{2}}\)
∴ x = 7 × 7 = 49
Hence, number of students in the class is 49.

8. 2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
Solution:
Let the number of rows be x.
Number of rows = Number of plants in each row
So, number of plants in a row = x
∴ Number of plants to be planted in a garden = x × x = x²
\(\begin{array}{l|r}
3 & 2025 \\
\hline 3 & 675 \\
\hline 3 & 225 \\
\hline 3 & 75 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
∴ x² = 2025
∴ \(\sqrt{x^{2}}=\sqrt{2025}\)
∴ x = \(\sqrt{3 \times 3 \times 3 \times 3 \times 5 \times 5}\)
∴ \(\sqrt{3^{2} \times 3^{2} \times 5^{2}}\)
∴ x = 3 × 3 × 5 = 45
Hence, the number of rows is 45 and the number of plants in each row is 45.

9. Find the smallest square number that is divisible by each of the numbers 4, 9 and 10.
Solution :
[Note: LCM is the number, which is divided by all factors of it without leaving remainder. ]
Here, the smallest square number divisible by each one of 4, 9 and 10 is equal to some multiple of the LCM of 4, 9 and 10.
\(\begin{array}{l|ll}
2 & 4, & 9, & 10 \\
\hline 2 & 2, & 9, & 5 \\
\hline 3 & 1, & 9, & 5 \\
\hline 3 & 1, & 3, & 5 \\
\hline 5 & 1, & 1, & 5 \\
\hline & 1, & 1, & 1
\end{array}\)
LCM of 4, 9 and 10 = 2 × 2 × 3 × 3 × 5 = 180
The prime factor 5 is unpaired.
So, 180 must be multiplied by 5.
∴ [180] × 5 = [2 × 2 × 3 × 3 × 5] × 5
∴ 900 = 2² × 3² × 5²
Hence, 900 is the required perfect square number.

10. Find the smallest square number that is divisible by each of the numbers 8, 15 and 20.
Solution:
[Note: LCM is the number, which is divided by all factors of it without leaving remainder.]
Here, the smallest square number divisible by each of 8, 15 and 20 is equal to some multiple of the LCM of 8, 15 and 20.
\(\begin{array}{r|rrr}
2 & 8, & 15, & 20 \\
\hline 2 & 4, & 15, & 10 \\
\hline 2 & 2, & 15, & 5 \\
\hline 3 & 1, & 15, & 5 \\
\hline 5 & 1, & 5, & 5 \\
\hline & 1, & 1, & 1
\end{array}\)
LCM of 8, 15 and 20 = 2 × 2 × 2 × 3 × 5 = 120
The prime factors 2, 3 and 5 are unpaired.
So, 120 should be multiplied by 2 × 3 × 5 = 30.
∴ [120] × 2 × 3 × 5 = [2 × 2 × 2 × 3 × 5] × 2 × 3 × 5
∴ 3600 = 2 × 2 × 2 × 3 × 5 × 2 × 3 × 5
∴ 3600 = 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5
Hence, 3600 is the required perfect square number.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 6 Squares and Square Roots Ex 6.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.2

1. Find the square of the following numbers:

Question (i).
32
Solution:
Let us use: (a + b)² = a² + 2ab + b²
(32)² = (30 + 2)²
= (30)² + 2 (30) (2) + (2)²
= 900 + 120 + 4
= 1024

Question (ii).
35
Solution:
(35)² = (30 + 5)²
= (30)² + 2 (30) (5) + (5)²
= 900 + 300 + 25
= 1200 + 25
= 1225
Second method :
[Note : The unit digit of 35 is 5.]
(35)² = 3 × (3 + 1) × 100 + 25
= 3 × 4 × 100 + 25
= 1200 + 25
= 1225

Question (iii).
86
Solution:
(86)² = (80 + 6)²
= (80)² + 2 (80) (6) + (6)²
= 6400 + 960 + 36
= 7396

Question (iv).
93
Solution:
(93)² = (90 + 3)²
= (90)² + 2 (90) (3) + (3)²
= 8100 + 540 + 9
= 8649

Question (v).
71
Solution:
(71 )² = (70 + 1)²
= (70)² + 2 (70) (1) + (1)²
= 4900 + 140 + 1
= 5041

Question (vi).
46
Solution:
(46)² = (40 + 6)²
= (40)² + 2 (40) (6) + (6)²
= 1600 + 480 + 36
= 2116

2. Write a Pythagorean triplet whose one member is:

Question (i).
6
Solution:
Here, 2n = 6
∴ n = 3

Now, n² – 1 = 3² – 1
= 9 – 1
= 8
and n² + 1 = 3² + 1
= 9 + 1 = 10
Thus, the required Pythagorean triplet is 6, 8, 10.

Question (ii).
14
Solution:
Here, 2n = 14
∴ n = 7
Now, n² – 1 = 7² – 1 = 49 – 1 = 48
and n² + 1 = 7² + 1 = 49 + 1 = 50
Thus, the required Pythagorean triplet is 14, 48, 50.

Question (iii).
16
Solution:
Here, 2n = 16
∴ n = 8
Now, n² – 1 = 8² – 1 = 64 – 1 = 63
and n² + 1 = 8² + 1 = 64 + 1 = 65
Thus, the required Pythagorean triplet is 16, 63, 65.

Question (iv).
18
Solution:
Here, 2n = 18
∴ n = 9
Now n² – 1 = 9² – 1 = 81 – 1 = 80
and n² + 1 = 92 + 1 = 81 + 1 = 82
Thus, the required Pythagorean triplet is 18, 80, 82.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 6 Squares and Square Roots Ex 6.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.1

1. What will be the unit digit of the squares of the following numbers?

Question (i).
81
Solution:
81
Here, the ending digit is 1.
1 × 1 = 1
∴ The unit digit of (81)² will be 1.

Question (ii).
272
Solution:
272
Here, the ending digit is 2.
2 × 2 = 4
∴ The unit digit of (272)² will be 4.

Question (iii).
799
Solution:
799
Here, the ending digit is 9.
9 × 9 = 81
∴ The unit digit of (799)² will be 1.

Question (iv).
3853
Solution:
3853
Here, the ending digit is 3.
3 × 3 = 9
∴ The unit digit of (3853)² will be 9.

Question (v).
1234
Solution:
1234
Here, the ending digit is 4.
4 × 4 = 16
∴ The unit digit of (1234)² will be 6.

Question (vi).
26387
Solution:
26387
Here, the ending digit is 7.
7 × 7 = 49
∴ The unit digit of (26387)² will be 9.

Question (vii).
52698
Solution:
52698
Here, the ending digit is 8.
8 × 8 = 64
∴ The unit digit of (52698)² will be 4.

Question (viii).
99880
Solution:
99880
Here, the ending digit is 0.
0 × 0 = 0
∴ The unit digit of (99880)² will be 0.

Question (ix).
12796
Solution:
12796
Here, the ending digit is 6.
6 × 6 = 36
∴ The unit digit of (12796)² will be 6.

Question (x).
55555
Solution:
55555
Here, the ending digit is 5.
5 × 5 = 25
∴ The unit digit of (55555)² will be 5.

2. The following numbers are obviously not perfect squares. Give reason:

Question (i).
1057
Solution:
1057
Here, the ending digit is 7, which is not one of the digits 0, 1, 4, 5, 6 or 9.
∴ 1057 is not a perfect square.

Question (ii).
23453
Solution:
23453
Here, the ending digit is 3, which is not one of the digits 0, 1, 4, 5, 6 or 9.
∴ 23453 is not a perfect square.

Question (iii).
7928
Solution:
7928
Here, the ending digit is 8, which is not one of the digits 0, 1, 4, 5, 6 or 9.
∴ 7928 is not a perfect square.

Question (iv).
222222
Solution:
222222
Here, the ending digit is 2, which is not one of the digits 0, 1, 4, 5, 6 or 9.
∴ 222222 is not a perfect square.

Question (v).
64000
Solution:
64000
Here, the number of zeros at the end is odd.
∴ 64000 is not a perfect square.

Question (vi).
89722
Solution:
89722
Here, the ending digit is 2, which is not one of the digits 0, 1, 4, 5, 6 or 9.
∴ 89722 is not a perfect square.

Question (vii).
222000
Solution:
222000
Here, the number of zeros at the end is odd.
∴ 222000 is not a perfect square.

Question (viii).
505050
Solution:
505050
Here, the ending digit is 0. (Number of odd zero.)
∴ 505050 is not a perfect square.

3. The squares of which of the following would be odd numbers ?

(i) 431
(ii) 2826
(iii) 7779
(iv) 82004
Solution:
[Note: The square of an odd natural number is odd and that of an even number is an even number.]
(i) 431
This is an odd number.
∴ (431)² is an odd number.

(iii) 7779
This is an odd number.
∴ (7779)² is an odd number.

4. Observe the following pattern and find the missing digits:

Solution :
Observing the above pattern, we can find the missing digits as follows :

5. Observe the following pattern and supply the missing numbers :

Solution:
Observing the above pattern, we can find the missing numbers as follows :

6. Using the given pattern, find the missing numbers:
1² + 2² + 2² = 3²
2² + 3² + 6² = 7²
3² + 4² + 12² = 13²
4² + 5² + …….² = 21²
5² + ……² + 30² = 31²
6² + 7² + ……² = ……²
[To find pattern:
Third number is related to first and second number. How?
Fourth number is related to third number. How?]
Solution:
(a)² + (a + 1)² + {a (a + 1 )}²
= {a (a + 1) + 1}²
The missing numbers are :
1² + 2² + 2² = 3²
2² + 3² + 6² = 7²
3² + 4² + 12² = 13²
4² + 5² + 20² = 21²
5² + 6² + 30² = 31²
6² + 7² + 42² = 43²

7. Without adding, find the sum:

Question (i).
1 + 3 + 5 + 7 + 9
Solution:
The sum of first five odd numbers = 5²
= 5 × 5
= 25

Question (ii).
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
Solution:
The sum of first ten odd numbers = 10²
= 10 × 10
= 100

Question (iii).
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23
Solution:
The sum of first twelve odd numbers = 12²
= 12 × 12
= 144

8.

Question (i).
Express 49 as the sum of 7 odd numbers.
Solution:
49 = 7² = Sum of first seven odd numbers
∴ 49 = 1 + 3 + 5 + 7 + 9 + 11 + 13

Question (ii).
Express 121 as the sum of 11 odd numbers.
Solution :
121 = 11² = Sum of first eleven odd numbers
∴ 121 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21

9. How many numbers lie between squares of the following numbers?
[Note : Between n² and (n + 1)², there are 2n non-square numbers.]

Question (i).
12 and 13
Solution:
Natural numbers between 12² and 13²
= 2 × 12
= 24. (2n, n = 12)

Question (ii).
25 and 26
Solution:
Natural numbers between 25² and 26²
= 2 × 25
= 50. (2n, n = 25)

Question (iii).
99 and 100
Solution:
Natural numbers between 99² and 100²
= 2 × 99
= 198. (2n, n = 99)

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 5 Data Handling InText Questions and Answers.

PSEB 8th Class Maths Solutions Chapter 5 Data Handling InText Questions

Textual (Textbook Page No. 69 – 70)

1. A Pictograph : Pictorial representation of data using symbols.

Question (i).
How many cars were produced in the month of July ?
Solution:
250 cars were produced in the month of July.

Question (ii).
In which month were maximum number of cars produced?
Solution:
Maximum number of cars were produced in the month of September.

2. A Bar Graph : A display of information using bars of uniform width, their heights being proportional to the respective values.

Question (i).
What is the information given by the bar graph ?
Solution:
Here, the bar graph gives information about number of students of class VIII in different academic years.

Question (ii).
In which year is the increase in the number of students maximum ?
Solution:
In year 2004-05, the increase in the number of students is maximum.

Question (iii).
In which year is the number of students maximum ?
Solution:
In year 2007 – 08, the number of students is maximum.

Question (iv).
State whether true or false:
‘The number of students during 2005 – 06 is twice that of 2003 – 04.’
Solution :
False, the number of students during 2005 – 06 is not twice that of 2003 – 04 but more than twice.

3. Double Bar Graph : A bar graph showing two sets of data simultaneously. It is useful for the comparison of the data.

Question (i).
What is the information given by the double bar graph?
Solution :
Here, the double bar graph provides information about marks obtained by a student in different subjects and comparison of his marks in year 2005 – 06 and 2006 – 07.

Question (ii).
In which subject has the performance improved the most?
Solution :
In the subject Maths, the performance has improved the most.

Question (iii).
In which subject has the performance deteriorated?
Solution :
In the subject English, the performance has deteriorated.

Question (iv).
In which subject is the performance at par?
Solution:
In the subject Hindi, the performance is at par.

Think, Discuss and Write (Textbook Page No. 71)

Question 1.
If we change the position of any of the bars of a bar graph, would it change the information being conveyed? Why?
Solution:
If the height of a bar remains unchanged, then changing of its position does not change the information being conveyed.

Try These (Textbook Page No. 71)

Question 1.
Draw an appropriate graph to represent the given information:

Solution:
To represent the given data by a bar graph, draw two axes perpendicular to each other. Let us represent ‘Months’ on \(\overrightarrow{\mathrm{OX}}\) and ‘Number of watches sold’ \(\overrightarrow{\mathrm{OY}}\) on OY. Let us make rectangles of same width. The heights of the rectangles are proportional to the number of watches, using a suitable scale :
Here, scale is 1 cm = 500 watches
Since, 500 watches = 1 cm
1000 watches = 2 cm
1500 watches = 3 cm
2000 watches = 4 cm
2500 watches = 5 cm

Question 2.

Children who prefer	School A	School B	School C
Walking	40	55	15
Cycling	45	25	35

Solution:
Since, a comparison of two activities is to be represented, therefore a double graph is drawn by taking the ‘Schools’ along X-axis and ‘Number of children’ along Y-axis, using a scale of 1 cm = 5 children.

Question 3.
Percentage wins in ODI by 8 top cricket teams.

Teams	From Champions Trophy to World Cup ’06	Last 10 ODI in ’07
South Africa	75%	78%
Australia	61 %	40%
Sri Lanka	54%	38%
New Zealand	47%	50%
England	46%	50%
Pakistan	45%	44%
West Indies	44%	30%
India	43%	56%

Solution:
To compare the percentage win in ODI achieved by various teams, we represent the data by a double bar graph. We represent the ‘Team’s Names’ along the X-axis and their ‘percentage win’ along Y-axis, using the scale 1 cm – 5%.

Try These (Textbook Page No. 72)

1. A group of students were asked to say which animal they would like most to have as a pet. The results are given below:
dog, cat, cat, fish, cat, rabbit, dog, cat, rabbit, dog, cat, dog, dog, dog, cat, cow, fish, rabbit, dog, cat, dog, cat, cat, dog, rabbit, cat, fish, dog.
Make a frequency distribution table for the same.
Solution:
Using tally-marks, we have

Try These (Textbook Page No. 73-74)

1. Study the following frequency distribution table and answer the questions given below.
Frequency Distribution of Daily Income of 550 Workers of a factory:

Class Interval (Daily Income in ₹)	Frequency (Number of workers)
100 – 125	45
125 – 150	25
150 – 175	55
175 – 200	125
200 – 225	140
225 – 250	55
250 – 275	35
275 – 300	50
300 – 325	20
Total	550

Question (i).
What is the size of the class intervals ?
Solution:
Class size = [Upper class limit] – [Lower class limit]
= 125 – 100
= 25

Question (ii).
Which class has the highest frequency ?
Solution:
The class 200 – 225 is having the highest frequency (140).

Question (iii).
Which class has the lowest frequency ?
Solution :
The class 300 – 325 has the lowest frequency (20).

Question (iv).
What is the upper limit of the class interval 250 – 275?
Solution:
The upper limit of the class interval 250 – 275 is 275.

Question (v).
Which two classes have the same frequency ?
Solution :
The classes 150 – 175 and 225 – 250 are having the same frequency (55).

2. Construct a frequency distribution table for the data on weights (in kg) of 20 students of a class using intervals 30 – 35, 35 – 40 and so on.
40, 38, 33, 48, 60, 53, 31, 46, 34, 36, 49, 41, 55, 49, 65, 42, 44, 47, 38, 39
Solution:
Lowest observation = 31
Highest observation = 65
Class intervals :
30-35, 35-40, 40-45, ……..
The frequency distribution table for above data can be prepared as follows :

Try These (Textbook Page No. 75 – 76)

1. Observe the histogram and answer questions given below:

Question (i).
What information is being given by the histogram ?
Solution:
This histogram represents the heights (in cms) of girls of class VII.

Question (ii).
Which group contains maximum girls ?
Solution:
The group 140- 145 contains maximum number of girls (7).

Question (iii).
How many girls have a height of 145 cms and more?
Solution:
7 girls have a height of 145 cm and more (4 + 2 + 1 = 7).

Question (iv).
If we divide the girls into the following three categories, how many would there be in each?
150 cm and more-Group A
140 cm to less
than 150 cm – Group B
Less than 140 cm – Group C
Solution:
Number of girls in
Group A : 150 cm and more = 2 + 1 = 3
Group B : 140 cm and less than 150 cm = 7 + 4 = 11
Group C : Less them 140 cm = 3 + 2 + 1 = 6

Try These (Textbook Page No. 78)

1. Each of the following pie charts gives you a different piece of information !; about your class. Find the fraction of the circle representing each of these information:

Solution:
(i) Fraction of the circle representing the ‘girls’ 50 % = \(\frac {50}{100}\) = \(\frac {1}{2}\)
Fraction of the circle representing the ‘boys’ 50% = \(\frac {50}{100}\) = \(\frac {1}{2}\)

(ii) Fraction of the circle representing ‘walk’ 40 % = \(\frac {40}{100}\) = \(\frac {2}{5}\)
Fraction of the circle representing ‘bus or car’ 40 % = \(\frac {40}{100}\) = \(\frac {2}{5}\)
Fraction of the circle representing ‘cycle’ 20 % = \(\frac {20}{100}\) = \(\frac {1}{5}\)

(iii) Fraction of the circle representing those who love mathematics = (100 – 15)%
= 85 %
= \(\frac {85}{100}\) = \(\frac {17}{20}\)
Fraction of the circle representing those who hate mathematics = 15%
= \(\frac {15}{100}\) = \(\frac {3}{20}\)

2. Answer the following questions based on the pie chart given:

(i) Which type of programmes are viewed the most?
(ii) Which two types of programmes have number of viewers equal to those watching sports channels ?
Solution:
From the given pie chart,

Type of viewers	Percentage
Sports viewers	25 %
News viewers	15 %
Information viewers	10 %
Entertainment viewers	50%

(i) The entertainment programmes are viewed the most (50 %).
(ii) The news and informative programmes have the number of viewers equal to those watching sports channels (15 % + 10 % = 25 %).

Try These (Textbook Page No. 81)

1. Draw a pie chart of the data given below : The time spent by a child during a day.
Sleep – 8 hours
School – 6 hours
Homework – 4 hours
Play – 4 hours
Others – 2 hours
Solution:
First we find the central angle corresponding to each of the given activities.

Activity	Duration of the activity in a day out of 24 hours	Central angle corresponding to the activity
Sleep	8 hours	\(\frac {8}{24}\) × 360° = 120°
School	6 hours	\(\frac {6}{24}\) × 360° = 90°
Home­ work	4 hours	\(\frac {4}{24}\) × 360° = 60°
Play	4 hours	\(\frac {4}{24}\) × 360° = 60°
Others	2 hours	\(\frac {2}{24}\) × 360° = 30°

The required pie chart is given below.
[Note: Dividing a circle into sectors with corresponding angle (with protractor) you get the required pie chart.]

Think, Discuss and Write (Textbook Page No. 81)

Which form of graph would be appropriate to display the following data.

Question 1.
Production of food grains of a state.

Solution :
A bar graph will be an appropriate representation to display given data.

Question 2.

Favourite food	Number of people
North Indian	30
South Indian	40
Gujarati	25
Others	25
Total	120

Solution :
A pie chart (circle graph) will be an appropriate representation to display given data.

Question 3.
The daily income of a group of a factory workers:

Daily income (in Rupees)	Number of workers (in a factory)
75 – 100	45
100 – 125	35
125 – 150	55
150 – 175	30

Solution :
A histogram will be an appropriate representation to display given data.

Try These (Textbook Page No. 83 – 84)

Question 1.
If you try to start a scooter, what are the possible outcomes ?
Solution:
It may start.
It may not start.

Question 2.
When a die is thrown, what are the six possible outcomes?
Solution:
When a die is thrown, the possible outcomes are: 1, 2, 3, 4, 5 or 6 on the upper face of the die.

Question 3.
When you spin the wheel shown, what are the possible outcomes ? (Fig 5.9)
List them.
(Outcome here means the sector at which the pointer stops.)

Solution:
When we spin the wheel shown, the possible outcomes are A, B or C.
[Note: The sector at which the pointer stops is outcome.]

Question 4.
You have a pot with five identical balls of different colours and you are to pull out (draw) a ball without looking at it; list the outcomes you would get (Fig 5.10).

Solution:
When we draw a ball from a bag with five identical balls of different colours, the possible outcomes are : W, R, B, G or Y.

Think, Discuss and Write (Textbook Page No. 84)

In throwing a die:

1. Does the first player have a greater chance of getting a six?
Solution:
No.

2. Would the player who played after him have a lesser chance of getting a six?
Solution:
No.

3. Suppose the second player got a six. Does it mean that the third player would not have a chance of getting a six ?
Solution:
No.

Try These (Textbook Page No. 86)

Suppose you spin the wheel:

1. ( i ) List the number of outcomes of getting a green sector and not getting a green sector on this wheel.
Solution:
Number of outcomes of getting a green sector = 5
Number of outcomes of not getting a green sector = 3

(ii) Find the probability of getting a green sector.
Solution :
∴ The total number of outcomes = 8
Number of outcomes of getting a green sector = 5
∴ Probability of getting a green sector = \(\frac {5}{8}\)

(iii) Find the probability of not getting a green sector.
Solution:
∴ The total number of outcomes = 8
Number of outcomes of not getting a green sector = 3
∴ Probability of not getting a green sector = \(\frac {3}{8}\)

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 11 Mensuration Ex 11.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.4

1. Given a cylindrical tank, in which situation will you find surface area and in which situation volume:

Question (a)
To find how much it can hold.
Solution:
To find how much a cylindrical tank can hold, we will find its volume.

Question (b)
Number of cement bags required to plaster it.
Solution:
To find number of cement bags required to plaster a cylindrical tank, we will find its surface area.

Question (c)
To find the number of smaller tanks that can be filled with water from it.
Solution:
To find the number of smaller tanks that can be filled with water from it, we will find volume of the tank.

2. Diameter of cylinder A is 7 cm and the height is 14 cm.

Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area?
Solution:
Radius of cylinder B is double them that of cylinder A.
∴ Volume of cylinder B should be more than that of cylinder A.

For cylinder A:
radius (r) = \(\frac{diameter}{2}\) = \(\frac{7}{2}\)
height (h) = 14 cm
Volume of cylinder A = πr²h
= \(\frac{22}{7}\) × (\(\frac{22}{7}\))² × 14
= \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) × 14
= 11 × 7 × 7
= 593 cm³

For cylinder B:

radius (r) = \(\frac{diameter}{2}\) = \(\frac{14}{2}\) = 7cm and
height (h) = 7 cm
Volume of cylinder B = πr²h
= \(\frac{22}{7}\) × 7² × 7
= \(\frac{22}{7}\) × 7 × 7 × 7
= 22 × 7 × 7
= 1078 cm³

Total surface area:
For cylinder A:

radius (r) = \(\frac{7}{2}\) cm
height (h) = 14 cm
Total surface area of cylinder A
= 2πr (r + h)
= 2 × \(\frac{22}{7}\) × \(\frac{7}{2}\)(\(\frac{7}{2}\) +14)
= 22(\(\frac{35}{2}\))
= 11 × 35
= 385 cm²

For cylinder B :
radius (r) = 7 cm, height (h) = 7 cm
Total surface area of cylinder B
= 2πr (r + h)
= 2 × \(\frac {22}{7}\) × 7(7 + 7)
= 44(14) = 616 cm²
So the surface area of cylinder B is greater than that of cylinder A. Hence, the cylinder with greater volume also has greater surface area.

3. Find the height of a cuboid whose base area is 180 cm² and volume is 900 cm³?
Solution:
Let the height of cuboid be h cm.
Now, = Area of base × Height
∴ 900 = 180 × h
∴ h = \(\frac {900}{180}\) = 5cm
Hence, height of cuboid is 5 cm.

4. A cuboid is of dimensions 60 cm × 54 cm × 30 cm. How many small cubes with side 6 cm can be placed in the given cuboid?
Solution:
Volume of a cuboid = 60 × 54 × 30 cm³
Volume of a cube = 6³ = 6 × 6 × 6 cm³
∴ Number of small cubes
= \(\frac{\text { Volume of cuboid }}{\text { Volume of one cube}}\)
= \(\frac{60 \times 54 \times 30}{6 \times 6 \times 6}\)
= 10 × 9 × 5 = 450
Hence, 450 cubes can be placed in the given cuboid.

5. Find the height of the cylinder whose volume is 1.54 m³ and diameter of the base is 140 cm?
Solution:
For given cylinder:
Volume = 1.54 m³
Radius(r) = \(\frac {diameter}{2}\) = \(\frac {140}{2}\) = 70cm = 0.7 m
Volume of cylinder = πr²h
∴ 1.54 = \(\frac {22}{7}\) × 0.7 × 0.7 × h
∴ h = \(\frac{1.54 \times 7}{22 \times 0.7 \times 0.7}\) = 1m
Hence, height of the cylinder is 1 m.

6. A milk tank is in the form of cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of milk in litres that can be stored in the tank?
Solution:
For given cylindrical milk tank:
Radius (r) = 1.5 m = \(\frac {15}{10}\) m
Height (h) = 7m
Volume of cylindrical milk tank
= πr²h
= \(\frac {22}{7}\) × (\(\frac {15}{10}\))² × 7
= \(\frac {22}{7}\) × \(\frac {15}{10}\) × \(\frac {15}{10}\) × 7
= \(\frac{11 \times 3 \times 3}{2}=\frac{99}{2}\) = 49.5m³
= 49.5 m³
1 m³ = 1000 litres
∴ 49.5 m³ = 49.5 × 1000 = 49500 litres
Hence, 49,500 litres of milk can be stored in the tank.

7. If each edge of a cube is doubled:

Question (i)
How many times will its surface area increase?
Solution:
Let the edge of the original cube be x.
Then, its new edge (by doubling) = 2x
Original surface area of the cube
= 6 (side)²
= 6 (x)²
= 6x²
New surface area of the cube
= 6 (side)²
= 6 (2x)²
= 6 (2x × 2x)
= 6 (4x²) = 24X²
= \(\frac{\text { New surface area of the cube }}{\text { Original surface area of the cube }}\) = \(\frac{24 x^{2}}{6 x^{2}}\) = 4
Hence, surface area of a cube will increase 4 times.

Question (ii)
How many times will its volume increase ?
Solution:
Original volume of the cube
= (side)³
= (x)³
= x³
New volume of the cube = (side)³
= (2x)³
= (2x × 2x × 2x)
= 8x³
Now,
\(\frac{\text { New volume of the cube }}{\text { Original volume of the cube }}\) = \(\frac{8 x^{3}}{x^{3}}\) = 8
Hence, volume of the cube will increase 8 times.

8. Water is pouring into a cuboidal reservoir at the rate of 60 litres per minute. If the volume of reservoir is 108 m³, find the number of hours it will take to fill the reservoir.
Solution:
Volume of the cuboidal reservoir =108 m³ 1 m³ = 1000 litres
∴ 108 m³ = 108 × 1000 litres
= 1,08,000 litres
Water poured in a minute = 60 litres
∴ Water poured in an hour
(∵ 1 hour = 60 minutes) = 60 × 60
= 3600 litres
Time taken to fill reservoir = \(\frac{\text { volume of reservoir }}{\text { water poured in an hour }}\) = \(\frac {108000}{3600}\)
= 30 hours
Hence, 30 hours it will take to fill the reservoir.

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 5 Data Handling Ex 5.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.3

1. List the outcomes you can see in these experiments:

Question (a).
Spinning a wheel

Solution :
Outcomes of spinning the given wheel are :
A, B, C or D.

Question (b).
Tossing two coins together
Solution:
Outcomes in tossing two coins together are : HH, HT, TT, TH
(H = Head, T = Tail)

2. When a die is thrown, list the outcomes of an event of getting

Question (i).
(a) a prime number.
(b) not a prime number.
Solution:
Possible outcomes are: 1, 2, 3, 4, 5 or 6
Prime numbers = 2, 3, 5
(a) Outcomes of getting a prime number are: 2, 3 or 5.
(b) Outcomes of getting not a prime number are : 1, 4 or 6.

(ii) (a) a number greater than 5.
(b) a number not greater than 5.
Solution:
(a) Outcomes of getting a number greater than 5 is 6.
(b) Outcomes of getting a number not greater than 5 are: 1, 2, 3, 4 or 5.

3. Find the:

Question (a).
Probability of the pointer stopping on D in (Question 1 – (a)) ?
Solution:
There are 5 sectors containing A, B, C and D.
Since, there is only 1 sector containing D.
∴ Favourable outcomes = 1
Number of total outcomes = 5
∴ Probability of the pointer stopping on D = \(\frac {1}{5}\)

Question (b).
Probability of getting an ace from a well shuffled deck of 52 playing cards ?
Solution:
Number of possible outcomes = 52
(Total number of cards in a deck = 52)
Since, there are 4 aces in a pack of 52 cards.
∴ Favourable outcomes = 4
∴ Probability of getting an ace = \(\frac{4}{52}=\frac{1}{13}\)

Question (c).
Probability of getting a red apple. (See figure below)

Solution:
Total number of apples = 7
∴ Possible number of ways = 7
Since, there are 4 red apples.
∴ Favourable outcomes = 4
∴ Probability of getting a red apple = \(\frac {4}{7}\)

4. Numbers 1 to 10 are written on ten separate slips (one number on one slip), kept in a box and mixed well. One slip is chosen from the box without looking into it. What is the probability of.

Question (i).
getting a number 6 ?
Solution :
We can get a slip written the number ‘6’ only once.
∴ Number of favourable outcome = 1
Probability of getting the number 6 = \(\frac {1}{10}\)

Question (ii).
getting a number less than 6 ?
Solution:
Numbers less than 6 are 1, 2, 3, 4 and 5. These are five numbers.
∴ Favourable outcomes = 5
Probability of getting the number less than 6 = \(\frac {5}{10}\) = \(\frac {1}{2}\)

Question (iii).
getting a number greater than 6 ?
Solution :
Numbers greater than 6 are 7, 8, 9 and 10. These are four numbers.
∴ Favourable outcomes = 4
Probability of getting the number greater than 6 = \(\frac {4}{10}\) = \(\frac {2}{5}\)

Question (iv).
getting a 1-digit number ?
Solution :
1-digit numbers are 1, 2, 3, 4, 5, 6, 7, 8 and 9. These are nine numbers.
∴ Favourable outcomes = 9
Probability of getting a 1-digit number = \(\frac {9}{10}\)

5. If you have a spinning wheel with 3 green sectors, 1 blue sector and 1 red sector, what is the probability of getting a green sector? What is the probability of getting a non-blue sector?
Solution:
There are 5 sectors in all.
(3 + 1 + 1 = 5)
∴ Number of total possible outcomes = 3
Probability of getting a green colour sector = \(\frac {3}{5}\)
There are 4 non-blue sectors. (5 – 1 = 4)
∴ Number of favourable outcomes = 4
Probability of getting a non-blue sector = \(\frac {4}{5}\)

6. Find the probabilities of the events given in Question 2.
Solution:
There are 6 outcomes.
(i) 2, 3 and 5 are prime numbers. These are three numbers.
∴ Favourable outcomes = 3
Probability of getting a prime number = \(\frac {3}{6}\) = \(\frac {1}{2}\)

(ii) 1, 4 and 6 are non-prime numbers. These are three numbers.
∴ Favourable outcomes = 3
Probability of getting a non-prime number = \(\frac {3}{6}\) = \(\frac {1}{2}\)

(iii) 6 is greater than 5. This is only one number.
∴ Favourable outcome = 1
Probability of a number greater than 5 = \(\frac {1}{6}\)

(iv) 1, 2, 3, 4 and 5 are not greater than 5. There are five numbers.
∴ Favourable outcomes = 5
Probability of a number which is not greater than 5 = \(\frac {5}{6}\)

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 11 Mensuration Ex 11.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3

1. There are two cuboidal boxes as shown in the figures. Which box requires the lesser amount of material to make?

Solution:
For 1st cuboidal box:
length (l) = 60 cm, breadth (b) = 40 cm and height (h) = 50 cm
Total surface area of a cuboid
= 2 (lb + bh + lh)
= 2 [(60 × 40) + (40 × 50) + (50 × 60)]
= 2 (2400 + 2000 + 3000)
= 2(7400)
= 14,800 cm²

For 2nd cuboidal box:
l = b = h = 50 cm
Total surface area of a cuboid
= 2 (lb + bh + lh)
= 2 [(50 × 50) + (50 × 50) + (50 × 50)]
= 2(2500 + 2500 + 2500)
= 2 × 7500
= 15,000 cm²
As, total surface area of cuboid (a) is less, so the box (a) requires the less amount of material to make.

2. A suitcase with measures 80 cm × 48 cm × 24 cm is to be covered with a tarpaulin cloth. How many metres of tarpaulin of width 96 cm is required to cover 100 such suitcases?
Solution:
Let us find total surface area of a suitcase (cuboidal in shape).
length (l) = 80 cm, breadth (b) = 48 cm and height (h) = 24 cm
∴ Total surface area of a suitcase = 2 (lb + bh + lh)
= 2 [(80 × 48) + (48 × 24) + (24 × 80)]
= 2(3840 + 1152 + 1920)
= 2 (6912)
= 13,824 cm²
Total surface area of such 100 suitcases = 13,824 × 100
= 13,82,400 cm²
Area of 1 metre trapezium
= length × breadth
= 100 × 96 = 9600 cm²
Tarpaulin required to cover 100 suitcases = \(\frac{1382400}{9600}\) = 144 metres
Hence, 144 m tarpaulin is required to cover 100 suitcases.

3. Find the side of a cube whose surface area is 600 cm².
Solution:
Let the side of the cube be x cm
Total surface area of a cube = 6x²
Total surface area of the cube = 600 cm² (Given)
∴ 6x² = 600
∴ x² = \(\frac {600}{6}\)
∴ x² = 100
∴ x² = 10²
∴ x = 10
Hence, the side of the cube is 10 cm.

4. Rukhsar painted the outside of the cabinet of measure 1 m × 2 m × 1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet.

Solution:
For given cabinet:
length (l) = 2 m, breadth (b) = 1 m and height (h) = 1.5 m
Total surface area of the cabinet
= 2 (lb + bh + lh)
= 2 [(2 × 1) + (1 × 1.5) + (2 × 1.5)]
= 2 (2 + 1.5 + 3)
= 2(6.5) = 13 m²
She has not painted bottom. So subtract area of bottom from total surface area of the cabinet.
Area of bottom = l × b = 2 × 1 = 2m²
∴ Painted surface area = (13 – 2) m² = 11 m²
Hence, she has painted 11 m² area of a cabinet.

5. Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth and height of 15 m, 10 m and 7 m respectively. From each can of paint 100 m² of area is painted. How many cans of paint will she need to paint the room?
Solution:
For given wall:
length (l) = 15 m, breadth (b) = 10 m and height (h) = 7 m
∴ Area to be painted
= Area of 4 walls + Area of ceiling
= [2 (l + b) × h] + l × b
= [2(15 + 10) × 7] + 15 × 10
= [2(25) × 7] + 150
= 350 + 150 = 500 m²
Now, one can of paint covers 100 m² area.
∴ Number of paint cans needed
= \(\frac{\text { Area to be painted }}{\text { Area painted by one can }}=\frac{500 \mathrm{~m}^{2}}{100 \mathrm{~m}^{2}}\)
Hence, 5 cans of paint will be needed.

6. Describe how the two figures given are alike and how they are different. Which box has larger lateral surface area?

Solution:
Here, figure (i) is cylinder and figure (ii) is cube.
Similarity: Both have the same height.
Difference: One is the cylinder and the other is a cube.
For cylinder:
Radius = \(\frac{\text { diameter }}{2}=\frac{7}{2}\) = cm
Height = 7 cm
∴ Lateral (curved) surface area of cylinder
= 2πrh
= 2 × \(\frac{22}{7} \times \frac{7}{2}\) × 7
= 22 × 7 = 154 cm²

For given cube:
side = 7 cm
Lateral surface area of the cube
= 4l² = 4 × 7²
= 4 × 49 = 196 cm²
Hence, cubical box has a larger area.

7. A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How much sheet of metal is required?
Solution:
For given cylindrical tank:
radius (r) = 7 m, height (h) = 3 m
Total surface area of tank
= 2πr (r + h)
= 2 × \(\frac {22}{7}\) × 7(7 + 3)
= 44(10) = 440 m²
Hence, 440 m² sheet of metal is required.

8. The lateral surface area of a hollow cylinder is 4224 cm². It is cut along its height and formed a rectangular sheet of width 33 cm. Find the perimeter of rectangular sheet?
Solution:
Lateral surface area of a hollow cylinder = 4224 cm² (Given)
Let length of a rectangular sheet made from hollow cylinder be l cm.
∴ l × b = 4224
∴ 1 × 33 = 4224
∴ l = \(\frac {4224}{33}\) = 128 cm
∴ Length of rectangular sheet =128 cm

Perimeter of rectangular sheet
= 2 (l + b)
= 2 (128 + 33)
= 2 (161) = 322 cm
Hence, perimeter of rectangular sheet is 322 cm.

9. A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road levelled if the diameter of a road roller is 84 cm and length is 1 m.
Solution:
Shape of road roller is cylindrical.

For given cylinder:
Radius (r) = \(\frac{\text { diameter }}{2}\) = \(\frac {84}{2}\) = 42cm
length (height) (h) = 1 m = 100 cm
∴ Curved surface area of a roller
= 2 πrh
= 2 × \(\frac {22}{7}\) × 42 × 100
= 26,400 cm²
Roller covers area of 26,400 cm² in 1 revolution.
∴ Area of covered by roller in 750 revolutions
= 26400 × 750 cm²
= \(\frac{26400 \times 750}{100 \times 100}\) m²
= 1980 m²
Hence, area of road levelled is 1980 m².

10. A company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm.

Company places a lable around the surface of the container (as shown in the figure). If the lable is placed 2 cm from top and bottom, what is the area of the label.
Solution:
For given cylindrical container:
radius (r) = \(\frac {diameter}{2}\) = \(\frac {14}{2}\) = 7 cm
height (h) = 20 cm
Now, label is placed 2 cm away from top and bottom.
∴ Height of label = (20 – 2 – 2) cm
= (20 – 4) cm = 16 cm
For label:
radius (r) = 7 cm, height (h) = 16 cm
∴ Area of cylindrical label = 2πrh
= 2 × \(\frac {22}{7}\) × 7 × 16
= 44 × 16
= 704 cm²
Hence, area of the label is 704 cm².