Class 7

Punjab State Board PSEB 7th Class Hindi Book Solutions Chapter 17 राखी की चुनौती Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Hindi Chapter 17 राखी की चुनौती

Hindi Guide for Class 7 PSEB राखी की चुनौती Textbook Questions and Answers

(क) भाषा-बोध

1. शब्दार्थ

शब्दों के अर्थ सरलार्थों के साथ दिए गए हैं।

तड़ित = बिजली
घन = बादल
गगन = आकाश
पुष्प = फूल
आर्द = गीली
रुलाई = रोना
स्वाधीनता = आजादी
जालिम = अत्याचारी
गर्व = स्वाभिमान

2. इन मुहावरों के अर्थ लिखते हुए वाक्यों में प्रयोग करें :

फूले न समाना _____________ _________________
खिलना _______________ ______________________
धूनी तपना ____________ _____________________
मंगल मनाना _____________ ____________________
घायल हृदय _____________ ______________________
खूनी दर्द उठना _______________ ____________________
विषमता का बन्धन ______________ ____________________
उत्तर:
फूले न समाना (प्रसन्न होना) – सुभद्रा अपने भाई को देख कर फूली न समाई।
खिलना (प्रसन्न हो जाना) –  विदेश से आए अपने पुत्र को देखकर माँ का हृदय खिल उठा।
धूनी तपना (कष्ट झेलना) – देशभक्तों को देश को आजाद करवाने के लिए धूनी तापनी पड़ती है।
मंगल मनाना (शुभ कामना करना) – मैं आपके सुखी भविष्य के लिए मंगल मनाता हूँ।
घायल हृदय (अत्यन्त पीड़ा होना) – मेरा घायल हृदय माता-पिता को देखने के लिए तड़पता है।
खूनी दर्द उठना (तीखी पीड़ा होना) – राखी के दिन भी भाई को कैद में पाकर बहन के हृदय में खूनी दर्द उठता है।
विषमता का बन्धन (भेदभाव का बन्धन) – हमें पारस्परिक विषमता के बन्धनों को काट कर मिल-जुल कर रहना चाहिए।

3. तड़ित आज फूली समाती न घन में,
लता आज फूली समाती न वन में
कहीं बूंद है पुष्प प्यारे खिले हैं,
मैं हूँ, बहिन, किन्तु भाई नहीं है,
छीनी हुई माँ की स्वाधीनता को
वह जालिम के घर में से लाने गया है।

रेखांकित शब्दों के दो-दो पर्यायवाची (समानार्थक) शब्द लिखें

तड़ित = ____________ ________________
लता = _______________ ________________
घन = ___________ __________________
पुष्प = _______________ ___________________
बहिन = _______________ _________________
भाई = ________________ _________________
माँ = ____________ ________________
स्वाधीनता = ____________ _________________
जालिम = _____________ __________________
घर = ________________ ____________________
उत्तर:
तड़ित – बिजली, विद्युत्।
लता – बेल, वल्लरी।
घन- बादल, मेघ।
पुष्प- फूल, सुमन।
बहिन – भगिनी, सहोदरा।
भाई – भ्राता, सहोदर।
माँ – माता, जननी।
स्वाधीनता – स्वतन्त्रता, आज़ादी।
जालिम – दुष्ट, खल।
घर – गृह, सदन।

4. इन भाववाचक संज्ञाओं का मूल रूप लिखें :

चमक, सुहाई, खुशी, रुलाई, स्वाधीनता, विषमता।
उत्तर:
चमकीला, सुहावना, खुश, रोना, स्वाधीन, विषम।

(ख) विचार-बोध

1. उपयुक्त शब्द भरकर वाक्य पूरा करें:

1. बहिन …………. के कारण मन में अत्यन्त खुश है।
2. बिजली …………. के कारण बादल में अत्यन्त खुश है।
3. घटा …………. के कारण आकाश में अत्यन्त खुश है।
4. लता …………. के कारण वन में अत्यन्त खुश है।
5. मेरा बन्धु देश को आजाद कराने के लिए …………. में गया है। (जेलखाने, फूल खिलने, चमकने, राखी, वर्षा)

उत्तर:

1. राखी।
2. चमकने
3. वर्षा
4. फूल खिलने
5. जेलखाने

2. इन प्रश्नों के उत्तर एक या दो वाक्यों में लिखें :

प्रश्न 1.
राखी का त्योहार कब आता है ?
उत्तर:
राखी का त्योहार सावन महीने की पूर्णिमा को आता है।

प्रश्न 2.
बहनें उस दिन हर्षित क्यों होती हैं ?
उत्तर:
बहनें राखी के दिन अपने भाइयों की कलाइयों पर राखी बाँध कर हर्षित होती हैं।

प्रश्न 3.
लेखिका का भाई कहाँ गया है ?
उत्तर:
लेखिका का भाई देश की स्वतन्त्रता के लिए जेल गया है।

प्रश्न 4.
क्या भाई के सम्मुख न होने से वह दुखी है ?
उत्तर:
बहन भाई के सम्मुख न होने से दुखी नहीं है, क्योंकि उसका भाई महान् कार्य के लिए जेल गया है।

प्रश्न 5.
उसकी ‘राखी’ कैसी है ?
उत्तर:
बहन की राखी रेशम से कोमल नहीं है बल्कि एक लोहे की हथकड़ी के समान है।

3. इन प्रश्नों के उत्तर चार-पाँच वाक्यों में लिखें :

1. लेखिका राखी के पवित्र त्योहार के शुभ अवसर पर देश के नवयुवकों को क्या चुनौती देती है ?
उत्तर:
लेखिका राखी के पवित्र त्योहार के शुभ अवसर पर देश के युवकों को चुनौती देती है कि यदि राखी बंधवानी है तो देश के लिए त्याग करने के लिए तैयार हो जाओ। भारत माता को विदेशी अत्याचारी अंग्रेजों की गुलामी से आजादी दिलवाने के लिए जेल जाना पड़े तो जेल भी जाओ।

(ग) भाव-बोध

निम्न पद्यांशों का भाव स्पष्ट करें :

1. है भादो, घटा किन्तु छाई नहीं है,
नहीं है खुशी, पर रुलाई नहीं है।

2. हम मंगल मनावें, वह तपता है धूनी,
है घायल हृदय, दर्द उठता है खूनी।

3. आते हो भाई पुनः पूछती हूँ,
विषमता के बँधन की है लाज तुम को
तो बन्दी बनो देखो बन्धन है कैसा ?
चुनौती यह राखी की है आज तुमको॥
उत्तर:
इन पद्यांशों के सरलार्थ-भाग को देखिए।

(घ) रचना

रक्षा बन्धन के पवित्र त्योहार पर तुम्हारे भाई ने तुम्हें घड़ी का उपहार दिया है, इस उपहार की उपयोगिता बताते हुए उसका धन्यवाद पत्र के द्वारा करें।
उत्तर:
912-शिवाजी पार्क,
जालन्धर शहर।
दिनांक 22 जुलाई, 20…..
पूज्य भाई साहब,
सादर नमस्कार।
आपकी प्रतीक्षा कर रही थी कि आप रक्षाबन्धन पर अवश्य आएँगे, परन्तु मिला आप के द्वारा भेजा गया पैकेट। जब मैंने इसे खोला तो इसमें आकर्षक घड़ी प्राप्त कर मैं खुशी से झूम उठी। इस में अलार्म, डेट, महीना, दिन देखकर तो मेरी सभी समस्याएँ हल हो गईं। मैं समय पर सब कार्य कर सकूँगी तथा दिन, महीना, तारीख भी नहीं भूलूंगी। इसके लिए बहुत-बहुत धन्यवाद। आप अवसर निकाल कर शीघ्र आइएगा। आदरणीया भाभी जी को मेरा नमस्कार कहिए तथा हार्दिक और आद्या को मेरा प्यार भरा आशीर्वाद दीजिए।
आपकी प्यारी छोटी बहन
रश्मि ।

(ङ) करो
* अपने हाथ से राखी तैयार कर अपने भाई को भेजें।

PSEB 7th Class Hindi Guide राखी की चुनौती Important Questions and Answers

1. निम्नलिखित प्रश्नों के उत्तर उचित विकल्प चुनकर लिखिए

प्रश्न 1.
‘राखी की चुनौती’ कविता की रचनाकार कौन है ?
(क) सुभद्रा कुमारी चौहान
(ख) धर्मवीर भारती
(ग) सूर्यकांत त्रिपाठी निराला
(घ) सुमित्रा नंदन पंत
उत्तर:
(क) सुभद्रा कुमारी चौहान

प्रश्न 2.
कौन-से त्योहार पर बहन फूली नहीं समाती ?
(क) दीपावली
(ख) रक्षाबंधन
(ग) होली
(घ) दशहरा
उत्तर:
(ख) रक्षाबंधन

प्रश्न 3.
कवयित्री ने वीरों के लिए किसे चुनौती कहा है ?
(क) राखी को
(ख) माला को
(ग) घर को
(घ) धन को
उत्तर:
(क) राखी को

प्रश्न 4.
कवयित्री भाई को क्या प्रेरणा दे रही है ?
(क) बेटी बचाओ
(ख) खूब पढ़ो
(ग) भारत माता को गुलामी से मुक्त कराओ
(घ) कोई नहीं
उत्तर:
(ग) भारत माता को गुलामी से मुक्त कराओ।

प्रश्न 5.
देश को आजाद कराने के लिए बहन कौन-सी राखी बाँधने को तैयार
(क) हथकड़ी रूपी
(ख) फूल रूपी
(ग) धागारूपी
(घ) कोई नहीं
उत्तर:
(क) हथकड़ी रूपी

2. दिए गए शब्द का सही अर्थ से मिलान कीजिए

प्रश्न 1.
पूनो:
कार्तिक
अमावस्या
पूर्णिमा
उत्तर:
पूर्णिमा

प्रश्न 2.
भादों:
अंग्रेज़ी महीना
हिंदी महीना
भाग जा
उत्तर:
हिंदी महीना

प्रश्न 3.
घटा:
बादल
घाटी
खटाई
उत्तर:
बादल

प्रश्न 4.
तड़ित
बिजली
ताड़का
ताकना
उत्तर:
बिजली।

सप्रसंग सरलार्थ

1. बहिन आज फूली समाती न मन में,
तड़ित आज फूली समाती न घन में।
घटा है न फूली समाती गगन में,
लता आज फूली समाती न वन में।

शब्दार्थ:
फूली समाती न = बहुत प्रसन्न। तड़ित = बिजली। घन = बादल। घटा = बादलों का समूह । गगन = आकाश वन = जंगल। प्रसंग-यह पद्यांश श्रीमती सुभद्रा कुमारी चौहान द्वारा लिखित ‘राखी की चुनौती’ नामक कविता से लिया गया है। इसमें कवयित्री ने देशभक्त भाइयों को देश की आजादी के लिए जेल जा कर भारत माता को आजाद कराने की प्रेरणा दी है।

सरलार्थ:
कवयित्री कहती है कि आज राखी के त्योहार पर बहन मन में फूली नहीं समाती है, बहन बहुत ही प्रसन्न है। बिजली भी बादलों में चमकती हुई फूली नहीं समा रही। घटा आकाश में फूली नहीं समाती । काले बादलों का समूह आकाश में छाया हुआ है। लता आज वन में फूली नहीं समाती । लता पूरी तरह खिली हुई है। प्रकृति भी आज प्रसन्न है।

भाव:
रक्षा-बन्धन के अवसर पर मानव समाज के साथ प्रकृति भी आनन्द-मंगल मना रही है। बहनें भाइयों की कलाई पर आज राखी बाँधने के लिए प्रसन्न हैं।

2. कहीं राखियाँ हैं, चमक है कहीं पर,
कहीं बूंद है, पुष्प प्यारे खिले हैं।
ये आई है राखी, सुहाई है पूनी,
बधाई उन्हें जिनको भाई मिले हैं।।

शब्दार्थ:
पुष्प = फूल। सुहाई = शोभा देती है। पूनो = पूर्णिमा।

प्रसंग:
यह पद्यांश श्रीमती सुभद्रा कुमारी चौहान द्वारा लिखित ‘राखी की चुनौती’ नामक कविता से लिया गया है। इसमें कवयित्री ने देशभक्त भाइयों को देश की आज़ादी के लिए जेल जाकर भारत माता को आजाद कराने की प्रेरणा दी है।

सरलार्थ:
कवयित्री कहती है कि आज रक्षा बन्धन के अवसर पर स्थान-स्थान पर राखियाँ दिखाई देती हैं। कहीं उनकी चमक-दमक शोभा दे रही है तो कहीं सावन के महीने में वर्षा की फुहारें पड़ रही हैं और बूंदें गिर रही हैं। कहीं-कहीं सुन्दर प्यारे फूल खिले हए हैं। आज राखी का सुन्दर और पवित्र पर्व आ गया है। पूर्णिमा का यह पर्व बहुत सुन्दर लग रहा है। इस शुभ अवसर पर उन्हें बधाई है जिनके भाई उनके पास हैं।

भाव:
राखी के शुभ पर्व के अवसर पर मानव तथा प्रकृति दोनों प्रसन्न हैं।

3. मैं हूँ बहिन किन्तु भाई नहीं है,
है राखी सजी पर कलाई नहीं है।
है भादों, घटा किन्तु छाई नहीं है,
नहीं है खुशी पर रुलाई नहीं है।

शब्दार्थ:
सजी है = सुन्दर लगती है। कलाई = बाजू का अगला भाग। रुलाई = रोना। घटा = बादलों का समूह। छाई = फैला।

प्रसंग:
यह पद्यांश श्रीमती सुभद्रा कुमारी चौहान द्वारा लिखित ‘राखी की चुनौती’ नामक कविता से लिया गया है। इसमें कवयित्री ने देशभक्त वीरों को देश की आजादी के लिए जेल जाने के लिए प्रेरित किया है।

सरलार्थ:
कवयित्री कहती है कि मैं बहन अपने घर में हूँ, किन्तु मेरा भाई मेरे पास नहीं है। (वह देश की आज़ादी के लिए सत्याग्रह करके जेल गया हुआ है।) सुन्दर राखी तो मेरे हाथ में है, परन्तु भाई की कलाई नहीं है। ऐसा लगता है जैसे भादों का महीना है, फिर भी घटा छाई हुई नहीं है। इस समय न तो मुझे प्रसन्नता है और रोना है। भाई देश की आज़ादी के लिए जेल गया है। वह अच्छे उद्देश्य को पूरा करने के लिए जेल गया है, इसलिए दुःख नहीं है परन्तु उसके पास न होने से प्रसन्नता भी नहीं है।

भाव:
भाई को राखी न बाँध सकने के कारण बहन प्रसन्न नहीं है परन्तु देश को आज़ाद कराने के लिए भाई जेल गया है इसलिए वह दुखी भी नहीं है।

4. मेरा बन्धु माँ की पुकारों को सुनकर
के तैयार हो जेलखाने गया है।
छीनी हई माँ की स्वाधीनता को,
वह ज़ालिम के घर में से लाने गया है।

शब्दार्थ:
बन्धु = भाई। स्वाधीनता = आज़ादी। ज़ालिम = निर्दयी।

प्रसंग:
यह पद्यांश श्रीमती सुभद्रा कुमारी चौहान द्वारा लिखित ‘राखी की चुनौती’ नामक कविता से लिया गया है। इसमें कवयित्री ने देशभक्त वीरों को देश की आजादी के लिए जेल में बंदी होने के लिए प्रेरित किया है।

सरलार्थ:
कवयित्री कहती है मेरा भाई भारत माता की पुकार को सुनकर उसे गुलामी के बंधन से छुड़ाने के लिए तैयार हो कर जेल गया है। वह अंग्रेजों द्वारा छीनी गई भारत माता की आज़ादी को अत्याचारी अंग्रेज़ों के घर में से लाने के लिए ही जेल में गया है।

भाव:
बहन का भाई देश को स्वतंत्र कराने जेल गया है।

5. मुझे गर्व है किन्तु राखी है सूनी,
वह होता, खुशी तो क्या होती न दूनी।
हम मंगल मनावें, वह तपता है धूनी,
है घायल हृदय, दर्द उठता है खूनी॥

शब्दार्थ:
गर्व = अभिमान। किन्तु = लेकिन। दूनी = दुगुनी। धूनी = तपने की आग। दर्द = दुःख। खूनी – खून बहाने वाला। मंगल = कल्याण।

प्रसंग:
यह पद्यांश श्रीमती सुभद्रा कुमारी चौहान द्वारा लिखित ‘राखी की चुनौती’ नामक कविता से लिया गया है। इसमें कवयित्री ने देशभक्त वीरों को देश की आजादी के लिए जेल में बंदी होने के लिए प्रेरित किया है।

सरलार्थ:
कवयित्री कहती है कि मुझे भाई के जेल जाने का गर्व है, परन्तु भाई के पास न होने के कारण राखी सूनी पड़ी है। यदि भाई मेरे पास होता तो क्या मुझे दुगुनी खुशी न होती अर्थात् दुगुनी प्रसन्नता ज़रूर होती। हम यहाँ पर मंगल मना रही हैं और वह जेल में तपस्या कर रहा है। इस भेदभाव के कारण कवयित्री कहती है मेरा हृदय घायल है और उसमें से खून बहा देने वाली पीड़ा हो रही है।

भाव:
बहन अपने भाई के जेल में होने से दुखी है।

6. अब तो बढ़े हाथ, राखी पड़ी है,
रेशम की कोमल नहीं, यह कड़ी है।
अजी देखो लोहे की यह हथकड़ी है,
इसी प्रण को लेकर बहिन यह खड़ी है।

शब्दार्थ-कोमल = नरम। प्रण = प्रतिज्ञा, वचन। कड़ी = सख्त ।

प्रसंग:
यह पद्यांश श्रीमती सुभद्रा कुमारी चौहान द्वारा लिखित ‘राखी की चुनौती’ नामक कविता से लिया गया है। इसमें कवयित्री ने देशभक्त वीरों को देश की आजादी के लिए जेल में बंदी होने के लिए प्रेरित किया है।

सरलार्थ:
कवयित्री कहती है हे भाई! यदि तुम्हें दुःख है तो अपना हाथ आगे बढ़ाओ, यह राखी पड़ी हुई है। यह रेशम के समान कोमल नहीं है, यह बहुत सख्त है। अजी देखो, यह तो लोहे की हथकड़ी है। इसी प्रण को लेकर बहन राखी लेकर खड़ी हुई है।

भाव:
बहन भाई को देश को आजाद कराने के लिए रेशम की राखी के स्थान पर लोहे की हथकड़ी रूपी राखी बाँधने के लिए तैयार है।

7. आते हो भाई पुनः पूछती हूँ,
विषमता के बंधन की है लाज तुमको।
तो बन्दी बनो देखो बन्धन है कैसा,
चुनौती यह राखी की है आज तुमको॥

शब्दार्थ:
पुनः = फिर । विषमता = भेदभाव। लाज = शर्म । बन्दी = कैदी। बंधन = बाँधने का साधन। चुनौती = ललकार।

प्रसंग:
यह पद्यांश श्रीमती सुभद्रा कुमारी चौहान द्वारा लिखित ‘राखी की चुनौती’ नामक कविता से लिया गया है। इसमें कवयित्री ने वीरों को देश की आजादी के लिए जेल में बंदी होने के लिए प्रेरित किया है।

सरलार्थ:
कवयित्री कहती है कि हे भाई! क्या तुम आते हो? मैं तुम्हें फिर पूछती हूँ। तुम को इस विषम परिस्थिति के रक्षा के बन्धन की थोड़ी-सी भी लज्जा है, तो कैदी बनो, और देखो कि यह राष्ट्र रक्षा का कैसे बन्धन है? आज मेरी तुम को यह राखी एक चुनौती है कि तुम बन्दी बनकर भारत माता को गुलामी से छुड़ाओ।

भाव:
कवयित्री भाई को भारत माता को गुलामी के बन्धनों से मुक्त कराने की प्रेरणा दे रही है।

रारवी की चुनौती Summary

रारवी की चुनौती कविता का सार

‘राखी की चुनौती’ कविता सुभद्रा कुमारी चौहान द्वारा रचित है, जिस में कवयित्री ने रक्षा-बंधन के पर्व पर देश को स्वतंत्र कराने के लिए जेल में बन्द अपने भाई को राखी की चुनौती देते हुए भारत माँ की स्वाधीनता को वापस लाने के लिए कहा है। कवयित्री लिखती है कि आज राखी के दिन बहन मन में, बिजली बादलों में, घटा आकाश में और लता वन में फूली नहीं समा रही है। कहीं राखियाँ, कहीं वर्षा की बूंदे, कहीं फूल खिले हैं। पूर्णिमा के इस राखी पर्व पर उन्हें बधाई है, जिन्हें भाई मिले हैं। बहन घर में है पर उसका भाई यहाँ नहीं है, भादों है पर घटा छाई नहीं है, प्रसन्नता न होते हुए भी दुःख भी नहीं है। भाई भारत माता को गुलामी के बन्धनों से छुड़ाने के लिए जेल गया है। इसलिए गर्व तो है परन्तु भाई को राखी नहीं बांध सकती, वह होता तो खुशी दुगुनी हो जाती। यहाँ आनन्द मन रहा है और भाई जेल में तप रहा है, यही बहन को दुःख है। उस के पास भाई के लिए लोहे की हथकड़ी जैसी राखी है। वह चाहती है कि इस विषम परिस्थिति में यदि उसके भाई को कुछ भी लज्जा है तो वह इसका कैदी बन कर देखे कि राखी का बन्धन कैसा होता है? यही उसकी राखी उसे आज चुनौती दे रही है।

Punjab State Board PSEB 7th Class Hindi Book Solutions Chapter 16 हुसैनी वाला बार्डर Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Hindi Chapter 16 हुसैनी वाला बार्डर

Hindi Guide for Class 7 PSEB हुसैनी वाला बार्डर Textbook Questions and Answers

(क) भाषा-बोध

1. शब्दार्थ

अत्यन्त = बहुत अधिक
हर्ष = खुशी, प्रसन्नता
ग्रीष्म = गर्मी
भ्रमण = घूमना
दर्शनीय = देखने योग्य
सीमा = सरहद
दरिया = नदी
निकट = नज़दीक
मुक्ति = आज़ादी
जुल्म = अत्याचार
रोष = क्रोध
निर्धारित = निश्चित
पूर्व = पहले
परिजनों = रिश्तेदारों
आनन-फानन = तुरन्त
दाह-संस्कार = जलाने का कार्य
वंदनीय = सम्मान के योग्य
विभूषित = सुशोभित
बार्डर = सीमा, सरहद
रिट्रीट = पश्चगमन, वापसी
कुर्बानी = बलिदान
अजब = अनोखा
दास्तां = कहानी
बयान = वर्णन, बखाना
स्मृति = याद
शहादत = बलिदान
यादगार = स्मारक
अनपढ़ता = अशिक्षा

2. इन मुहावरों के अर्थ समझते हुए वाक्यों में प्रयोग करें:

प्राणों की बाज़ी लगाना – प्राण न्योछावर करना _______________________
ठाठे मारना – राष्ट्रीयता की भावनाएँ हृदय में जागृत होना ________________________
प्राण न्योछावर करना – शहीद होना _______________________
उत्तर:
वीर सैनिक अपने देश की रक्षा के लिए अपने प्राणों की बाज़ी लगा देते हैं।
शिशु को रोते देखकर माँ के हृदय में ममता का सागर ठाठे मारने लगा।
आतंकवादियों से मुठभेड़ में मेजर साहब ने अपने प्राण न्योछावर कर दिए।

3. इन शब्दों के विपरीत अर्थ वाले शब्द लिखें:

हर्ष = ………………
इच्छा = ………………..
न्याय = …………………
अनपढ़ = ……………
उत्तर:
शब्द विपरीत शब्द
हर्ष = शोक
इच्छा = अनिच्छा
न्याय = अन्याय
अनपढ़ = पढ़ा-लिखा

4. इन शब्दों में से मूल शब्द अलग करके लिखें:

दर्शनीय = …………………
वंदनीय = ……………….
आकर्षित = ………………..
शहीदी = ………………….
केन्द्रीय = …………………
सम्मानित = …………………
विभूषित = ………………….
उत्तर:
शब्द मूल शब्द
दर्शनीय = दर्शन
वंदनीय = वंदन
आकर्षित = कर्षित
शहीदी = शहीद
केन्द्रीय = केन्द्र
सम्मानित = सम्मान
विभूषित = भूषित
भारतीय = भारत

5. इन वाक्यों में उचित विशेषण शब्द लिखकर वाक्य पूरे करें :

1. फिरोज़पुर पंजाब का ……………. नगर है।
2. हुसैनीवाला में …………… भगतसिंह, राजगुरु और सुखदेव की समाधियाँ हैं।
3. यहाँ पर भगतसिंह के ……………. बटुकेश्वरदत्त और ……………. विद्यावती की भी समाधियाँ हैं।
4. शाने हिन्द देश की …………., ……………., ……………., ……………..  का प्रतीक है।
5. बर्की मैमोरियल 1965 के युद्ध में ………….. सैनिकों की ………… बयान करते हैं।
6. सारागढ़ी गुरुद्वारा ………….. सिक्ख सैनिकों की ………….. की यादगार है।

उत्तर:

1. फिरोजपुर पंजाब का बहुत प्राचीन नगर है।
2. हुसैनीवाला में देशभक्त भगतसिंह, राजगुरु और सुखदेव की समाधियाँ हैं।
3. यहाँ पर भगतसिंह के पुराने साथी बटुकेश्वरदत्त और पंजाब माता विद्यावती की भी समाधियाँ हैं।
4. शाने हिन्द देश की विशाल, महान, बड़े, शक्तिशाली का प्रतीक है।
5. बर्की मैमोरियल 1965 के युद्ध में भारतीय सैनिकों की वीरता बयान करते हैं।
6. सारागढ़ी गुरुद्वारा बहादुर सिक्ख सैनिकों की शहादत की यादगार है।

(ख) विचार-बोध

1. इन प्रश्नों के उत्तर एक या दो वाक्यों में लिखें :

प्रश्न 1.
फिरोज़पुर से हुसैनीवाला बार्डर कितनी दूर है ?
उत्तर:
फिरोज़पुर से हुसैनीवाला बार्डर लगभग ग्यारह किलोमीटर दूर है।

प्रश्न 2.
हुसैनीवाला में किन-किन शहीदों के समाधि स्थल हैं ?
उत्तर:
हुसैनीवाला में भगत सिंह, राजगुरु और सुखदेव की समाधियाँ हैं। इसके साथ भगतसिंह के मित्र बटुकेश्वर दत्त और भगत सिंह की माता पंजाब माता विद्यावती की समाधियाँ भी हैं।

प्रश्न 3.
इन शहीदों को ब्रिटिश सरकार ने निर्धारित समय से पूर्व फाँसी कब और क्यों दे दी ?
उत्तर:
ब्रिटिश सरकार ने भगत सिंह, राजगुरु और सुखदेव को फांसी 24 मार्च, 1931 से पहले 23 मार्च, सन् 1931 की शाम को इसलिए दे दी गई जिससे भारतीय जनता के रोष और विद्रोह का उन्हें सामना न करना पड़े।

प्रश्न 4.
किस व्यक्ति के प्रयासों से इस बार्डर पर रिट्रीट समारोह आरम्भ हुआ ?
उत्तर:
रिट्रीट समारोह का आरम्भ इंस्पैक्टर जनरल बी० एस० अश्वनी कुमार के प्रयासों से हुआ ।

प्रश्न 5.
सीमा रेखा पर शाने-हिन्द और फक्र-ए-पाक किसका प्रतीक है ?
उत्तर:
सीमा रेखा पर शाने-हिन्द और फक्र-ए-पाक भारत-पाकिस्तान के प्रतीक हैं।

प्रश्न 6.
बर्की मैमोरियल किनकी स्मृति में बनाया गया ?
उत्तर:
बी मैमोरियल सन् 1965 ई० में शहीद हुए सैनिकों की स्मृति में बनाया गया है।

प्रश्न 7.
सारागढ़ी गुरुद्वारा किस शहादत की यादगार है ?
उत्तर:
सारागढ़ी गुरुद्वारा वर्जिस्तान के सारागढ़ी किले की रक्षा में शहीद हुए 36 सिक्ख रेजीमेंट के 21 सिक्ख सैनिकों की यादगार में बनाया गया है।

2. इन प्रश्नों के उत्तर चार या पाँच वाक्यों में लिखें:

प्रश्न 1.
फिरोज़पुर के बारे में आप क्या जानते हैं ?
उत्तर:
फिरोज़पुर पंजाब का बहुत प्राचीन शहर है। इसे चौदहवीं शताब्दी में फिरोजशाह तुग़लक ने बसाया था। फिरोज़पुर शहर और छावनी दो भागों में बंटा हुआ है। फिरोज़पुर भारत-पाकिस्तान सीमा के नज़दीक बसा हुआ है। यहाँ से हुसैनीवाला बार्डर लगभग ग्यारह किलोमीटर दूर है। यहाँ सारागढ़ी काम्पलैक्स में बर्की मैमोरियल और सारागढ़ी मैमोरियल दर्शनीय स्थल हैं।

प्रश्न 2.
हुसैनीवाला बार्डर के निकट कौन-कौन से तीर्थ स्थल हैं ?
उत्तर:
हुसैनीवाला बार्डर के निकट वह तीर्थ है जहाँ भगत सिंह, राजगुरु और सुखदेव को फाँसी देकर उनका दाह संस्कार किया गया था। यहीं पर भगतसिंह, राजगुरु और सुखदेव की समाधियाँ बनाई गई हैं। इनके पास असैम्बली बम कांड के भगतसिंह के साथी शहीद बटुकेश्वर दत्त की समाधि है। पंजाब माता तथा भगतसिंह की माँ विद्यावती की समाधि भी यहीं बनाई गई है।

प्रश्न 3.
शहीदों का बलिदान हमें क्या याद दिलाता है ?
उत्तर:
शहीदों का बलिदान हमें याद दिलाता है कि हम उनके बलिदानों को व्यर्थ न जाने दें। हम भी अपने देश की रक्षा के लिए सदा तैयार रहें। जब भी देश को हमारी आवश्यकता हो; हम अपना निजी स्वार्थ त्याग कर देश के लिए कुर्बानी देने के लिए सबसे आगे हों; क्योंकि देश है तो हम हैं, देश नहीं तो कुछ भी नहीं।

प्रश्न 4.
आज हमें अपने देश का सम्मान और गौरव बढ़ाने के लिए क्या करना चाहिए ?
उत्तर:
हम अपने देश का गौरव और सम्मान बढ़ाने के लिए अशिक्षा, भ्रष्टाचार, अन्याय, कालाबाजारी, जमाखोरी आदि समाप्त करा के देशवासियों को उनके अधिकारों तथा कर्त्तव्यों के प्रति जागरूक करेंगे। सब को उन्नति के समान अवसर मिलेंगे तथा किसी प्रकार का ऊँच-नीच, जातिगत, अमीर-गरीब का भेद मिटा कर समतावादी समाज की स्थापना करने का प्रयास करेंगे, जिसमें सभी सुखी तथा देश के प्रति समर्पित होंगे।

(ग) रचना बोध

* अपने देश के लिए शहीद होने वाले महान् पुरुषों की जीवनियाँ पढ़ो और उन के गुण आचरण में लाओ।
* जब भी किसी शहीदी स्मारक को देखने जाओ तब अपने साथ डायरी लेकर जाओ ताकि संबंधित स्मारक के बारे में जानकारी नोट कर सको।
* ‘शहीद भगत सिंह’ पर लेख लिखो।
* देश भक्ति के बारे लिख कर कक्षा में टाँगें।
उत्तर:
अपने अध्यापक/अध्यापिका की सहायता से स्वयं कीजिए।

PSEB 7th Class Hindi Guide हुसैनी वाला बार्डर Important Questions and Answers

1. निम्नलिखित प्रश्नों के उत्तर उचित विकल्प चुनकर लिखिए

प्रश्न 1.
वाघा बार्डर के सामने कौन-सा समारोह होता है ?
(क) रिट्रीट समारोह
(ख) स्ट्रीट समारोह
(ग) भजन समारोह
(घ) भाषण समारोह
उत्तर:
(क) रिट्रीट समारोह

प्रश्न 2.
रश्मि ने किसे पत्र लिखा था ?
(क) रीटा
(ख) वैशाली
(ग) सीता
(घ) गीता
उत्तर:
(ख) वैशाली

प्रश्न 3.
वैशाली छुट्टियों में कहाँ घूमने गई थी ?
(क) दिल्ली
(ख) आगरा
(ग) शिमला
(घ) फ़िरोजपुर
उत्तर:
(ग) शिमला

प्रश्न 4.
रश्मि के भाई का क्या नाम था ?
(क) पंकज
(ख) अंकित
(ग) वैभव
(घ) राहुल
उत्तर:
(ख) अंकित

प्रश्न 5.
फिरोजपुर को किसने बसाया था ?
(क) जहाँगीर
(ख) शाहजहाँ
(ग) अकबर
(घ) फिरोजशाह तुगलक
उत्तर:
(घ) फिरोजशाह तुग़लक

2. निम्नलिखित रिक्त स्थानों की पूर्ति उचित विकल्पों से कीजिए

प्रश्न 1.
फिरोजपुर शहर और ………. दो भागों में बंटा है।
(क) छावनी
(ख) शहर
(ग) नगर
(घ) गांव
उत्तर:
(क) छावनी

प्रश्न 2.
भगतसिंह को उसके साथियों के साथ ………… को फांसी दी गई।
(क) 24 मार्च, 1931
(ख) 23 मार्च, 1931
(ग) 25 मार्च, 1931
(घ) 26 मार्च, 1931
उत्तर:
(ख) 23 मार्च, 1931

प्रश्न 3.
बी मैमोरियल …………….. के अमर शहीदों की याद में है।
(क) सन् 1965
(ख) सन् 1966
(ग) सन् 1967
(ग) सन् 1968
उत्तर:
(क) सन् 1965

प्रश्न 4.
36 सिक्ख रेजीमेंट के ………. सिक्खों ने अपना बलिदान दिया था।
(क) 22
(ख) 23
(ग) 21
(घ) 24
उत्तर:
(ग) 21

प्रश्न 5.
सारागढ़ी मैमोरियल ………. में है।
(क) फिरोजपुर
(ख) रामपुर
(ग) करनाल
(घ) गुरदासपुर
उत्तर:
(क) फिरोज़पुर

3. दिए गए शब्द का सही अर्थ से मिलान कीजिए

प्रश्न 1.
छावनी:
फ़ौजी ठिकाना
छाने वाला
छाता।
उत्तर:
फ़ौजी ठिकाना

प्रश्न 2.
शहादत:
शहद
बलिदान
शहतूत।
उत्तर:
बलिदान

प्रश्न 3.
तत्पर
तर बतर
तैरना
तैयार
उत्तर:
तैयार

प्रश्न 4.
रोष:
आशा
क्रोध
गर्मी
उत्तर:
क्रोध

हुसैनीवाला बार्डर Summary

हुसैनीवाला बार्डर पाठ का सार

‘हसैनीवाला बार्डर’ पत्र के रूप में लिखा पाठ है, जो रश्मि ने वैशाली को लिखा है। इस में फिरोज़पुर के पास पाकिस्तान सीमा पर स्थित हुसैनीवाला बार्डर के महत्त्व पर प्रकाश डाला गया है। वैशाली छुट्टियों में शिमला घूम आई थी जबकि रश्मि अपने अंकित भैया और पापा के साथ फिरोज़पुर रजनी दीदी के घर गई थी। वहाँ उसने फिरोज़पुर में देखे महत्त्वपूर्ण स्थलों का इस पत्र में वर्णन किया है।

फिरोज़पुर पंजाब का बहुत पुराना शहर है, जिसे चौदहवीं शताब्दी में फिरोज़शाह तुग़लक ने बसाया था। यह फिरोज़पुर शहर और छावनी दो भागों में बँटा हुआ है। भारतपाकिस्तान सीमा का हुसैनीवाला बार्डर यहाँ से लगभग ग्यारह किलोमीटर है। यह सतलुज नदी के किनारे पर स्थित है। यहाँ अमर शहीद भगतसिंह, राजगुरु और सुखदेव की समाधियाँ हैं। सांडर्स की हत्या के कारण इन्हें 24 मार्च, सन् 1931 को फाँसी देने की सज़ा सुनाई गई थी परन्तु ब्रिटिश सरकार ने इन्हें 23 मार्च, सन् 1931 की शाम को फाँसी देकर इनके शवों को यहीं जला दिया था, जिस कारण यह स्थान आज भी वंदनीय है। इन समाधियों के पास बटुकेश्वर दत्त तथा भगतसिंह की माता श्रीमती विद्यावती की समाधियां भी हैं। सन् 1962 तक बार्डर का एक किलोमीटर का यह क्षेत्र पाकिस्तान के पास था, जिसे सन् 1962 में फाजिल्का बार्डर के नज़दीक हैडसुलेमान के बारह गाँव पाकिस्तान को देकर इस अमर शहादत वाली भूमि को ले लिया था।

सन् 1970 से यहाँ वाघा बार्डर के समान रिट्रीट समारोह होने लगा है, जो देखने लायक होता है। यहाँ उस समय ‘वन्देमातरम्’ और ‘भारत माता की जय’ का स्वर गूंज उठता है तथा सीमा रेखा का शाने हिन्द, पाकिस्तान के फक्र-ए-पाक से ऊँचा होकर भारत की विशालता, महानता, बड़प्पन और शक्ति के गुण गाता है। फिरोजपुर के बर्की मैमोरियल और सारागढ़ी मैमोरियल भारतीय सैनिकों की वीरता और बलिदान के प्रतीक हैं। बर्की मैमोरियल सन् 1965 के अमर शहीदों की स्मृति में 11 सितम्बर, सन् 1969 को लै० ज० हरबख्श सिंह वी०सी० द्वारा स्थापित किया गया था तथा सारागढ़ी मैमोरियल 12 सितम्बर, सन् 1897 को वर्जिस्तान के सारागढ़ी किले की रक्षा करते हुए 36 सिक्ख रेजीमेंट के 21 सिक्ख सैनिकों की वीरता की याद दिलाता है।

इन समाधि स्थलों के दर्शनों से हम इन सैनिकों के बलिदान के प्रति नतमस्तक हो जाते हैं। हमें भी भारत-माता के गौरव और सम्मान के लिए सदा तत्पर रहने का प्रण लेना चाहिए।

Punjab State Board PSEB 7th Class Hindi Book Solutions Chapter 15 माँ का लाल Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Hindi Chapter 15 माँ का लाल

Hindi Guide for Class 7 PSEB माँ का लाल Textbook Questions and Answers

(क) भाषा-बोध

1. शब्दार्थ

लाल = पुत्र, सपूत
अधेड़ = ढलती उम्र की
कस्बा = छोटा शहर
सौदा = सामान
गिरफ़्तार = बंदी
झोला = थैला
अफवाह = उड़ती खबर
लारी = बस
मेंबर = सदस्य
अनन्यमनस्क = जिस का मन कहीं दूसरी ओर नहीं हो, एकाग्रचित, एक ही बात पर ध्यान लगाने वाला
पुलिस की दौड़ = पुलिस दल
नमक हलाल = स्वामी भक्त
सनद = प्रमाण-पत्र
तमगे = पदक, मैडल
हजूर = श्रीमान
दोषी = अपराधी
शामत = मुसीबत
गर्व = अभिमान
बुकनी = चूर्ण
ढेर हो जाना = मर जाना
आश्चर्यचकित = हैरान
फरजंदों = बेटों

2. इन मुहावरों के अर्थ लिखते हुए वाक्यों में प्रयोग करें:

पहाड़ खोदना ____________ ____________________
पसीना-पसीना होना ________________ ______________________
तितर-बितर होना ______________ _______________________
उत्तर:
पहाड़ खोदना (कठिन कार्य करना) – आई०ए०एस० में प्रथम आना पहाड़ खोदने के समान है।
पसीना-पसीना होना (पसीने से बिल्कुल तर होना) – ऐसी भयंकर गर्मी है कि ज़रासा बाज़ार जाते ही मैं पसीने-पसीने हो गया।
तितर-बितर होना (इधर-उधर होना) – पुलिस ने आँसू गैस छोड़ कर प्रदर्शनकारियों को तितर-बितर कर दिया।

3. दो-दो पर्यायवाची शब्द लिखें:

सौदा =	………………	………………
जेल =	………………	………………
आदमी =	………………	………………
साहस =	………………	………………
सभापति =	………………	………………
संग्राम =	………………	………………
ख़बर =	………………	………………
खुद =	………………	………………
शत्रु =	………………	………………
संकट =	………………	………………
बलिदान =	………………	………………

उत्तर:

	शब्द	पर्यायवाची शब्द
सौदा =	व्यवहार	क्रय-विक्रय
जेल =	कारागार	बन्दीगृह
आदमी =	मनुष्य	मानव
साहस =	हिम्मत	बहादुरी
सभापति =	अध्यक्ष	प्रधान
संग्राम =	युद्ध	लड़ाई
ख़बर =	समाचार	सूचना
खुद =	स्वयं	अपने आप
शत्रु =	दुश्मन	अरि
संकट =	विपत्ति	मुसीबत
बलिदान =	न्योछावर होना	कुर्बानी

4. प्रयोगात्मक प्रश्न

समस्त पद विग्रह

महात्मा महान् है जो आत्मा
महात्मा = महान् है आत्मा जिसकी (व्यक्ति विशेष)

उपुर्यक्त पहले उदाहरण में पूर्वपद (महान्) विशेषण है तथा उत्तर पद (आत्मा) विशेष्य है। यह कर्मधारय तत्पुरुष समास है। इसमें उत्तर पद की प्रधानता है तथा दोनों पदों में विशेषण-विशेष्य सम्बन्ध है।
अतएव जिस समास में उत्तर पद प्रधान हो तथा पूर्वपद व उत्तर पद में विशेषण विशेष्य सम्बन्ध हो, उसे कर्मधारय तत्पुरुष समास कहते हैं।
जबकि दूसरे उदाहरण में दोनों पद गौण हैं और प्रधान पद है व्यक्ति विशेष। इसमें समस्त पद किसी संज्ञा के लिए विशेषण का कार्य कर रहा है।
अतएव जिस समस्त पद में कोई भी पद प्रधान न होकर किसी अन्य पद की प्रधानता हो, वह बहुब्रीहि समास होता है। अन्य उदाहरण

समस्त पद	विग्रह	विशेष	समास का नाम
नीलकंठ	नीला है जो कंठ	विशेषण (नीला) और कंठ (विशेष्य) सम्बन्ध (दोनों पद प्रधान)	कर्मधारय
नीलकंठ	नीला है कंठ जिसका (शिवजी)	प्रधान पद (शिवजी)(दोनों पद गौण)	बहुब्रीहि
लम्बोदर	लम्बा है उदर	विशेषण (लम्बा) और उदर (विशेष्य) सम्बन्ध (दोनों पदप्रधान)	कर्मधारय
	लम्बा है उदर जिसका (गणेश)	प्रधान पद-गणेश (दोनों पद गौण)	बहुब्रीहि

विशेषण :-कर्मधारय समास में एक पद उपमान और दूसरा उपमेय भी हो सकता है। जैसे

समस्त पद विग्रह
घनश्याम घन के समान श्याम
उपर्युक्त,उदाहरण में पूर्वपद (धन) उपमान है तथा उत्तरपद श्याम (उपमेय) है।
उपमान :- वह वस्तु या व्यक्ति जिससे समता की जाये।
उपमेय :- वह वस्तु या व्यक्ति जिसकी समता की जाये।

समस्त पद विग्रह
1. तिरंगा तीन रंगों का समूह
2. तिरंगा तीन रंगों वाला अर्थात् भारत का राष्ट्रध्वज

उपर्युक्त पहले उदाहरण में पूर्वपद (तीन) संख्यावाचक शब्द है और विशेषण है तथा उत्तर पद (रंग) विशेष्य है। यह द्विगु समास है। अतएव जिस समास में पूर्व पद संख्यावाचक विशेषण हो और उत्तर पद विशेष्य हो, उसे द्विगु समास कहते हैं। जबकि दूसरे उदाहरण में दोनों पद गौण हैं और प्रधान पद है- भारत का राष्ट्रध्वज। यह बहुब्रीहि का उदाहरण है जिसकी पहले व्याख्या की जा चुकी है।

अन्य उदाहरण

समस्त पद विग्रह विशेष समास का नाम
पंजाब पाँच आबों का समूह । पाँच (विशेषण) संख्यावाचक है और आब (विशेष्य) से सम्बन्धित है द्विगु

पाँच आबों (नदियों) प्रधान पद- पंजाब प्रदेश बहुब्रीहि
वाला अर्थात् पंजाब प्रदेश (दोनों पद गौण)

अब इन समासों का विग्रह करके समास का नाम लिखें

समस्त पद	विग्रह	समास
सेनापति	……………	……………
पढ़ी-लिखो	……………	……………
रसोईघर	……………	……………
पुलिस कर्मी	……………	……………
दोपहर	……………	……………
हाथ-मुँह	……………	……………

उत्तर:

समस्त पद	विग्रह	समास
सेनापति	सेना का पति	तत्पुरुष समास
पढ़ी-लिखो	पढ़ो और लिखो	द्वंद्व समास
रसोईघर	रसोई के लिए घर	तत्पुरुष समास
पुलिस कर्मी	पुलिस का कर्मी	तत्पुरुष समास
दोपहर	दो पहरों का समाहार	द्विगु समास
हाथ-मुँह	हाथ और मुँह	द्वंद्व समास

(ख) विचार-बोध

1. इन प्रश्नों के उत्तर एक या दो वाक्यों में लिखें:

प्रश्न 1.
माधव ने अपनी माँ को क्या समाचार सुनाया ?
उत्तर:
माधव ने अपनी माँ को बताया कि गाँधी जी और सब नेता बंबई में कल, आठ अगस्त की रात को गिरफ्तार कर लिए गए।

प्रश्न 2.
उसकी माँ ने उस समाचार के प्रति क्या प्रतिक्रिया व्यक्त की ?
उत्तर:
माधव की माँ ने कहा कि यह तो होता ही रहता है। वे महात्मा हैं, कभी जेल में, कभी बाहर। वे जो चाहे करें, जहाँ चाहे रहें, सब ठीक है।

प्रश्न 3.
सोहनलाल को घर पहुँचने में कठिनाई क्यों हुई ?
उत्तर:
सोहन लाल को घर पहुँचने में कठिनाई इसलिए हुई क्योंकि किसी ने अफ़वाह उड़ा दी थी कि रेलगाड़ी उड़ा दी जाएगी। तब उसे लारी से आना पड़ा।

प्रश्न 4.
माधव ने सभापति से क्या कहा?
उत्तर:
माधव ने सभापति से कहा कि वे कल सभा में कह रहे थे कि महात्मा जी करो या मरो का नारा देकर जेल चले गए। क्या वह भी कुछ कर सकता है ?

प्रश्न 5.
सभापति ने माधव को क्या काम सौंपा ?
उत्तर:
सभापति ने माधव को यह काम सौंपा कि वह पुलिस वाले या फ़ौजी इधर आएँ तो उनका समाचार उन्हें दें तथा उनके बारे में किसी को पता न लगने दें।

प्रश्न 6.
छोटा आदमी भी बड़े काम में सहयोग दे सकता है, इसकी पुष्टि में कौन-सा किस्सा सुनाया ?
उत्तर:
छोटे आदमी के बड़े काम में सहयोग देने की पुष्टि में सभापति ने भगवान राम के लंका जाने के लिए समुद्र पर बनने वाले पुल में गिलहरियों के सहयोग का किस्सा सुनाया था।

प्रश्न 7.
फ़ौजी गाँव के लोगों से क्या पूछता है ?
उत्तर:
फ़ौजी गाँव के लोगों से तोड़-फोड़ में लगे लोगों के ठिकाने तथा उनकी सहायता करने वालों के बारे में पूछता है।

प्रश्न 8.
तोड़-फोड़ करने वालों की मदद करने वालों में माधव का नाम किसने बताया ?
उत्तर:
माधव का नाम दूसरे आदमी ने बताया था।

प्रश्न 9.
माधव ने फ़ौजी को क्या कहा ?
उत्तर:
माधव ने फ़ौजी को कहा कि इन्होंने जो कहा वह ठीक है। वह खुद यह बात बताने वाला था। गाँव को बचाने के लिए वह अपनी जान दे सकता है परन्तु किसी का नाम नहीं बताएगा।

प्रश्न 10.
सभापति ने क्या कह कर माधव की प्रशंसा की ?
उत्तर:
सभापति ने माधव को इस गाँव को बचाने वाला ही नहीं बल्कि देश को स्वतंत्र कराने में योगदान देने वाला भी बताया। उस के कारण गाँव तो बच गया परन्तु उसे हमने खो दिया।

2. इन पंक्तियों के भाव स्पष्ट करें:

(क) देश संकट में है, हम लोग भी कुछ करना चाहते हैं। यह किसने और क्यों कहा ?
उत्तर:
यह शब्द माधव ने अपनी साथी बालकों को मैदान में रात के पहले पहर में कहे हैं। उसने ऐसा इसलिए कहा क्योंकि देश के नेताओं को अंग्रेज़ी सरकार ने बन्दी बना लिया था तथा देश को आजाद कराना था।

(ख) गाँव तो बच गया पर इस गाँव में जो सबसे अच्छी चीज़ थी, उसे हम खो बैठे। यह किसने और कब कहा ?
उत्तर:
यह शब्द सभापति ने आज़ादी मिलने के बाद गाँव की सभा में माधव के कार्यों की प्रशंसा करते हुए कहे हैं।

(म) माधव के चरित्र की कोई दो विशेषताएं इस एकाँकी को पढ़कर लिखें।
उत्तर:
माधव देशभक्त तथा आत्मबलिदानी है। उसे गांधी जी का गिरफ्तार होना अच्छा नहीं लगता। वह स्वतंत्रता सेनानियों की सहायता करता है। उस से जब उन के गुप्त ठिकानों का फ़ौजी पता पूछना चाहते हैं तो वह विष खाकर अपने प्राण दे देता है।

योग्यता विस्तार

* माधव के समान ही ऐसे कई वीर हुए हैं जिन्होंने छोटी आयु में ही अपने देश के लिए प्राण न्योछावर कर दिए। उनके नाम पता करो तथा पुस्तकालय से पुस्तकें लेकर पढ़ो।
* आज देश आजाद हो चुका है। हम सब स्वतन्त्र भारत के नागरिक हैं। परन्तु फिर भी कई आन्तरिक और बाह्य शत्रु हमारे देश में सक्रिय हैं। कक्षा में चर्चा करो।
उत्तर:
अपने अध्यापक/अध्यापिका की सहायता से विद्यार्थी स्वयं करें।

PSEB 7th Class Hindi Guide माँ का लाल Important Questions and Answers

1. निम्नलिखित प्रश्नों के उत्तर उचित विकल्प चुनकर लिखिए

प्रश्न 1.
‘माँ का लाल’ किस प्रकार की विधा है ?
(क) एकांकी
(ख) नाटक
(ग) कहानी
(घ) रेखाचित्र
उत्तर:
(क) एकांकी

प्रश्न 2.
‘मां का लाल’ एकांकी में किसके बलिदान की बात कही गई है ?
(क) फ़ौजी
(ख) पुलिस
(ग) एक बालक
(घ) अध्यापक
उत्तर:
(ग) एक बालक

प्रश्न 3.
गाँधी जी को कब बंदी बना लिया गया था ?
(क) पाँच अगस्त
(ख) सात अगस्त
(ग) आठ अगस्त
(घ) दो अगस्त
उत्तर:
(ग) आठ अगस्त

प्रश्न 4.
रमा के पुत्र की आयु कितनी थी ?
(क) 14 वर्ष
(ख) 15 वर्ष
(ग) 16 वर्ष
(घ) 13 वर्ष
उत्तर:
(ख) 15 वर्ष

प्रश्न 5.
रमा के पुत्र का क्या नाम था ?
(क) माधव
(ख) राघव
(ग) रोहन
(घ) सोहन
उत्तर:
(क) माधव

2. निम्नलिखित रिक्त स्थानों की पूर्ति उचित विकल्पों से कीजिए

प्रश्न 1.
माधव के पिता …………….. पसीना-पसीना होकर आए।
(क) रोहन लाल
(ख) सोहनलाल
(ग) गोपाल राम
(घ) राघवराम
उत्तर:
(ख) सोहनलाल

प्रश्न 2.
सोहनलाल रेलगाड़ी की बजाए …………… से आए थे।
(क) कार से
(ख) साइकिल से
(ग) लॉरी से
(घ) रिक्शा से
उत्तर:
(ग) लॉरी से

प्रश्न 3.
पार्टी दफ्तर पर झंडा लगा हुआ था।
(क) तिरंगा
(ख) चरखा
(ग) अंग्रेजों
(ग) मुग़लों
उत्तर:
(क) तिरंगा

प्रश्न 4.
सभापति ने माधव को लड़कों का ……… बना दिया।
(क) भाई
(ख) नेता
(ग) सेवक
(घ) मालिक
उत्तर:
(ख) नेता

प्रश्न 5.
मंच पर गाँधी जी और …………… के चित्र थे।
(क) माधव
(ख) राघव
(ग) सोहनलाल
(घ) रमा
उत्तर:
(क) माधव।

3. दिए गए शब्द का सही अर्थ से मिलान कीजिए

प्रश्न 1.
सौदा:
सामान
सौगंध
शृंगार
उत्तर:
सामान

प्रश्न 2.
पहर:
4 घण्टे का
3 घण्टे का
5 घण्टे का
उत्तर:
3 घण्टे का

प्रश्न 3.
बुकनी:
चूर्ण
फूंकनी
बुर्का
उत्तर:
चूर्ण

प्रश्न 4.
नमक हराम:
स्वामी भक्त
स्वामी से धोखेबाज़ी
नमक खाने वाला
उत्तर:
स्वामी से धोखेबाज़ी

माँ का लाल Summary

माँ का लाल पाठ का सार

‘माँ का लाल’ एक एकांकी है, जिसमें लेखक ने एक देशभक्त बालक के आत्म बलिदान द्वारा देश के लिए बलिदान देने की प्रेरणा दी है। रमा रसोई बना रही थी तभी उस का पन्द्रह वर्षीय बेटा माधव बाज़ार में सौदा लेकर आया। रमा ने उसके देर से आने का कारण पूछा तो उसने बाजार से लगी भीड़ में हो रही चर्चा के विषय में बताया कि गाँधी जी आठ अगस्त की रात को बन्दी बना लिए गए हैं। उनके साथ हज़ारों दूसरे लोग भी गिरफ्तार हुए हैं। रमा उसे यह सब छोड़ कर अपना काम करने के लिए कहती है। तभी पसीना-पसीना हुए माधव के पिता सोहन लाल आए और उन्होंने बताया कि रेलगाड़ी उड़ाने की अफवाह सुनकर वे लारी से आए थे। रमा ने रेल उड़ाने पर कहा कि रेलें तो सबकी हैं, उन्हें उड़ाने की क्या तुक है? सोहन लाल इससे परेशान सब की बात बताई और कहा कि इस बार ज़रूर अंग्रेज़ सरकार से लड़ाई होगी। माधव अपने बारे में जानना चाहता था कि वे किसके साथ थे ? रमा ने उसे झिड़ककर अपना काम करने के लिए कहा। दूसरे दृश्य में पार्टी के दफ्तर पर तिरंगा झंडा लगा हुआ था। माधव ने वहाँ जा कर सभापति से पूछा कि महात्मा .. जी करो या मरो का नारा देकर चले गए थे, वह क्या करे, यही पूछने आया था। सभापति ने अभी उसे पढ़ने-लिखने के लिए कहा तथा स्वयं वहाँ से चले जाना चाहा, क्योंकि वहाँ पुलिस के आने की उन्हें सूचना मिल चुकी थी।

तीसरे दृश्य में माधव और गाँव के कई बालक रात के पहले पहर में एक मैदान में एकत्र होकर नेताओं की गिरफ्तारी तथा पुलिस की पकड़-धकड़ पर बातें कर रहे थे। स्कूल बन्द हो गए थे। वे देश के लिए कुछ करना चाहते थे। तभी वहाँ सभापति ने उन्हें काम बताया कि वे और उन के साथी यहाँ छिपकर रह रहे थे और देश को आजाद कराने की लड़ाई लड़ रहे थे। यदि पुलिस या फ़ौज इधर आए तो उस की सूचना उन्हें देने के लिए कहा। उन्होंने माधव को लड़कों का नेता बना दिया।

चौथे दृश्य में गाँव से लगे मैदान में फ़ौजी और पुलिस वाले गाँव वालों को सिर नीचा कर एक लाइन में बिठा कर तोड़-फोड़ करने वालों के विषय में पूछ रहे थे पर कोई कुछ बता नहीं पाया। फ़ौजी ने उन्हें फिर पूछा और धमकी दी कि बता दो नहीं तो सब मारे जाओगे। इस पर एक आदमी ने बताया कि एक लड़का माधव गाँववालों से खाना माँगकर उन्हें पहुँचाता है, उसे पता होगा। फ़ौजी ने माधव को उन में से अलग कर दिया। तो माधव ने उस आदमी के कथन का समर्थन करते हुए कहा कि वह गाँव वालों को बचाने के लिए अपनी जान दे देगा पर उन लोगों का नाम नहीं बताएगा। उसने कुछ बुकनी-सी निकालकर अपने मुँह में डाल लिया और देखते-ही-देखते मर गया। फ़ौजी ने सब को वहाँ से जाने दिया।

पाँचवां दृश्य बहुत दिनों बाद गाँव की सभा का था। मंच पर गाँधी जी और माधव के चित्र थे। सभापति देश को स्वतंत्र कराने में माधव का योगदान महत्त्वपूर्ण बताया, जिसने गाँव को बचाया, देश आज़ाद कराया परन्तु स्वयं चला गया। सब लोगों ने उनकी जय बोली और पर्दा गिर गया।

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 13 Exponents and Powers Ex 13.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 13 Exponents and Powers Ex 13.3

1. Write the following numbers in the expanded exponential form :

(i) 104278
Solution:
104278 = 1 × 10⁵ + 4 × 10³ + 2 × 10² + 7 × 10¹ + 8 × 10⁰

(ii) 20068
Solution:
20068 = 1 × 10⁴ + 6 × 10¹ + 8 × 10⁰

(iii) 120719
Solution:
120719 = 1 × 10⁵ + 2 × 10⁴ + 7 × 10² + 1 × 10¹ + 9 × 10⁰

(iv) 3006194
Solution:
3006194 = 3 × 10⁶ + 6 × 10³ + 1 × 10² + 9 × 10¹ + 4 × 10⁰

(v) 28061906
Solution:
28061906 = 2 × 10⁷ + 8 × 10⁶ + 6 × 10⁴ + 1 × 10³ + 9 × 10² + 6 × 10⁰

2. Find the number from each of the following expanded form :

(i) 4 × 10⁴ + 7 × 10³ + 5 × 10² + 6 × 10¹ + 1 × 10⁰
Solution:
4 × 10⁴ + 7 × 10³ + 5 × 10² + 6 × 10¹ + 1 × 10⁰
= 40000 + 7000 + 500 + 60 + 1
= 47561

(ii) 3 × 10⁴ + 7 × 10² + 5 × 10⁰
Solution:
3 × 10⁴ + 7 × 10² + 5 × 10⁰
= 30000 + 700 + 5 × 1
= 30705

(iii) 4 × 10⁵ + 5 × 10³ + 3 × 10² + 2 × 10⁰
Solution:
4 × 10⁵ + 5 × 10³ + 3 × 10² + 2 × 10⁰
= 400000 + 5000 + 300 + 2 × 1
= 4053202

(iv) 8 × 10⁷ + 3 × 10⁴ + 7 × 10³ + 5 × 10² + 8 × 10¹
Solution:
8 × 10⁷ + 3 × 10⁴ + 7 × 10³ + 5 × 10² + 8 × 10¹
= 80000000 + 30000 + 7000 + 500 + 80
= 80037580

3. Express the following numbers in standard form :

(i) 3,43,000
Solution:
3.43 × 10⁵

(ii) 70,00,000
Solution:
7.0 × 10⁶

(iii) 3,18,65,00,000
Solution:
3.1865 × 10⁹

(iv) 530.7
Solution:
5.307 × 10²

(v) 5985.3
Solution:
5.9853 × 10³

(vi) 3908.78
Solution:
3.90878 × 10³

4. Express the number appearing in the following statements in standard form :

(i) The distance between the earth and die moon is 384,000,000 m
Solution:
3.84 × 10⁸

(ii) The diameter of the earth is 1,27,56,000 m.
Solution:
1.2756 × 19⁷ m

(iii) The diameter of the sun is 1,400,000,000 m.
Solution:
1.40 × 10⁹ m

(iv) The universe is estimated to be about 12,000,000,000 years old.
Solution:
1.2 × 10¹⁰ years

(v) Mass of uranis is 86,800,000, 000,000,000,000,000,000 kg
Solution:
8.68 × 10²⁸ kg.

5. Compare the following numbers :

(i) 4.3 × 10¹⁴ ; 3,01 × 10¹⁷.
Solution:
Given numbers are 4.3 × 10¹⁴ and 3.01 × 10¹⁷ since the numbers are in standard form. As the power of 10 in 3.01 × 10¹⁷ is greater than the power of 10 in 4.3 × 10¹⁴.
∴ 3.01 × 10¹⁷ > 4.3 × 10¹⁴

(ii) 1.439 × 10¹² ; 1.4335 × 10¹².
Solution:
1.439 × 10¹² ; 1.4335 × 10¹²
The numbers are in standard form
As 1.439 > 1.433
∴ 1.439 × 10¹² > 1.4335 × 10¹²

Punjab State Board PSEB 7th Class Hindi Book Solutions Chapter 14 बुद्धि बल Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Hindi Chapter 14 बुद्धि बल

Hindi Guide for Class 7 PSEB बुद्धि बल Textbook Questions and Answers

(क) भाषा-बोध

1. शब्दार्थ:

सत्य – सच्ची
साहसी = हिम्मतवाला
जीवित = जिन्दा
टेढ़ीखीर = कठिन कार्य
अद्भुत = अनोखा
उपस्थित = हाज़िर
छल = धोखा
निगरानी = देखरेख
तैनात = नियुक्त
स्वतंत्र = आज़ाद
विश्वासघात = धोखा
घोषणा = ऊँचे स्वर में दी गई सूचना
उपलक्ष्य = उद्देश्य, प्रयोजन
इजाजत = आज्ञा

2. इन मुहावरों और लोकोक्तियों का अर्थ लिखते हुए वाक्य में प्रयोग करें:

पहाड़ से टकराना ________________ _________________________
आग में कूदना ___________________ __________________________
नाम होना __________________ _______________________
चंगुल में फँसना ________________ _____________________
चिकनी-चुपड़ी बातें ______________ __________________________
जाल में फँसाना ___________________ _______________________
विचारों के पँखों पर उड़ना ______________ ____________________
धोखा देना ________________ ______________________
हवा से बातें करना ______________________ ______________________
टेड़ी खीर ______________ ___________________________
एक और एक ग्यारह होना _________________ _______________________
घर का भेदी लंका ढाए ________________ _____________________
जैसे के साथ तैसा ____________ ________________________
उत्तर:
पहाड़ से टकराना (शक्तिशाली से मुकाबला करना) – दिलेर खाँ की सेना का छत्रपति शिवाजी की सेना के साथ टकराना पहाड़ से टकराना था।
आग में कूदना (मुसीबत में पड़ना) – भूकंप में घूमना-फिरना आग में कूदना है।
नाम होना (प्रसिद्ध होना) – भ्रष्टाचार आंदोलन से अन्ना हजारे का सब जगह नाम हो रहा है।
चंगुल में फँसाना (वश में करना) – वन कर्मियों ने खूखार शेर को बेहोशी का टीका लगाकर अपने चंगुल में फँसा लिया।
चिकनी-चुपड़ी बातें (ललचाना) – किसी की चिकनी चुपड़ी बातों में फँसना नहीं चाहिए।
जाल में फंसाना (वश में करना) – अपनी बातों से जयसिंह ने शिवाजी को जाल में फँसा लिया था।
विचारों के पंखों पर उड़ना (कल्पना करना) – मनुष्य का मन विचारों के पँखों पर उड़कर न मालूम कहाँ-कहाँ घूम आता है।
धोखा देना (छल करना, ठगना) – कपटी मित्र सदा धोखा देता है।
हवा से बातें करना (तेज़ दौड़ना) – महाराणा प्रताप का घोड़ा युद्ध भूमि में हवा से बातें करता था।
टेडी खीर (कठिन कार्य) – आजकल शिक्षित के लिए भी सरकारी नौकरी ढूंढना टेढ़ी खीर है ।
एक और एक ग्यारह होना (एकता दिखाना) – जब गांव वालों ने मिल कर डाकुओं का सामना किया तो एक और एक ग्यारह वाली बात चरितार्थ हुई।
घर का भेदी लंका ढाए (आपसी फूट का परिणाम बुरा होता है) – भारत की एकता में सेंध लगाने वाले भारत में ही हैं क्योंकि सच कहा है कि घर का भेदी लंका ढाए।
जैसे के साथ तैसा (बुरे के साथ बुरा व्यवहार) – छल करने वाले के साथ छल करना नीति है क्योंकि कहा भी गया है कि जैसे के साथ तैसा करो।

3. लिंग बदलो

टोकरा = ………………….
घोड़ा = ………………..
चूहा = ……………….
शेर = ………………….
पहाड़ = …………………
उत्तर:
टोकरा = टोकरी
घोड़ा = घोड़ी
चूहा = चुहिया
शेर = शेरनी
पहाड़ = पहाड़ी

4. विपरीत शब्द लिखें:

सत्य = …………………
जीवित = ………………….
उपस्थित = …………………
बहादुर = …………………
विश्वास = …………………..
स्वतन्त्र = …………………
पसन्द = ………………..
इनाम = ……………….
जीत = …………………
बंदी = ……………….
उत्तर:
शब्द विपरीत शब्द
सत्य = असत्य
जीवित = मृत
उपस्थित = अनुपस्थित
बहादुर = कायर
विश्वास = अविश्वास
स्वतन्त्र = परतन्त्र
पसन्द = नापसन्द
इनाम = सज़ा
जीत = हार
बंदी = आजाद

(ख) विचार-बोध

1. इन प्रश्नों के उत्तर एक या दो वाक्यों में लिखें:

प्रश्न 1.
दिलेर खाँ ने औरंगजेब से शिवाजी को जीवित पकड़ने के लिए जयसिंह के किस गुण की ओर संकेत किया ?
उत्तर:
दिलेर खाँ ने औरंगजेब से शिवाजी को जीवित पकड़ने के लिए जयसिंह के हिन्दू होने के गुण की ओर संकेत किया था।

प्रश्न 2.
औरंगज़ेब ने जयसिंह के साथ दिलेर खाँ को क्यों भेजना चाहा ?
उत्तर:
औरंगजेब ने जयसिंह के साथ दिलेर खाँ को इसलिए भेजना चाहा जिस से एक ही बुद्धि और दूसरे का बल मिल कर काम करे।

प्रश्न 3.
जयसिंह ने शिवाजी को क्या विश्वास दिलाया था ?
उत्तर:
जयसिंह ने शिवाजी को यह विश्वास दिलाया था कि औरंगज़ेब उनका स्वागत एक राजा के समान करेगा।

प्रश्न 4.
औरंगज़ेब ने शिवाजी को दरबार में देखकर क्या कहा ?
उत्तर:
औरंगजेब ने शिवाजी को दरबार में देखकर कहा कि क्या यही है वह पहाड़ी चूहा जो रात को चोरी-चोरी हमारे खज़ानों को कुतर डालता है।

प्रश्न 5.
जेल की कोठरी से बाहर निकलने के लिए शिवाजी ने मन में क्या सोचा?
उत्तर:
शिवाजी ने अपने जन्मदिन पर दान देने वाले फलों-मिठाइयों आदि के टोकरों के बहाने जेल की कोठरी से बाहर निकलने की बात सोची।

2. इन प्रश्नों के उत्तर चार या पाँच वाक्यों में लिखें:

प्रश्न 1.
दिलेर खाँ और औरंगज़ेब ने शिवाजी को जीवित पकड़ने के लिए क्या नीति अपनाई ?
उत्तर:
दिलेर खाँ और औरंगजेब ने शिवाजी को जीवित पकड़ने के लिए छल की नीति अपनाई। उन्होंने हिन्दू से हिन्दू को पकड़वाने के लिए जयसिंह का सहारा लिया। जयसिंह ने शिवाजी को विश्वास दिलाया कि आगरा जाने पर औरंगज़ेब उनके साथ राजाओं जैसा व्यवहार करेगा तो शिवाजी आगरा चलने के लिए तैयार हो गए थे।

प्रश्न 2.
शिवाजी को किस प्रकार बन्दी बनाया गया ?
उत्तर:
जब जयसिंह के विश्वास दिलाने पर कि औरंगज़ेब ने उनके साथ राजाओं जैसा व्यवहार करेगा तो शिवाजी औरंगजेब के दरबार में आए। उन्हें देखते ही औरंगजेब ने उन्हें पहाड़ी चूहा और उनके खज़ानों की चोरी करने वाला कह कर दिलेर खाँ से बन्दी बनवाकर आगरे के किले में कैदखाने में डाल दिया था।

प्रश्न 3.
शिवाजी किस प्रकार जेल की कोठरी से भागे ?
उत्तर:
शिवाजी का अप्रैल में जन्मदिन पड़ता है। उन्होंने अपने जन्मदिन पर दान करने के लिए इज़ाजत माँगी जो उन्हें मिल गई। वे बाहर से बड़े-बड़े टोकरों में फल, फूल, मिठाई, अन्न आदि मंगवाते और माँ भवानी की पूजा कर उन्हें बाहर पहरेदारों आदि में बंटवा देते। एक दिन वे एक बड़े मिठाई के टोकरे में बैठ कर जेल से बाहर आए और घोड़े पर सवार होकर अपने किले चले गए।

(ग) रचना बोध

(1) अभिनय : यह एक संवादात्मक कहानी है। स्कूल के वार्षिक उत्सव पर इसे एकाँकी के रूप में मंचन करें।
(2) अपने जन्मदिन पर कुछ ऐसा करने का सोचें जिससे आपकी बुद्धि की चारों ओर प्रशंसा हो।
उत्तर:
विद्यार्थी स्वयं करें।

PSEB 7th Class Hindi Guide बुद्धि बल Important Questions and Answers

1. निम्नलिखित प्रश्नों के उत्तर उचित विकल्प चुनकर लिखिए

प्रश्न 1.
किसके प्रयोग से बड़ी से बड़ी मुसीबत से पार पाया जा सकता है ?
(क) बुद्धि
(ख) घड़ी
(ग) धातु
(घ) पारा
उत्तर:
(क) बुद्धि

प्रश्न 2.
दिलेर खां किसका सेनापति था ?
(क) अकबर
(ख) जहाँगीर
(ग) औरंगजेब
(घ) शाहजहाँ
उत्तर:
(ग) औरंगजेब

प्रश्न 3.
शिवाजी को किस किले में कैद करके रखा गया था ?
(क) आगरा
(ख) दिल्ली
(ग) राजस्थान
(घ) मथुरा
उत्तर:
(क) आगरा

प्रश्न 4.
छत्रपति शिवजी का जन्म किस महीने में हुआ था ?
(क) मई
(ख) जून
(ग) जुलाई
(घ) अप्रैल
उत्तर:
(घ) अप्रैल

प्रश्न 5.
छत्रपति शिवाजी ने अपने जन्मदिन पर किस बात की इजाजत माँगी थी ?
(क) दान करने
(ख) भागने
(ग) घूमने जाने
(घ) कोई नहीं
उत्तर:
(क) दान करने

2. निम्नलिखित रिक्त स्थानों की पूर्ति उचित विकल्पों से कीजिए

प्रश्न 1.
औरगजेब ने शिवाजी को पकड़ने के लिए ………….. की नीति अपनाई।
(क) छल
(ख) गम
(ग) वीरता
(घ) पराक्रम
उत्तर:
(क) छल

प्रश्न 2.
शिवाजी किले से बाहर एक ………… की टोकरी में बैठकर निकले।
(क) मिठाई
(ख) फूलों
(ग) सब्जी
(घ) फलों
उत्तर:
(ख) फूलों

प्रश्न 3.
शिवाजी …………… के विश्वास दिलाने पर आगरा गए।
(क) शाइस्त खाँ
(ख) दिलेर खाँ
(ग) जयसिंह
(ग) औरंगजेब
उत्तर:
(ग) जयसिंह

प्रश्न 4.
किले के बाहर …………….. तैयार था ।
(क) एक तेज़ घोड़ा
(ख) एक तेज़ ऊंट
(ग) एक तेज़ घोड़ी
(घ) मोटर साइकिल
उत्तर:
(क) एक तेज़ घोड़ा।

प्रश्न 5.
शिवाजी ने मुग़लों को उन्हीं की ……….. नीति से मात देने की योजना बनाई।
(क) बल की
(ख) छल की
(ग) पराक्रम की
(घ) पौरूष की
उत्तर:
(ख) छल की

3. दिए गए शब्द का सही अर्थ से मिलान कीजिए

प्रश्न 1.
छल:
छलका
धोखा
छाला
उत्तर:
धोखा

प्रश्न 2.
कोठरी:
छोटा कमरा
बड़ा हॉल
बरामदा
उत्तर:
छोटा कमरा।

प्रश्न 3.
प्रयोजन:
प्रतियोजन
प्राण योजना
उद्देश्य
उत्तर:
उद्देश्य।

प्रश्न 4.
मात देना:
हरा देना
हरा रंग
माथा
उत्तर:
हरा देना

बुद्धि बल Summary

बुद्धि बल पाठ का सार

‘बुद्धि बल’ पाठ में लेखक ने छत्रपति शिवाजी की बुद्धिमत्ता की एक घटना का वर्णन किया है जिस का सन्देश यह है कि बुद्धि के प्रयोग से बड़ी-से-बड़ी मुसीबत से भी बचा जा सकता है। मुग़लों के समय की यह घटना है। एक दिन औरंगज़ेब ने अपने सेनापति दिलेर खाँ को शिवाजी को जीवित पकड़कर दरबार में लाने के लिए कहा तो उसने यह कार्य राजा जयसिंह से करवाने के लिए कहा। उसका मानना था कि हिन्दू होने के कारण शिवाजी जयसिंह की इस बात पर विश्वास कर लेंगे कि एक बार उनके आगरे के दरबार में आने से उन्हें स्वतंत्र राजा मान लिया जाएगा। शाइस्ता खाँ या अफज़ल खाँ का यकीन वे उनके मुसलमान होने के कारण नहीं करेंगे। औरंगज़ेब ने जय सिंह के साथ दिलेर खाँ को भी एक बहुत बड़ी सेना के साथ शिवाजी को लाने के लिए भेज दिया।

छत्रपति शिवाजी अफजल खाँ और शाइस्त खाँ की सेनाओं से पराजित तो नहीं हो सके थे परन्तु जयसिंह की बातों पर विश्वास कर औरंगजेब के दरबार में जब आ गए थे तो औरंगजेब ने उन्हें ‘पहाड़ी चूहा’ कह कर दिलेर खाँ से कह कर बन्दी बनाकर आगरे के किले में कैद करा दिया था। आगरे के किले के चारों ओर पूरी सेना तैनात कर दी गई थी, जिससे कोई बाहर न जा सके।

छत्रपति शिवाजी किले में कैद तो थे परन्तु वहाँ से निकलने के उपाय सोचते रहते थे। औरंगज़ेब ने उन्हें छल से बन्दी बनाया था इसलिए वे भी उसे छल से मात देना चाहते थे। अप्रैल का महीना था। इसी महीने शिवा जी का जन्म हुआ था। उन्होंने अपना जन्म दिन मनाने की घोषणा करते हुए कहा कि उन का जन्म दिन दस अप्रैल को है, जिसके उपलक्ष्य में वे दस दिन तक लोगों को फल-फूल, मिठाई-अन्न का दान करेंगे। औरंगज़ेब ने इस की आज्ञा दे दी। वे रोज़ दस-बीस बड़े-बड़े टोकरे फूल, फल, अन्न, मिठाई के मंगवाते और माँ भवानी की पूजा कर उन्हें छूकर बाहर बाँटने के लिए भेज देते। पहरेदार और उनके परिवार भी इन वस्तुओं का खूब आनन्द लेते। एक दिन शिवाजी मिठाई के टोकरे में छिप कर किले से बाहर निकल गए, जहाँ थोड़ी दूर पर एक तेज़ घोड़ा पहले से ही तैयार था, जिस पर सवार हो वे अपने किले में पहुँच गए। पहरेदारों ने जब उनकी कोठरी खाली देखी तो उनके होश उड़ गए।

Punjab State Board PSEB 7th Class English Book Solutions Chapter 3 A Glass of Milk Textbook Exercise Questions and Answers.

Class 7th English Solutions Chapter 3 A Glass of Milk Question Answers

A Glass of Milk Class 7 Questions and Answers

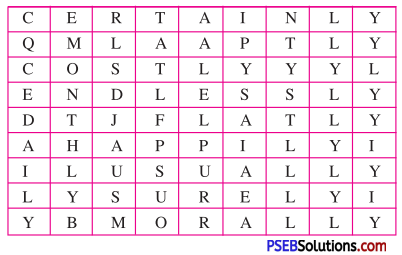
Activity 1.

Look up the following words in a dictionary. You should seek the following information about the words.
1. Meaning of the word as used in the play (adjective/noun/verb, etc.)
2. Pronunciation (The teacher may refer to the dictionary or the mobile phone for correct pronunciation.)
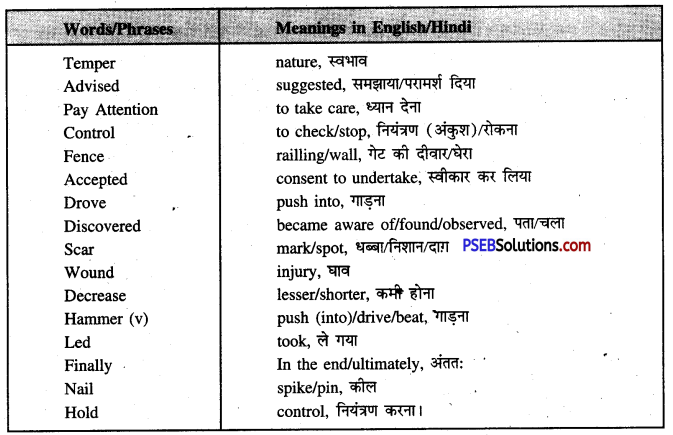
3. Words that normally go with the given word. For example, ‘owe’ goes with ‘money’, ‘bank’, ‘debt’, ‘apology’, etc.
4. Spellings

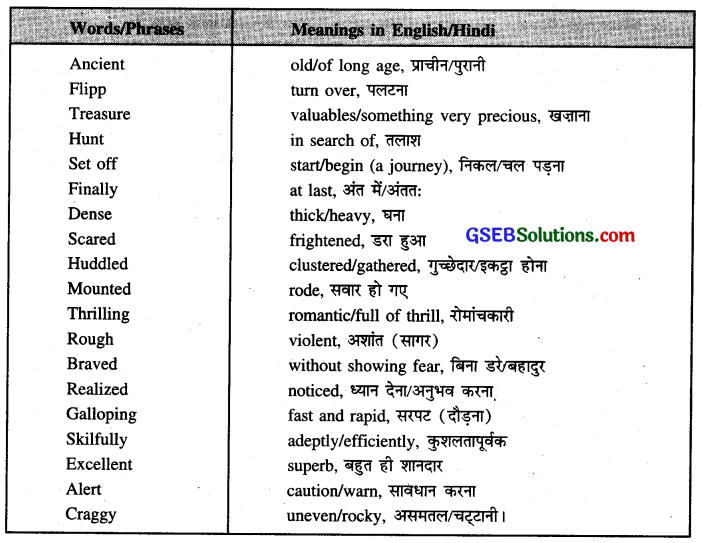
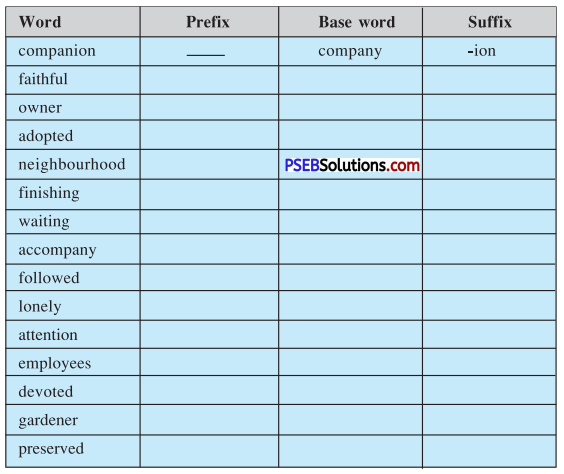
complicated	diagnose	surgery
attention	struggle	discuss

Vocabulary Expansion

Activity 2

Find suffixes in the following words.
1. complicated
2. hesitatingly
3. warmly
4. stronger
5. goodness
Answer:
1. -ated,
2. -ly,
3. ly,
4. -er,
5. ness.

Let us revise the prepositions besides’,’beside’, ‘between’ and ‘among’. ‘Besides’ means ‘in addition to’. “Beside’ means by the side of.,

1. What other sport do you play besides (के अतिरिक्त) hockey ?
2. She sat beside (के पास) her sick son all night.
‘Between (दो व्यक्तियों अथवा चीजों के बीच) is used for two people or things.
‘Among (दो से अधिक व्यक्तियों अथवा चीजों के बीच) is used for more than two people or things.

1. There is no love between the two brothers.
2. Distribute sweets among all the children.

Activity 3

Fill in the blanks choosing from the words given in the box.

beside

besides

between

among

1. The two brothers distributed the sweets …………………. themselves.
2. Radha came and sat ……………….. her mother.
3. The four thieves quarrelled ………………. themselves.
4. I have three other pens …………..
5. this. ……….. advising them, he gave them money also.
6. A beggar was sitting ………………. the temple gate.
Answer:
1. between
2. beside
3. among
4. besides
5. Besides
6. beside.

Learning to Read and Comprehend

Activity 4

Read the play carefully and write the answers.

Scene-1

Question 1.
Count and write the number of characters in Scene 1 of the play.
नाटक के दृश्य 1 में पात्रों की संख्या गिनो और लिखो।
Answer:
Two.

Question 2.
What are their names ?
उनके क्या नाम है?
Answer:
Howard Kelly and Anita.

Question 3.
What is the time ?
समय क्या है ?
Answer:
It is afternoon.

Question 4.
What does the boy say to himself ?
लड़का स्वयं से क्या कहता है ?
Answer:
He says that he must sell two more books to pay his school fee and ask for some water too.

Question 5.
Why does he sell books ?
वह पुस्तकें क्यों बेचता है ?
Answer:
He sells books to earn money for his school fee.

Question 6.
Why does he ring the bell ?
वह घंटी क्यों बजाता है ?
Answer:
He rings the bell to get the door opened.

Question 7.
Who opens the door ?
दरवाज़ा कौन खोलता है ?
Answer:
A lady opens the door.

Question 8.
What does he request the Lady for ?
वह औरत से किस चीज़ के लिए प्रार्थना करता है ?
Answer:
He requests the lady for some water.

Question 9.
What does the Lady give him ?
औरत उसे क्या देती है ?
Answer:
The lady gives him a glass of milk.

Question 10.
How much money does the Lady give the boy for the book ?
औरत लड़के को पुस्तक के कितने पैसे देती है ?
Answer:
She gives him 5 pounds.

Scene-2

Question 1.
Count and write the number of characters in Scene 2 of the play.
नाटक के दृश्य 2 में पात्रों की संख्या गिनो और लिखो।
Answer:
Two.

Question 2.
What is the profession of the characters of this scene ?”
इस दृश्य के पात्रों का क्या व्यवसाय है ?
Answer:
They are doctors.

Question 3.
Why had the Lady come to this hospital ?
औरत इस अस्पताल में क्यों आई है ?
Answer:
The lady had some complicated disease and had been referred to this hospital for treatment.

Question 4.
How did the Lady get ill ?.
औरत बीमार कैसे हुई ?
Answer:
The lady got ill because of food poisoning

Question 5.
What kind of treatment did she need ?
उसे किस प्रकार के इलाज की ज़रूरत थी ?
Answer:
She needed immediate surgery.

Scene-3

Question 1.
How much time did the patients get to pay the bill, as per the rules ?
नियमों के अनुसार मरीजों को बिल चुकाने के लिए कितना समय मिलता था ?
Answer:
They got two days to pay the bill.

Question 2.
Why did the Lady get worried ?
औरत चिन्ता में क्यों पड़ गई ?
Answer:
She got worried to see the heavy bill to pay within two days.

Question 3.
Why did the Lady have tears in her eyes ?
औरत की आँखों में आंसू क्यों आ गये थे ?
Answer:
These were the tears of happiness as the bill had already been paid.

Question 4.
Why did she not have to pay the bill ?
उसे बिल क्यों नहीं चुकाना था ?
Answer:
She did not have to pay the bill because Dr. Howard had already paid it.

Question 5.
Who had paid the bill ? Why ?
बिल किसने चुकाया था ? क्यों ?
Answer:
Dr. Howard had paid the bill. He had paid it to repay the goodness of the lady in the form of a glass of milk.

Question 6.
Why was the Lady happy in the end ?
अन्त में औरत प्रसन्न क्यों थी ?
Answer:
In the end, the lady was happy because her faith in God and goodness of people had become stronger.

Learning Language:
Degrees of Adjectives

Adjectives have three forms of comparison: Positive, Comparative and Superlative. Simple adjectives that make no comparisons are positive forms.
Most adjectives form the comparative by adding ‘-r’, ‘-er’, -ier’ and the superlative by adding ‘-st’, ‘-est’, ‘-iest to the positive.
Adjectives के तीन रूप (degrees) होते हैं। Positive degree आम विशेषता बताती है; जबकि Comparative तथा Superlative degrees का प्रयोग तुलना के लिए किया जाता है।
(i) अधिकतर adjectives के पीछे ‘-er’/’-ier’ तथा ‘-est’/’-iest’ जोड़ने से तथा आवश्यक परिवर्तन (विशेषकर अंतिम) करने से क्रमश: Comparative तथा Superlative degrees बनती हैं ; जैसे

Positive	Comparative	Superlative
quick	quicker	quickest
fine	finer	finest
nice	nicer	nicest
bold	bolder	boldest
clever	cleverer	cleverest
deep	deeper	deepest
dirty	dirtier	dirtiest
heavy	heavier	heaviest
happy	happier	happiest

(ii)Adverb “more” तथा “most” के प्रयोग से ; जैसे —

Positive	Comparative	Superlative
beautiful courageous difficult satisfactory useful	more beautiful more courageous more difficult more satisfactory more useful	most beautiful most courageous most difficult most satisfactory most useful

(iii) भिन्न – भिन्न शब्दों के प्रयोग से ; जैसे —

Positive	Comparative	Superlative
good\well	better	best
bad	worse	worst
little	less	least
far	farther/further	farthest/furthest
many	more	most

Activity 5

Complete the following sentences by choosing the correct comparative form of the words given in the brackets :
1. Australia is the ………………. island in the world. (large, larger, largest)
2. The class test was ……………… than we had expected. (easy, easier, easiest)
3. The elephant has the …………….. trunk. (long, longer, longest)
4. Kilimanjaro in Africa is ………………. than Mont Blanc in Europe. (tall, taller, tallest)
5. The white dog was the ……………… of all. (greedy, greedier, greediest)
Answer:
1. largest
2. easier
3. longest
4. talle
5. greediest.

Activity 6.

Fill in the blanks with the correct degree of comparison of the adjective. Use the adjective given in the brackets.

1. Shyam is …………… than Karan. Neil is the ……………….. of them all.
2. My room is …………….. than yours. (neat)
3. Pole star is the ………….. ….. star. (bright)
4. The sweets I ate at this sweetshop are ………………. than any other sweets I have ever eaten. (delicious)
5. Is the Prime Minister …………….. than the President ? (powerful)
Answer:
1. healthier, healthiest
2. neater
3. brightest
4. more delicious
5. more powerful.

Comparative and Superlative Adjectives

Activity 7

Rewrite each sentence below using the comparative or superlative form of the adjectives given in the brackets.
Example A : You are (tall) than me.
Answer A : You are taller than me.

Question 1.
The fish I caught is (big) than the one you caught.
Answer:
The fish I caught is bigger than the one you caught.

Question 2.
That is the (small) umbrella I have ever seen!
Answer:
That is the smallest umbrella I have ever seen.

Question 3.
She is the (pretty) girl I have ever seen.
Answer:
She is the prettiest girl I have ever seen.

Question 4.
My friend is (fabulous) than yours.
Answer:
My friend is more fabulous than yours.

Question 5.
That building is (large) than the one next to it.
Answer:
That building is larger than the one next to it.

Question 6.
Who has the (easy) job in our family ?
Answer:
Who has the easiest job in your family ?

Question 7.
Do you think a screwdriver is (useful) than a hammer ?
Answer:
Do you think a screwdriver is more useful than a hammer?

Learning to Speak

Activity 8 (Think-Pair-Share)

Think about what do you want to do to help someone ? Think of a good human value such as :

1. sharing food
2. caring for an injured animal
3. giving new clothes to the needy, etc.
Sit facing your partner. Tell your partner about it. Each pair will take 5 minutes to speak and listen to each other.
After five minutes, say what have you learnt about your partner in front of the class)?
नोट-छात्र स्वयं करें।

Learning to Write

Activity 9

Do some people, who want to sell something, ring your door-bell in the afternoons ? Do they disturb you ? How do you react ? Are you polite to them ? Most people are rude to them. Write about the time when a salesman rang a bell when you were sleeping. You can use some of the following words/phrases.

afternoon, bell, fast asleep, woke up, salesman, selling books, pestered, offered water, angry, close the door

Answer:
It was afternoon yesterday when a bell rang at our door. I was fast asleep. Suddenly I woke up and opened the door. A salesman with some books in his hand greeted me. He requested me to buy one. He asked for some water too. I gave him a glass of water and requested him to go away. But he stood there like a statue and went on speaking. I got irritated and angry and closed the door.

Learning to Use Language

Read the following paragraph on Blackpool :

Blackpool is a beautiful town in England. Tourists love going to Blackpool. Blackpool is situated at the seaside. The seawater of Blackpool is very salty and visibly black. That is why the town is called Blackpool. It is a place that children love going to. There is a lot that children may find amusing. There is a tall tower in the middle of the town which is also black.

Activity 10.

Write a paragraph on your village/town/city or Amritsar/Jalandhar/Patiala/Ludhiana etc.
You may talk about :

• where the place is located
• what the place is famous for
• what most people do when they visit the place.

Note : The teacher must help learners to get information about the city/ place they want to write about.
I live in Amritsar. It is one of the biggest cities of Punjab. It is holy place and a historical city as well. It is mainly known for the Sri Harmandir Sahib, the holiest shrine of the Sikhs. People from all over the world visit this place. They have a dip in the holy tank here. The Jallianwalla Bagh near this holy shrine reminds us of the martyrs of 1919. The Durgiana Mandir of Amritsar is also worth visiting.

Comprehension Of Passages

Read the following passages carefully and aswers the questions that follow each :

(1) A small and a narrow street, afternoon time, a small boy selling things from door to door.
Boy (to himself): I must sell two more books ! How will I give my school fee if I don’t sell these books ? But it is a hot afternoon ! I am so hungry and thirstly ! I think I must ask for some water from the next house!
The boy sees a small house. He rings the bell. A lady opens the door.
Boy (tired and hungry): Good afternoon, Ma’am!
Lady (politely) : Good afternoon ! Do you want something ?
Boy : My name is Howard, Howard Kelly. I am selling these books. Will you buy one of my books?

1. What was the small boy doing ?
छोटा सा लड़का क्या कर रहा था ?

2. How was he feeling ?
वह कैसा महसूस कर रहा या?

3. Choose true and false statements and write them in your note book.
(a) The street was big and narrow.
(b) The boy’s name was Howard Kelly.

4. Complete the sentences according to the meaning of the passage.
(a) I must ask for some water ……………….
(b) The boy was to pay his ………………

5. Match the words with their meanings :

(a) ask for	softly
(b) politely	demand
	quickly

Answer:
1. The small boy was selling books from door to door.
2. He was feeling very hungry, thirsty and tired.
3.
(a) False
(b) True.
4.
(a) I must ask for some water from the next house .
(b) The boy was to pay his school fee.
5.
(a) ask for — demand
(b) politely — softly.

(2) Lady : You are very small. You should be in school and not selling things !
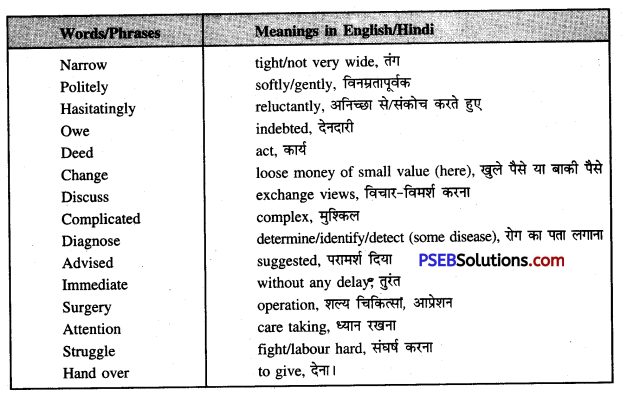
Boy : Yes, Ma’am. I need to pay for my fee. For this reason, I go door to door selling books. And, ah (hesitatingly) Can I get some water, please ? I am very thirsty.
The lady looks at him and says :
Lady : Sure! Just a few minutes, child. (goes inside and comes back with a glass) Here you are ! Here’s some milk. You are so weak. It appears you haven’t eaten for days !
Boy (taking the glass from the lady and drinking it) : Thank you so much, Ma’am. You are very kind ! How much, ehm… How much do I, ah… owe you for the milk ?

1. Why had the boy to sell books ?
लड़के को किताबें क्यों बेचनी पड़ती थीं ?

2. What did the Lady give the boy to drink ?
औरत ने लड़के को पीने के लिए क्या दिया ?

3. Choose true and false statements and write them in your note book.
(a) The boy appeared to be hungry.
(b) The boy asked the lady for some milk.

4. Complete the sentences according to the meaning of the passage.
(a) The Lady went inside and came back
(b) You should be in school and ……………….

5. Match the words with their meanings :

(a) sure	reluctantly
(b) hesitatingly	smilingly
	certainly

Answers
1. The boy had to sell books to earn money for his school fee.
2. The lady gave the boy a glass of milk to drink.
3.
(a) True
(b) False.
4.
(a) The Lady went inside and came back with a glass.
(b) You should be in school and not selling things.
5.
(a) sure — certainly
(b) hesitatingly – reluctantly.

(3) Dr. Brown (facing Dr Kelly) : She is from Blackpool. The doctors there advised her to come to this hospital as they could not understand her disease.
It started with food poisoning but got complicated. Perhaps, her liver has got affected.
Dr. Kelly : What ? From Blackpool ? That’s where I come from. Where is the lady ? (Dr Brown taking Dr Kelly to the hospital room)
Dr. Brown : There she is! She needs immediate surgery. I don’t think we can do much in this case even after surgery.
Dr. Kelly (peeps into the room and sees the sleeping woman, smiles) : We must do our best ! And, I’ll do my best to save her.
Dr. Brown : Sure doctor ! We’ll make all possible efforts to save her. Do you know her ? Dr Kelly smiles again.

1. What was the problem with the lady according to Dr. Brown ?
डॉ० ब्राउन के अनुसार औरत की क्या समस्या थी ?

2. What were the two doctors ready to do for the lady ?
दोनों डॉक्टर औरत के लिए क्या करने को तैयार थे ?

3. Choose true and false statements and write them in your note book.
(a) The lady needed immediate surgery.
(b) The Lady’s problem had started with over eating.

4. Complete the sentences according to the meaning of the passage.
(a) The Lady was from …………………
(b) The doctors in Blackpool hospital …………. the Lady’s disease.

5. Match the words with their meanings :

(a) efforts	damaged
(b) affected	attempts
	instruments

Answer.
1. According to Dr. Brown Lady’s liver was affected due to food poisoning.
2. The two doctors were ready to make all possible efforts to save the lady.
3.
(a) True
(b) False.
4.
(a) The Lady was from Blackpool.
(b) The doctors in Blackpool hospital could not understand the Lady’s disease.
5.
(a) efforts — attempts
(b) affected — damaged.

(4) Nurse (handing over the bill to the Lady) : Here is your medicine ! And, er… this is your bill. As per the hospital rules, you need to pay the bill in two days.
Lady (looking worried) : This hospital seems to be very expensive. Nurse : Yes, Madam. It is the most expensive hospital in London.
Lady (looks at the bill) : …It will take me a lifetime to pay the bill! It is signed by Dr Howard Kelly.
Nurse : Yes ! He’s very kind. He took special care of you. He’s from your city. Lady (looking interested) : Really ? Is he from Blackpool ?
Nurse : Yes, He is ! let me see your bill, Madam ! (takes the bill and looks at it, smiles) Yes, something is written on it. Did you see it?
Lady : No, let me see it again. (reads aloud with tears in her eyes). ‘Paid in full years ago with a glass of milk’. Dr Howard Kelly.

1. What were the hospital rules about payment of the bill ?
बिल चुकाने के बारे में अस्पताल के क्या नियम थे ?

2. What was written on the bill ?
बिल पर क्या लिखा था ?

3. Choose true and false statements and write them in your note book.
(a) The bill was signed by the Nurse.
(b) Dr. Howard Kelly was from Blackpool.

4. Complete the sentences according to the meaning of the passage.
(a) It is the ………………… in London.
(b) It will take me a lifetime …………..

5. Match the words with their meanings :

(a) expensive	anxious
(b) worried	interested
	costly

Answers
1. As per the hospital rules the bill was to be paid in two days.
2. ‘Paid in full years ago with a glass of milk.’
3.
(a) False
(b) True.
4.
(a) It is the most expensive hospital in London.
(b) It will take me a lifetime to pay the bill.
5.
(a) expensive – costly
(b) worried – anxious.

Use Of Words/Phrases In Sentences

1. Understand (to know) —
I can’t understand what you want.
मुझे समझ नहीं आता कि तुम क्या चाहते हो।

2. Disease (ailment) —
Corona has spread a fatal disease.
कोरोना ने घातक बीमारी फैला दी है।

3. Complicated (complex) —
Your problem is very complicated.
तुम्हारी समस्या बहुत ही जटिल है।

4. Faith (trust) —
I have deep faith in God.
मेरा परमात्मा में गहरा विश्वास है।

5. Accept (take) —
I don’t accept money for any social service.
मैं किसी सामाजिक कार्य के लिए धन स्वीकार नहीं करता।

6. Deed (act) —
Do a good deed daily.
प्रतिदिन एक अच्छा काम (कर्म) करो।

7. Hand over (to give) —
Do a good deed daily.
प्रतिदिन एक अच्छा काम (कर्म) करो

8. Discuss (exchange views) —
Let us discuss this problem.
आओ हम इस समस्या पर चर्चा/विचार-विमर्श करें।

9. Ask for (demand) —
He asked me for some money.
उसने मुझसे कुछ पैसे मांगे।

10. Expensive (costly) —
Your shirt is very expensive.
तुम्हारी कमीज़ बहुत कीमती है।

Word Meanings:

A Glass of Milk Summary in Hindi

Scene 1…………………… and feels stronger.

दृश्य-1.
समय : बाद दोपहर
स्थान : इंग्लैंड का एक छोटा सा शहर-ब्लैक पूल
पात्र : एक लड़का : हॉवर्ड केली
एक महिला : अनीता
दृश्य : एक छोटी और तंग गली, बाद दोपहर का समय, एक छोटा-सा लड़का एक दरवाज़े से दूसरे दरवाजे तक (घर-घर जाकर) सामान बेच रहा है।
लड़का (स्वयं से) : मुझे दो और किताबें अवश्य बेचनी पड़ेंगी। यदि मैं इन किताबों को नहीं बेचूंगा, तो मैं अपने
स्कूल की फीस कैसे भरूंगा। परन्तु दोपहर गर्म है। मैं बहुत प्यासा हूँ और मुझे तेज़ भूख भी लगी है। मैं सोचता हूँ कि मैं अगले घर से पानी माँग लूं।

लड़के को एक छोटा घर दिखाई देता है। वह घंटी (बैल) बजाता है। एक औरत दरवाजा खोलती है।
लड़का (थका हारा : गुड ऑफ्टरनून मैम !और भूखा)
औरत (विनम्रता से) : Good afternoon. तुम्हें कुछ चाहिए क्या ?
लड़का : मेरा नाम हॉवर्ड केली है। मैं ये पुस्तकें बेच रहा हूँ। क्या तुम मेरी कोई एक पुस्तक खरीदोगी।
औरत : तुम बहुत छोटे हो। तुम्हें स्कूल में होना चाहिए न कि कुछ बेचना चाहिए।
लड़का : हां ! मैम। मुझे अपनी फ़ीस भरनी है। इसी कारण मैं घर-घर जाकर किताबें बेचता हूँ। और, आह
(झिझकते हुए)। कृपया क्या मुझे कुछ पानी मिल सकता है ? मुझे बहुत प्यास लगी है। औरत उसकी ओर देखकर बोलती है।

औरत : अवश्य ! बच्चे ! कुछ क्षण (पल) रुको। (अंदर जाती है और एक गिलास लेकर वापिस आती है।) यह लो !
यह दूध है। तुम बहुत कमज़ोर हो। ऐसा लगता है तुमने कई दिनों से कुछ खाया नहीं है।
लड़का (औरत से : आपका बहुत-बहुत शुक्रिया मैम ! आप बहुत दयालु हैं। मुझे कितना ehm ………….. मुझे गिलास लेकर पीते हुए) कितना ah (आह) ………….. दूध के लिए मुझे कितना मूल्य चुकाना है? औरत (स्नेह से भरकर : कुछ भी नहीं ! तुम्हें मुझे कुछ भी नहीं देना। मेरी माँ ने मुझे सिखाया है कि किसी दयापूर्ण बोलते हुए) कार्य की कीमत नहीं लेनी चाहिए। मुझे तुमसे एक किताब खरीदनी है। इस पुस्तक का मूल्य
क्या है?

लड़का(मुस्कराते हुए) : धन्यवाद, मैम ! मैं इसे सदा याद रखूगा। इस पुस्तक का मूल्य 4 पौंड और 70 पैंस है। औरत पुस्तक ले लेती है और उस लड़के को 5 पौंड देकर शेष पैसे अपने पास रखने को कहती है। लड़का मुस्कराता है और उस घर से चल देता है। वह खुश है और उसे लगता है कि जैसे उसे और अधिक शक्ति मिल गई हो।

Scene 2 ………………………………….. smiles again.

दृश्य-2. (कई वर्षों के बाद)

समय : सुबह
स्थान : शहर का बड़ा अस्पताल
पात्र : डा० पीटर ब्राउन
डा० हॉवर्ड केली
(डा० ब्राउन और डा० केली एक केस पर विचार-विमर्श करते हुए)
डा० केली : डा० ब्राउन, क्या यह कठिन केस है?
डा० ब्राउन : हाँ, यह एक जटिल केस है। हम अभी तक इस समस्या को समझ नहीं पाये।
डा० केली (डा० ब्राउन : औरत कौन है? वह कहाँ से है? और वह इतनी बीमार कैसे हो गई?
के निकट आते हुए) डा० ब्राउन (डा० केली : वह ब्लैक पूल से है। वहाँ के डाक्टरों ने उसे इस अस्पताल में आने की सलाह दी है क्योंकि
की ओर वे उसकी बीमारी का पता नहीं लगा पाए। यह फूड पाइजनिंग (भोजन से जहर बन जाने) देखते हुए) से शुरू हुई लेकिन जटिल हो गयी। शायद उसका लीवर प्रभावित हो गया है।
डा० केली : क्या ? ब्लैक पूल से ? मैं भी तो वहीं से हूँ। कहाँ है औरत ?
(डा० ब्राउन डा० केली को अस्पताल के उस कमरे में ले जाते हुए)
डा० ब्राउन : यह रही, वह। इसे शीघ्र ही शल्य चिकित्सा (सर्जरी) की आवश्यकता है। मुझे नहीं लगता कि हम शल्य चिकित्सा के बाद भी इस केस में ज्यादा कुछ कर पाएं। डा० केली (कमरे में : हमें अपनी पूरी कोशिश करनी चाहिए। और मैं इसे बचाने के लिए अपना हर संभव सर्वश्रेष्ठ झांकता है और सोई हुई प्रयत्न करूंगा। महिला को देखकर मुस्कराता है) डा० ब्राउन : अवश्य, डॉक्टर ! हम इसे बचाने के लिए पूरा प्रयत्न करेंगे। क्या आप इसे जानते हो?
डा० केली फिर से मुस्कराते हैं।

Scene 3 ………………. become stronger today.

दृश्य-3.

स्थान : अस्पताल का एक कमरा
पात्र : औरत
: एक नर्स
: एक व्यक्ति (बिल विभाग से)
(नर्स औरत को दवाई देने लगती है।)
व्यक्ति (नर्स को कुछ : क्या यह अच्छा महसूस कर रही है? यह भाग्यशाली है कि इसका केस डा० हॉवर्ड केली कागज़ देते हुए) ने अपने हाथ में लिया था। यह इनका बिल है। इन्हें दो दिन में बिल का भुगतान करना है।
इन्हें बिल दिखा दो। नर्स (व्यक्ति से : तुम ठीक कह रहे हो। यह भाग्यशाली है।
और हाँ, यह पहले से बहुत अच्छा महसूस कर बिल लेते हुए) रही है और स्वस्थ है।
(नर्स औरत को दवाई देती है।) नर्स (औरत को : यह आपकी दवाई है।
और हां, यह आपका बिल है। अस्पताल के नियमानुसार आपको बिल बिल देते हुए) का भुगतान दो दिन में करना है।
औरत (चिन्तित : यह अस्पताल बहुत महंगा लगता है। दिखाई देती है)
नर्स : हां मैडम! यह लंदन का सबसे महँगा अस्पताल है।
औरत (बिल देखते : इस बिल को भरने में मेरा पूरा जीवन लग जाएगा। इस पर डा० हॉवर्ड के हस्ताक्षर हैं। हुए)
नर्स : हां। वह बहुत दयालु हैं। उन्होंने आपका विशेष ध्यान रखा है। वह आपके शहर से ही हैं। औरत (रुचि : वास्तव में ? क्या वह ब्लैक पूल से हैं? दिखाते हुए)
नर्स : हां, वह वहीं से हैं। मुझे अपना बिल दिखाओ, मैडम ! (बिल लेती है और देखकर मुस्कराती – है) हां, इस पर कुछ लिखा है। क्या आपने देखा है?
औरत : नहीं, मुझे फिर से देखने दो। (आंखों में आंसू लिए ऊंची आवाज़ में पढ़ती है।) ‘वर्षों पहले एक गिलास दूध द्वारा पूरा बिल चुका दिया गया था।’ डॉ० हॉवर्ड केली।
औरत : भगवान हॉवर्ड का भला करे। मैं बहुत खुश हूँ। आज मेरा भगवान और आदमी की अच्छाई पर भरोसा और भी मज़बूत हो गया है।

Retranslation Of Isolated Sentences

1. I must sell two more books.
मुझे दो और किताबें अवश्य बेचनी पड़ेंगी।

2. I think I must ask for some water.
मैं सोचता हूँ कि मैं पानी माँग लूं।

3. I am selling these books.
मैं ये पुस्तकें बेच रहा हूँ।

4. You should be in school and not selling things.
तुम्हें स्कूल में होना चाहिए न कि कुछ बेचना चाहिए।

5. It appears you haven’t eaten for days.
ऐसा लगता है कि तुमने कई दिनों से कुछ नहीं खाया है।

6. My mother has taught me not to accept payment for a deed of kindness.
मेरी माता ने मुझे सिखाया है कि दयापूर्ण कार्य की कीमत नहीं लेनी चाहिए।

7. The boy smiles and leaves the house.
लड़का मुस्कराता है और उस घर से चल देता है।

8. We have not yet been able to diagnose the problem.
हम अभी तक इस बीमारी को समझ नहीं पाए।

9. The doctors there advised her to come to this hospital.
वहाँ के डाक्टरों ने उसे इस अस्पताल में आने की सलाह दी है।

10. She needs immediate surgery.
इसे शीघ्र ही शल्य चिकत्सा (सर्जरी) की आवश्यकता है।

11. We will make all possible efforts to save her.
हम इसे बचाने के लिए पूरा प्रयत्न करेंगे।

12. This is her bill.
यह इनका बिल है।

13. It is the most expensive hospital in London.
यह लंदन का सबसे महंगा अस्पताल है।

14. It will take me a lifetime to pay the bill.
इस बिल को भरने में मेरा पूरा जीवन लग जाएगा।

15. Paid in full years ago with a glass milk.
वर्षों पहले एक गिलास दूध द्वारा पूरा बिल चुका दिया गया था।

16. My faith in God and goodness of people has become stronger today.
मेरा भगवान और आदमी की अच्छाई पर भरोसा और .भी मज़बूत हो गया है।

English Guide for Class 7 PSEB Prose

• Rent for Water Question Answer
• Birbal’s Khichdi Question Answer
• A Glass of Milk Question Answer
• Mountaineers Question Answer
• The Princess Who Never Smiled Question Answer
• A Treasure Hunt Question Answer
• A Hole in the Fence Question Answer
• Hachiko-The World’s Most Loyal Dog Question Answer

Punjab State Board PSEB 7th Class English Book Solutions Chapter 6 A Treasure Hunt Textbook Exercise Questions and Answers.

Class 7th English Solutions Chapter 6 A Treasure Hunt Question Answers

A Treasure Hunt Class 7 Questions and Answers

Activity 1

Look up the following words/phrases in a dictionary. You should seek the following information about the words and put them in your WORDS notebook.

1. Meaning of the word as used in the story (adjective/noun/verb, etc.)
2. Pronunciation (The teacher may refer to the dictionary or the mobile phone for correct pronunciation.)
3. Spellings

ancient	treasure	swept across	huddled	skilfully
mounted	set off	thrilling	braved	realized

Vocabulary Expansion

Activity 2

Question 1.
Choose suitable phrases from the box to write below each image a dense forest

a dense forest	a galloping camel
craggy mountains	a swimming turtle

Answer:
a dense forest
a craggy mountain
a galloping camel
a swimming turtle

Learning to Read and Comprehend

Activity 3

What is meant by the bold words in the following sentences? The first one has been done for you.

Question 1.
The eagle agreed and joined the two.
Answer:
The word ‘two’ refers to the lion and Sagar.

Question 2.
The eagle watched every step they took with his sharp eyes.
Answer:
The word ‘they’ refers to Sagar and the lion.

Question 3.
There, they met a sheep.
Answer:
The word ‘they’ refers to Sagar, the lion and the eagle.

Question 4.
Will you join us in a treasure hunt and keep us warm when it’s cold ?
Answer:
The word ‘you’ refers to the sheep.

Question 5.
You are called the ship of the desert.
Answer:
The word ‘You’ refers to the camel.

Question 6.
The four finally reached the desert.
Answer:
The word ‘four’ refers to Sagar, the lion, the eagle and the sheep.

Question 7.
The rough waves almost drowned them.
Answer:
The word ‘them’ refers to Sagar, the lion, the eagle, the sheep and the camel.

Question 8.
Indeed, they had found the greatest treasure ever!
Answer:
The word “they’ refers to Sagar, the lion, the eagle, the sheep, the camel and the turtle.

Activity 4

Answer the following questions.

Question 1.
What did Sagar find in the library ?
सागर को लाइब्रेरी में क्या मिला ?
Answer:
Sagar found an ancient book in the library.

Question 2.
What did he plan to do ?
उसने क्या करने की योजना बनाई ?
Answer:
He planned to go in search of the treasure.

Question 3.
Where did Sagar go first? Whom did he meet there?
सागर सबसे पहले कहां गया ? वहां वह किससे मिला ?
Answer:
Sagar went to a forest first. He met a lion there.

Question 4.
Why did Sagar feel scared in the forest ?
वन में सागर डर क्यों गया था ?
Answer:
Sagar felt scared because the forest was dense and dark.

Question 5.
Where did Sagar and the lion go from the forest ?
सागर तथा शेर वन से कहां गए ?
Answer:
They went to a mountain from the forest.

Question 6.
What did Sagar ask the eagle to do ? Why ?
सागर ने गिद्ध से क्या करने को कहा ? क्यों ?
Answer:
Sagar asked the eagle to alert them against the danger because the eagle had very good eyesight.

Question 7.
Who did they meet in the valley ?
घाटी में वे किससे मिले ?
Answer:
In the valley, they met a sheep.

Question 8.
How would the sheep help Sagar and others ?
भेड़ सागर तथा उसके अन्य साथियों की सहायता कैसे कर सकती थी ?
Answer:
The sheep would keep them warm in cold.

Question 9.
How did the camel help them ?
ऊँट ने उनकी सहायता कैसे की ?
Answer:
The camel helped them cross the vast desert.

Question 10.
What did the turtle do to help them ?
कछुए ने उनकी सहायता करने के लिए क्या किया ?
Answer:
The turtle took them across the ocean.

Activity 5

Discuss the following in groups and explain it in the given space. . “Congratulations ! You have found the treasure !” What did the owl want to tell Sagar and his companions ?
ऊपर दिया गया वाक्य कह कर उल्लू सागर तथा उसके साथियों को क्या बताना चाहता था ?
Answer:
The owl wanted to tell them that friendship is a great blessing. It is the greatest treasure ever. They were lucky to find it.

Learning Language

Parts of Speech

Till now, we have done nouns, pronouns, verbs, adjectives, adverbs, prepositions etc. They are called Parts of Speech.

Activity 6

Read each sentence below and look carefully at the underlined words.

If the word names a person, place, thing or idea, it is a NOUN. Write N in the given space.
If the word shows an action, it is a VERB. Write V in the given space.
If the word describes a noun, it is an ADJECTIVE. Write A in the given space.
Answer:
1. Maria picked a fresh rose from the garden for her aunt. — N
2. Does anyone have a rose garden? — A
3. The puppy rose and patted his mother for attention. — V
4. He will book a hotel room for you. — V
5. I bought a new book. — N
6. Do you know of a book club ? — A
7. Corner the mouse if you want to catch it. — V
8. Corners of my book were torn. — N
9. I live in the corner house. — A
10. Some paper yellow with age. — V
11. Diana needs yellow paint to make the painting. — A
12. Yellow is a nice colour. — N
13. I like baby pink colour. — A
14. The baby kept crying. — N
15. My grandmother likes to baby me. — V

Learning to Listen Dictation

Activity 7

Your teacher will speak some words from the story. Listen carefully and write their spellings.
Answer:
1. ancient
2. treasure
3. swept
4. huddled
5. mounted
6. thrilling
7. braved
8. realized
9. ocean
10. galloped.
नोट :-विद्यार्थी इन शब्दों की spellings याद करें और ये शब्द लिखने का अभ्यास करें।

Activity 8

Read the following poem with proper pronunciation. Put more STRESS on the bold words in each line. Remember poems are to be read and not sung like nursery rhymes.
(The teacher must help the students.)

Sympathy
I lay in sorrow, deep distressed
My grief a proud man heard
His looks were cold.
He gave me gold.
But not a kindly word.
My sorrow passed – I paid him back
The gold he gave to me.
Then stood erect and spoke my thanks
And blessed his charity.
I lay in want, in grief and pain.
A poor man passed my way.
He bound my head.
He gave me bread.
He watched me night and day.
How shall I pay him back again
For all, he did to me ?
Oh ! Gold is great. But greater far
Is heavenly sympathy ! -Charles Mackay

नोट :-अध्यापक की सहायता से स्वयं करें।

Learning to Write

Activity 9

Read the following messages that people write for their friends and family on their birthdays.
1. May your special day be filled with love, laughter and happiness. You deserve it.
2. Choose to celebrate your birthday, the way you like. May your birthday bring you the happiness and the good health you deserve.
3. Wishing you happiness and success in your lifelin the coming years.
4. It is always good to remember you, my friend, especially on your birthday. Enjoy! Make it unforgettable!
5. I am so sorry that I forgot your birthday. Belated Happy Birthday.
6. I can’t believe, I missed your birthday. I am so sorry. Wishing you a very happy birthday and success in everything you do.

Activity 10

You forgot to wish your friend on his or her birthday. Write a birthday message for your friend in the card given below.

You must :
1. say sorry to your friend for forgetting to wish him/her
2. give belated wishes to your friend in the message
3. wish your friend happiness, success in life and good health
Some useful words/phrases
1. apologise
2. forget
3. wish
4. deserve
5. celebrate
6. belated
7. many happy returns
8. happiness
9. sincerely
10. success/successful
11. future
12. good health

You may begin your message with :

Dear/Dearest Anshu/Anshika How forgetful I am to forget your birthday on May 22, 2020, So I failed to wish you. I am very sorry for this. However, nothing has gone wrong yet. I can still give you my heartly wishes, belated this may be. I always wish for your happiness and success in life. Enjoy good health always. I promise never to forget your birthday in future. Anshika 24 May, 2020

Learning to Use Language
Writing a story

Activity 11.

Write a short story (100 words) using the following words. An outline is given below.
Your story must have :
a beginning
a middle/ the main story
a conclusion
Outline
the sun and the wind–friends–one day-an argument—who is stronger-decided to test their strength—saw a man walking—the challenge—to remove the coat-using the strength wind used its strength blew hard-man caught hold of his coat-the wind grew tired—could not remove the coat—the sun’s turn-started shining very brightly-used its heat—man felt hot-removed his coat–the sun became the winner.
Answer:
Once a dispute arose between the sun and the wind. The wind boasted that it was stronger than the sun. But it refused to accept the wind’s superiority. Just then they saw a passerby. He was wearing a coat. Both claimed that they would make the traveller remove his coat. First, it was the wind’s turn to try. It blew as hard as it could. The faster it blew, the tighter the man wrapped up his coat. The wind failed to make the man take off his coat.

Then it was the sun’s turn to show its strength. It started shining brightly. The man who was shivering with cold, felt relieved. Soon he started sweating all over and removed his coat. Thus the sun won the contest. The wind accpeted its defeat.
Moral : Gentleness is better than pride.
Or
Pride hath a fall.

Comprehension Of Passages:

Read the following passages carefully and answer the questions that follow each :

(1) One day, Sagar went to a library. There, he found an ancient book. He flipped through the pages of the book. In the book, he saw a big sheet folded neatly. He opened the sheet and saw that it was a treasure map. “Hurray! I’m going to find this treasure and have some fun”, he said to himself. Sagar set off for the treasure hunt.

He walked and walked and finally reached a forest. In the forest, he met a lion. “You are strong and brave! I am going on a treasure hunt. Will you come with me ?” said Sagar to the lion. The lion agreed to go with him. They both went into the forest. The forest was dense and dark. Sagar was scared, but they crossed the forest easily because the lion was by his side.

1. What did Sagar see in the book ? What was it ?
सागर ने किताब में क्या देखा ? यह क्या था ?

2. Where did Sagar meet the lion ? How did he praise him ?
सागर को शेर कहां मिला ? उसने शेर की प्रशंसा कैसे की ?

3. Choose true and false statements and write them in your note book.
(a) Sagar found a new book in the library.
(b) Sagar became happy to see a treasure map.

4. Complete the sentences according to the meaning of the passage.
(a) The lion agreed to ……………
(b) Sagar crossed the forest easily because ……

5. Match the words with their meanings :

(a) hunt	hurry
(b) scared	search
	afraid

Answers
1. Sagar saw a big sheet folded neatly. It was a treasure map.
2. Sagar met the lion in the forest. He praised him by saying that he was strong and brave.
3.
(a) False
(b) True
4.
(a) The lion agreed to go with them.
(b) Sagar crossed the forest easily because the lion was by his side.
5.
(a) hunt — search
(b) scared — afraid

(2) Then the two of them reached a mountain. There, they met an eagle. “You have excellent eyesight and you can alert us to dangers! We are looking for treasure. Will you come with us?” said Sagar to the eagle. The eagle agreed and joined the two.

The mountains were tall and craggy. The lion slipped on the mountain but Sagar quickly caught him and gave him a hand. The lion thanked Sagar when he pulled him up. The eagle watched every step they took with his sharp eyes. Soon, they reached a valley.

There, they met a sheep. “Will you join us in a treasure hunt and keep us warm when it’s cold?” Sagar asked the sheep. The sheep agreed and joined the lion, the eagle and Sagar. A cold wind swept across the valley. They all huddled against the sheep who kept them warm and cosy.

1. What could the eagle do for Sagar and his companions ? How ?
गिद्ध सागर तथा उसके साथियों के लिए क्या कर सकता था ? कैसे ?

2. Who could keep them warm in cold ?
ठंड में उन्हें कौन गर्मी दे सकता या

3. Choose true and false statements and write them in your note-book.
(a) The mountains were tall and craggy.
(b) The lion had sharp eyes.

4. Complete the sentences according to the meaning of the passage.
(a) The eagle watched their every step with ……
(b) ……………. swept across the valley.

5. Match the words with their meanings.

(a) swept	crowded
(b) huddled	blew
	walked

Answer:
1. The eagle could alert them to dangers with his sharp eyes.
2. The sheep could keep them warm in cold.
3.
(a) True
(b) False
4.
(a) The eagle watched their every step with his sharp eyes.
(b) A cold wind swept across the valley.
5.
(a) swept — blew
(b) huddled — crowded.

(3) The five finally reached the ocean where they met a turtle. “Can you help us to cross the ocean? We are on a treasure hunt!” said Sagar to the turtle. The turtle agreed and joined the lion, the eagle, the sheep, the camel and Sagar. The rough waves almost drowned them but the turtle swam skilfully and took them across the ocean.

The six of them met an owl on the other side. The old owl spoke from his ancient wisdom, “Congratulations! You have found the treasure!” “Where is it?” they all asked in surprise. “Together, you have crossed the forest, climbed the mountains, braved the desert and swum across the ocean.

You could never have done it without the help of one another!” said the owl. They all looked at one another and realized that the owl was right. They had found friendship! Indeed, they had found the greatest treasure ever !

1. What was going to drown them ? Who came to their help?
उन्हें क्या चीज़ डुबोने लगी थी ? उनकी सहायता के लिए कौन आगे आया ?

2. Who told them about the real treasure ? What was it ?
उन्हें सच्चे खजाने के बारे में किसने बताया ? यह क्या था ?

3. Choose true and false statements and write them in your note-book.
(a) They had crossed the forest and the ocean together.
(b) They were six before they met a turtle.

4. Complete the sentences according to the meaning of the passage.
(a) They realized that the …………..
(b) They had found the ……………

5. Match the words with their meanings.

(a) skilfully	adeptly
(b) finally	in the beginning
	in the end

Answer:
1. The rough waves were going to drown them. The turtle came to their help.
2. The owl told them about the real treasure. It was ‘friendship’.
3.
(a) True
(b) False
4.
(a) They realized that the owl was right.
(b) They had found the greatest treasure ever!
5.
(a) skilfully – adeptly
(b) finally – in the end.

Use Of Words/Phrases In Sentences

1. Neatly (clearly) —
Please write the letter neatly.
कृपया पत्र साफ़-साफ़ लिखें।

2. Folded (wrapped) —
He thanked me with folded hands.
उसने हाथ जोड़ कर मेरा धन्यवाद किया।

3. Give someone a hand (help) —
He gave me his hand while we were crossing the river.
उसने नदी पार करते समय मेरी सहायता की।

4. Realize (to feel) —
He realized his mistake.
उसने अपनी गलती महसूस की।

5. Galloping (running fast) —
The galloping horses were soon out of sight.
तेज़ दौड़ते घोड़ें जल्दी ही अदृश्य हो गए।

6. Braved (faced bravely) —
He braved the danger.
उसने खतरे का वीरतापूर्वक सामना किया।

7. Set off (start) —
They set off on a long journey.
वे एक लंबी यात्रा पर चल पड़े।

8. Excellent (superb) —
He gave an excellent performance.
उसने बहुत ही शानदार प्रदर्शन किया।

Word Meanings

A Treasure Hunt Summary in Hindi

One day, Sagar ……………..warm and cosy.

एक दिन सागर एक पुस्तकालय गया। वहाँ उसे एक प्राचीन पुस्तक मिली। उसने पुस्तक के पन्नों को पलटा। पुस्तक में उसने एक बड़ा सफ़ाई से मुड़ा हुआ कागज़ देखा। उसने उस कागज़ को खोला और देखा। वह एक ख़जाने का नक्शा (मानचित्र) था। उसने खुशी से चिल्लाते हुए अपने आप से कहा, “मैं खज़ाना ढूंढने जाऊंगा, कुछ मज़ा भी आएगा।” सागर खज़ाने की तलाश में निकल पड़ा। वह चलता गया और अन्ततः एक जंगल में पहुँच गया।

जंगल में वह एक शेर से मिला। सागर ने शेर से कहा, “तुम ताकतवर और बहादुर हो! मैं एक खजाने की तलाश में जा रहा हूँ। क्या तुम मेरे साथ चलोगे।” शेर उसके साथ चलने के लिए सहमत हो गया। दोनों जंगल में गए। जंगल घना तथा अंधेरा था। सागर डर गया, परन्तु उन्होंने आसानी से जंगल पार कर लिया क्योंकि शेर उसके साथ था। तब वे दोनों एक पहाड़ पर पहुँचे। वहां वे एक गिद्ध (Eagle) से मिले। सागर ने गिद्ध से कहा, “तुम्हारी दृष्टि बहुत ही शानदार है और तुम हमें आने वाले खतरों से सावधान कर सकते हो।

हम खज़ाने की खोज पर हैं। क्या तुम हमारे साथ चलोगे ?” गिद्ध ने अपनी सहमति दी और उनके साथ शामिल हो गया। पहाड़ ऊँचे तथा असमतल थे। शेर पहाड़ पर फिसल गया परन्तु सागर ने शीघ्रता से उसे पकड़ लिया और उसे सहारा दिया। जैसे ही सागर ने शेर को खींचा उसने उसका धन्यवाद किया। गिद्ध उनके प्रत्येक कार्य को अपनी तीव्र दृष्टि से देखता रहा। शीघ्र ही वे एक घाटी में पहुँच गए। वे एक भेड़ से मिले ।

सागर ने भेड़ से पूछा, “क्या तुम खजाने की खोज में हमारे साथ चलोगी और ठंड में हमें गर्मी प्रदान करोगी ?” भेड़ सहमत हो गई और शेर, गिद्ध और सागर के साथ शामिल हो गई। घाटी में ठंडी हवा चल रही थी। वे सभी भेड़ के साथ जुड़ (चिपक) कर बैठ गए जिसने उनके शरीर को गर्मी दी और आराम पहुँचाया।

The four finally ……………. treasure ever !

चारों अन्ततः एक रेगिस्तान पहुँचे जहाँ उन्होंने एक ऊँट को देखा। सागर ने ऊँट से कहा, “तुम्हें रेगिस्तान का जहाज़ कहा जाता है! क्या तुम खज़ाना खोजने में हमारे साथ चलोगे और रेगिस्तान को पार करवाने में हमारी सहायता करोगे ?” ऊँट सहमत (मान) हो गया। शेर, भेड़ और सागर ऊँट पर सवार हो गए और खुशी-खुशी बड़े रेगिस्तान को पार करने के लिए चल पड़े। गिद्ध उनका मार्गदर्शन करता रहा। ऊँट सरपट दौड़ने लगा। ऊँट पर बैठ कर रेगिस्तान को पार करना रोमांचक (अनुभव) था।

पाँचों आखिरकार महासागर पर पहुँच गए जहाँ उन्हें एक कछुआ मिला। सागर ने कछुए से कहा, “क्या तुम महासागर को पार करने में हमारी मदद करोगे ? हम खजाने की खोज पर हैं।” कछुआ मान गया और शेर, गिद्ध, भेड़, ऊँट और सागर के साथ चल पड़ा। अशांत/कष्टदायक लहरों ने उन्हें लगभग डुबो ही दिया था, परन्तु कछुए ने कुशलतापूर्वक तैर कर उन्हें सागर पार करवा दिया।

सभी छ: को दूसरी ओर एक उल्लू मिला। बूढ़ा उल्लू अपनी प्राचीन बुद्धिमत्ता दिखाते हुए बोला, “बधाई हो! तुम्हें खजाना मिल गया।” उन सभी ने हैरानी से पूछा, “कहाँ है वह ?” उल्लू ने कहा, “तुम सबने एक साथ जंगल पार किया, पहाड़ पर चढ़े, बहादुरी से रेगिस्तान और तैरकर यह सागर पार किया है। तुम एक-दूसरे की मदद के बिना यह नहीं कर सकते थे।” उन सबने एक-दूसरे की ओर देखा और अनुभव किया कि उल्लू ठीक कह रहा है। उन्हें ‘मित्रता’ मिल गई थी। वास्तव में उन्हें अब तक का सबसे बड़ा खज़ाना मिल गया था।

Retranslation Of Isolated Sentences

1. There he found an ancient book. — वहाँ उसे एक प्राचीन पुस्तक मिली।
2. I am going to find this treasure. — मैं इस खज़ाने को ढूंढने जा रहा हूँ।
3. Sagar set off for treasure hunt. — सागर खज़ाने की तलाश में निकल पड़ा।
4. They both went into the forest. — वे दोनों जंगल में गए।
5. You have excellent eyesight. — तुम्हारी दृष्टि बहुत ही अच्छी है।
6. The eagle agreed and joined the two. — गिद्ध सहमत हो गया और दोनों में शामिल हो गया।
7. A cold wind swept across the valley. — घाटी में शीत लहर चल रही थी।
8. You are called the ship of the desert. — तुम्हें रेगिस्तान का जहाज़ कहा जाता है।
9. You have found the treasure. — तुम्हें खज़ाना मिल गया है।
10. You could never have done it without the help of one another. — तुम एक-दूसरे की सहायता के बिना यह काम नहीं कर सकते थे।
11. They all huddled against the sheep. — वे सभी भेड़ के साथ चिपक कर बैठ गए।
12. The forest was dense and dark. — वन सघन और अंधेरा था।

English Guide for Class 7 PSEB Prose

• Rent for Water Question Answer
• Birbal’s Khichdi Question Answer
• A Glass of Milk Question Answer
• Mountaineers Question Answer
• The Princess Who Never Smiled Question Answer
• A Treasure Hunt Question Answer
• A Hole in the Fence Question Answer
• Hachiko-The World’s Most Loyal Dog Question Answer

Punjab State Board PSEB 7th Class English Book Solutions Poem 1 Trains Textbook Exercise Questions and Answers.

Class 7th English Solutions Poem Chapter 1 Trains Question Answers

Trains Class 7 Questions and Answers

Activity 1.

Look up the following words in a dictionary. You should seek the following information about the words and put them in your WORDS notebook.
1. Meaning of the word as used in the poem (adjective/noun/verb, etc.)
2. Pronunciation (The teacher may refer to the dictionary or the mobile phone for correct Pronunciation.)
3. Spellings

Passenger	Precious	mail	freight
dusk	dawn	without	fail

Post-reading

Vocabulary Expansion

Trains are a very important means of land transport in India. India has a large network of trains.

Activity 2.

Given below are some more means of transport. Put them under the right box.

car	aeroplane	scooter	helicopter	boat	auto
bus	ship	submarine	train	jeep	bicycle

Land	sky	water
car bus scooter train auto jeep bicycle	aeroplane helicopter	ship submarine boat

Activity 4

Read the following lines and answer the questions that follow : Through day and darkness, Through dusk and dawn.

Question 1.
What do the above lines refer to ?
Answer:
The above lines refer to trains running day and night.

Question 2.
What do the day and darkness’ and dusk and dawn’ in the poem tell the readers ?
Answer:
They tell us about the different times of the day. They also form pairs of opposite time.

Learning Language

Conjunctions : ‘so’, ‘because’. “although’. ‘and’, ‘yet
We use Conjunctions like ‘and, “or”, “but, “because’ and although’ to join two parts of sentences.
नोट:-वाक्य के दो या अधिक भागों को जोड़ने के लिए जिन शब्दों का प्रयोग किया जाता है, उन्हें Conjunctions कहते हैं।

Activity 5

1 Complete the sentences given below with ‘so’ or ‘because’. Here are a few examples. Read them before you do the activity.
Examples :
1. Rajan is happy because he has stood first in the race.
2. It was raining, so I did not go to school.
3. I went to the cinema because it was a holiday.
We use ‘because‘ for giving reasons, and ‘so’ for talking about results or purposes.

1. My dog was hungry …………. it stole biscuits from the shelf.
2. I am feeling sleepy …………….. I am very tired.
3. Babli bought new clothes ………….. she wanted to wear them on Diwali.
4. It was raining, …………. my books got wet.
5. He did not study hard, …………… he failed the test.
6. I asked for directions ………….. I was lost.
7. I did not clean the room, ………… it became dirty.
8. I met with an accident …………….. I was driving fast.
9. Deepa went to the doctor …………… she was feeling sick.
10. Mohan did not help Sohan …………….. he was not well.
Answer:
1. so
2. because
3. because
4. so
5. so
6. because
7. so
8. because
9. because
10. because.

Activity 6.

Combine the sentences given below using “although’ and ‘yet’. Write them in your notebook. Here are a few examples. Read them before you do the activity.

Examples :
1. Rajan did not win the race. Rajan was happy.
Although Rajan did not win the race, yet he was happy.

2. It was raining. I went to school.
Although it was raining, yet I went to school.

3. It was a holiday. I did not go to the cinema.
Although it was a holiday, yet I did not go to the cinema.
We use ‘although’ and ‘yet in the same sentence for unexpected or different information.

1. My dog was hungry. It did not eat biscuits.
2. He is very sleepy. He is watching a movie.
3. Babli wanted to wear new clothes on Diwali. Babli did not buy them.
4. It was raining. I did not take an umbrella.
5. He did not study hard. He passed the test.
6. I was lost. I did not ask for directions.
7. My room was dirty. I did not clean the room.
8. I was ill. I did not go to the doctor.
9. Mohan and Sohan were friends. Mohan did not help Sohan.
10. I went to the market. I did not buy anything.
Answer:
1. Although my dog was hungry. yet it did not eat biscuits.
2. Although he is very sleepy. yet he is watching a movie.
3. Although Babli wanted to wear new clothes on Diwali, yet she did not buy them.
4. Although it was raining, yet I did not take an umbrella.
5. Although he did not study hard, yet he passed the test.
6. Although I was lost, yet I did not ask for directions.
7. Although my room was dirty, yet I did not clean it.
8. Although I was ill, yet I did not go to the doctor.
9. Although Mohan and Sohan were friends, yet Mohan did not help Sohan.
10. Although I went to the market, yet I did not buy anything.

Learning to Listen

Activity 7.

Listen to the teacher, recite the following poem and repeat after her/him.

Clouds

White sheep. white sheep,
On a blue hill,
When the wind stops,
You all stand still.
When the wind blows.
You walk away slow,
White sheep,
white sheep
Where do you go?
नोट : विद्यार्थी स्वयं करें।

Learning to Speak

Activity 8

Speak the following pairs aloud. (ऊंची आवाज़ में बोलें)
1. mail — fail
2. dawn — lawn
3. plains — trains

Activity 9 (Pairwork)

Discuss with your partner about how you would like to travel. You can discuss the following questions with each other.
1. Do you like to travel by train/ship/plane ?
2. How would you like to travel if you have to go from Punjab to Mumbai ? Why ?
3. If you decide to go by train, what would you like to take with you ?

Learning to Write

Activity 10

Paragraph Writing:

पैराग्राफ़ किसी विषय की संक्षिप्त व्याख्या होती है। यह लगभग 100 शब्दों में लिखा जाता है। इसके पहले वाक्य में विषय का परिचय दिया जाता है, जबकि इसका अंतिम वाक्य विषय का निष्कर्ष होता है। पैराग्राफ़ के मध्य भाग में विषय से जुड़ी मुख्य बातों का वर्णन किया जाता है। ध्यान रहे कि यह पैराग्राफ़ एक ही विचार या बिन्दु पर केंद्रित हो।

A Journey by Bus I went to Jalandhar by bus last month. I hired an e-rickshaw and reached the bus stand. I went to the booking window. There was a great rush. I got the ticket on my turn. The bus came and I got into the bus. There was no room in the bus. Many people were standing.

I could not get any seat. It was very hot. I was sweating. Soon the conductor whistled. The bus started. I felt easy. Some passengers got down at Phagwara. Now I got a seat near the window. I looked out of the window. Greenfields looked very beautiful. Farmers were at their work. Cattle were grazing. Our bus crossed many bridges on the way. At last the bus reached Jalandhar. It took me three hours to reach there. I enjoyed the journey but I got tired.

Stanzas For Comprehension

Read the stanzas given below and answer the questions that follow each :

(1) Over the mountains,
Over the plains,
Over the rivers,
Here come the trains.
Carrying passengers,
Carrying mail,
Bringing their precious loads
In without fail.

(i) Where do the trains move?
रेलगाड़ियां कहाँ चलती हैं ?

(ii) What do they carry ?
वे क्या उठाती है।?

(iii) Name the poem and the poet.
कविता और कवि का नाम बताओ।
Answer:
(i) The trains move over the mountains, plains and rivers.
(ii) They carry passengers, goods and precious loads.
(iii) The name of the poem is ‘Trains’ and that of the poet is James S. Trippett.

(2) Thousands of freight cars
All rushing on Through day and darkness,
Through dusk and dawn,
Over the mountains,
Over the plains,
Over the rivers,
Here come the trains.

(i) What is rushing on ?
क्या – क्या चीज़ दौड़ती रहती है ?

(ii) When do they rush on?
वे कब दौड़ती हैं?

(iii) What is the central idea of the poem?
कविता का केन्द्रीय भाव क्या है ?
Answer:
(i) Thousands of freight cars are rushing on.
(ii) They rush on all through day and night.
(ii) Trains run day and night. They provide a great service to the country by carrying people and their costly load.

Word Meanings.

Trains Summary in Hindi

यह कविता रेलगाड़ियों के बारे में है। रेलगाड़ियाँ दिन-रात दौड़ती रहती हैं। वे कभी नहीं रुकतीं। वे पर्वत, नदियाँ, मैदान सब कुछ पार कर जाती हैं। वे डाक, यात्रियों तथा उनके कीमती सामान को लाद कर ले जाती हैं। वे माल (भारी सामान) को ढोती हैं। वे सुबह शाम कुछ नहीं देखतीं। वे दौड़ती ही रहती हैं।

Class 7 PSEB Solutions Poetry

• Poem 1 Trains Question Answer
• Poem 2 The Hunter and the Deer Question Answer
• Poem 3 An Earthquake Question Answer
• Poem 4 There was a Naughty Boy Question Answer

Punjab State Board PSEB 7th Class English Book Solutions Poem 4 There was a Naughty Boy Textbook Exercise Questions and Answers.

Class 7th English Solutions Poem Chapter 4 There was a Naughty Boy Question Answers

There was a Naughty Boy Class 7 Questions and Answers

Activity 1.

Look up the following words in a dictionary. You should seek the following information about the words and put them in your WORDS notebook.
1. Meaning of the word as used in the poem (adjective/noun/verb, etc.)
2. Pronunciation (The teacher may refer to the dictionary or the mobile phone for correct pronunciation.)
3. Spellings

Scotland

ground

yard

weighty

fourscore

wondered

Vocabulary Expansion

Activity 2

The naughty boy ran away to Scotland from England to see the people there. There, he found that things in Scotland were just the same as in England. To show that things were similar, the poet uses the word “as’. Write about the things that are similar in the space given. One example is given.

1. The naughty boy found that the ground in Scotland was as hard as in England
2. The naughty boy found that the yard in Scotland was as long as in England.
3. The naughty boy found that the song in Scotland was as merry as in the England.
4. The naughty boy found that the cherry in Scotland was as red as in England.
5. The naughty boy found that as weighty as in England.
6. The naughty boy found that the fourscore in Scotland was as eighty as in England.
7. The naughty boy found that the door in Scotland was as wooden as in England.

Activity 3.

Read the following lines from the poem.

That a door
Was as wooden
The door in the poem was ‘wooden’. Let us see some other things which are made of wood. Select the things in the box below that are made of wood and underline them.

table	car	mobile phone	television
boat	laptop	bed	cupboard

Answer:
table, boat, bed, cupboard.

Activity 4.

Three words are given in each column. Fill in the blanks with the names of the material with which the things in each column are made of.

Answer:
stell, Wood, cloth, rubber.

Learning to Read and Comprehend

Activity 5.

Answer the following questions.

Question 1.
Where did the naughty boy run away from ?
शरारती लड़का कहाँ से भाग कर आया था ?
Answer:
The naughty boy ran away from England.

Question 2.
Where did the naughty boy go?
शरारती लड़का कहाँ गया ?
Answer:
He went to Scotland.

Question 3.
Why did he go there ?
वह वहाँ क्यों गया ?
Answer:
He went there to see the people living there.

Question 4.
What different things did the boy see in Scotland ?
लड़के को स्काटलैंड में कौन-सी भिन्न चीजें देखीं ?
Answer:
The boy saw nothing different in Scotland.

Question 5.
What did the boy wonder about ?
लड़के को किस बात की हैरानी हुई ?
Answer:
He wondered that everything in Scotland was the same as it was in England. Learning Language

Activity 6.

The poem “There was a Naughty Boy’ is very interesting. It describes many things. To describe the things, the poet uses many adjectives. The title of the poem “There was a Naughty Boy’ also has an adjective to describe the boy. Find some more adjectives from the grid given below.

Look at the following two sentences.
1. I am hungry.
2. I am starving.

What is the difference between ‘hungry’ and ‘starving’ here?
Here, sentence 2 tells the reader that ‘I am very hungry (starving). ‘Starving’ means “very hungry’. ‘Starving’, ‘therefore’, is the stronger adjective.

Activity 7.

Match the adjective in Column A with its stronger adjective in Column B. Column A

Column A Adjective	Column B Stronger Adjective
hungry	starving
tired	beautiful
pretty	enraged
nice	exhausted
intelligent	excellent
angry	brilliant
clean	spurious
bad	hygienic
fake	dreadful

Answer:
Hungry — starving, tired – exhausted, pretty – beautiful, nice – excellent, intelligent – brilliant, angry – enraged, clean – hygienic, bad – dreadful, fake – spurious.

Learning to Listen (Class Activity)

Activity 8.

The teacher will speak clearly and give instructions to the students. Students will close their books and listen to the instructions and follow them.
Now repeat the same activity. The teacher will ask a student to come to the front and read the instructions to other students.
Appendix

Learning to Speak (Pairwork)

Activity 9.

Read the following pairs of words aloud with proper stress.
1. hard, yard हाँअड्, याअड्)
2. long, song (लँग,साँग))
3. red, lead (रेड, लैड)
4. weighty, eighty (वेराटी, राअटी)
5. found, ground (फउंड, ग्राउंड)
नोट – विद्यार्थी स्वंय करें

Activity 10.

Discuss in your group what the naughty boy would like to see in Punjab if he came to India and what he would do here.
Some hints :
1. The Golden Temple
2. Vaisakhi Fair
3. Giddha
4. Bhangra
Answer:
Punjab is a land of ten great Sikh Gurus, Gurudwaras and temples. People here are very brave, hard-working and cheerful. The naughty boy, therefore, would see, a scene totally different from England. He would visit the Golden Temple, Jallianwalla Bagh and famous Durgyana Temple. If he came in April, he would visit the Vaisakhi Fair. He would enjoy Giddha and Bhangra, the classical dances of the Punjab. He would also like to see the green and golden fields of wheat crop. Moreover, he would do heavy shopping and take back with him a number of symbols of the Punjabi Culture.

Learning to Use Language (Group work)

Activity 11.

Discuss in your group which places would you like to see in London and why ? Here are some pictures.

Buckingham Palace where the Queen of United Kingdom lives

Westminster Abbey and the Big Ben Clock Tower

London Eye – a giant wheel, riding on which you can see the whole of London
Answer:
London, the capital of England is a beautiful city to visit. There are many places worth visiting. If I go to London. I would like to visit Buckingham Palace, the Westminster Abbey, the Big Ben Clock Tower and the London eye first.

The Buckingham Palace is a majestic building. It is the royal palace of the Queen of U.K. The Westminster Abbey is a huge royal church. It is situated in the centre of the city offering daily services for all. It is also – World Heritage cite.

The Big Ben Tower is another building worth visiting. Big Ben is the nickname of the striking clock of the tower. The clock is known for it accuracy. The London Eye is a giant wheel. It is thrilling to have a ride on it. The ride enables you to see the whole of London.

Stanzas For Comprehension

Read the following stanzas carefully and answers the questions that follow each :

(1) There was a naughty boy,
And a naughty boy was he
He ran away to Scotland
The people there to see.

1. Why did the naughty boy run to Scotland ?
शरारती लड़का स्कॉटलैंड क्यों भाग गया ?

2. Why does the poet repeat the word ‘naughty’.
कवि लडके के लिए ‘naughty’ शब्द को क्यों देहराता है|

3. Name the poem and the poet.
कविता और कवि का नाम लिखें।
Answers
1. The naughty boy ran to Scotland to see the people there.
2. The poet repeats the word ‘naughty’ to say that the boy was most mischievous or the naughties one.
3. The name of the poem is ‘There was a Naughty Boy’ and that of the poet is John Keats.

(2) Was as weighty,
That fourscore
Was as eighty,
That a door
Was as wooden,
As in England
So he stood in his shoes
And he wondered,
He wondered,
He stood in his shoes,
And he wondered.

1. What ‘similarity’ did he find about the ground, the door there ?
वहां धरती और दरवाजे के बारे में क्या (किस समानता का) पता चला ?

2. What wondered him ? What words show he surprise ?
उसे किस बात की हैरानी हुई ? कौन-से शब्द उसकी हैरानी को व्यक्त करते हैं ?

3. What is the central idea of the poem ? कविता का केन्द्रीय भाव क्या है ?
Answer.
1. He found that the ground was as hard and the door was as wooden as in England.
2. Similarity in everything in England and in the place where he was (Scotland) wondered him. The words ‘He stood in his shoes’ show his surprise.
3. The poem brings out that no places are different, no men are different in the world. Their way of life is the same. The things they use and the activities they are involved in are similar. :

Word Meanings

There was a Naughty Boy Summary in Hindi

एक शरारती लड़का (इंग्लैंड) का था। वह यह देखने के लिए स्कॉटलैंड भाग गया कि वहां के लोग कैसे हैं। वह देख कर हैरान रह गया कि वहाँ की धरती इंग्लैंड की धरती की तरह सख्त है। वहां के गज़ की लम्बाई भी उतनी है जितनी कि इंग्लैंड में। स्कॉटलैंड तथा इंग्लैंड के गीतों, फलों तथा धातुओं के गुणों में भी समानता थी।

उदाहरण के लिए गीत आनन्द भरे थे, चैरी लाल थी तथा सीसा भारी था। वहां की गणना का मानक कोड़ी (20 वस्तुएं) भी एक जैसा था। वास्तव में यह सब कुछ हैरान कर देने वाला था।

Class 7 PSEB Solutions Poetry

• Poem 1 Trains Question Answer
• Poem 2 The Hunter and the Deer Question Answer
• Poem 3 An Earthquake Question Answer
• Poem 4 There was a Naughty Boy Question Answer

Punjab State Board PSEB 7th Class English Book Solutions Chapter 5 The Princess Who Never Smiled Textbook Exercise Questions and Answers.

Class 7th English Solutions Chapter 5 The Princess Who Never Smiled Question Answers

The Princess Who Never Smiled Class 7 Questions and Answers

Activity 1.

Look up the following words in a dictionary. You should seek the following information about the words and put them in your WORDS note work.
1. Meaning of the word as used in the story (adjective/noun/verb, etc.)
2. Pronunciation (The teacher may refer to the dictionary or the mobile phone for correct pronunciation.)
3. Spellings:

Princess	amuse	tricks	clown	mime
Journey	scarce	nervous	appeared	magician

Activity 2.

Rearrange the jumbled words given in capitals on the right side to mean the following.

Activity 3.

Answer the following questions :

Question 1.
Why was the king worried about Tanya, the princess ?
राजकुमारी तान्या के बारे में राजा चिंतित क्यों था ?
Answer:
The King was worried because Tanya never smiled.

Question 2.
What did he do to amuse his daughter ?
पुत्री को खुश करने के लिए उसने क्या किया ?
Answer:
He called a magician and a clown to amuse her.

Question 3.
What did the magician do ?
जादूगर ने क्या किया ?
Answer:
The magician showed the princess some tricks.

Question 4.
What did the clown do ?
मस्खरे (जोकर) ने क्या किया ?
Answer:
The clown tried to make the princess laugh with a mime.

Question 5.
What did the king do when the princess did not smile ?
राजकुमारी के न मुस्कराने पर राजा ने क्या किया ?
Answer:
At this, the king declared that anyone who made the princess laugh would get to marry her.

Question 6.
Who was Ivan ?
इवान कौन था ?
Answer:
Ivan was a poor boy who worked for a farmer.

Question 7.
What did Ivan want to do?
इवान क्या करना चाहता था ?
Answer:
Ivan wanted to take a chance to make the princess laugh.

Question 8.
Who all did he meet on his way to the palace ?
महल की ओर जाते हुए वह रास्ते में किस-किस से मिला ?
Answer:
He met a fish, a mouse and a grass-hopper.

Question 9.
What did they want ?
वे क्या चाहते थे ?
Answer:
They wanted to have a new home.

Question 10.
What did Ivan give each of them ?
इवान ने प्रत्येक को क्या दिया ?
Answer:
Ivan gave a gold coin to each of them.

Question 11.
Where was the princess ?
राजकुमारी कहां थी ?
Answer:
The Princess was standing by her window.

Question 12.
What was she doing ?
वह क्या कर रही थी ?
Answer:
She was looking at Ivan.

Question 13.
What happened when Ivan fell into a hole ?
जब इवान सुराख/बिल में गिरा तो क्या हुआ ?
Answer:
The princess started laughing at this.

Question 14.
Why did she start laughing ?
वह हँसने क्यों लगी ?
Answer:
She started laughing because it was the funniest thing she had ever seen.

Question 15.
What did the king do ?
राजा ने क्या किया ?
Answer:
The king became very happy and started laughing.

Activity 4

Select the correct option and fill it in the given blank :

Question 1.
Princess Tanya was a pretty girl but she did not
(a) smile
(b) walk
(c) speak
Answer:
(a) smile

Question 2.
The king called …….. to amuse her.
(a) a magician
(b) a clown
(c) a magician and a clown
Answer:
(c) a magician and a clown

Question 3.
The farmer gave Ivan three ………. coins.
(a) silver
(b) copper
(c) gold
Answer:
(c) gold

Question 4.
Ivan met a ……….. first of all.
(a) mouse
(b) fish
(c) grass-hopper
Answer:
(b) fish

Question 5.
Ivan gave .. …………. to the mouse.
(a) one coin
(b) two coins
(c) three coins
Answer:
(a) one coin

Question 6.
The princess was standing by her ………..
(a) window
(b) garden
(c) tower
Answer:
(a) window

Question 7.
Ivan fell into a ………
(a) river
(b) lake
(c) hole
Answer:
(c) hole

Question 8.
The princess laughed on seeing the small animals the fish, the mouse and the grass hopper trying to ………………….. Ivan to save him.
(a) pull up
(b) push down
(c) push away
Answer:
(a) pull up.

Learning Language

Tenses (verb)
हमें क्रिया का समय बताते हैं। यहां Present continuous Tense के बारे में बात की गई है। इस Tense के बारे में जानने के लिए नीचे दिए गए Format का चयन करें

Affirmative

I	am	laughing (first form of the verb + -ing).
He/She/It/Singular Nouns	is
We/You/They/Plural Nouns	are

Negative.

I	am not
He/She/Singular Nouns	is not	watching (verb in its first	a film
We/You/They/Plural Nouns	are not	form + ing).

Interrogative
Is/am/are + subject + first form of the verb + -ing ?

Activity 5

Complete the following sentences using Present Continuous Tense of the verb given in the brackets (Capitalize when needed).

1. My teacher………. talk on the phone right now.
2. …….. you ……………. (dance) ?
3. Cheeku ………………………… (do) his homework at the moment.
4. Shanti …………………………… (work) on a project nowdays.
5. My kids ………………………… (play) in the garden now.
6. Some people ………………. ……… (wait) to talk to you.
7. I ……………… (not go) for a walk today.
8 Leena ……………… (study) for his exam right now ?
9 Uma ……………… (play) the piano now ?
10. Mohan and I ……………… (paint) the fence today.
11. Amita ……………… (help) me at present.
12. My children ……………… (not listen) to the radio now.
13. Saira ……………… (not drink) tea now.
14. I ……………… (vacuum) the carpet right now.
15. My father ……………… (watch) TV now.
16. What she ……………… (eat) right now ?
17. ……. your dog ……… (hide) from me ?
18. Which book ………………………… you ……………….. (read) nowadays?
19. Thomas ………………………. (drive) me home now.
20. I …………………………. (wash) my hands at the moment.
Answer:
1. is talking
2. Are, dancing
3. is doing
4. is working
5. are playing
6. are waiting
7. am not going
8. Is, studying
9. Is, playing
10. are painting.
11. is helping
12. are not listening
13. is not drinking
14. am vacuuming
15. is watching
16. is eating
17. Is, hiding
18. are, reading
19. is driving
20. am washing.

Now Read the following :

Princess Tanya was watching everything from her window. She started laughing. It was the funniest thing she had ever seen. She laughed and laughed. She kept laughing. The King was passing by her room. He saw that the princess was laughing. The King became very happy. He also started laughing. Within no time, the queen was laughing, the ministers were laughing, the servants were laughing, the guards were laughing and all the people were laughing. Ivan was also laughing.

ऊपर के passage में past (बीते हुए समय की क्रिया, जो उस समय जारी थी) का प्रयोग किया गया है। यह Past Continuous Tense में है। इस Tense के Patterm का अध्ययन नीचे दिए गए वाक्यों में करें।
नोट : Interrogative Sentences में was/were + Subject + first form of the verb + ing ? का Pattern अपनाएं।

Affirmative.

I/He/She/Singular Nouns	was	watching (verb in its first Torm + -ing).	a film.
We/You/They/ Plural Nouns	were

Negative.

I/He/She/Singular Nouns	was not	watching (verb in its first form +-ing).	a film.
We/You/They/ Plural Nouns	were not

Activity 6

Supply the suitable forms of verbs given in the brackets. The first one is done for you.
1. I was shopping (shop) when you called.
2. Students …………………………… (play) happily when I reached the class.
3. I told him but he didn’t hear me as he ………………. (watch) the news.
4. Sheela and Khyati ………………………… (work) in the office when the boss walked in.
5. The Knight Riders ……………………… (warm-up) when the Mumbai Indians arrived at the stadium.
6. While Minesh was praying, Kiran ………………………. (bake) a cake.
7. I ……………………. (drive) when you called, so I couldn’t answer.
8. I saw Meena yesterday when she …………….. (walk) by the river.
9. My mother ……………. (cook) and my father …………………………. (dust) the house yesterday.
10. Shanti ……………………….. (boil) milk when Rita came.
Answer:
2. were playing
3. was watching
4. were working
5. were warming up
6. was baking
7. was driving
8. was walking
9. was cooking, was dusting
10. was boiling.

Learning to Listen

Activity 7.

Let us play a game today. Get up from your seats. The name of the game is, “The Princess Says…. You will follow the commands of your teacher. She/he will give you commands to follow. Commands will begin with the phrase “The Princess Says …. If the teacher does not say “The Princess Says…….. before a command (i.e. hold your left ear); you will not follow the command. If you still follow the command, you will be out of the game. The last person left wins.

नोट: अपने teacher के साथ मिलकर स्वयं करें।

Learning to Speak (Pair work)

Activity 8

Imagine that you are talking to your friend on the phone. Tell each other about four things that you and your family members are doing. You can pick words from the following table.

wash	dance	cook	pray	dust	jump
watch	laugh	clean	make	draw	help

A: Hello, I am ………. X ……… (name) speaking ! Who is on the line ?
B: Hello, I am …….. Y …….. (name) speaking !
A: Oh! What are you doing?
B: I am watching T.V.
A: What is your mother doing ?
B: She is washing clothes. And, what is your mother doing ?
A: She is cooking food.
B: What is your younger brother doing?
A: He is drawing. He is making a dog.
B: What is your elder sister doing? And what about your father?
A: My younger sister is helping mother in the kitchen. My father is praying to God.
B: What is the noise about that is coming ?
A: My younger sister is jumping, dancing and laughing.
B: Good afternoon. Now I am putting the phone down.

Learning to Write

Activity 9

A mind map of a story is given below. The name of the story is “The Three Pigs’. Using the mind map, write your story about the three pigs and the wolf . All the hints and useful words are given in the mind map.

Answer:
The Three Pigs : Once there were three pigs. One lived in a straw house and one in a wooden. Their houses were not strong as they were quickly built. But the third one lived in a brick house that was very strong. One day a big bad wolf came there. It was hungry for pigs. It blew down the straw and the wooden houses easily and ate the pigs. But she could not break down the brick house. Therefore, it climbed down the chimney of the house. Soon she got buried by hot water and ran away crying.

Learning to use language

Activity 10

Read the dialogue between a dinosaur and a sparrow. Dinosaur is an extinct animal and sparrow is about to become extinct. Radiation from mobile phone towers has harmed sparrows and other birds.

Complete the dialogue by taking information from the given table.

1. First appeared	235 million years ago
2. Class	Reptile
3. Size	Different sizes, 20 inches to 39.7 meters
4. Height	59 feet (largest dinosaurs)
5. Life on Earth	150 million years
6. Extinction	66 million years ago
7. Cause of Extinction	Asteroid hit on Earth
8. Result of the asteroid hit	Mass extinction of most species on Earth

Dialogues

Sparrow : Hello, stranger! You are so huge. How can I help you ?
Dinosaur : Oh, hello! Actually I am not a stranger. I used to live here 66 million years ago.
Humans call us Dinosaurs. So I’m just exploring how much the planet has changed.
Sparrow : Oh, really! How much has it changed ?
Dinosaur : Oh, it has changed so much. I don’t like the change. There were no humans and buildings when I used to live no pollution, no global warming.
Sparrow : Oh, tell me more, Sir !
Dinosaur : There were trees all around. We were everywhere – on land, in the air and in water.
Sparrow : Oh, wow! What were they called ?
Dinosaur : Humans have named the flying Dinosaurs as PTERODACTYL.
Sparrow And what about the ones that lived in the water ?
Dinosaur : They have been named as SPINOSAURUS.
Sparrow : Mr Dinosaur, I have so many questions to ask you.
Dinosaur : Don’t worry, I know what is in your mind.
Here I am going to tell you all about me and our family.

We were reptiles. We appeared on earth 235 million years ago. We were of different sizes — from 20 inches to 39.7 meters. The largest member of our family was 59 feet tall. We lived about 150 million years on earth. But about 66 million years ago an asteroid hit the earth that caused our extinction. This incident also led to the extinction of most species of this planet.

Comprehension Of Passages

Read the following passage carefully and answer the questions that follow each.

(1) This is a very old story from Russia. There was a princess in Russia. Her name was Tanya. Tanya was very beautiful but she never smiled or laughed. Her father, the king, loved her very much but he kept worrying because she never smiled. Even the queen was worried.

King (said to himself): I must find a way to make my daughter happy. I want to see her smiling! And he had an idea. He called a magician to amuse his daughter. The magician showed the princess some tricks.

1. What kind of girl was Tanya ?
तान्या कैसी लड़की थी ?

2. What did Tanya’s father wish ?
तान्या के पिता की क्या इच्छा थी ?

3. Choose true and false statements and write them in your note-book.
(a) Tanya’s father was a king.
(b) Queen never got worried.

4. Complete the sentences according to the meaning of the passage.
(a) Tanya was a …………..
(b) The magician showed the princess …………..

5. Match the words with their meanings.

(a) worried	entertain
(b) amuse	anxious
	show

Answer:
1. Tanya was very beautiful but she never smiled or laughed.
2. Tanya’s father wished to see his daughter (Tanya) smiling.
3.
(a) True
(b) False
4.
(a) Tanya was a princess in Russia.
(b) The magician showed the princess some tricks.
5.
(a) worried — anxious
(b) amuse — entertain

(2) Very far from the palace, there lived a poor boy. His name was Ivan. He worked for a farmer. When he heard about the king’s promise, he wanted to take a chance at making the princess laugh. He thought that he could make her laugh. The farmer gave the boy three gold coins for the journey.
On his way, he found a lake. In the lake, there was a fish. The fish called him.
Fish (to Ivan) : Oh ! Can you help me, please ?
Ivan (to the fish) : How can I help you, fish ?
Fish (to Ivan) : I have lived in this lake for a long time.
Now the water is getting dirty. I don’t want to live here anymore, but I am too poor to find a new house.
Ivan (to the fish): I am so sorry, Fish. I have three gold coins. I can give you one. I’ll still have two for my journey. I am going to meet the princess.

1. Who was Ivan ? Where did he live ?
इवान कौन था ? वह कहां रहता था ?

2. What did Ivan saw on his way?
रास्ते में उसे क्या दिखाई दिया ?

3. Choose true and false statements and write them in your note-book.
(a) The fish had lived in the lake for a long time.
(b) The fish wanted the princess to help it.

4. Complete the sentences according to the meaning of the passage.
(a) The farmer gave the boy ………….. for the journey.
(b) I am too poor to

5. Match the words with their meanings.

promise	saw
found	made
	word

Answers
1. Ivan was a poor boy who worked for a farmer. He lived very far from the king’s palace.
2. On his way, Ivan saw a lake with a fish in it.
3.
(a) True
(b) False
4.
(a) The farmer gave the boy three gold coins for the journey.
(b) I am too poor to find a new house.
5.
(a) promise — word
(b) found — saw.

(3) Ivan continued travelling. He was hungry and very tired. He had no money to buy food. He reached the palace. He saw the princess. She was standing by her window. She was looking at him. He became nervous because the princess was looking at him. He fell into a hole.
Ivan (shouting) : Help! Someone, help me!
Suddenly, the fish, the mouse and the grass-hopper appeared.
All three (fish, mouse and grasshopper) : Don’t worry! We will save you !
The three of them pulled the boy from the hole.

1. In what condition was Ivan when he reached the palace ?
महल तक पहुँचने पर इवान की क्या दशा थी ?

2. Why did he become nervous ?
वह घबरा क्यों गया ?

3. Choose true and false statements and write them in your note-book.
(a) The princess was standing.
(b) The three of them pulled the boy.

4. Complete the sentences according to the meaning of the passage.
(a) The princess was standing …………………..
(b) The three of them pulled the boy …………..

5. Match the words with their meanings.

(a) nervous	confused
(b) appeared	became invisible
	became visible

Answer:
1. Ivan was very hungry and thirsty when he reached the palace.
2. He became nervous because the princess was looking at him.
3.
(a) False
(b) True
4.
(a) The princess was standing by her window.
(b) The three of them pulled the boy out from the hole.
5.
(a) nervous — confused
(b) appeared — became visible

(4) Princess Tanya was watching everything from her window. She started laughing. It was the funniest thing she had ever seen. She laughed and laughed. She kept laughing. The king was passing by her room. He saw that the princess was laughing. The king became very happy. He also started laughing. Within no time, the queen was laughing, the ministers were laughing, the servants were laughing, the guards were laughing and all the people were laughing. Ivan was also laughing. The king kept his promise. The kingdom came to know that Ivan and the princess were getting married. They got married. Ivan became a prince. He went to the king.

1. How did the King feel ?
राजा ने कैसा महससू किया ?

2. Who were getting married ?
किसकी शादी हो रही थी ?

3. Choose true and false statements and write them in your note-book.
(a) The king did not keep his promise.
(b) Ivan became a prince.

4. Complete the sentences according to the meaning of the passage.
(a) Within …………….. the queen was laughing.
(b) The king saw that ………….

5. Match the words with their meanings.

(a) funniest	smile
(b) watch	most amusing
	see

Answer:
1. The king became very happy.
2. The princess and Ivan were getting married.
3.
(a) False
(b) True
4.
(a) Within no time the queen was laughing.
(b) The king saw that the princess was laughing.
5.
(a) funniest — most amusing
(b) watch — see

Use Of Words/Phrases In Sentences

1. Amuse (entertain) –
Mother amused her child with toys.
माँ ने खिलौनों से अपने बच्चे का मनोरंजन किया।

2. Tricks. (feats) –
The tricks of the magician were funny.
जादूगर के करतब मज़ाकिया थे।

3. Nervous (confused) –
Why are you so nervous ?
आप इतने घबराए हुए क्यों हैं ?

4. Scarce (not enough, scanty) –
Water is getting scarce here.
यहां पानी की कमी होती जा रही है।

5. Worried (anxious) –
You look worried. What is the problem ?
तुम चिंतित दिखाई देते हो। क्या समस्या है ?

6. Journey (trip) –
We went on a long journey last year.
पिछले साल हम एक लंबी यात्रा पर गए।

7. Princess (royal maiden) –
The princess was married to a handsome prince.
राजकुमारी की शादी एक सुंदर राजकुमार से कर दी गई।

8. Appeared (came in front of) –
The thief appeared before the judge.
चोर जज के सामने आया।

9. Pulled (dragged) –
We pulled the heavy fish with a rope.
हमने भारी मछली को एक रस्सी से खींचा।

Word Meanings

The Princess Who Never Smiled Summary in Hindi

This is very old …………………….. them could do it.

यह रूस की एक बहुत पुरानी कहानी है। रूस में एक राजकुमारी थी। उसका नाम तान्या था। तान्या बहुत सुंदर थी लेकिन वह कभी भी हंसती या मुस्कराती नहीं थी। उसके पिता राजा थे और उसे बहुत प्यार करते थे परन्तु वह चिंतित रहते थे क्योंकि वह कभी मुस्कराती नहीं थी। यहां तक कि रानी भी चिंतित थी। राजा (अपने आप से कहा) : मुझे कोई रास्ता ढूंढना चाहिए ताकि मैं अपनी बेटी को खुश कर सकू। मैं उसे मुस्कराते हुए देखना चाहता हूँ। और उसे एक विचार सूझा। उसने अपनी बेटी को बहलाने के लिए एक जादूगर को बुलाया। जादूगर ने राजकुमारी को कुछ कतरब दिखाए। राजा

(राजकुमारी से) : हा, हा, हा …… क्या यह मनोरंजक नहीं ?
राजकुमारी (राजा से) : हाँ, पिता जी। करतब अच्छे हैं परन्तु वे मेरे चेहरे पर मुस्कान नहीं ला सकते।
उन्होंने एक जोकर को भी बुलाया ताकि वह मुस्करा सके।
राजा (राजकुमारी से) : हा, हा, हा …… क्या यह मज़ेदार नहीं ?
राजकुमारी (राजा से) : हाँ पिता जी। जोकर मजाकिया है, परन्तु वह मुझे मुस्कराहट नहीं दे सकता।जोकर उसे हंसाने के लिए नकलें भी उतारता है।

राजा (राजकुमारी से) : हा, हा, हा ………. क्या यह मज़ाकिया नहीं है ?
राजकुमारी (राजा से) : वह अच्छा है परन्तु वह मेरी मुस्कराहट नहीं ला सकता।
अन्ततः उसने अपने देश के सभी लोगों को यह बताने का निर्णय लिया कि जो कोई भी राजकुमारी को हँसा देगा, उसका विवाह राजकुमारी से कर दिया जाएगा। रूस भर से लोग राजा के महल गए और उन्होंने राजकुमारी को हँसाने का प्रयत्न किया, परन्तु कोई भी ऐसा न कर सका।

Very far from ………………. meet the princess.

महल से बहुत दूर एक गरीब लड़का रहता था। उसका नाम इवान था। वह एक किसान के पास काम करता था। जब उसने राजा के वचन के बारे में सुना, तो उसने राजकुमारी को हँसाने का एक अवसर पाने की सोची। वह सोचता था वह उसे हँसा सकता है। किसान ने यात्रा के लिए लड़के को तीन स्वर्ण मुद्राएं दीं। रास्ते में उसे एक झील मिली। झील में एक मछली थी। मछली ने उसे पुकारा। मछली (इवान से) : ओह! कृपया आप मेरी मदद कर सकते हैं ?
इवान (मछली से) : मछली, मैं तुम्हारी क्या मदद कर सकता हूँ ?

मछली (इवान से) : मैं एक लम्बे समय से इस झील में रह रही हूँ। अब पानी गंदा हो रहा है। मैं यहाँ और
अधिक नहीं रहना चाहती, परंतु मैं इतनी गरीब हूँ कि अपने लिए नया घर नहीं ले
सकती। इवान (मछली से) : मछली, मैं माफी चाहता हूँ। मेरे पास तीन स्वर्ण मुद्राएं हैं। मैं एक तुम्हें दे सकता हूँ।
मेरे पास यात्रा के लिए फिर भी दो बच जाएंगी। मैं राजकुमारी से मिलने जा रहा हूँ।
मछली (इवान से) : मैं तुम्हारा धन्यवाद कैसे कर सकती हूँ ?

इवान (मछली से) : चिंता मत करो। मुझे तुम्हारी मदद करके खुशी हुई। मुझे आशा है कि तुम्हें एक नया और अच्छा घर मिल जाएगा। इवान ने अपनी यात्रा जारी रखी। उसने एक बड़ा सा खेत
देखा। खेत में एक चूहा था। चूहे ने उसे पुकारा। चूहा (इवान से) हैलो नवयुवक! क्या तुम मेरी सहायता कर सकते हो ?
इवान (चूहे से) : चूहे, मैं तुम्हारी मदद कैसे कर सकता हूँ?
चूहा (इवान से) : मैं लम्बे समय से इस खेत में रह रहा हूँ। अब यहां भोजन कम होता जा रहा है। मैं अब यहां और अधिक नहीं रहना चाहता, परन्तु मैं गरीब हूँ।

इवान (चूहे से) : चूहे, मैं माफी चाहता हूँ। मेरे पास दो स्वर्ण मुद्राएं हैं। मैं एक तुम्हें दे सकता हूँ। मेरे
पास यात्रा के लिए फिर भी एक रह जाएगी। मैं राजकुमारी से मिलने जा रहा हूँ।
चूहा (इवान से) : तुम बहुत दयालु हो। मैं किस प्रकार तुम्हारा आभार व्यक्त करूं?
इवान : चिंता मत करो। मैं तुम्हारी मदद करके खुश हूँ। मुझे आशा है कि तुम्हें एक अच्छा और नया घर मिल जाएगा।

Ivan continued ………………….. from the hole.

इवान ने यात्रा जारी रखी। वह एक जंगल में पहुंचा। जंगल में एक टिड्डा रहता था। टिड्डे ने उसे पुकारा।
टिड्डा (इवान से) : सुनिये! क्या तुम मेरी मदद कर सकते हो ?
इवान (टिड्डे से) : टिड्डे, मैं तुम्हारी क्या मदद कर सकता हूँ ?

टिड्डा (इवान से) : मैं लम्बे समय से इस जंगल में रह रहा हूँ। अब बहुत अधिक गर्मी होती जा रही है। मैं अब यहां नहीं रहना चाहता, परन्तु मैं गरीब हूँ।
इवान (टिड्डे से) : टिड्डे, मैं माफी चाहता हूँ। मेरे पास एक स्वर्ण मुद्रा है। मैं वह तुम्हें दे सकता हूँ। मैं अपना काम चला लूंगा। मैं राजकुमारी से मिलने जा रहा हूँ।

टिड्डा (इवान से) : तुम बहुत दयालु हो। मैं तुम्हारा आभार किस प्रकार व्यक्त करूं।
इवान (टिड्डे से) : चिंता मत करो। मैं तुम्हारी मदद करके खुश हूँ। मैं आशा करता हूँ कि तुम्हें एक अच्छा
और नया घर मिल जायेगा। इवान ने यात्रा जारी रखी। वह भूखा और बहुत थक चुका था। उसके पास भोजन के लिए पैसे नहीं थे। वह महल पहुंच गया। उसने राजकुमारी को देखा। वह अपनी खिड़की में खड़ी थी। वह उसे देख रही थी। वह घबरा गया क्योंकि राजकुमारी उसकी ओर ही देख रही थी। वह एक सुराख में जा गिरा।

इवान (चिल्लाया) : सहायता! कोई मेरी सहायता करो। अचानक ही मछली, चूहा तथा टिड्डा प्रकट हो गए।
तीनों मिलकर (मछली, : चिन्ता मत करो। हम तुम्हारी रक्षा करेंगे। चूहा तथा टिड्डा), तीनों ने मिलकर उसे सुराख से बाहर खींच लिया।

Princess Tanya ………….. People were smiling.

राजकुमारी तान्या यह सब कुछ अपनी खिड़की से देख रही थी। वह हँसने लगी। यह उसके लिए सबसे मनोरंजक बात थी, जो कुछ भी उसने अब तक देखा था। वह जोर से हँसने लगी और वह लगातार हँसती रही। राजा उसके कमरे के पास से गुजर रहा था। उसने देखा कि राजकुमारी हँस रही है। राजा बहुत खुश हुआ। वह भी हँसने लगा। तुरंत ही रानी हँसने लगी, मंत्री हँसने लगे, नौकर हँसने लगे, सुरक्षाकर्मी हँसने लगे और सभी लोग हँसने लगे। इवान भी हँसने लगा।
राजा ने अपना वचन निभाया। राज्य को पता चल गया कि इवान और राजकुमारी की शादी हो रही है। उनकी शादी हो गई। इवान राजकुमार बन गया। वह राजा के पास गया।

इवान (राजा से) : मुझे मेरे मित्र बहुत प्रिय हैं। मैं उन्हें महल में रख रहा हूँ।
राजा (इवान से) : मुझे कोई परेशानी नहीं है। उन्होंने भी राजकुमारी को हँसाया है।
उस दिन से महल एक खुशी भरा स्थान बन गया। चारों ओर हँसी और मुस्कराहटें बिखरी हुई थीं। इवान, राजकुमारी तान्या और उसके मित्र मुस्करा रहे थे, राजा मुस्करा रहा था, रानी मुस्करा रही थी, मंत्री मुस्करा रहे थे, नौकर मुस्करा रहे थे, सुरक्षाकर्मी मुस्करा रहे थे और सभी लोग मुस्करा रहे थे।

Retranslation Of Isolated Sentences

1. There was a princess in Russia. — रूस में एक राजकुमारी थी।
2. Her father, the king loved her very much. — उसके पिता, राजा उसे बहुत प्यार करते थे।
3. Even the queen was worried. — यहां तक कि रानी भी चिंतित थी।
4. I want to see her smiling. — मैं उसे मुस्कराते हुए देखना चाहता हूं।
5. The magician showed the princess some tricks. — जादूगर ने राजकुमारी को कुछ करतब दिखाए।
6. He called a clown to make her smile.– उसने उसकी मुस्कराहट लाने के लिए एक जोकर (मस्खरे) को बुलाया।
7. He is good, but he does not make me smile.– यह अच्छा है, परन्तु यह मुझे मुस्कराहट प्रदान नहीं कर सकता।
8. People from all over the Russia went to the king’s palace. — रूस भर से लोग राजा के महल में गए।
9. He worked for a farmer. — वह किसान के पास काम करता था।
10. The farmer gave the boy three gold coins for the journey. — किसान ने यात्रा के लिए लड़के को तीन मुद्राएं दीं।
11. The king kept his promise. — राजा ने अपना वचन निभाया।
12. She kept laughing. — वह लगातार हँसती रही।
13. I am happy to help you. — मुझे तुम्हारी मदद करके खुशी हुई।
14. He was hungry and very tired. — वह भूखा था और बहुत थका हुआ था।
15. He fell into a hole. — वह एक सुराख में गिर गया।
16. Three of them pulled the boy from the hole. — तीनों ने मिलकर उसे सुराख से खींच लिया।
17. Princess Tanya was watching everything from her window. — राजकुमारी तान्या यह सब कुछ अपनी खिड़की से देख रही थी।

English Guide for Class 7 PSEB Prose

• Rent for Water Question Answer
• Birbal’s Khichdi Question Answer
• A Glass of Milk Question Answer
• Mountaineers Question Answer
• The Princess Who Never Smiled Question Answer
• A Treasure Hunt Question Answer
• A Hole in the Fence Question Answer
• Hachiko-The World’s Most Loyal Dog Question Answer