Punjab State Board PSEB 10th Class Physical Education Book Solutions ਕ੍ਰਿਕਟ (Cricket) Game Rules.
ਕ੍ਰਿਕਟ (Cricket) Game Rules – PSEB 10th Class Physical Education
ਯਾਦ ਰੱਖਣ ਵਾਲੀਆਂ ਗੱਲਾਂ
(Points to Remember)
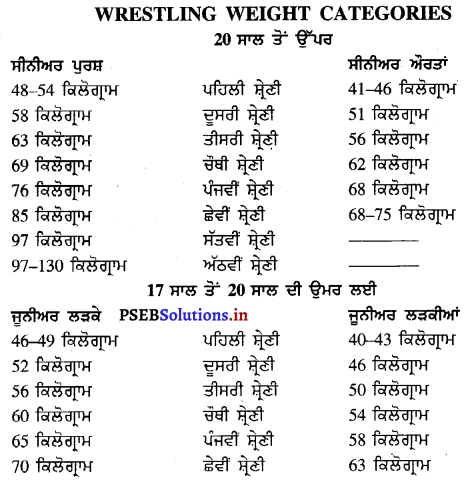
- ਕ੍ਰਿਕਟ ਟੀਮ ਵਿਚ ਖਿਡਾਰੀਆਂ ਦੀ ਗਿਣਤੀ = 16 (11 + 5)
- ਵਿਕਟਾਂ ਦੇ ਵਿਚਾਲੇ ਦੀ ਦੂਰੀ = 22 ਗਜ਼ ਜਾਂ 20.12cm
- ਪਿੱਚ ਦੀ ਚੌੜਾਈ = 4′ 4″
- ਵਿਕਟਾਂ ਦੀ ਚੌੜਾਈ = 9 ਇੰਚ
- ਕ੍ਰਿਕਟ ਗੇਂਦ ਦਾ ਘੇਰਾ = 8 ਤੋਂ 9 ਇੰਚ
- ਕ੍ਰਿਕਟ ਗੇਂਦ ਦਾ ਭਾਰ = 5 \(\frac{1}{2}\) ਐੱਸ ਤੋਂ 5\(\frac{3}{4}\) ਐੱਸ
- ਬੈਟ ਦੀ ਚੌੜਾਈ = 4 \(\frac{1}{4}\) ਇੰਚ
- ਬੈਟ ਦੀ ਲੰਬਾਈ = 38 ਇੰਚ
- ਗੋਂਦ ਦਾ ਰੰਗ = ਦਿਨ ਦੇ ਮੈਚ ਲਈ ਲਾਲ ਅਤੇ ਰਾਤ ਦੇ ਮੈਚ ਲਈ ਸਫ਼ੈਦ
- ਕੇਂਦਰ ਤੋਂ ਵੱਡੇ ਚੱਕਰ ਦੀ ਦੂਰੀ = 75 ਗਜ਼ ਤੋਂ 85 ਗੰਜ਼ (68 ਤੋਂ 58 ਮੀ.).
- ਵਿਕਟਾਂ ਦੀ ਜ਼ਮੀਨ ਤੋਂ ਉਚਾਈ = 28 ਇੰਚ
- ਮੈਚ ਦੀਆਂ ਕਿਸਮਾਂ = 20-20, ਇਕ ਦਿਨ ਦਾ ਮੈਚ, ਪੰਜ ਦਿਨ ਦਾ ਟੈਸਟ ਮੈਚ
- ਮੈਚ ਦੇ ਅੰਪਾਇਰਾਂ ਦੀ ਗਿਣਤੀ = 2
- ਤੀਜਾ ਅੰਪਾਇਰ = ਇਕ ਮੈਚ ਰੈਫ਼ਰੀ
- ਕੇਂਦਰੀ ਵਿਕਟ ਤੋਂ ਦੋਨੋਂ ਤਰਫ਼ ਪਿਚ ਦੀ ਚੌੜਾਈ = 4 ਫੁੱਟ 4 ਇੰਚ
- ਸਕੋਰਰ ਦੀ ਗਿਣਤੀ = 2
- ਪਾਰੀ ਬਦਲਣ ਦਾ ਸਮਾਂ = 10 ਮਿੰਟ
- ਖਿਡਾਰੀ ਬਦਲਣ ਦਾ ਸਮਾਂ = 2 ਮਿੰਟ
- ਛੋਟੇ ਸਰਕਲ ਦਾ ਰੇਡੀਅਸ = 2.7 ਮੀ.

ਖੇਡ ਸੰਬੰਧੀ ਮਰੰਡਵਪੂਰਨ ਜਾਣਕਾਰੀ
- ਮੈਚ ਦੋ ਟੀਮਾਂ ਵਿਚਕਾਰ ਖੇਡਿਆ ਜਾਂਦਾ ਹੈ । ਹਰੇਕ ਟੀਮ ਵਿਚ 11 ਖਿਡਾਰੀ ਹੁੰਦੇ ਹਨ ।
- ਮੈਚ ਲਈ ਦੋ ਅੰਪਾਇਰ ਨਿਯੁਕਤ ਕੀਤੇ ਜਾਂਦੇ ਹਨ । ਦੋਵੇਂ ਪਾਸੇ ਇਕ-ਇਕ ਅੰਪਾਇਰ ਹੁੰਦਾ ਹੈ ।
- ਦੌੜਾਂ ਦਾ ਰਿਕਾਰਡ ਸਕੋਰਰ ਰੱਖਦਾ ਹੈ ।
- ਜ਼ਖ਼ਮੀ ਜਾਂ ਬਿਮਾਰ ਹੋਣ ਦੀ ਹਾਲਤ ਵਿਚ ਖਿਡਾਰੀ ਤਬਦੀਲ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਪਰ ਉਸ ਨੂੰ ਬੈਟ ਜਾਂ ਬਾਉਲਿੰਗ ਕਰਨ ਦੀ ਆਗਿਆ ਨਹੀਂ ਹੁੰਦੀ । ਉਹ ਵਿਕਟਾਂ ਦੇ ਵਿਚਾਲੇ ਦੂਜੇ ਖਿਡਾਰੀ ਲਈ ਦੌੜ ਸਕਦਾ ਹੈ ਜਾਂ ਫ਼ੀਲਡ ਕਰ ਸਕਦਾ ਹੈ ।
- ਬਦਲਿਆ ਹੋਇਆ ਖਿਡਾਰੀ ਆਪਣੀ ਖ਼ਾਸ ਜਗ੍ਹਾ (Special Position) ਤੇ ਫੀਲਡ ਨਹੀਂ ਕਰ ਸਕਦਾ ।
- ਬੈਟ ਕਰਨ ਲਈ ਜਾਂ ਫ਼ੀਲਡ ਕਰਨ ਲਈ ਟੀਮ ਦੇ ਕੈਪਟਨ ਨਿਰਣਾ ਕਰਦੇ ਹਨ ।
- ਹਰੇਕ ਇਨਿੰਗ ਦੇ ਸ਼ੁਰੂ ਵਿਚ ਨਵਾਂ ਬਾਲ ਲਿਆ ਜਾਂਦਾ ਹੈ । 200 ਰਨ ਬਣਨ ਪਿੱਛੋਂ ਜਾਂ 75 ਓਵਰਜ਼ ਦੇ ਪਿੱਛੋਂ ਵੀ ਨਵਾਂ ਬਾਲ ਲਿਆ ਜਾ ਸਕਦਾ ਹੈ | ਬਾਲ ਗੁੰਮ ਹੋ ਜਾਣ ‘ਤੇ ਜਾਂ ਖਰਾਬ ਹੋ ਜਾਣ ‘ਤੇ ਵੀ ਨਵਾਂ ਬਾਲ ਲੈ ਸਕਦੇ ਹਾਂ, ਪਰ ਇਸ ਦੀ ਹਾਲਤ ਗੁੰਮ ਹੋਏ ਜਾਂ ਖ਼ਰਾਬ ਹੋਏ ਬਾਲ ਨਾਲ ਮਿਲਦੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।
- ਅੱਜ-ਕਲ 20-20 (ਟਵੰਟੀ-ਟਵੰਟੀ) ਮੈਚ ਦਿਨ-ਰਾਤ ਨੂੰ ਖੇਡੇ ਜਾਂਦੇ ਹਨ, ਜਿਸ ਵਿਚ ਗੁਲਾਬੀ ਰੰਗ ਦਾ ਬਾਲ ਇਸਤੇਮਾਲ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 1.
ਕ੍ਰਿਕਟ ਦੀ ਖੇਡ ਵਿਚ ਕਿੰਨੇ ਖਿਡਾਰੀ, ਨਿਰਣਾਇਕ ਅਤੇ ਸਕੋਰਰ ਤੇ ਉਨ੍ਹਾਂ ਦੀ ਕ੍ਰਿਕਟ ਕਿੱਟ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਕ੍ਰਿਕਟ ਦੀ ਖੇਡ ਵਿਚ ਖਿਡਾਰੀਆਂ ਦੀ ਗਿਣਤੀ, ਨਿਰਣਾਇਕ ਅਤੇ ਸਕੋਰਰ ਤੇ ਉਨ੍ਹਾਂ ਦੀ ਕ੍ਰਿਕਟ ਕਿੱਟ-
- ਕ੍ਰਿਕਟ ਮੈਚ ਦੋ ਟੀਮਾਂ ਵਿਚਕਾਰ ਖੇਡਿਆ ਜਾਂਦਾ ਹੈ । ਹਰੇਕ ਟੀਮ ਦੇ ਖਿਡਾਰੀਆਂ ਦੀ ਗਿਣਤੀ 11-11 ਹੁੰਦੀ ਹੈ । ਹਰੇਕ ਟੀਮ ਦਾ ਇਕ ਕਪਤਾਨ ਹੁੰਦਾ ਹੈ, ਜੋ ਪਾਰੀ ਲਈ ਟਾਸ ਹੋਣ ਤੋਂ ਪਹਿਲਾਂ ਆਪਣੇ ਖਿਡਾਰੀ ਨਾਮਜ਼ਦ ਕਰਦਾ ਹੈ ।
- ਕਿਸੇ ਖਿਡਾਰੀ ਦੇ ਜ਼ਖਮੀ ਜਾਂ ਬੀਮਾਰ ਹੋ ਜਾਣ ਕਾਰਨ ਉਸ ਦੀ ਥਾਂ ‘ਤੇ ਕਿਸੇ ਦੂਜੇ ਖਿਡਾਰੀ ਨੂੰ ਲਏ ਜਾਣ ਦੀ ਆਗਿਆ ਹੈ । ਨਵੇਂ ਖਿਡਾਰੀ ਨੂੰ ਸਬਸਟੀਚਿਉਟ ਖਿਡਾਰੀ ਕਹਿੰਦੇ ਹਨ । ਸਬਸਟੀਚਿਊਟ ਖਿਡਾਰੀ ਕੇਵਲ ਫੀਲਡ ਹੀ ਕਰ ਸਕਦਾ ਹੈ । ਉਹ ਬੈਟ ਜਾਂ ਬਾਉਲ ਨਹੀਂ ਕਰ ਸਕਦਾ ।
- ਪਾਰੀ ਲਈ ਟਾਸ ਤੋਂ ਪਹਿਲਾਂ ਦੋਵੇਂ ਸਿਰਿਆਂ ਲਈ ਇਕ-ਇਕ ਨਿਰਣਾਇਕ ਨਿਯੁਕਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ, ਜੋ ਖੇਡ ਦਾ ਨਿਰਪੱਖ ਨਿਰਣਾ ਕਰਦਾ ਹੈ ।
- ਸਾਰੀਆਂ ਦੌੜਾਂ ਦਾ ਵੇਰਵਾ ਰਿਕਾਰਡ ਰੱਖਣ ਲਈ ਦੋ ਸਕੋਰਰ ਨਿਯੁਕਤ ਕੀਤੇ ਜਾਂਦੇ ਹਨ । ਉਹ ਅੰਪਾਇਰਾਂ ਦੇ ਸਾਰੇ ਇਸ਼ਾਰਿਆਂ ਅਤੇ ਆਦੇਸ਼ਾਂ ਦੀ ਪਾਲਨਾ ਕਰਦੇ ਹਨ ।
ਕ੍ਰਿਕਟ ਕਿੱਟ (Cricket Kit) – ਕ੍ਰਿਕਟ ਦੇ ਖਿਡਾਰੀ ਲਈ ਕਿੱਟ ਪਹਿਨਣਾ ਜ਼ਰੂਰੀ ਹੈ । ਕਿੱਟ ਤੋਂ ਭਾਵ ਸਫ਼ੈਦ ਪੈਂਟ, ਕਮੀਜ਼, ਬੂਟ, ਜੁਰਾਬਾਂ, ਪੈਡ, ਅਬਡੌਮਨਲ ਗਾਰਡ, ਗਲਵਜ ਅਤੇ ਬੈਟ ਹਨ ।

ਪ੍ਰਸ਼ਨ 2.
ਕ੍ਰਿਕਟ ਬਾਲ, ਬੈਟ (ਬੱਲਾ), ਪਿੱਚ, ਵਿਕਟਾਂ, ਬਾਊਲਿੰਗ ਅਤੇ ਪਾਪਿੰਗ ਕੀਜ਼, ਪਾਰੀ, ਖੇਡ ਦਾ ਆਰੰਭ, ਇੰਟਰਵਲ ਅਤੇ ਅੰਤ ਬਾਰੀ, ਖੇਡ ਬਾਰੇ ਲਿਖੋ ।
ਉੱਤਰ-
ਕ੍ਰਿਕਟ ਬਾਲ, ਬੈਟ (ਬੱਲਾ), ਪਿੱਚ, ਵਿਕਟਾਂ, ਬਾਊਲਿੰਗ ਅਤੇ ਪਾਪਿੰਗ ਕੀਜ਼ਾਂ, ਪਾਰੀ, ਖੇਡ ਦਾ ਆਰੰਭ, ਅੰਤ ਅਤੇ ਇੰਟਰਵਲ ।
ਗੇਂਦ (Ball) – ਕ੍ਰਿਕਟ ਗੇਂਦ ਦਾ ਭਾਰ 5\(\frac{1}{2}\) ਐੱਸ (155.9 ਗ੍ਰਾਮ ਤੋਂ ਘੱਟ ਅਤੇ 5\(\frac{3}{4}\) ਐੱਸ (163 ਗ੍ਰਾਮ ਤੋਂ ਵੱਧ ਨਹੀਂ ਹੋਵੇਗਾ । ਇਸ ਦੀ ਗੋਲਾਈ 88 \(\frac{13}{16}\)“(22.4 ਸਮ) ਤੋਂ ਘੱਟ ਤੇ 9” (22.9 ਸਮ ਤੋਂ ਵੱਧ ਨਹੀਂ ਹੋਵੇਗੀ । ਇਹ ਚਮੜੇ ਦੀ ਬਣੀ ਹੋਵੇਗੀ, ਜਿਸ ਤੇ ਲਾਲ ਚਮਕਦਾਰ ਰੰਗ ਕੀਤਾ ਹੋਵੇਗਾ । ਰਾਤ ਸਮੇਂ ਖੇਡੇ ਜਾਣ ਵਾਲੇ ਮੈਚਾਂ ਵਿਚ ਚਿੱਟੇ ਰੰਗ ਦੀ ਗੇਂਦ ਵਰਤੀ ਜਾਂਦੀ ਹੈ । ਹਰੇਕ ਕਪਤਾਨ ਨਵੀਂ ਪਾਰੀ (Innings) ਸ਼ੁਰੂ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਨਵੀਂ ਗੇਂਦ ਮੰਗ ਸਕਦਾ ਹੈ । ਗੇਂਦ ਗੁੰਮ ਹੋ ਜਾਣ ਜਾਂ ਖ਼ਰਾਬ ਹੋਣ ਤੇ ਅੰਪਾਇਰ ਦੁਸਰੀ ਗੇਂਦ ਦੀ ਵਰਤੋਂ ਦੀ ਇਜਾਜ਼ਤ ਦੇਣਗੇ ਪਰੰਤੂ ਉਸ ਦੀ ਹਾਲਤ ਗੁੰਮ ਹੋਏ ਗੇਂਦ ਜਾਂ ਖ਼ਰਾਬ ਹੋਏ ਬਾਲ ਵਰਗੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।
ਬੈਟ (Bat) – ਬੈਟ ਦੀ ਲੰਬਾਈ ਹੈਂਡਲ ਸਮੇਤ 38” ਹੁੰਦੀ ਹੈ ਅਤੇ ਇਸ ਦੀ ਚੌੜਾਈ ਵੱਧ ਤੋਂ ਵੱਧ ਚੌੜੀ ਥਾਂ 4\(\frac{1}{4}\) ਤੋਂ ਵੱਧ ਨਹੀਂ ਹੋ ਸਕਦੀ । ਸਧਾਰਨ ਕ੍ਰਿਕਟ ਬੈਟ ਦਾ ਭਾਰ 2\(\frac{1}{2}\) ਪੜ ਹੁੰਦਾ ਹੈ ।
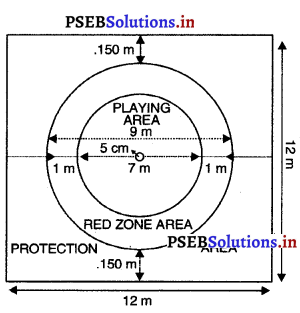
ਪਿੱਚ (Pitch) – ਬਾਊਲਿੰਗ (ਗੇਂਦਬਾਜ਼ੀ ਕਰਨ ਵਾਲੀਆਂ ਥਾਂਵਾਂ ਦੇ ਵਿਚਕਾਰ ਵਾਲੀ ਗਰਾਊਂਡ ਪਿੱਚ ਅਖਵਾਉਂਦੀ ਹੈ । ਵਿਕਟ ਦੇ ਵਿਚਕਾਰ ਸਟੰਪਾਂ ਦੇ ਮਿਲਣ ਵਾਲੀ ਕਲਪਿਤ ਰੇਖਾ ‘ਤੇ ਇਸ ਦੀ ਦੋਵੇਂ ਪਾਸੇ ਚੌੜਾਈ 5 ਫੁੱਟ (1.52 ਮੀਟਰ) ਹੁੰਦੀ ਹੈ ਤੇ ਕੁੱਲ ਪਿੱਚ ਦੀ ਚੌੜਾਈ 8’-8” ਹੁੰਦੀ ਹੈ ।
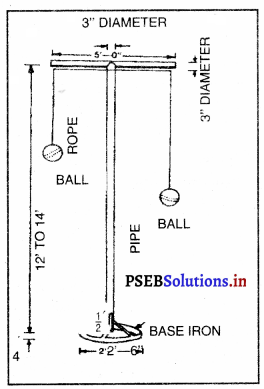
ਵਿਕਟਾਂ (Wickets) – ਪਿੱਚ ਦੇ ਆਹਮਣੇ-ਸਾਹਮਣੇ ਤਿੰਨ-ਤਿੰਨ ਵਿਕਟਾਂ ਗੱਡੀਆਂ ਜਾਣਗੀਆਂ
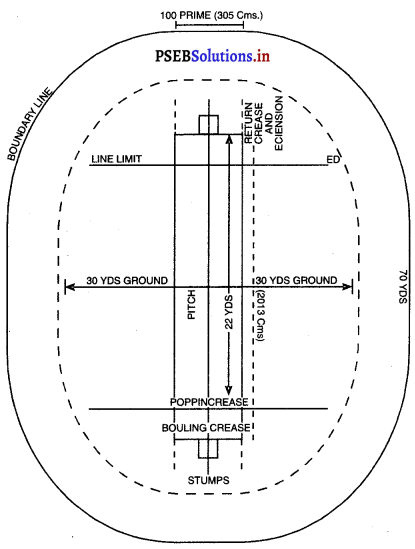
ਤੇ ਆਹਮੋ-ਸਾਹਮਣੇ ਗੱਡੀਆਂ ਵਿਕਟਾਂ ਦਾ ਫ਼ਾਸਲਾ 22 ਗਜ਼ ਹੋਵੇਗਾ । ਵਿਕਟਾਂ ਦੀ ਚੌੜਾਈ 9” ਹੋਵੇਗੀ ਅਤੇ ਉਸ ਦੇ ਤਿੰਨ ਸਟੰਪ ਅਤੇ ਉੱਪਰ ਰੱਖਣ ਵਾਲੀਆਂ ਦੋ ਗੁੱਲੀਆਂ (Baiss) ਹੋਣਗੀਆਂ । ਸਟੰਪ ਬਰਾਬਰ ਹੋਣਗੇ ਅਤੇ ਇੰਝ ਗੱਡੇ ਜਾਣਗੇ ਕਿ ਗੇਂਦ ਉਨ੍ਹਾਂ ਦੇ ਵਿਚਕਾਰੋਂ ਪਾਰ ਨਾ ਜਾ ਸਕੇ ।
ਧਰਤੀ ਤੋਂ ਉਨ੍ਹਾਂ ਦੀ ਉੱਚਾਈ 28 ਇੰਚ ਹੋਵੇਗੀ । ਹਰੇਕ ਗਿੱਲੀ 4\(\frac{3}{8}\) ਇੰਚ ਲੰਬੀ ਹੋਵੇਗੀ ਅਤੇ ਸਟੰਪ ਦੇ ਉੱਪਰ ਰੱਖੀ ਹੋਈ ਗੁੱਲੀ ਉਸ ਨਾਲੋਂ \(\frac{1}{2}\) ਇੰਚ ਤੋਂ ਬਾਹਰ ਵਧੀ ਨਹੀਂ ਹੋਵੇਗੀ ।
ਬਾਊਲਿੰਗ ਅਤੇ ਪਾਪਿੰਗ ਕ੍ਰੀਜ਼ਾਂ (Bowling and Popping Creases) – ਬਾਊਲਿੰਗ ਝੀਜ਼ ਸਟੰਪਾਂ ਦੇ ਨਾਲ 8 ਫੁੱਟ 8 ਇੰਚ ਲੰਮੀ ਖਿੱਚੀ ਜਾਵੇਗੀ । ਸਟੰਪਾਂ ਵਿਚਕਾਰ ਹੋਣਗੀਆਂ | ਪਾਪਿੰਗ ਗ਼ਜ਼ ਬਾਊਲਿੰਗ ਕੀਜ਼ ਦੇ ਸਮਾਨਾਂਤਰ 3 ਫੁੱਟ ‘ਤੇ ਖਿੱਚੀ ਜਾਵੇਗੀ ਅਤੇ ਇਹ ਸਟੰਪਾਂ ਦੇ ਦੋਵੇਂ ਪਾਸੇ
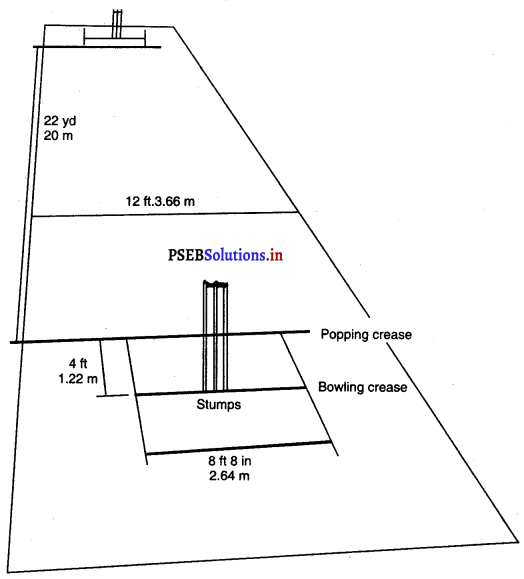
6 ਫੁੱਟ ਵਧਾਈ ਜਾਵੇਗੀ ।ਰਿਟਰਨ ਭੀਜ਼ ਬਾਊਲਿੰਗ ਕੀਜ਼ ਦੇ ਦੋਨਾਂ ਸਿਰਿਆਂ ‘ਤੇ ਸਮਕੋਣ ਤੇ ਖਿੱਚੀ ਜਾਵੇਗੀ ਅਤੇ ਇਸ ਨੂੰ ਪਾਪਿੰਗ ਕੀਜ਼ ਦੇ ਮਿਲਣ ਲਈ ਵਧਾਇਆ ਜਾਵੇਗਾ | ਪਾਪਿੰਗ ਕ੍ਰੀਜ਼ ਤੇ ਰਿਟਰਨ ਭੀਜ਼ ਦੋਨੋਂ ਹੀ ਲੰਬਾਈ ਵਿਚ ਅਸੀਮਿਤ ਮੰਨੀਆਂ ਜਾਂਦੀਆਂ ਹਨ ।
ਪਾਰੀ (Innings) – ਹਰੇਕ ਟੀਮ ਨੂੰ ਵਾਰੀ-ਵਾਰੀ ਨਾਲ ਦੋ ਵਾਰ ਖੇਡਣਾ ਪੈਂਦਾ ਹੈ । ਇਸ ਦਾ ਫੈਸਲਾ ਟਾਸ ਦੁਆਰਾ ਕੀਤਾ ਜਾਵੇਗਾ ਕਿ ਕਿਹੜੀ ਟੀਮ ਪਹਿਲੇ ਖੇਡੇ । ਜੋ ਵੀ ਟੀਮ ਪਹਿਲੇ ਖੇਡੇਗੀ, ਜੇਕਰ ਉਸ ਨੇ ਵਿਰੋਧੀ ਟੀਮ ਤੋਂ ਪੰਜ ਦਿਨ ਜਾਂ ਵਧੇਰੇ ਦੇ ਮੈਚ ਵਿਚ 200 ਦੌੜਾਂ, ਤਿੰਨ ਦਿਨ ਦੇ ਮੈਚ ਵਿਚ 150, ਦੋ ਦਿਨ ਦੇ ਮੈਚ ਵਿਚ 100 ਅਤੇ ਇਕ ਦਿਨ ਦੇ ਮੈਚ ਵਿਚ 25 ਦੌੜਾਂ ਵਧੇਰੇ ਬਣਾ ਲਈਆਂ ਹਨ, ਤਾਂ ਉਹ ਦੂਸਰੀ ਟੀਮ ਨੂੰ ਦੁਬਾਰਾ ਖੇਡਣ ਲਈ ਕਹਿ ਸਕਦੀ ਹੈ। ਅਰਥਾਤ Follow on ਕਰਵਾ ਸਕਦੀ ਹੈ । ਬੈਟਿੰਗ ਕਰਨ ਵਾਲੀ ਟੀਮ ਦਾ ਕਪਤਾਨ ਸਮੇਂ ਤੋਂ ਪਹਿਲਾਂ ਵੀ ਪਾਰੀ ਦੀ ਸਮਾਪਤੀ ਦੀ ਘੋਸ਼ਣਾ (Declare) ਕਰ ਸਕਦਾ ਹੈ ।
ਖੇਡ ਦਾ ਆਰੰਭ, ਅੰਤ ਅਤੇ ਇੰਟਰਵਲ (Start and close of Play and Intervals) – ਹਰੇਕ ਪਾਰੀ ਦੇ ਆਰੰਭ ’ਤੇ ਪ੍ਰਤੀ ਦਿਨ ਖੇਡ ਆਰੰਭ ਕਰਨ ਤੋਂ ਪਹਿਲਾਂ ਕੈਪਟਨ ਕਹਿੰਦਾ ਹੈ ‘ਖੇਡੋ’ ਅਤੇ ਜੇਕਰ ਟੀਮ ਖੇਡਣ ਤੋਂ ਇਨਕਾਰ ਕਰੇ, ਤਾਂ ਉਹ ਮੈਚ ਹਾਰ ਜਾਵੇਗੀ । ਹਰੇਕ ਪਾਰੀ ਵਿਚ 10 ਮਿੰਟ ਅਤੇ ਹਰੇਕ ਨਵੇਂ ਬੈਟਸਮੈਨ ਦੇ ਆਉਣ ਵਿਚ ਵੱਧ ਤੋਂ ਵੱਧ ਦੋ ਮਿੰਟ ਦਿੱਤੇ ਜਾਣਗੇ । ਭੋਜਨ ਲਈ ਇੰਟਰਵਲ ਅਕਸਰ 45 ਮਿੰਟ ਤੋਂ ਵੱਧ ਨਹੀਂ ਹੋਵੇਗਾ । ਚਾਹ ਲਈ ਇੰਟਰਵਲ 20 ਮਿੰਟ ਤੋਂ ਜ਼ਿਆਦਾ ਨਹੀਂ ਹੋਵੇਗਾ । ਜੇਕਰ ਚਾਹ ਦੇ ਨਿਰਧਾਰਿਤ ਸਮੇਂ ਤੇ 9 ਖਿਡਾਰੀ ਆਊਟ ਹੋਏ ਹੋਣ ਤਾਂ ਖੇਡ ਨੂੰ 30 ਮਿੰਟ ਤੱਕ ਜਾਂ ਪਾਰੀ ਦੀ ਸਮਾਪਤੀ ਤਕ ਜਾਰੀ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ ।

ਪ੍ਰਸ਼ਨ 3.
ਕ੍ਰਿਕਟ ਦੀ ਖੇਡ ਵਿਚ ਤੁਸੀਂ ਹੇਠ ਲਿਖਿਆਂ ਤੋਂ ਕੀ ਸਮਝਦੇ ਹੋ ?
ਸਕੋਰ, ਬਾਊਂਡਰੀ, ਗੇਂਦ ਦਾ ਗੁੰਮ ਹੋ ਜਾਣਾ, ਨਤੀਜਾ, ਓਵਰ, ਵਿਕਟਾਂ ਦਾ ਡਿੱਗਣਾ, ਰੈੱਡ ਬਾਲ, ਨੋ ਬਾਲ, ਵਾਈਡ ਬਾਲ, ਬਾਈ ਅਤੇ ਲੈਗ ਬਾਈ, ਆਪਣੇ ਖੇਤਰ ਤੋਂ ਬਾਹਰ, ਬੈਟਸਮੈਨ ਦਾ ਰਿਟਾਇਰ ਹੋਣਾ, ਬਾਊਲਡ, ਕੈਚ, ਗੇਂਦ ਨੂੰ ਹੱਥ ਲਾਉਣਾ, ਗੇਂਦ ‘ਤੇ ਦੋ ਵਾਰ, ਵਿਕਟ ‘ਤੇ ਵਾਰ, ਐਲ. ਬੀ. ਡਬਲਿਊ, ਖੇਡ ਵਿਚ ਰੋਕ, ਸਟੰਪਡ, ਰਨ ਆਊਟ, ਵਿਕਟ ਰੱਖਿਅਕ, ਖੇਤਰ ਰੱਖਿਅਕ ।
ਉੱਤਰ-
ਸਕੋਰ (Score) – ਪਹਿਲਾਂ ਬੈਟਸਮੈਨ ਗੇਂਦ ਨੂੰ ਚੋਟ ਲਗਾਉਣ ਦੇ ਬਾਅਦ ਗੇਂਦ ਮੈਦਾਨ ਵਿਚ ਰਹਿਣ ਦੇ ਸਮੇਂ ਵਿਚ ਇਕ ਸਾਈਡ ਤੋਂ ਦੂਸਰੀ ਸਾਈਡ ਤਕ ਦੌੜਦਾ ਹੈ । ਉਹ ਜਿੰਨੀ ਵਾਰ ਅਜਿਹਾ ਕਰੇਗਾ, ਉੱਨੇ ਰਨ ਹੋ ਜਾਂਦੇ ਹਨ | ਸਕੋਰ ਲਈ ਦੌੜਾਂ ਦੀ ਗਿਣਤੀ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਜਦੋਂ ਬੈਟਸਮੈਨ ਗੇਂਦ ਨੂੰ ਹਿੱਟ ਕਰਨ ਮਗਰੋਂ ਇਕ ਸਿਰੇ ਤੋਂ ਦੂਸਰੇ ਸਿਰੇ ‘ਤੇ ਪਹੁੰਚ ਜਾਂਦਾ ਹੈ, ਤਾਂ ਇਕ ਦੌੜ ਪੂਰੀ ਸਮਝੀ ਜਾਂਦੀ ਹੈ । ਜੇਕਰ ਕੋਈ ਬੈਟਸਮੈਨ ਦੂਜੇ ਪਾਸੇ ਪਹੁੰਚੇ ਬਿਨਾਂ ਰਾਹ ਤੋਂ ਵਾਪਸ ਪਰਤ ਜਾਂਦਾ ਹੈ, ਉਹ ਦੌੜ ਨਹੀਂ ਗਿਣੀ ਜਾਂਦੀ । ਇਸ ਨੂੰ ਸ਼ਾਰਟ ਰਨ (Short Run) ਕਹਿੰਦੇ ਹਨ । ਜੇਕਰ ਰਨ ਬਣਾਉਂਦੇ ਸਮੇਂ ਬਾਲ ਹਵਾ ਵਿਚ ਹੋਵੇ, ਉਹ ਲਪਕ ਲਿਆ ਜਾਵੇ, ਤਾਂ ਉਹ ਰਨ (ਦੌੜ) ਗਿਣੀ ਨਹੀਂ ਜਾਵੇਗੀ । ਇਸੇ ਤਰ੍ਹਾਂ ਜੇਕਰ ਬੈਟਸਮੈਨ ਦੌੜ ਬਣਾਉਂਦੇ ਸਮੇਂ ਰਨ ਆਊਟ (Run Out) ਹੋ ਜਾਵੇ, ਤਾਂ ਉਹ ਦੌੜ ਨਹੀਂ ਗਿਣੀ ਜਾਵੇਗੀ ।
ਬਾਊਂਡਰੀ (Boundary) – ਜੇਕਰ ਬੈਟਸਮੈਨ ਦੇ ਹਿਟ ਕਰਨ ‘ਤੇ ਗੇਂਦ ਮੈਦਾਨ ਨੂੰ ਛੰਹਦੀ ਹੋਈ ਸੀਮਾ ਰੇਖਾ ਦੇ ਪਾਰ ਚਲੀ ਜਾਂਦੀ ਹੈ ਤਾਂ ਉਸ ਨੂੰ ਬਾਊਂਡਰੀ ਕਹਿੰਦੇ ਹਨ । ਬਾਊਂਡਰੀ ਦਾ ਚਾਰ ਸਕੋਰ ਹੁੰਦਾ ਹੈ । ਜੇਕਰ ਗੇਂਦ ਜ਼ਮੀਨ ਨੂੰ ਲੱਗੇ ਬਿਨਾਂ ਬਾਊਂਡਰੀ ਤੋਂ ਬਾਹਰ ਜਾ ਕੇ ਡਿੱਗੇ ਤਾਂ 6 ਦੌੜਾਂ ਹੋ ਜਾਂਦੀਆਂ ਹਨ । ਬਾਊਂਡਰੀ ਜੇਕਰ ਓਵਰ ਥਰੋ ‘ਤੇ ਹੋਈ ਹੈ, ਜਾਂ ਖੇਤਰ ਰੱਖਿਅਕ ਨੇ ਜਾਣ ਬੁੱਝ ਕੇ ਕੀਤੀ ਹੈ ਤਾਂ ਬਣੇ ਹੋਏ ਹਨ ਅਤੇ ਬਾਊਂਡਰੀ ਦਾ ਸਕੋਰ ਫਲਅੰਕਣ ਵਿਚ ਜੋੜੇ ਜਾਣਗੇ ।
ਗੇਂਦ ਦਾ ਗੁੰਮ ਹੋ ਜਾਣਾ (Lost Ball) – ਜੇਕਰ ਗੇਂਦ ਗੁੰਮ ਹੋ ਜਾਵੇ ਤਾਂ ਕੋਈ ਵੀ ਖੇਤਰ ਰੱਖਿਅਕ ਗੁੰਮ ਹੋ ਜਾਣ ਦਾ ਐਲਾਨ ਕਰ ਦਿੰਦਾ ਹੈ । ਅਜਿਹੀ ਹਾਲਤ ਵਿਚ ਅੰਪਾਇਰ ਗੁੰਮ ਹੋਈ ਗੇਂਦ ਨਾਲ ਮਿਲਦੀ-ਜੁਲਦੀ ਹਾਲਤ ਵਾਲੀ ਗੇਂਦ ਨਾਲ ਖੇਡ ਮੁੜ ਸ਼ੁਰੂ ਕਰਵਾ ਦਿੰਦਾ ਹੈ ।
ਨਤੀਜਾ (Results) – ਜੋ ਵੀ ਟੀਮ ਦੋ ਪਾਰੀਆਂ (ਇਨਿੰਗਜ਼) ਵਿਚ ਜ਼ਿਆਦਾ ਦੌੜਾਂ ਬਣਾ ਲੈਂਦੀ ਹੈ ਉਸ ਨੂੰ ਜੇਤੂ ਮੰਨਿਆ ਜਾਵੇਗਾ | ਪਰ ਜੇਕਰ ਮੈਚ ਪੂਰਾ ਨਾ ਹੋ ਸਕੇ, ਤਾਂ ਇਹ ਬਰਾਬਰ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ ।
ਓਵਰ (Over) – ਇਕ ਓਵਰ ਵਿਚ 6 ਵਾਰ ਗੇਂਦ ਸੁੱਟੀ ਜਾਂਦੀ ਹੈ । ਇਹ ਓਵਰ ਵਿਕਟ ਦੇ ਸਿਰੇ ‘ਤੇ ਵਾਰੀ-ਵਾਰੀ ਦਿੱਤੇ ਜਾਂਦੇ ਹਨ | ਜੇਕਰ ਪਹਿਲਾਂ ਨਿਸਚਿਤ ਕਰ ਲਿਆ ਜਾਵੇ, ਤਾਂ ਇਕ ਵਾਰ ਓਵਰ ਵਿਚ ਅੱਠ ਗੇਂਦਾਂ ਖੇਡੀਆਂ ਜਾ ਸਕਦੀਆਂ ਹਨ । “ਨੋ ਬਾਲ’ ਅਤੇ ‘ਵਾਈਡ ਬਾਲ’ ਓਵਰ ਵਿਚ ਨਹੀਂ ਗਿਣੇ ਜਾਣਗੇ । ਜਿੰਨੇ ਨੋ ਬਾਲ ਉਸ ਓਵਰ ਵਿਚ ਹੋਣਗੇ, ਉਨੀਆਂ ਹੀ ਹੋਰ ਗੇਂਦਾਂ ਸੁੱਟੀਆਂ ਜਾਣਗੀਆਂ । ਇਕ ਇਨਿੰਗਜ਼ ਵਿਚ ਕੋਈ ਵੀ ਬਾਊਲਰ ਲਗਾਤਾਰ ਦੋ ਓਵਰ ਬਾਉਲ ਨਹੀਂ ਕਰ ਸਕਦਾ । ਜੇਕਰ ਅੰਪਾਇਰ ਤੋਂ ਓਵਰ ਦੀਆਂ ਬਾਲਾਂ ਦੀ ਗਿਣਤੀ ਵਿਚ ਭੁੱਲ ਹੋ ਜਾਂਦੀ ਹੈ ਤਾਂ ਅੰਪਾਇਰ ਦੁਆਰਾ ਗਿਣਿਆ ਗਿਆ ਓਵਰ ਨਹੀਂ ਮੰਨਿਆ ਜਾਵੇਗਾ ।
ਵਿਕਟਾਂ ਦਾ ਡਿੱਗਣਾ (Fall of wickets) – ਜਦੋਂ ਬੈਟਸਮੈਨ ਖੁਦ ਜਾਂ ਉਸ ਦਾ ਬੈਟ ਜਾਂ ਗੇਂਦ ਸਟੰਪਜ਼ ਦੇ ਉੱਪਰ ਦੀਆਂ ਦੋਨੋਂ ਗੁੱਲੀਆਂ ਡੇਗ ਦੇਣ ਜਾਂ ਜ਼ੋਰ ਨਾਲ ਸਟੰਪ ਧਰਤੀ ਤੋਂ ਉੱਖੜ ਜਾਵੇ ਤਾਂ ਵਿਕਟ ਡਿੱਗਣਾ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਰੈੱਡ ਬਾਲ (Dead Ball)-
- ਜਦ ਗੇਂਦ ਬਾਊਲਰ ਜਾਂ ਵਿਕਟ ਕੀਪਰ ਨੇ ਠੀਕ ਤਰ੍ਹਾਂ ਨਾਲ ਫੜ ਲਿਆ ਹੋਵੇ ।
- ਜਦ ਉਹ ਸੀਮਾ ਤਕ ਪਹੁੰਚ ਜਾਵੇ ਜਾਂ ਠੱਪਾ ਖਾ ਲਵੇ ।
- ਉਹ ਖੇਡੇ ਜਾਂ ਬਿਨਾਂ ਖੇਡੇ ਅੰਪਾਇਰ ਜਾਂ ਬੈਟਸਮੈਨ ਦੇ ਕੱਪੜਿਆਂ ਵਿਚ ਫਸ ਜਾਵੇ ।
- ਬੈਟਸਮੈਨ ਆਉਟ ਹੋ ਜਾਵੇ ।
- ਗੇਂਦ ਸੁੱਟਣ ਵਾਲਾ ਗੇਂਦ ਫਿਰ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਉਪਰੰਤ ਅੰਪਾਇਰ ਖੇਡ ਨੂੰ ਜੇਕਰ ਰੋਕਣਾ ਚਾਹੇ ।
- ਅੰਪਾਇਰ ਦੁਆਰਾ ਸਮੇਂ ਜਾਂ ਓਵਰ ਦਾ ਐਲਾਨ ਕਰਨ ਤੇ ।
ਨੋ ਬਾਲ (No Ball) – ਗੇਂਦ ਕਰਦੇ ਸਮੇਂ ਦੇ ਗੇਂਦਬਾਜ਼ ਦਾ ਅਗਲਾ ਪੂਰਾ ਪੈਰ ਬੈਟਿੰਗ ਝੀਜ਼ ਤੋਂ ਅੱਗੇ ਟੱਪ ਜਾਂਦਾ ਹੈ ਜਾਂ Returning Crease ਨੂੰ ਕੱਟਦਾ ਹੈ ਤਾਂ ਅੰਪਾਇਰ ਨੋ ਬਾਲ ਘੋਸ਼ਤ ਕਰ ਦਿੰਦਾ ਹੈ । ਬੇਟਸਨ ਨੇ ਬਾਲ ’ਤੇ ਹਿੰਟ ਲਗਾ ਕੇ ਜਿੰਨੀਆਂ ਵੀ ਦੌੜਾਂ ਸੰਭਵ ਹੋਣ, ਬਣਾ ਸਕਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਬਣੀਆਂ ਦੌੜਾਂ ਨੂੰ ਭੁੱਲ ਸਕੋਰ ਵਿਚ ਜੋੜ ਲਿਆ ਜਾਵੇਗਾ । ਜੇਕਰ ਕੋਈ ਦੌੜ ਨਾ ਬਣੀ ਹੋਵੇ ਤਾਂ ਕੇਵਲ ਇਕ ਦੌੜ ਹੀ ਸਕੋਰ ਵਿਚ ਜੋੜੀ ਜਾਵੇਗੀ । ਅੰਪਾਇਰ ਆਪਣੀ ਇਕ ਭੁਜਾ ਫੈਲਾ ਕੇ ਨੋ ਬਾਲ ਦਾ ਇਸ਼ਾਰਾ ਦਿੰਦਾ ਹੈ ।
ਵਾਈਡ ਬਾਲ (Wide Ball) – ਜੇਕਰ ਬਾਊਲਰ ਬਾਲ ਨੂੰ ਵਿਕਟ ਤੋਂ ਇੰਨੀ ਉਚਾਈ ‘ਤੇ ਜਾਂ ਚੌੜਾਈ ‘ਤੇ ਸੁੱਟਦਾ ਹੈ ਕਿ ਅੰਪਾਇਰ ਦੇ ਵਿਚਾਰ ਵਿਚ ਇਹ ਬੈਟਸਮੈਨ ਦੀ ਪਹੁੰਚ ਤੋਂ ਬਾਹਰ ਹੈ, ਤਾਂ ਉਹ ਵਾਈਡ ਬਾਲ ਦੀ ਘੋਸ਼ਣਾ ਕਰ ਦਿੰਦਾ ਹੈ । ਜੋ ਦੌੜਾਂ ਵਾਈਡ ਬਾਲ ਦੇ ਸਮੇਂ ਬਣਨ ਉਨ੍ਹਾਂ ਨੂੰ ਵਾਈਡ ਬਾਲ ਵਿਚ ਗਿਣਿਆ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਕੋਈ ਵੀ ਦੌੜ ਨਾ ਬਣੇ ਤਾਂ ਇਕ ਦੌੜ ਸਮਝੀ ਜਾਂਦੀ ਹੈ । ਵਾਈਡ ਬਾਲ ਦਾ ਇਸ਼ਾਰਾ ਅੰਪਾਇਰ ਆਪਣੀਆਂ ਦੋਵੇਂ ਭੁਜਾਵਾਂ ਸਿੱਧੀਆਂ ਫੈਲਾ ਕੇ ਕਰਦਾ ਹੈ ।
ਬਾਈ ਅਤੇ ਲੈਗ ਬਾਈ (Bye and Leg-Bye) – ਜੇਕਰ ਕੋਈ ਚੰਗੀ ਤਰ੍ਹਾਂ ਨਾਲ ਸੁੱਟੀ ਗੇਂਦ ਜਾਂ ਬੈਟਸਮੈਨ (ਸਟਰਾਈਕਰ) ਦੇ ਬੈਟ ਜਾਂ ਸਰੀਰ ਨੂੰ ਬਿਨਾਂ ਛੂਹੇ ਕੋਲੋਂ ਲੰਘ ਜਾਵੇ ਅਤੇ ਦੌੜ ਬਣ ਜਾਵੇ ਤਾਂ ਅੰਪਾਇਰ ਬਾਈ ਘੋਸ਼ਿਤ ਕਰੇਗਾ | ਪਰ ਨੋ ਬਾਲ ਜਾਂ ਵਾਈਡ ਬਾਲ ਨਹੀਂ ਹੋਣਾ ਚਾਹੀਦਾ | ਪਰ ਜੇਕਰ ਗੇਂਦ ਬੈਟਸਮੈਨ ਦੇ ਬੈਟ ਵਾਲੇ ਹੱਥ ਨੂੰ ਛੱਡ ਕੇ ਸਰੀਰ ਦੇ ਕਿਸੇ ਭਾਗ ਨੂੰ ਛੂਹ ਕੇ ਕੋਲੋਂ ਲੰਘ ਜਾਵੇ ਅਤੇ ਦੌੜ ਬਣ ਜਾਵੇ ਤਾਂ ਅੰਪਾਇਰ ਲੈ ਬਾਈ ਘੋਸ਼ਿਤ ਕਰੇਗਾ ।
ਆਪਣੇ ਖੇਤਰ ਤੋਂ ਬਾਹਰ – ਬੈਟਸਮੈਨ ਆਪਣੇ ਖੇਤਰ ਤੋਂ ਬਾਹਰ ਮੰਨਿਆ ਜਾਵੇਗਾ, ਜਦੋਂ ਤਕ ਉਸ ਦੇ ਹੱਥ ਦੇ ਬੈਟ ਦਾ ਕੁੱਝ ਭਾਗ ਜਾਂ ਉਸ ਦਾ ਸਰੀਰ ਕਲਪਿਤ ਮੰਜ ਰੇਖਾ ਦੇ ਪਿੱਛੇ ਜ਼ਮੀਨ ‘ਤੇ ਨਾ ਹੋਵੇ ।
ਬੈਟਸਮੈਨ ਦਾ ਰਿਟਾਇਰ ਹੋਣਾ – ਬੈਟਸਮੈਨ ਕਿਸੇ ਵੀ ਸਮੇਂ ਜ਼ਖ਼ਮੀ ਜਾਂ ਬੀਮਾਰੀ ਦੀ ਹਾਲਤ ਵਿਚ ਰਿਟਾਇਰ ਹੋ ਸਕਦਾ ਹੈ । ਉਹ ਬੱਲੇਬਾਜ਼ੀ ਤਾਂ ਕਰ ਸਕਦਾ ਹੈ ਪਰ ਉਸ ਨੂੰ ਵਿਰੋਧੀ ਕਪਤਾਨ ਤੋਂ ਆਗਿਆ ਲੈਣੀ ਹੋਵੇਗੀ ਕਿ ਕਿੰਨਵੇਂ ਨੰਬਰ ‘ਤੇ ਬੱਲੇਬਾਜ਼ੀ ਕਰੇ ।
ਬਾਊਲਡ (Bowled) – ਜੇਕਰ ਵਿਕਟ ਗੇਂਦ ਕਰ ਕੇ ਡੇਗ ਦਿੱਤੀ ਜਾਵੇ, ਤਾਂ ਗੇਂਦ ਖੇਡਣ ਵਾਲਾ ਬਾਊਲਡ (Bowled Out) ਅਖਵਾਉਂਦਾ ਹੈ, ਭਾਵੇਂ ਗੇਂਦ ਪਹਿਲੇ ਉਸ ਦੇ ਪੈਰ ਜਾਂ ਸਰੀਰ ਨੂੰ ਛੂਹ ਚੁੱਕੀ ਹੋਵੇ । | ਕੈਚ (Catch-ਜੇਕਰ ਗੇਂਦ ਬੈਟ ਦੇ ਨਾਲ ਜਾਂ ਬੈਟ ਵਾਲੇ ਹੱਥ ਨਾਲ ਕਲਾਈ ਨਾਲ ਨਹੀਂ ਲਗ ਕੇ ਧਰਤੀ ਨੂੰ ਛੂਹਣ ਤੋਂ ਪਹਿਲਾਂ ਕਿਸੇ ਫੀਲਡਰ ਦੁਆਰਾ ਬੋਚ ਲਈ (ਲਪਕ) ਲਈ ਜਾਵੇ ਤਾਂ ਬੈਟਸਮੈਨ ਕੈਚ ਆਊਟ ਹੋਵੇਗਾ | ਕੈਚ ਦੇ ਸਮੇਂ ਰੱਖਿਅਕ ਦੇ ਦੋਵੇਂ ਪੈਰ ਪੂਰੀ ਤਰ੍ਹਾਂ ਖੇਡ ਦੇ ਮੈਦਾਨ ਵਿਚ ਹੋਣ । ਜੇਕਰ ਖੇਤਰ-ਰੱਖਿਅਕ ਸੀਮਾ ਰੇਖਾ ਤੋਂ ਬਾਹਰ ਕੈਚ ਫੜਦਾ ਹੈ ਤਾਂ ਬੈਟਸਮੈਨ ਆਊਟ ਨਹੀਂ ਮੰਨਿਆ ਜਾਂਦਾ, ਸਗੋਂ ਉਸ ਨੂੰ 6 ਰਨ ਮਿਲਦੇ ਹਨ । ਜੇਕਰ ਗੇਂਦ ਵਿਕਟ ਕੀਪਰ ਦੇ ਪੈਰਾਂ ਵਿਚ ਜਾ ਵਸੇ ਤਾਂ ਵੀ ਬੈਟਸਮੈਨ ਆਉਟ ਮੰਨਿਆ ਜਾਵੇਗਾ ।
ਗੇਂਦ ਨੂੰ ਹੱਥ ਲਾਉਣਾ (Handle the Ball) – ਜੇਕਰ ਹੱਥਾਂ ਨਾਲ ਖੇਡਦੇ ਸਮੇਂ ਕੋਈ ਬੈਟਸਮੈਨ ਗੇਂਦ ਨੂੰ ਛੂਹ ਲੈਂਦਾ ਹੈ ਤਾਂ ਉਸ ਨੂੰ ਗੇਂਦ ਦੇ ਨਾਲ ਹੱਥ ਲਗਾਇਆ ਆਊਟ ਮੰਨਿਆ ਜਾਵੇਗਾ ।
ਗੇਂਦ ‘ਤੇ ‘ਦੋ ਵਾਰ’ (Hit the Ball twice) – ਬੈਟਸਮੈਨ ਗੇਂਦ ‘ਤੇ ਦੋ ਵਾਰ ਆਊਟ ਹੋਵੇਗਾ ਜੇਕਰ ਗੇਂਦ ਉਸ ਦੇ ਸਰੀਰ ਦੇ ਕਿਸੇ ਭਾਗ ਨੂੰ ਲਗ ਕੇ ਰੁਕ ਜਾਂਦੀ ਹੈ ਜਾਂ ਉਹ ਉਸ ਤੇ ਦੁਬਾਰਾ ਜਾਣ-ਬੁਝ ਕੇ ਵਾਰ ਕਰਦਾ ਹੈ । ਕੇਵਲ ਆਪਣੀ ਵਿਕਟ ਦੇ ਬਚਾਅ ਲਈ ਵੀ ਵਾਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਪਰੰਤੂ ਇਹ ਸ਼ਰਤ ਹੈ ਕਿ ਅਜਿਹਾ ਵਿਕਟ ਦੇ ਬਚਾਅ ਲਈ ਕੀਤਾ ਗਿਆ ਹੋਵ, ਇਸ ਪ੍ਰਕਾਰ ਜੇ ਕੋਈ ਰਨ ਬਣ ਵੀ ਜਾਵੇ ਤਾਂ ਉਹ ਗਿਣਿਆ ਨਹੀਂ ਜਾਂਦਾ ।
ਵਿਕਟ ‘ਤੇ ਵਾਰ (wicket is down or Hit wicket) – ਜੇਕਰ ਗੇਂਦ ਖੇਡਦੇ ਸਮੇਂ ਬੈਟਸਮੈਨ ਆਪਣੇ ਬੈਟ ਜਾਂ ਸਰੀਰ ਦੇ ਕਿਸੇ ਭਾਗ ਨਾਲ ਵਿਕਟਾਂ ਡੇਗਦਾ ਹੈ, ਤਾਂ ਉਸ ਨੂੰ ‘ਵਿਕਟ ਤੇ ਵਾਰ’ ਆਉਟ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਉਸ ਦੀ ਵਿਕਟ ਟੋਪੀ ਜਾਂ ਹੈਟ ਡਿੱਗਣ ਜਾਂ ਬੈਟ ਦੇ ਟੁੱਟੇ ਹੋਏ ਕਿਸੇ ਭਾਗ ਦੇ ਵੱਜਣ ਨਾਲ ਡਿੱਗ ਜਾਂਦੀ ਹੈ, ਤਾਂ ਉਸ ਨੂੰ ਵੀ ‘ਵਿਕਟ ਤੇ ਵਾਰ’ ਆਉਟ ਮੰਨਿਆ ਜਾਵੇਗਾ ।
ਐੱਲ. ਬੀ. ਡਬਲਿਉ. (ਲੈਗ ਬਿਛੋਰ ਵਿਕਟ) – ਬੈਟਸਮੈਨ ਉਸ ਸਮੇਂ ਐੱਲ. ਬੀ. ਡਬਲਿਉ. ਆਊਟ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ, ਜਦੋਂ ਉਹ ਗੇਂਦ ਨੂੰ ਬੱਲੇ ਨਾਲ ਛੂਹਣ ਤੋਂ ਪਹਿਲਾਂ ਸਰੀਰ ਦੇ ਕਿਸੇ ਭਾਗ ਨਾਲ ਰੋਕਣ ਦਾ ਯਤਨ ਕਰਦਾ ਹੈ ਅਤੇ ਅੰਪਾਇਰ ਅਨੁਸਾਰ ਗੇਂਦ ‘ਤੇ ਵਿਕਟ ਸਿੱਧੀ ਰੇਖਾ ਵਿਚ ਹੈ । ਜੇਕਰ ਬੈਟਸਮੈਨ ਇਸ ਨੂੰ ਆਪਣੇ ਸਰੀਰ ਦੇ ਕਿਸੇ ਭਾਗ ਨਾਲ ਨਾ ਰੋਕਦਾ ਤਾਂ ਗੇਂਦ ਵਿਕਟ ‘ਤੇ ਹੀ ਲਗਦੀ ।
ਖੇਤਰ ਵਿਚ ਰੋਕ – ਕੋਈ ਵੀ ਬੈਟਸਮੈਨ ਖੇਤਰ ਵਿਚ ਰੋਕ ਆਊਟ ਹੋ ਸਕਦਾ ਹੈ, ਜੇਕਰ ਉਹ ਜਾਣ-ਬੁਝ ਕੇ ਕਿਸੇ ਫੀਲਡਰ ਨੂੰ ਗੇਂਦ ਫੜਨ ਤੋਂ ਰੋਕਦਾ ਹੈ ।
ਸਟੰਪਡ (Stumped) – ਬੈਟਸਮੈਨ ਦੇ ਹੱਥ ਦਾ ਬੈਟ ਜਾਂ ਉਸ ਦਾ ਪੈਰ ਮੰਨੀ ਗਈ ਮੁੰਜ ਰੇਖਾ ਦੇ ਪਿੱਛੇ ਧਰਤੀ ‘ਤੇ ਨਾ ਹੋਵੇ, ਤਾਂ ਉਹ ਖੇਤਰ ਤੋਂ ਬਾਹਰ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਬੈਟਸਮੈਨ ਉਸ ਸਮੇਂ ਸਟੰਪਡ ਆਊਟ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ, ਜਦੋਂ ਗੇਂਦ ਨੋ ਬਾਲ ਨਾ ਹੋਵੇ ਅਤੇ ਬਾਊਲਰ ਦੁਆਰਾ ਟੁੱਟੀ ਗਈ ਹੋਵੇ ਅਤੇ ਉਹ ਦੌੜ ਬਣਾਉਣ ਦੀ ਕੋਸ਼ਿਸ਼ ਦੀ ਸਥਿਤੀ ਤੋਂ ਇਲਾਵਾ ਖੇਤਰ ਤੋਂ ਬਾਹਰ ਚਲਿਆ ਜਾਵੇ ਅਤੇ ਵਿਕਟ ਕੀਪਰ ਵਿਕਟ ਉਖਾੜ ਸੁੱਟੇ ਜਾਂ ਵਿਕਟਾਂ ਦੇ ਉੱਪਰ ਰੱਖੀਆਂ ਗੱਲੀਆਂ ਉਤਾਰ ਦੇਵੇ ।
ਰਨ ਆਊਟ (Run Out) – ਜਿਸ ਸਮੇਂ ਗੇਂਦ ਮੈਦਾਨ ਵਿਚ ਹੋਵੇ ਤਾਂ ਬੈਟਸਮੈਨ ਭੱਜਦੇ ਹੋਏ ਖੇਤਰ ਤੋਂ ਬਾਹਰ ਚਲਿਆ ਜਾਏ ਅਤੇ ਵਿਰੋਧੀ ਟੀਮ ਦਾ ਖਿਡਾਰੀ ਉਸ ਦੀ ਵਿਕਟ ਡੇਗ ਦੇਵੇ, ਤਾਂ ਬੈਟਸਮੈਨ ਰਨ ਆਉਟ ਹੋ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਬੈਟਸਮੈਨ ਇਕ ਦੂਜੇ ਨੂੰ ਪਾਰ ਕਰ ਜਾਣ, ਤਾਂ ਉਸ ਬੈਟਸਮੈਨ ਨੂੰ ਆਉਟ ਮੰਨਿਆ ਜਾਵੇਗਾ, ਜੋ ਡਿੱਗੀ ਹੋਈ ਵਿਕਟ ਵਲ ਦੌੜ ਰਿਹਾ ਹੋਵੇ ।
ਵਿਕਟ ਰੱਖਿਅਕ (wicket Keeper) – ਵਿਕਟ ਕੀਪਰ ਸਦਾ ਵਿਕਟਾਂ ਦੇ ਪਿੱਛੇ ਰਹੇਗਾ ਜਦੋਂ ਤਕ ਕਿ ਬਾਊਲਰ ਦੁਆਰਾ ਟੁੱਟੀ ਹੋਈ ਗੇਂਦ ਨੂੰ ਬੈਟਸਮੈਨ ਦੇ ਬੈਟ ਜਾਂ ਸਰੀਰ ਦੇ ਕਿਸੇ ਹਿੱਸੇ ਨਾਲ ਛੋਹ ਨਹੀਂ ਜਾਂਦੀ ਜਾਂ ਵਿਕਟ ਦੇ ਪਾਰ ਨਹੀਂ ਜਾਂਦੀ ਜਾਂ ਬੈਟਸਮੈਨ ਆਊਟ ਨਹੀਂ ਹੋ ਜਾਂਦਾ, ਵਿਕਟ ਰੱਖਿਅਕ ਗੇਂਦ ਨੂੰ ਨਹੀਂ ਪਕੜ ਸਕਦਾ ।
ਖੇਤਰ ਰੱਖਿਅਕ (Fielders) – ਖੇਤਰ ਰੱਖਿਅਕ ਆਪਣੇ ਸਰੀਰ ਦੇ ਕਿਸੇ ਵੀ ਹਿੱਸੇ ਨਾਲ ਗੇਂਦ ਨੂੰ ਰੋਕ ਸਕਦਾ ਹੈ । ਉਸ ਨੂੰ ਆਪਣੀ ਟੋਪੀ ਨਾਲ ਗੇਂਦ ਰੋਕਣ ਦੀ ਆਗਿਆ ਨਹੀਂ ।
ਜੇਕਰ ਉਹ ਇਸ ਤਰ੍ਹਾਂ ਕਰਦਾ ਹੈ, ਤਾਂ ਇਸ ਦੀ ਸਜ਼ਾ ਚਾਰ ਦੌੜਾਂ ਹੋਣਗੀਆਂ । ਜੇਕਰ ਉਸ ਦੀ ਕੋਈ ਦੌੜ ਨਾ ਬਣੀ ਹੋਵੇ, ਤਾਂ ਚਾਰ ਦੌੜਾਂ ਜੋੜ ਦਿੱਤੀਆਂ ਜਾਣਗੀਆਂ ।
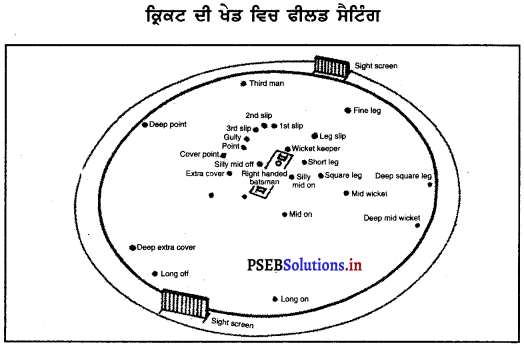
A.
- Wickets.
- Bowling crease
- Return crease
- Popping crease.
B. Position of Players-
- Slips
- 3rd man
- Gully
- Point
- Cover-point
- Extra-cover.
- Mid-off
- Bowler.
- Straight
- Mid-on
- Long-on
- Mid-wicket
- Square leg
- Fine leg
- Leg-slips
- Short leg
- Silly mid-off.
- Silly mid-on
- Silly point
- Backward point
- Wicket Keeper.
ਖੇਤਰ, ਮੌਸਮ ਅਤੇ ਰੌਸ਼ਨੀ – ਮੈਚ ਸ਼ੁਰੂ ਹੋਣ ਤੋਂ ਪਹਿਲਾਂ ਟੀਮਾਂ ਦੇ ਕਪਤਾਨ ਖੇਡ ਲਈ ਖੇਤਰ, ਮੌਸਮ ਅਤੇ ਰੌਸ਼ਨੀ ਦੇ ਉੱਚਿਤ ਹੋਣ ਨੂੰ ਨਿਸਚਿਤ ਕਰਨ ਲਈ ਚੋਣ ਕਰਨਗੇ । ਜੇਕਰ ਇਸ ਸੰਬੰਧੀ ਪਹਿਲਾਂ ਸਹਿਮਤੀ ਨਾ ਕੀਤੀ ਗਈ ਹੋਵੇ, ਤਾਂ ਉਸ ਦਾ ਫੈਸਲਾ ਅੰਪਾਇਰ ਕਰਨਗੇ ।
ਅਪੀਲ – ਅੰਪਾਇਰ ਕਿਸੇ ਬੈਟਸਮੈਨ ਨੂੰ ਆਉਟ ਨਹੀਂ ਦੇਵੇਗਾ ਜਦੋਂ ਤਕ ਕਿਸੇ ਫੀਲਡਰ ਦੁਆਰਾ ਅਪੀਲ ਨਹੀਂ ਕੀਤੀ ਗਈ ਹੋਵੇ । ਇਹ ਅਪੀਲ ਅਗਲੀ ਗੇਂਦ ਸੁੱਟਣ ਅਤੇ ਸਮਾਂ ਪੁਕਾਰਨ ਤੋਂ ਪਹਿਲਾਂ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਅਪੀਲ ਕਰਦੇ ਸਮੇਂ ਫੀਲਡਰ ਅੰਪਾਇਰ ਨੂੰ ਕਹਿੰਦੇ ਹਨ ਇਹ ਕਿਵੇਂ ਹੋਇਆ | ਅੰਪਾਇਰ ਆਉਟ ਦਾ ਨਿਰਣਾ ਅਪੀਲ ਨਿਰਦੇਸ਼ਕਾਂ ਉਂਗਲਾਂ ਉਠਾ ਕੇ ਦਿੰਦਾ ਹੈ ।
ਮੈਂਡਟੇਰੀ ਓਵਰ (Mandatory Over) – ਮੈਚ ਦੇ ਆਖ਼ਰੀ ਦਿਨ ਮੈਚ ਸਮਾਪਤ ਹੋਣ ਤੋਂ ਇਕ ਘੰਟਾ ਪਹਿਲਾਂ ਅੰਪਾਇਰ ਮੈਂਟੇਰੀ ਓਵਰ ਦਾ ਸੰਕੇਤ ਦਿੰਦਾ ਹੈ । ਉਸ ਤੋਂ ਬਾਅਦ 20 ਓਵਰਾਂ ਦੀ ਇਕ ਹੋਰ ਖੇਡ ਖੇਡੀ ਜਾਂਦੀ ਹੈ । ਹਰ ਇਕ ਓਵਰ ਵਿਚ 6 ਬਾਲ ਖੇਡੇ ਜਾਂਦੇ ਹਨ । ਜੇਕਰ ਮੈਚ ਬਰਾਬਰ ਹੁੰਦਾ ਪ੍ਰਤੀਤ ਹੋਵੇ, ਤਾਂ ਇਨ੍ਹਾਂ ਓਵਰਾਂ ਤੋਂ ਪਹਿਲਾਂ ਵੀ ਖੇਡ ਸਮਾਪਤ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ ।
ਡੈੱਡ ਬਾਲ (Dead Ball) – ਬਾਲ ਉਨ੍ਹਾਂ ਹਾਲਤਾਂ ਵਿਚ ਹੀ ਰੈੱਡ ਮੰਨੀ ਜਾਂਦੀ ਹੈ, ਜਦ ਕਿ ਉਹ ਠੀਕ ਤਰ੍ਹਾਂ ਬਾਊਲਰ ਜਾਂ ਵਿਕਟ ਕੀਪਰ ਦੇ ਕਾਬੂ ਹੋ ਜਾਏ ਜਾਂ ਸੀਮਾ ‘ਤੇ ਪਹੁੰਚ ਜਾਵੇ, ਅੰਪਾਇਰ ਜਾਂ ਬੈਟਸਮੈਨ ਦੇ ਕੱਪੜਿਆਂ ਵਿਚ ਉਲਝ ਜਾਵੇ ਜਾਂ ਅੰਪਾਇਰ ਦੁਆਰਾ ਸਮੇਂ ਜਾਂ ਓਵਰ ਦੀ ਘੋਸ਼ਣਾ ਕਰ ਦਿੱਤੀ ਜਾਵੇ ; ਇਨ੍ਹਾਂ ਤੋਂ ਇਲਾਵਾ ਜਦ ਖਿਡਾਰੀ ਆਊਟ ਹੋ ਜਾਂਦਾ ਹੈ ਜਾਂ ਉਸ ਨੂੰ ਗੰਭੀਰ ਸੱਟ ਲੱਗ ਜਾਂਦੀ ਹੈ ।
ਮੈਦਾਨ ਦੀ ਅੜਚਨ (Obstructing the Field) – ਜੇ ਕੋਈ ਬੱਲੇ-ਬਾਜ਼ ਜਾਣ-ਬੁੱਝ ਕੇ ਦੂਸਰੀ ਟੀਮ ਦੀ ਖੇਡ ਵਿਚ ਅੜਚਨ ਪਾਉਂਦਾ ਹੈ, ਜਿਸ ਕਾਰਨ ਵਿਰੋਧੀ ਟੀਮ ਨੂੰ ਬਾਲ ਫੜਨ ਵਿਚ ਰੁਕਾਵਟ ਆਉਂਦੀ ਹੈ ਤਾਂ ਰੋਕਣ ਵਾਲੇ ਬੈਟਸਮੈਨ ਨੂੰ ਆਊਟ ਮੰਨਿਆ ਜਾਂਦਾ ਹੈ । ਅਜਿਹਾ ਕਰਨ ਨੂੰ ਮੈਦਾਨ ਦੀ ਅੜਚਨ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ।
ਇਕ ਦਿਨ ਦਾ ਮੈਚ (One Day Match) – ਰਾਸ਼ਟਰੀ ਅਤੇ ਅੰਤਰ-ਰਾਸ਼ਟਰੀ ਇਕ ਦਿਨ ਦਾ ਟੈਸਟ ਮੈਚ ਹੁੰਦਾ ਹੈ । ਜਿਸ ਵਿਚ ਦੋਵੇਂ ਟੀਮਾਂ 40-40 ਜਾਂ 50-50 ਓਵਰ ਦੇ ਮੈਚ ਖੇਡਦੀਆਂ ਹਨ, ਜੋ ਟੀਮ ਵੱਧ ਰਨ ਬਣਾ ਜਾਵੇ, ਉਹ ਜਿੱਤ ਜਾਂਦੀ ਹੈ ।
ਖੇਤਰ ਰੱਖਿਅਕ ਦੀ ਵਿਉ ਰਚਨਾ – ਫੀਲਡ ਸੈਟਿੰਗ ਵਿਚ ਆਮ ਤੌਰ ‘ਤੇ ਮੈਦਾਨ ਵਿਚ ਖੇਤਰ ਰੱਖਿਅਕ ਪਿੱਛੇ ਦਿੱਤੇ ਚਿੱਤਰ ਅਨੁਸਾਰ ਥਾਂ ਹਿਣ ਕਰਦੇ ਹਨ ।
ਕ੍ਰਿਕਟ ਦੀ ਖੇਡ ਵਿਚ ਅੰਪਾਇਰ ਦੁਆਰਾ ਦਿੱਤੇ ਜਾਣ ਵਾਲੇ ਸੰਕੇਤ ।

ਪ੍ਰਸ਼ਨ 4.
ਕ੍ਰਿਕਟ ਦੀ ਖੇਡ ਦੀਆਂ ਕੁੱਝ ਮਹੱਤਵਪੂਰਨ ਤਕਨੀਕਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਕ੍ਰਿਕਟ ਦੀ ਖੇਡ ਦੀਆਂ ਕੁੱਝ ਮਹੱਤਵਪੂਰਨ ਤਕਨੀਕਾਂ
ਕ੍ਰਿਕਟ ਵਿਚ ਬੈਟਿੰਗ ਮੁਹਾਰਿਤ ਅਤੇ ਤਕਨੀਕਾਂ ਕਿਸੇ ਵੀ ਹਿਟ ਨੂੰ ਸਫਲਤਾ ਪੂਰਵਕ ਖੇਡਣ ਲਈ ਬੈਟਸਮੈਨਾਂ ਨੂੰ ਤਿੰਨ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ : ਉਸ ਨੂੰ ਜ਼ਰੂਰ ਹੀ ਪਹਿਲਾਂ ਬਾਲ ਨੂੰ ਲੱਭਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਫਿਰ ਬਾਲ ਵੱਲ ਧਿਆਨ ਰੱਖਣਾ । ਉਸ ਨੇ ਇਹ ਫੈਸਲਾ ਕਰਨਾ ਹੁੰਦਾ ਹੈ ਕਿ ਕਿਹੜੀ ਹਿੱਟ ਠੀਕ ਤਰ੍ਹਾਂ ਖੇਡਣ ਲਈ ਆਪਣੇ ਬਦਨ ਨੂੰ ਮੋੜਨਾ ਚਾਹੀਦਾ ਹੈ ।

ਕਹਿਣ ਨੂੰ ਤਾਂ ਕਾਫੀ ਆਸਾਨ ਹੈ, ਪਰ ਅਸਲ ਵਿਚ ਏਨਾ ਆਸਾਨ ਨਹੀਂ ਹੈ । ਇਹ ਗੱਲ ਸੋਚਣ ਲਈ ਤਾਂ ਆਸਾਨ ਹੈ ਕਿ ਤੁਸੀਂ ਬਾਲ ਵੱਲ ਵੇਖ ਰਹੇ ਹੋ । ਸੱਚਮੁੱਚ ਕਿਸੇ ਆ ਰਹੇ ਬਾਲ ਨੂੰ ਤੱਕਣਾ ਆਸਾਨ ਹੈ, ਬਸ਼ਰਤੇ ਕਿ ਤੁਸੀਂ ਆਪਣਾ ਮਨ ਬਣਾਇਆ ਹੋਇਆ ਹੋਵੇ । ਪਰ ਪੂਰੀ ਪਾਰੀ ਵਿਚ ਹਰੇਕ ਬਾਲ ਦੀ ਜਾਂਚ ਕਰਨ ਦੀ ਆਦਤ ਬਣਾਉਣੀ, ਸਹੀ ਅਰਥਾਂ ਵਿਚ ਜਾਂਚ ਕਰਨ ਦੀ, ਇਕ ਬੜਾ ਔਖਾ ਕੰਮ ਹੈ । ਤੁਸੀਂ ਅਜਿਹਾ ਸਿਰਫ ਆਪਣੇ ਹੱਥਾਂ ਵਿਚਲੇ ਕੰਮ ਉੱਤੇ ਧਿਆਨ ਕੇਂਦਰਿਤ ਕਰਨਾ ਸਿੱਖ ਕੇ ਹੀ ਕਰ ਸਕਦੇ ਹੋ । ਇਹ ਸੱਚਮੁੱਚ ਬੜਾ ਔਖਾ ਹੈ, ਪਰ ਜੇ ਤੁਸੀਂ ਇਸ ਤਰ੍ਹਾਂ ਕਰਨਾ ਸਿੱਖ ਲੈਂਦੇ ਹੋ, ਤਾਂ ਇਹ ਤੁਹਾਨੂੰ ਕ੍ਰਿਕਟ ਵਿਚ ਹੀ ਸਹਾਈ ਸਿੱਧ ਨਹੀਂ ਹੋਵੇਗਾ, ਸਗੋਂ ਜ਼ਿੰਦਗੀ ਵਿਚ ਵੀ ।
ਠੀਕ ਇਸ ਤਰ੍ਹਾਂ ਇਹ ਫੈਸਲਾ ਕਰਨਾ ਕਿ ਕਿਸੇ ਵਿਸ਼ੇਸ਼ ਬਾਲ ਨੂੰ ਕਿਸ ਤਰ੍ਹਾਂ ਹਿੱਟ ਕਰਨਾ ਹੈ, ਇਹ ਇਕ ਤਰ੍ਹਾਂ ਨਾਲ ਅੰਤਰ-ਪ੍ਰੇਰਨਾ ਦਾ ਮਾਮਲਾ ਹੈ, ਜਾਂ ਜਿਸ ਨੂੰ ਅਕਸਰ ਕ੍ਰਿਕਟ ਵਿਚ “ਬਾਲ ਸੁਝ’ ਕਿਹਾ ਜਾਂਦਾ ਹੈ । ਪਰ ਇਹ ਮੁੱਖ ਤੌਰ ‘ਤੇ ਤਜਰਬੇ ਦਾ ਕੰਮ ਹੈ ।
ਖਿਡਾਰੀ ਦੀ ਸਥਿਤੀ
ਇਕ ਖਿਡਾਰੀ ਦੀ ਆਰਾਮਦਾਇਕ, ਤਨਾਅ-ਰਹਿਤ ਅਤੇ ਸੰਤੁਲਿਤ ਸਥਿਤੀ ਬੜੀ ਜ਼ਰੂਰੀ ਹੈ, ਬਾਲ ਦੀ ਸਹੀ ਪਰਖ ਕਰਨੀ ਅਤੇ ਹਰੇਕ ਸਰੋਕ ਲਈ ਪੈਰਾਂ ਦੀ ਹਿਲ-ਜੁਲ ਇਸ ਉੱਤੇ
ਹੀ ਨਿਰਭਰ ਕਰਦੀ ਹੈ । ਪੈਰ ਸਾਧਾਰਨ ਤੌਰ ‘ਤੇ ਕਰੀਜ਼ ਦੇ ਪਾਸਿਆਂ ਵੱਲ ਸਮਾਨਾਂਤਰ ਹੋਣੇ | ਚਾਹੀਦੇ ਹਨ ਅਤੇ ਉਨ੍ਹਾਂ ਦੇ ਪੰਜੇ ਨਿਸ਼ਾਨੇ ਵੱਲ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।

ਬੈਕ ਲਿਫਟ
ਇਕ ਸਹੀ ‘ਬੈਕ ਲਿਫਟ ਦੀ ਬਹੁਤ ਮਹੱਤਤਾ ਹੈ । ਖੱਬੀ ਬਾਂਹ ਅਤੇ ਗੁੱਟ ਨੂੰ ਹੀ ਸਾਰਾ ਕੰਮ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਬੈਟ ਦਾ ਸਾਹਮਣਾ ਪਾਸਾ ਨਿਸ਼ਾਨੇ ਵੱਲ, ਜਿਵੇਂ ਕਿ ਬੈਟ ਉਭਰਦਾ ਹੈ ।
ਸਿਰ ਅਤੇ ਬਦਨ ਬਿਲਕੁਲ ਸਥਿਰ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ | ਉਭਾਰ ਦੇ ਅਖੀਰ ‘ਤੇ ਸੱਜੀ ਕੁਹਣੀ ਬਦਨ ਤੋਂ ਥੋੜ੍ਹੀ ਜਿਹੀ ਹਟੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਖੱਬਾ ਹੱਥ ਪੈਂਟ ਦੀ ਸੱਜੀ ਜੇਬ ਦੇ ਬਿਲਕੁਲ ਸਾਹਮਣੇ ਉੱਪਰ ਵੱਲ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
ਬੈਟ ਹੇਠਾਂ ਵੱਲ ਇੱਛਤ ਹਿੱਟ ਦੀ ਰੇਖਾ ‘ਤੇ ਘੁੰਮਣਾ ਚਾਹੀਦਾ ਹੈ । ਹਮਲੇ ਸਮੇਂ ਬੈਕ ਲਿਫ਼ਟ ਕੁਦਰਤੀ ਹੈ ਕਿ ਵਧੇਰੇ ਪੱਕੀ ਹੋਵੇਗੀ ।
ਸਿੱਧੇ ਬਾਲ ਲਈ ਸਾਹਮਣੀ ਸੁਰੱਖਿਆ ਹਿੱਟ
ਸਾਹਮਣੀ ਹਿੱਟ ਸੁਰੱਖਿਆ ਵਿਚ ਨਾ ਸਿਰਫ ਬਹੁ-ਕੀਮਤੀ ਹੈ, ਸਗੋਂ ਸਾਰੀਆਂ ਹਿੱਟਾਂ ਦਾ ਆਧਾਰ ਵੀ ਹੈ, ਇਸ ਨੂੰ ਠੀਕ ਢੰਗ ਨਾਲ ਖੇਡਣਾ ਲਗਪਗ ਅੱਧਾ ਬੈਟਸਮੈਨ ਬਣਨ ਦੇ ਤੁਲ ਹੈ । ਉਦੇਸ਼ ਬਾਲ ਨੂੰ ਜਿੰਨਾ ਪੁਆਇੰਟ ਦੇ ਨੇੜੇ ਤੋਂ ਨੇੜੇ ਸੰਭਵ ਹੋ ਸਕੇ ਖੇਡਣਾ ਹੈ ।

ਸਿਰ ਅੱਗੇ ਵੱਲ ਵਧਾਉਂਦਿਆਂ, ਖੱਬਾ ਕੂਲ੍ਹਾ ਤੇ ਮੋਢਾ ਬਾਲ ਦੀ ਰੇਖਾ ਤੋਂ ਬਾਹਰ ਰੱਖ ਕੇ ਬਾਲ ਨੂੰ ਬੈਟ ਤੇ ਖੱਬੇ ਪੈਰ ਦੇ ਕੁੱਝ ਇੰਚ ਸਾਹਮਣੇ ਲੈਣਾ ਹੁੰਦਾ ਹੈ ਅਤੇ ਪੈਰ ਮਿਡ-ਆਫ ਅਤੇ ਐਕਸਟਰਾ ਕਵਰ ਦੇ ਵਿਚਕਾਰ ਦੀ ਸੇਧ ਵਿਚ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਬਦਨ ਦਾ ਭਾਰ ਮੁੜੇ ਹੋਏ ਖੱਬੇ ਗੋਡੇ ਨਾਲ ਬਿਲਕੁਲ ਸਾਹਮਣੇ ਵੱਲ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
ਬਾਲ ਦੀ ਸਾਰਾ ਰਸਤਾ ਪਰਖ ਕਰੋ । ਇਸ ਤਰ੍ਹਾਂ ਕਰਨ ਲਈ ਤੁਹਾਨੂੰ ਆਪਣਾ ਸਿਰ ਜਿੱਥੇ ਤਕ ਹੋ ਸਕੇ ਸੰਤੁਲਨ ਵਿਚ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ । ਸਿਰ ਉੱਪਰ ਚੁੱਕਣ ਲਈ ਲਾਲਚ ਨੂੰ ਘੱਟ ਕਰੋ ।
ਹਿੱਟਾਂ ਵਿਚ ਕੰਟਰੋਲ ਲਾਜ਼ਮੀ ਹੈ-ਜੇ ਤੁਸੀਂ ਮਜ਼ਬੂਤ ਹਿੱਟ ਮਾਰਨੀ ਚਾਹੁੰਦੇ ਹੋ, ਤਾਂ ਤੁਹਾਡੀ ਹਿੱਟ ਘੁੰਮਣ ਦੀ ਬਜਾਏ ਵਧੇਰੇ ਲੰਬੀ ਹੋ ਸਕਦੀ ਹੈ ।
ਬਾਲ ਨੂੰ ਸਾਫ-ਸਾਫ ਤੇ ਸੌਖੀ ਤਰ੍ਹਾਂ ਹਿੱਟ ਕਰਨ ਲਈ, ਉਸ ਨੂੰ ਸੀਮਾ (ਬਾਊਂਡਰੀ) ਵੱਲ ਸੁੱਟਣ ਨਾਲੋਂ ਮੈਦਾਨ ਵਿਚ ਸੁੱਟਣਾ ਚਾਹੀਦਾ ਹੈ ।
ਜੇ ਬਾਲ ਕਾਫੀ ਦੂਰ ਉੱਪਰ ਹੈ ਤਾਂ ਹਿੱਟ ਇਕੋ ਲੰਬੇ ਕਦਮ ਨਾਲ ਮਾਰੀ ਜਾ ਸਕਦੀ ਹੈ, ਪਰ ਤੁਹਾਨੂੰ ਪਿੱਚ ਉੱਤੇ ਘੱਟ ਰਫਤਾਰ, ਤੇਜ਼ ਅਤੇ ਅਧੂਰੇ (Shorter) ਬਾਲ ਨੂੰ ਖੇਡਣ ਲਈ ਪੈਰ ਦੀ ਵਰਤੋਂ ਕਰਨੀ ਵੀ ਸਿੱਖਣੀ ਜ਼ਰੂਰੀ ਹੈ ।

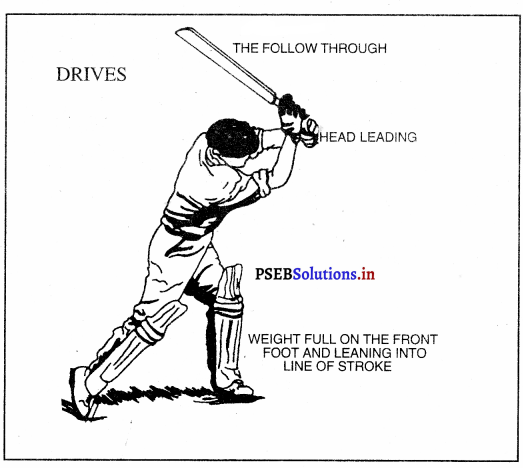
ਆਫ ਭਾਈਵ
ਆਫ ਡਾਈਵਿੰਗ ਵਿਚ ਸਭ ਤੋਂ ਜ਼ਰੂਰੀ ਗੱਲ ਇਹ ਹੈ ਕਿ ਤੁਹਾਡਾ ਸਿਰ, ਖੱਬਾ ਮੋਢਾ ਅਤੇ | ਕਮਰ ਬਾਲ ਦੀ ਰੇਖਾ ਉੱਤੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ । ਜੇ ਇਹ ਠੀਕ ਦਿਸ਼ਾ ਵਿਚ ਹੋਣਗੇ ਤਾਂ ਖੱਬਾ ਪੈਰ ਆਪਣੇ ਆਪ ਹੀ ਠੀਕ ਦਿਸ਼ਾ ਵਿਚ ਕੰਮ ਕਰੇਗਾ | ਪਹੁੰਚ ਤੋਂ ਬਾਹਰ ਬਾਲ ਅਤੇ ਸਧਾਰਨ ਬਾਲ ਨੂੰ ਪ੍ਰਾਪਤ ਕਰਨ ਲਈ ਖੱਬੇ ਮੋਢੇ ਦੀ ਪਿੱਠ ਗੇਂਦ ਕਰਨ ਵਾਲੇ ਵੱਲ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ | ਅਤੇ ਆਫ-ਸਾਈਡ ਵੱਲ ਹਿੱਟ ਦਾ ਨਿਸ਼ਾਨਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਬੈਟ ਅਸਲ ਵਿਚ ਆਪਣੀ ਹੇਠਾਂ ਵੱਲ ਚਾਲ ਫਾਈਨ ਲੈਗ ਦੀ ਰੇਖਾ ਤੋਂ ਸ਼ੁਰੂ ਕਰੇਗਾ । ਜਿੱਥੋਂ ਤੱਕ ਸੰਭਵ ਹੋ ਸਕੇ ਬੈਟ ਦਾ ਪੂਰਾ ਹਿੱਸਾ ਹਿੱਟ ਦੀ ਰੇਖਾ ਰਾਹੀਂ ਘੁੰਮਣਾ ਚਾਹੀਦਾ ਹੈ ।
ਆਨ ਝਾਈਵ
ਲੜਕਿਆਂ ਵਿਚ ਆਨ ਡਾਈਵ ਦੀ ਯੋਗਤਾ ਬੜੀ ਘੱਟ ਹੈ, ਪਰ ਜੇ ਉਹ ਉਸ ਨੂੰ ਹਾਸਿਲ ਕਰ ਲੈਣ ਤਾਂ ਆਪਣੇ ਰਨ ਬਨਾਉਣ ਦੀ ਤਾਕਤ ਨੂੰ ਵਧਾ ਸਕਦੇ ਹਨ ।
ਇਸ ਵਿਚ ਪਹਿਲੀ ਹਰਕਤ ਖੱਬੇ ਮੋਢੇ ਨੂੰ ਹਲਕਾ ਜਿਹਾ ਨੀਵਾਂ ਰੱਖਣਾ, ਇਸ ਤਰ੍ਹਾਂ ਖੱਬੇ ਪੈਰ ਅਤੇ ਸੰਤੁਲਨ ਦੀ ਰੇਖਾ ਨੂੰ ਸਹੀ ਰੱਖਣ, ਸਿਰ ਨੂੰ ਅੱਗੇ ਵੱਲ ਕਰਦਿਆਂ ਬਾਲ ਦੀ ਰੇਖਾ ਉੱਤੇ ਆਉਣ ਵਿਚ ਮਦਦ ਮਿਲੇਗੀ । ਖੱਬਾ ਪੈਰ ਰੇਖਾ ਤੋਂ ਥੋੜ੍ਹਾ ਜਿਹਾ ਲਾਂਭੇ ਹੋਵੇਗਾ ।
ਬੈਟਸਮੈਨ ਨੂੰ ਹਿੱਟ ਦਾ ਨਿਸ਼ਾਨਾ ਲੈਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਅਖੀਰ ਬੈਟ ਦਾ ਪੂਰਾ ਚੌੜਾ ਪਾਸਾ ਰੇਖਾ ਵੱਲ ਹੇਠਾਂ ਘੁੰਮਣਾ ਚਾਹੀਦਾ ਹੈ । ਬੈਟਸਮੈਨ ਨੂੰ ਆਪਣੀ ਆਨ ਡਾਈਵਜ਼ ਵਿੱਚ ਸੱਜੇ ਹੱਥ ਅਤੇ ਸੱਜੇ ਮੋਢੇ ਤੋਂ ਜ਼ਿਆਦਾ ਕੰਮ ਲੈਣ ਦੀ ਰੁਚੀ ਨੂੰ ਮਜ਼ਬੂਤੀ ਨਾਲ ਘਟਾਉਣਾ ਹੋਵੇਗਾ । ਉਸ ਨੂੰ ਆਪਣੇ ਖੱਬੇ ਕੂਲ਼ੇ ਨੂੰ ਵੀ ਦੂਰ ਹੋਣ ਦੀ ਇਜਾਜ਼ਤ ਨਹੀਂ ਦੇਣੀ ਚਾਹੀਦੀ ।

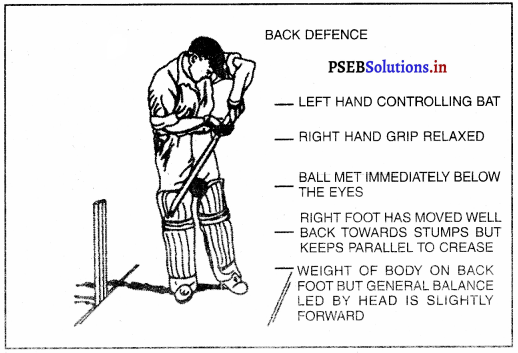
ਜਦੋਂ ਤੱਕ ਇਕ ਬੈਟਸਮੈਨ ਬਾਲ ਦੀ ਪਿੱਚ ਦੀ ਚੰਗੀ ਤਰ੍ਹਾਂ ਪਰਖ ਨਹੀਂ ਕਰ ਲੈਂਦਾ ਉਦੋਂ ਤਕ ਉਸ ਨੂੰ ਬੈਕ ਸਟਰੋਕ ਨਾਲ ਹੀ ਖੇਡਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਇਸ ਤਰ੍ਹਾਂ ਉਸ ਨੂੰ ਬਾਲ ਦੀ ਪਿੱਚ ਤੋਂ ਬਾਅਦ ਜਾਂਚ ਕਰਨ ਦਾ ਸਮਾਂ ਵੀ ਮਿਲੇਗਾ । ਹੌਲੀ ਬਾਲ ਅਤੇ ਵਧੇਰੇ ਮੁਸ਼ਕਿਲ ਵਿਕਟ ਵਿਚ ਉਸ ਨੂੰ ਜ਼ਰੂਰ ਹੀ ਬੈਕ ਸਟਰੋਕ ਉੱਤੇ ਨਿਰਭਰ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।
ਸੱਜਾ ਪੈਰ ਕਰੀਜ਼ ਵੱਲ ਪੰਜਾ ਸਮਾਨਾਂਤਰ ਰਹਿੰਦਿਆਂ ਬਾਲ ਦੀ ਰੇਖਾ ਦੇ ਅੰਦਰ ਅਤੇ ਪਿੱਛੇ ਵੱਲ ਚੰਗੀ ਤਰ੍ਹਾਂ ਹਿਲ-ਜੁਲ ਕਰ ਸਕਦਾ ਹੈ | ਬਦਨ ਦਾ ਭਾਰ ਇਸ ਪੈਰ ਉੱਤੇ ਬਦਲੀ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ, ਪਰ ਸਿਰ ਅੱਗੇ ਵੱਲ ਥੋੜਾ ਝੁਕਿਆ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ । ਖੱਬਾ ਪੈਰ ਪੰਜੇ ਭਰਨੇ ਹੁੰਦਿਆਂ ਹੋਇਆਂ ਇਕ ਸੰਤੁਲਨਕਾਰ ਵਜੋਂ ਕੰਮ ਕਰਦਾ ਹੈ ।


ਬਾਲ ਨਜ਼ਰਾਂ ਤੋਂ ਥੋੜ੍ਹਾ ਜਿਹਾ ਹੇਠਾਂ ਮਿਲਣਾ ਚਾਹੀਦਾ ਹੈ, ਜਿਹੜਾ ਕਿ ਜਿੰਨਾ ਸੰਭਵ ਪੱਧਰ ਹੋ ਸਕੇ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ, ਕਿਉਂਕਿ ਉਹ ਬਾਲ ਨੂੰ ਹੇਠਾਂ ਪਿੱਚ ਵੱਲ ਤੱਕਦੀਆਂ ਹਨ । ਹਿੱਟ ਉੱਤੇ ਕੰਟਰੋਲ ਖੱਬੇ ਹੱਥ ਤੇ ਬਾਂਹ ਵਲੋਂ ਕੂਹਣੀ ਉੱਪਰ ਚੁੱਕ ਕੇ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਸੱਜਾ ਹੱਥ ਅੰਗੂਠੇ ਤੇ ਉਂਗਲਾਂ ਦੀ ਪਕੜ ਵਿਚ ਅਰਾਮਦਾਇਕ ਹੁੰਦਾ ਹੈ । ਬਦਨ ਨੂੰ ਜਿੰਨਾ ਸੰਭਵ ਹੋ ਸਕੇ ਪਾਸਿਆਂ ਵੱਲ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ।
ਇਕ ਲੜਕਾ ਜਦ ਤੱਕ ਸਿੱਧੀ ਹਿੱਟ ਮਾਰਨੀ ਨਹੀਂ ਸਿੱਖਦਾ, ਤਦ ਤੱਕ ਬੈਟਸਮੈਨ ਨਹੀਂ ਬਣਦਾ, ਪਰ ਉਸ ਨੂੰ ਮਾੜੇ ਭਾਵ ਗਲਤ ਬਾਲ ਨਾਲ ਖੇਡਣ ਦੀ ਜਾਂਚ ਵੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ। ਅਤੇ ਉਹ ਗੱਲ ਕਰਾਸ-ਬੈਟ ਹਿੱਟਾਂ ਰਾਹੀਂ ਅਕਸਰ ਵਧੇਰੇ ਅਸਰਦਾਰ ਹੋ ਸਕਦੀ ਹੈ । ਇਹ ਗੱਲ ਵਿਸ਼ੇਸ਼ ਕਰਕੇ ਲੰਬੇ ਟੱਪਿਆਂ ਅਤੇ ਪੂਰਨ ਉਛਾਲ ਵਿਚ ਸੱਚੀ ਲੱਗਦੀ ਹੈ ਅਤੇ ਖ਼ਾਸ ਕਰਕੇ ਜੂਨੀਅਰ ਕ੍ਰਿਕਟ ਵਿਚ ਚੌਕੇ ਮਾਰਨ ਦੇ ਉੱਤਮ ਮੌਕੇ ਪ੍ਰਦਾਨ ਕਰਦੀ ਹੈ ।
ਇਹ ਹਿੱਟਾਂ ਵਧੇਰੇ ਆਸਾਨ ਹੁੰਦੀਆਂ ਹਨ, ਕਿਉਂਕਿ ਇਹ ਸਿੱਧੀਆਂ ਬੈਟ ਹਿੱਟਾਂ ਨਾਲੋਂ | ਵਧੇਰੇ ਕੁਦਰਤੀ ਹੁੰਦੀਆਂ ਹਨ, ਪਰ ਇਨ੍ਹਾਂ ਨੂੰ ਦ੍ਰਿੜ੍ਹਤਾ ਨਾਲ ਖੇਡਣ ਵਾਸਤੇ ਤੁਹਾਨੂੰ ਦਰੁਸਤੀ | ਨਾਲ ਖੇਡਣ ਦੀ ਜਾਂਚ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ।
ਪਿਛਲੇ ਪੈਰ ਦਾ ਸੁਕਏਅਰ ਕੱਟ
ਬਾਲ ਰੇਖਾ ਅਤੇ ਪੁਆਇੰਟ ਉੱਤੇ ਸਾਹਮਣੇ ਤੋਂ ਜਾਂ ਪਿੱਛੇ ਮਿਲਦੇ ਬਾਲ ਨਾਲ ਨਿਪਟਣ | ਲਈ ਸੱਜਾ ਪੈਰ ਕੂਲ੍ਹੇ ਦੀ ਰੇਖਾ ਦੇ ਆਰ-ਪਾਰ ਘੁੰਮਦਾ ਹੈ । ਫਿਰ ਗੁੱਟ ਅਤੇ ਹੱਥਾਂ ਨੂੰ ਇਕ | ਉੱਚੇ ਬੈਟ-ਲਿਫਟ ਤੋਂ ਹੇਠਾਂ ਮੋੜਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਸਿਰ ਤੇ ਬਦਨ, ਝੁਕੇ ਹੋਏ ਸੱਜੇ ਗੋਡੇ ਤੇ ਸਟਰੋਕ ਦੀ ਰੇਖਾ ਵਿਚ ਘੁੰਮਦਾ ਹੈ ।

ਲੇਟ ਕੱਟ:
ਇਹ ਹਿੱਟ ਵੀ ਉੱਪਰ ਵਾਲੀ ਹਿੱਟ ਵਰਗੀ ਹੀ ਹੈ, ਸਿਵਾਏ ਇਸ ਦੇ ਕਿ ਇਹ ਖੱਬੇ ਮੋਢੇ ਦੇ ਵਧੇਰੇ ਮੋੜ ਨਾਲ ਸ਼ੁਰੂ ਹੁੰਦੀ ਹੈ ਅਤੇ ਸੱਜਾ ਪੈਰ ਥਰਡ ਸਲਿਪ ਵੱਲ ਪੰਜੇ ਦੇ ਰੁਖ ਨਾਲ | ਧਰਤੀ ਉੱਤੇ ਹੁੰਦਾ ਹੈ । ਬਾਲ ਵਿਕਟਾਂ ਦੀ ਸਤਹਿ ਦੇ ਬਰਾਬਰ ਮਿਲਦਾ ਹੈ ਅਤੇ ਗੁੱਟ ਅੱਗੇ ਵਧਾਉਂਦਿਆਂ ਬੈਟਸਮੈਨ ਇਸ ਨੂੰ ਗਲੀ ਜਾਂ ਸੈਕਿੰਡ ਸਲਿਪ ਦੀ ਦਿਸ਼ਾ ਵਿਚ ਹਿੱਟ ਕਰਦਾ
ਹੈ ।
ਇਨ੍ਹਾਂ ਦੋਹਾਂ ਕੱਟਾਂ ਵਿਚ ਖੱਬਾ ਪੈਰ ਪੰਜੇ ਉੱਤੇ ਆਰਾਮ ਦੀ ਹਾਲਤ ਵਿਚ ਰਹਿੰਦਾ ਹੈ ਅਤੇ | ਭਾਰ ਲੁਕੇ ਹੋਏ ਸੱਜੇ ਗੋਡੇ ਉੱਤੇ ਪੂਰੀ ਤਰ੍ਹਾਂ ਰਹਿੰਦਾ ਹੈ ।
![]()
![]()