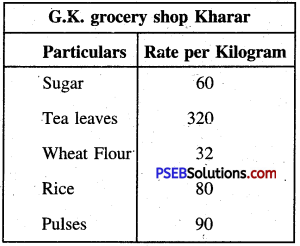
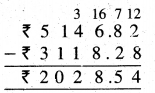
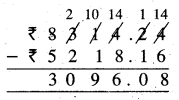
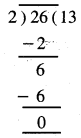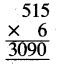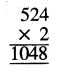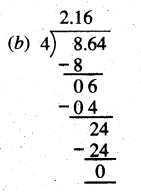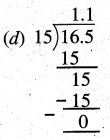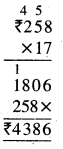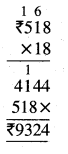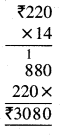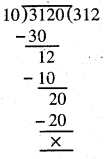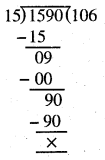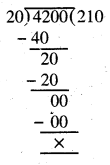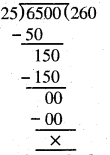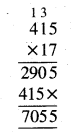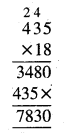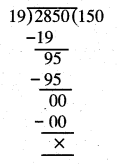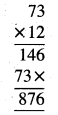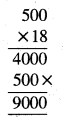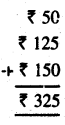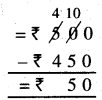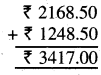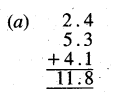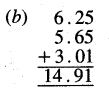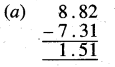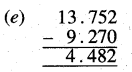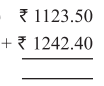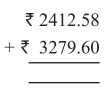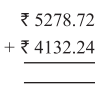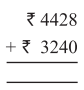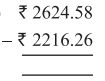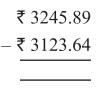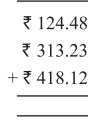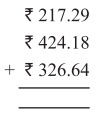Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 4 Fractions Ex 4.6 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 5 Maths Chapter 4 Fractions Ex 4.6
Question 1.
Find the greater fraction for each pair of the following :
(a) \(\frac{2}{5}\), \(\frac{2}{3}\)
(b) \(\frac{7}{9}\), \(\frac{7}{12}\)
(c) \(\frac{1}{8}\), \(\frac{1}{4}\)
(d) \(\frac{4}{6}\), \(\frac{4}{8}\)
(e) \(\frac{3}{7}\), \(\frac{3}{11}\)
(f) \(\frac{7}{9}\), \(\frac{4}{9}\)
(g) \(\frac{3}{4}\), \(\frac{1}{4}\)
(h) \(\frac{5}{8}\), \(\frac{7}{8}\)
Solution:
(a) \(\frac{2}{5}\), \(\frac{2}{3}\)
The numerator of both the fractions are equal. So, the fraction whose denominator is smaller will be greater.
Hence, \(\frac{2}{3}\) is greater than \(\frac{2}{5}\).
(b) \(\frac{7}{9}\), \(\frac{7}{12}\)
The numerator of both the fractions are equal. So, the fraction whose denominator is smaller will be greater.
Hence, \(\frac{7}{9}\) is greater than \(\frac{7}{12}\).
(c) \(\frac{1}{8}\), \(\frac{1}{4}\)
The numerator of both the fractions are equal. So, the fraction whose denominator is smaller will be greater.
Hence, \(\frac{1}{4}\) is greater than \(\frac{1}{8}\)
(d) \(\frac{4}{6}\), \(\frac{4}{8}\)
The numerator of both the fractions are equal. So, the fraction whose denominator is smaller will be greater.
Hence, \(\frac{4}{6}\) is greater than \(\frac{4}{8}\)
(e) \(\frac{3}{7}\), \(\frac{3}{11}\)
The numerator of both the fractions are equal. So, the fraction whose denominator is smaller will be greater.
Hence, \(\frac{3}{7}\) is greater than \(\frac{3}{11}\).
(f) \(\frac{7}{9}\), \(\frac{4}{9}\)
The denominator of both the fractions are equal. So, the fraction whose numerator is greater will be greater.
Hence, \(\frac{7}{9}\) is greater than \(\frac{4}{9}\)
(g) \(\frac{3}{4}\), \(\frac{1}{4}\)
The denominator of both the fractions are equal. So, the fraction whose numerator is greater will be greater.
Hence, \(\frac{3}{4}\) is greater than \(\frac{1}{4}\).
(h) \(\frac{5}{8}\), \(\frac{7}{8}\)
The denominator of both the fractions are equal. So, the fraction whose numerator is greater will be greater.
Hence, \(\frac{7}{8}\) is greater than \(\frac{5}{8}\)

Question 2.
Find the smaller fraction for each part of the following :
(a) \(\frac{3}{5}\), \(\frac{3}{4}\)
(b) \(\frac{5}{8}\), \(\frac{5}{12}\)
(c) \(\frac{7}{9}\), \(\frac{4}{9}\)
(d) \(\frac{3}{6}\), \(\frac{3}{8}\)
(e) \(\frac{5}{7}\), \(\frac{5}{11}\)
(f) \(\frac{8}{12}\), \(\frac{5}{12}\)
(g) \(\frac{9}{4}\), \(\frac{7}{4}\)
(h) \(\frac{9}{8}\), \(\frac{7}{8}\)
Solution:
(a) \(\frac{3}{5}\), \(\frac{3}{4}\)
The numerator of both the fractions are equal. So, the fraction whose denominator is greater will be smaller.
Hence, \(\frac{3}{5}\) is Smaller than \(\frac{3}{4}\)
(b) \(\frac{5}{8}\), \(\frac{5}{12}\)
The numerator of both the fractions are equal. So, the fraction whose denominator is greater will be smaller.
Hence, \(\frac{5}{12}\) is Smaller than \(\frac{5}{8}\)
(c) \(\frac{7}{9}\), \(\frac{4}{9}\)
The denominator of both the fractions are equal. So, the fraction whose numerator is greater will be smaller.
Hence, \(\frac{3}{5}\) is Smaller than \(\frac{3}{4}\)
(d) \(\frac{3}{6}\), \(\frac{3}{8}\)
The numerator of both the fractions are equal. So, the fraction whose denominator is greater will be smaller.
Hence, \(\frac{3}{8}\) is Smaller than \(\frac{3}{6}\)
(e) \(\frac{5}{7}\), \(\frac{5}{11}\)
The numerator of both the fractions are equal. So, the fraction whose denominator is greater will be smaller.
Hence, \(\frac{5}{11}\) is Smaller than \(\frac{5}{7}\)
(f) \(\frac{8}{12}\), \(\frac{5}{12}\)
The denominator of both the fractions are equal. So, the fraction whose numerator is greater will be smaller.
Hence, \(\frac{5}{12}\) is Smaller than \(\frac{8}{12}\)
(g) \(\frac{9}{4}\), \(\frac{7}{4}\)
The denominator of both the fractions are equal. So, the fraction whose numerator is greater will be smaller.
Hence, \(\frac{7}{4}\) is Smaller than \(\frac{9}{4}\)
(h) \(\frac{9}{8}\), \(\frac{7}{8}\)
The denominator of both the fractions are equal. So, the fraction whose numerator is greater will be smaller.
Hence, \(\frac{7}{8}\) is Smaller than \(\frac{9}{8}\)
Question 3.
Write the following in increasing (ascending) order :
(a) \(\frac{7}{12}\), \(\frac{4}{12}\), \(\frac{1}{12}\), \(\frac{5}{12}\)
(b) \(\frac{5}{12}\), \(\frac{5}{9}\), \(\frac{5}{7}\), \(\frac{5}{4}\)
(c) \(\frac{6}{11}\), \(\frac{4}{11}\), \(\frac{9}{11}\), \(\frac{3}{11}\)
(d) \(\frac{7}{8}\), \(\frac{7}{12}\), \(\frac{7}{4}\), \(\frac{7}{2}\)
(e) \(\frac{12}{15}\), \(\frac{12}{13}\), \(\frac{12}{17}\), \(\frac{12}{10}\)
Solution:
(a) \(\frac{7}{12}\), \(\frac{4}{12}\), \(\frac{1}{12}\), \(\frac{5}{12}\)
The denominators of all of these fractions are equal. Therefore, the fraction which has the lowest numerator, will be the smallest.
Among these fractions, \(\frac{1}{12}\) is the smallest.
Ascending order is \(\frac{1}{12}\), \(\frac{4}{12}\), \(\frac{5}{12}\) and \(\frac{7}{12}\).
(b) \(\frac{5}{12}\), \(\frac{5}{9}\), \(\frac{5}{7}\), \(\frac{5}{4}\)
The numerator of all of these fractions are equal. Therefore, the fraction whose denominator is the largest, is the smallest fraction.
Among these fractions, \(\frac{5}{12}\) is the smallest.
Ascending order is \(\frac{5}{12}\), \(\frac{5}{9}\), \(\frac{5}{7}\) and \(\frac{5}{4}\)

(c) \(\frac{6}{11}\), \(\frac{4}{11}\), \(\frac{9}{11}\), \(\frac{3}{11}\)
The denominators of all of these fractions are equal. Therefore, the fraction which has the lowest numerator, will be the smallest fraction.
Among these fractions, \(\frac{3}{11}\) is the smallest.
Ascending order is \(\frac{3}{11}\), \(\frac{4}{11}\), \(\frac{6}{11}\) and \(\frac{9}{11}\).
(d) \(\frac{7}{8}\), \(\frac{7}{12}\), \(\frac{7}{4}\), \(\frac{7}{2}\)
The numerator of all of these fractions are equal. Therefore, the fraction whose denominator is the largest, is the smallest fraction.
Among these fractions, \(\frac{7}{12}\) is the smallest.
Ascending order is \(\frac{7}{12}\), \(\frac{7}{8}\), \(\frac{7}{4}\) and \(\frac{7}{2}\)
(e) \(\frac{12}{15}\), \(\frac{12}{13}\), \(\frac{12}{17}\), \(\frac{12}{10}\)
The numerator of all of these fractions are equal. Therefore, the fraction whose denominator is the largest, is the smallest fraction.
Among these fractions, \(\frac{12}{17}\) is the smallest.
Ascending order is \(\frac{12}{17}\), \(\frac{12}{15}\), \(\frac{12}{13}\) and \(\frac{12}{10}\)
![]()
![]()
![]()
![]()
![]()