Punjab State Board PSEB 9th Class Science Important Questions Chapter 11 Work and Energy Important Questions and Answers.
PSEB 9th Class Science Important Questions Chapter 11 Work and Energy
Long Answer Type Questions:
Question 1.
What is potential energy? Deduce an expression for the gravitational potential energy of a body of mass’m’ placed at height ‘h’ above the ground. Give some practical examples.
Answer:
Potential Energy: It is the energy possessed by an object when it is raised above or below the surface of earth.
Mathematical Expression: Consider a body of mass ‘m’ raised to a height ‘h’ above the surface of earth to a position ‘B’. In order to lift the body to this height we have to apply minimum force equal to mg, the weight of the body in the upward direction from position ‘A’.
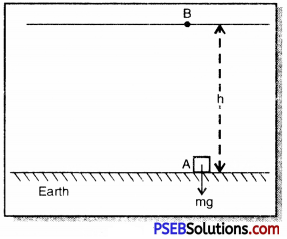
∴ Work done on the body against the force of gravity (W) = Force × Displacement
W = F × S
But F = mg and S = h
W = mg × h
= mgh
The work done (W = mgh) on the body is against the force of gravity
∴ Ep = W = mgh
Since this work done is against the force of gravity, so this energy is called gravitational potential energy. This potential energy does not depend on the path along which the body is moved.
Practical Examples:
1. In olden days there were no digital watches and the watches used to be wound up. When its spring is open then the watch does not work. When its spring is wound up then it starts working.
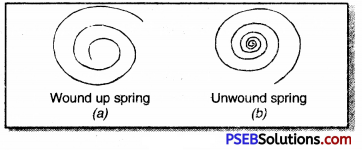
As is shown in Fig. on winding the spring closes and potential energy is stored up. This potential energy due to change in size and shape of the spring helps to move the hands of watch.
2. Try to open a spring with your both hands. Work is, therefore, being done by your hands. By doing this the spring extends in its length and as such potential energy is stored in it.
![]()
Question 2.
What is kinetic energy? Derive a mathematical expression for kinetic energy.
Answer:
Kinetic Energy: It is defined as the energy possessed by a body due to velocity, if body is not in motion then it does not possess kinetic energy.
Mathematical Expression: Suppose a football of mass ‘m’ is at rest and force ‘F’ is applied. Due to the force acting on it, the football covers a distance ‘S’ in’t’ seconds and attains a velocity υ. Thus, acceleration produced in the football is ‘a’
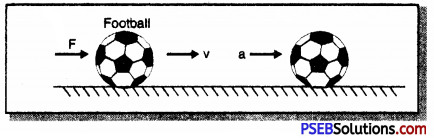
Work done on the football W = F × S ………..(1)
According to Newton’s second law of motion,
F = m × a …………. (2)

Equation (8) proves that the work done on the football is stored in it as kinetic energy.
∴ kinetic energy stored = Work done = \(\frac {1}{2}\)mv2
Question 3.
What is law of conservation of energy? Explain the law with the help of an example and prove its reality.
Answer:
Law of conservation of energy: According to this law total energy always remain constant or total energy always remains the same. Though one form of energy can be transformed to some other form of energy but total energy still remains constant.
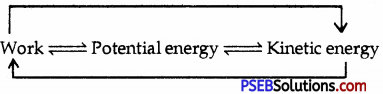
Explanation with example: Throw a ball vertically upwards from the surface of earth. You do some work on the ball. This work gets stored in the form of potential energy. This is called gravitational potential energy. As the ball moves up and up its velocity continue to decrease and its kinetic energy continue to decrease and potential energy goes on increasing. When ball reaches the maximum height its kinetic energy becomes minimum i.e. zero but potential energy becomes maximum. We can prove mathematically that at any position in the path of motion of the ball the sum of potential energy and kinetic energy remains same.
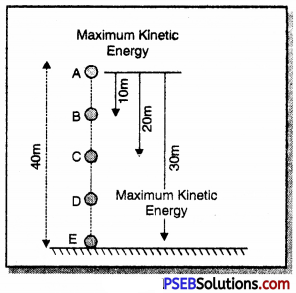
Mathematical Proof for law of conservation of energy:
Consider a ball of mass 10 kg situated at a point 30 m above the surface of earth i.e. point A. Let it be dropped from point A or shown in fig.
At point A
potential energy of ball (P.E.) = m × g × h
= 10 × 10 × 30
= 3000 J
Since, ball is at rest initially thus, at point A it kinetic energy (K.E.) = 0
∴ Total mechanical energy of ball = P.E. + K.E.
= 3000 + 0 = 3000 J ………….(i)
At point B
Ball is above the surface of earth by 20 m.
potential energy (P.E.) = m × g × h
= 10 × 10 × 20
= 2000 J
Using υ2 – u2 = 2gh
υ2 = u2 + 2gh
υ2 = 0 + 2 × 10 × 10
∴ υ2 = 200
∴ Kinetic energy at point B (K.E.) = \(\frac {1}{2}\)mυ2
= \(\frac {1}{2}\) × 10 × (200)
= 1000 J
∴ Total mechanical energy of ball at point B = potential energy + kinetic energy
= 2000 + 1000
= 3000 J. ……………… (ii)
Similarly, at point C and D total mechanical energy will be 3000 J.
These equation prove that total energy is always conserved.
![]()
Question 4.
If the force acting on the object is not in the direction of motion then how will you consider the work done? Explain giving example and also tell when will the work done be minimum and when it will be maximum?
Answer:
When the force acting on the object is not in the direction of motion. A gardener pushes the lawn mower in the forward direction. He applies force F on the handle HH’ facing the ground.
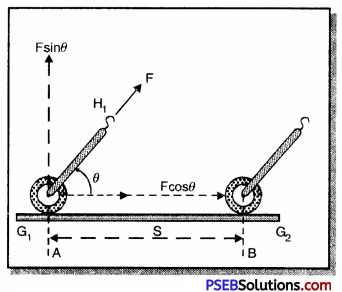
As is clear from the figure, the gardener is not applying force in the horizontal direction but applies force in a direction making angle θ with the direction of force. In such situation the force acting on the machine drives the roller in the horizontal direction from A to B.
Here the effective force is F cos θ and not F and the vertical component F sin θ balances the weight of the lawn mower.
∴ Work done by the lawnmower (W) = Component of Force × Displacement
= F cos θ × S
1. When the force acts along the direction of displacement then θ = 0° and cos θ = cos 0° = 1
∴ W = F cos θ × S
= F × 1 × S
W = F × S
This time the work done will be maximum.
2. When the force acting on the object is in a direction perpendicular to the direction of motion then θ = 90° and cos θ = cos 90° = 0
∴ W = F cos θ x S
= F cos 90° x S
= F x 0 x S
⇒ W = 0
This time the work done is minimum.
Short Answer Type Questions:
Question 1.
What is work? How can you calculate it? Also give the unit of work.
Answer:
Work: Work done by a force or by an object in the product of applied force and the displacement taking place in the direction of applied force.
If F = force acting on the body
S = displacement of the body in the direction of force
Work done by force, W = F × S ……(i)
we know, when a force acts on a body acceleration is produced in the body.
Thus, if m = mass of body
a = acceleration produced in the body then from Newton’s second law of motion
F = m × a ….(ii)
Using (i) and (ii),
W = m × a × S ………….(iii)
Unit of work: When force is measured in Newton (N) and displacement in metre (m), the
work = Newton × Metre
W = N × m
W = Joule (J)
∴ S.I. unit of work is Joule (J) and C.G.S. unit is erg.
1 Joule = 107 erg.
Question 2.
Show by giving an example that if force acting in the body does not produce any displacement then the work done will be zero?
Answer:
This statement can be understood by the following example.
If a child tries to push a car by applying his, maximum force but the car does not displace even through 1 centimeter, then in the language of physics we can say that the child has done no work.
In this situation suppose the child applies force F and displacement S = 0 then
∴ Work done by the child, W = F × S
= F × 0
⇒ W = 0
Question 3.
A stone tied to one end of string is moved in a circle. How much work is done by the centripetal force in this circular motion?
Answer:
A stone is made to move in a circle as shown the fig. then the finger with which you hold the string will experience some force. The force acting on the moving stone is known as centripetal force.
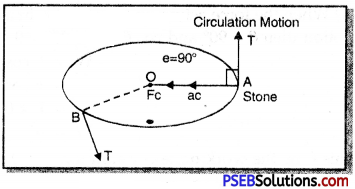
This force acts radially inwards towards the centre of the circle. If in this situation the stone gets detached then it will fly off in the direction tangential along AT or BT as shown in fig. Now, the centripetal force acts perpendicular to the direction of motion, thus no work is done by the centripetal force.
![]()
Question 4.
What is power? Write its SI unit also.
Answer:
Power. Harish and Karan climbed up a tree to pluck 60 mangoes each. They started climbing at the same moment of time. Harish got his 60 mangoes in 30 minutes whereas Karan got his 60 mangoes in 60 minutes. That means Karan took more time to do the same work. Both did the same work, both had same energy but their power was not same i.e. Power of Harish is more than that of Karan.
Power: Power of an object or a machine is its time rate of doing work i.e. Power is defined as rate of doing work with time.
∴ Power = \(\frac{\text { Work done }}{\text { time taken }}\)
or P = \(\frac{\text { w }}{\text { t }}\)
If work is measured in joule and time in second then unit of power is ‘watt’.
∴ 1 watt = \(\frac{\text { 1 Joule }}{\text { 1 second }}\)
commercial unit of power is kilowatt.
1 kilowatt = 1000 watt = 1000 joule/second
Question 5.
Prove by an experiment that mechanical energy can be transformed into heat energy.
Or
When we hammer a nail into a wooden block the nail gets heated up? Why?
Answer:
Place a nail on a wooden block and hammer it, some part of the nail goes into the wooden block, when nail is completely into the block due to hammering, when nail in further hammered then nail, hammer and block all gets heated up. When hammer is lifted up for hammering, its potential energy increases due to its position.
When it falls on the nail then its whole energy is transformed into kinetic energy of the nail and the nail goes into the wooden block. When nail is completely embedded into the block then mechanical energy of the hammer converts into heat energy of the nail, block and hammer meaning thereby that mechanical energy gets converted or transformed into heat energy.
Question 6.
Differentiate between Potential Energy and Kinetic Energy.
Answer:
Difference between Potential energy (P.E.) and Kinetic energy (K.E.)
| Potential Energy | Kinetic Energy |
| 1. The potential energy of an object depends upon its position and size. | The kinetic energy of an object is due to its motion or velocity. |
| 2. Potential energy (P.E.) = m × g × h | Kinetic energy (K.E.) = \(\frac {1}{2}\)mυ2 |
| 3. Potential energy of an object depends upon its height above the ground or its depth below the ground surface. | The kinetic energy of an object depends upon its velocity. |
![]()
Question 7.
A horse and a dog are running with the same velocity. If the mass of horse is ten times the mass of the dog then what will be ratio of their kinetic energy?
Solution:
Suppose the mass of dog = m
∴ Mass of the horse = 10m
Velocity of horse = Velocity of dog = υ (say)

Question 8.
Two masses m and 2m are dropped from height h and 2h. On reaching the ground, which will have a greater kinetic energy and why?
Answer:
K.E. of mass m = P.E. lost by mass m = mgh
K.E. of mass 2m = P.E. lost by mass 2m
= 2m × g × 2h = 4mgh
Hence, mass 2 m will have a greater kinetic energy on reaching the ground.
Question 9.
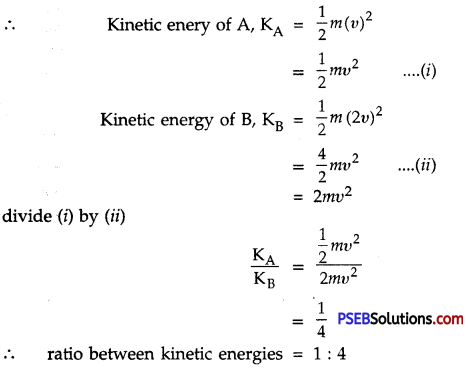
Two objects having same mass’m’ are moving with velocities υ and 2υ. Find ratio of their kinetic energies.
Answer:
Let bodies A and B each have same mass m and their respective velocities are υ and 2υ
Question 10.
In what conditions the physical capacity of a man to do work decreases?
Answer:
After sickness and in old age the physical capacity of a man to do work decreases because the energy of his body muscles becomes less.
![]()
Question 11.
Explain clearly the difference between energy and power with the help of an example.
Answer:
- Energy: Energy is the ability to do work and is equal to the magnitude of total work which could be done by the energy. It has no relation with the time.
- Power: It is the rate of doing work. It has no relation with the magnitude of total work.
- Example: A worker taken one hour to complete a piece of work, whereas the other worker takes 2 hours to complete the same piece of work. In this case, both the workers are doing the same work i.e. both are consuming same amount of energy.
But first worker did the same work in half the time as compared to other worker thus. First worker has doubled the power than the other worker.
Important Formulae:
- Kinetic Energy = \(\frac {1}{2}\) mυ2
- Potential Energy = mgh
Here m = Mass of the object; g = Acceleration due to gravity, h = Height - Work (W) = Force (F) × Displacement (S)
- Power (P) = \(\frac{\text { Work Done (W) }}{\text { Time taken (t) }}\)
Or Power (P) = \(\frac{\text { F × S }}{\text { t }}\)
= F × \(\frac{\text { S }}{\text { t }}\) (∵ υ = \(\frac{\text { S }}{\text { t }}\))
= F × υ - 1 Joule = 1 Newton × 1 metre
- 1 watt = \(\frac{\text { 1 Joule }}{\text { 1 Second }}\)
- Horse Power = 746 watt
- 1 Kilowatt hour = 36,00,000 Joule = 3.6 × 106 Joule
- 1 watt hour = 3600 Joule
Numerical Problems (Solved):
Question 1.
J of energy is applied to lift a box of mass 0.5 kg. How much high it would be raised?
Solution:
Potential energy (P.E.) = 1 J
Mass of the box (m) = 0.5 kg
Acceleration due to gravity, (g) = 10 m/s2
Height to which box is raised, (h) = ?
We know, potential energy (P.E.) = m × g × h
1 = 0.5 × 10 × h
1 = 5 × h
or h = \(\frac {1}{5}\) = 0.2
∴ Height to which box would be raised, (h) = 0.2 m
![]()
Question 2.
A woman pulls water-filled bucket weighing 5 kg from a well 10 m deep in 10 s. What is her power?
Solution:
Mass of water filled bucket, (m) = 5 kg
Depth of well(h) = 10 m
Acceleration due to gravity, (g) = 10 m s-2
Work done by woman(W) = P.E
= m × g × h
= 5 × 10 × 10
= 500 J
Time (t) = 10 s
Now, power = \(\frac{\text { Total work done(W) }}{\text { Total time taken(t) }}\)
= \(\frac {500J}{10s}\)
= 50 J/s
= 50 watt
Question 3.
A boy weighing 50 kg climbs up a vertical height of 100 m. Calculate the amount of work done by him. How much potential energy does he gain? Take r = 9.8 m/s2?
Solution:
Here, m = 50kg, g = 9.8 m/s2, h = 100m
Work done by the body = mgh
= 50 × 9.8 × 100
= 49000 J
= 4.9 × 104 J
Gain in P.E. = Work done = 4.9 × 104 J
Question 4.
A man drops a 10 kg rock from the top of a 20 m ladder. What will be its kinetic energy when it reaches the ground? What will be its speed just before it hits the ground? Does the speed depend on the mass of the rock? (Take g = 10 m s-2)
Solution:
Here u = 0, m = 10 kg, h = 20 m, g = 10 m s-2
We know, υ2 – u2 = 2gh
∴ υ-2 – 0-2 = 2 × 10 × 20
or υ = \( \sqrt{{400}} \)
= 20 m s-1
K.E. = \(\frac {1}{2}\)mυ2
= \(\frac {1}{2}\) × 10 × (20)2
= 2000 J
Speed does not depends on the mass of the rock because the acceleration due to gravity under which the rock falls does not depend on mass.
Question 5.
A rocket of 3 × 106 kg mass takes off from a launching pad and acquires a vertical velocity of 1 km/s at an altitude of 25 km. Calculate the potential energy, and the kinetic energy. (Take g = 10 m s-2).
Solution:

![]()
Question 6.
An electric heater of 1000 W is used for 2 hours a day. What is the cost of using it for a month of 28 days, if 1 unit costs ₹ 3.00?
Solution:
Here, P = 1000 W
= 1 kW
Total time, t = 2 × 28 hours
= 56 hours
Total energy consumed = P × t
= 1kW × 56h
= 56kWh
∴ Cost of 1 kWh = ₹ 3.00
∴ Cost of using electricity for Feb = 3 × 56
= ₹ 168.
Question 7.
The power of a motor pump is 5 kW. How much water per minute the pump an raise to height of 20 m? Take g = 10 ms-2.
Solution:
Here, P = 5 kW = 5000 W, t = 1 min = 60s, h = 20 m, g = 10 ms-2

Question 8.
Calculate the electricity bill amount for the month of November of a family if 4 tube lights of 40 W each for seven hours, a TV of 150 W for three hours and two bulbs of 60 W each for four hours are used per day. The cost per unit is ₹ 3.50.
Solution:
Power of each tube light = 40 W
∴ Total power of 4 tube lights = 4 × 40 W
= 160 W
Energy consumed by 4 tube lights each day
= 160 W × 7 h
= 1120 Wh
= \(\frac {1120}{1000}\) = 1.112kWh
Energy consumed by T.V. per day = 150W × 3h
= 450 Wh
= \(\frac {450}{1000}\) = 0.45 kWh
Energy consumed by 2 bulbs per day = 60W × 4h × 2
= 480 Wh
= \(\frac {480}{1000}\) = 0.48 kWh
Total energy consumed per day by all appliances = 1.12 + 0.45 + 0.48 = 2.05 kWh
Total energy consumed in 30 days = 2.05 kWh × 30
= 61.50 kWh
Cost of 1 kWh = ₹ 3.50
Cost of 61.50 kWh = 3.50 × 61.50
= ₹ 215.25
![]()
Question 9.
A person carrying 10 bricks each of man 2.5 kg. on his head moves to a height 20 metres in 50 seconds. Calculate the power spent in carrying bricks of the person. (g = 10 ms-2)
Solution:
Total mass (m) = 10 × 2.5 kg
= 25 kg.
Time (t) = 50 s
Displacement (S) = 20m
g = 10 ms-1
Force exerted by person (F) = mg
= 25kg × 10 ms-2
= 250 N
Work done = Force × Displacement
= F × S
= 250 N × 20 m
= 5000 J
Power = \(\frac{\text { Work done }}{\text { Time }}\)
= \(\frac {5000J}{50s}\)
= 100 w.
Question 10.
A car of 1000 kg moving with a velocity of 30 m/s stops with uniform acceleration after covering a distance of 50 m on application of brakes. Find the force applied by the brakes on the car and also work done.
Solution:
u = 30 ms-1
υ = 0
S = 50m
Now υ2 – u2 = 2aS
(0)2 – (30)2 = 2 × a × 50
– (30 × 30) = 100 × a
a = –\(\frac {900}{100}\)
∴ a = – 9m/s2
Force, F = m × a
= 1000 × 9
= 9000 N
work done by the brakes, W = F × S
= 9000 × 50
= 450000 N-m
= 4.5 x 105 J
Question 11.
A freely falling hammer of mass 1 kg 7 falls on a nail fixed in a block of wood. If the hammer falls from a height of 1 m then what will be the kinetic energy just before striking the nail? (Take g = 10 m s-2)
Solution:
Mass of the hammer, (m) = 1kg
Height of the hammer (h) = 1 m
Acceleration due to gravity (g) = 10ms-2
using υ2 – u2 = 2gS
υ2 – (0)2 = 2 × 10 × 1
υ2 = 20 ………..(i)
Now kinetic energy of hammer (K.E.) = \(\frac {1}{2}\) × m × υ2
= \(\frac {1}{2}\) × 1 × 20 [From (i)]
= 10 J
![]()
Question 12.
A car is moving with a speed of 54 km/h. What will be the kinetic energy of the boy of mass 40 kg sitting in the car?
Solution:
Speed of the boy = speed of the car
= 54 km/h
= 54 × \(\frac {5}{18}\)m s-1
= 3 × 5 m s-1
= 15 m s-1
Mass of the boy (m) = 40kg
∴ kinetic energy (K.E.) of the boy = \(\frac {1}{2}\)mυ2
= \(\frac {1}{2}\) × 40 × (15)2
= 20 × 15 × 15
= 4500 J
Question 13.
1 Joule of energy is used for one heart beat. Calculate the power of the heart if it throbs 72 times in one minute.
Solution:
Work done in 1 heart beat = 1 J
∴ Total work done by heart in 72 beats = 72 × 1 J
= 72 J
Time (t) = 1 min
= 1 × 60 s
= 60 s
Power = \(\frac{\text { Work done }}{\text { Time taken }}\)
= \(\frac {72 J}{60s}\)
= 1.2 J/s
= 1.2 Watt
Very Short Answer Type Questions:
Question 1.
State the relation between commercial unit of energy and joules.
Answer:
1 commercial unit of energy (or 1 kWh) = 3.6 × 106 Joule.
![]()
Question 2.
How much work is done on a body of mass 1 kg whirling on a circular path of radius 5m?
Answer:
Work done is zero.
Question 3.
What is the SI unit of power?
Answer:
The SI unit of power is Watt.
Question 4.
A ball is thrown vertically upwards. Its velocity keeps on decreasing. What happens to its kinetic energy when it reaches the maximum height?
Answer:
The kinetic energy of the body changes into its potential energy.
Question 5.
If the heart works 60 joules in one minute, what is its power?
Answer:
Power = \(\frac{\text { Energy }}{\text { Time }}\)
= \(\frac {60J}{60s}\)
= 1 W
![]()
Question 6.
Name the term used for the sum of kinetic energy and potential energy of a body.
Answer:
Mechanical energy.
Question 7.
How many joules make one-kilowatt hour?
Answer:
1 kilowatt-hour = 3.6 × 106 J.
Question 8.
What should be the change in velocity of a body required to increase its kinetic? energy to four times of its initial value?
Answer:
The velocity of the body should doubled at constant mass.
Question 9.
Under what conditions the work done by a force is zero inspite of displacement being taking place?
Answer:
When displacement is in a direction perpendicular to the applied force.
Question 10.
What is the power of a machine which does 2000 joules of work in 10 seconds?
Solution:
Power of a machine = \(\frac{\text { Work done }}{\text { time }}\)
= \(\frac {2000J}{10s}\)
= 200 W
Question 11.
What is the SI unit of kinetic energy?
Answer:
Joule.
![]()
Question 12.
Water flows down the mountains to the plains. What happens to the potential energy of water?
Answer:
Potential energy of water will decrease. It will change to kinetic energy of water.