Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 7 Triangles Ex 7.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 7 Triangles Ex 7.4
Question 1.
Show that in a right angled triangle, the hypotenuse is the longest side.
Answer:
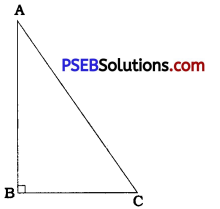
In ∆ ABC, ∠ B is a right angle.
∴ ∠ B = 90° and AC is the hypotenuse.
In ∆ ABC,
∠A + ∠B + ∠C = 180°
∴ ∠ A + 90° + ∠ C = 180°
∴ ∠ A + ∠ C = 90°
Now, ∠ A and ∠ C are both positive (in degrees) and their sum is 90°.
∴ ∠ A < 90° and ∠ C < 90°
∴ ∠ A < Z B and ∠ C < ∠ B
∴ BC < AC and AB < AC (Theorem 7.7)
Hence, hypotenuse AC is greater than each of the other two sides BC and AB. Thus, the hypotenuse is the longest side in a right angled triangle.
![]()
Question 2.
In the given figure, sides AB and AC of ∆ ABC are extended to points P and Q respectively. Also, ∠PBC < ∠ QCB. Show that AC > AB.
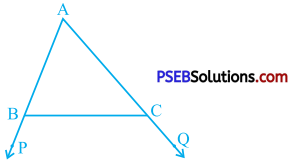
Answer:
∠ PBC < ∠ QCB (Given)
∴ – ∠ PBC > – ∠ QCB (Multiplying an inequality by (-1), it reverses)
∴ 180° – ∠ PBC > 180° – ∠ QCB (Adding 180° on both the sides) …………. (1)
Now, ∠ ABC and ∠ PBC as well as ∠ ACB and ∠ QCB from a linear pair.
∴ ∠ ABC = 180° – ∠ PBC and
∠ ACB = 180° – ∠ QCB
Substituting these values in (1), we get
∠ ABC > ∠ ACB
Now, in ∆ ABC, ∠ ABC > ∠ ACB A
∴ AC > AB (Theorem 7.7)
![]()
Question 3.
In the given figure, ∠ B < ∠ A and ∠ C < ∠ D. Show that AD < BC.
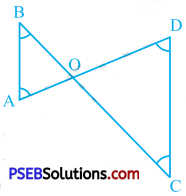
Answer:
In ∆ OAB, ∠ B < ∠ A
∴ OA < OB (Theorem 7.7) …………….. (1)
In ∆ OCD, ∠ C < ∠ D
∴ OD < OC (Theorem 7.7) ……………… (2)
Adding (1) and (2),
OA + OD < OB + OC
∴ AD < BC (As O is the point of intersection of AD and BC, it lies on both the line segments.)
![]()
Question 4.
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD ,(see the given figure). Show that ∠A > ∠C and ∠B > ∠D.
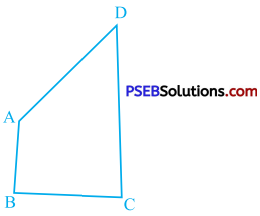
Answer:
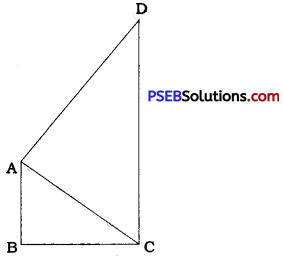
Construction: In quadrilateral ABCD, draw diagonal AC.
AB is the smallest side of ABCD and CD is the longest side of ABCD.
∴ AB < BC and AD < CD.
In ∆ ABC, AB < BC
∴ ∠ ACB < ∠ BAC …… (1)
In ∆ CDA, AD < CD
∴ ∠ DCA < ∠ DAC ……… (2)
Adding (1) and (2),
∠ ACB + ∠ DCA < ∠ BAC + ∠ DAC
∴ ∠ BCD < ∠ BAD
∴ ∠ BAD > ∠ BCD
Thus, in quadrilateral ABCD, ∠ A > ∠ C. Similarly, after constructing diagonal BD and using the inequalities in A ABD and A CBD, it can be proved that ∠ B > ∠ D.
![]()
Question 5.
In the given figure, PR > PQ and PS bisects ∠ QPR. Prove that ∠ PSR > ∠ PSQ.
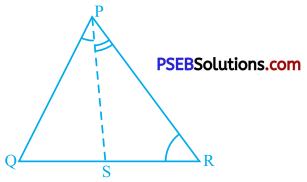
Answer:
PS is the bisector of ∠QPR.
∴ ∠QPS = ∠RPS = \(\frac{1}{2}\) ∠QPR ……………. (1)
∠ PSR is an exterior angle of A PQS and ∠ PSQ is an exterior angle of A PRS.
∴ PSR = ∠ Q + ∠QPS and
∠PSQ = ∠R + ∠RPS …………….. (2)
Now, in A PQR, PR > PQ
∴ ∠ Q > ∠ R
∴ ∠Q + \(\frac{1}{2}\) ∠ QPR > ∠R + \(\frac{1}{2}\) ∠ QPR
∴ ∠Q + ∠QPS > ∠R + ∠RPS [from (1)]
∴ ∠PSR > ∠PSQ
![]()
Question 6.
Show that of all line segments drawn from a given point not on a given line, the perpendicular line segment is the shortest.
Answer:
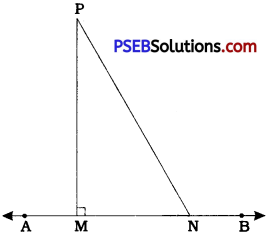
AB is a line and P is a point not on AB.
PM is the perpendicular line segment drawn from P to line AB.
N is any point on AB, other than M.
In ∆ PMN, ∠ M = 90°
∴ ∠ N < 90°
Thus, in ∆ PMN, ZN < ZM.
∴ PM < PN
This is true for any location of point N.
Hence, of all the line segments drawn from a point not on a given line, the, perpendicular line segment is the shortest.