PSEB 9th Class Maths Solutions Chapter 1 Number Systems Ex 1.5

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 1 Number Systems Ex 1.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5

Question 1.
Classify the following numbers as rational or irrational:
(i) 2 – √5
Answer:
2 – √5 is an irrational number as it is the difference of rational number (2) and irrational number (√5).

(ii) (3 + √23) – √23
Answer:
Thus, (3 + √23) – √23 is a rational number even if it is the difference of two irrational numbers (3 + √23) and √23.

(iii) \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\)
Answer:
\(\frac{2 \sqrt{7}}{7 \sqrt{7}}\) = \(\frac{2}{7}\), Thus, \(\frac{2 \sqrt{7}}{7 \sqrt{7}}\) is a rational number even if it is a quotient of two irrational numbers 2√7 and 7√7.

(iv) \(\frac{1}{\sqrt{2}}\)
Answer:
\(\frac{1}{\sqrt{2}}\) is an irrational number as it is the quotient of rational number (1) and irrational number (√2).

(v) 2π
Answer:
2π is an irrational number as it is the product of rational number 2 and irrational number π.

Question 2.
Simplify each of the following expressions:
(i) (3 + √3) (2 + √2)
Answer:
(3 + √3) (2 + √2) = 6 + 3√2 + 2√3 = √6

(ii) (3 + √3) (3 – √3)
Answer:
(3 + √3) (3 – √3) = (3)² – (√3)² = 9 – 3 = 6

(iii) (√5 + √2)²
Answer:
(√5)² + 2(√5) (√2) + (√2)²
= 5 + 2√10 + 2
= 7 + 2√10

(iv) (√5 – √2) (√5 + √2)
Answer:
(√5 – √2) (√5 + √2) = (√5)² – (√2)²
= 5 – 2 = 3

Question 3.
Recall, π is defined as the ratio of the circumference (say c) of a circle to its diameter (say d). That is, π = \(\frac{c}{d}\). This seems to contradict the fact that π is irrational. How will you resolve this contradiction?
Answer:
π is defined as the ratio of circumference (C) of a circle to its diameter (d). As seen in the process of successive magnification used to represent real numbers on the number line, we see that more and more accuracy can be obtained by successive magnification. But, since the real numbers exhibit gaps. we can never measure the exact length of the circumference and the diameter. Any one or both may be having length represented by an irrational number. Hence, there is no contradiction that π being the ratio of c and d is still an irrational number.

Note: in the study of mathematics at higher level, you may study that π is a transcendental number and also the proof of π being an irrational number.

Question 4.
Represent √9.3 on the number line.
Answer:

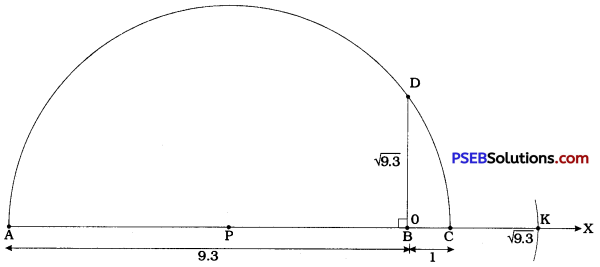
Steps of construction:

• Draw ray AX.
• Mark B on ray AX such that AB = 9.3 cm.
• Mark C on ray BX such that BC = 1 cm.
• By drawing perpendicular bisector of seg AC, obtain its midpoint P.
• Draw a semicircle with centre P and radius AP.
• Draw perpendicular to seg AC at B intersecting the semicircle at D.
• Then, BD = √9.3.
• Let line AX be the number line on which B corresponds to 0 and BC = 1 unit.
• Draw an arc with centre B and radius BD to intersect ray BX at K.
• Point K represents √9.3 on the number line.

Question 5.
Rationalise the denominators of the following:
(i) \(\frac{1}{\sqrt{7}}\)
Answer:
\(\frac{1}{\sqrt{7}}\) = \(\frac{1}{\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}}\)
= \(\frac{\sqrt{7}}{7}\)

(ii) \(\frac{1}{\sqrt{7}-\sqrt{6}}\)
Answer:
\(\frac{1}{\sqrt{7}-\sqrt{6}}\) = \(\frac{1}{\sqrt{7}-\sqrt{6}} \times \frac{\sqrt{7}+\sqrt{6}}{\sqrt{7}+\sqrt{6}}\)
= \(\frac{\sqrt{7}+\sqrt{6}}{7-6}\)
= √7 + √8

(iii) \(\frac{1}{\sqrt{5}+\sqrt{2}}\)
Answer:
\(\frac{1}{\sqrt{5}+\sqrt{2}}\) = \(\frac{1}{\sqrt{5}+\sqrt{2}} \times \frac{\sqrt{5}-\sqrt{2}}{\sqrt{5}-\sqrt{2}}\)
= \(\frac{\sqrt{5}-\sqrt{2}}{5-2}\)
= \(\frac{\sqrt{5}-\sqrt{2}}{3}\)

(iv) \(\frac{1}{\sqrt{7-2}}\)
Answer:
\(\frac{1}{\sqrt{7-2}}\) = \(\frac{1}{\sqrt{7}-2} \times \frac{\sqrt{7}+2}{\sqrt{7}+2}\)
= \(\frac{\sqrt{7}+2}{7-4}\)
= \(\frac{\sqrt{7}+2}{3}\)