Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 1 Number Systems Ex 1.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.3
Question 1.
Write the following in decimal form and say
what kind of decimal expansion each has:
(i) \(\frac{36}{100}\)
Answer:
The decimal expansion of \(\frac{36}{100}\) is terminating.
![]()
(ii) \(\frac{1}{11}\)
Answer:

Thus, \(\frac{1}{11}\) = 0.0909…. = \(0.\overline{09}\)
The decimal expansion of \(\frac{1}{11}\) is non- terminating.
(iii) 4\(\frac{1}{8}\)
Answer:
4\(\frac{1}{8}\) = \(\frac{33}{8}\)

Thus, 4\(\frac{1}{8}\) = 4.125
The decimal expansion of 4\(\frac{1}{8}\) is terminating.
(iv) \(\frac{3}{13}\)
Answer:

Thus, \(\frac{3}{13}\) = 0.230769230769…. = \(0.\overline{230769}\)
The decimal expansion of 4\(\frac{2}{11}\) is non-terminating recurring.
![]()
(v) \(\frac{2}{11}\)
Answer:

Thus, \(\frac{2}{11}\) = 0.1818….. = \(0 . \overline{18}\)
The decimal expansion of \(\frac{2}{11}\) is non-terminating recurring.
(vi) \(\frac{329}{400}\)
Answer:

Thus, \(\frac{329}{400}\) = 0.8225
The decimal expansion of \(\frac{329}{400}\) is terminating recurring.
Question 2.
You know that \(\frac{1}{7}\) = \(0 . \overline{142857}\). Can you predict what the decimal expansions of \(\frac{2}{7}\), \(\frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}\) are, without actually doing the long division? if so, how? [Hint: Study the remainders while finding the value of \(\frac{1}{7}\) carefully.]
Answer:
While finding the decimal expansion of \(\frac{1}{7}\) by long division, we observe that the remainder 3, 2, 6, 4, 5 and 1 repeat in that order and the digits 1, 4, 2, 8, 5 and 7 repeat in that order in the quotient. So, in the decimal expansion of \(\frac{2}{7}\), the same digits recur beginning with 2. Thus,
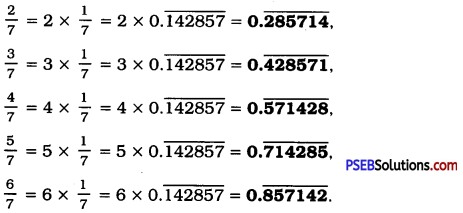
![]()
Question 3.
Express the following in the form \(\frac{p}{q}\), where p and q are integers and q ≠ 0:
(i) 0.\(\overline{6}\)
Answer:
Let x = 0.\(\overline{6}\)
∴ x = 0.6666…
∴ 10x = 6.6666…
∴ 10x = 6 + x
∴ 10x – x = 6
∴ 9x = 6
∴ x = \(\frac{6}{9}\)
∴ x = \(\)
Thus. 0.\(\overline{6}\) = \(\frac{2}{3}\)
(ii) 0.4\(\overline{7}\)
Answer:
Let x = 0.4\(\overline{7}\)
∴ x = 0.4777…..
∴ 10x = 4.7777…..
∴ 10x = 4.3 + 0.4777…..
∴ 10x = 4.3 + x
∴ 9x = 4.3
∴ 9x = \(\frac{43}{10}\)
∴ x = \(\frac{43}{90}\)
Thus, 0.4\(\overline{7}\) = \(\frac{43}{90}\)
(iii) 0.\(\overline{001}\)
Answer:
Let x = 0.\(0 . \overline{001}\)
∴ x = 0.001001001 ……
∴ 1000 x = 1.001001001 ……
∴ 1000 x = 1 + 0.001001001 ……
∴ 1000 x = 1 + x
∴ 999 x = 1
∴ x = \(\frac{1}{999}\)
Thus, \(0 . \overline{001}\) = \(\frac{1}{999}\)
![]()
Question 4.
Express 0.99999 ….. in the form \(\frac{p}{q}\). Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Answer:
Let x = 0.99999 …..
∴ 10x = 9.99999 ……
∴ 10x = 9 + 0.99999 ……
∴ 10x = 9+x
∴9x = 9
∴ x = 1
Thus, 0.99999 ….. = 1
in other words, 0.\(\overline{9}\) = 1.
This also follows the rule mentioned in ‘Remember’ section that 0.\(\overline{m}\) = \(\frac{m}{9}\). As per rule, 0.\(\overline{9}\) = \(\frac{9}{9}\) = 1.
The answer seems to be tricky. Actually, there is no situation that gives the decimal expansion of a rational number \(\left[\frac{p}{q}\right]\) as 0.\(\overline{9}\).
This is an imaginary illustration of recurring decimal number.
You may say that 0.\(\overline{3}\) + 0.\(\overline{6}\) = 0.\(\overline{9}\) But in simple fraction form 0.\(\overline{3}\) and 0.\(\overline{6}\) add up to give 1. Thus, 0.\(\overline{9}\) = 1.
Question 5.
What can the maximum number of digits be in the repeating block of digits in the decimal expansion of \(\frac{1}{17}\)? Perform the division to check your answer.
Answer:
The maximum number of digits in the repeating block of digits in the decimal expansion of \(\frac{1}{17}\) can be 16(17 – 1).

Thus, \(\frac{1}{17}\) = \(0.\overline{0588235294117647}\)
Here, 17 – 1 16 gives the maximum possible number of digits in the repeating block of digits in the decimal expansion of \(\frac{1}{17}\). In some other cases, the number of digits in the repeating block of digits in the decimal expansion of \(\frac{1}{m}\) can be smaller than (m – 1), where m is a natural number.
For example, \(\frac{1}{13}\) = \(0 . \overline{076923}\) has only 6 digits (not 12) in the repeating block of digits in the decimal expansion.
![]()
Question 6.
Look at several examples of rational numbers in the form \(\frac{p}{q}\) (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?
Answer:
\(\frac{1}{2}\) = 0.5, \(\frac{1}{5}\) = 0.2, \(\frac{1}{10}\) = 0.1,
\(\frac{1}{4}\) = 0.25, \(\frac{1}{8}\) = 0.125, \(\frac{1}{16}\) = 0.0625,
\(\frac{1}{25}\) = 0.04, \(\frac{1}{125}\) = 0.008, \(\frac{1}{625}\) = 0.0016,
\(\frac{1}{20}\) = 0.05, \(\frac{1}{50}\) = 0.02 etc.
But, \(\frac{1}{3}\) = 0.\(\overline{3}\), \(\frac{1}{7}\) = \(0 . \overline{142857}\), \(\frac{1}{6}\) = 0.1\(\overline{6}\) etc.
This suggest that the decimal expansion of a rational number \(\frac{\boldsymbol{P}}{\boldsymbol{q}}\) is terminating if and only if q has no prime factors other than 2 and 5. in other words, q = 2m5n, where m and n are whole numbers.
Question 7.
Write three numbers whose decimal expansions are non-terminating non-recurring.
Answer:
We know that the decimal expansion of an irrational number is non-terminating non recurring. There are infinitely many irrational numbers. We can state few of them as below:
o.o1001000100001 …,
0.02002000200002…., 0.50500500050000… are a few required numbers in the decimal form. The decimal expansions of numbers like √2, √3, √5, \(\sqrt[3]{10}\), etc. are also non- terminating non-recurring.
Question 8.
Find three different irrational numbers between the rational numbers \(\frac{5}{7}\) and \(\frac{9}{11}\)
Answer:
We know that \(\frac{5}{7}\) = \(0 . \overline{714285}\) and \(\frac{9}{11}\) = \(0 . \overline{81}\)
There are actually infinitely many irrational numbers between these recurring decimals. Three irrational numbers between them can be stated as below:
0.720720072000 …, 0.750750075000 …
0.780780078000….
As you see, the above numbers are non-terminating non-recurring. Hence, they are irrational numbers.
Question 9.
Classify the following numbers as rational or irrational:
(i) √23
Answer:
√23 is an irrational number.
(ii) √225
Answer:
√225 = 15 is a rational number
![]()
(iii) 0.3796
Answer:
0.3796 is a rational number.
(iv) 7.478478……..
Answer:
7.478478…… = \(7 . \overline{478}\) is a rational number.
(v) 1.101001000100001…….
Answer:
1.101001000100001……. is an irrational number.