PSEB 8th Class Maths Solutions Chapter 7 Cubes and Cube Roots InText Questions

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 7 Cubes and Cube Roots InText Questions and Answers.

PSEB 8th Class Maths Solutions Chapter 7 Cubes and Cube Roots InText Questions

Try These (Textbook Page No. 111)

Find the one’s digit of the cube of each of the following numbers:
(i) 3331
(ii) 8888
(iii) 149
(iv) 1005
(v) 1024
(vi) 77
(vii) 5022
(viii) 53
Solution:

Sl. No.	Number	Number ending in	Units place digit of the cube
(i)	3331	1	1
(ii)	8888	8	2
(iii)	149	9	9
(iv)	1005	5	5
(v)	1024	4	4
(vi)	77	7	3
(vii)	5022	2	8
(viii)	53	3	7

Some interesting patterns: (Textbook Page No. 111)

Observe the following pattern of sums of odd numbers.

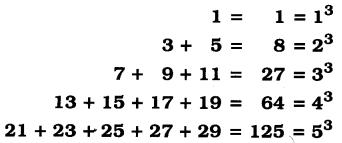
Try These (Textbook Page No. 111)

1. Express the following numbers as the sum of odd numbers using the above pattern ?
(a) 6³
(b) 8³
(c) 7³
Solution:
From above pattern, we can conclude n³ = [n(n – 1) + 1] + [n(n – 1) + 3] + [n(n – 1) + 5]… + n terms
(a) 6³
Here, n = 6, n- 1=5
6 (6 – 1) + 1 → 6 × 5 + 1 → 31

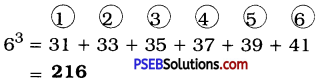
OR
= [6(6 – 1) + 1] + [6(6 – 1) + 3] + [6(6 – 1) + 5] + [6(6 – 1) + 7] + [6(6 – 1) + 9] + [6(6 – 1) + 11]
= (6 × 5 + 1) + (6 × 5 + 3) + (6 × 5 + 5) + (6 × 5 + 7) + (6 × 5 + 9) + (6 × 5 + 11)
= (30 + 1) + (30 + 3) + (30 + 5) + (30 + 7) + (30 + 9) + (30 + 11)
= 31 +33 + 35 + 37 + 39 + 41
= 216

(b) 8³
Here, n = 8, n – 1 = 7
8 (8 – 1) + 1 → 8 × 7 + 1 → 57

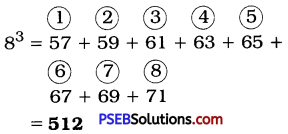
OR
= [8(8 – 1) + 1] + (8(8 – 1) + 3] + [8(8 – 1) + 5] + [8(8 – 1) + 7] + [8(8 – 1) + 9] + [8(8 – 1) + 11] + [8(8 – 1) + 13] + [8(8 – 1) + 15]
= (8 × 7 + 1) + (8 × 7 + 3) + (8 × 7 + 5) + (8 × 7 + 7) + (8 × 7 + 9) + (8 × 7 + 11) + (8 × 7 + 13) + (8 × 7 + 15)
= (56 + 1) + (56 + 3) + (56 + 5) + (56 + 7) + (56 + 9) + (56 + 11) + (56 + 13) + (56 + 15)
= 57 + 59 + 61 + 63 + 65 + 67 + 69 + 71
= 512

(c) 7³
Here, n = 7, n – 1 = 6
7 × 6 + 1 → 42 + 1 → 43

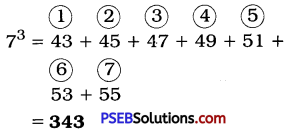
OR
= [7(7 – 1) + 1] + [7(7 – 1) + 3] + [7(7 – 1) + 5] + [7(7 – 1) + 7] + [7(7 – 1) + 9] + [7(7 – 1) + 11] + [7(7 – 1) + 13]
= (7 × 6 + 1) + (7 × 6 + 3) + (7 × 6 + 5) + (7 × 6 + 7) + (7 × 6 + 9) + (7 × 6 + 11) + (7 × 6 + 13)
= (42 + 1) + (42 + 3) + (42 + 5) + (42 + 7) + (42 + 9) + (42 + 11) + (42 + 13)
= 43 + 45 + 47 + 49 + 51 + 53 + 55
= 343

Consider the following pattern:
2³ – 1³ = 1 + 2 × 1 × 3
3³ – 2³ = 1 + 3 × 2 × 3
4³ – 3³ = 1 + 4 × 3 × 3
Using the above pattern, find the value of the following:
(i) 7³ – 6³
(ii) 12³– 11³
(iii) 20³ – 19³
(iv) 51³ – 50³
Solution:
From above pattern, we can conclude
n³ – (n – 1)³ = 1 + n × (n – 1) × 3
(i) 7³ – 6³ = 1 + 7 × 6 × 3
= 1 + 126
= 127

(ii) 12³ – 11³ = 1 + 12 × 11 × 3
= 1 + 396
= 397

(iii) 20³ – 19³ = 1 + 20 × 19 × 3
= 1 + 1140
= 1141

(iv) 51³ – 50³ = 1 + 51 × 50 × 3
= 1 + 7650
= 7651

Try These (Textbook Page No. 112)

1. Which of the following are perfect cubes?

Question (1).
400
Solution:
\(\begin{array}{l|l}
2 & 400 \\
\hline 2 & 200 \\
\hline 2 & 100 \\
\hline 2 & 50 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
400 = 2 × 2 × 2 × 2 × 5 × 5
Here, the prime factors 2 and 5 do not appear in triples.
∴ 2 × 5 × 5 is left over.
∴ 400 is not a perfect cube.

Question (2).
3375
Solution:
\(\begin{array}{l|l}
3 & 3375 \\
\hline 3 & 1125 \\
\hline 3 & 375 \\
\hline 5 & 125 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
3375 = 3 × 3 × 3 × 5 × 5 × 5
Here, the prime factors 3 and 5 appear in triples.
No factor is left over.
∴ 3375 is a perfect cube.
3375 = 3³ × 5³

Question (3).
8000
Solution:
\(\begin{array}{l|l}
2 & 8000 \\
\hline 2 & 4000 \\
\hline 2 & 2000 \\
\hline 2 & 1000 \\
\hline 2 & 500 \\
\hline 2 & 250 \\
\hline 5 & 125 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
8000 = 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5
Here, the prime factors 2 and 5 appear in triples.
No factor is left over.
∴ 8000 is a perfect cube.
8000 = 2³ × 2³ × 5³

Question (4).
15625
Solution:
\(\begin{array}{l|l}
5 & 15625 \\
\hline 5 & 3125 \\
\hline 5 & 625 \\
\hline 5 & 125 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
15625 = 5 × 5 × 5 × 5 × 5 × 5
Here, the prime factor 5 appear in triples.
No factor is left over.
∴ 15625 is a perfect cube.
15625 = 5³ × 5³

Question (5).
9000
Solution:
\(\begin{array}{l|l}
2 & 9000 \\
\hline 2 & 4500 \\
\hline 2 & 2250 \\
\hline 3 & 1125 \\
\hline 3 & 375 \\
\hline 5 & 125 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
9000 = 2 × 2 × 2 × 3 × 3 × 5 × 5 × 5
Here, among the prime factors 2 and 5 appear in triples but 3 does not appear in triple.
3 × 3 is left over.
∴ 9000 is not a perfect cube.

Question (6).
6859
Solution:
\(\begin{array}{l|l}
19 & 6859 \\
\hline 19 & 361 \\
\hline 19 & 19 \\
\hline & 1
\end{array}\)
6859 = 19 × 19 × 19
Here, the prime factor 19 appears in triple.
No factor is left over.
∴ 6859 is a perfect cube.
6859 = 193

Question (7).
2025
Solution:
\(\begin{array}{l|l}
3 & 2025 \\
\hline 3 & 675 \\
\hline 3 & 225 \\
\hline 3 & 75 \\
\hline 5 & 25 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
2025 = 3 × 3 × 3 × 3 × 5 × 5
Here, the prime factor 3 appears in triple, but 3 × 5 × 5 is left over.
∴ 2025 is not a perfect cube.

Question (8).
10648
Solution:
\(\begin{array}{r|l}
2 & 10648 \\
\hline 2 & 5324 \\
\hline 2 & 2662 \\
\hline 11 & 1331 \\
\hline 11 & 121 \\
\hline 11 & 11 \\
\hline & 1
\end{array}\)
10648 = 2 × 2 × 2 × 11 × 11 × 11
Here, the prime factors 2 and 11 appear in triples.
No factor is left over.
∴ 10648 is a perfect cube.
10648 = 2³ × 11³

Think, Discuss and Write (Textbook Page No. 113)

1. Check which of the following are perfect cubes:
(i) 2700
(ii) 16000
(iii) 64000
(iv) 900
(v) 125000
(vi) 36000
(vii) 21600
(viii) 10000
(ix) 27000000
(x) 1000
What pattern do you observe in these perfect cubes ?
Solution:
(i) 2700
The number is ending with two zeros. If a number ends with three zeros or a multiple of 3 zeros, it may be a perfect cube.
∴ 2700 is not a perfect cube.

(ii) 16000
The number is ending with three zeros.
So it may be a perfect cube.
But, 16 is not a perfect cube.
∴ 16000 is not a perfect cube.

(iii) 64000
The number is ending with three zeros.
So it may be a perfect cube.
64 is a perfect cube. (∵ 4³ = 64)
∴ 64000 is a perfect cube.

(iv) 900
The number is ending with two zeros.
So it is not a perfect cube.
∴ 900 is not a perfect cube.

(v) 125000
The number is ending with three zeros.
So it may be a perfect cube.
125 is a perfect cube. (∵ 5³ = 125)
∴ 125000 is a perfect cube.

(vi) 36000
The number is ending with three zeros.
So it may be a perfect cube.
But, 36 is not a perfect cube.
∴ 36000 is not a perfect cube.

(vii) 21600
The number is ending with two zeros.
So it is not a perfect cube.
∴ 21600 is not a perfect cube.

(viii) 10000
The number is ending with four zeros.
So it is not a perfect cube.
∴ 10000 is not a perfect cube.

(ix) 27000000
The number is ending with six zeros.
So it may be a perfect cube.
27 is a perfect cube. (∵ 3³ = 27)
∴ 27000000 is a perfect cube.

(x) 1000
The number is ending with three zeros.
So it may be a perfect cube.
1 is a perfect cube, (∵ 1³ = 1)
∴ 1000 is a perfect cube.

Think, Discuss and Write (Textbook Page No. 115)

1. State true or false for any integer m, m² < m³. Why ?
Solution:
It seems true, but not always true.
m × m = m² and m × m × m = m³
∴ m² < m³
e.g. if m = 1
∴ m² = 1² = 1 and m³ = 1³ = 1
∴ m² ≮  m³, but m² = m³
If m = (- 1)
∴ m² = (- 1)² = 1 and m³ = (- 1)³ = (- 1)
∴ m² ≮  m³, but m2 > m³
So the above statement is not always true.