Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 5 Fractions Ex 5.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 6 Maths Chapter 5 Fractions Ex 5.3
1. Write the fraction for the shaded part and check whether these fractions are equivalent or not?
Question (i)
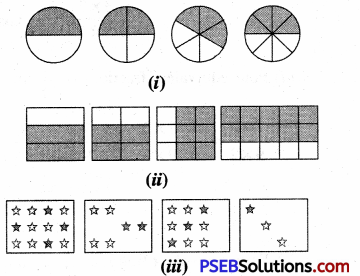
Solution:

![]()
2. Find four equivalent fractions of the followings:
Question (i)
(i) \(\frac {1}{4}\)
(ii) \(\frac {3}{5}\)
(iii) \(\frac {7}{9}\)
(iv) \(\frac {5}{11}\)
(v) \(\frac {2}{3}\)
Solution:
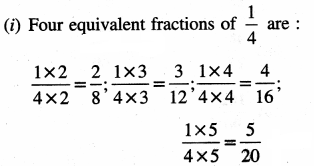
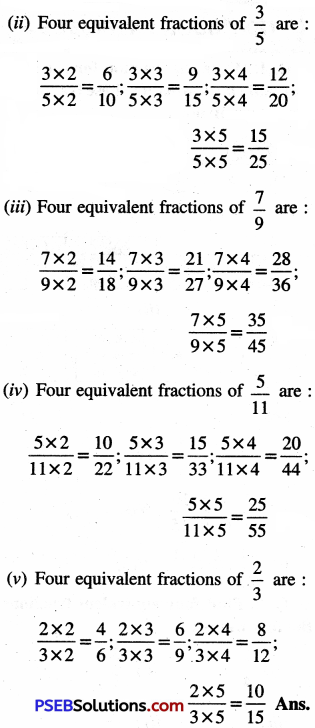
![]()
3. Write the lowest equivalent fraction (simplest form) of :
Question (i)
(i) \(\frac {10}{25}\)
(ii) \(\frac {27}{54}\)
(iii) \(\frac {48}{72}\)
(iv) \(\frac {150}{60}\)
(v) \(\frac {162}{90}\)
Solution:

4. Are the following fractions equivalent or not?
Question (i)
\(\frac{5}{12}, \frac{25}{60}\)
Solution:
We have

By cross product,
5 × 60 = 300 and 12 × 25 = 300
Since two cross products are same
So, the given fractions are equivalent.
![]()
Question (ii)
\(\frac{6}{7}, \frac{36}{42}\)
Solution:
We have

By cross product,
6 × 42 = 252 and 7 × 36 = 252
Since two cross products are same
So, the given fractions are equivalent.
Question (iii)
\(\frac{7}{9}, \frac{56}{72}\)
Solution:
We have
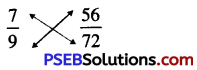
By cross product,
7 × 72 = 504 and 9 × 56 = 504
Since two cross products are same
So, the given fractions are equivalent.
5. Replace [ ] 1 in each of the following by the correct number.
Question (i)
\(\frac{2}{7}\) = 12 / [ ]
Solution:
Observe the numerators we have 12 ÷ 2 = 6
So, we multiply both numerator and denominator of \(\frac {2}{7}\) by 6
We get \(\frac{2}{7}=\frac{2 \times 6}{7 \times 6}=\frac{12}{42}\)
Hence, the correct number in [ ] 1 is 42
Question (ii)
\(\frac{5}{8}\) = 35 / [ ]
Solution:
Observe the numerators we have 35 ÷ 5 = 7
So, we multiply both numerator and denominator of \(\frac {5}{8}\) by 7
We get \(\frac{5}{8}=\frac{5 \times 7}{8 \times 7}=\frac{35}{56}\)
Hence, the correct number in [ ] is 56.
Question (iii)
\(\frac{24}{36}\) = 6 / [ ]
Solution:
Observe the numerators we have 24 ÷ 6 = 4
So, we divide both numerator and denominator of \(\frac {24}{36}\) by 4
We get \(\frac{24}{36}=\frac{24 \div 4}{36 \div 4}=\frac{6}{9}\)
Hence, the correct number in [ ] is 9
![]()
Question (iv)
\(\frac{30}{48}\) = 8 / [ ]
Solution:
Observe the denominators we have 48 ÷ 8 = 6
So, we divide both numerator and denominator of \(\frac {30}{48}\) by 6
We get \(\frac{30}{48}=\frac{30 \div 6}{48 \div 6}=\frac{5}{8}\)
Hence, the correct number in ⊇ is 5
Question (v)
\(\frac{7}{4}\) = 42 / [ ]
Solution:
Observe the numerators we have 42 ÷ 7 = 6
So, we multiply both numerator and denominator of \(\frac {7}{4}\) by 6
We get \(\frac{7}{4}=\frac{7 \times 6}{7 \times 6}=\frac{42}{24}\)
Hence, the correct number in [ ] is 24
6. Find the equivalent fraction of \(\frac {3}{5}\), having
Question (i)
numerator 18
Solution:
(i) Equivalent fraction of \(\frac {3}{5}\), having numerator 18 is
\(\frac{3}{5}\) = 18 / [ ]
Observe the numerators, we have 18 ÷ 3=6
So, we multiply both numerator and denominator of \(\frac {3}{5}\) by 6
∴ \(\frac{3}{5}=\frac{3 \times 6}{5 \times 6}=\frac{18}{30}\)
Thus, required equivalent fraction of \(\frac{3}{5}=\frac{18}{30}\)
![]()
Question (ii)
denominator 20
Solution:
Equivalent fraction of \(\frac {3}{5}\), having denominator 20 is \(\frac{3}{5}\) = [ ] / 20
Observe the denominators, we have 20 ÷ 5 = 4
So, we multiply both numerator and denominator of \(\frac {3}{5}\) by 4
Thus, required equivalent fraction of \(\frac{3}{5}=\frac{12}{20}\)
∴ \(\frac{3}{5}=\frac{3 \times 4}{5 \times 4}=\frac{12}{20}\)
Thus, required equivalent fraction of
\(\frac{3}{5}=\frac{12}{20}\)
Question (iii)
numerator 24.
Solution:
Equivalent fraction of \(\frac {3}{5}\) , having numerator 24 is
\(\frac{3}{5}\) = 24 / [ ]
Observe the numerators, we have 24 ÷ 3 = 8
So, we multiply both numerator and denominator of \(\frac {3}{5}\) by 8
∴ \(\frac{3}{5}=\frac{3 \times 8}{5 \times 8}=\frac{24}{40}\)
Thus, required equivalent fraction of
\(\frac{3}{5}=\frac{24}{40}\)
7. Find the equivalent fraction of \(\frac {24}{40}\), having
Question (i)
(i) numerator 6
(ii) numerator 48
(iii) denominator 20
Solution:
(i) Equivalent fraction of \(\frac {24}{40}\), numerator 6 is
\(\frac{24}{40}\) = 6 / [ ]
Observe the numerators, we have 24 ÷ 6 = 4
So, we divide both numerator and denominator of \(\frac {24}{40}\) by 4
∴ \(\frac{24}{40}=\frac{24 \div 4}{40 \div 4}=\frac{6}{10}\)
Thus, required equivalent fraction of
\(\frac{24}{40}=\frac{6}{10}\)
![]()
Question (ii)
numerator 48
Solution:
Equivalent fraction of \(\frac {24}{40}\), having numerator 48 is
\(\frac{24}{40}\) = 48 / [ ]
Observe the numerators, we have 48 ÷ 24 = 2
So, we multiply both numerator and denominator of \(\frac {24}{40}\) by 2
∴ \(\frac{24}{40}=\frac{24 \times 2}{40 \times 2}=\frac{48}{80}\)
Thus, required equivalent fraction of
\(\frac{24}{40}=\frac{48}{80}\)
Question (iii)
denominator 20
Solution:
Equivalent fraction of \(\frac {24}{40}\), having denominator 20 is
\(\frac{24}{40}\) = [ ] / 20
Observe the denominators, we have 40 ÷ 20 = 2
So, we divide both numerator and denominator of \(\frac {24}{40}\) by 2
\(\frac{24}{40}=\frac{24 \div 2}{40 \div 2}=\frac{12}{20}\)
∴ Thus, required equivalent fraction of
\(\frac{24}{40}=\frac{12}{20}\)